首页
登录
注册
-
金属材料在高应变率加载下的断裂行为是国防领域和力学学科前沿关注的焦点问题。20世纪40年代，Mott[1]指出，金属环（柱壳）的破片尺寸与断裂应变的统计规律密切相关。Grady[2]进一步发展了Mott的理论，并假定断裂应变ε满足韦伯分布，即
式中：k为形状参数，λ为尺度参数，Pd为断裂应变的累计概率因子。Robson[3]建立了一个简单的仿真模型，初步验证了Mott[1]和Grady[2]的碎裂理论。Todinov[4]提出，断裂应变存在统计属性的原因是材料存在微观缺陷。当材料内部缺陷演化的应力相关性近似遵循幂律分布时，韦伯分布能够有效预测这些缺陷引发的局部失效概率，但相关理论的正确性并未得到实验的有效支撑，并且Grady[2]也承认其采取的韦伯分布假设缺乏实验支撑。
Niordson[5]发展的电磁膨胀环实验技术被广泛应用于金属材料的动态断裂行为研究，具有应变率易调、操作简便、重复性好等优势，且可配套多种诊断技术以获得金属电磁膨胀环的断裂应变。学者们最初通过测量回收破片的尺寸计算断裂应变，但回收过程中不可避免地会对破片造成二次损伤。Zhang等[6–7]和Janiszewski[8]利用破片回收技术研究金属延展性是否具有应变率依赖性时，甚至给出了完全相反的结论。Zhang等[6]利用高速摄影技术获得了膨胀环的断裂过程图像，但由于幅间距高达11 μs，得到的断裂应变的不确定度过大。Dan等[9]和Jiang等[10]采用磁探针获得了样品环中电压信号的突变点，但只能获得第一个断口的高精度断裂时刻。近年来，光子多普勒测速仪（photonic Doppler velocimetry，PDV）[11–15]也被用于研究膨胀环的断裂行为，但主要用于获取膨胀环的运动速度历史。
本研究将建立一种新型密排PDV阵列测试技术，将其应用于6061铝电磁膨胀环断裂信息的原位诊断，以期获得膨胀环多个断裂位置的断裂应变的高精度统计分布信息；在此基础上，建立含概率统计的仿真模型，通过大规模计算研究6061铝环动态断裂应变分布规律；最后，通过实验与数值模拟相结合，探讨Grady[2]提出的断裂应变满足韦伯分布假设的合理性。
-
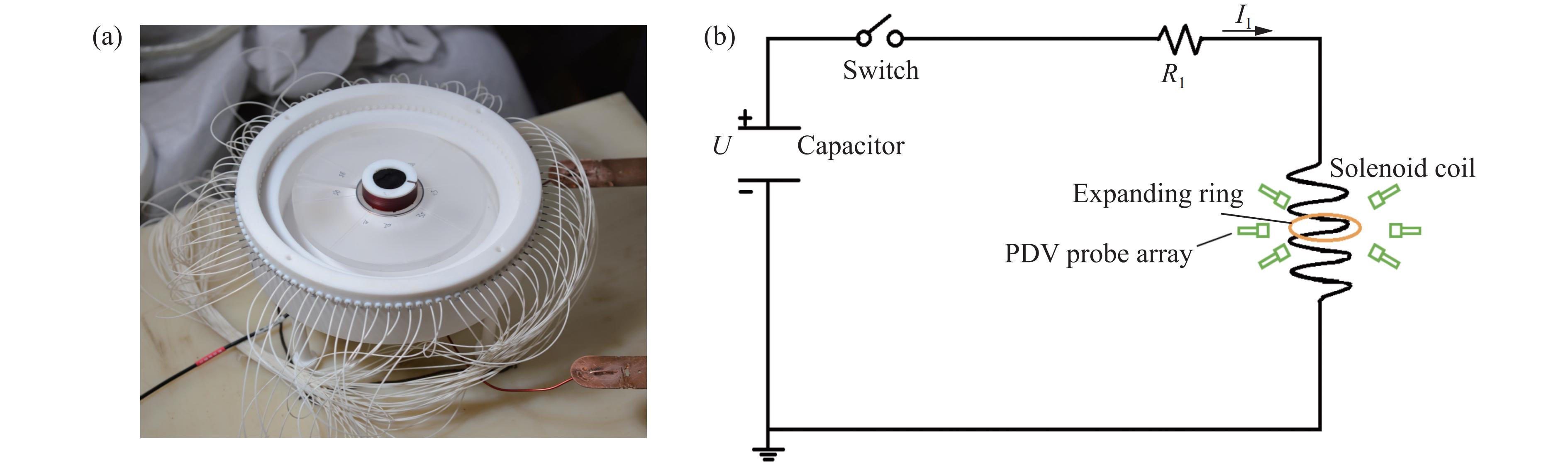
如图1(a)所示，实验样品环材料为6061铝，样品环外半径为21 mm，内半径为20 mm，高度为1 mm。在装置外围布设密排PDV阵列以获取样品环膨胀断裂的高空间分辨率实验数据，所有测点均向心均匀排列，共计100个测点，初始时刻相邻测点在样品环外表面的弧长间距为1.2 mm。
电磁膨胀环测试原理如图1(b)所示。将样品环固定于螺线圈外围中部，并与螺线圈保持同轴，以确保样品环均匀膨胀及变形。螺线管线圈由15匝线圈组成，可实现较高的电磁加载力。电容器充电至预定电压后，闭合开关，高强度电流流经螺线管，产生快速变化的强磁场，在样品环中产生反向电流，导致样品环在安培力的驱动下沿径向膨胀。当样品环膨胀至一定程度时，由于内部结构的不均匀性，产生了应变局域化，并最终发生断裂。
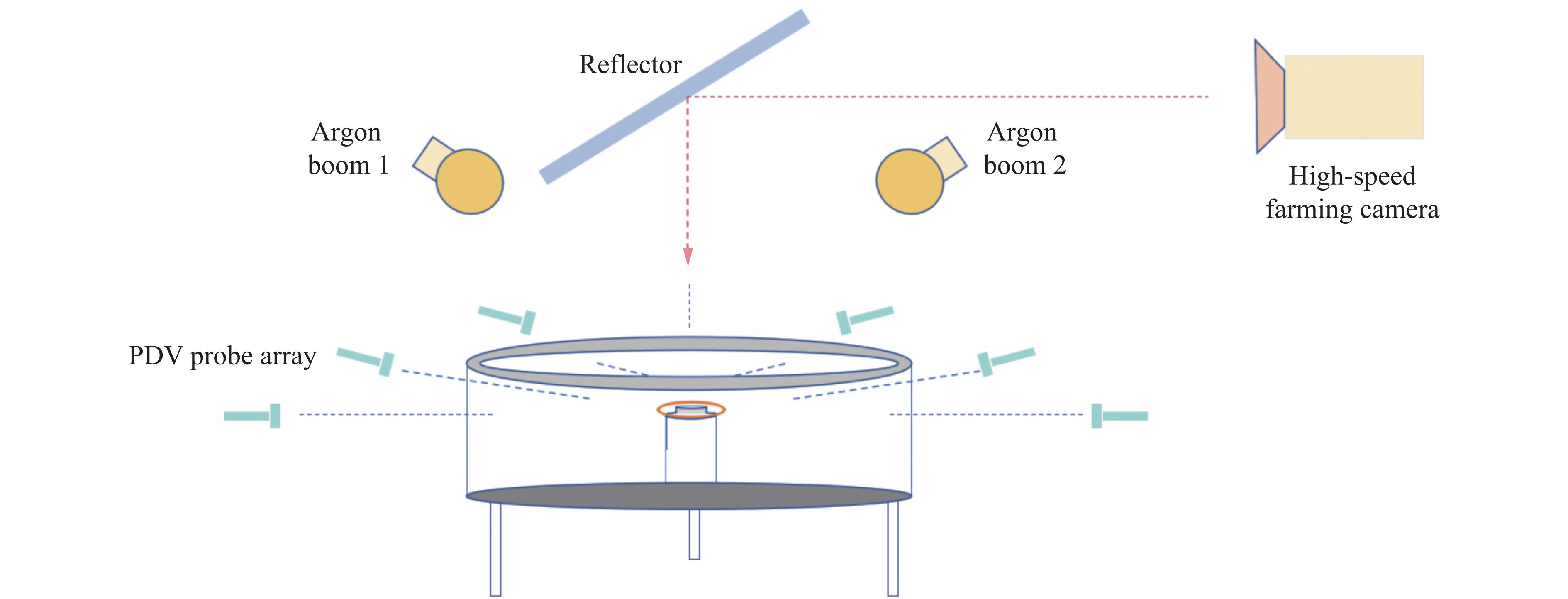
实验装置布局如图2所示。除密排PDV测速技术外，还采用高速相机从轴向拍摄样品环的膨胀断裂全过程。脉冲氙灯为高速摄影提供了充足的照明，反光镜实现光路的折转。
-
共进行了7发实验，通过调整电容器的充电电压实现不同应变率加载，通过激光测速获取膨胀环的运动速度历史曲线，通过高速摄影和样品回收获取断口数量，结果见表1。
以第7发实验为例，介绍利用密排PDV阵列测试技术获得断裂时刻的方法。图3展示了相邻4个PDV探针获得的典型速度谱图，可以看出，所有速度谱图在早期均呈单一速度曲线特征，从约40 μs开始出现不同程度的弥散现象。分析认为，该弥散现象与膨胀环的断裂密切相关：膨胀环断裂瞬间，断口附近材料在高电流的烧蚀作用下变为等离子体，高速膨胀运动的等离子体导致测速谱图呈弥散特征，且越靠近断口位置，弥散程度越高。断口通常会出现在相邻2个测点之间，因此测速谱图中出现弥散信号的时刻总是晚于断裂时刻。通常等离子体的初始运动速度超过6 km/s，相邻测点的初始弧长间隔为1.2 mm，所以等离子体从断口运动到最近测速探头的时间小于0.1 μs。在本次实验中，测速通道13、14、15、16观测到弥散信号的时刻分别为42.7、42.5、42.8和43.1 μs，因此，判定最早出现弥散信号的通道14距离断口最近，该断口的断裂时刻为42.5 μs。
图4为40.1和43.1 μs相邻时刻的高速摄影图像，膨胀环测速编号10～20（图4(b)中的黑框区域）观测到了等离子体发光现象，与PDV测速判读的弥散信号出现时刻相符，进一步验证了速度谱图信号解读的合理性。
根据PDV测点获得的速度历史曲线v(t)，计算得到断裂时刻对应的断裂应变εf[9–10]
式中：tf为断裂时间，t为时间，r0为样品环的初始外半径。
采用上述方法可得到一发实验中膨胀环多个断口位置的断裂应变。据此开展了7发不同应变率实验获得的所有断裂应变数据，如图5所示，并与Zhang等[6]和Altynova等[13]所获得的6061铝实验数据进行对比。
需要说明的是，虽然本研究与Zhang等[6]和Altynova等[13]实验采用的电磁膨胀环材料均为6061铝，但材料的晶粒尺寸、热处理工艺、样品环尺寸并不相同。此外，Zhang等[6]和Altynova等[13]的断裂应变是通过测量回收破片断口处的横截面积或破片长度变化获得的，因此，不同实验获得的断裂应变的绝对值存在差异。
通过图5可以看到，与Zhang等[6]和Altynova等[13]的实验结果相比，本研究在同样的加载应变率下获得了多个断口位置的断裂应变，进而可分析其统计特性。此外，随着应变率的增加，断裂应变的中值呈增大趋势，与Zhang等[6]和Altynova等[13]的实验结果吻合。Zhang等[6]曾认为，由于金属环的不均匀变形，颈缩和断口处的应变不能完全描述金属本身的延性，应变率与断裂应变并无明显关系[6]，这与Janiszewski[8]的结论相反。但Zhang等[7]在随后的研究中发现，其不均匀变形是由于样品自身的尺寸差异影响了结果，修改了之前的结论。
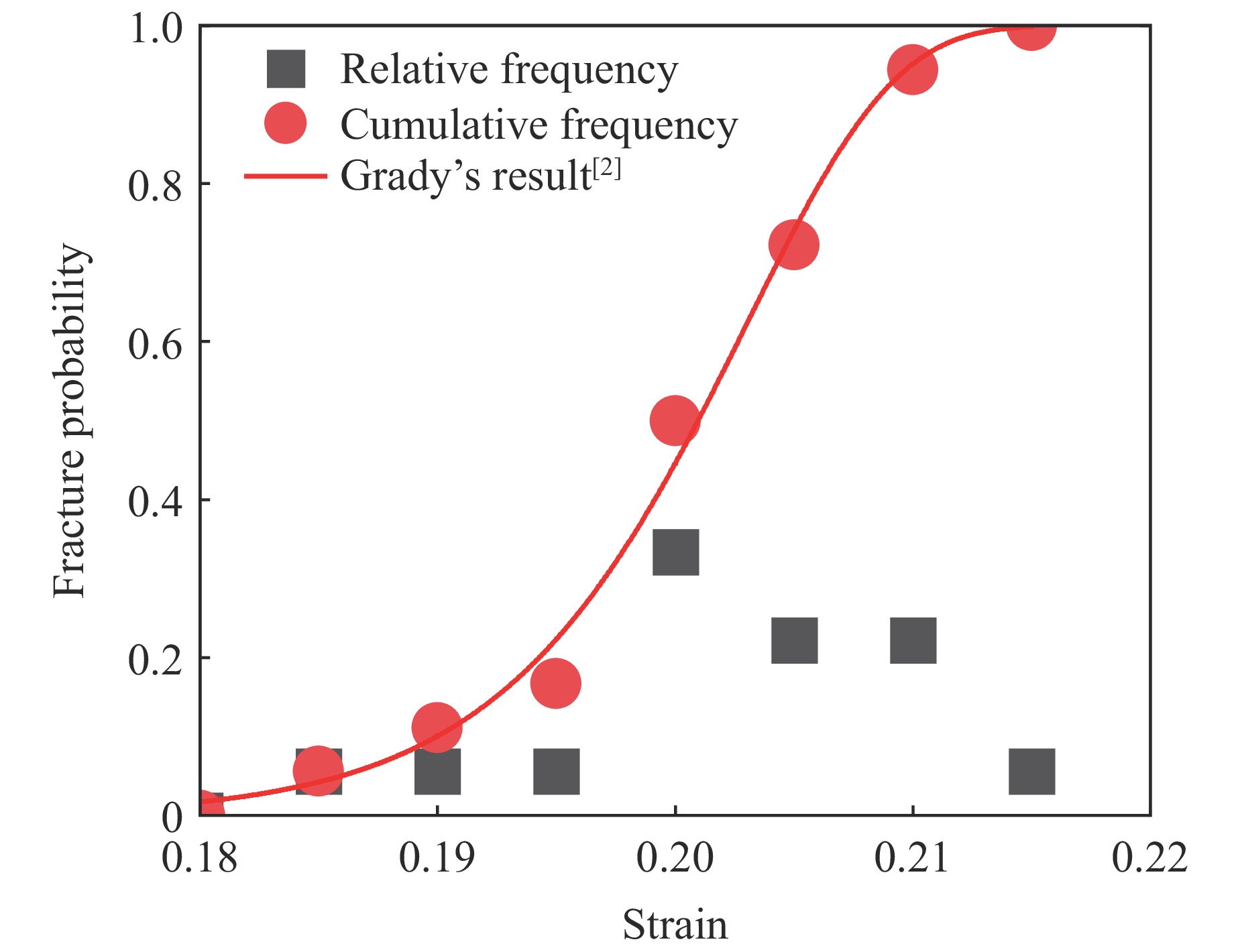
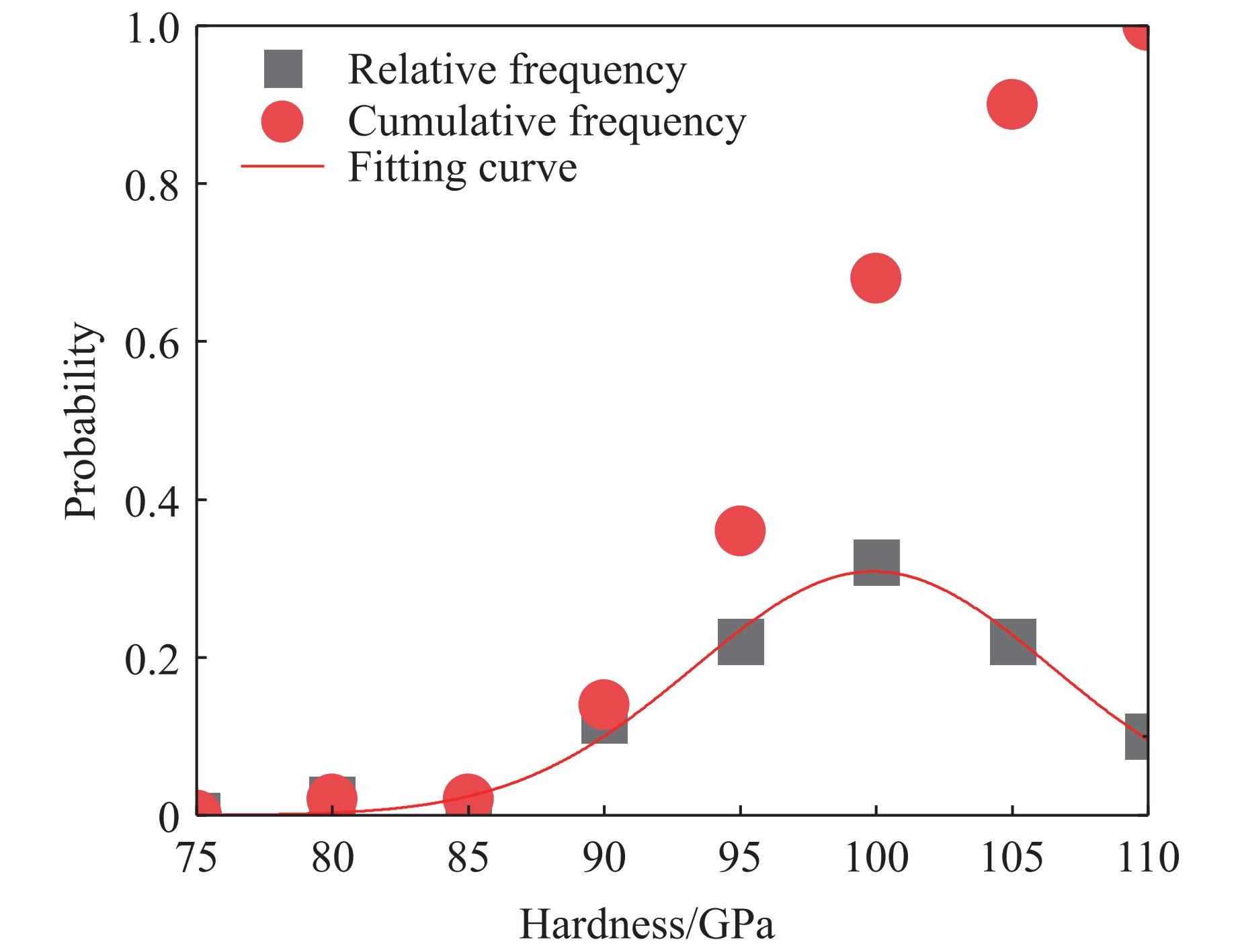
为了进一步验证Grady[2]提出的断裂应变分布，假设式(1)合理，选取实验6和实验7（最大运动速度约为180 m/s）的结果进行统计处理，将实验数据划分为8个区间，计算每个区间的相对频率和累计频率，如图6所示。可以看出，韦伯分布可以较好地描述实验数据的统计分布，韦伯分布参数中，形状参数k=33，尺度参数λ=0.2。
-
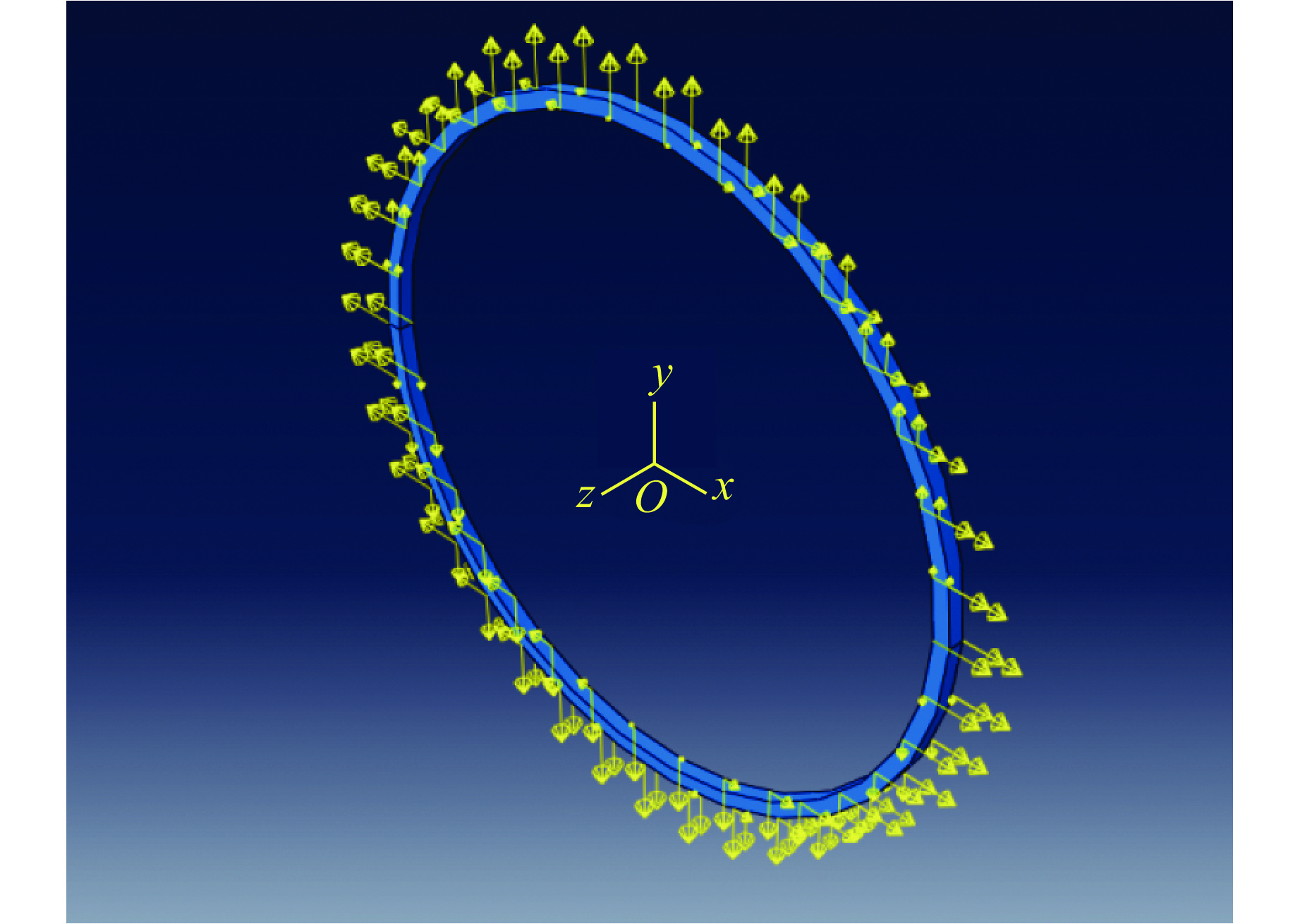
采用ABAQUS/Explict软件对电磁膨胀环的断裂行为进行数值模拟。样品环的材料、尺寸与实验保持一致，网格采用C3D8R类型，网格尺寸为0.125 mm，网格数为
64000 。采用体力边界条件施加在样品环上，以模拟整个运动过程，体力沿膨胀环径向且所有单元均相同，如图7所示。体力曲线根据实验测得的速度曲线进行计算迭代获得。采用Zhang等[16]基于VUMAT（动力学自定义材料子程序）二次开发的材料模型进行力学场求解。材料本构模型在传统J-C模型的基础上增加了损伤软化项，采用Lovinger等[17]提出的基于能量的损伤演化模型进行计算，即
式中：σy为屈服应力，εp为等效塑性应变，A、B、n、C和m为J-C本构参数，
${{ \dot \varepsilon }_0} $ 为参考应变率，Tm为材料熔化温度，T为单元的温度，Tr为室温，D为软化系数，W为单元变形引起的塑性功，Wi和Wf分别为材料变形失稳时刻和失效时刻对应的塑性功，TW为塑性变形导致的温升，cp为比定压热容，ρ为密度。6061铝的材料参数列于表2[18]，其中：G为剪切模量。膨胀环的断裂行为与材料的微介观不均匀性密切相关。Liu等[14]通过在本构中引入概率因子P描述材料的微介观不均匀性，成功再现了金属柱壳的膨胀断裂与压缩剪切过程，采用的本构形式为
式中：
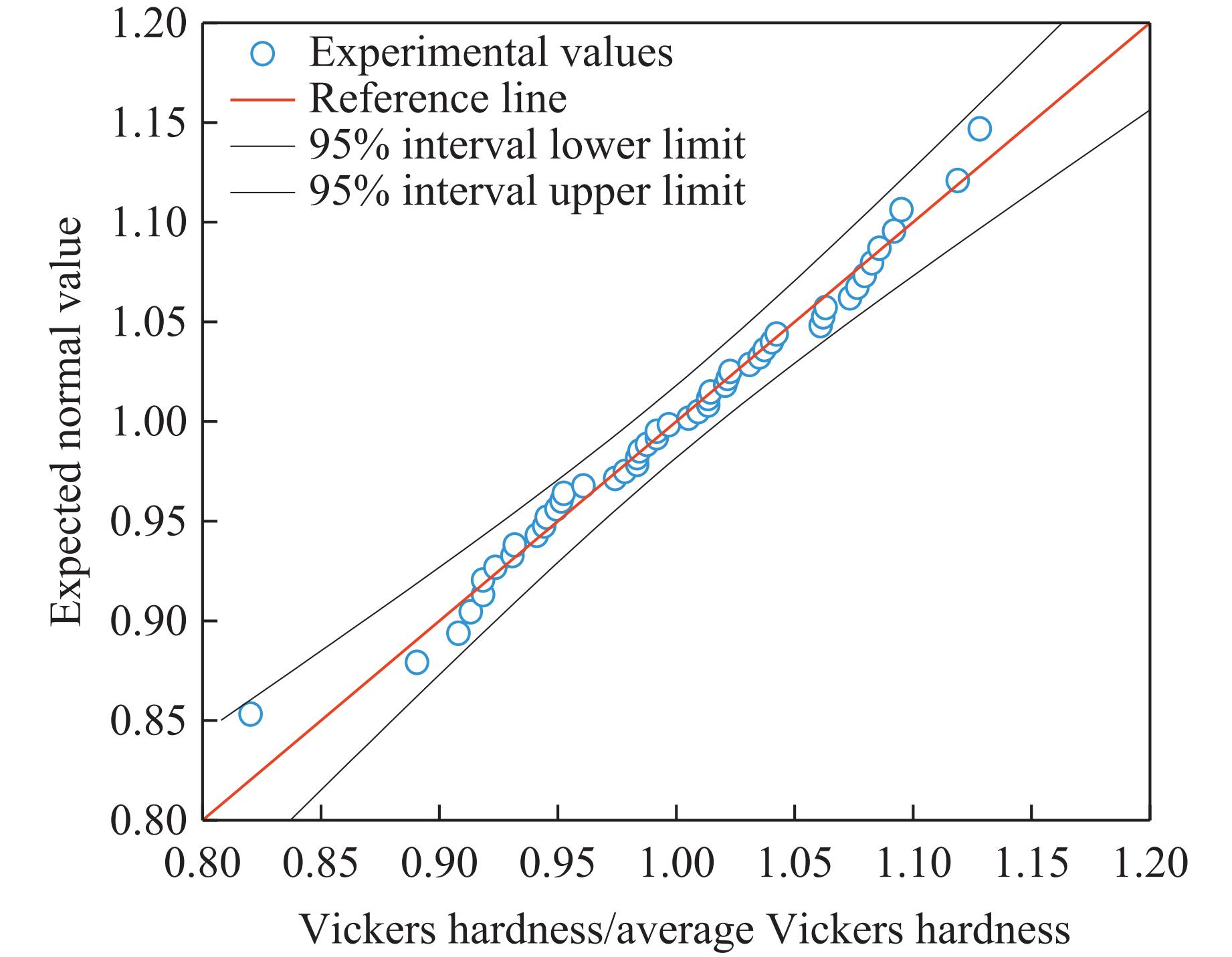
${\sigma }_{\text{y}}' $ 为特定单元的屈服应力。每个单元的概率因子不同，假定其满足以1为中值的分布。Cai等[19]的研究发现，韧性金属材料的硬度与准静态屈服强度呈正相关，而6061铝的动态屈服强度对应变率不敏感[18]。Altynova等[13]也发现，6061铝在不同速度下的硬度与准静态拉伸试样结果接近，因此，可以采用表征维氏硬度的方式获得材料的动态屈服强度进行统计。将表面抛光的6061铝样品环固定在显微硬度计平台上，选用10 g载荷在样品环表面等间隔测量。采用正四棱锥金刚石压头作用于样品表面，通过测量压痕区域的面积，计算材料的维氏硬度，如图8所示。实验共测得50个硬度数据，对其进行统计处理，结果如图9和图10所示。图10中，平均值μ=1，断裂应变的标准差σ=
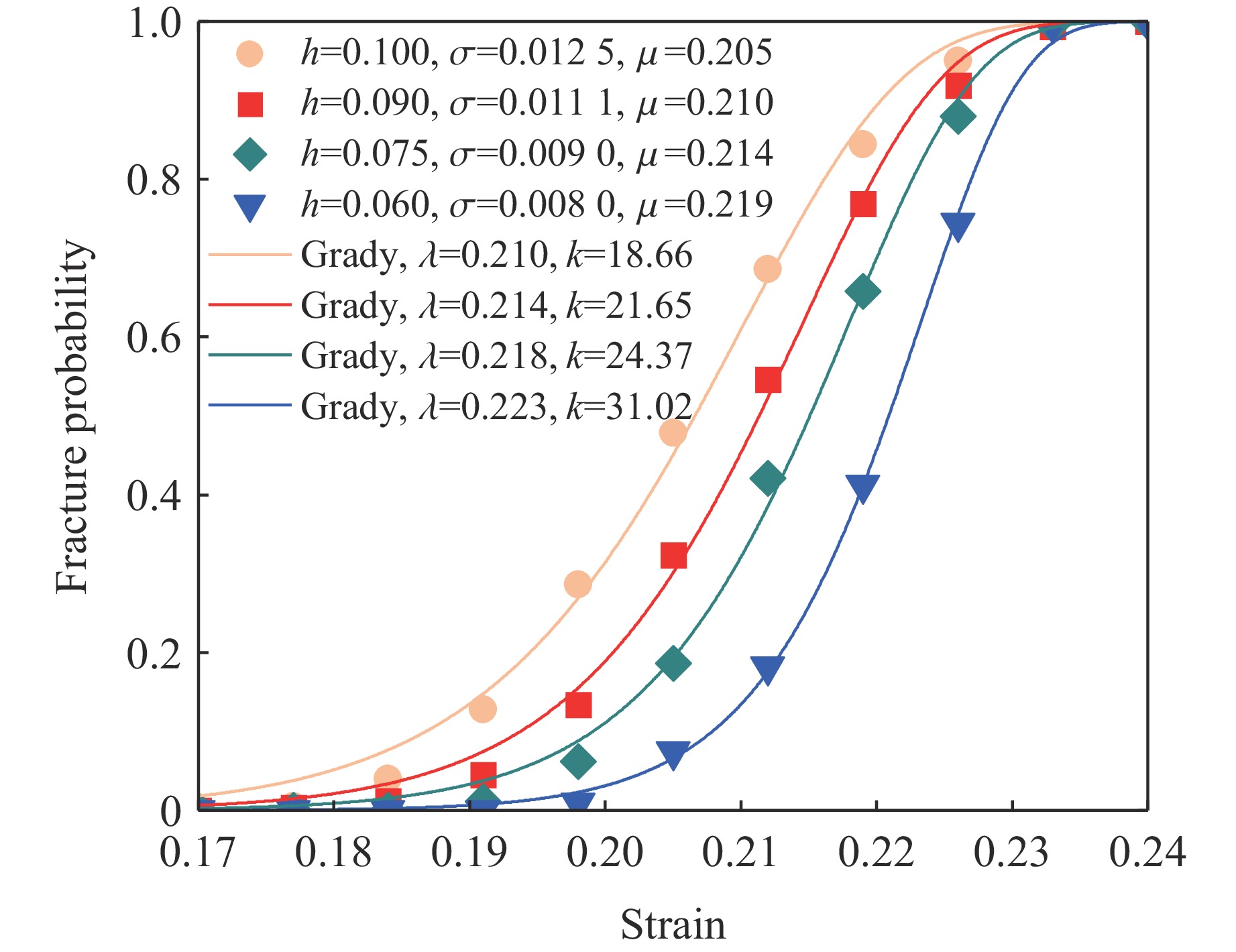
0.06544 ，P=0.7663 。Q-Q图（用于评估数据是否符合特定分布假设）统计结果表明：6061铝的硬度表现出明显的正态分布规律，P远大于0.05，正态分布的标准差为0.065。因此，可认为6061铝的动态屈服强度符合标准差为0.065的正态分布。在数值模拟中，按照正态分布N(1,h2)生成随机数，标准差h分别设置为0.100、0.090、0.075和0.060，在2倍标准差范围内选取单元的概率因子P。为了分析断裂应变满足韦伯分布假设的合理性，针对每个标准差开展200次计算，由于每次概率因子的具体分布情况不同，所以200次计算的结果各不相同，对结果进行分析可获得断裂应变的统计分布信息，如图11所示。
采用Grady模型对模拟结果进行拟合，结果也绘于图11。可以看出，韦伯分布可以同时较好地描述4种均匀性下断裂应变的统计规律。标准差h为0.06时，数值模拟结果拟合得到韦伯分布参数k=31、λ=0.22，与实验得到的k=33、λ=0.2吻合。
-
通过基于新型密排PDV阵列测试技术的电磁膨胀环实验及含概率统计的大规模数值模拟，研究了6061铝膨胀环断裂应变的统计分布规律。利用新型密排PDV阵列测试技术，首次成功获取了电磁膨胀环不同位置处的高精度原位断裂应变实验数据，为6061铝环断裂应变统计规律的分析提供了可靠的实验数据。实验结果表明，随着应变率的增大，6061铝的断裂应变平均值逐渐增大。考虑材料不均匀性的数值模拟成功再现了膨胀环的膨胀断裂过程，通过大规模计算获得了大量的断裂应变模拟结果。实验与模拟结果的统计分析均表明，Grady假定的韦伯分布可以较好地描述6061铝断裂应变的统计规律。
6061铝电磁膨胀环的动态断裂应变统计规律
Statistical Law of Dynamic Fracture Strain Distribution of 6061 Aluminum Electromagnetic Expansion Ring
-
摘要: 研究延性金属环在动态加载下的断裂应变分布规律具有重要意义，电磁膨胀环装置是常用的实验加载手段。然而，目前实验上缺乏有效的原位观测技术，无法获得高精度的断裂应变统计数据。为此，将新研制的密排光子多普勒测速仪阵列应用于电磁膨胀环实验，获得了大量高置信度的断裂应变实验数据；通过硬度测量获得了材料屈服强度的统计分布规律，建立了含概率的本构模型，并进行了大规模计算，得到了大量的断裂应变模拟结果。结合实验与模拟结果，分析了6061铝电磁膨胀环动态断裂应变的应变率效应以及断裂应变韦伯分布假设的合理性。
-
关键词:
- 密排多普勒测速仪阵列 /
- 电磁膨胀环 /
- 断裂应变统计规律 /
- 应变率效应
Abstract: The fracture strain distribution of ductile metal rings under dynamic loading has significant application value, and the electromagnetic expansion ring is a commonly used experimental loading method. However, currently there is a lack of effective in-situ observation technology in experiments, making it impossible to obtain high-precision fracture strain statistical data. In this paper, the newly developed close-packed photonic Doppler velocimetry (PDV) array testing technology was applied to the electromagnetic expanding ring experiment, and a large amount of high-confidence fracture strain experimental data were obtained. The statistical distribution of material yield strength was obtained through hardness measurements, a probabilistic constitutive model was established, and large-scale computations were carried out to obtain a wealth of fracture strain simulation results. By combining experiments with simulations, the strain rate effect of dynamic fracture strain in 6061 aluminum electromagnetic expanding ring and the rationality of the Weibull distribution assumption for fracture strain were analyzed. -
-
图 1 (a)密排PDV阵列测点布局及装配实物，(b)膨胀环实验装置原理
Figure 1. (a) Densely packed PDV array measurement points and assembly of the experimental setup; (b) principle of the expansion ring experimental device
图 4 (a) 40.1 μs和 (b) 43.1 μs时刻6061铝电磁膨胀环的高速摄影照片
Figure 4. High-speed photographs of the electromagnetic expansion ring made of 6061 aluminum alloy at 40.1 μs (a) and 43.1 μs (b)
图 5 6061铝电磁膨胀环断裂应变的实验测量结果
Figure 5. Experimental measurement results of the fracture strain for electromagnetic expansion rings
图 6 6061铝电磁膨胀环实验数据统计分布
Figure 6. Cumulative frequency distribution curve of the electromagnetic expansion ring experimental data
图 8 6061铝样品的维氏硬度测量界面
Figure 8. Vickers hardness measurement interface of the 6061 aluminum ring
图 9 6061铝环的维氏硬度频率分布
Figure 9. Vickers hardness frequency distribution of the 6061 aluminum ring
图 11 6061铝电磁膨胀环数值模型断裂应变累计频率分布
Figure 11. Cumulative frequency distribution of the fracture strain of numerical simulation models for the 6061 aluminum electromagnetic expansion ring
表 1 实验样品的最大扩展速度及断口数量
Table 1. Maximum expansion velocity and number of fractures of experimental samples
Test No. Charging voltage/kV Maximum expansion velocity/(m·s–1) Number of fractures 1 5.25 113 1 2 5.50 120 3 3 5.50 130 4 4 6.00 145 4 5 6.00 150 6 6 6.25 175 10 7 6.50 190 8 
下载: 导出CSV
表 2 6061铝的J-C模型参数
Table 2. Parameters of the J-C model of the 6061 aluminum
ρ/(g·cm−3) G/GPa A/GPa B/GPa n C $ \dot{\varepsilon}_0/\mathrm{s}^{-1} $ Tm/K Tr/K m cp/(J∙kg−1∙K−1) 2.703 27 0.278 0.245 0.817 0.0256 1.0 925 300 1.34 876
下载: 导出CSV
-
[1] MOTT N F. Fragmentation of shell cases [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1947, 189(1018): 300–308. doi: 10.1098/rspa.1947.0042 [2] GRADY D. Fragmentation of rings and shells: the legacy of N. F. Mott [M]. Berlin, Heidelberg: Springer, 2006. [3] ROBSON J D. Exploring effects of property variation on fragmentation of metal rings using a simple model [J]. Defence Technology, 2023, 23: 1–7. doi: 10.1016/j.dt.2022.08.014 [4] TODINOV M T. Is Weibull distribution the correct model for predicting probability of failure initiated by non-interacting flaws? [J]. International Journal of Solids and Structures, 2009, 46(3/4): 887–901. doi: 10.1016/j.ijsolstr.2008.09.033 [5] NIORDSON F I. A unit for testing materials at high strain rates: by using ring specimens and electromagnetic loading, high strain rates are obtained in a tension test in a homogeneous, uniaxial strain field [J]. Experimental Mechanics, 1965, 5(1): 29–32. doi: 10.1007/BF02320901 [6] ZHANG H, RAVI-CHANDAR K. On the dynamics of necking and fragmentation—Ⅰ. real-time and post-mortem observations in Al 6061-O [J]. International Journal of Fracture, 2006, 142(3): 183–217. doi: 10.1007/s10704-006-9024-7 [7] ZHANG H, RAVI-CHANDAR K. On the dynamics of necking and fragmentation—Ⅱ. effect of material properties, geometrical constraints and absolute size [J]. International Journal of Fracture, 2008, 150(1): 3–36. doi: 10.1007/s10704-008-9233-3 [8] JANISZEWSKI J. Ductility of selected metals under electromagnetic ring test loading conditions [J]. International Journal of Solids and Structures, 2012, 49(7/8): 1001–1008. doi: 10.1016/j.ijsolstr.2012.01.005 [9] DAN J K, GUO Z L, CHEN Y, et al. Preliminary investigations on dynamic fracture of ductile metals by using electromagnetically driven expanding ring [J]. AIP Advances, 2020, 10(10): 105001. doi: 10.1063/5.0016527 [10] JIANG Y, CHEN Y, GUO Z L, et al. Effect of strain rate on ductility of Cu TU1 in electromagnetic ring expansion [J]. International Journal of Impact Engineering, 2024, 184: 104832. doi: 10.1016/j.ijimpeng.2023.104832 [11] BARKER L M, HOLLENBACH R E. Laser interferometer for measuring high velocities of any reflecting surface [J]. Journal of Applied Physics, 1972, 43(11): 4669–4675. doi: 10.1063/1.1660986 [12] STRAND O T, GOOSMAN D R, MARTINEZ C, et al. Compact system for high-speed velocimetry using heterodyne techniques [J]. Review of Scientific Instruments, 2006, 77(8): 083108. doi: 10.1063/1.2336749 [13] ALTYNOVA M, HU X Y, DAEHN G S. Increased ductility in high velocity electromagnetic ring expansion [J]. Metallurgical and Materials Transactions A, 1996, 27(7): 1837–1844. doi: 10.1007/BF02651933 [14] LIU M T, REN G W, FAN C, et al. Experimental and numerical studies on the expanding fracture behavior of an explosively driven 1045 steel cylinder [J]. International Journal of Impact Engineering, 2017, 109: 240–252. doi: 10.1016/j.ijimpeng.2017.07.008 [15] HUANG S, CHEN H Y, ZHANG R, et al. Uncovering the fracture behavior of metallic cylindrical shells under internal explosive loadings via careful design of densely-arranged multi-point photon Doppler velocimetry measurements [J]. International Journal of Impact Engineering, 2023, 180: 104679. doi: 10.1016/j.ijimpeng.2023.104679 [16] ZHANG H, PEI X Y, PENG H, et al. Phase-field modeling of spontaneous shear bands in collapsing thick-walled cylinders [J]. Engineering Fracture Mechanics, 2021, 249: 107706. doi: 10.1016/j.engfracmech.2021.107706 [17] LOVINGER Z, RITTEL D, ROSENBERG Z. Modeling spontaneous adiabatic shear band formation in electro-magnetically collapsing thick-walled cylinders [J]. Mechanics of Materials, 2018, 116: 130–145. doi: 10.1016/j.mechmat.2017.01.010 [18] 邓云飞, 张永, 吴华鹏, 等. 6061-T651铝合金动态力学性能及J-C本构模型的修正 [J]. 机械工程学报, 2020, 56(20): 74–81. doi: 10.3901/JME.2020.20.074 DENG Y F, ZHANG Y, WU H P, et al. Dynamic mechanical properties and modification of J-C constitutive model of 6061-T651 aluminum alloy [J]. Journal of Mechanical Engineering, 2020, 56(20): 74–81. doi: 10.3901/JME.2020.20.074 [19] CAI J Z, GRIESBACH C, AHNEN S G, et al. Dynamic hardness evolution in metals from impact induced gradient dislocation density [J]. Acta Materialia, 2023, 249: 118807. doi: 10.1016/j.actamat.2023.118807 -
计量
- 文章访问数: 182
- HTML全文浏览数: 182
- PDF下载数: 0
- 施引文献: 0