-
岩爆是深部地下工程发展中一种常见的动力失稳地质灾害,对人员安全、设备完整性和操作连续性构成巨大威胁。目前,大长度、大断面和大埋深已成为地下工程发展的重要趋势,矿山、隧道等工程位于地下深层高地应力区,极易发生岩爆[1–2]。因此,准确预报预警岩爆,能有效降低风险和损失。
岩爆分类预测研究一直是岩土工程领域的热点和难点之一。目前,国内外专家针对岩爆发生机理及影响因素开展了大量研究。常见的岩爆预测方法可大致分为判据预测法、现场监测预测法和综合预测法3类。判据预测法主要基于岩爆机理,建立岩体物理力学参数与岩爆发生之间的相关性,包括Russense判据[3]和Hoek判据[4]。然而,由于岩爆机理十分复杂,采用单一指标很难全面、准确地解释岩爆的发生机理和严重程度。现场监测预测法可以直接实时获取相关参数,包括微震检测法[5]、声发射(acoustic emission, AE)法[6]。综合预测法是利用机器学习和深度学习方法,构建岩爆影响因子与岩爆之间的非线性相关模型。温廷新等[7] 利用海林格距离过采样增加少数类样本数目,然后基于粒子群优化(particle swarm optimisation,PSO)算法,引入自适应种群间距和变异算子设计自适应混合差分粒子群优化(adaptive hybrid differential particle swarm optimization,AHDPSO)算法,利用AHDPSO算法优选极限学习机(extreme learning machine,ELM)的输入层权值和隐藏层阈值,构建岩爆烈度等级预测模型。李明亮等[8]首先对岩爆经典案例数据进行归一化处理,得到其无量纲数据,然后利用混沌映射和交叉变异算子对Harris hawks优化算法进行改进,最终建立了IHHO-ELM岩爆烈度等级预测模型。侯克鹏等[9]运用自适应平衡机制调节多元宇宙算法(multi-verse optimizer,MVO)中的虫洞存在概率(VWEP)和旅行距离率(VTDR)2个重要参数,改进后的算法比传统模型的寻优能力更强,精度更高。满轲等[10]根据灰色关联分析结果对4种评价方案进行比选,以确定最优预测指标,采用基本麻雀搜索算法(sparrow search algorithm,SSA)优化随机森林(random forest,RF)模型,提高了预测模型的准确率和泛化性。高梅等[11]采用SMOTEENN和CGAN算法,以过采用、欠采样、对抗生成的方法处理原始数据,随后采用10种经典算法验证了SMOTEENN-CGAN模型的有效性。
上述方法主要集中于岩爆指标权重和算法创新研究,在一定程度上忽视了由于各地工况差异大、数据测量方法不当等导致的岩爆数据中存在离群值及类别不均衡等问题。然而,在机器学习中,类别不均衡将导致预测结果偏向于以多数类为中心的样本,其他少数类样本的值则没有得到很好地捕捉。同时,单一数据集预处理或算法改进很难避免自身的局限性,因此,对岩爆预测性能的提升不显著。针对上述不足,本研究将两者进行结合,首先,通过数据预处理剔除异常值和均衡各类岩爆数据,采用极限梯度提升树(XGBoost)、随机森林、多层感知机(multi-layer perceptron,MLP)3类模型进行对比分析,验证数据预处理前后对模型准确率的提升;其次,采用Sine混沌映射,引入动态自适应权重,结合柯西变异混合策略改进麻雀搜索算法,选用8个基准函数对PSO、灰狼算法(grey wolf optimizer, GWO)、遗传算法(genetic algorithm,GA)、基本麻雀搜索算法和改进麻雀搜索算法(improved sparrow search algorithm,ISSA)进行性能测试、对比和分析;最后,采用ISSA对3类预测模型进行参数寻优,引入5折交叉验证评估模型的泛化能力,再次提高模型预测的准确率。通过分析讨论多个评价指标,阐明算法改进与数据预处理结合的重要性,选出最优模型,以期为岩爆预测提供一种新思路。
-
岩爆作为一类复杂非线性的动力失稳地质灾害,数据集的质量和岩爆特征指标的选取会直接影响岩爆预测模型的性能。因此,综合考虑诱发岩爆的内因和外因(即岩性条件和应力条件),结合特征指标整体性原则、代表性原则、定量分析性原则和可操作性原则,选取围岩最大切向应力σθmax、抗压强度σc、抗拉强度σt和弹性能量指数λwet作为模型的输入,其中:抗压强度、抗拉强度和弹性能量指数反映岩性条件,围岩最大切向应力代表应力条件[12]。通过文献检索和数据整理,收集岩爆地下开采过程中的174例作为数据集,如表1所示,其中:15例来自Zhou等[13],41例来自武立文[14],50例来自田睿[1],其余68例来自刘剑等[2]、李明亮等[8]和刘晓悦等[15]。
依据岩爆烈度等级划分依据和破坏特征,如表2和表3所示。将岩爆烈度等级分为Ⅰ级(无岩爆)、Ⅱ级(轻微岩爆)、Ⅲ级(中等岩爆)、Ⅳ级(强烈岩爆)。数据集统计参数的基本描述见表4。
-
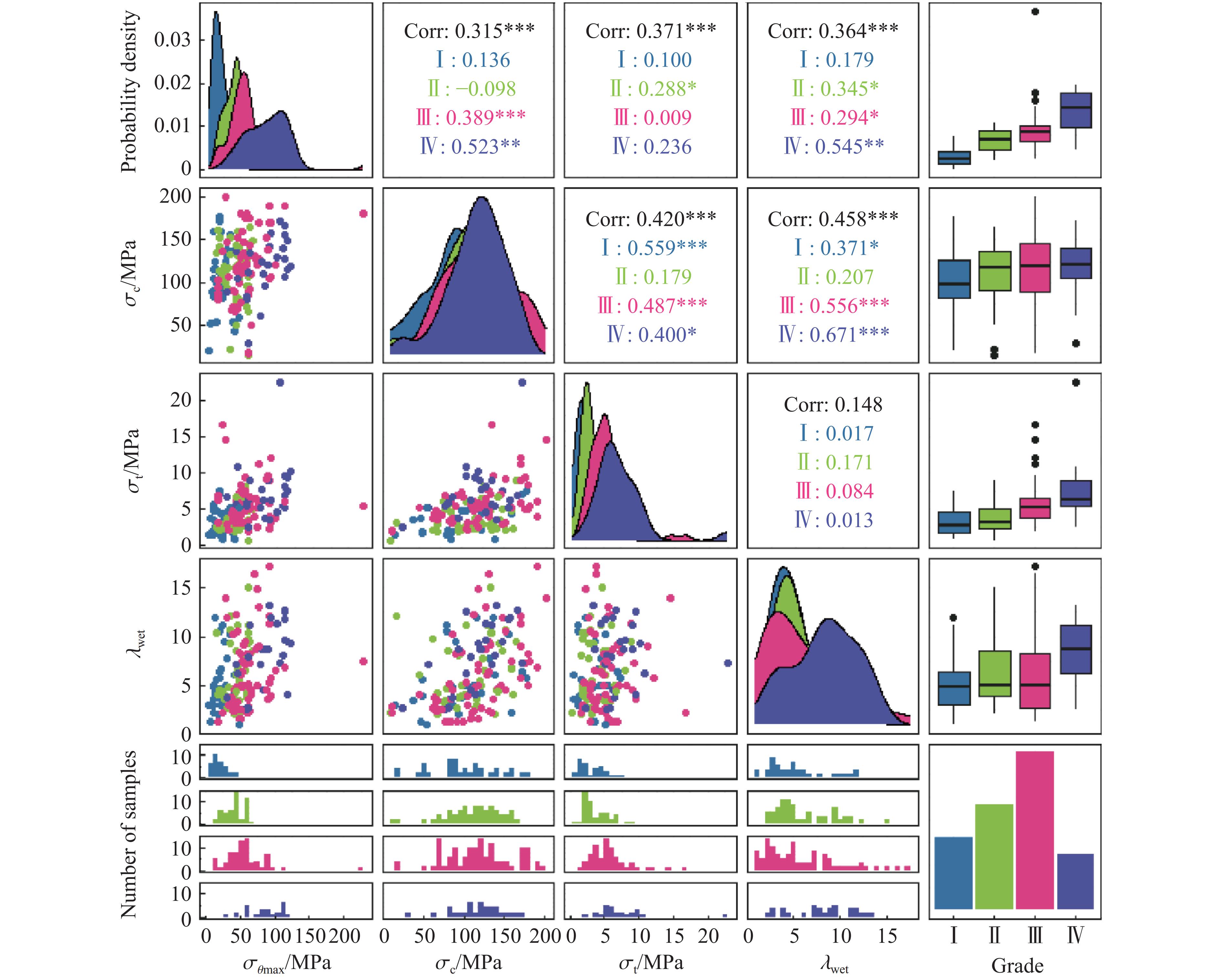
为更加直观地了解各个指标间的统计学关系,利用R语言对数据集进行可视化分析,如图1所示。图1中,对角线和第5行分别表示各指标叠合核密度曲线和单核密度直方图,反映了各指标的分布特征。从对角线下方的散点图可以看出,数据集的分布较为散乱,其中随着散点与原点距离的增大,岩爆烈度趋于增强。同时,为了探究各指标间的相关性,利用皮尔曼相关性分析,得到图1右上角所示的相关性系数图。根据相关系数可以看出,4个指标之间呈弱相关性。从图1中最右列的箱线图可以看出,箱线图的黑点代表异常值,说明原始数据集中含有离群样本。
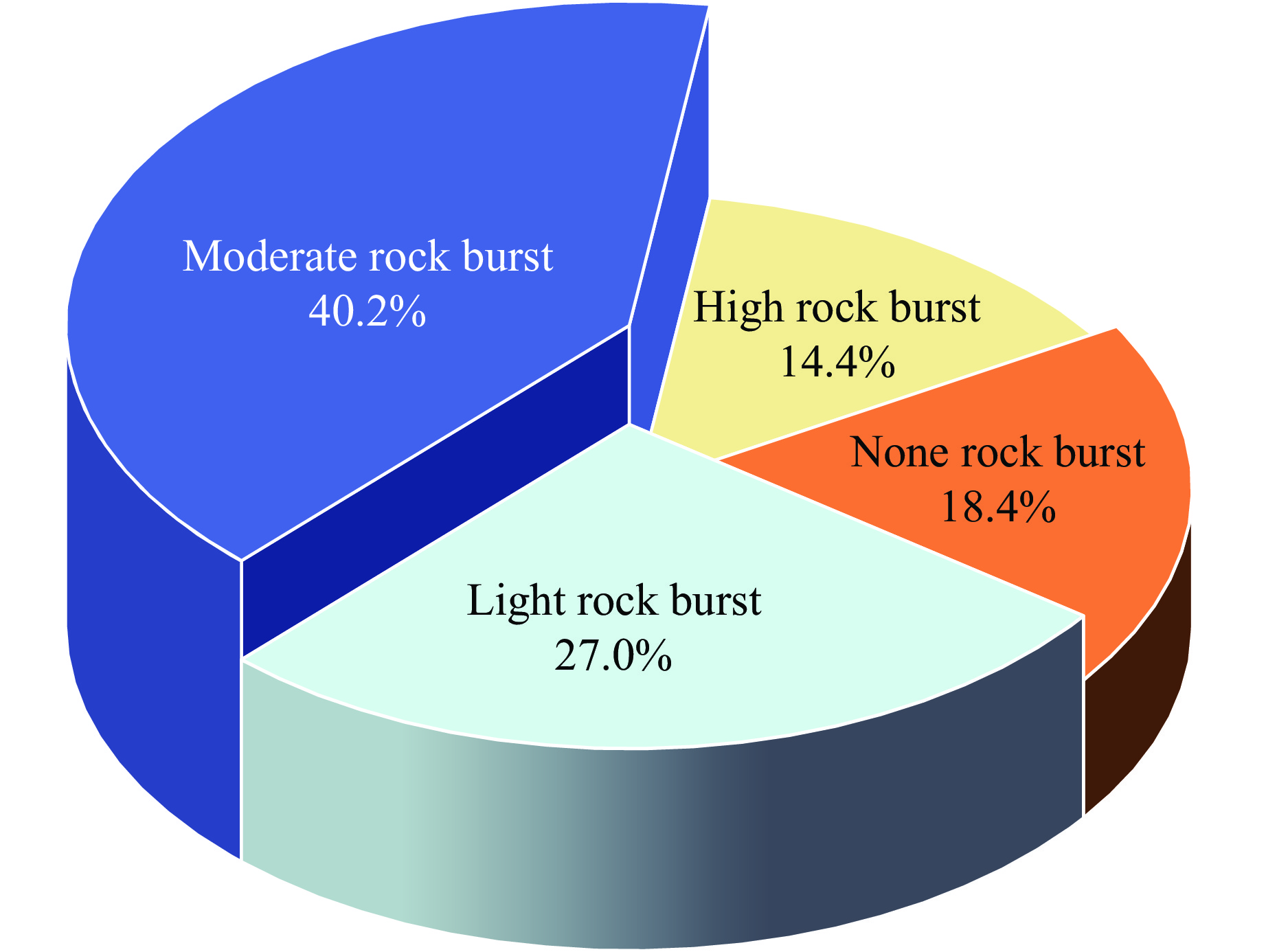
不平衡的数据分类存在多数类和少数类。当多数类的样本数远大于少数类的样本数时,必须实现均衡类分布设计,以保证少数类在整体样本中的必要性。由图2可见,本研究中Ⅰ级岩爆样本32组,占比为18.4%;Ⅱ级岩爆样本47组,占比为27.0%;Ⅲ级岩爆样本70组,占比为40.2%;Ⅳ级岩爆样本25组,占比为14.4%;样本数目比例为1.28∶1.88∶2.8∶1,最大样本量为最小样本量的2.8倍,各类样本数目不均衡。
-
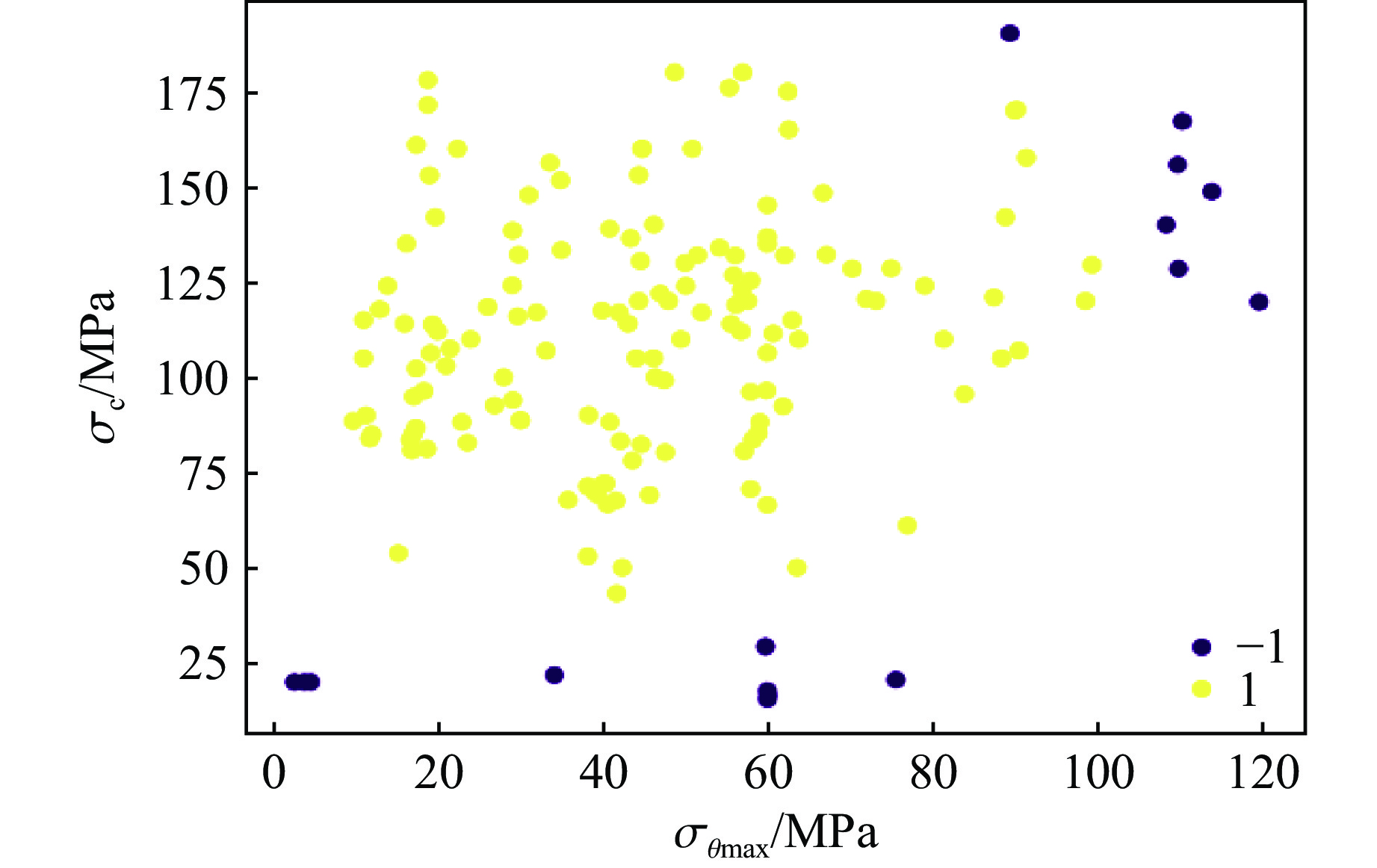
为消除离群样本对预测模型性能的影响,引入局部离群因子(local outlier factor,LOF)算法剔除异常值。LOF算法是基于密度的离群点检测方法,通过计算每个数据与其周围邻域数据点的密度之比,来判断当前数据点是否为异常值[16]。按照4种岩爆预测指标,根据岩爆等级逐级检测并剔除离群样本,利用Python编制程序并绘制离群样本散点图,如图3所示(“1”表示正常样本,“−1”表示离群样本)。
通过逐级分类对比,共剔除16例离群样本,余下158例非离群样本。剔除的部分离群样本如表5所示。
同时,考虑到样本数目不均衡,本研究选用自适应过采样(ADASYN)增加少数类样本数目。该方法根据少数类样本在多数类样本中的分布情况,可以自适应地改变不同少数类样本的权重,为难以学习的少数类样本生成更多的合成样本,能够较好地保持原有的数据结构[17]。过采样后的数据集由原来的158例扩充为251例,其中Ⅰ级岩爆样本65组,Ⅱ级岩爆样本60组,Ⅲ级岩爆样本62组,Ⅳ级岩爆样本64组,各等级岩爆的比例接近1∶1∶1∶1。最后,为避免不同数量级和量纲的影响,加快模型收敛速度,提高模型训练率,采用最大-最小值对平衡后的数据库进行归一化处理,作为后续模型输入。
-
SSA的灵感来源于自然界麻雀觅食,通过模拟麻雀种群的群体觅食活动、预警和反捕食行为设计构建群智能算法,具体步骤参考文献[18]。
-
传统的SSA中种群位置是随机产生的,而随机初始化种群的初始值可能呈密集状态,导致种群分布不均。因此,本研究引入Sine混沌映射代替随机映射,使初始麻雀种群能够较均匀地分布在搜索空间内,提高解的质量及收敛速度。Sine混沌映射原理表示为
式中:
$ {x}_{i} $ 为第i个混沌数;$ \mu $ 为系统参数,$ \mu \in [0, 1] $ 。 -
在SSA中,随着迭代次数的增加,发现者逐渐向全局最优解靠近,麻雀个体搜索范围逐渐缩小,发现者聚集,从而陷入局部最优。为了进一步平衡算法的全局搜索和局部开发能力,本研究在发现者位置更新方式中引入动态权重因子w,当预警值小于安全值时,w在迭代初期有较大值,提高了算法的全局搜索范围,增强全局寻优能力;当预警值大于安全值时,w自适应地减小,增强了局部搜索能力[19]。权重因子和改进发现者计算公式为
式中:
$ {t}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 为最大迭代次数,$ t $ 为当前迭代次数,R为标准正态随机数,$ {X}_{i,j}^{t} $ 为第$ i $ 个麻雀在第$ j $ 维的位置,$ {f}_{j,g}^{t} $ 为上一代中第$ j $ 维的全局最优解,$ Q $ 为服从[0,1]正态分布的随机数,$ {R}_{2}\in \left[\mathrm{0,1}\right] $ 为预警值,$ S\in [0.5, 1.0] $ 为安全值。 -
柯西变异来源于柯西分布,函数分布特点为两端形状又长又扁,在原点处的峰值小,逼近原点速度缓慢,因而可以产生更大的扰动。本研究引入柯西算子,充分利用柯西分布函数两端变异的效果发挥扰动能力,改善了算法易陷入局部最优的缺陷[20]。新的目标更新位置
式中:
$ {X}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}\left(t\right) $ 为第$ t $ 代全局最优位置,$ C\left(\mathrm{0,1}\right) $ 为标准柯西分布函数,$\otimes $ 表示相乘含义。融合Sine混沌映射、动态自适应权重和柯西变异扰动策略的ISSA的具体执行步骤如下:
(1) 设定初始参数,包括种群数大小
$ N $ 、最大迭代次数$ {t}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 、发现者比例$ {P}_{\mathrm{D}} $ 、侦察者比例$ {S}_{\mathrm{D}} $ 、警戒阈值$ {R}_{2} $ 、安全阈值$ S $ 等;(2) 执行Sine混沌映射初始化种群;
(3) 根据计算得出每只麻雀的适应度值,按照由小到大排序,确定当前最优适应度值和最差适应度值以及对应的位置;
(4) 在适应度值较优的麻雀中选取比例为
$ {P}_{\mathrm{D}} $ 的麻雀作为发现者,并按照式(3)更新位置;(5) 余下的麻雀个体作为追随者,根据基本SSA追随者公式更新位置;
(6) 随机从麻雀种群中选取比例为
$ {S}_{\mathrm{D}} $ 的麻雀作为侦察者,根据SSA侦察者公式更新位置;(7) 选择柯西变异扰动策略对当前最优解扰动,产生新解;
(8) 计算适应度值,更新麻雀位置;
(9) 判断是否达到迭代循环结束条件,若满足,进行下一步,否则跳转步骤(3);
(10) 程序结束,输出最优解。
-
为了验证ISSA的优越性,选取PSO、GWO、GA、SSA进行寻优性能对比,5种群体智能优化算法的参数设置如表6所示。其中:c1、c2分别为个体学习因子和社会学习因子,w为惯性权重,a为收敛因子,r1、r2为[0, 1]范围内的随机向量,Pc为交叉概率,Pm为变异概率。选取8个基准测试函数,F1~F4为单峰函数,F5~F8为多峰函数。其中,单峰函数用来测试算法的收敛速度和局部开发能力,多峰函数验证算法W避免陷入局部最优的能力。基准测试函数范围和最优解等信息如表7所示。
为降低偶然误差带来的影响,设置相同的通用条件,种群个数均为20,迭代次数为500,独立运行30次,记录平均值和标准差。观察表8可知:5种算法无论是在单峰函数和多峰函数中,ISSA在平均值和标准差中都优于其他算法,在求解F5和F7函数时,平均值和标准差都为零,相比于其他算法至少提升2个数量级,提升程度明显。从表4的最优解可知,ISSA在8种基准测试函数实验中所求平均值相较于其余4种算法更接近理论全局最优解。同时,标准差数值大小代表求解数据过程中波动的大小。对比5种算法多次寻优实验结果可得,ISSA的平均值和标准差更小,说明ISSA寻优过程的鲁棒性更强,精度更高。
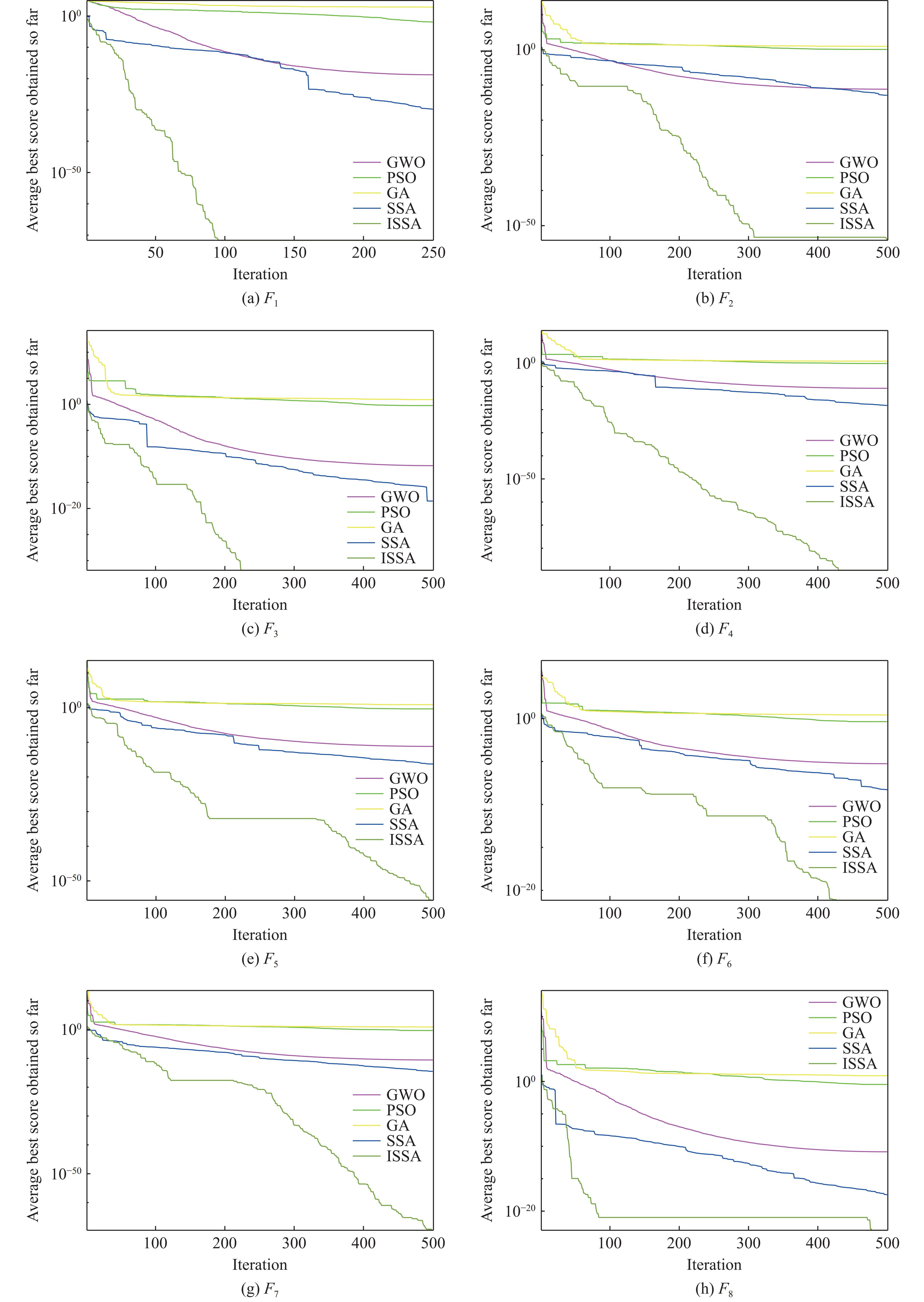
同时,为了更加直观地对比5种算法的收敛速度和收敛精度,绘制了8种测试函数迭代收敛曲线,结果如图4所示。观察图形可知:相较于其他算法的收敛曲线,ISSA收敛曲线一直处于下方且数值较小,说明无论在收敛速度还是求解精度上,ISSA均较高。
-
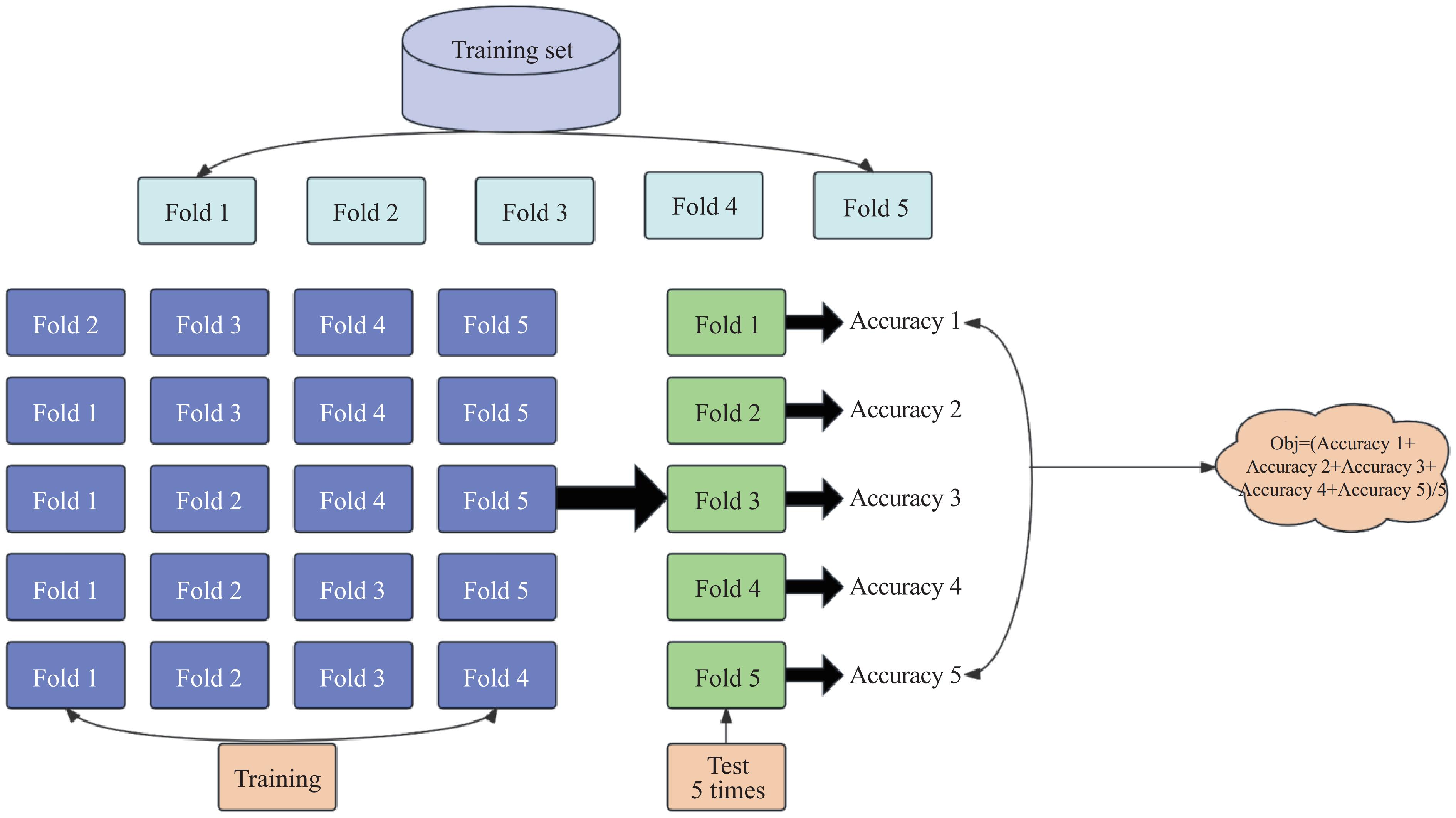
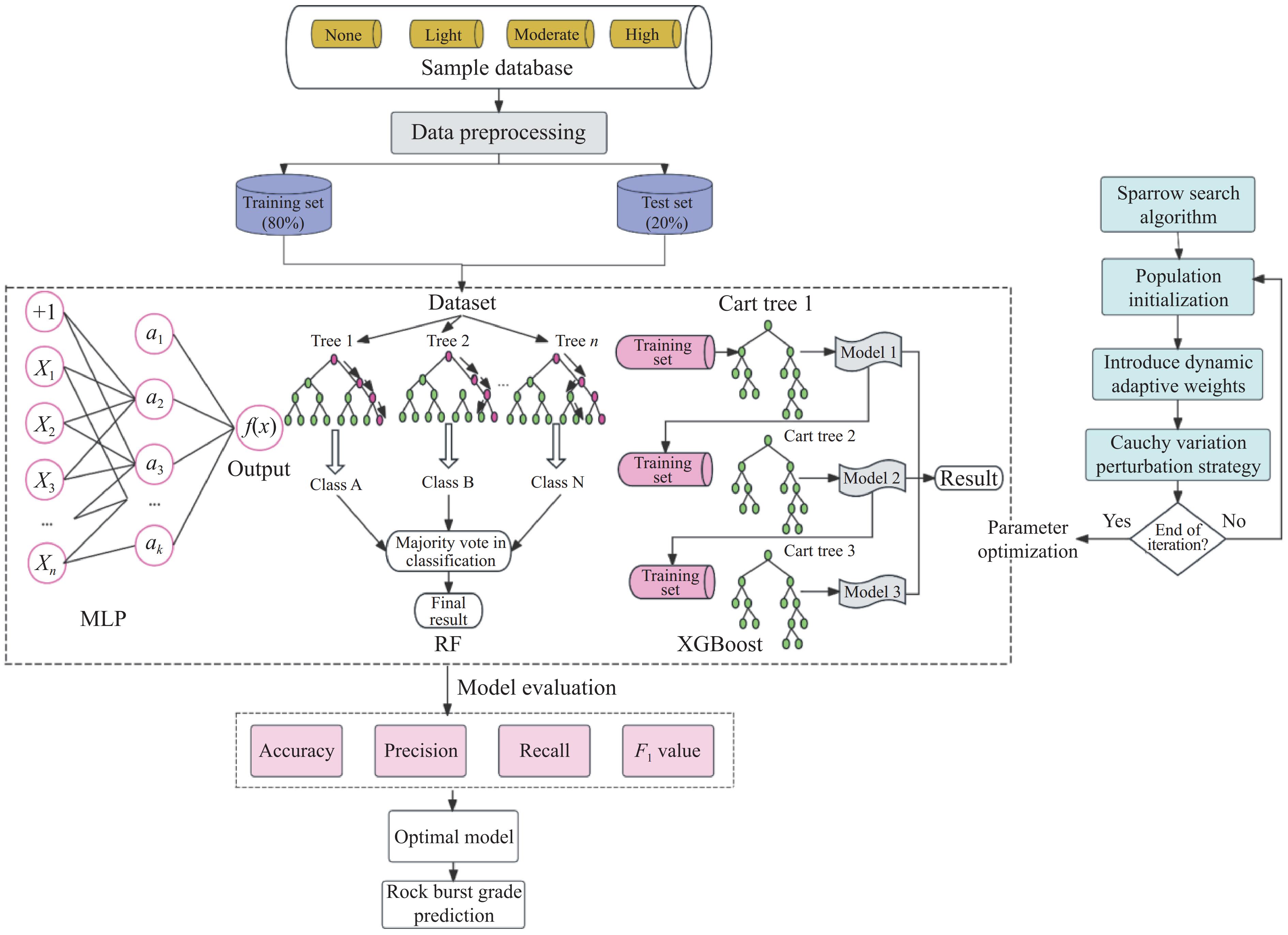
近年来,机器学习被广泛应用于岩爆预测的研究,本研究选取非线性学习性能优秀的RF、MLP、XGBoost 3类算法构建岩爆等级预测模型。为了提升模型的泛化能力,对174组原始岩爆数据集和251组预处理后的岩爆数据集进行分层抽样处理,按照8∶2的比例随机划分训练集和测试集。采用5折交叉验证对模型参数进行择优,将训练集划分为5份,计算5种组合参数的平均准确率,从而得到最优参数[21],交叉验证和目标函数计算流程如图5所示。
-
为实现从各岩爆等级到整体评估模型的分类性能,采用准确率、精确率、召回率、F1得分作为评价指标。模型具体预测流程如图6所示。
具体步骤如下:
(1) 采用LOF与自适应过采样方法对原始数据集预处理,按照8∶2划分训练集和测试集;
(2) 将处理前后的数据集代入3种机器学习模型对比分析;
(3) 引入SSA,设定初始SSA参数;
(4) 采用3种混合策略ISSA,输出最优解;
(5) 引入5折交叉验证,提升模型泛化能力,选出最优参数;
(6) 选取4种评价指标对模型评价,选出最优模型进行岩爆等级预测。
-
为验证数据预处理对岩爆预测准确率的提升效果,将原始数据和预处理后的样本分别输入3种算法的岩爆预测模型进行训练、对比和验证,各模型测试集的准确率如表9所示。由表9可知,岩爆数据集经过预处理后,MLP、RF、XGBoost模型的预测准确率分别提升8.05%、14.37%、15.52%。因此,基于LOF剔除离群样本和ADASYN均衡样本数目的数据预处理算法对提升模型性能具有明显效果。
为了进一步对比ISSA对岩爆预测模型性能的提升作用,分别选取SSA和ISSA算法对3种模型学习器的参数进行优化。将预处理后的岩爆数据集输入模型,通过统计各模型优化后在测试集上的分类性能指标,选出最优模型,测试集结果以4种岩爆等级展开,结果如表10所示。
由表10可知,相较于SSA,经过ISSA的参数优化后,3种模型的准确率分别提高了3.89%、3.93%和7.12%,说明采用ISSA优化其超参数和提升模型性能是可行的。分等级观察表10发现,ISSA对XGBoost模型性能的提升最大。选取数据集时可以发现,Ⅱ级岩爆和Ⅲ级岩爆数据相近,机器学习模型训练时容易发生误判,而Ⅰ级岩爆和Ⅳ级岩爆数据分布稳定,故ISSA-XGBoost模型对Ⅰ级和Ⅳ级岩爆预测准确率达到100%,可以精确判断Ⅰ级和Ⅳ级岩爆;模型对Ⅱ级岩爆和Ⅲ级岩爆的误判率较高,但仍优于其他模型,处于可接受的误差范围,表现出极好的性能,因此,本研究选择ISSA-XGBoost模型作为预测岩爆等级的最优模型。
-
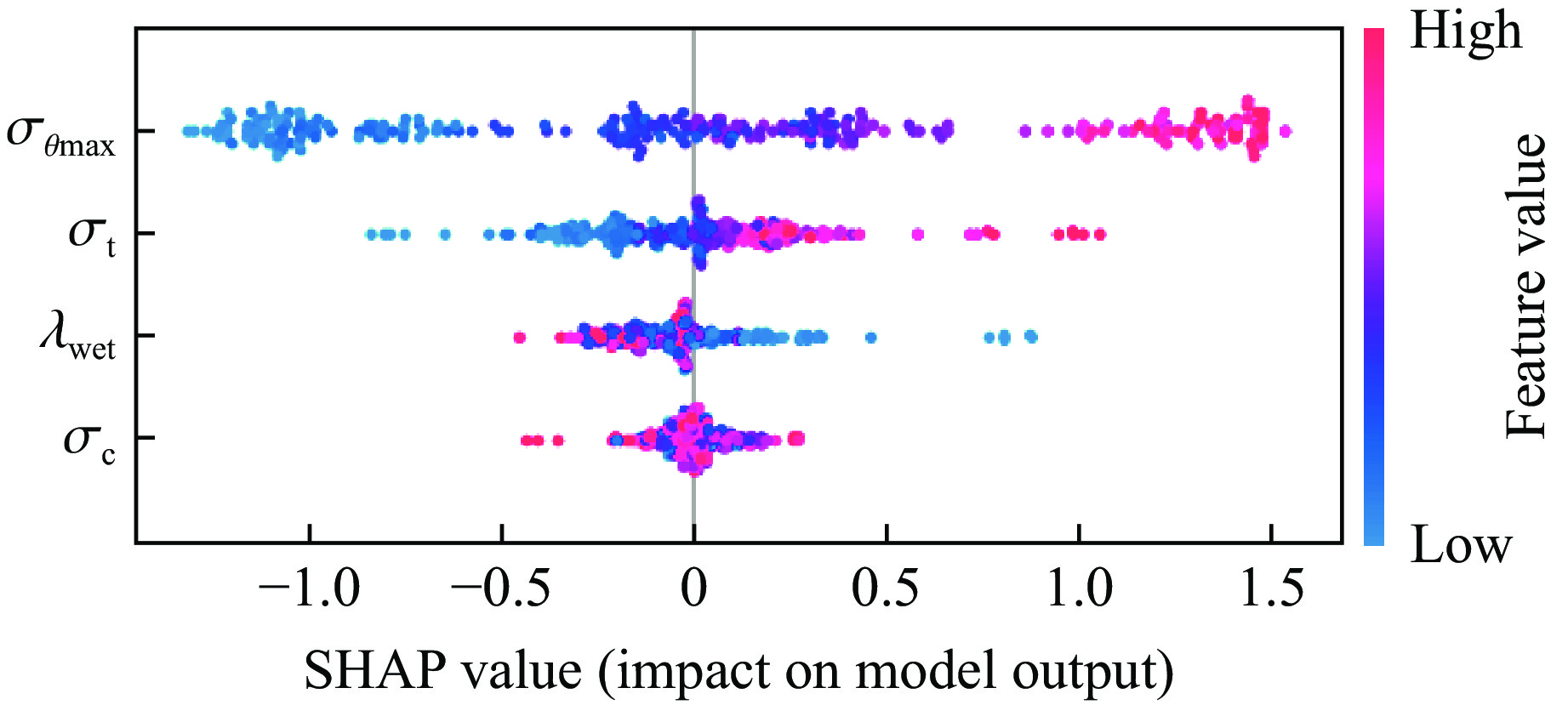
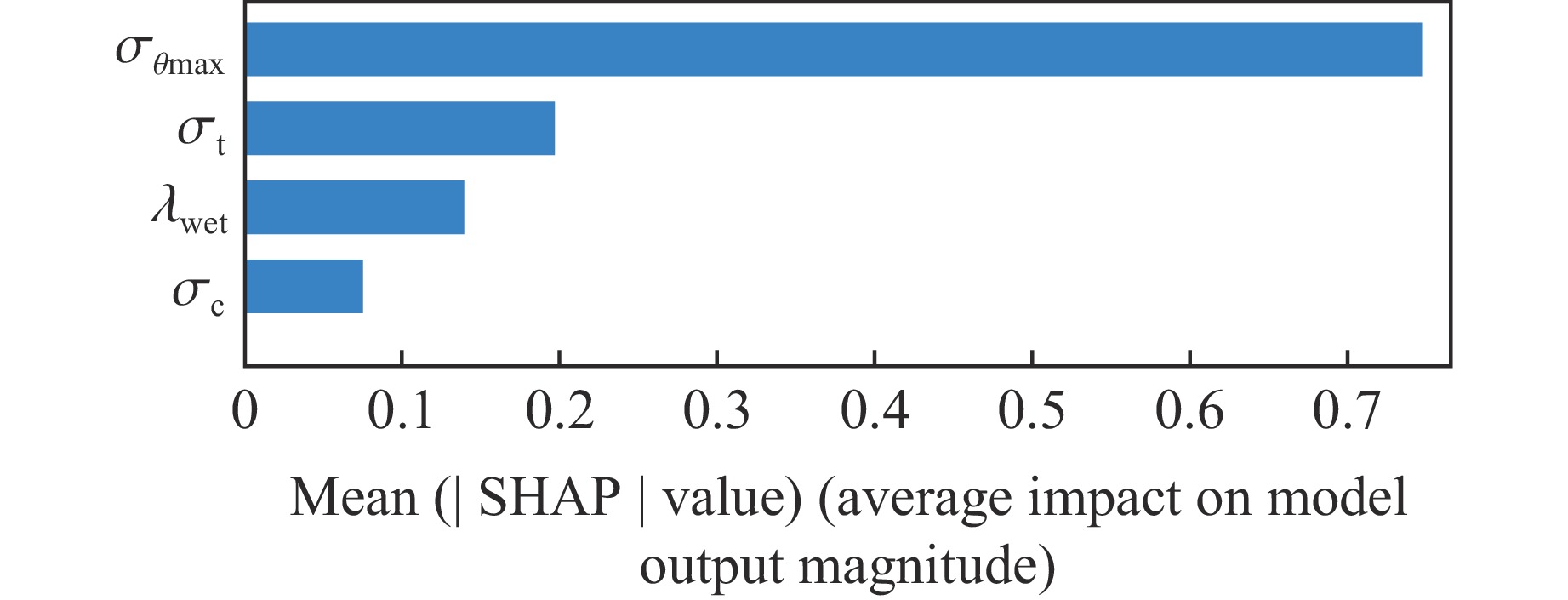
相较于分析变量间线性相关程度的皮尔曼相关性分析,SHAP(shapley additive explanations)特征重要性分析不仅能够揭示特征之间的非线性关系,而且用于解释不同模型中的特征重要性和影响机制,结果如图7和图8所示。SHAP特征摘要图说明了不同岩性指标对岩爆等级预测的正负关系。该线上的每个标记表示此图中的一个示例数据点,较高的值显示为红色,较低的值显示为蓝色。每个标记沿水平轴的位置表示特征值对预测的贡献度大小。从图7可以看出:围岩最大切向应力和抗拉强度与岩爆等级预测呈正相关,表明这2个指标对模型正确输出具有较大的正向影响;弹性能量指数与岩爆等级呈负相关,说明当弹性能量指数值越小的时候,岩爆等级预测正确的可能性越低;抗压强度指标SHAP趋于零,表明其对区分岩爆等级的贡献较小。图8中的每个特征重要性通过平均SHAP值的绝对值确定,围岩最大切向应力是影响岩爆预测等级的最重要因素,其次是抗拉强度、弹性能量指数和抗压强度。以上结果表明:在ISSA-XGBoost岩爆等级预测模型中,本研究所选的4个指标作为模型输入是合理的,其中围岩最大切向应力是最重要的影响因素。
-
(1) 收集了174组岩爆工程实例建立岩爆数据库,采用LOF与自适应过采样方法对原始数据集进行预处理,同时采用XGBoost、RF、MLP机器学习模型对数据处理前后进行对比分析,数据处理后3种模型的准确率分别提升15.52%、14.37%、8.05%。
(2) ISSA能够有效跳出局部最优。通过Sine混沌映射、引入动态自适应权重、结合柯西变异混合策略改进SSA,选取8个基准测试函数,并与4种经典智能优化算法进行仿真实验测试,证实了算法改进的优越性。
(3) 采用ISSA对3种机器学习模型参数进行择优,3种模型的准确率分别提高了3.89%、3.93%和7.12%,通过对比各分类指标,阐明了算法改进与数据预处理结合的重要性,选择ISSA-XGBoost模型为预测岩爆等级最优模型,为岩爆预测提供了一种新思路。
(4) 在特征重要性分析中,基于所构建模型,发现围岩最大切向应力是最重要的影响因素,然而 SHAP值可能会随着模型变化出现差异。随着越来越多的工程数据累积和机器学习理论的日渐成熟,大数据、多指标的岩爆等级预测会得到更广泛的应用。
基于数据预处理和改进麻雀算法的岩爆预测
Rock Burst Prediction Based on Data Preprocessing and Improved Sparrow Algorithm
-
摘要: 为解决机器学习岩爆预测中存在离群样本、样本不均衡、麻雀搜索算法易陷入局部最优等问题,从数据预处理和算法改进2个角度建立岩爆预测模型。首先,基于岩性条件和应力条件,选取围岩最大切向应力、抗压强度、抗拉强度和弹性能量指数作为特征指标,采用3种机器学习算法,结合5折交叉验证方法构建预测模型。在数据预处理阶段,收集了174组国内外岩爆案例建立数据库,针对离群样本,引入局部离群因子(LOF)算法,根据岩爆等级逐级检测并剔除离群样本;针对样本不均衡问题,引入自适应过采样方法(ADASYN)增加少数类样本数目。采用3种混合策略改进麻雀搜索算法,利用改进的麻雀搜索算法(ISSA)对极限梯度提升树(XGBoost)、随机森林(RF)、多层感知机(MLP)3种机器学习算法参数寻优,分析准确率、精确率等多个评价指标,对模型进行有效性验证。结果表明,新构建的最优模型ISSA-XGBoost的准确率达到了94.12%,具有较高的预测准确率。此外,对4种特征指标进行特征重要性分析,确定了围岩最大切向应力是最重要特征。Abstract: To solve the problems of outlier samples, imbalanced samples, and local optimal of sparrow search algorithm in machine learning rockburst prediction, this paper established a rockburst prediction model from two perspectives of data preprocessing and algorithm improvement. First, based on lithology conditions and stress conditions, selected the maximum tangential stress, compressive strength, tensile strength and elastic energy index of surrounding rock as the characteristic indexes, and used three kinds of machine learning algorithms combined with 5-fold cross-validation method to construct the prediction model. In the data pre-processing stage, collected 174 groups of domestic and international rock burst cases to establish a database; for outlier samples, introduced the local outlier factor (LOF) algorithm to detect and eliminate outlier samples step by step according to the rock burst class; for sample imbalance, the adaptive synthetic sampling method (ADASYN) was introduced to increase the number of minority class samples. Three hybrid strategies were employed to improve sparrow search algorithm (ISSA) was used to optimize the parameters of three machine learning algorithms, namely limit gradient lift tree (XGBoost), random forest (RF) and multi-layer perceptron (MLP). Multiple evaluation indexes such as accuracy rate and precision rate were analyzed and discussed to verify the effectiveness of the model. The results show that the accuracy of the newly constructed optimal model, ISA-XGBoost, reaches 94.12%, indicating high prediction accuracy. In addition to the feature importance analysis of the four feature indexes, it was determined that the maximum tangential stress of the surrounding rock is the most important feature.
-
Key words:
- rockburst prediction /
- data preprocessing /
- algorithm improvement /
- feature importance /
- machine learning .
-

-
表 1 岩爆经典案例
Table 1. Classic rock burst cases
Sample σθmax/MPa σc/MPa σt/MPa λwet Rock burst grade 1 18.80 178.00 7.40 5.70 Ⅰ 2 31.05 147.85 3.00 11.96 Ⅲ 3 91.43 157.63 6.27 11.96 Ⅳ 4 61.91 92.40 5.43 8.28 Ⅲ 5 58.20 83.60 5.90 2.60 Ⅳ 6 60.00 136.79 2.12 10.42 Ⅱ 7 44.40 120.00 5.10 5.00 Ⅱ … … … … … … 170 61.46 135.67 9.02 11.20 Ⅳ 172 110.55 106.20 9.59 12.51 Ⅳ 172 41.90 143.01 6.68 4.30 Ⅱ 173 109.40 190.00 6.10 6.90 Ⅲ 174 48.00 59.00 5.23 0.88 Ⅰ 表 2 岩爆分类等级特征描述
Table 2. Characteristics of rock burst grade
Rock burst
gradeFeature description Motion feature Sweep depth/m Acoustic signature Ⅰ No rockburst activities 0 No sound Ⅱ Rock deforms, cracks or spalls, but no ejection
phenomenon occurs<0.5 Weak sound Ⅲ Rock deforms and fractures with a considerable amount
of chip ejecting, loosening and sudden destruction0.5–1.0 Crisp crackling Ⅳ Rock deforms and fractures with a considerable amount
of chip ejecting, loosening and sudden destruction>1.0 Strong bursts and
roaring sounds表 3 岩爆分级标准
Table 3. Rock burst classification criteria
Rock burst grade Rock burst evaluation index σθmax/MPa σc/MPa σt/MPa λwet Ⅰ 0–24 0–80 0–5 0–2.0 Ⅱ 24–60 80–120 5–7 2.0–3.5 Ⅲ 60–126 120–180 7–9 3.5–5.0 Ⅳ 126–200 180–320 9–30 5.0–20.0 表 4 数据集统计参数
Table 4. Statistical parameters of data sets
Rock burst index σθmax/MPa σc/MPa σt/MPa λwet Maximum value 221.00 200.72 22.60 17.13 Minimum value 3.80 15.50 0.70 0.88 Mean value 50.42 113.68 4.94 6.16 Standard deviation 29.42 38.51 2.88 3.57 Sample size 174 174 174 174 表 5 剔除离群样本
Table 5. Removes outlier samples
Sample No. σθmax/MPa (outlier value) Rock burst grade Sample No. σθmax/MPa (outlier value) Rock burst grade 11 108.40 Ⅳ 95 75.60 Ⅲ 25 110.35 Ⅳ 96 59.77 Ⅳ 36 2.60 Ⅰ 122 119.69 Ⅳ … … … 表 6 算法参数
Table 6. Algorithm parameters
PSO GWO GA SSA ISSA c1=c2=2, w=0.9 a $\in $ [0, 2]; r1, r2$\in $ [0, 1]Pc=0.8, Pm=0.05 PD=20%, SD=10%,
S=0.8PD=20%, SD=10%,
S=0.8, wmin=1, wmax=3表 7 测试函数
Table 7. Test functions
Function Type Value range Optimal solution F1 Sphere [–100, 100] 0 F2 Schwefel′2.22 [–10, 10] 0 F3 Schwefel′1.2 [–100, 100] 0 F4 Quartic [–1.28, 1.28] 0 F5 Rastrigrin [–5.12, 5.12] 0 F6 Ackley [–32, 32] 0 F7 Griewing [–600, 600] 0 F8 Foxholes [–65, 65] 1 表 8 ISSA与经典算法实验结果的对比
Table 8. ISSA experimental results compared with classical algorithms
Algorithm Mean value F1 F2 F3 F4 F5 F6 F7 F8 PSO 1.21×103 1.84×1010 5.42×1010 6.20×109 8.18×1010 6.52×1010 1.45×108 2.21×109 GWO 1.23×103 2.19×1011 2.63×1011 1.93×1010 2.88×106 6.40×108 1.31×1010 2.10×108 GA 8.28×103 3.66×1011 3.12×1011 7.00×1011 7.97×108 6.17×107 1.64×1011 3.19×1011 SSA 5.60×10−3 2.50×10−2 1.71×10−2 7.74×10−2 7.02×10−2 5.19×10−2 2.23×10−2 4.15×10−2 ISSA 6.11×10−4 1.39×10−2 1.08×10−2 1.75×10−2 0 7.67×10−3 0 2.87×10−2 Algorithm Standard deviation F1 F2 F3 F4 F5 F6 F7 F8 PSO 7.21×103 4.11×1011 1.21×1012 1.39×1011 1.83×1012 1.46×1012 3.25×109 4.94×1010 GWO 7.71×103 4.88×1012 5.88×1012 3.52×1011 4.54×107 1.20×1010 2.89×1011 4.08×109 GA 1.41×104 5.58×1012 6.80×1012 9.64×1012 1.43×1010 4.46×108 2.14×1012 5.11×1012 SSA 6.32×10−2 3.01×10−1 2.95×10−1 9.80×10−1 8.46×10−1 7.58×10−1 2.15×10−1 5.78×10−1 ISSA 8.20×10−3 1.47×10−1 1.89×10−1 2.75×10−1 0 7.48×10−2 0 4.48×10−1 表 9 数据预处理前后3种机器学习模型准确率
Table 9. Accuracy of three machine learning models before and after data preprocessing
Data class Model accuracy/% MLP RF XGBoost Raw rock burst data set 55.17 60.34 62.07 Preprocessing rock burst data set 63.22 74.71 77.59 表 10 SSA改进前后模型预测结果的对比
Table 10. Comparison of model prediction results before and after SSA improvement
Algorithm Rock burst grade Precision rate Recall rate F1 value Sample size/group SSA-MLP
(Accuracy, 82.36%)Ⅰ 1.00 1.00 1.00 13 Ⅱ 0.75 0.75 0.75 12 Ⅲ 0.80 0.68 0.74 12 Ⅳ 0.75 0.86 0.80 14 SSA-RF
(Accuracy, 84.31%)Ⅰ 1.00 1.00 1.00 13 Ⅱ 1.00 0.83 0.91 12 Ⅲ 0.68 0.68 0.68 12 Ⅳ 0.75 0.86 0.80 14 SSA-XGBoost
(Accuracy, 87.00%)Ⅰ 0.83 0.92 0.87 13 Ⅱ 0.91 0.77 0.83 12 Ⅲ 0.82 0.75 0.78 12 Ⅳ 0.85 0.93 0.89 14 ISSA-MLP
(Accuracy, 86.25%)Ⅰ 1.00 1.00 1.00 13 Ⅱ 0.83 0.83 0.83 12 Ⅲ 0.80 0.68 0.74 12 Ⅳ 0.81 0.93 0.87 14 ISSA-RF
(Accuracy, 88.24%)Ⅰ 1.00 0.92 0.96 13 Ⅱ 0.84 0.83 0.83 12 Ⅲ 0.79 0.91 0.85 12 Ⅳ 0.92 0.86 0.89 14 ISSA-XGBoost
(Accuracy, 94.12%)Ⅰ 1.00 1.00 1.00 13 Ⅱ 1.00 0.83 0.91 12 Ⅲ 0.80 1.00 0.89 12 Ⅳ 1.00 0.93 0.96 14 -
[1] 田睿. 基于机器学习的岩爆烈度等级预测模型研究与应用 [D]. 包头: 内蒙古科技大学, 2020. TIAN R. Research and application of rockburst intensity classification prediction model based on machine learning algorithms [D]. Baotou: Inner Mongolia University of Science and Technology, 2020. [2] 刘剑, 周宗红, 刘军, 等. 基于主成分分析和改进Bayes判别的岩爆等级预测 [J]. 采矿与岩层控制工程学报, 2022, 4(5): 053014. doi: 10.13532/j.jmsce.cn10-1638/td.2022.05.004 LIU J, ZHOU Z H, LIU J, et al. Prediction of rockburst grade based on principal component analysis and improved Bayesian discriminant analysis [J]. Journal of Mining and Strata Control Engineering, 2022, 4(5): 053014. doi: 10.13532/j.jmsce.cn10-1638/td.2022.05.004 [3] 孙飞跃, 刘希亮, 郭佳奇, 等. 岩爆预测评估方法的动力数值分析 [J]. 应用力学学报, 2022, 39(1): 26–34. doi: 10.11776/j.issn.1000-4939.2022.01.004 SUN F Y, LIU X L, GUO J Q, et al. Dynamic numerical calculation analysis of rockburst prediction assessment methods [J]. Chinese Journal of Applied Mechanics, 2022, 39(1): 26–34. doi: 10.11776/j.issn.1000-4939.2022.01.004 [4] 曲宏略, 刘哲言, 杨龙, 等. 基于应力判据的隧道岩爆预测评估研究 [J]. 地下空间与工程学报, 2020, 16(Suppl 2): 934–938,956. QU H L, LIU Z Y, YANG L, et al. Prediction and evaluation of rock burst in tunnel based on stress criterion [J]. Chinese Journal of Underground Space and Engineering, 2020, 16(Suppl 2): 934–938,956. [5] DOU L M, CAI W, CAO A Y, et al. Comprehensive early warning of rock burst utilizing microseismic multi-parameter indices [J]. International Journal of Mining Science and Technology, 2018, 28(5): 767–774. doi: 10.1016/j.ijmst.2018.08.007 [6] CAO A Y, JING G C, DING Y L, et al. Mining-induced static and dynamic loading rate effect on rock damage and acoustic emission characteristic under uniaxial compression [J]. Safety Science, 2019, 116: 86–96. doi: 10.1016/j.ssci.2019.03.003 [7] 温廷新, 陈依琳. 基于海林格距离和AHDPSO-ELM的岩爆烈度等级预测模型 [J]. 中国安全科学学报, 2022, 32(11): 38–46. doi: 10.16265/j.cnki.issn1003-3033.2022.11.1915 WEN T X, CHEN Y L. Prediction model of rockburst intensity grade based on Hellinger distance and AHDPSO-ELM [J]. China Safety Science Journal, 2022, 32(11): 38–46. doi: 10.16265/j.cnki.issn1003-3033.2022.11.1915 [8] 李明亮, 李克钢, 秦庆词, 等. 岩爆烈度等级预测的机器学习算法模型探讨及选择 [J]. 岩石力学与工程学报, 2021, 40(Suppl 1): 2806−2816. LI M L, LI K G, QIN Q C, et al. Discussion and selection of machine learning algorithm model for rockburst intensity grade prediction [J]. Chinese Journal of Rock Mechanics and Engineering, 201, 40(Suppl 1): 2806−2816. [9] 侯克鹏, 包广拓, 孙华芬. 改进的MVO-GRNN神经网络岩爆预测模型研究 [J]. 安全与环境学报, 2024, 24(3): 923–932. doi: 10.13637/j.issn.1009-6094.2023.0341 HOU K P, BAO G T, SUN H F. Research on improved MVO-GRNN neural network rockburst prediction model [J]. Journal of Safety and Environment, 2024, 24(3): 923–932. doi: 10.13637/j.issn.1009-6094.2023.0341 [10] 满轲, 武立文, 刘晓丽, 等. 基于灰色关联分析和SSA-RF模型的岩爆等级预测 [J]. 金属矿山, 2023(5): 202–212. doi: 10.19614/j.cnki.jsks.202305021 MAN K, WU L W, LIU X L, et al. Rockburst grade prediction based on grey correlation analysis and SSA-RF model [J]. Metal Mine, 2023(5): 202–212. doi: 10.19614/j.cnki.jsks.202305021 [11] 高梅, 张成良, 张华超, 等. 基于SMOTEENN-CGAN-Stacking的岩爆烈度等级预测研究 [J]. 工程地质学报, 2024, 32(6): 2264–2276. doi: 10.13544/j.cnki.jeg.2024-0112 GAO M, ZHANG C L, ZHANG H C, et al. Rockburst intensity level prediction based on SMOTEENN-CGAN-Stakcing [J]. Journal of Engineering Geology, 2024, 32(6): 2264–2276. doi: 10.13544/j.cnki.jeg.2024-0112 [12] 苏焕博. 数据缺失和不均衡下的IDPSO-ELM岩爆烈度等级预测模型研究 [D]. 阜新: 辽宁工程技术大学, 2022. SU H B. Research on IDPSO-ELM rockburst intensity grade prediction model with missing and unbalanced data [D]. Fuxin: Liaoning Technical University, 2022. [13] ZHOU J, LI X, MITRI H S. Classification of rockburst in underground projects: comparison of ten supervised learning methods [J]. Journal of Computing in Civil Engineering, 2016, 30(5): 04016003. doi: 10.1061/(ASCE)CP.1943-5487.0000553 [14] 武立文. 基于SSA-RF模型的岩爆预测方法及应用研究 [D]. 北京: 北方工业大学, 2024. WU L W. Research on rockburst prediction method and application based on SSA-RF model [D]. Beijing: North China University of Technology, 2024. [15] 刘晓悦, 杨伟, 张雪梅. 基于改进层次法与CRITIC法的多维云模型岩爆预测 [J]. 湖南大学学报(自然科学版), 2021, 48(2): 118–124. doi: 10.16339/j.cnki.hdxbzkb.2021.02.015 LIU X Y, YANG W, ZHANG X M. Rockburst prediction of multi-dimensional cloud model based on improved hierarchical analytic method and critic method [J]. Journal of Hunan University (Natural Sciences), 2021, 48(2): 118–124. doi: 10.16339/j.cnki.hdxbzkb.2021.02.015 [16] 谭文侃, 叶义成, 胡南燕, 等. LOF与改进SMOTE算法组合的强烈岩爆预测 [J]. 岩石力学与工程学报, 2021, 40(6): 1186–1194. doi: 10.13722/j.cnki.jrme.2020.1035 TAN W K, YE Y C, HU N Y, et al. Severe rock burst prediction based on the combination of LOF and improved SMOTE algorithm [J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(6): 1186–1194. doi: 10.13722/j.cnki.jrme.2020.1035 [17] 王宇航, 周宗红, 李国才, 等. 基于数据预处理的岩爆等级预测模型及精度优化 [J]. 矿业研究与开发, 2024, 44(11): 101–109. doi: 10.13827/j.cnki.kyyk.2024.11.009 WANG Y H, ZHOU Z H, LI G C, et al. Prediction model and accuracy optimization of rockburst grade based on data preprocessing [J]. Mining Research and Development, 2024, 44(11): 101–109. doi: 10.13827/j.cnki.kyyk.2024.11.009 [18] 翁嘉诚, 周晓杰, 叶蓓蕾, 等. 基于改进麻雀搜索算法的K-means聚类 [J]. 数学的实践与认识, 2024, 54(2): 152–166. WENG J C, ZHOU X J, YE B L, et al. K-means clustering based on improved sparrow search [J]. Mathematics in Practice and Theory, 2024, 54(2): 152–166. [19] 杜云, 周志奇, 贾科进, 等. 混合多项自适应权重的混沌麻雀搜索算法 [J]. 计算机工程与应用, 2024, 60(7): 70–83. doi: 10.3778/j.issn.1002-8331.2307-0254 DU Y, ZHOU Z Q, JIA K J, et al. Chaotic sparrow search algorithm with mixed multinomial adaptive weights [J]. Computer Engineering and Applications, 2024, 60(7): 70–83. doi: 10.3778/j.issn.1002-8331.2307-0254 [20] 毛清华, 张强. 融合柯西变异和反向学习的改进麻雀算法 [J]. 计算机科学与探索, 2021, 15(6): 1155–1164. doi: 10.3778/j.issn.1673-9418.2010032 MAO Q H, ZHANG Q. Improved sparrow algorithm combining cauchy mutation and opposition-based learning [J]. Journal of Frontiers of Computer Science and Technology, 2021, 15(6): 1155–1164. doi: 10.3778/j.issn.1673-9418.2010032 [21] 张建涛, 刘志祥, 张双侠, 等. 基于WOA-RF的边坡稳定性预测模型 [J]. 高压物理学报, 2024, 38(3): 035301. doi: 10.11858/gywlxb.20230837 ZHANG J T, LIU Z X, ZHANG S X, et al. Slope stability prediction based on WOA-RF hybrid model [J]. Chinese Journal of High Pressure Physics, 2024, 38(3): 035301. doi: 10.11858/gywlxb.20230837 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: