采用真空感应磁悬浮熔炼炉制备具有强韧性的CrCoNiSi_0.3中熵合金。原材料的纯度为99.9%，在真空度为1×10⁻³ Pa的环境下熔炼，铸成直径为80 mm、高度为100 mm的铸锭。检测结果显示，铸锭的实际化学成分（质量分数）为Co（33.10%）、Cr（28.73%）、Ni（33.74%）、Si（4.44%）^[15]。采用电火花切割方法切割铸锭，得到厚度为8 mm的圆片合金板，于1200 ℃均匀化热处理5 h，室温轧制至厚度减少62.5%，然后在1100 ℃的温度下退火热处理1 h，使合金再结晶。所有热处理均在氩气气氛中进行，每次热处理结束后进行水淬处理。

室温准静态压缩实验在Instron万能试验机上进行，应变率范围为10⁻⁴～10⁻² s⁻¹。高温准静态压缩实验在力试科仪LE5105万能试验机上进行，先将样品随炉升温，达到指定温度后保温10 min，然后开始压缩，测试完成后随炉冷却至约500 ℃，开炉取出试样，空气冷却，压缩应变率为10⁻³ s⁻¹，当应变达到50%时终止压缩。采用块状压缩试样，理论尺寸为3 mm×4 mm×5 mm，其示意图和实物如图1(a)所示。

室温动态压缩实验在SHPB上开展^[16]，动态压缩试样与准静态压缩试样一致。实验前，采用2000目砂纸对试样表面进行磨抛处理，遴选表面无孔洞和裂纹的试样。每次实验至少重复3次。实验中，首先测量试样的应力-应变曲线，根据极限屈服应变计算各应变率下的极限压缩应变，然后使用合适高度的止动环限制压缩，保证压缩应变小于极限压缩应变。例如：通过样品1得到某应变率下的应力-应变曲线，获得极限屈服应变ε_y，然后测量样品2的高度h，通过ε_yh求得此应变率下样品2的极限压缩应变，则所用止动环的高度为$ h-{\varepsilon }_{\mathrm{y}}h $。止动环由高强马氏体钢制成，其示意图和实物如图1(b)所示。将样品放入止动环中进行压缩实验，当样品压缩变形后的高度达到止动环高度时，停止加载，由此获得经过一次应力波加载的压缩变形样品，用于试样变形后的微观表征。在1776、4039和5196 s⁻¹应变率下分别获得应变为17.3%、38.1%和49.0%的变形试样，由此开展不同应变率加载下的变形机理研究。

采用Empyrean型X射线衍射仪测量铸锭的相组成，利用JEOL JSM-7100 F型场发射扫描电子显微镜（field emission scanning electron microscope，FESEM）、电子背散射衍射（electron backscatter diffraction，EBSD）、JEM-2100 F型透射电子显微镜（transmission electron microscope，TEM）对试样的微观结构进行表征。TEM和SEM观测前，首先通过机械法和金相法抛光试样，然后在20 ℃、15 V的温度和电压下使用抛光液（高氯酸与无水乙醇的体积比为1∶9）进行电解抛光，其中，压缩试样的TEM离子减薄样品取自试样中心。

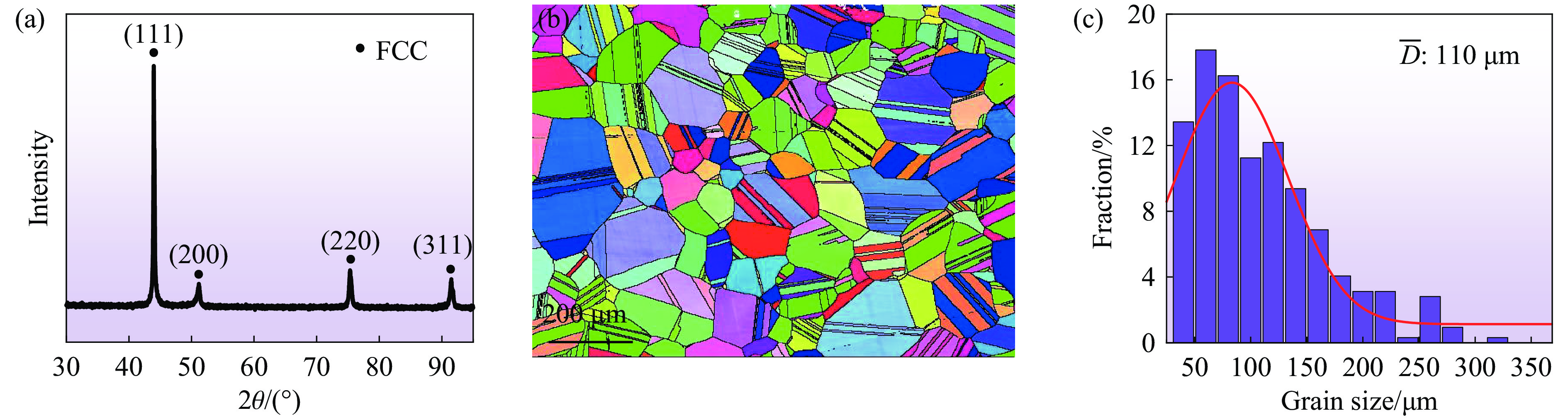
为了分析合金的初始组织，对其进行了X射线衍射（X-ray diffraction，XRD）和EBSD微观表征和统计。退火处理后CrCoNiSi_0.3中熵合金的XRD谱如图2(a)所示，根据衍射峰，确定试样为单相FCC结构。CrCoNiSi_0.3中熵合金的EBSD反极图如图2(b)所示，可以发现，CrCoNiSi_0.3中熵合金具有随机取向晶粒和丰富的退火孪晶。因此，试样的初始组织为完全再结晶的单相FCC结构。对其晶粒尺寸进行统计，结果如图2(c)所示，包含孪晶界在内的平均晶粒尺寸$\overline D $约为110 μm。

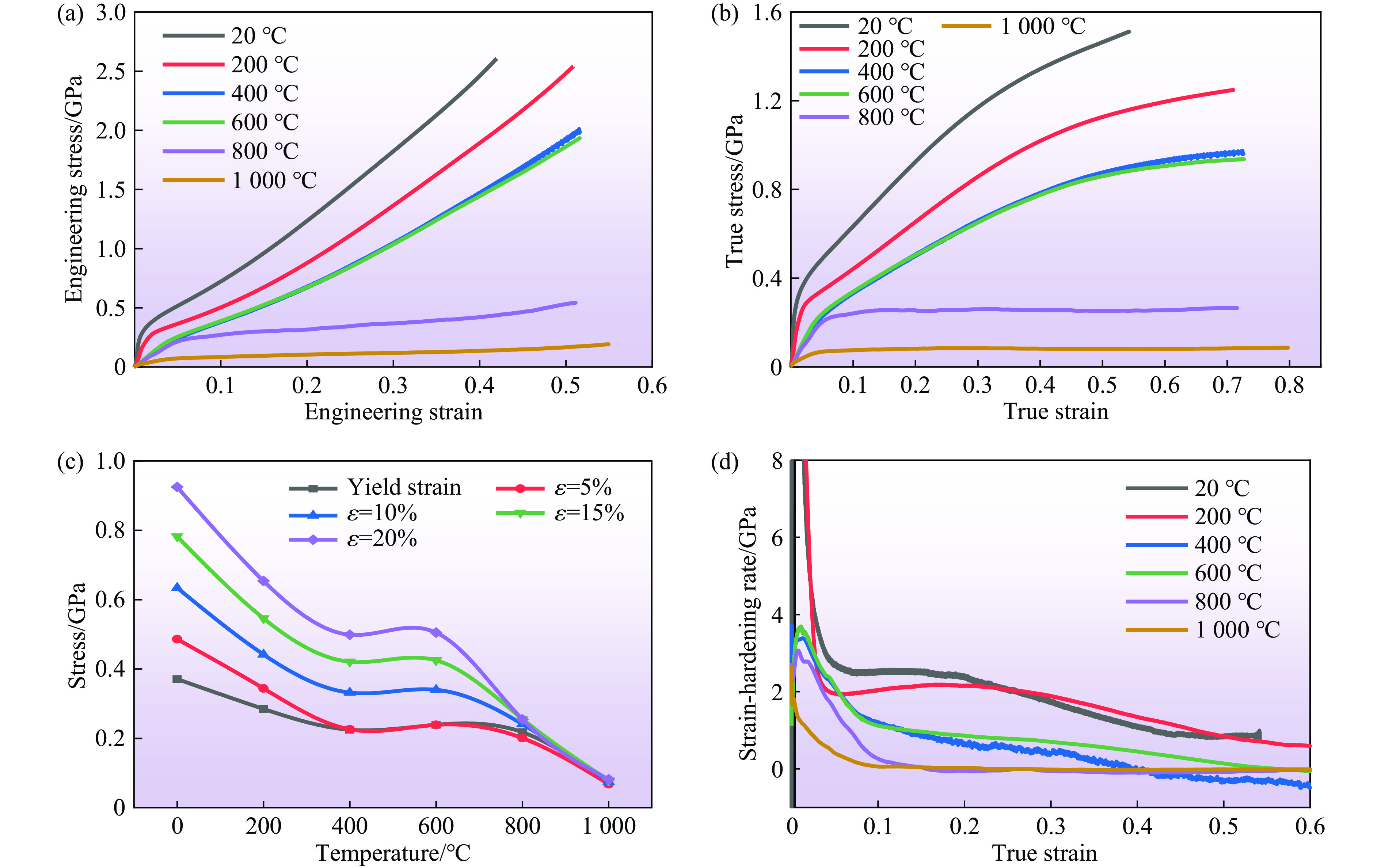
图3(a)和图3(b)分别为准静态压缩（应变率$ \dot{\varepsilon } $为10⁻⁴、10⁻³、10⁻² s⁻¹）和动态压缩（应变率为1776、3231、4039、5196 s⁻¹）下试样的工程应力-工程应变曲线。当应变率为5196 s⁻¹时，CrCoNiSi_0.3中熵合金发生失效；在其他应变率条件下，工程应力-工程应变曲线末端出现的应力下降均归因于应力波卸载。

不同应变率下CrCoNiSi_0.3中熵合金的压缩真实应力-真实应变（$ \sigma $-$ \varepsilon $）曲线如图3(c)所示。根据曲线的变化趋势，可将CrCoNiSi_0.3中熵合金的动态力学行为分为3个阶段：首先，合金经历弹性变形阶段（OA段），当真实应变低于0.02时，应力呈线性增长，直至达到屈服强度；而后，由于应变硬化效应与热软化效应的相互竞争，且应变硬化效应更强，应力随位移增加而缓慢增加，属于应变硬化阶段（AB段）；最后，随着应力波的卸载或者材料失效，应力迅速下降，即BC段。随着动态应变率升高，CrCoNiSi_0.3中熵合金的屈服强度增大，呈现应变率强化效应。不同应变率下合金的屈服强度统计如图3(d)所示：准静态压缩下合金的屈服强度随应变率的变化较小，维持在350 MPa；在应变率为1776、3231、4039、5196 s⁻¹的动态压缩下，合金的屈服强度分别增至409、517、525、682 MPa。应变率达到5196 s⁻¹时，试样出现明显裂纹，表明试样发生破坏。

准静态和动态载荷下CrCoNiSi_0.3中熵合金的应力-应变率双对数曲线如图3(e)所示，其中，直线斜率表示不同应变率对应的应变率敏感系数（$ m=\partial \mathrm{ln}\,\sigma /\partial \mathrm{ln}\,\dot{\varepsilon } $），屈服强度在准静态和动态载荷下的平均应变率敏感系数分别为0.0109和0.5944，说明该合金在高应变率下具有更强的应变率敏感性，合金的变形行为与加载应变率存在强相关性。此外，随着应变率的升高，在5196 s⁻¹应变率下，CrCoNiSi_0.3中熵合金表现出明显的应变硬化率降低现象。

对CrCoNiSi_0.3中熵合金在不同应变率下的应变硬化行为进行分析，探究其塑性变形行为。图3(f)呈现了CrCoNiSi_0.3中熵合金在不同应变率下的应变硬化曲线，可见，合金的硬化行为受加载应变率的影响。应变硬化曲线主要分为3个阶段：在第1阶段，曲线急剧下降，直至2～3 GPa停止下降，试样的变形机制为位错滑移主导的塑性变形；在第2阶段，应变硬化率曲线在准静态加载曲线附近波动，整体变化趋势与准静态加载曲线一致，即随真实应变的增加而减小，试样变形机制转变为孪晶主导的塑性变形^[17]；第3阶段中，应变硬化率降至零。图3(f)中的插图呈现了不同加载应变率下试样的平均应变硬化率，可以看出，平均应变硬化率随着应变率的升高先小幅增大而后减小。CrCoNi中熵合金在10⁻³、2000、3000、4000、5000 s⁻¹应变率下的平均应变硬化率分别约为2.30、2.35、2.40、2.55、1.50 GPa^[18]，CrCoNiSi_0.3中熵合金在不同应变率下的平均应变硬化率的整体变化趋势与CrCoNi中熵合金一致，但变化幅度更小，表明Si的加入减弱了应变率对中熵合金应变硬化率的影响。动态加载时，应变硬化率曲线出现多个明显波动，其原因是：宏观上看，高速加载时，应力波传播波系复杂，样品所受的应力和应变率随时间的变化也非常复杂，导致应变硬化率曲线出现波动^[19–20]。

对CrCoNiSi_0.3中熵合金在20～1000 ℃温度范围内进行准静态（10⁻³ s⁻¹）压缩实验，得到的工程应力-工程应变曲线和真实应力-真实应变曲线如图4(a)和图4(b)所示。可以看出，温度的升高使合金屈服，流动应力下降，塑性变形阶段的应变硬化率减小，与多数材料的热变形变化趋势^{[7–8, 12]}一致。800 ℃时，合金的应变硬化率趋于零，说明此时合金的应变硬化能力与热软化能力接近。在室温至600 ℃条件下，CrCoNiSi_0.3中熵合金表现出明显的应变硬化，在800～1000 ℃条件下则表现为理想的弹塑性变形模式，温度达到1000 ℃时合金仍未出现明显的软化现象，该性能优于大部分传统合金和中/高熵合金^[21–23]。值得注意的是，400 ℃下CrCoNiSi_0.3中熵合金在压缩过程中出现了锯齿流变现象。由于锯齿流变会降低材料的塑性，破坏局部塑性变形的稳定性，使得塑性变形进入不均匀模式^[24]，因此，材料失效可能首先发生在这些局部不稳定区域，导致合金塑性降低，这可能是导致400 ℃时材料的力学性能与600 ℃时相似的原因。

为了研究合金强度随温度的变化规律，对应变为5%、10%、15%、20%以及屈服应变下的应力随温度的变化进行分析。图4(c)显示了压缩屈服应力随温度的变化。当温度从室温升高至200、400、600、800、1000 ℃时，CrCoNiSi_0.3中熵合金的屈服强度也由345 MPa分别降至285、225、239、218和70 MPa。准静态加载下，合金的流动应力随温度的升高整体呈下降趋势；但是，在某一温度区域内，流动应力随温度的升高几乎没有下降，甚至出现反常增大。这一现象使得金属的流动应力-温度曲线出现反常峰，该现象被称为“第三型应变时效”（the third-type strain aging，3rd SA），通常由运动位错与扩散的溶质原子相互作用引起^[25]。已有研究证明，Si因原子半径较小，主要以间隙原子的形式存在于固溶体中，适当添加Si对于改善合金的显微组织和力学性能有建设性作用^[9–10]。因此推测，加入Si元素后，扩散的Si溶质原子运动并与位错发生相互作用，导致“第三型应变时效”发生。

图4(d)为CrCoNiSi_0.3中熵合金在不同温度下的应变硬化率-真实应变曲线。可以发现：温度的升高使得材料的应变硬化能力不断减弱；温度低于600 ℃时，应变硬化能力随着真实应变的增加不断变小；当温度达到800 ℃及以上时，应变硬化率曲线呈平直状态，即表现为理想塑性流动模式。

首先，对准静态压缩变形机理进行研究。图5为室温准静态压缩（10⁻³ s⁻¹）下应变达到45.8%时试样的TEM图像。从图5(a)可以观察到大量的层错（stacking faults，SFs）、孪晶（twin），以及交叉孪晶（multiplc twining）。图5(b)所示的衍射图样和图5(c)所示的高分辨图像进一步证明了其存在。图5(d)为图5(c)矩形区域的放大图。从图5(b)和图5(d)可以观察到密排六方（hexagonal close packed，HCP）组织，表明试样发生了FCC到HCP的相变。此外，从图5(d)还可以看到交叉层错形成的Lomer-Cottrells（LCs）位错锁。这些机制的综合作用促使合金形成较强的加工硬化能力。从图5(e)观察到严重变形的组织，形成剪切带（shear band，SB）。图5(f)中未完全成形的纳米环表明，剪切带内部为纳米晶雏形。

为了研究不同应变率下的压缩变形机理，对动态加载下（1776、4039和5196 s⁻¹）变形后的试样进行SEM表征，分析其微结构变形机制和剪切带的形成。图6(a)和图6(b)分别给出了应变率为1776 s⁻¹、应变为17.3%以及应变率为4039 s⁻¹、应变为38.1%的2个试样的SEM-BSD图像。观察图6(a)发现，1776 s⁻¹应变率下CrCoNiSi_0.3中熵合金的晶粒变形较小，晶粒内部存在交错的滑移（cross-slip）。从图6(b)观察到，4039 s⁻¹应变率下材料晶粒变形明显，存在弯曲交叉的变形孪晶（bending deformation twin）。图6(c)为应变率为5196 s⁻¹、应变为49.0%的试样的SEM-BSD图像，可以观察到清晰的宽度约为6.5 μm的绝热剪切带（adiabatic shear band，ASB），且在绝热剪切带中形成了微裂纹（crack）。绝热剪切带是指在高速变形、冲击载荷或其他高应变率加载条件下，材料局部区域因塑性变形功转化为热能且热量来不及散失，导致该区域温度急剧升高，进而发生剧烈的局部剪切变形，形成的一条窄带状变形区域^[26]。图6(d)为图6(c)中剪切带方框区域的放大图。绝热剪切带的内部发生明显的晶粒细化，两侧为严重变形的细长晶粒，绝热剪切带中心到两侧形成梯度纳米晶（gradient nanocrystals），裂纹处于梯度纳米晶的中间。微观上看，高应变率加载下，位错运动更加剧烈，位错密度不断变化，其增殖、运动和交互作用更加复杂。位错之间的相互交割、缠结等会使位错运动阻力不断变化，导致材料的应变硬化率发生波动。同时，即使没有形成明显的绝热剪切带，高速变形过程中产生的热量也会使材料温度升高，而温度变化会影响材料的力学性能，如使材料的屈服强度降低、应变硬化能力改变等。试件不同部位的温度升高情况可能不同，这是导致动态加载下应变硬化率曲线出现波动的另一原因^{[10, 27]}。

选择5196 s⁻¹应变率下动态压缩变形后的试样进行TEM精细表征。图7(a)和图7(b)显示了5196 s⁻¹应变率下压缩变形后试样的TEM图像，可以观察到宽约300 nm的剪切带，其内部存在明显的晶粒细化；图7(c)为选区电子衍射图像；图7(d)、图7(e)和图7(f)分别为图7(a)中剪切带附近高应变区的高分辨图像和衍射图，可观察到高密度层错，交叉层错形成位错锁，且存在孪晶和纳米尺度的HCP结构。SEM和TEM测得的绝热剪切带的宽度不同，说明动态加载下样品变形后不仅存在较微观（6.5 μm）的剪切带，也存在纳微观（300 nm）的剪切带。

图8(a)为600 ℃准静态压缩后试样的TEM图像。从图8(a)～图8(d)可以发现，试样在高温变形后仍然存在较多的多级纳米孪晶和丰富的层错网，以及局部变形导致的纳米晶区（见图8(d)），但整体层错密度较室温准静态条件下低。从图8(c)可以观察到层错网和位错锁，位错锁在加固和增韧方面的有效性取决于它们积累脱位的能力^[28]。CrCoNiSi_0.3中熵合金在600 ℃下仍存在高密度层错和位错锁，该现象在其他合金中很少见，可能是导致其力学性能与400 ℃时相似的另一个原因。从图8(d)可以发现，材料中存在宽度约为500 nm的剪切变形区，并且剪切变形区宽度较室温准静态下大，所形成的纳米环也更加完整。这是由于动态再结晶的发生需要克服一定的能量障碍，高温下原子的活动能力增强，使得位错更容易通过攀移、滑移等方式运动和重新排列；高温下，晶界的迁移能力增强，晶界处的原子扩散速度加快，更容易发生晶界的弓出、迁移等现象，从而促进了动态再结晶的发生^[29–30]。图8(e)～图8(h)为1000 ℃高温准静态压缩实验后试样的TEM图像。在1000 ℃高温下，试样出现较大的再结晶晶粒，晶粒尺寸约为4 μm，但仍比原始晶粒小。晶粒内部含有密度较小的位错、少量的层错和σ析出相（见图8(f)和图8(g)），σ析出相表现为Cr、Si元素的富集（见图8(f)）。

选择合适的本构模型描述材料的力学性能是工程应用不可或缺的一步。Johnson-Cook（J-C）模型是一种经验型黏塑性本构模型，能较好地描述金属材料的应变硬化效应、应变率强化效应和温度软化效应。J-C模型的形式简单，使用方便，在工程中得到了广泛应用。本研究采用J-C模型描述CrCoNiSi_0.3中熵合金在一维应力状态下的本构关系。

J-C本构模型将流动应力$ \overline{\sigma } $表示为应变硬化$ {f}_{1}\left(\varepsilon \right) $、应变率强化$ {f}_{2}\left(\dot{\varepsilon }\right) $和热软化$ {f}_{3}\left(T\right) $ 3个函数的乘积，即$ \overline{\sigma }={f}_{1}\left(\varepsilon \right){f}_{2}\left(\dot{\varepsilon }\right){f}_{3}\left(T\right) $，具体形式为^[31]

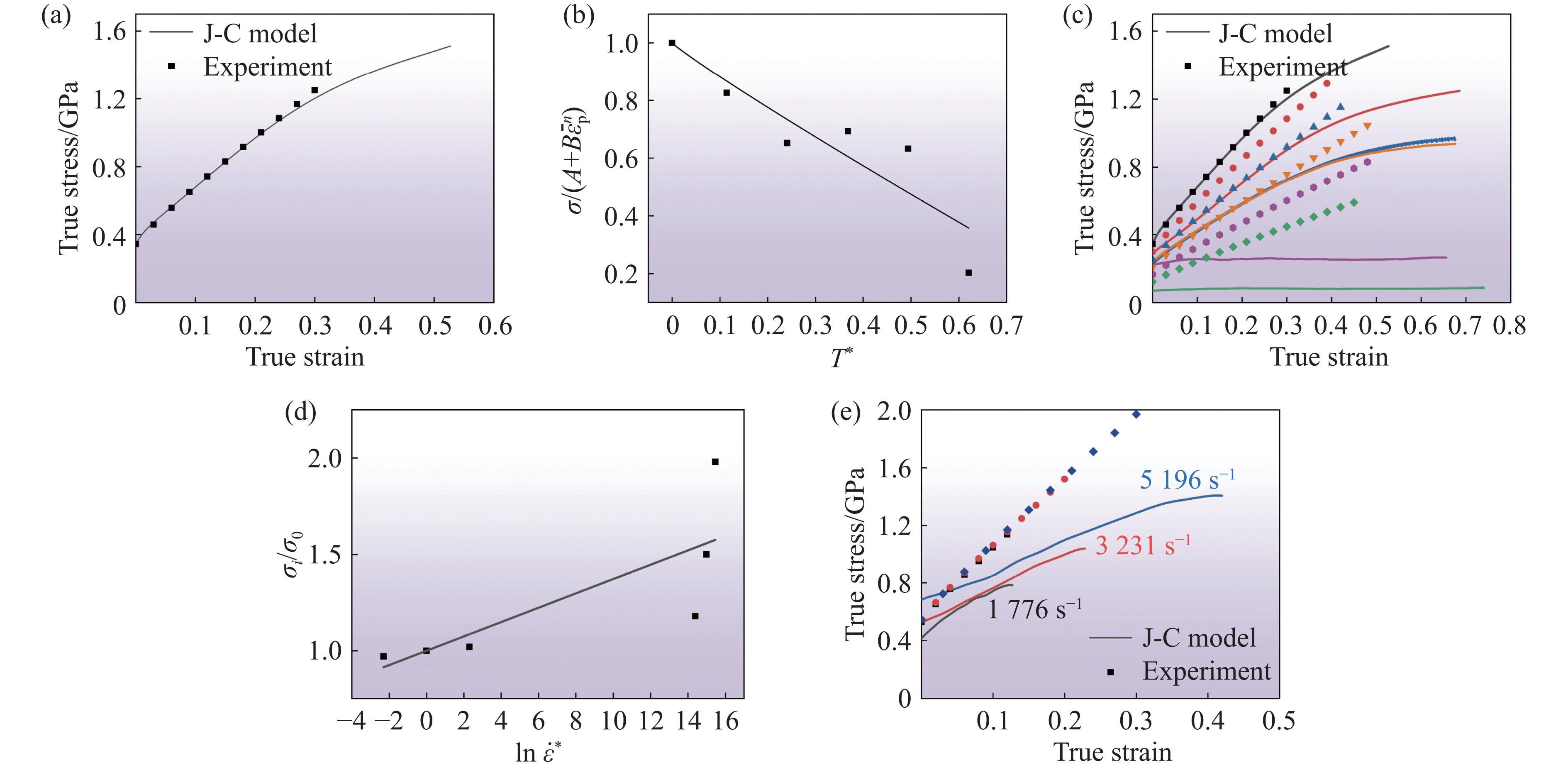
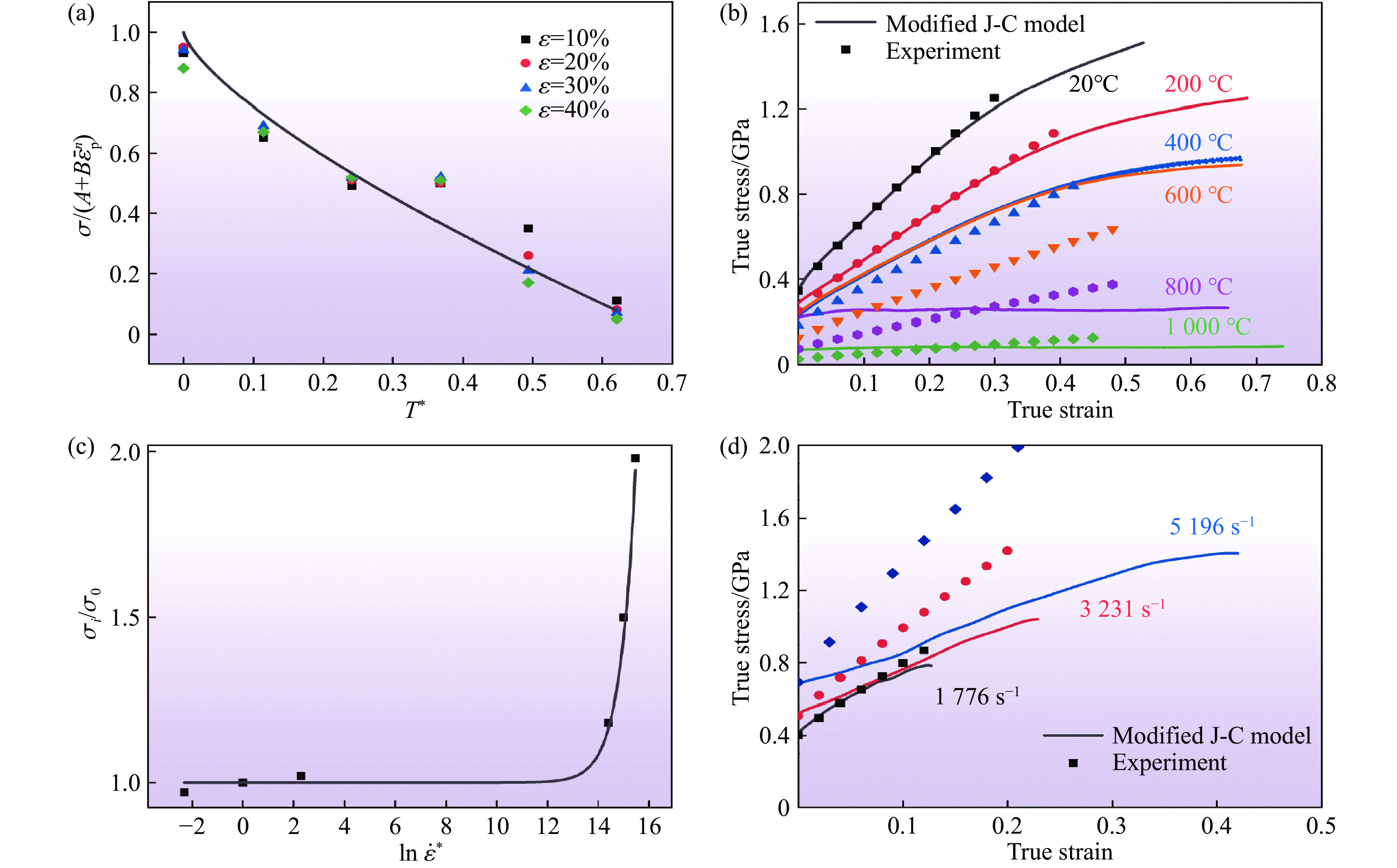
式中：$ {\overline{\varepsilon }}_{\mathrm{p}}^{} $为等效塑性应变；A为参考应变率和参考温度下的初始屈服应力；B和n分别为材料应变硬化模量和硬化指数；C为材料的应变率强化参数；m为材料的热软化指数；$ {\dot{\varepsilon }}^{*}=\dot{\varepsilon }/{\dot{\varepsilon }_{0}} $为无量纲塑性应变率，$ {\dot{\varepsilon }_{0}} $为参考应变率；$ {T}^{*}=(T-{T}_{\mathrm{r}})/({T}_{\mathrm{m}}-{T}_{\mathrm{r}}) $为同系温度，$ {T}_{\mathrm{r}} $为参考温度，$ {T}_{\mathrm{m}} $为熔化温度。对室温准静态（10⁻³ s⁻¹）加载下试样的实验数据进行拟合，得到参数A=345 MPa、B=2675 MPa、n=0.9，如图9(a)所示。

根据Hume-Rothery规则，计算CrCoNiSi_0.3中熵合金的理论熔点：$ {T}_{\mathrm{m}}=\sum\limits _{i}{w}_{i}{T}_{{\rm m}i} $=1 598 ℃，其中，$ {w}_{i} $为第i个元素的质量分数，$ {T}_{{\rm m}i} $为第i个元素的熔点。取同一应变率下合金的高温屈服强度$ {\sigma }_{\rm Y}\left({T}^{*}\right) $与参考温度下屈服强度$ {\sigma }_{\rm Y}\left({T}_{\mathrm{r}}\right) $之比

得到不同$ {T}^{*} $的$ {f}_{3}\left({T}^{*}\right) $。根据不同温度下的准静态压缩实验（10⁻³ s⁻¹），得到$ {f}_{3}\left({T}^{*}\right) $，结果如图9(b)所示。采用$ {f}_{3}\left({T}^{*}\right)=1-{{T}^{*}}^{m} $进行拟合，得到m=0.9294。高温准静态真实应力-真实应变实验结果与拟合曲线如图9(c)所示。

室温下J-C本构方程可以简化为$ {\sigma }_{i}={\sigma }_{0}\left(1+C\mathrm{ln}\dfrac{\dot{\varepsilon }}{{\dot{\varepsilon }_{0}}}\right) $，其中，$ {\sigma }_{i} $为不同应变率下的屈服应力，$ {\sigma }_{0} $为准静态加载时的屈服应力，$ {\dot{\varepsilon }_{0}} $=10⁻³ s⁻¹。通过动态压缩实验获得$ {\sigma }_{i}/{\sigma }_{0} $-$ \mathrm{ln}\,{\dot{\varepsilon }}^{*} $拟合曲线，如图9(d)所示，由此得到$ C= $0.03721。此时，所得到的J-C本构方程为

观察图9可以发现，无论是温度还是应变率，传统的J-C本构模型都不能很好地描述CrCoNiSi_0.3 中熵合金。其中，温度项的拟合差距主要是由于600和800 ℃的2个屈服应力反常点严重影响了曲线拟合；在应变率项中，室温下传统J-C本构方程的$ {\sigma }_{i} $与$ \mathrm{ln}({\dot{\varepsilon }}/{{\dot {\varepsilon }_{0}}}) $为线性关系，但对于CrCoNiSi_0.3中熵合金，$ {\sigma }_{i}/{\sigma }_{0} $与$ \mathrm{ln}\,{\dot{\varepsilon }}^{*} $的线性拟合效果不佳，曲线呈指数增长。

为了获得更好的预测效果，对J-C本构模型进行了修正。针对温度项，用不同真实应变下的真实应力进行参数拟合。引入参数t，采用函数$ {f}_{3}\left({T}^{*}\right)=1-t{{T}^{*}}^{m} $，拟合得到m=0.72，t=1.3，拟合曲线如图10(a)所示。图10(b)给出了实验与拟合得到的高温准静态真实应力-真实应变曲线，可以发现，除了600 和800 ℃，拟合曲线与实验曲线符合良好。600 ℃时，变形后样品内部存在大量的多级纳米孪晶、丰富的层错网及位错锁结构，大幅提高了材料在此温度下的力学性能，推测800 ℃时也如此。

CrCoNiSi_0.3中熵合金中$ {\sigma }_{i}/{\sigma }_{0} $随$ \mathrm{ln}\,{\dot{\varepsilon }}^{*} $呈指数形式增长，因此，忽略温度项，得到应变率强化公式^[32–33]

$ {\sigma }_{i}/{\sigma }_{0} $-$ \mathrm{ln}\,{\dot{\varepsilon }}^{*} $的实验和拟合结果如图10(c)所示，拟合得到$ C=1+8.24\times {10}^{-12} $，$ l=1.65 $。此时，J-C本构方程为

室温动态加载下实验与拟合的真实应力-真实应变曲线如图10(d)所示。对比发现，拟合曲线与实验曲线相差较大，误差主要发生在加工硬化阶段。其主要原因是实验曲线塑性段的应变硬化随应变率的升高而降低。

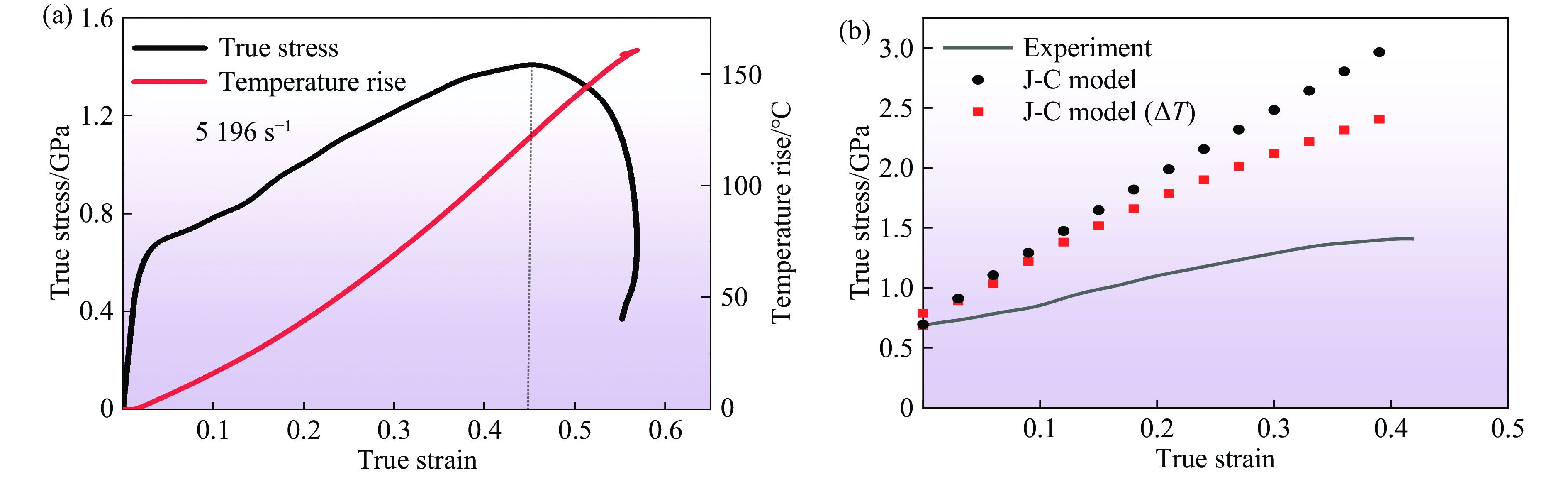
分析认为，初始J-C本构模型的预测误差较大，且误差随着应变率的增加而变大，其原因在于加工硬化项B与应变率存在相关性。考虑动态加载过程中温度变化的影响，以5196 s⁻¹为例，通过公式$ \Delta T=\dfrac{\beta }{\rho {c}_{p}}\displaystyle \int \tau \mathrm{d}{{ Y}}_{\mathrm{p}} $计算绝热温升（$ \Delta T $为绝热温升；c_p为比定压热容；$ \rho $为密度；β为塑性功转化为热的泰勒-昆纳系数，对于绝热剪切，β=0.9；$ {{Y}}_{\mathrm{p}} $为塑性剪切应变；$ \tau $为剪切应力），结果如图11(a)所示。将引入温度因素的J-C数据与未引入温度因素的J-C数据及实验数据进行对比，结果如图11(b)所示，可以发现，温度并非动态加载下应变硬化率下降的主要原因。

应变率对应变硬化率的影响在于其塑性变形机制。应变率较低时，位错有足够的时间运动和增殖，通过位错滑移等方式使材料发生塑性变形，位错之间的交互作用相对稳定，应变硬化效果明显。当应变率升高时，位错运动速度加快，位错的增殖和湮灭过程变得复杂，位错之间的交互作用也更加剧烈，导致大量交滑移和孪晶组织产生，致使位错运动阻力增大，位错难以持续有效地增加材料的塑性变形，表现为应变硬化率下降。应变率为5196 s⁻¹时动态再结晶机制导致应变硬化降低^[34]。

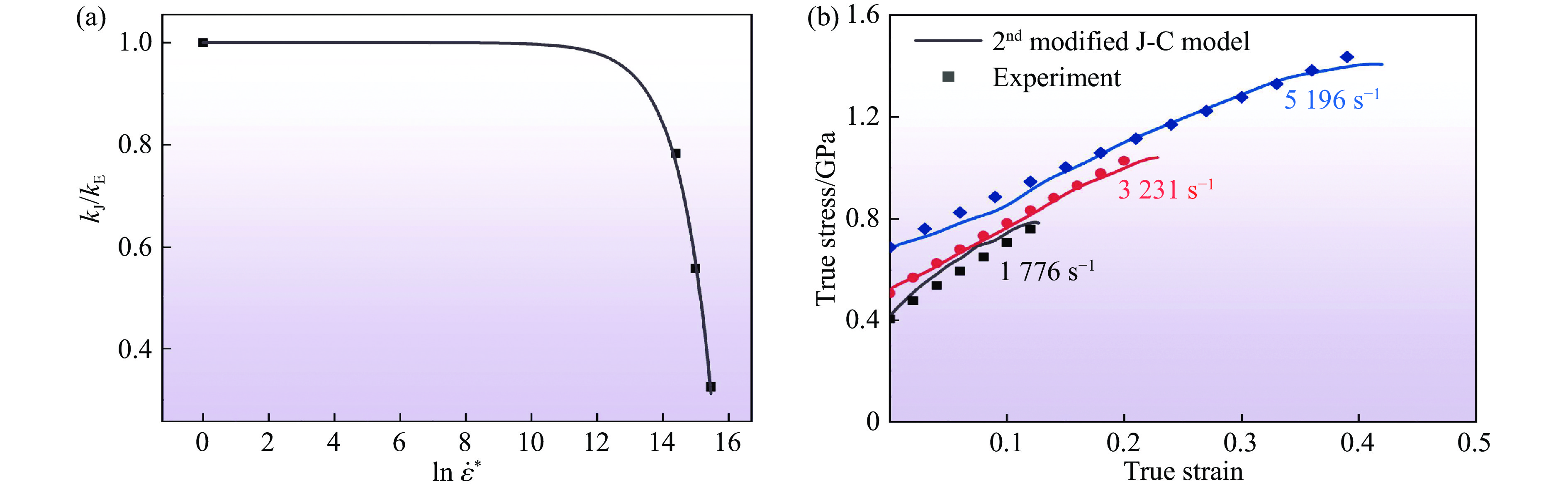
因此，对J-C方程进行第2次修正，将应变硬化常数$ B $改为关于应变率$ \mathrm{ln}\,{\dot{\varepsilon }}^{*} $的函数，参考应变率下的$ B $命名为$ {B}_{0} $，得到不同应变率与参考应变率下真实应力-真实应变曲线屈服段斜率之比$ {k}_{\mathrm{J}}/{k}_{\mathrm{E}} $，拟合曲线如图12(a)所示。其表达式为

最终得到修正的J-C本构方程

式中：$ B=2\,675(1-1.22\times {10}^{-7}{{\dot{\varepsilon }}}^{*1.005}) $，单位MPa。

室温动态加载下试样的真实应力-真实应变曲线的实验结果和修正J-C模型拟合曲线如图12(b) 所示。

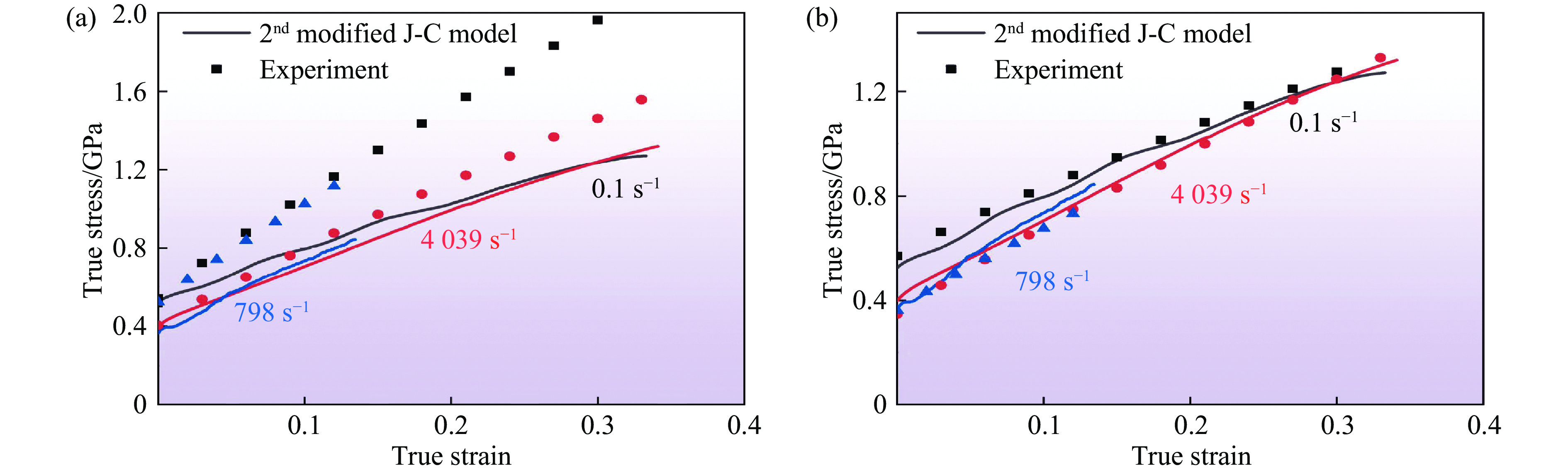
分别采用修正前和修正后的J-C本构方程进行拟合，得到其他应变率下的真实应力-应变曲线，如图13(a)和图13(b)所示。对比发现，修正后的J-C本构方程的拟合效果良好。

采用Instron万能试验机和SHPB对CrCoNiSi_0.3中熵合金在室温、不同应变率（1776～5196 s⁻¹）加载下的力学行为进行了研究，采用LE5105试验机对CrCoNiSi_0.3中熵合金在高温（200～1000 ℃）准静态压缩下的力学行为进行了研究，结合显微组织表征，揭示了高应变率和高温压缩下CrCoNiSi_0.3中熵合金的变形机理，并对J-C本构模型进行了修正，得到如下主要结论。

(1) 在动态压缩载荷作用下，CrCoNiSi_0.3中熵合金的屈服强度随着应变率的升高而增大。准静态加载时，屈服强度为350 MPa；动态加载时，随着应变率从1 776 s⁻¹增加到5 196 s⁻¹，屈服强度从409 MPa增加到682 MPa。CrCoNiSi_0.3中熵合金在宽应变率范围内表现出较高的应变硬化能力。平均应变硬化率先随应变率升高而略微增加，随后在5 196 s⁻¹时显著下降，并伴有明显的内部结构变化，如绝热剪切带和微裂纹。准静态加载和动态加载下屈服强度的应变率敏感系数分别为0.010 9和0.594 4，表明动态加载下屈服强度的应变率敏感性更高。

(2) 在准静态加载下，CrCoNiSi_0.3中熵合金的屈服应力和流动应力随温度的升高而减小。CrCoNiSi_0.3中熵合金在高温下具有良好的抗压性能，在1000 ℃时仍表现出应变强化。在600 ℃下，除晶粒细化外，变形孪晶、层错和位错锁的共同作用促使CrCoNiSi_0.3中熵合金表现出较强的动态应变硬化行为。

(3) 为了更好地预测CrCoNiSi_0.3中熵合金的力学行为，对J-C本构模型的温度和应变率项进行了修正。针对CrCoNiSi_0.3中熵合金的应变硬化随应变率升高而降低的力学行为，通过引入应变硬化函数进行了修正。修正的J-C本构模型对于不同应变率下CrCoNiSi_0.3中熵合金的力学行为均有较好的拟合效果。