由于高压引线的存在，在分压器的顶端出现频率低、衰减慢的振荡波，使得测量的波形畸变严重。因此，需要在引线中串联一个阻尼电阻来减小振荡波对测量的影响，而电阻及引线电感等会造成测量系统的响应时间增加，使得纳秒级脉冲电压的测量不准确^[15]。同时，如果是分立式电容分压器，高压臂和低压臂之间需用电缆相接，这段电缆上的波过程会在低压臂的电压上叠加高频振荡^[16]。因此，需要尽可能减小电缆长度或者改变电容分压器的结构。

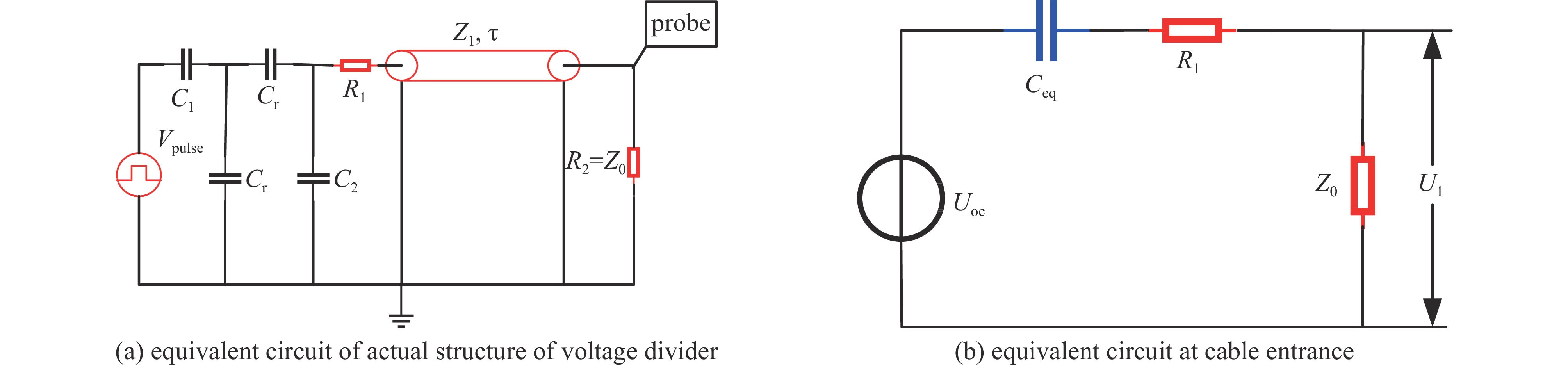
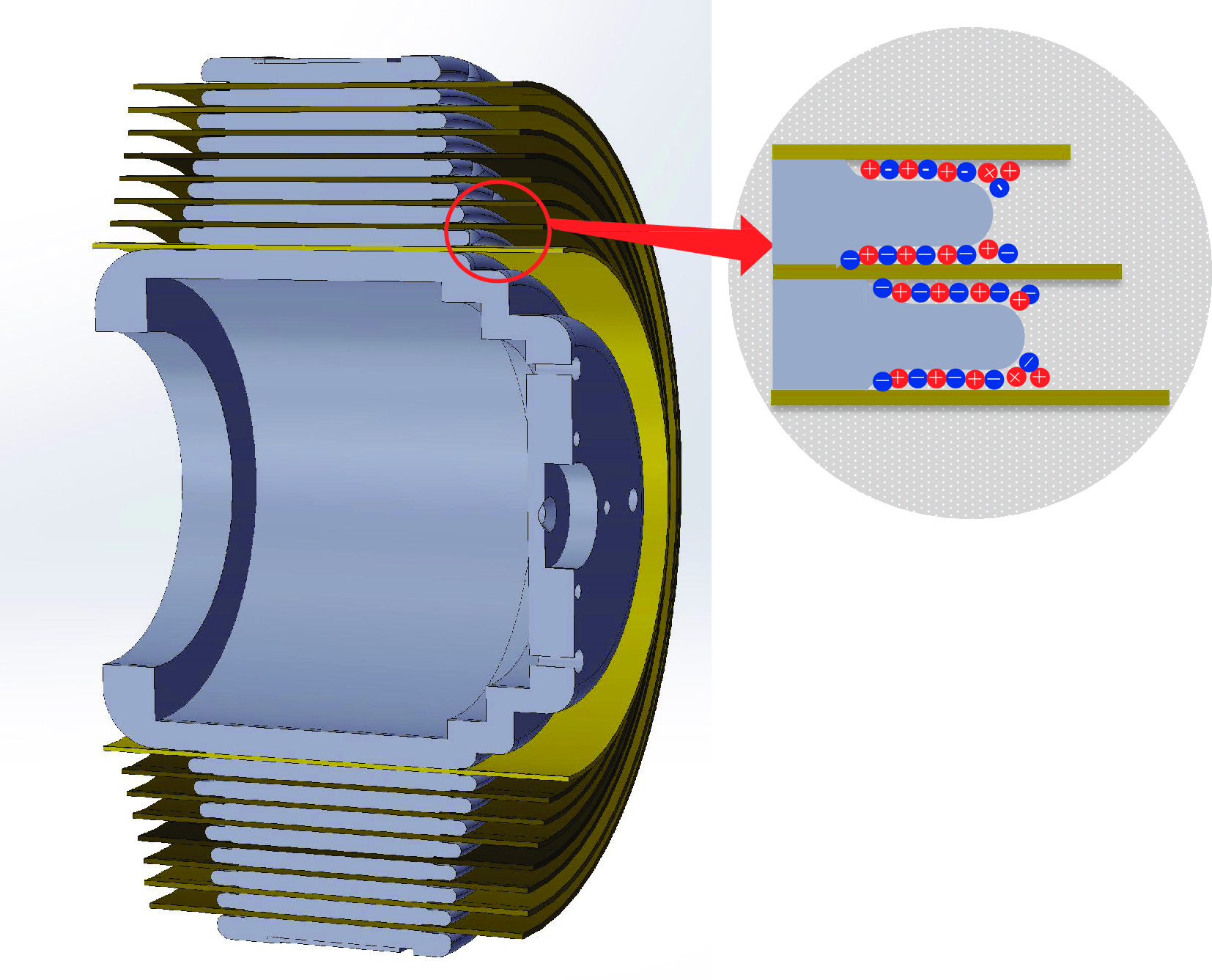
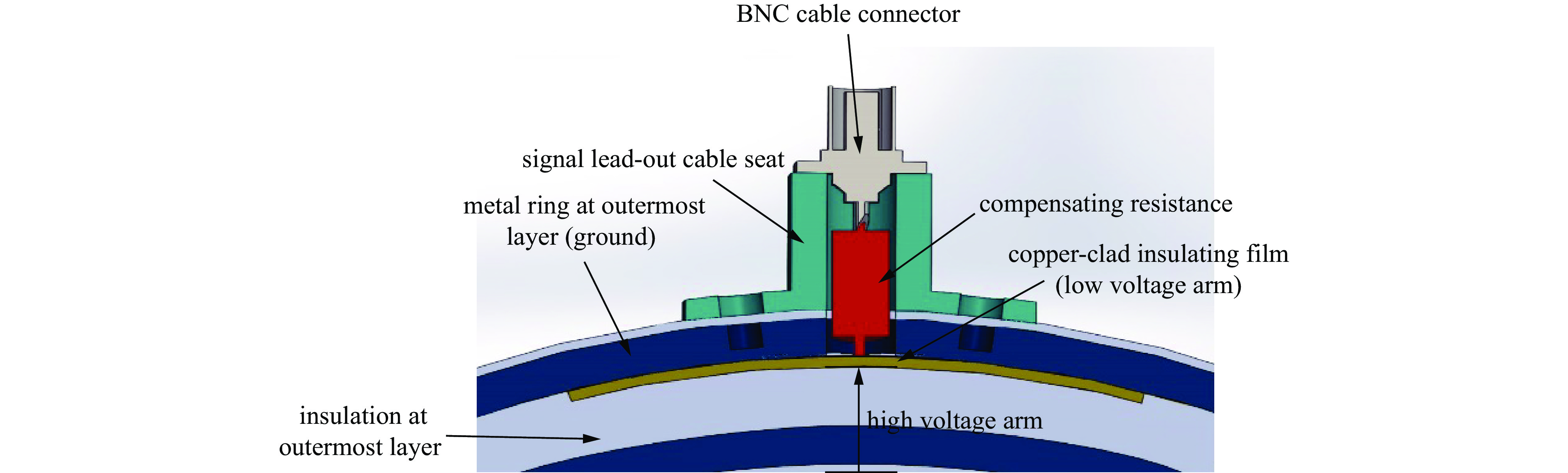
为了解决上述问题，本文设计了一种耦合式电容分压器。分压器主要由一个8层峰化电容器、覆铜薄膜和补偿电阻组成。峰化电容器作为该电容分压器的基础，结合覆铜薄膜形成一体化结构，同时采用电阻补偿的方式达到自积分的目的。如图1所示。其中，覆铜薄膜由金属膜和绝缘膜组成，它是该电容分压器的关键元件。为了防止绝缘膜沿面闪络，金属膜的面积应该比绝缘膜稍小^[16]。此外，绝缘膜应选取相对介电常数高、韧性好、耐压性能好的材料。因此，本文金属膜长宽均比绝缘膜小10 mm，绝缘膜选取聚酰亚胺薄膜。峰化电容器的最外层金属环为接地端，将覆铜薄膜贴附于峰化电容最外层绝缘层与最外层金属环的地电极之间，峰化电容器其他结构保持不变。覆铜薄膜介质金属部分与峰化电容靠近内径侧多层薄膜介质所形成的电容为电容分压器高压臂，覆铜薄膜介质电容作为电容分压器低压臂。为了避免杂散电感影响分压器的高频响应，补偿电阻采用无感的碳芯电阻，一端与低压臂覆铜薄膜信号引出端连接，一端与同轴电缆接头（BNC）连接将测量信号引出。

为了分析比较不同低压臂电容与补偿电阻参数下的探头响应特性，本文设计了两个探头（1#探头和2#探头），低压臂覆铜绝缘膜分别为厚度为50 μm和25 μm的聚酰亚胺薄膜。低压臂电容可近似为

式中：ε₀为真空介电常数，取8.85×10⁻¹² F/m；ε_r为聚酰亚胺相对介电常数，取3.2；l为覆铜的纵向长度，取60 mm；θ(z)为覆铜的圆周张角；r₁、r₂分别为峰化电容电极轴心到覆铜薄膜的距离和峰化电容最外层金属内径，单位为mm。可以计算出1#探头和2#探头的低压臂的电容分别为5.44 nF和10.88 nF。由于低压臂的r₁和r₂非常接近，因此在测量时会引入测量误差，同时还存在加工工艺带来的厚度误差，上述理论公式计算的误差可能比较大。因此，在确定低压臂电容时，一般由平衡电桥实测得来，表1为低压臂电容与补偿电阻实测值。

由于峰化电容一体化电容分压器的低压臂是嵌入到了峰化电容器的最后一层绝缘介质中，则其结构不是简单的高低压臂串联，而是图2（a）和图2（b）所示的结构及等效分布电容。其中，C₁为前7层电容器的串联电容；C₂为薄膜介质低压臂电容；C_s为第7层金属环到金属绝缘膜一侧金属之间的电容；C_ri(i=1,2,…,n)为第8层电容除嵌入部分电容的其它部分的电容，并联总电容为C_r。

根据分压器的实际结构可得到图3（a）所示的等效电路。由电路理论可知，补偿电阻R₁左端可等效为电压U_oc与电容的串联C_eq。电压信号进入电缆端口前的等效电路如图3（b）所示。若输入电压为单位阶跃信号，则其阶跃响应为

式中：U_oc(s)=C₁C_ss⁻¹/[C₂C_s+(C₁+C_r)(C₂+C_s)]；C_eq=C₂+C_a，C_a=C_s(C₁+C_r)/(C₁+C_r+C_s)。由Laplace反变换可知

由于C₂$\gg $C_a且R₁+Z₀$\gg $1/sC_eq，则式（2）可简化为

由彼德逊法可以得到，电压波在从电缆端口输出时的输出信号为

由此可知，峰化电容分压器的测量输出为

式中：R₂等于电缆的特性阻抗Z₀。因此分压器分压比为

由式（3）可知，分压器的低频响应由等效电容C_eq与补偿电阻与波阻抗之和(R₁+Z₀)的乘积决定。由于C₂$\gg $C_a且R₁$\gg $Z₀，则低频响应主要由补偿电阻R₁和低压臂电容C₂决定。由于峰化电容器紧凑型结构限制，一般较大的低压臂电容难以实现，因此，若实际设计时要提高峰化电容一体化电容分压器的测量脉宽，一般采用增大补偿电阻的方法。同时，由分压比k的表达式（7）可知，电压信号经由电容分压器分压后，由R₁和R₂组成的电阻分压器进行二次衰减。若满足(C₁+C_r)(C₂+C_s)$\gg $C₂C_s时，输出电压信号可近似看作输入信号经由两级电容分压器分压后，由电阻分压器再进行衰减得到的信号。因此，相对于传统电容分压器，这种分压器大大提高了其分压比。

为了验证上述理论分析，利用了Pspice进行分压器分压比的仿真计算，其电路模型如图3（a）所示。其中，脉冲方波信号的幅值为1 kV，脉冲上升沿和下降沿均为10 ns，脉宽1 μs。峰化电容一体化电容分压器是整体结构，难以实现用数字电桥测得各部分电容值，因此可以根据式（1）计算出各个部分的理论结构电容，其中电容C₁为102.9 pF，C_s、C_r分别取103.2 pF和616.8 pF，低压臂电容C₂以及积分电阻R₁按照表1取值，末端匹配电阻R₂取50 Ω。传输电缆的参数为特性阻抗50 Ω，传输延时τ为100 ns。

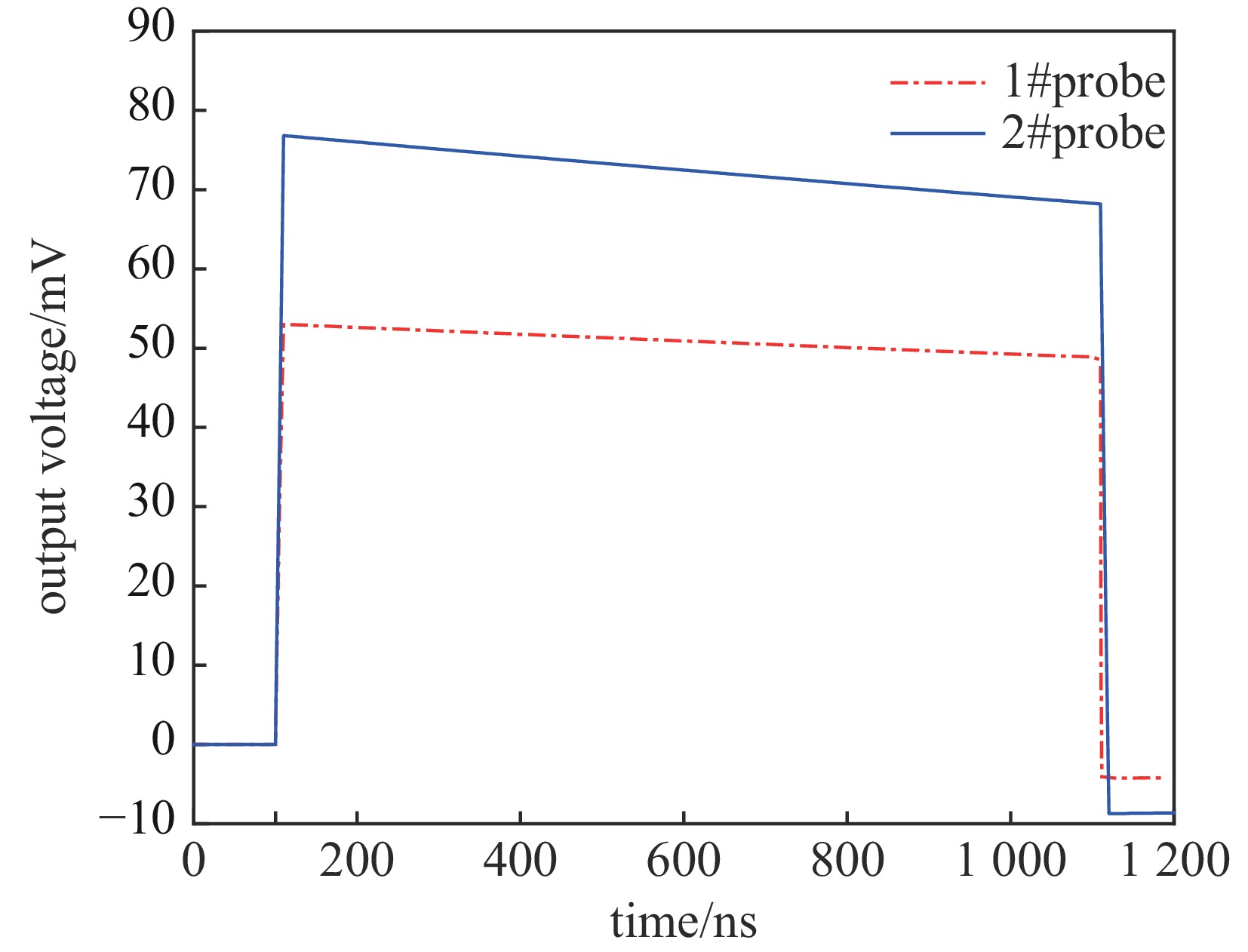
两探头输出信号PSpice仿真结果如图4所示。由图4可知，1#探头输出信号的幅值为76.82 mV，2#探头输出信号的幅值为53.07 mV，分压比分别为13020和18843。根据理论分析得出的分压比计算式（7），1#探头分压比应为13010，2#探头分压比应为18835，即输出电压信号分别为76.86 mV和53.09 mV，这与仿真得出的分压比大小相差不大且分压比的相对误差不超过0.1%，可忽略不计。因此，可按照式（7）对峰化电容一体化电容分压器的分压比进行理论分析。

同时，由表1可知，1#探头的时间常数R₁C₂为8.2 μs，2#探头的时间常数为11.7 μs，因此，2#探头相对于1#探头低频响应较好，且理论上1#探头可测脉宽为800 ns左右的脉冲信号，2#探头可测脉宽为1.2 μs左右的脉冲信号。为了分析两个电压探头对不同脉宽信号的响应，仿真分析了脉冲方波信号脉宽分别为100 ns、500 ns以及1 μs时电压探头的输出信号，可以得到表2所示结果。其中两个电压探头在脉宽为100 ns时平顶降最小，低频响应最佳，1#探头方波响应波形的平顶倾斜为1.0%，而2#探头的平顶倾斜为0.8%，而在脉宽为1 μs时平顶降最大，低频响应较差，1#探头方波响应波形的平顶倾斜为10.0%，而2#探头的平顶倾斜为6.6%，由此可以得出时间常数R₁C₂为方波脉宽τ的倍数越大，两个电压探头低频响应越好，且相比于1#探头，2#探头的低频响应更好。因此由仿真结果可知，本文分压器仿真与理论分压比一致，且低频响应主要由补偿电阻R₁和低压臂电容C₂决定。

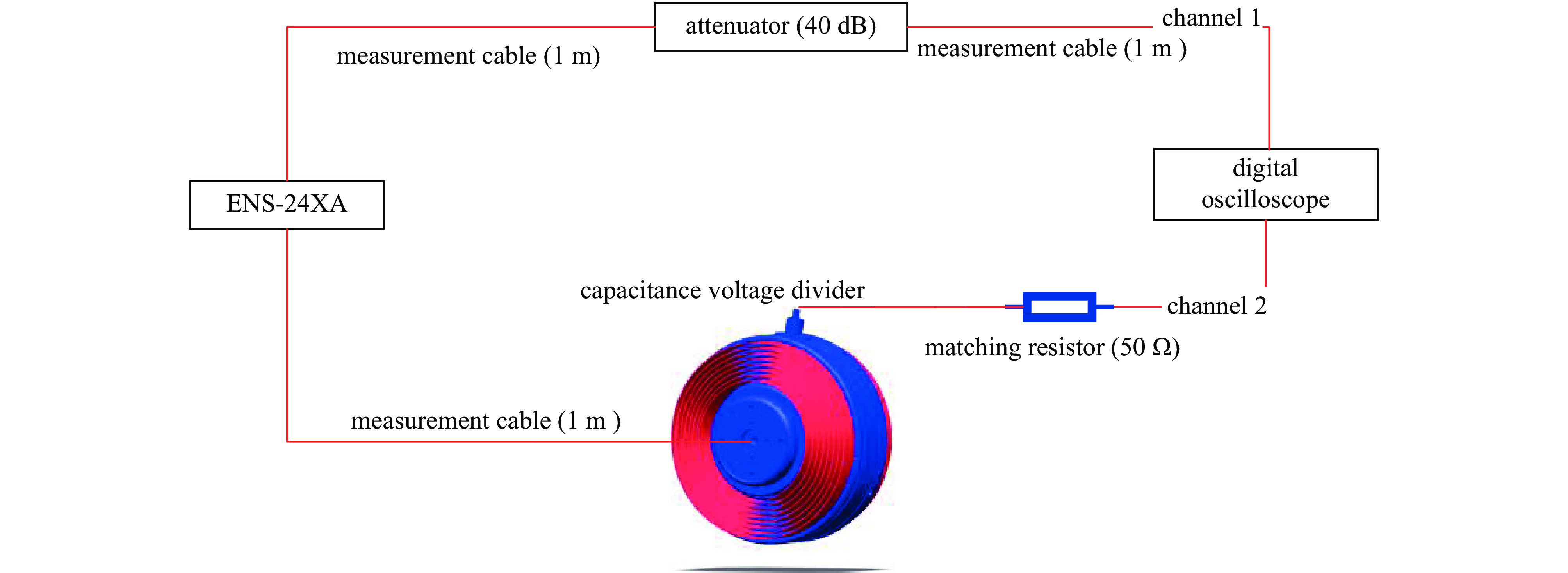
对峰化电容一体化电容分压器进行响应时间和分压比的标定，需如图5所示的标定系统。该标定系统主要由ENS-24XA方波发生器、待标定电容分压器、衰减器（带宽4 GHz）、数字示波器MSO44（带宽1 GHz）、50 Ω匹配头以及信号测量电缆等组成。其中，方波发生器ENS-24XA产生的脉冲经由两路进入示波器（1 MΩ高阻模式）。一路通过40 dB衰减器直接进入示波器通道1，另一路经由电容分压器后进入示波器通道2。通过通道1的源信号对分压器输出信号进行标定。

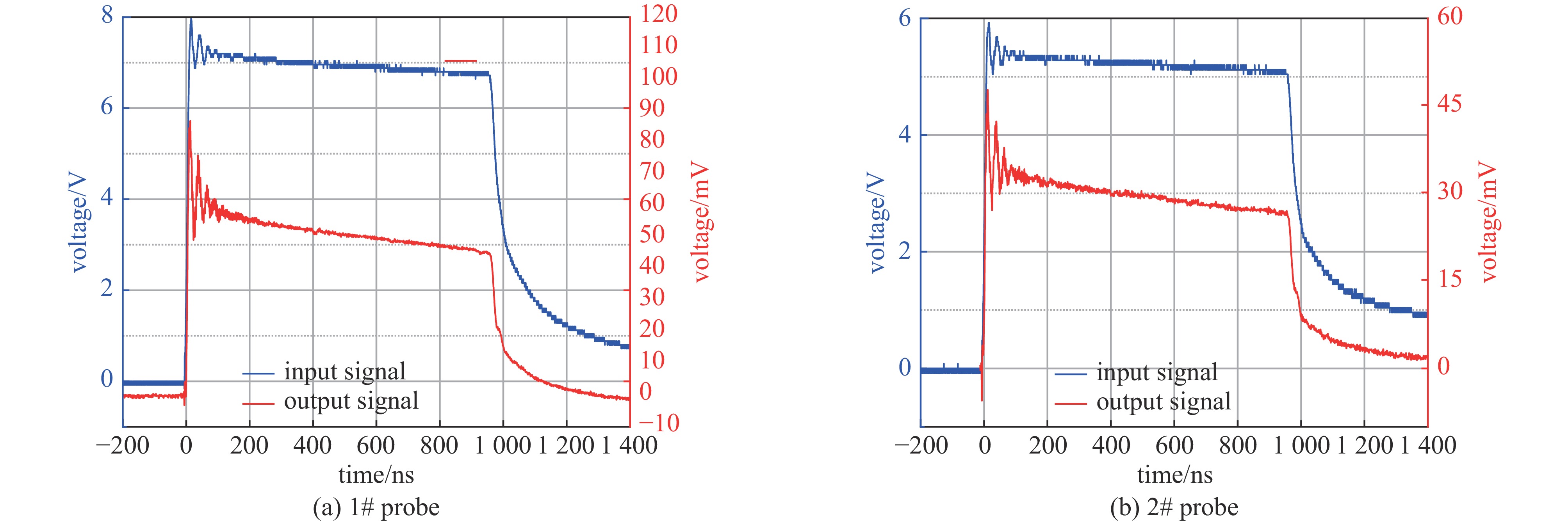
当方波发生器产生幅值约0.6 kV、脉宽1 μs的脉冲信号时，对两个探头分别进行标定，示波器测得的经衰减的源脉冲信号以及电容分压器探头的输出信号如图6所示。由于方波发生器的调压步长较大，在调节电压时可能会造成幅值在0.6 kV上下浮动，但低压标定下电压幅值对分压比的标定几乎不影响，可忽略不计。

由标定波形可以看出，输出电压波形与方波跟随一致，响应良好。但输出电压会出现一定平顶降的现象，这主要是由低频响应造成的。电容分压器的低频响应主要由低压臂容值C₂以及输入阻抗之积得到的时间常数决定，两探头设计的输入阻抗相近，则低频响应主要是由低压臂容值C₂决定。

由图6可看出，1#探头方波响应波形的平顶倾斜为5.7%，而2#探头的平顶倾斜为4.4%，由此可以得出：相比于1#探头，2#探头的低频响应更好，这在图4中仿真输出波形中也有所体现。由图6可以看出1#探头明显比2#探头的平顶倾斜严重，低频响应更差。而且由图7（a）可以看出1#探头出现了一定的负电压偏置现象，这主要是因为1#探头的低频响应较差、平顶倾斜较严重导致的。由此可知，2#探头低压臂电容C₂及时间常数较大、低频响应良好，且若两探头用于百纳秒脉宽的脉冲信号时低频响应会更好，平顶倾斜也会更小。

因此，采用高频振荡中心光滑后的平顶电压得出分压比。由图6可知，1#探头输出幅值约为50 mV，2#探头的输出幅值约为33 mV。对两个探头分别进行十次标定，取平均值作为其分压比结果，表3为探头的标定响应时间及分压比。由表3可知，两探头的分压比与理论分压比之间存在一定的误差，这主要是因为低压臂嵌入到了峰化电容中，未考虑边缘效应引起的电容估算误差，同时还存在衰减器以及分压器的响应造成的误差。

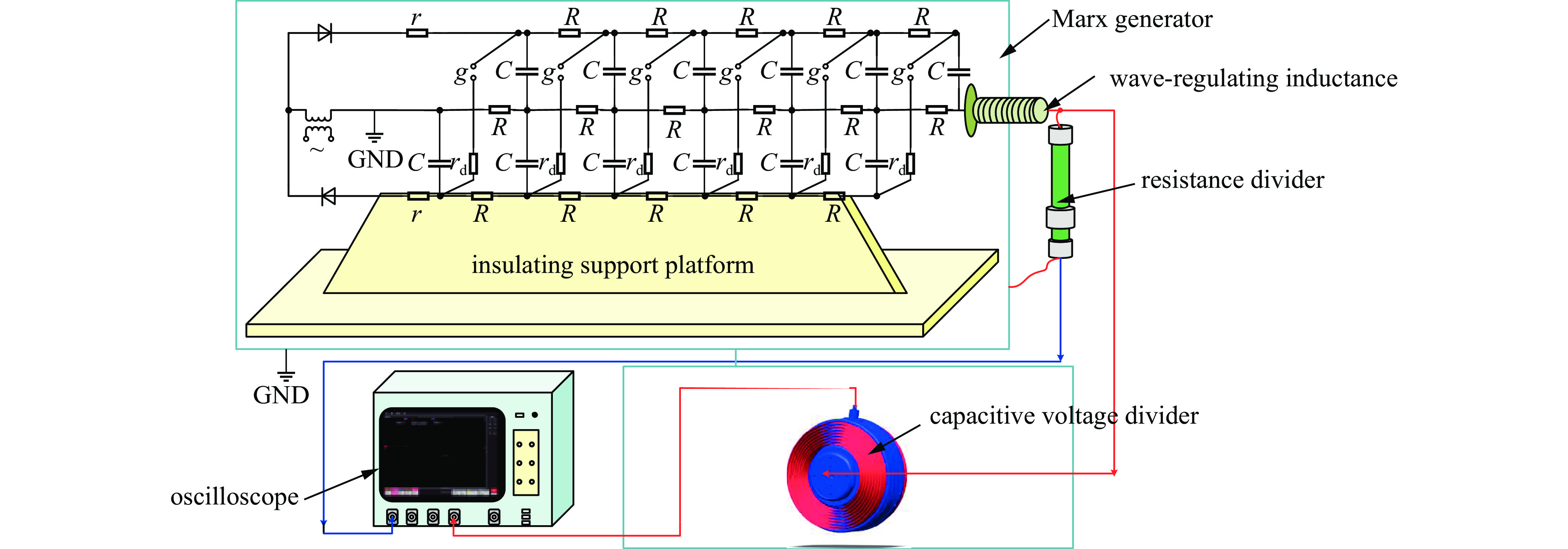
由于受方波发生器输出幅值限制以及峰化电容一体化电容分压器分压比大的影响，测量输出电压信号较小，受干扰比较严重，信噪比小，从而分压比测量不够准确。因此，分压器的分压比需在Marx脉冲源工作平台再进行在线标定。且为了验证峰化电容分压器的绝缘要求，须在较高电压下进行实验，图7为Marx平台的示意图。

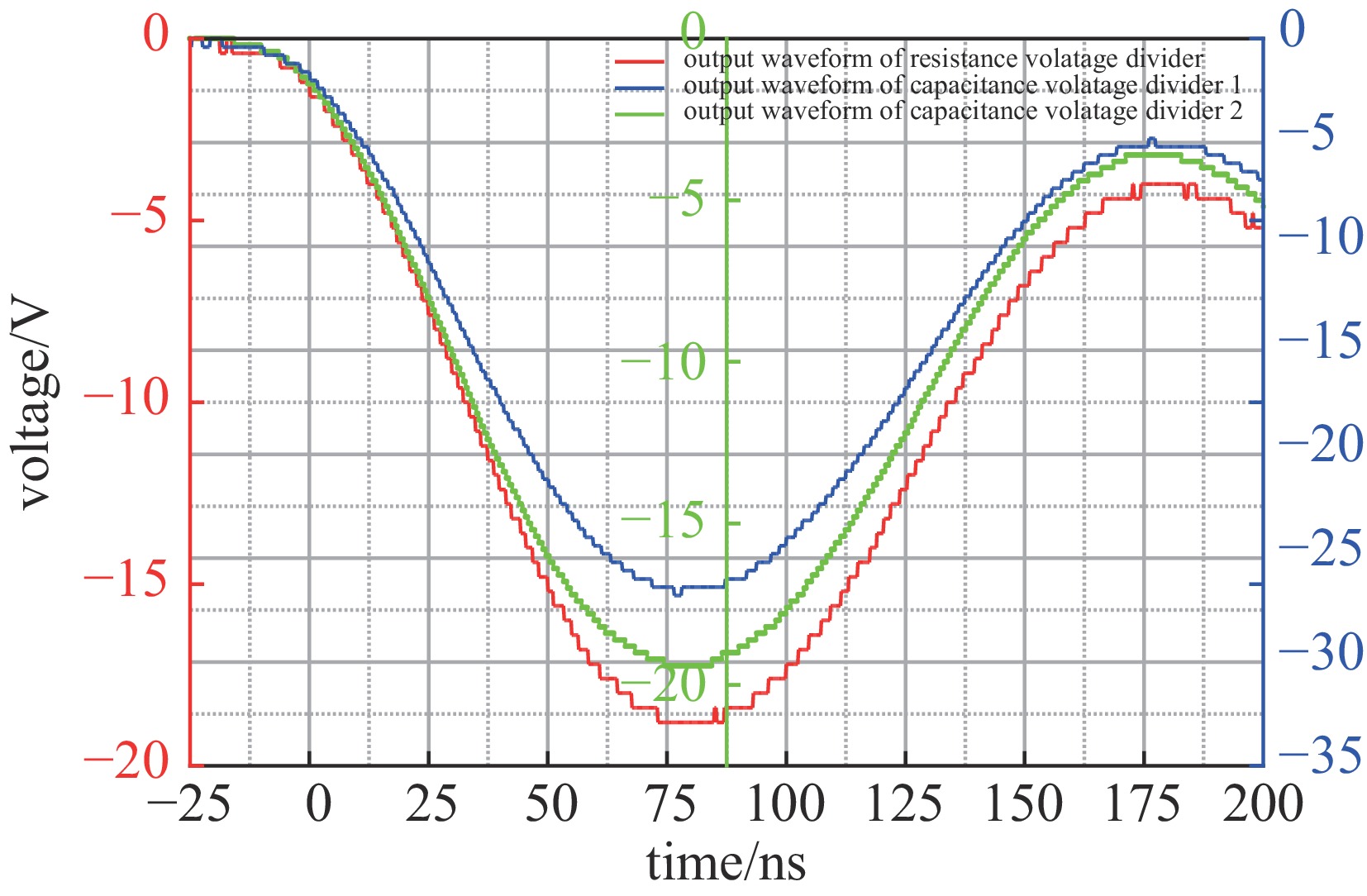
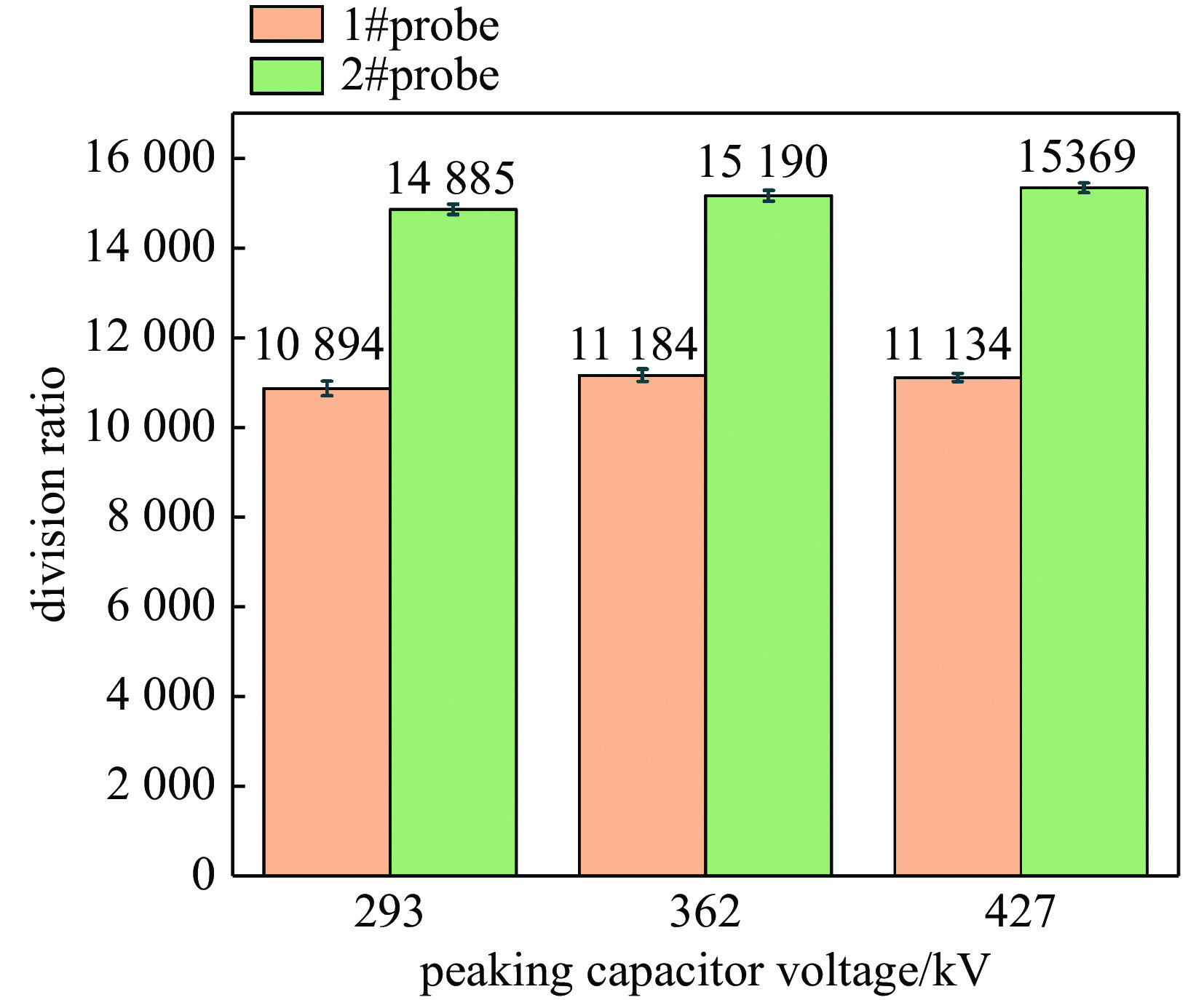
上述图7中装于调波电感后的电阻分压器的分压比已标定好，其分压比为1490。因此拟采用此电阻分压器对峰化电容一体化电容分压器进行在线标定。图8是Marx平台高压在线标定的典型波形，可以看出峰化电容一体化电容分压器的输出波形与电阻分压器的波形跟随一致，响应良好。

高压在线标定是通过提高峰化电容器耐受电压来标定分压器在不同电压等级下的分压比。本实验主要通过提高Marx主回路充电电压达到提高峰化电容电压，分别在主回路充电电压为20～28 kV，步长为4 kV时标定了3个电压等级状态，其分压比如图9所示。由图可知，两个探头在峰化电容器耐受电压为293、362、427 kV的作用下，分压比变化较小。1#探头分压比分布于11000左右，且2#探头分布于15100左右。因此，取各个探头3个电压等级下的平均值作为其最终分压比，即1#探头分压比为11071，2#探头分压比为15148。

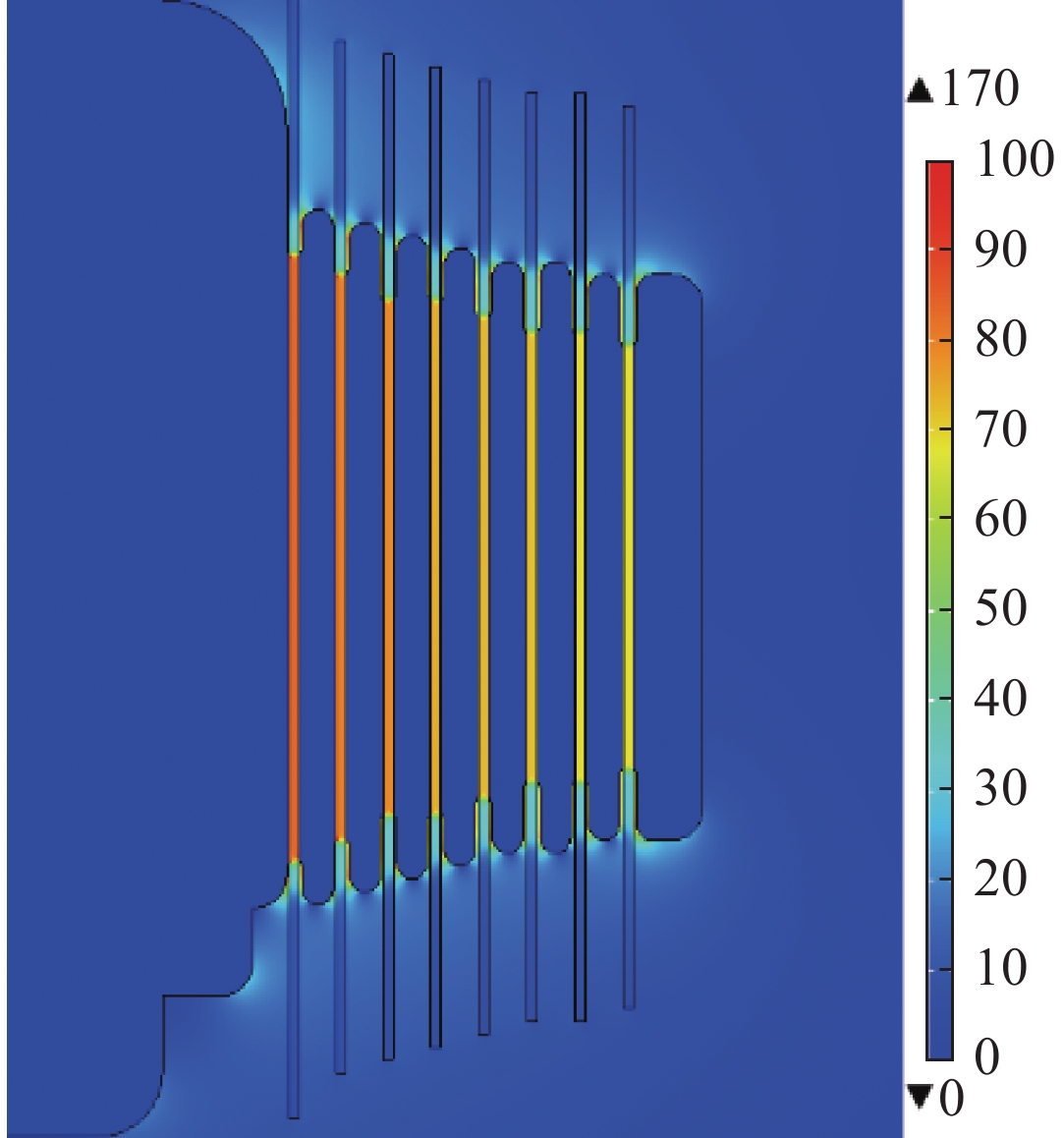
由高压在线标定结果可知，两探头的分压比与低压方波标定和理论的分压比具有一定的误差，除了低频响应引起的读数误差之外，其主要原因是峰化电容器本身设计的结构所导致。本文中MV级峰化电容器由一系列同心电容器串联而成，整个电容器由8层绝缘介质和8个等间隔的金属环组成。为了使峰化电容器电压均匀分布，要求每一个电容器的电容值一致，同时为了使每部分的电容值和场强保持一致，设计的每个金属环都有各自不同的长度和直径^[17]。为了优化金属环轴向两端的电场分布，采取了倒圆角来减小局部场强。利用有限元仿真软件计算在峰化电容器上施以1 MV电压下的电场分布，如图10所示。可以看出各层电容器平均场强不超过85 kV/mm，但金属环与绝缘介质之间气隙的场强会比较高。因此，较高电压下在场强达到一定值时，该气隙会发生局部放电甚至击穿并形成放电非平衡等离子体^[18-19]，这在一定程度上会增大峰化电容器的电容值，如图11所示。

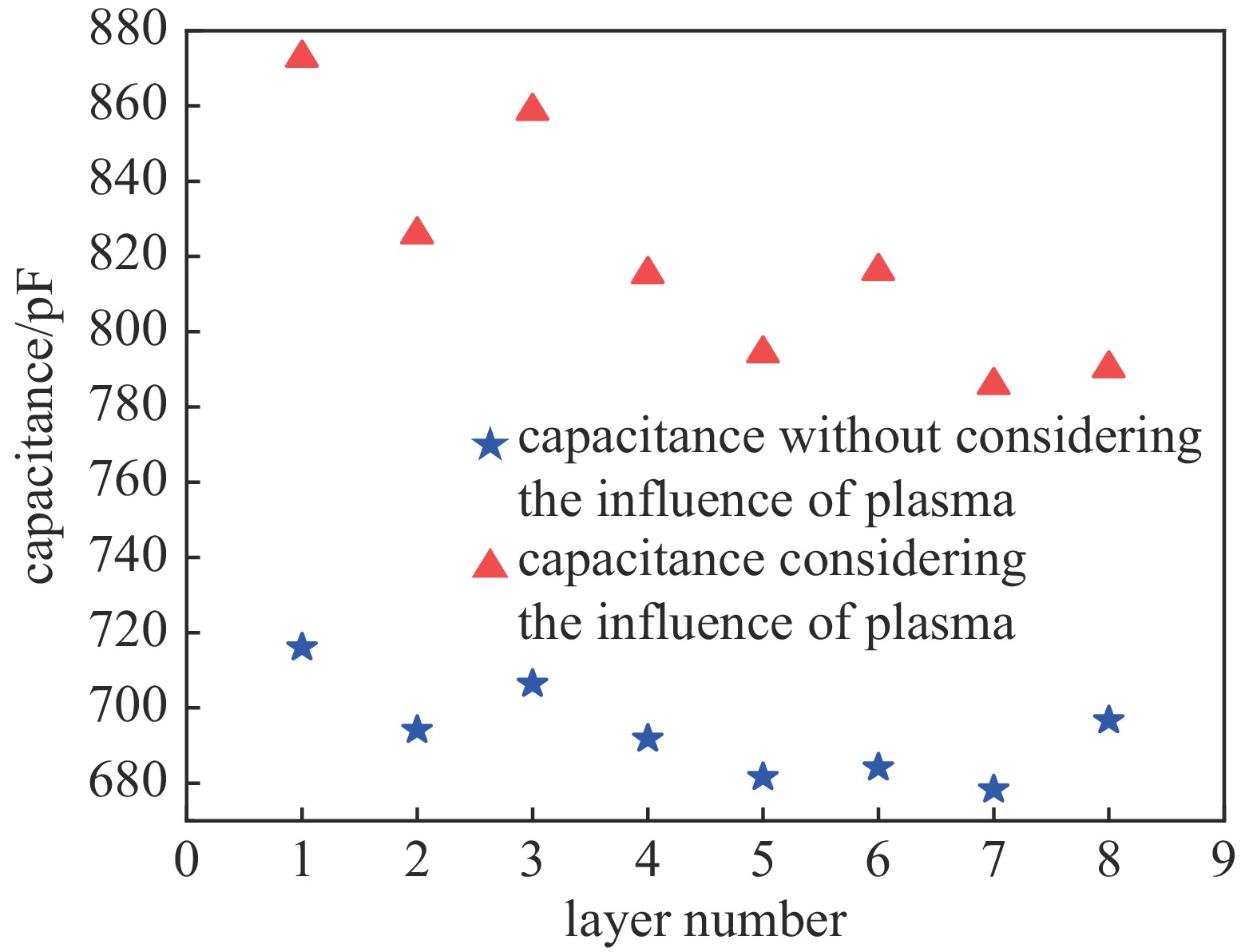
为了考虑高压作用下形成的等离子体对结构电容的影响，对各电极间的等离子体气隙进行电极延伸并利用有限元仿真软件进行电容仿真计算，可以得到8层电容器的每层电容如图12所示。根据图12可知，峰化电容器容值在高压等离子的影响下会相应增大，因此按照原仿真电路图4（a）进行重新赋值仿真，各部分电容同样按照式（5）计算得到，其中C₁取115.9 pF，C_r和C_s分别取137.8 pF和735.0 pF，其它参数不变。由仿真可以得到1#探头分压比为10495，2#探头分压比15150，相比于实验标定的分压比分别相差5.20%和0.02%。因此，由上述分析可知峰化电容容值在高压下受等离子体变化是影响其分压比的主要因素之一。由于峰化电容器工作电压通常达到数百kV至MV量级，因而在实际测量中通常采用高压在线标定的分压比作为分压器的分压比。

为了探究在更高电压等级的作用下探头分压比的变化趋势，在Marx充电电压更高时进行了标定实验。考虑到更高电压等级下峰化电容绝缘耐受性能，在峰化电容器后需连接气体输出开关和400 Ω负载电阻以实现脉冲信号在首个波峰截断，实验平台示意图如图13所示。由表3标定结果可知，峰化电容一体化电容分压器的两个探头，两者测量的峰化电容电压之差变化不大，且未随电压升高呈线性变化。这可能是由于金属环与绝缘介质之间的气隙较小，在较小的耐受电压下，气隙已经击穿形成等离子体，即该峰化电容器一体化电容分压器在耐受较低电压下分压比已经比较稳定而在高压下不会造成较大的误差。

在Marx主回路充电电压为48 kV时，出现了两探头电压之差增长较大的情况，这主要是受气体开关耐受脉冲电压幅值的限制，开关在脉冲前沿击穿造成的。由于2#探头比1#探头的响应时间较大，则其高频响应相对较差，导致最终输出波形前沿变缓，上升时间由81.0 ns增至83.4 ns。当输出开关击穿之时，2#探头所测幅值相对真实值较小，最终导致2#探头输出电压幅值偏小。若调整实验参数使开关在峰值击穿时，可有效减小两探头所测的电压之差。

依据1#探头所测电压对2#探头进行高压在线标定，由表4中数据分析可知，2#探头的分压比在不同电压等级下，分压比维持在15200左右，除上述分析Marx充电电压48 kV时开关前沿击穿导致的分压比偏大外，其它都比较稳定且平均分压比为15283，相较于低电压等级下分压比(15128)的相对误差低于0.9%，可忽略不计。因此，该分压器在较高电压等级下分压比稳定性良好。

本文设计了一种用于测量峰化电容上脉冲电压的一体化电容分压器，该分压器实现了峰化电容电压的直接测量，并成功运用于Marx脉冲源的峰化电容电压测量。主要结论如下：以峰化电容器为基础，巧妙地在峰化电容最外层同心电容器的接地端嵌入合理设计的聚酰亚胺覆铜薄膜，形成了一种新型结构的峰化电容一体化电容分压器；根据峰化电容一体化电容分压器实际结构，分析了分压器的响应特性，给出了理论计算公式并进行了仿真计算，且仿真分压比与理论分压比一致，且其低频响应与结构电容C₁、C_s、C_r及C₂和补偿电阻R₁有关，而本电容分压器主要由时间常数R₁C₂决定；开展了方波标定实验，得到了两个探头的分压比及响应时间，1#探头响应时间为4.45 ns，2#探头响应时间为6.28 ns。同时为了得到正常工作状态下的分压比进行了高压在线标定实验，得到了1#探头分压比为11071，2#探头分压比为15148。高压在线标定分压比与方波标定和理论分压比相差较大，主要是峰化电容容值在高压作用下受等离子体的影响，因此在考虑该因素的影响下通过仿真计算分析得到了两探头理论与标定的分压比一致，相对误差均小于5.20%，且试验验证在更高压等级下，一体化电容分压器分压比随电压变化较小，不随电压呈线性变化，且该分压器的分压比相对误差较小，因而该分压器的分压比稳定性良好。