线圈型电磁发射器一般是指用脉冲或交变电流在驱动线圈上产生磁行波来驱动带有线圈或导磁材料制成的运动电枢的发射装置。它利用驱动线圈和发射体间的磁耦合机制工作，其本质为直线电机^[14]。磁阻型电磁线圈发射器系统由驱动线圈、铁磁电枢、发射管、储能器、续流二极管、可控开关及外部放电与控制电路组成，如图1（a）发射器2D模型图所示。

磁阻型线圈发射器工作原理为，当可控开关K₁导通，电容组C₁向驱动线圈释放脉冲电流，脉冲强磁场产生电磁吸力驱动电枢向右加速，因磁路有趋使自身磁阻变小的特性，线圈中磁路磁阻随电枢向右运动先减后增，当电枢与线圈中心面重合时最小。若电枢过驱动线圈中心面后，线圈中仍存在磁场，则会产生电磁制动力阻碍电枢向右运动，所以当电枢与驱动线圈中心面将要重合时需关断开关K₁，使驱动线圈与续流二极管D1构成续流回路以迅速消耗线圈中剩余电流，以减小甚至消除电磁制动力，使电枢以惯性运动直至出膛。

为简化模型并抓住影响系统性能的主要因素，便于进行有效的理论分析和工程设计，忽略储能电容器组、触发电路导线以及续流二极管的等效电阻与等效电感，只考虑驱动线圈的电感及等效电阻，任何放电电路在未关断储能器前都可等效为如图1（b）所示的储能电容两端并联一个续流二极管D的RLC放电电路。

放电回路的电压方程

式中：L为驱动线圈等效电感值，C为脉冲储能电容器电容值，$U(t)$为脉冲储能电容器电压值随时间变化函数，R为驱动线圈等效电阻值。

线圈发射器电路工作条件需要RLC电路满足:$ R < 2\sqrt {\dfrac{L}{C}} $，又由电路的初始状态$ U(0_+)=U\mathrm{_c},\dfrac{\mathrm{d}U(t)}{\mathrm{d}t}\left|_{t=0_+}\right.=0 $（$ U\mathrm{_c} $为脉冲储能电容器初始电压），可以确定

式中：$ \; \beta = \dfrac{R}{{2L}},\omega = \sqrt {\dfrac{{4L - C{R^2}}}{{4C{L^2}}}} $，$I(t)$为脉冲储能电容器电压值随时间变化函数；当RCL回路中驱动线圈等效电阻值R小到可以忽略时，有

当$t = \dfrac{\pi }{2}\sqrt {LC} $时，驱动线圈的放电电流达到峰值$ I_{\mathrm{dm}}=U_{\mathrm{c}}\sqrt{\dfrac{C}{L}} $，若系统能量得到最大化利用，需要在电枢未达到驱动线圈中心面时，脉冲电流达到峰值。

放电电路的后期等效电路取决于各电路的结构性质，放电电路类型可按电路是否关断分类，也可按剩余能量消耗方式分类。

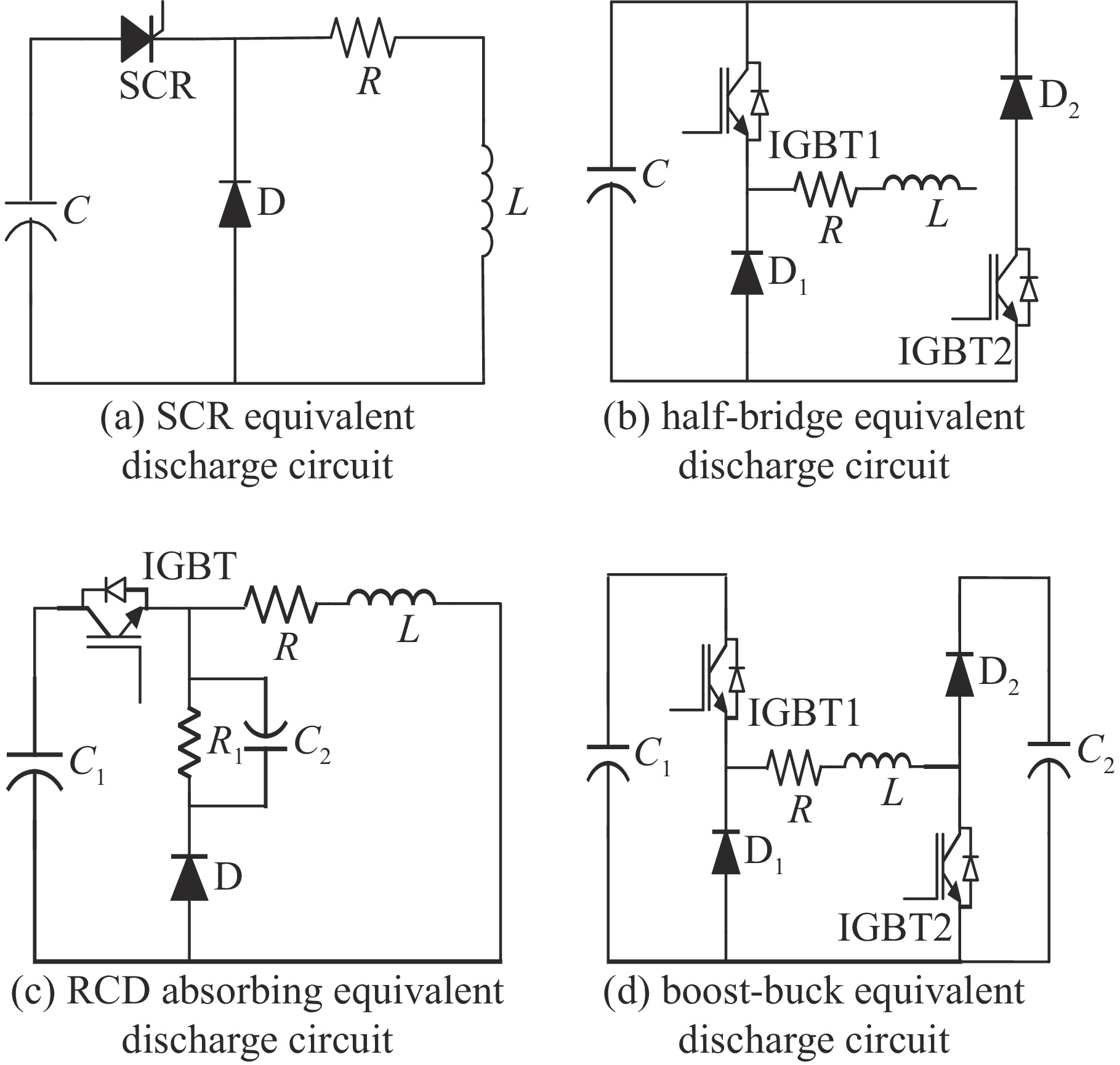
本文分析了磁阻型电磁线圈发射系统中不同放电电路结构对发射性能的影响，研究了SCR式放电电路、半桥式放电电路、RCD吸收式放电电路、Boost-Buck式放电电路这四种电路模型，其电路中开关类型与电路功能如表1所示，四种放电电路原理如图2所示。

图2（a）中SCR式放电电路采用SCR即半可控开关为电路控制开关，该开关只能控制电路导通，不可控制电路关断，电路结构简单，其工作原理为：当SCR接收到外部脉冲信号时SCR导通形成RCL电路，驱动线圈上流过脉冲电流在驱动线圈上形成脉冲磁场，根据磁阻最小原理，驱动线圈吸引电枢加速运动，当储能电容组中电能消耗完，驱动线圈则与续流二极管构成RL续流回路，在此阶段驱动线圈中的剩余电流需要自然衰减到零，会对电枢产生很大且持续时间较长的电磁制动力阻碍电枢加速，影响系统的发射性能。

考虑到全控开关的寿命和性能，本文电路中的全控开关采用IGBT^[15]。为后期试验研究的安全性考虑，电容器选型中其最大充电电压不能高于当前IGBT额定电压的90%，根据驱动电路的传导电流峰值$ I_{\mathrm{dm}}=U_{\mathrm{c}}\sqrt{\left(C/L\right)} $，不能超过IGBT最大栅极驱动电压${V_{{\mathrm{GE}}}}$下的钳位感性负载电流${I_{{\mathrm{LM}}}}$，可得到电容器电容值及驱动线圈等效电感的范围。

图2（b）中半桥式放电电路，在放电时两个可控开关同时接收到外部触发信号，IGBT导通并与储能电容组和驱动线圈形成RCL电路，驱动线圈在此阶段将吸引铁磁电枢向磁阻减小方向做加速运动，当电枢将要与驱动线圈中心面重合时，可控开关接收到外部关断信号，驱动线圈与两个续流二极管和该级储能电容器构成续流回路，该阶段将驱动线圈存储剩余电磁能转换成电能回收到该级储能电容器中，并可使驱动线圈中电流迅速降至为零。此电路可减小甚至消除电枢受到的电磁制动力，可较大提高系统的发射性能，也可减小下次发射时储能器的充电时长。但该电路需要设计两个可控开关的驱动及保护电路较为复杂，且成本相对较高。

文献[12]的放电电路中存在一个全控型开关与一个半控型开关，电路复杂且冗余。将传统驱动电路中控制开关SCR换成IGBT，将并联在储能电容器旁的续流二极管替换成RCD吸收支路，如图2（c）所示该电路放电时，根据磁阻最小原理驱动线圈吸引铁磁电枢加速运动，IGBT关断后，驱动线圈与RCD支路构成续流回路，线圈中的大部分剩余电磁能将以充电的形式转移到RCD支路中的储能电容器内，小部分能量则通过RCD支路中的耗能电阻消耗掉，当驱动线圈中剩余电磁能消耗完后，RCD支路中的储能电容则与耗能电阻构成新的回路以将储能电容中的能量消耗完，其驱动线圈中剩余能量的消耗速度取决于续流回路中电容与电阻参数的选取，该驱动电路通过耗能电阻迅速消耗驱动线圈中的剩余电磁能，虽然抑制了电枢加速过程中受到的电磁制动力，从而提高了电枢出口速度，但未对剩余能量进行回收再利用，导致系统能量利用率的提升不明显。

半桥式放电电路虽可回收的驱动线圈中剩余能量，但该回收能量不能运用到本次发射中^[13]，不利于多级发射器设计，考虑到之后的多级发射器的研究，本文基于Boost升压电路原理拓扑一种可将驱动线圈中剩余能量回收到下一级驱动线圈的储能器中的放电电路，如图2（d）所示。该电路放电时，IGBT1与IGBT2同时接收到外部触发信号，IGBT导通并与储能电容组和驱动线圈形成RCL电路，驱动线圈在此阶段将吸引铁磁电枢向磁阻减小方向做加速运动，当电枢将要与驱动线圈中心面重合时，可控开关接收到外部关断信号，驱动线圈与下一级的脉冲储能电容器构成续流回路，并通过充电的方式将线圈中的剩余电磁能转换为下级储能电容器的电能，该电路相较于半桥式放电电路更适合作为多级发射器的放电电路。

由文献[16]可知电枢出口速度与脉冲储能电容器的初始电压和电容值成正比，而系统能量利用率随着电容器初始电压与电容值的增大皆呈先增后减的趋势；由文献[17]中可知电枢的受力与驱动线圈中脉冲电流的平方成正比，减小匝数可增大脉冲电流峰值，还可减小驱动线圈等效电阻值；考虑到器件的绝缘性需增大驱动线圈的绕线半径以适配脉冲电流的增大^[18]；文献[19]表明电枢长度和驱动线圈轴向长度相近时可提高系统发射性能，且高导磁率材料的电枢还可提高其出口动能^[20]。

综上使用有限元法，对单级磁阻型电磁线圈发射器进行2D模型建立，系统各变量参数选取如表2所示。

发射系统2D模型如图3所示，模型中包含空气域、驱动线圈域、电枢域和发射管四个部分。模型驱动电路采用外部脉冲激励电路，驱动线圈采用软件延时触发。定义驱动线圈底部为电枢位移参考坐标零点，电枢沿Z轴正方向运动，电枢底端距参考零点距离记为电枢初始触发位置。

以电枢初始触发位置为−115 mm，可关断电路系统延时时长为15 ms为例，分析单级磁阻发射器在上述四种电路激励下驱动线圈的电流、电枢所受电磁力、电枢速度及储能电容器电压变化，如图4所示。

图4（a）中，使用传统电路在放电过程中，驱动线圈中电流在15～25 ms范围内衰减平缓，是因为电枢受到电磁制动力又将电枢的动能通过电磁场逆转了驱动线圈中的磁能，这也是传统电路下发射器发射性能不高的原因之一；发射器在放电阶段可提高驱动线圈中传导电流的峰值，是因为使用了可关断电路，关断电路能够有效地控制电流的变化速率。当电磁线圈中的磁场需要被迅速削减时，关断电路可以迅速切断电流流动，从而快速减小磁场的能量，导致磁场崩溃。这种突然的磁场崩溃会诱导出更高的感应电动势，从而导致更高的电流峰值。

可控开关电路在关断可控开关后，驱动线圈中剩余电磁能都可以近似看成通过充电的形式转换成电容中的电能。因此可定性分析${t_0}$时刻关断后，驱动线圈中传导电流$I(t)$的衰减变化与回收能量的储能电容器初始电压的关系为

式中：$ {\alpha _2} = \dfrac{{ - R}}{{2L}} $，$ \;{ \beta _2} = \dfrac{{\sqrt {4CL - {{(RC)}^2}} }}{{2CL}} $，$ {\varphi _2} = \arctan \left( {\dfrac{{{\alpha _2}A - C{U_{{\mathrm{c}}1}}({\alpha _2}^2 + {\beta _2}^2)}}{{{\beta _2}A}}} \right) $，A为关断时刻电流值。

由公式（6）可知，其他参数相同时，剩余能量回收阶段中储存剩余能量的储能电容器初始电压值$ {U_{{\text{c}}1}} $越大，驱动线圈中的传导电流衰减速率就越快，如图4（a）所示。

由图4（b）可以看出，可关断电路可以大幅度提高电枢受到的电磁驱动力，且各可关断电路下电枢受到的电磁驱动力大致相同，在缩短电枢受到电磁制动力时长的同时也增大了电磁制动力的峰值，结合图4（a）可知，续流阶段驱动线圈中电流衰减为零的速度越快，电枢受到的电磁制动力的时间越短，电磁制动力的峰值也越小，即衰减速率与电枢所受电磁制动力的大小和时间都成反比。

图4（c）中在其他参数相同时，电枢出口速度峰值与电枢受到的电磁驱动力有关，电磁驱动力与其作用时间的积分值越大，电枢速度峰值越大，即电枢速度峰值与电磁驱动力及其作用时间积分成正比；电枢到达峰值后都又一段速度下降时间后趋于稳定，电枢出口速度与电枢峰值间的速度差值是由于电枢受到电磁制动力造成的，电磁制动力与其作用时间的积分值越大，速度差值越大，即电枢出口速度与电磁制动力及其作用时间积分成反比。

由图4（d）可以看出，半桥式与Boost-Buck式放电电路是可将驱动线圈中剩余能量进行回收，且回到电容器的初始电压越小，回收的能量越多。

由图4可知，可关断电路可以有效抑制电枢受到的电磁制动力，但电枢仍受到电磁制动力，因此需对可关断电路下发射器参数进行优化，又因发射器结构参数已给定，只能通过更改电枢的初始触发位置和可控开关导通时长来优化发射性能。基于文献[8]中均匀实验法对可关断电路中IGBT元件工作延时以及电枢初始触发位置进行确定，并考虑到IGBT元件的响应速度及后期的试验研究，以0.5 ms为步长改变IGBT导通时长，以1 mm为步长，改变电枢触发位置，两个试验因素皆有n个试验水平，放电时长${t_i}$与触发位置${x_j}$会得到电枢出口速度${v_{i,j}}$。在参数优化过程中，电枢出口速度呈先增后减的趋势，会得到电枢最大出口速度$ {v}=\max\left\{{{v}}_{{1},{1}}{{,v}}_{{1},{2}}{,}\cdots {{,v}}_{{n,n}}\right\} $，该速度下对应的放电时长t和触发位置x就为该发射器模型在此均匀实验法下IGBT1与IGBT2元件最优同步延时时长与电枢触发位置。

以此思想得到最佳参数如表3所示，由表3可知，关断电路下，电枢的最佳触发位置相对于未关断时都产生后移，在最佳触发参数下驱动线圈的电流、电枢所受电磁力、电枢速度及储能电容器电压变化如图5所示。

由图5（a）可知，优化后的发射器中驱动线圈中电流在关断后其电流下降速度进一步加快，由图5（b）可知，最优参数下可关断电路下的发射器其电枢受到的电磁制动力可以完全被抑制，部分电磁制动力未被抑制，一方面可能是因为放电电路中续流回路的电子元器件参数与发射器参数不适配，导致驱动线圈中剩余电流衰减速度相对过慢；另一方面可能是遏制电枢受到的电磁制动力不仅需要通过改变电路结构、触发位置和放电时长，还需对发射器的其他参数进行优化。由图5（c）可知，当电枢受到的电磁制动力被近乎完全抑制时，电枢的峰值速度就可作为电枢的出口速度，且三种可关断电路下电枢出口速度大体相同。

从图5（d）可知，Boost-Buck式电路在关断后可将驱动线圈剩余能量回收到另一组储能电容中以提高电容组初始电压，相较半桥式电路其应用在多级发射中更具灵活性。

发射装置在四种不同激励电路下，其系统的各自能量利用率以及三种可关断电路下发射器性能相较传统SCR式放电电路下发射性能提升比例如表4所示。

文献[5，11，13]中，发射器系统效率在0.786%～7.76%，对电枢初始触发位置、电路结构及电路参数等因素进行优化后，系统效率可达0.981%到11.61%，与表4中SCR电路效率4.84%，进行关断设计后效率可达15.52%～18.63%具有较好的一致性，从一定程度上也反应了文中四种放电电路设计的正确性。从表4中可以看出，可关断电路相较SCR式电路可以极大程度地提高电枢出口速度及发射系统性能。在可关断电路中，当电枢出口速度相近时，半桥式与Boost-Buck式的电路性能皆优于RCD吸收式电路的性能。

本文分析了磁阻型电磁线圈发射器在不同的放电电路结构下对发射性能的影响，采用有限元方法进行仿真分析得到以下结论：（1）电枢出口速度与其总冲量成正比、电枢反向冲量与电流衰减速率成反比；可关断的放电电路相对不可关断电路在相同参数下可大幅度提高发射器的系统性能，其中Boost-Buck式放电电路相对SCR式放电电路的出口速度提升最少为78.77%，RCD式放电电路相对SCR式放电电路的能量利用率提升最少为220.66%；（2）3种可关断电路中，剩余能量可回收的电路性能优于剩余能量损耗的电路性能，即半桥式放电电路与Boost-Buck式放电电路性能优于RCD吸收式电路，半桥式电路可回收更多的能量，Boost-Buck式更具灵活性。

本文仿真分析了四种放电电路对单级线圈发射器的性能影响，为后期对多级电磁线圈发射系统的电路设计与性能优化提供理论支撑。下一步的主要工作是进行系统性实验来分析三种可关断电路在相同工作条件下的实际性能，重点研究Boost-Buck式放电电路在多级发射器上的性能提升策略，通过实验数据优化电路参数，并测试各电路在不同应用场景下的表现，评估放电电路长期工作的稳定性