在HPM器件实验研究中，最大输出脉宽受限于谐振腔体表面的尖端场强。这是因为微波在腔体内传输过程中，前向波与反向波发生周期性叠加，当腔体内微波幅值达到一定程度时，金属表面的尖端位置会产生超过真空击穿场强阈值的强场击穿现象，从而导致脉冲缩短。此外，由于实验中器件内部并不是完全真空的状态，电场击穿阈值会有所下降，腔体中的金属尖端位置更易发生击穿，严重影响HPM器件的正常工作。

金属表面是否易发生击穿取决于多方面因素，例如器件表面最大场强，结构的材料、形状、粗糙度和微波器件内真空度等，在设计器件的时候，需要理论分析电场分布，合理选择腔体工作模式以降低最大表面场强，同时将器件尖锐位置进行倒角以减弱场强尖端效应。衡量输出功率水平与器件内部击穿风险最主要的参量是功率容量（PHC），功率容量为HPM器件稳定工作时，传输功率P_f与轴向最大表面场强绝对值E_m(z)的相对大小^[11]，即

当传输功率大小一定时，腔体金属轴向表面场强越大，那么功率容量越小，反之亦然。当轴向表面场强一定时，传输功率越大，说明功率容量也越大，反之则越小。

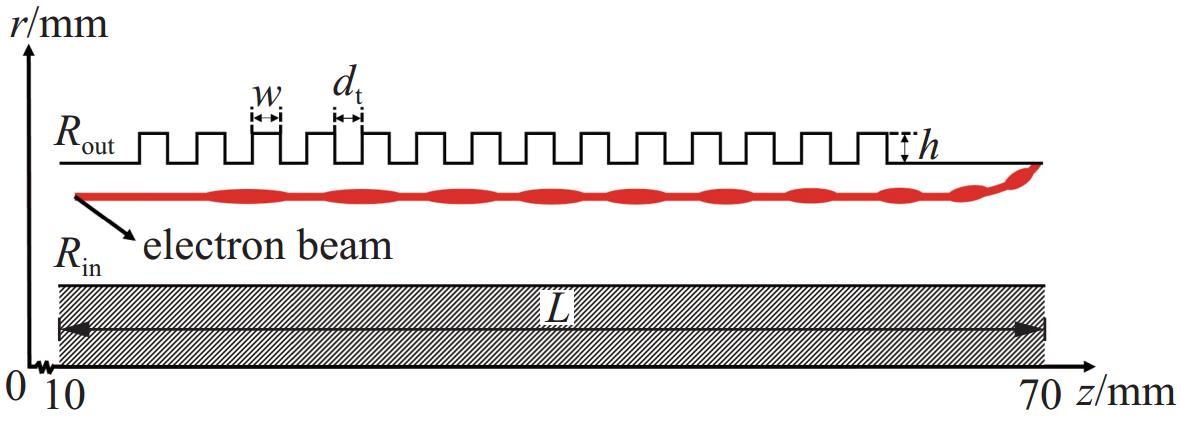
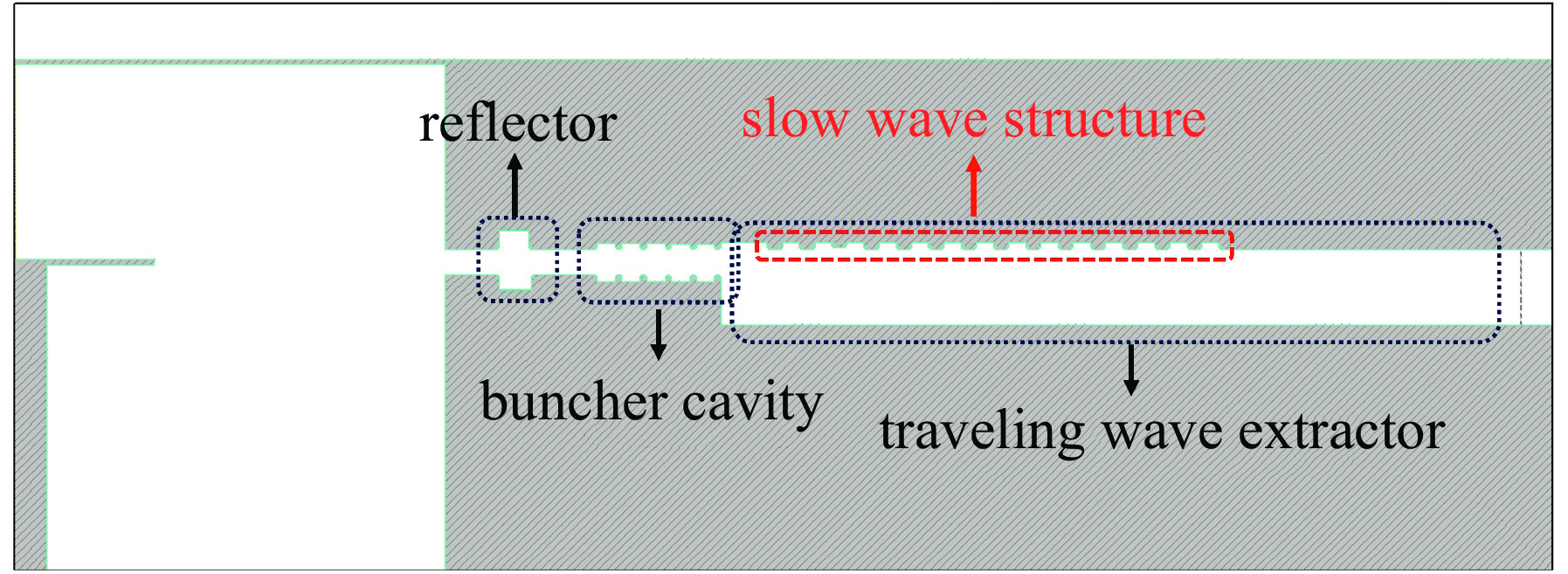
本课题组前期工作基础^[13,15-16]为在400 kV工作电压下，采用TM₀₂模式工作的大过模行波输出腔降低器件轴向表面场强，提升功率容量，并进行了实验验证^[18]。为了进一步降低器件轴向表面场强，提升功率容量，基于本课题前期工作基础，本文拟设计的HPM器件将采用TM₀₃模式工作的行波输出腔，且环形阴极中心半径和慢波结构外导体半径分布为28.8 mm和30.0 mm，过模比约为12，中心波长为4.82 mm，相应微波频率62.25 GHz。为了提升器件的起振时间，保留了传统TTO中的反射腔和调制腔，HPM器件整管结构见图1。为了增强器件对电子束的调制能力，选取调制腔的周期数为5，腔体高度和周期长度分别为3.6、2.3 mm。本文重点介绍器件行波提取腔和其中慢波结构的设计，如图2所示，图中R_in、R_out分别为腔体的内外导体半径；w、d_t分别为慢波结构的腔宽和腔体之间漂移段的长度；h为慢波结构的高度。接下来给出一些关键尺寸参数的具体设计。

将器件设计频点f代入到同轴结构TM₀₁截止波长经验公式可得

式中：c为光速。那么TM₀₂、TM₀₃模式的截止波长约为TM₀₁的二倍和三倍，由此得到

将TM₀₁、TM₀₂和TM₀₃模式的束通道宽度，即内外导体径向间距ΔR=R_out−R_in可以分别设置为2.4 mm、4.6 mm和7.1 mm。

在行波提取腔中，电子速度v_b需要与慢波结构中微波相速度v_p同步，且略大于微波相速度，即v_b≥v_p。微波相速度可近似表示成

式中：p为慢波结构单个周期长度，即慢波结构的腔宽w和腔体之间漂移段的长度d_t之和，φ为工作模式稳定后相邻周期电磁波相位变化大小，在本文中器件慢波结构的工作模式为TM₀₃模，一般位于−1次谐波区，因此φ的取值可以从π到2π。电子在二极管加速电压下的速度公式可表示为

式中：U₀为二极管加速电压，大小为400 kV。将参数代入到公式（5）和（6）中求得的慢波结构周期大小p可取值2 mm至4 mm，因此初步设置p大小为3 mm进行优化，单个周期中腔体宽度w和间隙宽度d_t大小分别设置为1.6 mm和1.4 mm。通过设计计算获得器件行波提取腔和其中慢波结构的主要尺寸参数如表1所示，表中N为慢波结构的周期个数。

下面拟用HFSS软件电磁仿真模块，得到工作模式为TM₀₁、TM₀₂、TM₀₃的三种腔体结构的轴向表面电场分布，然后从功率容量的角度，来确定对TM₀₃的选择。图3所示为模拟结果，横坐标为器件轴向长度，纵坐标为轴向表面电场大小。在相同的慢波结构尺寸下保持同轴结构外导体半径不变，通过改变同轴结构内导体半径，仿真得到的横向模式依次为TM₀₁、TM₀₂、TM₀₃模，同时获得三个模式在谐振频率相近时其轴向电场E_z在近外导体表面（R_out=30.0 mm）位置的分布。表2给出了HFSS仿真中每个模式在注入功率为1 W微波信号时的轴向最大表面场强数值。可以看出，3个横向模式中TM₀₃模的腔体轴向最大表面场强最小，根据公式（1），说明TM₀₃模式理论上在三个模式中具有最高的功率容量，并且工作在TM₀₃模式的腔体内外导体间距较宽，能够存储相对多的能量。由此分析可知，相对于其他模式，工作在TM₀₃模式的V波段同轴渡越时间振荡器有望获得更大的输出功率和输出脉宽。

HPM器件的基本结构如图1所示，二极管包括石墨阴极和阴极基座，阳极包含前置反射腔、5间隙调制腔和14周期行波提取慢波结构。为了进一步降低电子束空间电荷效应、提升器件的功率容量，器件往往设置为较大的过模比，这会导致行波提取腔内可能激励起的模式随之变多。工作在TM₀₃模式的腔体具有大过模、大腔宽，因此纵向模式间隔很小，在腔体中很容易导致杂模在起振的过程中被放大。因此，为了使TM₀₃模式成功在行波提取腔中起振，还需要进行优化设计。我们首先通过设计慢波结构的周期与腔深，计算结构场分布、同步条件来获得冷腔色散以此确定工作频点。然后，通过优化腔体结构调节耦合阻抗、微波群速度、起振电流，使TM₀₃模式具有较高的耦合阻抗、较小的群速度以及较小的起振电流，从而使TM₀₃模式能够优先起振并达到饱和。

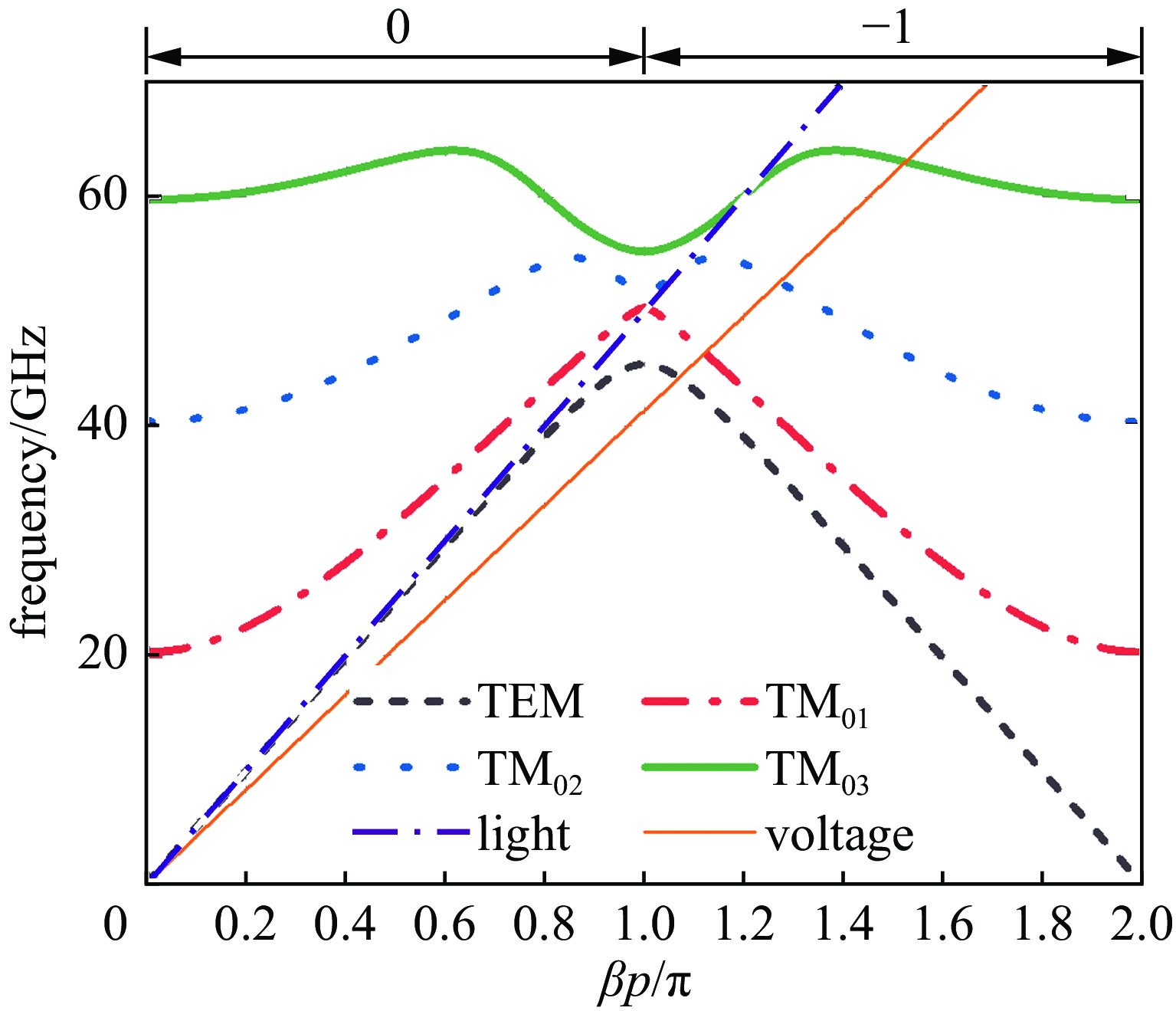
色散曲线是慢波结构设计最基本的依据^[19]。图3所示为基于表1中的慢波结构尺寸参数计算的慢波结构色散曲线，横坐标为纵向传播常数β_n和周期长度p的乘积，图中斜率较低的黄色直线为电子束线，60 GHz附近的实心曲线为TM₀₃模式色散曲线，它们的交点为400 kV同步电压下的器件工作点，其中电子束线的斜率代表微波相速，色散曲线上该点切线的斜率代表微波群速。由图可以看出，电子束线交TM₀₃模式曲线于–1次谐波区的（21/14）π模工作点，对应坐标横轴1.53，近似取值1.5。

为了表示电子束与微波本征模式间相互作用的强弱程度，耦合阻抗是研究HPM器件束波互作用时人为定义的一个具有阻抗量纲的参数^[20]，耦合阻抗越大，表示电子束可以更有效地将能量交给本征电场，从而激励起所需要的电磁波，第n次空间谐波的耦合阻抗计算公式为

在式（7）中，$ {{E}_{n}^{2}({\textit{z}})} $为器件主要工作模式的第n次谐波在腔体间隙中电子束半径位置的轴向电场的平方，$ \;{ \beta }_{n} $为工作模式n次谐波的相位传播常数，它与慢波结构周期长度的乘积就是色散曲线上的工作点所对应的横坐标，在图4中，电子束线与TM₀₃模式色散曲线交于−1次谐波区，$ \;{ \beta }_{0} $为该模式0次谐波所对应的相位传播常数；P为单个周期慢波结构中的功率流，该功率可由慢波结构周期长度p、电磁波群速度v_g和单个周期长度容纳的微波能量W来表示。

式（7）中群速度v_g表示的是电磁波能量传输的速度，数值大小为色散曲线上某点切线斜率的绝对值，方向由切线斜率的正负来表示。群速度的定义

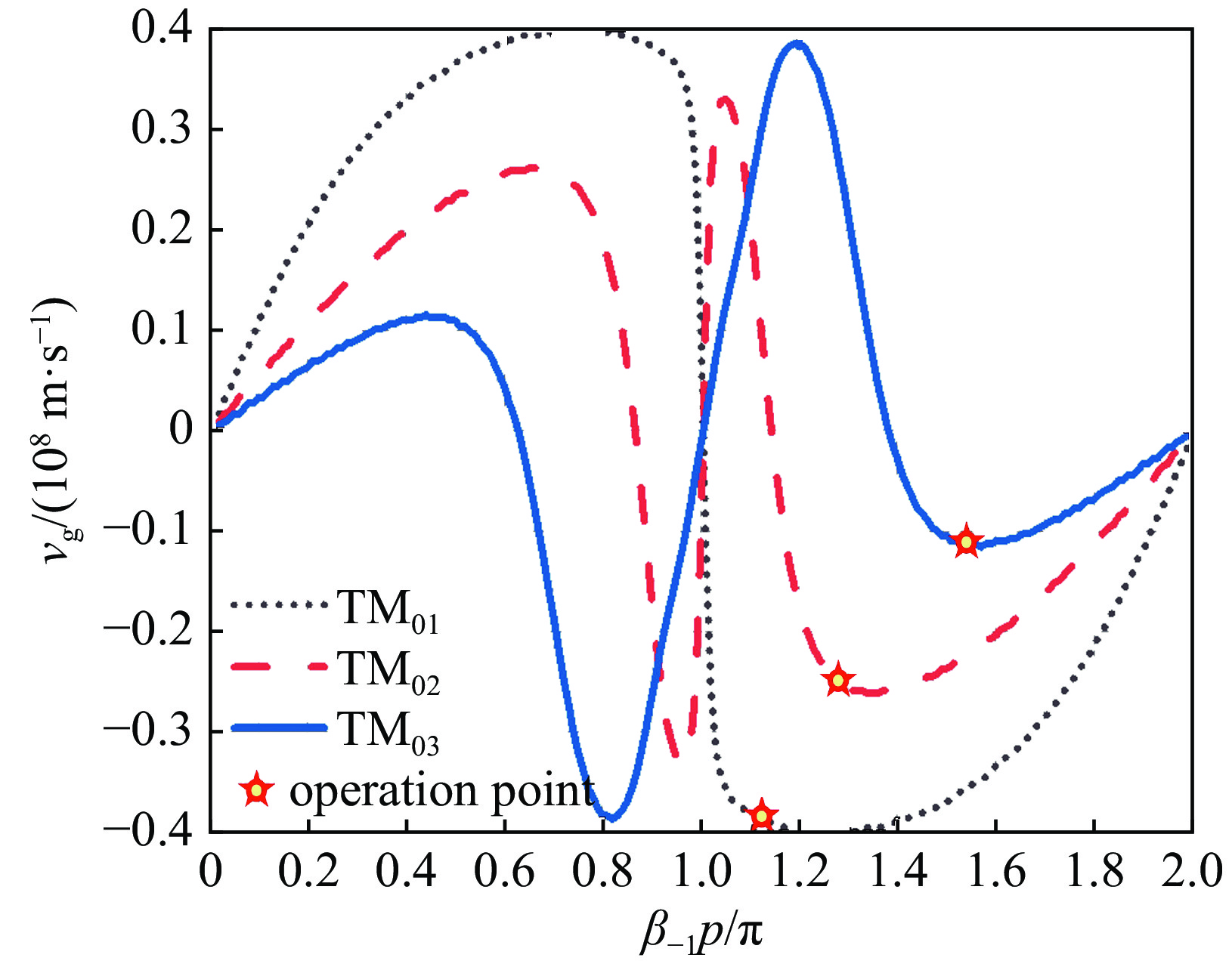
式中：$ \omega $是微波角频率。

图4给出了由式（9）得到的三个模式的群速度与相位常数的对应关系，并在图中标出了每个模式的工作点。计算得到TM₀₁、TM₀₂、TM₀₃三个模式的群速度大小分别为3.8×10⁷ m/s，2.5×10⁷ m/s，1.1×10⁷ m/s，可以看出TM₀₃模式在工作点附近具有绝对值最小的群速度。

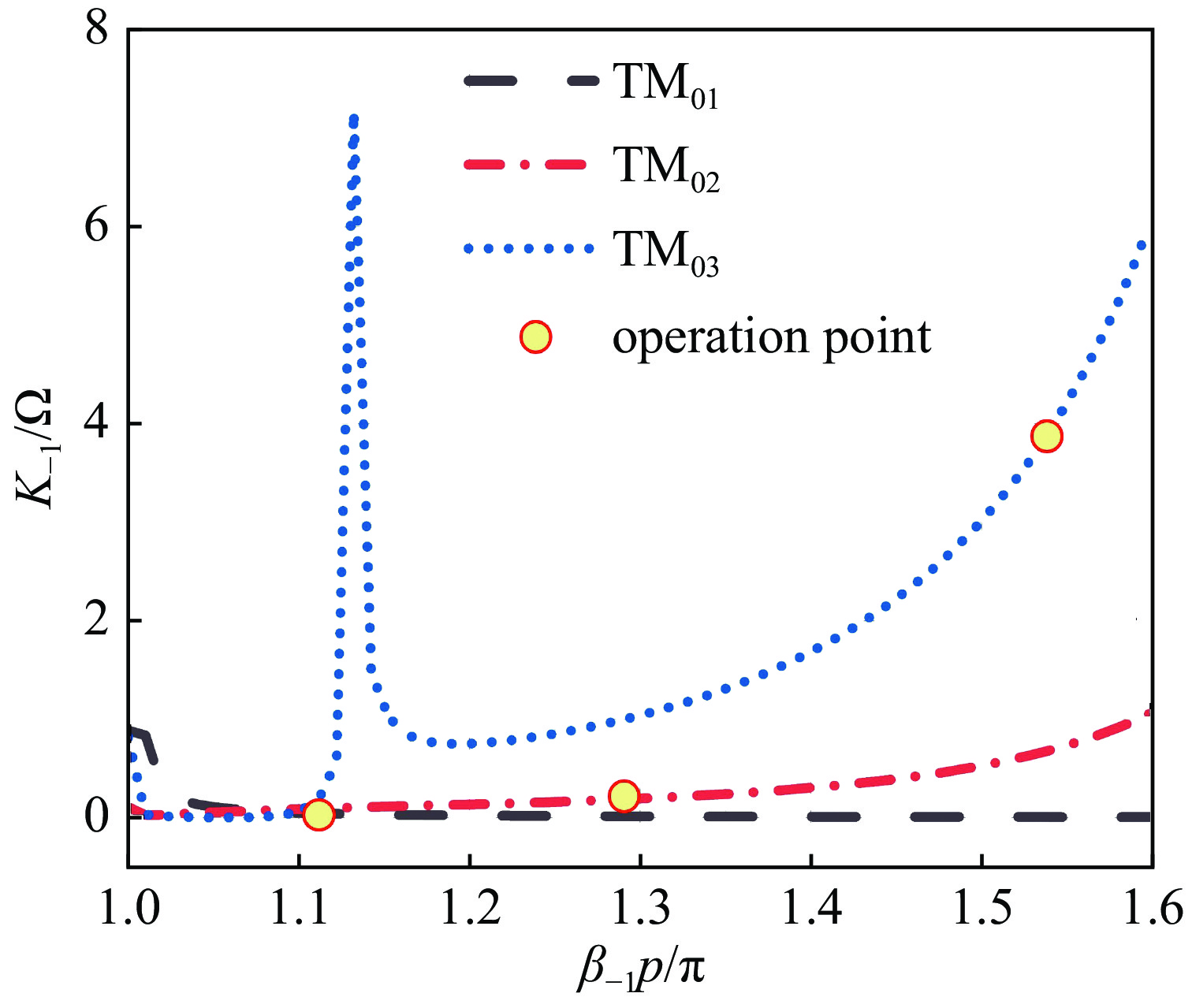
从图4得到群速度的数值大小后，对不同模式的耦合阻抗进行了计算。图5是每个模式的耦合阻抗随纵向传播常数的变化趋势，纵坐标K₋₁为TM₀₁、TM₀₂、TM₀₃模式的−1次谐波工作点的耦合阻抗，大小分别为0.03、0.18、3.9 Ω，可以看出TM₀₃模式的耦合阻抗高于其他模式，说明在束波互作用区，TM₀₃模式电磁波与电子束的换能效果最好。因此在这三个可能被激励的横向工作模式中，TM₀₃模式具有最大的耦合阻抗从而将优先被激励起来并成为主要工作模式。

起振电流描述了某个模式起振时在HPM器件腔体中所需的最小电流，因而当该模式具有相对其他模式较小的起振电流时，该模式将能够优先起振并成为主要工作模式。起振电流表达式^[20]

式中：N为慢波结构周期个数，$ C\left({r}_{\mathrm{b}}\right) $为电子束在中心半径处与慢波结构轴向电场的耦合系数，它的数值大小趋势与耦合阻抗完全一致，β₋₁即微波模式轴向传播常数，由前面色散曲线给出，γ为相对论因子，$ \eta\mathrm{_{lin}} $是由器件的尺寸定义的线性效率，Q为腔体的品质因数。$ {I}_{A}=m{c}^{3}/e $，其中m和e分别为电子质量和电荷，c为真空中光速。该式中需要重点关注的是腔体个数N与品质因数Q，这两个参数能够极大地影响模式的起振时间，N即表1中的慢波结构周期数14，Q值的表达式如下

式中：L为互作用区间的总长度，如图2所示。R为慢波结构末端处，即图2从左到右第14个慢波周期处的微波反射系数。由于在确定基本慢波结构参数和色散曲线后，不同模式之间只有群速度的区别较大，因此由公式（10）、(11)，可得TM₀₃模式在同步电压下由于群速度小而具有高Q值和低起振电流。

由此可见TM₀₃模式比起TM₀₁和TM₀₂模式具有更大的耦合阻抗和更易达到的小起振电流，因而在模式竞争中具有优先起振的优势。

根据前面对HPM器件结构参数的设计和模式控制分析，下面将使用PIC粒子模拟软件CHIPIC对HPM器件整管结构进行模拟仿真。为了贴合开展实验时的实际条件，代入了由磁场仿真软件SUPERFISH仿真得到的螺线管磁场位型曲线，磁场峰值大小为1.2 T，在收集极位置逐渐降低，从而将电子束引导至收集极。

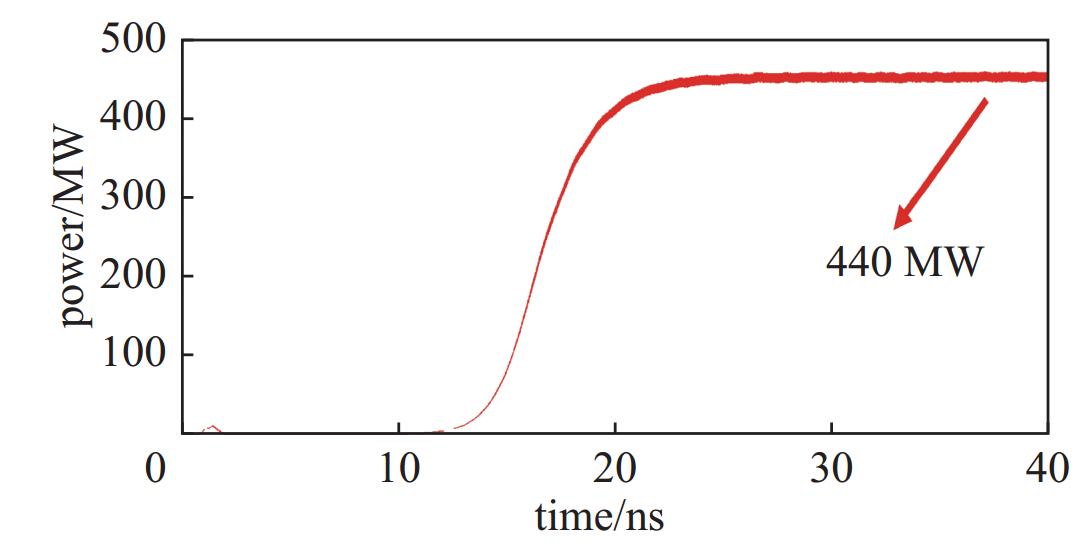
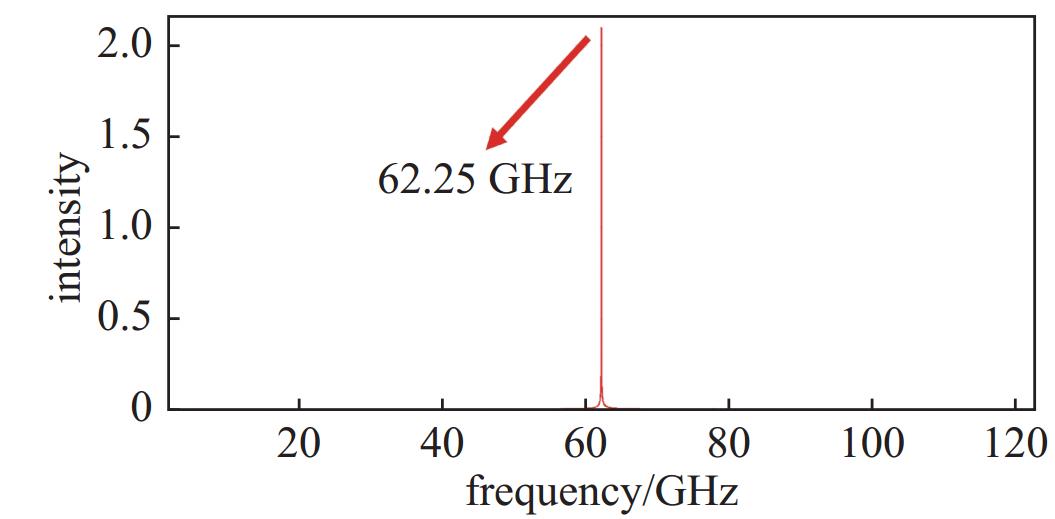
将导体材料设置为带损耗的金属材料，馈入电压400 kV、电流5 kA、总功率为2 GW的电脉冲进行仿真。图6为通过粒子模拟仿真获得的电磁波输出微波功率曲线，由图可知微波输出功率为440 MW，饱和时间25 ns，效率22%。图7为输出微波频谱图，说明该器件工作频点为设计频点62.25 GHz且频谱纯净，验证了设计结果的合理性。

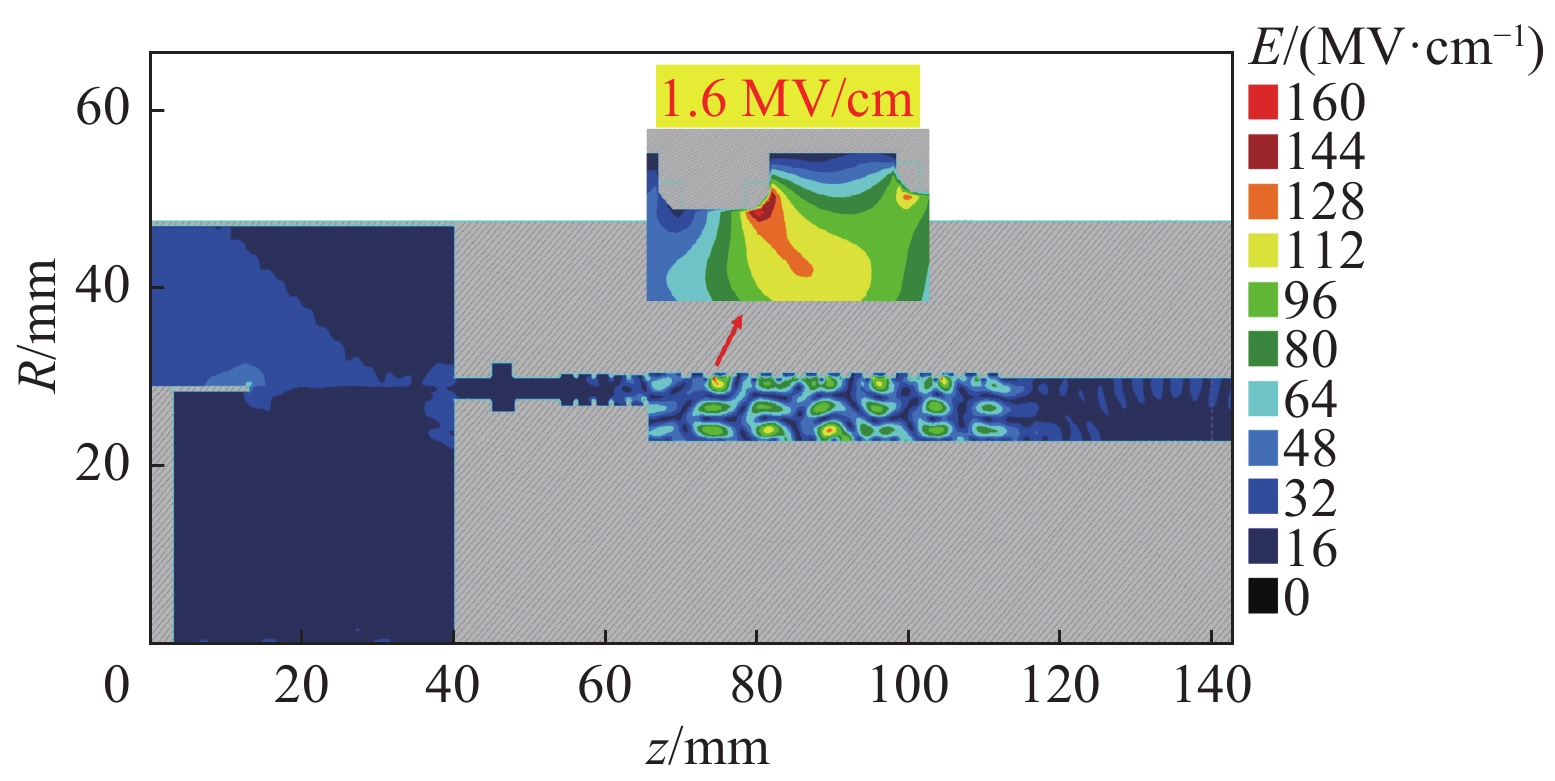
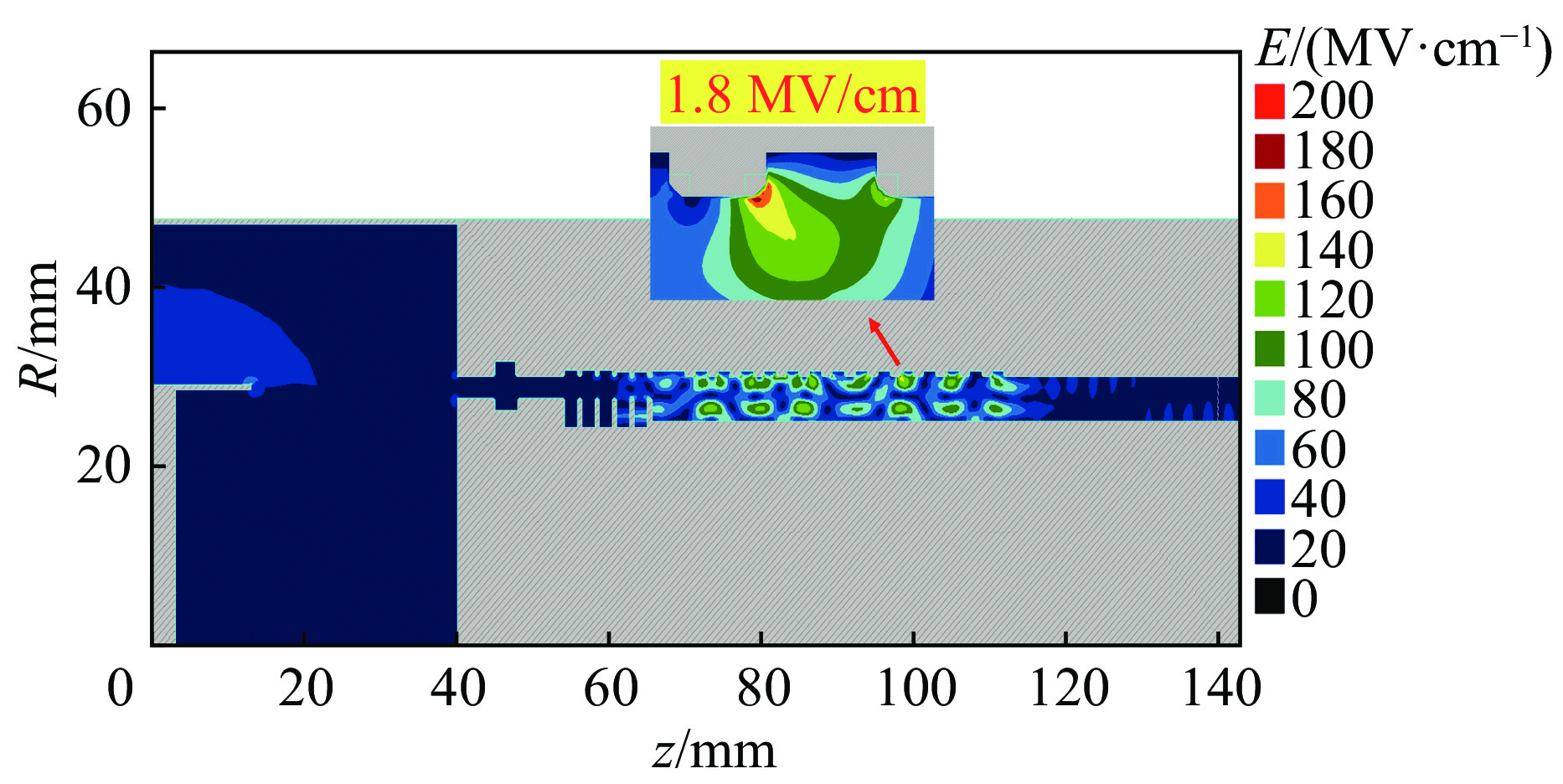
通过粒子模拟获得，器件在提取结构的束波互作用区的横向工作模式为TM₀₃模式，基于TM₀₃模式工作的结构轴向最大表面场强出现在第一腔体与第二腔体之间的间隙位置，如图8所示，数值大小为1.6 MV/cm。对比本课题组之前的研究工作^[18]，基于TM₀₂模式工作的结构轴向最大表面场强出现在倒数第三腔体与第四腔体之间的间隙位置，如图9所示，数值大小为1.8 MV/cm。应用TM₀₃模式后腔体轴向最大表面场强由1.8 MV/cm下降到了1.6 MV/cm，下降比例11%。由此可见，对比基于TM₀₂模式工作的腔体结构，TM₀₃模式能够在更大的腔体尺寸下，保持更低的表面场强，从而有望降低实验中射频击穿风险，获得更高的器件输出功率、更长的脉冲宽度。

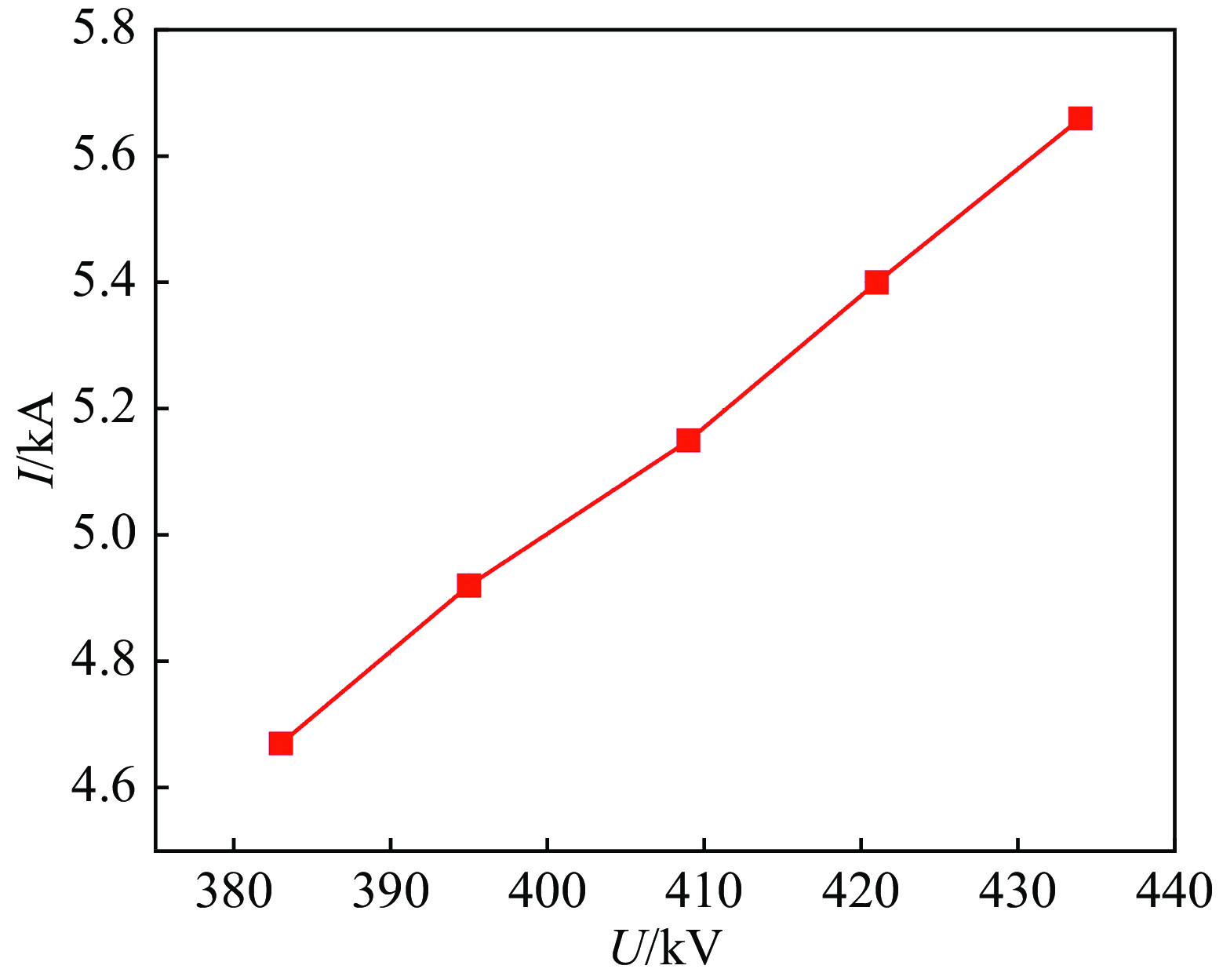
接下来进行了器件工作区间、敏感性参数研究等仿真工作，图10为器件伏安特性曲线，可以看出在电压380～440 kV的范围内未达到发射饱和，二极管发射能力正常，并能够在400 kV的电压下提供5 kA的粒子束流。

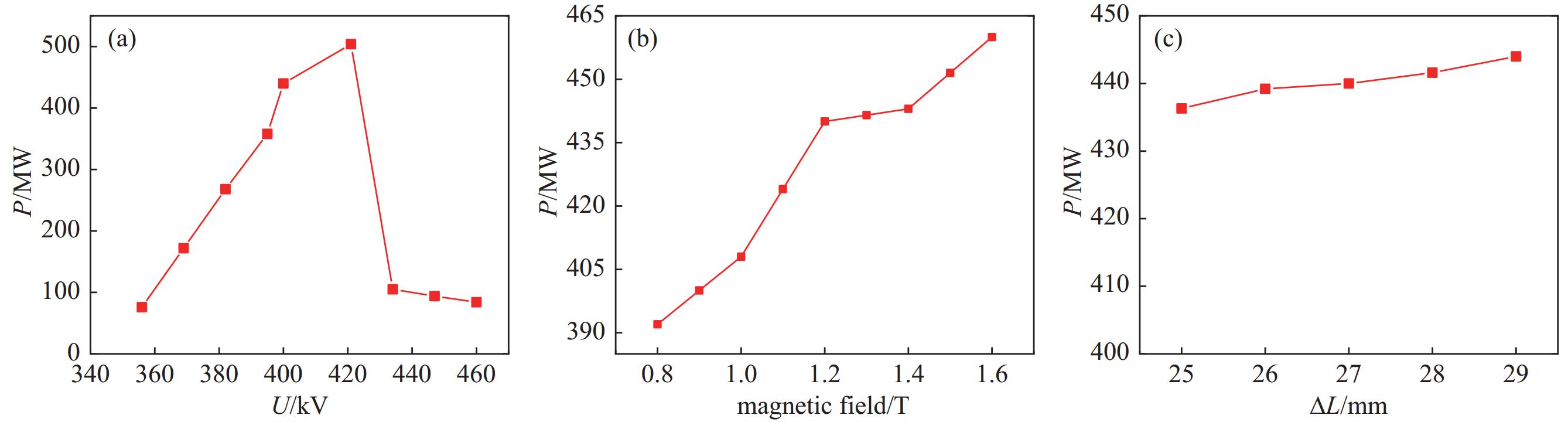
图11分别计算了输出功率随二极管电压、外加磁场及阴阳极间距的变化趋势。由此可以得到结论：（1）二极管电压从350 kV到420 kV时，输出功率逐渐增大，并在工作电压为400 kV时达到440 MW；当二极管电压大于420 kV时，输出功率骤降至百兆瓦以下，这是由于腔体内模式发生跳变的缘故；（2）磁场大小从0.8 T到1.6 T，输出功率从390 MW增长至460 MW，但是过大的磁场会大幅提升实验中磁路系统的体积重量，导致整个装置过于复杂，因此这种选择了1.2 T；（3）通过改变阴阳极间距ΔL来改变二极管阻抗时，输出功率能够始终保持在425 MW以上，证明了器件在一定范围内的稳定性。

为了提升V波段HPM器件的功率容量，论文提出了一种基于TM₀₃模式的大横向尺寸束波互作用结构的V波段同轴渡越时间振荡器，并进行了结构参数设计。从计算TM₀₁ 、TM₀₂和TM₀₃三个模式的冷腔场分布、色散曲线、群速度，到耦合阻抗和起振电流分析表明，在该设计参数下TM₀₃模式相对TM₀₁和TM₀₂等其他模式能够优先起振，且采用TM₀₃模式能在一定程度上提升腔体的功率容量，证明了设计结果的正确性。通过粒子模拟在束波互作用结构中成功激励起TM₀₃模式，器件工作电压为400 kV，工作电流为5 kA，磁场大小为1.2 T，获得了440 MW的高功率微波输出，器件效率为22%，轴向最大表面场强不超过1.6 MV/cm，验证了设计结果的合理性，为后续实验研究奠定了基础。