本文选用了最简易的波导分支元件——波导T型转接头作为功率合成器^[12]，为满足磁控管功率合成系统的对等特性^[9]，则可进一步确定为H-T分支接头合成器，后续称为H-T功率合成器。H-T功率合成器的S参数矩阵^[12]为

若两路功率信号${P_{{\text{H-T}}.1}}{{\text{e}}^{{\text{j}}{\varphi _1}}}$和${P_{{\text{H-T}}.2}}{{\text{e}}^{{\text{j}}{\varphi _2}}}$同时入射H-T功率合成器，根据H-T功率合成器的S参数矩阵，H-T功率合成器的合成输出为

式中：P_H-T.1，P _H-T.2为入射信号的功率；${\varphi _1}$和${\varphi _2}$为信号入射至H-T功率合成器端面处的相位。

则H-T功率合成器的合成效率为

式中：k为功率比，$ k = \dfrac{{{P_{{\text{H-}} {\text{T}}{\text{.1}}}}}}{{{P_{{\text{H-}} {\text{T}}{\text{.1}}}}}} $。

从式（2）和（3）可知，当入射H-T功率合成器的信号功率相等且相位相同时，合成器的合成效率最高且达到了100%；随着两路功率信号的入射相位差从0°变化到180°时，H-T功率合成器的合成功率从$ \left( {{P_{{\text{H-}} {\text{T}}{\text{.1}}}} + {P_{{\text{H-}} {\text{T}}{\text{.1}}}}} \right) $线性减小为0。故功率合成系统可以通过控制入射H-T功率合成器的信号相位来实现输出功率的实时控制。

从前文可知，合成输出功率实时控制的本质是控制入射H-T功率合成器的信号相位，下面讨论建立注入频率与高功率磁控管输出相位的关系，实现通过注入频率实时控制合成系统的输出功率。

在注入锁定的合成系统中，外注入与互注入效应并存。延续先前的工作^[9]，则可先考虑两只对等磁控管的互注入效应，假设两只磁控管各体差异可以忽略，外观品质因数相近，功率合成网络互易对称，则根据Adler理论^[13]可知，磁控管入射至H-T功率合成器的相位差Δφ将满足如下方程

式中：${\omega _1}$和${\omega _2}$分别是两只磁控管各自的自由振荡频率；$\Delta \omega $为频差；Q是外观品质因数；${\varphi _1}$和${\varphi _2}$是两只磁控管的输出相位；${\xi _{12}}$表示自由振荡频率为${\omega _2}$的磁控管对自由振荡频率为${\omega _1}$的磁控管的耦合强度；${\xi _{21}}$表示自由振荡频率为${\omega _1}$的磁控管对自由振荡频率为${\omega _2}$的磁控管的耦合强度；${\mathit{\Phi}} $则代表互注入路径上带来的相位超前或者滞后。

在稳态情况下，${{{\text{d}}\Delta \varphi } \mathord{\left/ {\vphantom {{{\text{d}}\Delta \varphi } {{\text{d}}t}}} \right. } {{\text{d}}t}} = 0$，又因为$\left| {\sin \left( {{\mathit{\Phi}} + \Delta \varphi } \right)} \right| \leqslant 1$，则其中任一只磁控管的互注入锁定条件^[13]为

式中：i≠j，i=1、2，j=1、2；${\omega _i}$为第i只磁控管的自由振荡频率；${\xi _{ij}}$表示第j只磁控管对第i磁控管的耦合强度。

则锁定输出频率都为

然后，在注入锁定的合成系统中，两只磁控管都还有外注入信号，且两只磁控管还可分别被各自的外注入信号锁定，根据Adler理论^[13]，任一只磁控管输出信号φ_i将满足如下方程

式中：$ {\rho _{{\text{inj}}\_i}} = \sqrt {{{{P_{{\text{inj}}\_i}}} \mathord{\left/ {\vphantom {{{P_{{\text{inj}}\_i}}} {{P_i}}}} \right. } {{P_i}}}} $，i≠j，i=1、2，j=1、2；φ_i和φ_j是磁控管输出相位，${\varphi _{{\text{inj}}}}$是注入信号的相位，$ {\rho _{{\text{inj\_}}i}} $是第i只磁控管的注入比，P_i是第i只磁控管的输出功率。

最终，根据线性叠加原理或N. Shinohara理论^[14]，合成系统中两路磁控管输出的瞬时相位差（即入射至H-T功率合成器的相位差Δφ）满足下述方程

从式（8）可知，两只磁控管的输出相位差（即入射至H-T功率合成器的相位差Δφ）与磁控管自由振荡频率及注入功率的关系如下：1）当两只磁控管的自由振荡频率频差$\Delta \omega $近似为0，且注入功率一致时，此时两只磁控管的输出相位必然满足同步条件，式（8）简化为Adler方程^[13]，故即使注入频率在锁定区域移动，合成系统的输出功率维持不变，此状态不可实现注入频率控制合成输出功率，故本文后续不对此情况进行讨论；2）当两只磁控管的自由振荡频率频差$\Delta \omega $近似为0，且注入功率不一致时，则注入频率在锁定区域移动，合成系统的输出功率维持不变，若注入频率移动至低注入功率磁控管的外注入锁定边界时，该只磁控管的输出相位相对于外注入信号相位会快速翻转180°，则系统的合成输出功率也跟随快速降低，此状态可注入频率控制合成输出功率；3）当两只磁控管的自由振荡频率频差$\Delta \omega $不为0，但满足互注入锁定条件，且注入功率相等时，则注入频率在锁定区域移动，两只磁控管的输出相位差为不同常数，此状态也可实现注入频率控制合成输出功率。因此，当磁控管功率合成系统的自由振荡频率和注入功率满足条件2）或条件3）时，可通过控制注入频率实现两路磁控管输出相位差的控制，也即实现H-T功率合成器入射端面的信号相位控制，从而实现通过注入频率控制系统的合成功率输出。由于该原理实现的功率合成系统是通过注入频率控制系统的输出功率，故将这种微波源称之为频控功率源。

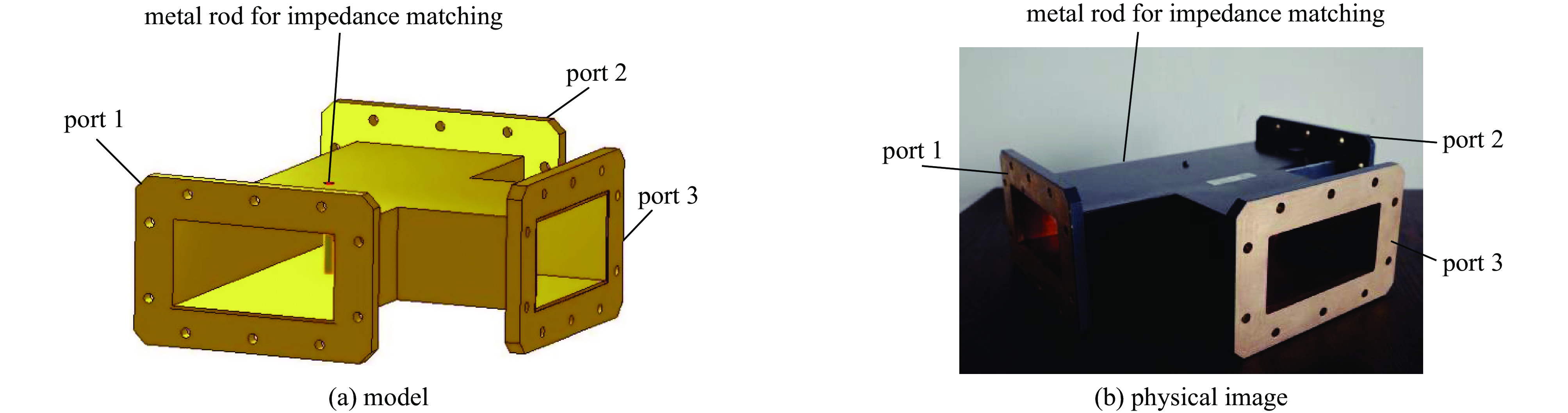
根据节1中H-T功率合成器的S参数矩阵，H-T功率合成器无法同时匹配所有端口，为实现高效的功率合成，只需对H-T功率合成器的输出端口进行匹配设计，故本文的设计思路是在传统WR430 H-T分支波导的基础上，插入一个圆柱形的销钉，实现输出端口的阻抗匹配。所设计的H-T功率合成器模型及加工实物如图1所示。H-T功率合成器的端口1和端口2为信号的入射端口，端口3为合成信号的输出端口，输出端口3的中间为用于匹配的圆柱形销钉。

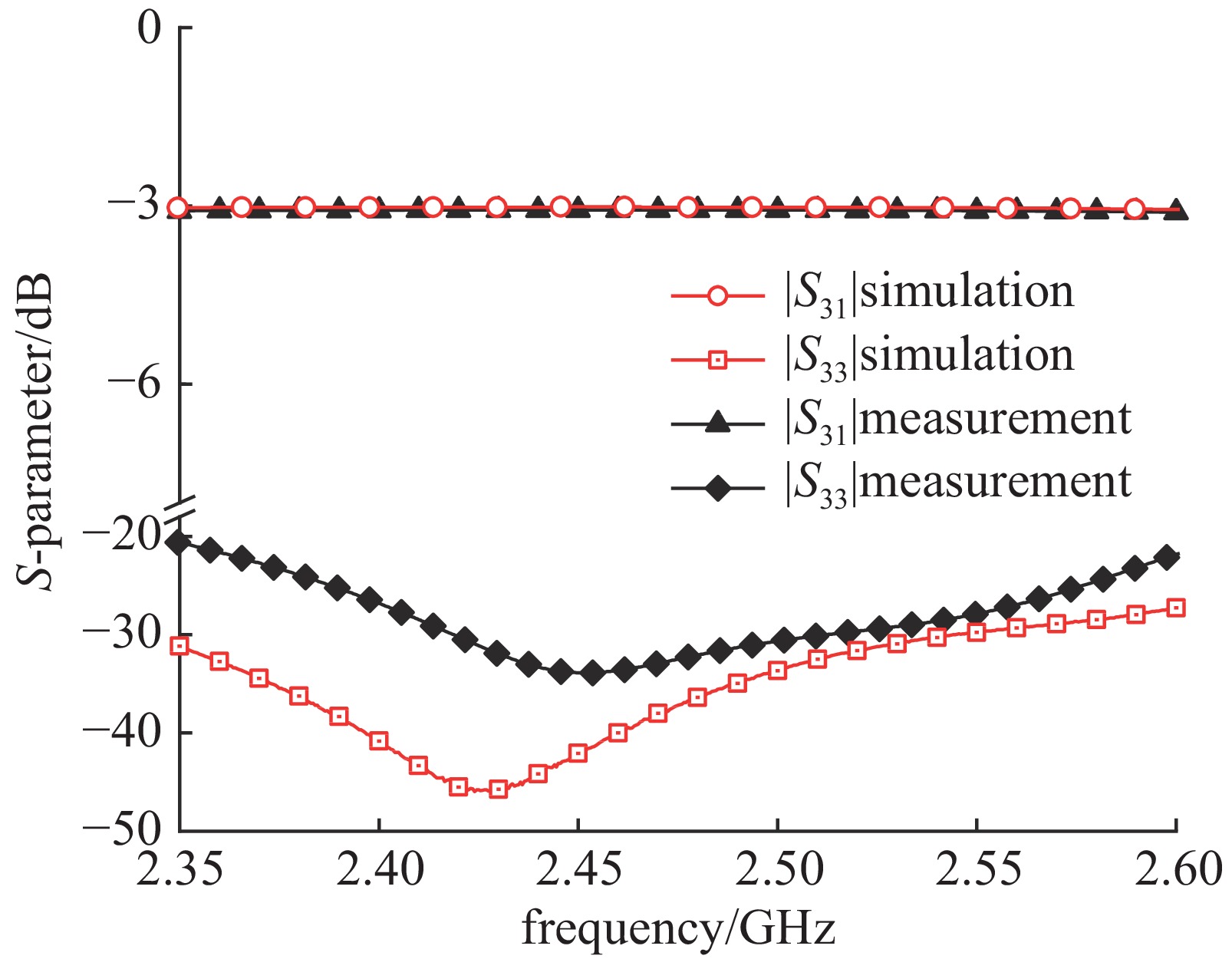
H-T功率合成器因匹配销钉引入了不连续性，该不连续性会引起H-T功率合成器中激励起高次模，从而增大了H-T功率合成器的损耗，故使用商业软件反复优化设计，尽量抑制高次模效应，优化后的设计和实测S参数结果如图2所示。从图2可知，输出端口的S参数S₃₃仿真时低于−30 dB，输出端口的实测S参数也低于−20 dB，匹配特性良好；传输系数|S₃₁|接近3 dB，插入损耗小于0.05 dB，性能理想。

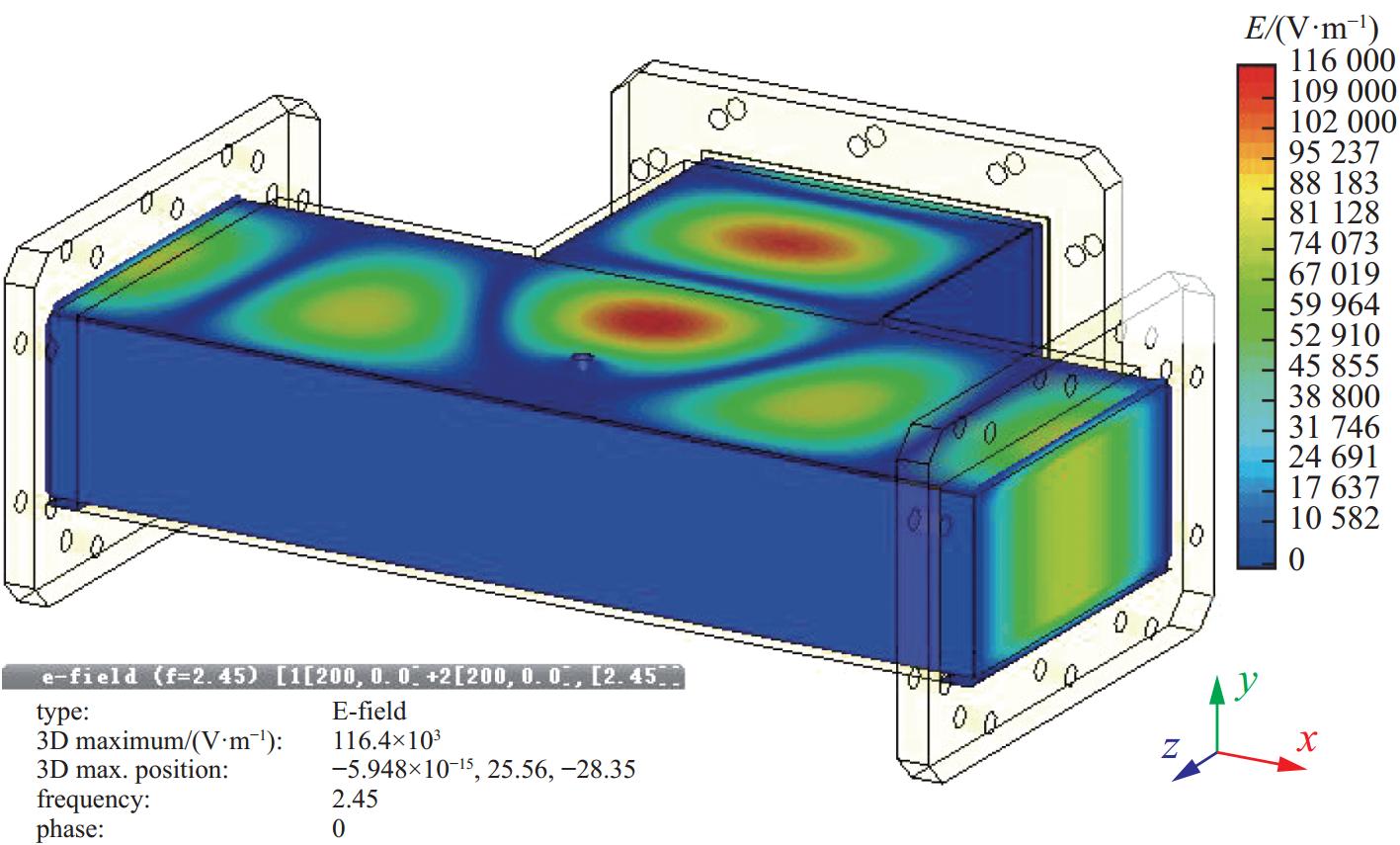
为了验证H-T的功率容量，在商业仿真软件中用两路等功率同相的20 kW信号同时激励H-T功率合成器，其电场分布结果如图3所示。

从图3中可知，输入端口处的电场分布对称，输出端口处的电场约为输入端口的$\sqrt 2 $倍，通过坡印亭矢量公式^[15]求出H-T功率合成器合成端口输出功率约为39.72 kW，则可计算出合成效率高达99.3%；合成电场最强的位置位于输出端口和销钉之间，电场强度为116 kV/m，远远小于连续波击穿空气的场强30 kV/cm，所以H-T功率合成器功率容量明显高于40 kW。

利用上节中的H-T功率合成器，构建了基于20 kW S波段注入锁定磁控管的频控功率源系统，其原理框图如图4所示。

频控功率源系统的高功率部分见图4中白色框图部分所示，两只20 kW CK-2091连续波磁控管的输出信号分别经过各自的四端口环行器导向（四端口环行器一方面将磁控管的高功率信号与注入信号隔离，并导入注入信号至磁控管，另一方面实现磁控管的输出保护，防止磁控管输出反射功率过大而烧毁磁控管）后，分别传输至60 dB波导定向耦合器，耦合采样后的两路高功率信号送至H-T功率合成器，合成后的功率信号由一个60 dB波导定向耦合器采样后流向大功率水负载，绝大部分微波功率被该负载所吸收，剩余的少部分功率反射回四端口环行器，由隔离负载吸收。图4中大箭头指示了磁控管的高功率信号传输路径，小箭头指示了磁控管之间互相耦合的信号传输通道。

频控功率源系统的注入部分由图4黄色框图部分表示，注入信号由安捷伦矢量信号源产生，经3 dB功分器等分为两路等功率同相信号，等分后的两路信号分别经过200 W功率放大器放大后，再分别由20 dB的耦合器采样后，最后通过环行器注入磁控管。磁控管的注入功率则是通过调节功放的增益来实现。

频控功率源的测试部分如图4中绿色部分所示，两只20 dB耦合器的耦合端接至功率计，采样外注入信号的功率；3只60 dB耦合器的耦合端接至功率计采样H-T的入射信号功率与合成信号功率，60 dB耦合器的反向耦合端接至频谱仪用于采样该系统的频谱质量。

按照之前的工作，先从对等磁控管的功率合成开始^[9]，分别开启两只磁控管，利用频率推移实现20 kW磁控管自由振荡频率的牵引，即分别调节两路磁控管的阳极电流，分别记录两只磁控管在不同阳极电流下的工作参数与状态。随后，选取了分别满足第二节中条件2）和条件3）的两种初始状态，在这两种初始状态下，同时开启两只磁控管，确认并记录此时对等功率合成的工作状态。最终，把满足第二节中条件2）和条件3）的两种初始状态标记为初始状态（1）和初始状态（2），其工作特性参数列入了表1。

根据第二节的理论分两种情况进行实验研究：

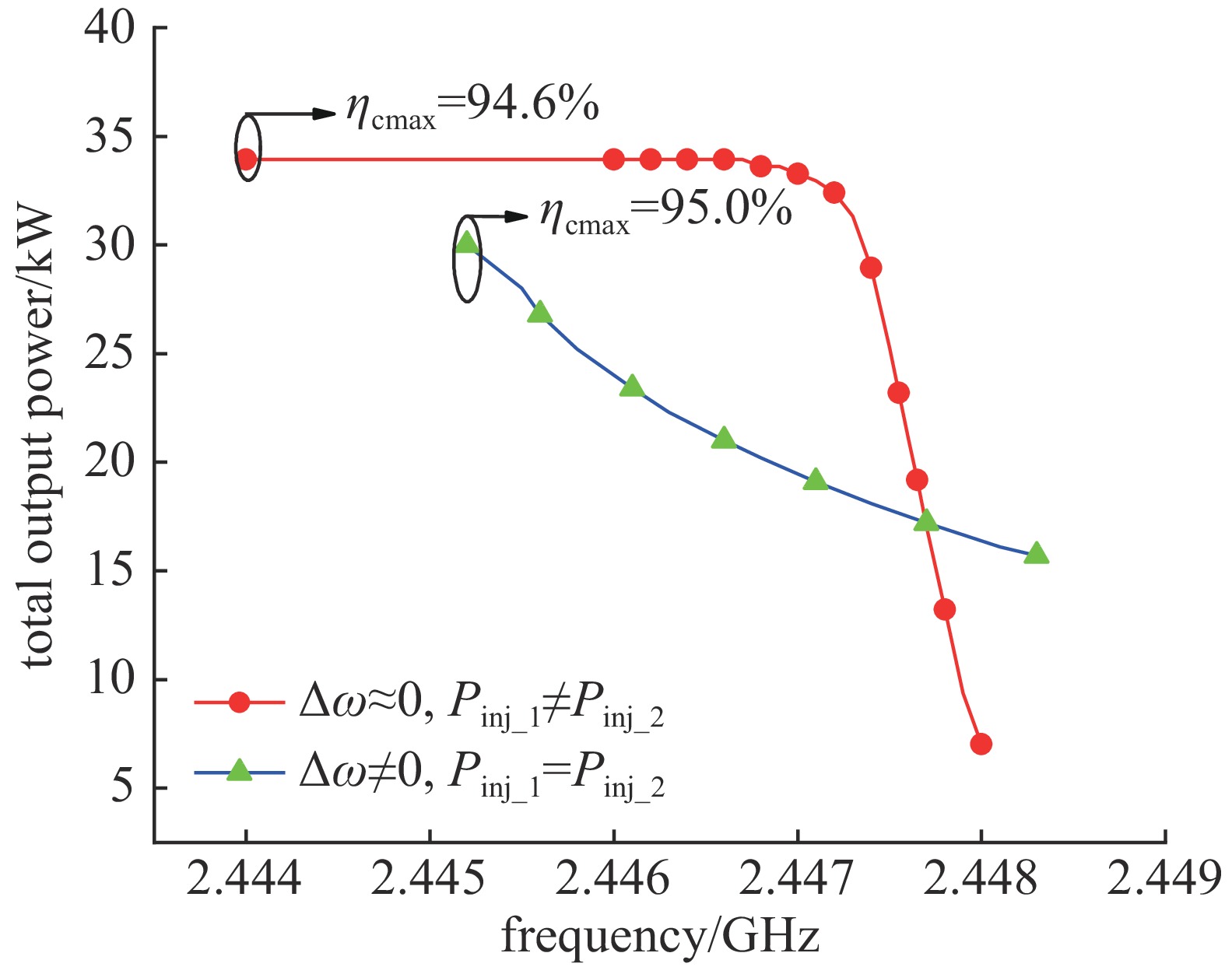
第一种情况：在第（1）种初始状态下，保持一路注入功率为100 W，另一路通过调节功率放大器的增益，将注入功率降低至70 W左右，则可实现条件2）描述的频控功率源，实验结果如图5中红色曲线所示，频控功率源系统的锁定范围为2.4440～2.4480 GHz，双管的注入锁定带宽达到了4.0 MHz。在2.444～2.4469 GHz的锁定频率范围内，H-T总合成输出的功率约为33.9 kW，H-T功率合成器的合成效率为94.6%；当进一步提高注入频率，若注入频率高于2.4469 GHz，随着注入频率增加，H-T合成输出功率快速降低，当注入频率增加至2.4480 GHz时，H-T的合成功率降低至7 kW左右，功率控制范围约6 dB。造成这种现象的原因是外注入信号功率较低的一路磁控管已经处于外注入信号的锁定边界，此时其对应注入的磁控管输出相位相对于外注入信号相位会快速翻转180°，导致H-T入射相差从0°向180°移动，实现了第二节中条件2）描述的频控功率源。

第二种情况：在第（2）种初始状态下，两只磁控管的自由振荡频率差约为1.2 MHz，两只磁控管之间的自由振荡频率差异不可忽略，两只磁控管之间互注入的功率分别为200.0 W和183.5 W，满足式（5）互注入锁定条件，两路磁控管互注入锁定于2.4460 GHz，与式（6）计算结果一致。通过H-T功率合成器后端的60 dB耦合器确认磁控管都振荡在2.4460 GHz以后，连接注入支路并打开信号源，对两只磁控管注入100 W等功率同相的信号，并在2.4460 GHz附近移动注入频率，测得注入锁定频率与H-T功率合成器的合成功率关系，如图5中蓝色曲线所示。频控功率源的注入锁定范围为3.1 MHz，随着注入频率的增加，H-T合成器合成功率降低，当注入频率为2.4452 GHz时，双管合成效率最大，约为95.0%，合成输出功率为30.0 kW；当注入频率为2.4483 GHz时，双管合成效率最小，约为48.4%，合成输出功率约为15.2 kW，功率控制范围约为3 dB，实现了第二节中条件3）描述的频控功率源。

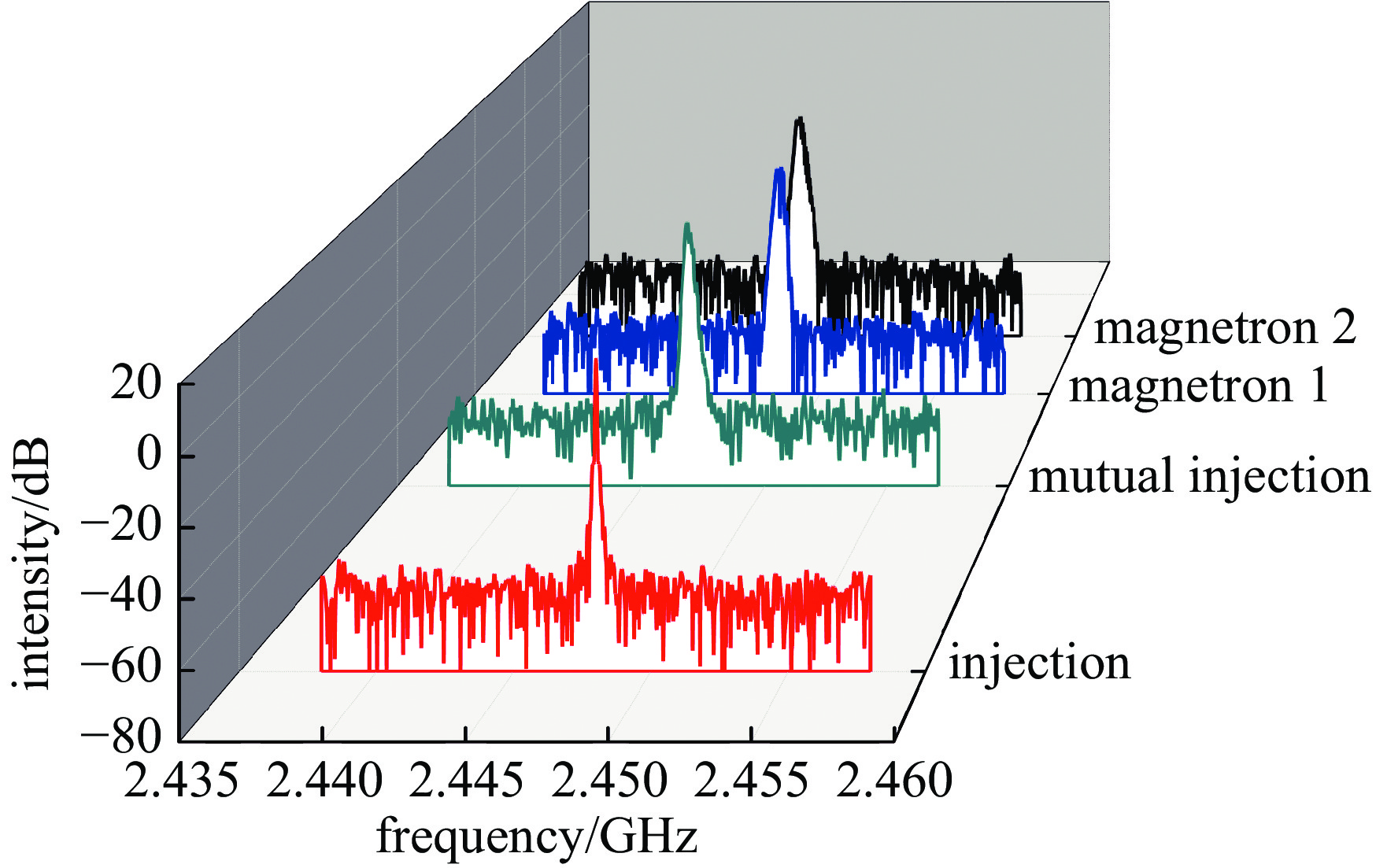
为了说明此频控功率源的优越性，进一步对基于注入锁定频控功率源的输出频谱特性进行了表征与对比，如图6所示。当两只磁控管处于自由振荡状态时，磁控管输出振荡频谱谱宽较宽，各自的输出频率漂移现象明显；当两只磁控管达到互注入锁定之后，磁控管输出频谱稍微收窄，且磁控管输出的调频噪声被抑制；当两路磁控管的注入功率都为100 W时，该微波源的合成输出频谱更加尖锐，输出频谱中不存在任何的杂散频谱或啁啾颤噪，磁控管的输出频谱杂散抑制大于−65.0 dBc@500 kHz，该输出频谱特性远远优于先前工作报道结果^[8-9]。

针对互注入与外注入功率合成系统的局限性，本文基于注入锁定技术，提出了一种利用注入频率实时控制合成输出功率的解决方案，完成了理论分析并进行了实验验证。在两种不同的情况下分别实现了两种不同的频控功率源。频控功率源的功率控制范围达到了3 dB，注入锁定带宽达到了4.0 MHz，杂散抑制比为−65.0 dBc@500 kHz，系统总功率达到33.9 kW，H-T合成器合成功率94.6%，系统效率约为86.6%。目前尚未见到国际上报道类似S波段磁控管频控功率源系统，也尚未见到国际上S波段两路连续波磁控管无移相器功率合成系统达到类似性能的报道。