近年来水下目标正朝着多样化、规模化、隐形化快速发展, 目标辐射噪声级不断减低, 加之目标数量不断增多, 这种复杂的信号环境给目标检测与跟踪带来极大挑战^[1-3]。现有的目标检测与跟踪通常分成两步进行, 先利用最小方差无失真响应(MVDR)^[4]、多重信号分类(MUSIC)^[5]、稀疏贝叶斯学习(SBL)^[6]等阵列信号处理方法检测有无目标以及目标的方位角, 再将检测结果作为观测输入, 通过递归贝叶斯滤波、数据关联等方法得到时间上连续的目标运动轨迹^[3]。然而, 这种分步处理方式会带来信息损失, 特别在低信噪比、密集多目标等非理想信号环境下存在一定的局限性。一方面, 在低信噪比条件下会漏检一些弱目标, 同时产生大量虚假目标, 这大大增加了数据关联的难度, 一旦出现关联错误将导致轨迹偏离甚至错跟; 另一方面, 当多个目标方位历程出现交叉时, 受阵列孔径和算法性能限制, 空间谱呈现单峰形态, 往往只能输出一个方位检测结果, 连续多次的漏检将导致轨迹中断。

检测前跟踪(TBD)^[7]技术直接对声呐原始数据进行联合检测与跟踪处理, 避免了阈值检测带来的信息损失, 也无需复杂的数据关联, 为解决复杂信号环境下检测跟踪问题提供了新的思路。声呐原始数据提供了更加丰富的信息, 但具有较强的非线性、非高斯特性, 同时也受到场景中多个目标与环境噪声的共同作用, 任一目标状态或噪声的变化均会对其产生影响。因此, 如何处理这种非标准观测成为TBD技术亟待解决的瓶颈问题。作为非线性、非高斯递归贝叶斯滤波的基本工具之一, 研究人员尝试利用粒子滤波(PF)解决该问题, Northardt等提出了基于空间谱观测的粒子滤波检测前跟踪(PF-TBD)方法, 使用波束形成输出的空间谱作为观测, 引入点扩散函数描述空间谱与目标状态的映射关系, 用于构建似然函数并更新粒子权重, 海试结果表明该方法在多达8个目标场景下实现了稳定跟踪^[8-9]。金盛龙等对PF-TBD算法的重采样环节进行改进, 利用遗传算子和准蒙特卡罗方法解决粒子多样性匮乏问题, 提升了跟踪精度和鲁棒性^[10]。王燕等采用并行分区的思想提升邻近目标的跟踪性能^[11]。然而, 上述粒子滤波方法仅适用目标数固定不变的理想场景。

为应对目标数未知且时变的复杂场景, Mahler创新性地引入了随机有限集(RFS)理论, RFS是元素互异、无序且数目可变的有限集合, 非常适合描述多目标状态的不确定性以及目标新生、消亡和演变等过程^[12-14]。RFS-TBD方法可以分为两类, 一类是无标签RFS-TBD方法, 包括概率假设密度 (PHD) 滤波器^[15]和集势概率假设密度(CPHD) 滤波器^[16-17]等, 这类算法仅递归传递多目标概率密度函数的统计矩及势分布, 这与卡尔曼滤波器仅传递统计矩的思想类似。但是, 对于声呐数据这类特殊观测, 需要计算多维的集合积分, 通常不存在解析解。针对该问题, Saucan等^[16]和Masnadi-Shirazi等^[17]提出了基于叠加近似的CPHD-TBD算法, 利用变量替换与Campbell定理消除多维的集合积分, 并推导出了统计矩及势分布的近似解表达式, 侧扫声呐实测数据验证了算法的有效性。针对多目标状态提取时聚类算法会影响跟踪性能的问题, Zhang等将每个单目标概率密度函数单独近似为伯努利分布, 提出了基于叠加近似的多伯努利检测前跟踪(MB-TBD)算法, 避免了多目标状态提取时聚类算法对跟踪性能的影响, 有效提升了跟踪精度^[18]。由于集合的元素是无序的, 因此无标签RFS方法只能估计多目标状态, 不能形成时间连续的运动轨迹。为此, Vo等对每个目标状态加入特定标签, 用来表示目标状态与某条轨迹的隶属关系^[19-20], 以区分不同目标的运动轨迹, 标签RFS-TBD方法包括标签多伯努利(LMB)滤波器^[21]、广义标签多伯努利(GLMB)滤波器^[22]等。但是, 非线性和非标准观测带来的多维积分在计算上依然难以处理, 需要启发式或者原理性近似方法。针对该问题, Li等提出了基于目标分组的近似LMB-TBD方法^[21], 该方法假设不同目标对观测的影响可以相互分离, 通过目标分组将高维积分降为多组一维积分, 雷达及室内声学传感器数据验证了算法的有效性。但是, 声呐数据是所有目标入射信号与背景噪声的叠加, 观测与所有目标状态具有强相关性, 因此这种启发式的目标分组方法并不适用。

本文面向方位历程交叉场景, 提出了一种广义标签多伯努利检测前跟踪(GLMB-TBD)方法。该方法无需波束形成、峰值检测等预处理, 直接将声呐基阵接收数据构造的协方差矩阵作为观测, 保留了目标方位、入射信号功率等信息, 由于协方差矩阵观测服从复威沙特分布(Complex Wishart, CW), 本文利用复威沙特分布与复逆威沙特分布(Complex Inverse Wishart, CIW)的共轭性质, 通过变量替换推导得出了后验分布近似解表达式, 解决了多维积分难以计算的问题。仿真和海试试验分别对比了GLMB-TBD方法与其他方法的目标数估计与方位跟踪精度, 验证了所提方法在方位历程交叉场景下的有效性和可行性。

在复杂的多目标场景下, 目标数量和对应目标状态均具有随机性, k时刻多目标状态可表示为有限集合的形式:

式中, n表示目标数量, ${\boldsymbol{x}} = (\widetilde {\boldsymbol{x}},\ell )$表示单目标状态, 由运动状态向量$\widetilde {\boldsymbol{x}} \in \mathbb{X}$和标签$\ell \in \mathbb{L}$组合构成, $ \mathbb{X} $表示状态空间, $ \mathbb{L} $表示离散且可数的标签空间。标签$\ell = ({t_{\text{B}}},j)$由有序整数对表示, ${t_{\text{B}}} \leqslant k$表示目标新生时刻, 索引$j$用来区分${t_{\text{B}}}$时刻新生的目标。$\mathcal{L}:\mathbb{X} \times \mathbb{L} \to \mathbb{L}$表示从超空间$\mathbb{X} \times \mathbb{L}$到标签空间$ \mathbb{L} $的投影, ${X_k}$的标签投影表示成$\mathcal{L}({X_k}) = \{ {\ell _1}, \cdots ,{\ell _n}\} $。为确保各个目标标签的唯一性, 避免标签重复出现, 标签RFS要求多目标状态与其标签集合的元素数量相同, 即$|{X_k}| = |\mathcal{L}({X_k})|$。定义标签互异检测器用于保证标签RFS中所有元素的标签互异:

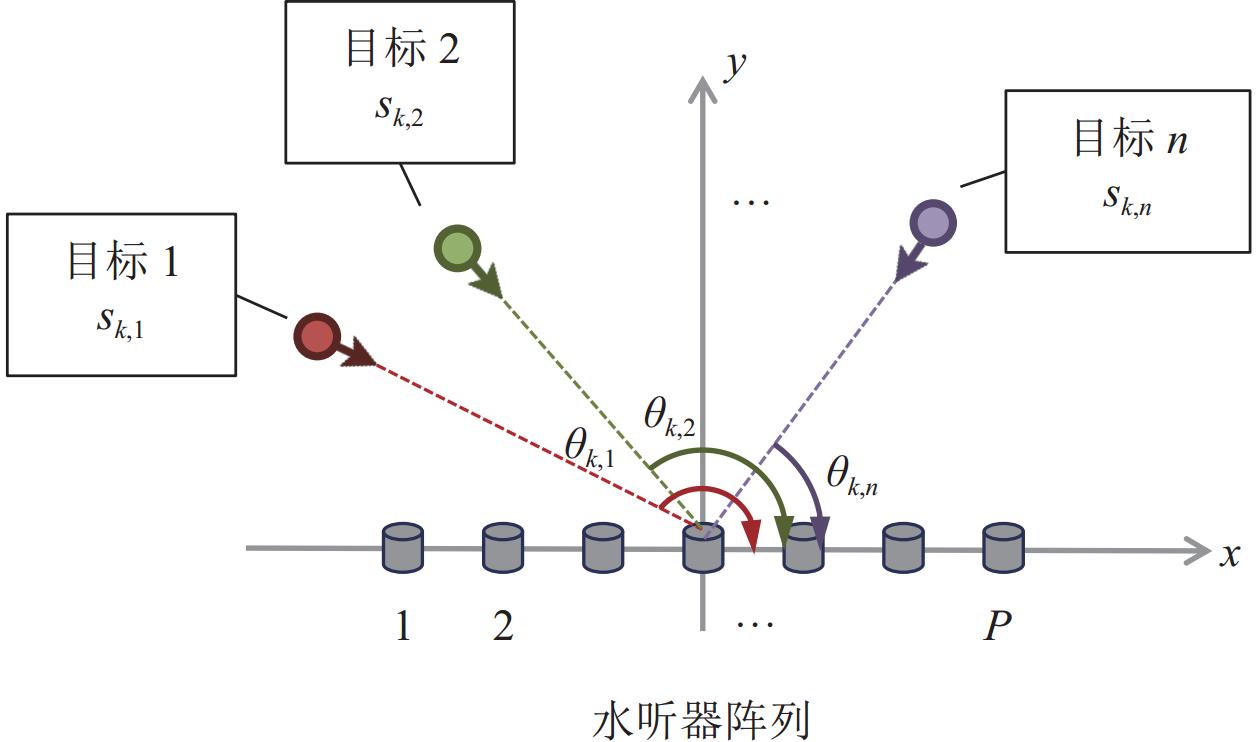
水听器阵列由P元各向同性的水听器均匀排列而成, k时刻有n个目标位于阵列远场, 阵列接收信号是各个目标从${\theta _{k,1}}, \cdots ,{\theta _{k,n}}$方向入射的窄带信号与各向同性环境噪声构成, 如图1所示。

假设相邻时刻的时间周期内有M个连续快拍, 则k时刻第p个水听器的接收信号为

式中, f_c是入射信号频率, d是阵元间距, c是声波的传播速度, $ {{\boldsymbol{s}}_{k,i}} = [{s_{k,i}}(1), \cdots ,{s_{k,i}}(M)] \in {\mathbb{C}^{1 \times M}} $是第i个目标的入射信号, 服从均值为0方差为$\sigma _{k,i}^2{{\boldsymbol{I}}_M}$的多元复高斯分布, ${{\boldsymbol{I}}_M}$表示$ M \times M $维单位矩阵, 写作$\mathcal{C}\mathcal{N}({{\boldsymbol{s}}_{k,i}};{\boldsymbol{0}},\sigma _{k,i}^2{{\boldsymbol{I}}_M})$, $ {{\boldsymbol{v}}_{k,p}} = [{v_{k,p}}(1), \cdots ,{v_{k,p}}(M)] \in {\mathbb{C}^{1 \times M}} $是第p个传感器的观测噪声, 服从均值为0方差为$\sigma _v^2{{\boldsymbol{I}}_M}$的多元复高斯分布, 写作$ \mathcal{C}\mathcal{N}({\boldsymbol{v}_{k,p}};{\boldsymbol{0}},\sigma _v^2{{\boldsymbol{I}}_M}) $, 假设不同时刻和不同阵元上的观测噪声相互独立。

水听器阵列接收信号为

式中, $ {\boldsymbol{a}}({\theta _i}) = {[1,{{\rm{e}}^{ -{\rm{ j}}2\pi {f_c}d\cos {\theta _i}/c}}, \cdots ,{{\rm{e}}^{ - {\rm{j}}2\pi {f_c}(P - 1)d\cos {\theta _i}/c}}]^{\rm{T}}} \in {\mathbb{C}^{P \times 1}} $表示第i个目标入射信号的阵列响应向量, 上角标T表示矩阵转置, $ {{\boldsymbol{V}}_k} = {[{{\boldsymbol{v}}_{k,1}},{{\boldsymbol{v}}_{k,2}}, \cdots ,{{\boldsymbol{v}}_{k,P}}]^{\text{T}}} \in {\mathbb{C}^{P \times M}} $表示阵列的观测噪声矩阵。

对于先检测后跟踪方法, 检测过程存在漏检、虚警等情况, 检测到的方位角数量具有随机性, 因此观测也可以表示成有限集合形式, 记作$ {\varTheta _k} = \{ {\hat {\theta} } _{k,1}, \cdots ,{\hat {\theta} } _{k,m} \} $, m表示检测到的方位角数量。由于观测集合由目标生成的检报集和噪声导致的虚警集构成, 因此可以表示成如下的并集形式:

式中, $ {C_k} $表示虚警集, $ {D_k}({\boldsymbol{x}}) $表示目标$ x $生成的检报集, 只可能为空集或只包含一个元素, 当集合为空表示目标$ {\boldsymbol{x}} $漏检, 即$ {D_k}({\boldsymbol{x}}) = \emptyset $, 集合内只包含一个元素表示目标$ {\boldsymbol{x}} $被检测到且对应方位角为$\hat{\theta } $, 即$ {D_k}({\boldsymbol{x}}) = \hat{\theta}$。

对于检测前跟踪方法, 观测是阵列接收信号$ {{\boldsymbol{Z}}_k} $构造的协方差矩阵:

式中, 上角标H表示矩阵的共轭转置, ${{\boldsymbol{R}}_{{Z_k}}}$是$ P \times P $维对称正定矩阵, 且服从自由度为M, 尺度矩阵为${\boldsymbol{\varGamma}} $的CW分布^[23], 写作$\mathcal{C}{\mathcal{W}_P}({{\boldsymbol{R}}_{{Z_k}}};M,{\boldsymbol{\varGamma}} )$。

假设环境噪声功率$\sigma _v^2$已知, 未知目标状态包括方位$\theta $和入射信号功率${\sigma ^2}$, 单目标运动状态建模为${\widetilde {\boldsymbol{x}}_{k,i}} = {[{\theta _{k,i}},{\dot \theta _{k,i}},\sigma _{k,i}^2]^{\rm{T}}}$。给定多目标状态${X_k}$, 多目标似然函数为

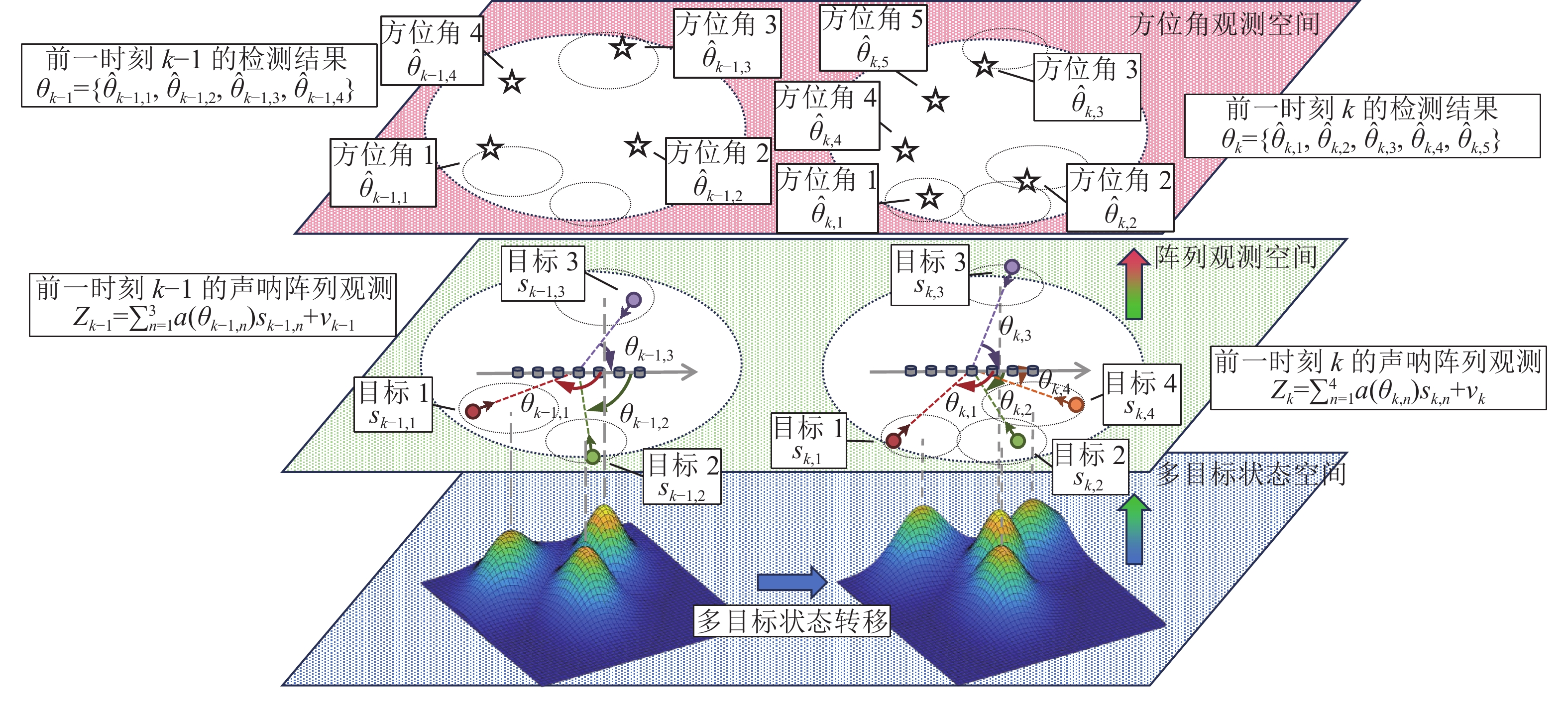
式中, ${\text{tr(}} \cdot {\text{)}}$表示矩阵的迹, $ {\widetilde \varGamma _P}[M] $表示多变量复伽马函数^[24], 尺度矩阵表示为

先检测后跟踪与检测前跟踪的观测空间对比如图2所示。先检测后跟踪方法对应方位角观测空间, 方位角检测结果用五角星表示, k−1时刻共有4个方位角, 其中2个位于目标的误差半径内, 说明是目标生成的方位角, 另外2个是虚警, k时刻共有5个方位角, 其中3个位于目标的误差半径内, 说明是目标生成的方位角, 另外2个是虚警。检测前跟踪方法对应阵列观测空间, 声呐阵列观测包含了所有目标的完整信息。

在最优多目标贝叶斯滤波框架下, 广义标签多伯努利(GLMB)分布提供了一种闭式解形式, 也就是说, 假设多目标概率密度函数服从GLMB分布, 在贝叶斯框架下进行预测、更新后, 得到的多目标概率密度函数仍服从GLMB分布。GLMB分布定义为^[25-26]

式中, 求和符号表示该分布由多种假设构成, 对于其中任意一种假设, $\mathcal{L}(X) = \{ {\ell _1}, \cdots ,{\ell _n}\} $表示$X$的标签集, ${w^{(I)}}$表示对应的假设权重, $ {[{p^{(I)}}]^X} \triangleq \prod\nolimits_{{\boldsymbol{x}} \in X} {{p^{(I)}}({\boldsymbol{x}})} $表示$X$中所有目标概率密度函数的累乘, 且满足$\sum\nolimits_{I \in \mathcal{F}(\mathbb{L})} {{w^{(I)}}} = 1$以及$ \int {{p^{(I)}}({\boldsymbol{x}}){\rm d}{\boldsymbol{x}}} = 1 $。$\mathcal{F}(\mathbb{L})$表示标签空间全体有限子集构成的超空间, 狄拉克函数${\delta _I}(\mathcal{L}(X))$用于保证标签集$\mathcal{L}(X)$属于标签空间, 当且仅当$I = \mathcal{L}(X) \in \mathcal{F}(\mathbb{L})$时${\delta _I}(\mathcal{L}(X)) = 1$。

给定先验GLMB分布${\pi _{k - 1}} \, (\,{X_{k - 1}} \,|\, {\boldsymbol{R}}_Z^{[k - 1]} \,)$, 预测GLMB分布为^[22]

式中

式中, 预测标签集表示成并集形式$I = {L_{\rm{S}}} \cup {L_{\rm{B}}}$, 其中${L_{\rm{S}}}$表示存活目标的标签集, 等于预测标签集$I$与0到$k - 1$时刻标签空间的交集, 记作${L_{\rm{S}}} = I \cap {\mathbb{L}_{{\text{0}}:k - 1}}$; ${L_{\rm{B}}}$表示新生目标标签集, 等于预测标签集$I$与$k$时刻标签空间的交集, 记作${L_{\rm{B}}} = I \cap {\mathbb{L}_k}$。预测假设权重$w_{k|k - 1}^{(I)}$等于存活假设权重$w_{\rm{S}}^{(I)}(I \cap {\mathbb{L}_{{\text{0}}:k - 1}})$与新生假设权重$ w_{\rm{B}}^{}(I \cap {\mathbb{L}_k}) $的乘积。对于预测的单目标概率密度$p_{k|k - 1}^{(I)}({{\boldsymbol{x}}_{k,i}})$, 当${1_{{\mathbb{L}_{0:k - 1}}}}(\ell ) = 1$, 即预测目标为存活目标时, $p_{k|k - 1}^{(I)}({{\boldsymbol{x}}_{k,i}}) = p_{\rm{S}}^{(I)}({{\boldsymbol{x}}_{k,i}})$, 当${1_{{\mathbb{L}_k}}}(\ell ) = 1$, 即预测目标为新生目标时, $p_{k|k - 1}^{(I)}({{\boldsymbol{x}}_{k,i}}) = p_{\rm{B}}^{}({{\boldsymbol{x}}_{k,i}})$。${1_L}(\ell )$是包含函数, 当$\ell \in L$时等于1, 否则为零。

存活假设权重和存活单目标概率密度函数表示为

式中, 权重$w_{\rm S}^{(I)}({L_{\rm S}})$是标签空间${\mathbb{L}_{0:k}}$任意子集$J$中所有包含${L_{\rm S}}$的先验权重$w_{k - 1}^{(I)}(J)$加权求和; $ {P_{\rm S}}({\boldsymbol{x}}') $表示目标$ {\boldsymbol{x}}' $的存活概率, $\eta _{\rm S}^{(I)}(\ell ) = \int {{P_{\rm S}}({\boldsymbol{x}}')p_{k - 1}^{(I)}({\boldsymbol{x}}'){\rm d}{\boldsymbol{x}}'}$是其归一化因子。当目标存活概率与其状态无关时, 即$ {P_{\rm S}}({\boldsymbol{x}}') \triangleq {P_{\rm S}} $, 归一化因子等于常数, 写作$ \eta _{\rm S}^{(I)}(\ell ) = {P_{\rm S}} $, 此时, 式(14)的存活单目标概率密度函数变成标准的Chapman-Kolmogorov预测, 写作$ p_{\rm S}^{(I)} \, ({\boldsymbol{x}},\, \ell ) \,= \int {{f_{k|k - 1}}({\boldsymbol{x}}|{\boldsymbol{x}}') \, p_{k - 1}^{(I)}({\boldsymbol{x}}') \, {\rm d}{\boldsymbol{x}}'} $。

新生假设权重$w_{\mathrm{B}}^{}({L_{\mathrm{B}}})$和新生单目标概率密度函数$p_{\mathrm{B}}^{}({x_{k,i}})$通常需要预先定义, 对于无源声呐应用场景, 新生目标的先验信息很难精确已知, 为解决该问题, 2.4节给出了一种自适应新生目标模型。

给定预测GLMB分布和观测${{\boldsymbol{R}}_{{Z_k}}}$, 后验GLMB分布表达式如下^[22]:

式中

式中, 后验权重$w_k^{(I)}$正比于预测权重$w_{k|k - 1}^{(I)}$, 比例因子$\eta _{{{\boldsymbol{R}}_{{Z_k}}}}(I)$的计算需要边缘化所有目标的影响, 后验单目标概率密度函数$\widehat p_k^{(I)}({{\boldsymbol{x}}_{k,i}})$的计算需要边缘化除当前目标以外其他所有目标的影响。当各个目标对于观测的影响可以分离时, 多目标似然函数可以写作多个单目标似然函数相乘的形式, 从而多维积分变成多个一维积分相乘, 但是对于阵列观测, 各个目标对于观测的影响不可分离, 因此, 如何求解多维积分成为关键问题。

针对多维积分问题, 本节利用CW分布与CIW分布的共轭性质, 通过变量替换可以推导后验GLMB分布的近似解。

给定标签集$I$, 后验权重的表达式如下:

式中, $\mathcal{C}\mathcal{G}\mathcal{B}_P^{II}({{\boldsymbol{R}}_{{Z_k}}};M,\widehat \rho ,\widehat {\boldsymbol{\varPhi}} )$表示复广义Ⅱ型贝塔分布, $\widehat \rho $和$\widehat{\boldsymbol{ \varPhi}} $分别表示该分布的自由度和尺度矩阵估计值:

式中, b是任意的$P \times 1$维非零复向量, ${\mathrm{vec}}( \cdot )$表示矩阵的向量化, ${{\boldsymbol{M}}_{\boldsymbol{Y}}}$和${{\boldsymbol{C}}_{\boldsymbol{Y}}}$表示为

证明: 当标签集$|I| = 0$时, 即目标数等于0, 式(16)的后验权重为

当标签集$|I| > 0$时, 即目标数大于0, 式(16)的后验权重为

式中, $ {\boldsymbol{\varGamma}} ({X_k}) $是关于多目标状态${X_k}$的函数, 如式(8)所示。定义$P \times P$维对称正定的复随机矩阵${\boldsymbol{Y}} = {\boldsymbol{\varGamma}} ({X_k})$, 根据变量替换定理, 式(27)的向量积分可简化成如下的矩阵积分:

式中, $p({\boldsymbol{Y}})$是复随机矩阵${\boldsymbol{Y}}$的概率密度函数。${\boldsymbol{Y}}$的均值和协方差矩阵分别为

假设${\boldsymbol{Y}}$服从CIW分布, 记作$ p({\boldsymbol{Y}}) = \mathcal{C}\mathcal{I}{\mathcal{W}_P}({\boldsymbol{Y}};\rho ,{\boldsymbol{\varPhi}} ) $, $\rho $和${\boldsymbol{Y}}$分别是自由度和尺度矩阵。已知${\boldsymbol{Y}}$的均值和协方差矩阵, 可以估计CIW分布的自由度和尺度矩阵, 如式(20)和式(21)所示, 具体推导过程见附录A。利用CW分布与CIW分布的共轭性质, 式(28)的积分可简化为

给定标签集I, 只有当目标数大于等于1时才存在后验单目标概率密度函数, 因此只考虑目标数等于1和大于1两种情况, 后验单目标概率密度函数表达式如下:

式中, ${\widehat \rho _i}$和${\widehat{\boldsymbol{ \varPhi}} _i}$分别表示广义Ⅱ型贝塔分布的自由度和尺度矩阵:

式中, b是任意的$P \times 1$维非零复向量, 参数${{\boldsymbol{M}}_{{{\boldsymbol{Y}}_i}}}$和${{\boldsymbol{C}}_{{{\boldsymbol{Y}}_i}}}$表示为

证明: 当标签集$|I| = 1$时, 即目标数等于1, 式(17)的后验单目标概率密度函数为

当标签集${\text{|}}I{\text{|}} > 1$时, 即目标数大于1, 式(17)的后验单目标概率密度函数为

式中, ${{\boldsymbol{\varGamma}} _i}({X_k})$是关于多目标状态${X_k}$的函数, 表示为

定义$ P \times P $维对称正定的复随机矩阵$ {{\boldsymbol Y}_i} = {{\boldsymbol \varGamma} _i}({X_k}) $, $ {{\boldsymbol Y}_i} $的均值和协方差矩阵分别为

假设${{\boldsymbol{Y}}_i}$服从CIW分布, 记作$ p({{\boldsymbol{Y}}_i}) = \mathcal{C}\mathcal{I}\mathcal{W}({{\boldsymbol{Y}}_i};{\rho _i}, {{\boldsymbol{\varPhi}} _i}) $。已知${{\boldsymbol{Y}}_i}$的均值和协方差矩阵, 可估计CIW分布的自由度和尺度矩阵, 如式(33)和式(34)所示。同理, 式(38)的积分可简化为

至此, 推导了后验GLMB分布近似解表达式, 消除了多维积分运算。

本节给出基于粒子滤波的数值计算实现方法, 实现流程如表1所示。给定当前时刻的先验GLMB分布, 写作$ {\pi _{k - 1}} = {\{ w_{k - 1}^{(I')},{[p_{k - 1}^{(I')}]_{\ell \in I'}}\} _{I' \in \mathcal{F}\left( {{\mathbb{L}_{0:k - 1}}} \right)}} $, 其中, 单目标概率密度函数使用J个加权粒子集表示, $\widetilde {\boldsymbol{x}}_{k - 1}^{(j)}$表示粒子采样, $ \omega _{k - 1}^{(j)} $表示粒子权重, 如下所示:

预测过程如表1的1~11行所示, 预测标签集$ I $是存活标签集与新生标签集的并集, 写作$ I = {L_{\text{S}}} \cup {L_{\text{B}}} $。给定前一时刻标签集合$ I' $, 最多可衍生出$ {2^{|I'|}} $个存活假设, 以两个目标为例$ I' = \{ {\ell _1},{\ell _2}\} $, 可以衍生出4个存活假设, 对应的标签集分别是: 1) 无目标存活$ L_{\text{S}}^{(1)} = \emptyset $; 2) 标签为$ {\ell _1} $的目标存活$ L_{\text{S}}^{(2)} = \{ {\ell _1}\} $; 3) 标签为$ {\ell _2} $的目标存活$ L_{\text{S}}^{(3)} = \{ {\ell _2}\} $; 4) 两个目标均存活$ L_{\text{S}}^{(4)} = \{ {\ell _1},{\ell _2}\} $。预测过程会导致存活假设的数量呈指数增长, 为减轻运算量, 可以采用K最短路径方法^[20]保留其中K_S个权重较大的存活假设。

新生目标模型为$ {\pi _{\mathrm{B}}} = \{ {r_{{\mathrm{B}},i}},{p_{{\mathrm{B}},i}}\} _{i = 1}^{{n_{\mathrm{B}}}} $, $ {n_{\mathrm{B}}} $为新生目标个数, $ {r_{{\mathrm{B}},i}} $为目标新生概率, $ {p_{{\mathrm{B}},i}}(\widetilde {\boldsymbol{x}}) $为新生目标概率密度函数。采用文献[27]的最大似然方法构造新生目标模型, 给定当前时刻的阵列观测$ {{\boldsymbol{R}}_{{Z_k}}} $, 扫描方位空间得到各个方位的入射信号功率估计, 扫描间隔为$0.5\text{°}$, 表达式如下:

式中, ${\boldsymbol{\varSigma }}$是关于前一时刻多目标状态估计${\widehat X_{k - 1}}$的函数, 写作${\boldsymbol{\varSigma }} \,=\, {\boldsymbol{ \varGamma}} ({\widehat X_{k - 1}}) \,=\, \sigma _v^2{{\boldsymbol{I}}_P} \,+\, \sum\nolimits_{{x_{k - 1}} \in {{\widehat X}_{k - 1}}} {\sigma _{k - 1}^2{\boldsymbol{a}}({\theta _{k - 1}}){{\boldsymbol{a}}^{\rm{H}}}({\theta _{k - 1}})} $。挑选入射信号功率大于门限$ \sigma _{}^2 > \sigma _{{\text{threshold}}}^2 $的峰值, $ \{ {\theta _{{\text{peak}},i}},\sigma _{{\text{peak}},i}^2\} _{i = 1}^{{n_B}} $分别是峰值处的方位及对应的信号功率, 利用高斯分布采样新生粒子, 记作$ {p_{{\mathrm{B}},i}}(\widetilde {\boldsymbol{x}}) = \mathcal{N}(\widetilde {\boldsymbol{x}};{{\boldsymbol{m}}_{{\rm{B}},i}},{{\boldsymbol{P}}_{\rm{B}}}) $, 均值为$ {{\boldsymbol{m}}_{{\rm{B}},i}} = [{\theta _{{\text{peak}},i}},0,\sigma _{{\text{peak}},i}^2] $, 方差为$ {{\boldsymbol{P}}_{\rm{B}}} $。新生过程最多可衍生出$ {2^{{n_{\rm{B}}}}} $个新生假设, 为减轻运算量, 也可以采用K最短路径方法保留其中K_B个权重较大的新生假设。

更新过程如表1的12~23行所示, 给定后验标签集$ I $, 后验权重分成两种情况进行计算, 分别是目标数等于0和大于等于1。当目标数等于0时, 可以直接求出后验权重。当目标数大于等于1时, 根据式(24)和式(25), 每个单目标$ {\ell _i} \in I $的${{\boldsymbol{M}}_i}$和${{\boldsymbol{C}}_i}$分别为

根据式(22)和式(23), 可以计算出参数$ \boldsymbol{M_Y} $和$ \boldsymbol{C_Y} $, 从而估计出自由度和尺度矩阵, 得到后验权重。

后验单目标概率密度函数的粒子集分两种情况进行计算, 分别是目标数等于1和大于1。当目标数等于1时, 可以直接求出粒子的后验权重。当目标数大于1时, 根据式(35)和式(36), 每个粒子对应的$ {\boldsymbol{M}}_{{{\boldsymbol{Y}}_i}}^{(j)} $和${{\boldsymbol{C}}_{{{\boldsymbol{Y}}_i}}}$分别为

根据式(33)和式(34), 可以计算出每个粒子的自由度和尺度矩阵估计值, 用于更新粒子权重。根据更新粒子权重$ \omega _k^{(j)} $重采样, 得到归一化权重的后验单目标状态粒子集$p_k^{(I)}(\widetilde {\boldsymbol{x}}) = \{ 1/J,\widetilde {\boldsymbol{x}}_k^{(j)}\} _{j = 1}^J$, 进而得到单目标状态估计, ${\widehat {\boldsymbol{x}}_k} = \sum\nolimits_{j = 1}^J {\widetilde {\boldsymbol{x}}_k^{(j)}} /J$。多目标轨迹提取过程如下, 首先估计目标数:

然后遍历所有目标数等于$ \widehat n $的后验假设, 寻找权重最大的假设, 提取对应的标签集合和多目标状态。

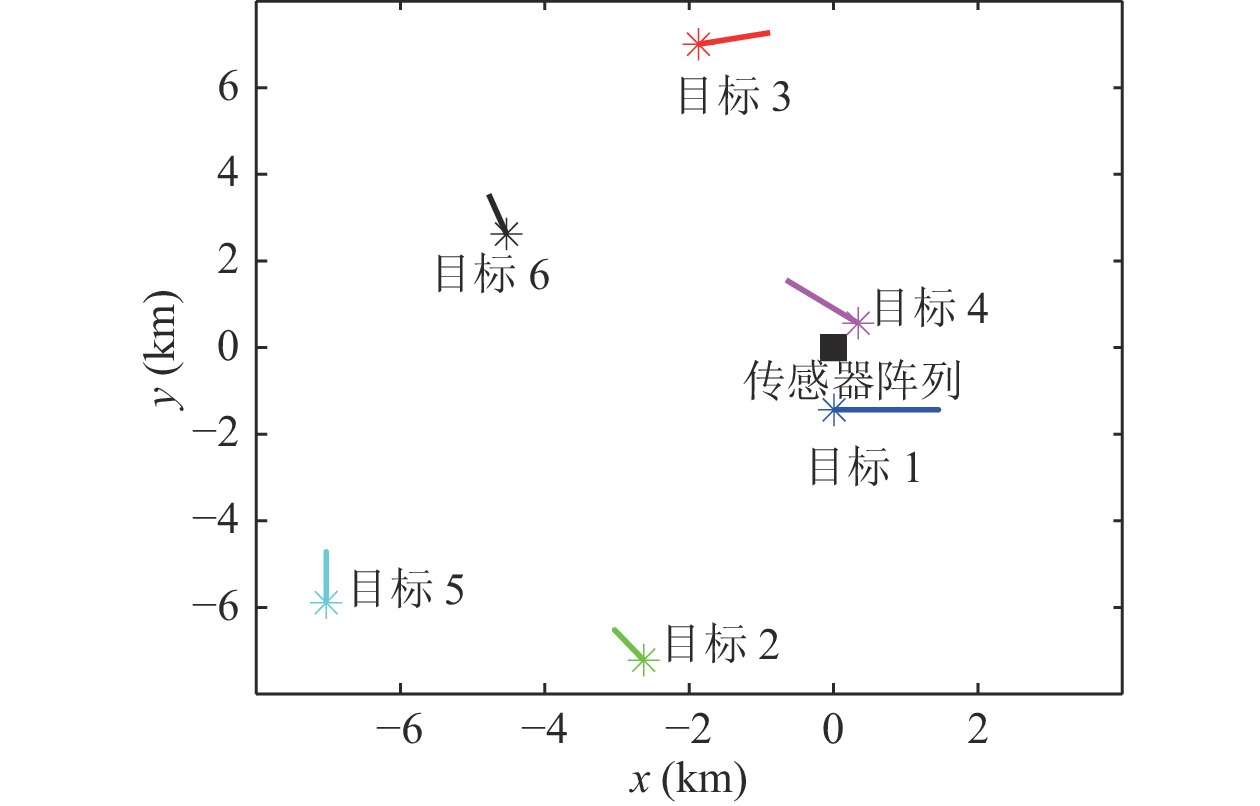
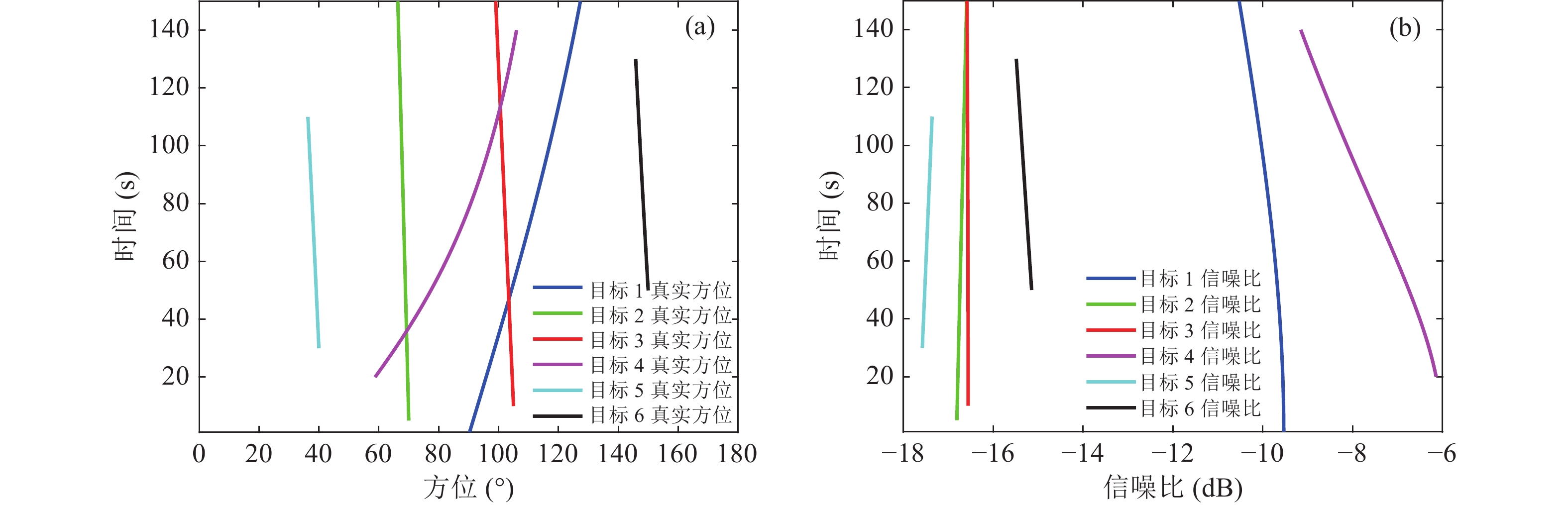
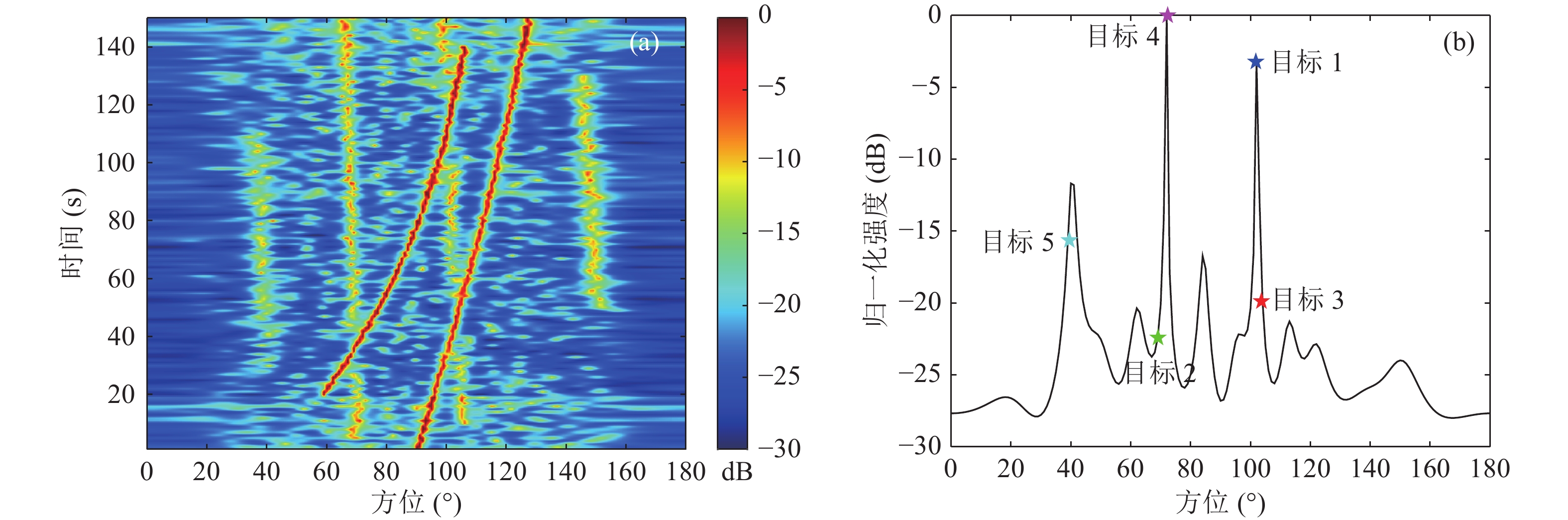
仿真场景如图3所示, 水听器阵列是16个阵元组成的均匀直线阵, 阵元间距满足半波长, 位于坐标原点, 由符号“■”表示, 总观测时间长度为150 s, 监视区域内有6个目标在不同时刻以及不同位置出现, 假设所有目标均做匀速直线运动, 符号“*”表示目标初始位置, 各个目标的初始状态、运动参数以及出现与消失时刻见表2。图4(a)是目标方位随时间变化曲线, 假设各向同性的环境噪声场, 环境噪声级和目标辐射噪声的声源级在观测时间保持不变, 传播损失服从柱面波扩展衰减$ {\text{PL}} = 10\lg r $, $ r $是目标与阵列之间的距离, 图4(b)为信噪比随时间变化曲线, 假设环境噪声功率已知, $ \sigma _v^2 = 5 $, 入射信号功率为$ {\sigma ^2} = 10^{{\rm SNR}/10} \sigma _v^2 $。30~55 s时间段内, 有2组目标方位历程交叉, 110~130 s内, 有1组目标方位历程交叉, 且目标1与目标4距离阵列较近, 入射信号功率较强, 目标2与目标3距离阵列较远, 入射信号功率较弱, 强弱目标信噪比相差最大可达10 dB。

设置每帧的时间周期为1 s, 每帧有效快拍数为100, 图5(a)为SBL方法得到的方位历程图, 扫描间隔为$0.5\text{°}$, 按dB量化。在方位历程交叉区间内, 目标1与目标4的入射信号功率较强, 方位轨迹十分明显, 几乎掩盖了目标2与目标3, 仅能凭借人眼视觉累积大致估计各个目标的方位轨迹。图5(b)为第40秒的SBL空间谱切片, 由于SBL算法分辨率限制, 当2个目标方位邻近时仅出现1个峰值, 若采用峰值检测方法会丢失其中1个目标信息。

对于检测后跟踪方法, 单目标运动状态定义为$ {\widetilde {\boldsymbol x}_k} = {[{\theta _k},{\dot \theta _k}]^{\rm T}} $, 其中$ {\theta _k} $表示目标方位, $ {\dot \theta _k} $表示其方位变化率, 状态转移方程采用常速度运动模型:

式中, $ \Delta T = 1{\text{ s}} $是一帧的时间周期, $ {\varepsilon _{\ddot \theta }} $是方位加速度的高斯噪声, 标准差设置为$ 0.03~(\text{°})/{{\text{s}}^2} $。观测输入是每帧SBL空间谱切片的方位检测结果, 表示成有限集合形式$ {\varTheta _k} = [{\hat \theta } _{k,1}, \cdots ,{\hat \theta } _{k,m}] $, 检测门限设置为$ - 20{\text{ dB}} $, 观测方程为

式中, $ {\boldsymbol H} = [ 1~~0 ]^{\text{T}} $, $ {v_k} \sim \mathcal{N}(0,\sigma _v^2) $是观测高斯噪声, 标准差设置为$ {\sigma _v} = 2{\text{°}} $。

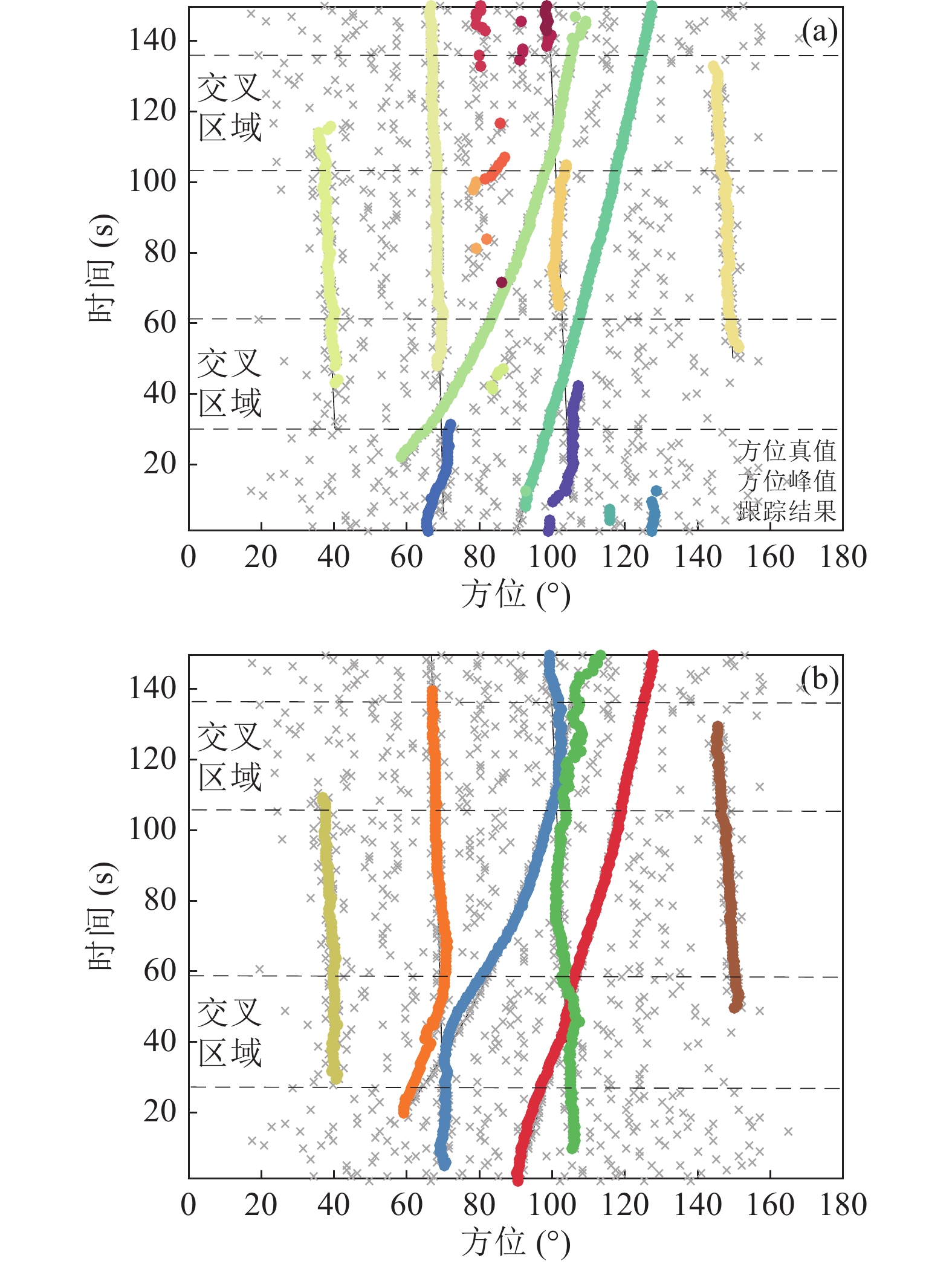
分别采用联合概率数据关联(JPDA)滤波器^[28]和标准GLMB滤波器^[20]对方位检测结果进行处理, JPDA滤波器需要精确已知6个目标的出现与消失时刻。标准GLMB滤波器的参数设置如下: 目标存活概率$ {P_{\text{S}}} = 0.99 $, 新生目标模型由当前时刻方位检测结果$ {\varTheta _k} $决定, 满足$ {\pi _{\mathrm{B}}} = \{ r_{\mathrm{B}}^{(i)},p_{\mathrm{B}}^{(i)}\} _{i = 1}^m $, $ m = |{\varTheta _k}| $是方位峰值数量, 目标新生概率$ r_{\mathrm{B}}^{(i)} = 0.001 $, 新生目标状态分布满足$ p_{\mathrm{B}}^{(i)}(\widetilde {\boldsymbol{x}}) = \mathcal{N}(\widetilde {\boldsymbol{x}};{\boldsymbol{m}}_{\mathrm{B}}^{(i)},{\boldsymbol{P}}_{\mathrm{B}}^{}) $, 均值$ {\boldsymbol{m}}_{\mathrm{B}}^{(i)} = {[{\theta _{k,i}},0]^{\mathrm{T}}} $, 方差$ {{\boldsymbol{P}}_{\mathrm{B}}} = {\text{diag}}{([3,0.3])^2} $。每个目标分配的粒子数300, 检测概率$ {P_{\text{D}}} = 0.9 $, 平均虚警数设置为$ 3 $。

图6为检测后跟踪方法的多目标方位跟踪结果, 黑色实线是方位真值, 灰色 × 是方位检测结果, 对应观测输入, 不同颜色的点迹表示不同目标的方位轨迹。在方位历程交叉时, GLMB滤波器判断弱目标消失, 交叉过后判断新目标出现, 点迹颜色发生变化说明轨迹标签发生变化, 不属于同一个目标。JPDA滤波器由于精确已知目标出现与消失时刻, 因此未出现轨迹中断, 但是在方位历程交叉区域, 错误的数据关联导致目标1~4方位轨迹与真值不同, 说明出现了误跟。

分别采用PF-TBD滤波器^[9,10]、MB-TBD滤波器^[18]、本文所提GLMB-TBD滤波器对阵列数据进行处理, PF-TBD滤波器的状态转移方程与式(50)相同, 不能估计信号功率, 同时需要精确已知6个目标的出现与消失时刻。

MB-TBD和GLMB-TBD滤波器的状态转移方程如下, k时刻单目标运动状态定义为$ {\widetilde {\boldsymbol{x}}_k} = {[{\theta _k},{\dot \theta _k},\sigma _k^2]^{\rm T}} $, 状态转移方程采用常速度运动模型:

式中, $ {\varepsilon _{{\sigma ^2}}} $是信号功率的高斯噪声, 标准差与前一时刻的信号功率相关, 即$ {\varepsilon _{{\sigma ^2}}} = 0.1\sigma _{k - 1}^2 $。观测输入是阵列数据协方差矩阵${{\boldsymbol{R}}_{{Z_k}}}$, 观测方程如式(6)所示。

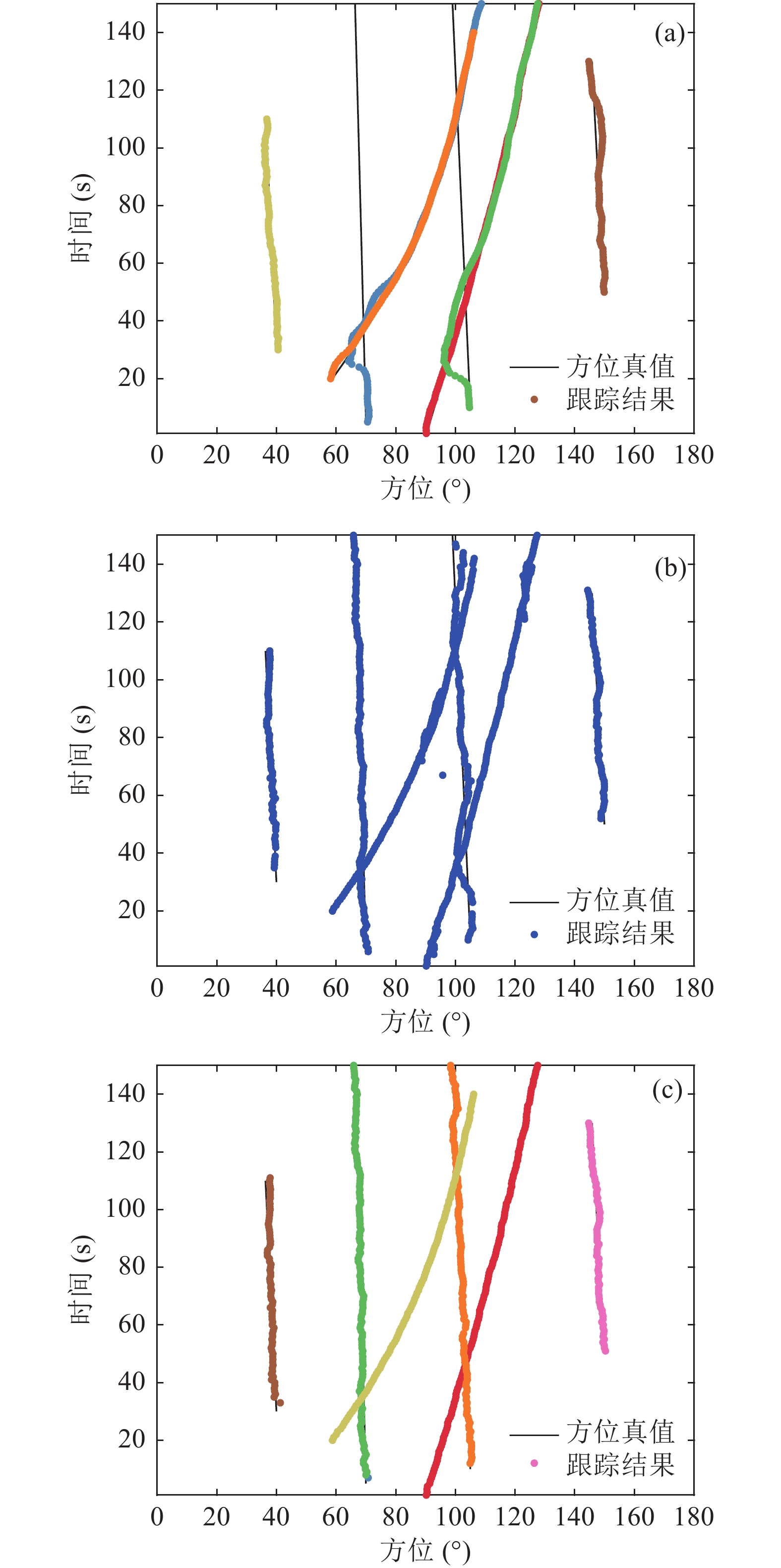
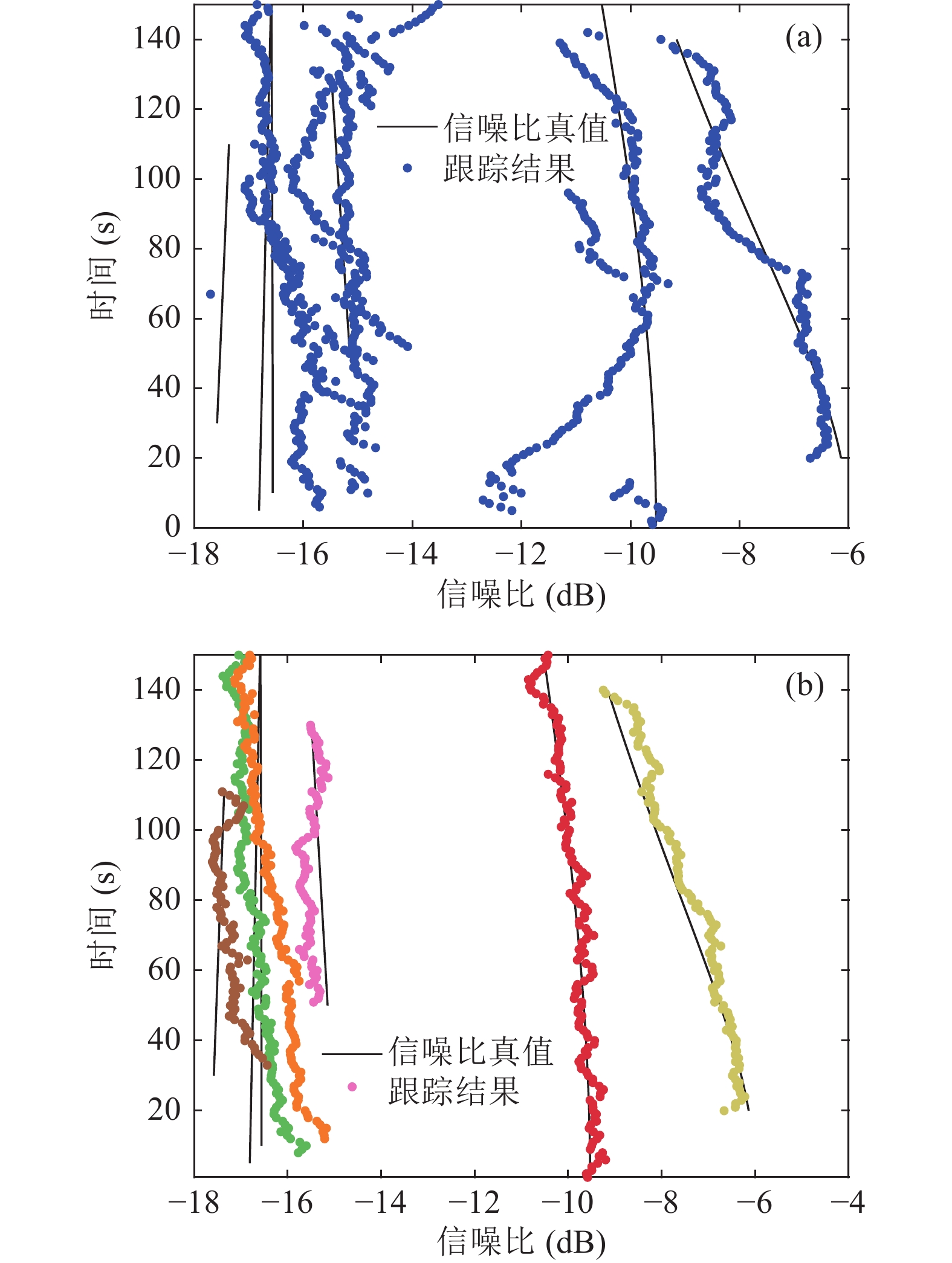
滤波器的参数设置如下: 存活概率$ {P_{\rm S}} = 0.99 $, 存活假设数量$ {K_{\text{S}}} = 50 $, 新生目标模型由当前时刻阵列数据协方差矩阵${{\boldsymbol R}_{{Z_k}}}$决定, 满足$ {\pi _{\mathrm{B}}} = \{ r_{\mathrm{B}}^{(i)},p_{\mathrm{B}}^{(i)}\} _{i = 1}^m $, $ m $是信号功率峰值大于门限$ \sigma _{{\text{threshold}}}^2 = 0.01 $的数量, 即$ {\mathrm{SNR}} > - 27\;{\mathrm{dB}} $的数量, 目标新生概率为$ r_{\mathrm{B}}^{(i)} = 0.001 $, 新生目标状态分布满足$ p_{\mathrm{B}}^{(i)}(\widetilde {\boldsymbol{x}}) = \mathcal{N}(\widetilde {\boldsymbol{x}};{\boldsymbol{m}}_{\mathrm{B}}^{(i)},{\boldsymbol{P}}_B^{}) $, $ {{\boldsymbol{m}}_{{\mathrm{B}},i}} = [{\theta _{{\text{peak}},i}},0,\sigma _{{\text{peak}},i}^2]_{i = 1}^{{n_{\mathrm{B}}}} $, 方差$ {{\boldsymbol{P}}_{\mathrm{B}}} = {\text{diag}}{([3,0.3,0.1])^2} $, 新生假设数量$ {K_{\text{B}}} = 50 $, 每个目标分配的粒子数为300。

图7为检测前跟踪方法的多目标方位跟踪结果。由于PF-TBD滤波器已知目标的出现与消失时刻, 因此未出现轨迹中断现象, 如图7(a)所示, 但弱目标方位出现了误跟, 原因是该滤波器根据波束能量计算每个目标状态粒子的似然函数, 当方位历程交叉时, 目标1和目标4方位的波束能量更强, 粒子的似然程度更高, 导致弱目标的方位轨迹偏向强目标, 直至完全重合。图7(b)和图8(a)分别为MB-TBD滤波器方位跟踪与信噪比跟踪结果, 该方法一定程度上解决了方位历程交叉下的连续跟踪问题, 但是在部分时刻错误估计目标数量, 原因是该方法递归过程中仅保留了多目标后验分布的一阶矩信息, 跟踪性能表现不佳。与之相比, GLMB-TBD滤波器递归过程中保留了一阶矩和目标数分布信息, 目标数估计更加准确, 不仅可以准确检测目标出现与消失, 而且能够精确且稳定地输出各个方位轨迹, 如图7(c)所示; 同时也能跟踪各个目标信噪比变化, 如图8(b)所示, 较好地解决了强弱目标方位历程交叉场景下的连续跟踪问题。

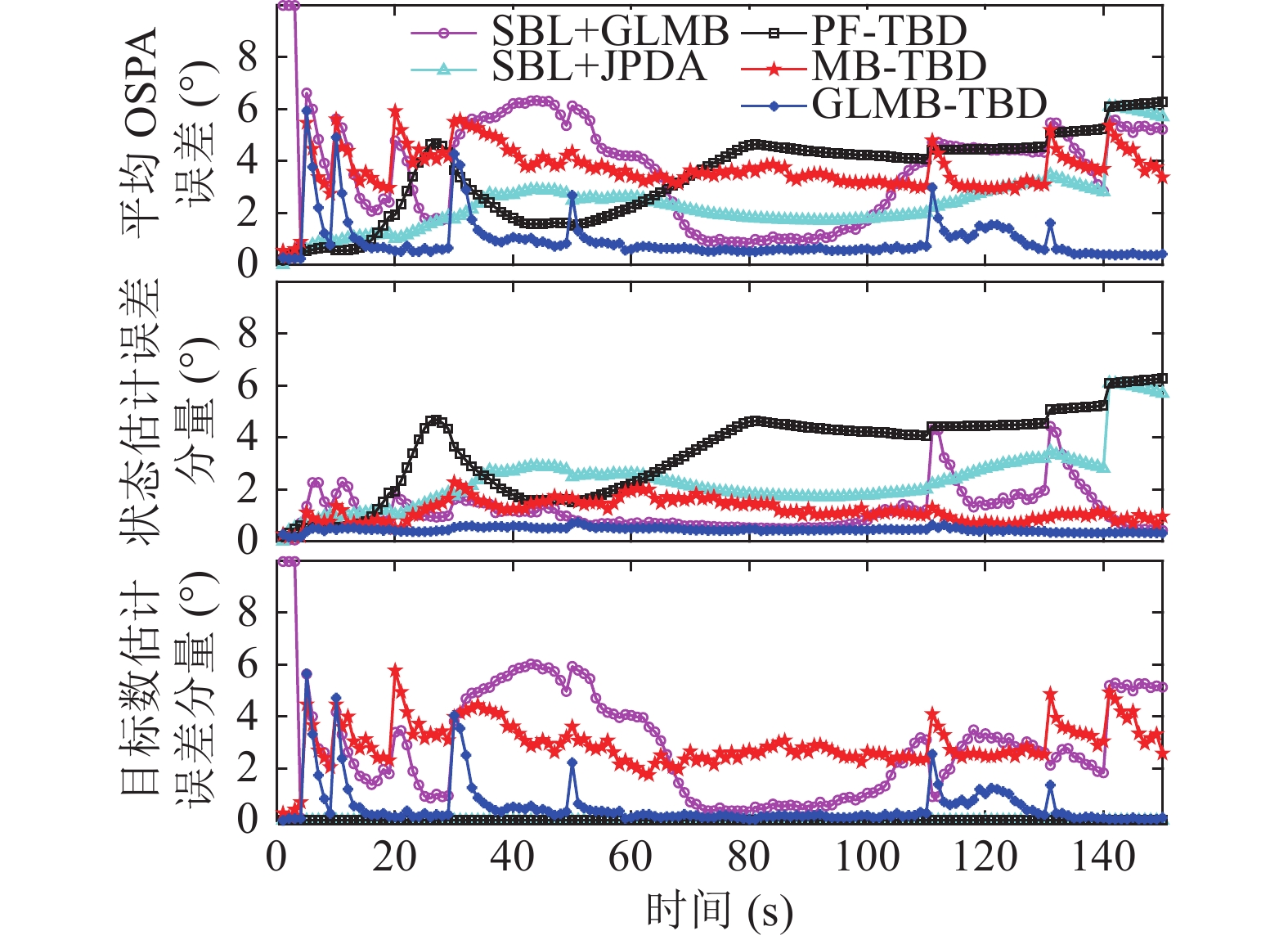
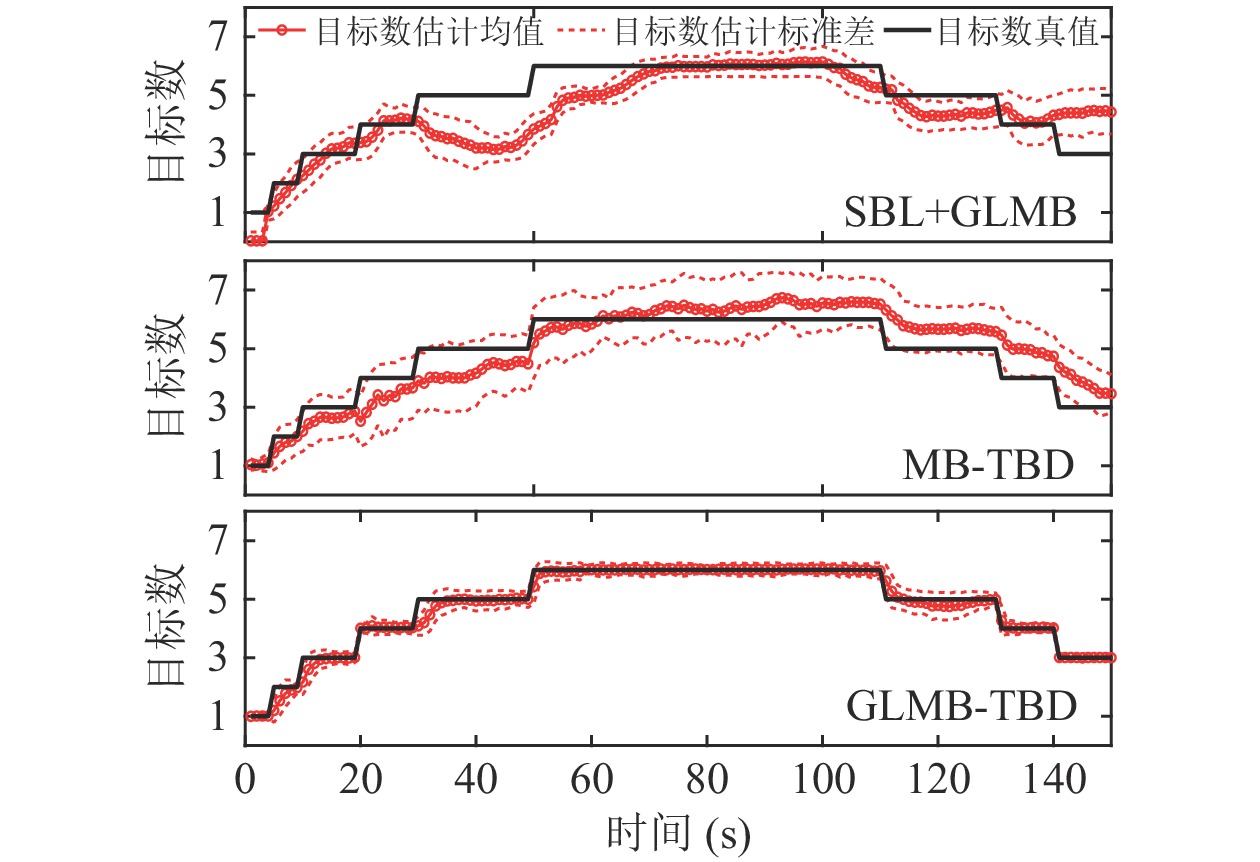
下面通过100次独立的蒙特卡罗实验验证各个方法的统计性能, 性能评价指标采用最优子模式分配(OSPA)误差准则^[29], 该误差由状态估计误差分量和目标数估计误差分量构成, 设置截断参数等于10°, 阶数等于2。图9为平均OSPA误差随时间变化曲线, SBL+GLMB滤波器在方位历程交叉区间, 轨迹中断导致目标数估计误差分量迅速上升; SBL+JPDA和PF-TBD滤波器精确已知目标数, 目标数估计误差分量等于零, 但是误跟导致方位历程交叉后状态估计误差分量迅速上升。MB-TBD滤波器的目标估计误差分量维持在较高水平, 说明目标数估计性能不佳; 而GLMB-TBD滤波器的目标数估计误差分量仅在目标出现和消失时刻剧烈增大, 随后快速收敛至较低水平, 说明能够较好地处理目标数变化带来的不确定性影响, 并且在跟踪稳定时状态估计误差分量维持在1°附近, 状态估计精度远远优于其他滤波器。图10为SBL+GLMB、MB-TBD和GLMB-TBD滤波器的目标数估计统计结果随时间变化曲线, 红色○是目标数估计均值, 虚线是目标数估计标准差, 黑色实线是目标数真值。GLMB-TBD滤波器的目标数估计结果更加准确, 标准差更小。

在实际应用场景中, 目标辐射噪声的声源级与其方位、航行速度、机动方式等多种因素有关^[30], 很难保持稳定不变, 导致入射信号功率可能发生突变。为了验证信噪比突变对所提算法的影响, 仿真场景中假设目标3在第36秒信噪比突然增加6 dB, 目标6在第100秒信噪比突然降低6 dB。图11为GLMB-TBD滤波器的多目标跟踪结果, 信噪比突降时滤波器判定目标3消失, 随后判定新目标出现, 两个目标轨迹颜色不同, 标签发生变化, 说明不是同一个目标。信噪比突增时滤波器判定新目标出现, 新目标方位与目标6方位基本重合, 两个目标的入射信号功率之和接近真值。信噪比突变情况下检测前跟踪方法会错误判断目标出现与消失, 此时需要借助频谱等特征保证跟踪轨迹的连续性。

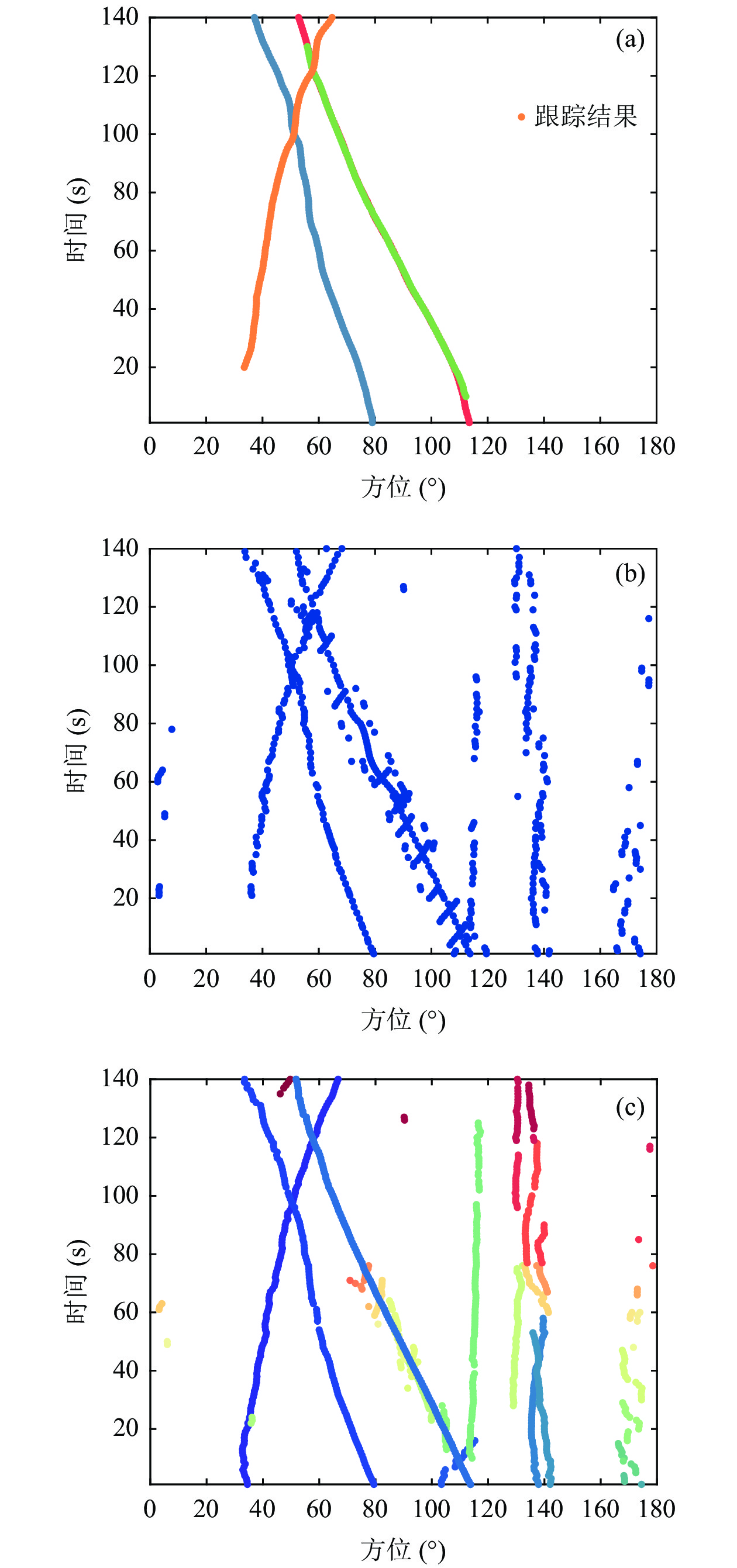
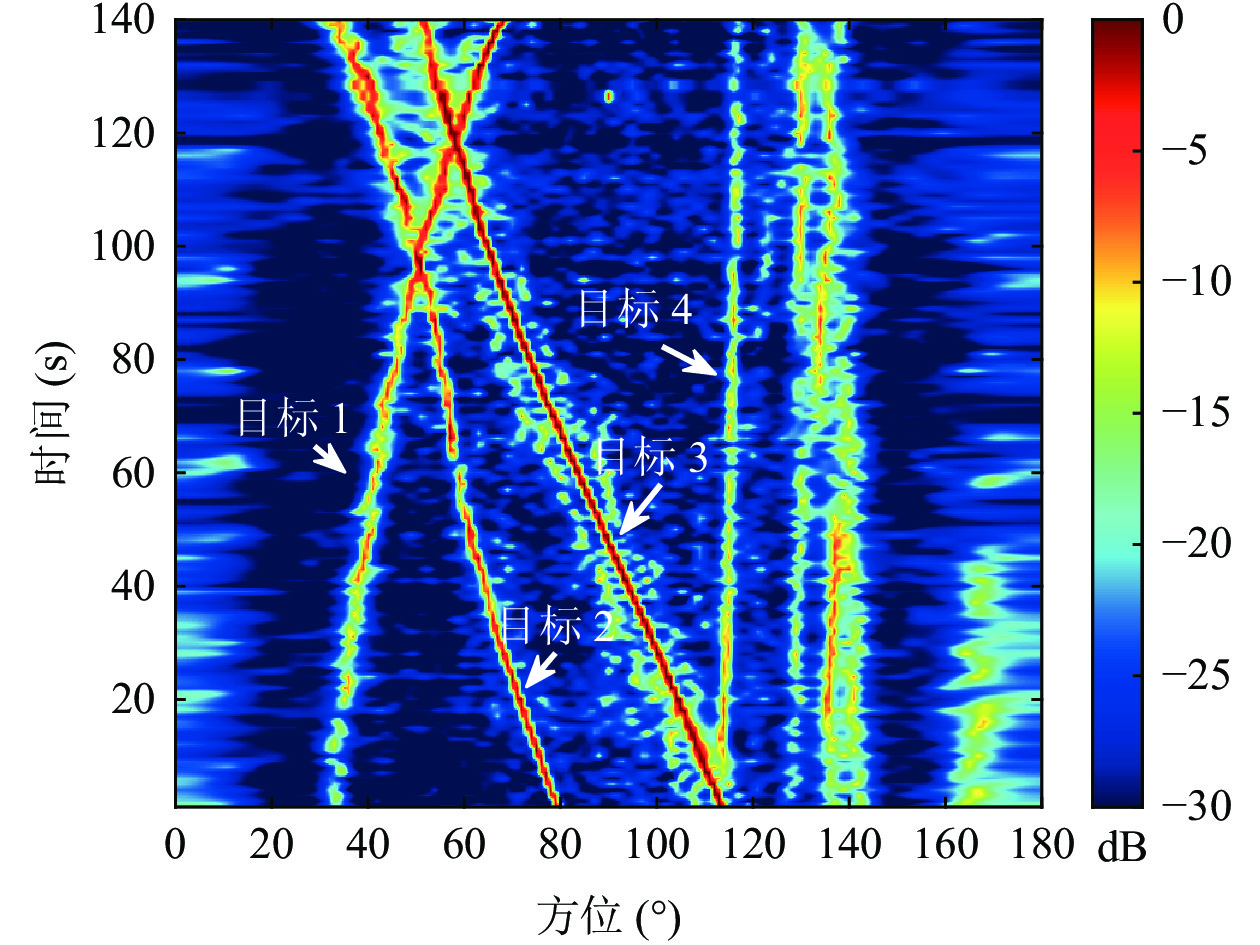
2017年在中国近海某海域进行了试验, 海底布放32元水听器构成的均匀线阵, 阵元间距2 m, 处理的子频带中心频率为400 Hz, 分析数据长度为140 s, 每帧时间周期为1 s, 每帧的有效快拍数为200, 环境噪声功率已知, $ \sigma _v^2 = 5 $。场景中目标数量众多, 各个目标入射信号功率不同, 目标类型和方位真值未知。图12为SBL方法的方位历程图, 可以观测到4条较为清晰完整的方位轨迹, 目标1方位从32°缓慢移动到65°, 目标2方位从80°缓慢移动到40°, 目标3方位从110°缓慢移动到55°, 目标4方位一直保持在115°附近。此外, 140°方位有至少3个弱目标出现, 160°方位有1个弱目标出现, 方位轨迹较为模糊。

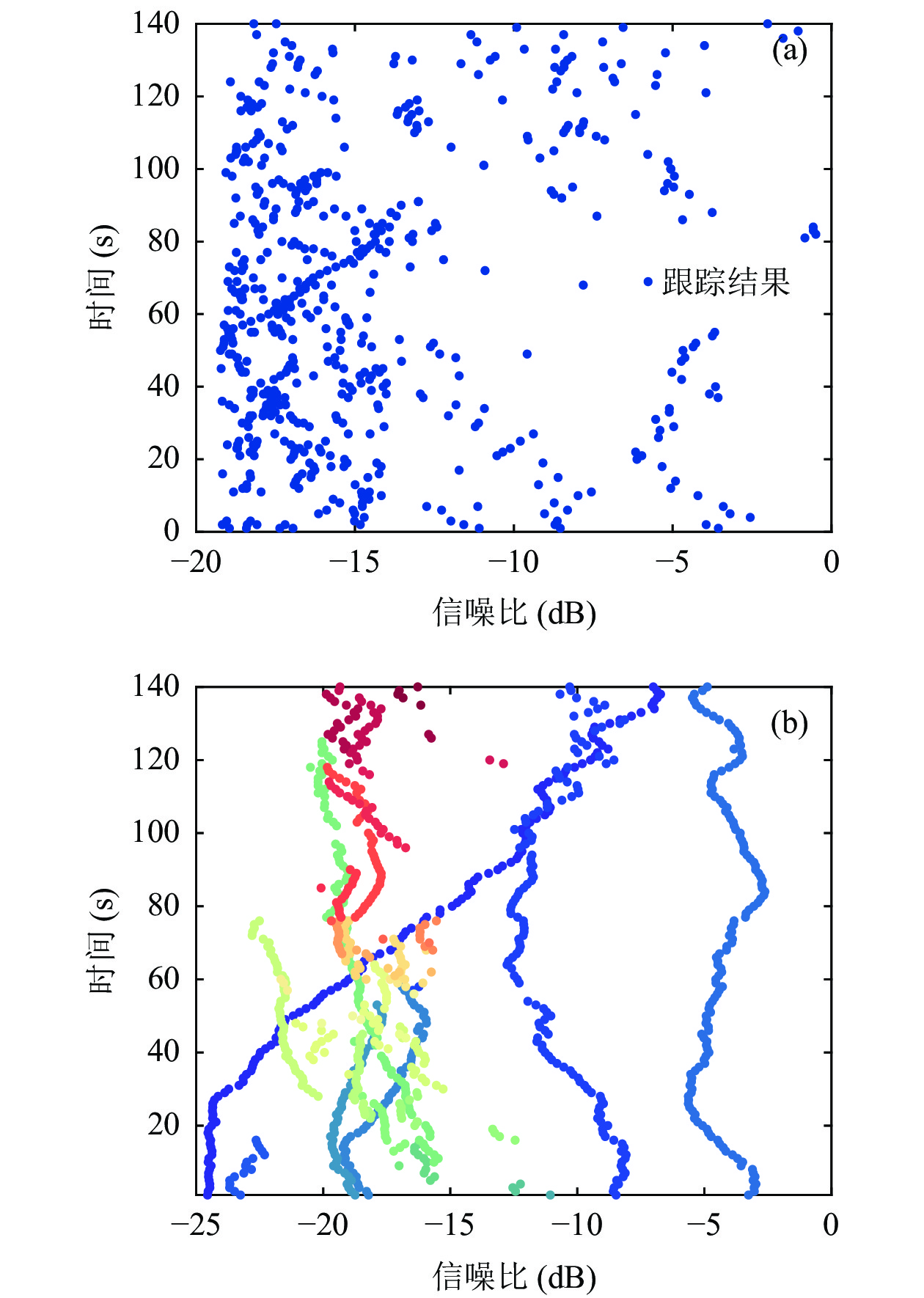
检测后跟踪方法的状态空间模型与3.2节相同, SBL空间谱峰值检测门限为$ - 20{\text{ dB}} $, JPDA滤波器精确已知4个目标的出现与消失时刻, 标准GLMB滤波器的存活与新生模型参数设置与3.2节相同, 检测概率设置为$ {P_{\text{D}}} = 0.9 $, 每帧的平均虚警数设置为$ 1 $。图13为检测后跟踪方法的多目标方位跟踪结果, 检测后跟踪方法均能给出4个目标连续的方位轨迹。SBL+GLMB滤波器能够检测到140°的3个目标以及160°的目标, 但是在方位历程交叉时目标1与目标2的方位轨迹出现一定偏差; SBL+JPDA滤波器在目标数精确已知的条件下, 能够较好给出4个目标的方位轨迹, 但不具备新生目标检测能力, 无法给出场景中其他目标的方位轨迹。

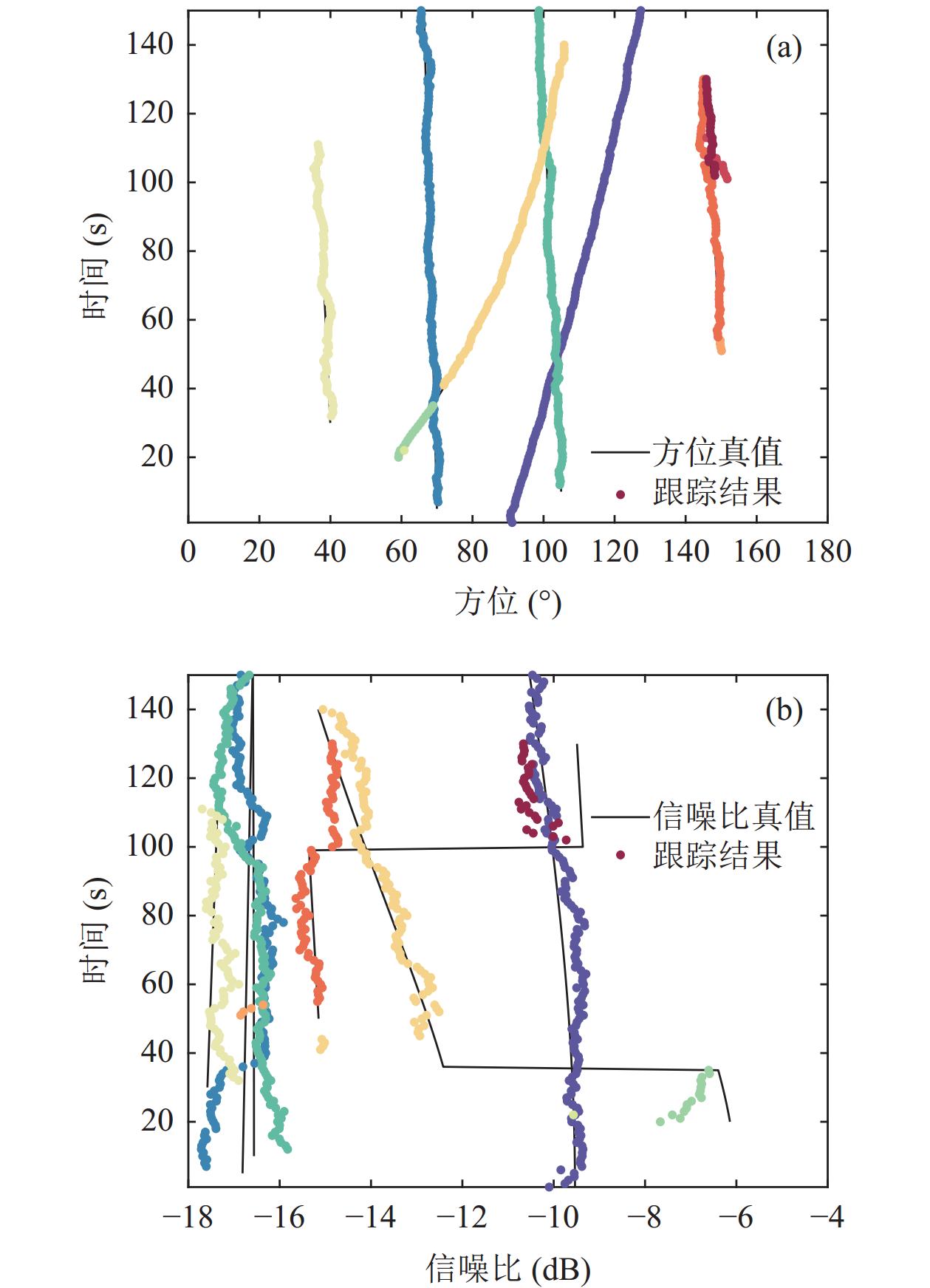
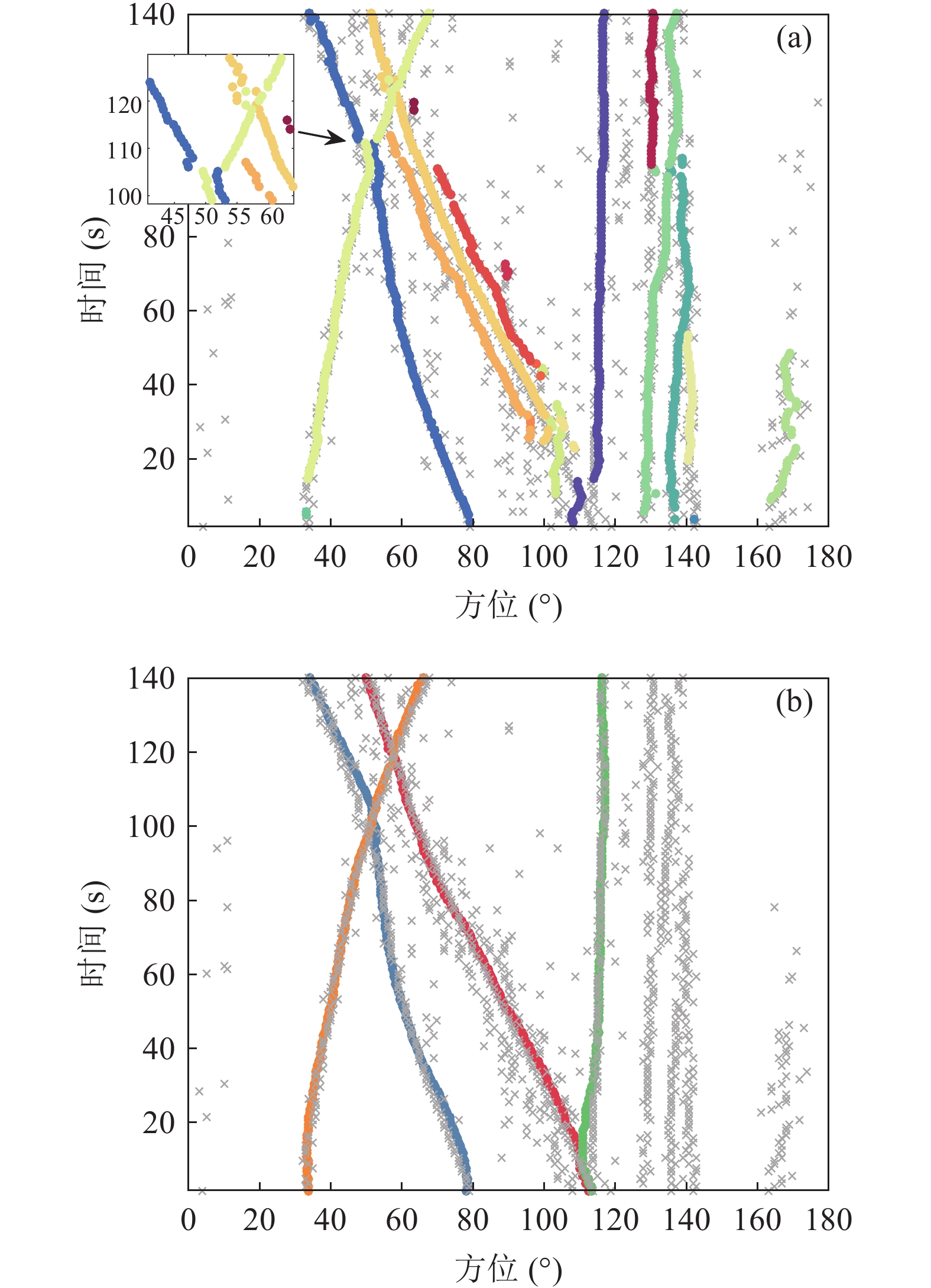
检测前跟踪方法的状态空间模型与3.3节相同, 新生目标模型由当前时刻阵列数据协方差矩阵${{\boldsymbol{R}}_{{Z_k}}}$决定, 信号功率峰值检测门限设置为$ \sigma _{{\text{threshold}}}^2 = 0.01 $的数量, 即$ {\mathrm{SNR}} > - 27\;{\mathrm{dB}} $。图14为检测前跟踪方法的多目标方位跟踪结果, PF-TBD滤波器在目标数精确已知的条件下, 目标4出现了误跟, 其方位轨迹与目标3完全重合。MB-TBD滤波器在第120秒轨迹交叉时目标1出现漏检, 跟踪效果不佳。GLMB-TBD滤波器不仅能连续、稳定地输出4个目标的方位轨迹, 在方位历程交叉区域仍具备较好的跟踪稳定性和连续性, 而且能够检测到140°方位的3个目标以及160°方位的目标, 并给出较为连续的方位轨迹。图15(b)为多目标信噪比跟踪结果, 目标1信噪比从−25 dB一直上升至−7 dB左右; 目标2初始信噪比约为−8 dB, 从第30秒开始下降, 随后上升至−10 dB左右; 目标3的信噪比维持在−5 dB附近; 目标4初始信噪比约为−15 dB, 随后下降至−20 dB直至消失; 140°方位的3个目标信噪比均在−20 dB附近。

针对方位历程交叉场景下多目标检测与跟踪问题, 提出一种基于广义标签多伯努利滤波的多目标检测前跟踪方法, 该方法直接将阵列数据协方差矩阵作为输入, 融合了航迹新生、消亡及演变等模型, 实现了联合多目标滤波与航迹管理。仿真和海试数据处理结果表明, 在方位历程交叉的情况下, 所提方法能够准确检测目标的出现与消失, 连续、稳定地跟踪目标方位, 并输出准确的方位航迹, 有效克服了轨迹中断和误跟问题, 在低信噪比(−18 dB)条件下具有较好的检测跟踪性能, 但在信噪比突变条件下所提算法会错误判断目标出现与消失, 此时需要借助频谱等特征保证目标轨迹的连续性。

定义$P \times P$维对称正定的复随机矩阵$ {\boldsymbol{Y}} $服从复逆威沙特分布, 记作$ {\boldsymbol{Y}}\sim \mathcal{C}\mathcal{I}\mathcal{W}({\boldsymbol{Y}};\rho ,{\boldsymbol{\varPhi }}) $, $ \rho \geqslant P $是自由度, $ {\boldsymbol{\varPhi}} $是$P \times P$维对称正定的尺度矩阵。假设复随机矩阵$ {\boldsymbol{Y}} $的期望${\rm{E}}[{\boldsymbol{Y}}]$和协方差矩阵$ {\rm{Cov}}[{\rm{vec}}({\boldsymbol{Y}})] $已知, 推导其自由度$ \widehat \rho $和尺度矩阵$ \widehat {\boldsymbol{\varPhi}} $的估计值。

根据共轭性质^[23], 复随机矩阵$ Y $的逆服从复威沙特分布, 即

根据复威沙特分布的性质, 复随机矩阵$ {\boldsymbol{Y}} $的期望为

根据文献[17]推论3.1.1, 对于任意$P \times 1$维的非零复向量$ {\boldsymbol{b}} $, 随机变量${\boldsymbol{\varLambda}} = {{({{\boldsymbol{b}}^{\rm H}}{\boldsymbol{Yb}})} / {({{\boldsymbol{b}}^{\rm H}}{\boldsymbol{\varPhi b}})}}$服从逆伽马(inverse Gamma, IG)分布, 写作$ \mathcal{I}\mathcal{G}(\varLambda ;\rho - P + 1) $, 其概率密度函数为

根据IG分布的性质, 随机变量$ \varLambda $的方差为

根据概率统计理论, 随机变量$ \varLambda $的方差为

联立式(A4)和式(A5), 可得

根据矩阵向量化的性质${\rm{vec}}({\boldsymbol{AC}}) = ({{\boldsymbol{C}}^{\rm{T}}} \otimes {{\boldsymbol{I}}_k}){\rm{vec}}({\boldsymbol{A}})$, 式中$ {\boldsymbol{A}} $和$ {\boldsymbol{C}} $分别是$k \times n$维和$n \times m$维的矩阵, $ \otimes $表示克罗内克积。则式(A6)写为

经推导, 自由度的估计值为

将$ \widehat \rho $代入式(A2), 可以得到尺度矩阵的估计值, 即

则式(20)和式(21)得证。