随着越来越多的水声传感器网络^[1-4]部署在水下通过水声通信链路执行海洋数据采集、资源探测以及助潜作业等任务, 非合作的水声通信信号必须得到有效地监测识别, 利用监测识别出的通信信号调制方式可以实现干扰对抗及探测定位等。水声正交频分复用(OFDM)是水下高速通信的常用手段, 对水声OFDM进行类内调制识别有重要研究意义。

目前, 无线电中已有多个方法^[5-9]可以实现OFDM类内调制识别, 这些方法基本都是通过提取子载波映射符号的高阶累积量特征实现识别。然而在水声多径信道下, OFDM子载波映射符号是混乱、发散的, 高阶累积量识别特征稳健性不足^[10], 导致识别方法失效。由于OFDM类内调试识别相关文献较少, 对OFDM的类内调制识别方法可以参考同样包括映射符号的MPSK类内调制识别。MPSK类内调制识别除直接提取映射符号的高阶累积量特征进行识别外, 还可以先从盲均衡的角度降低信道对映射符号的影响, 再提取特征实现识别。在无线电信道中, 文献[11-14]针对MPSK通信信号提出了多种盲均衡方法来克服信道干扰的影响, 从而能够更好地实现MPSK调制识别或解调。但这些盲均衡方法通常需要满足两个先验条件: 一是信道条件为平坦衰落信道; 二是MPSK原本映射符号是已知的。然而, 本文中的信道条件为水声多径信道, 且是在无任何先验信息的非合作条件下进行识别, 这两个先验条件均无法满足。在水声信道中, 文献[15]提出了一种分块子载波信道估计的水声OFDM类内调制识别方法, 该方法将整个OFDM子载波分为若干个大的分块, 并假设各子块内子载波映射符号受到相同信道衰落系数的影响, 对每个子块分别进行处理估计出对应的信道衰落系数, 从而降低水声信道的影响。但是在实际的水声信道下, 仅相干带宽内的相邻若干个子载波上的映射符号才能等效为受到相同信道衰落系数的影响, 显然该方法的假设并不合理, 未能充分利用子载波信道的特点, 识别性能受到了严重限制。

本研究从盲均衡的角度实现水声多径信道下OFDM类内调制识别, 提出了最大似然(Maximum Likelihood, ML)分类器框架下基于子载波信道模型盲均衡的非合作水声OFDM类内调制识别方法, 实现子载波BPSK、QPSK、8PSK及16QAM的调制识别。首先, 根据水声OFDM各子载波信道的特点, 对OFDM的子载波映射符号进行分块, 将各分块内子载波映射符号对应的信道衰落系数和噪声功率等效为相同。然后, 利用期望最大化(Expectation Maximization, EM)算法^[16-17], 分别对各分块内的子载波映射符号进行处理, 估计出信道衰落系数和噪声功率, 为了进一步提高EM算法的收敛速度, 利用K均值聚类(K-means)算法^[18]对该分块映射符号对应的信道衰落系数进行粗估计, 并将该信道衰落系数作为EM算法的初始值, 使EM算法能快速收敛, 结合估计结果, 利用ML分类器实现OFDM类内调制识别。最后, 通过仿真和海试数据验证提出的识别方法的有效性。

在多径信道下, 由于频率选择性衰落, 水声OFDM各子载波映射符号对应的信道衰落系数都不相同^[19-20]。假设调制的一个水声OFDM符号共包含$ K $个子载波, 符号周期为$ T $, 即子载波间隔为$ 1/T $, 系统载波频率为$ {f_c} $, 则第$ k $个子载波对应的载波频率为$ {f_k} = {f_c} + k/T, \; k = 0,\cdots ,K - 1 $。这里定义$ {c_k} $是第$ k $个子载波上对应的映射符号, 生成的OFDM调制信号可以表示为

取其实部可以获得最终的发送信号$ y\left( t \right) $。假设信道参数在一个 OFDM 符号持续时间内保持不变, 典型的水声多径信道模型可以表示为

其中, $ {N_p} $表示多径信道路径的个数, $ {A_p} $和$ {\tau _p} $分别表示路径$ p $的衰落系数和时延。在水声多径信道和噪声的影响下, 接收信号$ u(t) $可以表示为

其中, $ w(t) $是噪声。这里假设已经对接收信号去除了循环前缀并经过DFT恢复出了子载波映射符号。因此, 频域的基带子载波映射符号可以表示为

其中, $ {\boldsymbol{r }}= {\left[ {{r_0},\cdots,{r_{K - 1}}} \right]^{\text{T}}} $, $ {\boldsymbol{H}} $是维度为$ K \times K $的对角矩阵, 反映的是信道的频域信息, 第$ k $行的第$ k $列元素用$ {g_k} $表示, $ {\boldsymbol{c}} = {\left[ {{c_0},\cdots,{c_{K - 1}}} \right]^{\text{T}}} $, $ {\boldsymbol{v}} $是频域噪声向量。由式(4)可知, 在每个子载波上都存在一个信道衰落系数$ {g_k} $。与平坦信道衰落下映射符号仅对应一个信道衰落系数不同, 本文无法直接利用平坦衰落信道下的盲均衡方法解决映射符号发散、混乱的问题, 这里需要对每个子载波上的信道衰落系数进行估计, 利用估计值实现对子载波映射符号的均衡, 从而解决水声多径信道造成子载波映射符号混乱、发散的问题。

本文中的OFDM类内调制方式包括BPSK、QPSK、8PSK及16QAM, $ {M_i}\left( {i = 1,{\text{ }}2,{\text{ }}3,{\text{ }}4} \right) $代表各调制方式的映射符号种类个数, $ i $, $ {M_i} $取值与OFDM类内调制方式的对应关系如表1中所示, $ i $代表各类内调制方式, 取1时代表BPSK; 取2时代表QPSK; 取3时代表8PSK。BPSK共有两种不同的映射符号, 即$ {M_1} = 2 $; QPSK共有4种不同的映射符号, 即$ {M_2} = 4 $; 8PSK共有8种不同的映射符号, 即$ {M_3} = 8 $; 16QAM共有16种不同的映射符号, 即$ {M_4} = 16 $。

假设OFDM中的子载波映射符号都来自同一种调制方式, 将调制的单个OFDM符号的情况扩展到多个OFDM符号的情况。假设接收信号共包含$ L $个OFDM符号, 则$ {\boldsymbol{r}} = {\left[ {{{\boldsymbol{r}}_0},\cdots ,{{\boldsymbol{r}}_k},\cdots ,{{\boldsymbol{r}}_{K - 1}}} \right]^{\text{T}}} $, 其中, $ {{\boldsymbol{r}}_k} = \left[ {{{{r}}_{k,0}},\cdots ,{{{r}}_{k,L - 1}}} \right] $。若多径信道是时不变的, 由OFDM的调制原理可知, 这$ L $个OFDM符号中处于同一子载波位置的映射符号会受到相同的信道衰落系数$ {g_k} $的影响。由于无法确认接收映射符号$ {r_{k,l}} $来源于当前类内调制方式下的何种映射符号, 此时的似然值可以利用$ {{{r}}_{k,l}} $与各候选类内调制方式中的所有种类映射符号的平均似然值^[11]来替代。因此, 当给定$ {g_k} $和$ \sigma _k^2 $后, 似然值的计算公式可表示为

其中, $ {{\boldsymbol{s}}^{(i)}} =[ {s_0^{(i)},\cdots ,s_{{M_i} - 1}^{(i)}}] $表示第$ i $种候选调制方式下的原始映射符号, $ \sigma _k^2 $是处于第$ k $个子载波位置上对应映射符号的噪声功率。OFDM类内调制方式的识别可以通过比较各候选类内调制方式的似然值的大小来确定, 即

其中, $ \ln \left\{ \cdot \right\} $表示取对数运算, $ \widehat i $对应识别出的类内调制方式。

根据OFDM类内调制方式中对应映射符号的特点, 可以将接收的子载波映射符号$ {{\boldsymbol{r}}_k} $建模为高斯混合模型(GMM) ^[21]。假设建模的GMM由$ {M_i} $个高斯模型组成, 且$ {{\boldsymbol{r}}_k} $中映射符号$ {r_{k,l}} $映射到各高斯模型的概率相等, 则GMM的概率密度函数可以表示为

其中, $ {\mathcal{N}_m}\left( {{r_{k,l}}|{g_k},\sigma _k^2} \right) $是第$ m $个高斯模型的概率密度函数。由于无法确定映射符号$ {r_{k,l}} $来源于哪个高斯模型, 这里引入隐变量$ {\textit z} \triangleq {\left\{ {{{\textit z}_{l,m}}} \right\}_{L \times {M_i}}} $, 其中$ {{\textit z}_{l,m}} $表示映射符号$ {r_{k,l}} $来源于第$ m $个模型。$ {{\textit z}_{l,m}} $可以表示为

引入的隐变量$ {{\textit z}_{l,m}} $可将数据展开为完整数据, 即确定了$ {r_{k,l}} $来自于哪个高斯模型, 从而确保EM算法中的E-step顺利地展开。因此, 引入隐变量的似然函数可表示为

公式两边取对数可得到

定义$ Q $函数, 表示当给定映射符号$ {{\boldsymbol{r}}_k} $、前一次迭代的信道衰落系数$ g_k^p $以及噪声功率$ {(\sigma _k^2)^p} $时, 式(10)中的对数似然函数对$ {\boldsymbol z} $的期望, 具体可表示为

其中

令式(12)的结果为$ {\gamma _{l,m}} $, 它表示$ {{\boldsymbol{r}}_k} $中映射符号$ {r_{k,l}} $来源于各高斯模型的可能性。用$ {{\mathrm{Re}}} \{ {g_k}\} + {\rm j}\cdot{{\mathrm{Im}}} \{ {g_k}{\text{\} }} $表示信道衰落系数$ {g_k} $, 则$ Q $函数变为

利用式(12)实现对$ {{\textit z}_{l,m}} $的估计后, 式(13)中不再含有隐变量, EM中的M-step就归结为通过当前$ Q $函数的最大化来实现信道衰落系数和噪声功率的估计。对上式分别求关于$ {{\mathrm{Re}}} \{ {g_k}\} $, $ {{\mathrm{Im}}} \{ {g_k}\} $, $ \sigma _k^2 $的偏导数, 并令其为零, 可得

其中, $ {\widehat g_k} $和$ \widehat \sigma _k^2 $是新的估计值。因此, 可以利用式(12)(14)(15)(16)以迭代的方式求出信道衰落系数和噪声功率。在迭代过程中可以发现, EM算法需要设置信道衰落系数的初始值$ g_k^0 $, 一个相对准确的初始值$ g_k^0 $会使EM算法收敛的速度更快。本文提出利用K-means算法实现$ g_k^0 $的粗估计, 使EM算法能够快速地收敛, 提高算法的效率。K-means算法通过建立一个目标函数实现$ g_k^0 $的粗估计, 目标函数可表示为

分别对目标函数中$ {{\mathrm{Re}}} \{ {g_k}\} $和$ {{\mathrm{Im}}} \{ {g_k}\} $求偏导, 并令其值为零, 可得

K-means算法也是一种迭代算法, 一般设置迭代次数, 在迭代次数到达预设的门限时, 迭代会终止, 最终将K-means算法估计得到的$ {\widehat g_k} $作为EM算法的初始值$ g_k^0 $。EM算法先预设类内调制方式, 通过在预设的类内调制方式中设置的子载波映射符号和估计出的信道衰落系数解决原始子载波映射符号未知的问题。

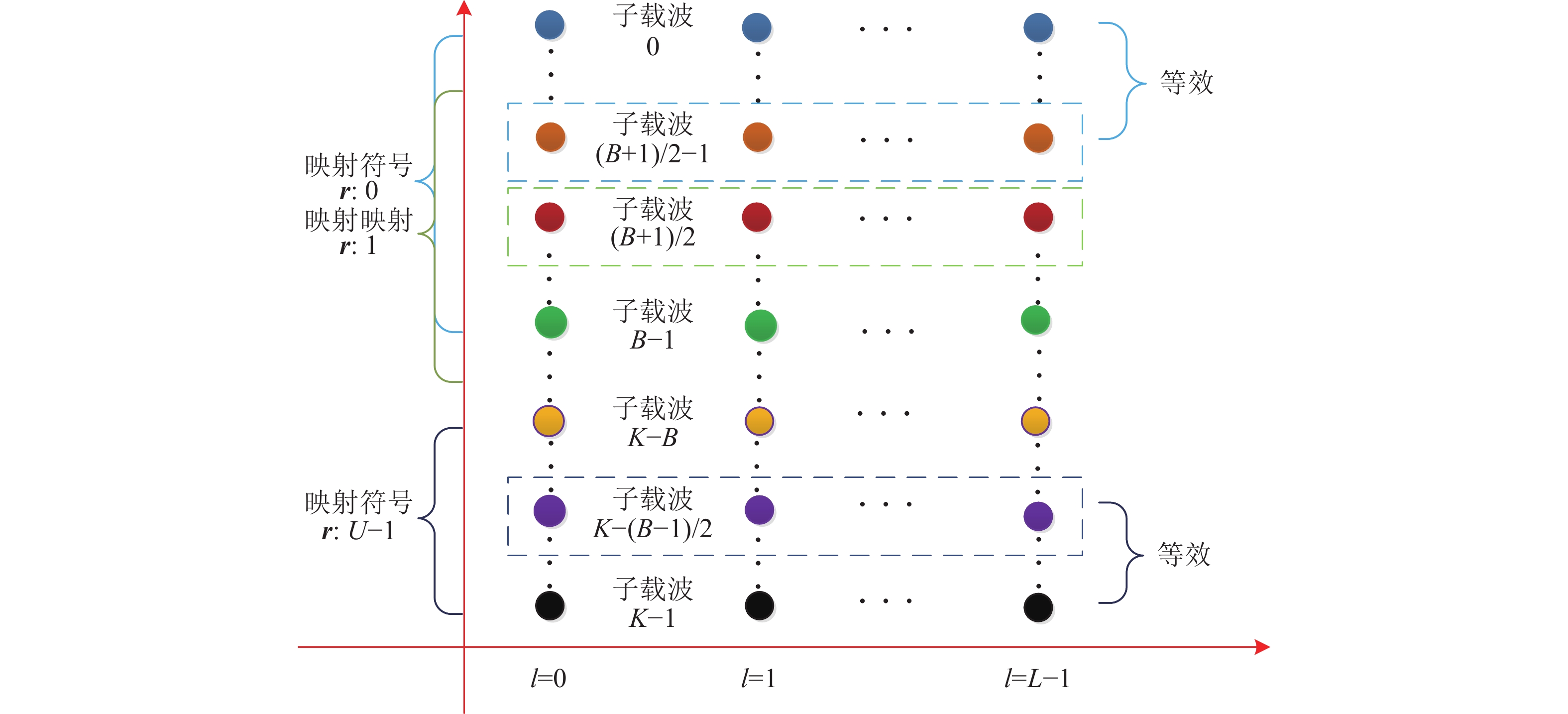
在EM算法的基础上进一步结合水声OFDM子载波信道模型, 提出一种分块策略, 实现高可靠的信道衰落系数和噪声功率的估计。从前述推导过程可知, 为保证信道衰落系数和噪声功率的准确性, EM算法实际上是分别对各子载波上的映射符号$ {{\boldsymbol{r}}_k} $进行处理。然而若要EM算法的性能得到保证, $ {{\boldsymbol{r}}_k} $中的映射符号个数需要达到一定要求, 这就需要对大量的OFDM符号进行处理。但在实际中, 尤其在非合作下接收到的OFDM符号个数有限, 且受时变多径信道的影响, 若将大量OFDM符号中同一个子载波位置上的映射符号利用EM算法进行处理, EM算法会由于映射符号个数不足或时变信道的影响导致可靠性降低。考虑到在一定的多径扩展下, 信道存在相干带宽, 而相邻多个子载波的频率变化是缓慢的, 在相干带宽内可以认为相邻多个子载波的映射符号受相同信道衰落系数的影响。因此, 为了同时兼顾OFDM子载波信道特点和EM算法对映射符号个数的要求, 这里假设相邻若干个子载波上的信道衰落系数是相同的, 利用EM算法处理多个相邻子载波上的映射符号, 在所提分块策略下, 信道衰落系数估计的可靠性将大大提高。本文称该方法为EM-Block, 具体的分块策略示意如图1所示。需要注意的是文献[15] 是将子载波分为几个大块, 同时将各大块内子载波映射符号对应的信道衰落系数等效为相同, 在一定的多径扩展下, 各大块内子载波对应的带宽势必会高于信道的相干带宽, 最终造成识别性能降低的问题。而本文完全考虑了水声多径信道、盲均衡算法以及子载波信道模型间的关系, 以一种类似于STFT中重叠的方式对子载波进行分块, 估计出每一个子载波对应的信道衰落系数, 识别性能将得到明显提高。

采用子载波重叠的方式进行分块, 步长为1个子载波, 根据提出的分块策略, EM-Block算法可分为以下几个步骤实现:

步骤1　对子载波映射符号$ {\boldsymbol{r }}$分块, 假设每个分块内对应的子载波个数为$ B $ ($ B $为奇数), 则总的分块个数为$ U = K - \left( {B - 1} \right) $。

步骤2　取前0至$ B - 1 $个子载波对应的映射符号作为分块映射符号$ {\boldsymbol{r}}:0 $, 利用EM算法估计出该分块映射符号下的信道衰落系数和噪声功率作为子载波$ \left( {B + 1} \right)/2 - 1 $对应的$ {g_{\left( {B + 1} \right)/2 - 1}} $和$ \sigma _{\left( {B + 1} \right)/2 - 1}^2 $; 取$ 1 $至$ B $个子载波对应的映射符号作为分块映射符号$ {\boldsymbol{r}}:1 $, 利用EM算法估计出该分块映射符号下的信道衰落系数和噪声功率作为子载波$ \left( {B + 1} \right)/2 $对应的$ {g_{\left( {B + 1} \right)/2}} $和$ \sigma _{\left( {B + 1} \right)/2}^2 $; 依次类推估计出所有分块映射符号$ {\boldsymbol r} = \left[ {{\boldsymbol{r}}:0,\cdots ,{\boldsymbol{r}}:u,\cdots ,{\boldsymbol{r}}:\left( {U - 1} \right)} \right] $下的信道衰落系数和噪声功率。

步骤3　利用子载波重叠的方式分块会出现前后多个子载波的信道衰落系数和噪声功率无法估计的情况, 这里直接将前、后多个子载波的信道衰落系数和噪声功率分别与子载波$ \left( {B + 1} \right)/2 - 1 $、子载波$ K - \left( {B - 1} \right)/2 $等效进行计算。

具体的算法流程如表2所示。EM-Block算法的计算量主要集中在第7, 12, 13步, 在每个分块下K-means算法中的$ {\widehat g_u} $在第$ n\_{\rm Kmeans} $次迭代以及EM算法中的$ {\gamma _{l,m}} $, $ {\widehat g_u} $, $ \widehat \sigma _u^2 $在第$ n\_{\text{EM}} $次迭代的计算量如表3所示。

因此, 在提出的分块策略下, 估计得到所有子载波映射符号的信道衰落系数和噪声功率后, 利用式(5)和式(6)可以实现OFDM类内调制识别。本文将分块策略下EM算法结合ML分类器实现OFDM类内调制识别的方法称为EM-Block-ML。

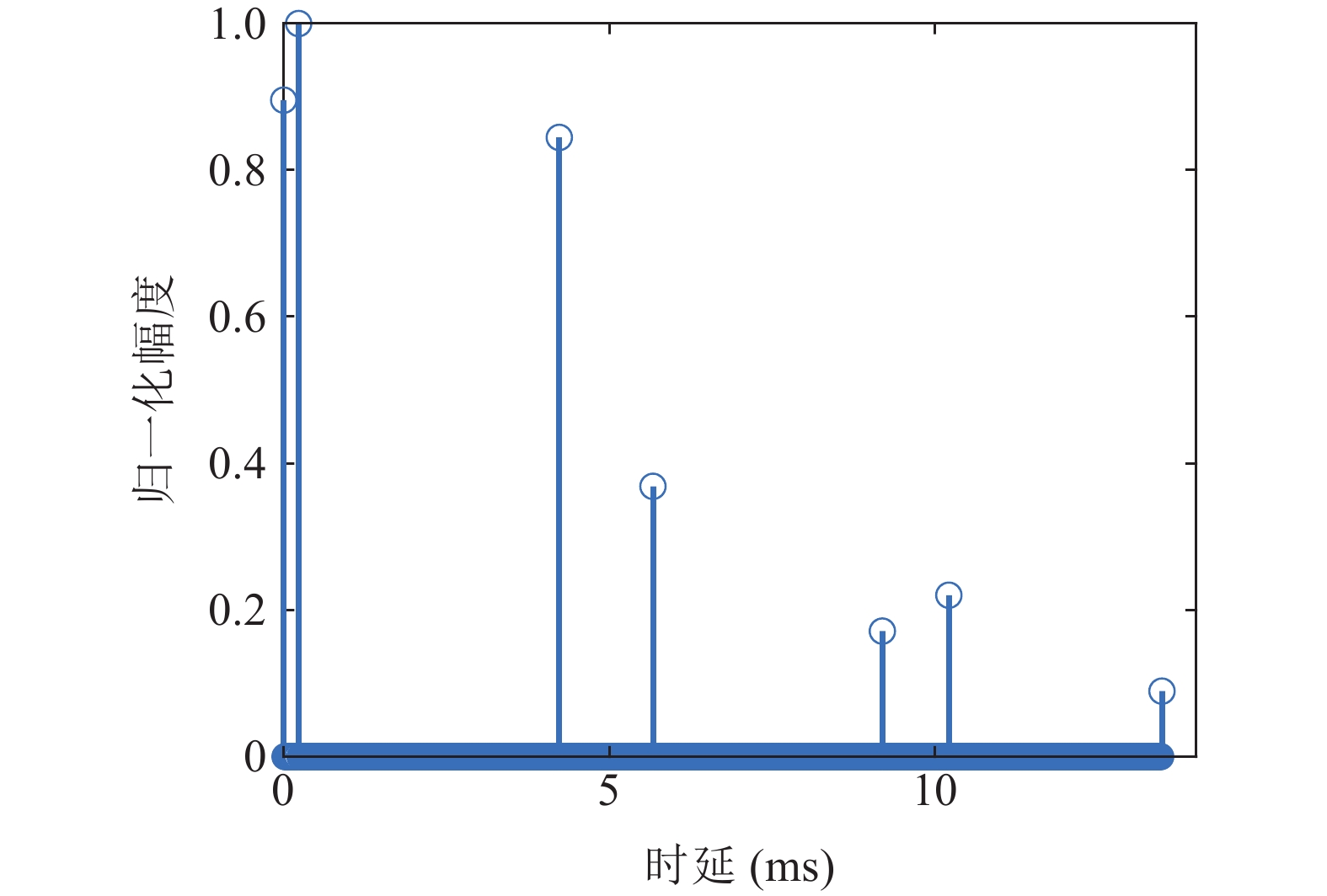
通过仿真信号对提出的识别方法进行验证。仿真中的水声多径信道引自文献[22], 假设信道的路径个数为7, 相邻路径的时延差服从均值为3 ms的指数分布, 平均多径时延扩展为21 ms。生成的信道冲激响应(CIR)如图2所示, 仿真中的噪声为带内噪声。

仿真的水声OFDM通信信号参数如表4所示, 假设接收到的OFDM通信信号已经去除循环前缀并经过DFT恢复出了子载波映射符号。为了减少计算量, 对每个接收信号处理时, 仅取2048个子载波映射符号进行计算。仿真中每个分块内的信道衰落系数的初始值设置为1。此外, 考虑到非合作情况下, 类内调制方式的原始映射符号未知, 为了与表4中的原始子载波映射符号有所区别, 设置BPSK的子载波映射符号为{j, –j}; 设置QPSK的子载波映射符号为{0.707+0.707j, –0.707+0.707j, –0.707–0.707j, 0.707–0.707j}; 设置8PSK的子载波映射符号为{0.924+0.383j, 0.383+0.924j, –0.383+0.924j, –0.924+0.383j, –0.924–0.383j, –0.383–0.924j, 0.383–0.924j, 0.924–0.383j}, 因为16QAM映射符号一般是统一的, 所以直接设置其子载波映射符号与表中原始子载波映射符号相同。在识别率的计算上, 分别在各信噪比(SNR)下取BPSK、QPSK、8PSK及16QAM类内调制下的300组数据用于计算最终的识别率, 因此每个SNR下的通信信号个数为1200。

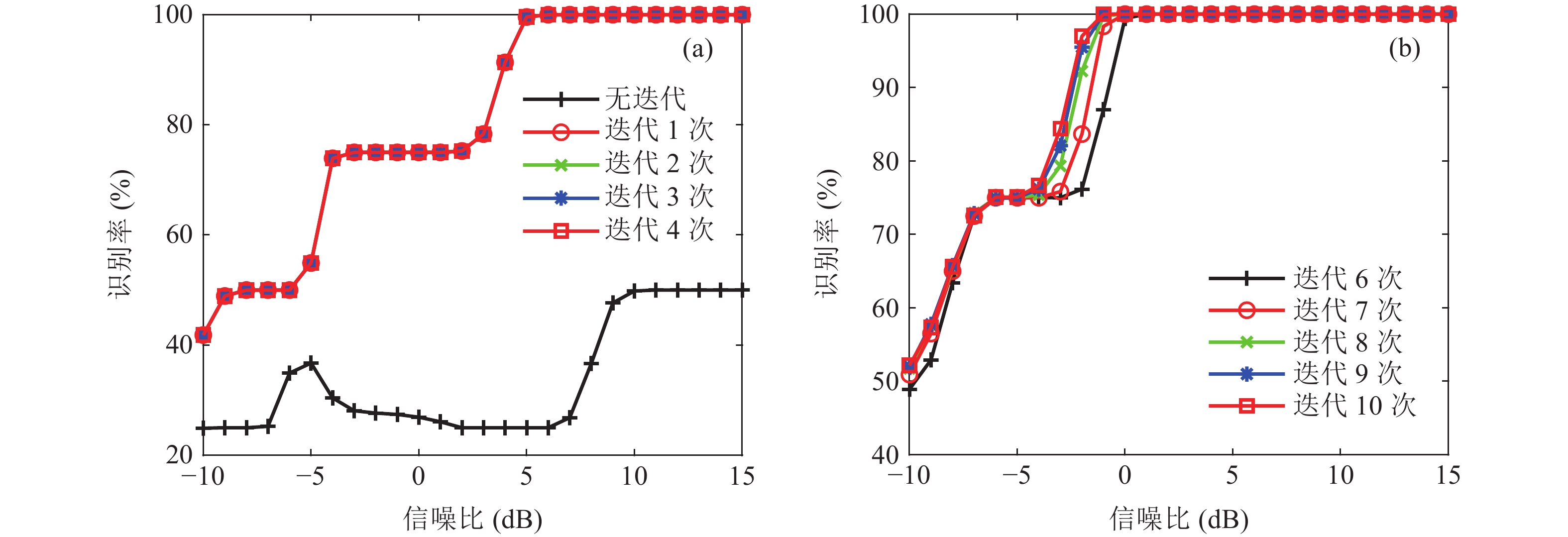
根据提出的分块策略, 对子载波映射符号进行分块。假设接收到的信号包含16个OFDM符号, 每个分块内包含5个子载波, 因此分块内的映射符号个数为80。又因为仅对2048个子载波映射符号进行计算, 所以共需子载波128个, 仿真中直接取全部OFDM符号的前128个子载波映射符号进行处理。根据理论推导可知, K-means算法能得到一个粗略的初始信道衰落系数, 可加快EM算法的收敛速度, 这里在仿真中固定EM算法的迭代次数为1, 设置K-means算法的迭代次数为0, 1, 2, 3, 4。当K-means算法的迭代次数为0时, 表示EM算法未用K-means算法获取信道衰落系数作为初始信道衰落系数, 而是用1作为初始信道衰落系数。图3(a)是当K-means算法取不同迭代次数时, EM-Block-ML方法的识别率随SNR的变化曲线。当K-means算法迭代次数为0时, 即使在较高的SNR下, 仅1次迭代的EM算法难以实现OFDM类内调制识别; 当K-means算法的迭代次数从0变为1或者更高时, 识别率明显提高, 说明K-means算法能够提供一个较为准确的信道衰落系数初始值。此外, 当K-means算法迭代次数为1或更高时识别率的提升不明显, 说明此时K-means算法已经基本收敛, 因此在后面的仿真中设置K-means算法的迭代次数为1。

在确定了K-means算法的迭代次数后, 通过比较在不同迭代次数EM算法下提出方法的识别性能来确定EM算法的迭代次数。设置EM的迭代次数为6, 7, 8, 9, 10。图3(b)为EM算法取不同迭代次数时, EM-Block-ML方法的识别率随SNR的变化曲线。随着EM算法迭代次数的增加识别率不断提高, 当EM算法的迭代次数为9或更高时, 识别率的提升不明显, 说明此时EM算法已经基本收敛, 因此在后面的仿真中设置EM算法的迭代次数为9。

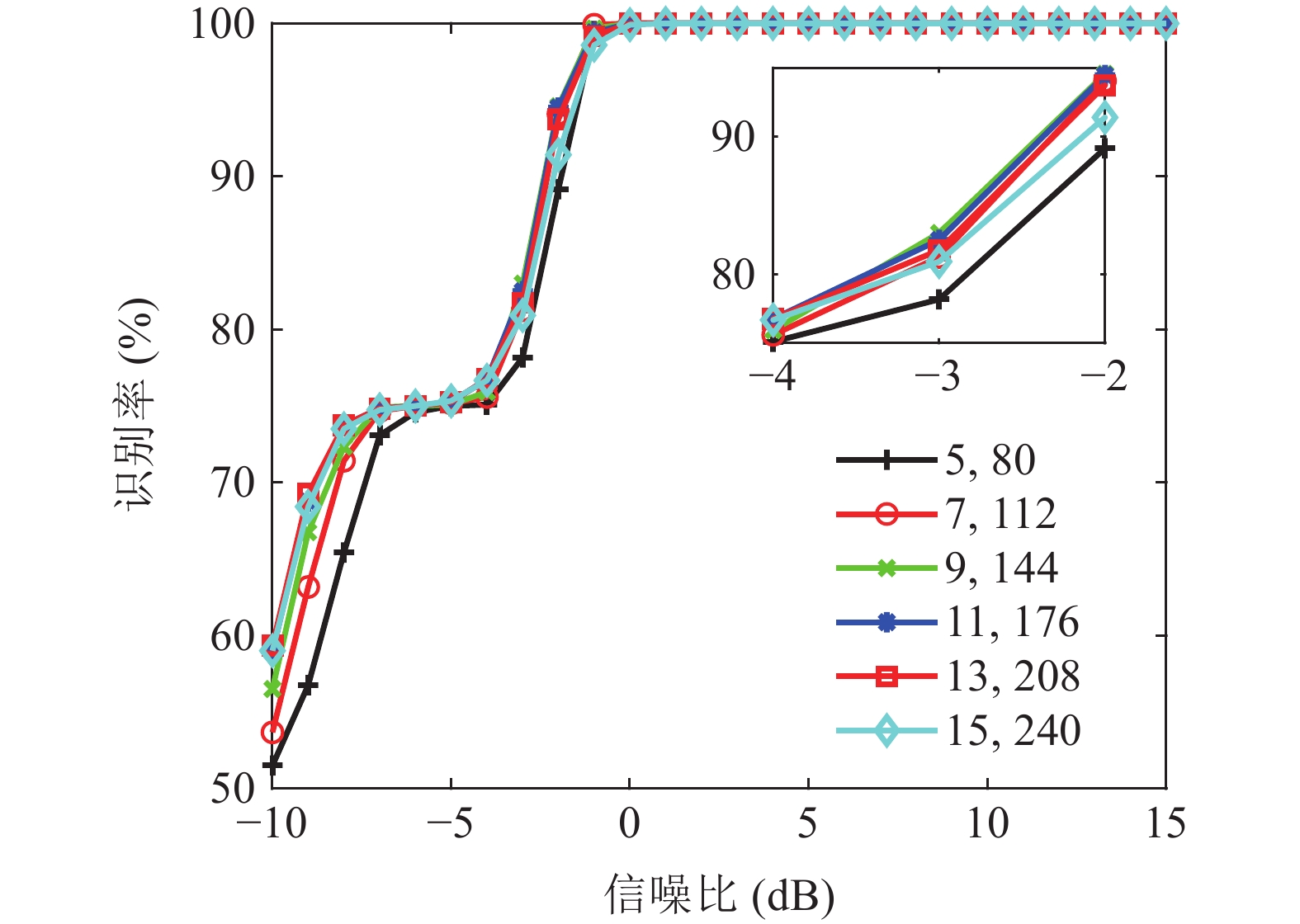
本文提出的分块策略需要同时兼顾OFDM子载波信道特点和EM算法对映射符号个数的要求, 即分块内子载波个数与分块内映射符号个数如何设置才能达到最优的识别性能。因为仿真部分仅对2048个子载波映射符号进行计算, 且接收信号包含16个OFDM符号, 所以共取全部OFDM符号的前128个子载波处理。仿真中共比较了六种不同参数设置下的识别率情况: 分别是分块内子载波个数为5, 分块内映射符号个数为80; 分块内子载波个数为7, 分块内映射符号个数为112; 分块内子载波个数为9, 分块内映射符号个数为144; 分块内子载波个数为11, 分块内映射符号个数为176; 分块内子载波个数为13, 分块内映射符号个数为208; 分块内子载波个数为15, 分块内映射符号个数为240。图4是不同分块内子载波个数与分块内映射符号个数设置下, EM-Block-ML方法的识别率随SNR的变化曲线。分块内子载波个数与分块内映射符号个数对识别率的影响是相互制约的, 当接收信号的OFDM符号个数一定时, 分块内子载波个数越少, 即分块个数越多, 在EM算法对映射符号个数满足要求时识别率就越高; 当EM算法映射符号个数无法满足要求时, 适量增加分块内子载波个数, 即减少分块个数, 增加EM算法的映射符号个数, 也能达到较高的识别率。根据以上分析, 在下面的仿真中设置分块内子载波个数为9, 分块内映射符号个数为144。

分析所提EM-Block方法的盲均衡性能, 具体是将恢复出的子载波映射符号除以对应估计出的每个分块内的信道衰落系数, 得到均衡后的子载波映射符号。仿真中SNR为10 dB。图5—图8分别是利用提出的EM-Block算法处理的各类内调制方式的盲均衡结果。所提EM-Block方法实现了高可靠的盲均衡, 均衡后的映射符号基本都收敛在对应类内调制方式下设置的子载波映射符号中。可见, 提出的EM-Block方法不仅可以实现盲均衡, 还能解决非合作情况下原始子载波映射符号未知的问题。接着利用这些收敛后的子载波映射符号结合设置的子载波映射符号计算似然值, 最大似然值对应的预设类内调制方式即为最终的识别结果。

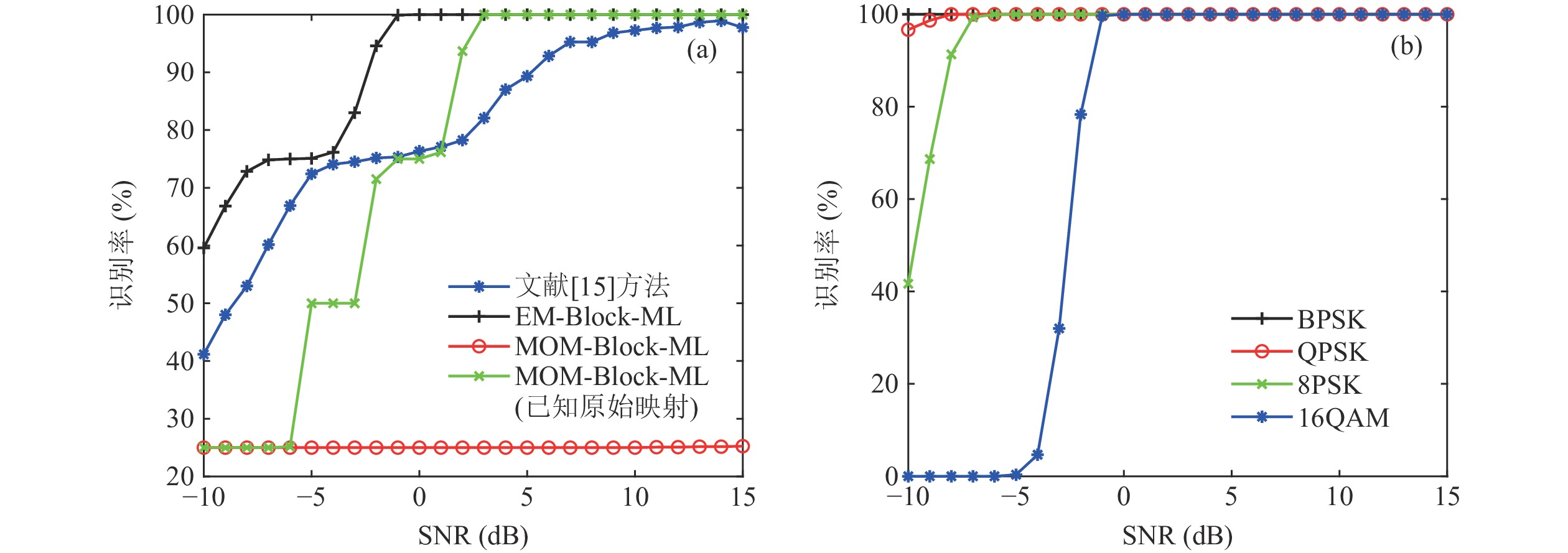
分析所提EM-Block-ML方法的识别性能, 仿真中加入了矩量法(MOM) ^[11]-Block-ML、已知原始子载波映射符号的MOM-Block-ML以及文献[15]中的方法作对比。EM-Block-ML识别方法的参数设置是从前文仿真中得到的, MOM-Block-ML和已知原始映射的MOM-Block-ML的分块策略与EM-Block-ML相同, 文献[15]中方法设置分块个数为4, 分块内子载波映射符号为256。EM-Block-ML、MOM-Block-ML、已知原始映射的MOM-Block-ML以及文献[15]中方法随SNR变化的识别率曲线如图9(a)所示。EM-Block-ML和已知原始映射的MOM-Block-ML均能较好地实现类内调制方式识别, 其中EM-Block-ML的识别性能优于已知原始映射的MOM-Block-ML, 但在非合作下原始子载波映射符号是未知的, MOM-Block-ML无法实现类内调制方式识别, 仿真中红色标记的识别率曲线说明了该点。此外, 文献[15]中方法在SNR大于5 dB时达到了90%以上的识别率, 而本文提出的方法在SNR大于−3 dB就能达到90%以上的识别率, 且从仿真结果来看, 本文提出方法在SNR大于−2 dB时就已经达到了100%的识别率, 而文献[15]中方法无法实现100%识别率, 仿真结果充分说明了该方法将分块内所有映射符号等效为受相同信道衰减系数影响的分块设计并不合理, 制约了算法的性能。图9(b)所示分别为BPSK、QPSK、8PSK及16QAM等OFDM类内调制方式在EM-Block-ML识别方法下各自的识别率曲线。BPSK在所有SNR下识别率均为100%; 当SNR大于–8 dB时, QPSK达到了100%的识别率; 当SNR大于–7 dB时, 8PSK达到了100%的识别率; 当SNR大于–1 dB时, 16QAM达到了100%的识别率。

由图9可知, 分块策略能有效地提高盲均衡的性能, 极大提高了识别率; MOM信道衰落系数和噪声功率估计方法无法解决原始子载波映射符号未知的问题, 无法应用于本文的非合作场景中; EM算法不仅能实现信道衰落系数和噪声功率的估计, 还能解决原始子载波映射符号未知的问题, 保证了ML分类器的有效性, EM-Block-ML识别方法实现了高可靠的非合作水声OFDM类内调制方式识别。

为进一步说明本文方法的有效性, 利用海试实验数据对EM-Block-ML识别方法进行验证。在南海陵水采集得到实验数据, 其中一只船抛锚作为目标节点接收测试信号, 另一只船作为移动节点在不同距离处发射测试信号。实验处水深60~70 m, 海况良好, 海面有小幅涌, 抛锚船有起伏, 偶有大晃动, 发射换能器深27 m, 接收水听器深30 m, 收发船距离约为5 km。发送的OFDM信号的调制参数如表5所示。

实验时连续发送了5帧OFDM信号, 图10是分别利用这5帧信号中的LFM信号做拷贝相关处理计算得到的信道冲激响应。实验时的信道具有明显的多径结构, 其中有两根能量较强的路径, 多径时延扩展在20 ms以内, 第1~5帧的多径结构较为稳定, 并无明显的变化。

图11(a)—图15(a)分别为这5帧OFDM信号的子载波映射符号。由图可见, 映射符号较为混乱、分散, 无法直接识别出原始的子载波调制方式。在此, 利用提出的EM-Block-ML方法处理这5帧OFDM信号的子载波映射符号。首先, 按照提出的分块策略对子载波映射符号进行分块, 每帧OFDM信号的子载波映射符号共包含595个数据子载波, 且有8个OFDM符号, 考虑到实际的海洋信道时变严重, 这里设置各分块内的子载波个数为5, 分块内的映射符号个数为40。此外, 考虑到非合作情况下, 原始类内调制方式对应的映射符号未知, 为与表5的原始子载波映射符号有所区别, 在处理映射符号时设置QPSK的子载波映射符号为{1, j, –1, –j}。然后, 利用EM-Block算法分别估计这些分块子载波映射符号对应的信道衰落系数, 利用得到的信道衰落系数对这5帧OFDM信号的子载波映射符号进行均衡, 均衡结果如图11(b-e)—图15(b-e)所示。EM-Block算法中当预设的类内调制方式为QPSK时, 得到的信道衰落系数能有效地使混乱、发散的子载波映射收敛到设置的映射符号{1, j, –1, –j}中。最后, 将对这5帧信号估计得到的信道衰落系数和噪声功率代入ML分类器的公式中, 通过比较预设不同类内调制方式下似然值的大小进行类内调制方式识别, 这5帧OFDM数据在预设不同类内调制方式时对应的似然值如表6所示。在预设QPSK时, 对应的似然值最大, 因此识别结果全部正确。

利用EM-Block-ML识别方法处理接收的5帧OFDM信号, 由结果可知, EM-Block方法能够有效地实现盲均衡, 使接收到的混乱、发散的子载波映射符号收敛到设置的子载波映射符号中, 保证了ML分类器的有效性; 这5帧OFDM信号类内调制方式的识别结果验证了所提识别方法的有效性。

受水声多径信道的影响, 接收到的OFDM子载波映射符号总体上是混乱、发散的, 这使原本可用于OFDM类内调制识别的特征稳健性不足, 导致识别方法失效。针对上述问题, 本文从盲均衡的角度, 提出了EM-Block-ML的水声OFDM类内调制识别方法。仿真和实验数据处理结果表明, K-means算法能加快EM-Block算法的收敛速度; EM-Block算法实现了高可靠的盲均衡, 使混乱、发散的子载波映射符号收敛, 解决了原始子载波映射符号未知的问题; EM-Block-ML方法实现了水声多径信道下高可靠的OFDM类内调制识别。