正交频分复用(OFDM)由于其特有的循环前缀和各子载波相互正交的结构以及良好的抗多途能力和高频带利用率, 近年来广泛应用于水声通信中^[1–5]。海洋环境复杂多变, 无论是自然界的生物运动还是人工作业, 都不可避免产生高强度脉冲干扰, 严重影响OFDM水声通信性能^[6–8]。因此, 如何在脉冲干扰环境中实现精确的信道估计和均衡, 改善OFDM通信系统性能是当前的一个重要研究方向^[9–11]。

根据脉冲干扰功率通常远大于信号功率且持续时间短的特性, 非线性预处理成为脉冲干扰环境中接收端常用方法之一。此类方法利用一定准则设置阈值, 按照阈值判决结果确定接收信号中脉冲干扰位置, 对这些位置的信号幅值进行裁剪、消隐或非线性滤波等操作, 缓解接收信号中脉冲干扰的影响, 随后再进行基于高斯白噪声的信道估计与均衡^[12]。文献[13]利用阈值法确定脉冲干扰位置, 然后在导频处采用最小二乘(LS)方法实现了信道和脉冲干扰的联合估计, 在阈值法基础上提高了估计精度。文献[14]针对含脉冲噪声的接收信号设计了多重阈值分段估计器, 结果表明其效果优于传统的裁剪、消隐估计器。虽然此类方法复杂度低, 但是确定阈值需要预先确定脉冲干扰的相关参数, 而参数往往会根据信道条件而变化, 即阈值的选取标准难以确定。同时, 对于OFDM信号而言, 其高峰值平均功率比破坏了用于缓解脉冲干扰的阈值法性能, 消隐后的OFDM信号不再是正交的, 由此产生的载波间干扰也会降低系统性能。还有一类常用的接收端处理方法是迭代干扰抑制, 通过一些准则迭代更新脉冲干扰的位置和大小, 直至获得脉冲干扰的最优估计, 将其从接收信号中减去以消除脉冲干扰影响。文献[15]基于因子图和置信传播设计了迭代消息传递结构, 缓解脉冲干扰影响。文献[16]首先根据信号幅值确定脉冲噪声在时域的位置, 然后基于LS算法, 利用OFDM空子载波估计脉冲干扰样本, 最后在现有信道估计和初步数据符号决策的基础上, 进一步开发了迭代接收机。

近年来, 越来越多的学者开始关注水声信道和脉冲干扰的稀疏性, 引入压缩感知进行稀疏信号重构与恢复^[17-18]。文献[19]提出时频测量的OFDM框架结构, 基于压缩感知同时抑制窄带干扰和脉冲噪声, 从OFDM的零子载波中获得脉冲干扰的测量向量对信号进行重构。文献[20-21]提出利用正交匹配追踪(OMP)算法, 在迭代过程中引入施密特正交化, 准确估计信道状态信息并抑制脉冲噪声, 但是OMP算法需要预先假设脉冲噪声稀疏度已知。为进一步提高脉冲干扰下的OFDM通信性能, 文献[22-23]采用基于期望最大化(EM)的稀疏贝叶斯学习(SBL)算法, 在接收端将信道向量和脉冲干扰向量合并为一个向量进行估计, 从接收信号中减去估计出的脉冲干扰, 再根据估计信道进行均衡。经过仿真和试验验证, 该方法可实现良好系统性能, 但存在两方面的问题: 一是没有考虑到脉冲干扰和信道各自的稀疏性, 将二者作为一个联合向量进行估计, 引入了一定的估计误差; 二是联合向量的维度较高, 导致迭代求解时系统的计算复杂度较高。此外, 文献[24]在SBL信道估计的基础上, 进一步提出了联合的稀疏贝叶斯学习(JSBL)算法, 在迭代中完成信道和符号的联合估计。虽然该文献给出了一种JSBL的低复杂度递归实现方法, 但没有考虑脉冲干扰存在时的应对策略。

考虑到脉冲干扰向量和信道向量具有不同的稀疏度, 本文提出了基于变分贝叶斯推断(VBI)的水声OFDM信道估计方法。该方法利用平均场变分贝叶斯推断, 使用简单概率分别对脉冲干扰向量和信道向量复杂后验概率进行拟合, 得到最大后验估计。考虑到脉冲干扰向量和信道向量具有独立性, 本文将二者分离估计, 提高了估计精度。同时, 相比基于SBL的干扰、信道联合估计方法, 本文方法显著降低了迭代过程的计算复杂度。为充分利用全部子载波信息, 区别于传统线性均衡方法, 本文进一步提出了基于VBI的干扰、信道和符号联合估计方法, 将符号估计融入VBI框架, 与干扰向量和信道向量一起迭代求解, 利用三者之间的耦合关系, 进一步提升系统性能。

考虑一个卷积编码, 采用梳状导频的OFDM系统, 假设每个符号包含$ N $个子载波, 其中导频子载波数目为$ {N_p} $, 数据子载波数目为$ {N_d} $, 空子载波数目为$ {N_{\textit z}} $, 满足$ N = {N_p} + {N_d} + {N_{\textit z}} $。设每个OFDM符号持续时间为$ T $, 循环前缀长为$ {T_{cp}} $, 通带信号的起始频率为${f_0}$, 则通带OFDM符号可以表示为

式中, $\mathrm{Re}(\cdot)$表示取实部, $ x\left[ k \right] $表示第$ k + 1 $个子载波上传输的符号, ${f_k} = {f_0} + k/T$表示第$ k + 1 $个子载波的中心频率。假设基带的水声信道长度为L, 满足${\boldsymbol{h}} = {\left[ {h\left[ 0 \right],h\left[ 1 \right], \cdots ,h\left[ {L - 1} \right]} \right]^{\text{T}}}$, 且$ {T_{cp}} > L $。则基带的频域接收OFDM符号${\boldsymbol{Y}} = {\left[ {Y(0),Y(1),\cdots,Y(N - 1)} \right]^{\text{T}}}$满足以下关系:

式中, $ {X} $为频域OFDM符号构成的$ N \times N $维的对角矩阵。$ {H}{\text{ = }}{{F}_L}{h} $为信道的频率响应, $ {F} $为$ N \times N $维的归一化傅里叶矩阵, $ {{F}_L} $为$ {F} $的前$L$列, $ {\boldsymbol{I}} = [I(0),I(1),\cdots, I(N - 1)]^{\text{T}} $和$ {\boldsymbol{W}} = {[W(0),W(1),\cdots,W(N - 1)]^{\text{T}}} $分别为$ N \times 1 $维频域的脉冲干扰向量和背景高斯白噪声向量, $ {\boldsymbol{i}} = {[i(0),i(1),\cdots,i(N - 1)]^{\text{T}}} $是$ N \times 1 $的时域脉冲干扰向量。

受文献[23]的启发, 为了简化估计维度, 引入${N_p} \times {N_p}$维的归一化傅里叶矩阵${{\boldsymbol{F}}_p}$, 令${{\boldsymbol{i}}_p} = {\boldsymbol{F}}_p^{\text{H}}{{\boldsymbol{I}}_p}$, 下标$p$表示导频位置, 此时${{\boldsymbol{i}}_p}$可以看作是对时域脉冲干扰的欠采样。导频处的接收信号可以表示为

式中, ${{\boldsymbol{Y}}_p}$表示${\boldsymbol{Y}}$导频所在行构成的$ {N_p} \times 1 $列向量, $ {X_p} $是$ {N_p} \times {N_p} $的对角阵, 其对角元素为已知导频符号, ${N_p} \times L$维的${{{\overline {\boldsymbol{F}}}}_L}$是${\boldsymbol{F}}$导频所在行对应的前$L$列, $ {{\boldsymbol{M}}_p} = {{\boldsymbol{X}}_p}{{\boldsymbol{\overline F}}_L} $, ${{\boldsymbol{W}}_p}$为导频处对应的频域高斯白噪声。

常见的脉冲噪声统计模型有高斯混合模型(GMM)和对称$\alpha $稳定分布模型等, 背景噪声与脉冲噪声共同构成了GMM分布。其中, GMM具有闭式的概率密度函数, 且一阶矩和二阶矩均有限, 便于分析; 对称$\alpha $稳定分布模型稳定性强, 能较为准确地描述脉冲噪声概率密度函数拖尾特征, 但无闭式的概率密度函数。为了能够更有效简便地完成后续的变分近似, 本文将脉冲噪声的先验分布设定为0均值的高斯分布, 与背景噪声共同构成了二分量的GMM分布。因此, 定义信道$ {\boldsymbol{h}} $和脉冲干扰$ {{\boldsymbol{i}}_p} $的先验分布分别为

式中, $ \mathcal{C}\mathcal{N} $表示复高斯分布, $ {{\boldsymbol{\lambda }}_{1:L}} = {\left[ {{\lambda _1},{\lambda _2}, \cdots ,{\lambda _L}} \right]^{\text{T}}} $为信道$ {\boldsymbol{h }}$的超参数, $ {{\boldsymbol{\lambda }}_{L + 1:L + {N_p}}} = {[ {{\lambda _{L + 1}},{\lambda _{L + 2}}, \cdots ,{\lambda _{L + {N_p}}}} ]^{\text{T}}} $为脉冲干扰$ {{\boldsymbol{i}}_p} $的超参数, 各参数相互独立。进一步定义超参数的先验概率分布:

式中, $ \mathcal{G} $表示伽马分布, $\varGamma \left( a \right) = \int_0^\infty {{t^{a - 1}}{\text{exp}}\left( { - t} \right){\rm d}t} $。令${\boldsymbol{\lambda }} = {[ {{\boldsymbol{\lambda }}_{1:L}^{\text{T}},{\boldsymbol{\lambda }}_{L + 1:L + {N_p}}^{\text{T}}} ]^{\text{T}}}$。定义背景高斯白噪声${{\boldsymbol{W}}_p}$的先验分布满足:

式中, ${W_i}$表示${{\boldsymbol{W}}_p}$中第$i$个元素。进一步定义$\varepsilon $的先验满足伽马分布:

根据变分贝叶斯推断原理, 引入变分分布$ q\left( {{\boldsymbol{h}},{{\boldsymbol{i}}_p},{\boldsymbol{\lambda }},\varepsilon } \right) $拟合后验分布$ p\left( {{\boldsymbol{h}},{{\boldsymbol{i}}_p},{\boldsymbol{\lambda }},\varepsilon |{Y_p}} \right) $, 利用平均场理论将$ q\left( {{\boldsymbol{h}},{{\boldsymbol{i}}_p},{\boldsymbol{\lambda }},\varepsilon } \right) $分解为如下形式^[25]:

问题转化为寻找式(8) 满足的最佳分布$ {q^*}\left( {{\boldsymbol{h}},{{\boldsymbol{i}}_p},{\boldsymbol{\lambda }},\varepsilon } \right) $, 使二者的后向KL (Kullback-Leibler)散度最小^[25]。令${\boldsymbol{\varLambda}} = \left\{ {{\boldsymbol{h}},{{\boldsymbol{i}}_p},{\boldsymbol{\lambda }},\varepsilon } \right\}$表示待估计参数集合, $ {\varLambda _j} $表示${\boldsymbol{\varLambda }}$中第$ j $个元素, 变分分布$ q\left( {{\varLambda _j}} \right) $的最优解$ {q^*}\left( {{\varLambda _j}} \right) $满足

式中, 符号$ \propto $表示正比关系, $\langle\cdot\rangle_{q(\boldsymbol{\varLambda}) / q\left(\varLambda_j\right)}=E_{\prod_{i \neq j}^4 q\left(\Lambda_i\right)}[\cdot]$表示对$ (\cdot) $求除了$ q\left( {{\varLambda _j}} \right) $外其他$ q\left( {{\varLambda _i}} \right) $乘积的期望。

由于任一$ {q^*}\left( {{\varLambda _j}} \right) $的求解依赖于其他参数$ {\varLambda _i} $, 因此可迭代更新各参数, 依次求得各参数的最优解。

设${{\boldsymbol{\mu}} }_{(\cdot)}$和$ {{\boldsymbol{\varSigma }}}_{(\cdot)} $分别表示期望和协方差, 则${\boldsymbol{h}}$中第$j$个元素平方的期望可以表示为$ {\mu _{{\boldsymbol{h}}_j^2}} = {\langle {{{| {{{\boldsymbol{h}}_j}} |}^2}} \rangle _{q( {\boldsymbol{h}} )}} = {{\boldsymbol{\varSigma }}_{\boldsymbol{h}}}( {j,j} ) + {[ {{{\boldsymbol{\mu }}_{\boldsymbol{h}}}( j )} ]^2},j = 1,2, \cdots ,L $, 同理$ {\boldsymbol{i}} $中第$j$个元素平方的期望可以表示为$ {\mu _{{\boldsymbol{i}}_j^2}} = {\langle {{{| {{{\boldsymbol{i}}_{p,j - L}}} |}^2}} \rangle _{q( {{{\boldsymbol{i}}_p}} )}} = {{\boldsymbol{\varSigma }}_{\boldsymbol{i}}}( {j - L,j - L} ) + {[ {{{\boldsymbol{\mu }}_{\boldsymbol{i}}}( {j - L} )} ]^2} $, $ j = L + 1, \cdots ,L + {N_p} $。令$ {\widehat \lambda _m} = {\langle {{\lambda _m}} \rangle _{q({\lambda _m})}}, \; m = 1, \cdots , L + {N_p} $, $ {{\boldsymbol{\widehat \lambda }}_{1:L}} = {[ {{{\widehat \lambda }_1},{{\widehat \lambda }_2}, \cdots ,{{\widehat \lambda }_L}} ]^{\text{T}}} $, $ {{\boldsymbol{\widehat \lambda }}_{{L+1} : {L+N_p}}} = [ {{\widehat \lambda }_{L + 1}}, {{\widehat \lambda }_{L + 2}}, \cdots ,{{\widehat \lambda }_{L + {N_p}}} ]^{\text{T}} $, 由附录A可得$ q( \varepsilon ) $, $ q( {\boldsymbol{h }}) $, $ q( {{{\boldsymbol{i}}_p}} ) $和$ q( {\boldsymbol{\lambda }}) $分别满足

式中

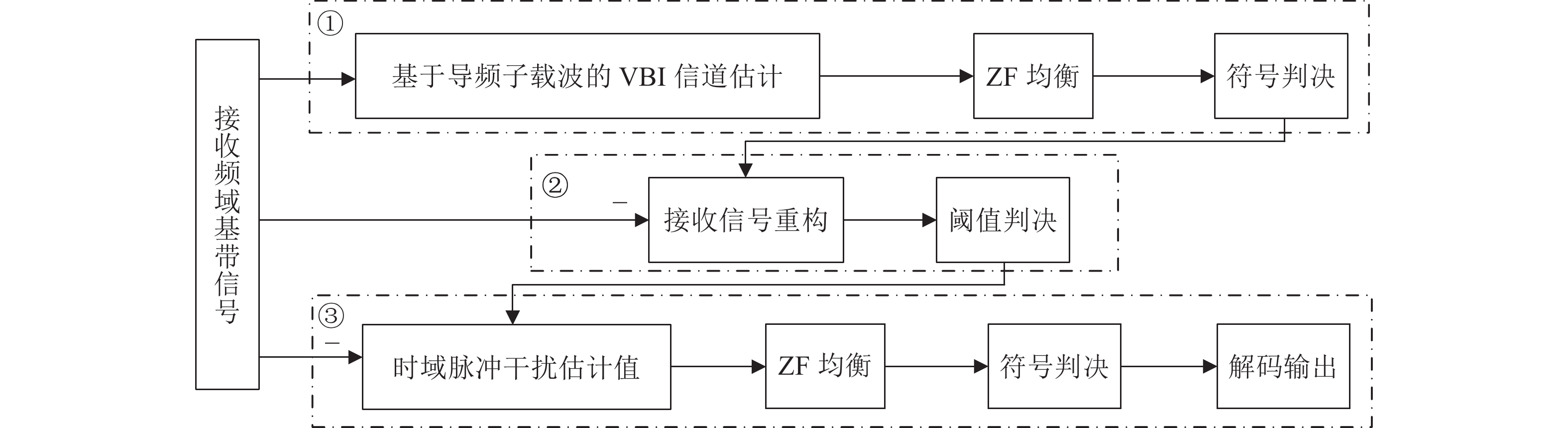
总结基于VBI的信道估计方法步骤如表1所示。按照表1步骤迭代收敛后得到信道估计值$ {{\boldsymbol{\widehat h}}_{{\text{VBI}}}} $, 此时可利用迫零(Zero-forcing, ZF)均衡^[26]在OFDM接收端得到均衡后的符号, 然后根据发射端规则重构接收信号$\overline y$, 与实际接收信号相减, 设置合理阈值$T$, 即可估计出时域全部的脉冲干扰$ \widehat i $:

将该脉冲干扰从实际接收信号中减去, 然后直接进行均衡即可。图1为基于VBI的信道估计和脉冲干扰抑制流程。ZF均衡的目的主要是用于产生符号的估计值, 以提供给后续的联合估计方法作为迭代的初始值。同样地, 也可以选取其他均衡器来产生符号的初始估计值, 出于简化考虑, 本文选取了较为简单的ZF均衡, 从而不额外增加系统的复杂度。

本节考虑将符号估计代入VBI框架, 第2节中基于导频的信道估计可扩展为基于全部子载波的信道、干扰和符号联合估计(JVBI), 进一步提升符号估计精度。令$ {\boldsymbol{M}} = {\boldsymbol{X}}{{\boldsymbol{F}}_L} $, 由式(2)可得

定义$ \boldsymbol i $的先验分布为

式中, ${{\boldsymbol{\lambda }}_{L + 1:L + N}} = {[ {{\lambda _{L + 1}},{\lambda _{L + 2}}, \cdots ,{\lambda _{L + N}}} ]^{\text{T}}}$。定义$ {{\boldsymbol{\lambda }}_{L + 1:L + N}} $先验概率分布为

令${\boldsymbol{\lambda }} = {[ {{\boldsymbol{\lambda }}_{1:L}^{\text{T}},{\boldsymbol{\lambda }}_{L + 1:L + N}^{\text{T}}} ]^{\text{T}}}$, ${\boldsymbol{ \varLambda}} = \left\{ {{\boldsymbol{h}},{\boldsymbol{i}},{\boldsymbol{\lambda }},\varepsilon ,{\boldsymbol{X}}} \right\} $, 则联合概率分布可以表示为

引入分布$ q\left( {{\boldsymbol{X}},{\boldsymbol{h}},{\boldsymbol{i}},{\boldsymbol{\lambda }},\varepsilon } \right) $拟合后验分布$ p\left( {{\boldsymbol{X}},{\boldsymbol{h}},{\boldsymbol{i}},{\boldsymbol{\lambda }},\varepsilon |{\boldsymbol{Y}}} \right) $, 由式(8) 同理可得

与${\boldsymbol{\varLambda }}$中的其他参数不同, 由于待估计符号${\boldsymbol{X}}$的复杂性, 其变分分布无法由某一确定分布给出, 因此可以根据下式求解${\boldsymbol{X}}$的最大似然估计:

式中, $ i \in {{\boldsymbol{\varDelta }}_{{N_d}}} $为数据符号索引, ${\boldsymbol{\varPsi }}$为星座图映射符号集合, $ {{\boldsymbol{F}}}_{L}\left(i,\cdot \right) $代表$ {{\boldsymbol{F}}_L} $的第$i$行, $ {\boldsymbol{C}} = {{\boldsymbol{F}}_L}{{\boldsymbol{\varSigma }}_{\boldsymbol{h}}}{\boldsymbol{F}}_L^{\text{H}} $, $ {\boldsymbol{D}} = {\boldsymbol{F}}{{\boldsymbol{\varSigma }}_{\boldsymbol{i}}}{\boldsymbol{F}}_{}^{\text{H}} $。

与第2节推导类似, 令$ q\left( {{\boldsymbol{X}},{\boldsymbol{h}},{\boldsymbol{i}},{\boldsymbol{\lambda }},\varepsilon } \right) $与$ p( {\boldsymbol{X}},{\boldsymbol{h}},{\boldsymbol{i}},{\boldsymbol{\lambda }}, \varepsilon |Y ) $之间的后向KL散度最小, 可分别得到变分分布$ q\left( \varepsilon \right) $, $ q\left( h \right) $, $ q\left( i \right) $, $ q\left( {\boldsymbol{\lambda }} \right) $为

式中

总结基于全部子载波的信道、干扰和符号联合估计步骤如表2所示。在VBI框架中代入未知符号进行估计时, 需要给出全部子载波上符号的初始迭代值, 为了避免累积误差, 本文将第2节中VBI方法得到的判决符号作为初值传递给JVBI方法。

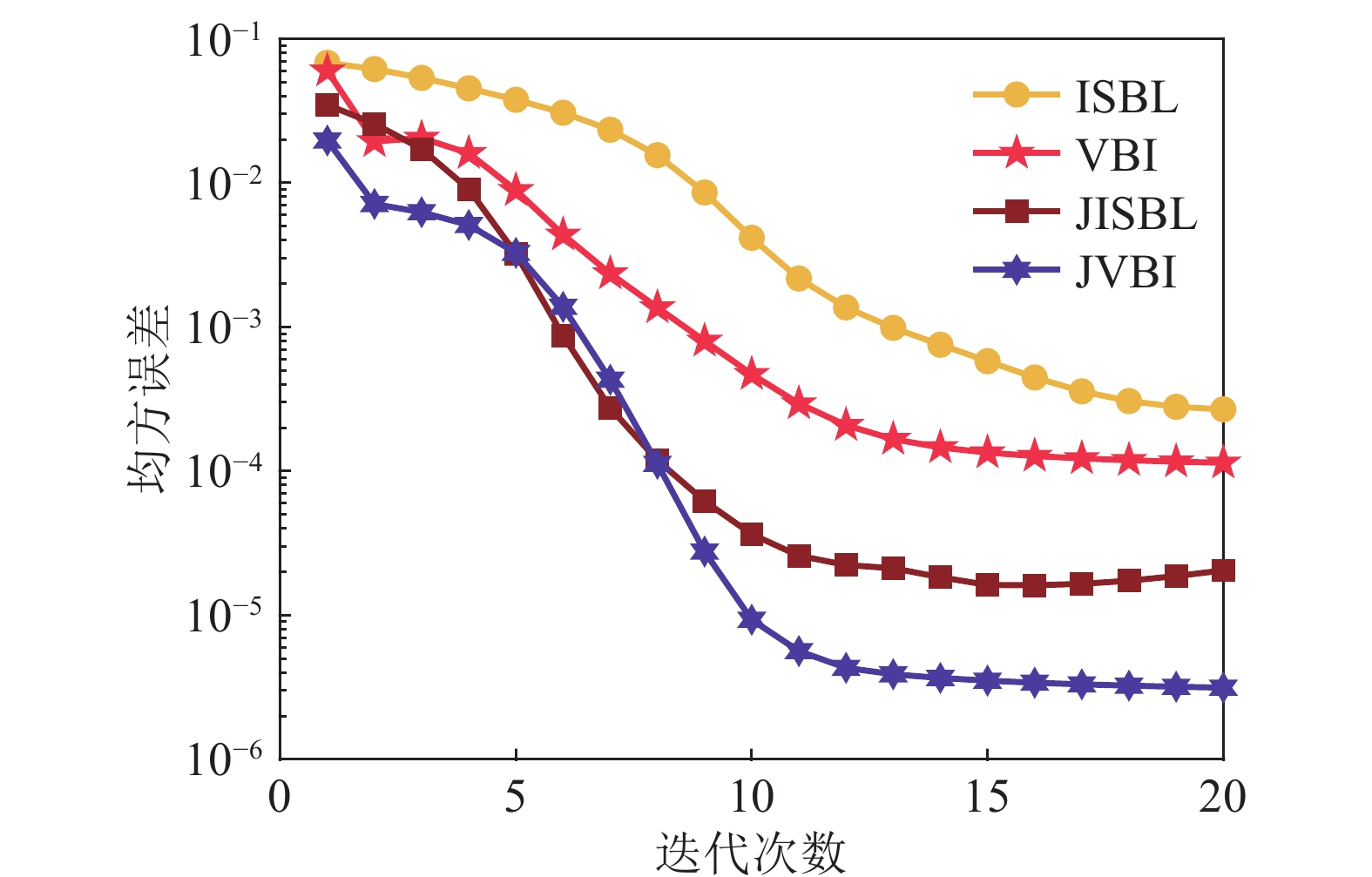
对所提方法与文献[23]中基于导频的SBL的联合估计方法进行复杂度对比分析。虽然文献[23]中信道长度为${N_p}$, 但其有效信道长度仍为$L$, 因此可将联合向量的维度由$2{N_p}$简化为$L + {N_p}$。表3对比了基于SBL的联合估计方法和本文所提方法一次迭代的计算复杂度, 其中, ISBL方法表示采用文献[23]中基于导频子载波的SBL干扰、信道联合估计方法得到信道估计值后, 再利用本文方法进行干扰抑制, JISBL表示文献[23]中的基于全部子载波的SBL干扰、信道和符号联合估计方法, VBI表示基于导频子载波的VBI信道估计和干扰抑制方法, JVBI表示基于全部子载波的VBI干扰、信道和符号联合估计方法。由于本文所提方法分离了脉冲干扰向量和信道向量, 因此VBI和JVBI计算复杂度远小于ISBL和JISBL。

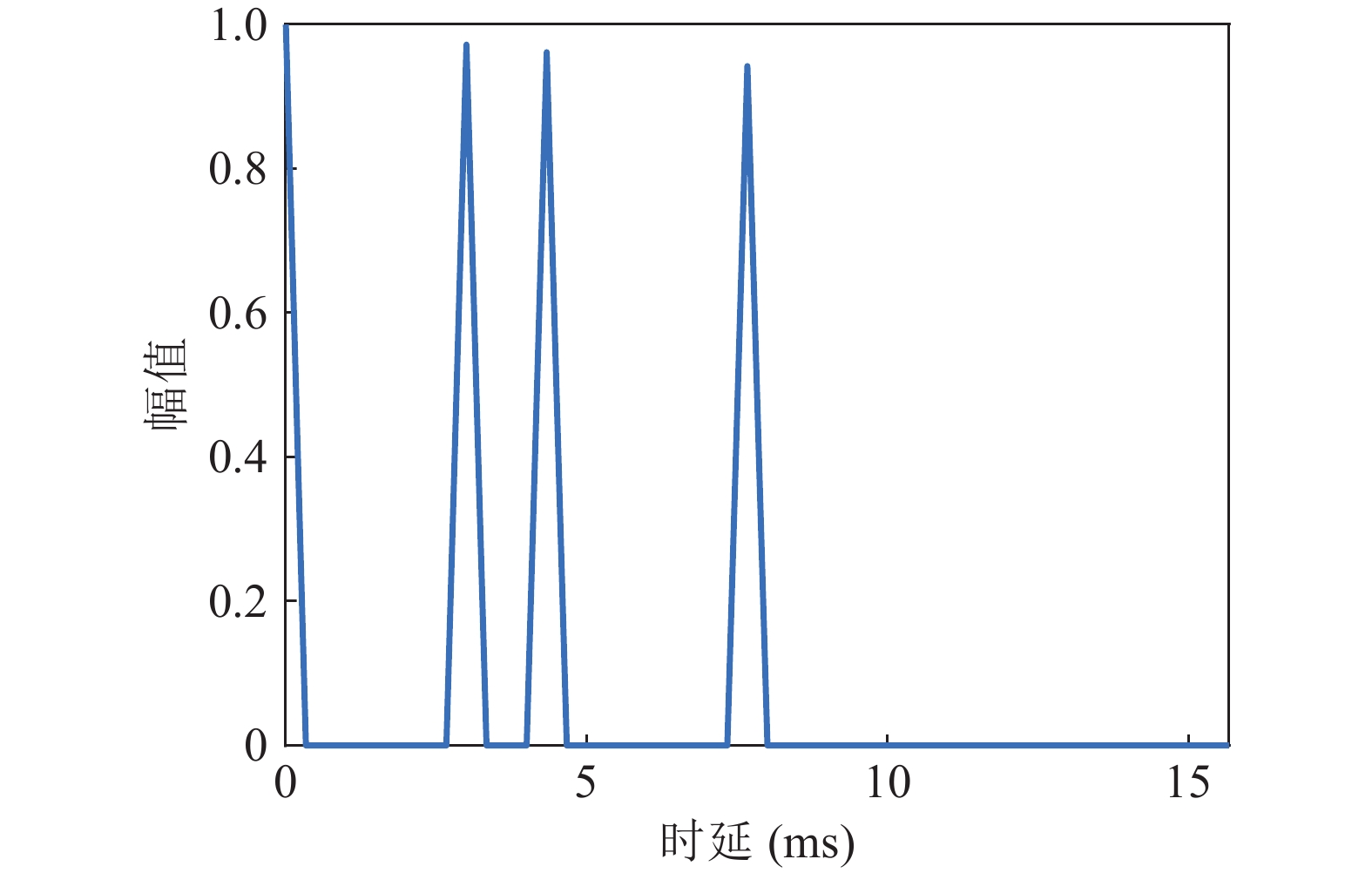
图2为上述四种方法的收敛速度曲线, 其中纵轴代表信道估计结果与图3仿真信道之间的均方误差(MSE), 其中$ {\text{MSE}} = \left( {1/L} \right)\left\| {{\boldsymbol{h}} - {{\boldsymbol{h}}_{\rm real}}} \right\|_2^2 $, $ {{\boldsymbol{h}}_{\rm real}} $表示真实信道向量, $ {\Vert \cdot \Vert }_{2} $表示求向量的2范数。图中结果表明, 几种方法的收敛速度相近, 并且VBI和JVBI的方法能够达到更低的MSE。

仿真时采用Bellhop软件生成信道, 设置参数为水深200 m, 发射换能器和水听器分别布放于水下10 m和15 m, 水平相距2 km。生成的信道冲激响应如图3所示, 四条声线经由不同路径达到接收端, 最大多途时延为7.67 ms。本节采用高斯混合模型作为脉冲噪声仿真模型进行算法验证。定义干噪比(INR)为

式中, $ E(\cdot) $表示能量。假设脉冲干扰在混合噪声中出现的概率为$ p $, 令$ v $表示总噪声, 包括脉冲干扰和背景高斯噪声, 则其概率密度可以表示为

式中, $p$表示脉冲干扰出现的概率, $ \sigma _i^2 $为脉冲干扰的方差, $ \sigma _w^2 $为加性高斯白噪声的方差。

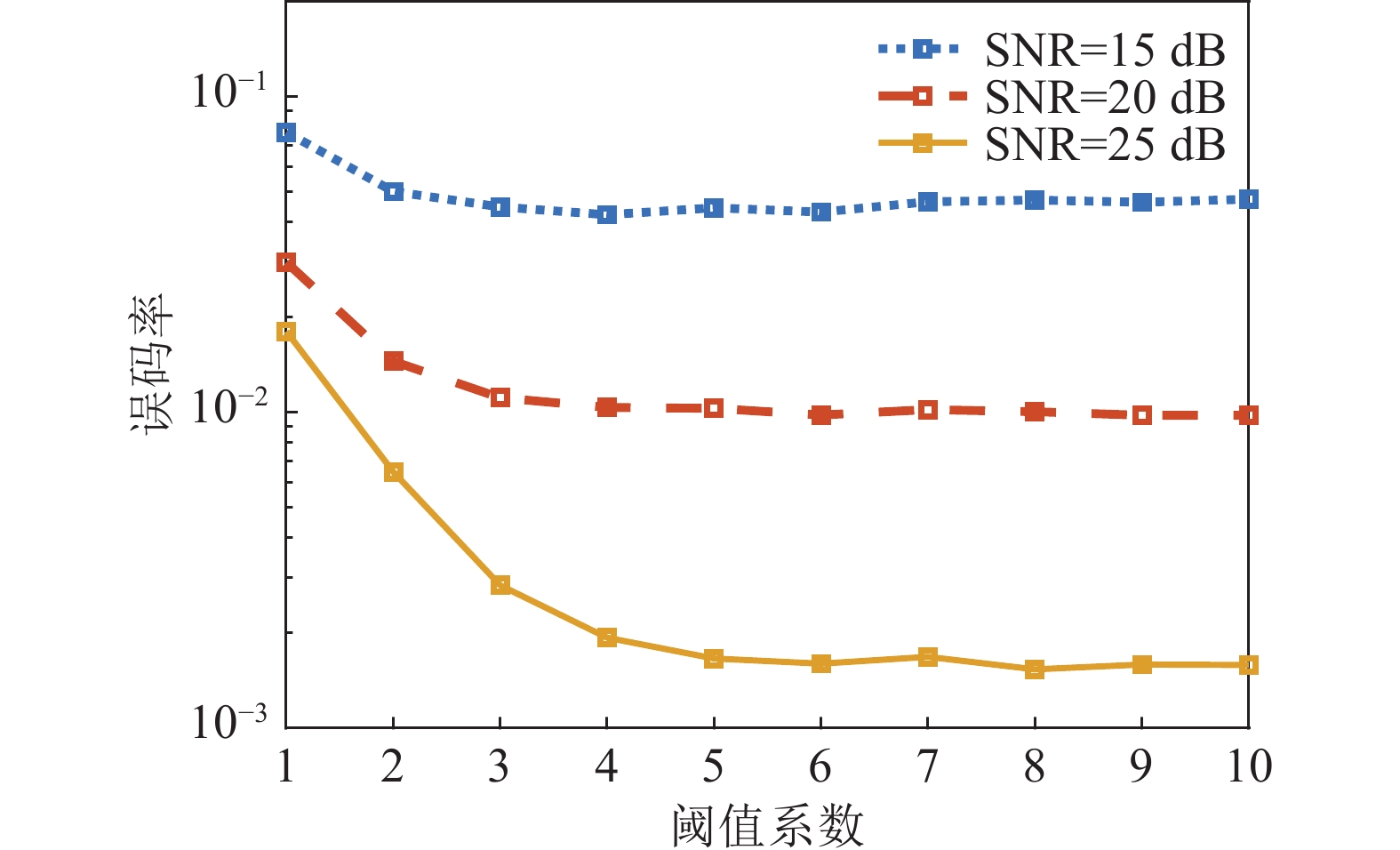
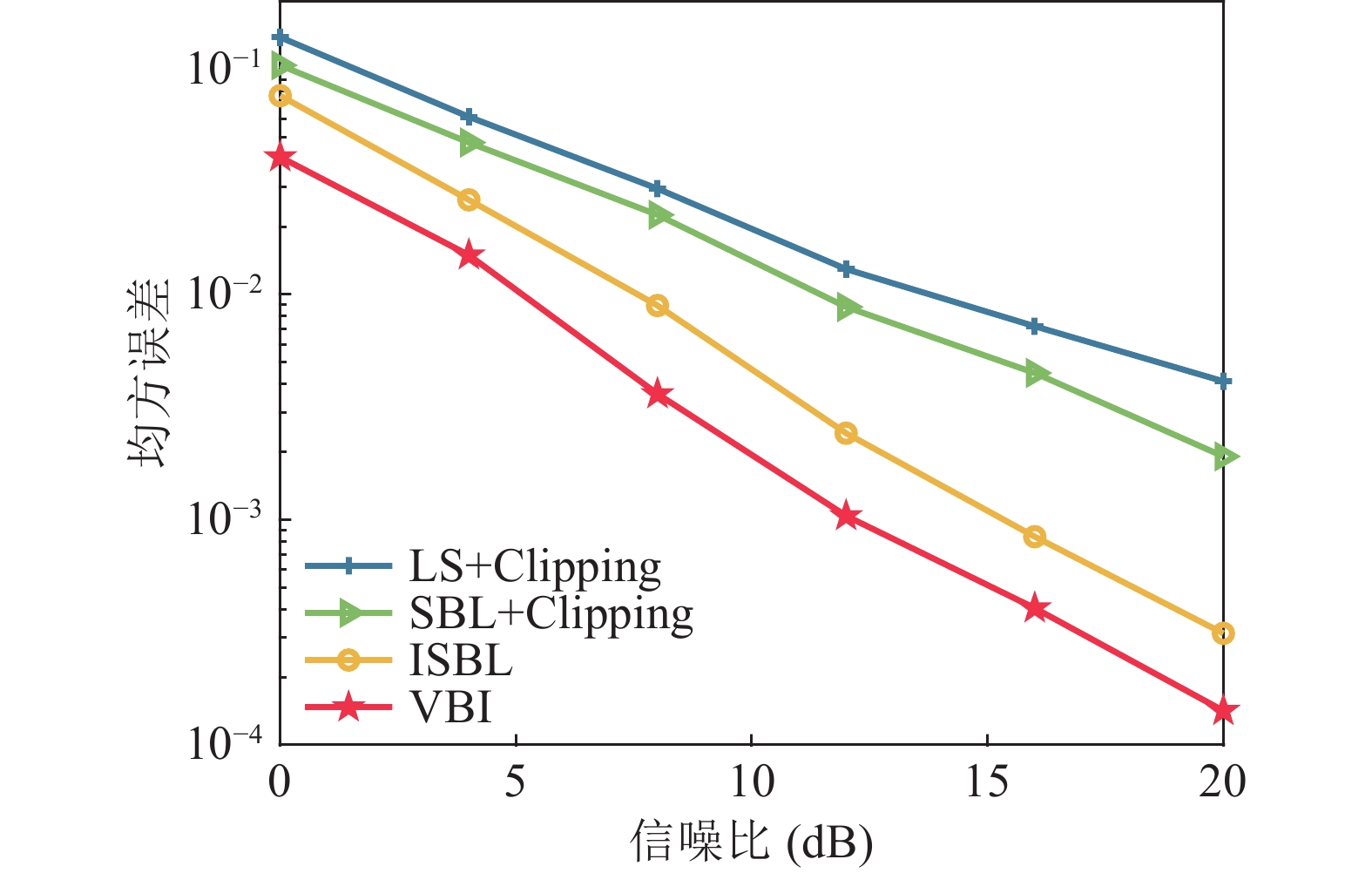
仿真共设置512个子载波, 其中40个导频子载波均匀分布。一个OFDM的符号长度为128 ms, 循环前缀长度为32 ms, 频带为3~7 kHz, 采样频率48 kHz, 调制方式采用BPSK, 采用1/2码率的卷积码进行信道编码。OFDM信号经过水声多途信道后加入$ p = 0.03 $的GMM模拟脉冲噪声。本文脉冲干扰阈值$T$以OFDM符号的平均功率$\overline P$作为基准, 令$T{\text{ = }}\sqrt {\zeta \overline P} $, 其中$\zeta $为阈值系数。图4以经过裁剪预处理后的LS信道估计为例, 给出了信噪比(SNR)固定时叠加GMM脉冲噪声后系统误码率随系数$\zeta $变化情况, 其中INR=20 dB。随着SNR增大, 系统误码率随阈值系数变化的波动范围越大。总体来看, 在${\text{5}} \leqslant \zeta \leqslant {\text{10}}$的情况下, 系统误码率波动较小, 因此本文统一选择脉冲干扰阈值系数$\zeta {\text{ = 5}}$。

图5为不同信道估计算法下随信噪比变化的均方误差曲线, 其中LS+Clipping和SBL+Clipping分别表示经过裁剪预处理的LS和SBL信道估计方法。结果表明, 经过裁剪预处理的LS方法MSE最高, 性能最差。SBL+Clipping方法优于前者, 但相比于ISBL方法仍有差距, 表明信道与脉冲干扰的联合估计方法效果好于简单的裁剪预处理。VBI方法性能最好, 在仿真中, MSE相比ISBL方法进一步提升了约3 dB。

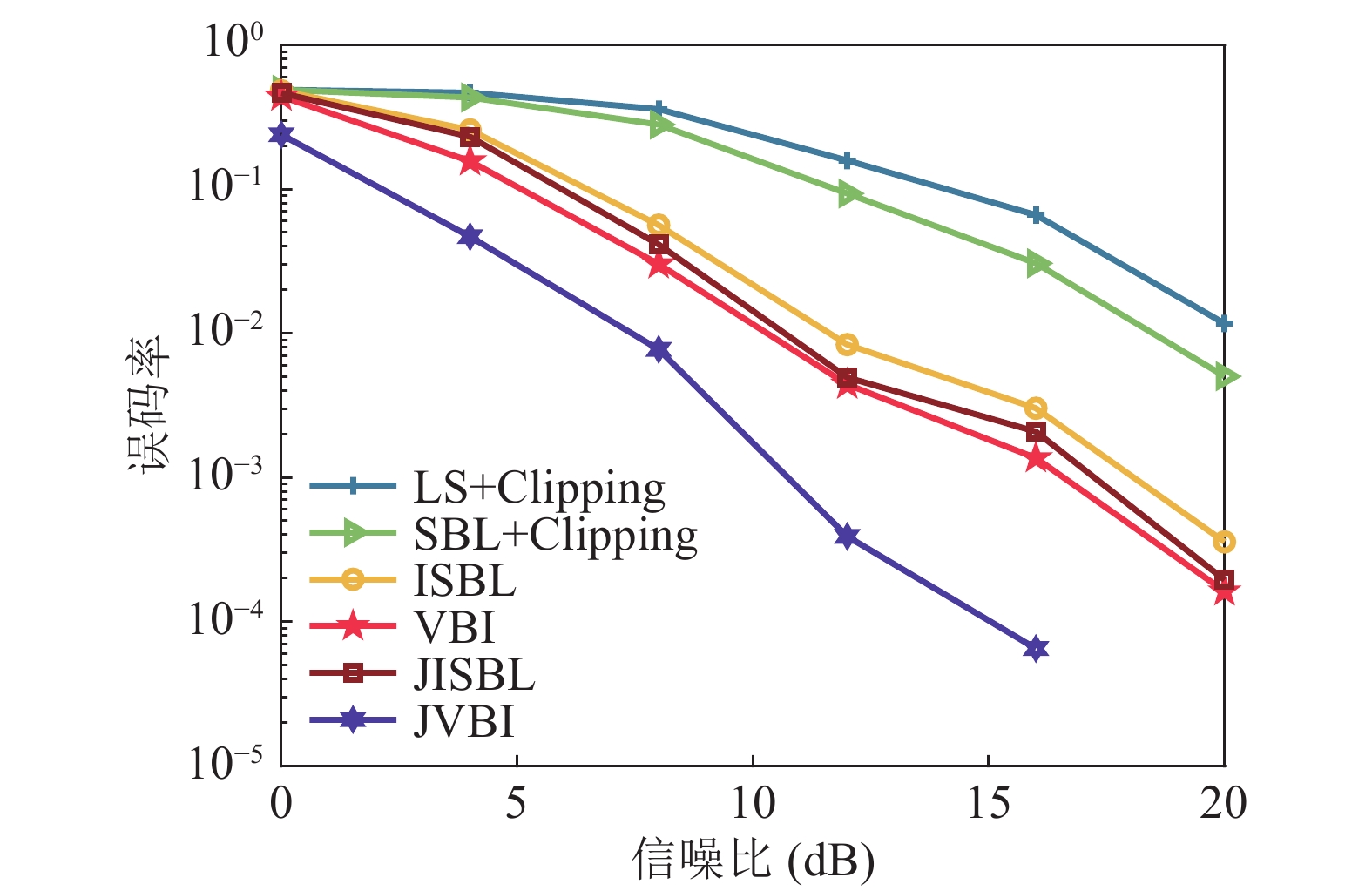
图6进一步展示了不同算法下随信噪比变化的误码率曲线。结果表明, 经过裁剪预处理的LS和SBL方法误码率最高, ISBL和JISBL方法的误码率水平较前两者显著下降。相较之下, 本文所提基于VBI的脉冲干扰抑制方法由于分离估计信道向量和干扰向量, 误码率性能优于ISBL。最后, JVBI方法进一步提升了符号估计精度, 降低了系统误码率。随着SNR增大, JVBI的性能优势也愈发显著。

为进一步验证本文所提方法在实际脉冲干扰环境中的鲁棒性, 本节将利用松花江试验得到的通信数据叠加实际采集到的鼓虾噪声进行验证。2023年2月2日, 在黑龙江省哈尔滨市松花江上进行了单输入多输出(SIMO)水声通信试验。声源处松花江深度6.4 m (包括冰层厚度), 地理位置位于$ {45^ \circ }47'53''{\text{N}} $, $ {\text{12}}{{\text{6}}^ \circ }39'7''{\text{E}} $, 上层冰层厚度0.7 m, 发射换能器深度4 m。接收阵处松花江深度8.4 m (包括冰层厚度), 地理位置为$ {45^ \circ }47'{\text{38''N}} $, $ {\text{12}}{{\text{6}}^ \circ }39'{\text{49''E}} $, 冰层厚度0.7 m, 6阵元的自容式水听器均匀线阵于水深2 m处等间距(相邻阵元间隔1 m)向下布放。收发两端水平距离约800 m。

图7为松花江试验中的OFDM信号帧结构示意图。发射信号共包括512个子载波, 其中406个数据子载波, 74个导频子载波, 其余32个为空子载波。中心频率12 kHz, 带宽4 kHz, 其余参数与仿真一致。试验时一帧信号包括5个OFDM符号, 每个帧首尾均添加10 kHz至14 kHz的双曲调频(Hyperbolic Frequency Modulation, HFM)信号, 作为同步信号和多普勒估计信号, HFM的持续时间为500 ms, 与OFDM块之间的零保护间隔是200 ms。试验中, 接收的OFDM信号首先基于帧前后的HFM信号进行了块多普勒补偿^[26-27], 之后采用了本文涉及的几种算法处理信号。

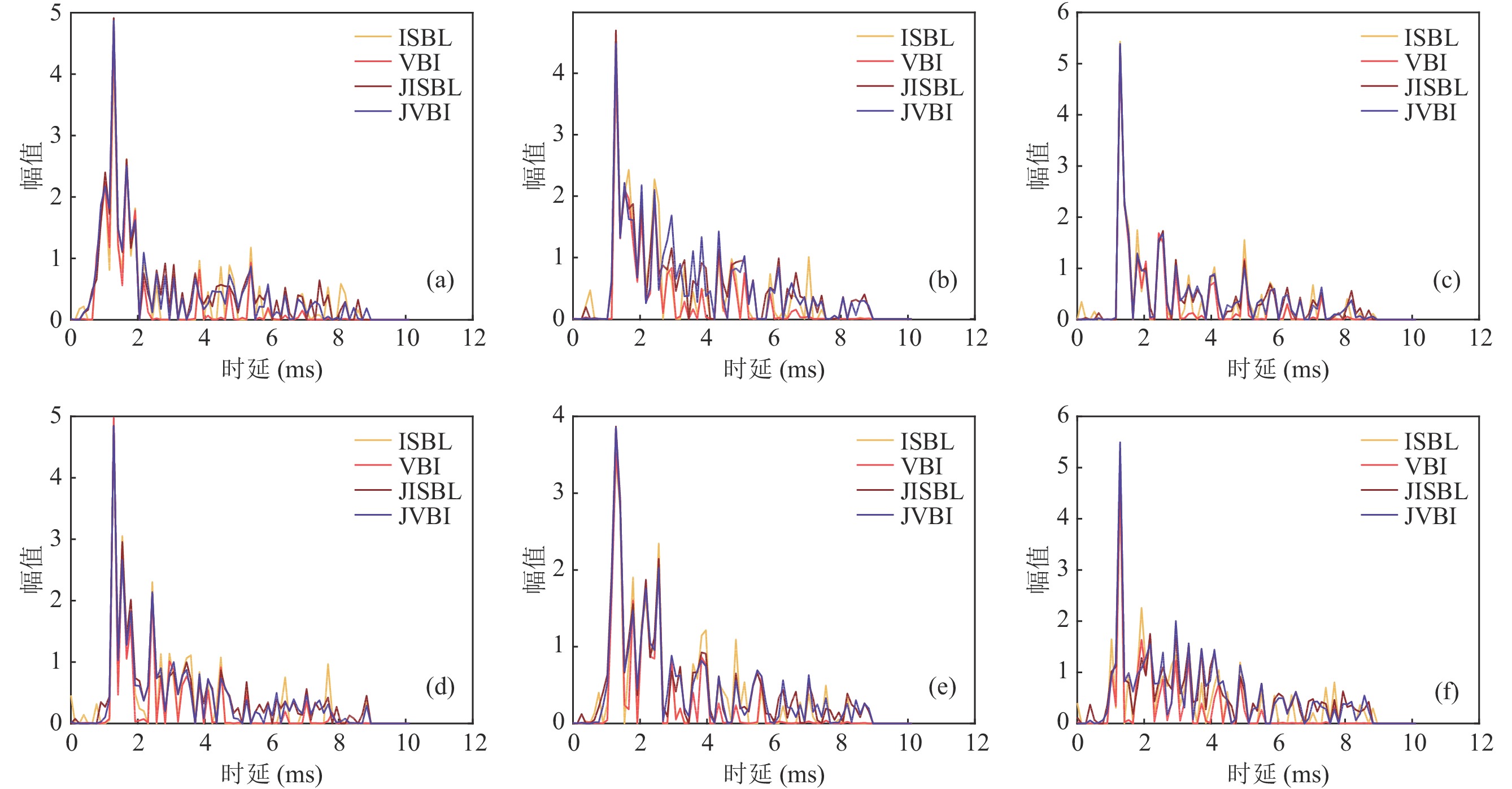
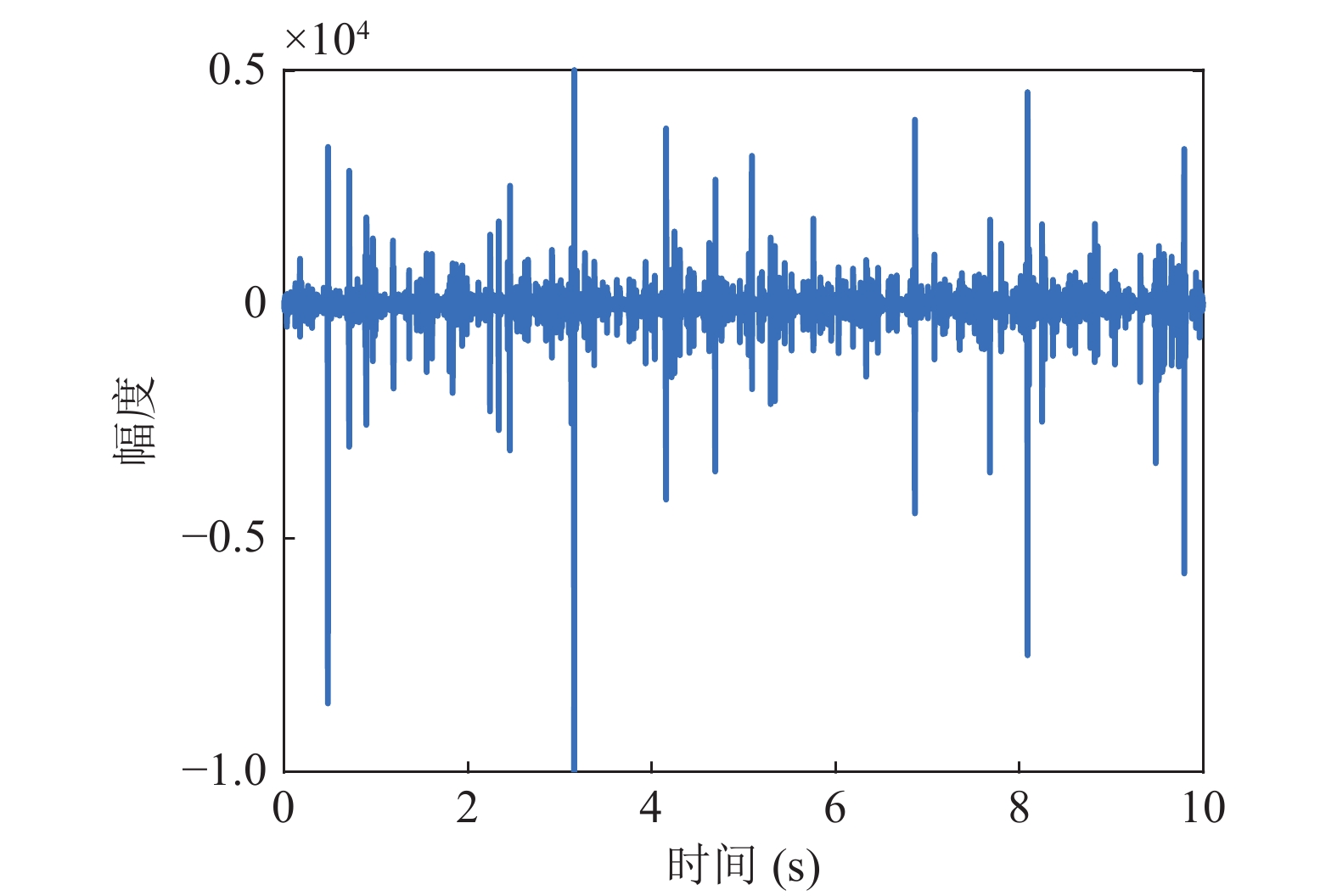
图8为接收一帧信号的时频图, 试验共接收到150帧信号。图9为松花江不同水听器处的信道估计结果, 结果表明试验水域多途结构较为复杂, 不同方法估计得到的信道冲激响应在整体结构上类似, 但仍存在一定的差异。图10为新加坡附近海域采集到的鼓虾噪声, 可以看出其中存在诸多强干扰。由于无法分离该鼓虾噪声中的背景高斯白噪声和强脉冲干扰, 因此将其分别以不同的信干噪比(SINR)叠加在实际数据中, 以验证本文所提方法性能。

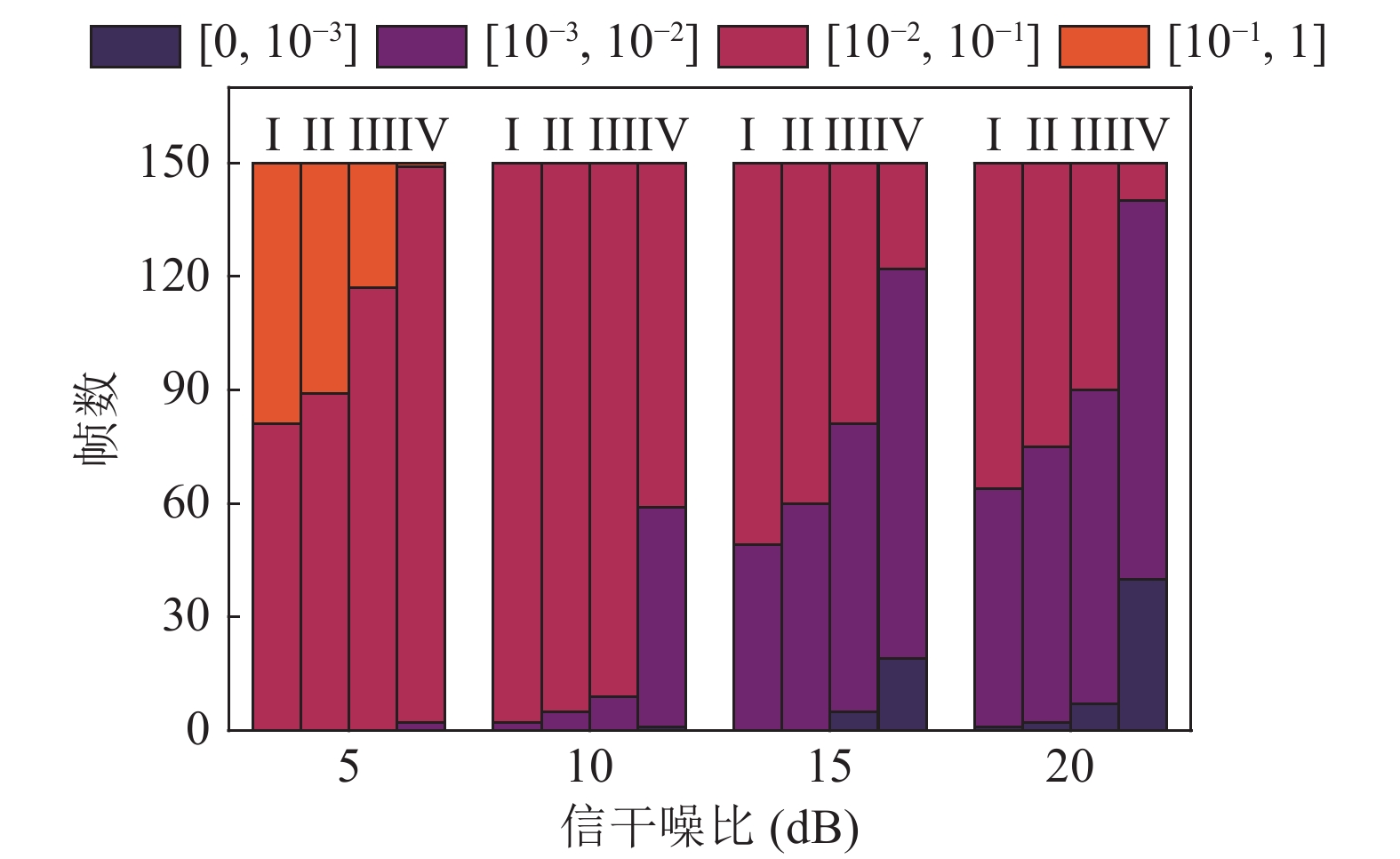
接收数据包的误码率统计情况如图11所示, 本次试验仅对比ISBL、JISBL、VBI和JVBI四种干扰抑制方法。图中I、II、III、IV分别代表ISBL、JISBL、VBI、JVBI, 不同颜色的柱状图表示维特比解码后的误码率所处误码区间不同([0,10⁻³], [10⁻³,10⁻²], [10⁻²,10⁻¹], [10⁻¹,1]), 纵轴表明解码后的不同误码区间所占据的帧数。可以看出, 在该半仿真试验中, 随着SINR增加, 各方法解码后系统的误码率均呈现下降趋势, 且JISBL相比ISBL、JVBI相比VBI的性能增益均逐渐加大。四种方法表现出的性能排序依次为JVBI>VBI>JISBL>ISBL, 说明所提基于VBI的两种干扰抑制方法相比两种ISBL方法表现出更好的鲁棒性。

针对脉冲干扰环境中水声OFDM性能下降的问题, 本文提出了基于VBI的信道估计和符号联合估计方法。基于VBI中的平均场理论, 分离了干扰向量和信道向量, 利用简单的分布拟合待求的后验概率分布, 迭代更新各分布直至收敛, 得到信道向量的最优估计, 重构接收信号后利用阈值判决分离脉冲干扰, 有效抑制了脉冲干扰对于接收信号影响, 克服了SBL方法中联合向量带来的性能损失, 降低了计算复杂度, 提高了脉冲干扰下水声OFDM性能。在此基础上, 利用全部子载波上的符号信息, 将基于导频的VBI方法均衡得到的符号作为初值输入VBI框架迭代求解, 进一步提升了符号估计精度。仿真及试验结果表明, 本文所提方法在脉冲干扰环境下具有良好的鲁棒性。

根据式(11) 和式(12) , 可分别更新$ q\left( \varepsilon \right) $, $ q\left( {\boldsymbol{h}} \right) $, $ q\left( {{{\boldsymbol{i}}_p}} \right) $, $ q\left( {\boldsymbol{\lambda }} \right) $:

(1)更新$ q\left( \varepsilon \right) $

式中, $ \Vert\cdot \Vert $表示向量的模。令$ {{\boldsymbol{\mu }}_{\boldsymbol{h}}} = {\left\langle {\boldsymbol{h}} \right\rangle _{q\left( {\boldsymbol{h}} \right)}} $, $ {{\boldsymbol{\mu }}_{\boldsymbol{i}}} = {\left\langle {{{\boldsymbol{i}}_p}} \right\rangle _{q\left( {{{\boldsymbol{i}}_p}} \right)}} $, $ {{\boldsymbol{\varSigma }}_{\boldsymbol{h}}} = {\left\langle {{{\left\| {{\boldsymbol{h}} - {{\boldsymbol{\mu }}_{\boldsymbol{h}}}} \right\|}^2}} \right\rangle _{q\left( {\boldsymbol{h}} \right)}} $, $ {{\boldsymbol{\varSigma }}_{\boldsymbol{i}}} = {\left\langle {{{\left\| {{{\boldsymbol{i}}_p} - {{\boldsymbol{\mu }}_{\boldsymbol{i}}}} \right\|}^2}} \right\rangle _{q\left( {{{\boldsymbol{i}}_p}} \right)}} $, 有

令$\rho = \dfrac{1}{2}{\left\| {{{\boldsymbol{Y}}_p} - {{\boldsymbol{M}}_p}{{\boldsymbol{\mu}} _{\boldsymbol{h}}} - {{\boldsymbol{F}}_p}{{\boldsymbol{\mu}} _{\boldsymbol{i}}}} \right\|^2} + \dfrac{1}{2}{\rm tr}\left( {{{\boldsymbol{M}}_p}{{\boldsymbol{\varSigma}} _{\boldsymbol{h}}}{\boldsymbol{M}}_p^{\text{H}} + {{\boldsymbol{F}}_p}{{\boldsymbol{\varSigma }}_{\boldsymbol{i}}}{\boldsymbol{F}}_p^{\text{H}}} \right) + d$, 则式(A1) 可写为

式(A3) 两边同取${\text{e}}$指数并忽略常数项, 可得

因此$\varepsilon $的期望可表示为

(2)更新$q\left( {\boldsymbol{h}} \right)$

式(A6) 两边同取${\text{e}}$指数, 得

式中, 信道${\boldsymbol{h}}$的期望和协方差分别为

(3)更新$q\left( {{{\boldsymbol{i}}_p}} \right)$

式(A9) 两边同取${\text{e}}$指数, 得

式中, 脉冲干扰${{\boldsymbol{i}}_p}$的期望和协方差分别为

(4)更新$ q\left( {\boldsymbol{\lambda }} \right) $

$ {\boldsymbol{\lambda }} $包括$ {{\boldsymbol{\lambda }}_{1:L}} $和$ {{\boldsymbol{\lambda }}_{L + 1:L + {N_p}}} $两部分, 在此分别进行更新。

式(A12) 两边同求${\text{e}}$指数, 得

且

同理

式(A15) 两边同求${\text{e}}$指数, 得

且

至此, $ q\left( \varepsilon \right) $, $ q\left( {\boldsymbol{h}} \right) $, $ q\left( {{{\boldsymbol{i}}_p}} \right) $和$ q\left( {\boldsymbol{\lambda }} \right) $的更新公式全部推导完毕。