-
随着海洋资源开发和海洋探测技术的发展, 高速水下信息传输的需求日益提升。然而, 由于水声信道具有较强多径、较长时延的特点, 引起较大的符号间干扰, 导致严重的频率选择性衰落, 降低了水下信息传输的可靠性[1-3]。单载波时域均衡技术因为具有高速信息传输速率和良好的符号间干扰抑制能力被广泛应用于高速水声通信系统中[4-5]。Turbo判决反馈均衡算法通过迭代译码器和均衡器之间的软信息, 可进一步降低单载波时域均衡水声通信系统的误码率, 实现稳定可靠的高速水下信息传输[6-9]。
Turbo判决反馈均衡可以分为基于信道估计Turbo判决反馈均衡和直接自适应Turbo判决反馈均衡[10-13]。虽然基于信道估计Turbo判决反馈均衡可以依据最小均方误差(MMSE)准则, 通过估计信道冲激响应获得最优均衡器系数, 但是由于存在大量矩阵求逆计算, 使得计算复杂度大大增加[14]。此外, 当信噪比较低时, 信道估计精度降低进而影响最优均衡器系数, 使得均衡性能变差。而直接自适应Turbo判决反馈均衡则基于维纳滤波原则, 自适应更新均衡器系数, 通过多次迭代获得最优均衡器系数, 具有较低的计算复杂度。因此, 直接自适应Turbo判决反馈均衡器具有收敛速度慢的特点。为此, 文献[15]通过采用双层迭代结构(即内层迭代基于软判决的均衡器参数和接收滤波信号, 外层迭代均衡器和解码器之间的外部对数似然比), 提高收敛速度。文献[16]采用分数间隔迭代软均衡器, 通过内部软判决器、内部软均衡器、用于抑制突发噪声的去噪器和MMSE估计器迭代交互符号外部信息, 获得自迭代增益, 加快收敛速度。此外, 常规的判决反馈均衡器存在误差传递现象, 通过时间反转处理, 将正向均衡器和反向均衡器加以融合, 采用双向均衡结构抑制误差传递, 获得更好的均衡性能[17-18]。但是, 上述Turbo判决反馈均衡器均没有利用水声信道的稀疏特性, 系统计算复杂度高, 且均衡性能有待进一步提高。
针对这一问题, 利用水声信道稀疏特性的自适应均衡算法得到了学者的广泛关注[19-22]。文献[19]通过在迭代最小二乘(RLS)自适应均衡算法的代价函数中引入
$ {l_0} $ 和$ {l_1} $ 范数, 提高自适应均衡算法在常规稀疏信道条件下的收敛速度, 降低最小均方误差。文献[20]通过在RLS自适应均衡算法中引入$ {l}_{1, 0} $ 和$ {l}_{2, 0} $ 范数, 提高自适应均衡算法在簇稀疏条件下的均衡性能。文献[21]提出了一种稀疏性已知条件下的正则化子带稀疏自适应均衡算法, 通过分别调整自适应均衡算法的步长和权重因子, 使系统具有更快的收敛速度和更低的均方误差(MSE)。文献[22]提出了一种联合参数优化的稀疏自适应RLS算法(JO-S-RRLS), 通过联合优化遗忘因子和代价函数, 使RLS自适应算法在稀疏信道条件下具有更低的均方误差和更好的跟踪性能。通过利用水声信道稀疏特性, 进一步降低均方误差, 从而提升双向Turbo判决反馈中前馈滤波器和反馈滤波器的均衡性能。但是, 上述自适应均衡算法没有应用于双向Turbo自适应判决反馈均衡器中, 降低了均衡器的均衡性能。针对以上问题, 本文提出了一种参数自适应调整稀疏迭代最小二乘(Parameter-Adaptive Adjustment Sparse Recursive Least-Square, PAA-S-RLS)自适应算法的双向Turbo均衡器。首先, 通过联合优化遗忘因子和稀疏约束参数更新迭代系数, 提高RLS自适应算法在稀疏水声信道中的均衡性能, 为双向Turbo自适应均衡器提供更好的前馈和反馈滤波性能。此外, 将参数自适应调整稀疏自适应RLS算法应用于双向Turbo自适应判决反馈均衡器中, 改善单一方向Turbo自适应判决反馈均衡器误差传递的问题, 提高了在稀疏水声信道条件下的均衡性能。仿真和海试结果表明在稀疏水声信道中, 参数自适应调整稀疏自适应RLS算法的双向Turbo均衡器可以获得更低的误码率。
-
由于水声信道具有严重的符号间干扰, 常通过自适应均衡器来抑制, 与传统的基于线性均衡器相比, 在忽略误差的前提下判决反馈均衡器性能由于引入反馈结构, 其性能远优于线性均衡器。
然而, 在判决反馈均衡器中, 如果判决器产生错误判决, 则会导致误差传递现象, 降低均衡器的均衡性能。因此, 通过采用双向判决反馈均衡器的结构改善误差传递问题。该种结构均衡器采用一个正向判决反馈均衡器和一个时间反转判决反馈均衡器, 反向均衡器的输出结果通过时间反转, 再通过合并器将正向和反向均衡器输出的判决信息加以合并。在双向判决反馈均衡器中, 由于处理过程中产生的突发性错误是在相反的方向上, 具有较低的相关性, 即在同一位置处两个均衡方向同时产生错误的概率很低, 因此, 采用双向判决反馈均衡器结构, 可以降低均衡器错误传播的概率, 提高判决反馈均衡器的均衡性能。
-
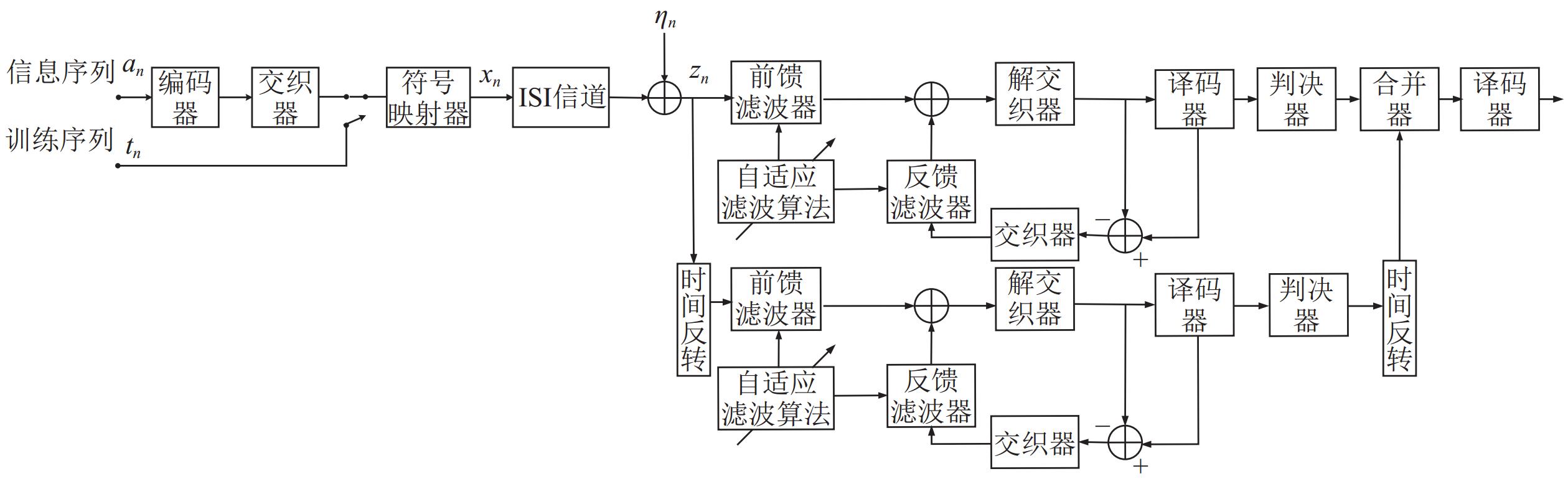
为进一步提高双向判决反馈均衡器的性能, 将均衡器和译码器联合起来, 采用双向判决反馈Turbo均衡算法, 典型的双向判决反馈Turbo水声通信系统模型如图1所示。在双向判决反馈均衡器的基础上, 双向判决反馈Turbo均衡器首先将估计出的发送符号映射成软信息, 输入到软入软出译码器之中; 然后, 将译码器输出的软信息反馈给均衡器, 这样就形成了一种软入软出的迭代接收机结构, 通过不断地迭代软信息有效地提高双向判决反馈均衡器的均衡性能。双向判决反馈Turbo均衡器由一个正向Turbo判决反馈均衡器和一个时间反转的Turbo判决反馈均衡器构成。双向判决反馈Turbo均衡器不但可以减少误差传递, 还可以通过联合均衡器和译码器, 提高均衡器抑制符号干扰的能力。再通过加权因子合并正向和反向均衡器输出软信息, 可以依据均方误差最小化原则, 选择正向和反向Turbo均衡器在合并中比重均为1/2, 获得最佳的输出结果[23]。在双向判决反馈Turbo均衡器中, 正向和反向Turbo判决反馈均衡器结构相同, 但反向Turbo均衡结构中增加时间反转处理。此外, 虽然双向判决反馈Turbo均衡器在帧结构中增加了反方向训练序列部分, 但是由于正向判决反馈Turbo均衡器和反向判决反馈Turbo均衡器是并行进行的, 并不影响用户速率。
-
双向判决反馈Turbo均衡结构中的自适应均衡的算法部分, 通常采用LMS和RLS自适应均衡算法, 相比于LMS算法, RLS算法具有更快的收敛速度, 可应用于本文采用的双向判决反馈Turbo均衡器中。传统的RLS算法没有考虑水声信道稀疏特性, 普遍存在收敛慢的问题, 通过将
$ {l_0} $ 范数项、$ {l_1} $ 范数项和$ {l}_{1, 0} $ 范数项、$ {l_{2,0}} $ 范数项引入算法的迭代更新表达式中, 将抽头更新值更快地向零点方向吸引, 加快算法对稀疏约束项的收敛性[24-25]。本文在文献[17-18]的基础上, 对自适应均衡算法加以改进, 通过利用水声信道的稀疏性, 在代价函数中引入稀疏约束, 不仅可以使RLS自适应均衡算法更快地收敛到更低的均方误差, 还可以在不进行信道估计、不了解信道稀疏结构的条件下, 通过联合参数优化思想, 自适应调整罚函数中稀疏约束的权重系数, 匹配常规稀疏(或簇稀疏)水声信道结构, 改善自适应RLS均衡算法在稀疏水声信道结构未知条件下均衡算法的性能。假设均衡器的输入为
$ {{\boldsymbol{x}}_n} = {\left[ {{x_n},{x_{n - 1}}, \cdots ,{x_{n - L + 1}}} \right]^{\text{T}}} $ , 其中$ L $ 是滤波器长度, 滤波输出信号为$ {y_n} $ , 均衡器期望输出信号$ {d_n} $ 。则根据横向滤波器的结构可知$ {y_n} = \sum\nolimits_{i = 0}^{L - 1} {{w_{i,n}}{x_{n - i}}} $ , 其中$ {w_{i,n}} $ 是RLS自适应均衡器系数。先验误差$ {e_n} $ 可以表示为$ {e_n} = {d_n} - {y_n} $ 。不同于文献[22], 本文算法可以在未知信道稀疏结构的条件下, 通过自适应调整常规稀疏和簇稀疏特性所占比重大小的权重因子$ {\alpha _n} \geqslant 0 $ ,$ {\beta _n} \geqslant 0 $ 计算均衡器系数。此外, 相比于文献[22], 本文算法增加了代价函数中表征簇稀疏信道特性的约束项$ g({{\boldsymbol{w}}_n}) $ , 即根据最小二乘法, 代价函数可表示为其中,
$ {\varepsilon }_{n}=\Vert {{\boldsymbol{y}}}_{n}-{{\boldsymbol{w}}}_{n}^{\text{T}}{{\boldsymbol{x}}}_{n}{\Vert }_{2}^{2}=\Vert {({{\boldsymbol{h}}}_{n}-{{\boldsymbol{w}}}_{n})}^{\text{T}}{{\boldsymbol{x}}}_{n}{\Vert }_{2}^{2} $ ;$ f({{\boldsymbol{w}}_n}) $ 为表征信道常规稀疏特性的凸函数, 即$ f({{\boldsymbol{w}}}_{n})=\Vert {{\boldsymbol{w}}}_{n}{\Vert }_{1} $ , 或$ f({{\boldsymbol{w}}}_{n})=\Vert {{\boldsymbol{w}}}_{n}{\Vert }_{0} $ ;$ g({{\boldsymbol{w}}_n}) $ 为表征信道簇稀疏特性的凸函数, 即$ g({{\boldsymbol{w}}}_{n})=\Vert {{\boldsymbol{w}}}_{n}{\Vert }_{2,0} $ , 或$ g({{\boldsymbol{w}}}_{n})=\Vert {{\boldsymbol{w}}}_{n}{\Vert }_{1,0} $ 。则有令
$ \partial {J_n}/\partial {{\boldsymbol{w}}_n} = {\boldsymbol{0}} $ , 则有其中,
$ {{\boldsymbol{\varPhi }}_n} = \lambda {{\boldsymbol{\varPhi }}_{n - 1}} + {{\boldsymbol{x}}_n}{\boldsymbol{x}}_n^{\rm T} $ ,$ {{\boldsymbol{r}}_n} = \lambda {{\boldsymbol{r}}_{n - 1}} + {y_n}{{\boldsymbol{x}}_n} $ ,$ \lambda $ 为遗忘因子。令
则有
再令
$ {\boldsymbol{P}}_n^{ - 1} = {{\boldsymbol{\varPhi }}_n} $ , 根据矩阵求逆定理, 可知其中
为增益向量。由于
$ {{\boldsymbol{\widehat w}}_n} = {{\boldsymbol{P}}_n}{{\boldsymbol{\theta }}_n} $ , 则有令
$ {{\boldsymbol{\widehat \varepsilon }}_n} = {{\boldsymbol{\widehat w}}_n} - {{\boldsymbol{w}}_n} $ ,$ {{\boldsymbol{\widetilde \varepsilon }}_n} = {{\boldsymbol{\widetilde w}}_n} - {{\boldsymbol{w}}_n} $ , 其中,$ {{\boldsymbol{\widetilde w}}_n} $ 为在无稀疏约束下RLS算法均衡器系数。由于在实际水声信道中,$ {{\boldsymbol{w}}_n} $ 未知, 可通过一阶近似来获得$ {\alpha _n} $ ,$ {\beta _n} $ 。并假设$ {\alpha _n} $ ,$ {\beta _n} $ ,$ {{\boldsymbol{P}}_n}\partial f({{\boldsymbol{\widehat w}}_n})/\partial {{\boldsymbol{\widehat w}}_n} $ ,$ {{\boldsymbol{P}}_n}\partial g({{\boldsymbol{\widehat w}}_n})/\partial {{\boldsymbol{\widehat w}}_n} $ ,$ {\text{tr}}\left( {{{\boldsymbol{P}}_n}} \right)/N $ ,$ f({{\boldsymbol{w}}_n}) $ ,$ g({{\boldsymbol{w}}_n}) $ 具有时不变性或者缓慢时变, 则有在稀疏自适应RLS均衡器中, 根据先验误差
$ {\xi _n} = {y_n} - {\boldsymbol{\widehat w}}_{n - 1}^{\rm T}{{\boldsymbol{x}}_n} $ 和后验误差$ {e_n} = {y_n} - {\boldsymbol{\widehat w}}_n^{\rm T}{{\boldsymbol{x}}_n} $ , 有$ {e_n} = {\xi _n}(1 - {\boldsymbol{x}}_n^{\rm T}{{\boldsymbol{k}}_n}) $ 。令$ {\rm E}\{ e_n^2\} = \sigma _{{e_n}}^2 $ , 并且令$ {\rm E}\{ v_n^2\} = \sigma _{{v_n}}^2 $ 为系统的噪声方差, 则有假设输入信号和误差信号是相互独立的, 则有
其中, 令
$ {q_n} = {\boldsymbol{x}}_n^{\rm T}{{\boldsymbol{P}}_{n - 1}}{{\boldsymbol{x}}_n} $ ,$ {\rm E} \{ q_n^2\} = {\sigma _{{q_n}}} $ 。再假设输入信号与先验误差信号也是不相关的, 并且$ \lambda $ 是具有一定的时变性, 则估计的能量可更新为[22]其中,
$ {\alpha _0} $ ,$ \alpha = 1 - 1/\left( {{K_a}N} \right) $ ,$ \beta = 1 - 1/\left( {{K_b}N} \right) $ 是权重因子,$ {K_a} \geqslant 2,{K_b} > {K_a} $ 。有其中,
$ \tau > 0 $ ,$ {\lambda _{{\text{max}}}} $ 为变遗忘因子的最大值。通过联合遗忘因子和稀疏约束系数, 优化稀疏RLS自适应均衡算法。算法流程框图如表1所示。 -
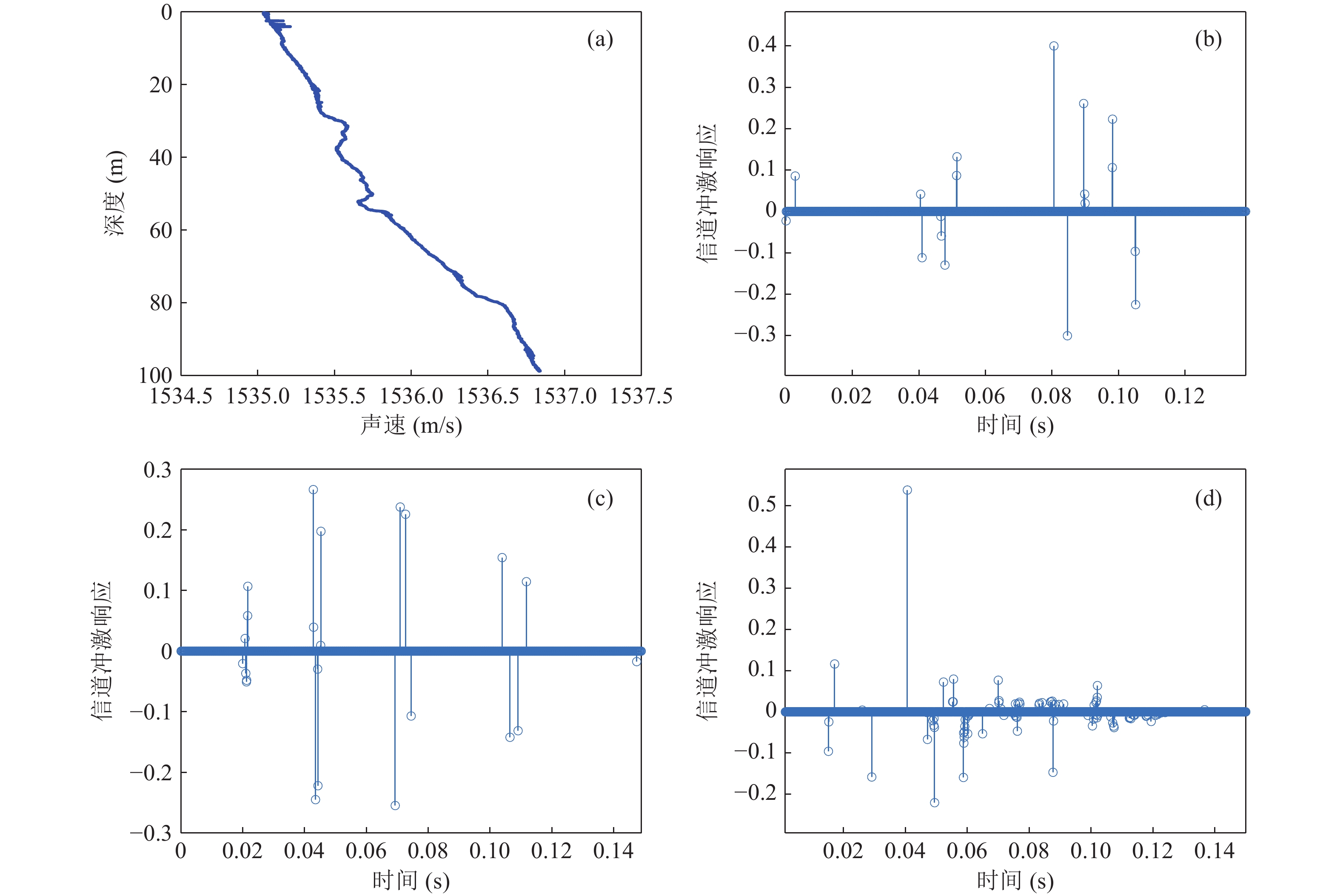
为验证算法性能, 基于2015年11月南海试验声速剖面, 通过Bellhop仿真信道冲激响应。设定发射声源深度40 m, 接收基元深度分别为40 m, 60 m, 80 m, 收发间距离为30 km, 海底声速1500 m/s, 底质密度1.8 g/cm3, 底吸收系数0.8
$ {\text{dB}}/\lambda $ 。图2为南海试验声速剖面以及接收基元深度分别为40 m, 60 m, 80 m时的信道冲击响应。由图2(b)(c)可知, 信道多途扩展约为100 ms, 由于接收深度不同, 信道的稀疏结构不同, 图2(b)是一种常规稀疏信道结构, 图2(c)是一种簇稀疏信道结构。图2(d)是一种常规稀疏和簇稀疏组成的混合稀疏信道结构, 0.04 s前属于稀疏信道结构, 0.04 s后属于簇稀疏信道结构。
仿真系统参数如表2所示, 采用8PSK调试方式, 发送符号率为250 sym/s, 信息序列为2319 比特, 前向和反向训练序列长度均为500 sym, 编码方式为码率为1/2的卷积码编码, 采用随机交织器。信号帧结构如图3所示。
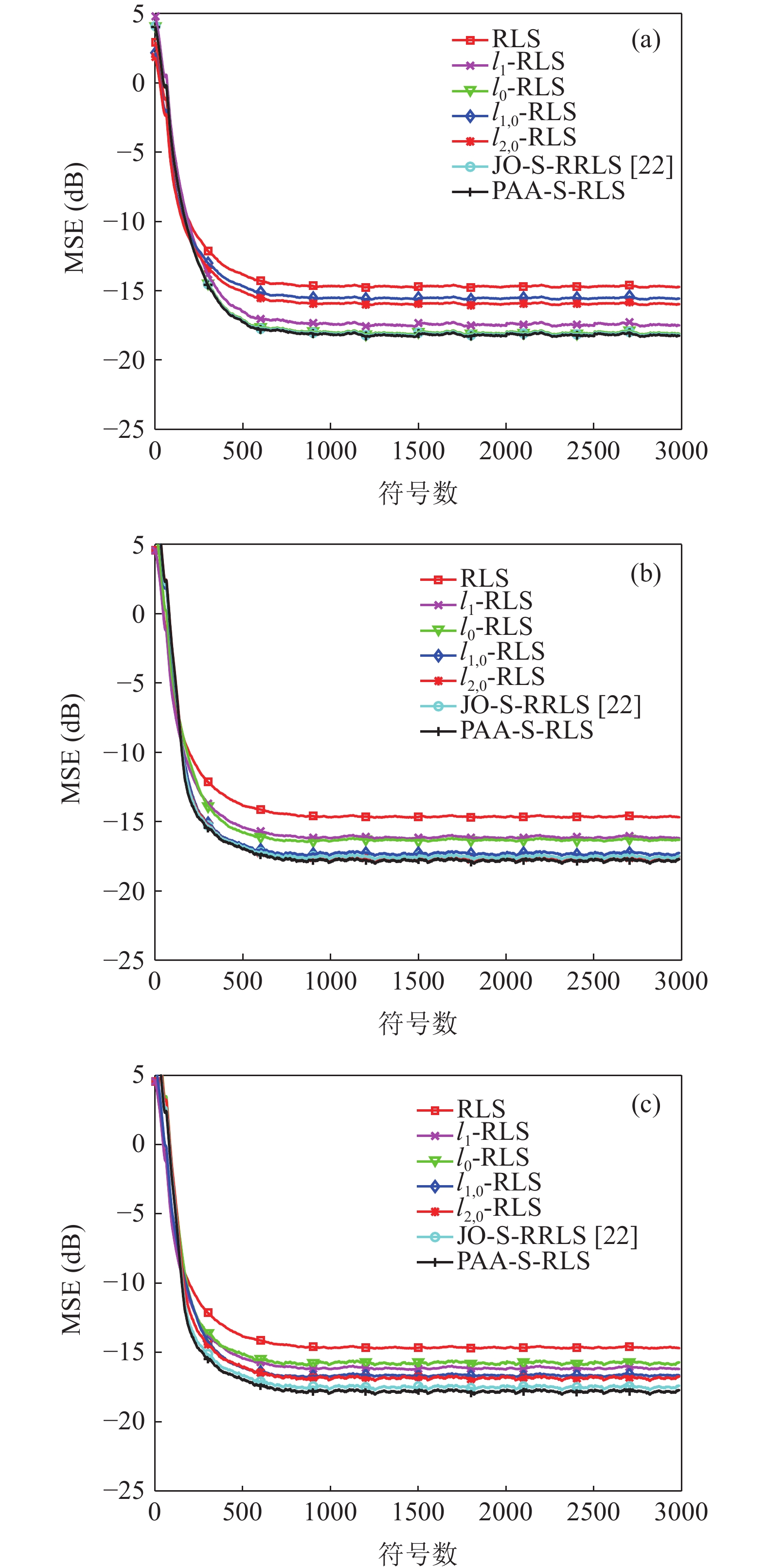
图4为在表2参数设置条件下, 不同自适应均衡RLS算法(常规RLS算法,
$ {l_0} $ -RLS[19],$ {l_1} $ -RLS[19],$ {l}_{1, 0} $ -RLS[20],$ {l}_{2, 0} $ -RLS[20], JO-S-RRLS[22])与PAA-S-RLS算法, 在信道冲击响应分别为图2(b)(c)(d),$ {\gamma _n} $ ,$ {\alpha _n} $ ,$ {\beta _n} $ 的初始值为0, 信噪比为15 dB条件下的均方误差仿真结果。在常规稀疏条件下(图2(b)), PAA-S-RLS算法略优于常规系数类RLS算法和JO-S-RRLS算法, 比簇稀疏类RLS算法均方误差低2 dB左右。在簇稀疏条件下(图2(c)), PAA-S-RLS算法略优于簇稀疏类RLS算法, 比常规稀疏类RLS算法均方误差低1.5 dB左右, 比JO-S-RRLS算法低0.5 dB左右。在混合稀疏信道条件下(图2(d)), PAA-S-RLS算法比常规稀疏类RLS算法均方误差低2 dB左右, 比簇稀疏类RLS算算法均方误差低1 dB左右, 比JO-S-RRLS算法低0.5 dB左右。这是由于PAA-S-RLS可以自适应调节优化参数, 使滤波器均衡系数更快迭代更新到与信道稀疏结构相匹配的数值, 可以在信道结构未知的实际信道中获得更好的均衡性能。图5为不同自适应均衡RLS算法(常规RLS算法,
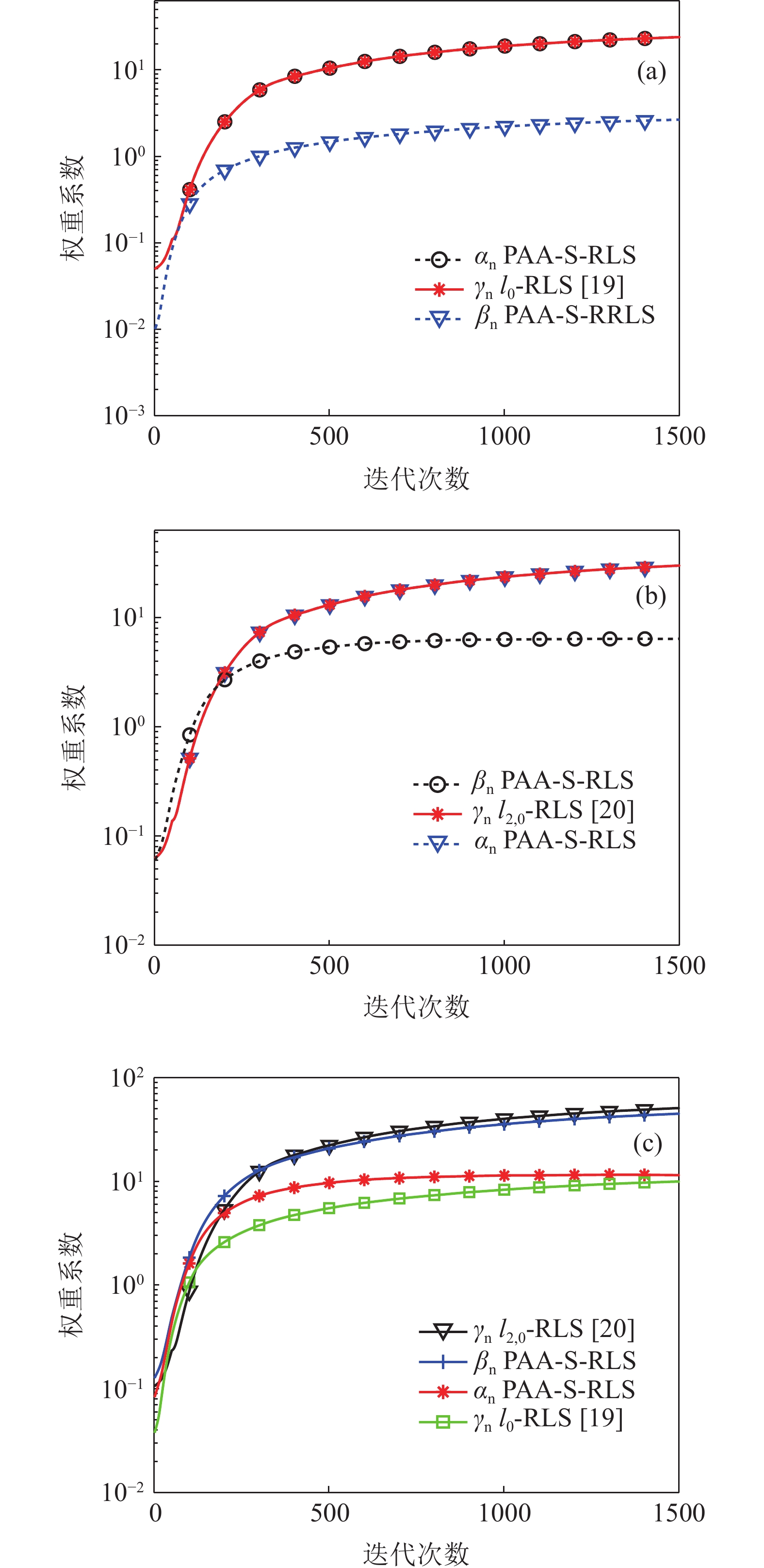
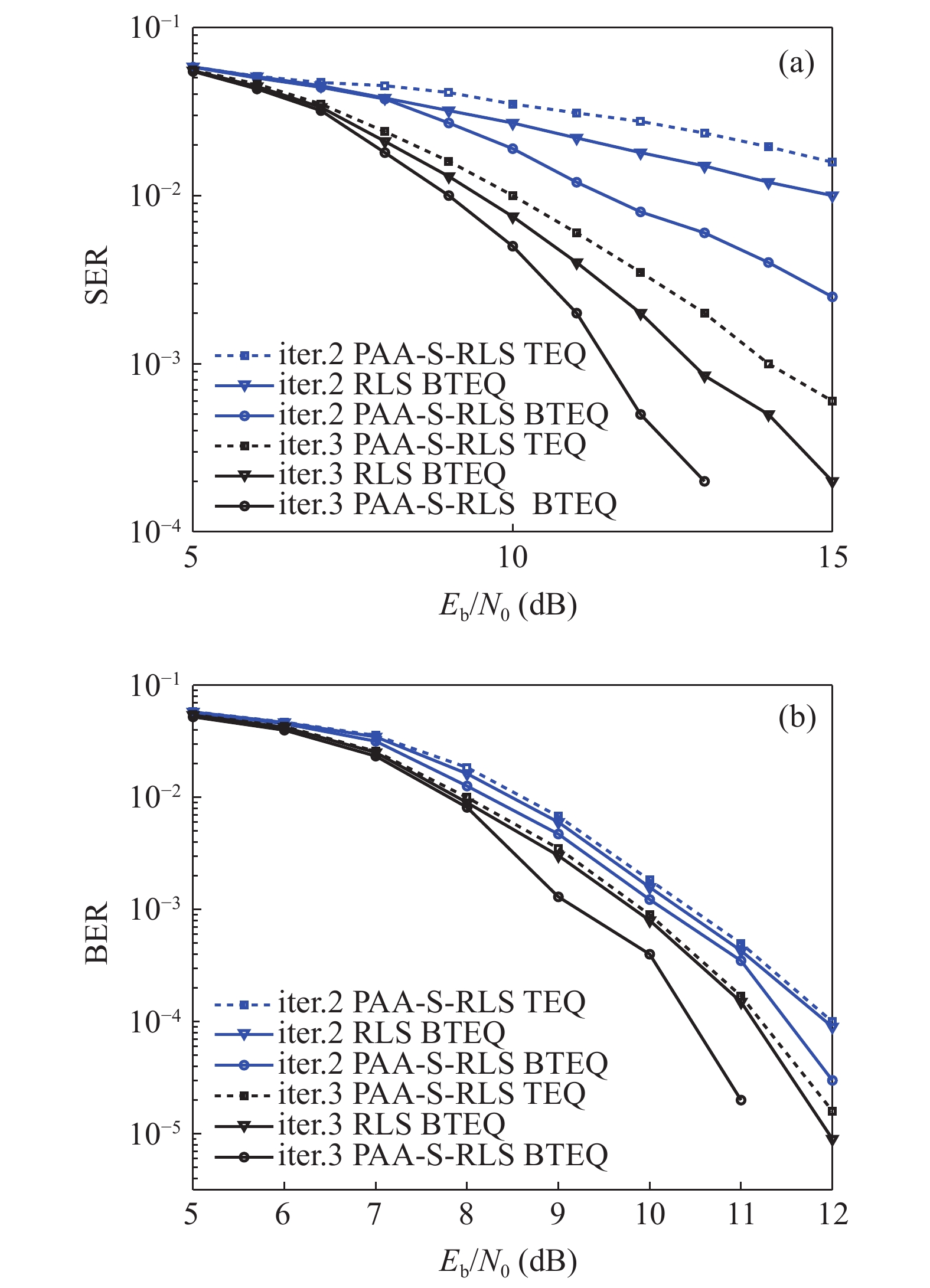
$ {l_0} $ -RLS[19],$ {l}_{2, 0} $ -RLS[20])与PAA-S-RLS算法, 在信道冲击响应分别为图2(b)(c)(d),$ {\gamma _n} $ ,$ {\alpha _n} $ ,$ {\beta _n} $ 的初始值为0, 信噪比为15 dB条件下稀疏约束参数$ {\gamma _n} $ ,$ {\alpha _n} $ ,$ {\beta _n} $ 随迭代次数变化情况。由图5(a)可知, 在常规稀疏信道条件下, PAA-S-RLS算法稀疏约束参数$ {\alpha _n} $ 与$ {l_0} $ -RLS的稀疏约束参数相同,$ {\beta _n} $ 稳态值很小近似于1, 使得$ {l_0} $ -RLS算法稳态均方误差和PAA-S-RLS算法稳态均方误差相同(图4(a))。由图5(b)可知, 在簇稀疏信道条件下, PAA-S-RLS算法稀疏约束参数$ {\beta _n} $ 与$ {l}_{2, 0} $ -RLS的稀疏约束参数相同,$ {\alpha _n} $ 稳态值较小, 使得$ {l}_{2, 0} $ -RLS算法稳态均方误差和PAA-S-RLS算法稳态均方误差相同(图4(b))。由图5(c)可知, 在混合稀疏信道条件下, PAA-S-RLS算法稀疏约束参数$ {\beta _n} $ 与$ {l}_{2, 0} $ -RLS的稀疏约束参数相近, 稀疏约束参数$ {\alpha _n} $ 与$ {l_0} $ -RLS的稀疏约束参数相近, 使得PAA-S-RLS算法稳态均方误差比$ {l_0} $ -RLS和$ {l}_{2, 0} $ -RLS具有更低的均方误差(图4(c))。因此, PAA-S-RLS可以自适应调节稀疏约束权重参数, 适应不同稀疏结构水声信道, 获得更好的均衡性能。图6是图2(b)的信道条件下, 基于PAA-S-RLS单向Turbo判决反馈均衡器(TEQ)、基于常规RLS双向判决反馈Turbo均衡器(BTEQ)和基于PAA-S-RLS双向判决反馈Turbo均衡器在不同比特信噪比(Eb/N0)条件下的误符号率(SER)和译码后的误码率(BER)。由图6(a)可见, 在同一迭代次数、均衡算法采用PAA-S-RLS算法的条件下, 双向判决反馈Turbo均衡优于单向Turbo判决反馈均衡处理; 在同一迭代次数、均采用双向判决反馈Turbo均衡器的条件下, 采用PAA-S-RLS算法比常规RLS算法具有更好低的误符号率。仿真结果表明, 基于PAA-S-RLS的BTEQ的收敛速度更快, 在相同比特信噪比条件下具有更低的误符号率。图6(b)为图6(a)中算法译码后的误码率曲线, 基于PAA-S-RLS双向判决反馈Turbo均衡器在较低信噪比条件下具有更低的误码率。
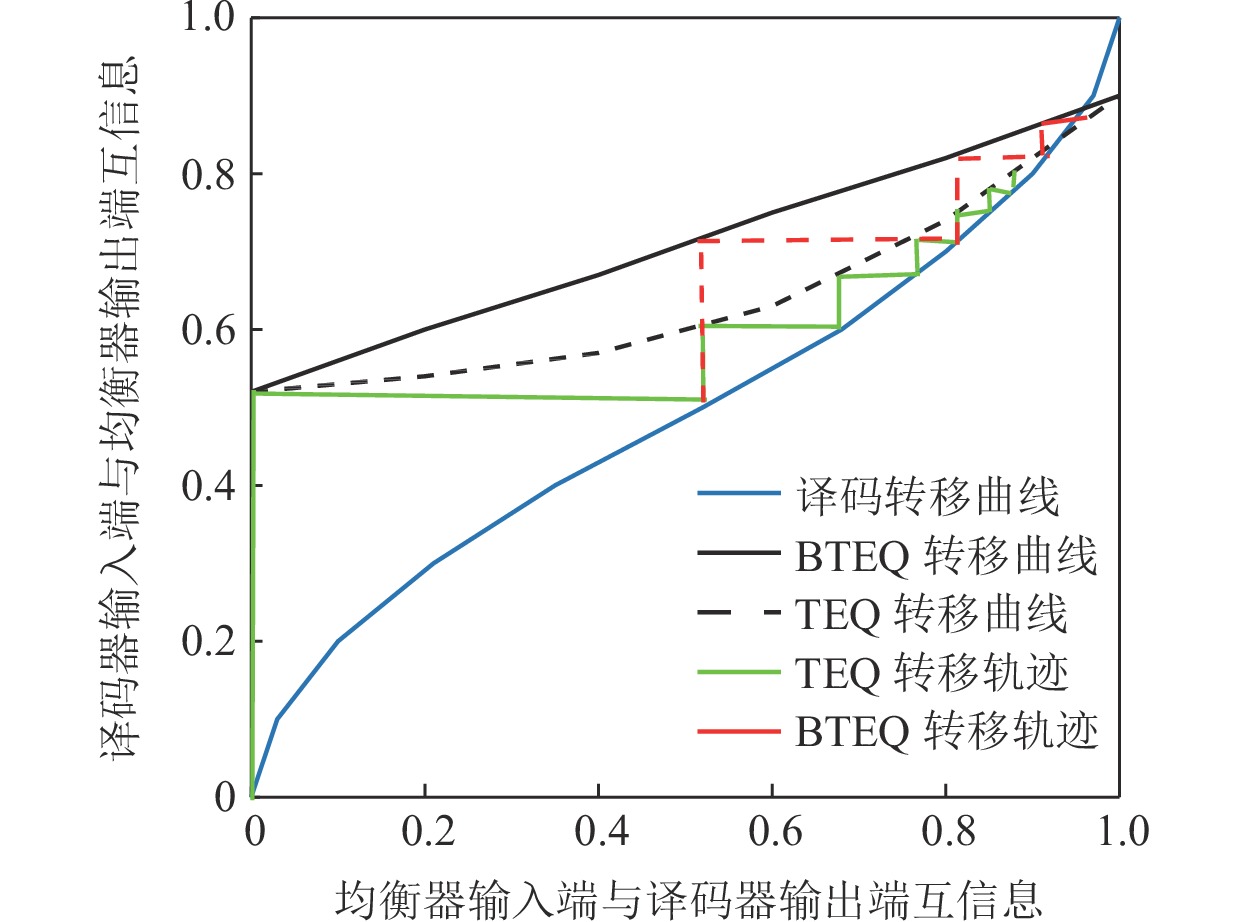
为了进一步衡量Turbo判决反馈均衡器的收敛性, 通过外信息转移图衡量均衡器的迭代译码性能。在高斯白噪声条件下, 假设输入均衡器的先验信息是相互独立的, 则均衡器输入的软信息
$ {L_i} $ 的条件概率为其中,
$ l $ 为随机变量,$ \sigma_{i}^{2} $ 为其方差。同理, 均衡器的输出软信息$ L_0^{} $ 也可以通过正态分布的随机变量进行表示。均衡器的输入软信息$ L_i^{} $ 和$ X $ 的互信息计算方法为同理,
$ L_0^{} $ 和$ X $ 的互信息也通过同样的方式获得。则当输入端互信息$ {I_i} $ 取某一特定值时, 可对应于输出端互信息$ {I_o} $ 的某一取值。通过这些成对的互信息取值点$ \left( {{I_i},{I_o}} \right) $ 就可以描绘外信息的交换。图7是在比特信噪比为10 dB的条件下的外信息转移图, 可见基于PAA-S-RLS算法的BTEQ比基于PAA-S-RLS算法的TEQ在达到较高互信息的情况下需要迭代的次数更少, 基于PAA-S-RLS算法的双向判决反馈Turbo均衡算法收敛性更好。 -
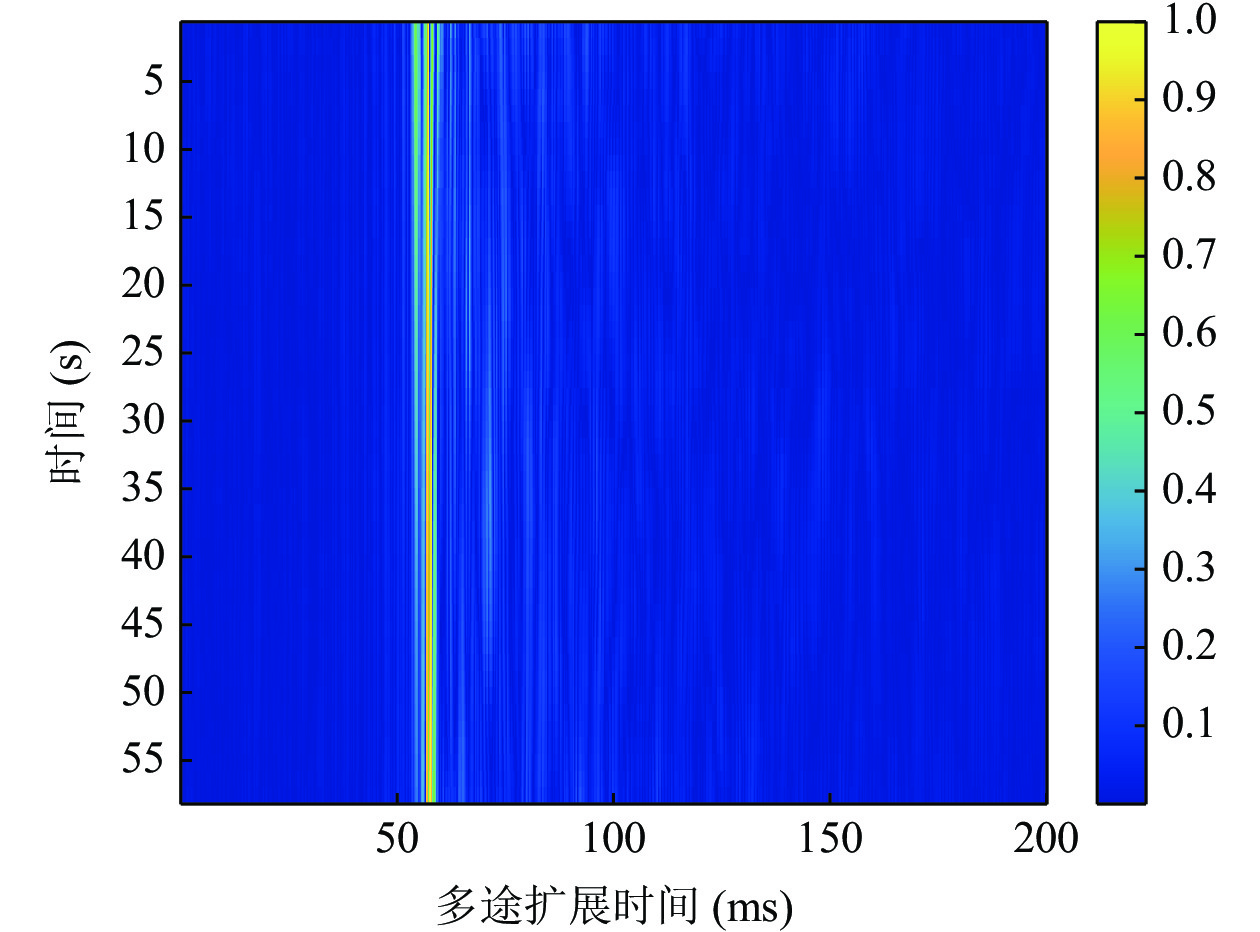
为验证上述算法在实际单载波水声通信系统中的性能, 处理了2015年11月的南海试验数据。海试中采用单发单收模式, 发射船通过锚系固定不动, 发射换能器位于水下40 m, 接收水听器通过锚系固定于水下80 m位置, 收发距离约为30 km。水声单载波通信系统参数与表1中参数相同, 发射数据帧结构和图3相同。带通滤波后, 接收信号信噪比约为11.2 dB。
图8为通过匹配滤波获得的归一化信道冲击响应, 可见信道能量主要集中于直达途中, 信道多途扩展大约为20 ms左右。根据信道冲击响应情况, 前向判决反馈滤波器前馈长度和反馈长度分别为40和10, 反向判决反馈滤波器前馈长度和反馈长度的长度分别为10和30, 锁相环参数
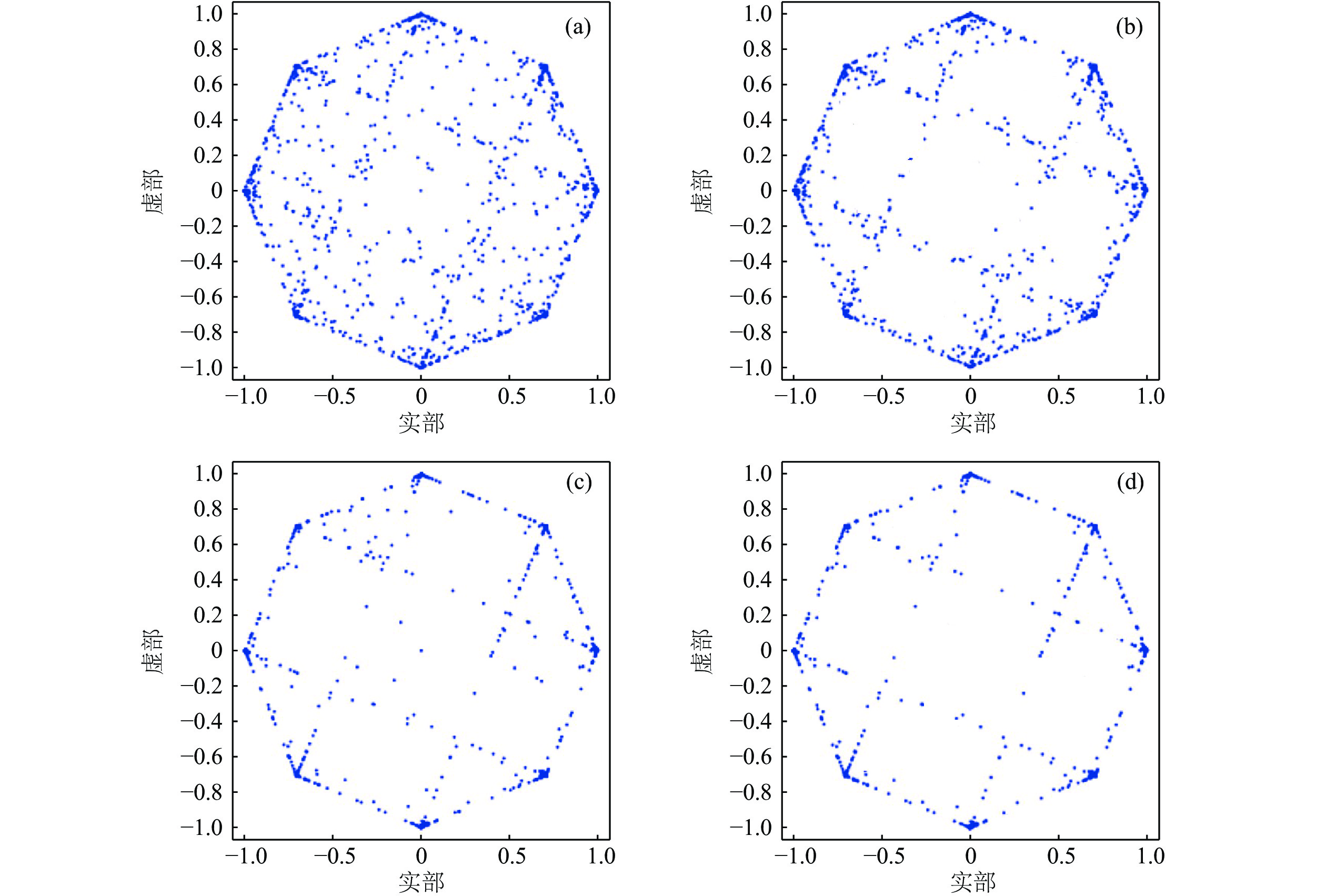
$ {K_{f1}} $ 和$ {K_{f2}} $ 分别为0.0005和0.00005, 遗忘因子初始值为0.995, 总迭代次数为3次。图9为迭代次数为2时, RLS TEQ、RLS BTEQ、PAA-S-RLS TEQ和PAA-S-RLS BTEQ均衡器译码后的星座图。基于RLS TEQ和RLS BTEQ算法的星座图均较为发散, 引入稀疏约束的TEQ和BTEQ算法(即基于PAA-S-RLS TEQ和PAA-S-RLS BTEQ算法)有更多的点收敛于星座点上, 具有更好的均衡效果。
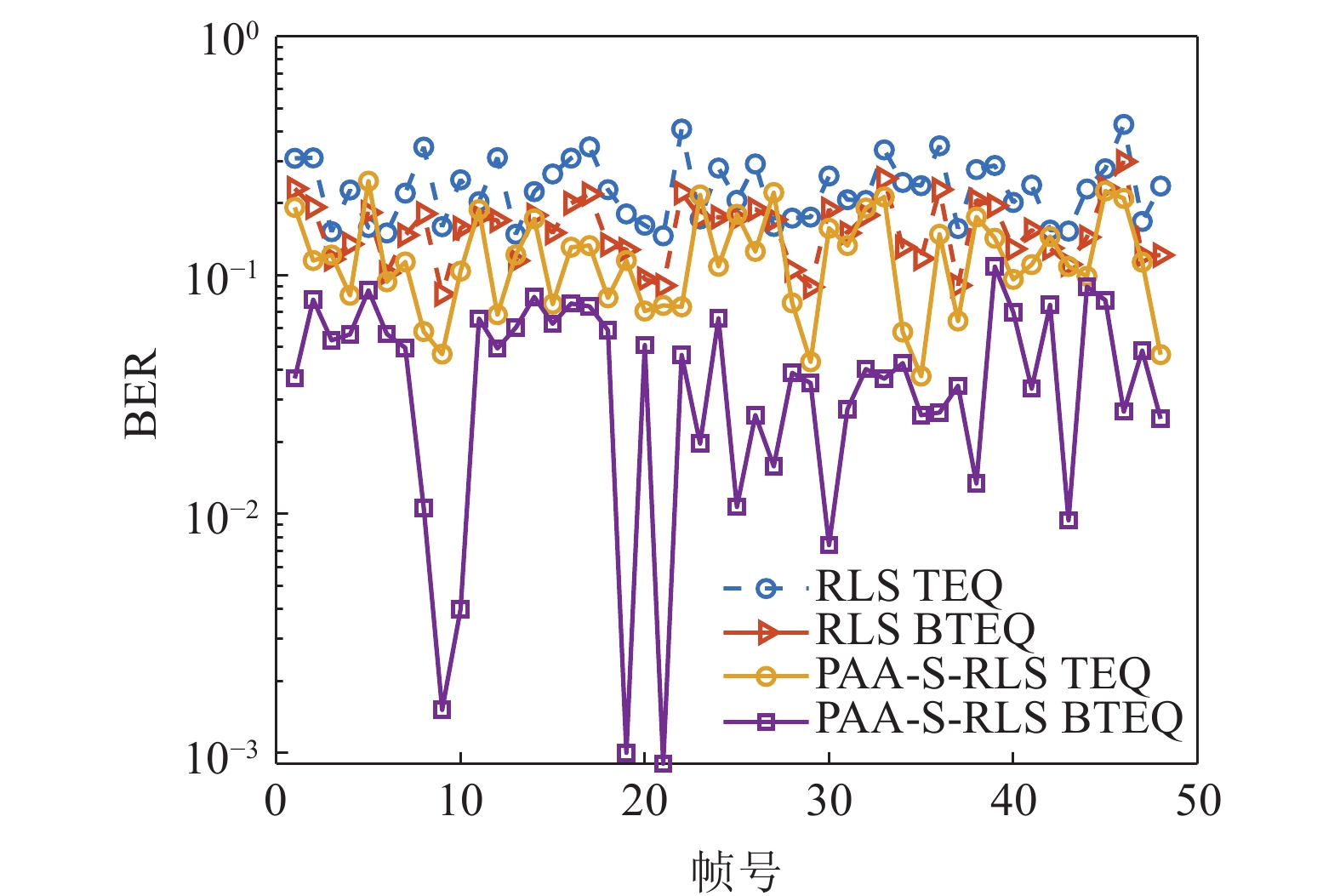
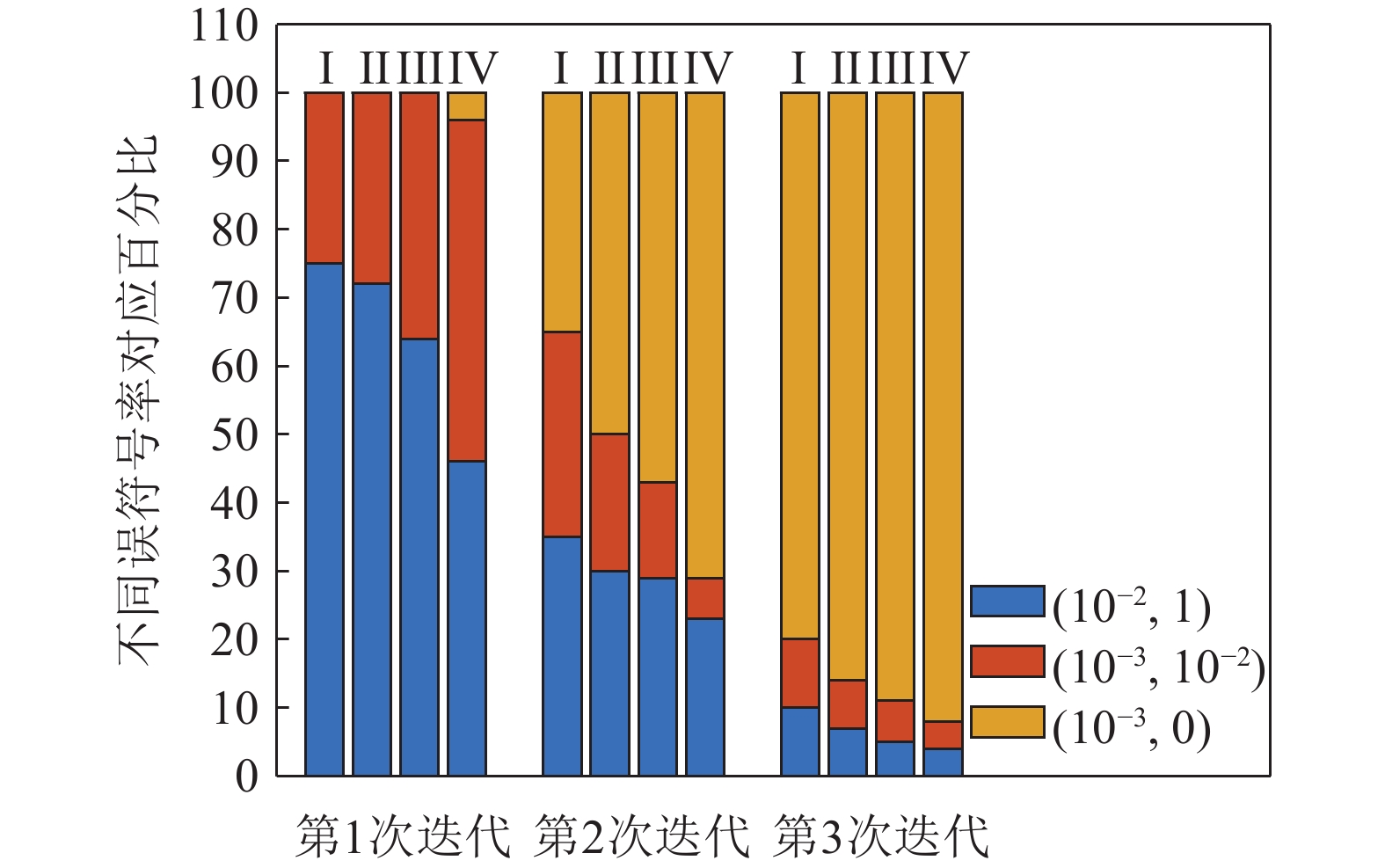
图10和图11为8PSK调制下48帧数据误码率统计结果。图10为迭代次数为1时RLS TEQ、RLS BTEQ、PAA-S-RLS TEQ和PAA-S-RLS BTEQ的误码率结果, 可见PAA-S-RLS BTEQ具有更低的误码率。图11为不同迭代次数下不同误码率所占百分比的统计, 其中I, II, III, IV分别为通过RLS TEQ、RLS BTEQ、PAA-S-RLS TEQ和PAA-S-RLS BTEQ进行处理, 可见在不同段BER, PAA-S-RLS BTEQ具有更低的误码率。
-
本文提出了一种参数自适应调整稀疏迭代最小二乘算法的双向Turbo均衡器。在均衡过程中, 通过联合优化遗忘因子和稀疏约束参数提升稀疏信道均衡性能; 然后通过双向判决反馈Turbo均衡结构, 降低误差传递, 减小迭代均衡次数。仿真和海试结果表明, 在稀疏水声信道中, 相比于传统的单向Turbo均衡算法, 本文算法在收敛速度和系统误码率方面具有更好的均衡性能。
联合稀疏自适应滤波的水声通信双向迭代均衡算法
A bidirectional iterative equalization algorithm for underwater acoustic communication based on sparse adaptive filtering
-
摘要: 针对具有稀疏性的水声信道, 提出了一种参数自适应调整稀疏迭代最小二乘自适应算法。通过联合优化遗忘因子和稀疏约束参数, 实现不同结构特性稀疏信道的自适应匹配, 使均衡算法更快地收敛到稳态; 针对常规均衡算法和单一方向Turbo判决反馈均衡器存在误差传递的问题, 设计了一种稀疏自适应迭代最小二乘算法与双向迭代Turbo判决反馈均衡器相结合的均衡器结构, 改善了常规均衡算法和单一方向Turbo判决反馈均衡器误差传递的问题, 提高了在稀疏水声信道条件中自适应均衡器的收敛速度和均衡性能。仿真和试验数据结果表明, 在稀疏水声信道中, 基于参数自适应调整稀疏迭代最小二乘算法的双向Turbo均衡算法具有更快的收敛性能、更低的误比特率和更好的均衡效果。Abstract: This paper proposes a parameter-adaptive adjustment sparse recursive least-square (PAA-S-RLS) adaptive algorithm for the sparse underwater acoustic channel. Firstly, the proposed algorithm can achieve adaptive matching of sparse channels with different structures by jointly optimizing the forgetting factor and sparse penalty parameters, which enables the equalization algorithm converge to the steady-state faster. Secondly, a robust sparse adaptive RLS algorithm combined with bidirectional iterative Turbo decision feedback equalizer is designed to address the issue of error propagation caused by the conventional equalization algorithms and conventional Turbo decision feedback equalizer, which can improve the convergence rate and the performance of adaptive equalizers in sparse underwater acoustic channels. Simulation and experimental results show that the bidirectional iterative equalization algorithm based on adaptive adjustment sparse RLS has faster convergence rate, lower bit error rate, and better equalization performance in the sparse underwater acoustic channel.
-
Key words:
- Channel equalization /
- Sparsity .
-

-
表 1 参数自适应调整稀疏RLS自适应均衡算法
输入: $ {{\boldsymbol{x}}_n} $ ,

$ {y_n} $ ,

$ {d_n} $ 

初始化:$ {{\boldsymbol{P}}_n} = \delta {{\boldsymbol{I}}_N} $ ,

$ {\boldsymbol{\widehat w}}_{ - 1}^{} = {\boldsymbol{0}} $ 

1. 计算增益向量$ {{\boldsymbol{k}}_n} = \dfrac{{{{\boldsymbol{P}}_{n - 1}}{{\boldsymbol{x}}_n}}}{{\lambda + {\boldsymbol{x}}_n^{\rm T}{{\boldsymbol{P}}_{n - 1}}{{\boldsymbol{x}}_n}}} $ 

2. 计算先验误差$ {\widehat \xi _n} = {y_n} - {\boldsymbol{\widehat w}}_{n - 1}^{\rm T}{{\boldsymbol{x}}_n} $ 

3. 更新权重因子$ {{\boldsymbol{\widehat w}}_n} = {{\boldsymbol{\widehat w}}_{n - 1}} + {\widehat \xi _n}{{\boldsymbol{k}}_n} - {\alpha _{n - 1}}(1 - \lambda ){{\boldsymbol{P}}_n}\dfrac{{\partial f({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}} - {\beta _{n - 1}}(1 - \lambda ){{\boldsymbol{P}}_n}\dfrac{{\partial g({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}} $ 

4. 估计能量$ \sigma _{{q_n}}^2 = {\alpha _0}\sigma _{{q_{n - 1}}}^2 + (1 - {\alpha _0})q_{n - 1}^2 $ 

$ \sigma _{{e_n}}^2 = \alpha \sigma _{{e_{n - 1}}}^2 + (1 - \alpha )e_{n - 1}^2 $ 

$ \sigma _{{v_n}}^2 = \beta \sigma _{{v_{n - 1}}}^2 + (1 - \beta )e_{n - 1}^2 $ 

5. 更新遗忘因子$ {\lambda _n} = {\text{min}}\left\{ \dfrac{{{\sigma _{{q_n}}}{\sigma _{{v_n}}}}}{{\tau + {\text{|}}{\sigma _{{e_n}}} - {\sigma _{{v_n}}}{\text{|}}}},{\lambda _{{\text{max}}}}\right\} $ 

6. 更新正则化系数$ {\alpha _n} $ ,

$ {\beta _n} $ 

$ {\alpha _n} = \max (0,{{\widehat \alpha }_n}) = \max \left( {0,{{\widehat \alpha }_{n - 1}} + \dfrac{{{\text{tr}}\left( {{{\boldsymbol{P}}_{n - 1}}} \right)}}{N}\dfrac{{\left( {f({{{\boldsymbol{\widehat w}}}_n}) - f({{\boldsymbol{w}}_{n - 1}})} \right)\left\| {{{\boldsymbol{P}}_n}\dfrac{{\partial g({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}}} \right\|_2^2 - \left( {g({{{\boldsymbol{\widehat w}}}_n}) - g({{\boldsymbol{w}}_{n - 1}})} \right){{\left[ {{{\boldsymbol{P}}_n}\dfrac{{\partial g({{{\boldsymbol{\widehat w}}}_n})}}{{\partial {{{\boldsymbol{\widehat w}}}_n}}}} \right]}^{\rm T}}\left[ {{{\boldsymbol{P}}_n}\dfrac{{\partial f({{{\boldsymbol{\widehat w}}}_n})}}{{\partial {{{\boldsymbol{\widehat w}}}_n}}}} \right]}}{{\left\| {{{\boldsymbol{P}}_{n - 1}}\dfrac{{\partial f({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}}} \right\|_2^2\left\| {{{\boldsymbol{P}}_{n - 1}}\dfrac{{\partial g({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}}} \right\|_2^2 - \left\| {{{\left[ {{{\boldsymbol{P}}_{n - 1}}\dfrac{{\partial f({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}}} \right]}^{\rm T}}\left[ {{{\boldsymbol{P}}_{n - 1}}\dfrac{{\partial g({{\widehat {\boldsymbol{w}}}_{n - 1}})}}{{\partial {{\widehat {\boldsymbol{w}}}_{n - 1}}}}} \right]} \right\|_2^2}}} \right) $ 

$ {\beta _n} = \max (0,{{\widehat \beta }_n}) = \max \left( {0,{{\widehat \beta }_{n - 1}} + \dfrac{{{\text{tr}}\left( {{{\boldsymbol{P}}_{n - 1}}} \right)}}{N}\dfrac{{\left( {g({{{\boldsymbol{\widehat w}}}_n}) - g({{\boldsymbol{w}}_{n - 1}})} \right)\left\| {{{\boldsymbol{P}}_n}\dfrac{{\partial f({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}}} \right\|_2^2 - \left( {f({{{\boldsymbol{\widehat w}}}_n}) - f({{\boldsymbol{w}}_{n - 1}})} \right){{\left[ {{{\boldsymbol{P}}_n}\dfrac{{\partial f({{{\boldsymbol{\widehat w}}}_n})}}{{\partial {{{\boldsymbol{\widehat w}}}_n}}}} \right]}^{\rm T}}\left[ {{{\boldsymbol{P}}_n}\dfrac{{\partial g({{{\boldsymbol{\widehat w}}}_n})}}{{\partial {{{\boldsymbol{\widehat w}}}_n}}}} \right]}}{{\left\| {{{\boldsymbol{P}}_{n - 1}}\dfrac{{\partial f({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}}} \right\|_2^2\left\| {{{\boldsymbol{P}}_{n - 1}}\dfrac{{\partial g({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}}} \right\|_2^2 - \left\| {{{\left[ {{{\boldsymbol{P}}_{n - 1}}\dfrac{{\partial f({{{\boldsymbol{\widehat w}}}_{n - 1}})}}{{\partial {{{\boldsymbol{\widehat w}}}_{n - 1}}}}} \right]}^{\rm T}}\left[ {{{\boldsymbol{P}}_{n - 1}}\dfrac{{\partial g({{\widehat {\boldsymbol{w}}}_{n - 1}})}}{{\partial {{\widehat {\boldsymbol{w}}}_{n - 1}}}}} \right]} \right\|_2^2}}} \right) $ 

7. 更新向量 $ {{\boldsymbol{P}}_n} $ :

$ {{\boldsymbol{P}}_n} = \lambda _{}^{ - 1}\{ {{\boldsymbol{P}}_{n - 1}} - {{\boldsymbol{k}}_n}{\boldsymbol{x}}_n^{\rm T}{{\boldsymbol{P}}_{n - 1}}\} $ 

表 2 仿真系统参数
参数名称 参数设置 信号带宽 500 Hz 符号率 250 sym/s 前向训练序列长度 500 sym 反向训练序列长度 500 sym 数据长度 2550 sym -
[1] 王海斌, 汪俊, 台玉朋, 等. 水声通信技术研究进展与技术水平现状. 信号处理, 2019; 35(9): 1441−1449 doi: 10.16798/j.issn.1003-0530.2019.09.001 [2] 武岩波, 朱敏, 朱维庆, 等. 接近非相干水声通信信道容量的信号处理算法. 声学学报, 2015; 40(1): 117−123 doi: 10.15949/j.cnki.0371-0025.2015.01.015 [3] Zhao S, Yan S, Xi J. Adaptive Turbo equalization for differential OFDM systems in underwater acoustic communications. IEEE Trans. Veh. Technol., 2020; 69(11): 13937−13941 doi: 10.1109/TVT.2020.3017778 [4] Singer A C, Nelson J K, Kozat S S. Signal processing for underwater acoustic communications. IEEE Commun. Mag., 2009; 47(1): 90−96 doi: 10.1109/MCOM.2009.4752683 [5] Leinhos H A. Block-adaptive decision feedback equalization with integral error correction for underwater acoustic communications. OCEANS 2000, IEEE, Providence, RI, USA, 2000: 817−822 [6] Tüchler M, Singer A C, Koetter R. Turbo equalization: Principles and new results. IEEE Trans. Commun., 2002; 50(5): 432−447 doi: 10.1109/TCOMM.2002.1006557 [7] Choi J W, Drost R, Singer A C, et al. Iterative multi-channel equalization and decoding for high frequency underwater acoustic communications. 5th IEEE Sensor Array Multichannel Signal Process Workshop, IEEE, Darmstadt, Germany 2008: 127−130 [8] Choi J W, Riedl T J, Kim K, et al. Adaptive linear Turbo equalization over doubly selective channels. IEEE J. Oceanic Eng., 2011; 36(4): 473−478 doi: 10.1109/JOE.2011.2158013 [9] Tao J, Zheng R, Xiao C, et al. Channel equalization for single carrier MIMO underwater acoustic communications. EURASIP J. Adv. Signal Process., 2010; 2010: 281769 doi: 10.1155/2010/281769 [10] Otnes R, Tuchler M. Iterative channel estimation for Turbo equalization of time-varying frequency-selective channels. IEEE Trans. Wirel. Commun., 2005; 3(6): 1918−1923 doi: 10.1109/TWC.2004.837421 [11] Zheng Y R, Wu J, Xiao C. Turbo equalization for single-carrier underwater acoustic communications. IEEE Commun. Mag., 2015; 53(11): 79−87 doi: 10.1109/MCOM.2015.7321975 [12] Laot C, Glavieux A, Labat J. Turbo equalization: Adaptive equalization and channel decoding jointly optimized. IEEE J. Sel. Areas Commun., 2001; 19(9): 1744−1752 doi: 10.1109/49.947038 [13] Singer A. Adaptive equalization, tracking, and decoding for high-rate underwater acoustic communications. J. Acoust. Soc. Am., 2012; 131(4S): 3276 doi: 10.1121/1.4708247 [14] Wu J, Wang L, Xiao C. Low-complexity soft-interference cancellation Turbo equalization for multi-input-multi-output systems with multilevel modulations. Comm. Lett., 2015; 9(5): 728−735 doi: 10.1109/GLOCOM.2013.6831590 [15] Duan W, Tao J, Zheng Y R. Efficient adaptive Turbo equalization for multiple-input-multiple-output underwater acoustic communications. IEEE J. Oceanic Eng., 2018; 43(3): 792−804 doi: 10.1109/JOE.2017.2707285 [16] Li D, Wu Y, Zhu M, et al. An enhanced iterative receiver based on vector approximate message passing for deep-sea vertical underwater acoustic communications. J. Acoust. Soc. Am., 2021; 149(3): 1549−1558 doi: 10.1121/10.0003625 [17] Song H C. Bidirectional equalization for underwater acoustic communication. J. Acoust. Soc. Am., 2012; 131(4): EL342−EL347 doi: 10.1121/1.3695075 [18] Xi J, Yan S, Xu L, et al. Soft direct-adaptation based bidirectional Turbo equalization for MIMO underwater acoustic communications. China Commun., 2017; 14(7): 1−12 doi: 10.1109/CC.2017.8010969 [19] Eksioglu E M, Tanc A K. RLS algorithm with convex regularization. IEEE Signal Process. Lett., 2011; 18(8): 470−473 doi: 10.1109/LSP.2011.2159373 [20] Eksioglu E M. Group sparse RLS algorithms. Int. J. Adapt. Control Signal Process., 2014; 28(12): 1398−1412 doi: 10.1002/acs.2449 [21] Yu Y, Huang Z, He H, et al. Sparsity-aware robust normalized subband adaptive filtering algorithms with alternating optimization of parameter. IEEE Trans. Circuits Syst. II Express Briefs, 2022; 69(9): 3934−3938 doi: 10.1109/TCSII.2022.3171672 [22] Yu Y, Lu L, Zakharov Y, et al. Study of robust sparsity-aware RLS algorithms with jointly-optimized parameters for impulsive noise environments. IEEE Signal Process. Lett., 2022; 29: 1037−1041 doi: 10.1109/LSP.2022.3166395 [23] Shi K, Shi P. Convergence analysis of sparse LMS algorithms with l1-norm penalty based on white input signal. Signal Process., 2010; 90(12): 3289−3293 doi: 10.1016/j.sigpro.2010.05.015 [24] Freitag L, Johnson M, Stojanovic M. Efficient equalizer update algorithms for acoustic communication channels of varying complexity. OCEANS '97, IEEE, Halifax, NS, Canada, 1997: 580−585 [25] Shi K, Shi P. Adaptive sparse Volterra system identification with l0-norm penalty. Signal Process., 2011; 91(10): 2432−2436 doi: 10.1016/j.sigpro.2011.04.028 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: