流致噪声是水听器接收信号的主要噪声成分, 对流致噪声进行有效抑制可以显著提升拖曳阵列声呐的探测性能。目前抑制拖曳阵列流致噪声主要通过物理途径, 如增大水听器与护套之间的距离或增加护套厚度等。然而拖曳阵小直径化的发展趋势限制了护套表面到水听器的距离, 上述方法不再适用。因此, 通过信号处理来抑制水听器接收数据中的流噪声成为提升拖曳阵列声呐探测性能的重要方法。

流噪声的物理模型与噪声特性分析是实现拖曳阵列流噪声抑制的前提。 Corcos等^[1]研究了平板表面上的湍流流动, 建立了湍流边界层(TBL)压力脉动的二维波数−频率谱模型。Carpenter等^[2]提出更加拟合拖曳阵列护套管的细长圆柱TBL压力起伏模型, 计算了拖曳阵列流噪声并进行试验测量。Linderman等^[3]推导了在护套外表面有TBL压力起伏时护套层对其响应的传递函数。汤渭霖等^[4]详细分析了流噪声的产生机理, 并讨论了不同水听器参数与护套参数对流噪声的影响。王斌等^[5] 详细比较了不同的TBL压力起伏模型, 并给出了流噪声功率谱的解析表达式。王晓林等^[6]通过分析大量实验数据对Carpenter压力起伏模型的参数进行修正, 更为准确地计算了拖曳阵列护套管内的流致噪声响应。杨秀庭等^[7-8]利用护套管内流致噪声的空间相关性, 计算了不同形状矢量水听器和水听器阵列接收的流噪声。

近年来, 通过阵列信号处理技术抑制拖曳阵列流噪声并提高阵处理性能受到关注。孟彧仟等^[9]分析了流噪声在声压、轴向振速和径向振速三个分量之间的相关性, 提出了基于声强流的拖曳阵列流噪声抑制方法。李磊等^[10-11]通过设计信号模拟器仿真拖曳阵列声呐工作时的不同噪声, 并提出了噪声抑制的相关算法, 但该算法主要针对本舰噪声与其他海洋环境噪声。张宾等^[12]采用经验模式分解的方法分解水听器的接收信号, 并分离出拖船噪声分量, 从而达到消除噪声的目的。针对水下目标特征提取与噪声源的识别, 如瞬时频率变化率算法^[13]、波束域时频分析方法^[14]等声源信号分析技术被提出并广泛应用。此外, 如正交匹配追踪波达方向估计法^[15]、利用期望最大算法的多频带声信号时延估计法^[16]等提升阵列定位性能的方法也被尝试用于拖曳阵列声呐探测中。韩东等^[17]将匹配场定位和平面波目标方位估计相结合, 设计了具有强噪声抑制功能的空域矩阵滤波器, 减小了处理后探测盲区的范围并提升了盲区外的探测能力。

上述基于阵列信号处理的流噪声抑制方法, 无论是利用信号的相关性或是从目标方位估计出发减少流噪声的影响, 均未实现拖曳阵列流噪声的有效抑制, 所带来的目标方位估计结果增益也十分有限。且上述流噪声模型研究中, 传统的TBL模型基于稳态的建模方法, 即仅为统计量上的建模, 没有考虑复杂噪声的概率密度分布, 而流噪声的准确建模以及信号成分的正确提取可实现噪声的有效抑制。Meng等^[18]提出通过高斯混合模型与低秩矩阵分解的方法模拟复杂噪声, 并通过最大似然法估计混合高斯模型中的参数。Yong等^[19]在此基础上引入分帧的概念, 让模型通过学习先前帧完成逐帧在线更新以更加鲁棒并适应现实场景的噪声变化情况。Yu等^[20-21]将混合高斯噪声模型引入传声器阵列测量与声成像中, 并通过分帧处理进行噪声的混合高斯模型构建与低秩矩阵分解, 实现了复杂噪声情况下的谐波信号去噪。

针对上述问题, 本文从拖曳阵列流致噪声的产生机理与噪声统计特性出发, 根据拖曳阵列流噪声表现出的非高斯的复杂统计特性, 建立了流噪声的高斯混合模型(Gaussian Mixture Model, GMM)。同时对低秩信号时频矩阵建模, 发展了混合高斯模型与期望最大(Gaussian Mixture Model-Expectation Maximum, GMM-EM)算法, 并对模型中的参数进行更新, 将水听器接收声压数据中的噪声与信号分离, 并完成信号的重建。仿真和实验结果表明, 所提方法可实现拖曳阵列流噪声的有效抑制, 提升拖曳阵列探测定位性能。

拖曳阵列流致噪声的主要来源可看作是TBL压力起伏激发线列阵振动产生的噪声信号, 其结果直接作用在水听器上, 成为拖曳阵列声呐主要的自噪声源。在拖曳阵列声呐探测工作过程中, 假设用于收集信号的水听器有M个, 水听器的接收信号是由远场平面波信号和背景噪声两部分组成, 在t时刻所有传声器接收信号$ \boldsymbol{y}\left(t\right)\in {\mathbb{R}}^{M\times 1} $可表示为

其中, $ \boldsymbol{A}\in {\mathbb{R}}^{M\times I} $为阵列流形矩阵, I为信号源的等效源数量, $ \boldsymbol{x}\left(t\right)\in {\mathbb{R}}^{I\times 1} $为t时刻水听器接收的远场平面波信号, $ \boldsymbol{n}\left(t\right)\in {\mathbb{R}}^{M\times 1} $表示t时刻的背景噪声, 即TBL压力起伏产生的流噪声。在实际工作环境中强烈的背景噪声$ \boldsymbol{n}\left(t\right) $会严重影响目标探测的结果。由于TBL压力起伏的复杂性, 拖曳阵列流噪声表现出非高斯的复杂统计特性, 对背景噪声进行建模与抑制十分困难。本文基于拖曳阵列流致噪声的非高斯特性, 建立精确的噪声拟合模型并对信号进行重建。通过将噪声成分从接收信号中分离以对实现拖曳阵列流噪声的抑制, 使用降噪后的信号进行波束形成能够显著提升拖曳阵列探测性能。

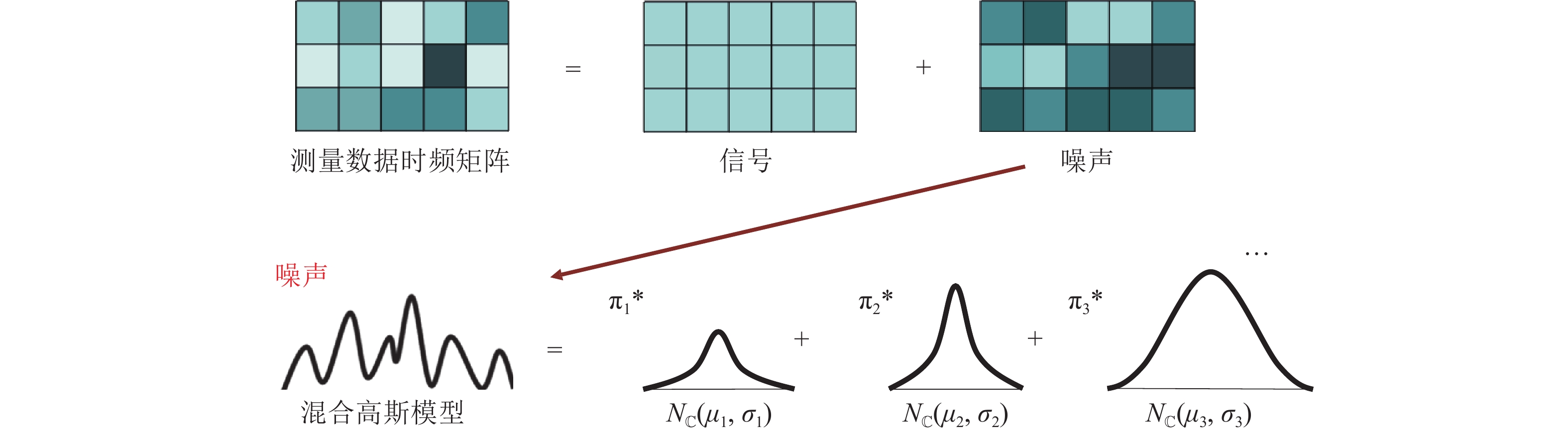
实际工作环境中背景噪声非常强, 严重影响目标探测结果, 并且由于TBL压力起伏的复杂性, 拖曳阵列流噪声表现出非高斯的复杂统计特性。拖曳阵列流噪声抑制的基本思想是通过分别对测量声压数据中的噪声与信号两部分建模, 实现信号与噪声的分离。

如图1所示, 对于流噪声部分的建模是针对拖曳阵列流噪声表现出的非高斯的复杂统计特性, 将噪声成分建模为几个不同参数不同权重的高斯模型叠加而成。而对于信号部分, 谐波信号在时频矩阵上会表现出低秩特性, 时频矩阵的秩取决于正弦曲线的数量^[22-23], 因此可对信号进行低秩矩阵分解, 从而与混合高斯建模的噪声相分离。

式(1)中, 需将水听器接收信号分离成远场平面波信号$ \boldsymbol{x}\left(t\right) $与噪声$ \boldsymbol{n}\left(t\right) $, 即对信号部分完成低秩建模, 对噪声成分进行混合高斯建模。整个过程需要在时频域完成, 将M个水听器通道中的第m个通道采集到的声压数据通过短时傅里叶变换(STFT)转换到时频域:

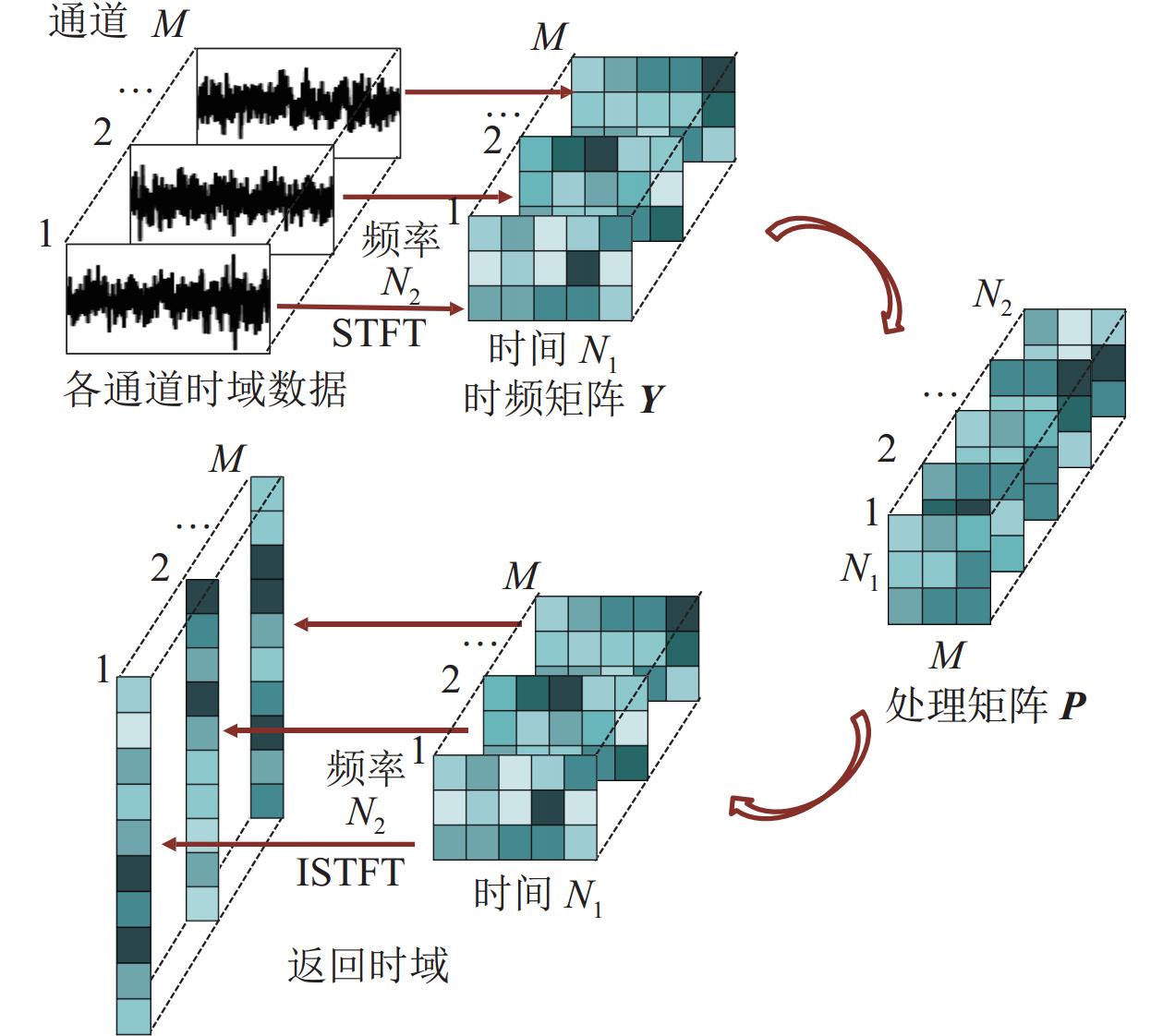
其中, $ \tau $和$ f $分别表示STFT过程中的时间参数与频率参数, $ w\left(t\right) $是STFT的窗口函数, $ {\mathrm{e}}^{-2\mathrm{j}\mathrm{\pi }f(t-\tau )} $是基函数。$ {Y}_{m} $是测量信号$ {y}_{m} $的时频表示, 其组成的矩阵$ {\boldsymbol{Y}} \in {\mathbb{C}^{{N_1} \times {N_2}}} $, $ {N}_{m} $是噪声$ {n}_{m} $的时频表示, 其组成的矩阵$ N \in {\mathbb{C}^{{N_1} \times {N_2}}} $, N₁, N₂分别为时频矩阵的时间与频率维度大小, $ {y}_{m} $为t时刻水听器接收信号$ \boldsymbol{y} $的第m个分量, $ {n}_{m} $为背景噪声$ \boldsymbol{n} $的第m个分量。

通过STFT得到的时频矩阵在完成模型构建与抑制算法求解后通过逆短时傅里叶变换(ISTFT)转换回时域, 转换过程如图2所示。通过STFT将每个通道的声压时域数据转换得到时频矩阵, 其中时频矩阵的大小由STFT过程中的时间参数$ \tau $与频率参数$ f $决定。将M个通道的时频矩阵拼接在一起, 数据维度为M × N₁ × N₂。然后, 通过矩阵维度的转换将M个通道的时频矩阵转换为N₂个矩阵$ \boldsymbol{P}\in {\mathbb{C}}^{M\times {N}_{1}} $作为后续建模与噪声抑制处理的数据矩阵, 即$ \{ {{\boldsymbol{P}}_1}, {{\boldsymbol{P}}_2},\cdots,{{\boldsymbol{P}}_{N2}} \} $。矩阵转换的目的在于可对时频矩阵中的每个频率点做后续建模与噪声抑制处理, 相当于在频域上对于宽带信号其整个频段都能够实现噪声建模与抑制, 使得算法能够处理宽带信号而不需要发射信号频率这一先验信息。由此得到的处理矩阵数据可以看成是信号低秩矩阵与噪声矩阵的叠加, 之后则对矩阵$ \boldsymbol{P}$分别进行低秩矩阵分解与混合高斯建模, 以实现信号的重构。

采用U和V矩阵分解的形式来表示信号部分, 其中U矩阵为子空间矩阵, V矩阵为系数矩阵, U矩阵的维度为r × N₁, V矩阵的维度为r × N₂, r为STFT得到时频矩阵的秩。可以将上述时频变换后得到的处理矩阵$ \boldsymbol{P}$的每个元素表示为

其中, $ {\boldsymbol{u}}^{\boldsymbol{i}} $代表U矩阵的第i行, $ {\boldsymbol{v}}^{\boldsymbol{j}} $代表V矩阵的第j行, 1 ≤ i ≤ N₁, 1 ≤ j ≤ N₂, ${\varepsilon _{ij}}$代表单元内的噪声信号, 每一个${\varepsilon _{ij}}$都假设满足混合高斯模型, 而总体噪声信号则表述为

其中, $[ \cdot ]$表示随机变量的概率密度函数, ${N_\mathbb{C}}(\varepsilon |0,\sigma _k^2)$ 表示均值为0, 方差为$\sigma _k^2$的高斯分布。$ {\pi }_{k} $是混合系数, 表示每一个高斯模型在总体模型中所占的权重, $0 \leqslant {\pi _k} \leqslant 1, \; \sum \nolimits_{k = 1}^K {\pi _k} = 1$。每一个单元的概率${p_{ij}}$表示为

其中, $[{p_{ij}}|k] = {N_\mathbb{C}}({p_{ij}}|{\left( {{{\boldsymbol{u}}^i}} \right)^{\text{T}}}{{\boldsymbol{v}}^j},\sigma _k^2)$, ${\boldsymbol{\varPi}} = \left\{ {{\pi _1},{\pi _2}, \cdots ,{\pi _K}} \right\}$, ${\boldsymbol{\varSigma}} = \left\{ {{\sigma _1},{\sigma _2}, \cdots ,{\sigma _K}} \right\}$。因此, $ \boldsymbol{P}$的似然函数为

在混合高斯模型的构建过程中, 主要包含三类未知参数: 第一类是每个高斯分布函数的均值和方差; 第二类是每个高斯分布函数占整个分布的权重; 第三类是用来逼近任意概率密度函数分布的高斯函数的个数。为达到信号与噪声分离的目的, 需要将混合高斯模型中的各参数以及信号模型中的U和V矩阵进行求解计算。

可采用EM算法迭代求解上述模型参数, 模型的整体构建与求解过程主要包括: 构建复杂噪声的概率密度函数, 对任意概率分布的复杂噪声进行自适应建模, 提出高斯分量参数的先验假设。初始化$ \boldsymbol{\varPi },\boldsymbol{\varSigma } $和$ \boldsymbol{U},\boldsymbol{V} $等参数, 确定混合高斯模型个数, 对混合高斯模型中各个高斯分量选取分配权重, 之后迭代求解混合高斯模型参数与$ \boldsymbol{U},\boldsymbol{V} $矩阵。

首先引入一个隐变量${\gamma _{ijk}}$, 引入隐变量的目的在于补齐样本来源于哪类高斯模型, 其表达式为

加入隐变量后可获得完全数据$ \left( { \boldsymbol{P},\gamma } \right) $, 其似然函数为

其中 , ${N_k} = \mathop \sum \nolimits_{ij} {\gamma _{ijk}}$, $N = \mathop \sum \nolimits_{i = 1}^K {N_k}$。

算法需更新的参数包括混合高斯模型中每个单一高斯分布的方差集合${\boldsymbol{\varSigma}} = \left\{ {{\sigma _1},{\sigma _2}, \cdots ,{\sigma _K}} \right\}$、总体模型中的混合系数${\boldsymbol{\varPi }}= \left\{ {{\pi _1},{\pi _2}, \cdots ,{\pi _K}} \right\}$以及U, V矩阵, 因此需要假设更新参数的先验信息。

混合高斯模型中的方差与混合系数的先验可分别假设为逆伽马分布与迪利克雷分布, 而U和V矩阵中的行向量$ {u}^{i},{v}^{i} $则可设置为高斯分布, 参数的先验分布如下:

其中, $ \text{Inv-Gamma}(\cdot) $为逆伽马分布, $ \text{Dir}(\cdot) $为迪利克雷分布, $ \mathrm{Gamma}(\cdot) $为伽马分布。C, d, α为逆伽马分布与迪利克雷分布中的参数, $ {\boldsymbol{I}}_{N} $是维度为N₁ × N₂的单位矩阵, 超参数$ {\gamma _n} $满足参数为a, b的伽马分布。似然函数可从假设的参数先验信息中计算得到每一步的参数后验函数, 并作为下一次更新的参数先验信息, 以此实现参数的迭代更新。

获得完全数据的似然函数之后, 分E步与M步两步进行计算与迭代求解。算法的E步即计算确定数据来源于哪一类高斯模型。计算给定一组数据下对各类高斯模型的响应度, 即对隐变量${\gamma _{ijk}}$进行估计, 首先需定义Q函数^[24-25]:

其中, $ \theta $表示估计参数$ \boldsymbol{\varPi },\boldsymbol{\varSigma } $和$ \boldsymbol{U},\boldsymbol{V} $的集合, $ {\theta }^{\left(i\right)} $表示迭代前的参数, $E\left( {{\gamma _{ijk}}} \right)$是指在混合高斯模型中, 观测数据${p_{ij}}$来自于第k个高斯分布模型, 称为对第k个模型的响应度, 算法的E步求解具体为估计隐变量的期望值。Q函数被用于计算当前迭代的似然值, 也称为完全数据的对数似然, 通过最大化Q函数可以逐步优化模型中需要求解的参数, 直到收敛。

估计隐变量之后, 剩余部分参数只与样本有关, 此时算法进入M步的计算, 即通过最大似然进行估计, 在最大化模型参数$ \boldsymbol{\varPi },\boldsymbol{\varSigma } $和$ \boldsymbol{U},\boldsymbol{V} $之间进行迭代。将上述Q函数最大化:

其中, ${\theta }^{\left(i + 1\right)}$代表迭代后的参数, $ \boldsymbol{\varPi },\boldsymbol{\varSigma } $的迭代需对Q函数进行最大化, 以得到参数的求解公式, 即得到混合高斯模型中每一个高斯模型的方差与模型的混合系数。参数的迭代求解公式为

其中, $ {N}_{k}={ \sum }_{i,j\in \varOmega }E\left({\gamma }_{ijk}\right) $。对于$ \boldsymbol{\varPi },\boldsymbol{\varSigma } $的迭代即求解得到$ {\pi }_{k},{\sigma }_{k}^{2} $, 将其代入重新计算来进行$ \boldsymbol{U},\boldsymbol{V} $的迭代, 通过最大化下述方程来实现$ \boldsymbol{U},\boldsymbol{V} $的迭代求解:

其中

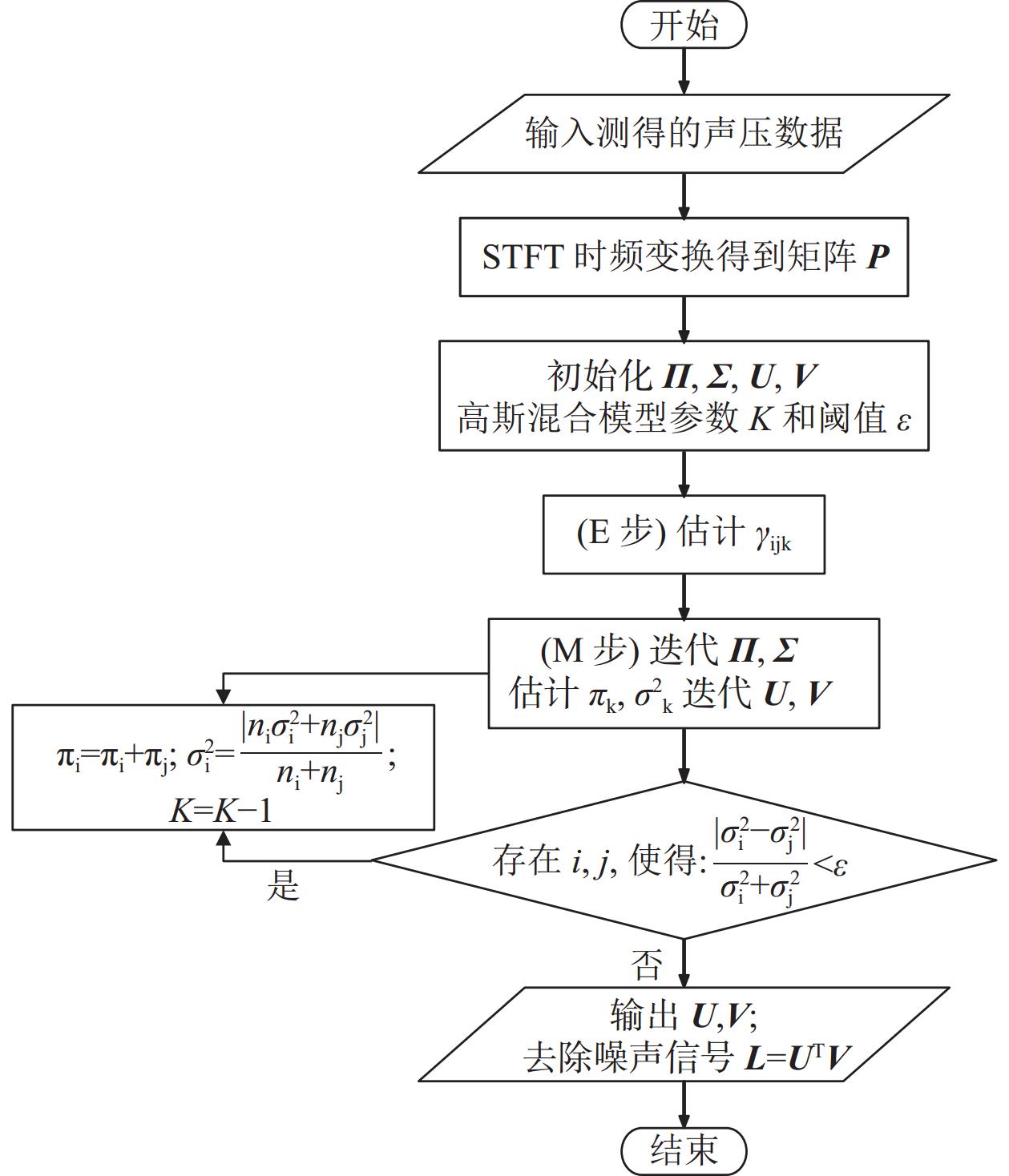
符号$ \odot $表示矩阵的Hadamard乘积, $|| \cdot |{|_2}$表示矩阵的$ {L}_{2} $范数。式(16)的求解可以通过交替最小二乘法(ALS)^[26]实现。在完成参数的闭式迭代求解之后, 再重建得到去除噪声之后的信号。

综上所述, 基于混合高斯模型的拖曳阵列流噪声抑制算法的整体流程步骤如图3所示。首先通过STFT将测得的声压时域数据转换到时频域, 并得到处理矩阵$\boldsymbol{P}$, 之后初始化$ \boldsymbol{\varPi },\boldsymbol{\varSigma } $和$ \boldsymbol{U},\boldsymbol{V} $等参数, 确定混合高斯模型个数与阈值, 对混合高斯模型中各个高斯分量选取分配权重。通过迭代$ \boldsymbol{\varPi },\boldsymbol{\varSigma } $计算$ {\pi }_{k},{\sigma }_{k}^{2} $从而进一步实现$ \boldsymbol{U},\boldsymbol{V} $矩阵的迭代, 直至满足迭代终止准则, 此时输出矩阵$ \boldsymbol{U},\boldsymbol{V} $, 最终得到重建信号$ \boldsymbol{L}= {\boldsymbol{U}}^{\rm T}\boldsymbol{V} $。

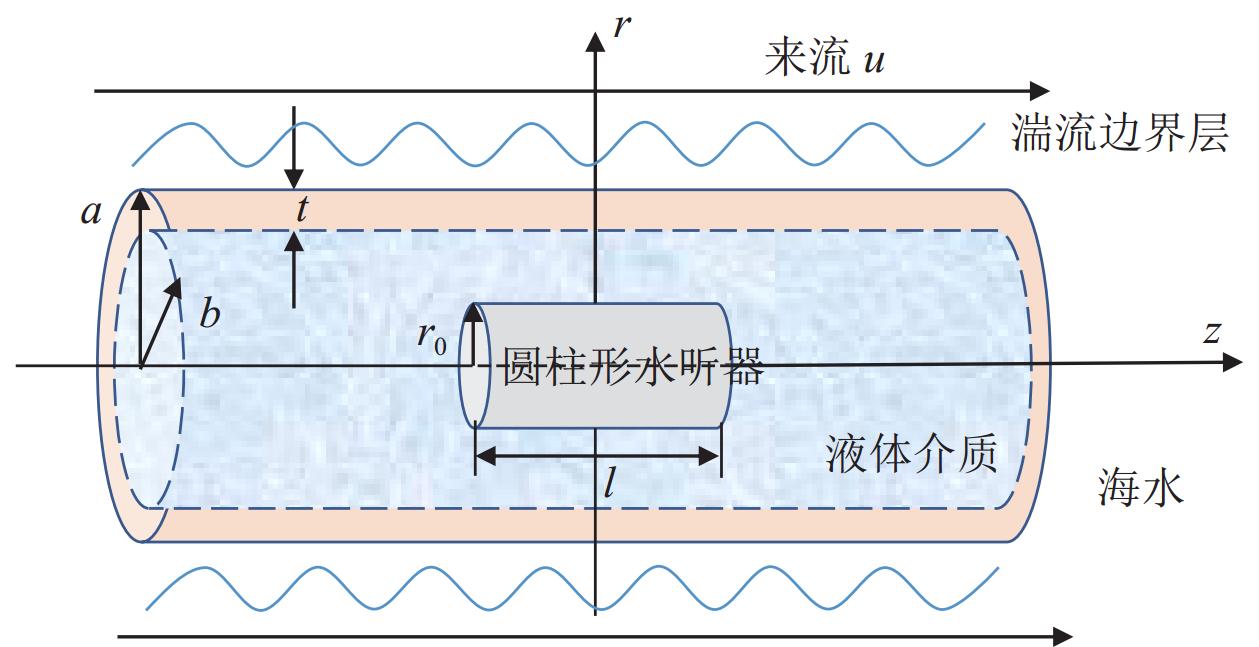
对含流噪声的谐波以及宽带信号进行仿真, 验证方法的有效性。采用拖曳阵列流噪声的自功率谱模型^[4]仿真流噪声信号。基于图4所示湍流边界层压力起伏激励圆柱壳内噪声场结构, 将模型简化为无限长弹性圆柱管, 即仅与纵向z及径向r相关的二维问题。

根据TBL压力起伏模型、护套传递函数模型以及由水听器形状得到的水听器函数等, 计算得到流噪声声压的自功率谱:

式中

是系统的波数−频率谱传递函数, $ {\varPhi _s}\left( {{k_{\textit z}},\omega } \right) $是TBL压力起伏的波数−频率谱, 其中$ k $为波数, $ \omega $为频率, $ {k}_{\textit z} $为z轴方向的波数, $ {k}_{1} $是对应管内流体介质中的波数, $ T(k,w) $为护套传递函数, 以圆柱形水听器为例, $ {r}_{0} $为水听器半径, b为护套内径, $ {\mathrm{J}}_{0}(\cdot) $为0阶Bessel函数, $ {a_p}\left( {{k_{\textit z}}} \right) = \sin \left( {{k_{\textit z}}l/2} \right)/({k_{\textit z}}l/2) $为单个水听器的波数响应函数, l为水听器长度。基于此模型, 已知拖曳阵护套表面TBL压力起伏的波数−频率谱和护套的传递函数, 即可得到压力起伏激励下的拖曳阵流噪声自功率谱。

采用基于细长圆柱体外表面TBL压力起伏理论模型^[2], 其中涉及的参数是由大量实验所得测量结果拟合而得。Carpenter压力起伏模型的波数−频率谱为

其中, R是圆柱护套的外径, $ {\rho }_{2} $为外部流体的密度, $ {U}_{c} $为迁移波数, 根据测量结果拟合得$ {U}_{c} $≈0.75U, U是自由流速, V_*为TBL剪切速度, V_*=0.04U。c, h, b可由实验数据测得, 王晓林等^[7-8]使用掌握的实验数据修正Carpenter压力起伏模型的参数, 本文采用修正后的参数, 具体见表1。

护套传递函数采用内部充液护套传递函数模型^[3],近似传递函数公式为

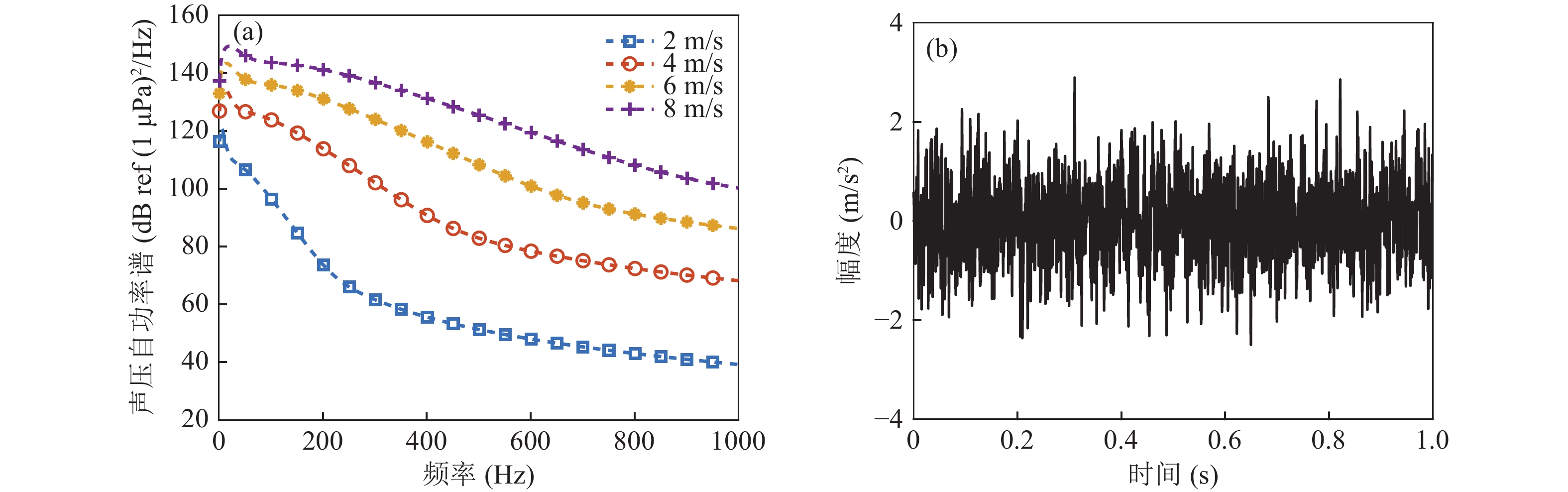
其中, k_b为呼吸波波数, 由此可得到拖曳阵列流噪声的自功率谱。图5(a)为此模型下得到的不同拖曳速度下(2 m/s, 4 m/s, 6 m/s, 8 m/s)拖曳阵列流噪声的自功率谱。选取拖曳速度为8 m/s的拖曳阵列流噪声自功率谱, 计算信号幅值并输入随机相位得到时域信号, 如图5(b)所示。由图5(a)可见, 随着频率的增加, 声压的自功率谱逐渐降低, 且在较低频段处下降速度较快。比较不同拖曳速度下的声压自功率谱也可以看出, 拖曳速度提高1倍, 声压的自谱值增加约20~40 dB。

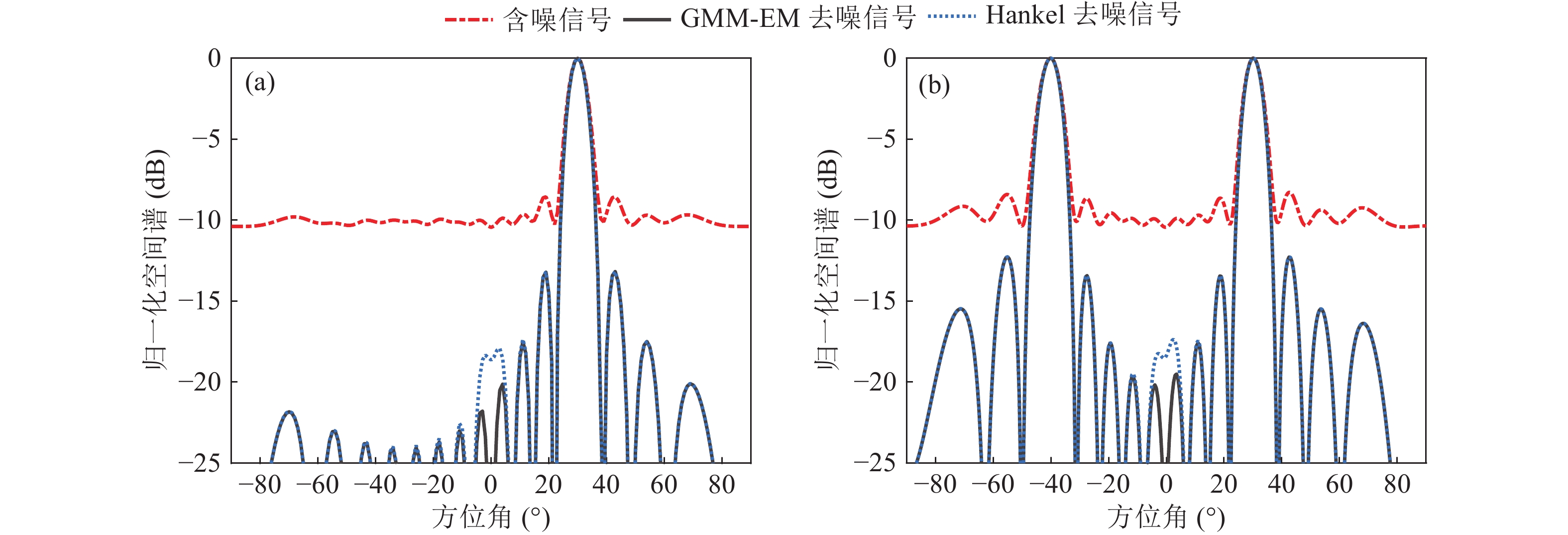
在上节所得拖曳阵列流噪声信号中添加不同频率的谐波信号, 用GMM-EM方法对含噪信号进行抑制处理, 再通过时域波束形成的目标方位估计方法验证噪声抑制效果。仿真中, 采样频率$ {f}_{s} = 4000$ Hz, 添加谐波信号信噪比$ {R}_{\text{SN}} = -5.85$ dB, 谐波信号频率分别设置为300 Hz, 500 Hz, 700 Hz, 900 Hz, 时域波达方向估计采用阵元数为8的均匀直线阵, 入射角度设置为30°的单入射角度和−40°, 30°的双入射角度两种情况。图6(a)为入射角度30°情况下含流噪声信号与经GMM-EM方法降噪后的信号分别做时域DOA的结果, 谐波信号频率为700 Hz; 并与Hankel矩阵降噪方法^[27]相比较, Hankel矩阵降噪方法通过SVD分解从谐波信号的Hankel矩阵提取特征向量以实现目标信号的重建。该方法被广泛应用于谐波信号的去噪。图6(b)为双入射角度−40°, 30°的仿真结果。

如图6所示, 在信号频率为700 Hz情况下, 经GMM-EM方法进行噪声抑制后的信号, 在单入射角度和双入射角度两种仿真条件下都能准确定位到目标, 且全角度背景级都能有效降低。对于单入射角度, 在不影响定位精度的情况下, 空间谱的背景级与含噪信号相比能够降低10~13 dB, 最大旁瓣级能够降低5 dB, 对于双入射角度, 背景级的降低也可达5~8 dB, 最大旁瓣级能够降低4 dB。而Hankel矩阵去噪信号的定位结果在多数角度虽也表现出更低的背景级, 但某些角度会出现错误的伪峰。其他谐波信号频率下的结果与图6类似。

采用信号噪声功率谱密度比来反映水听器接收信号中噪声的抑制情况:

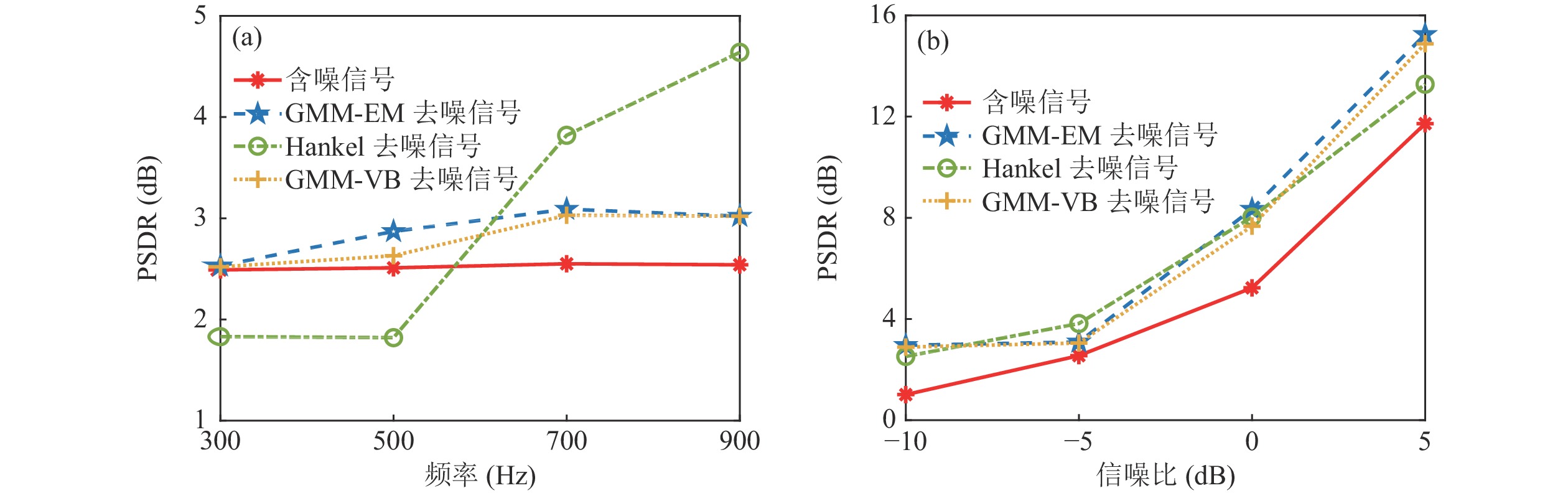
其中, PSDR表示信号噪声功率谱密度比, $ {\mathrm{P}\mathrm{S}\mathrm{D}}_{\mathrm{X}} $表示发射信号频率处信号的功率谱密度, $ {\mathrm{P}\mathrm{S}\mathrm{D}}_{\mathrm{N}} $表示流噪声所在低频频段内信号的功率谱密度。图7为不同目标信号频率以及不同信噪比下经各方法抑制前后的PSDR折线图。

图7(a)为仿真不同频率目标信号情况下的PSDR, 各频率下GMM-EM降噪处理后的信号噪声功率谱密度比均高于未经降噪处理的信号, 这表示接收信号中的噪声成分得到有效抑制, 且在高频段提升效果明显, 而GMM-EM方法与GMM-VB方法结果较为相近, GMM-EM在旁瓣抑制上效果稍好于GMM-VB。Hankel方法则会在高频段带来更好的提升, 而目标信号频率较低时噪声抑制效果较差。图7(b)为不同信噪比下的PSDR结果, 各抑制方法相较未降噪的信号均有一定提升, 并且随着添加目标信号信噪比的提高, 信号噪声功率谱密度比显著增大。

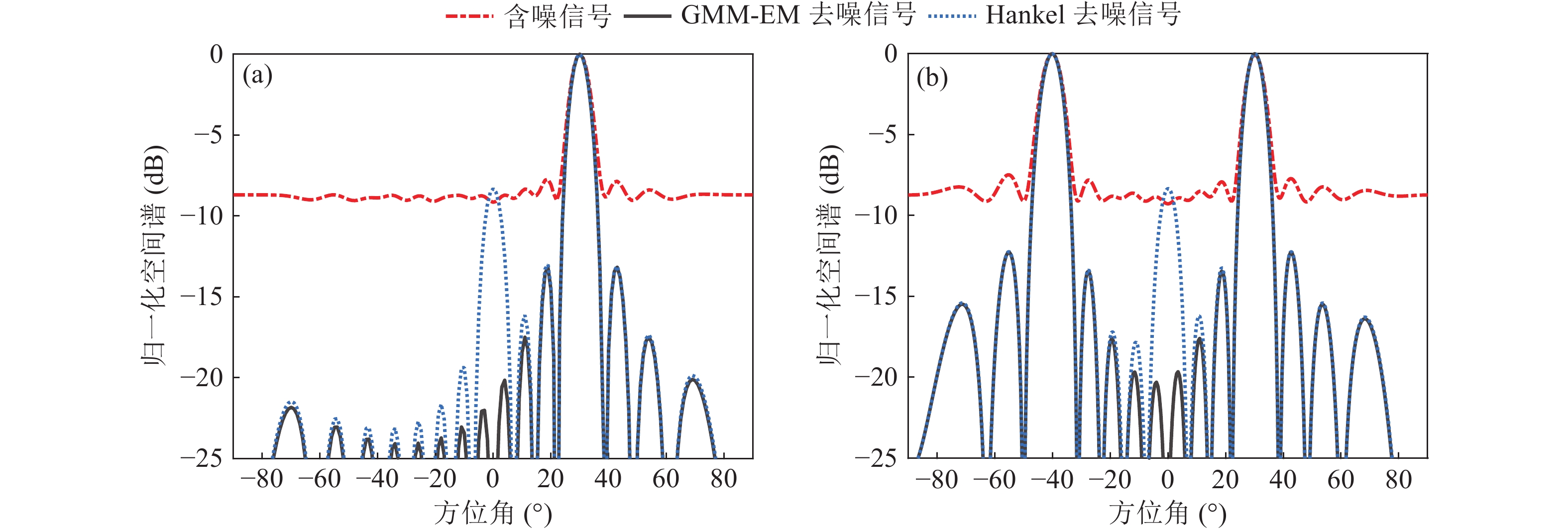
实际场景中多为宽带信号, 且信号频率可能存在于流噪声频段, 设置不同带宽和带宽频率的仿真信号, 以验证GMM-EM方法的有效性和实用性。仿真中, 采样频率${f_s}$=4000 Hz, 宽带信号频率分别设置为300~500 Hz, 600~800 Hz, 200~600 Hz, 500~900 Hz, 时域DOA采用阵元数为16的均匀直线阵, 入射角度设置为30°的单入射角度和−40°, 30°的双入射角度两种情况。图8(a)为入射角度30°情况下含流噪声信号与经GMM-EM方法降噪后的信号分别做时域DOA的结果, 并与Hankel矩阵去噪后的结果进行对比, 宽带信号频率为600~800 Hz。图8(b)为双入射角度−40°, 30°的仿真结果。

如图8所示, 在信号频率为600~800 Hz (其他频率结果类似)情况下, 经GMM-EM方法抑制噪声后的信号, 在单入射角度和双入射角度两种仿真条件下都能准确定位到目标, 且全角度其背景级都能有效降低。对于单入射角度, 在不影响定位精度的情况下, 空间谱的背景级与含噪信号相比能够降低10~15 dB, 最大旁瓣级能够降低10 dB; 对于双入射角度, 背景级的降低也能够达到5~10 dB, 最大旁瓣级能够降低8 dB。而Hankel矩阵去噪信号的定位结果在多数角度虽也表现出更低的背景级, 但在某些角度会出现更强的错误角度估计伪峰。由此可见, 本文方法可有效抑制拖曳阵列流噪声, 且显著提升拖曳阵列声呐定位目标的性能。

为验证所提方法在实际应用场景下的噪声抑制效果, 采用莫干山试验站湖试实验所得数据进行处理与分析, 包括不同拖速下的流噪声数据以及不同发射信号下的水听器接收数据。湖试实验的设置与工况如下: 载有拖曳阵列的船只静止于湖中, 通过船上电机设备设定收绳速度对连接的水下阵列进行拖曳, 载有换能器的船只距离拖曳船200 m时发射信号, 实验阵列共16个阵元。实验发射信号分别设置为单一谐波信号和带宽500 Hz的宽带信号, 拖曳速度分别设定为10 kn, 12 kn, 14 kn, 16 kn以模拟不同船速下的流噪声测定, 下述实验说明以及图片中涉及的具体频率信息均根据实验采样频率进行了归一化处理。图9为拖曳阵列探测湖试实验示意图。

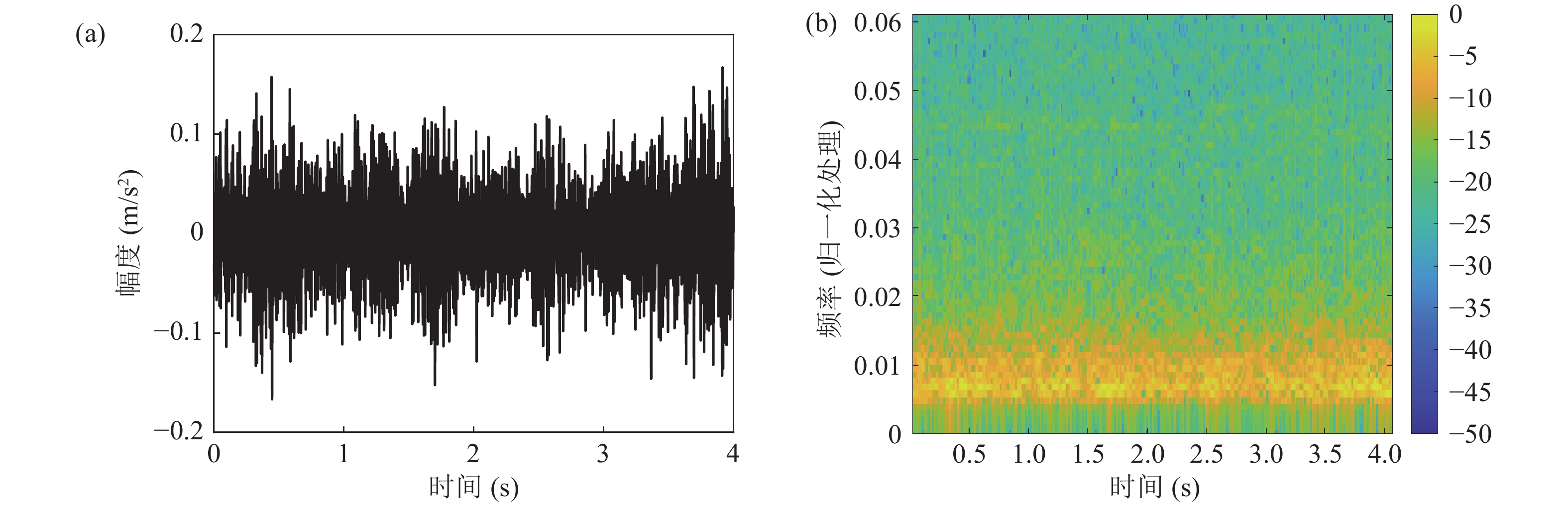
未发射信号时所测拖曳阵列噪声数据如图10所示。图10(a)是拖速为14 kn时实验测得的流噪声信号时域波形, 图10(b)是噪声信号的时频谱, 流噪声基本集中在低频范围附近。

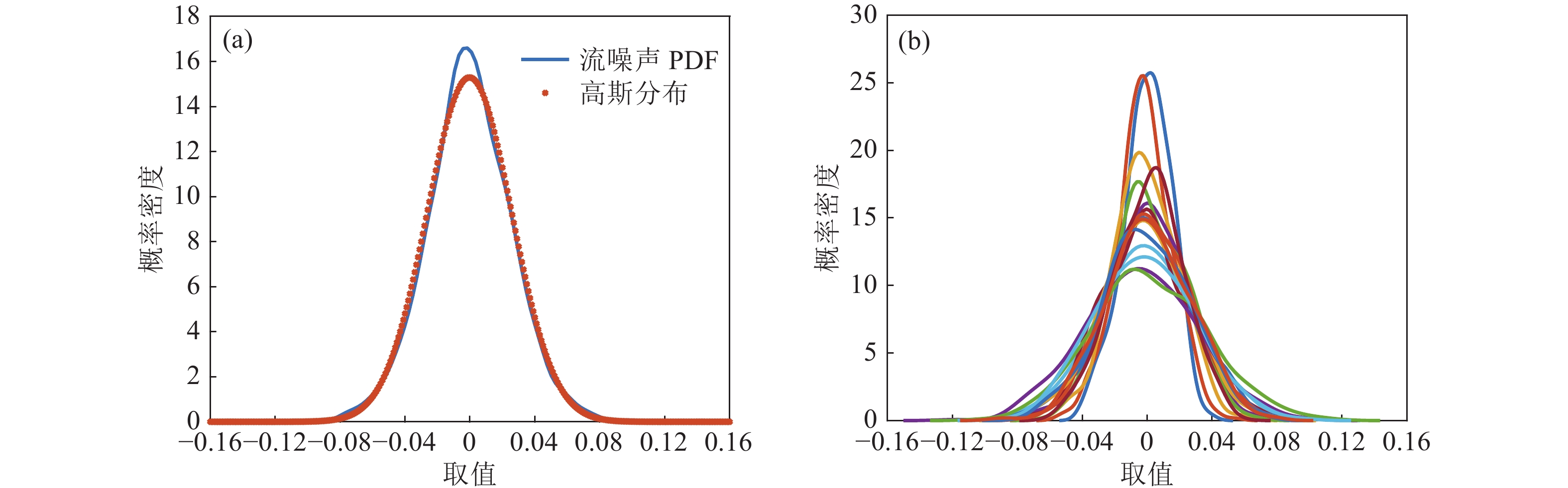
分析流噪声数据的非高斯性。对单通道噪声数据快拍矩阵的实部(虚部结果类似)进行概率密度函数(PDF)拟合, 结果如图11(a)所示, 实测流噪声数据的概率密度函数峰度高于高斯分布, 且较高斯分布更加陡峭。实验所有16通道噪声数据快拍矩阵的实部(虚部结果类似)概率密度分布函数的拟合结果如图11(b)所示, 不同通道的分布差异很大, 且存在数据分布偏离中心位置等复杂情况。通过计算实测信号的峰度与偏度来分析其是否满足高斯分布, 高斯分布峰度值应为3, 偏度值应等于0。分别计算16通道信号的峰度值与偏度值, 与高斯分布差异最大的通道信号峰度值低达1.82, 而不对称性最高的信号偏度值为0.97, 体现出明显的非高斯性。因此, 采用混合高斯模型拟合流噪声能够更加准确地考虑到流噪声的非高斯特性, 以及实际测量过程中通道之间噪声概率密度分布差异大的问题。

选取拖曳速度为14 kn, 发射信号为谐波信号的数据进行分析。处理的信号数据有65536个样本, 选取长度为1024个数据样本的汉明窗对每个通道的数据做STFT, 窗口重叠率为3/4, 得到的时频矩阵大小为513 × 253。将16个通道的时频矩阵拼接并转换矩阵的维度, 得到各频点的处理矩阵大小为16 × 253, 对每个频点的处理矩阵使用GMM-EM方法进行噪声抑制处理, 再改回通道数乘时频矩阵的形式, 最后对每个通道做ISTFT, 得到降噪处理后的时域信号。

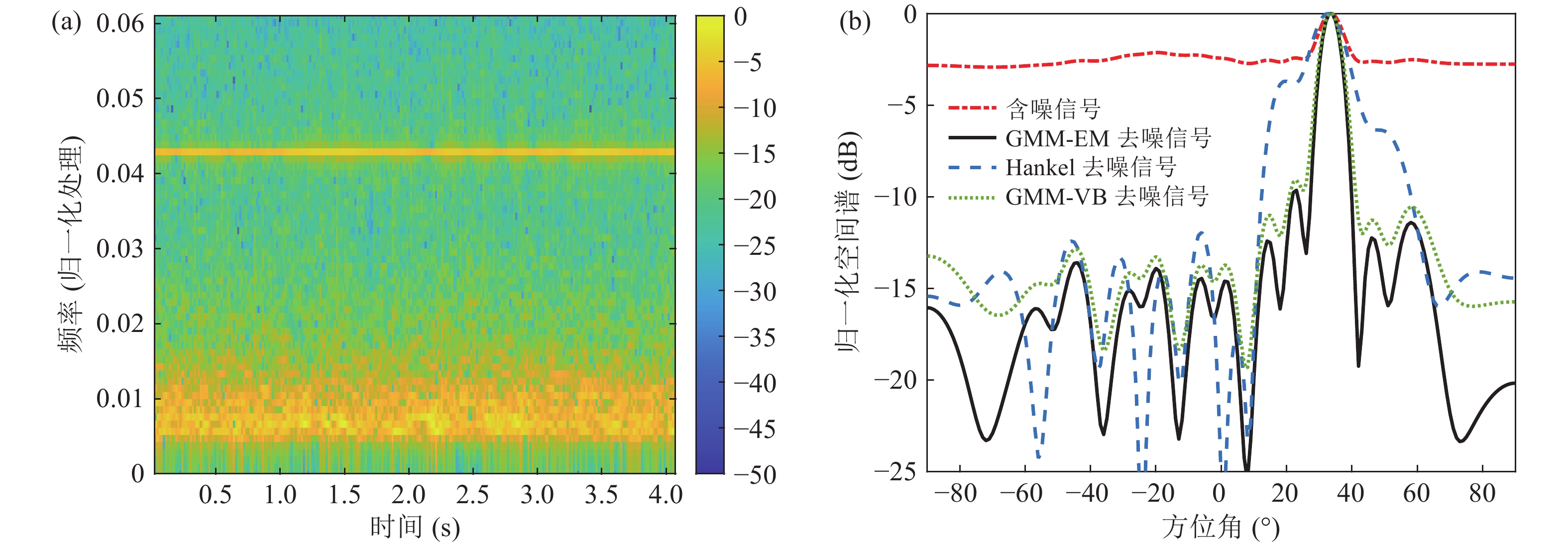
对测量信号做时频分析观察信号的时频特征。图12(a)为测量信号的时频谱, 其中谐波信号的信噪比较高。将处理前后的数据分别使用时域波束形成进行DOA估计, 通过定位结果验证本文方法对流噪声的抑制效果。湖试实验中, 声源静止而拖曳阵列不断移动, 声源相对于阵列的位置和角度随时间变化, 而本研究仅截取很短时间内的数据进行目标方位估计, 不考虑阵列的动态过程, 即本文的DOA估计不考虑多普勒效应的影响。图12(b)为测量信号经降噪处理前后的波束形成结果, 经GMM-EM降噪处理的信号, 在DOA结果没有发生偏移的情况下, 其最大旁瓣级能够有效抑制8~10 dB左右。GMM-EM方法与GMM-VB方法的结果较为相近, 但在某些方位角上的旁瓣级抑制表现更好; 而与Hankel矩阵降噪方法相比, 其在主瓣宽度减小的同时, 最大旁瓣级抑制效果能够提升2~5 dB左右。

表2为发射谐波信号时各方法抑制噪声后的信号噪声功率谱密度比。经GMM-EM方法抑制噪声后, 接收信号中信号噪声功率谱密度比从0.07 dB提升至3.04 dB, 与GMM-VB方法近似, 较Hankel方法提升更多。

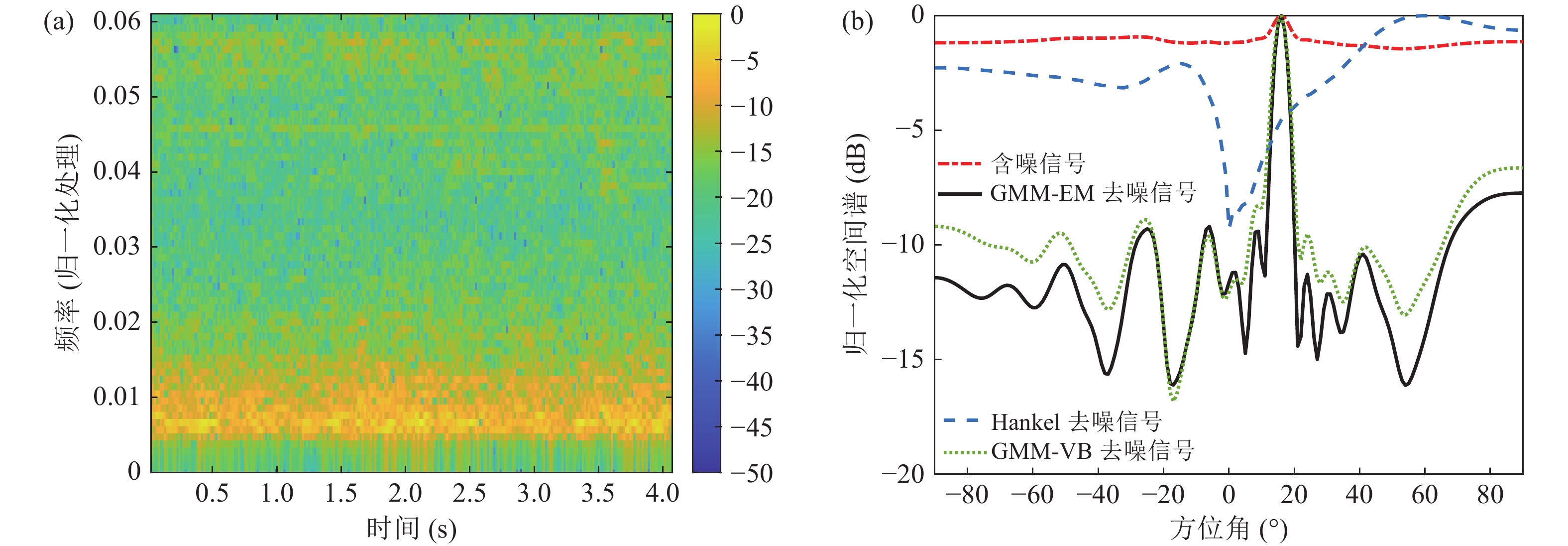
选取拖曳速度为14 kn, 发射信号为宽带信号的数据进行分析, 数据的时频转换和处理过程与发射谐波信号情况相同。图13(a)为测量信号的时频谱, 与发射信号为谐波信号的情况相比, 信噪比较低, 已无法准确分辨发射信号的频带范围。使用GMM-EM方法对测量信号进行噪声抑制处理, 再将处理前后的数据分别使用时域波束形成进行DOA估计。图13(b)为测量信号经降噪处理前后的波束形成结果。经GMM-EM方法降噪处理的信号, 在DOA结果没有发生偏移的情况下, 其最大旁瓣级能够有效抑制8~10 dB左右。并且在宽带信号情况下, 相较于GMM-VB方法最大旁瓣级抑制效果能够提升2~5 dB左右, 经Hankel矩阵降噪方法处理的信号已无法准确定位。

表3为发射宽带信号时各方法抑制噪声后的信号噪声功率谱密度比。经GMM-EM与GMM-VB方法抑制后, 接收信号中信号噪声功率谱密度比提升较大, 且PSDR值相近, 而Hankel方法在宽带信号的情况下未能有效抑制噪声成分。

综上可知, 在发射信号为谐波和宽带情况下, 所提方法均可有效抑制流噪声; 在低信噪比情况下, 经降噪处理后的信号定位效果显著提升。即所提方法能够实现实际拖曳阵列流噪声的有效抑制, 提升拖曳阵列声呐的定位性能。

利用阵列信号处理抑制拖曳阵列流噪声时, 由于TBL噪声特性与传播过程复杂, 难以准确建模与抑制。本文采用GMM的建模方法对拖曳阵列流噪声进行抑制处理, 利用流噪声的非高斯特性, 使用混合高斯模型对流噪声进行拟合。通过EM算法求解出混合高斯模型参数, 将流噪声部分从测量信号中分离。该方法解决了现有流噪声模型拟合不准确的问题, 发射信号为谐波信号和宽带信号时, 该方法均能有效抑制流噪声, 重建后的信号可实现目标的准确定位, 且最大旁瓣级可抑制8~10 dB。湖试实验进一步验证了所提方法的有效性, 该方法与GMM-VB方法的噪声抑制结果相近, 某些条件下抑制效果稍好, 但GMM-VB方法的求解速度更快; 与Hankel矩阵去噪方法相比, 该方法在发射谐波信号和发射宽带信号时均可实现流噪声的有效抑制。