声学方法测量海面波浪最早源于20世纪出现的声学波潮测量仪和多普勒声呐^[1], 使用声波测量重力为回复力的海洋表面波场中海面起伏和水体往复运动速度, 实现海面波浪参数估计。声学多普勒流速剖面仪(ADCP)综合运用声学多普勒测流速(测流)和声学表面跟踪测海表起伏(测高)进行海表波浪观测, 通过声束投射点组成的时间空间阵列估计海面波浪方向谱。海表波浪参数对水声学研究具有重要意义, 波浪谱可引入到环境噪声谱模型进行海洋环境噪声预报^[2]和垂直相关性研究^[3], 波浪方向谱可用于海面反射损失建模^[4]。

Haren^[5]使用坐底600 kHz ADCP测量海表波浪并估计风应力, 定义了海浪涂抹现象(wave smearing), 海洋表面层回声强度与波浪有效波高成反比, 次表层回声强度与海表气泡量有关且与有效波高成正比, 导致近表层流速测量方差较大, 海表位置估计误差等。 Wang等^[6]通过实验验证了表面波浪引起的气泡垂直分布对反向散射强度的影响。除了波浪参数相关的气泡层分布特性, 海表几何特征^[7]和ADCP声波束旁瓣反射能量^[8]也是影响声学表面跟踪准确度的两个重要因素。

由于ADCP倾斜波束测量海面起伏、水体沿波束流速时易受旁瓣能量干扰和近表层回声强度弱影响, 配置中间竖直波束的ADCP在波浪测量方面优势更强, 并被用于近岸波浪非方向参数和方向参数测量^[9-10]。按照波束配置, 测波浪ADCP有“4+1”波束基于声学流速法的Sentinel V 型ADCP和Signature1000型ADCP ^[11], “3+1”波束基于声学海表面跟踪方法(AST)的AWAC型ADCP。按照工作原理, ADCP波浪方向谱估计方法分为RDI的流速阵列法和Nortek的AST-UV法(属于单点三物理量法), 两种方法有着各自优势, 但都没有将“N+1”波束ADCP的: (1)中间竖直波束测高的高信噪比^[12], (2)倾斜波束阵列测点多、数据连续性好^[10], 这两方面优势充分结合。

已有研究中ADCP测波浪方法使用单测点多物理量或者多测点单物理量测量, 缺乏声学测高测流数据融合和分时采样阵列联合的方向谱估计研究。本研究提出空时联合的声学测高测流阵列海浪方向谱估计方法, 通过构建声学海表跟踪测高、声学多普勒测流的分时采样的空时联合阵列估计海浪方向谱。依据线性波浪理论和阵列测波时空等效原理, 引入时间空间传递函数和采样时延补偿项到数据协方差矩阵计算, 实现三维非同步采样阵列的等效二维同步采样阵列数据协方差矩阵重构。不同于波达方向估计中角度失配时波束域重构^[13]和空间谱加权迭代重构^[14], 本文方法属于建模法采样时延补偿的协方差矩阵重构, 能有效补偿采样时延、减小估计误差, 实现空时联合的声学测高测流阵列数据有效融合, 提升方向谱估计上限截止频率和准确度。

海洋表面波是重力为回复力的海水波动形式, 除一些海底地形突变和近岸斜坡导致的非线性情况外, 波高$h$与波长$\lambda $比值满足$h/\lambda < 0.05$的波浪可被视为线性波浪。海表波动引起海表起伏和水体往复运动是一个随机过程, 在典型波浪过程时间长度(一般小于3小时)内是广义平稳随机过程。Longuet-Higgins将海浪表面起伏$\zeta $模型化为随机过程^[15], 看作不同方向、不同周期、初相位$ {\varphi _{mn}} $不同且服从均匀分布、相互独立的子波双重叠加, 复函数形式表示为

其中, $M$为选定频段内子波频带划分个数、$N$为子波方向划分个数, ${a_{mn}}$表示在第$m$个子频带、第$n$个方向对应的离散化子波的幅值, ${{{\boldsymbol{k}}}_{mn}}$为子波波数矢量, $ {\varphi _{mn}} $为在$(0,2\pi )$上服从均匀分布的随机相位, $\omega = 2\pi f$为圆频率, ${a_{mn}}^2/2$描述子波能量, 从而可引入波浪频率方向谱:

其中, $ S\left( {{\omega _m},{\theta _n}} \right) $表示第$ mn $个子波分量的能量密度, 单位为${{\text{m}}^{\text{2}}}/\left( {{\text{Hz}} \cdot {\text{rad}}} \right)\;$。将式(3)代入式(1)后, 海表起伏可使用波浪频率方向谱描述为二重积分形式:

其中, $ {\omega _{\max }} $和$ {\omega _{\min }} $是海表风、涌浪的圆频率上下限, ${{\boldsymbol{k}}}$是含方向的波数矢量, ${{\boldsymbol{r}}}$是空间位置矢量, 不同水深或特征周期的波浪传播速度不同, 海表波浪呈现非线性的频散关系:

其中, $g$为重力加速度, $\gamma $为表面张力, $h$为水深, $\omega $为角频率, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. } \lambda }$为波数。ADCP观测对象风浪、涌浪的波长$\lambda \gg 5\;{\text{cm}}$, 表面张力作用可忽略, 频散关系简化为

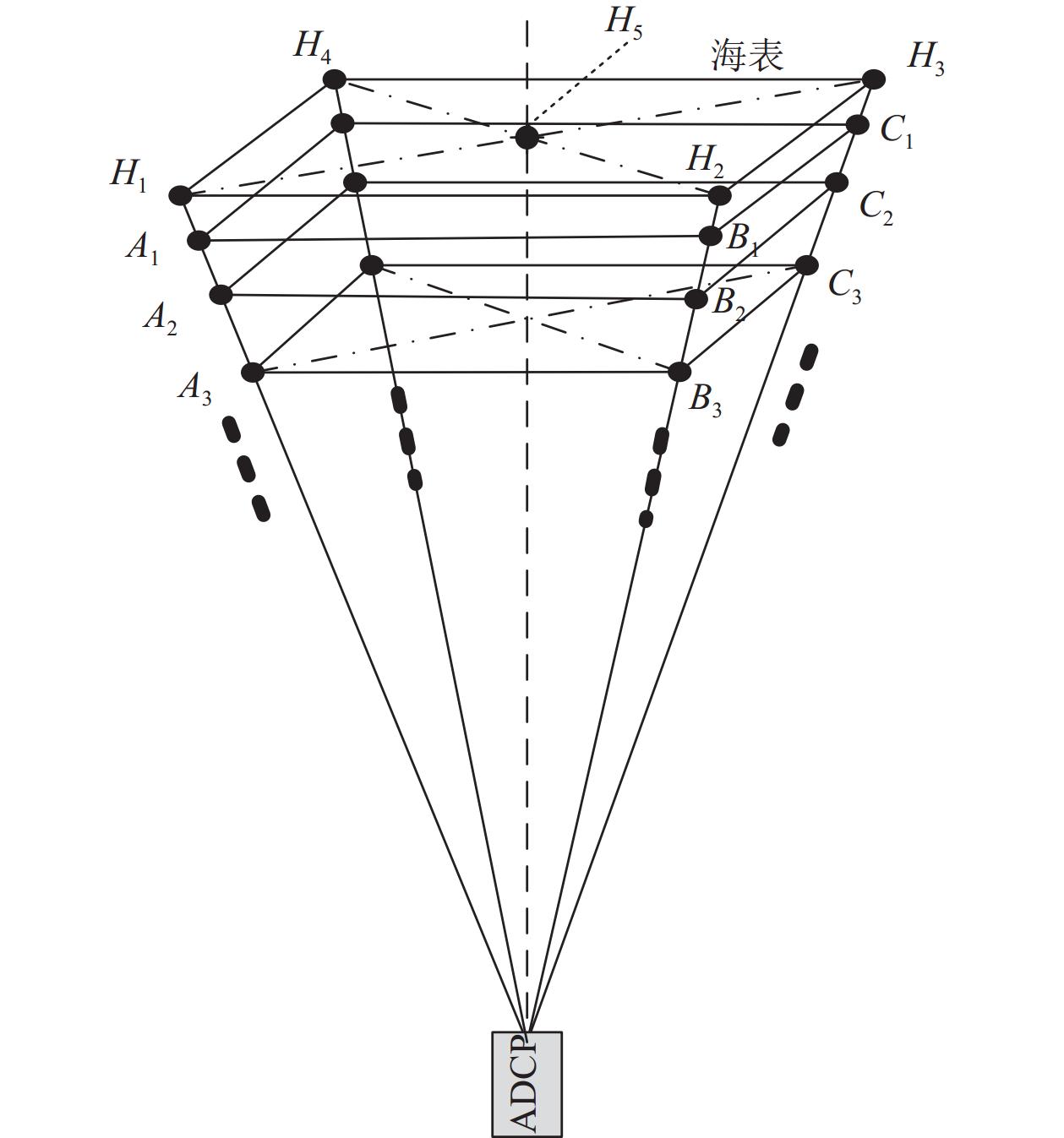
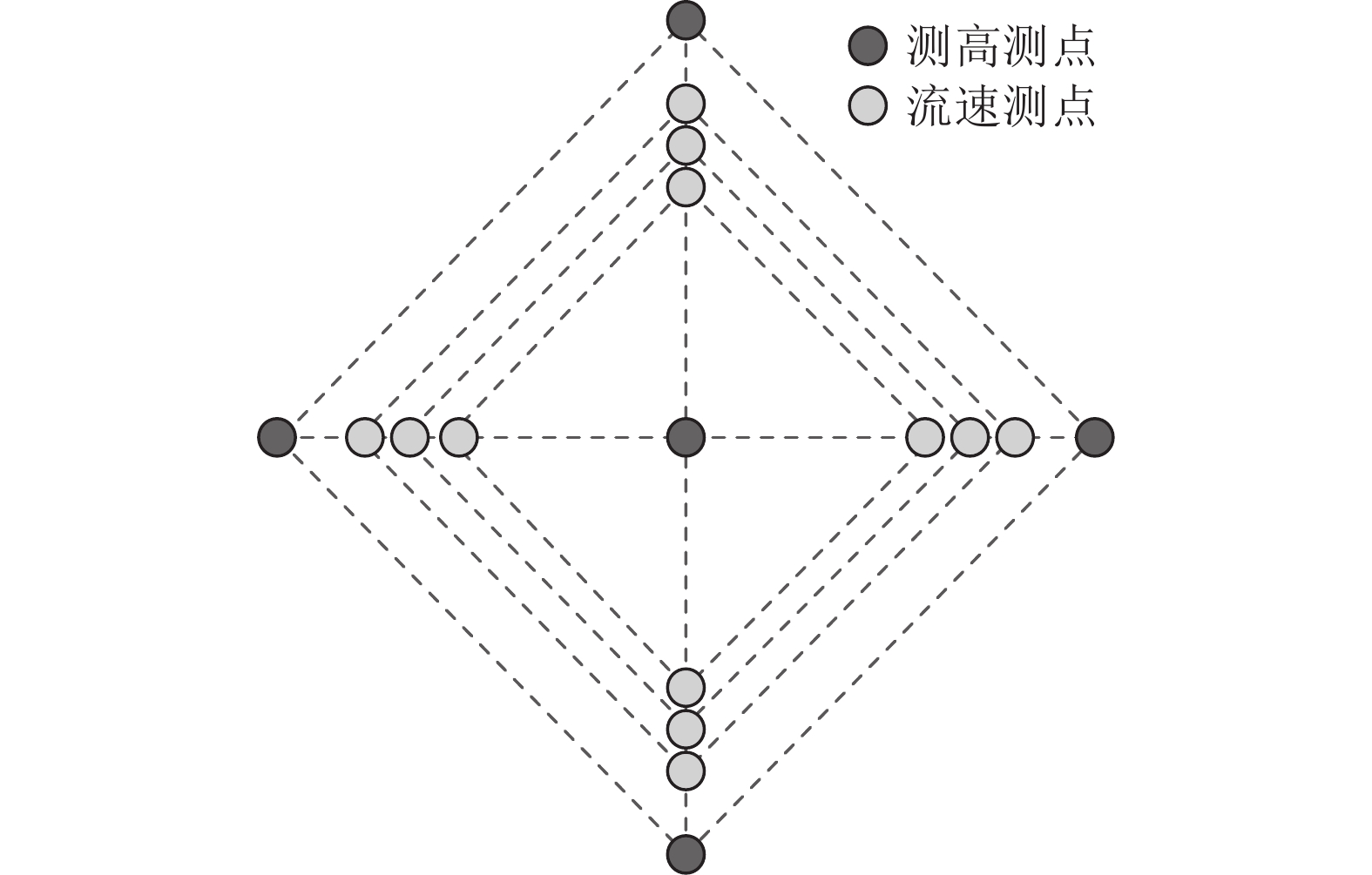
基于ADCP的海浪方向谱估计属于阵列法方式, 通过采集波浪场中的空间多点的多种物理量的时间序列, 图1为“4+1”波束ADCP测波浪的空间测点阵列在海面投影示意图。

假设相位随机, 任意两测点的海浪表面起伏测量序列的互相关函数:

其中, ${\eta _1}$和${\eta _2}$表示测点计数角标, ${\text{*}}$表示取共轭, 结合式(4)得到两测点测量序列的互谱$ {S_{{\eta _1}{\eta _2}}}\left( \omega \right) $和频率方向谱$ S\left( {\omega ,\theta } \right) $的关系:

ADCP测波阵列孔径尺度小于波长, 波浪传播衰减可忽略, 即海表各点的波面起伏数据自谱具有一致性可表达为${S_{\eta \eta }}\left( \omega \right){\text{ = }}S\left( \omega \right)$, 则互谱$ {S_{{\eta _1}{\eta _2}}}\left( \omega \right) $可与自谱$ {S_{\eta \eta }}\left( \omega \right) $、方向扩散函数$ G\left( {\theta ;\omega } \right) $ 建立联系:

其中, 方向扩散函数$ G\left( {\theta ;\omega } \right) $为方向分布函数$ g\left( {\theta ;\omega } \right) $与扩展因子的乘积, 满足$ S\left( {\omega ,\theta } \right) = S\left( \omega \right)G\left( {\theta ;\omega } \right) $和$ \int_{ - \pi }^\pi G \left( {\theta ;\omega } \right){\rm d}\theta = 1 $, 其中方向分布函数$ g\left( {\theta ;\omega } \right) $表征波浪能量分布, 典型如COS-2S型分布$ g\left( {\theta ;\omega } \right) = {c_N} \cdot {\cos ^{2s}}\left[ {{{\left( {\theta - {\theta _m}\left( \omega \right)} \right)} / 2}} \right] $, ${c_N}$为归一化系数, $s$为模型系数, ${\theta _m}$为平均方向。阵列孔径小于半波长, 忽略波浪传播的方向扩展, 即扩展因子取1。

不同测点间的互信息/互谱中可提取波浪方向信息, 对于海表起伏$\zeta $以外的其他物理量(如水体流速、压力等)的测量序列, 需要引入各测点的海表投影点表面起伏物理量$\zeta $到该测点的物理量$x$的传递函数$ T\left( \omega \right) = {{{\text{FT}}\left[ {x\left( t \right)} \right]} \mathord{\left/ {\vphantom {{{\text{FT}}\left[ {x\left( t \right)} \right]} {{\text{FT}}\left[ {\zeta \left( t \right)} \right]}}} \right. } {{\text{FT}}\left[ {\zeta \left( t \right)} \right]}} $, 并将方向$\theta $积分替换为含方向的波数矢量${{\boldsymbol{k}}}$积分, 则复合阵列中任意两测点${l_1}$和${l_2}$的任意物理量采样序列交叉谱$ {C_{{l_1}{l_2}}} $:

波浪方向谱(波数−频率谱)估计是式(10)的逆过程, 最大似然方向谱估计方法中, 连续积分可用有限累加近似, 方向谱估计式可表述为

其中, $L$元复合阵列数据的交叉谱$ {C_{{\eta _1}{\eta _2}}} $组成交叉谱矩阵$ {\boldsymbol{C}} \in {\mathbb{C}^{L \times L}} $, 任意物理量测点组成复合阵列的传递函数矩阵$ {\boldsymbol{T}} = \left[ {{T_1}, \cdots , {T_L}} \right] \in {\mathbb{C}^{L \times 1}} $, $K$为似然调节因子。

$ \widehat S\left( {{\boldsymbol{k}},\omega } \right) $的估计方法有多种: 速度快和稳定性好的最大似然法(MLM)及其扩展(EMLM)或迭代(IMLM)^[16], 精度高的贝叶斯估计(BDM), 还有扩展最大熵法(EMEP)、扩展本征矢法(EEV)、小波估计(WLM)等。最后, 使用波数−频率谱$ S\left( {{{\boldsymbol{k}}},\omega } \right) $计算频率−方向谱$ S\left( {\omega ,\theta } \right) $, 基于经典线性波浪理论或实际实验测量^[17]的海洋波浪频散关系:

典型“N+1”型五波束ADCP发射五个声波束, 对波束投射区域中海表到换能器距离或水体沿波束方向速度等物理量进行时间离散采样。如图2所示, H₁, H₂, H₃, H₄为倾斜波束测量海表起伏数据的测点, H₅为竖直波束测量海表起伏数据的测点, A_1~n, B_1~n, C_1~n, D_1~n为倾斜波束测量照射区域各层水体的沿波束方向速度测点, 以上测点构成了测量波浪场多种物理量的时间空间复合阵列。

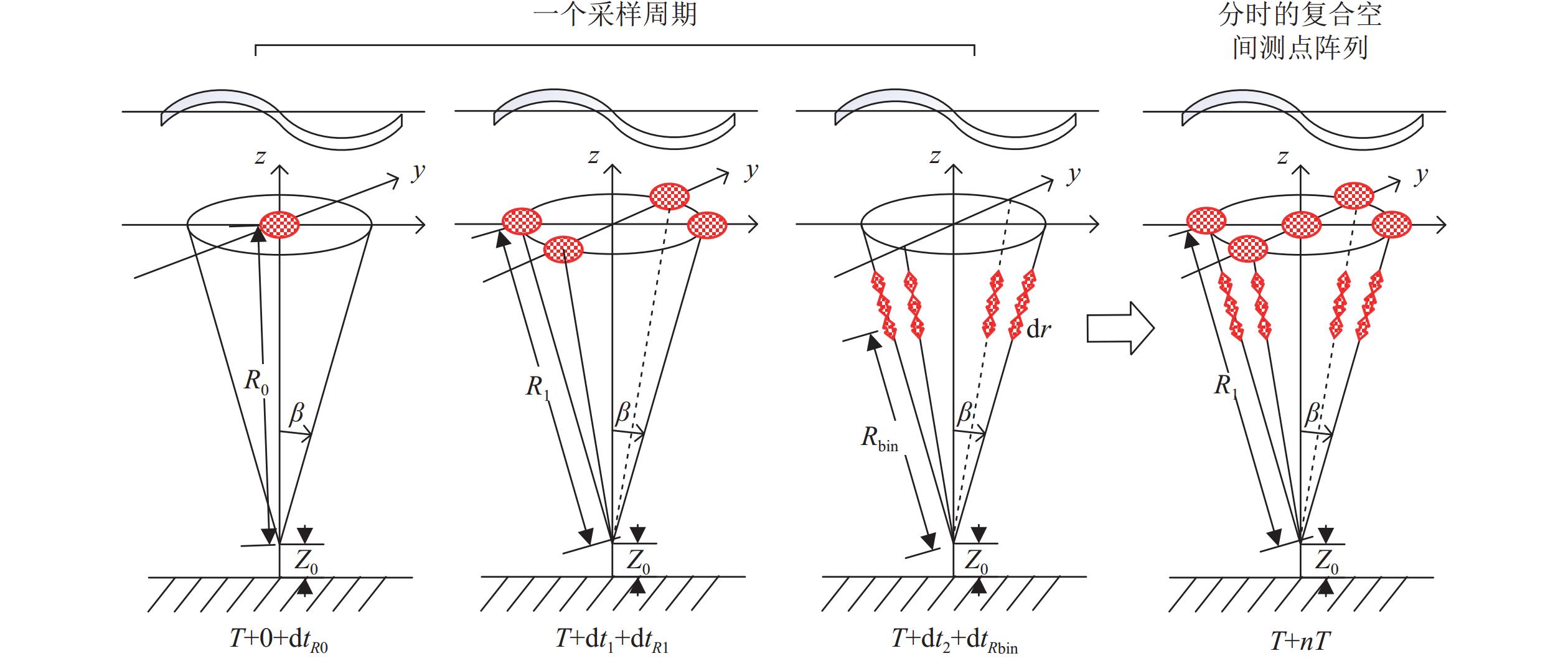
由于倾斜波束与竖直波束之间夹角较小, 同步工作时存在旁瓣直达波产生的相互影响(cross talk)^[18], 因此分时工作进行波浪场中物理量采样。并且, 由于海表和水体散射强度的巨大差异, 波面起伏和沿波束速度两种物理量测量也采用分时工作方式依次测量。每个采样周期内, 依次进行测海表起伏的竖直波束声脉冲发射接收、测海表起伏的倾斜波束声脉冲发射接收和测沿波束各层流速的倾斜波束声脉冲发射接收。由此构建五波束ADCP测量波浪物理场测量的空时阵列, 如图3所示, 其中$ R_0, \; R_1, \; R_{\rm bin} $分别为各物理量测点到ADCP换能器的声程, $ \mathrm{d}t_1,\; \mathrm{d}t_2$为声脉冲发射时间差, $ \mathrm{d}t_{R0}, \; \mathrm{d}t_{R1}, \; \mathrm{d}t_{R{\rm bin}} $为声传播时间。提出基于五波束ADCP声学海表面跟踪和声学多普勒测速的空时联合阵列波浪方向谱估计方法, 该方法的基本原理和主要步骤如下。

ADCP坐底向上观测海表, 以竖直波束向上投影到海表点为原点, 竖直向上为z方向, 建立三维空间坐标系, $g$是重力加速度值, $d$为观测点水深。测点坐标组成二维位置矢量${{{\boldsymbol{r}}}_{xy}}$, ${\textit{z}}$取正方向竖直向上, 海底为${\textit{z}} = - d$, 海面为${\textit{z}} = 0$。

根据式(1)可将波面起伏表示为

根据有限水深小振幅波动的运动方程组, 可计算速度势函数为

将频散关系式(6)变换形式:

其中, $\cosh $和${\rm{tanh }}$为双曲函数, 将频散关系变换式(15)代入式(14), 得到子波作用下的波场速度势函数:

对于波高测点, 特定的波数−角频率的子波能量对应的海表二维平面中波面起伏:

对于流速测点, 由式(16)可计算波数−角频率的子波对应波场质点水平和竖直运动速度:

由式(18)和式(19)可得倾斜波束测量的各层沿波束速度为

其中, ${\textit{z}}$为测点深度坐标值, $\alpha $为不同波束声波发射方向的方位角, $\beta $为倾斜波束的倾斜角, 传递函数$T$为时间无关变量, 空间传递函数, 记为${T_{\rm spat}}$, 离散化子波表述下, 满足$ {T_{\rm spat}}\left( {{\omega _n}} \right) \,=\, {{{\text{FT}}\left[\, {{u_{\rm Beam}}\left( t \right)} \, \right]} \,/\, {{\text{FT}}\left[\, {\zeta \left( t \right)} \,\right]}} = {{{\text{FT}}\left[ {{T_{\rm spat}}\zeta \left( t \right)} \right]} / {{\text{FT}}\left[ {\zeta \left( t \right)} \right]}} $, 据线性波浪理论的表面起伏−沿波束速度的空间传递函数$ {T_{\rm spat}} $:

其中, ${u_{{\rm Beam} - mn}}$为空时阵列测点处子波产生的轨迹流速沿波束分量, ${T_{\rm spat}}$为沿波束轨迹流速分量到竖直投影点波面起伏的空间传递函数, ${T_{\rm spat}}$的推导在Herbers^[19]的推导式基础上做了进一步深入, 并引入时间延迟项${T_\tau }$, 构建适用空时联合阵列的时空传递函数, 记为${T_{\rm spat - temp}}$。

在时间空间联合的复合空间测点阵列测量波浪中, 对于空时联合采样循环内各个物理量测量的时间延迟不同, 将时间延迟项${T_\tau }$加入到空间传递函数$ {T_{\rm spat}} $得到时空传递函数${T_{\rm spat - temp}}$, 用于不同物理量分时测量的时间联合补偿, 时延采样的倾斜波束上阵列测点获取的沿波束速度为

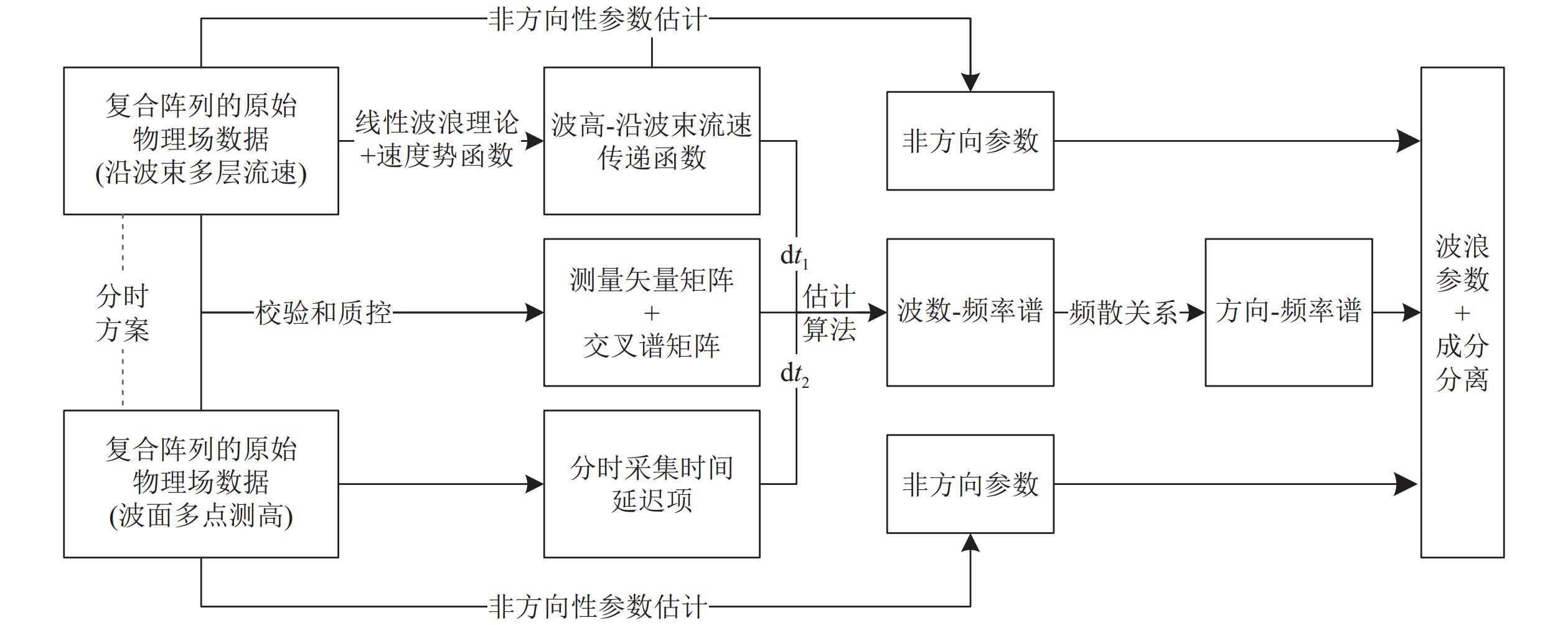
其中, $ \Delta t $为时延采样脉冲相对于首个脉冲的发射时间间隔, 取值为图3和图4中$ {\rm d}t_1, \; {\rm d}t_2 $, ${T_{\rm spat - temp}}$为波浪测量中的时空传递函数:

以式(21)—式(23)共同构建了不同物理量时间空间传递函数关系, 在采样矩阵协方差矩阵计算时, 使用时空传递函数关系可补偿时间延迟项, 减小方向谱估计误差。ADCP空时联合阵列海浪方向谱估计方法的主要步骤流程, 如图4所示。

由此, 空时联合的测高测流多参数的海浪方向谱估计过程可表示为

其中, ${\boldsymbol{A}} = \left[ {\exp \left( {{\rm i}{\boldsymbol{k}}{{\boldsymbol{r}}_1}} \right), \cdots ,\exp \left( {{\rm i}{\boldsymbol{k}}{{\boldsymbol{r}}_L}} \right)} \right]$为空间三维阵列投影到海表面二维阵列的导向矢量矩阵, 其中第$l$个测点投影点位置矢量$ {{{\boldsymbol{r}}}_l} = \left( {{x_l},{y_l},{{\textit{z}}_l} = 0} \right) $以阵列中心点为坐标原点, $ \oplus $为矩阵Hadamard积的计算符, 右上角标${\text{H}}$表示矩阵Hermitian共轭。$ {{\boldsymbol{T}}_{\rm spat - temp}} $为时间空间传递函数, $ {{\boldsymbol{C}}^{ - 1}} $是阵列数据交叉谱矩阵求逆, 本方法是迭代最大似然方向谱估计方法(IMLM)与基于频散关系建模采样时延相位补偿的结合, 关键在于构建了时间空间传递函数, 实现采样时间延迟项补偿和空间三维阵列到二维阵列映射, 形成对空时联合的测高测流复合阵列在波浪方向谱估计中时空耦合的解算。

使用靶谱划分网格子波叠加方法, 仿真数据包括倾斜波束测点波面起伏$\zeta \left( {x,y,{\textit{z}} = 0,t} \right)$、时延采样中间波束测点波面起伏$\zeta \left( {x,y,{\textit{z}} = 0,t + \tau } \right)$和各层沿波束速度${V_{\rm Beam - Bin}}\left( {x,y,{\text{z}},t} \right)$。仿真使用线性波浪理论线性叠加方法生成波面起伏数据和水体流动数据, 叠加潮位、潮流变化和测量噪声, 生成仿真的ADCP测波原始测量数据, 测高测流偏差^[20]和潮位潮流变化一般在数据预处理中作为固定偏差和线性趋势被去除。

基于窄带假设, 将有限带宽且一定方向扩展的海表波浪场看作多个不同方向和频率的远场窄带子波的叠加, 阵列有L个测点, ADCP测波应用中L等于4, 5, 12, 13等, 每测点采集数据长度为${N_{\rm data}}$, 即每组测量原始数据包含$L \times {N_{\rm data}}$的阵列数据。

第$l$测点时间序列数据为

其中, $m$和$n$是频率和方向划分的下标, $l$为测点序号, t是指复合阵列单帧采样时间点, $ {a_{mn}} $为子波在该测点的幅值, $ {T_l} $为第$l$测点的海表投影点表面起伏物理量到该测点的物理量的传递函数, ${{{\boldsymbol{r}}}_l}$为第$l$测点的相对参考原点的二维位置矢量, $ {\varphi _{mn}} $为各子波的随机初相位, ${\varepsilon _l}$为第$l$测点的相位随机的高斯白噪声。为简化问题, 基于窄带假设取${F_i}$频带进行分析, 原始测量数据时间序列可表示为

其中, X为阵列数据, ${\boldsymbol{X}} \in {\mathbb{R}^{L \times {N_{\rm data}}}}$, $s\left( {t;\theta } \right)$表示各方向的子波引起阵列原点处波面起伏的时间序列, $T$为时空传递函数, ${{\boldsymbol{k}}}\left( \theta \right)$为二维空间各方向子波的波数矢量。

对于典型“4+1”波束ADCP在波浪观测时, 4个倾角$\beta $的倾斜波束与1个中间竖直波束采样周期内小时延伪同步发射, 即非同步采样时间差$\tau $小于循环采样周期$ {T_{{\text{sample}}}} $。各波束在海表测高点和水体测流速对海表投影点组成了十字型复合测波阵列, 阵列空间导向矢量矩阵A和采样时间延迟项$ {{\boldsymbol{T}}_\tau } $、空间传递函数$ {{\boldsymbol{T}}_{\rm spat}} $组合计算。对于频点${f_0}$、入射方向${\theta _0}$的子波方向谱值为$S\left( {{f_0},{\theta _0}} \right)$, 使用原始阵列数据的协方差矩阵估计值R, 经过时空传递函数计算映射构建的二维等效阵列的数据协方差矩阵估计值$ {{\boldsymbol{R}}_{\rm spat - temp}} $, 表示为

仿真研究中, 复合阵列模型的假设条件:

(1)复合阵列采集了三类物理量, 测量噪声水平有差异, 结合理论和实际观测设定;

(2)不考虑因波束一致性差异导致的同类测点噪声不一致性, 即同类物理量测点测量数据噪声水平相同;

(3)不考虑阵列各测点的声学表面跟踪测量波面起伏数据中空间相关噪声, 源于声波束与方向性海表起伏相互关系导致的测量误差周期性变化。对于阵列空间相关噪声影响下的方向估计, 文献[21]给出了一种可行计算方法;

(4)忽略竖直声速剖面差异导致的空间测点位置误差, 即阵列孔径扩张和收缩的影响。

结合海试数据特点仿真坐底上看式ADCP观测海浪, 构造具有一定方向扩散度和符合实际观测实验数据信噪比水平的采样数据。为简化问题, 仿真实验不引入海浪物理场中潮、流、湍、波相互作用影响及这类影响下频率方向谱重映射修正问题。

仿真模拟水深20 m条件下, 倾斜波束倾角为20°的五波束ADCP坐底向上发射声脉冲进行波浪观测, 换能器距底0.8 m, 模拟观测对象波浪的有效波高为1 m, 峰值周期为4 s, 该水深条件下海浪特征波长约为25.0 m, 五波束ADCP各个波束在海面投影点组成的阵列的声学表面跟踪测波面起伏的阵列特征孔径为7.0 m, 声学多普勒测量次表层流沿波束流速的阵列特征孔径为7.7 m, 满足阵列孔径小于观测目标半波长的准则。

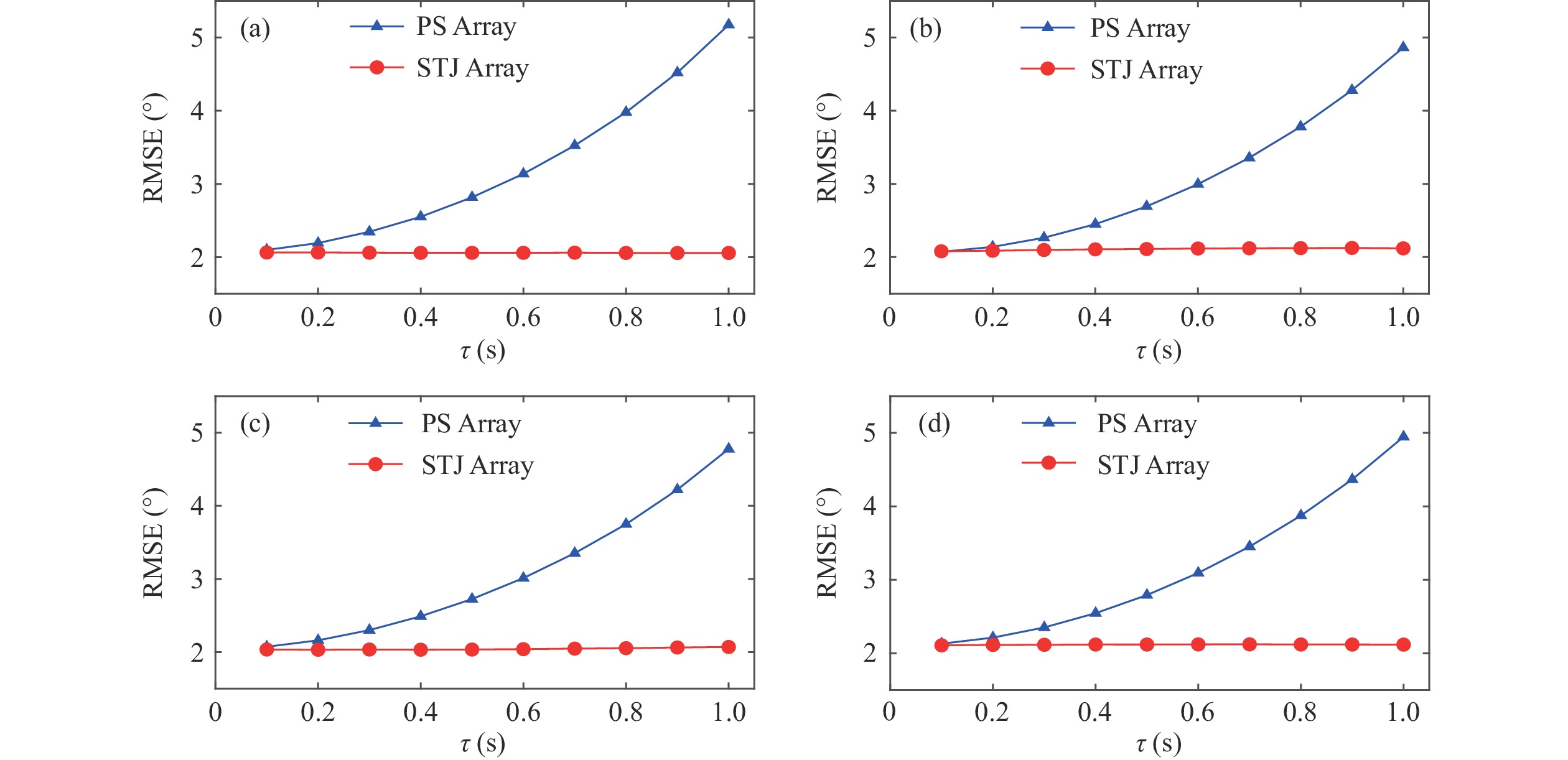
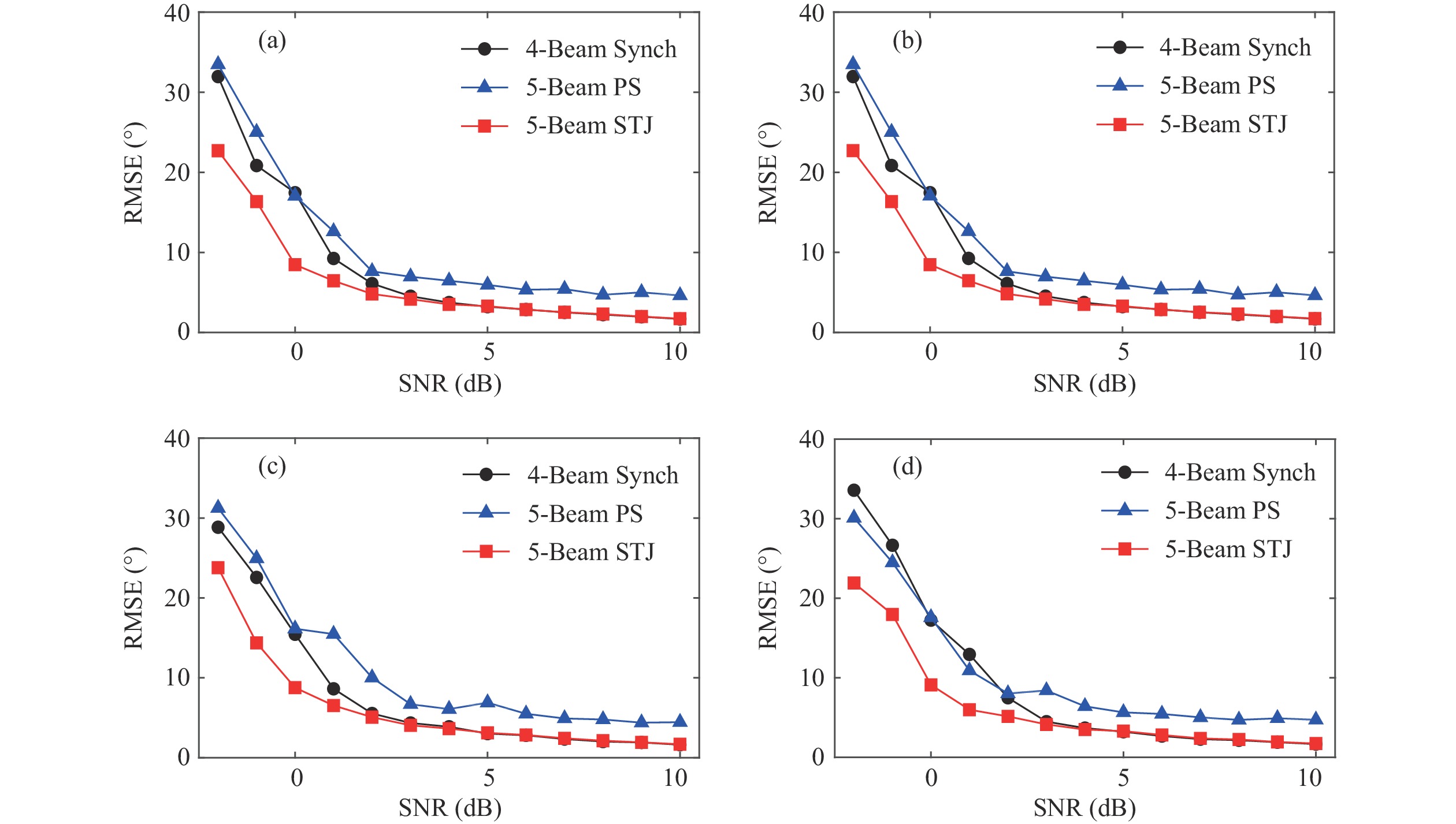
仿真1: 分析方向谱峰估计误差与采样时延$\tau $的关系。根据时空等效性和空间“采样定理”的防混叠条件, 采样时延值满足$\tau < {{{T_{\rm cut}}} / 2}$, 其中${T_{\rm cut}}$为可估方向谱的最短波周期。实际应用中, 采样时延值限制为$ \tau < {{{T_{\rm sample}}} / 2} < \left( {{{{T_{\rm cut}}} / 2}} \right)/2 $, 其中$ {T_{\rm sample}} $为采样周期。仿真数据信噪比设定为带内信噪比0 dB, 采样时延取值0.1~1.0 s、步长0.1 s, 目标波浪的谱峰周期${T_p}$为4 s, 数据采样率为4 Hz, 采样长度足够长为4096 s。五波束采样时延无补偿的方法, 属于一类伪同步阵列(PS Array), 五波束采样时延有补偿方法为空时联合阵列(STJ Array), 均使用五点波高数据, 相同的反演方法、频点划分、迭代次数等参数设置下, 500次仿真结果统计波浪方向谱的谱峰方向估计值${\widehat D_p}$均方根误差(RMSE)随采样时延的变化, 如图5所示。根据五元十字阵列的对称特点, 只需分析$\left[ {0\text{°},\;45\text{°}} \right]$入射方向, 因此仿真设定波浪入射方向分别为0°, 15°, 30°, 45°。

仿真1中采样点数足够长, 其估计结果的均方误差(MSE)可表征此仿真条件下方向估计方差水平, 最大似然方向估计方法(IMLM)的测量方差$ {{\mathrm{var}}} \left( {{\theta _k}} \right) \propto {1 \mathord{\left/ {\vphantom {1 {{{\text{N}}_{{\text{data}}}}}}} \right. } {{{{N}}_{{\text{data}}}}}} $, 由此可进一步估计快拍数更短时方向谱峰估计误差量级。

由图5可知, 采样时延补偿的空时联合阵列法能取得较好时延补偿效果, 在采样时延记录准确时, 方向谱谱峰估计值的RMSE几乎不随时延值变化。伪同步阵列法没有进行采样时延补偿, 方向谱谱峰估计值的RMSE会随采样时延值增大而增大, 采样时延$\tau {\text{ = }}{T_p}/4$时, 方向谱参数${\widehat D_p}$的RMSE达5°。在估计误差的方向差异方面, 由图5(a-d)对比可知, 对于此类等效二维阵列使用IMLM方法估计二维方向谱, 带内信噪比0 dB条件下, 入射方向不同时, 方向谱谱峰估计值的RMSE差异性较小。

仿真2: 分析方向谱峰估计误差与数据信噪比的关系。仿真波浪峰值周期${T_p}$设定为4 s, 中间波束测高采样时延设为$ \tau = 0.5{\text{ }}{\mathrm{s}} $。仿真参数: 循环采样率为$ {F_s} = 2{\text{ Hz}} $, 采样长度1024 s, 中间竖直波束测表面起伏的噪声水平比倾斜波束低2.5 dB^[22]。仿真2数据使用三种方法处理: (1) 同步四波束阵列法(4-Beam Synch), 使用4个倾斜波束的波高测点组成同步阵列; (2) 五波束伪同步阵列法(5-Beam PS Array), 使用1个中间波束的波高测点和采样时延的4个倾斜波束的波高测点, 无采样时延补偿, 组成伪同步阵列; (3) 五波束空时联合阵列法(5-Beam STJ Array), 使用1个中间波束的波高测点和采样时延的4个倾斜波束的波高测点组成空时联合阵列。

评价指标使用反演估计所得方向谱的谱峰方向${\widehat D_p}$与预设真值${D_p}$之差作为估计误差, 对比三种阵列方法的结果, 统计500次仿真结果方向谱的谱峰方向估计值${\widehat D_p}$均方根误差(RMSE)随信噪比的变化, 如图6所示。

由图6可知: (1)中间波束测高采样时延$\tau = 0.5{\text{ s}} = {T_p}/8$, 频带内信噪比(SNR)为3 dB时, 五波束伪同步阵列法(5-Beam PS Array)无采样时延补偿, 方向谱谱峰估计值${\widehat D_p}$的RMSE大于8°; (2)采样原始数据带内信噪比范围0~5 dB对应小波浪条件下, 五波束空时联合阵列法(5-Beam STJ Array)方向谱谱峰估计值${\widehat D_p}$的均方根误差更小。

使用中国科学院声学研究所国产自研的五波束IOA Wave ADCP进行了波浪水池测试和多次海上波浪观测试验, 为验证实际数据处理中空时联合阵列法的方向谱估计性能, 选取水深较深、波浪能量分布范围较宽的2020年威海市褚岛北侧的国家浅海海洋综合试验场的30 m水深水域五波束ADCP坐底上看式测波浪的海试数据进行分析。

海试中波浪测量ADCP的配置、应用环境参数和阵列特征等参数如表1所示。将实验场台站波浪浮标作为参照的标准仪器, 浮标测量结果显示实验期间波浪条件: 最大有效波高为2.8 m, 波浪谱峰周期2.8 s至8.0 s, 方向为0°~360°分布。

海试数据处理中, 使用两项检验指标评价空时联合阵列法的测波向性能。

检验1: 方向谱峰度。由于实地海试缺少标准的方向谱真值, 且不同仪器间固有偏差无法确认, 因此对比反演参数配置相同条件下不同阵列方法的方向谱结果, 选用方向谱峰方向$ {D_P} \pm {45\text{°} } $范围内谱值的kurtosis峰度$ {K_s} $用于评价方向谱的集中度。同类估计方法, 相同的参数和迭代次数设定下, 方向谱峰度越高, 说明估计方法的精度越好^[23]。

检验2: 方向谱谱峰方向结果序列相关系数检验。不同阵列方法在相同反演参数配置时谱峰方向${\widehat D_p}$与台站波浪浮标${D_p}$估计结果做相关性分析, 计算结果序列相关系数:

其中, $ \sigma $表示序列标准差, $ {\rm cov} $表示两序列的协方差。同类估计方法, 相同的参数和迭代次数设定下, 相关系数越大, 说明估计方法的准度越好。

海试数据信噪比水平主要随波浪有效波高H_s增大而增大, 将所有测次按有效波高H_s划分为四组进行横向对比。海试数据使用三种方法处理: (1)同步四波束阵列法(波高), 使用倾斜波束的4个波高测点; (2)同步四波束阵列法(流速), 使用倾斜波束的同层4个流速测点; (3)五波束空时联合阵列法, 使用1个中间波束的波高测点和采样时延的4个倾斜波束的波高测点组成空时联合阵列。

海试原始数据统计表明, 该海试环境、布放方式和仪器状态条件下, 观测波浪有效波高越大, 观测序列噪声强度增长速率显著小于观测序列强度增长速率, 即ADCP测波原始数据带内信噪比水平是随着波高增大而增大。首先, 对比不同阵列方法估得的方向谱峰度, 证明空时联合阵列在精度方面的相对优势。

由表2可知, 空时联合阵列法得到的方向谱相比于同步四波束阵列法(波高)、同步四波束阵列法(流速), 方向谱峰度相对更高, 从2.21提升至2.80。由于空时联合阵列方法增加了中间波束测高的1个测点, 并且联合了该测点的高质量数据, 因此在不同信噪比条件下均表现出相对优势。

由于波浪浮标原始测波数据类别和方向谱估计原理均不同于ADCP, 无法直接将ADCP估计波浪方向谱与浮标方向谱进行对比, 因此选用谱参数中谱峰方向${D_p}$序列用于相关性检验。将IOA Wave ADCP测波数据使用三种方法进行方向谱反演, 提取${D_p}$序列与实验场台站波浪浮标测波结果${D_p}$序列进行对比。作为参照的浮标测波结果序列被认为全部有效, 因此两者测波结果进行全部组次的相关性分析。

对于周期为4 s、有效波高为0.35 m的实验期间典型小波浪, 原始数据的信噪比估计: IOA Wave ADCP测波时, 测流速层厚为1 m时单ping测流误差的标准差约为7 cm/s, 实验数据统计倾斜波束声学表面跟踪的单ping测高误差的标准差为10 cm, 理论海表起伏序列标准差${\sigma _\zeta }$约为9 cm, 计算式${\sigma _\zeta } \approx {{{H_S}} \mathord{\left/ {\vphantom {{{H_S}} 4}} \right. } 4}$, 次表层波生往复流速序列标准差$ {a_{v - {\rm beam}}} $约为7 cm/s, 计算式为$ {\sigma _{v - {\rm beam}}} = {{\rm sqrt}({a^2}_{u - H}{{\cos }^2}\beta + {a^2}_{u - V}{{\sin }^2}\beta )} / {{\rm sqrt}\left( {a_\zeta ^2} \right)}\cdot {\sigma _\zeta } $。数据采样率约为方向谱分析带宽的4倍, 由此有效波高为0.35 m的实验期间典型小波浪, 阵列数据的带内信噪比估计范围为5~6 dB。因此选择H_s <0.35 m作为小波浪划分范围, 对应阵列数据带内信噪比水平小于6 dB。

三种阵列方法计算${D_p}$序列与浮标结果${D_p}$序列的相关系数结果如表3所示, 在H_s ≥ 0.35 m条件下, 五波束空时联合阵列法与同步四波束阵列方法, 计算得到方向谱谱峰方向D_p结果序列与波浪浮标D_p结果序列的相关系数相差较小, 两种方法性能相当。H_s < 0.35 m条件下, 相对于同步四波束阵列法, 五波束空时联合阵列法估计结果D_p序列与波浪浮标D_p序列相关系数从0.80提升至0.83, 即小波浪条件下五波束空时联合阵列法的方向谱估计准确度相对更高。

基于波浪频散理论和阵列最小孔径小于等于半波长准则, 可计算不同水深下, 四波束阵列和五波束阵列的测波截止频率上限, 如表4所示。对于超出截止频率上限的波浪谱段, 虽然可以估计方向谱, 但在主峰方向关于测量位矢线的对称方向, 会出现方向谱估计能量泄露。

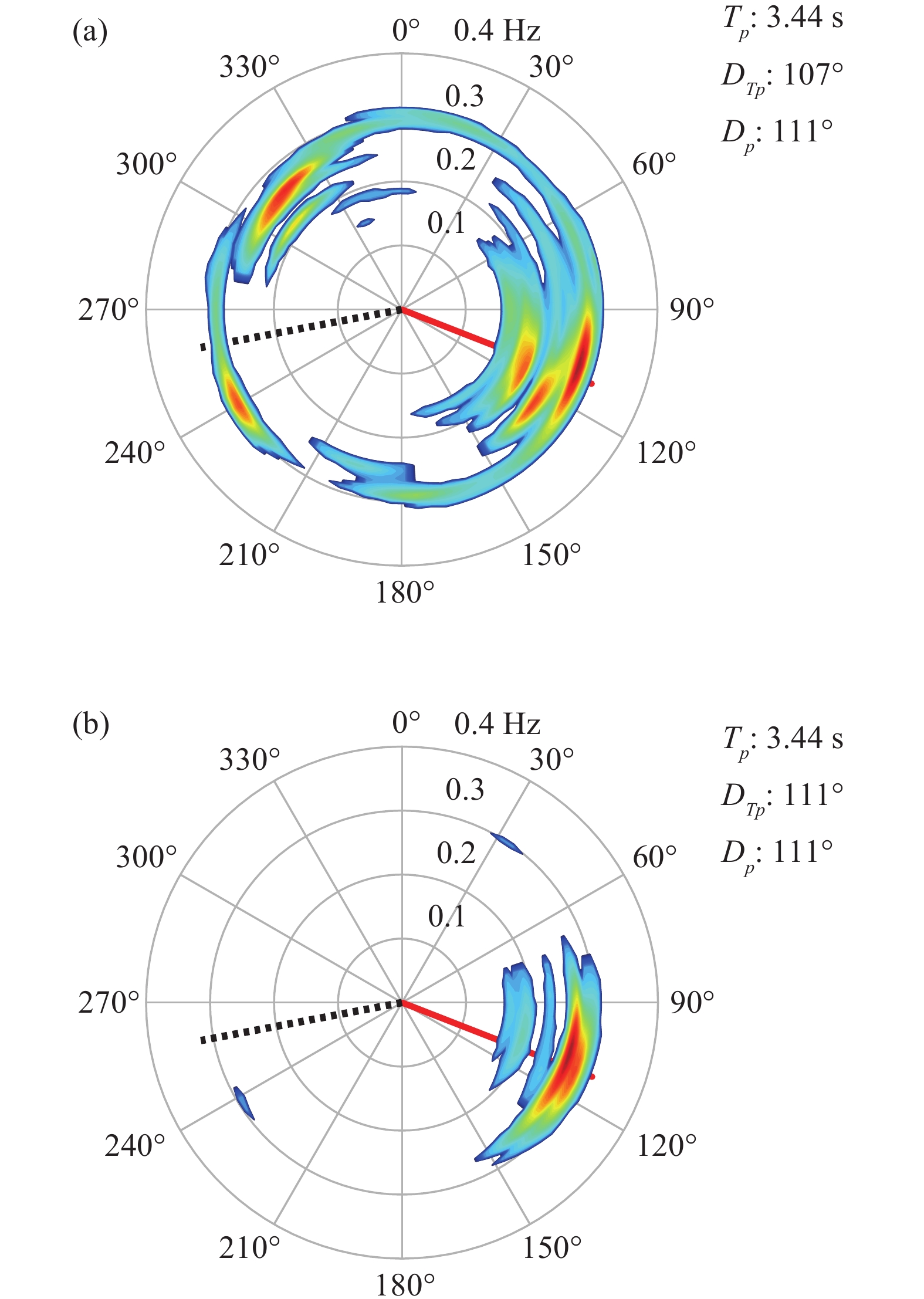
选取波谱谱峰频率大于同步四波束阵列法上限截止频率的组次, 用于说明空时联合阵列方法能提升五波束ADCP可测波浪方向谱的上限截止频率。如2019年12月威海IOA Wave ADCP坐底测波浪实验的第167组观测结果, 对于同步四波束阵列数据反演方向谱上限截止频率为0.22 Hz (可测方向波周期T > 4.46 s), 而五波束空时联合阵列数据反演方向谱上限截止频率为0.27 Hz (可测方向波周期T >3.75 s), 五波束空时联合阵列法在短波长、短周期的风浪观测方面具有明显优势, 图7为同步四波束阵列法与五波束空时联合阵列法的方向谱估计结果对比。

如图7所示, 波浪参数为有效波高H_s = 0.25 m (典型小波浪海况条件), 波谱峰周期T_P = 3.44 s, 超出四波束阵列的最小可测方向波周期下限, 略低于五波束联合阵列的最小可测周期下限。同步四波束阵列法估得反演方向谱呈现出方向模糊, 而空时联合阵列法能有效反演这类短周期、小波高的波浪方向谱。此类结果表明, 对于H_s < 0.35 m的55组数据中3.3 s < T_P < 4.4 s的所有组次, 同步四波束阵列法估得反演方向谱均表现出不同程度的方向模糊, 而空时联合阵列法结果相对更优。低信噪比数据条件下空时联合阵列法的D_P估计精度的改进, 是源于有效引入了精准度更优的中间波束测高数据序列。

现有研究中ADCP使用单点多物理量法或多点单物理量法, 没有将高信噪比测高和多测点测流结合, 海浪方向谱估计能力受限。本研究提出了一种空时联合的声学测高测流阵列海浪方向谱估计方法, 能对测高测流两类数据采样时延进行补偿, 实现空时联合复合阵列测波。此方法方向谱谱峰估计误差更小、方向谱峰度提升, 且在有效波高小于0.35 m (对应阵列数据带内信噪比小于6 dB)的小波浪组次谱峰波向估计准确度得到提升。同等布放条件下, 此法可估方向谱的有效波高更低、上限截止频率更高, 提升了ADCP声学海浪方向谱估计能力。