多站联合非合作定位方法是利用多个观测站同时对非合作目标进行观测, 获得目标的探测信息和识别信息, 并将获得的所有信息进行关联处理获得目标位置的方法。多站联合非合作定位方法具有扩展性好、隐蔽性强等特点, 适用于不便于加装合作信标的水中目标定位^[1–4]。非合作观测的一类重要信息是宽带辐射噪声信息, 其可能来自水中目标的被动辐射或主动发声, 携带包括频谱信息在内的多种特征, 充分利用这些特征信息定位目标是多站联合非合作定位方法的一个重点问题。在复杂环境中, 基于到达方向(DOA)估计的算法是对目标量测进行区分的有效算法^[5-6], 随着高分辨方位技术的发展, 使得基于DOA估计的算法在多站联合非合作定位问题的应用更具优势。

对于非合作目标定位问题, 充分利用历史信息是一项重要手段, 但在观测初始阶段由于缺乏有效历史信息, 只能利用量测信息对目标直接定位。在获取目标量测信息后, 需将目标在同一时刻发出的信息进行关联, 才能进行精确定位。因此, 多站联合定位中的关联问题可以分为两类, 一类是将多站的量测信息进行批号关联, 另一类是将目标在同一时刻的信息进行时空关联。水下目标通常在低速运动, 可忽略时空关联问题, 本文着重考虑目标批号关联问题。传统的批号关联算法通过空间量测信息来解决目标关联问题^[7]。其中较为典型的有多维分配的算法^[8]和分治贪心算法^[9], 此类算法是基于目标在空间的最小代价或最小距离进行量测关联, 在目标数目较少时性能较好, 但当目标数目增多时性能退化。除了空间信息之外, 还有相关文献提出利用附加的特征信息解决目标批号关联问题, Swartling等提出使用盲源分离提取特征来关联不同阵列的方位量测^[10], 但该算法只能在两个观测站的场景工作。为了解决观测站数目受限问题, Alexandridis等提出一种基于直方图特征的贪婪关联的算法^[11], 将不同观测站获得的相似特征聚类成组而实现关联, 但该方法仍对虚警较为敏感。Dang等在其基础上提出了一种基于直方图特征的二维分配方法^[12], 该算法在虚警场景性能较好。这些基于特征信息的算法都是针对室内声学场景提出的, 但由于水声信道具有复杂的时变空变特性, 利用上述特征的关联算法性能退化。针对水声定位场景, 曲光宇提出利用功率谱特征或时频窗特征的关联算法^[13], 此算法在特征稳定时性能较好, 但同样存在性能退化问题。

针对多站联合定位中的批号关联问题, 本文提出了一种多站联合观测非合作目标的定位批号关联算法。该算法立足于充分利用目标特征信息, 并考虑了场景内存在漏报和虚警等目标关联的不利条件, 利用模糊数学理论, 分别构建不同观测站量测之间的方位信息、连续谱特征和线谱特征之间的模糊关系矩阵, 旨在通过综合模糊关系矩阵找到不同观测站中模糊隶属度最大的量测, 即最清晰的量测。在数学上, 模糊关系的最大化是一个组合优化问题, 可以逐次求解进而转化成一个二维优化问题, 使用匈牙利算法进行求解, 并通过隶属度门限在关联过程中剔除模糊隶属度低的关联。在获得不同观测站的正确关联后, 即可利用方位信息来估计目标位置。仿真及试验结果表明, 本文算法在存在漏报虚警场景中优于传统算法, 且在试验中能够实现正确关联, 可以应用到真实的水声场景。

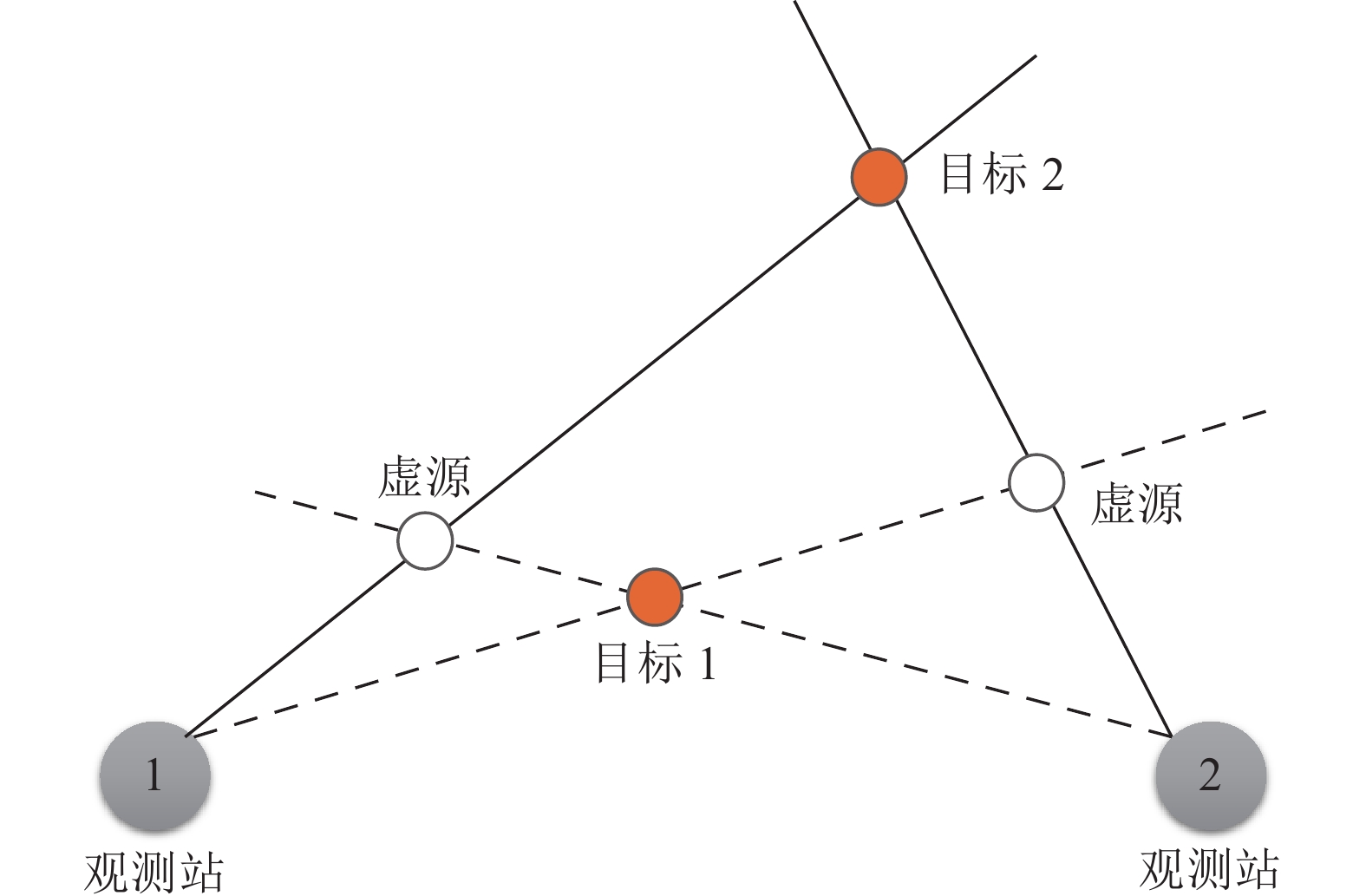
批号是观测站给融合中心上传数据的编号方式, 如观测站1某时刻上传的数据将其批号命名为量测1-1、量测1-2, 而观测站2某时刻上传的数据将其批号命名为量测2-1、量测2-2, 将四个批次的数据进行批号关联是多目标定位的一个重要问题。利用两个观测站估计两个目标的位置给出该问题的描述, 如图1所示, 虚线表示第1个目标的测向线, 实线表示第2个目标的测向线。来自观测站的测向线相交导致4个可能的目标位置。当测向线正确关联会得到目标真实位置(彩色圆圈), 而错误关联产生虚源(白色圆圈)。当找到从观测站到目标的正确测向线关联时, 多目标定位问题分解成多个单目标定位问题, 可以通过单目标位置估计算法进行求解。

考虑由$S$个已知位置的观测站组成的水声定位场景, 假设环境中同时存在$N$个目标, $N$是未知的, 目标在不同观测站观测方位不重叠。观测站$ s \in \left\{ {1,2, \cdots ,S} \right\} $获得的量测集$ {\mathcal{Z}_s} $表示为

式中, $ {n_s} $和${i_s}$分别表示观测站$s$获得的批号总数和观测站$s$观测到的第i个量测的批号, $ {\boldsymbol{z}}_{s,{i_s}} \triangleq \{ {\theta _{s,{i_s}}}, {H_{s,{i_s}}}, f_{s,{i_s}}^m \} $是第$s$个观测站的第${i_s}$个量测集合, 其中$ {\theta _{s,{i_s}}} $表示方位量测, $ {H_{s,{i_s}}} $和$ f_{s,{i_s}}^m $分别表示在该方位获取的功率谱分布函数和线谱频率。同时定义$ {{\boldsymbol{Z}}_{s - 1,q}},s = 2, \cdots ,S; $ $ q = 1, \cdots ,Q $为第$q$个已关联的量测集合, $Q$是已关联集数目, $ {\ell _{s - 1,q}} $表示前$s - 1$个观测站第$q$个已关联集的批号索引。

空间关系是指不同观测站对同一个目标的方位量测线会在空间相交, 这是纯方位定位的一个重要依据。由于方位量测会受到噪声的干扰, 观测到的目标空间位置存在模糊区域, 因此需要构建空间模糊关系矩阵来描述不同观测站的方位量测之间的模糊关系。

从全局关联角度出发, 以S元组$ \left\{ {{i_1}{i_2} \cdots {i_S}} \right\} $的形式表示观测站的方位量测集的关联结果^[14], 同一个S元组不能同时包含来自同一个观测站的多个量测值, 并且如果它不包含来自观测站s的任何量测值, 那么$ {i_s} = 0 $对应于一个虚拟量测值。每个S元组对应一个方位关联代价$ {c_{{i_1}{i_2} \cdots {i_S}}} $, 反映了该S元组中的量测值表示相同目标的广义可能性。定义$ {c_{{i_1}{i_2} \cdots {i_S}}} $为^[8]

式中, $ P{D_{s,{i_s}}} $表示目标检测概率; $ {\varPhi _s} $表示虚警分布; $ {\sigma _s} $表示方位量测的标准差; $ {\widehat \theta _{s,{i_s}}} $表示S元组估计位置到观测站的方位; $ u\left( {{i_s}} \right) $表示二进制关联变量, 当观测站s出现漏报即$ {i_s} = 0 $时$ u\left( {{i_s}} \right) = 0 $, 否则$ u\left( {{i_s}} \right) = 1 $。将所有$ {c_{{i_1}{i_2} \cdots {i_S}}} $由小到大进行排列的列向量$ {\boldsymbol\rho} = [{\rho _1}, {\rho _2}, \cdots ,{\rho _{\prod _{\text{1}}^S({n_s} + 1)}}]^{\rm T} $。

根据式(2), 若已关联集$ {{\boldsymbol{Z}}_{s - 1,q}} $中的空间模糊关系子集$ {\varTheta _{s - 1,q}} $和待关联方位$ {\theta _{s,{i_s}}} $之间的关联代价为$ {\varGamma _{{\ell _{s - 1,q}},{i_s}}} $, 利用模糊数学中的Zadeh取小算子$ \wedge $定义其为

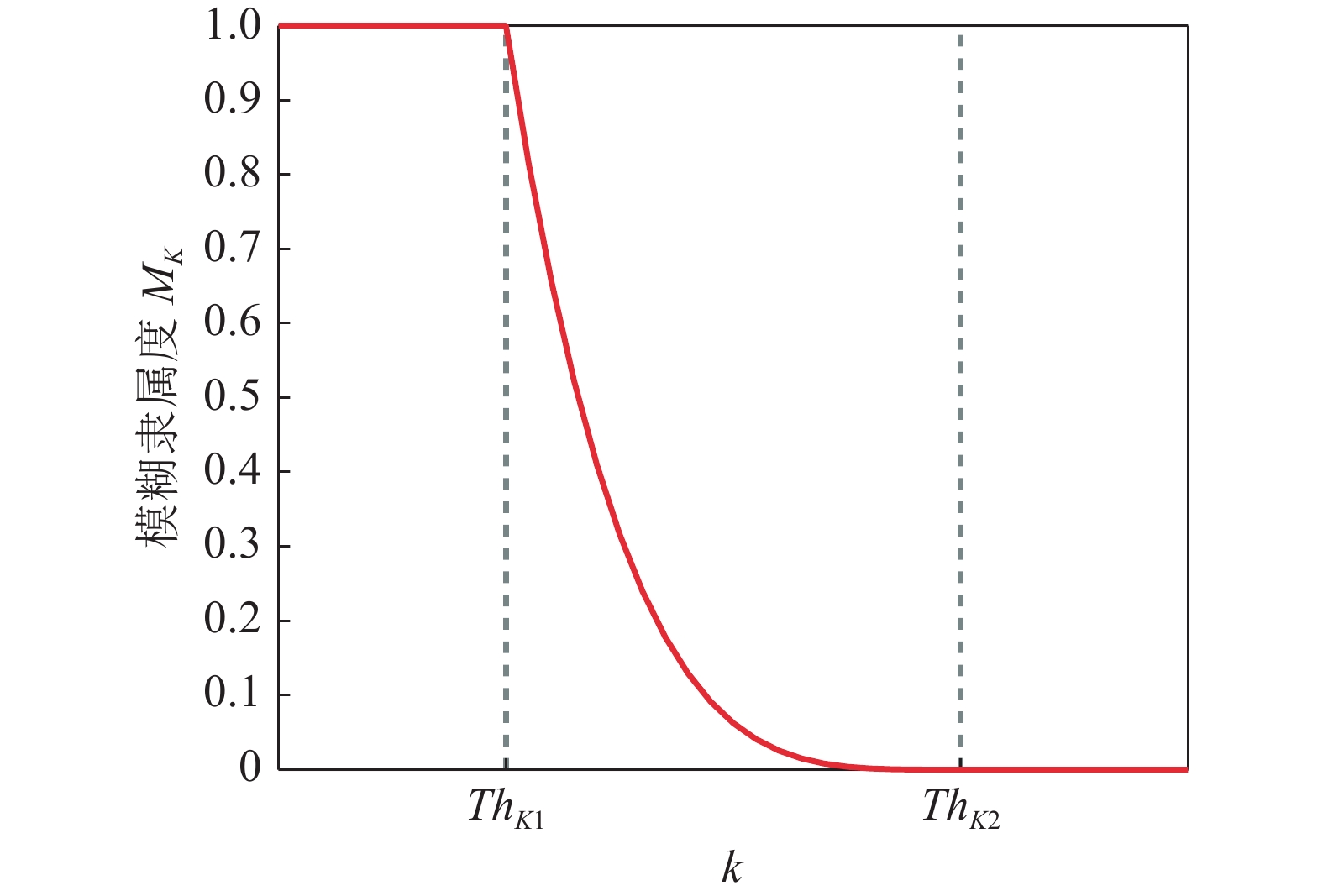
利用模糊数学思想, 引入模糊隶属函数概念, 将空间模糊关系的模糊隶属函数$ {M_K}\left( k \right) \in \left[ {0,1} \right] $定义为^[15]

式中, $ T{h_{K1}} = {\rho _{\mathop {\max }\limits_s ({n_s})}} $为模糊度的保守阈值, $ T{h_{K2}}{\text{ = }} - \sum\nolimits_{s = 1}^S {\ln \left( {1 - P{D_{s,{i_s}}}} \right)} $为模糊度的分割阈值, 隶属度函数的具体表示如图2所示。将代价$ {\varGamma _{{\ell _{s - 1,q}},{i_s}}} $代入模糊隶属函数$ {M}_{K}(\cdot) $, 计算空间模糊关系矩阵$ r_{{\ell _{s - 1,q}},{i_s}}^\mathbb{K} $元素:

则在观测站s进行关联时, 已关联集的方位特征子集$ {\varTheta _{s - 1,q}} $和待关联方位特征$ {\theta _{s,{i_s}}} $的空间模糊关系矩阵为$ R_s^\mathbb{K} = {\left( {r_{{\ell _{s - 1,q}},{i_s}}^\mathbb{K}} \right)_{Q \times {n_s}}} $。

由于目标辐射噪声到达不同观测站所传输的信道不同, 不同观测站量测的连续谱特征之间也存在模糊关系, 因此通过构建连续谱模糊关系矩阵来描述连续谱特征之间的模糊关系。选用滤波器参数法^[16]对目标辐射噪声的连续谱进行特征提取。首先获得目标辐射噪声连续谱估计, 对其进行平滑处理, 得到用于设计滤波器的参数, 包括峰值频率$ {f_0} $及其两侧区间进行倍频程采样频点和频点对应的谱级, 进而将幅度进行处理得到功率谱关于频率的分布函数, 即为连续谱特征。

若观测站s获得的第$ {i_s} $个量测中的功率谱分布函数为$ {H_{s,{i_s}}} $, 则连续谱特征定义为

观测站s获得的所有连续谱集合为$ \mathcal{F}_s^\mathbb{C} = \{ F_{s,1}^\mathbb{C},F_{s,2}^\mathbb{C}, \cdots , F_{s,{n_s}}^\mathbb{C}\} $。同时定义已关联集$ {{\boldsymbol{Z}}_{s - 1,q}} $中的连续谱特征子集为$ {\boldsymbol{F}}_{s - 1,q}^\mathbb{C} $, 由于同一目标在不同观测站的连续谱分布具有结构相似的特性, 利用Wasserstein距离^[17]构建用于表示已关联集的连续谱特征子集$ {\boldsymbol{F}}_{s - 1,q}^\mathbb{C} $和待关联连续谱特征$ F_{s,{i_s}}^\mathbb{C} $之间的隶属程度的模糊隶属函数$ {M_C}\left( {{\boldsymbol{F}}_{s - 1,q}^\mathbb{C},F_{s,{i_s}}^\mathbb{C}} \right) $。若分布u和分布v之间的Wasserstein距离为$ {d_W}\left( {u,v} \right) $, 则分布集合$ U = \left\{ {{u_1},{u_2}, \cdots } \right\} $和分布v之间的最小Wasserstein距离$ {d_C}\left( {U,v} \right) $为

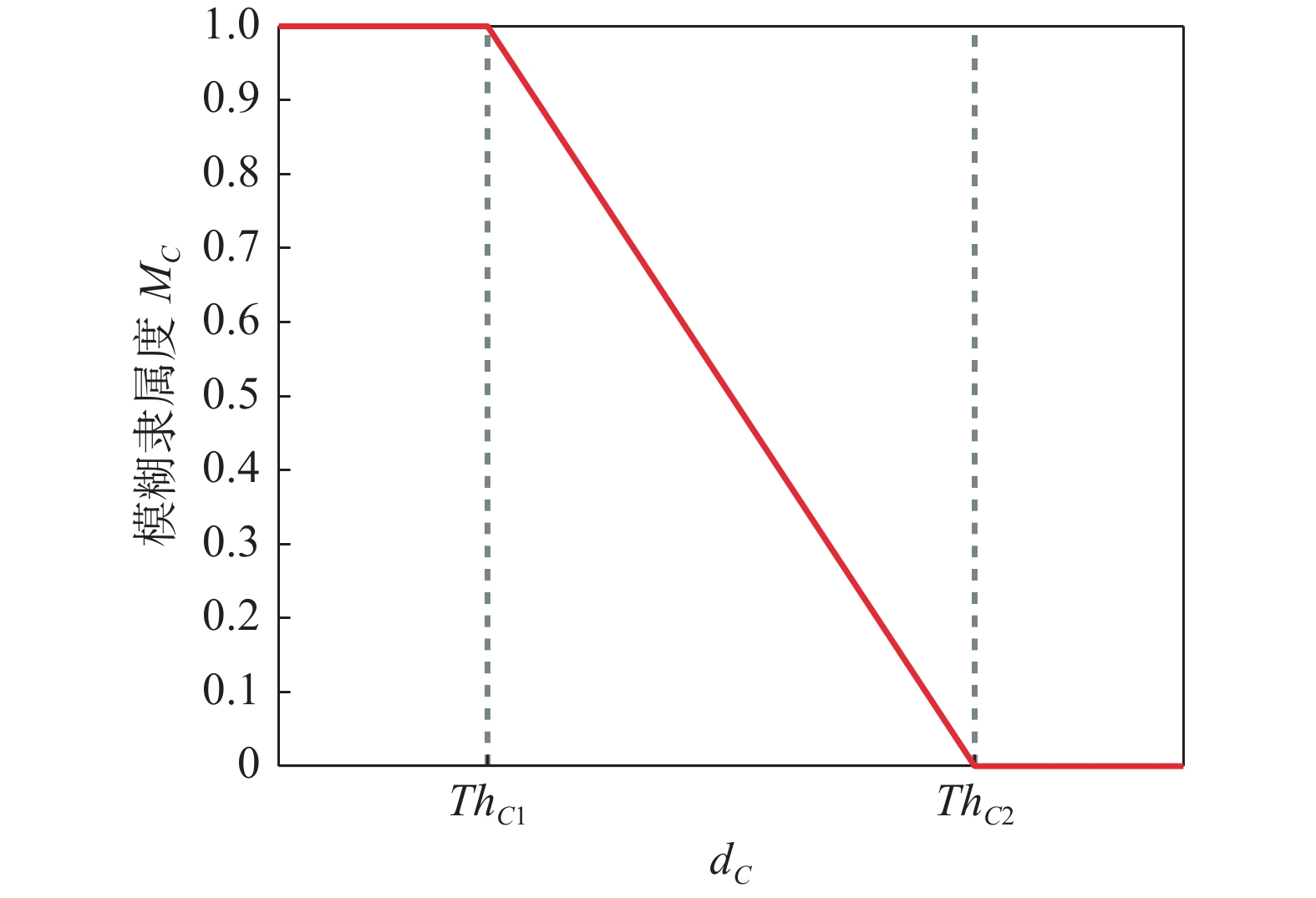
由于最小Wasserstein距离$ {d_C}\left( {U,v} \right) $变化范围较小且数值越小表示连续谱越相似, 因此将连续谱特征的模糊隶属函数构建成形状平缓的偏小型。连续谱特征的模糊隶属函数$ {M_C}\left( {U,v} \right) \in \left[ {0,{\text{ }}1} \right] $定义为

式中, $ T{h_{C1}} $(=3), $ T{h_{C2}} $(=10)分别为连续谱模糊度的保守阈值和分割阈值, 隶属度函数的具体表示如图3所示。将$ {\boldsymbol{F}}_{s - 1,q}^\mathbb{C} $和$ F_{s,{i_s}}^\mathbb{C} $代入模糊隶属函数, 计算连续谱模糊关系矩阵元素$ r_{{\ell _{s - 1,q}},{i_s}}^\mathbb{C} $为

则在观测站s进行关联时, 已关联集的连续谱特征子集$ {\boldsymbol{F}}_{s - 1,q}^\mathbb{C} $和待关联连续谱特征$ F_{s,{i_s}}^\mathbb{C} $的连续谱模糊关系矩阵为$ R_s^\mathbb{C} = {\left( {r_{{\ell _{s - 1,q}},{i_s}}^\mathbb{C}} \right)_{Q \times {n_s}}} $。

水中目标的辐射噪声中通常包含稳定线谱^[18], 但线谱强度随机起伏, 且受到传播距离等因素影响, 不同观测站接收到同一线谱的强度差异大, 强度信息不适合用于目标关联。同时由于观测站和运动目标之间的径向速度存在差异, 线谱频率会受到多普勒频移的影响, 不同观测站量测中的线谱特征之间存在模糊关系。因此选用线谱频率特征构建线谱模糊关系矩阵, 进而描述不同观测站的线谱特征之间的模糊关系。

若观测站s在第$ {i_s} $个量测中存在$ {M_{s,{i_s}}} $根线谱, $ f_{s,{i_s}}^m $表示第$ m $根线谱的频率。由于不同观测站获得的线谱受到多普勒频移影响, 因此将线谱根据相对多普勒频移进行扩展, 记$ \Delta f $是$ f_{s,{i_s}}^m $的最大容忍频偏, 则定义扩展线谱区间为

因此, 线谱特征$ F_{s,{i_s}}^\mathbb{L} $定义为

根据式(11)观测站s获得的所有线谱集合为$ \mathcal{F}_s^\mathbb{L} = \left\{ {F_{s,1}^\mathbb{L},F_{s,2}^\mathbb{L}, \cdots ,F_{s,{n_s}}^\mathbb{L}} \right\} $, 定义已关联集$ {{\boldsymbol{Z}}_{s - 1,q}} $中的线谱特征子集为${\boldsymbol{ F}}_{s - 1,q}^\mathbb{L} $, 由于同一目标的线谱特征具有线谱频率相似的特性, 因此利用重叠相似度^[19]构建用于表示已关联集的线谱特征子集$ {\boldsymbol{F}}_{s - 1,q}^\mathbb{L} $和待关联线谱特征$ F_{s,{i_s}}^\mathbb{L} $之间的隶属程度的模糊隶属函数$ {M_L}\left( {{\boldsymbol{F}}_{s - 1,q}^\mathbb{L},F_{s,{i_s}}^\mathbb{L}} \right) $。若定义集合$ {A_j} $和集合B之间的重叠相似度为$ {d_O}\left( {{A_j},B} \right) $, 利用取大算子$ \vee $定义多重集合$ \Xi = \left\{ {{A_1},{A_2}, \cdots } \right\} $和集合B之间重叠相似度的最大值$ {d_L}\left( {\Xi ,B} \right) $为

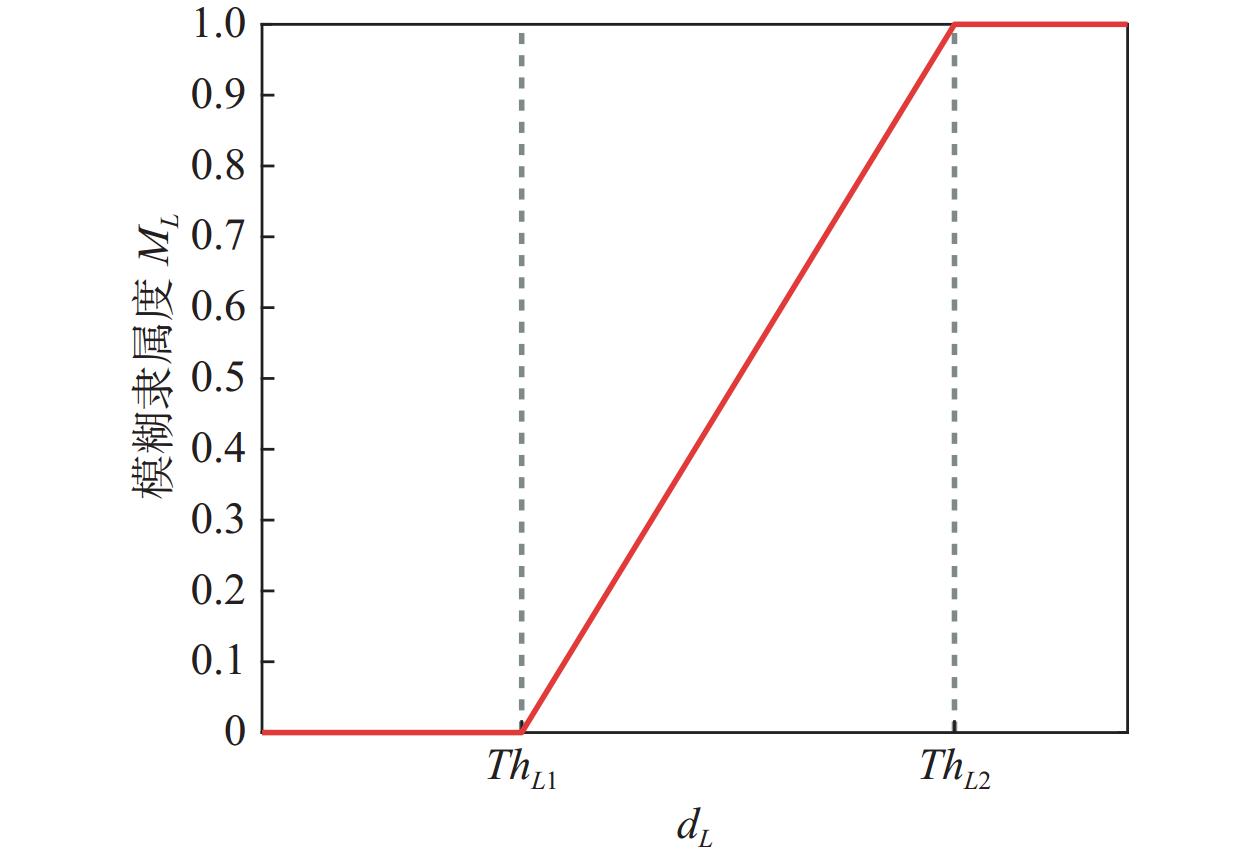
由于最大重叠相似度$ {d_L}\left( {\Xi ,B} \right) $数值越大表示量测之间来自同一目标可能性越大, 因此将线谱特征的模糊隶属函数构建为形状平缓的偏大型。线谱特征的模糊隶属函数$ {M_L}\left( {\Xi ,B} \right) \in \left[ {0,{\text{ }}1} \right] $定义为

式中, $ T{h_{L1}} $(=0.2), $ T{h_{L2}} $(=0.8)分别为模糊度的保守阈值和分割阈值, 隶属度函数的具体表示如图4所示。将$ {\boldsymbol{F}}_{s - 1,q}^\mathbb{L} $和$ F_{s,{i_s}}^\mathbb{L} $代入模糊隶属函数, 计算线谱模糊关系矩阵元素$ r_{{\ell _{s - 1,q}},{i_s}}^\mathbb{L} $为

则在观测站s进行关联时, 已关联集的线谱特征子集$ {\boldsymbol{F}}_{s - 1,q}^\mathbb{L} $和待关联线谱特征$ F_{s,{i_s}}^\mathbb{L} $的模糊关系矩阵为$ R_s^\mathbb{L} = {\left( {r_{{\ell _{s - 1,q}},{i_s}}^\mathbb{L}} \right)_{Q \times {n_s}}} $。

在获得空间信息和谱特征的模糊关系矩阵后, 确定待关联量测和已关联集之间的综合模糊关系矩阵。根据式(5)、式(9)和式(14)中分别获得的模糊关系矩阵元素, 通过对连续谱模糊关系矩阵元素和线谱模糊关系矩阵元素取大选取最清晰的特征, 再与空间模糊关系矩阵元素进行取小处理, 平衡空间模糊关系和特征模糊关系。定义关联的模糊系统中的综合模糊关系矩阵元素$ {r_{{\ell _{s - 1,q}},{i_s}}} $为

在进行关联时, 用$ {R_s} $表示观测站s的综合模糊关系矩阵:

定义二元关联决策变量$ {\zeta _{{\ell _{s - 1,q}},{i_s}}} $, 用来表示已关联集$ {{\boldsymbol{Z}}_{s - 1,q}} $和待关联量测$ {{\boldsymbol{z}}_{s,{i_s}}} $是否来自同一个目标的判定结果, 其定义为

因此, 多站联合观测非合作定位的目标批号关联问题可以被定义为

约束为

式(18)的优化问题可以用匈牙利算法^[20]求解。式(19)中, 第1个条件表示观测站s上最多有一个量测与已关联集$ {{\boldsymbol{Z}}_{s - 1,q}} $关联; 第2个条件表示最多有一个已关联集$ {{\boldsymbol{Z}}_{s - 1,q}} $与量测$ {{\boldsymbol{z}}_{s,{i_s}}} $关联。约束源于已关联集和待关联量测最多只能被关联一次。

当进行第一步关联时, 将第1个观测站的量测放入已关联集, 将第2个观测站量测与第1个观测站进行关联, 此时$ s=2 $, 已关联集数等于观测站1量测数, 即$ Q={n_1} $。已关联集和索引集可表示为

在之后关联中, 更新已关联集和索引集如下所示:

i. 如果关联结果$ {\zeta _{{\ell _{s - 1,q}},{i_s}}} = 1 $且$ {r_{{\ell _{s - 1,q}},{i_s}}} \geqslant \delta $ ($ \delta $是定义的隶属度门限), 已关联集和索引集更新:

ii. 如果关联结果$ {\zeta _{{\ell _{s - 1,q}},{i_s}}} = 1 $且$ {r_{{\ell _{s - 1,q}},{i_s}}} < \delta $, 将关联失败将判决变量进行重置:

iii. 如果$ \sum\nolimits_{{i_s} = 1}^{{n_s}} {{\zeta _{{\ell _{s - 1,q}},{i_s}}}} = 0 $, 表示观测站s上没有任何量测与$ {{\boldsymbol{Z}}_{s - 1,q}} $关联, 已关联集和索引集更新:

iv. 如果$ \sum\nolimits_{q = 1}^Q {{\zeta _{{\ell _{s - 1,q}},{i_s}}}} = 0 $, 表示没有任何已关联集与量测$ {{\boldsymbol{z}}_{s,{i_s}}} $关联, 已关联集数目增加:

所有观测站获取的量测完成关联后, 从S个观测站获取了Q个已关联集$ {{\boldsymbol{Z}}_{S,q}} $和索引集$ {\ell _{S,q}} $。估计二维空间的单个目标至少需要两个方位量测, 因此将至少有两个观测站量测的已关联集用来定位。同时, 若最终的已关联集中S元组方位关联代价大于$ T{h_{K2}} $, 则将其视为由多个观测站同时虚警产生并将已关联集置空, 最后估计的目标数目等于非空集合数。

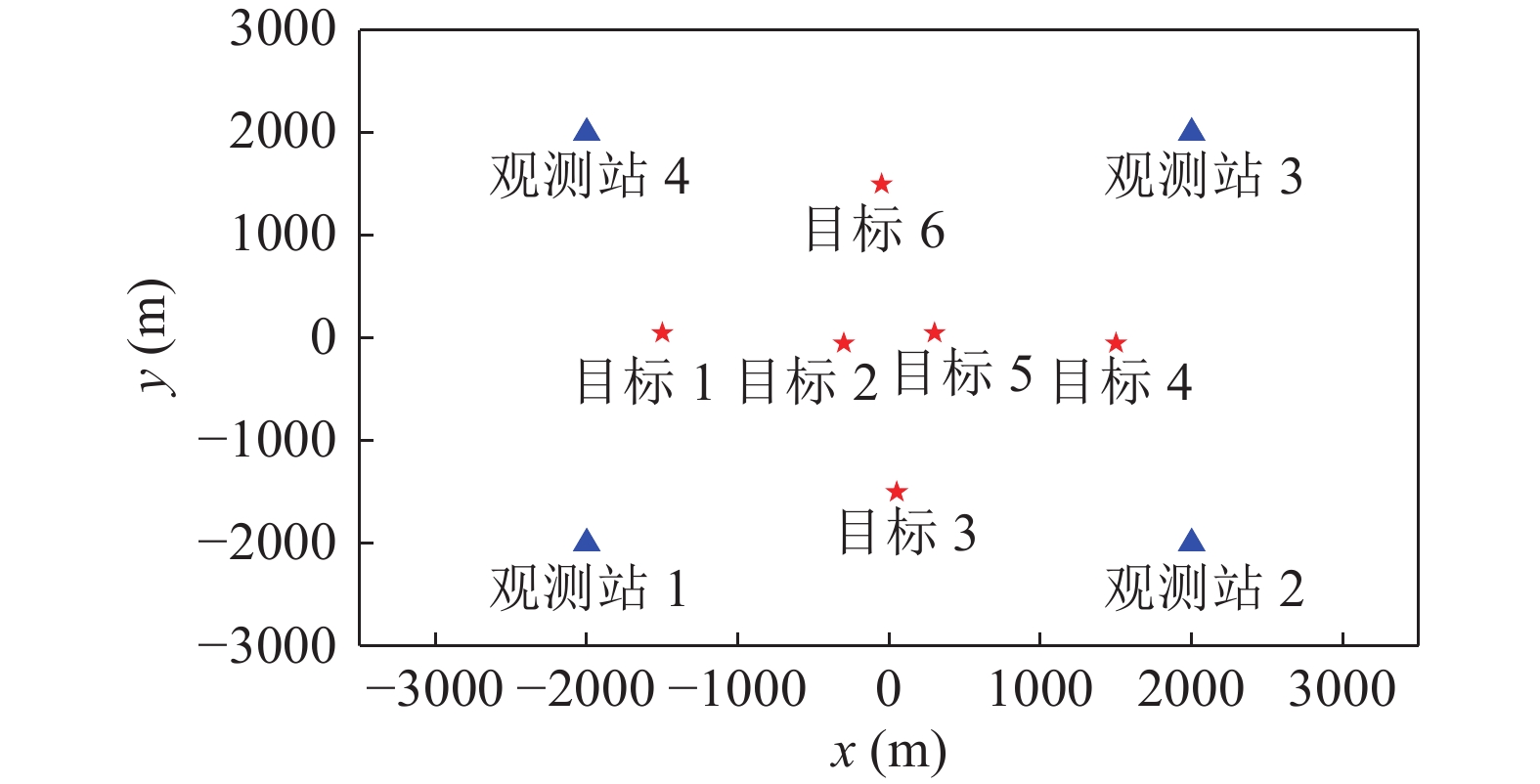
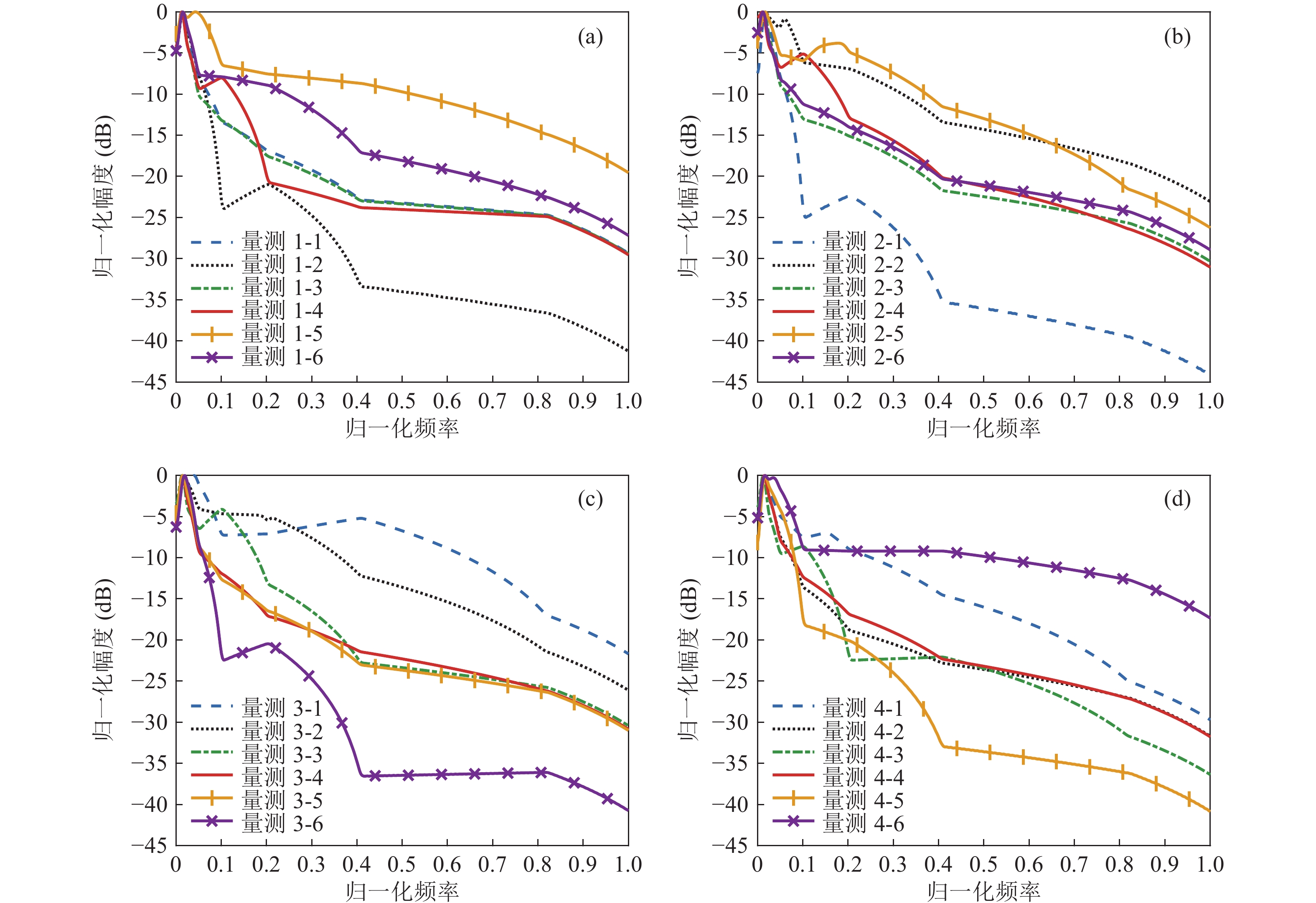
为了评估所提出算法的正确性, 考虑一个观测站数目为4、边长为4 km的正方形拓扑结构的多站联合非合作定位场景。每个观测站由多元阵列组成, 对区域内目标进行独立观测, 并提取探测到目标的方位信息、功率谱分布函数和线谱频率, 方位量测服从于均值为0、标准差为$ 1^\circ $的高斯分布, 虚警个数服从期望为$\lambda $的泊松分布, 虚警在每个观测站的观测视角$[0,\pi {\text{/2}})$内服从均匀分布, 模糊度隶属门限$\delta {\text{ = 0}}{\text{.3}}$, 最大容忍频偏$ \Delta f = 6 $ Hz, 在定位过程中采用最大似然算法^[7]。目标辐射噪声取自ShipsEar水下船舶噪声数据库^[21], 首先选取其中六种船舶噪声并分别提取其连续谱和线谱特征信息构建本文所用的目标辐射噪声信号, 然后将其根据布放位置分别通过浅海水声信道到达观测站并添加输出谱级信噪比约为10~30 dB的高斯白噪声, 最后对接收的舰船辐射噪声进行方位量测和特征提取, 获得观测站的量测集。其中目标辐射噪声信号的功率谱如图5所示, 目标和观测站布放如图6所示, 目标1~6对应的功率谱即分别为图5(a-f)。

观测站提取的连续谱特征和线谱分别如图7和表1所示, 观测站量测批号和目标真实序号的对应关系如表2所示。量测1-5、量测2-2、量测3-1、量测4-6的连续谱特征的峰值频率较为一致且异于其他量测, 因此属于同一目标的模糊隶属度较大。同时, 在量测1-2、量测2-1、量测3-6、量测4-5的线谱中均包含295.4 Hz, 301.4 Hz的稳定线谱, 因此这些量测属于同一目标的模糊隶属度较大。

图8是所有观测站对目标检测概率为1, 虚警期望为0时, 本文算法的关联定位结果。在设置的仿真条件下, 本文算法能够准确地估计出空间中的目标个数, 这表明本文算法在观测站提供信息准确时, 能够有效实现目标关联定位。

进一步分析本文算法的关联性能, 选用基于纯方位的多维分配算法^[8]、分治贪心算法^[9]和基于特征的功率谱关联算法^[13]、时频窗关联算法^[13]进行比较。其中多维分配算法是将不同观测站量测构建全局关联约束而逐步松弛优化的关联算法, 分治贪心算法利用最小距离原则寻找最优关联交点再根据贪心思想将交点集合进行合并获得正确关联的算法, 功率谱关联算法根据目标的功率谱直接计算相似度而进行匹配关联, 时频窗关联算法利用图像处理中的哈希算法对目标的时频窗特征进行匹配关联。

根据文献[8]中定义的标准, 提出两类标准用以评估本文提出算法的关联成功率。两类指标分别被命名为关联结果精度和关联结果召回率, 其定义为

式中, $ {\widehat N_{\rm real}} $表示正确关联组合的数量, $ \widehat N $表示估计目标数量, N表示真实目标数量。这两个指标取值范围均为[0, 1]。

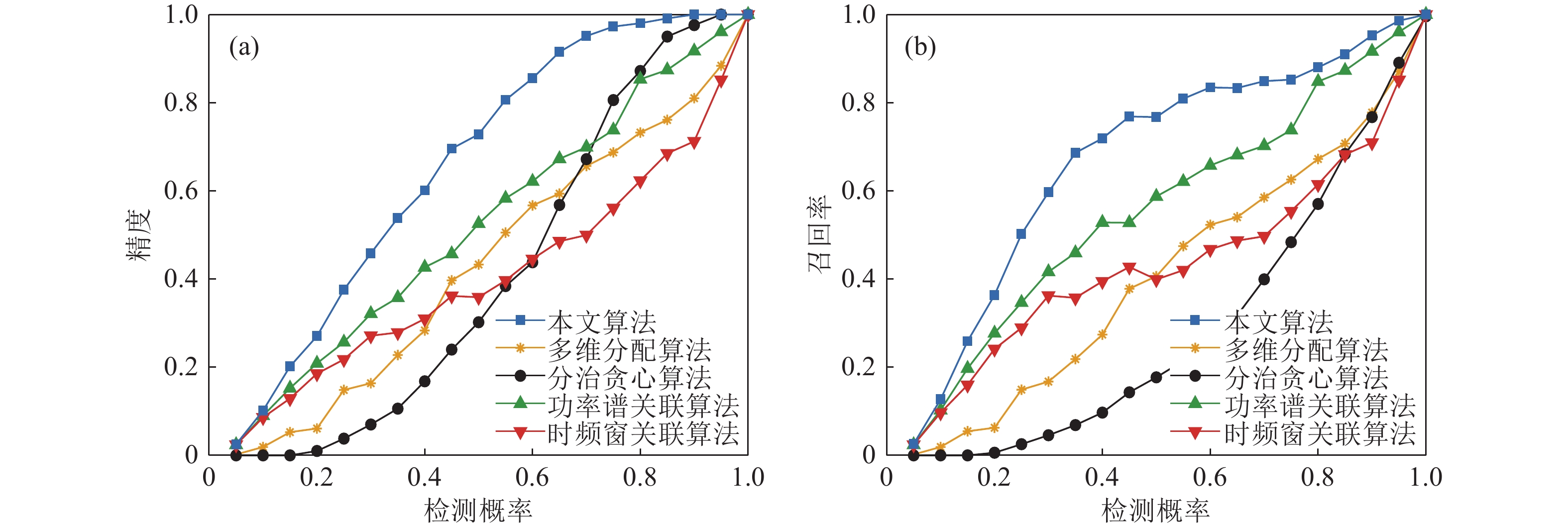
分析漏报对多目标关联算法的影响, 考虑3.1节区域内存在目标1、目标3和目标4三个目标的情况, 进行500次蒙特卡罗试验。为简化计算, 令所有观测站的虚警期望$\lambda = 0$, 研究所有观测站的目标检测概率$P{D_{s,{i_s}}} = 0.05,0.1, \cdots ,1$时算法的关联性能。

在目标出现不同漏报情况下, 五种目标关联方法的性能如图9所示。在检测概率为0.65以上时, 本文算法的关联精度保持在0.9以上, 而分治贪心算法、功率谱关联算法、多维分配算法、时频窗关联算法分别在检测概率为0.90, 0.90, 0.95, 0.95以上时, 达到同样关联精度; 在检测概率为0.55以上时, 本文算法的关联召回率保持在0.8以上, 而功率谱关联算法、分治贪心算法、多维分配算法、时频窗关联算法分别在检测概率为0.80, 0.95, 0.95, 0.95以上时, 达到此关联召回率。

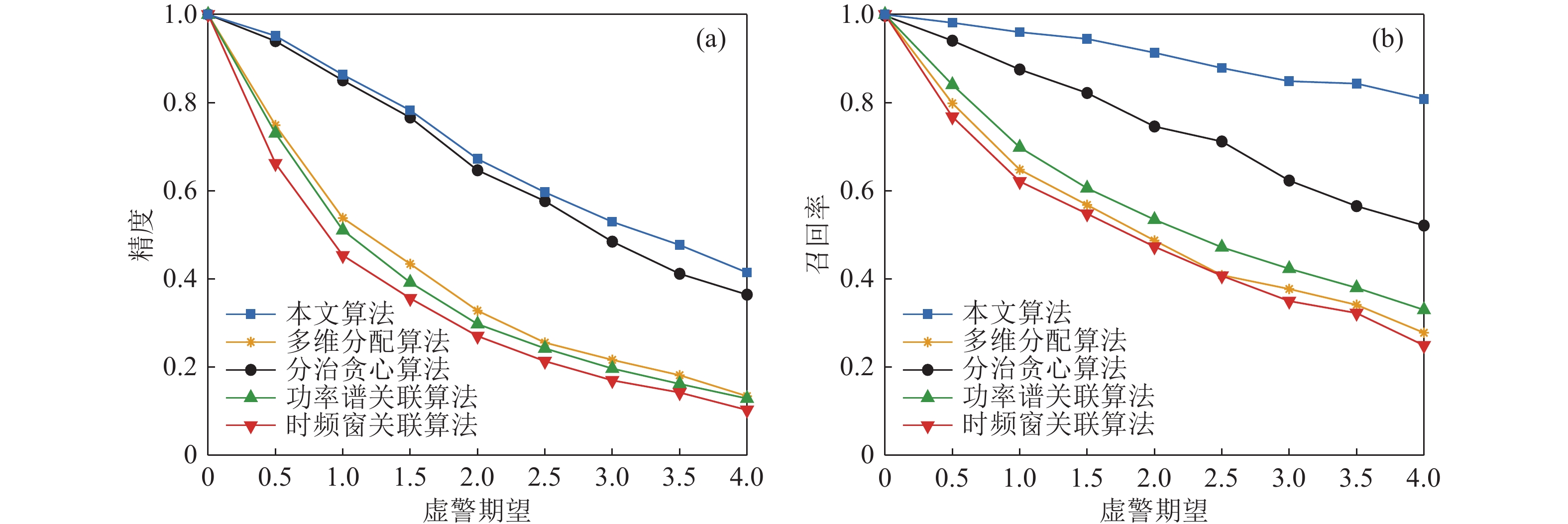
考察观测站量测信息中包括虚警时多目标关联算法的性能, 对本文算法和上述四种关联算法进行性能比较。考虑3.1节区域内存在目标1、目标3和目标4三个目标的情况, 进行500次蒙特卡罗试验。所有观测站目标检测概率为$P{D_{s,{i_s}}} = 1$, 虚警期望分为$\lambda = 0.5,1, \cdots ,4$。试验中若产生虚警, 则在观测站的观测范围内随机产生一个方位并根据接收信号提取其对应的特征。不同虚警期望情况下, 五种目标关联方法性能如图10所示。本文算法的召回率均能保持在0.8以上, 精度保持在0.4以上; 分治贪心算法的精度和召回率分别能保持在0.5和0.35以上, 其他三种算法的性能对虚警较为敏感。本文算法通过设置隶属度门限和输出门限, 取消了低隶属度关联并取消输出空间代价低的关联组合, 所以关联精度和召回率较高。

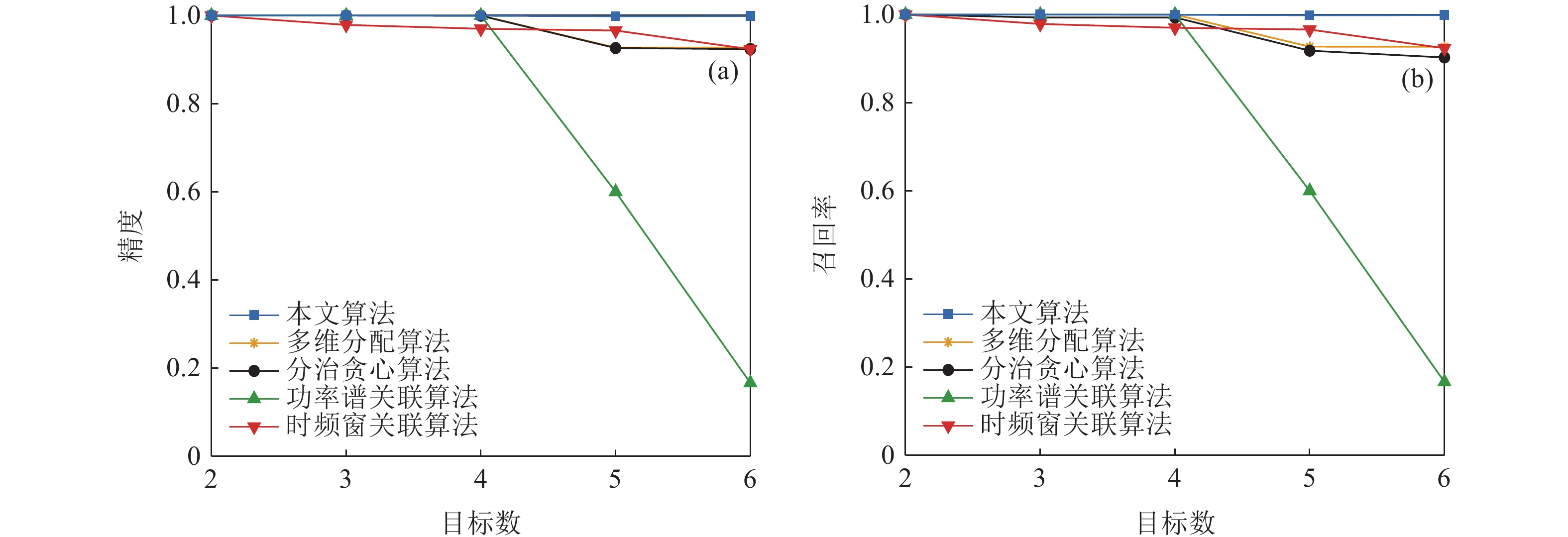
分析不同目标数对多目标关联算法的影响, 在3.1节区域内分别存在2, 3,…, 6个目标情况, 分别进行500次蒙特卡罗试验。所有观测站目标检测概率$P{D_{s,{i_s}}} = 1$, 虚警期望$\lambda = 0$。在两个目标场景存在目标1和目标2, 在三个目标场景增加目标3, 依此类推。

上述五种关联算法在不同目标数场景中的关联性能如图11所示。本文算法综合利用了空间信息和特征信息, 因此关联精度和关联召回率均一直保持在1; 多维分配算法、分治贪心算法和时频窗关联算法的关联精度和关联召回率能维持在0.9以上; 功率谱关联算法在目标数大于4时性能退化。

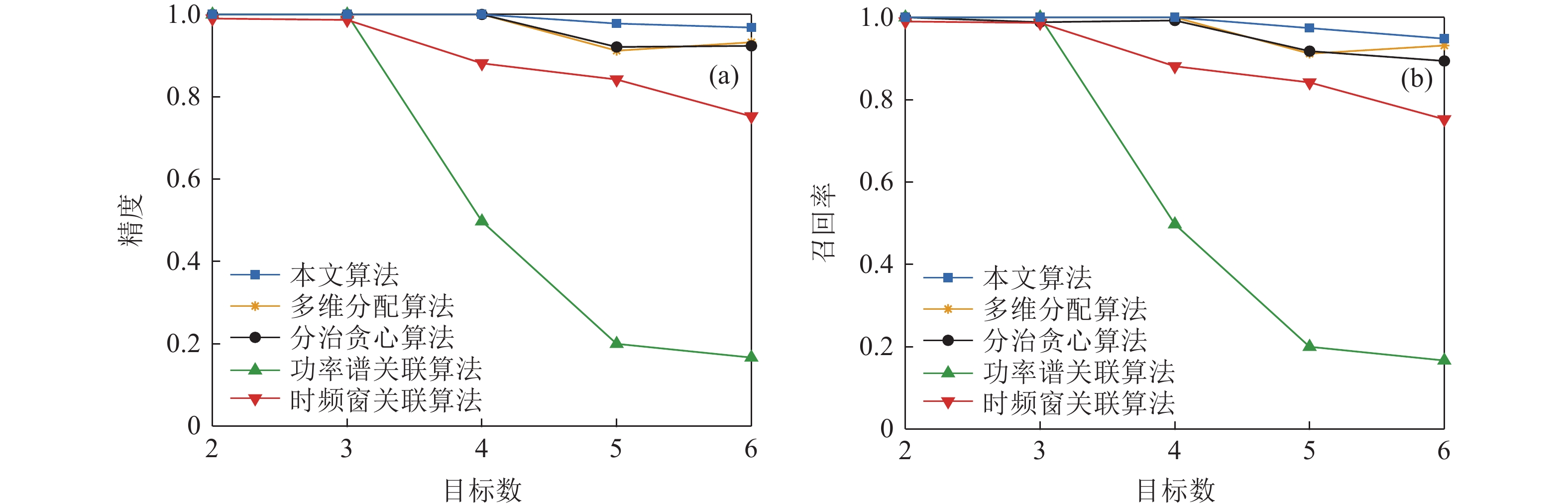
进一步分析本文算法的召回率边界, 在其他条件不变时, 添加输出谱级信噪比约为0~20 dB的高斯白噪声, 设置模糊度隶属门限$\delta {\text{ = 0}}{\text{.05}}$, 进行500次蒙特卡罗试验。

上述五种关联算法在此场景中关联性能如图12所示, 本文算法的关联结果精度和关联结果召回率在目标数大于4时性能下降。由于本方法对输入特征准确度有一定要求, 因此在信噪比低时性能下降。

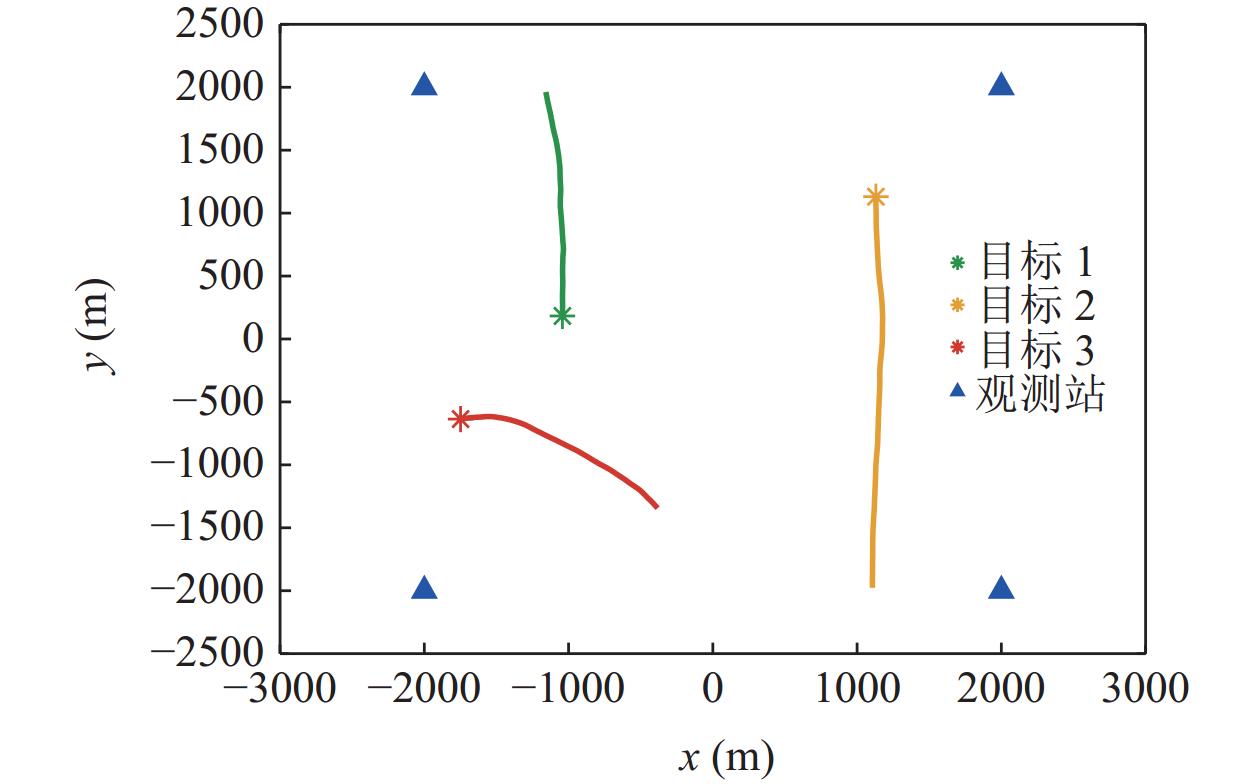
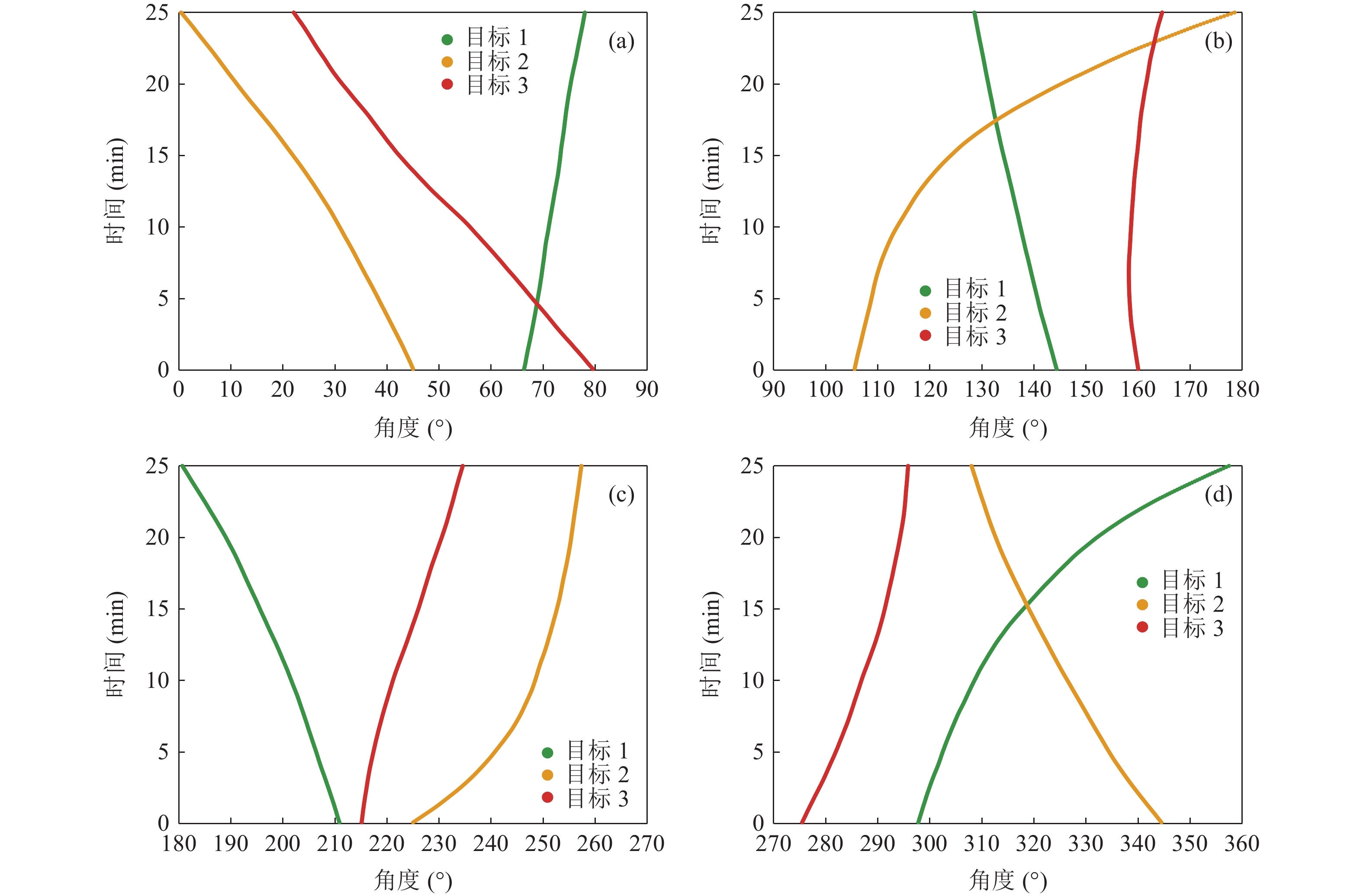
最后, 分析目标运动对多目标关联算法的影响。考虑图13所示的三个目标场景, 在观测极坐标系下目标存在轨迹交叉情况, 如图14所示。目标1~3对应的功率谱分别为图5(a)(c)(d)。仿真中, 所有观测站的目标检测概率$P{D_{s,{i_s}}} = 1$, 虚警期望$\lambda = 0$。目标关联过程中, 对每帧所有观测站提供数据进行独立关联。所有算法进行100次蒙特卡罗试验, 利用最优子模式分配(OSPA)误差^[22]来检验算法性能。

选取某次仿真试验中, 观测站在第3.5分钟获取的连续谱特征和线谱, 分别如图15和表3所示, 目标和量测的真实对应关系如表4所示。此时观测站1视野中目标1和目标3临近, 对应的量测为量测1-2和量测1-3, 由图15(a)可见, 量测1-2的谱形状受到量测1-3影响, 在归一化频率0.2处升幅较小。同样由表3可知, 在观测站1的量测2和量测3中出现相近频率的线谱。

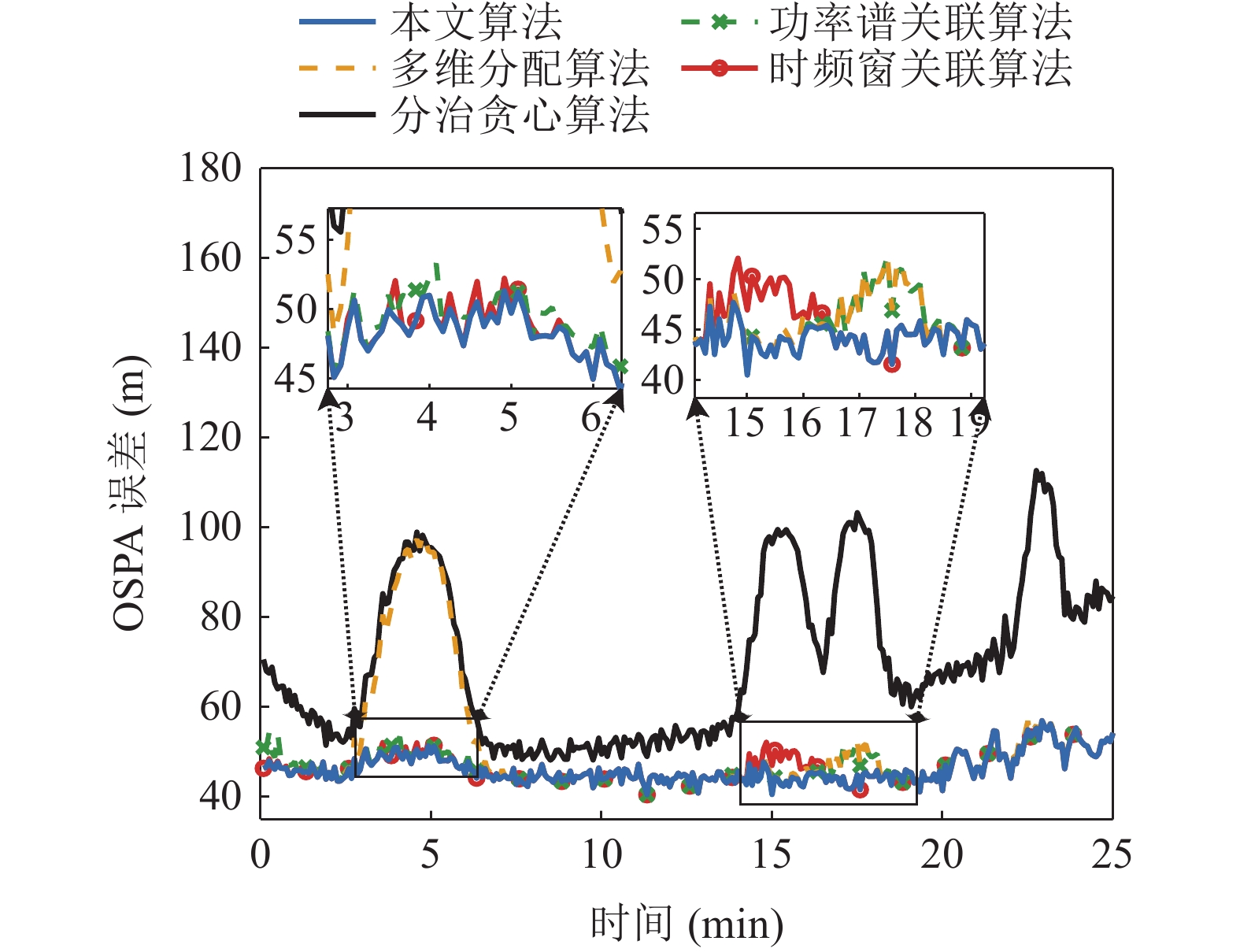
五种算法不同时间的OSPA误差(参数p = 1, c = 200)如图16所示, 在最初几分钟所有算法性能相近, 在5分钟左右由于观测站1视野中目标1和目标3临近, 多维分配算法和分治贪心算法出现输出结果数目错误而导致误差较高; 而在15分钟左右观测站2和观测站4视野中的目标1和目标2临近, 在23分钟后观测站2视野中的目标2和目标3临近, 分治贪心算法同样出现输出结果数目错误而导致OSPA误差急剧升高。而在目标临近而出现量测相互影响时, 本文算法、功率谱关联算法、时频窗关联算法OSPA误差略有升高, 而一个观测站发生量测合并时, 本文算法将合并量测与一个已关联集关联, 其他已关联集在此观测站上没有量测与之关联。在关联完成后, 虽然一个已关联集中有漏报损失部分定位精度, 但利用其他观测站信息仍可进行定位。所有时间平均OSPA误差如表5所示, 本文算法、功率谱关联算法、时频窗关联算法的平均OSPA误差相近。

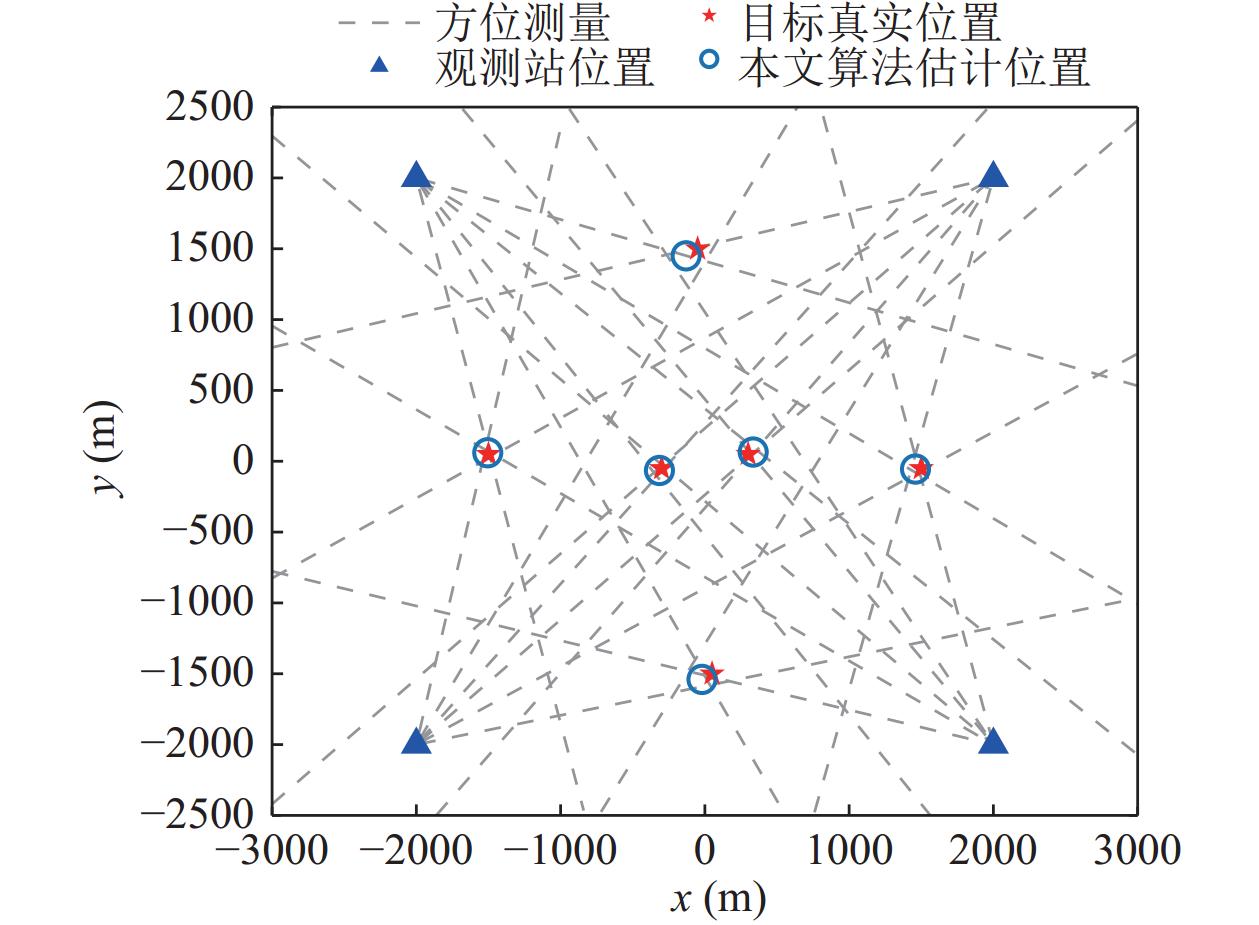
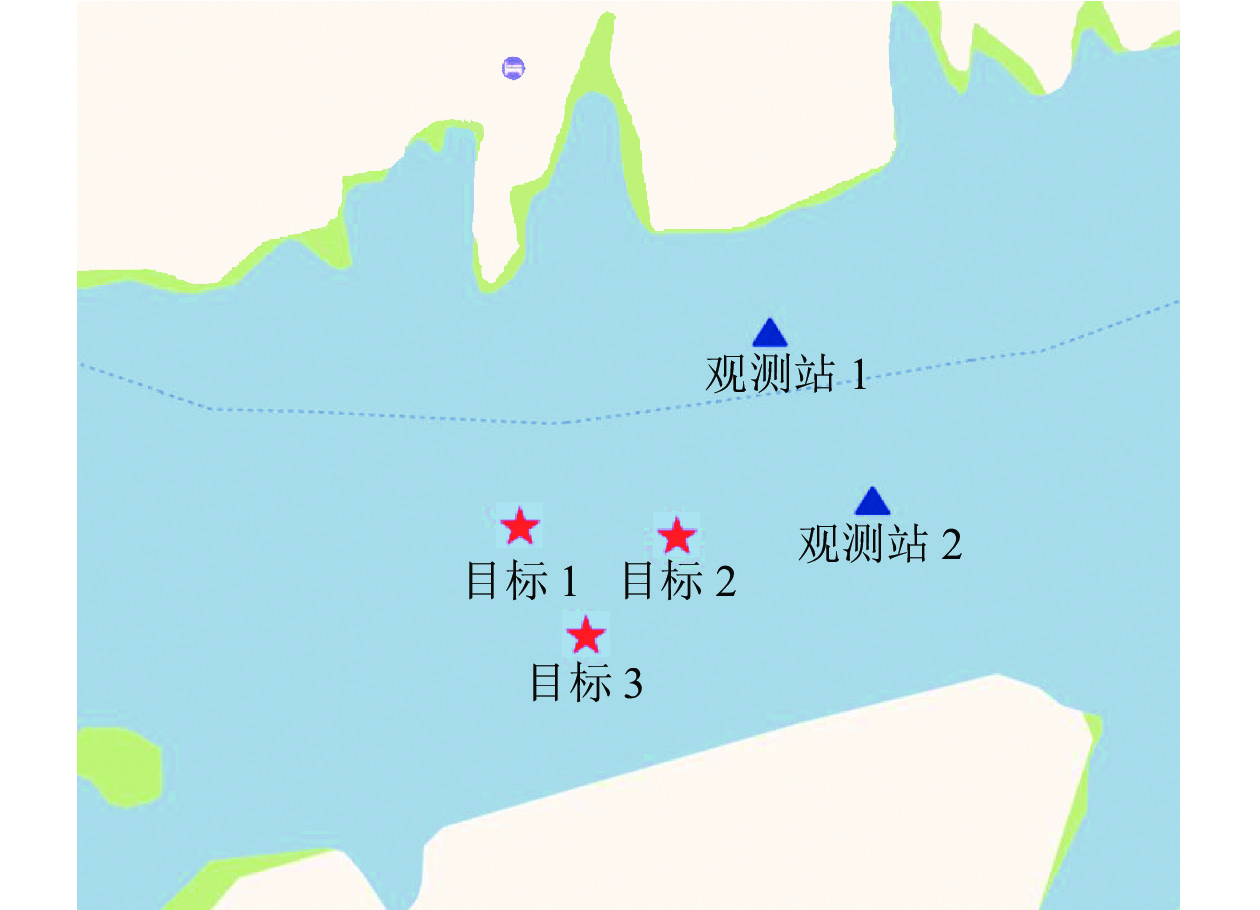
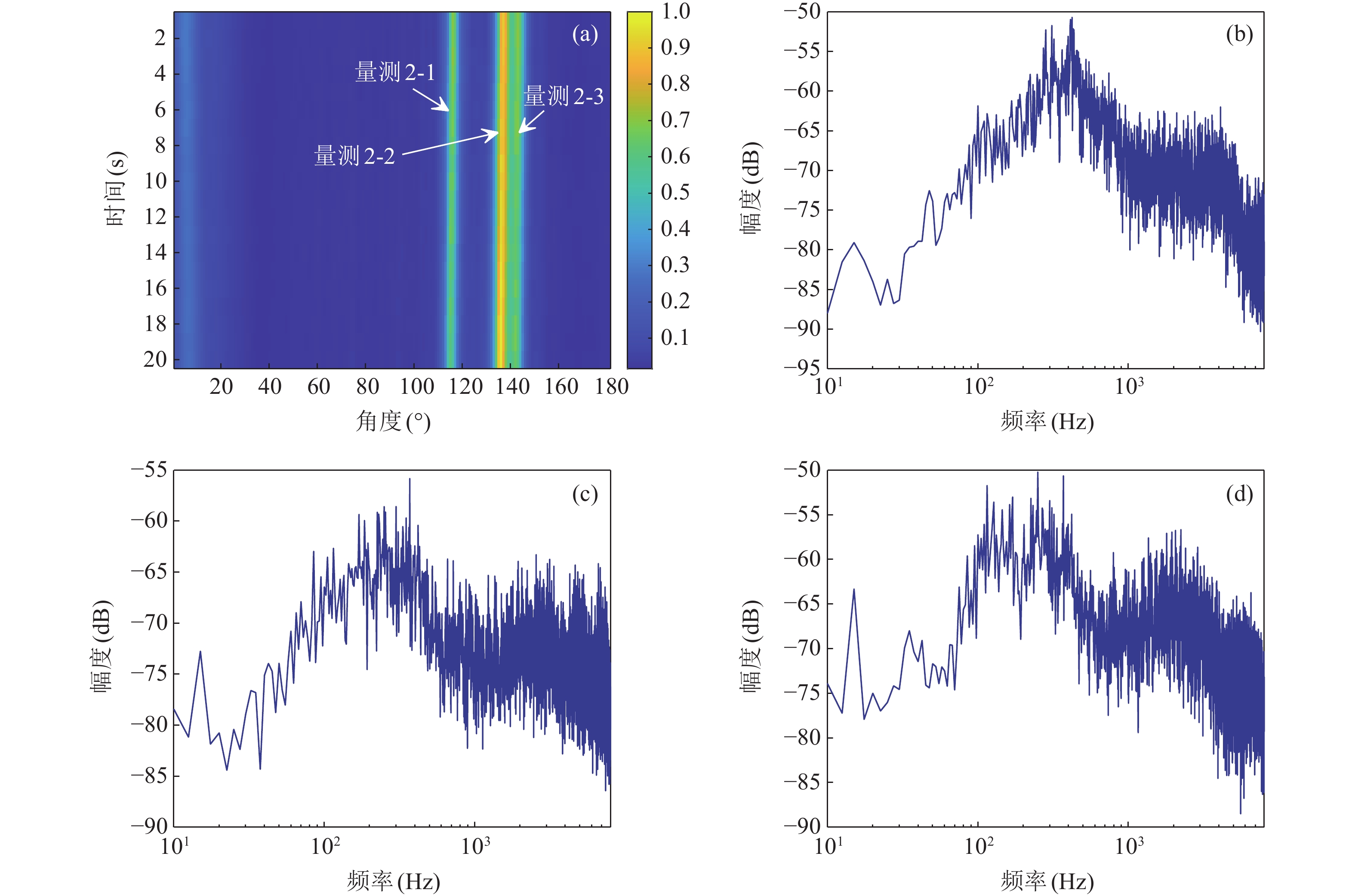
利用2022年11月在吉林省松花湖进行的多站非合作定位试验来验证本文算法性能。试验中采用2条固定吊放在水下的观测站对监测区域内的非合作目标进行监测。选取某段观测时间内的20 s观测数据进行处理, 其间目标和观测站均相对静止。通过对该观测时间内的全球定位系统信息进行提取, 位置关系如图17所示。

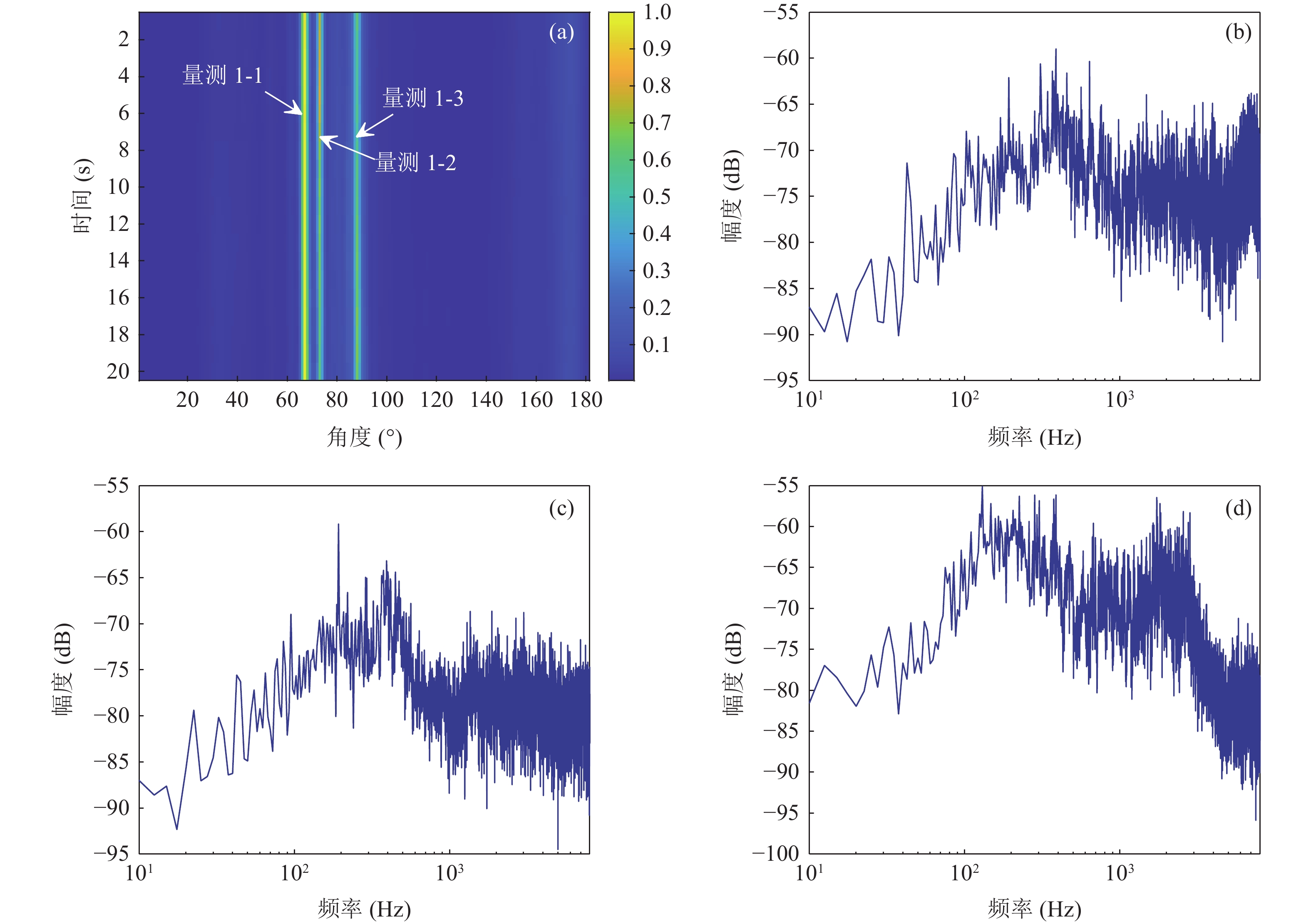
对选取观测时间内观测站阵列的接收信号进行目标方位谱估计, 对场景中的目标进行阈值检测并对通过门限的方位进行功率谱提取, 获取目标工作频段的辐射噪声功率谱, 两个观测站获得的极坐标系下方位谱和功率谱如图18和图19所示。

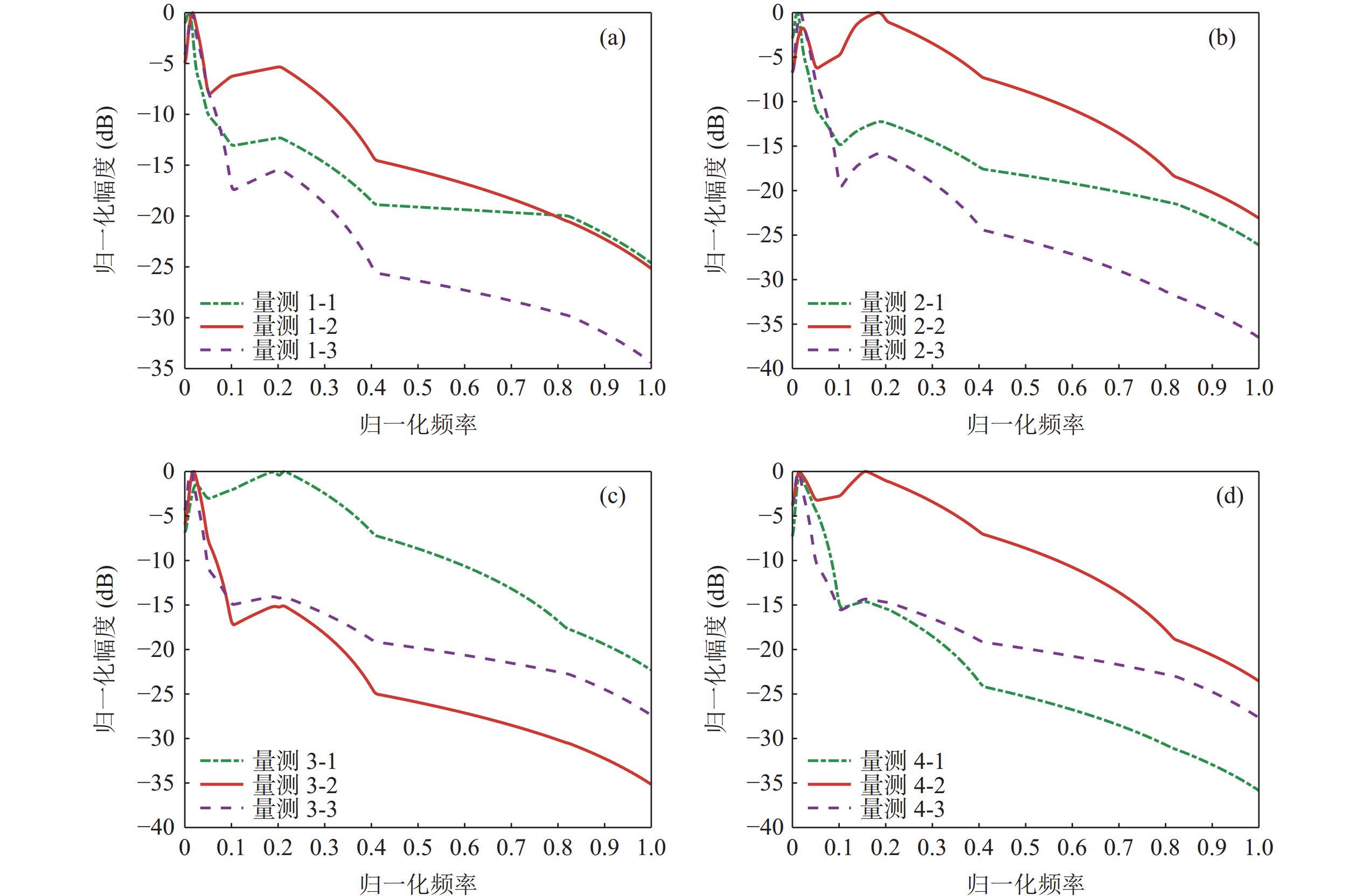
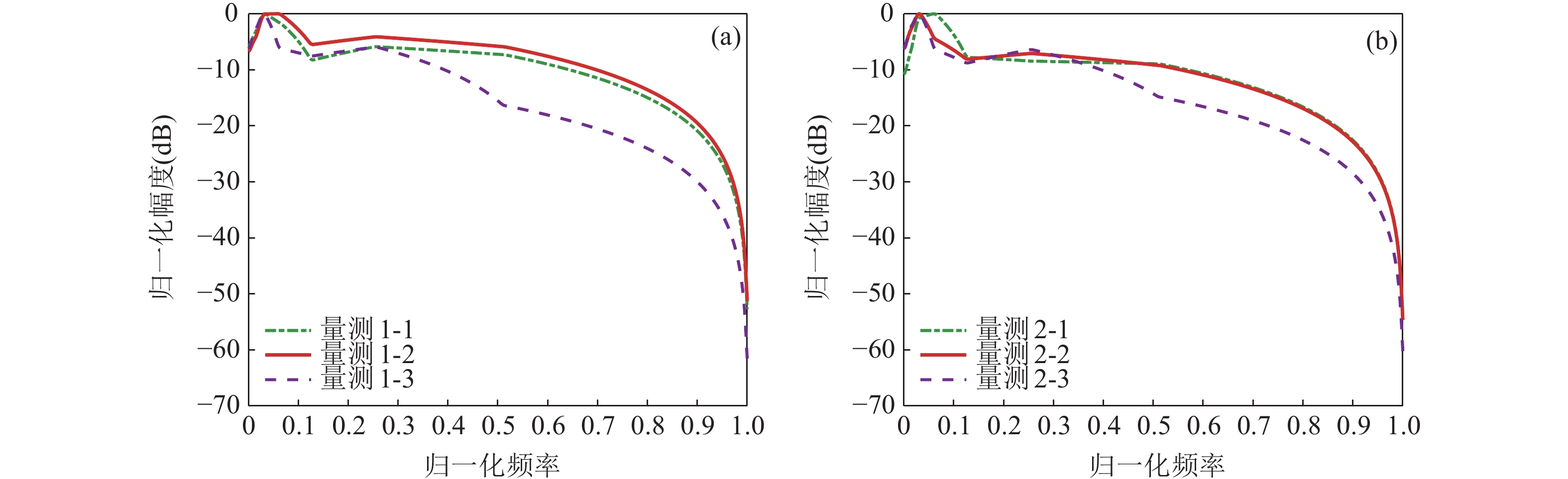
观测站提取的连续谱特征和线谱分别如图20和表6所示, 观测站量测批号和目标真实序号的对应关系如表7所示。量测1-2与量测2-1、量测1-3和量测2-3的连续谱特征形状更为相似, 其间的模糊隶属度较高。但量测1-1、量测1-2、量测2-1和量测2-2这四个批次的线谱量测区分程度并不明显, 这是由于目标在观测站的视野中方位临近而产生线谱串扰, 使得线谱特征模糊。

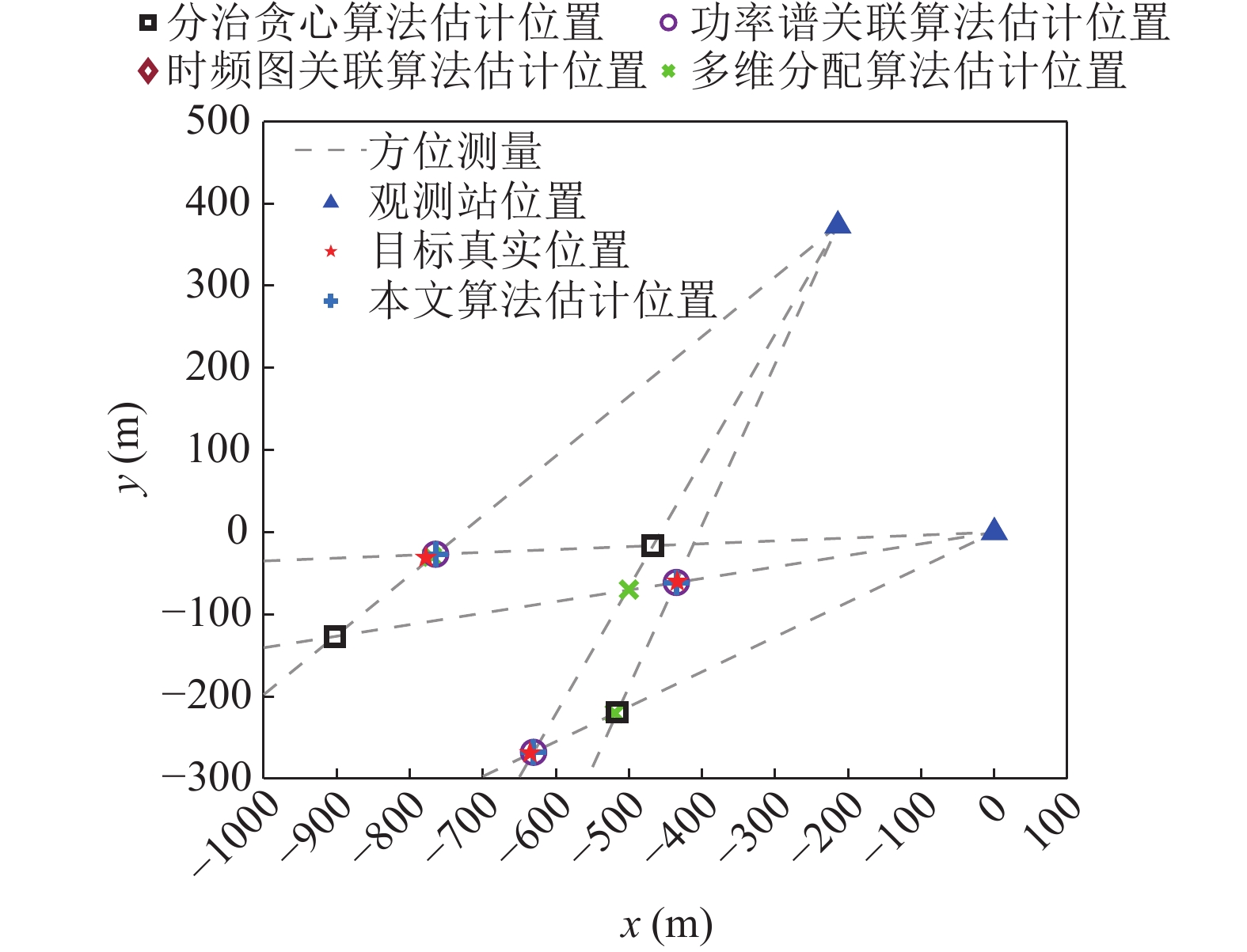
同样选用多维分配算法、分治贪心算法、功率谱关联算法、时频窗关联算法与本文算法进行关联比较, 其中模糊度隶属门限$\delta {\text{ = 0}}{\text{.3}}$, 最大容忍频偏$ \Delta f = 6 $ Hz。如图21所示, 此场景中只有本文算法和功率谱关联算法能够正确关联, 本文算法选择连续谱特征和线谱特征中最清晰的特征进行关联, 可以在一定程度上避免方位临近的干扰。该结果表明, 本文算法在实际试验场景中可以成功关联。

本文针对分布式水声非合作定位算法目标关联问题, 提出了一种多站联合观测非合作目标的定位批号关联算法。该方法利用模糊数学理论分别构建方位、连续谱特征以及线谱特征的模糊关系矩阵; 利用匈牙利算法对合成的综合模糊关系矩阵进行二维关联; 通过隶属度门限和方位门限取消低隶属度关联。仿真结果表明, 在一定虚警和漏报的场景下, 本文算法的关联召回率超过0.8, 而关联结果精度均高于对比的传统算法。在湖试场景中, 本文算法也能成功对目标进行关联。本文算法充分利用目标特征信息, 适用于复杂的水下场景。