-
目前, 噪声治理中广泛使用以无机纤维为代表的多孔吸声材料和以微穿孔板为代表的共振吸声结构。前者中低频吸声能力不足, 且质轻、性脆、易折断飞扬, 环境友好度和耐候性能不佳; 后者由穿以大量微孔的薄板附加背腔构成[1-2], 其中低频吸声性能良好, 无需填充多孔材料, 耐候性能优良。微穿孔板有较高的理论吸声带宽极限[3], 但其实际有效吸声频带一般较窄, 且面板厚度较薄, 机械强度有限, 微孔尺寸较小、数目庞大, 加工制备困难, 制约了微穿孔板吸声结构的大规模推广应用。在噪声控制领域, 获得宽频、高效、实用的微穿孔板吸声结构一直都颇具挑战性[4]。
高穿孔率的微穿孔薄板结构易于在较宽频带内获得足够的声阻和较小的声抗以匹配传播介质的特性阻抗, 进而最大限度地接近吸声性能理论极限。但几何参数的严苛要求使得一般的微穿孔板结构难以获得宽频吸声性能, 为此学者们提出了很多改进方案, 如设置微穿孔板串联[5-6]、并联[7-8]结构, 形成多重共振峰拓展吸声频带宽度; 借助微穿孔板与多孔材料[9-11]、机械阻抗[12]、亥姆霍兹共鸣器[13]等的复合, 引入高频耗能作用或低频共振装置, 拓展结构在高频或低频段的吸声性能; 在背腔内设置分割[14]、蜂窝[15]、卷曲空间[16-17]等结构, 改变声波传播路径, 拓展吸声带宽。上述方案均需引入微穿孔板之外的因素或改变孔板几何参数, 使系统变得复杂。
于是, 学者们致力于在孔、板本身找到解决问题的方案。针对圆形孔的研究已比较成熟, 其他孔型性能类似[18]。Ning等[19]对比研究了圆形孔、方形孔、三角孔的吸声性能, 指出相同截面积下三角孔吸声性能更优。在单位面积孔数不变的情况下, 微缝孔具备相同声阻下声抗最小的优势, 较小的声抗有利于扩大吸声结构的作用频带范围[4,20]。
薄板易于平衡好微穿孔板的声阻和声抗而获得良好的吸声性能, 却难以具备较高的机械强度。吕世明[21]制作了一种孔内结构复杂突变的微孔金属吸音板, 在厚板上实现了较好的吸声性能。Jiang等[20]通过热黏性声学仿真发现变截面微孔的能量损失主要集中在小孔段, 其突变处产生了额外的声阻抗, 而大孔段的吸声作用较小但起到了很好的支撑作用。
微穿孔板能否大规模推广应用主要取决于微孔实现的难易。目前, 常用的微孔制作方法包括冲压机械加工、激光打孔、电化学腐蚀和增材加工技术等。这些方法在加工高穿孔率超微孔时成本依然较高, 且在厚板上加工远小于板厚的微孔时难以保证加工质量。
本文将微穿孔板分离为支撑部件(大孔基板)和吸声部件(微缝薄膜), 在大孔基板上贴覆薄膜并于薄膜表面对应基板通透处连续机械作用, 自然快速形成大量微裂缝, 形成微裂缝吸声板[22]。根据微裂缝的几何特点提出了一般化的几何结构, 然后分别从大孔基板和微缝薄膜两方面理论计算板膜整体的声阻抗率, 使用热黏性声学仿真分析孔缝内外声场, 量化分析入口端、孔内段、孔缝连接处、缝内段和出口端的声阻抗率, 给出了考虑热黏性作用的狭长缝声阻抗末端修正模型, 并讨论了微裂缝板的等效几何参数和几何参数对吸声性能的影响。
-
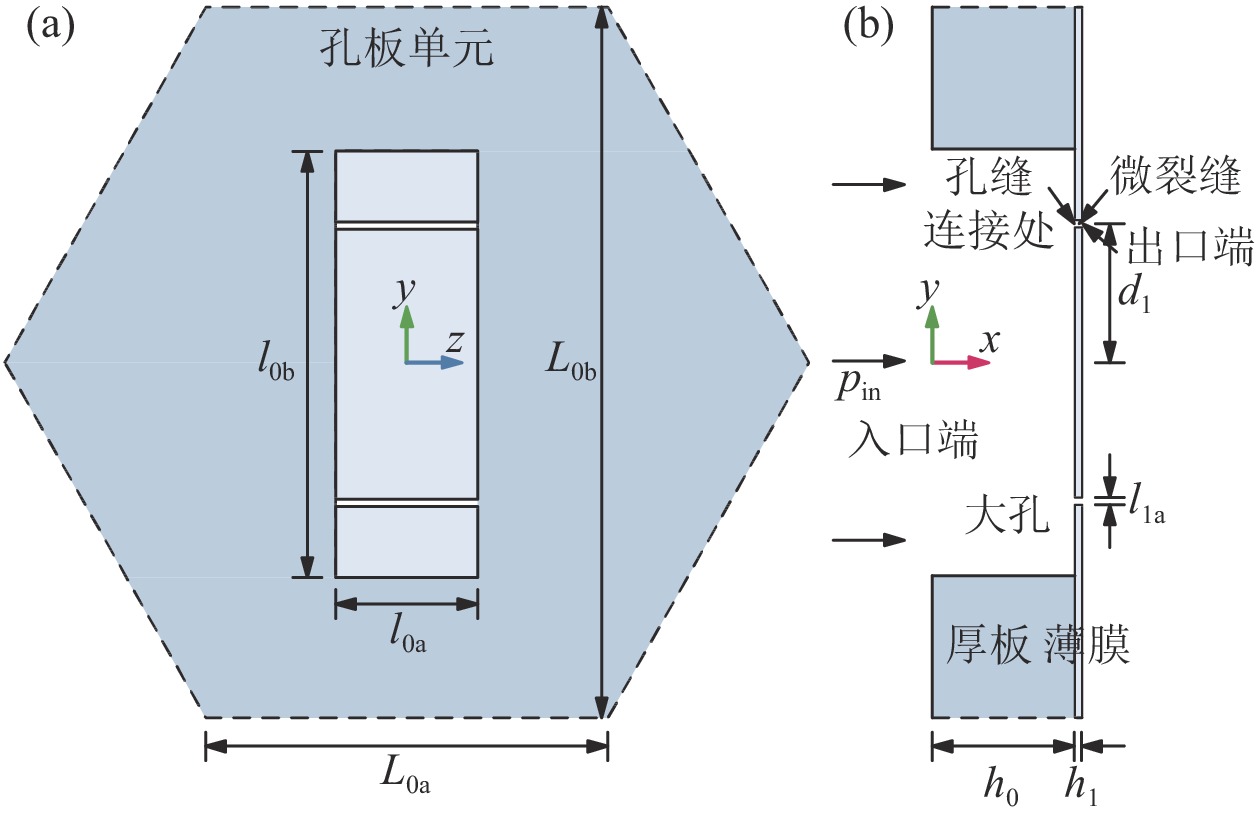
基板上的大孔一般为圆形孔或矩形孔, 前者宜于加工, 便于实际工程应用; 后者刻划产生的微裂缝的缝长是定值, 在缝长、工艺等参数不变的情况下, 缝宽基本保持不变。本文对矩形孔进行分析。在矩形孔基板上贴覆一层铝箔, 在铝箔上间隔一定距离对应大孔位置处运用刀具刻划, 每个大孔产生2 ~ 3条微裂缝, 如图1所示。矩形孔尺寸为
$ {l_{{\text{0a}}}} \times {l_{{\text{0b}}}} $ , 呈周期性六边形晶格分布, 孔短边、长边的间距分别为$ {L_{{\text{0a}}}} $ 和$ {L_{{\text{0b}}}} $ , 板厚为$ {h_{\text{0}}} $ , 膜厚为$ {h_{\text{1}}} $ , 单个孔板单元如图2所示。微裂缝的空间形态比较复杂, 主要由水平方向的撕裂和垂直方向的错位形成, 图1给出了工业CT (型号: Nano Voxel 4000)扫描的单孔剖面图。将微裂缝简化为一般的直通型狭长缝, 缝宽为$ {l_{{\text{1a}}}} $ , 缝长为矩形孔的短边长度$ {l_{{\text{0a}}}} $ , 每个大孔对应2条缝, 缝的位置偏离矩形孔长边中心线$ d_1 $ 处。微裂缝吸声板的一般化几何参数如表1所示。 -
微穿孔板吸声结构主要通过结构与声波发生孔−腔共振而消耗声能。其声能耗散作用主要包括两部分, 一是孔内效应, 主要由孔内的黏滞摩擦所引起; 二是末端效应, 由声波出入微孔时沿障板流动产生的摩擦损失、孔内空气柱振动产生的末端声辐射、声线弯折以及孔间相互作用所引起[1]。微穿孔板结构具有较高的理论吸声带宽极限, 当最大吸声系数达1.0时, 有效吸声频程(有效吸声上限频率与下限频率的比值)极限值达5.78; 当最大吸声系数降为0.9时, 有效吸声频程极限值提升为7.60[3]。微裂缝吸声板本质上仍是一种微穿孔板, 主要由大孔基板和微缝薄膜两部分构成。
-
声波作用于圆形孔时, 孔内黏滞摩擦引起的声阻抗率为[1-2]
其中,
$ \omega $ 为角频率;$ {\rho _0} $ 为空气密度;$ {\text{j}} $ 为虚数单元;${{\text{J}}_0}( \cdot )$ 和${{\text{J}}_1}( \cdot )$ 分别为零阶和一阶贝塞尔函数;$ h_0 $ 为圆形孔所在板的厚度;$ {k_{\text{0}}} $ 为穿孔常数, 正比于半径与黏滞边界层厚度的比值,$ {k_{\text{0}}} = {r_0}\sqrt {{{{\rho _0}\omega } \mathord{\left/ {\vphantom {{{\rho _0}\omega } \eta }} \right. } \eta }} $ ,$ {r_0} $ 为圆形孔的半径,$ \eta $ 为空气的剪切黏滞系数(1.79 × 10−5 N·s/m2, 20 ℃, 标准大气压)。空气出入微孔时一部分沿障板流动, 产生摩擦损失, 引起声阻抗末端修正; 孔内空气柱振动引起孔外空气跟随振动, 延伸了有效孔长, 引起声质量末端修正; 微孔出入口处声线弯折产生静态流阻; 气流通过微孔时影响旁边微孔通过的气流, 导致声线弯折区域减少, 影响声阻抗末端修正。Li[23]综合考虑上述四方面作用, 运用黏热理论提出圆形孔的单侧声阻抗末端修正为
其中, 式(2a)等号右侧第1项表示摩擦损失引起的声阻抗末端修正, 第2项表示声线弯折引起的声阻末端修正; 式(2b)等号右侧第1项表示声辐射引起的声抗末端修正, 第2项与式(2a)右边第1项一致。
$ {R_S} $ 表示振荡流在无限延伸的平面上产生的表面阻抗,$ {R_S} = {\sqrt {2\omega {\rho _0}\eta } }/2 $ 。矩形孔也具有类似圆形孔的作用, 其孔内黏滞摩擦引起的声阻抗率为[10]
其中,
$ {\alpha _m} = \left( {2m + 1} \right){\pi \mathord{\left/ {\vphantom {\pi {{l_{{\text{0a}}}}}}} \right. } {{l_{{\text{0a}}}}}} $ ,$ {\beta _n} = \left( {2n + 1} \right){\pi \mathord{\left/ {\vphantom {\pi {{l_{{\text{0b}}}}}}} \right. } {{l_{{\text{0b}}}}}} $ ,$ m $ ,$ n $ 为自然数。当矩形孔的长宽比较小时, 可以将其等效为圆形孔(直径为等效水力直径)计算其声阻抗末端修正[20]。
-
当矩形微孔一边无限长时, 微孔变为微缝, 缝内黏滞摩擦引起的声阻抗率为[24]
其中,
$ {k_{\text{1}}} = {{{l_{{\text{1a}}}}\sqrt {{{{\rho _0}\omega } \mathord{\left/ {\vphantom {{{\rho _0}\omega } \eta }} \right. } \eta }} } \mathord{\left/ {\vphantom {{{l_{{\text{1a}}}}\sqrt {{{{\rho _0}\omega } \mathord{\left/ {\vphantom {{{\rho _0}\omega } \eta }} \right. } \eta }} } 2}} \right. } 2} $ 。第1节中介绍的微缝的长宽比达到11.1, 可以近似看作一边无限延伸的微缝。缝内声阻抗率也可用近似式进行计算:缝的声阻抗末端修正比圆形孔更复杂。Ingard[25]基于模态展开法推导了矩形孔位于矩形通道中的声质量末端修正。马大猷[24]认为缝的声阻末端修正与圆形孔一致, 并将缝近似为椭圆端口求解其声抗末端修正。Zieliński等[26]运用等效流体法预测了微缝吸声结构的声阻抗率。Aulitto等[27]分别运用二维流的保角变换和薄边界层近似等方法计算了微缝的声阻抗末端修正。上述声阻抗末端修正均未考虑黏热的影响, 声阻抗末端修正有一定误差, 尤其对于缝宽较小且长宽比较大的狭长缝, 声阻末端修正与实际出入较大。
经典理论很少考虑板振动的影响, 而对于轻薄材料制成的微穿孔板, 其自身振动的影响不容忽视。Bravo等[28]和侯九霄等[29]利用耦合模态法研究了薄板振动对微穿孔板吸声性能的影响。薄膜上穿孔也能实现类似微穿孔板的吸声性能, Li等[30]根据穿孔边界的速度连续性分析了考虑薄膜振动的圆孔薄膜结构的声阻抗率。这些研究中板或薄膜周界施加了约束, 其面积远大于单孔面积, 板或薄膜的最大振动速度与孔内质点振动速度比较接近。
基板通透孔处对应薄膜的运动方程为[31]
其中,
$ \xi $ 为薄膜的横向位移,$ E $ 为膜材质的杨氏模量,$ \rho $ 为薄膜的密度,$ \sigma $ 为泊松比,$ T $ 为薄膜的张力,$ t $ 表示时间。本文中薄膜平铺在基板上, 未预先张紧, 通透孔内薄膜恢复平衡的力主要由自身劲度产生, 薄膜四周均受到通透孔的约束。以未开缝四边简支的矩形铝箔为例, 其振动的一阶简正频率为
可以计算出,
$ {f_{{\text{11}}}} $ 为1.4 × 104 Hz, 远高于正常关注的中低频吸声频率。薄膜开微缝后, 边界条件发生改变, 其一阶简正频率略有变化[32], 仍远高于关注频率。因此, 可忽略薄膜振动的影响。 -
孔缝结构可看作是由入口端、孔内段、孔缝连接处、缝内段和出口端共5部段构成, 孔缝结构本身的声阻抗率可由5部段声阻抗率的线性叠加而构成。考虑到各部段的穿孔率差异, 大孔基板对板膜整体声阻抗率的贡献为
其中,
$ {Z_0} $ ,$ {Z_{{\text{in}}}} $ 分别表示孔内段、入口端的声阻抗率。孔缝连接处和缝的出口端均为微缝的末端, 微缝薄膜对整体声阻抗率的贡献为
其中,
$ {Z_1} $ ,$ {Z_{10}} $ ,$ {Z_{{\text{out}}}} $ 分别表示为缝内段、孔缝连接处和出口端的声阻抗率。板膜整体的声阻抗率为大孔基板和微缝薄膜的声阻抗率之和,
$ Z = {Z'_{\text{0}}} + {Z'_{\text{1}}} $ 。板后部设置一定厚度的密闭空腔便构成了微裂缝吸声结构, 空腔的声阻抗率为$ {Z_D} = - {\text{j}}{\rho _0}{c_0}\cot \left( {{{\omega D} \mathord{\left/ {\vphantom {{\omega D} {{c_0}}}} \right. } {{c_0}}}} \right) $ , 其中$ D $ 为空腔深度。相对于空气特性阻抗, 微裂缝吸声板的相对声阻抗为$ {\textit{z}} = {Z \mathord{\left/ {\vphantom {Z {{\rho _0}{c_0}}}} \right. } {{\rho _0}{c_0}}} $ , 空腔的相对声阻抗为$ {{\textit{z}}_{\text{D}}} = {{{Z_{\text{D}}}} \mathord{\left/ {\vphantom {{{Z_{\text{D}}}} {{\rho _0}{c_0}}}} \right. } {{\rho _0}{c_0}}} $ 。在声波作用下, 微裂缝吸声结构的法向吸声系数为其中,
$ {\text{Re}} (\cdot)$ 和$ {\mathrm{Im}}(\cdot) $ 分别表示实部和虚部。 -
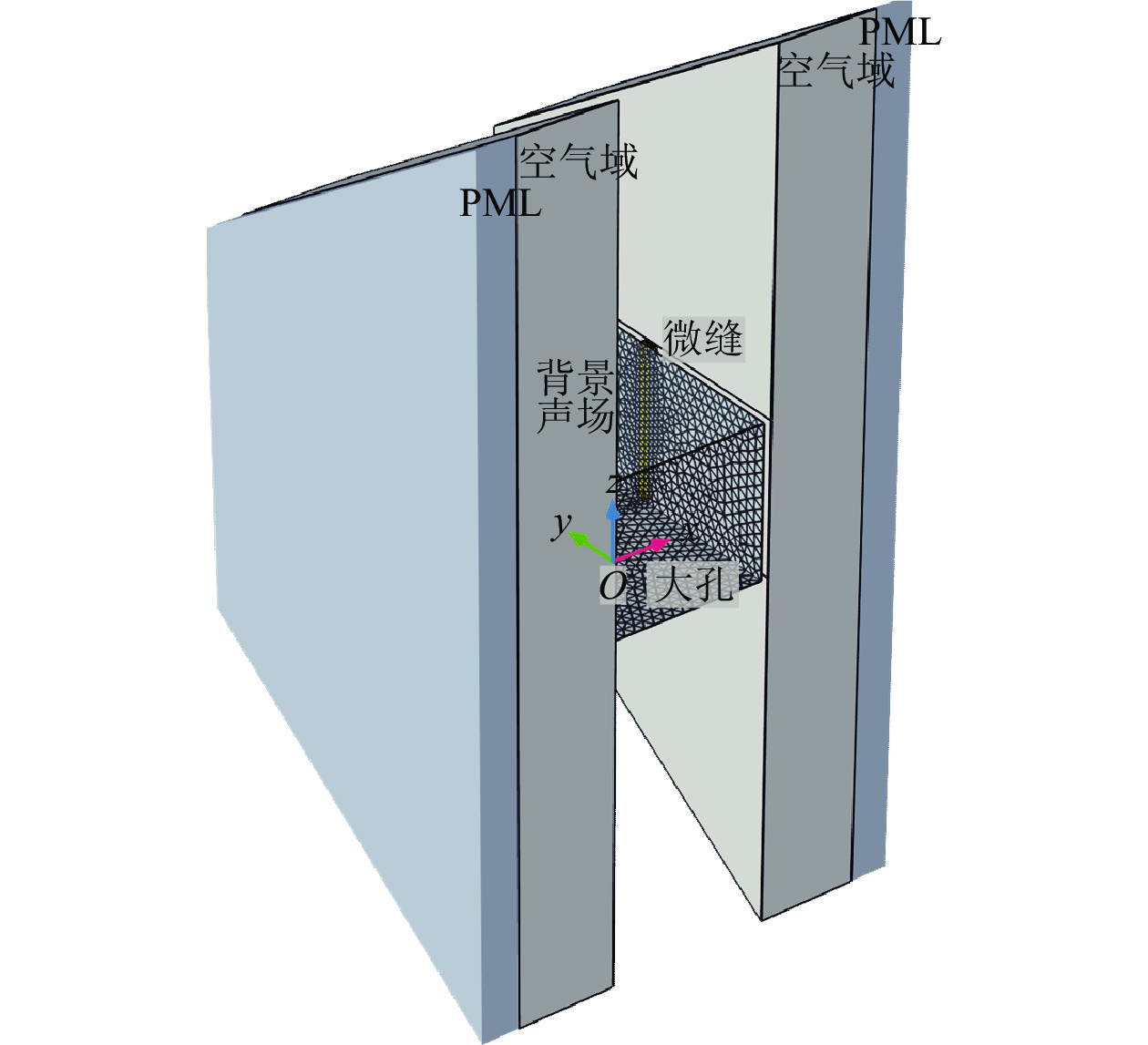
考虑到计算成本, 仅对产生黏热物理现象的系统组件进行仿真。一般微孔呈周期性分布, 选择一个基本单元进行研究, 由于单元呈对称分布, 使用COMSOL Multiphysics®对1/2单元进行热黏性声学频域物理场接口的三维数值仿真。仿真单元由孔隙、孔隙两端的空气域、空气域两端的完美匹配层(PML)构成, 完美匹配层是模拟开放域或无限域的特殊介质层, 其声阻抗与相邻介质完全匹配, 声波可以无反射地穿过分界面而进入完美匹配层, 并被完全吸收无反射波。设置坐标原点位于大孔左端面的中心,
$ x < 0 $ 的空气域设置为单位幅值的平面波入射的背景声场, 即声波从大孔端入射。空气域和完美匹配层的厚度分别设置为10倍和4倍缝宽。与板、膜接触的边界均设置为无滑移、等温壁面边界条件, 对称面($ y = 0 $ )设置为对称边界条件, 其他均设置为滑移、绝热边界条件。大孔、微缝和空气域均划分为自由四面体网格, 其中与板、膜接触的网格最大尺寸设置为黏性边界层厚度($ {\delta _{{\text{visc}}}} = \sqrt {{{2\eta } \mathord{\left/ {\vphantom {{2\eta } {\omega {\rho _0}}}} \right. } {\omega {\rho _0}}}} $ ), 其他网格最大尺寸均设置为$ {{{l_{{\text{0a}}}}} \mathord{\left/ {\vphantom {{{l_{{\text{0a}}}}} 6}} \right. } 6} $ , 完美匹配层的网格采用扫掠法进行划分, 网格层数不少于6层, 如图3所示, 其中展示了微缝和部分大孔的网格。 -
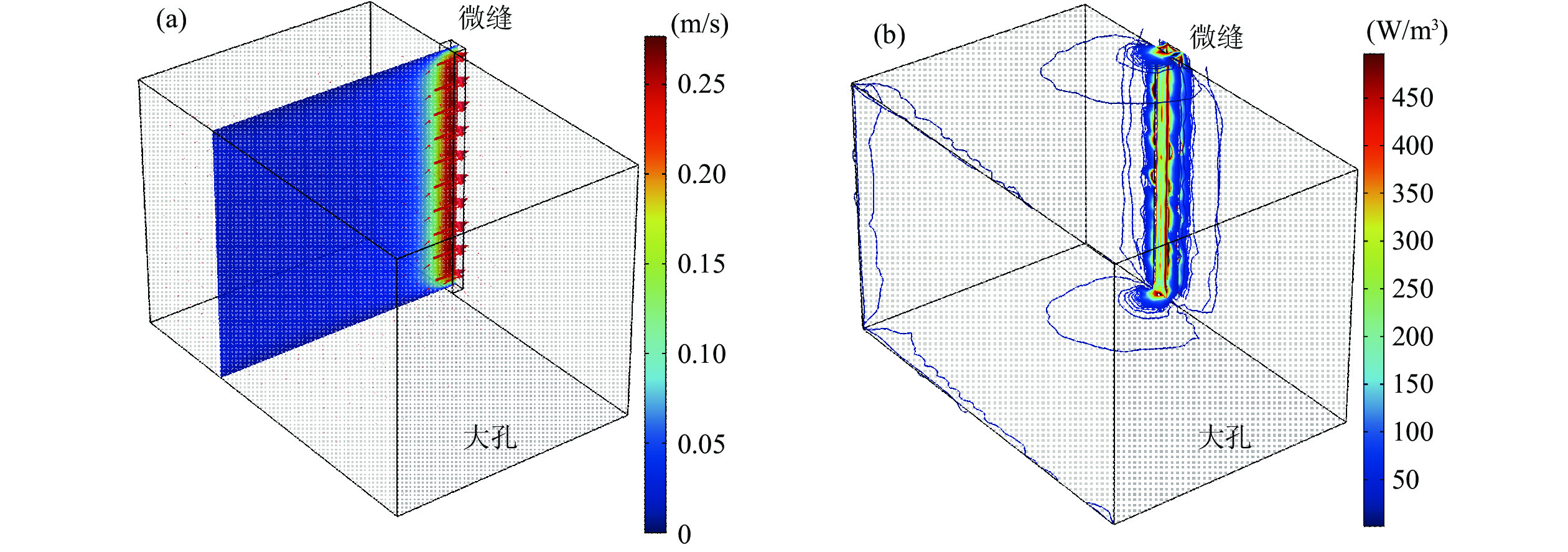
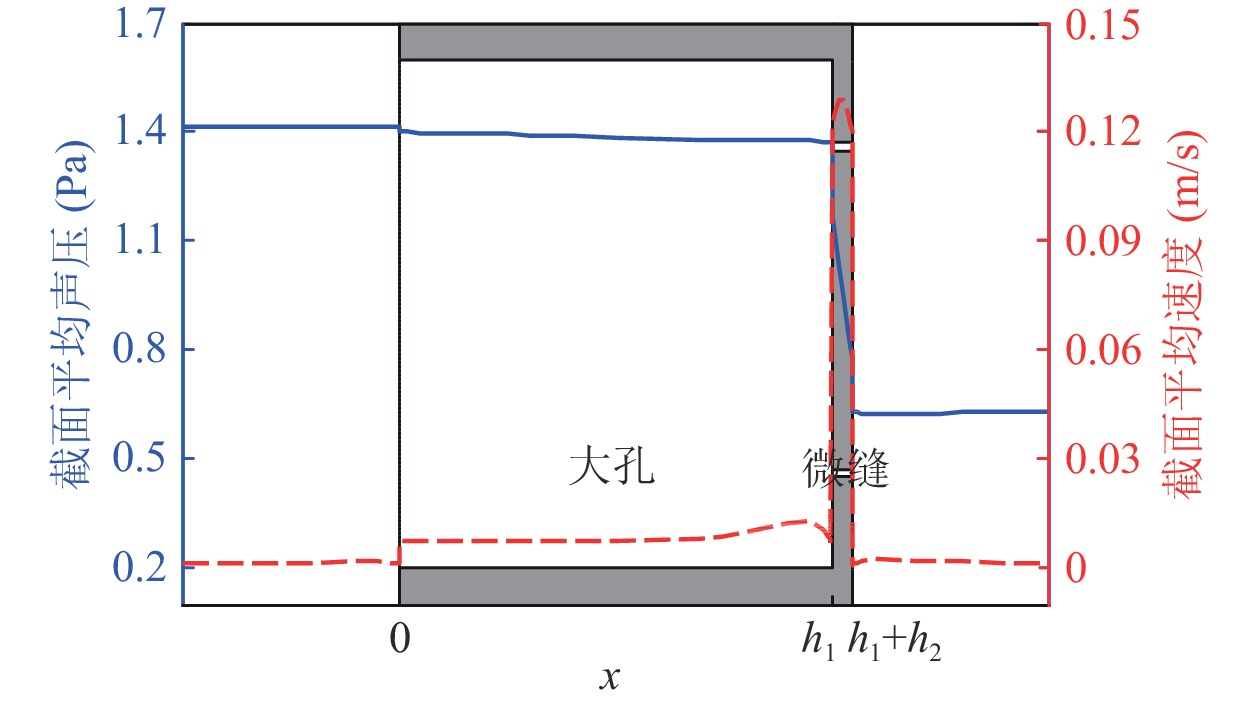
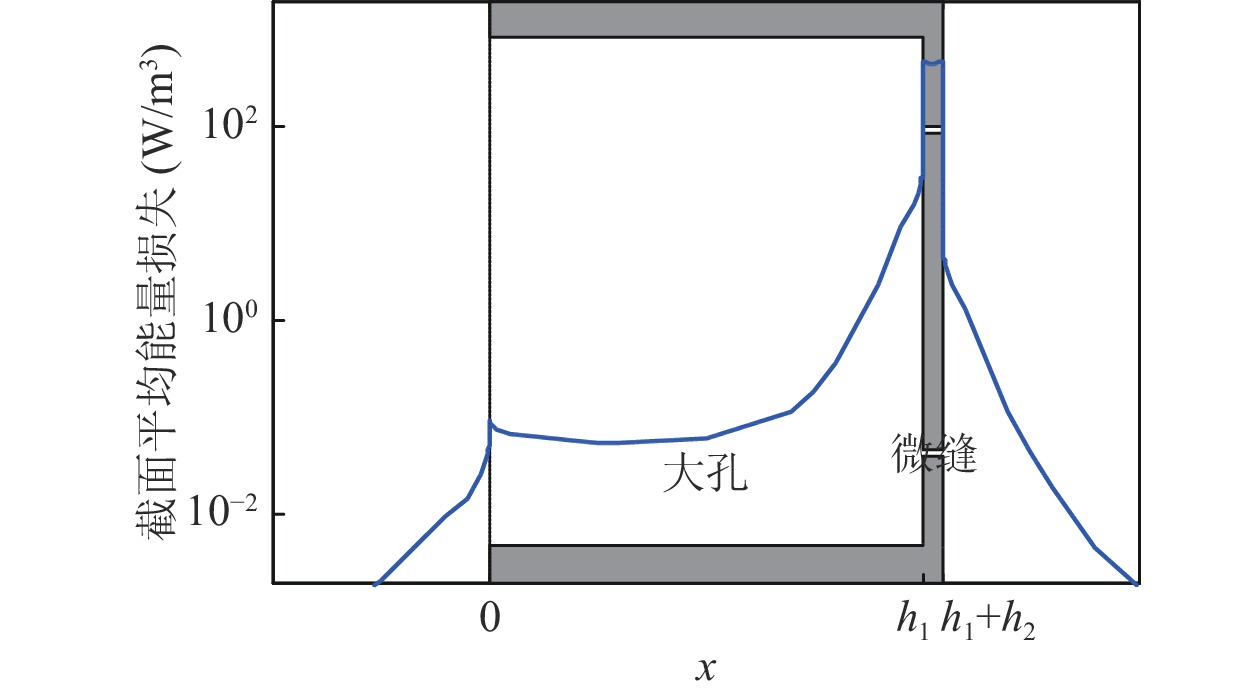
仿真得到频率1000 Hz时孔缝内速度矢量分布和总黏热能量损失密度的等值线分布, 如图4所示, 其他频率处规律相似。由图可见, 大孔内速度矢量逐渐向微缝汇聚, 且速度大小逐步递增, 直至在微缝内速度达到最大, 孔、缝壁面处速度均为零, 黏热能量损失主要集中在缝内外壁面处。图5和图6分别给出了孔、缝内外总声压、总瞬时速度和总黏热能量损失密度的截面平均值沿厚度方向的变化规律。可以看出, 声压沿x轴正方向逐渐递减, 大孔内声压衰减缓慢, 微缝内声压变化剧烈, 孔缝连接处和缝出口端声压骤降, 孔、缝外声压基本保持不变。在声压差的驱动下, 微缝内速度显著偏高, 对应的黏热能量损失密度显著偏高, 均远大于大孔内对应的值。
-
板膜整体的声阻抗率可通过结构两侧声压差与孔内平均速度之比计算得到:
其中,
$ \Delta p $ 为入口端和出口端两侧总声压的截面积分值之差,$ \Delta p = \iint_{{S_{{\text{in}}}}} {{p_{\text{t}}}{\text{d}}S} - \iint_{{S_{{\text{out}}}}} {{p_{\text{t}}}{\text{d}}S} $ ,$ {p_{\text{t}}} $ 为总声压, 表示入射声压与反射声压之和,$ {S_{{\text{in}}}} $ 和$ {S_{{\text{out}}}} $ 分别表示入口端和出口端孔板单元截面;$ U $ 为孔缝内轴向速度的截面积分, 对于大孔和微缝组成的变截面结构:其中,
$ {u_x} $ 表示孔、缝内轴向速度,$ \varOmega $ 表示孔、缝组成的区域。仿真计算得到板膜整体的声阻抗率, 难以直接剥离出各部段贡献的声阻抗率。参考上述方法, 分别对仅含有大孔和微缝的结构进行仿真, 其他设置均保持一致。经计算可得到仅含大孔和仅含微缝结构的声阻抗率。一般, 直通型微孔结构的入口端声阻抗末端修正与出口端一致[23]。经代数运算, 可计算出孔缝连接处的声阻抗率。仅含大孔和微缝结构的声阻抗率分别减去孔内声阻抗率(式(3))和缝内声阻抗率(式(4)), 可得入口端和出口端的声阻抗率。
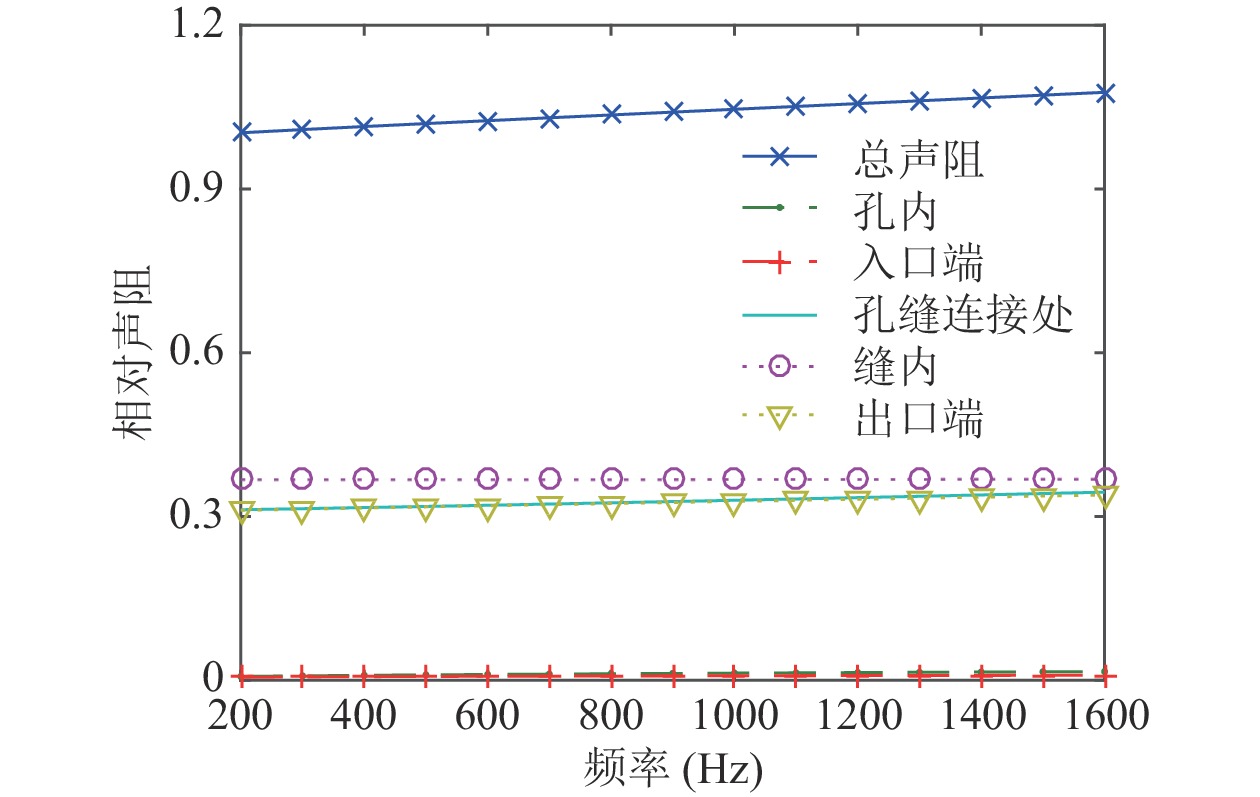
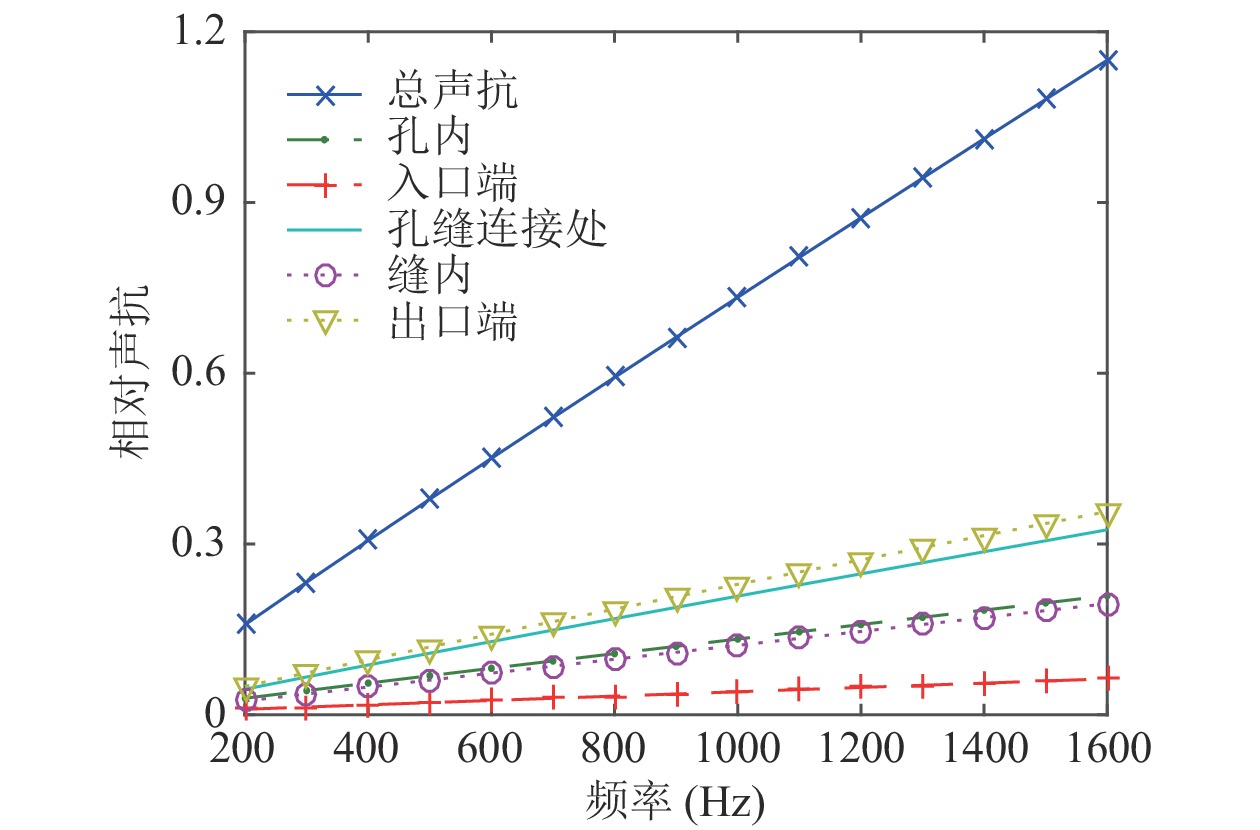
各部段和板膜整体的声阻抗率如图7和图8所示。随着频率的增加, 声阻变化较小, 而声抗变化较大; 孔内段和入口端贡献的声阻非常小, 可忽略不计, 但两者尤其前者对声抗的贡献量不可忽略; 缝内段是声阻的最大贡献者, 而缝的出口端是声抗的最大贡献者; 孔缝连接处和出口端的声阻末端修正几乎一致, 而后者的声抗末端修正则略微偏大。吸声良好的微穿孔板结构需要面板在较宽的频带范围内获得足够的声阻和较小的声抗以匹配空气特性阻抗, 准确获得微裂缝吸声板各部段的声阻抗率贡献有助于吸声结构的优化设计。
孔缝连接处和出口端均是缝的末端, 两处的声阻末端修正之和和声抗末端修正之和对板膜整体的声阻抗率贡献均超过了50%, 其准确计算非常关键。前述微缝声阻抗末端修正模型并未考虑黏热效应的作用, 对缝宽小且长宽比大的狭长缝的适应性较差。
-
对狭长缝开展系列仿真, 拟合确定其声阻抗末端修正模型。结合微裂缝生产工艺的特点, 仿真参数设置为: (1) 缝宽
$ {l_{{\text{1a}}}} $ 分别为0.08 mm, 0.10 mm, 0.12 mm, 缝的长宽比$ {r_{{\text{ab}}}} $ 分别为10, 20, 30, 穿孔率$ {\phi _{\text{1}}} $ 分别为0.6%, 1%, 2%, 4%, 6%; (2) 仿真单元内设置2条缝且分别偏离矩形孔长边中心线$ {{{l_{{\text{0b}}}}} \mathord{\left/ {\vphantom {{{l_{{\text{0b}}}}} 3}} \right. } 3} $ 处, 充分考虑缝之间的相互作用和缝相对于末端的位置对声阻抗的影响; 计算频率分别设置为200 Hz, 500 Hz, 1000 Hz, 2000 Hz, 4000 Hz, 缝末端边界设置为滑移、绝热边界条件, 共设计225个算例。参考3.1节和3.3节, 计算各算例的声阻和声抗末端修正值。根据2.1节理论可知, 声阻末端修正主要取决于表面阻抗作用(与频率相关)、声线弯折机制(与缝宽相关)和孔间相互作用(与穿孔率相关), 声抗末端修正主要取决于末端声辐射(与缝宽和频率相关)、表面阻抗作用(与频率相关)和孔间相互作用(与穿孔率相关)。假设狭长缝的声阻抗末端修正具有与圆形孔类似的基本形式, 使用非线性最小二乘法的优化算法进行拟合, 狭长缝的单侧声阻抗末端修正经验模型为
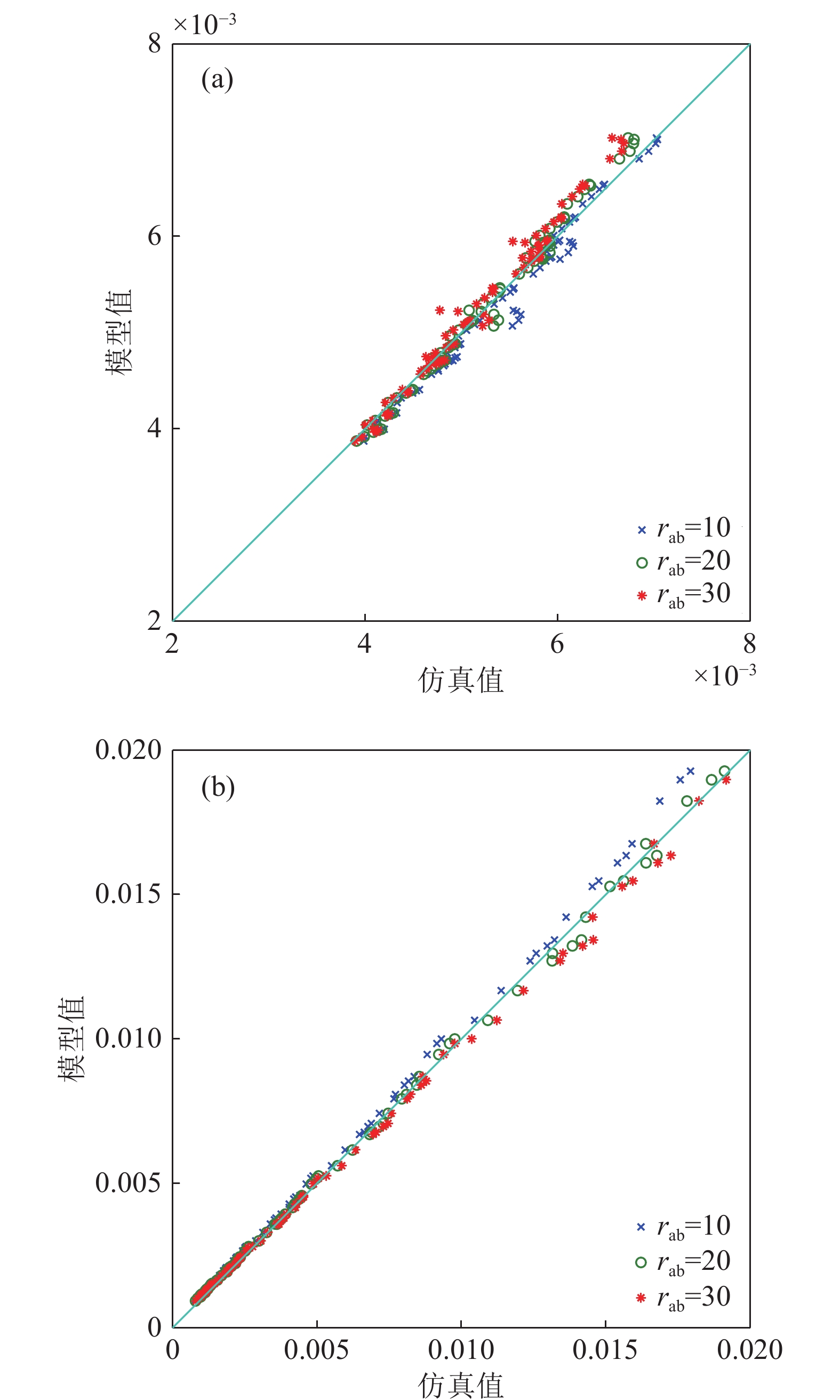
上述拟合的相关系数分别为0.9867和0.9985。由式(13a)和式(13b)计算出的225组算例的声阻和声抗末端修正值与仿真结果的一致性较好, 如图9所示。不同长宽比的仿真结果差异较小, 因此模型并未考虑长宽比的影响。上述模型适用的缝宽范围为0.08 ~ 0.12 mm, 穿孔率范围为0.6% ~ 6.0%, 长宽比范围为10以上, 频率范围为200 ~ 4000 Hz。
由式(13a)和式(13b)可知, 当缝宽很小时, 声线弯折机制起主要作用; 穿孔率对声阻末端修正影响较小, 而对声抗末端修正影响较大, 故出口端和孔缝连接处的声阻几乎一致而后者声抗偏高。出口端和孔缝连接处均是缝的末端, 两者主要差别在于: (1) 前者的穿孔率较小, 后者的截面积比较大; (2) 前者为自由末端, 边界为滑移、绝热边界条件, 后者为受约束末端, 边界为无滑移、等温边界条件。穿孔率对声阻抗末端修正的影响较大, 而边界条件的影响较小[33]。因此, 孔缝连接处的声阻抗末端修正也可参考上述模型进行计算。
-
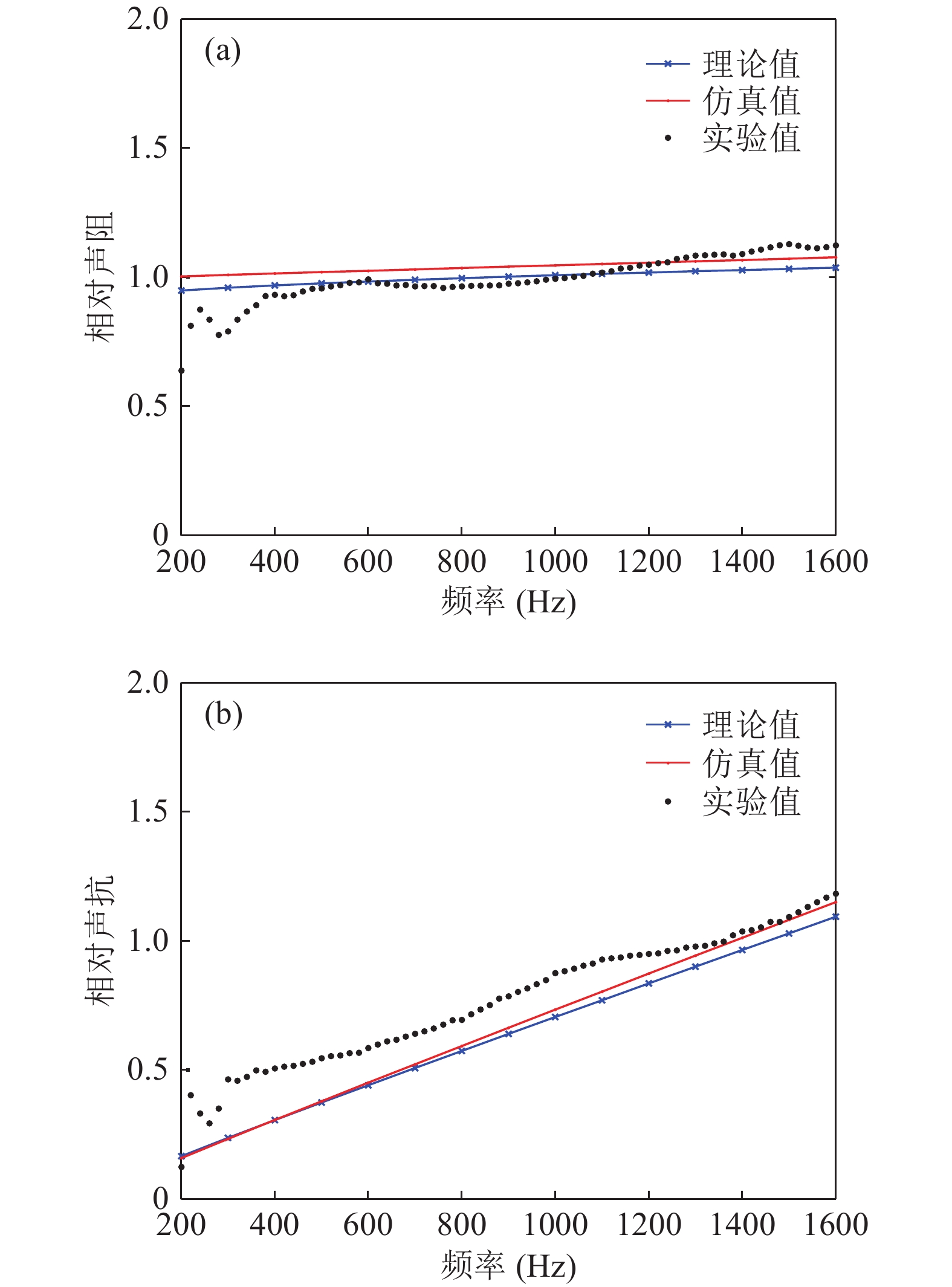
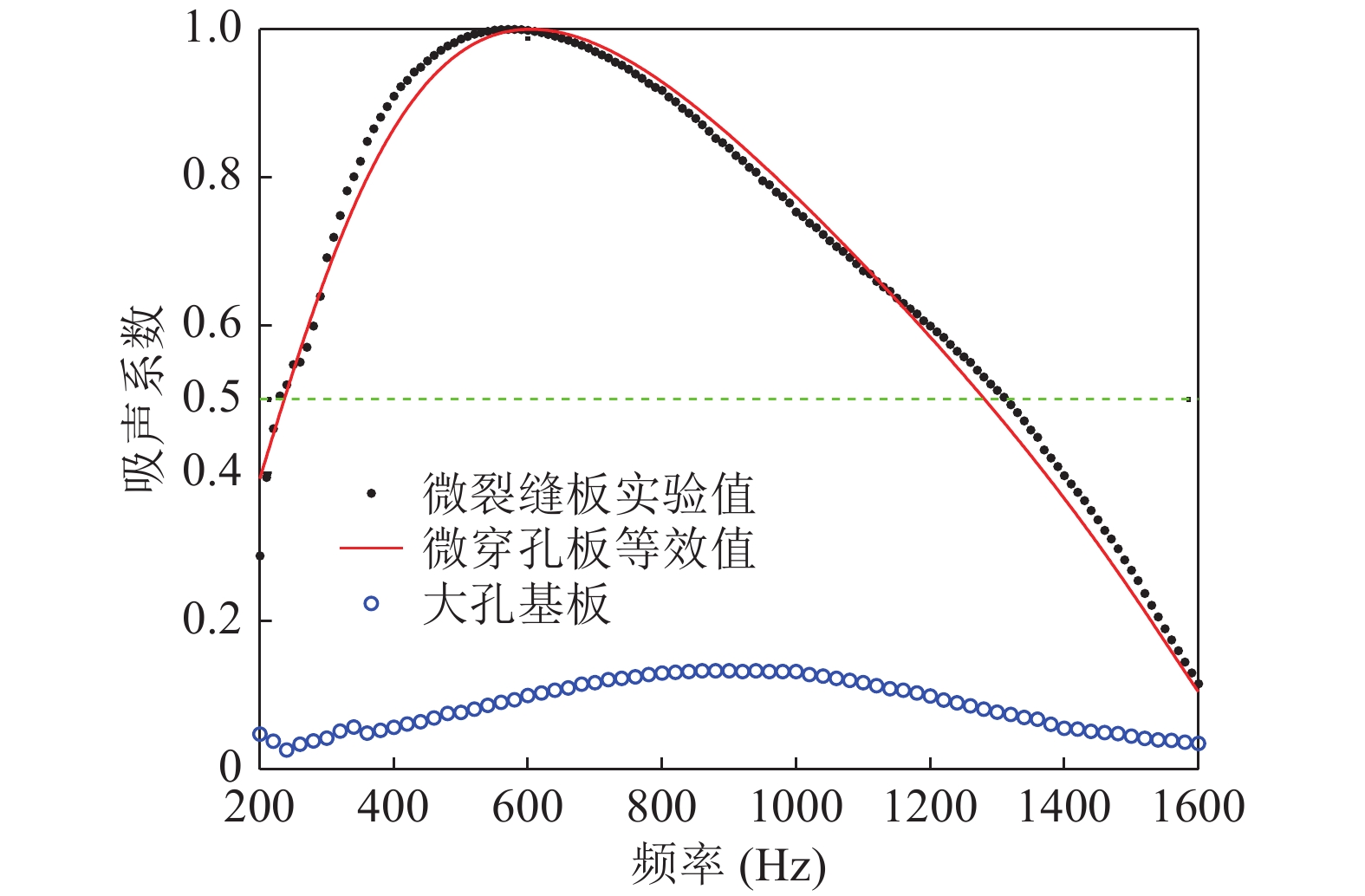
采用双传声器法测试第1节加工试件的法向声阻抗率, 使用阻抗管(BK4206), 背腔设置为100 mm, 测试频率范围为200 ~ 1600 Hz。相对声阻和声抗的实验结果如图10所示, 图中还展示了声阻抗率的理论值和仿真值。理论值与仿真值一致性较好, 两者与实验数据基本吻合, 预测的声抗略偏低, 主要原因在于: (1) 几何结构的简化引入一定的误差; (2) 试件由手工制作而成, 几何参数的不稳定带来一定的误差。法向吸声系数实验结果如图11所示, 试件吸声性能优异, 最大吸声系数
$ {\alpha _{{\text{max}}}} $ 超过0.99, 共振吸声频率为576 Hz, 有效吸声频程达5.3, 接近单层微穿孔板结构的吸声性能极限[3]。作为对比, 大孔基板在相同背腔下的吸声性能如图中圆形符号所示, 其因无法提供足够大的声阻, 吸声性能较差, 而覆膜加工成微裂缝板后, 吸声性能显著提升。 -
假定微裂缝板吸声性能可由直通型圆形孔微穿孔板等效而得到, 使用非线性最小二乘法的优化算法拟合最接近微裂缝板吸声性能的等效几何参数[34], 目标函数设定为
式中,
$ {\alpha _{{\text{cir}}}} $ 表示直通型圆形孔微穿孔板的理论吸声系数, 可参考式(1)和式(2)计算得到;$ {\alpha _{{\text{mea}}}} $ 表示微裂缝板的实测吸声系数。考虑到实际应用需要一定的结构强度, 设置板厚$ h $ 不低于1.0 mm。背腔深度保持一致, 其他参数不设置约束条件。优化得到直通型圆形孔微穿孔板的吸声系数曲线如图11中实线所示, 与微裂缝板的吸声性能相当。对应的等效几何参数: 板厚
$ h $ = 1.0 mm、孔径$ d $ = 0.22 mm、穿孔率$ \phi $ = 3.5%, 相当于在1 mm厚度单位面积板上加工92万个直径为0.22 mm的圆形微孔。以目前的工艺水平, 其大规模实现难度很大。因此, 微裂缝吸声板提供了一种易于工程实现且性能接近单层微穿孔板吸声极限的结构方案。 -
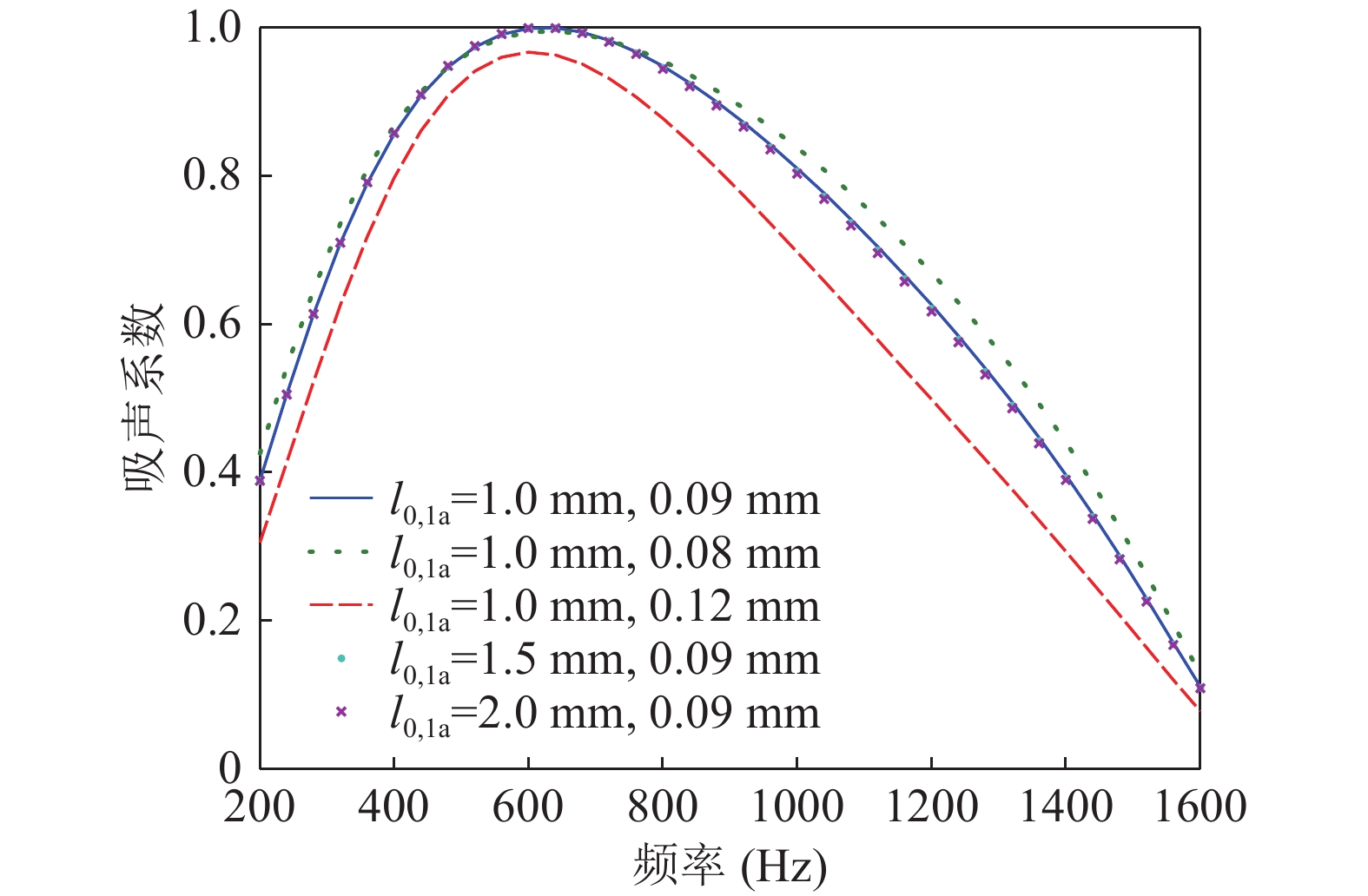
缝宽是微裂缝吸声板的关键几何参数, 缝宽
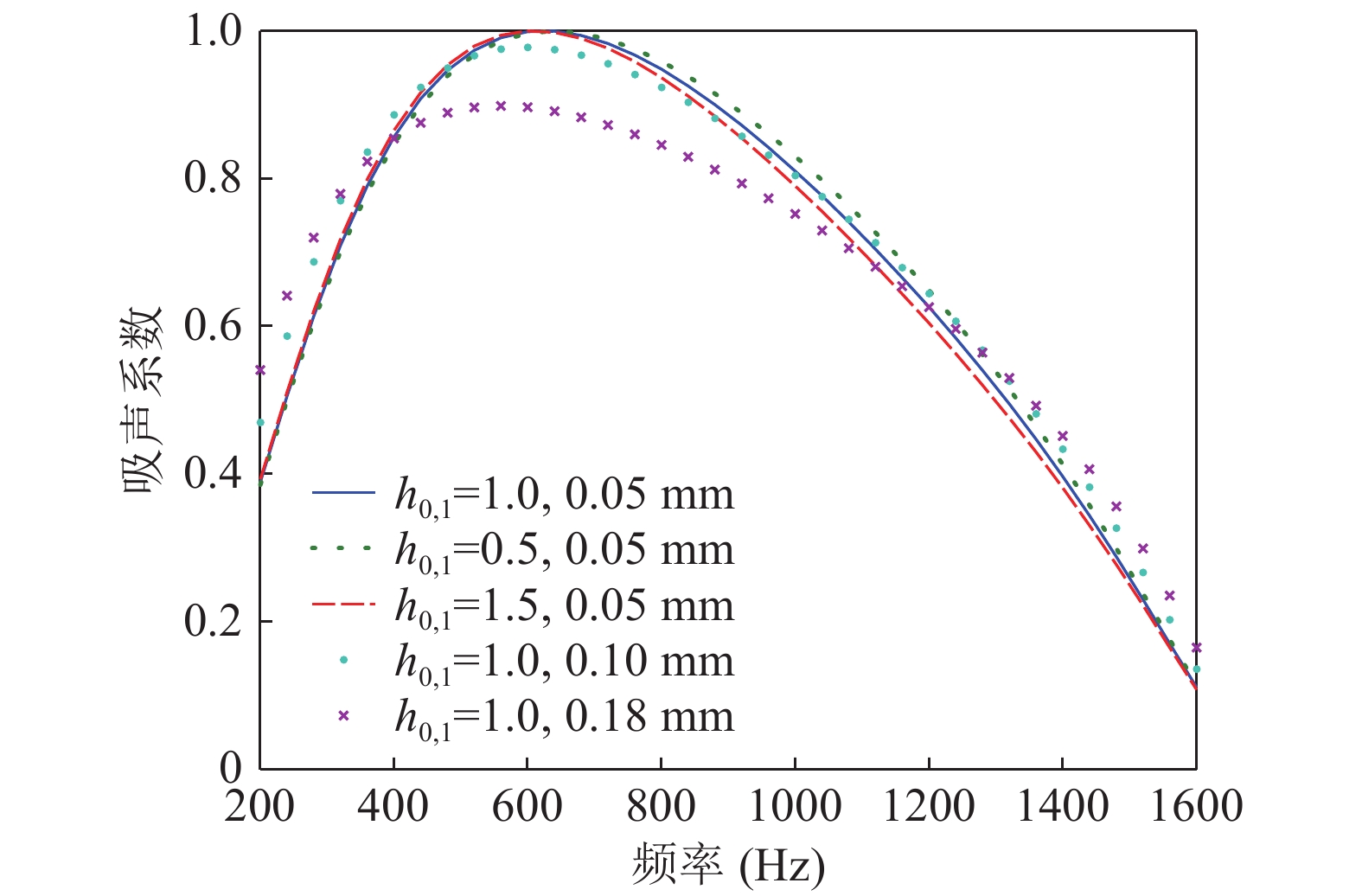
$ {l_{{\text{1a}}}} $ 分别取0.08 mm, 0.09 mm, 0.12 mm, 并保持基板大孔尺寸、板膜厚度和穿孔率等其他参数恒定, 缝宽对吸声系数的影响如图12所示。随着缝宽的增大, 吸声带宽显著降低, 吸声峰值频率向低频方向略微移动, 最大吸声系数有所改变。改变基板孔尺寸$ {l_{{\text{0a}}}} $ 为1.0 mm , 1.5 mm, 2.0 mm并保持其他参数恒定, 吸声系数曲线基本不变, 如图12所示。虽然仅改变基板孔尺寸对吸声性能影响较小, 但考虑到微裂缝的成型工艺, 基板孔尺寸决定了缝宽和缝长等参数, 其影响不可忽略。薄膜厚度一般较小, 改变膜厚
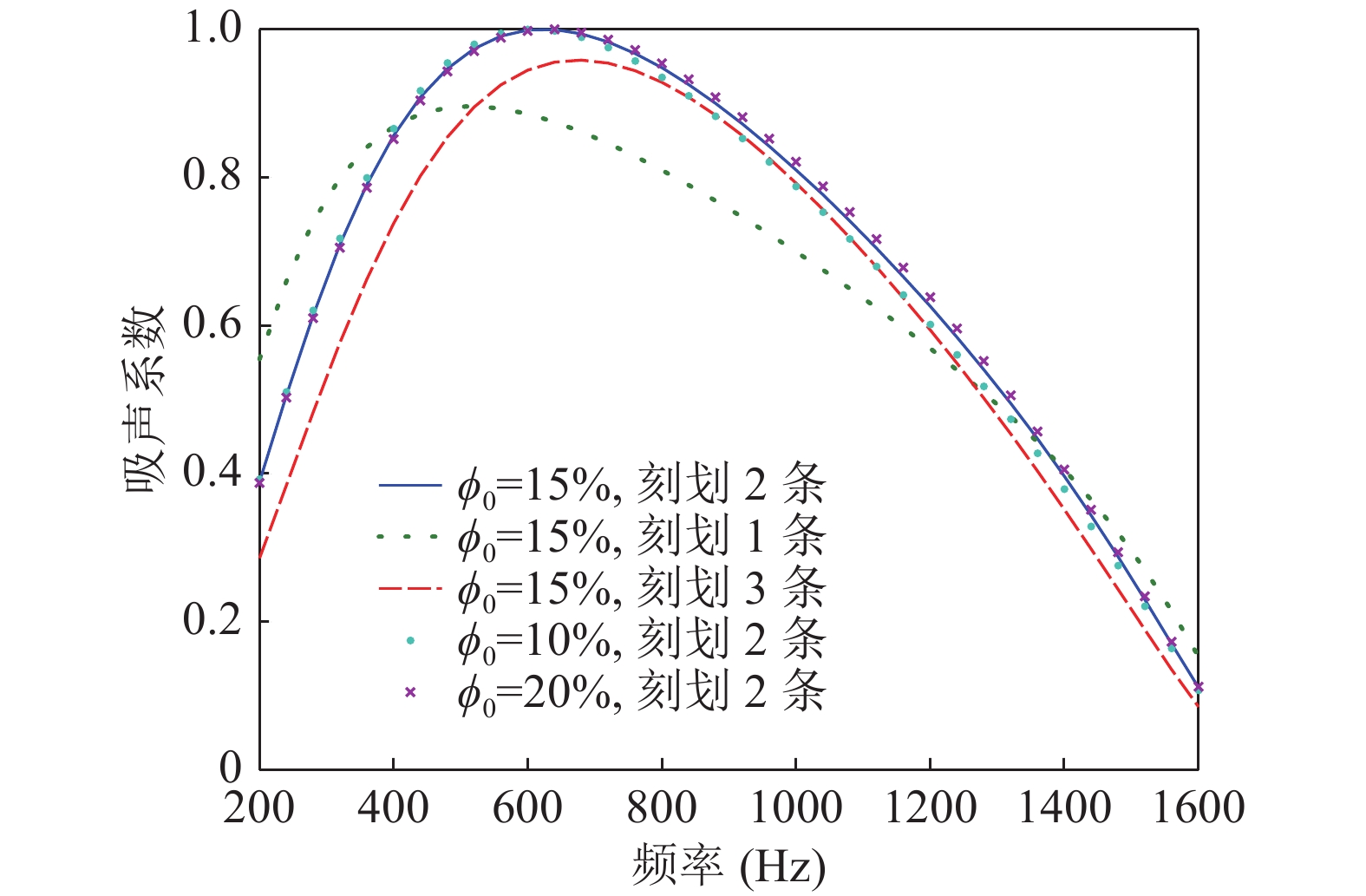
$ {h_{\text{1}}} $ 为0.05 mm, 0.10 mm, 0.18 mm, 并保持其他参数恒定, 膜厚对吸声系数的影响如图13所示。随着膜厚的增大, 最大吸声系数降低, 吸声带宽有所拓展, 吸声峰值频率向低频方向移动。当膜厚达0.18 mm时, 最大吸声系数$ {\alpha _{{\text{max}}}} $ 超过0.89, 有效吸声频程达7.3, 接近单层微穿孔板结构的吸声性能极限并进一步拓展了有效吸声带宽。改变板厚$ {h_{\text{0}}} $ 为0.5 mm, 1.0 mm, 1.5 mm, 并保持其他参数恒定, 吸声系数曲线基本不变, 如图13所示。微裂缝吸声板的机械强度主要取决于大孔基板, 其厚度对吸声性能影响较小, 因此适当增加其厚度可提升整体结构的机械强度。微缝穿孔率主要取决于单孔刻划微裂缝条数、缝宽、缝长和大孔穿孔率等参数。改变单孔刻划条数为1, 2, 3, 并保持其他参数恒定, 单孔刻划条数对吸声系数的影响如图14所示。单孔刻划条数对吸声性能影响显著, 仅刻划1条或3条均未能获得优异的吸声性能; 进一步改变基板大孔的穿孔率为10%, 15%, 20%并保持其他参数恒定, 吸声系数曲线基本不变, 如图14所示。一般地, 穿孔率主要是配合缝宽、膜厚等参数平衡好声阻和声抗的关系从而获得良好的吸声, 仅通过选择刻划条数便可灵活调节穿孔率的特点增强了微裂缝吸声板的可调控性。
微裂缝的空间形态比较复杂, 主要由水平方向的撕裂和垂直方向的错位形成。缝宽主要取决于基板孔尺寸、薄膜厚度、缝长和成型工艺等因素; 缝长主要取决于基板孔尺寸、刻划位置和成型工艺等因素; 从工艺的角度来看, 缝宽、膜厚、穿孔率等参数并不独立, 上述讨论未充分考虑工艺参数的影响, 具有一定的局限性。
-
本文理论计算了微裂缝吸声板的声阻抗率, 仿真了孔缝内外声场, 量化分析了入口端、孔内段、孔缝连接处、缝内段和出口端的声阻抗率贡献, 提出了考虑热黏性作用的狭长缝的声阻抗末端修正模型。
研究表明, 大孔基板对声压梯度、速度、黏热能量损失密度和声阻的贡献均较小, 但其厚度占比超过95%, 为整体结构提供了很好的支撑、通透和保护作用; 微缝薄膜的厚度占比不足5%, 但对声压梯度、速度、黏热能量损失密度和声阻抗率的贡献均较大, 为整体结构提供了良好的声学功能。
有别于常规孔板构型设计, 本文将微穿孔板分离为支撑部件(大孔基板)和吸声部件(微裂缝薄膜), 并运用刻划工艺加工形成微裂缝。微裂缝板是特殊的微穿孔板, 膜薄、缝细且穿孔率高, 拓展了亥姆霍兹共振原理对应的吸声带宽, 其兼具宽频吸声和力学承载的功能, 且便于加工, 有助于突破制约微穿孔板结构大规模推广应用的技术瓶颈。
微裂缝板吸声性能研究
Sound absorption performance of micro-ripped panel
-
摘要: 宽频微穿孔板结构因面板较薄、孔径较小且穿孔率较高难以大规模推广应用, 因此提出将微穿孔板分离为支撑部件和吸声部件, 形成大孔基板复合微缝薄膜的微裂缝吸声板。理论计算了该结构的声阻抗率, 仿真分析了孔缝内外声场以及各部段的声阻抗率, 并基于仿真数据提出了考虑热黏性效应的狭长缝声阻抗末端修正模型。实验验证了微裂缝板的吸声性能, 理论、仿真和实验结果一致性良好。研究表明, 大孔基板的厚度占比较大, 声学贡献较小, 为整体结构提供了良好的支撑、通透和保护作用; 微缝薄膜的厚度占比较小, 为整体结构提供了优异的吸声功能。
-
关键词:
- 43.50
Abstract: A wideband micro-perforated plate (MPP) resonant absorber usually requires a combination of thin plates, minute holes and high perforation rates, which is difficult to apply on a large scale. To solve the challenge, the MPP was divided into two parts, a supporting one and a sound absorbing one. A micro-ripped panel (MRP) was formed by combining a thick baseplate with large holes and a thin film with micro rips. The acoustic impedance of the MRP was theoretically calculated. The acoustic behaviors inside and outside the aperture, and the acoustic impedance of each part of the MRP were analyzed using simulation tools. Models were established to calculate the impedance end corrections of a micro-slit with large aspect ratio considering the effect of thermal viscosity. It is found that the thick baseplate with large holes could provide good supportive, permeable, and protective effects with small acoustic contributions, and the thin film with micro rips could provide excellent sound absorption performance.-
Key words:
- Micro-ripped panel .
-

-
表 1 微裂缝吸声板的一般化几何参数
部位 参数 数值 板 板厚度 $ {h_{\text{0}}} $ 

1.0 mm 膜 膜厚度 $ {h_{\text{1}}} $ 

0.05 mm 孔 孔短边 $ {l_{{\text{0a}}}} $ 

1.0 mm 孔长边 $ {l_{{\text{0b}}}} $ 

3.0 mm 孔短边间距 $ {L_{{\text{0a}}}} $ 

2.5 mm 孔长边间距 $ {L_{{\text{0b}}}} $ 

5.0 mm 穿孔率 $ {\phi _{\text{0}}} $ 

15% 缝 缝宽 $ {l_{{\text{1a}}}} $ 

0.09 mm 缝与孔中心轴线的平均距离 $ {d_{\text{1}}} $ 

0.9 mm 缝长 $ {l_{{\text{1b}}}} $ 

1.0 mm 穿孔率 $ {\phi _{\text{1}}} $ 

0.9% 缝孔截面积比 6% -
[1] Maa D Y. Potential of microperforated panel absorber. J. Acoust. Soc. Am., 1998; 104(5): 2861−2866 doi: 10.1121/1.423870 [2] 马大猷. 微穿孔板吸声结构的理论和设计. 中国科学, 1975; 18(1): 38−50 [3] 马大猷. 微穿孔板的实际极限. 声学学报, 2006; 31(6): 481−484 doi: 10.15949/j.cnki.0371-0025.2006.06.001 [4] 李贤徽, 蒋从双, 王芳, 等. 微穿孔板吸声结构——理论与应用. 北京: 化学工业出版社, 2022: 73−79 [5] Sakagami K, Matsutani K, Morimoto M. Sound absorption of a double-leaf microperforated panel with an air-back cavity and a rigid-back wall: detailed analysis with a Helmholtz–Kirchhoff integral formulation. Appl. Acoust., 2010; 71: 411−417 doi: 10.1016/j.apacoust.2009.11.014 [6] Cobo P, Colina C, Roibás-Millán E, et al. A wideband triple-layer microperforated panel sound absorber. Appl. Acoust., 2019; 226: 111226 doi: 10.1016/j.compstruct.2019.111226 [7] Li X, Wu Q, Kang L, et al. Design of multiple parallel-arranged perforated panel absorbers for low frequency sound absorption. Materials, 2019; 12(13): 2099 doi: 10.3390/ma12132099 [8] Huang S B, Zhou Z L, Li D T. Compact broadband acoustic sink with coherently coupled weak resonances. Sci. Bull., 2020; 65: 373−379 doi: 10.1016/j.scib.2019.11.008 [9] Liu Z Q, Zhan J X, Fard M, et al. Acoustic measurement of a 3D printed micro-perforated panel combined with a porous material. Measurement, 2017; 104: 233−236 doi: 10.1016/j.measurement.2017.03.032 [10] Li X, Liu B L, Chang D Q. An acoustic impedance structure consisting of perforated panel resonator and porous material for low-to-mid frequency sound absorption. Appl. Acoust., 2021; 108: 108069 doi: 10.1016/j.apacoust.2021.108069 [11] Ma X W, Liu X W, Xin F X. Sound absorption performance of gradiently slit-perforated double-porosity materials. Chinese Journal of Acoustics, 2021; 40(1): 1−17 doi: 10.15949/j.cnki.0217-9776.2021.01.001 [12] Zhao X D, Li X, D R. Enhancement of low-frequency sound absorption of microperforated panels by adding a mechanical impedance. Chinese Journal of Acoustics, 2015; 34(1): 27−36 doi: 10.15949/j.cnki.0217-9776.2015.01.003 [13] Park S H. Acoustic properties of micro-perforated panel absorbers backed by Helmholtz resonators for the improvement of low-frequency sound absorption. J. Sound Vib., 2013; 332(20): 4895−4911 doi: 10.1016/j.jsv.2013.04.029 [14] Min H Q, Guo W C. Sound absorbers with a micro-perforated panel backed by an array of parallel-arranged sub-cavities at different depths. Appl. Acoust., 2019; 149: 123−128 doi: 10.1016/j.apacoust.2019.01.013 [15] 张丰辉, 唐宇帆, 辛锋先, 等. 微穿孔蜂窝−波纹复合声学超材料吸声行为. 物理学报, 2018; 67(23): 234302 doi: 10.7498/aps.67.20181368 [16] Li Y, Assouar B M. Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl. Phys. Lett., 2016; 108: 063502 doi: 10.1063/1.4941338 [17] 李东庭, 黄思博, 莫方朔, 等. 基于微穿孔板和卷曲背腔复合结构的低频宽带吸声体. 科学通报, 2020; 65(15): 1420−1427 doi: 10.1360/TB-2019-0703 [18] Stinson M R. The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape. J. Acoust. Soc. Am., 1991; 89: 550−558 doi: 10.1121/1.400379 [19] Ning J F, Ren S W, Zhao G P. Acoustic properties of micro-perforated panel absorber having arbitrary cross-sectional perforations. Appl. Acoust., 2016; 111: 135−142 doi: 10.1016/j.apacoust.2016.04.012 [20] Jiang C S, Li X H, Xiao W M, et al. Acoustic characteristics of microperforated plate with variable cross-sectional holes. J. Acoust. Soc. Am., 2021; 150(3): 1652−1662 doi: 10.1121/10.0006044 [21] 吕世明. 在金属板材制作微孔的方法: CN 102439239A. 2012-05-02 [22] 蒋从双, 李贤微, 肖伟民. 板膜复合吸声板及其加工方法: CN 112497858A. 2021-03-16 [23] Li X H. End correction model for the transfer impedance of microperforated panels using viscothermal wave theory. J. Acoust. Soc. Am., 2017; 141(3): 1426−1436 doi: 10.1121/1.4976090 [24] 马大猷. 微缝吸声体理论. 声学学报, 2000; 25(6): 481−485 doi: 10.15949/j.cnki.0371-0025.2000.06.001 [25] Ingard U. On the theory and design of acoustic resonators. J. Acoust. Soc. Am., 1953; 25(6): 1037−1061 doi: 10.1121/1.1907235 [26] Zieliński T G, Chevillotte F, Deckers E. Sound absorption of plates with micro-slits backed with air cavities: analytical estimations, numerical calculations and experimental validations. Appl. Acoust., 2019; 146: 261−279 doi: 10.1016/j.apacoust.2018.11.026 [27] Aulitto A, Hirschberg A, Arteaga I L. Influence of geometry on acoustic end-corrections of slits in microslit absorbers. J. Acoust. Soc. Am., 2021; 149(5): 3073−3085 doi: 10.1121/10.0004826 [28] Bravo T, Maury C, Pinhede C. Vibroacoustic properties of thin micro-perforated panel absorbers. J. Acoust. Soc. Am., 2012; 132(2): 789−798 doi: 10.1121/1.4733555 [29] 侯九霄, 朱海潮, 袁苏伟. 耦合条件下微穿孔板吸声特性研究. 振动与冲击, 2020; 39(15): 156−162 doi: 10.13465/j.cnki.jvs.2020.15.021 [30] Li C X, Ben C, Anthony Z. Acoustic impedance of micro perforated membranes: Velocity continuity condition at the perforation boundary. J. Acoust. Soc. Am., 2016; 139(1): 93−103 doi: 10.1121/1.4939489 [31] Werner S. Vibrations of Shells and Plates. 3rd ed. CRC Press, 2004 [32] 石焕文. 裂纹及水介质对薄板振动和辐射声场特征的影响. 博士学位论文, 陕西: 陕西师范大学, 2004 [33] Jiang C S, Li X H, Cheng W Y, et al. Acoustic impedance of microperforated plates with stepwise apertures. Appl. Acoust., 2020; 157: 106998 doi: 10.1016/j.apacoust.2019.106998 [34] Liu J, Hua X, Herrin D W. Estimation of effective parameters for microperforated panel absorbers and applications. Appl. Acoust., 2014; 75: 86−93 doi: 10.1016/j.apacoust.2013.07.009 -


 首页
首页 登录
登录 注册
注册




 下载:
下载: