-
ELF是一种新型的电推进技术,利用等离子体团产生的角向电流与装置外加的径向磁场相互耦合产生轴向洛伦兹力加速等离子体产生推力。该推进技术潜在的优势可用于空间高功率、大推力和高比冲电推进系统,且可实现推力和比冲连续可变,不存在由于电极溅射和污染导致的寿命问题[1]。
作为脉冲工作模式的ELF推力器可实现较高的功率,气体储供单元、初级电离单元和场反构型(FRC)加速单元是该类型推力器的三个主要工作单元。推力器工作时工质气体由气体储供单元注入到初级电离单元之后电离产生最开始少量的等离子体,此后在装置中等离子体作为能量载体由初级电离单元进入场反构型加速单元。此阶段旋转磁场(Rotating Magnetic Field,RMF)由推力器靠近外层的两对正交射频天线共同作用产生,至此等效旋转磁场加速驱动带电粒子产生角向电流
${J_\theta }$ 。高能粒子在推力器腔体内与中性气体碰撞过程中进一步提高工质气体电离率,在外加磁场和等效旋转磁场的磁约束作用下等离子体产生场反构型等离子体团,等离子体团在${J_\theta } \times {B_r}$ 产生的作用力下加速喷出产生推力[2]。
全文HTML
-
ELF推力器是美国MSNW公司2008年在美国宇航局(NASA)项目支持下进行研发的一款新型场反构型电磁推力器,随后美国华盛顿大学和美国空军实验室也开启了场反构型推力器的研发工作[3-4]。最初MSNW公司成功利用氩气实现了1 kW的ELF推力器单脉冲和多脉冲工作模式,ELF-vl、ELF-v2、ELF-250等ELF系列衍生产品都曾利用氙气进行试验。采用氮气工质的ELF-300推力器比冲为6000 s,效率可达50%,等离子体最大温度为12 eV[5],目前200 kW级的ELF-375推力器效率高达65%~85%,已接近85%的理论可达效率,推力为7~15 N。
为了研究ELF系列推力器能够采用的更为广泛的推进器工质气体,同时探究火星大气作为工质气体的可能,MSNW公司在用ELF-v2作为实验样机的研究中,以95%CO2,3%N2和2%Ar组成的混合工质气体模拟火星大气,为探究30 kW级的 ELF-v2当混合工质气体以100~500 mL/min(标准状态)的流量注入时的实际功率,试验得到的运行功率为5.4 kW。ELF-160是ELF-v2基础上的改进型产品,MSNW公司以ELF-160为测试样机进行进一步测试,开展了多种不同工质推进剂对推力器性能影响的实验,并且测试验证了H2O、CO2、CH4等工质气体作为推进剂的可行性[6]。同时研究还发现虽然分子推进剂在平均分子质量较低的情况下仍可实现较高的比冲和推力器效率,但是放电室内等离子体耦合效率与氙气和氩气等相比较差,后续实验也证明了纯氙气的功率调节单元能量效率可达80%以上,而采用分子气体推进的效率普遍仅有20%~50%。
MSNW公司还研制了功率为1~5 kW的小功率ELF推力器EMPT,此型推力器在单脉冲模式运行时测得的元冲量为0.02 mN·s,在其最新测试结果中显示采用氙气工质气体比冲优于7000 s[7]。此外,美国爱德华空军实验室和密歇根大学还分别研制出了RP3-X、UM-RMF样机[8-9], 其中UM-RMF原理样机的最大设计功率为150 kW,此型推力器目前已经完成了30 kW级的实验测试。
空军研究实验室(AFRL)在数值模拟和实验测试方面做出了许多工作,MSNW LLC公司已经开发了推进器的原型,并对其进行了测试。此外,他们还推导出了简单的缩放表达式来深入了解推力器的性能[9]。
与美国研制思路不同的是日本采用螺旋波放电来获得更高的工质气体电离率并且进一步等离子体密度,JAXA在此思路基础上提出HEAT(Helicon Electrodeless Advanced Thruster)计划,并联合日本多所高校开展相关研究,旨在利用螺旋波放电激发等离子体并通过旋转磁场加速的方法产生推力的原理研究出无电极高性能电磁推进技术。日本东京农工大学等高校针对这种螺旋波放电的放电模式、放电管长度、天线位形以及螺旋波传播机理等多方面进行研究[10],实验结果表明,双鞍形射频天线、m=0线圈的激发模式、较长的放电管长度等条件,可以降低装置等离子体的输入功率,提高螺旋波放电源的等离子体密度,以此为FRC单元提供更加有效的能量耦合条件。不过从前期的试验反馈结果看,HEAT型推力器没有达到预期的加速效果。因此,JAXA仍在开展相关场反构型电推进技术研究[11]。
新加坡南洋理工大学在核聚变Rotamak装置的研究基础上提出GER(Gradually Expanded Rotamak-like Plasma)概念,究其概念本质也是基于场反构型原理的电磁推进。目前已经开展了对称结构稳态 RMF 射频放电的研究,并完成了GER样机方案的设计[12]。
Woods等利用等效电路模型分析了RMF-FRC推力器加速机制,推导出了效率、推力和脉冲的解析表达式。对于高RMF场强的情况可以忽略等离子体对驱动电路带来的负载损失,进而用恒定密度的圆柱体等效表示等离子体,求出了冲量推力器的表达式。结果表明在保持所有参数不变的情况下,存在一个最佳的输入能量以实现最大效率,电子完全磁化时产生最大角向电流,增加电子的磁化强度就能提高推理效率[13]。
国内场反构型等离子体技术主要应用于磁约束核聚变,近几年才开始在电推进领域开展相关的研究。目前仅有兰州空间技术物理研究所开展了ELF推力器的相关研究,已研制出了5 kW功率的原理样机,并且完成了相关放电测试[14-15]。此外兰州物理研究所在对目前国内外四种先进无电极推力器发展现状调研的基础上分析了基于ISRU应用的FRC推进器的显著优点和目前存在的有待解决的问题[16]。
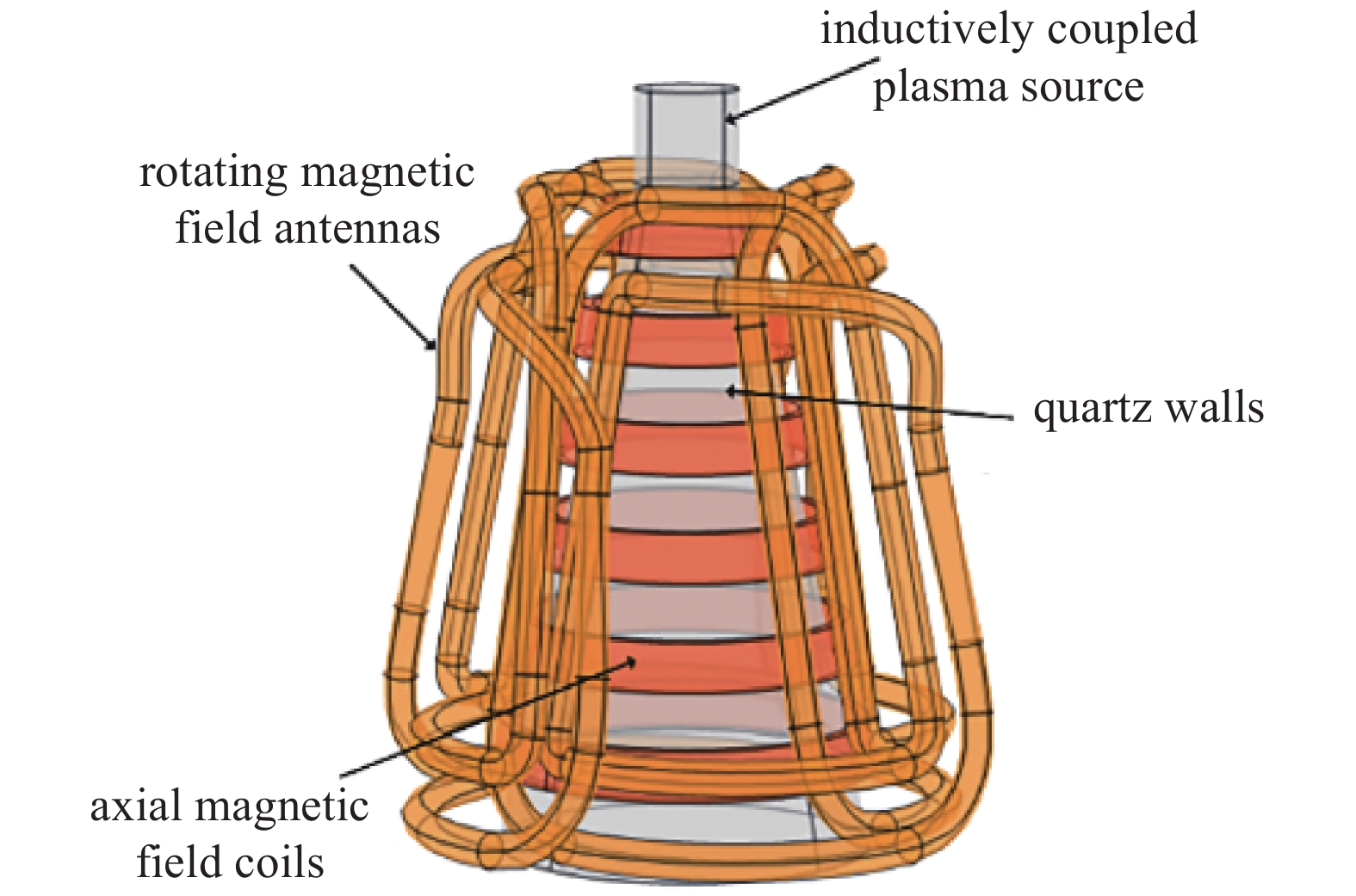
本文首先回顾了推力器的工作原理,国内外研究现状,然后建立了由推力器的关键元件组成的等效电路,目的是为了确定物理参数之间的关系,接下来求解电气和控制系统的相关物理方程,最后用数值方法求解方程组,本文在此基础上构建的模型图如图1,主要模型部件如图2、3所示 。
-
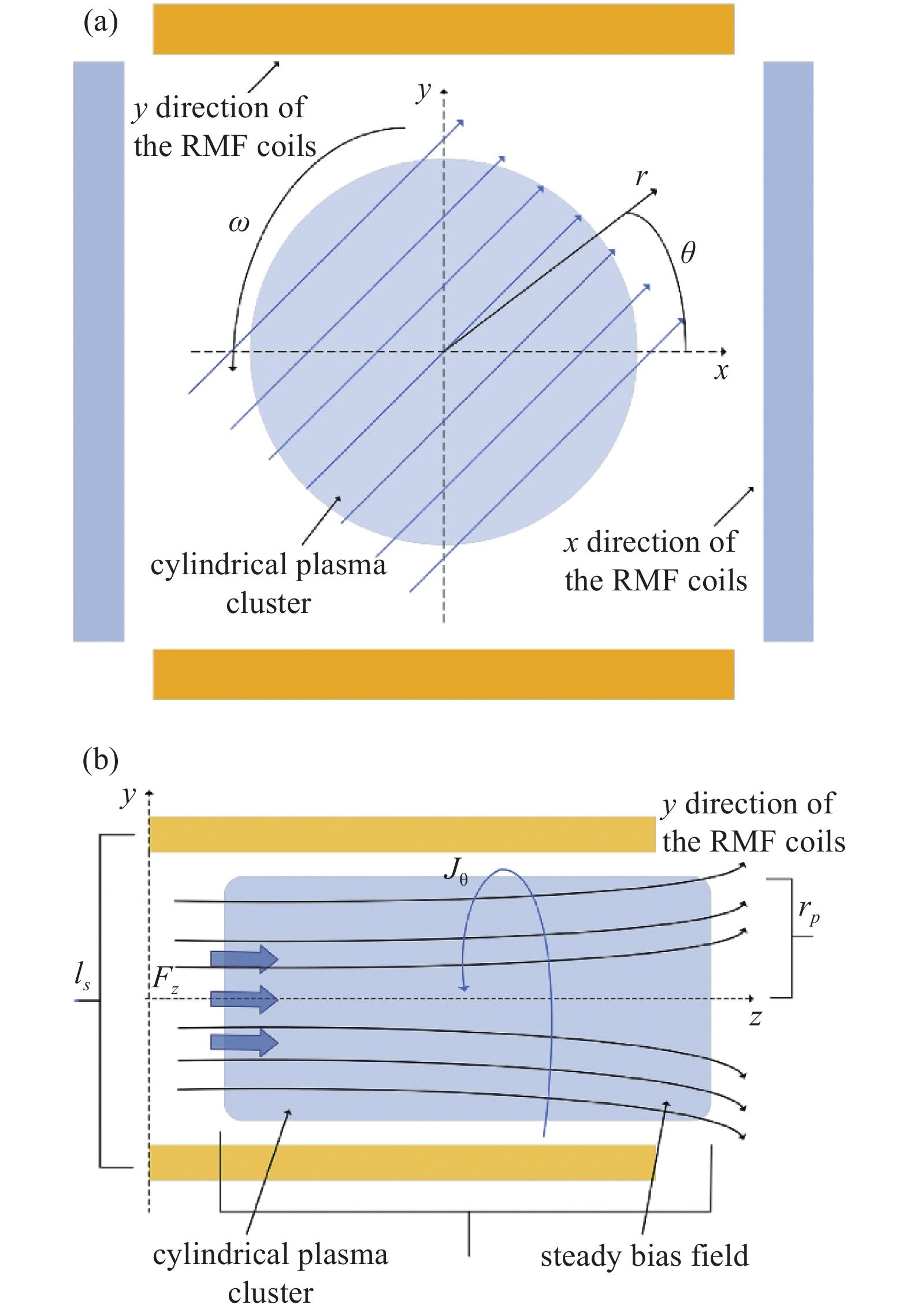
ELF通过在稳定背景磁场限制的等离子体柱中诱导方位电流来工作,方位角电流产生的磁场使等离子体中心线附近的背景轴向场反转,从而产生一个由高密度等离子体构成的独立结构,当等离子体中的方位角电流与背景场相互作用时,这个磁化等离子体被洛伦兹力加速,电离气体充满了推进器的背景稳定的磁场的形式。
式中Bs,r和Bs,z分别是偏置场的径向和轴向分量。两组线圈垂直排列,产生相位相差90°的旋转磁场。旋转磁场为以下形式:
式中B0是磁场的振幅,ω是磁场旋转的频率。这是一个理想化的RMF。这些场没有径向或轴向依赖关系。在本文的模型中,假设RMF是式2给出的理想化形式。这是为了定性地说明器件的性能,以便找到B场的简化形式。假设它们在放电过程中不受等离子体负载的影响,并保持正弦θ依赖性。等离子体负载对RMF的唯一影响是由于其电流大小的变化。使用法拉第感应定律和广义欧姆定律,对于轴向和方位压力梯度可以忽略不计的无限长等离子柱,时变磁场产生驱动轴向和方位电流的电场。
这里n是电子密度(在本研究中被假定为常数)、e是基本电荷,η是电阻率,定义为
在这里,νei是电子离子碰撞频率,m是电子的质量。方位电流与稳态偏置场的径向分量相互作用,产生轴向洛伦兹力,将等离子体高速喷出推进器
该推力器的加速是由角向电流与外部的磁场耦合产生的,通过为这些参数找到简单的模型,评估其性能。
-
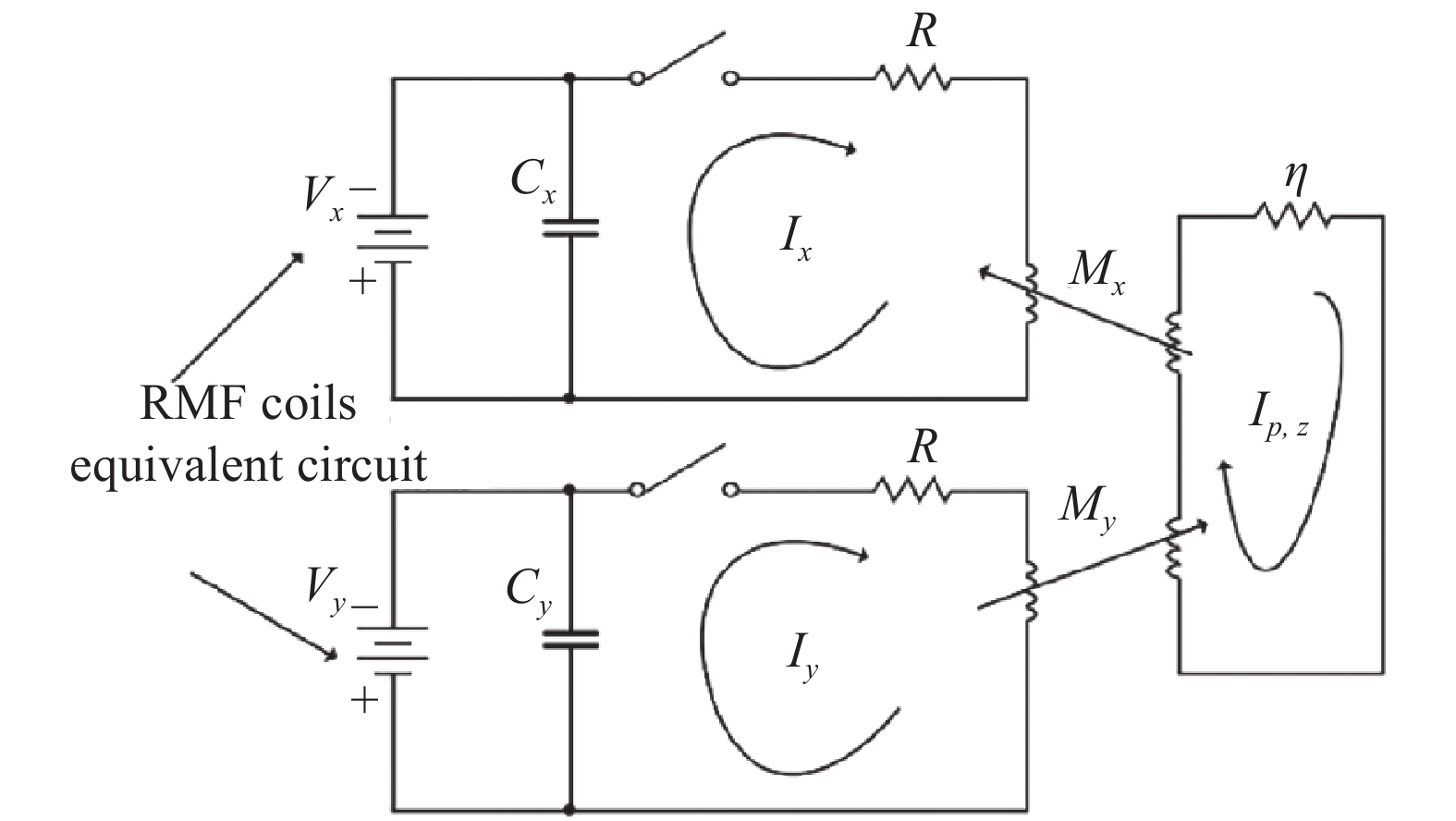
在最简单的形式中,ELF用两个驱动电路建模表示,每个驱动电路代表一对RMF线圈,并耦合到代表等离子体的圆柱形导电弹头。图4为集总电路的示意图。在每个驱动电路中,电容器被充电到初始电压V0。 在t = 0时,x方向线圈的一组电容器开始放电,四分之一周期后,y方向线圈的一组电容器开始放电。像所有RLC电路一样,系统将产生电流振荡。由于每个电路使用相同的器件,放电之间的延迟将导致电流的相位彼此相差
$ {\text{90}}^{\text{o}} $ 。图5说明了模型中使用的简化几何形状。 -
以图4作为电路模板,使用基尔霍夫电压定律为每个RMF线圈构建电路方程
式中k为RMF线圈与等离子
${V_x}(t)$ 和$ {V_y}(t) $ 体之间的耦合因子,它表示考虑了耦合中的非理想性,如非均匀场,并在分析中作为自由参数,${V_x}(t)$ 和$ {V_y}(t) $ 定义为Φx(t)和Φy(t)分别为等离子体在x和y方向RMF线圈的产生的通量的时间导数。可以根据线圈电流来定义RMF,为了简化模型,本文假设了无限长等离子柱的理想情况,根据线圈电流来定义RMF:
当由式(11)来表示磁场的作用时,弹头将产生自己的旋转磁场。这个场将与RMF线圈耦合,可以计算弹头产生的磁通量。再次使用式(7)与法拉第感应定律和广义欧姆定律相结合,可以根据RMF线圈电流、Ix和Iy重新推导轴向电流密度如式(12):
使用Biot-Savart定律,可以计算与RMF线圈相交的轴向等离子电流产生的磁通量。为了进一步简化这个问题,作者假设RMF线圈在每个方向的中心线产生的磁场在整个通量区域都是恒定的。这个区域只是横截面区域,并且随着等离子体团加速离开感应区域而变化。将其表示为式(13):
rp和lp是等离子体的半径和长度,而z(t)是等离子体尾端的位置,lp也是感应区的长度,感应区域反映了电离气体最初充满整个腔室的情况。
RMF线圈的x和y方向的通量方程如下式(14)(15):
y 方向 RMF 线圈的电容器与x方向 RMF 线圈失相
$ {\text{90}}^{\text{o}} $ 。方位角电流可以用 RMF 线圈电流来表示,因为z(t)可以用式(6) 所定义的等离子体的加速度来计算。首先,本文根据电路参数来计算方位角电流:y方向RMF线圈的相位和x方向RMF线圈的相位相差
$ {\text{90}}^{\text{o}} $ ,方位角电流可以使用RMF线圈的电流来表示。z(t)可以用式(6)定义的等离子体加速度来计算,方位角电流用等离子体参数的形式定义如下:利用式(16),对在感应区加速的等离子体进行积分,可以计算出等离子体的加速度,从而得到等离子体弹头在时间 t时的轴向位置:
式中 M 是等离子体弹头的质量。 最后,使用喷出推力器的等离子体弹头的动能和初始储存在电容器的总能量计算了效率。
这里uex是等离子体的出口速度,V0是电容器的初始电压。
其中本文在此处研究选取以下值:
n=1018 m−3, η=5.89×10−6 Ω·m, Bs, r=0.6 T, ls=0.2 m
rp=0.1 m, lp=0.4 m, R=0.3 Ω, C=0.04 nF
经研究可知电压从0到20000 V增加,而耦合因子k从0增加到1000。
实验选取工质流率ni=1.3 mg/s,最大偏置磁场为120 G,RMF幅值为2 kA,脉冲重复率为50 Hz,RMF频率为400 kHz,得到等离子体耦合效率η为60%~74%,比冲τ=2000 s,实验结果与本模型高度相符。
3.1. 集总电路建模
3.2. 系统方程
-
本文简述了ELF的原理,并构建了一个代表推力器工作的电路模型。并使用假设来简化系统,推导了性能模型方程,并分析了解析计算结果。结果表明,随着耦合因子的增加,性能也有所增加。比冲在低输入能量下迅速增加,在高输入能量下逐渐稳定。当输入能量较低时,效率也会迅速提高。在后续的模型中,将会考虑等离子体自感、径向稳定磁场和无限长圆柱形等离子体假设,以便更深入地理解推力器。

 首页
首页 登录
登录 注册
注册




 下载:
下载: