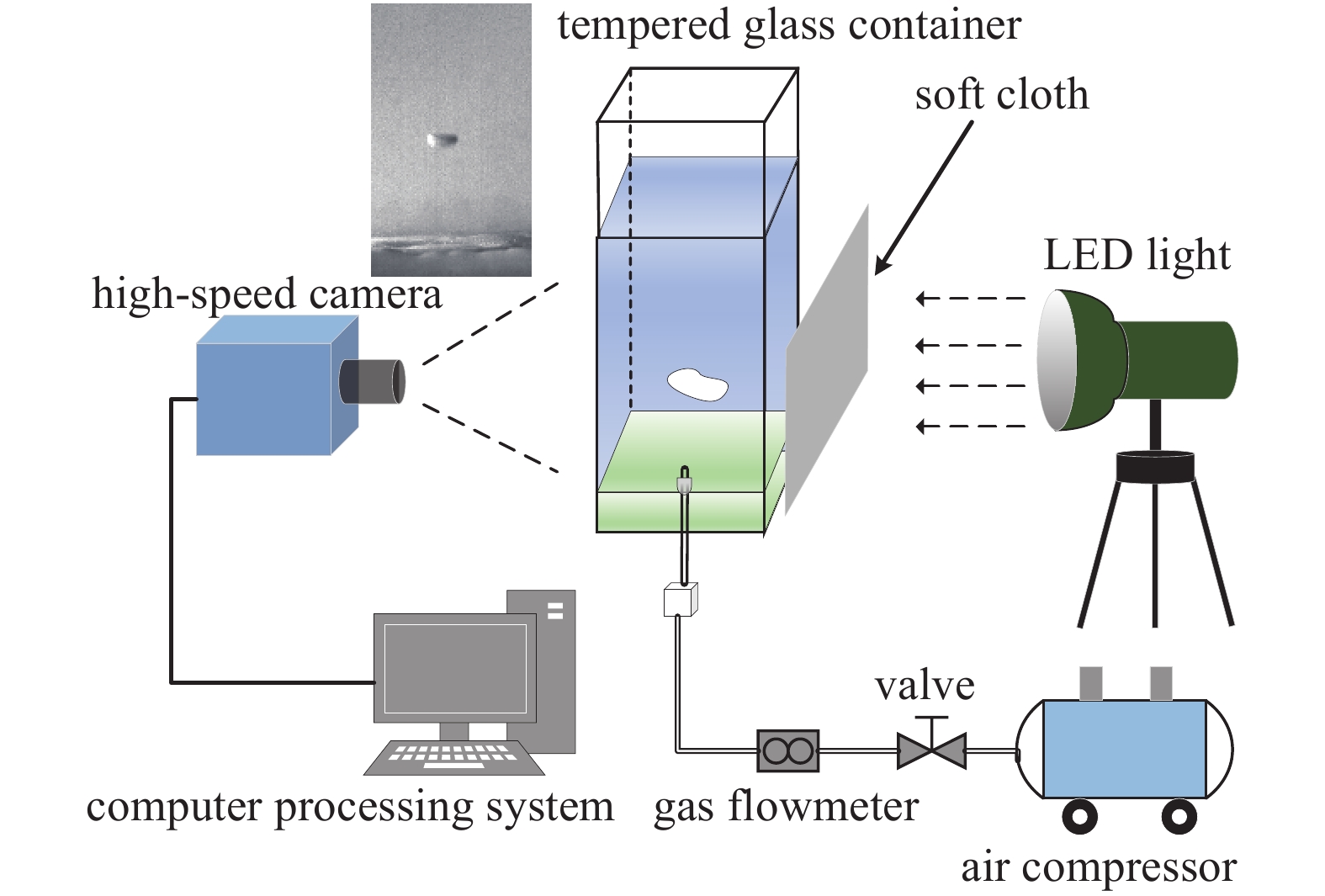
本次实验是在内蒙古科技大学气液两相流实验系统下进行的。如图1所示，该实验主要包含控制气泡系统和图像信息采集两部分。

实验过程主要是利用自行搭建的气泡上升行为特性可视化实验平台，展开对气液两相流中气泡穿过底层的固体颗粒物后，在常温常压下的形态的变化和运动状态的实验研究，利用高速摄像机进行拍摄气泡在液池容器中上升的运动过程，并将图片储存在计算机中。实验中用于配置固液悬浮液的固体颗粒选用粒径为15~45 µm的玻璃微珠，即气泡底层的固体颗粒物。在液池容器中装入一定量的纯水后开启无油静音空压机阀门，空压机提供气体通过胶管使气体传输到平口管中，然后调节流量计直至进气流量准确。因为实验过程中，液池容器中的气泡上升速度比较快，无强光源照射的情况下，拍摄的图片显示为黑色且气泡上升的过程无法清晰的显示，为此，增加了LED太阳灯来辅助拍摄气泡上升过程，以获得更清晰的气泡图像。

1.高速摄像机

在数据采集过程中，利用高速摄像机拍摄气泡在液池底部穿过底层颗粒物后运动上升过程。对于高数摄像机的参数如下。

在实验过程中高速摄像机采用的国产千眼狼OSG030-815VM，详细参数如表1所示，可以提高数据的采集效率和照片像素，提高计算的精确度，加快实验的进程，避免时间的浪费。摄像机的镜头为Canon EF 100 mm/2.8LIS.USM微距镜头，该镜头可以产生一定的防抖效果，大大的减少了实验的不确定性。

2.无油静音空压机

实验中，模拟的气体是通过无油静音空压机产生的，即基本的特征其自身带有消音设备，工作时可以减少噪声。并且罐内具有防锈防菌功能，可以保证原始气体产生的洁净度，从而使得结果更加准确，减小误差。

3.电子天平

在模拟液池底层的悬浮物时，采用不同颗粒直径的玻璃圆珠颗粒进行实验。而进行实验前，需要利用电子天平称量（精确度达到0.1 mg）出不同颗粒直径范围的质量，然后将称取后的颗粒放入玻璃容器内，充分搅拌，待其静止再用直尺测量出颗粒物所堆积的长、宽和高的值，计算出颗粒堆积的体积，进而计算出不同颗粒直径范围的密度。

4.LED太阳灯

在实验过程中，气泡穿过固体颗粒层在液体中运动时速度快，拍摄时常常与液体背景相混合，不能清晰的将运动过程显示出来。因此需要通过利用EF-200LED太阳灯来增加曝光度，增加液体背景的效果，该太阳灯发光管响应时间短，抗干扰性强等特点。

图像处理技术在流体动力学、医学、气象学、材料力学、船舶力学等方面都有很多应用。SVD分解在图像处理中可实现的功能包括降维^[17]、去噪^[18]和转换^[19]等。

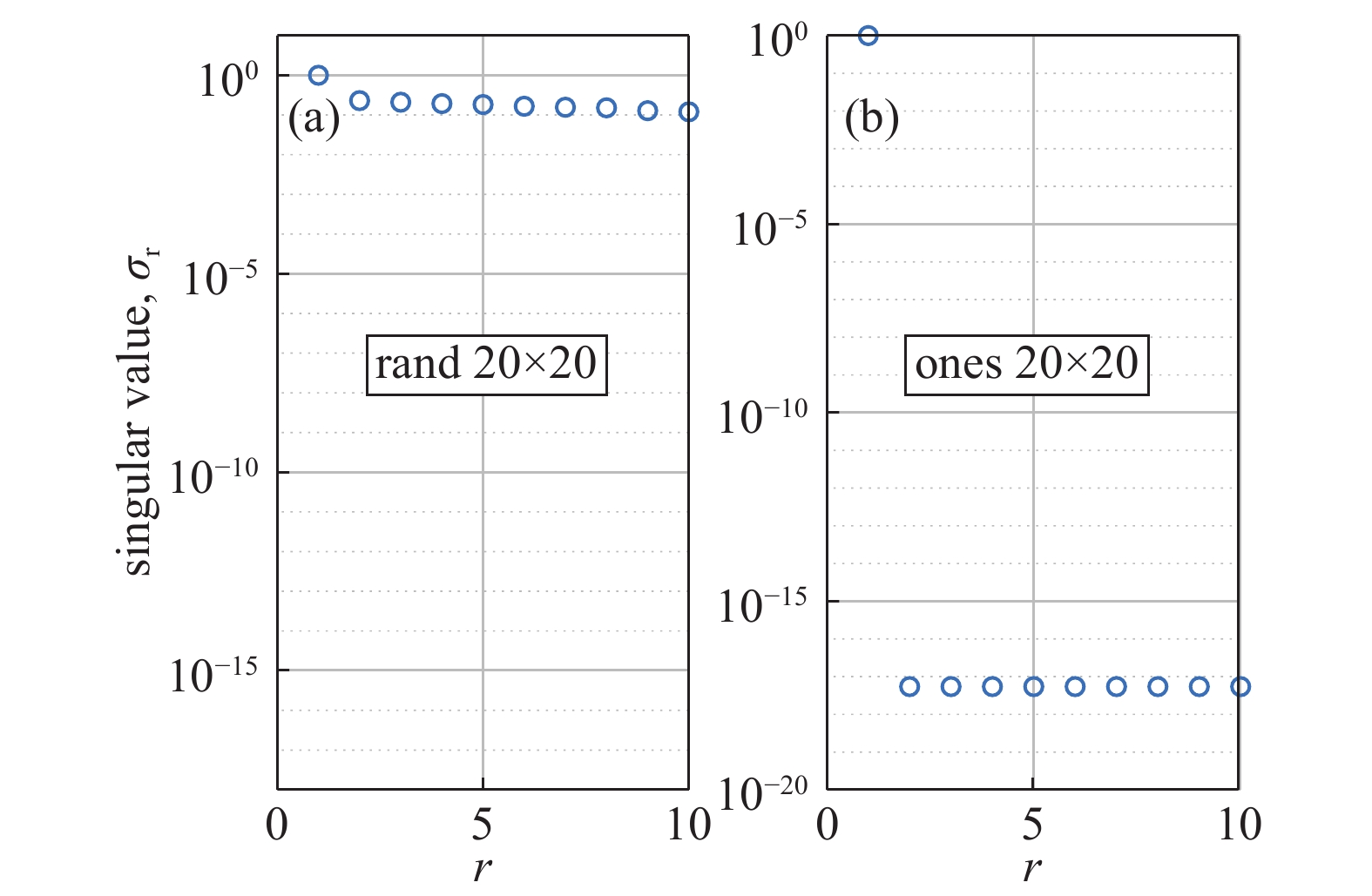
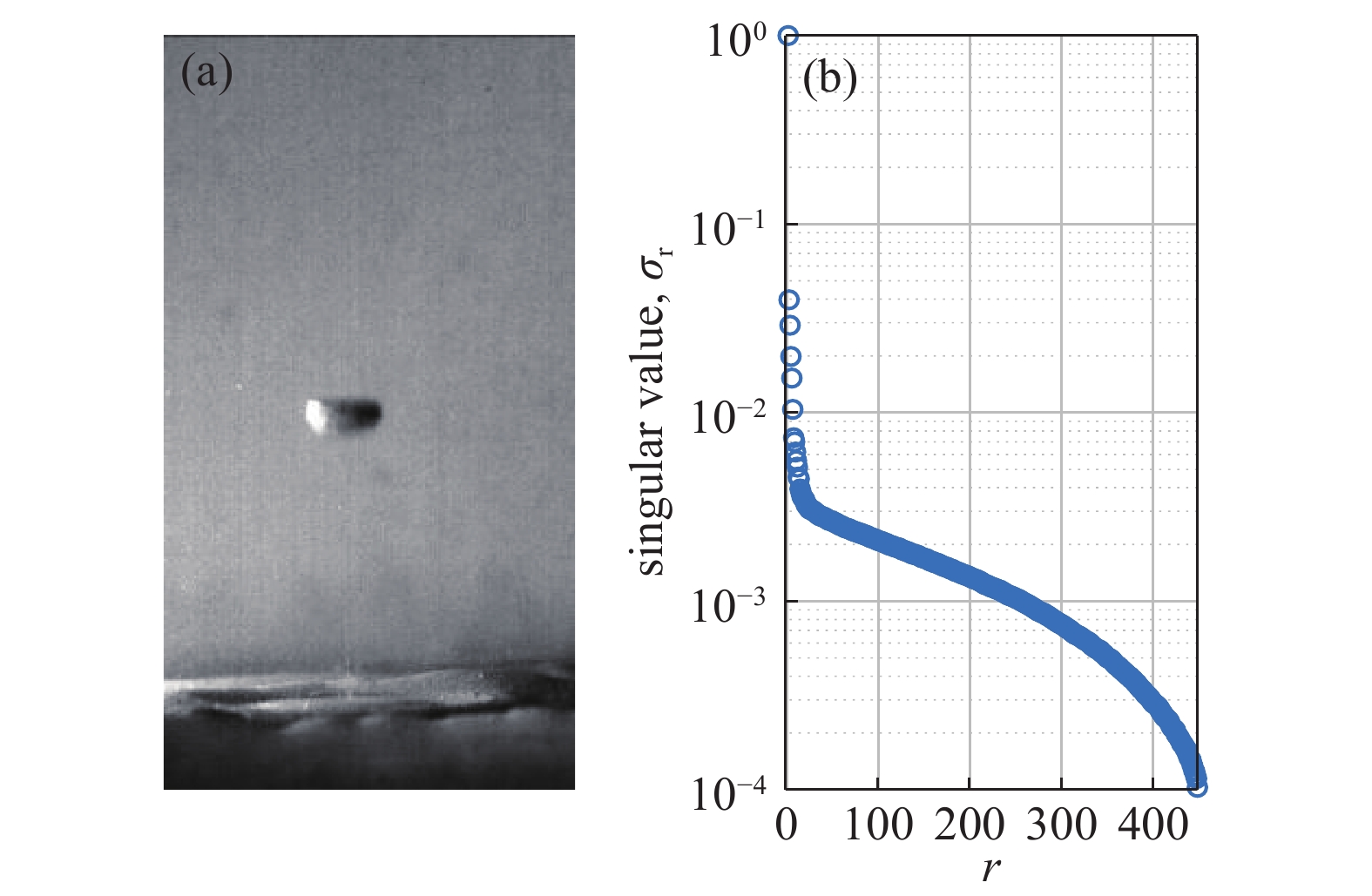
式(1)是将图像矩阵X分解成一个${{U}},{{V}},\sum$，分别是左奇异矩阵、右奇异值矩阵和单值分解矩阵。分解后的矢量$ {u_1},{u_2}, \cdots {u_r} $是图像矩阵所组成的列空间向量的向量基，$ {v_1},{v_2}, \cdots ,{v_r} $是行空间向量基，$ {\sigma _1},{\sigma _2}, \cdots {\sigma _r} $为单值，$ r $为矩阵的秩。秩在数学上定义表示最大不相关的向量个数，单值$ \sigma $的分布可以表示矩阵的复杂程度。图2是将随机生成的20×20的矩阵进行单值分布与数值全为1的20×20的矩阵分布进行对比，会发现对于矩阵的复杂程度不同，形成的单值分布是有很大区别的。

如图所示，发现图2（a）中的单值分解图像出现平缓的连续点，而图2（b）中的仅有一个1值点，且从第二个点后图像的点值趋近于0，这是由于矩阵的低秩成分造成的。于是图3，将一张气泡图像进行SVD分解来探索其图像的丰富程度。

如图3所示，其原始气泡的拍摄图像通过SVD分解后得到单值分布曲线，图中曲线的前一部分是陡然下降的不连续的点，后一部分是连续的平滑线段，且曲线较为平缓，这就表明原始的气泡图片包含的两种部分，即低秩部分和稀疏部分。而矩阵的秩是对储存在矩阵中的独特信息的度量，秩越高，信息越丰富。如图所示单值分解的图像反映出气液两相流图像中气泡与液体背景的信息丰富度。

对原始气泡图像进行SVD分解：

如图4所示，原始矩阵$ X $被分解成单个奇异值向量相加，并且单值从主要成分到次要成分依次排列，于是将原始气泡图像进行SVD分解后，图像也是从低秩成分到稀疏成分进行显示，图中$ {\sigma _1}{u_1}{v_1} $对应的图像是液体背景和底部颗粒层，$ {\sigma _2}{u_2}{v_2} $对应的图像成分中液体背景消失，$ {\sigma _3}{u_{_3}}{v_3} $对应图像成分中气泡成分，证明主要成分是液体背景，次低秩成分是颗粒物表面，通过矩阵低秩的近似截断相加来对原始气泡图像进行分析，形成图4的气泡低秩提取图像。

如图5，将原始气泡图像进行SVD分解后，选取五种不同的秩进行图像显示，会发现在秩为1和2时的气泡图像，只剩下液体背景图像，气泡图像被丢弃，随着秩的逐渐增大，图像显示的信息丰富程度越来越$ {\sigma _1}{u_1}{v_1} $接近于原始图像，且秩为1时的图像与图4中第二幅所对应的图像一样。对比上式可知，将气泡图像矩阵进行奇异值分解后，矩阵形成各个奇异值向量相加，单值由主要成分到次要成分进行以此排列，逐渐增大秩的提取，会发现液体背景图像占原图像的主要成分，而气泡图像是需要秩达到一定程度后才会出现。

这也就表明，在气泡图像中，气泡图像单值分解的低秩部分是具有相关性的信息的液体背景图像，稀疏部分是指单纯的气泡图像。

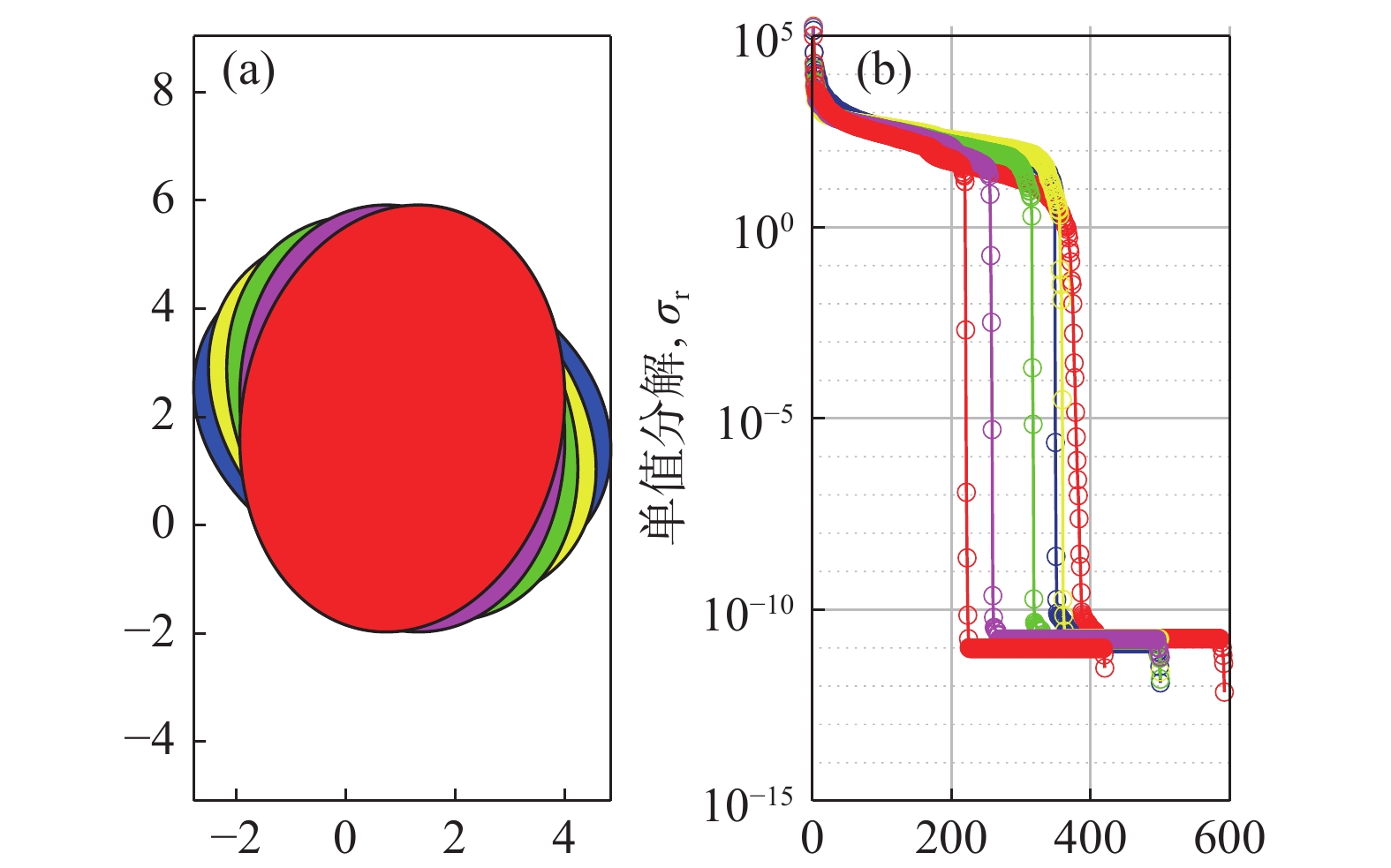
理想气泡的图像是绝对对称的图形，由浮力、重力、水压力等多种力的混合作用下，才出现挤压变形、翻转运动，甚至消失的状态。不同的因素，导致实气泡的运动过程是非常复杂的。先取一个对称的椭圆形来初步探索理想状态下小气泡在只有旋转因素下，物体的单值分解图像。

如图6所示，（a）图中的椭圆形状图像按其中心点每次旋转30°，然后对旋转后的椭圆图像分别进行SVD分解，并将逐条的单值分布曲线合并成图（b），按照颜色一一对应，椭圆形状图像的旋转变化可以清晰的在单值分解的图像中表现出来，随着旋转角度的变化，单值分布曲线由右向左移动，即可以推理出当气泡受到单一因素的影响时，单值分解图像可以表示出来。

在实际应用中，比如图像处理、网络数据分析、生物信息学中，经常会由于采样、环境和传感器等多种原因导致获得的数据与真实数据由很大的出入，而传统的PCA处理大误差是很脆弱的，不具有鲁棒性，甚至仅仅因为一个元素的测量错误而使得到的低秩矩阵和真实的低秩矩阵相差很大。RPCA技术的提出改善了这一缺点。其主要思想就是利用凸形规划法，在数据矩阵的最优化准则下，将数据矩阵$ X $分解成一个低秩矩阵$ L $和稀疏矩阵$ S $。在图像矩阵中，RPCA算法中的稀疏矩阵可以描述源图像中的显著信息，从而有效的实现图像的主成分提取。

式（2）中当矩阵$ L $的秩取到最小时，则认为$ L $是低秩的，$ S $是稀疏的。$ S $的0范数是指$ S $矩阵中非零元素的个数，当非零元素的个数越少时，$ S $越稀疏，因此，要求低秩矩阵$ L $和稀疏矩阵$ S $的0范数都取到最小。然而，式（2）是一个非凸的优化问题，目前还没有一个最直接的优化方法。但可以通过将矩阵S的零范数用1范数来代替，将低秩部分用核范数来代替。这样做可以实现矩阵的逼近，从而将等式实现凸优化求解，其中参数λ起平衡因子的作用。

式（3）中通过矩阵$ L $的核范数来近似表示矩阵$ L $的秩，核范数是指$ L $的奇异值的和，所以当核范数越小时，可近似认为矩阵$ L $的秩越低。$ S $的1范数是指当矩阵中某一列的元素的绝对值取最大的时候，这一列的元素的绝对值的和。则当1范数趋向于0时，也就说明其他列的元素的绝对值也很小，也就近似认为非0元素的个数很少，而非0元素的个数越少，矩阵$ S $越稀疏。

而式（3）解法又是一个高可能性的NP问题，对于松弛问题也被认为是主成分追踪，可以利用增广拉格朗日乘子算法（ALM）来解决问题。Lin^[20]就提出了增广拉格朗日乘子算法（ALM），并且在一定条件下证明ALM算法比奇异值收缩算法（SVT）^[21]和加速近端梯度算法（APG）收敛性更准确、收敛速度更快，更重要的是ALM算法的迭代次数经常不超过最低秩矩阵的大小。

增广拉格朗日算法主要解决的是如下问题：

其构建增广拉格朗日函数是：

为了将有约束问题转化为无约束问题，增加了惩罚项

其中$ Y \in {R^n} $为拉格朗日乘子。式（6）中新增的第二项是$ Y $和$ X - L - S $的一个内积，$ Y $应该要足够大时，此时的$ L $和$ S $才能更加精确的趋向于$ X $。第三项是由于为了将有约束问题转换为无约束问题而增加的一个惩罚项，$ \mu $为惩罚参数，同理，需要$ \mu $足够大。为了找到满足这个拉格朗日函数取最小的时候所对应的$ Y $、$ {L_k} $和$ {S_k} $，通过不断迭代$ {Y_{K + 1}} = {Y_K} + \mu (X - {L_K} - {S_K}) $，直至函数达到收敛。

增广拉格朗日乘子法相比于传统的拉格朗日法的最大的特点时求解带有特定结构的非光滑等式约束优化问题，即可求得最优解，大大缩短了计算速度，减少储存量。对于这种特殊的结构，本文使用一种简单的程序取求解L和S，即交替方向法（ADM）^[23]。

为高效求解式（6）问题，交替投影法最为合适，可以交替投影求解以下两个变量优化问题。

式中$ \varOmega $表示投影算子，就是向$ \varOmega $空间投影，即：

对于交替方向加权主成分追踪方法的实验证明与具体算法流程可以参考kton的研究成果^[25]。其基本思想是由于背景结构在图像光谱中是不变的，因此在结构组成的矩阵中，背景图像对应的矩阵可以看做是低秩矩阵，这也是图像成分分析技术（PCA）可以实现“人脸识别”的重要原因^[15]，相比于PCA，RPAC算法的特点是可以从低秩成分中恢复图像背景图，并且突出图像的稀疏成分。

本文通过RPCA的基本思想，将气泡的运动图像通过高速摄像机的拍摄，得到一个很大的关于气泡运动的数据库X，经过鲁棒主成分分析法，将气泡图像中的背景和气泡有效的分离出来。通过不断调整阈值，使得低秩部分包含的更多的信息，即使得分离出来的矩阵S更贴合气泡的运动过程。

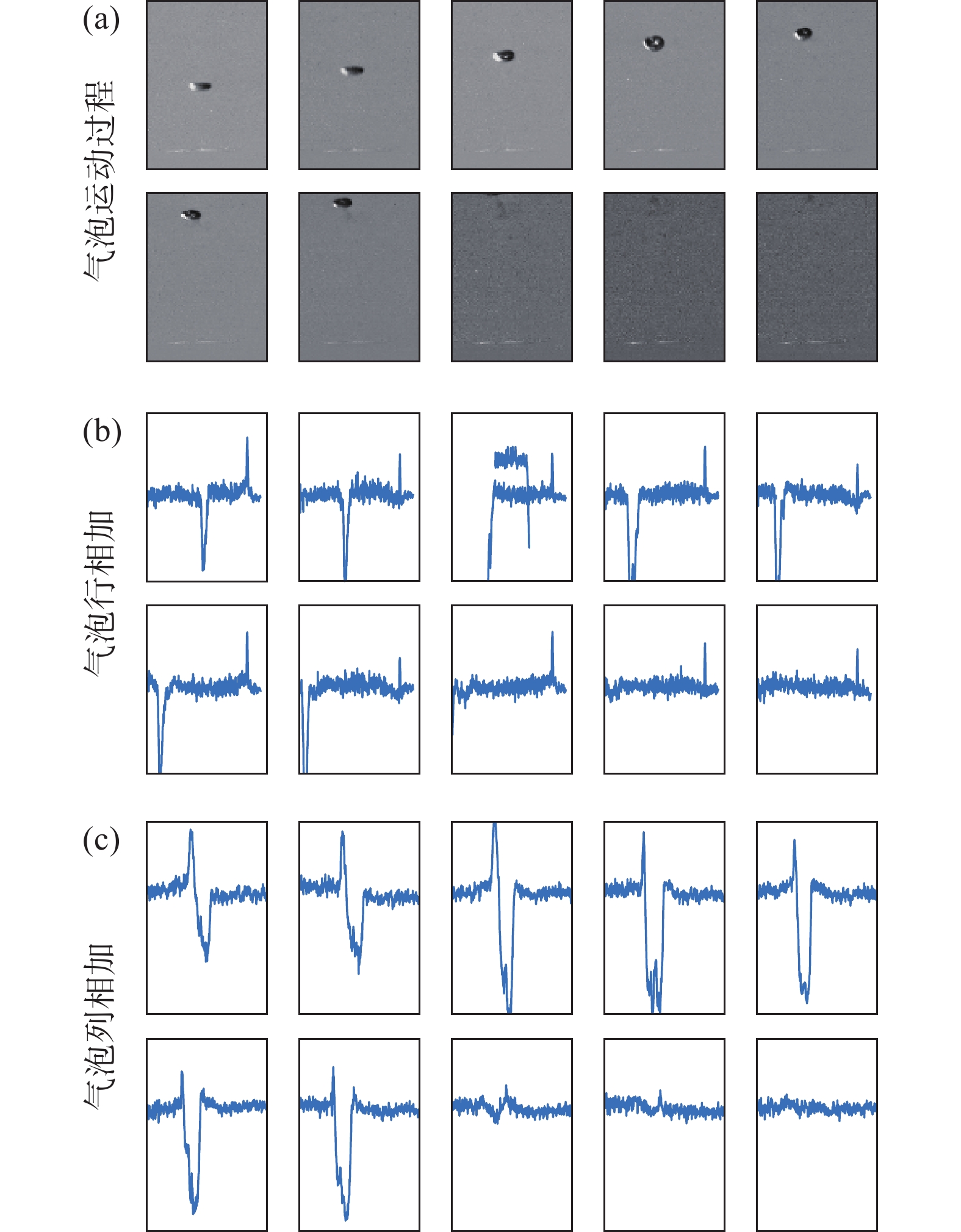
由于利用数据采集中高速摄像机拍摄的气泡过程产生的照片是大量的，本文选取了以一组气泡的运动过程为例，提取了气泡运动的部分图像，本文示图采用间隔显示的方法，即运动过程的三十张图片中，每间隔三张图片进行图片显示，形成如图7的气泡运动过程。

如图7所示，可以看出运用RPCA技术对图像进行背景分离是非常准确有效的。即通过RPCA技术可以对气泡图像矩阵的稀疏成分和低秩部分进行分离。当气泡有效分离后，可以通过稀疏矩阵来探索气泡的运动的无背景干扰运动过程。

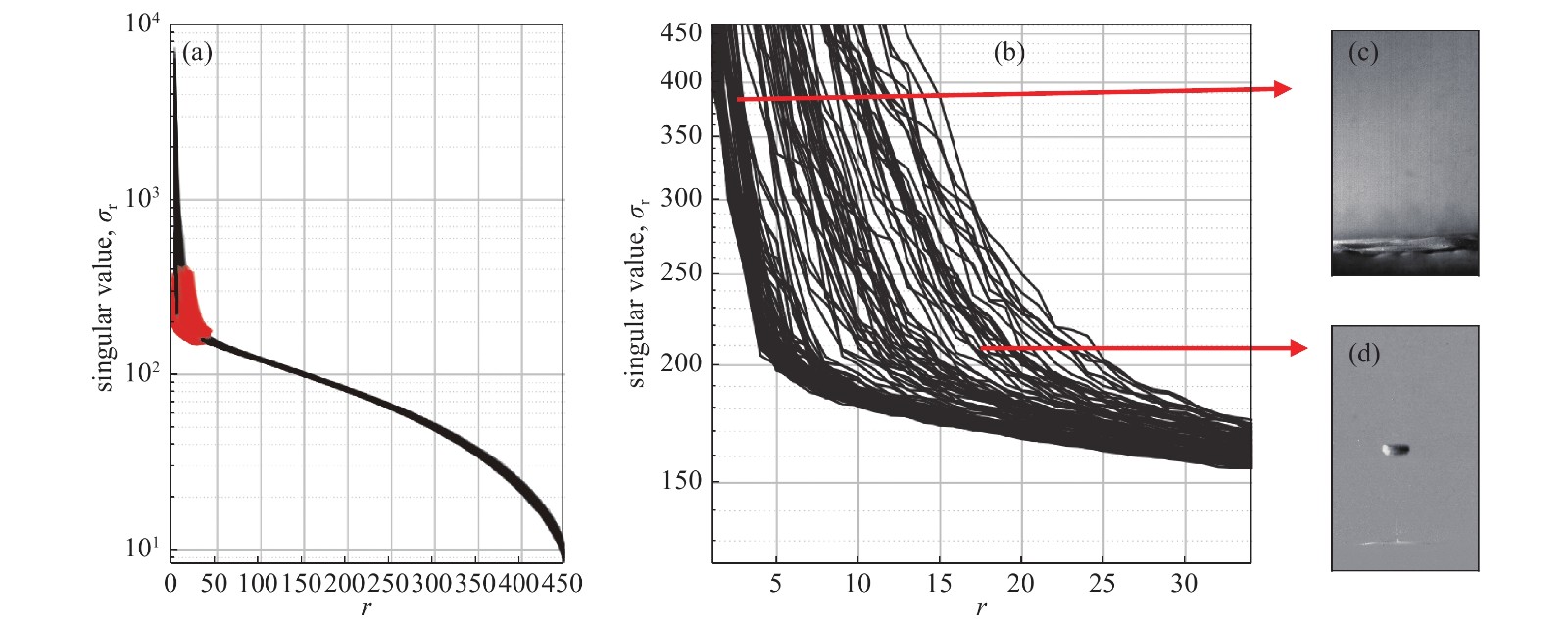
SVD分解对于输入一组图像信息时，其可以将这组图像转变为一个大容量的矩阵组合X，分解后可以很好的表现出一组图像的公共特征。于是，将经过处理后无背景的气泡图像形成的稀疏矩阵进行SVD分解后来观察其公共特征。

如图8所示，将图中单值分解图像的拐点处（红色标记处）进行放大，气泡图像进行低秩分解后的线条出现明显的重合部分和稀疏部分。逐个图像对比得出线条的重合部分，正是无气泡的图像，而稀疏线条也对应着气泡的运动线条的结论，这与理论分析是完全符合的。

提取后的气泡图像可以近似表示气泡运动全特征。即通过稀疏矩阵来探索气泡的运动过程。由于稀疏矩阵中气泡所对应的矩阵位置出现明显的异常值，当通过矩阵逐行累加和逐列累加后，矩阵异常值的位置区域也就对应气泡在背景图的相对位置。

数学原理:

式（9）中X_i1表示矩阵i行中的第一个值，X_i2表示i行中的第二个值，以此类推，进行矩阵依次行相加。

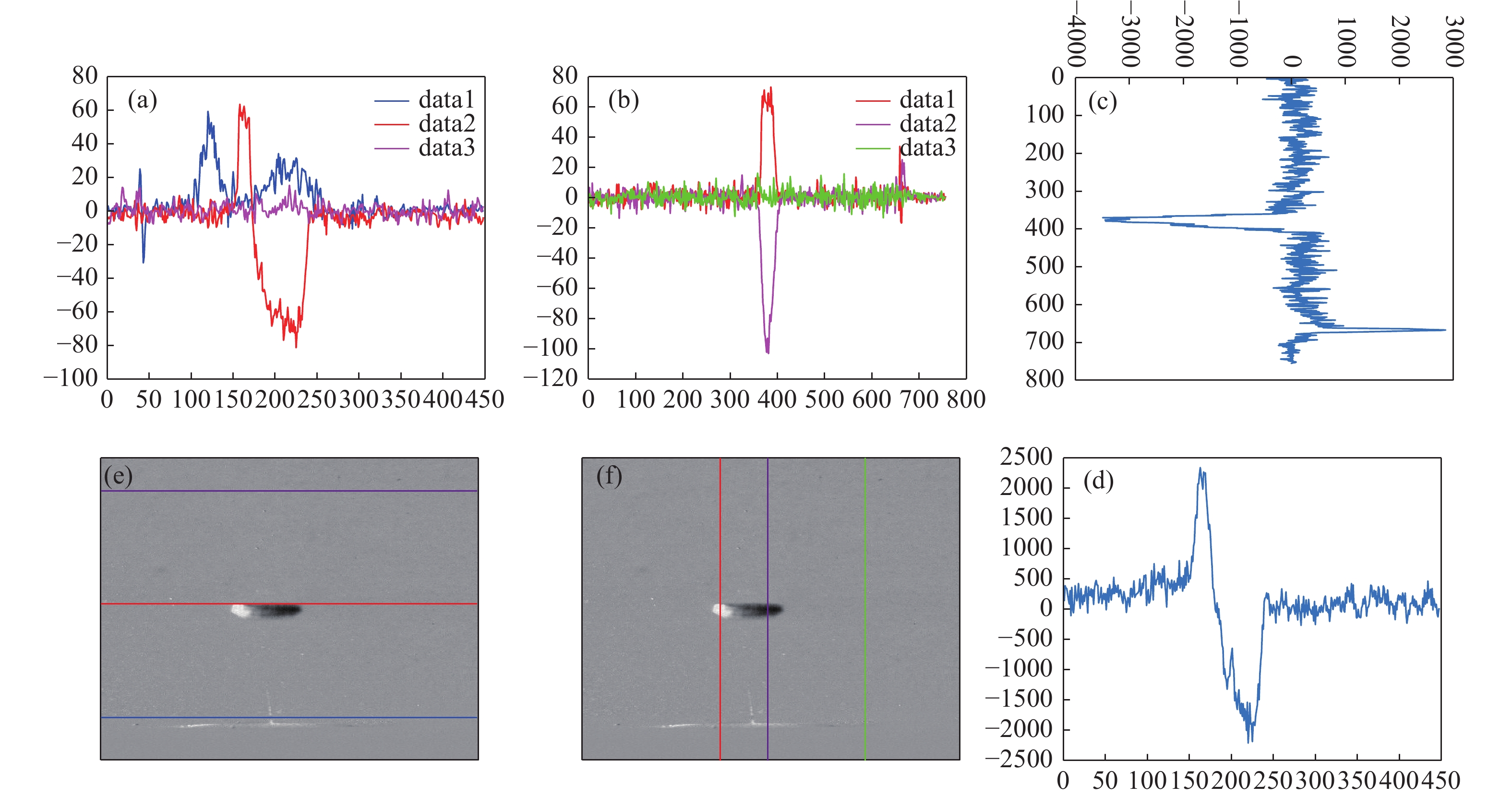
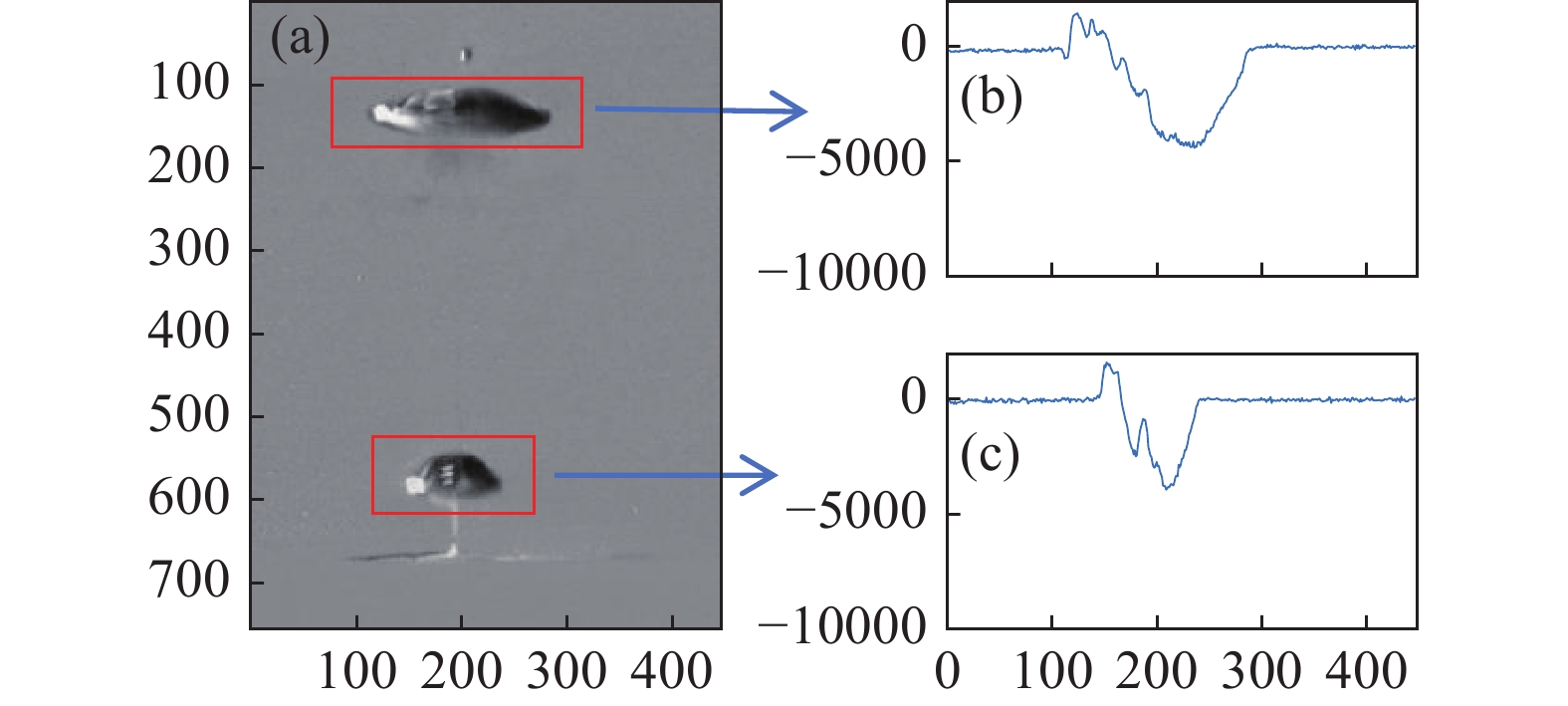
式（10）X_1j表示矩阵j列中的第一个值，X_2j表示矩阵j列中的第二值，以此类推，进行列相加。如图9所示，对一张去除背景的气泡图像进行分析，以图中三种颜色的横竖线代表着对这张图像中某一组数据的行相加和列相加。取图像中三种特殊位置的数据先进行比较，（a）图的三条线条对应三组数据，三组数据由颜色一一对应。通过（a）图和（b）图会发现对于特殊位置的行数据和列数据都会出现异常的波动值，于是将图像中所有数据进行逐行相加和逐列相加，会形成图中的（c）图和（d）图。

如图9所示，图像的行相加图像和列相加图像都出现明显的峰值。（c）图中的低峰值和高峰值分别表示图像中的气泡相对上升位置和底部液体产生的相对扰动位置。同理，（d）图中的峰值移动位置反映气泡的左右相对移动位置。通过气泡的峰值移动可以判断气泡的位置运动轨迹过程。（d）图中的高低峰值分别是由于气泡的拍摄而形成的明暗面，即气泡的边界面，通过高低峰值的跨度范围可以反映气泡的轮廓范围。

为探索气泡运动过程，取一组去除背景的气泡连续运动图像过程进行分析，通过对气泡矩阵进行逐行累加和逐列累加后，形成如下图的各自对应的10张行相加和列相加对比图。

如图10所示，通过间隔采样法，提取一组气泡的运动过程进行分析，图（b）中1到7张图像表现的气泡向上运动过程，低峰值也从随气泡上升的运动从右向左移动（图11（a）解释的气泡上升的X轴的位置点），而高峰值的位置几乎不变（图11解释的气泡脱离底层颗粒物后在液体中最初的扰动点）。8到10张图片是只有液体背景的行相加，即图像基本一样。图（c）中的1到7张图基本趋势也大致相同，反映气泡的上升过程（图11（b）解释的气泡上升的Y轴位置点）8到10张是无气泡图像。

当气泡图片矩阵进行RPCA分解后，气泡图片的稀疏矩阵能有效反映气泡的运动过程。将气泡完整的一组运动过程形成的图片进行分析，每张形成的矩阵进行逐行相加和逐列相加，来观察其运动过程中图片矩阵的变化，尤其是图片高低峰值的变化过程。

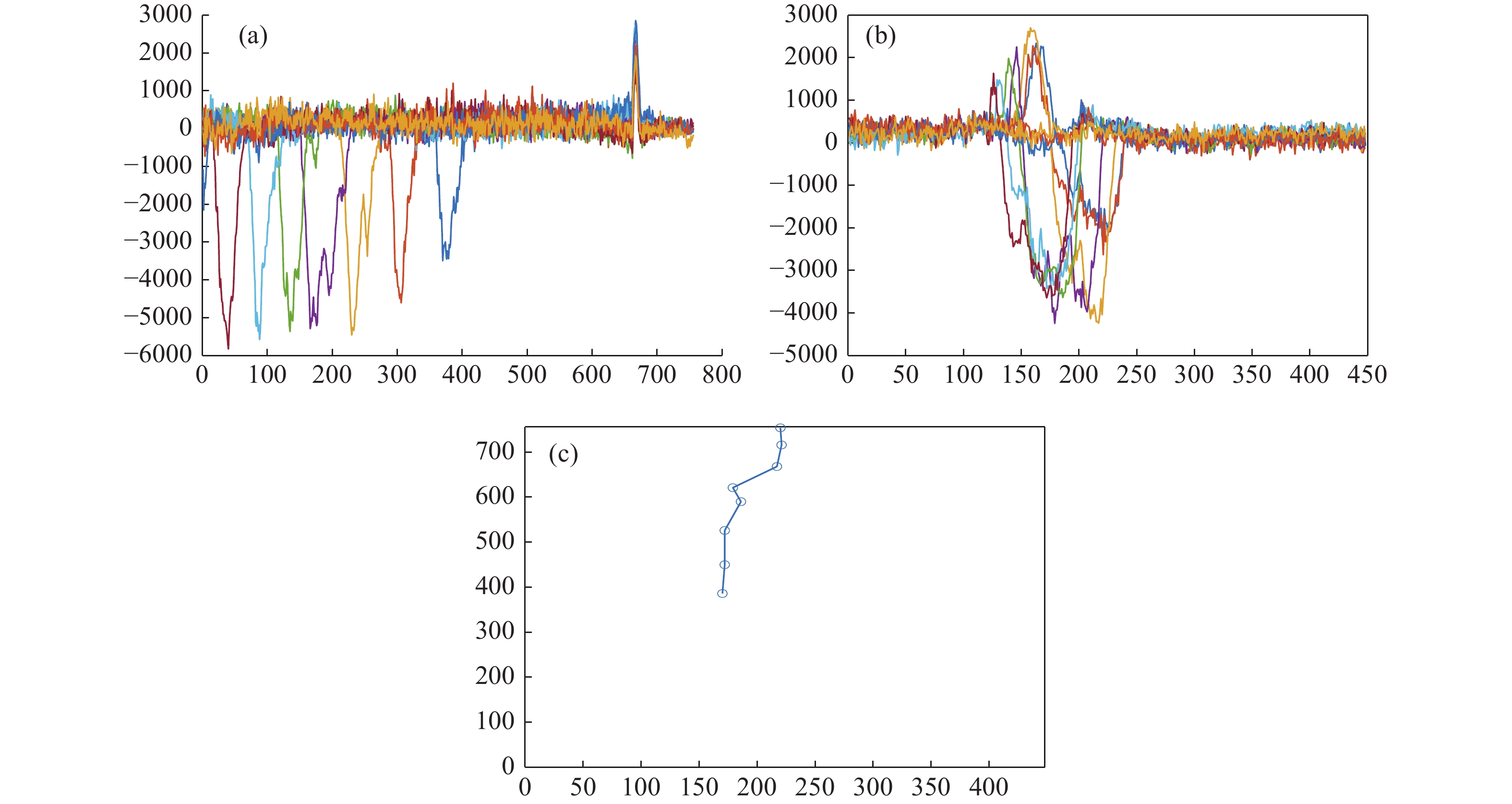
如图11所示，矩阵行相加的最大值点在气泡运动的过程中是几乎不变的，即最大值所取值与气泡运动无关，对比原图发现，是由底部扰动产生的正值点。将气泡上升运动的全过程通过矩阵数值去表示时，会发现矩阵行相加后形成一列数值，将其对应二维坐标系的Y轴数据，矩阵列相加后形成一行数据，对应二维坐标系的X轴数据。

图11（a）中最小值点的移动过程是由右向左运动的，研究发现，对应气泡向上Y轴移动的过程。而图11（b）矩阵列相加的峰值位置，对应气泡向上X轴移动的过程。将图10中的单个气泡上升运动用上述方法去表示时，形成图11（c）气泡的运动轨迹。

综上所述，气泡的相对位置在矩阵突出点的转变来显示出其运动轨迹，当气泡的运动轨迹知道后，即可通过每张图片拍摄的间隔时间，来表达气泡的相对速度，从而反应气泡的运动快慢。

数学原理：

式中t表示气泡图像在高速摄像机拍摄的图像间隔的时间，s表示气泡在拍摄间隔时间内在背景图像中运动的相对距离，V表示气泡在背景图像每过一段时间后运动的速度。

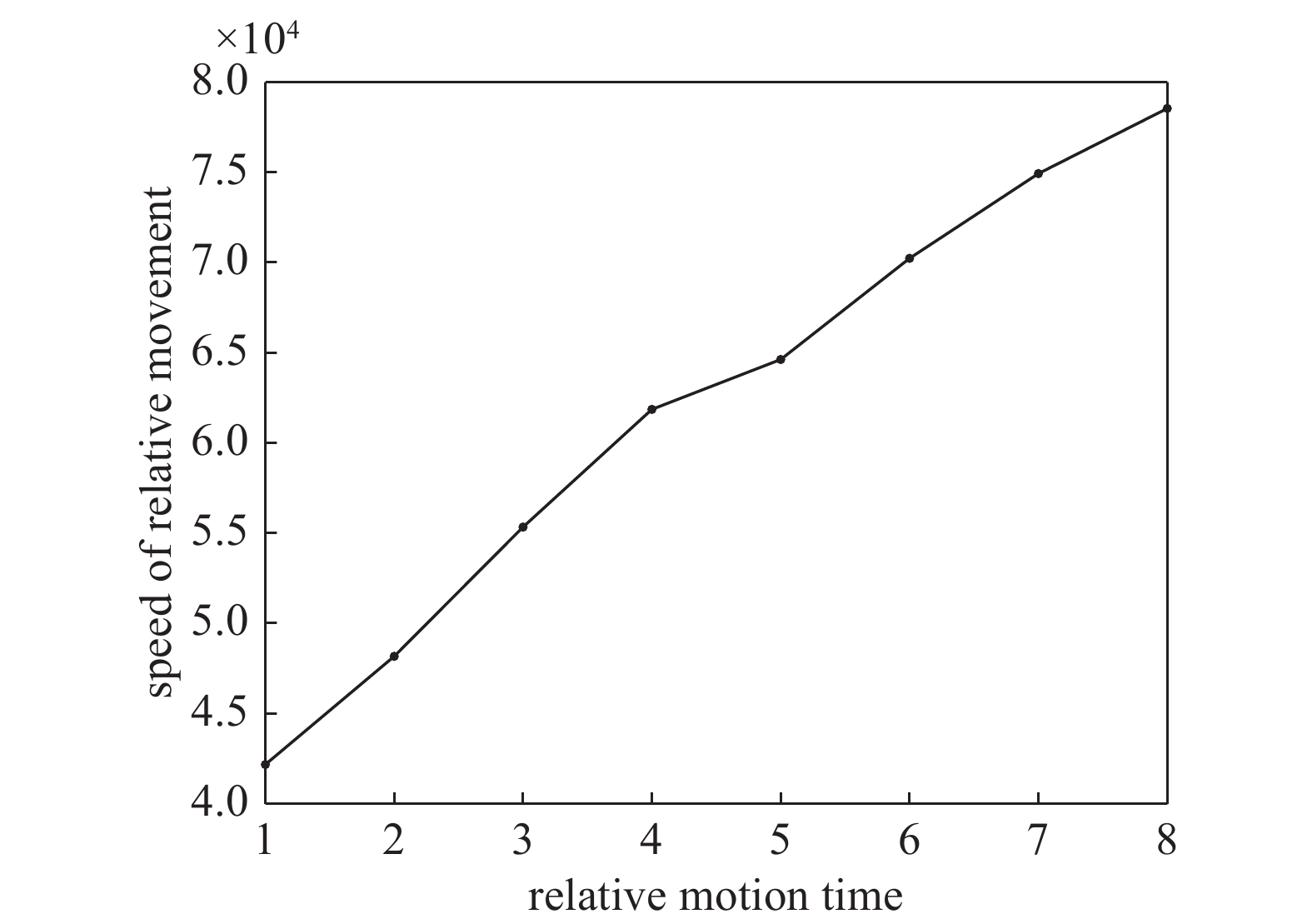
如图12气泡的相对移动速度变化曲线，取一段气泡的运动过程进行速度变化分析，会发现不同时间段气泡的运动速度是有所变化的，当气体从脱离底层颗粒物表面向上运动后，气泡在相对时间间隔相同时，气泡的运动轨迹跨度范围增大，相对运动速度增大。即证明了气泡多重力的作用下形成一定的运动趋势，呈一定的加速度向上运动。通过控制变量法比较速度大小，可以探索不同工况下对气泡的影响因素。

由单张图片中矩阵列相加矩阵图像与气泡图像一一对应，会发现图片中的高低峰值是研究所感兴趣的重要部分，气泡的亮暗面对应峰值所处的矩阵位置，于是，就可以利用峰值与峰值间的起始位置与结尾位置间的宽度来大致计算气泡的宽度，实验结果如下图：

如图13将一张图像中红色边框所圈出的两个气泡进行宽度对比，会发现右图中上面气泡对应的红色线条的跨越距离要大于下面气泡所对应的线条的跨越距离，这与实际图像中上面的气泡比下面的气泡更大相符合。即高低峰值间的宽度范围来表示气泡的薄扁度，研究发现，宽度范围越大气泡越扁，宽度范围越小气泡越宽。

将鲁棒性主成分分析算法运用于气液两相流气泡图像分离技术，该方法将气泡与背景图像合理的分离。通过稀疏矩阵对气泡运动过程进行分析，提出逐行相加和逐列相加的算法，来突出气泡图像矩阵数值的突出点相对位置，与原始气泡运动过程进行对比，证明此次算法的合理有效性。

(1)本文应用了SVD分解技术分析了气泡与背景图像分离的可能性，利用RPCA技术来实现了气泡在原始图像中的自动提取。相比于原本的图像分离技术^[26]，SVD分解和RPCA技术可以弥补处理单一图像和不可自动化的缺陷。

(2)本文提出逐行相加和逐列相加的新算法，实现对气泡相对位置的确定，描绘气泡的运动轨迹，计算气泡的相对运动速度，对比气泡的形变大小。