首页
登录
注册
下载:
-
低真空管道磁浮技术相对于铁路轮轨式运输是一项革新性的技术，是一项巨大的系统工程，此项技术可以极大的减少阻力，而空气动力学是目前管道磁浮列车必须解决的关键问题之一[1]。
列车在管道内运行时存在一系列气动特性问题[2]，目前国内外很多学者进行了大量的数值仿真计算。周晓等[3-4]采用粘性流体 Navier-Stokes 方程和 k-ε 湍流模型，研究不同阻塞比对管道的影响，当列车以不同速度运行时管道车体受到的空气阻力，其结果显示阻力随阻塞比的增大而增大，阻塞比较小时，对阻力的影响较小。刘元森[5]采用二维、定常、可压缩湍流研究方法，利用动网格方法将磁悬浮列车置于真空度管道中，然后通过分段铺设在轨道下方的直线电机加速，磁悬浮列车可以在数倍于飞机的速度运行。陈绪勇[6]通过对不同头车、尾车的流线型设计，研究不同真空度和不同阻塞比对磁浮列车空气阻力的影响规律。米百刚等[7]基于动网格技术，并且建立二维、可压缩、非定常的 Navier-Stokes 方程及SST k-ω 湍流模型，研究真空管道阻塞比和真空度与空气阻力的关系。
但与此同时面对气流阻塞效应，激波效应等一系列新的瓶颈难题接踵而来，Kim等[8]基于Navier-Stokes 方程和 SST k-ω 湍流模型，研究明线磁悬浮列车不同速度阻力数据对比，同时提出管道内产生激波的速度标准，结果表明激波的临界速度仅是与阻塞比相关的函数，管道压力的影响几乎为零。Kim等[9]建立二维模型，基于非定常、可压缩的 Navier-Stokes 方程和SST k-ω 湍流模型研究了管道内激波现象，结果表明管道的直径和环境压力对激波影响较大，管道的长度不影响激波。张晓涵等[10] 建立二维亚音速真空管道列车数值模型，结合重叠网格技术研究了真空管道列车运行前方的气动壅塞现象与尾部的激波现象。Zhou等[11-12]根据可压缩 Navier-Stokes 方程和 SST k-ω 湍流模型，研究激波簇结构及管道内激波演变规律。Niu等[13-15]建立二维计算仿真模型，受管道激波的影响对列车压力、流速和温度的变化进行研究，并分析列车速度对激波强度及位置的影响。黄尊地等[16]建立管道列车二维计算模型，基于验证的网格和湍流模型开展超声速列车运行时管道激波特性分析，探究了管道内激波反射特性，运行时间和马赫数对管道列车头车正激波和车尾激波串的演变规律。
综上所述，列车在管道内运行可以减少气动阻力，但存在激波问题，目前国内外很多学者已研究列车的激波演变规律，但单管双线运输能力远远大于单线，且关于双线还鲜有研究。因此本文建立二维管道列车交会数值仿真模型，采用非定常 SST k-ω 湍流模型并结合滑移网格技术，分析管道列车交会时激波演变特性。
-
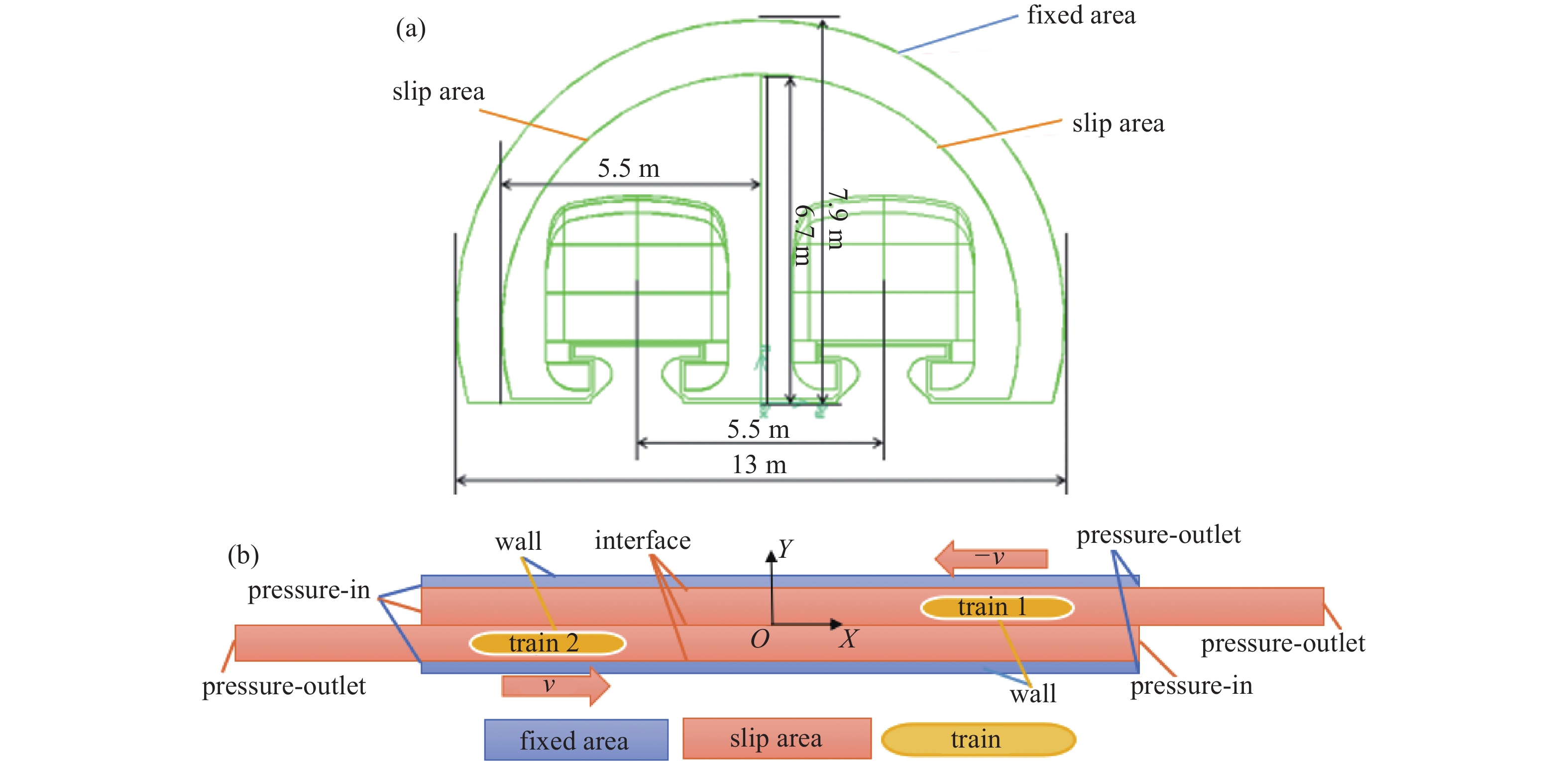
选择磁浮列车TR08，采用gambit软件建立三维模型，三维模型侧视图如1 (a) 所示，计算区域由两个涵盖列车的滑移区域（管道）和一个涵盖管道空间的固定区域（隧道）组成。
磁浮列车长度79.5 m，宽度3.7 m，高4 m，两车线间距5.5 m，固定区域最大宽度13 m，单个滑移区域最大宽度5.5 m。水平投影方法得到整个二维平面数值计算仿真模型如1 (b) 所示，两车起始交会距离为x m，列车尾部距离固定区域端口300 m，两列车在隧道中央处等速交会。
-
建立二维计算模型进行流场仿真，鉴于流场仿真来流速度较高，空气压缩效应较为明显，因此采用理想气体。采用隐式密度求解器，选择AUSM+格式处理对流通量，可以准确捕捉激波不连续性[17]，动量、湍动能、比耗散率均采用二阶迎风离散格式。
计算区域边界条件设置如1 (b) 所示，固定区域与滑移区域重叠壁面设置为交换面interface，无重叠壁面、列车表面设置为固定壁面wall，计算区域入口端为压力入口，出口端为压力出口；涵盖车1区域定义为右滑移区域，涵盖车2区域定义为左滑移区域，右滑移区域运行速度为-ν，左滑移区域速度为ν，环境气压为1 atm，初始温度为288.15 K。
-
本文采用非结构化与结构化混合网格对计算域进行网格剖分，并对流动复杂区域进行网格加密，加密长度为300 m，尺寸为8 mm，为防止网格尺寸对数值仿真的影响，本文建立起始交会距离500 m，分析粗中细三种不同的网格尺寸对管道压力、列车阻力的影响。
设置棱柱层厚度为20 mm，列车表面为14层棱柱层网格，拉伸比为1.2，背景域网格基础尺寸分别为100、80、60 mm，最小尺寸分别为40、30、20 mm，列车基础尺寸为8 mm，最小尺寸分别为7、5、3 mm，网格数量大约分别为180万、250万、330万。
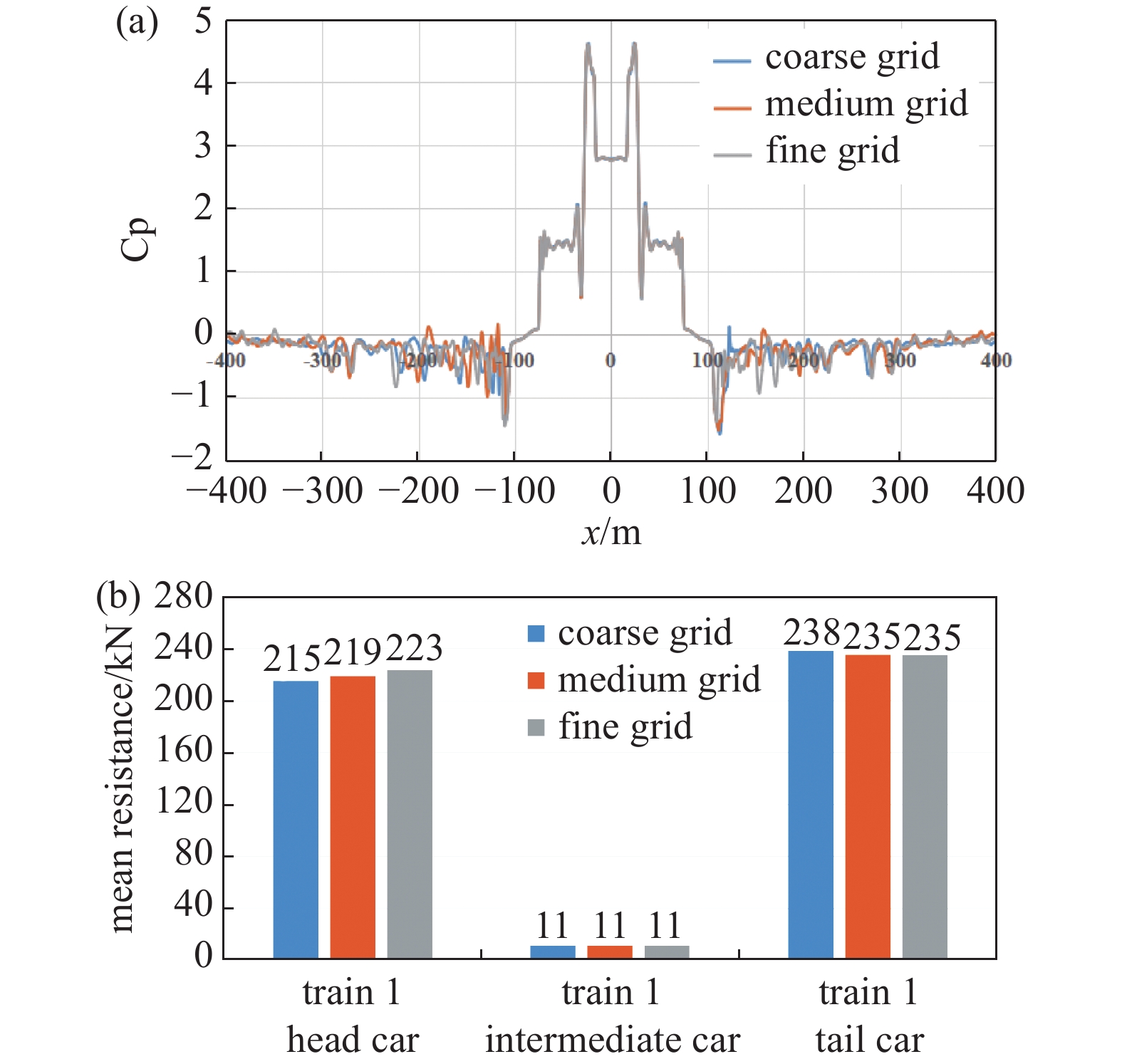
两车以速度
1000 km/h在隧道中央处等速交会，环境压力p=1 atm，初始温度为288.15 K，管道内y=0处压力系数曲线如图2 (a) 所示，t=0.8 s时，列车前方正激波前锋相互干涉，压力系数激增，列车运行一段时间后，当两车间距大于100 m时，压力存在波动，当两车间距小于100 m时误差较小。选取车1的平均阻力进行分析，如图2(b) 所示，头车误差相对中间车和尾车误差略大，以车1头车平均阻力为例，粗网格与细网格误差为3.58%，中网格与细网格误差为1.79%，由图可知平均阻力均满足误差范围要求，本文选取中等网格。
-
气体在较长的管道中传播，气流受到管道壁面的约束，堆积到列车前方形成高压区，因气体的可压缩性，管道内气体长时间被压缩，造成壅塞现象，形成正激波。在车肩车尾处，横断面相对增大，导致流速急剧增大而压力急剧减小，形成膨胀波。
分别对列车前方区域和尾流区域的流动特点进行描述，管道内气压p=1 atm，初始温度T=288.15 K。起始交会距离为500、
1000 、1500 和2000 m，管道列车运行速度等级包括1000 、1100 、1200 、1500 和1750 km/h，设起始交会距离为x，两车运行后相距为x1。分析两列车在隧道中央处等速交会时激波特性及列车气动阻力演变规律。 -
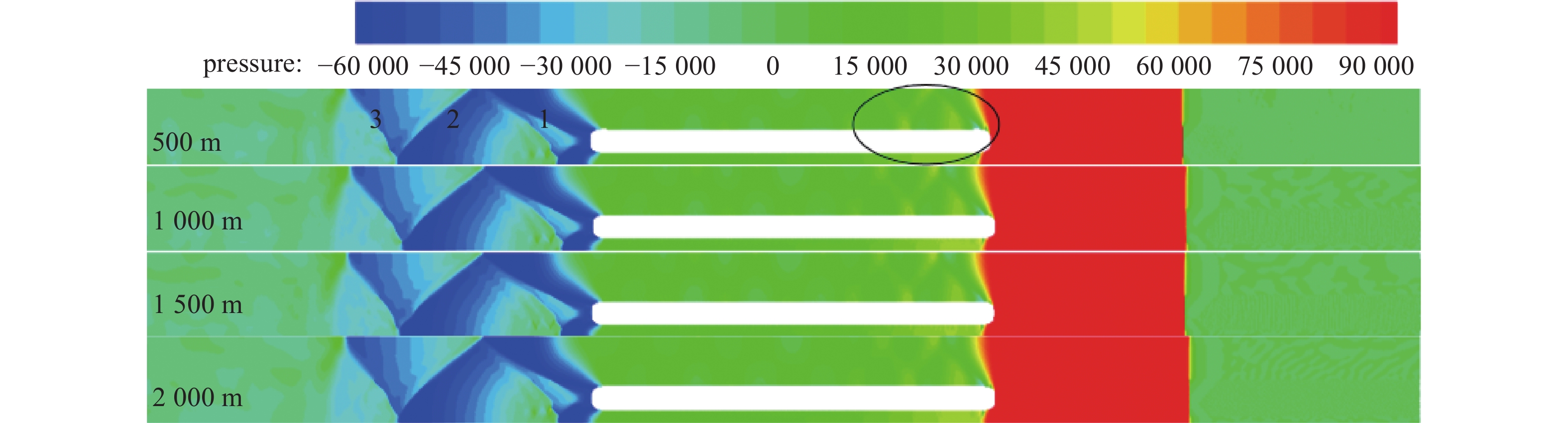
两车均以
1500 km/h速度运行，以车2为例，当起始交会距离为500 m~2000 m时，对运行时间t=0.4 s管道内列车激波演变规律进行分析。如图3所示，车2前方正激波还未相互影响，当x=500 m时，车肩处横断面相对增大，压力急剧下降，由于管道壁面的约束，车身与管道壁面产生激波反射现象，但反射强度较弱，列车尾部受膨胀波影响，车尾产生激波1，激波1与管道壁面反射生成激波2，激波2再次射生成激波3，形成激波串现象，激波串强度沿车尾方向逐渐减弱。
当起始交会距离x为
1000 、1500 和2000 m时，列车前方壅塞长度、车身激波与管道壁面反射现象、车尾激波串演变规律及管道内压力变化与x=500 m基本一致。结果表明，管道列车以相同速度交会时，当两车相距较远，即列车前方正激波还未相互交叉干涉时，管道列车运行相同时间，起始交会距离x对激波演变特性影响较小（可以忽略）。随运行时间的推移，两车交会间距相对减小，分析两车以车速
1500 km/h从不同起始交会距离x运行到相同位置x1，如图4 (a)(b)(c) 所示，分别为交会前、中、后三个时间段内管道激波演变规律。由4 (a) 可知，两车交会前，当x=500 m，正激波前锋延伸到头车，车尾激波与管道多次反射形成激波串，沿车尾方向激波串强度减弱；随着x的增加，x=
1000 m时，列车尾部激波串长度增加；x=1500 m时，正激波前锋从头车延伸到中间车，列车尾部激波串再次增加；x=2000 m时，正激波前锋延伸到车尾，车尾出现激波-膨胀波相互干涉，由于两车相距一定的距离，列车尾部以膨胀波为主，车尾部激波串长度再次增加，沿车尾方向激波强度减弱。两车身交会时，如图4(b) 所示，x=500 m时，车1尾部膨胀波和车2头部压缩波相互影响，正激波延伸到车尾，正激波和车尾膨胀波相结合与管道壁面反射形成激波-膨胀波，列车尾部受膨胀波影响，正激波消失后，继续产生激波串。随x的增加，激波演变规律相似，激波-膨胀波长度增加，管道内波系复杂，沿车尾方向，复杂波强度逐渐减弱至负压，并又以激波形式与管道壁面多次反射形成激波串。
如图4 (c) 所示，当两车交会完成时，截面积增大，车尾受膨胀波影响，压力降低，列车尾部呈现激波串，沿两车运行方向，压力有所回升。随交会距离x的增加，壅塞长度增加，车身激波-膨胀波反射现象明显，压力增大，车尾激波串强度减弱。
-
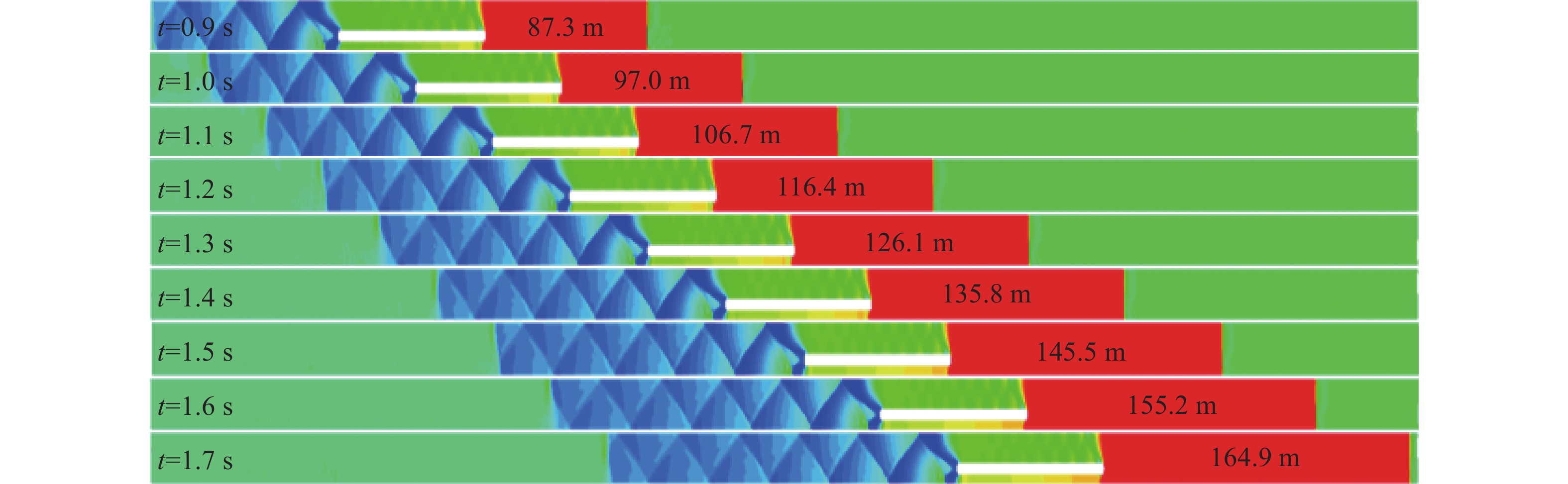
两车均以1500 km/h速度运行，起始交会距离为2000 m，列车前方正激波长度为d，当两车间距较远时，两车流场相互影响较小（可以忽略）。以车2为例，分析t=0.9 s至t=1.7 s管道内激波演变规律如图5所示。
当t=0.9 s时，列车前方正激波长度d=87.3 m，正激波长度随时间线性增加，t=1.7 s时，d=164.9 m。以图5不同时间节点正激波长度得以推出d=97 t，运行时间每增加0.1 s，则正激波长度增加大约9.7 m。
当两车相距较远时，列车前方正激波未相互干涉，不同时间节点管道激波演变过程相似，壅塞长度随运行时间呈线性递增关系。随运行时间的推移，车身附近压力增加，车身与管道壁面多次激波反射，但激波反射强度较弱，沿管道列车车尾方向，激波串反射长度增加，反射强度逐渐减弱。
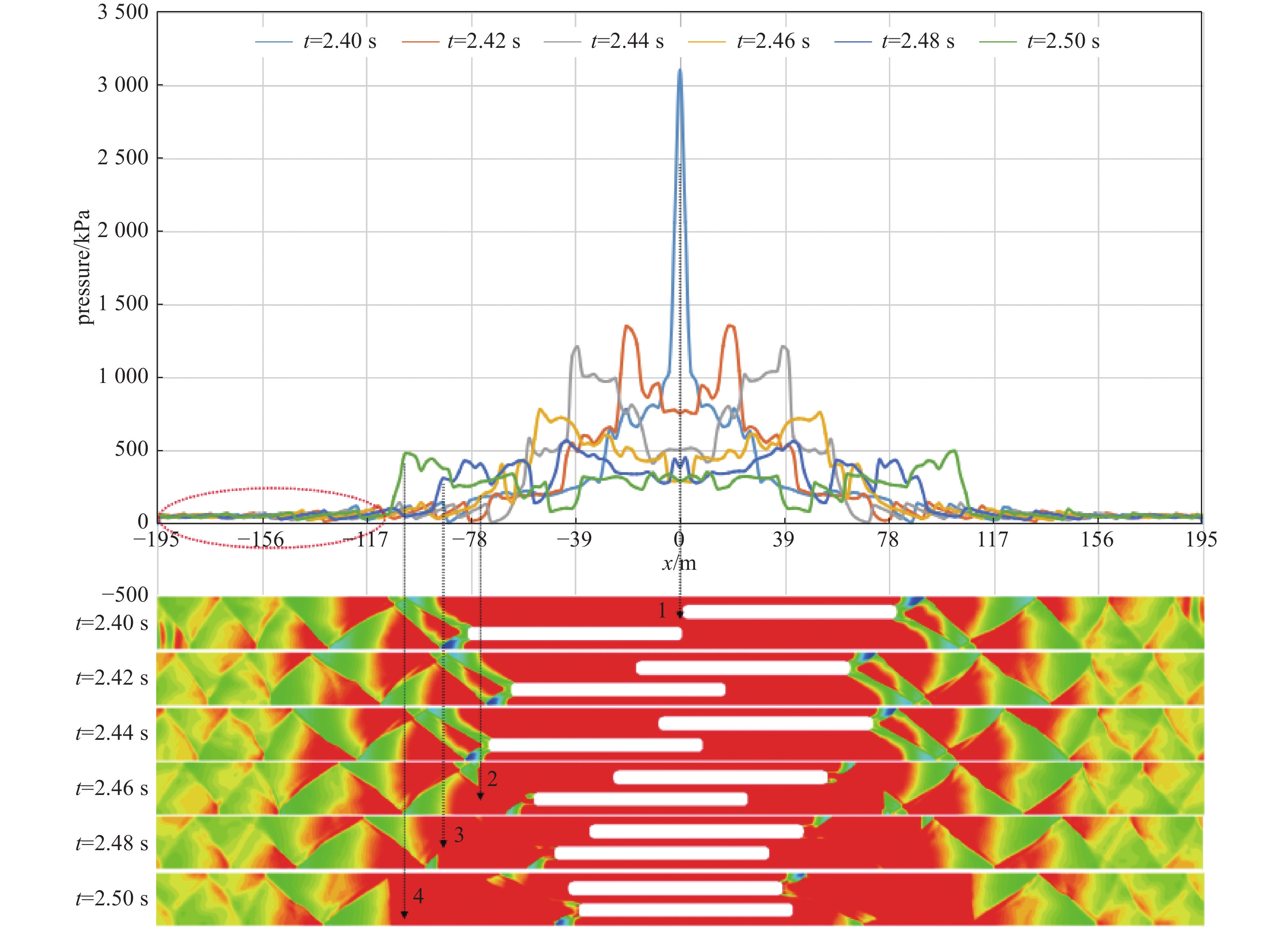
两车交会管道激波特性如图6所示，其图中曲线为两车交会中间管道y=0 处的压力变化规律。分析t=2.40 s至t=2.50 s不同时刻管道列车交会时激波演变规律，列车前后激波相互交叉干涉，同时壅塞范围被车尾膨胀波及激波分成若干小的范围，波系较为复杂，且正激波前锋已完全包围交会列车。
由图6可知，当t=2.40 s时，以车2为例，如浅蓝色曲线所示，两车鼻尖点1处压力激增，达到
3002 KPa，列车尾部有少量膨胀波出现，激波-膨胀波相互干涉，沿车2尾部方向与管道壁面进行多次反射，沿车尾方向强度减弱，管道内压力降低；t =2.46 s时，列车尾部2处出现较短的壅塞区段，如黄色曲线所示，管道内压力增大。反射，沿车尾方向强度减弱，管道内压力降低；t=2.46 s时，列车尾部2处出现较短的壅塞区段，如黄色曲线所示，管道内压力增大。
随运行时间的增加，车2头车逐渐远离，车1头车逐渐靠近，压缩波的存在导致管道内压力增大，车2尾部壅塞区段增加。整个过程如压力曲线所示，远离管道列车区域压力降低，如红色圆圈区域所示，列车尾部呈现激波反射现象，激波强度逐渐减弱。
选取整个交会时间区段，分析两车交会前、交会中、交会后整个过程管道激波特性，如图7所示，以黑色虚线右侧车1为例展开研究。
整个交会过程随运行时间的推移，列车前方正激波从头车延伸到列车尾部，由于车尾横截面积相对增大导致压力急剧降低，列车尾部生成的膨胀波与管道壁面多次发生反射，最终呈现大量的激波串。
列车运行到t=2.20 s时，正激波前锋延伸到车头，车肩处横断面增大，压力降低，车身与管道壁面发生激波反射现象，强度较弱，列车尾部激波串与管道壁面进行多次反射直到a1位置，之后压力又有所回升；t=2.25 s时，正激波前锋已延伸到中间车，列车尾部激波串达到a2处，激波串相对前0.05 s长度缩短；t=2.30 s时，正激波前锋延伸到车尾，正激波前锋已完全包围列车，列车尾部出现较短的激波与膨胀波相互干涉区段，如d1处所示，由于车1尾部主要存在膨胀波，b1处激波与管道壁面发生激波反射直到a3处。
t=2.35 s至t=2.45 s时，激波演变规律与之前时刻基本一致，列车前后激波相互交叉干涉，同时壅塞区段被车尾膨胀波及激波分成若干小的范围，波系较为复杂，车尾激波-膨胀波相互干涉反射长度增加，激波串长度缩短；t=2.50 s时，车1车尾与车2头车刚完成交会，车2列车前方开始出现壅塞区段，从d5处到c1处为壅塞区段，c1到b5呈现激波-膨胀波与管道壁面多次反射，b5到a7由于膨胀波的存在，又出现激波反射；t=2.55 s时，两车车身压力降低，车2前方壅塞长度较前0.05 s增加，b6到a8处的激波串长度逐渐缩短，两车尾部出现激波，强度增加，列车车身与管道壁面之间进行多次激波-膨胀波反射；t=2.60 s时，两车完成交会，与前0.05 s相比，列车前方壅塞区段长度增加，车身激波-膨胀波反射现象明显，两车尾部因膨胀波导致管道压力急剧降低，车尾出现激波反射现象。
-
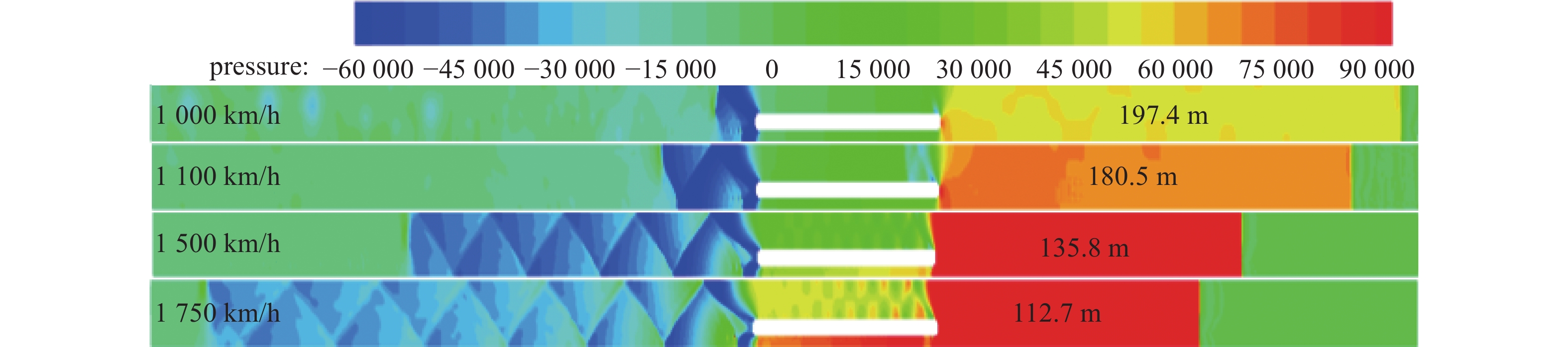
选取起始交会距离2000 m，列车运行相同时间1.4 s，如图8所示，此时两车相距较远，两车流场相互影响较小（可以忽略）。以车2为例，随运行速度的增加，管道内压力整体增大，头车正激波壅塞长度缩短，车身逐渐呈现激波反射现象，沿车尾方向，激波串长度增加，激波强度减弱。
由图8可知，两车均以
100 0 km/h速度运行时，列车前方壅塞长度为197.4 m，车尾存在较短的激波现象；当两车以1100 km/h运行时，头车壅塞长度缩短到180.5 m，管道内压力增大，车尾激波串长度增加；当车速为1500 km/h时，壅塞长度为135.8 m，与1000 km/h和1100 km/h相比，车尾激波串长度明显增加，激波强度减弱；车速达到1750 km/h时，壅塞长度为112.7 m，车身出现明显的激波反射现象，车尾激波串再次增加，激波强度减弱。研究结果表明当两车相距较远时，随速度的提高，列车前方壅塞长度缩短，管道内压力增大，车尾激波串长度增加，激波反射强度减弱。
选取起始交会距离
2000 m，两车均以1750 km/h运行，在隧道中央处等速交会，与3.1.2节图7管道列车运行速度1500 km/h相比，如图9所示，分析t=1.90 s至t=2.25 s各时间节点管道内激波演变规律。当列车运行到t=1.90 s至t=2.00 s时，车身激波反射现象比较明显，正激波逐渐向车尾方向延伸；t=2.05 s至t=2.25 s管道列车前方正激波壅塞区段增加，激波串长度缩短。
研究结果表明，当管道列车运行速度过高，会导致正激波占比较大，管道内压力明显增大，激波前锋包围列车现象明显，车身与管道壁面进行多次激波反射现象，车尾呈现较短的激波-膨胀波相互交叉干涉现象。
-
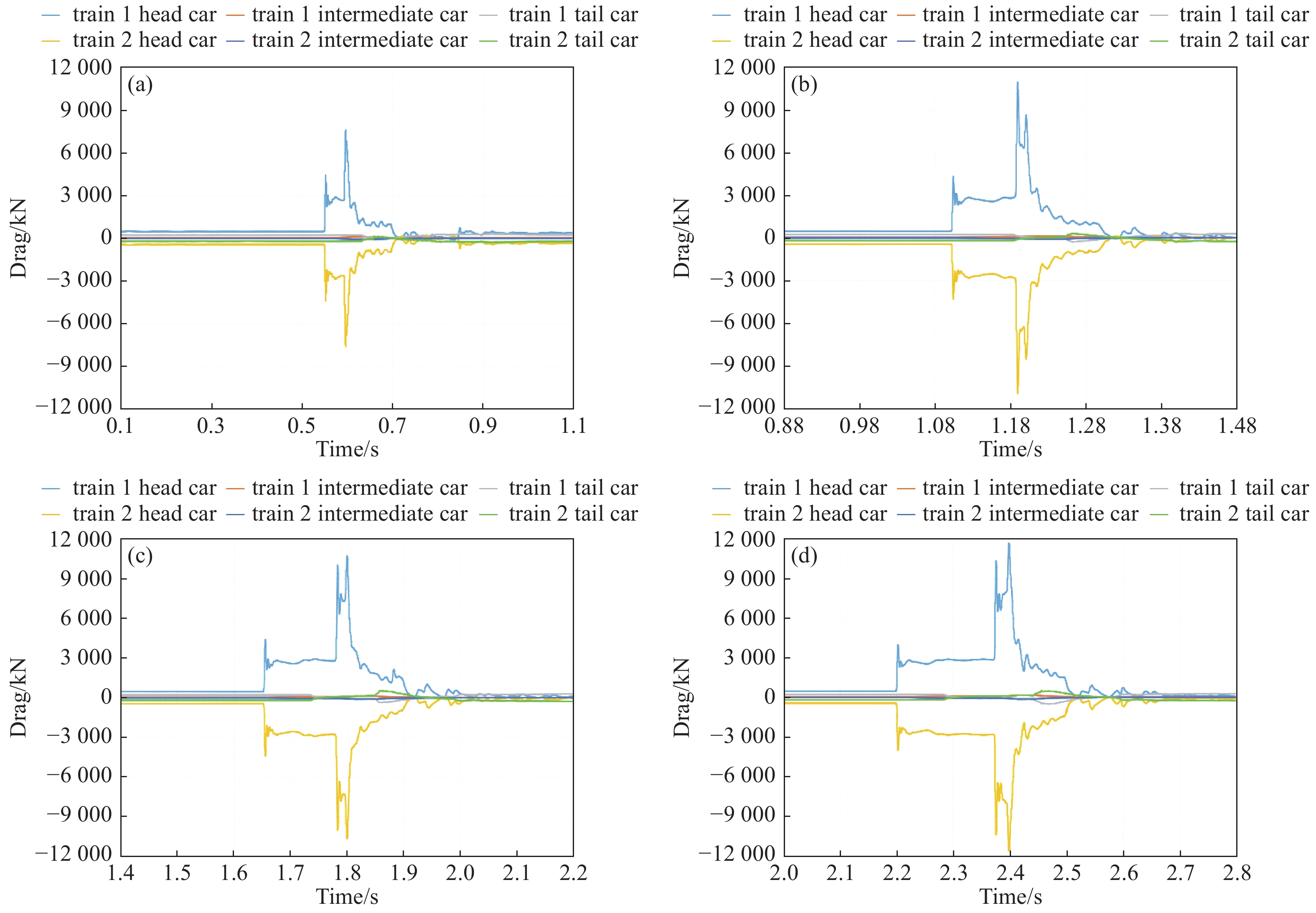
两列车均以1000 km/h在隧道中央处交会，分析不同起始交会距离对管道列车气动阻力的影响。如 图10 (a)-(d)分别为不同起始交会距离500、1000、1500和2000 m状态下的列车气动阻力分布。
如图10 (a) 所示，以车1为例，起始交会距离x=500 m时，t=0.55 s之前列车各部位处于相对平稳阶段，头车平均阻力为449 KN；t=0.55 s至t=0.6 s之间，两车运行间距相对减小，列车前方正激波已相互交叉干涉，车1头车平均阻力为2740 KN，比两车激波相互干涉前激增83.6%；t=0.6 s时，两车间距已接近0 m，此时车1头车阻力激增到最大值
7590 KN，阻力再次激增63.9%；当t=0.78 s，两车基本完成交会，两车头车阻力逐渐恢复到相对平稳状态，与头车相比，中间车和尾车每个时间节点阻力变化相对较小。由图10(a)-(d) 可知，以头车为例，两车相距较远时，正激波相互干涉前，起始交会距离对阻力影响较小。两车正激波前锋相互干涉（未交会时），车1头车阻力急剧增大，车2头车阻力急剧降低，起始交会距离越长，两车正激波相互干涉时间越长，头车阻力绝对值增大。随列车的运行，两车间距相对减小，当两车准备交会时，头车阻力绝对值再次激增；当两车车尾分离较远时，两车激波相互影响较小，列车阻力恢复到单车运行状态，整个交会过程中间车和尾车阻力值受起始距离影响较小。
当两车相距较远时，起始交会距离对管道列车气动阻力影响较小（可以忽略），两车在管道内运行一段时间后，两车间隔距离较近，两车正激波前锋相互交叉干涉时，起始交会距离会对气动阻力产生影响。管道列车速度过高时，列车气动阻力会急剧增加，但固定区域隧道过短会对列车最大阻力有所抑制，即当起始交会距离为500 m、
1000 m时会低估最大阻力，因此起始交会距离选择大于1500 m较为合适。通过以上分析，结果表明列车行驶在短、中长隧道（x<
150 0 m）阻力/压力最大绝对值变化剧烈，长隧道（x>1500 m）阻力/压力最大绝对值变化幅值较小。两车交会完成后，由于两车车尾膨胀波相互干涉，列车阻力绝对值急剧下降至相对平稳状态，但阻力变化幅值存在波动。 -
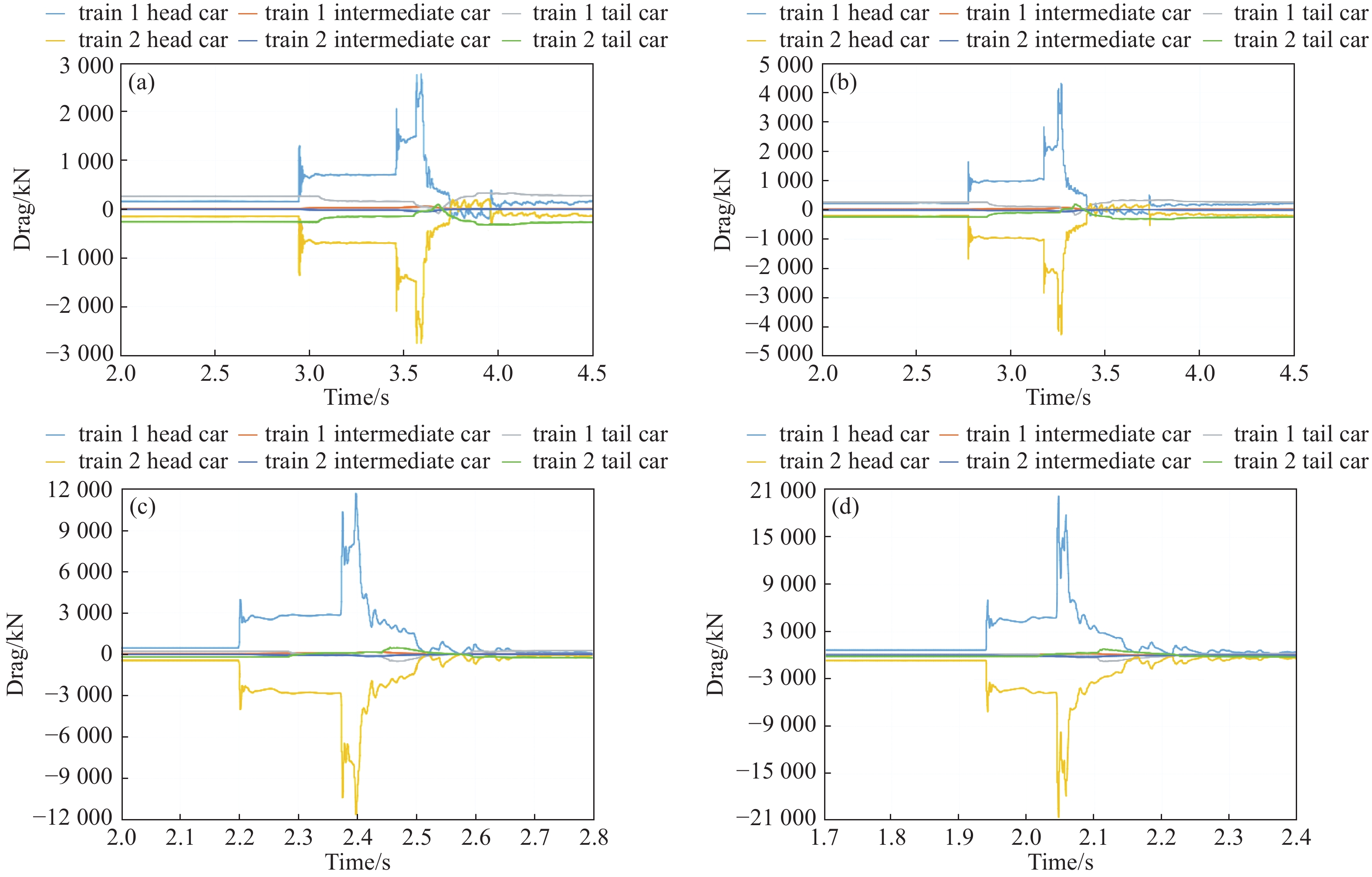
取起始交会距离距离
2000 m，如图11(a)-(d)分别为1000、1100、1500和1750 km/h速度下列车气动阻力分布。由图11可知，不同速度下列车气动阻力变化规律基本一致。当两列车均以1000 km/h在隧道中央处等速交会，由图11(a) 可知，t=2.95 s时，两车正激波前锋相互干涉，车1头车出现激增又急剧下降到相对稳定状态，阻力大约为700 KN；t=3.46时两车相对间隔距离较小，阻力再次激增，正激波包围两车；当两车运行到t=3.6 s时车1头部阻力激增到最大值2766 KN，随时间的推移，两车交会阻力急剧下降之后又恢复到相对平稳状态。如图11 (b) 所示，两车均以
1100 km/h运行，正激波前锋相互干涉，阻力值达到1000 KN左右；当两车运行到t=3.26 s时，车1头部阻力激增到约4119 KN，与1000 km/h相比，阻力绝对值增加。由图11 (c) 可知，两车1500 km/h运行时，两车交会前正激波前锋相互影响区段阻力激增到3000 KN左右；t=2.4 s时车1阻力再次激增到11668 KN。两车均以
1750 km/h运行时，由图11 (d) 可知，列车正激波前锋处于相互交叉干涉阶段，阻力激增到大约4800 KN；t=2.05 s时车1阻力再次激增到20170 KN。以上分析可推断，列车运行速度对列车阻力影响较为明显，随列车速度的提高，其阻力绝对值增大。管道列车以
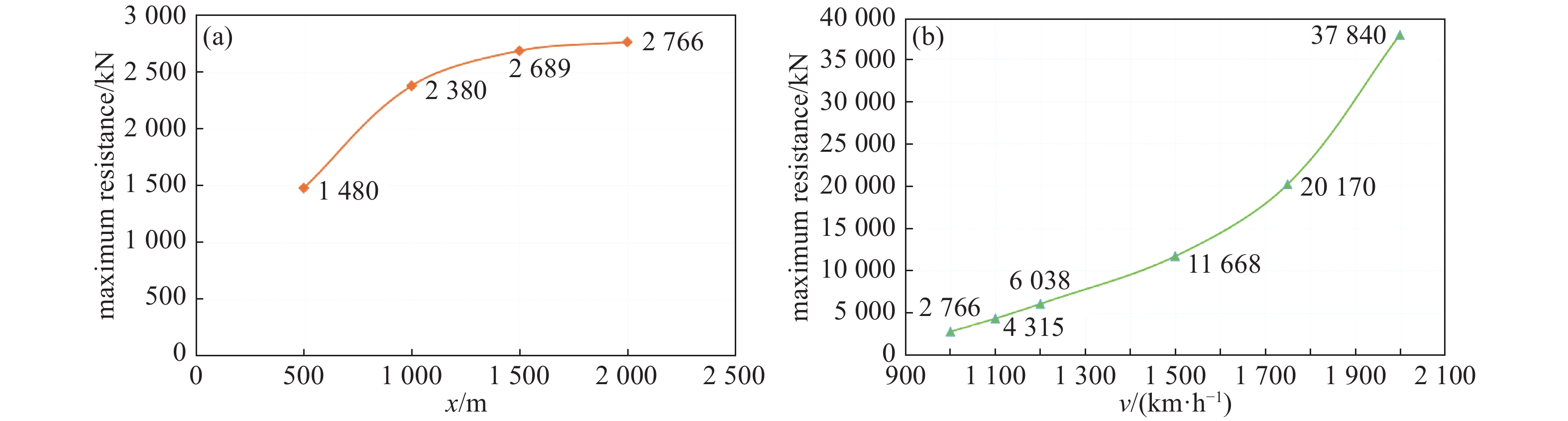
1000 km/h速度运行，如图12 (a) 所示，分析起始交会距离距离对列车气动阻力的影响，起始交会距离x=500 m时，最大阻力达到1480 KN；当x增加到1000 m时，最大阻力达到2380 KN，比500 m增加37.82%；当x=1500 m时，列车最大阻力值达到2689 KN，比x=1000 m增加11.49%；起始交会距离x达到2000 m时，最大阻力达到2766 KN，比x=1500 m增加2.78%。仿真结果表明列车行驶在短、中长隧道内（x<1500 m）最大阻力变化剧烈，长隧道内（x>1500 m）最大阻力变化幅值较小。由图11可知速度对列车阻力影响较为明显，其不同速度最大阻力变化曲线如图12 (b) 所示，当两车均已
1000 km/h运行时，列车最大阻力达到2766 KN；当以1100 km/h运行时，列车最大阻力达到4315 KN，较100 0 km/h增加35.89%；当1200 km/h运行时最大阻力达到6038 KN，较1100 km/h增加28.53%；当管道列车运行速度为2000 km/h，最大阻力达到37840 KN。结果表明与起始交会距离相比，列车运行速度对阻力影响较大，随速度的提高，列车最大阻力持续增大。 -
建立二维管道列车交会数值仿真模型，详细分析了不同交会距离、时间和速度下管道列车交会前、中、后激波演变特性及对列车阻力的影响，根据流场仿真结果，得出以下结论：
（1）交会前，两车正激波前锋未相互交叉干涉，壅塞长度随运行时间线性递增，管道内压力影响较小；交会中，管道内压力整体增大，列车周围存在激波-膨胀波干涉现象；交会完成，列车周围压力较低，沿列车运行方向压力回升，逐渐恢复单车运行状态。
（2）随起始交会距离x的增加，阻力/压力绝对值增大，头车壅塞长度和车尾激波串长度增加。但起始交会距离过小会抑制列车最大阻力/压力，当列车行驶在短、中长隧道（x<
1500 m）阻力/压力变化剧烈，长隧道（x>1500 m）阻力/压力变化幅值相对较小。（3）列车运行速度对列车阻力影响较大，随速度的提高，阻力/压力绝对值增大，列车前方壅塞区段缩短，沿车尾方向，列车尾部激波串长度增加，激波反射强度减弱。
（4）本文研究了管道环境压力p=1 atm，线间距5.5 m时二维管道列车交会激波特性，下一步将研究三维管道列车在不同真空度、线间距交会时激波演变特性。
二维管道列车交会激波特性分析
Analysis on Shock Wave Characteristics of Two-Dimensional Rendezvous Train in Tube
-
摘要: 列车在低真空管道内运行可以极大的减少阻力，但同时面临激波效应等难题。建立二维管道仿真模型，采用可压缩非定常 SST k-ω 湍流模型并结合滑移网格技术，研究不同起始交会距离、速度、时间下管道内激波演变规律。结果表明：两车相距较远时，列车前方壅塞区段向前推进，壅塞长度随时间线性递增，正激波相互扰动时，阻力/压力绝对值激增；两头车交会时，阻力/压力绝对值再次激增达到最大值，随列车的运行又急剧下降到相对平稳状态，交会过程中阻力/压力沿车尾方向先降低后增大。车尾区域存在激波、膨胀波相互交叉干涉现象，波系较为复杂，沿车尾方向激波反射强度减弱。随交会距离的增加，列车行驶在短、中长隧道（<
1500 m）阻力/压力变化剧烈，长隧道（>1500 m）阻力/压力变化幅值较小。随速度的增加，列车前方壅塞区段长度缩短，阻力/压力绝对值增大，车尾激波串长度增加，强度减弱。Abstract: The train running in the low vacuum tube can greatly reduce the resistance, but it also faces the problem of the shock wave effect. We establish a two-dimensional tube simulation model. The compressible unsteady SST k-ω turbulence model combined with sliding mesh technology was used to study the evolution of shock waves in the tube under different initial intersection distance, velocity and time. The results show that when the two trains are far away from each other, the congestion section in front of the train moves forward, and the congestion length increases linearly with time. When the normal shock waves disturb each other, the absolute value of drag/pressure increases sharply. When the two locomotives meet, the absolute value of resistance/pressure increases sharply again to the maximum value and decreases sharply to a relatively stable state with the operation of the train. During the intersection, the resistance/pressure decreases first and then increases along the tail direction. Shock wave and expansion wave cross each other in the rear area; the wave system is more complex, and the intensity of the shock wave reflection is weakened along the rear direction. With the increase of the intersection distance, the resistance/pressure of the train running in short and medium tunnels (<1500 m) changes dramatically. Long tunnel (>1500 m) resistance/pressure change amplitude is small. As the speed increases, the length of the congestion section in front of the train is shortened, the resistance/pressure absolute value increases, the length of the rear shock train increases, and the intensity decreases.-
Key words:
- Tube train rendezvous /
- Congestion length /
- Aerodynamic drag /
- Shock wave characteristics .
-
-
图 1 几何模型图。（a）三维模型侧视图及尺寸，（b）二维平面图
Figure 1. Geometric model diagram. (a) Side view and dimensions of 3D model, (b) two-dimensional planar plan
图 2 不同网格尺寸。（a） t=0.8 s压力系数曲线，（b）车1平均阻力
Figure 2. Different grid sizes. (a) t= 0.8 s pressure coefficient curve, (b) average resistance of train 1
图 4 不同起始交会距离激波变化规律。（a）交会前，（b）交会中，（c）交会后
Figure 4. Variation law of shock waves with different initial intersection distances. (a) Before the rendezvous, (b) during the rendezvous, (c) after the rendezvous
图 5 t=0.9 s至t=1.7 s激波演变特性
Figure 5. Evolution characteristics of shock wave from t=0.9 s to t=1.7 s
图 6 t=2.40 s至t=2.50 s激波演变特性
Figure 6. Shock wave evolution characteristics from t=2.40 s to t=2.50 s
图 7 交会全过程激波演变特性
Figure 7. Shock wave evolution characteristics in the whole process of rendezvous
图 9 t=1.90 s至t=2.25 s管道激波演变特性
Figure 9. Evolution characteristics of tube shock wave from t=1.90 s to t=2.25 s
图 10 不同起始交会距离气动阻力分布。(a) 500 m，(b)
1000 m，(b)1500 m，(d)2000 mFigure 10. Aerodynamic drag distribution at different initial intersection distances. (a) 500 m, (b)
1000 m, (b)1500 m, (d)2000 m
图 11 不同列车速度气动阻力分布。(a) 1000 km/h，(b) 1100 km/h，(c) 1500 km/h，(d) 1750 km/h
Figure 11. Aerodynamic drag distribution of trains at different speeds. (a) 1000 km/h, (b) 1100 km/h, (c) 1500 km/h, (d) 1750 km/h
-
[1] Shen Z Y. Thoughts on the development of vacuum pipeline high-speed traffic in China[J]. Journal of Southwest Jiaotong University,2005,40(2):133−137 (沈志云. 关于我国发展真空管道高速交通的思考[J]. 西南交通大学学报,2005,40(2):133−137(in chinese) doi: 10.3969/j.issn.0258-2724.2005.02.001 Shen Z Y . Thoughts on the development of vacuum pipeline high-speed traffic in China [J]. Journal of Southwest Jiaotong University , 2005 , 40 (02): 133 − 137 doi: 10.3969/j.issn.0258-2724.2005.02.001 [2] Choi J K,Kim K H. Effects of nose shape and tunnel cross-sectional area on aerodynamic drag of train traveling in tunnels[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Re‐search,2014,41:62−73 doi: 10.1016/j.tust.2013.11.012 [3] Zhou X,Zhang D Y,Zhang Y P. Numerical study on the influence of blockage ratio on train air resistance in vacuum pipeline[J]. Journal of Vacuum Science and Technology,2008,26(6):535−538 (周晓,张殿业,张耀平. 真空管道中阻塞比对列车空气阻力影响的数值研究[J]. 真空科学与技术学报,2008,26(6):535−538(in chinese) Zhou X, Zhang D Y, Zhang Y P. Numerical study on the influence of blockage ratio on train air resistance in vacuum pipeline[J]. Journal of Vacuum Science and Technology,2008,26(6):535-538 [4] Zhou X. Numerical simulation of air resistance of high speed train in vacuum pipeline transportation [D]. Chengdu: Master's Thesis of Southwest Jiaotong University, 2008 周晓. 真空管道运输高速列车空气阻力数值仿真[D]. 成都: 西南交通大学硕士学位论文, 2008 [5] Liu Y S. Air resistance simulation and rescue research of vacuum tube maglev train [D]. Chengdu: Master Dissertation of Southwest Jiaotong University, 2010 刘元森. 真空管道磁悬浮列车空气阻力仿真及其救援研究[D]. 成都: 西南交通大学硕士学位论文, 2010 [6] Chen X Y. Simulation and analysis of aerodynamic problems of vacuum tube maglev train [D]. Chengdu: Master's Thesis of Southwest Jiaotong University, 2010 陈绪勇. 真空管道磁悬浮列车空气动力学问题仿真分析[D]. 成都: 西南交通大学硕士学位论文, 2010 [7] Mi B G,Zhan H,Zhu J. Research on resistance calculation method of high-speed train in vacuum pipeline based on dynamic mesh[J]. Journal of Vacuum Science and Technology,2013,33(9):877−882 (米百刚,詹浩,朱军. 基于动网格的真空管道高速列车阻力计算方法研究[J]. 真空科学与技术学报,2013,33(9):877−882(in chinese) doi: 10.3969/j.issn.1672-7126.2013.09.07 Mi B G, Zhan H, Zhu J. Research on resistance calculation method of high-speed train in vacuum pipeline based on dynamic mesh [J]. Journal of Vacuum Science and Technology , 2013 , 33(09): 877 − 882 doi: 10.3969/j.issn.1672-7126.2013.09.07 [8] Kim T K,Kim K H,Kwon H B. Aerodynamic characteristics of a tube train[J]. Journal of Wind Engineering and Industrial Aerodynamics,2011,99:1187−1196 doi: 10.1016/j.jweia.2011.09.001 [9] Kim D W,Kim T H,Kim H D. A study on characteristics of shock train inside a shock tube[J]. Theoretical and Applied Mechanics Letters,2017,7:366−371 doi: 10.1016/j.taml.2017.09.005 [10] Zhang X H,Li T,Zhang J Y,et al. Aerodynamic congestion and shock wave phenomenon of subsonic vacuum pipeline train[J]. chinese journal of mechanical engineering,2021,57(4):182−190 (张晓涵,李田,张继业,等. 亚音速真空管道列车气动壅塞及激波现象[J]. 机械工程学报,2021,57(4):182−190(in chinese) Zhang X H, Li T, Zhang J Y, etc . Aerodynamic congestion and shock wave phenomenon of subsonic vacuum pipeline train [J]. chinese journal of mechanical engineering , 2021 , 57(04): 182 − 190 [11] Zhou P,Li T,Zhang J Y,et al. Study on shock cluster structure of vacuum pipeline super train[J]. chinese journal of mechanical engineering,2020,56(2):86−97 (周鹏,李田,张继业,等. 真空管道超级列车激波簇结构研究[J]. 机械工程学报,2020,56(2):86−97(in chinese) Zhou P, Li T, Zhang J Y, etc . Study on shock cluster structure of vacuum pipeline super train [J]. chinese journal of mechanical engineering , 2020 , 56(02): 86-97 [12] Zhou P,Zhang J Y,Li T,et al. Numerical study on wave phenomena produced by the super high-speed evacuated tube maglev train[J]. Journal of Wind Engineering and Industrial Aerodynamics,2019,190:61−70 doi: 10.1016/j.jweia.2019.04.003 [13] Niu J Q,Sui Y,Yu Q J,et al. Numerical study on the impact of Mach number on the coupling effect of aerodynamic heating and aerodynamic pressure caused by a tube train[J]. Journal of Wind Engineering and Industrial Aerodynamics,2019,190:100−111 doi: 10.1016/j.jweia.2019.04.001 [14] Niu J Q,Sui Y,Yu Q J,et al. Effect of acceleration and deceleration of a capsule train running at transonic speed on the flow and heat transfer in the tube[J]. Aerospace Science and Technology,2020,105:1−12 doi: 10.1016/j.ast.2020.105977 [15] Sui Y,Niu J Q,Ricco P,et al. Impact of vacuum degree on the aerodynamics of a high-speed train capsule running in a tube[J]. International Journal of Heat and Fluid Flow,2021,88:1−14 doi: 10.1016/J.IJHEATFLUIDFLOW.2020.108752 [16] Huang Z D,Yi Y Y,Chang N. Analysis of shock wave characteristics of pipeline train in supersonic operation[J]. Vacuum,2022,59(5):55−62 (黄尊地,伊严严,常宁. 超声速运行时管道列车激波特性分析[J]. 真空,2022,59(5):55−62(in chinese) Huang Z D, Yi Y Y, Chang N . Analysis of shock wave characteristics of pipeline train in supersonic operation [J]. Vacuum , 2022 , 59(05): 55-62 [17] Zhou P,Zhang J Y. Aerothermal mechanisms induced by the super high-speed evacuated tube maglev train[J]. Vacuum,2020,173:109142 doi: 10.1016/j.vacuum.2019.109142 -
计量
- 文章访问数: 77
- HTML全文浏览数: 77
- PDF下载数: 1
- 施引文献: 0