首页
登录
注册
-
原子层沉积（Atomic Layer Deposition, ALD）是一种先进的薄膜沉积技术，由气相前驱体与基底上的活性位点进行交替的连续自终止反应，来沉积厚度可控的具有高度保形性的薄膜[1-3]。基于以上特性，ALD能在具有微纳结构（例如深孔）的基底内进行薄膜沉积，从而实现基底孔道尺寸和表界面性质的调节。因此，ALD已在微电子[4]、膜分离[5]、催化剂[6]等领域得到广泛的应用。
ALD可以通过对分离膜微结构的精确调控以及在膜通道中加入功能性薄膜来改善分离膜的性能[7,8]。在以分离膜为基底的薄膜沉积过程中，薄膜沉积情况取决于前驱体分子在孔道内的扩散和反应。然而，通过实验表征，仅能得到基底表面以及孔道内的形貌[7-9]，这些结构特征并不能反映薄膜沉积的扩散反应机理以及各个参数对沉积动力学影响。为了实现多孔基底内薄膜沉积分布的调控，可以借助数值模拟方法，预测薄膜沉积过程及其影响因素。基于Tsapatsis等[10]运用 ALD技术制备高性能丙烯/丙烷气体分离膜的研究，作者前期建立了介孔基底ALD薄膜沉积模型[11]，预测了孔道随ALD循环数逐渐收缩直至堵塞的动态过程。本文在此基础上，考察扩散、反应的动力学、基底特性、前驱体浓度等多种参数，对ALD薄膜沉积的影响，通过模拟结果对参数进行敏感性分析，最后拟合出解析公式，可用于预测多孔基底孔道内部和外部的薄膜沉积。
-
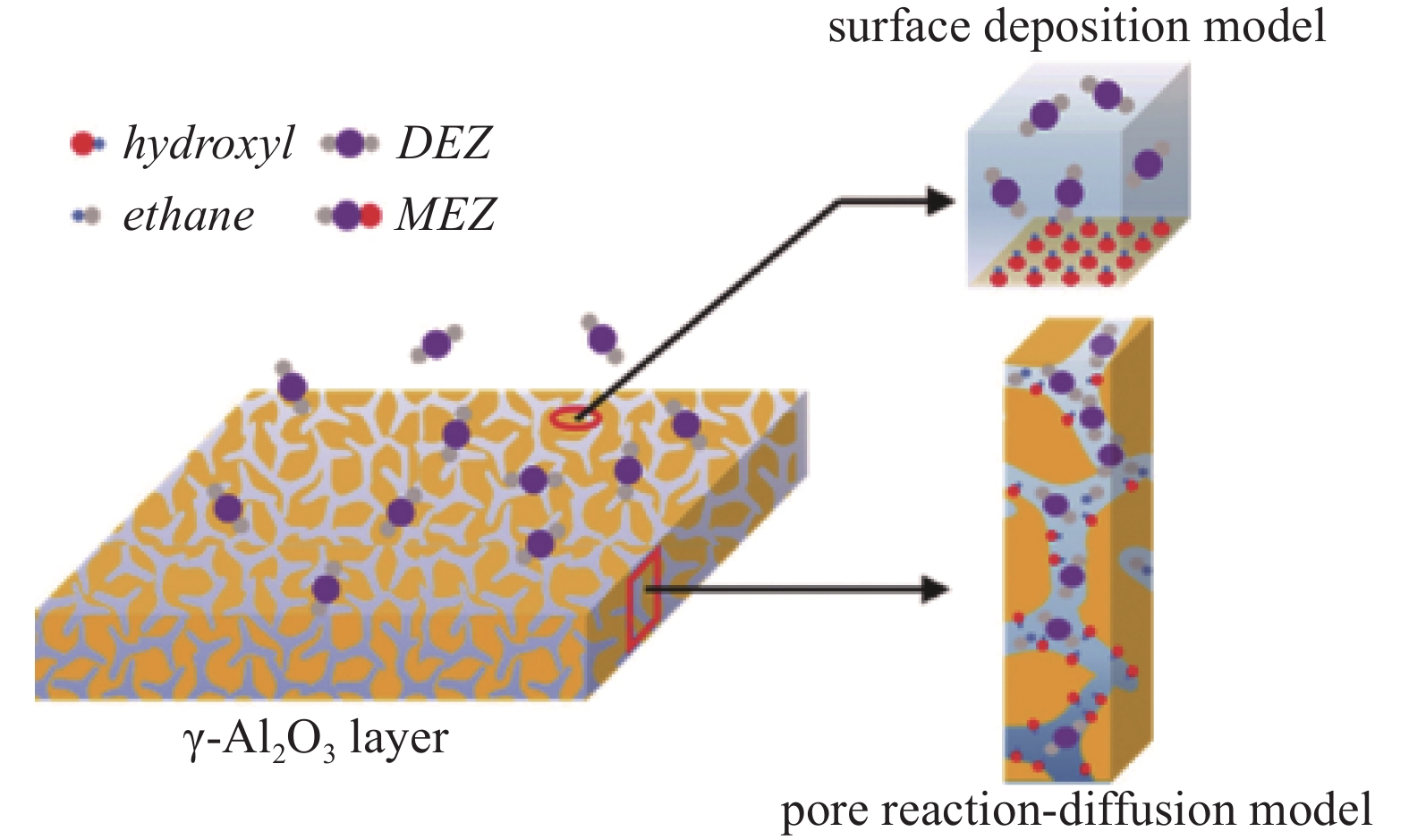
针对γ-Al2O3多孔基底的ALD过程进行建模，不考虑γ-Al2O3在横截面和深度方向的结构差异。基底外表面薄膜沉积，采用基于单个网格的表面沉积模型描述，基底表面每一个局部点都被视为一个网格；孔道内薄膜沉积，采用基于一维孔道反应-扩散模型，具体模型如图1所示。
-
由于介孔基底孔径很小，故ALD过程受空间位阻的影响较大，据研究[12]表明，其沉积过程动力学一般是由体积较大的前驱体的反应扩散决定的。因此，本次模拟只研究二乙基锌（DEZ）半ALD循环过程，假设H2O半循环可以将DEZ半循环中沉积的薄膜全部转化为ZnO薄膜，并将γ-AL2O3表面及孔道内恢复至被羟基覆盖的状态[13]。由于孔道尺寸较小，在目前操作条件下，DEZ在孔道内的扩散主要是表面扩散，且扩散系数可采用阿伦尼乌斯公式表示，主要受基底温度影响[14]。
DEZ半循环过程可以由以下三个方程表示：
其中，ZnO2是基底表面的单乙基锌（MEZ）继续与相邻羟基发生第二次配体交换反应，使得一个Zn原子与两个表面羟基位点结合生成的架桥锌，该反应会进一步降低表面的活性羟基数量。
反应过程中各物质浓度变化由式 (4)~(8) 给出，其中 (4)-(7) 为DEZ半循环的表面沉积方程，(5)-(8)为孔道沉积方程：
通过计算反应中消耗的羟基数量，可以得到DEZ半循环后基底内表面和外表面的覆盖率
$ \theta $ ：式中，ka -DEZ在γ-Al2O3基底表面的吸附速率常数，kd -脱附速率常数，k1 -DEZ*向MEZ转化速率常数，k2 -MEZ向ZnO2转化速率常数，Ci -各物质的浓度，ε -孔隙度，ι -曲折因子，Ds -扩散系数。
-
DEZ在表面沉积模型和孔道反应-扩散模型入口处的边界条件通过反应器尺度模拟来确定[15]。对于多孔基底，ε和ι会影响气体分子的扩散过程，在本模型中将这两个参数与Ds组成有效扩散系数来考虑多孔基底形状对沉积过程的影响。两种模型初始状态设置均匀的羟基浓度，其他各组分设置通量为零的边界条件。数值求解过程中，时间采用一阶隐式，空间采用一阶迎风的离散方案，时间步长范围通过独立性测试，确定为 1×10−6 s~1×10−4 s，具体参数设置请参考作者之前的工作[11]。
-
为了验证模型，按照文献中的反应机理，将本模型计算结果与文献中的可逆吸附表面沉积模型[16]、不可逆吸附表面沉积模型[16]、零反应概率的反应-扩散模型[17]、100%反应概率的反应-扩散模型[18]计算得到的值进行对比，对于可逆和不可逆表面沉积模型的偏差分别为1.21%和0.64%，孔道内的反应-扩散模型也有很好的一致性，具体对比结果可见之前的工作[11]。
-
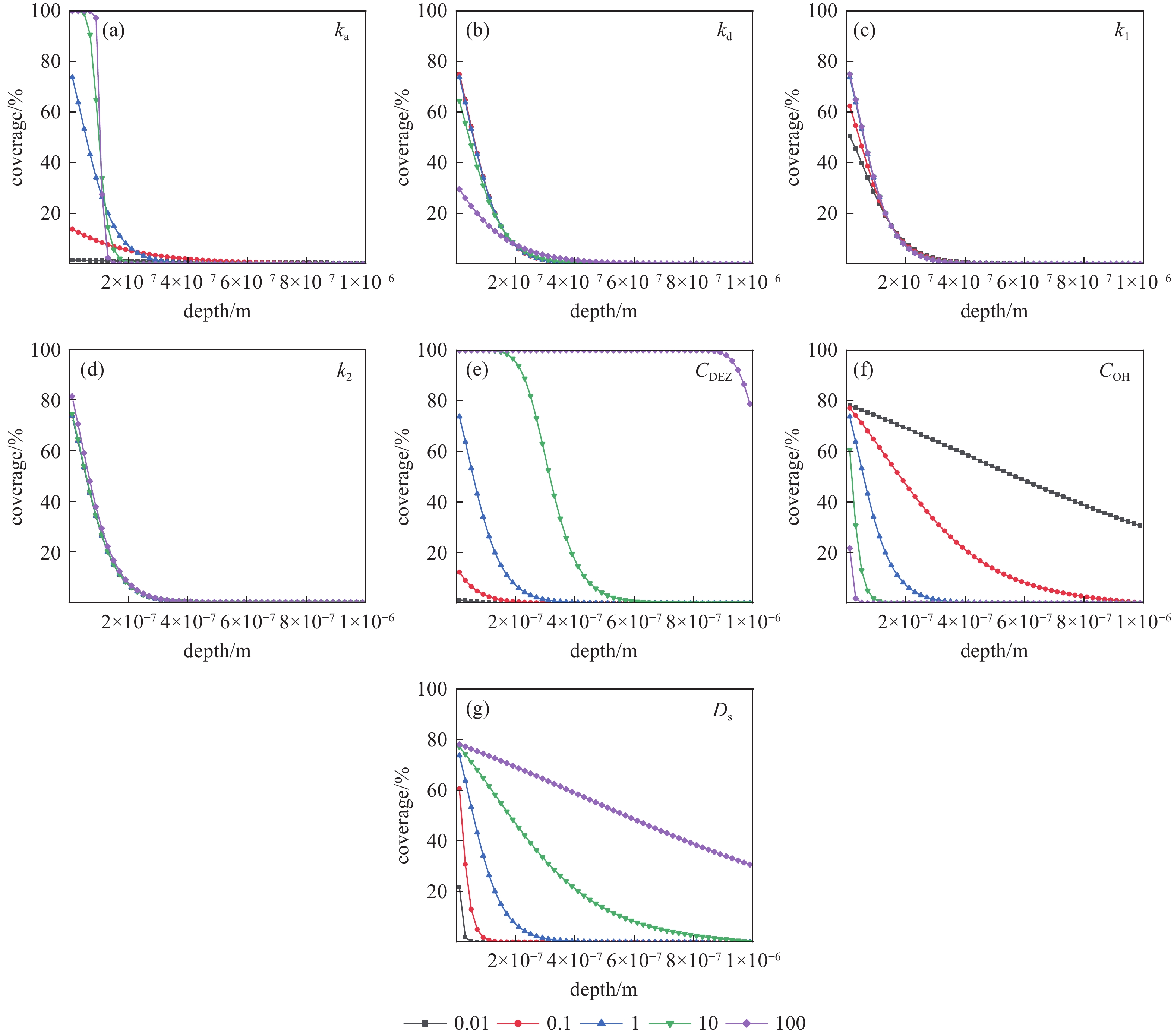
由于实际工艺中前驱体、基底、操作条件存在差别，为了充分研究参数变化对ALD过程的影响，本节对表面沉积过程中各种参数（ka，kd，k1，k2，CDEZ，COH）进行了单变量敏感性模拟测试，其中标准参数值见表1。通过对比结合其他研究者们的工作，作者发现目前ZnO的ALD窗口比较宽，可确定为70~250℃[19-21]。不同温度下ALD过程的反应速率常数及扩散系数可由阿伦尼乌斯公式形式计算，通过计算发现，温度对ka，kd，k1的影响很大。在ALD窗口内，ka的变化范围是0.04 ka,标准~147.67 ka,标准，kd的变化范围是0.04 kd,标准~147.67 kd,标准，k1的变化范围为0.01 k1,标准~596.84 k1,标准，Ds的变化范围为0.14 Ds,标准~19.29 Ds,标准。Holmqvist等[22]研究得到的反应速率常数也均在此范围内。γ-Al2O3基底表面的羟基浓度范围在3.3~12.6 nm−2[23]，在本研究中，根据情况本文取值7.8 nm−2。由于DEZ的浓度与通入前驱体的时间和前驱体的分压有关，不同的反应器也会影响DEZ的浓度，在此本文进行了大范围的研究。
基于以上的调研，再结合实际情况的多样性和复杂性，本文以基准参数为起点，计算了从0.01到100倍不同标准参数值的情况，并分析了参数变化对最终表面覆盖率
$ \theta $ 影响，目的是使得出的结论，能涵盖大量实际工艺中可能碰到的情况结果如图2所示。由计算结果可知：在模拟条件下，当ka的值在0.01ka标准 ~10 ka标准范围内增大时，
$ \theta $ 由$ 1.54\% $ 增加到$ 100\% $ ，此时，基底表面覆盖已经达到饱和，$ \theta $ 达到最大，当ka值继续增加时，$ \theta $ 不会再有变化。随着kd的值增大，$ \theta $ 由$ 79.80\% $ 降至$ 31.40\% $ 。ka与kd的大小会影响DEZ分子进入反应器后进行吸附的快慢以及吸附达到平衡时的位置，通常来说ka值越大， DEZ吸附速率越快，会在短时间内产生大量的DEZ*，缩短了周期时间。随着kd的增加，DEZ*脱附速率加快，在吸附达到平衡时DEZ*的浓度会降低，从而减慢薄膜沉积的速率。与吸附过程类似的，当k1的值在0.01k1标准 ~100 k1标准范围内增大时，
$ \theta $ 由52.70%增加到79.81%。k1的大小决定了DEZ*转变为MEZ速率的快慢，较小的k1会导致配体交换反应速率比较慢，不利于薄膜的沉积，同时导致基底上累积大量的DEZ*，这会使可逆吸附达到平衡时的位置发生变化，更有利于向脱附方向进行，造成较低的$ \theta $ 。对MEZ与羟基反应的速率常数k2模拟计算时发现，当k2的值在0.01k2标准 ~100 k2标准范围内变化时，$ \theta $ 并没有明显变化。这是因为表面的羟基在式（2）反应中被大量占据，在这种条件下，这步反应的反应速率很低[25]，k2的变化不能明显的改变反应的速率，此反应产生ZnO2消耗的表面羟基几乎可以忽略，不会对$ \theta $ 产生较大影响。由模拟计算结果可以发现，随着CDEZ的增加，
$ \theta $ 有大幅度增加，从1.54%变化到100%，与之相反，随着COH的增加，$ \theta $ 没有变化。这表明在高浓度DEZ前提下，COH越高，对薄膜沉积过程越有利，即表面覆盖率与羟基密度有紧密的联系。这一结果与Puurunen[26]关于TMA/H2O-ALD过程的定量研究结果相符，在不同温度下该过程中的单循环生长(GPC)均与表面羟基浓度之间存在线性关系。 -
本节对孔道内沉积过程中各种参数（ka，kd，k1，k2，CDEZ，COH，Ds）进行了单变量敏感性分析，结果如图3所示。由于孔口位置处接近于表面沉积，孔口位置的
$ \theta $ 随着ka增大而增加，这与上节表面沉积过程的模拟结果相符合。此外，不同ka值对应的沉积曲线斜率也不同，ka越大所对应的曲线的斜率越大，100 ka标准时的沉积曲线形状已经非常接近Gordon模型[18]中的阶梯状曲线，孔道内沉积严重受到扩散限制。从0.01 kd标准到10 kd标准，kd的变化对孔道内沉积的影响不明显，孔口位置的$ \theta $ 仅下降了10.62%，在100kd标准时孔口$ \theta $ 有明显降低，从64.48%降低为29.51%，沉积曲线的坡度也有所减小。较小的kd情况下，表面羟基活性位点浓度高，脱附的DEZ*可以在短时间内再次进行吸附，故沉积曲线的斜率不会发生明显变化。孔道内沉积受k1，k2影响较小，由于孔道内沉积受分子扩散限制，DEZ*向MEZ转化的速率较慢，脱附过程相对来说速率就更低，对孔道内沉积影响不显著，故孔道内沉积对k1，k2敏感性低。
在孔道内，DEZ的浓度只改变了薄膜的穿透深度[1]并没有改变沉积曲线的形状，在200 nm深度处，标准DEZ浓度的
$ \theta $ 为95.6%。Arts等[27]发现在孔道内沉积的薄膜，其剖面边缘轮廓的斜率由具有最低穿透深度的反应物的反应性（反应速率与扩散速率之比）决定，并由此提出了一种基于高长径比结构中沉积薄膜的厚度分布提取过程反应性的方法。在上节中可以发现，改变$ {C}_{\mathrm{D}\mathrm{E}\mathrm{Z}} $ 不会影响沉积过程的反应性，因此不同浓度DEZ的沉积曲线具有类似的形状。孔口位置的
$ \theta $ 不会受$ {C}_{\mathrm{O}\mathrm{H}} $ 和$ {D}_{\mathrm{S}} $ 的影响而发生变化，但是增大$ {C}_{\mathrm{O}\mathrm{H}} $ 可以增加反应活性位点，而减小$ {D}_{\mathrm{S}} $ 能降低前驱体在孔道里的扩散性，这两种情况都可以增加孔道内的反应性，使孔道内的沉积发生在较浅的位置，沉积曲线也更加陡峭。 -
为了评估在单ALD循环后，孔内的沉积物分布受过程参数的影响，本节基于Kim[12]、和Yanguas-Gil[28]等的报道进行了推导，具体过程如下：
当ALD过程开始时，由于基底表面高浓度的羟基活性位点，DEZ*将大量生成，表面羟基完全反应之前
${\rm{d}}{C}_{{\mathrm{D}\mathrm{E}\mathrm{Z}}^{\mathrm{*}}}/{\rm{d}}t\approx 0$ 。由Kim等[12]提出的ALD沉积ZnO过程中的吸附的动力学模型可得到MEZ浓度可用(3-1)式表示：由此可以计算得到ALD半循环的
$ \theta $ 的关系表达式：一般来说，
$ \dfrac{{k}_{1}+{k}_{\mathrm{d}}}{{k}_{\mathrm{a}}}\gg {C}_{\mathrm{D}\mathrm{E}\mathrm{Z}} $ ，这种情况下$ {C}_{\mathrm{D}\mathrm{E}\mathrm{Z}} $ 对$ \theta $ 的影响可以忽略。故式(3-3)可简化为：将沉积过程中和基底发生碰撞的前驱体分子与基底实现反应的概率定义为
$ {\beta }_{0} $ ，式中，
$ {v}_{\mathrm{t}\mathrm{h}} $ -分子平均热力学速度，$ \stackrel{-}{n} $ -平均分子浓度，$ {s}_{0} $ -单个反应位点所占表面积，$ d $ -平均孔径。孔道内的沉积曲线是典型的S形分布，故使用三参数的Sigmoidal函数来拟合不同参数下的沉积曲线：
式中，z -孔道深度，ω和σ为该曲线的两个形状参数。当z=0时，对应于表面沉积模型，结合式(12)和式(14)可得到ω的表达式：
将(15)式对z求导：
根据上节中的模拟结果进行拟合，得到：
Yanguas-Gil等[28]将纳米孔道特定位置覆盖达到饱和所需的时间分为前驱体从孔道入口扩散至该位置所需的传质时间和在表面发生饱和沉积所用时间，即：
式中，z -深度，
$ \gamma =\dfrac{{n}_{0}{s}_{0}}{\overline{s}} $ 表示每个特征结构内每单位面积前驱体分子的数量，通常对于多孔基底这个值远小于1。此时将θ=0.5代入式(19)得到:式中，
$ {N}_{\mathrm{A}} $ -阿伏伽德罗常数；$ {C}_{\mathrm{D}\mathrm{E}\mathrm{Z},\mathrm{c}} $ 为θ=0.5 时，DEZ只在多孔基底表面饱和沉积的浓度，并不在深孔内发生扩散，定义$ {C}_{\mathrm{D}\mathrm{E}\mathrm{Z},\mathrm{c}} $ 为θ=0.5 时的临界浓度，当$ {C}_{\mathrm{D}\mathrm{E}\mathrm{Z}} > {C}_{\mathrm{D}\mathrm{E}\mathrm{Z},\mathrm{c}} $ 时，沉积曲线会向孔道深处生长，生长的距离$ {z}_{0} $ 是：于是不同参数下的多孔基底沉积分布可以由下式预测：
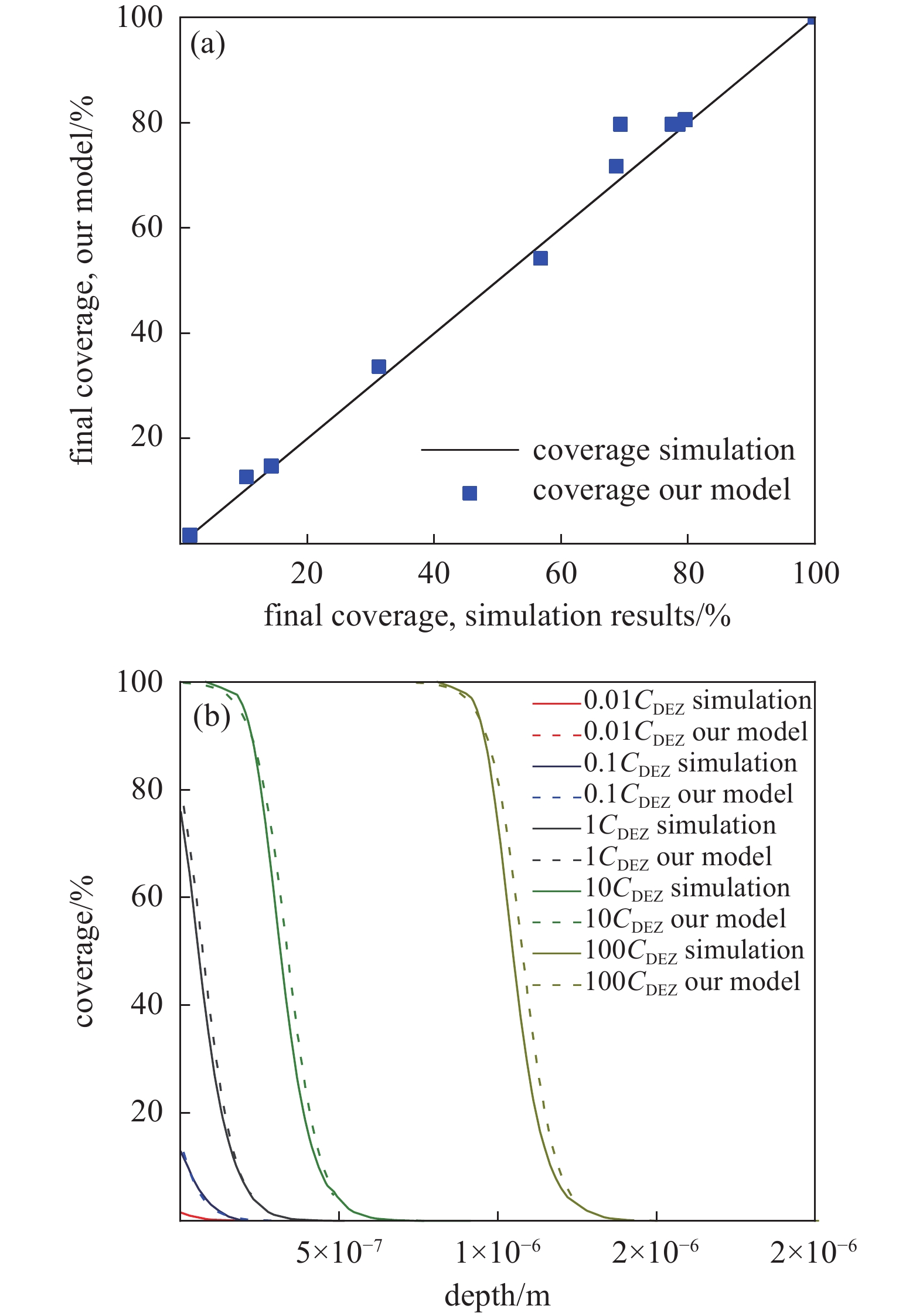
推导得到的解析模型包括式(12)和式(21)，将解析式计算与模拟结果进行对比，结果如图4所示，其中图4（a）是标准参数值对应的表面模型的覆盖率，图4（b）是不同
$ {C}_{\mathrm{D}\mathrm{E}\mathrm{Z}} $ 情况下孔道模型的覆盖率，计算值与模拟结果吻合较好。因此，在已知实验相关参数的情况下，可以通过上述解析式计算ALD过程的沉积覆盖率及其分布。 -
在孔径为5.08 nm，厚度为5 μm的γ-Al2O3多孔基底[11]表面和孔道内进行ALD沉积。经过对基底表面以及孔道内的ALD过程进行模拟，分析了过程参数变化对薄膜沉积的影响。结论如下：
表面沉积过程中，当COH为10200
$ \mathrm{m}\mathrm{o}\mathrm{l}{\mathrm{·}\mathrm{m}}^{-3} $ 不变的情况下，ka在11~1.1×104$ {\mathrm{m}}^{3} \cdot {(\mathrm{m}\mathrm{o}\mathrm{l} \cdot \mathrm{s})}^{-1} $ 范围内变化时，θ从1.54%增加至100%，此时表面覆盖达到饱和；当k1在0.2~20$ {\mathrm{s}}^{-1} $ 范围变化时，θ从52.70%变化为78.56%，继续增加k1时，θ变化不大； kd在0.006~60$ {\mathrm{s}}^{-1} $ 内增加时，θ从79.8%降低到31.40%；而在CDEZ一定的情况下，COH（1.02×102~1.02×106$ \text{mol}{\mathrm{·}\mathrm{m}}^{-3} $ ）的变化几乎没有影响基底表面的覆盖率。其中 ka，k1，CDEZ的增大对薄膜的生长起正作用，相反，kd的增加会抑制薄膜生长。孔道内的ALD过程，在CDEZ一定的情况下，基底表面的覆盖率对COH和DS$ （3.96\times {10}^{-9} \sim 3.96\times {10}^{-5}{\mathrm{m}}^{2} \cdot {\mathrm{s}}^{-1}） $ 的变化较为敏感，k1和kd的变化则对孔道内沉积过程影响很小。为了制备高性能气体分离膜，沉积物在外表面的厚度可以忽略，需要在ALD过程中降低沉积物孔道内的深度，即降低台阶覆盖率。根据参数敏感性分析可知，可以通过提高ka和降低CDEZ实现。前者可以采用提高操作温度或等离子体强化，后者可以通过提高载气流量或改装供气系统前驱体源瓶。
在敏感性分析的基础上，结合前人的研究，对ALD过程进行了半经验模型的推导，该解析式与模拟结果吻合较好，在已知相关参数的情况下，能准确计算出过程参数对ALD半循环覆盖率的影响，从而可以指导实验设计和优化。
符号解释 Ci —第i种物质的摩尔浓度，mol·m−3 t —时间，s CDEZ,c —临界DEZ浓度，mol·m−3 vth —分子热力学速度，m·s−1 d —平均孔径，m z —深度，m Ds —表面扩散系数，m2·s−1 z0 —平移距离，m ka —吸附速率常数，m3·mol−1·s−1 $ {\beta }_{0} $ —基本反应概率kd —脱附速率常数，s−1 $ \varepsilon $ —孔隙度k1 —DEZ*向MEZ反应速率常数，m3·mol−1·s−1 $ \tau $ —曲折因子k2 —MEZ向ZnO2 反应速率常数，s−1 $ \theta $ —表面覆盖率n0 —分子浓度，m−3 $ \gamma $ —前驱体分子过剩数NA —阿伏伽德罗常数，6.02×1023 $ \omega $ —无量纲参数s0 —单个反应位点所占表面积，m2 $ \sigma $ —模型参数，m−1$ \overline s $ —比表面积，m2·m−3
多孔基底原子层沉积薄膜分布的数值模拟
Numerical Simulation of the Film Distribution During Atomic Layer Deposition within Porous Substrates
-
摘要: 原子层沉积（ALD）技术能在多孔基底内沉积亚纳米精度的薄膜，从而调节孔道尺寸和界面性质。此类ALD薄膜沉积，同时受到前驱体扩散和反应的影响，这给沉积动力学研究带来了困难。本文对ALD制备ZnO 薄膜过程中前驱体在γ-Al2O3基底外表面沉积和孔道内沉积过程建立了模型，并通过数值模拟对表面和孔道两种模型进行了参数敏感性分析，拟合得到沉积物覆盖率公式。结果表明：在表面沉积过程中，随着吸附速率常数ka、吸附态的二乙基锌（DEZ*）向单乙基锌（MEZ）转化速率常数k1、羟基浓度COH的增大，和脱附速率常数kd的减小，基底表面的薄膜沉积加快；对于孔道内沉积过程，较大的羟基浓度COH和较小的扩散系数DS，驱使薄膜沉积在较浅位置；拟合所得解析式能准确预测多孔基底外表面和孔道内的沉积物覆盖率及其分布。Abstract: Atomic layer deposition (ALD) technology can deposit thin films on porous substrates with sub-nanometer precision, thereby adjusting the pore size and interface properties. Such ALD processes are affected by the diffusion and reaction of precursors, which causes difficulties in studying the reaction kinetics. In this paper, models were established for the depositions on the outer surface and inside the pores of the γ-Al2O3 substrate where ZnO films were formed via ALD. A sensitivity analysis was carried out for the two models through numerical simulation, which led to the formulas of surface coverage of the deposits. The results show that during the deposition on the outer surface of the substrate, with the increase of adsorption rate constant ka, the conversion rate constant k1 of adsorbed diethyl zinc to monoethyl zinc, the hydroxyl concentration COH, and the decrease of the desorption rate constant kd, the film deposition accelerates. For the deposition inside the pores, higher COH and lower diffusion coefficient DS result in deposit formation in a shallow position. The analytical formulas can accurately predict the deposit coverage and its distribution on the outer surface and inside the pores of porous substrates.
-
Key words:
- Atomic layer deposition /
- Numerical simulation /
- Coverage /
- Porous substrate /
- Reaction and diffusion .
-
-
图 2 不同参数对表面沉积模型表面覆盖率的影响
Figure 2. Effect of different parameters on the coverage of surface deposition model
图 3 孔内沉积模型对不同参数的敏感性(a) ka; (b) kd; (c) k1; (d) k2; (e) CDEZ; (f) COH; (g) Ds
Figure 3. Effect of different parameters on coverage of deposition model in pores (a) ka; (b) kd; (c) k1; (d) k2; (e) CDEZ; (f) COH; (g) Ds
图 4 解析模型与模拟结果对比。(a) 表面覆盖率， (b) 孔内覆盖率
Figure 4. Comparison between proposed analytical model and simulation results. (a) Surface coverage, (b) pore coverage
表 1 标准模型参数
Table 1. Detailed values of standard model parameters
参数 数值 参考文献 COH,0 $7.8 \; {\mathrm{n}\mathrm{m} }^{-2}, 10200 \; {\mathrm{m}\mathrm{o}\mathrm{l} \cdot \mathrm{m} }^{-3}$ [23] Ds $ 3.96 $ $\times {10}^{-7} \; {\mathrm{m} }^{2} \cdot {\mathrm{s} }^{-1}$ [24] ka $1100 \; {\mathrm{m} }^{3} \cdot {(\mathrm{m}\mathrm{o}\mathrm{l} \cdot \mathrm{s})}^{-1}$ [15] ε/ι 0.1 kd $0.6 \; {\mathrm{s} }^{-1}$ [15] k1 $20 \; {\mathrm{s} }^{-1}$ [15] k2 $0.0015 \; {\mathrm{m} }^{3} \cdot {(\mathrm{m}\mathrm{o}\mathrm{l} \cdot \mathrm{s})}^{-1}$ [15] 
下载: 导出CSV
符号解释 Ci —第i种物质的摩尔浓度，mol·m−3 t —时间，s CDEZ,c —临界DEZ浓度，mol·m−3 vth —分子热力学速度，m·s−1 d —平均孔径，m z —深度，m Ds —表面扩散系数，m2·s−1 z0 —平移距离，m ka —吸附速率常数，m3·mol−1·s−1 $ {\beta }_{0} $ —基本反应概率kd —脱附速率常数，s−1 $ \varepsilon $ —孔隙度k1 —DEZ*向MEZ反应速率常数，m3·mol−1·s−1 $ \tau $ —曲折因子k2 —MEZ向ZnO2 反应速率常数，s−1 $ \theta $ —表面覆盖率n0 —分子浓度，m−3 $ \gamma $ —前驱体分子过剩数NA —阿伏伽德罗常数，6.02×1023 $ \omega $ —无量纲参数s0 —单个反应位点所占表面积，m2 $ \sigma $ —模型参数，m−1$ \overline s $ —比表面积，m2·m−3
下载: 导出CSV
-
[1] Cremers V,Puurunen R L,Dendooven J. Conformality in atomic layer deposition: current status overview of analysis and modelling[J]. Applied Physics Reviews,2019,6(2):21302 doi: 10.1063/1.5060967 [2] Johnson R W,Hultqvist A,Bent S F. A brief review of atomic layer deposition: from fundamentals to applications[J]. Materials Today,2014,17(5):236−246 doi: 10.1016/j.mattod.2014.04.026 [3] Leskelä M,Ritala M. Atomic layer deposition chemistry: recent developments and future challenges[J]. Angewandte Chemie International Edition,2003,42(45):5548−5554 doi: 10.1002/anie.200301652 [4] Hwang C S. Atomic layer deposition for semiconductors. atomic layer deposition for semiconductors[M]. New York:Springer, 2014: 263 [5] Xiong S,Qian X,Zhong Z,et al. Atomic layer deposition for membrane modification, functionalization and preparation: a review[J]. Journal of Membrane Science,2022,658:120740 doi: 10.1016/j.memsci.2022.120740 [6] Wu F,Zhou L,Guo D,et al. Efficient modulation of electrocatalyst interfaces by atomic layer deposition: fundamentals to application[J]. Advanced Energy and Sustainability Research,2022,3(7):2200026 doi: 10.1002/aesr.202200026 [7] Kaindl R, Homola T, Rastelli A, et al. Atomic layer deposition of oxide coatings on porous metal and polymer structures fabricated by additive manufacturing methods (laser-based powder bed fusion, material extrusion, material jetting)[J]. Surfaces and Interfaces, 2022 [8] Li F,Li L,Liao X,et al. Precise pore size tuning and surface modifications of polymeric membranes using the atomic layer deposition technique[J]. Journal of Membrane Science,2011,385-386:1−9 doi: 10.1016/j.memsci.2011.06.042 [9] Nikkola J,Sievänen J,Raulio M,et al. Surface modification of thin film composite polyamide membrane using atomic layer deposition method[J]. Journal of Membrane Science,2014,450:174−180 doi: 10.1016/j.memsci.2013.09.005 [10] Ma X,Kumar P,Mittal N,et al. Zeolitic imidazolate framework membranes made by ligand-induced permselectivation[J]. Science,2018,361(6406):1008−1011 doi: 10.1126/science.aat4123 [11] Gu H, Lee D T, Corkery P, et al. Modeling of deposit formation in mesoporous substrates via atomic layer deposition: Insights from pore‐scale simulation[J]. AIChE Journal, 2022 [12] Kim S,Lee S,Ham S,et al. A kinetic study of ZnO atomic layer deposition: Effects of surface hydroxyl concentration and steric hindrance[J]. Applied Surface Science,2019,469:804−810 doi: 10.1016/j.apsusc.2018.11.064 [13] Yousfi E B,Fouache J,Lincot D. Study of atomic layer epitaxy of zinc oxide by in-situ quartz crystal microgravimetry[J]. Applied surface science,2000,153(4):223−234 doi: 10.1016/S0169-4332(99)00330-X [14] E. Baumgarten F W H H. Adsorption isotherms of hydrocarbons on γ-alumina[J]. Journal of Chromatography A,1977,138(2):347−354 doi: 10.1016/S0021-9673(00)94970-7 [15] Zhuang L,Corkery P,Lee D T,et al. Numerical simulation of atomic layer deposition for thin deposit formation in a mesoporous substrate[J]. AIChE Journal,2021,67(8) [16] Puurunen R L. Surface chemistry of atomic layer deposition: A case study for the trimethylaluminum/water process[J]. Journal of Applied Physics,2005,97(12):121301 doi: 10.1063/1.1940727 [17] Bird R, Stewart W, Lightfoot E. Transport phenomena (2nd Edition)[M]. New York: Wiley, 2002: 905 [18] Gordon R G,Hausmann D,Kim E,et al. A kinetic model for step coverage by atomic layer deposition in narrow holes or trenches[J]. Chemical vapor deposition,2003,9(2):73−78 doi: 10.1002/cvde.200390005 [19] Jeon S,Bang S,Lee S,et al. Structural and electrical properties of ZnO thin films deposited by atomic layer deposition at low temperatures[J]. Journal of the Electrochemical Society,2008,155(10):H738 doi: 10.1149/1.2957915 [20] Tapily K,Gu D,Baumgart H,et al. Mechanical and structural characterization of atomic layer deposition-based ZnO films[J]. Semiconductor science and technology,2011,26(11):115005 doi: 10.1088/0268-1242/26/11/115005 [21] Mousa M B M,Oldham C J,Jur J S,et al. Effect of temperature and gas velocity on growth per cycle during Al2O3 and ZnO atomic layer deposition at atmospheric pressure[J]. Journal of vacuum science & technology. A, Vacuum, surfaces, and films,2012,30(1) [22] Holmqvist A,Törndahl T,Magnusson F,et al. Dynamic parameter estimation of atomic layer deposition kinetics applied to in situ quartz crystal microbalance diagnostics[J]. Chemical engineering science,2014,111:15−33 doi: 10.1016/j.ces.2014.02.005 [23] Knözinger H,Ratnasamy P. Catalytic aluminas: surface models and characterization of surface sites[J]. Catalysis reviews. Science and engineering,1978,17(1):31−70 doi: 10.1080/03602457808080878 [24] Sladek K J,Gilliland E R,Baddour R F. Diffusion on surfaces. II. correlation of diffusivities of physically and chemically adsorbed species[J]. Industrial & engineering chemistry fundamentals,1974,13(2):100−105 [25] Weckman T,Laasonen K. Atomic layer deposition of zinc oxide: study on the water pulse reactions from first-principles[J]. The Journal of Physical Chemistry C,2018,122(14):7685−7694 doi: 10.1021/acs.jpcc.7b11469 [26] Puurunen R L. Correlation between the growth-per-cycle and the surface hydroxyl group concentration in the atomic layer deposition of aluminum oxide from trimethylaluminum and water[J]. Applied Surface Science,2005,245(1-4):6−10 doi: 10.1016/j.apsusc.2004.10.003 [27] Arts K,Vandalon V,Puurunen R L,et al. Sticking probabilities of H2O and Al(CH3)3 during atomic layer deposition of Al2O3 extracted from their impact on film conformality[J]. Journal of Vacuum Science & Technology A,2019,37(3):30908 [28] Yanguas-Gil A,Elam J W. Self-Limited reaction-diffusion in nanostructured substrates: surface coverage dynamics and analytic approximations to ALD saturation times[J]. Chemical Vapor Deposition,2012,18(1-3):46−52 doi: 10.1002/cvde.201106938 -
图( 4) 表( 2)
计量
- 文章访问数: 89
- HTML全文浏览数: 89
- PDF下载数: 1
- 施引文献: 0