-
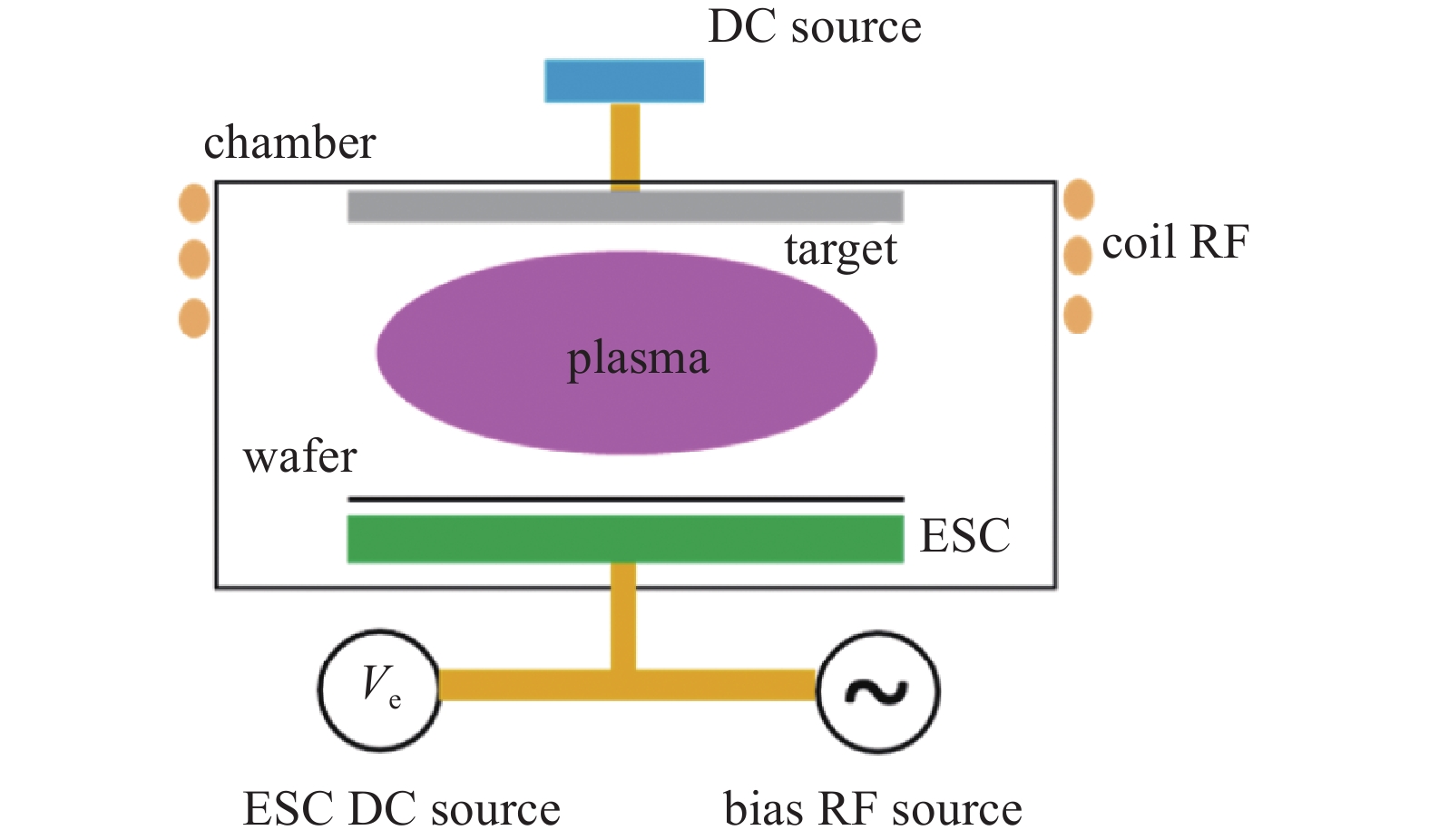
在半导体与光学领域中,部分工艺需要使用Electrostatic chuck静电卡盘等结构(ESC)来固定衬底进行工艺,通常静电卡盘通常处于下腔室位置,如图1所示。同时静电卡盘也可以实现快速加热以及加载射频功率调节等离子体状态的作用。同时静电卡盘在工艺过程中还具有高稳定性、低颗粒性、控温良好等性能,因此,静电卡盘在半导体、光学领域中受到越来越广泛的应用[1-7]。
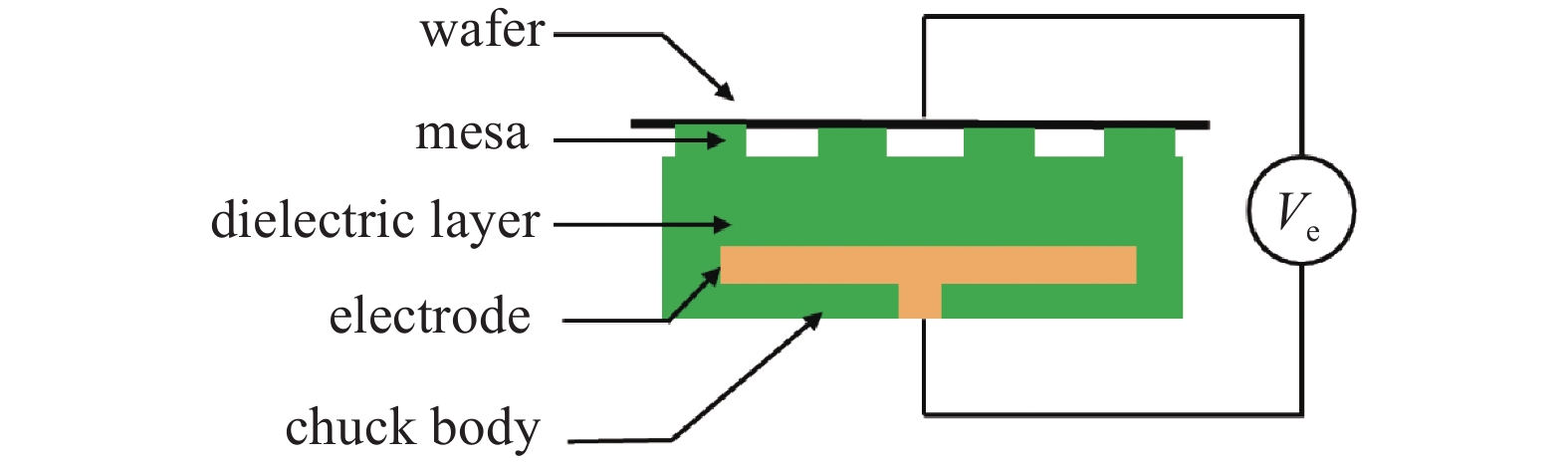
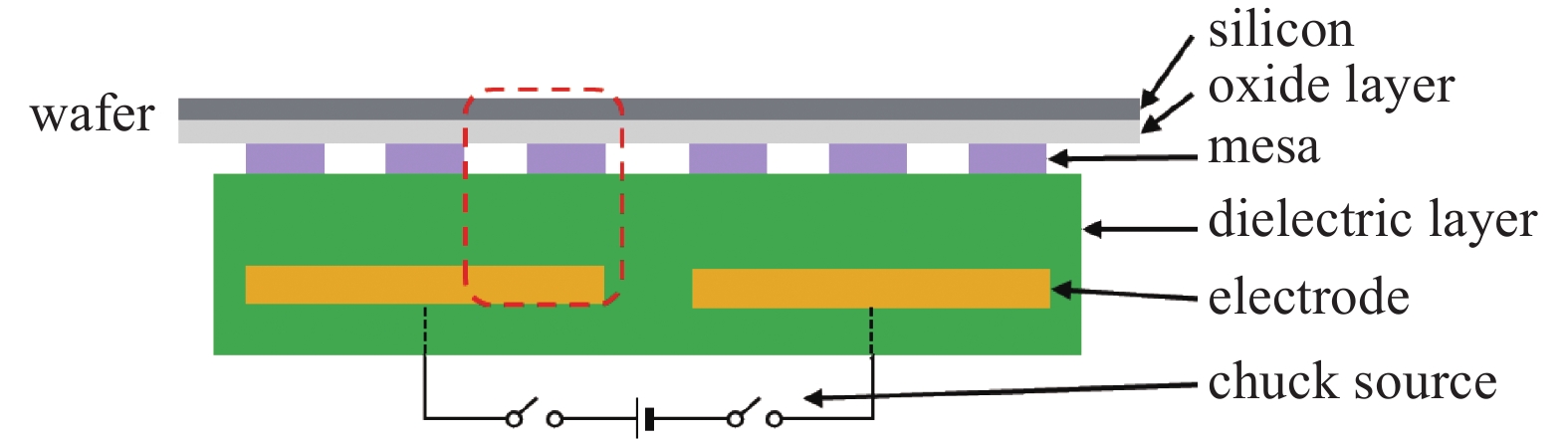
半导体设备领域中静电卡盘的基本结构如图2所示,其结构主要包括介电层、电极、静电卡盘主体结构。在静电卡盘工作中,晶圆、介电层、电极之间形成一个电容结构。当电容两极间接通吸附直流电压时,电极和晶圆之间存在一定的直流电压差,静电卡盘通过电极和晶圆之间的库仑力实现吸附晶圆的作用。
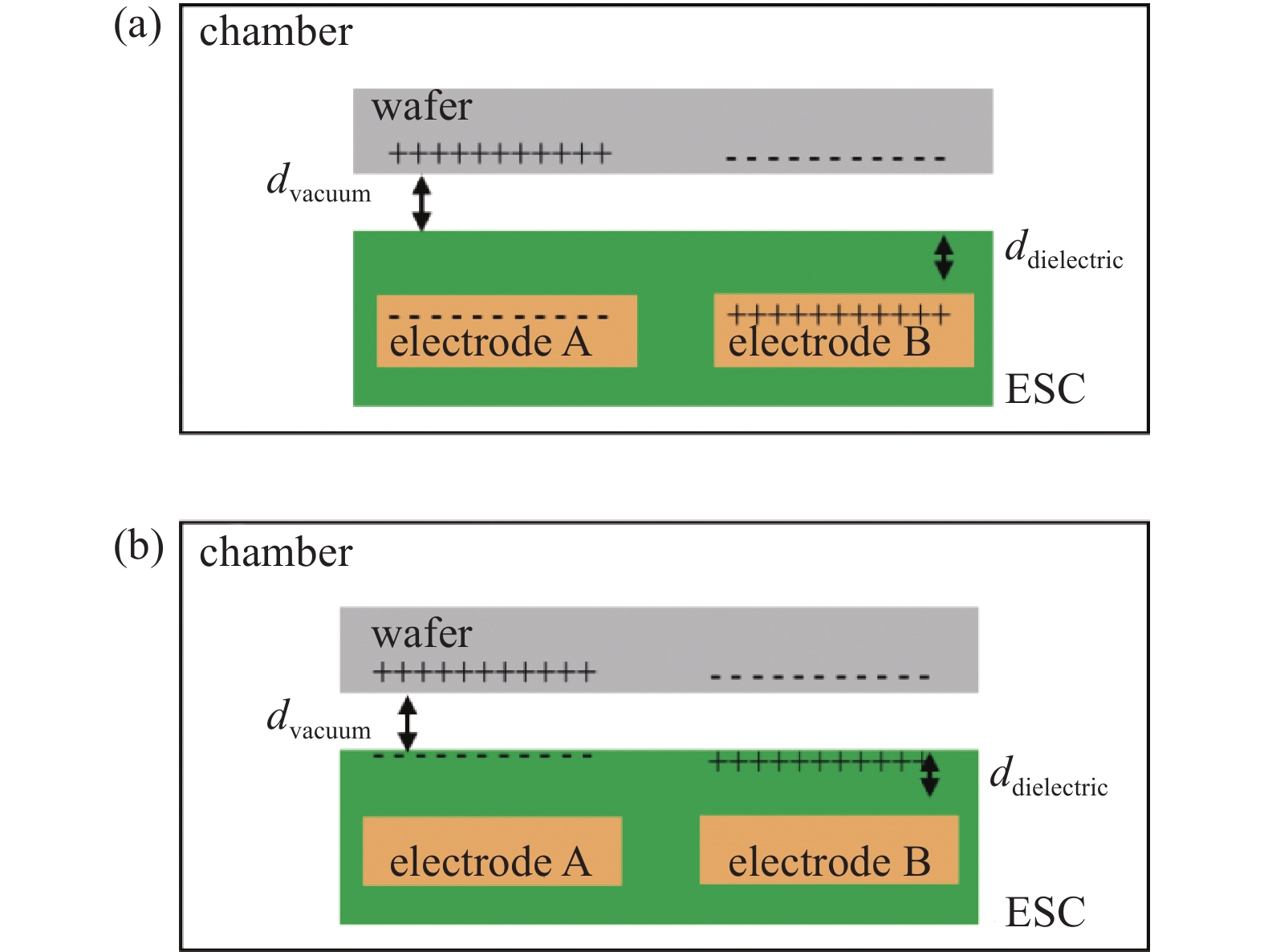
依据静电卡盘的吸附原理来对静电卡盘进行分类,静电卡盘可以分为库伦型静电卡盘以及Johnsen-Rahbek type 约翰逊-拉别克型(J-R型)静电卡盘[8-11]。库伦型静电卡盘的工作原理如图3 (a)所示,库伦型静电卡盘的介电层绝缘电阻的体电阻率较高,通常应大于
$ {\text{10}}^{\text{16}} $ Ω·cm,属于绝缘材料。在加载吸附电压时,静电荷聚集在吸附电极上,很难迁移到静电卡盘吸附面上。基于此,静电卡盘的吸附力主要来自于电极与晶圆之间的库仑力。J-R型静电卡盘工作原理如图3(b)所示,J-R型静电卡盘的主要特点是其介电层的体电阻率通常在
$ {\text{10}}^{\text{9}} $ Ω·cm~$ {\text{10}}^{\text{11}} $ Ω·cm范围内,属于半导体材料。通常静电卡盘介电层设计的响应时间τ<1 s,因此电极上的电荷可以在极短的时间内迁移到静电卡盘表面。静电卡盘表面电荷与晶圆之间存在库仑力,从而实现静电卡盘吸附晶圆的功能。库伦型静电卡盘制作难度低,选用的材料更简单(纯度高的氧化铝陶瓷即可实现),其应用较为广泛。相对于库伦型静电卡盘来说,J-R型静电卡盘实现吸附功能的静电荷距离晶圆的距离更近,因此在加载相同吸附电压的情况下,J-R型静电卡盘可以实现更高的吸附力。
综上所述J-R型静电卡盘结构在吸附晶圆的过程中使用的吸附电压更低,对晶圆造成静电损伤的影响更小。所以在更先进的半导体工艺中,双极J-R型静电卡盘受到越来越广泛的应用。
在某些半导体工艺中,晶圆会经过高温环境,在其表面形成一层致密的氧化层结构通常为氧化硅材料。而氧化层厚度与对应工艺的温度、时间、氧气含量有关,无法准确预估氧化层的厚度。晶圆背面氧化层的厚度直接影响静电卡盘对晶圆的吸附力,如果吸附力不足,会导致工艺过程中晶圆从静电卡盘上脱落,从而影响工艺结果甚至会损伤静电卡盘。因此在静电卡盘的设计上,不仅要考虑静电卡盘对纯硅材料晶圆吸附力的大小,还需要考虑静电卡盘对具有氧化层晶圆吸附力的大小。因此静电卡盘对具有氧化层晶圆吸附力的研究关乎半导体工艺的稳定性。但目前国内很少有对J-R型静电卡盘对具有氧化层晶圆吸附力的研究,这会对中国半导体工艺向先进制程上的发展造成一定的阻碍。因此开展J-R型静电卡盘对具有氧化层晶圆的研究至关重要。
本文接下来将搭建静电卡盘吸附力测试平台,测试静电卡盘对具有不同氧化层厚度晶圆吸附力的变化。并利用等效电容方法,建立计算静电卡盘对具有氧化层晶圆吸附力的仿真模型。
-
本文将利用气体背吹法测试静电卡盘对晶圆的吸附力。气体背吹法[12]的工作原理是:在静电卡盘内部的背吹气路中安装一个可以人为控制气体流量的流量计,同时在气路靠近静电卡盘的位置处,安装一个测试气压的真空规。在静电卡盘吸附晶圆时,缓慢增加静电卡盘的背吹气压,直到晶圆脱离静电卡盘,记录晶圆刚脱离静电卡盘时,背吹气压值。通过气压转换成背吹力,再减去晶圆的重力,即可得到静电卡盘的吸附力。该方法测试平台搭建简单,并且晶圆受力均匀,测试结果误差较小。
-
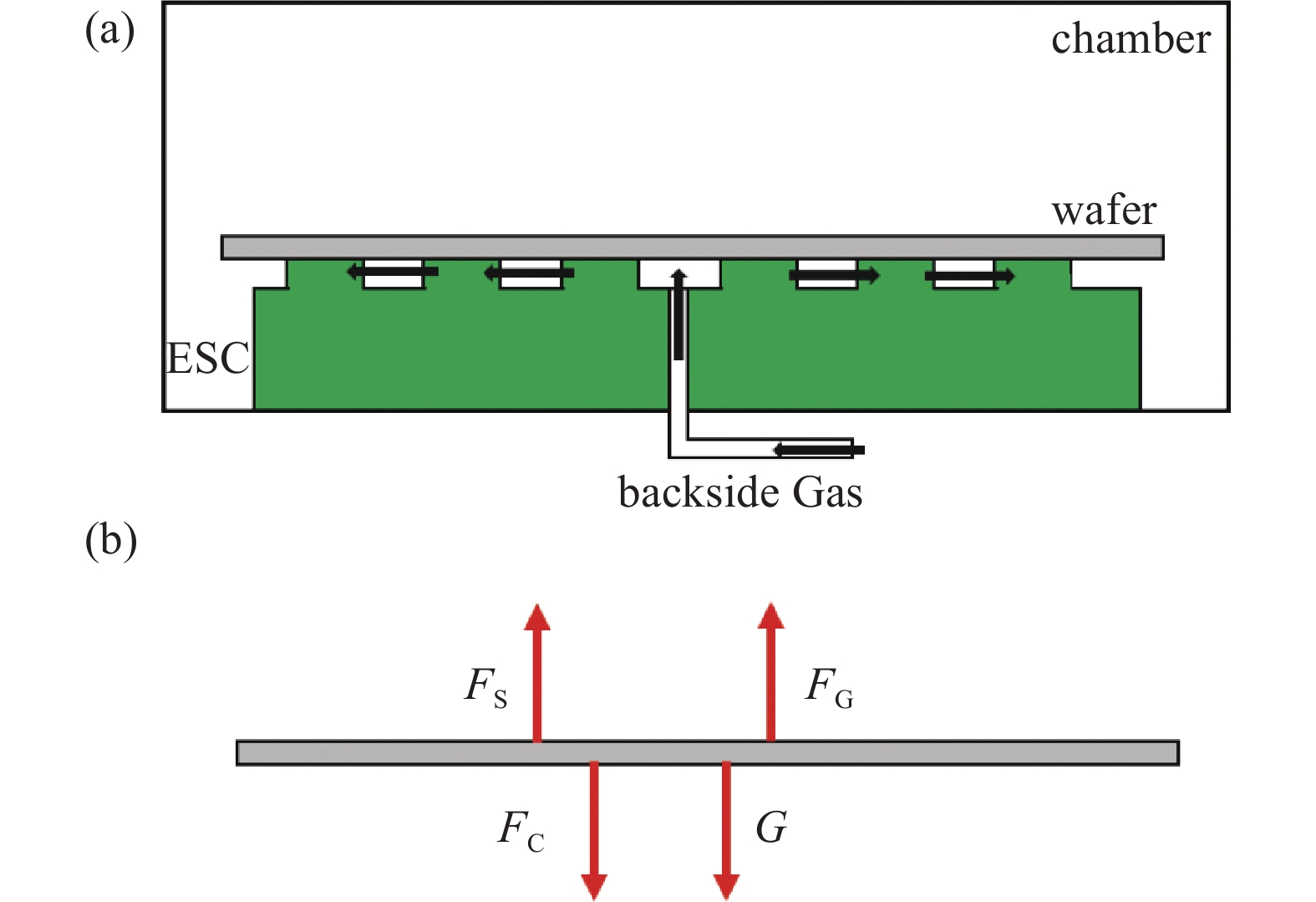
双极J-R型静电卡盘吸附力测试的基本原理如图4(a)所示。首先搭建好真空腔室结构,将晶圆放置在静电卡盘的吸附面结构上;之后把真空腔室抽真空到1×10−5 Pa环境下;然后给静电卡盘施加吸附电压,吸附表面的晶圆结构;下一步在静电卡盘与晶圆之间的孔隙中通入背吹气,通过背吹气路上的真空规读出此时背吹气压。由于此时腔室真空度(约<1×10−2 Pa)远小于背吹气压值(>100 Pa)这时背吹气产生的压力
${{F}}_{\text{G}}$ 加上凸点的支撑力$ {{F}}_{\text{S}} $ 等于静电卡盘的吸附力$ {{F}}_{\text{C}} $ 加上晶圆自身的重力G,如式(1)所示。其晶圆受力示意图如图4(b)所示。式中背吹气压力
$ {{F}}_{\text{G}} $ 可以通过背吹气压p乘以晶圆面积A得到。如式(2)所示。当逐渐增加背吹气的流量时,背吹气压升高,
$ {{F}}_{\text{G}} $ 增加,但是此时静电卡盘的吸附力$ {{F}}_{\text{C}} $ 和晶圆自身的重力G的大小不变,凸点的支撑力$ {{F}}_{\text{S}} $ 降低,如式(1)所示。当背吹气压增加到一定大小时,晶圆脱离静电卡盘,此时可以认为支撑力$ {{F}}_{\text{S}} $ 为0,晶圆刚好脱离静电卡盘时的背吹气压等于吸附力$ {{F}}_{\text{C}} $ 和晶圆重力G之和。由此即可测出静电卡盘的吸附力$ {{F}}_{\text{C}} $ 。 -
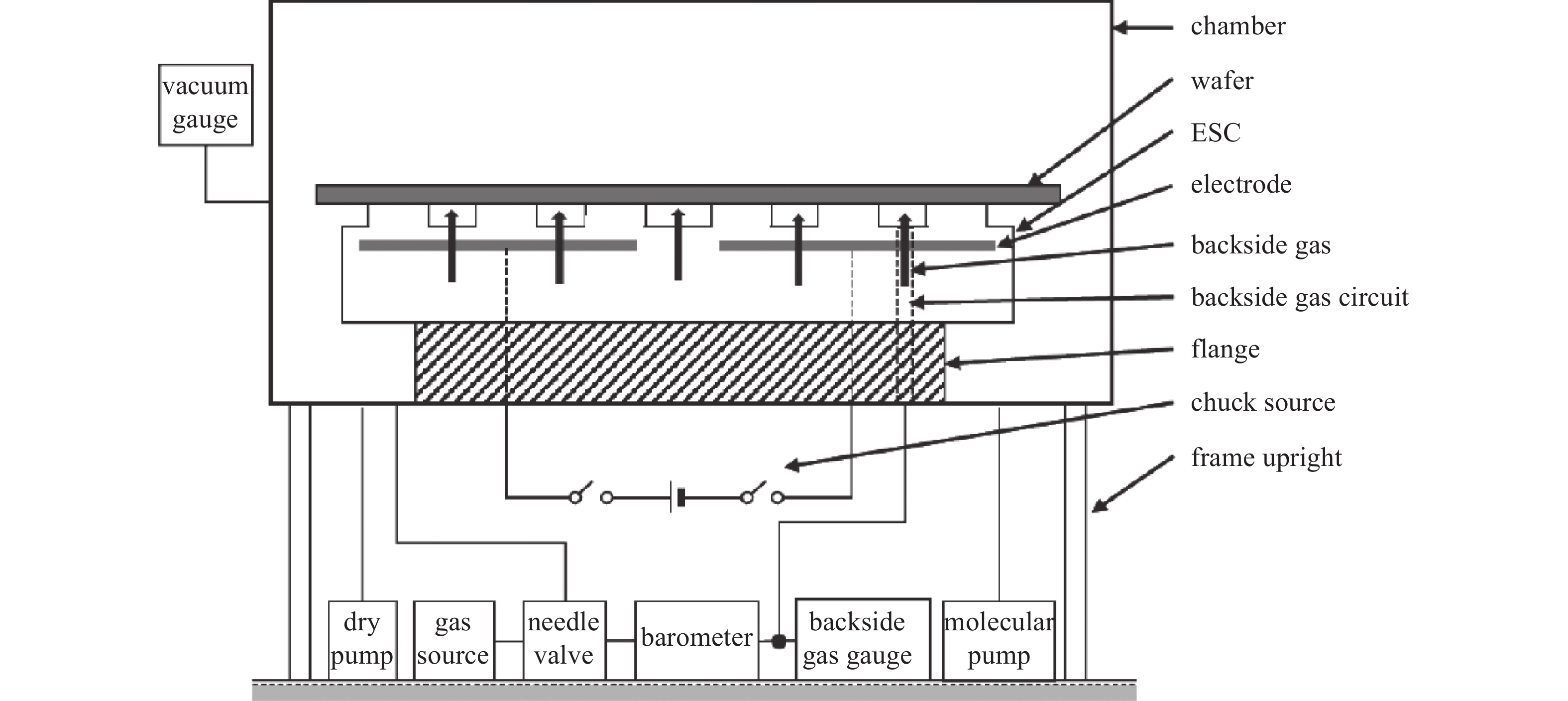
基于上述测试静电卡盘吸附力的原理以及所使用J-R型静电卡盘结构,本文搭建了包括软件控制系统和硬件测试系统的实验装置。其主要结构包括:真空腔室、干泵、分子泵、静电卡盘固定结构(具有封真空作用)、直流电源、气源、针阀、气体流量计、真空规、真空控制系统、气体流量控制系统、气压测试系统、吸附电压控制系统。具体的实验装置如图5所示。其中具体的软件、硬件控制系统的结构如示意图6所示。
实验装置的安装及测试过程如下,首先搭建好真空腔室结构、干泵、分子泵、真空规、背吹气压规、针阀、气路结构以及控制系统。将静电卡盘通过固定结构固定在真空腔室中,其中静电卡盘的电引入结构、及背吹气路在大气中,其吸附面被固定结构封在真空腔室中。将静电卡盘吸附面擦拭干净去除表面污渍及残余电荷,放上一片洁净的晶圆结构。直流电源接在静电卡盘的两极。静电卡盘背吹气路与气体流量计、真空规、以及气源相连。在本实验中,使用的是氩气作为静电卡盘的背吹气。安装好静电卡盘之后将腔室密封,并通过真空控制系统将腔室的气压抽到本底气压,并使腔室保持本底气压在两个小时以上,防止静电卡盘表面水汽干扰测试结果。开通直流电源,在静电卡盘的两极施加吸附电压,使静电卡盘吸附晶圆。通过控制增加通入静电卡盘气体流量的大小,来逐步增加背出气压的大小,直到晶圆脱离静电卡盘。在晶圆刚脱离静电卡盘时,(在晶圆脱离静电卡盘时,背吹气压会迅速降低)通过记录背吹气路上真空规的读数,得到背吹气的最大背压值,即可计算出静电卡盘吸附力的大小。
-
本文测试时所使用的12吋J-R型静电卡盘结构主要包括陶瓷盘基体结构、中心气孔、表面气道结构、以及表面凸点结构。其中静电卡盘工作时,晶圆被放置在凸点表面避免与陶瓷盘直接接触磨损陶瓷盘;陶瓷盘中的电极结构为双“D”型双极结构,制作在陶瓷盘结构内,电极上会加载直流电压吸附晶圆;背吹气从气孔中通入到气道以及晶圆和静电卡盘之间的空隙中;静电卡盘表面气道结构可以实现快速匀气作用,防止通入背吹气时晶圆背面气压不均匀。
而对于制作的凸点的结构以及对应电学性质,将会在下一章进行介绍,同时会研究凸点对晶圆吸附力的影响。
-
本文使用物理气相沉积的方法制作静电卡盘的凸点结构。实验制作的凸点结构主要材料为碳,其结构为金刚石结构,因此硬度较大(大于50 GPa),可以有效的防止晶圆对凸点的磨损,单个凸点的电阻率约为500 Ω为导体材料。本文中的实验和仿真主要针对于具有该凸点结构的J-R型静电卡盘结构。接下来本文将利用理论模型和实验测试的方法研究凸点尺寸、性能对J-R型静电卡盘吸附大小的影响。
制作的凸点结构在微米量级,在这一尺度上,使用白光干涉仪可以准确测量凸点轮廓形貌。
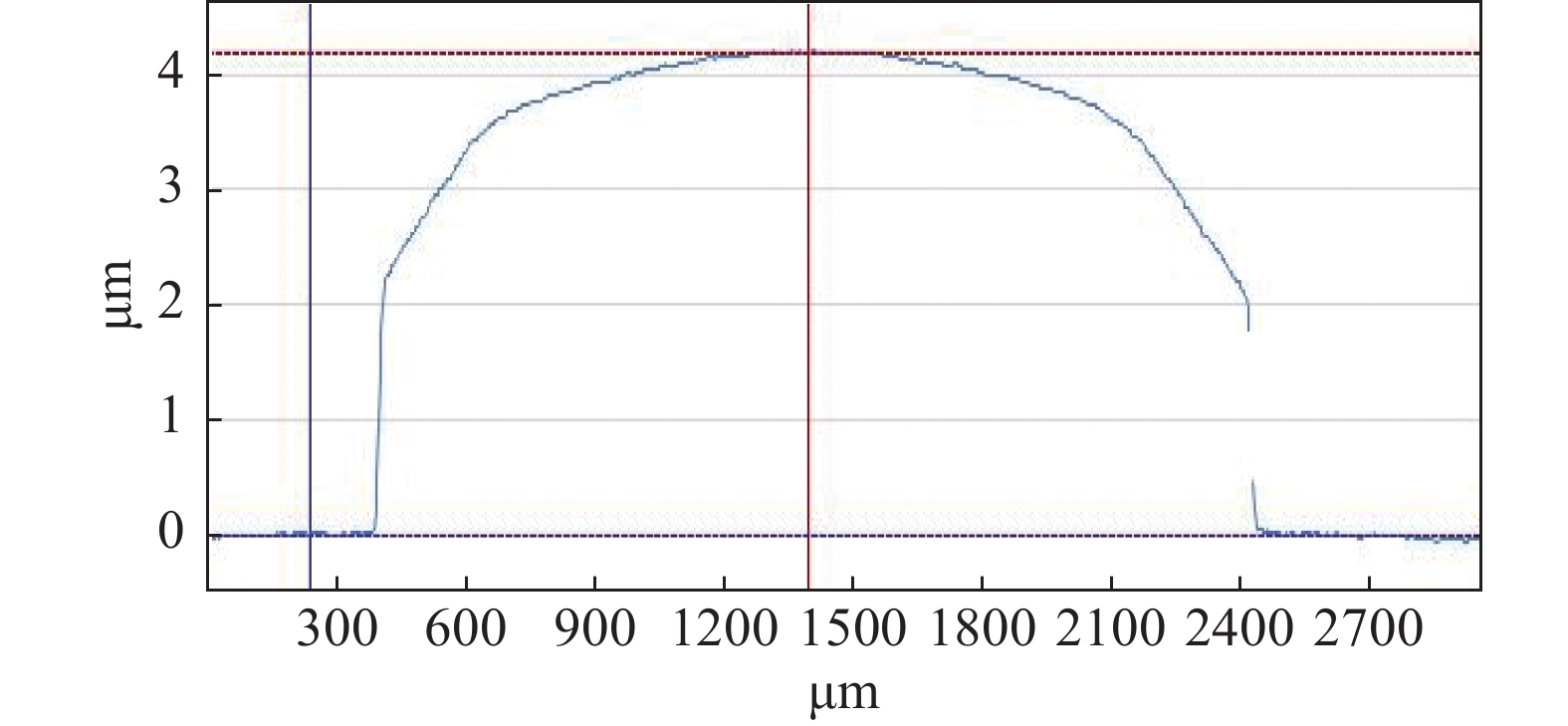
测量得到静电卡盘表面凸点形貌的一维轮廓图如图7所示,从图中可以测量得到凸点的高度、凸点的面积以及凸点的表面形貌。
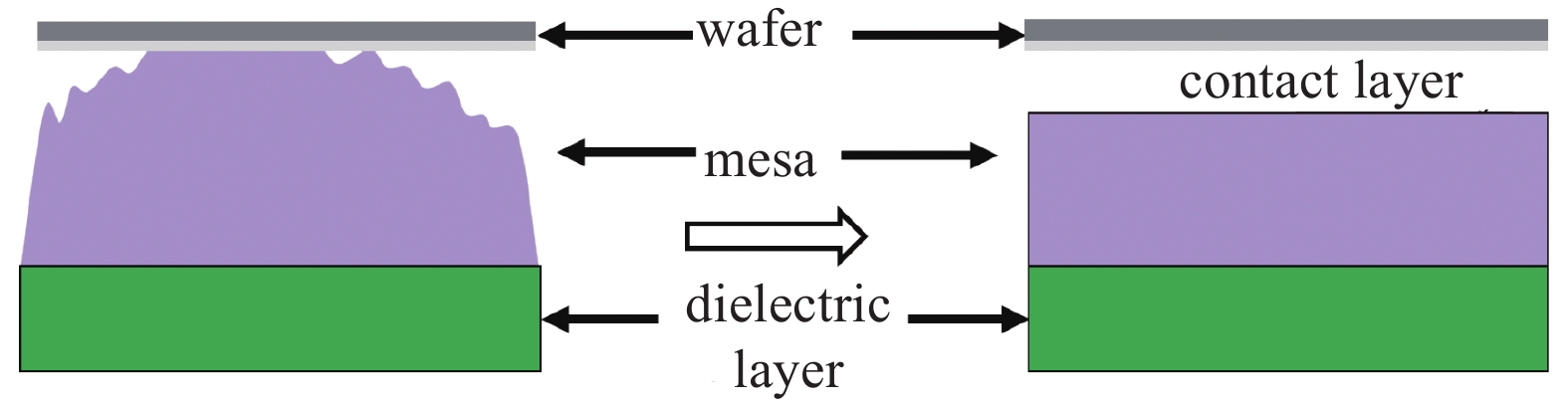
从图7可以看到,凸点表面具有一定弧度及粗糙度。依据J-R型静电卡盘的工作原理,凸点表面也会累积电荷,同时也会对晶圆产生吸附力。为了更好地研究凸点的吸附力,我们依据凸点表面到晶圆之间距离将凸点与晶圆之间的不规则间隙等效成一个光滑的接触层结构,如图8所示,其中
$ {h}_{\mathrm{M}} $ 为凸点的高度、$ {h}_{\mathrm{n}} $ 为某一凸点上等效的间隙层厚度,$ {\delta }_{\mathrm{n}} $ 为某一凸点上等效间隙层厚度。并且由于晶圆表面粗糙度远小于凸点及介电层表面粗糙度,在本研究中认为晶圆表面为光滑平面,因此可以认为静电卡盘上等效间隙层厚度δ都来自于凸点表面粗糙度。因此在本文中可以认为测量得到的第n个凸点的高度$ {h}_{\mathrm{M}\_\mathrm{n}} $ 为该凸点周围局部间隙层厚度$ {h}_{\mathrm{n}} $ 与接触层厚度$ {\delta }_{{\rm{n}}} $ 之和,见图8,即在使用干涉仪测量凸点高度发现,虽然不同凸点之间高度相差在±1 μm之间,但是测试发现在静电卡盘同一半径上凸点之间的高度相差在±0.05 μm范围内,而通常凸点高度的平均值约为4 μm,因此可以认为在静电卡盘同一半径上的凸点高度相同,通过该假设可以等效计算出式(3)中的
$ h+\delta $ 值与测量得到的凸点高度之间的关系,如式(4),即:其中
$ {r}_{1} $ 、$ {r}_{2} $ 、…、$ {r}_{n} $ 为静电卡盘某一半径上第1、2、…、n个凸点到静电卡盘中心的距离。$ {h}_{\mathrm{M}\_1} $ 、$ {h}_{\mathrm{M}\_2} $ 、…、$ {h}_{\mathrm{M}\_\mathrm{n}} $ 为静电卡盘某一半径上第1、2、……、n个凸点的高度。并且经等效计算得到,使用物理气相沉积法得到的凸点高度为4.5 μm时,凸点与晶圆之间接触层的厚度约为1.5 μm。由于需要计算的凸点结构较多,本文对接触层厚度进行如下假设:(1)在相同高度下,使用物理气相沉积法制备的凸点,经等效计算得到的接触层厚度相同。(2)使用物理气相沉积法制备的凸点,经等效计算得到的接触层厚度与凸点的高度成正比。本文通过上述两个假设,可以计算得到其他不同凸点对应的接触层厚度。
同时,还可以通过计算凸点的总面积与静电卡盘上的面积之比,计算出凸点面积的占比η。
-
对于J-R型静电卡盘来说,凸点与晶圆之间的接触电阻以及氧化层的绝缘电阻会极大的影响静电卡盘对晶圆的吸附力。在半导体领域中多数用到的晶圆为硅材料,但是在生产中也会用到具有不同氧化层厚度的晶圆结构,通常氧化层的厚度在100 nm到600 nm之间。在本文中,将会选取纯硅晶圆以及氧化层厚度为200 nm、500 nm的晶圆样品,来研究J-R型静电卡盘对晶圆吸附力影响的研究。
由静电卡盘的工作原理可知,J-R型静电卡盘主要利用静电卡盘表面电荷与晶圆内极性相反电荷之间的库仑力,来吸附晶圆。但是在背面为氧化硅的晶圆结构上,氧化硅为绝缘体材料,其内部几乎不存在自由电子或自由离子。因此J-R型静电卡盘表面电荷很难对氧化层产生吸附力。但是晶圆内部的硅材料为半导体材料含有自由电荷可以与静电卡盘产生吸附力。因此,在本文中认为晶圆的氧化为绝缘材料,在测试中不会发生电子迁移。但是可以将氧化层等效成一个电容结构来研究静电卡盘与晶圆之间的库仑力。
静电卡盘对晶圆的吸附力不仅需要考虑凸点到晶圆之间的电容值,还需要考虑凸点与晶圆之间的电压。而这部分电压主要取决于凸点到晶圆内硅材料的电阻,主要为凸点到晶圆表面的接触电阻与晶圆氧化层电阻的串联。由于晶圆氧化层为绝缘材料其体电阻率大于
$ {1\times 10}^{16} $ Ω·cm,因此我们先假定凸点与晶圆内硅材料的电阻主要来自于晶圆氧化层的绝缘电阻;基于此假设并依据电阻率计算公式,可以计算出电极到凸点之间介电层的电阻以及凸点到晶圆内硅材料的电阻,从而可以评估凸点与晶圆之间分压。依据体电阻率计算公式,如式(5)所示可以预估晶圆凸点到氧化层的电阻。其中
其中R为电阻值,ρ为电阻率,L为电阻材料的长度,S为电阻材料的面积。对于凸点对应晶圆氧化层电阻来说,L为对应氧化层厚度,S假定为凸点面积,其凸点直径约为2 mm,电阻率ρ大于
$ {1\times 10}^{16} $ Ω·cm。依据电阻率计算公式,评估500 nm厚度晶圆氧化层电阻大于$ {1.6\times 10}^{13} $ Ω;200 nm厚度晶圆氧化层电阻大于$ {6.3\times 10}^{12} $ Ω。而凸点对应介电层电阻小于$ {3\times 10}^{11} $ Ω,从电阻对比可以看到凸点对应氧化层电阻大于介电层电阻。依据图8可以看到,实际上凸点与晶圆的接触面积远小于凸点的面积,因此可以推断,对于氧化层厚度为500 nm、200 nm的晶圆,凸点与晶圆之间氧化层的电阻${{R}}_{\text{O}\text{x}}$ 远大于凸点与电极之间对应介电层的电阻$ {R}_{\mathrm{D}} $ 。接下来,将依据上述凸点结构及电学性能的研究,建立J-R型静电卡盘对具有不同氧化层厚度晶圆的吸附力大小计算的仿真模型。
-
本文依据等效电容理论建立静电卡盘吸附力计算模型。等效电容方法的原理是,将静电卡盘对晶圆的吸附,等效成电极、晶圆所成的平行板电容的两极之间的库仑力,并且将静电卡盘表面划分成有凸点的结构以及没有凸点的结构区域,分别计算这两个结构内,电极与晶圆之间的等效电容值。最后通过并联电容计算,得到静电卡盘整个电极与晶圆之间的等效电容值,并依据电容电极间库仑力计算公式,计算得到静电卡盘对晶圆的吸附力。
静电卡盘吸附背面是氧化硅材料的晶圆时,静电卡盘与晶圆组成的吸附结构如图9所示,对于J-R型静电卡盘主要考虑以下结构晶圆、晶圆背面氧化层的厚度、凸台、介电层、电极[13]。
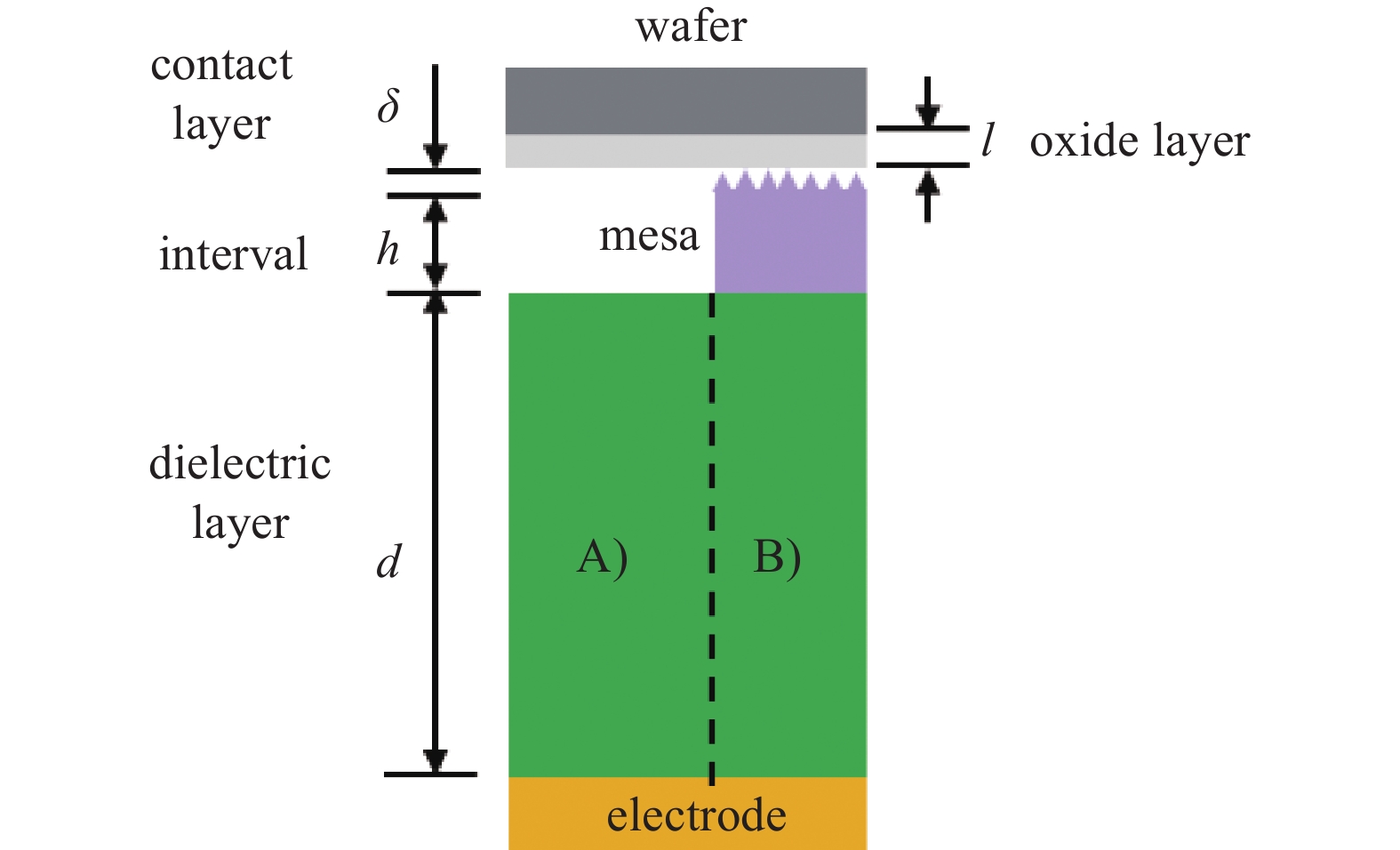
静电卡盘、凸点、晶圆局部结构图如图10所示。依据图10的结构和几何特征,其中关键的几何尺寸物理量包括介电层的厚度d,晶圆氧化层厚度l,间隙层高度h,以及接触层的厚度δ。其中晶圆背面氧化层的厚度l是已知的,并且可以使用膜厚测试仪测得氧化层的厚度。图10中间隙层高度h、介电层厚度d可以由静电卡盘结构尺寸得到。从图10静电卡盘局部结构来看,静电卡盘主要可以分为两部分结构:A)电极——介电层——间隙层——晶圆氧化层——晶圆结构;B)电极——介电层——凸点——接触界面——晶圆氧化层——晶圆结构。
-
本研究中的静电卡盘的介电层厚度d远大于凸点高度h以及晶圆绝缘层厚度l,因此忽略电极上电荷对晶圆吸附力的影响。
在A)电极——介电层——间隙层——晶圆氧化层——晶圆结构中,对晶圆的吸附力主要来自于介电层表面电荷对晶圆内硅材料的吸附力。这部分静电卡盘表面到晶圆内部硅材料电容可以等效为晶圆氧化层电容
${{C}}_{\text{O}\text{x}}$ 与间隙层电容${{C}}_{\text{I}}$ 串联;静电卡盘表面到晶圆内硅材料的电阻为晶圆氧化层电阻${{R}}_{\text{O}\text{x}}$ 与间隙层电阻$ {R}_{\text{I}} $ 串联之和;但是在电极与静电卡盘表面之间还串联介电层电阻$ {R}_{\mathrm{D}} $ 。对于B) 电极——介电层——凸点——接触界面——晶圆氧化层——晶圆结构上,静电卡盘对晶圆的吸附主要来自于凸点表面的电荷对晶圆内硅材料的吸引,忽略电极与静电卡盘界面对晶圆的吸附力的影响。凸点表面到晶圆内硅材料之间的电容等效为晶圆氧化层电容
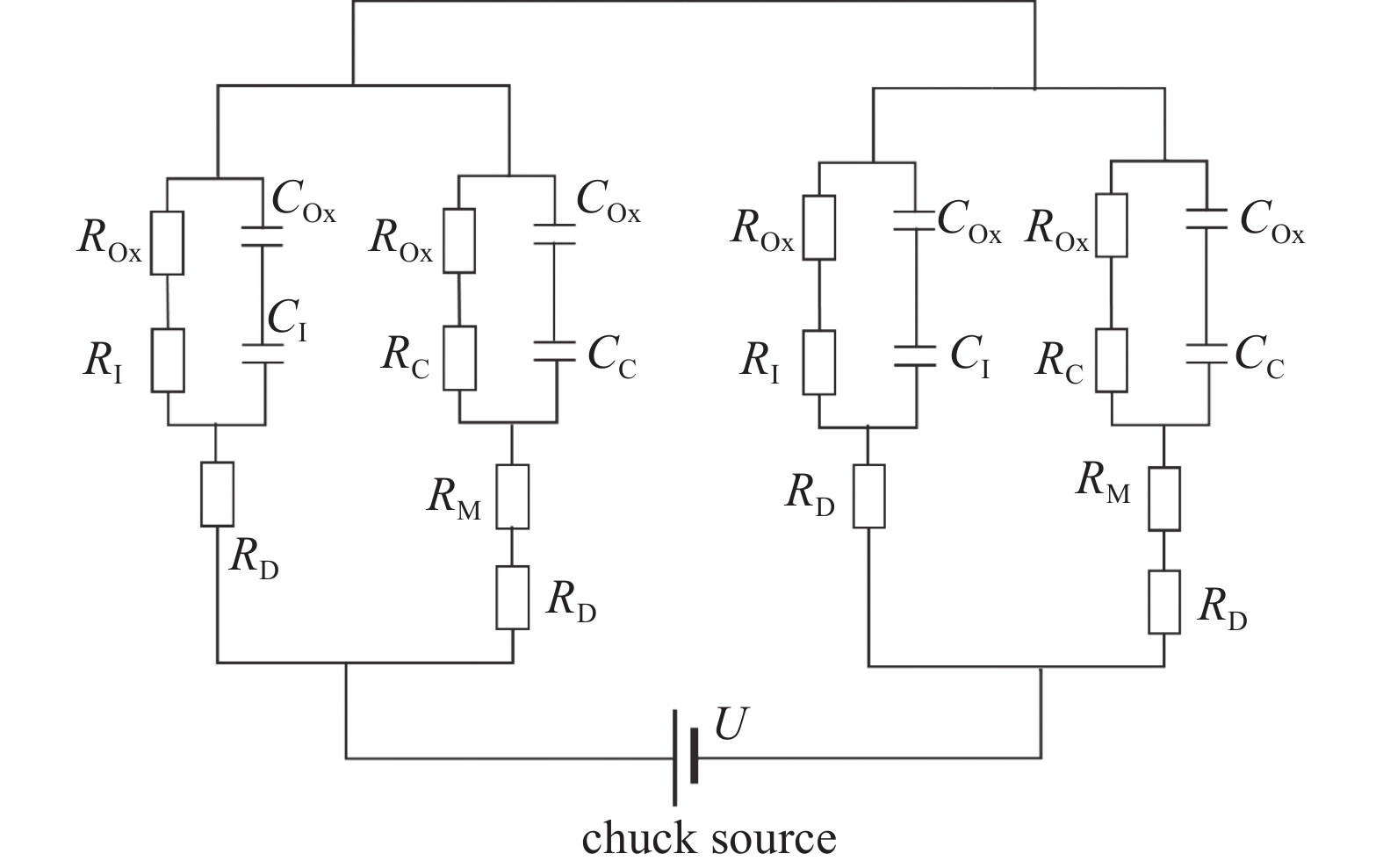
${{C}}_{\text{O}\text{x}}$ 与接触层电容${{C}}_{\mathrm{C}}$ 串联。凸点表面到晶圆内硅结构之间电阻的为晶圆氧化层电阻${{R}}_{\text{O}\text{x}}$ 与接触电阻${{R}}_{\mathrm{C}}$ 串联之和。但是电极与凸点表面之间还串联介电层电阻$ {R}_{\mathrm{D}} $ 与凸点电阻$ {R}_{\mathrm{M}} $ 。由上所述双极J-R型电路结构可以等效为电阻和电容如图11所示。在等效电路图11中,静电卡盘吸附电源的电压为U,静电卡盘正极和负极到晶圆之间的电阻几乎相同,并且正极到晶圆之间电阻与负极到晶圆之间电阻形成的是串联回路,因此每个电极到晶圆之间的电压
$ {U}_{\text{p}} $ 为:通过图11的等效电路,可以建立计算J-R型静电卡盘对晶圆吸附力大小的仿真计算公式。在A) 电极——介电层——间隙层——晶圆氧化层——晶圆结构中,间隙层的等效电容
${{C}}_{\mathrm{I}}$ 为:其中,
$ {\varepsilon }_{\mathrm{g}} $ 为间隙层和接触界面狭缝内填充气体的相对介电常数,$ {\varepsilon }_{0} $ 为真空介电常数,$ \varphi $ 为正电极或负电极有效面积与介电层表面积之比,在本研究中认为电极正极或负极占介电层表面积之比相同都为$ \varphi $ ,A为介电层表面积,$ \eta $ 为所有凸点的总面积占介电层表面积的比例,h为间隙层高度,δ为接触层的厚度。氧化层的等效电容
${{C}}_{\mathrm{I}}$ 可由式(8)计算出:其中,
$ {\varepsilon }_{\mathrm{O}\mathrm{x}} $ 为晶圆氧化层的相对介电常数,$ {\varepsilon }_{0} $ 为真空介电常数,$ {\varepsilon }_{\mathrm{O}\mathrm{x}} $ 为晶圆氧化层(即氧化硅)材料的相对介电常数通常该材料相对介电常数为3.5,$ \varphi $ 为正电极或负电极有效面积与介电层表面积之比,A为电极表面积,$ \eta $ 为所有凸点的总面积占介电层表面积的比例,l为晶圆氧化层的厚度。由此可以计算出静电卡盘表面到晶圆内硅结构的电容值
$ {C}_{S} $ 的大小,如式(9):由电阻分压公式计算静电卡盘表面到晶圆内硅材料之间的电压
$ {U}_{\text{S}} $ ,如式(10):其中,
$ {R}_{\text{I}} $ 为间隙层电阻,${{R}}_{\text{Ox}}$ 为氧化层电阻,$ {R}_{\mathrm{D}} $ 为介电层电阻,$ {U}_{\text{p}} $ 为电极到晶圆之间的电压。由3章晶圆氧化层的研究可以知道,晶圆氧化层电阻${{R}}_{\text{Ox}}$ 与间隙层电阻$ {R}_{\text{I}} $ 之和远大于介电层电阻$ {R}_{\mathrm{D}} $ 。由此可知电极到介电层表面几乎无分压,$ {U}_{\text{S}} $ 与电压$ {U}_{\text{p}} $ 相同。在B) 电极——介电层——凸点——接触界面——晶圆氧化层——晶圆结构中,接触层的电容值
$ {C}_{\mathrm{I}} $ ,如式(11)所示:其中,
$ {\varepsilon }_{\mathrm{g}} $ 为接触界面狭缝内填充气体的相对介电常数,$ {\varepsilon }_{0} $ 为真空介电常数,$ \varphi $ 为正电极或负电极有效面积与介电层表面积之比,A为介电层表面积,$ \eta $ 为所有凸点的总面积占介电层表面积的比例,h为间隙层高度,δ为接触层的厚度。氧化层的等效电容
$C_{ {{\rm{Ox\_M}} }}$ 可由公式(12)计算出:同样的方法可以得到凸点表面到晶圆内硅材料的电容值
$ {C}_{\mathrm{M}} $ ,如式(13)所示:由电阻分压公式,可以计算静电卡盘凸点表面到晶圆内硅材料之间的电压
$ {U}_{\text{M}} $ ,如式(14)所示:由第3章中的研究可以知道,凸点上对应晶圆绝缘层的电阻远大于凸点对应介电层的电阻与凸点本身电阻之和,因此计算可得电极到凸点表面几乎无分压,凸点表面到晶圆内硅材料之间的电压
$ {U}_{\text{M}} $ 与电压$ {U}_{\text{p}} $ 相同。由平行板电容计算两极之间库仑力的计算公式可以得到静电卡盘产生的吸附力大小,如式(15)所示:
其中,F为静电卡盘产生的静电力的大小,E为电极加载电压时静电卡盘与晶圆之间形成的平行板电容器的电势能,
$ {C}_{\mathrm{S}} $ 为静电卡盘表面到晶圆内硅结构总的电容值,$ {C}_{\mathrm{M}} $ 为所有的凸点表面到晶圆内硅材料总的电容值,$ {U}_{\text{p}} $ 为静电卡盘上电极与晶圆之间的电势差。由式(15)可以计算出J-R型静电卡盘对具有氧化层晶圆的吸附力,从公式中可以推断出,晶圆上氧化层的厚度会影响静电卡盘的吸附力。接下来作者将利用仿真模型与实验平台,来测试J-R型静电卡盘在不同电压下,对具有200 nm、500 nm氧化层厚度晶圆的吸附力。进而研究J-R静电卡盘对不同材料晶圆吸附力大小的影响。
-
吸附电压对静电卡盘吸附力的影响
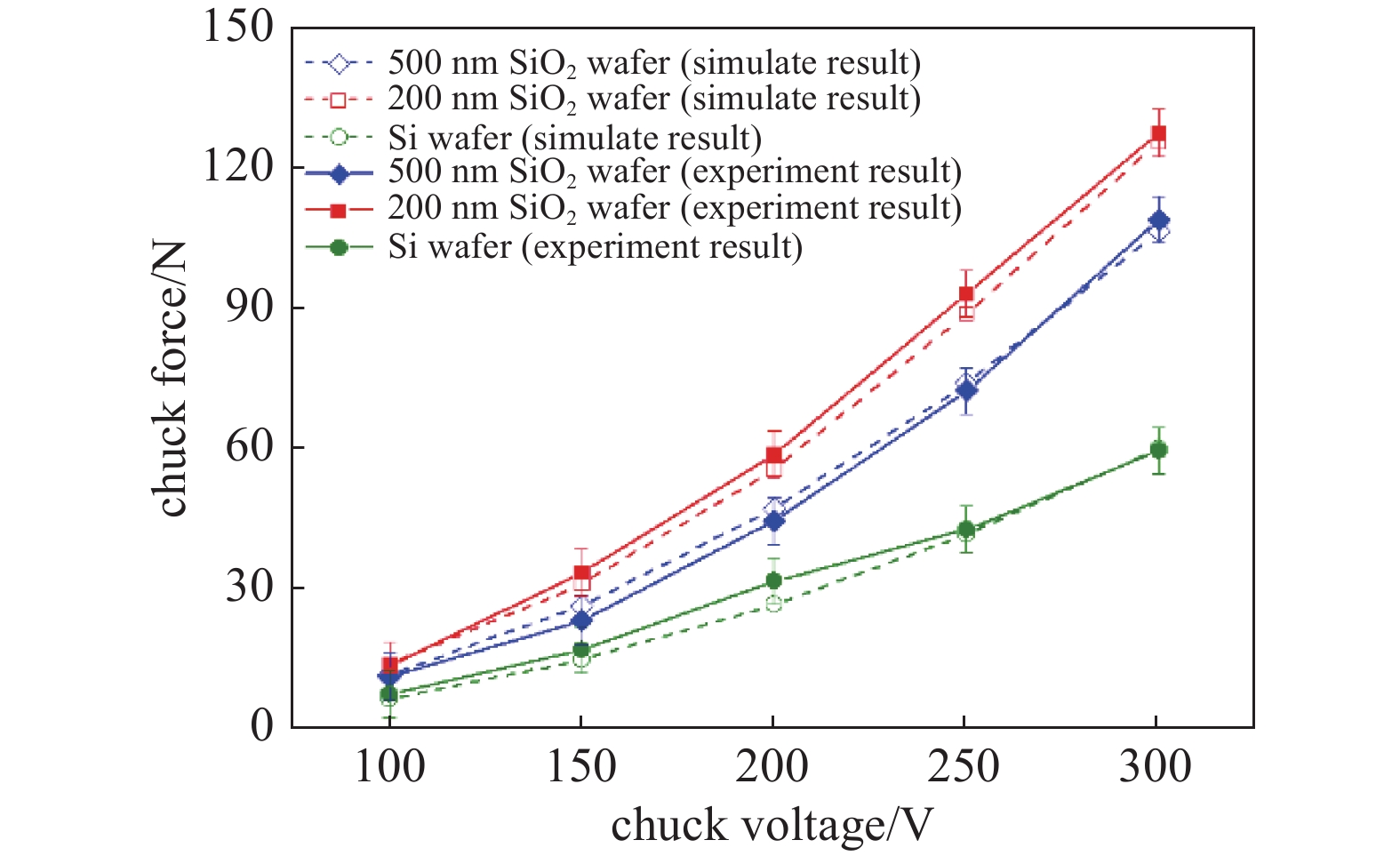
本文利用第2章中搭建的测试平台,利用背吹法测试静电卡盘的吸附力。其过程是在同一个静电卡盘上,在不同吸附电压下,吸附住纯硅晶圆以及具有200 nm、500 nm氧化层晶圆;然后逐步增加背出气量,直到晶圆脱离静电卡盘,记录此时背吹气路的气压值,然后利用式(2)计算得到静电卡盘的吸附力。从测试平台得到的实验结果与仿真计算得到的结果如图12所示。由于气路的控制,实验是非连续性增加背吹气量,因此实验测试的结果有着10 N的误差波动。
得到的实验与模型仿真结果如图12所示。限于气体流量计以及真空规的量程所限,测试吸附电压的大小最大能达到300 V。
从图12中可以看到,无论静电卡盘吸附哪种材料的晶圆,在实验结果中静电卡盘的吸附力都会随着吸附电压的升高而增长。仿真结果中吸附力大小随电压变化的趋势与实验结果一致,并且仿真结果在测试结果的误差范围内。
并且在相同电压下静电卡盘对具有一定厚度氧化层晶圆的吸附力大于静电卡盘对纯硅晶圆的吸附力。这是由于晶圆氧化层绝缘电阻较高,凸点到晶圆内硅材料之间分压较大导致的。
但从图12中同样可以看到,在相同吸附电压下,静电卡盘对具有200 nm氧化层晶圆的吸附力(图中红色曲线)大于具有500 nm氧化层晶圆的吸附力(图中蓝色曲线)。这是由于随着晶圆氧化层厚度增加,静电卡盘表面到晶圆内硅材料之间的电容降低,从而减少静电卡盘对晶圆的吸附力。从上述实验结果可以推断出,J-R型静电卡盘对晶圆的吸附力,随晶圆氧化层厚度的增加先增加后减少,因此可以依此结果及文中建立的仿真模型设计静电卡盘结构,使静电卡盘对不同材料的晶圆都具有足够的吸附力。
同时图12中实验与仿真结果证实了文中依据等效电容方法建立的仿真模型可以准确计算J-R型静电卡盘对不同材料晶圆的吸附力。
-
本文以物理气相沉积制备了J-R型静电卡盘的凸点,并以此静电卡盘为研究对象,研究了凸点结构及电学性能对凸点表面到晶圆内硅材料之间电阻的影响。
利用等效电容方法,描述了静电卡盘吸附具有氧化层晶圆的等效电路,从而建立了计算J-R型静电卡盘对不同材料晶圆吸附力的仿真计算模型。研究了凸点电性能、凸点结构、介电层厚度、介电层的体电阻率、晶圆氧化层厚度等参数对静电卡盘吸附的影响。即:(1)J-R型静电卡盘对具有一定氧化层厚度晶圆的吸附力大于纯硅晶圆的吸附力。(2)受氧化层电阻及电容的影响,随着晶圆氧化层厚度的增加,J-R型静电卡盘对晶圆的吸附力,先增加后减少。
本文所建立的仿真模型为今后静电卡盘对不同材料衬底吸附力的研究提供理论依据。但由于静电卡盘本身材料以及晶圆种类的局限性,对于静电卡盘吸附力的研究仍具有一定的局限性。接下来还需在如下方面对静电卡盘进行研究:(1)凸点形状、高度分布、面积占比等对J-R型静电卡盘吸附力的影响。(2)介电层体电阻率、厚度对J-R型静电卡盘吸附力的影响。(3)J-R型静电卡盘对氮化硅、蓝宝石等常见衬底材料吸附力的影响。
晶圆材料对J-R型静电卡盘吸附力影响的研究
Influence of Wafer Material on Chuck Force of J-R Type Electrostatic Chuck
-
摘要: 静电卡盘是半导体以及光学设备中关键器件之一,主要起到固定衬底快速加热的作用。本研究中搭建了真空腔室平台,并依据气体背吹法,测试了约翰逊-拉别克型静电卡盘对不同电压下不同材料晶圆的吸附力。本文通过对氧化层电学性质及静电卡盘凸点结构的研究,得出静电卡盘对具有氧化层晶圆的吸附力来自于静电卡盘表面电荷与晶圆内硅材料之间吸附力的结论。并且利用等效电容法,建立了计算不同材料晶圆对静电卡盘吸附力影响的仿真模型。通过实验与仿真的结果表明,相同吸附电压下,静电卡盘对具有氧化层晶圆的吸附力大于静电卡盘对纯硅晶圆的吸附力。静电卡盘对晶圆吸附力的大小随着氧化层厚度的增加,先增加后减少。本文的研究对J-R效应理论的完善以及静电卡盘的设计及优化具有重要指导意义。为半导体设备的发展提供重要的理论基础。Abstract: Electrostatic chuck is one of the most important elements in the semiconductor field, mainly used in integrated circuit equipment and optical equipment, which plays the role of carrying wafers and substrates. This research introduces the vacuum chamber and uses the back gas method to test the chuck force of the Johnsen-Rahbek type electrostatic chuck with different thicknesses of the oxide layer of the wafer and in different chuck voltages. In this article, we infer that the chuck force comes from the Coulomb force between the electrostatic chuck and the silicon in the wafer by studying the electrical properties of the oxide layer and the structure of the mesa. We built the mathematical model to study the effect of the thickness of the oxide layer of the wafer in chuck force with the equivalent capacitance method. The experiment and simulation results show that because of the low contact resistance, under the same chuck voltage, the chuck force of the electrostatic chuck to the wafer with the oxide layer is greater than that of the electrostatic chuck to the bare silicon wafer. And with increasing the thickness of the oxide layer of the wafer, the chuck force between the electrostatic chuck and wafer increases first and then decreases. This research has important guidance for the improvement of the Johnsen-Rahbek effect theory and the optimization of the structure of the electrostatic chuck, and provides a theoretical basis for the development of semiconductor equipment.
-
Key words:
- Electrostatic chuck /
- Johnsen-Rahbek effect /
- Oxide layer /
- Back gas method /
- Equivalent capacitance method .
-

-
-
[1] Choe H H. Basic study of a glass substrate in dry etching system[J]. Vacuum,2006,81(3):344−346 doi: 10.1016/j.vacuum.2006.06.010 [2] Goodman D L. Effect of wafer bow on electrostatic chucking and back side gas cooling[J]. Journal of Applied Physics,2008,104(12):124902 doi: 10.1063/1.3043843 [3] Wright D R,Chen L,Federlin P,et al. Manufacturing issues of electrostatic chucks[J]. Journal of Vacuum Science and Technology B,1995,13(4):1910−1916 doi: 10.1116/1.588108 [4] Kurkowski P, Drizlikh S, Sarver R, et al. Effects of wafer bow and warpage on performance of electrostatic chucks in high volume manufacturing [C]. Advanced Semiconductor Manufacturing Conference and Workshop, 2005 IEEE/SEMI. Munich: IEEE, 2005: 127-129 [5] Chang C H,Leou K C,Lin C,et al. Real-time control of ion density and ion energy in chlorine inductively coupled plasma etch processing[J]. Journal of Vacuum Science and Technology A,2003,21(4):1183−1187 doi: 10.1116/1.1575222 [6] Choi D Y,Kim N H,Kim S Y. Reduction of loading effects with the sufficient vertical profile for deep trench silicon etching by using decoupled plasma sources[J]. Journal of Materials Processing Technology,2009,209(17):5818−5829 doi: 10.1016/j.jmatprotec.2009.06.014 [7] Abraham I C,Woodworth J R,Riley M E,et al. Electrical and plasma property measurements of a deep reactive ion etching Bosch process[J]. Journal of Vacuum Science and Technology B,2003,21(3):1112−1117 doi: 10.1116/1.1565145 [8] Qin S,McTeer A. Wafer dependence of Johnsen-Rahbek type electrostatic chuck for semiconductor processes[J]. Journal of Applied Physics,2007,102(6):064901 doi: 10.1063/1.2778633 [9] Watanabe T,Kitabayashi T,Nakayama C. Electrostatic force and absorption current of alumina electrostatic chuck[J]. Japanese Journal of Applied Physics,1992,31(7):2145−2150 [10] Field J. Electrostatic wafer clamping for next-generation manufacturing[J]. Solid State Technology,1994,37(9):91−93 [11] Wardly G A. Electrostatic wafer chuck for electron beam microfabrication[J]. Review of Scientific Instruments,1973,44(10):1506−1509 doi: 10.1063/1.1685985 [12] Asano K,Hatakeyama F,Yatsuzuka K. Fundamental study of an electrostatic chuck for silicon wafer handling[J]. IEEE Transactions on Industry Applications,2002,38(3):840−845 doi: 10.1109/TIA.2002.1003438 [13] Wang K S,Cheng J,Zhong Y,Ji L H. A novel measuring method of clamping force for electrostatic chuck in semiconductor devices[J]. Journal of Semiconductors,2016,37:044012 doi: 10.1088/1674-4926/37/4/044012 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: