首页
登录
注册
-
多种能源产业排放的尾气中含有稀薄甲烷，例如稠油火驱采油尾气、煤层开发排放的乏风等。这些废气中甲烷含量非常少，难以直接回收或点燃利用，直接排放会造成严重的温室效应。因此探索高效辅助燃烧技术，降低稀薄甲烷点火难度，对这类废气利用有重要意义。非平衡态等离子体辅助燃烧技术可以使气体中产生大量活性物质，促进含有甲烷的混合气体快速发生氧化反应，从而降低燃烧的点火温度，提高火焰的稳定性。在工程上已经大量采用。但是由于燃烧过程和气体等离子体放电过程非常复杂，完整的理论分析研究相对较少。
目前对于等离子体辅助燃烧的数值模拟研究主要采用零维或者整体模型，例如2020年Bechane等[1]在对等离子体辅助燃烧进行数值模拟时采用整体模型进行求解，2022年，Barleon等[2]采用整体模型进行数值模拟，以上理论研究都验证了等离子体可以有效辅助燃烧过程。但是该方法将等离子体视为一个内部参数不存在梯度的整体，而将能量输入与等离子体反应过程相结合，忽略具体边界条件的影响，不能跟踪放电周期中荷电粒子和活性基团的分布变化，因此不能完全表征等离子体放电的完整过程。
与上述模拟方法相比，等离子体流体模型更适合描述等离子体放电空间内的各种过程，尤其适合描述介质阻挡放电 (Dielectric barrier discharge，DBD)[3]过程。本文采用一维等离子体流体模型对DBD辅助稀薄甲烷-空气燃烧点火过程进行数值模拟，研究了放电初始的数个放电周期内非平衡态等离子体对于燃烧过程的影响，增进了对该过程细节的了解。该研究为开发新型等离子体辅助处理稀薄甲烷尾气技术进行了理论探索。
-
甲烷-空气DBD等离子体中包含大量反应，其中主要包括甲烷燃烧反应和各种放电反应，需对其进行合理简化才能进行模拟计算。Larsson等[4]曾建立一个由80个反应组成的等离子体辅助甲烷燃烧模型。其中甲烷燃烧过程由42个不可逆反应组成(简称Z42，表1中反应R1-R42)，该简化机理与经典的GRI3.0[5]反应机理在火焰温度、火焰速度、主要物质预测等方面较为一致。他们的模型中还包括与等离子体放电相关的38组反应，包括臭氧O3反应、激发态氧分子O2*反应、化学电离、电子碰撞解离、电子碰撞电离、电子吸附解离等过程(表1中反应R43-R80)。其中O3和O2*的反应会显著影响H，O以及OH自由基的浓度，会增加甲烷点燃过程的反应速率，降低点火延迟时间[6]。在此基础上，本文参考Pancheshnyi等[7]提出的空气等离子体放电简化反应机理，补充N2相关反应(表1中反应R81-R101)，通过以上方法，我们将DBD非平衡态等离子体辅助甲烷燃烧反应进行简化，建立由36种反应物质和101种反应组成的简化反应体系，具体反应如表1所示。其中电子碰撞反应从Lxcat数据库[8]获得碰撞截面数据进行计算。
-
本文模拟研究主要考查等离子体对稀薄甲烷点火过程的影响，且模拟时间极短，放电间隙较小，因此忽略流动的影响，仅考虑等离子体放电、燃烧和传热过程。
等离子体流体模型将电子和重物质粒子分为两类连续流体。采用漂移-扩散方程描述等离子体的电子数密度和电子能量密度：
式中，ne和Nn分别是为电子和重粒子的数密度，1/m3；nε为能量密度，J/m³；xj 为第j个电子碰撞反应中重粒子反应物的摩尔分数；Δεj为第j电子碰撞反应中的反应能量，J。kj为第j电子碰撞反应中的反应速率系数，通过下式计算：
式中，me是电子质量，kg；ε是电子能量，eV；σ是碰撞截面积，m2；f是电子能量分布函数，取最常用的麦克斯韦分布(Maxwellian)。式(2)中电子迁移特性(μe，De，με，Dε)通过求解玻尔兹曼方程得到。
对于非电子物质的质量分数采用下式描述：
式中Dkm是有效二元扩散系数；Rk是与k组分相关反应的速率；ρ为气体混合密度，kg/m3；qk和wk分别为k组分的电荷数和质量分数。迁移率μ由爱因斯坦关系确定μk=(Dkm qk e)/(kb Tg) 其中，e为元电荷；Tg为气体温度，K；kB为玻尔兹曼常数。
静电场采用泊松方程计算：
式中，ε0为真空介电常数(ε0≈8.854×10−12)，εr为空气的相对介电常数；n+表示所有正离子浓度之和；n−表示所有负离子浓度之和。
传热方程如下：
式中，k是热导率，W/(m·K)；Q是热源项，W/m3；T是温度，K；Q通过反应物质热力学参数计算。
由于介质层不导电，因此需要考虑电介质表面的电荷累积过程，并考虑二次电子发射。二次发射系数γse受到表面特征和材料影响，通常难以确定，本计算中二次发射系数如表2所示。
-
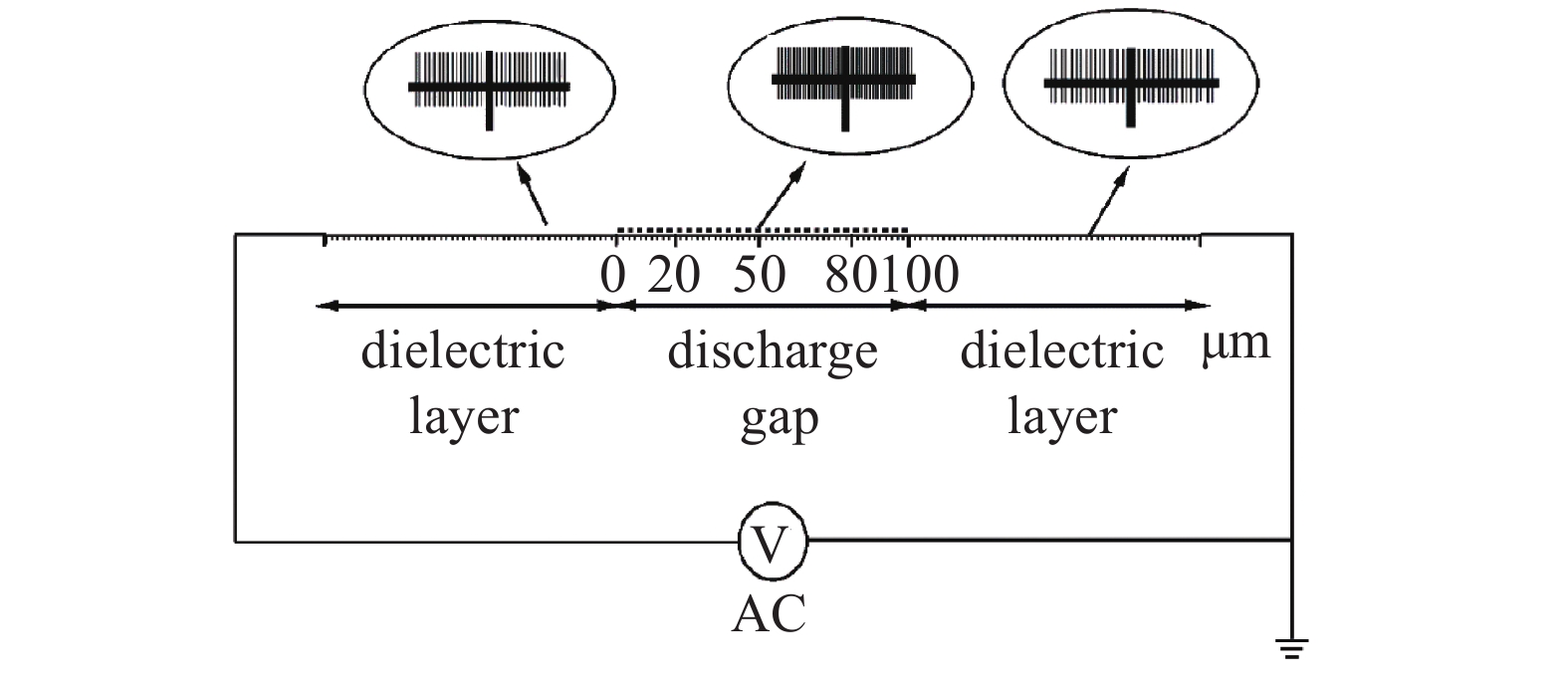
本文将圆形平板DBD放电器简化为一维模型，电极直径为10 cm，放电间隙和介质层厚度均为100 μm。本研究中选择较小的放电间隙可以获得较为稳定的放电状态[9]。在DBD放电器两端施加正弦高频交流电，频率为50 kHz。计算模型所划分网格如图1所示，在放电间隙区域采用高分辨率网格捕捉放电过程，在介质层区域使用较粗网格提高计算效率。本文利用COMSOL有限元软件进行计算。图1中放电间隙的左侧边界为0点，右侧边界为100 μm。图中50 μm位置为放电空间中间点处，图中20 μm和80 μm处为放电过程中电子数密度较高的区域，具体结果见2.1节。
在实际工程中，通常将含甲烷尾气与空气混合进行利用。以火驱尾气为例，通常为10% CH4、10% CO2和80% N2组成。为保证燃烧效果，通常要混入较多空气，在本文中主要考虑典型稀薄甲烷工况，即CH4与O2的摩尔比Φ=0.1时，气体中各组分CH4、CO2、O2和、N2的摩尔分数为1.74%、1.74%、17.36%和79.17%。其余各物质的初始摩尔分数均设定为1× 10−12，电子初始密度为1×1012 m−3，初始电子平能量为5 eV，气压为1 atm。由于模拟时长极短，可以近似将介质层边界设置为固定温度800 K。目前工程上或实验室中常用的DBD等离子体放电电压为10 kV~18 kV，若电压低于10 kV放电强度较低，若高于18 kV可能出现介质击穿，因此本文的模拟计算中选取10 kV~18 kV电压作为研究参数。
-
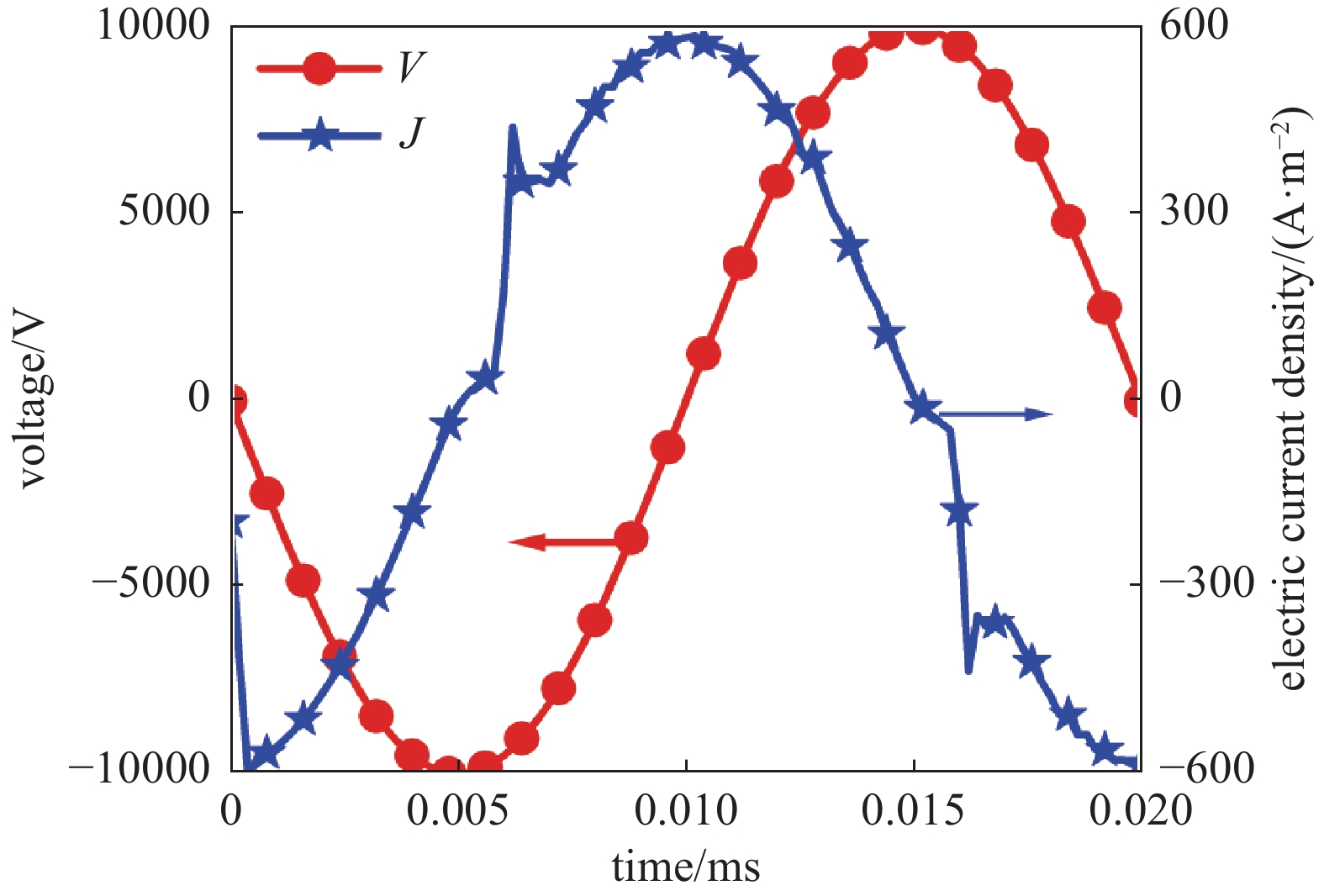
图2为外加电压10 kV，CH4与O2摩尔比Φ为0.1时放电特性。由于表面电荷累积的影响，电流周期比电压周期略早0.005 ms，约为1/4个放电周期。电流密度达到最大值时约为600 A∙m−2。图中电流密度存在少量毛刺，这些时刻由于间隙电压较大，导致瞬时电流较大。
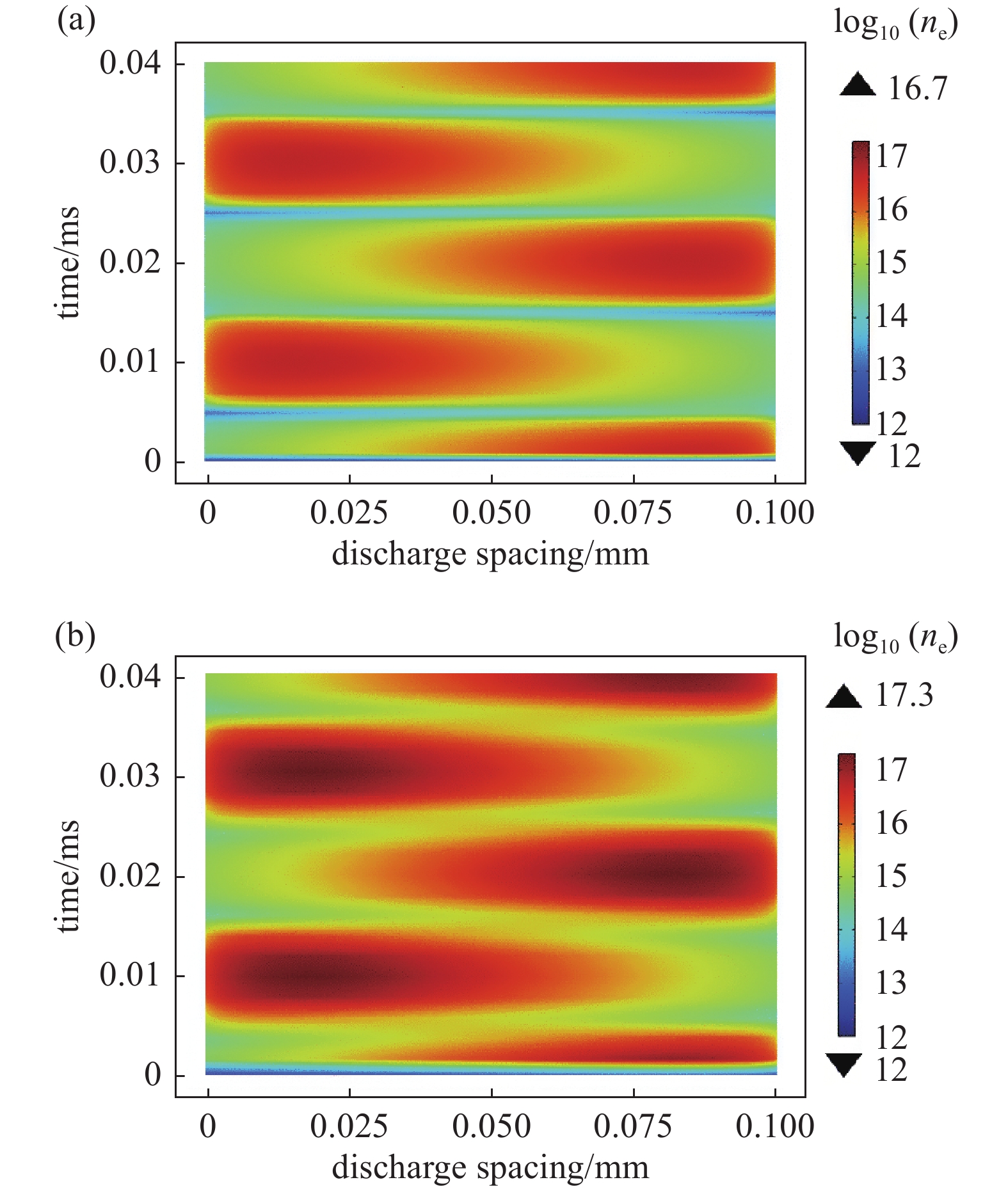
图3为不同电压下，两个放电周期即0.04 ms内电子数密度对数的时空变化情况，横坐标表示放电间距，纵坐标表示时间。从(a)、(b)中发现在相同周期内，随着外加电压幅值的增大，电子数密度峰值越大。电子数密度在靠近介质壁面约20 μm处达到最大值。外加电压幅值为10 kV时电子数密度达到5.32×1016 m−3，外加电压幅值为18 kV时电子数密度达到2.0×1017 m−3，约为前者的四倍。
-
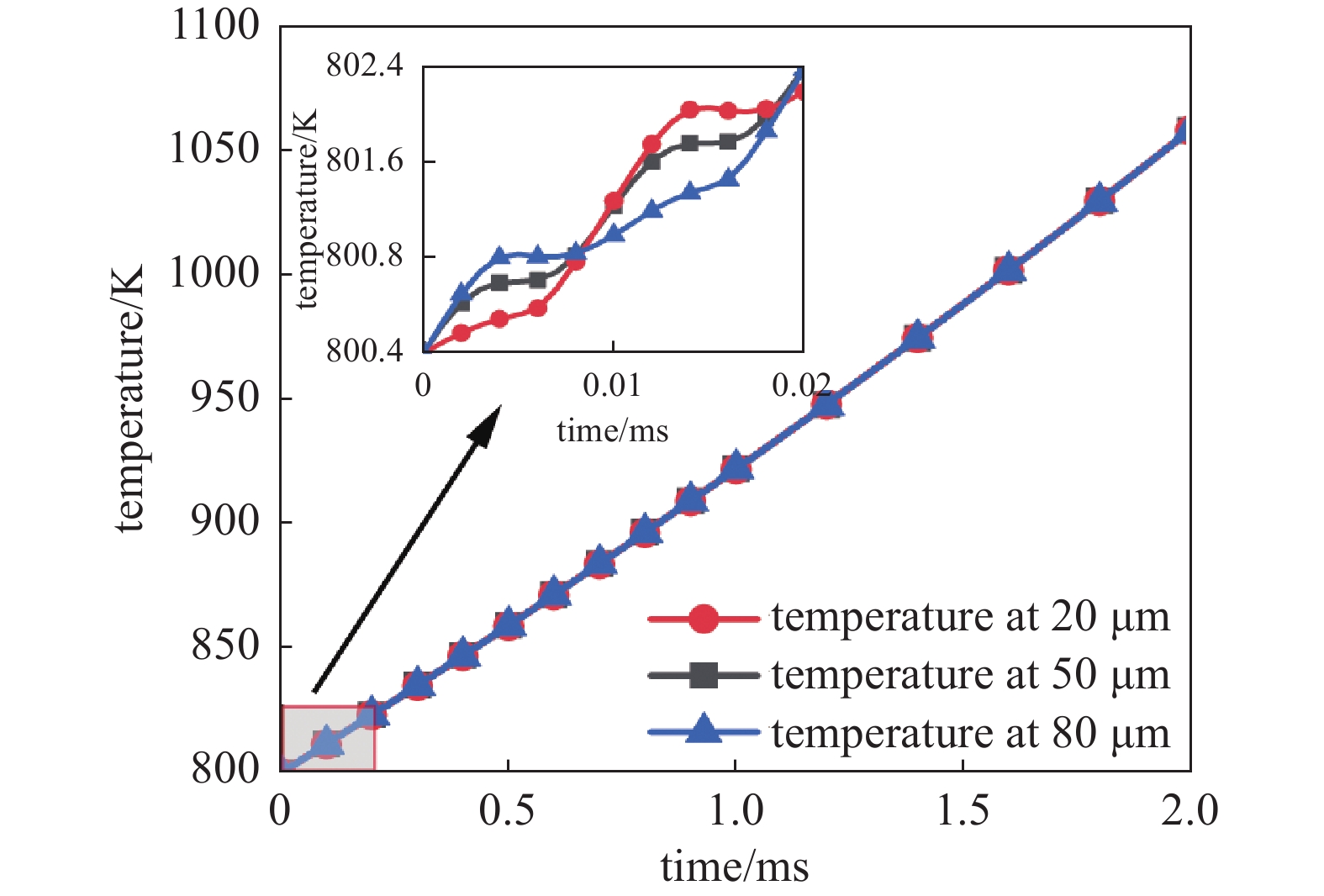
图4为2 ms时间内，10 kV电压下，CH4与O2摩尔比Φ为0.1时，不同位置处的温度变化情况。从图中可以看到，0.02 ms内，放电间隙中20 μm处、中间点处和80 μm处温度呈阶梯状上升趋势，主要是因为在电子密度增加阶段，等离子体对化学反应促进效果显著，放热反应明显加快，气体温度会快速上升；在两次放电的间隙电子密度保持在较低的位置，放热反应速率较慢，此时气体温度几乎保持不变。但在2 ms内可以发现它们之间的温度变化不大，差值在1 K以内，而中间点处工作气体燃烧温度变化较其他位置更为均匀，更能代表整个空间温度的变化趋势。据此，以下讨论中以放电间隙中间点位置温度代表整体放电温度。
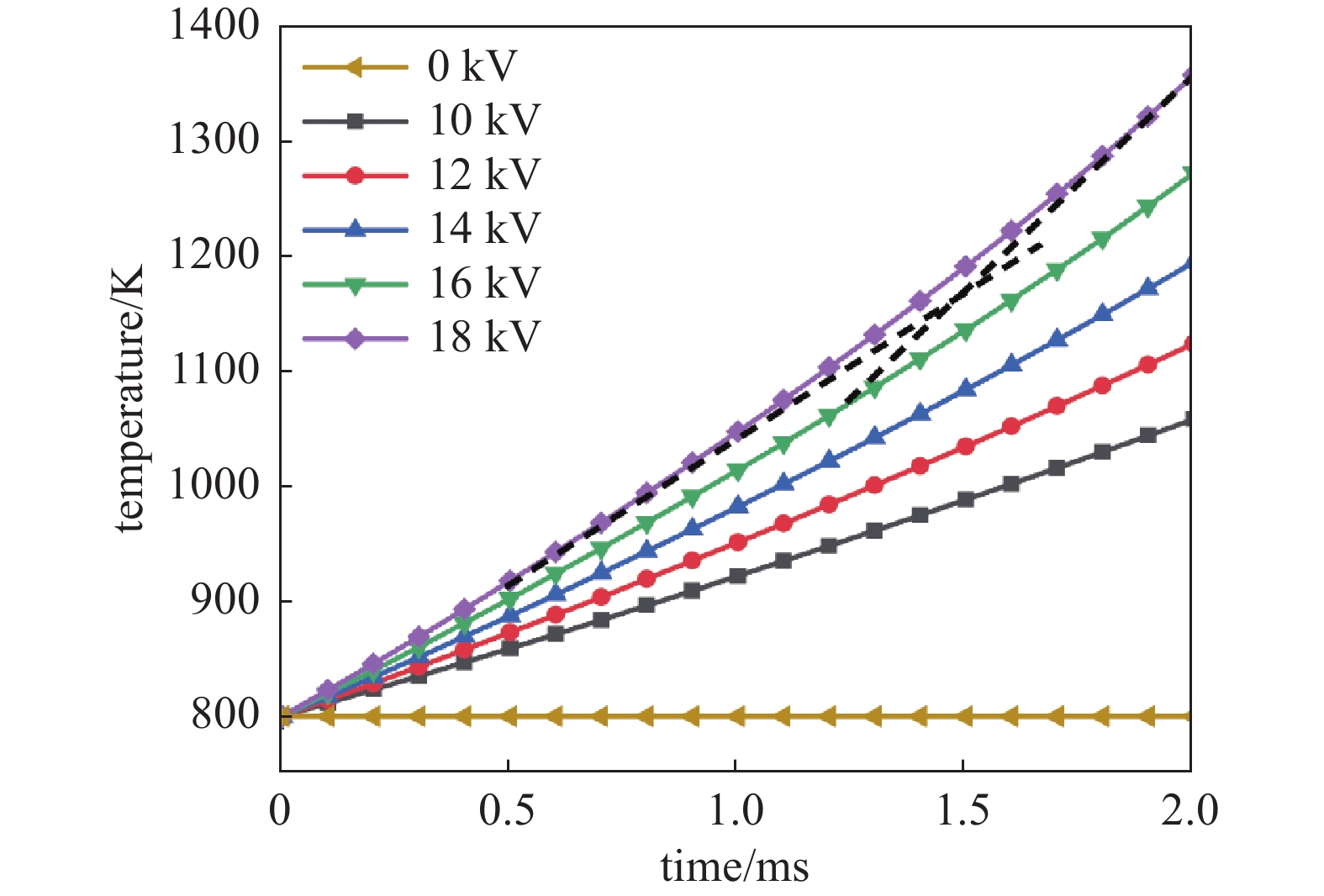
图5为 2 ms时间内，不同电压下，CH4与O2摩尔比Φ为0.1时，放电间隙中点温度随时间变化。图4中18 kV温度曲线根据其斜率变化近似可以分为两个阶段。大约在1.5 ms之前，气体温度增长较缓慢，温度从800 K上升至约1150 K。这一阶段由于等离子体放电产生大量活性基团，原本不会发生剧烈化学反应的过程也会产生少量的氧化反应，使气体温度缓慢上升。当气体温度到达1150 K后，CH4的燃烧过程将成为气体加热的主要热源，1.5~2 ms期间温度上升速度明显加快，温度从1150 K上升至1400 K。
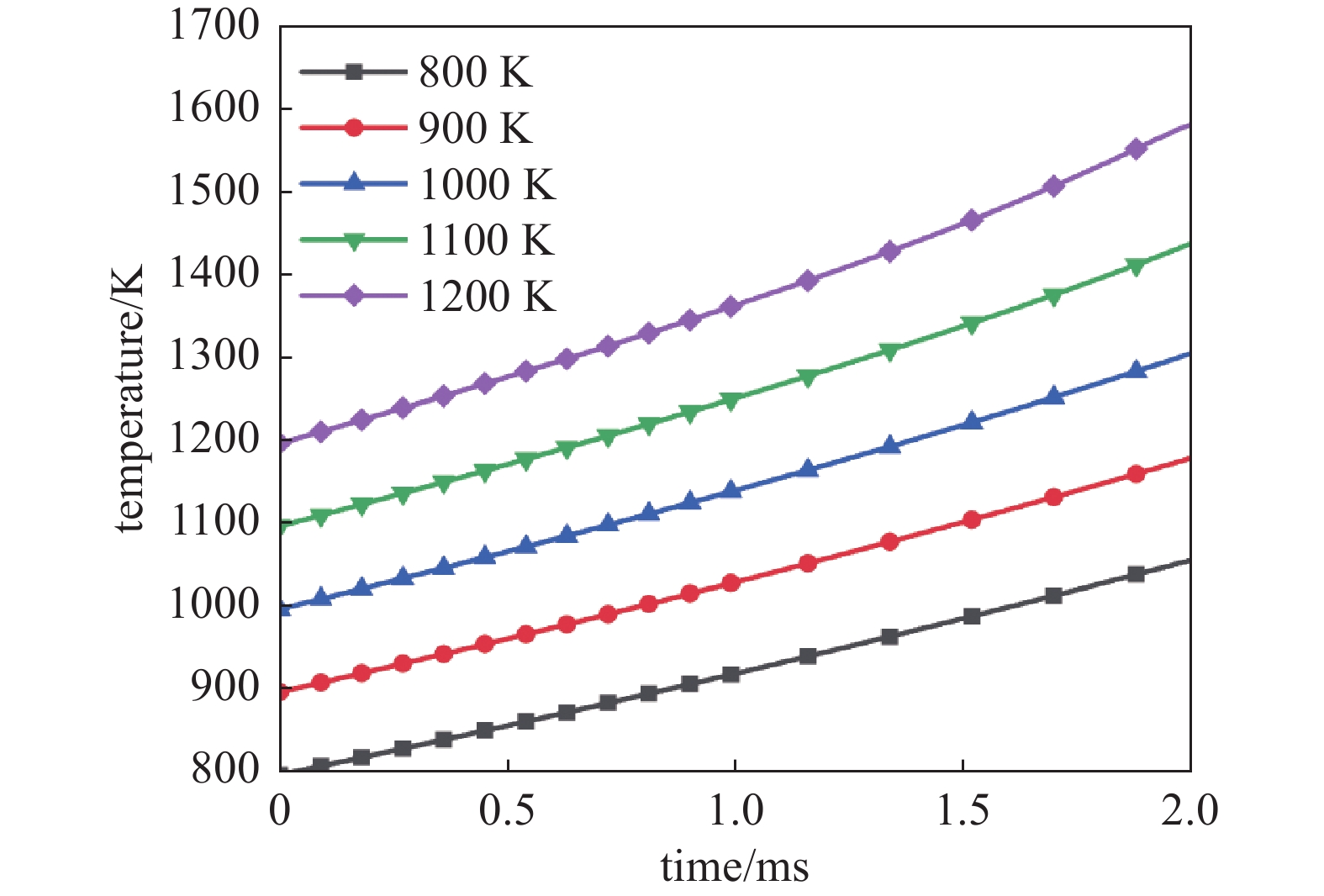
稀薄甲烷燃烧过程对温度非常敏感，工程上如果采用蓄热式氧化技术必须保持混合气体温度不少于1100 K。当采用DBD辅助燃烧技术时，初始温度对燃烧的影响并不大。图6为不同初始温度下稀薄甲烷燃烧中间点处温度变化。从图中可以看出，当初始温度在800~1200 K的范围内时，初始温度对燃烧温度上升斜率的影响非常小，换言之在这一阶段等离子体对燃烧的促进作用高于温度的影响。现在在工程上如果采用DBD非平衡态等离子体对稀薄甲烷空气燃烧过程进行辅助，可以在较低温度下进行点燃过程。后文计算中初始温度均为800 K。
-
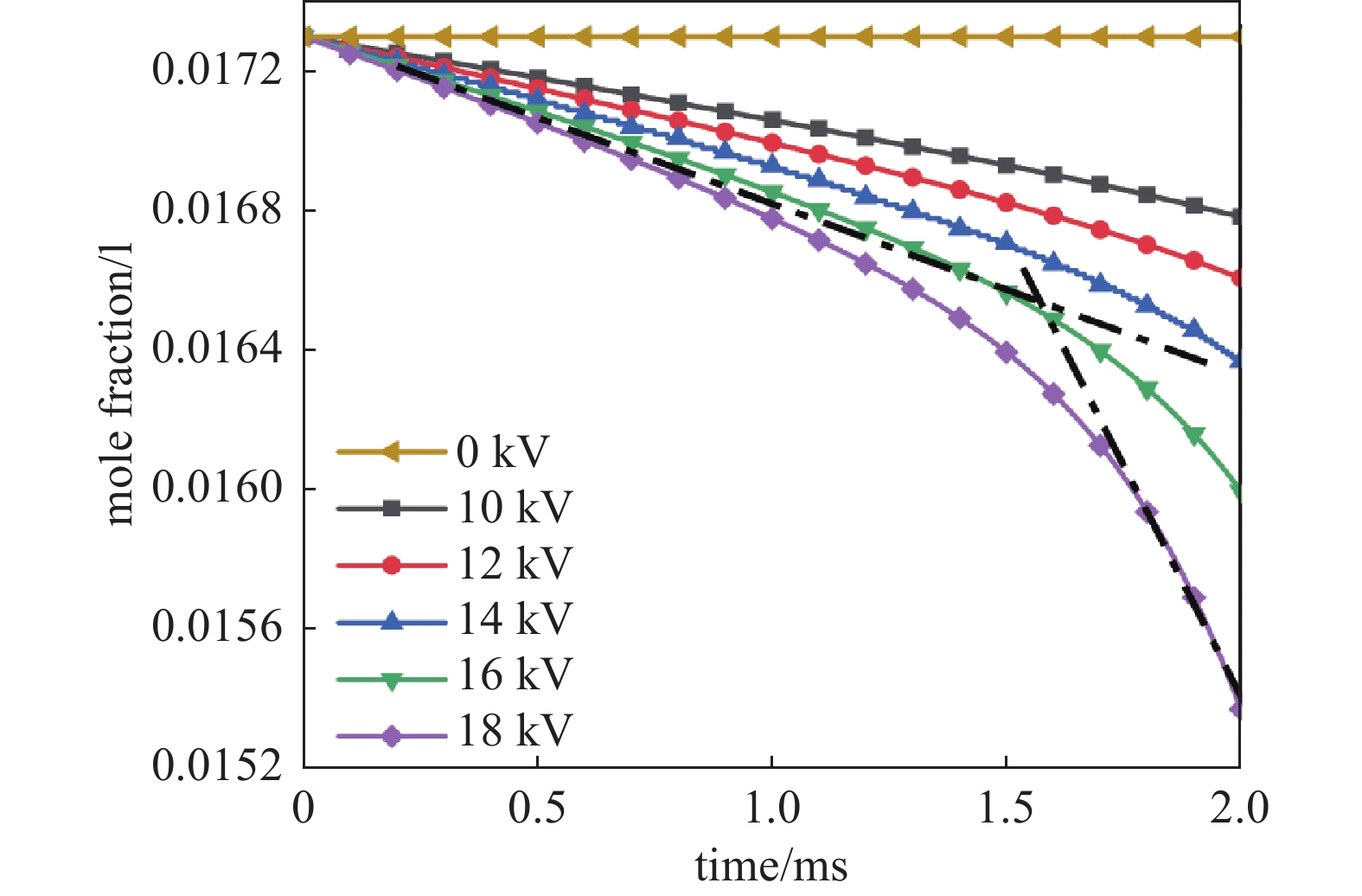
图7为在CH4与O2摩尔比Φ为0.1，放电2 ms时间内CH4的平均摩尔分数变化。从图7可以看出没有等离子体助燃时，不会发生燃烧反应，CH4的平均摩尔分数不发生变化。开始放电后，CH4的平均摩尔分数同样出现快速下降趋势，并且随着放电电压增加，下降速度加快。高放电电压情况下，CH4的摩尔分数变化呈现明显的快慢两个阶段，以外加电压幅值为18 kV为例，0~1.5 ms期间CH4的摩尔分数下降较慢，这一阶段主要受等离子体放电过程的影响，产生了大量活性基团，促进了化学反应，伴随着气体温度也缓慢升高；1.5 ms之后气体温度超过1250 K，CH4浓度下降速率显著增加，在这一阶段气体温度升高至CH4的点火温度，等离子体辅助作用相对减少，主要是由于燃烧过程消耗了大量CH4。
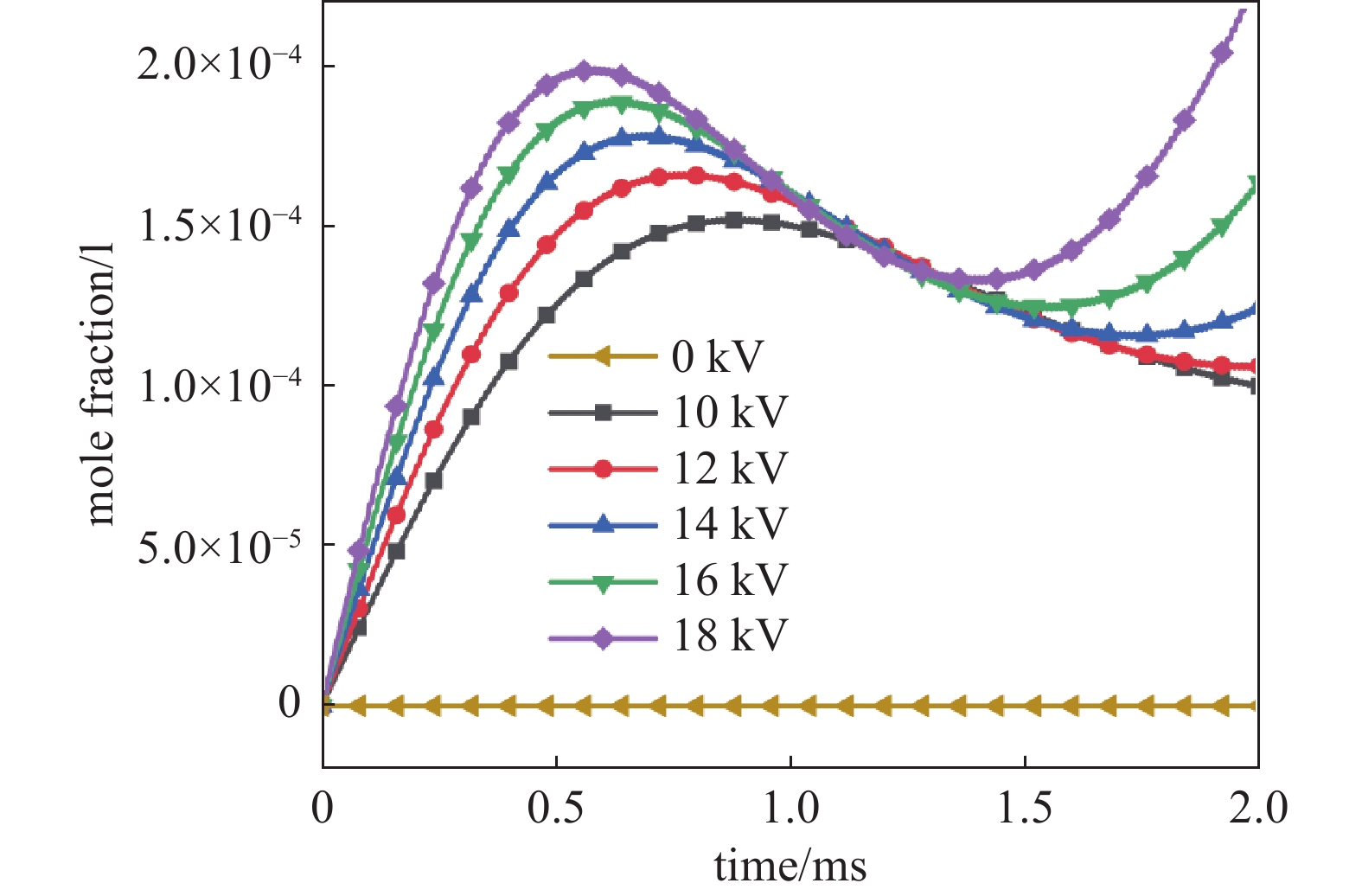
图8中CH3的平均摩尔分数的变化大体可以分为三个阶段。首先，当气体温度低于900 K时，CH3快速增加，随后在0.5~1.5 ms内CH3的摩尔分数又缓慢下降。在前两个阶段中，由于等离子体带来持续的反应过程，气体温度始终在上升。当气体温度超过1250 K之后，CH4三体反应明显加快，产生了大量CH3，因此其摩尔分数又开始快速增加。
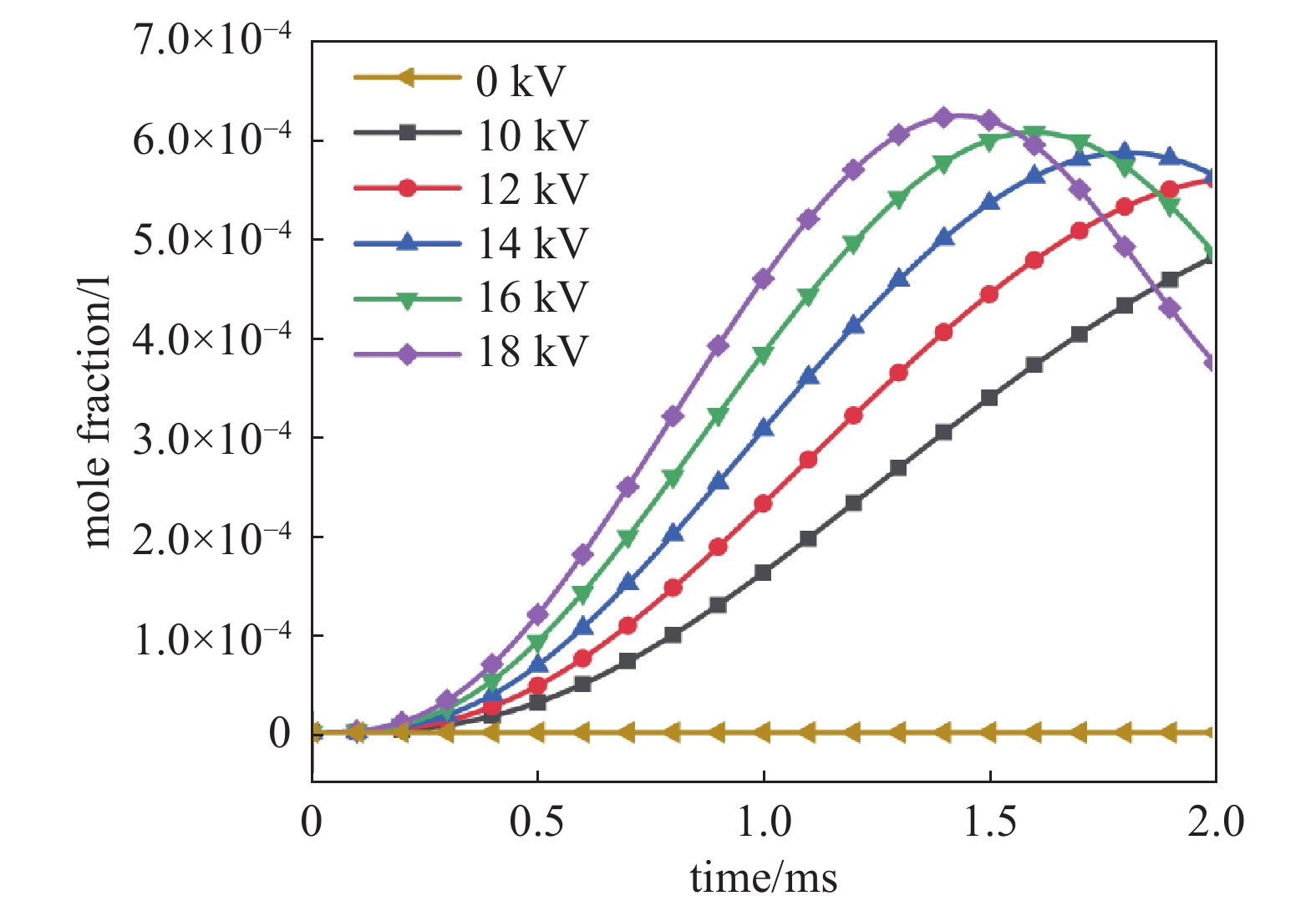
图9为CH3O平均摩尔分数的变化。如图所示，当电压为18 kV时，0~1.5 ms内CH3O摩尔分数快速上升达到峰值约6.5×10−4，1.5~3 ms内其摩尔分数又快速下降到3.5×10−4。在等离子体放电为主的阶段，CH3O快速积累，在温度升高后CH4开始快速燃烧后，CH3O是重要的反应物质被快速消耗。当放电电压较低时，由于气体温度升高较慢，前期CH3O的浓度升高速度也较慢。当放电电压为10~12 kV时，混合气体中的快速燃烧过程始终没有发生，CH3O摩尔分数在2 ms时仍未开始下降。
-
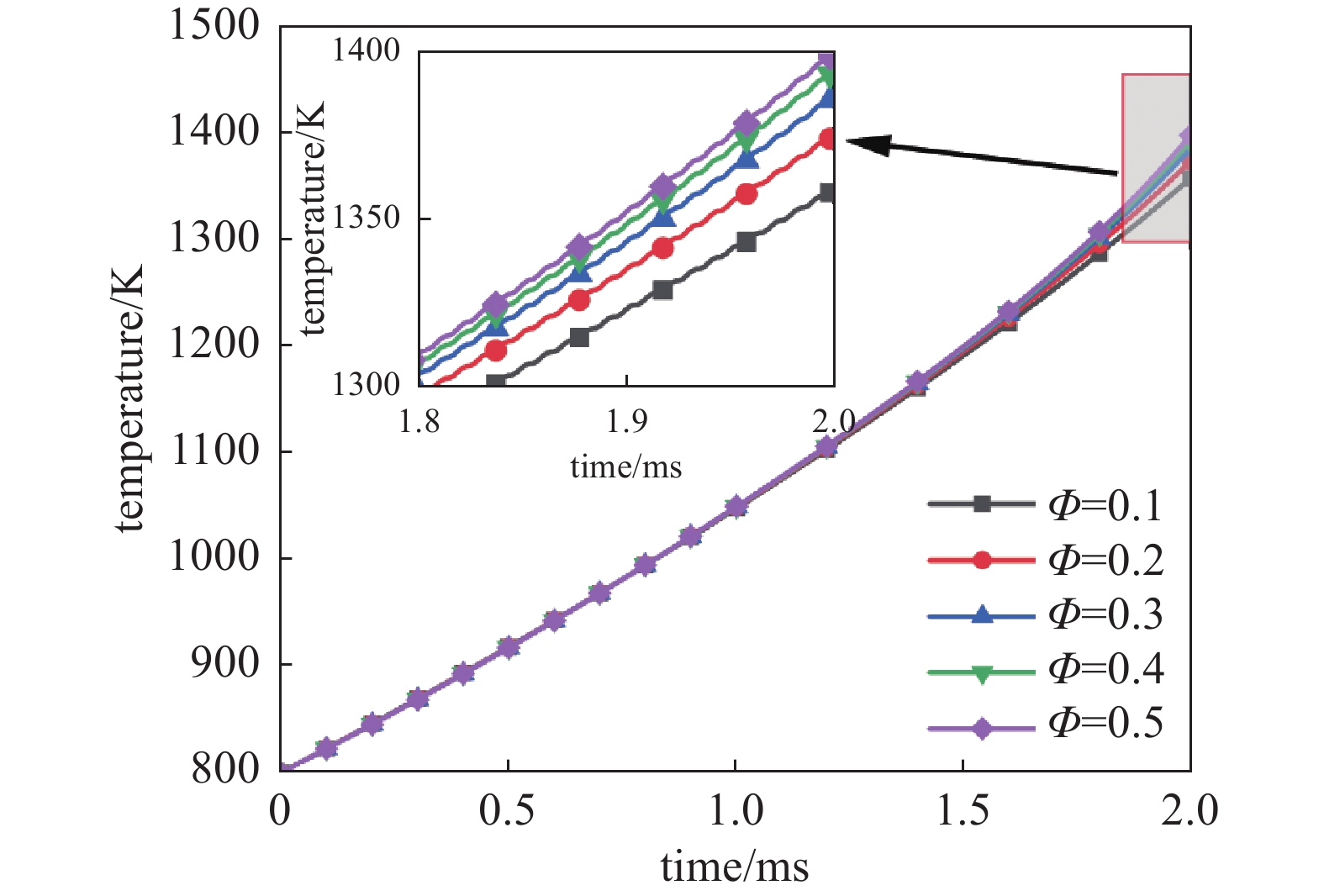
本节研究等离子体助燃条件下CH4与O2摩尔比对温度的影响。不同摩尔比工况和相应气体组成如如表3所示。图10为18 kV电压下， 2 ms内温度随摩尔比Ф的变化关系。从图中可以看到摩尔比Ф=0.1时，气体温度从800 K上升至1360 K；摩尔比Ф=0.5时，气体温度从800 K上升至1400 K，比前者提高约40 K。在点火阶段CH4与O2的摩尔比Ф对温度的影响较小。改变电压幅值后，发现该摩尔比Ф对燃烧的温度影响与图10类似；如果是放电电压更小的情况，这一差别将更小。
-
惰性气体Ar容易发生电离反应，是常用的等离子体放电气体。当工作气体中加入少量Ar，会降低击穿电压，提高电子数密度，增加放电的稳定性，在工程上补充Ar有可能会优化稀薄甲烷混合气体的燃烧情况。因此本节在稀薄甲烷混合气体等离子体反应的基础上(见表1)补充一组Ar的放电反应，通过数值模拟考察Ar含量对点燃过程的影响，为进一步优化等离子体辅助稀薄甲烷燃烧提供参考。增加的反应如表4所示，Ar的表面反应如表5所示。
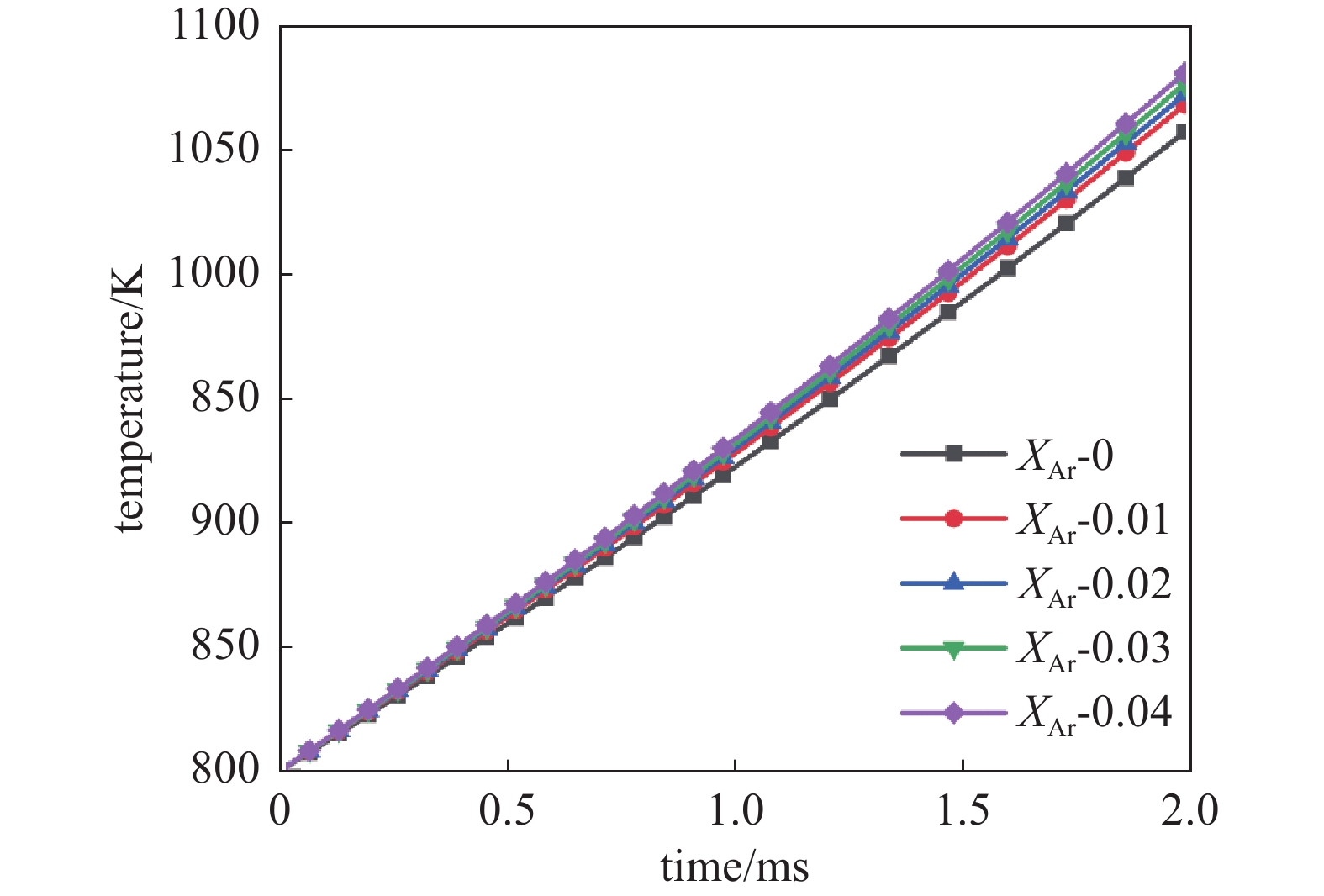
图11为10 kV电压下，摩尔比Ф=0.1时，2 ms内温度随Ar摩尔分数的变化情况。如图所示，当Ar摩尔分数为0时，甲烷-空气混合气体燃烧后温度从800 K上升至1050 K；当Ar摩尔分数为0.04时，甲烷-空气混合气体燃烧后温度从800 K上升至1080 K，比前者提高了30 K。说明Ar的含量对等离子体辅助甲烷-空气混合气体燃烧的具有一定的促进效果，但是影响并不大。需要指出由于本文整理的反应机理中，对激发态分子间的潘宁电离过程考虑较少，在实际过程中Ar 的影响可能会略大于本文结果。
-
本文采用一维流体模型对DBD非平衡态等离子体辅助稀薄甲烷-空气燃烧点火过程进行仿真，对等离子体与甲烷-空气燃烧反应机理进行了大幅简化，研究了电压电流放电特性和点火阶段主要活性粒子数密度变化以及探究了外加电压幅值、初始温度、Ar含量和甲烷氧气摩尔比对等离子体辅助燃烧的影响。本文模拟计算的时间和空间尺度都非常小，通过实验观测较为困难，通过本文理论计算其结果可以增加对该过程的了解。主要结论如下。
(1) 在DBD等离子体辅助稀薄甲烷-空气燃烧点火过程中，随着激励电压的加大，放电空间中电子数密度随之增加，电子数密度在靠近介质壁面约20 μm处达到最大值。
(2) 当初始温度为800 K时，稀薄甲烷-空气发生化学反应的速度很慢，但是加入DBD放电可以有效促进混合气体发生化学反应，典型的介质阻挡放电就可以使混合气体在2 ms气体温度最高可达1000~1400 K左右，即可以有效实现快速点火过程；在这一阶段等离子体对燃烧的促进作用高于温度的影响。
(3) 等离子体放电后，CH4的摩尔分数显著下降，下降速度受电子数密度影响明显。在2 ms内，当气体温度较低时，CH4的摩尔分数降低较慢，CH3首先快速增加达到极值后保持稳定，CH3O则持续快速积累；随着气体温度逐渐升高，剧烈燃烧过程消耗了大量CH4，同时CH3又开始快速增加，而CH3O被快速消耗。
(4) 在等离子体辅助甲烷-空气混合气体燃烧点火阶段，Ar的含量增加对燃烧的具有一定的促进效果，但是影响并不大，同时甲烷与O2摩尔比增加也会小幅增加燃烧温度，但是影响幅度较小。
介质阻挡放电辅助稀薄甲烷-空气燃烧点火过程的一维数值模拟
One-dimensional Numerical Simulation of the Ignition Process of Lean Methane-air Combustion Assisted by Dielectric Barrier Discharge
-
摘要: 非平衡态等离子体可以辅助稀薄甲烷-空气燃烧，但是目前对该过程的数值模拟尚不深入。本文建立了简化的等离子体辅助甲烷燃烧反应机理，并采用一维流体模型对微尺度DBD非平衡态等离子体辅助稀薄甲烷-空气燃烧过程进行数值模拟。模拟结果显示，等离子体放电可以在较低的初始温度下有效促进燃烧反应的发生，并且随着放电电压增加，放电空间中电子数密度明显增加，同时有效提高了燃烧温度。数值模拟结果可以反映主要活性粒子的变化趋势。在该阶段中，Ar含量增加或者CH4与O2摩尔比增加都会小幅增加燃烧温度，但是影响幅度较小。本研究结果增进了对该过程的了解。Abstract: Non-equilibrium plasma can assist lean methane-air combustion, but the numerical simulation of this process is not yet in-depth. This paper establishes a simplified plasma-assisted methane combustion mechanism, and a one-dimensional fluid model is used to simulate the micro-scale DBD non-equilibrium plasma-assisted lean methane-air combustion process. The simulation results show that plasma discharge can effectively promote the combustion reaction at a lower initial temperature. With the increase of discharge voltage, the number density of electrons in the discharge space increases significantly, and the combustion temperature is effectively increased. The numerical simulation results can reflect the changing trend of the primary active particles. In this stage, the increase of Ar content or the molar ratio of CH4 to O2 will slightly increase the combustion temperature, but the impact is negligible. The results of this study enhance the understanding of this process.
-
-
图 2 外加电压为10 kV时电压和电流密度变化
Figure 2. Change of voltage and current density with the applied voltage 10 kV
图 3 不同电压下0.04 ms内电子数密度的时空分布。(a) 外加电压为10 kV; (b) 外加电压为18 kV
Figure 3. The spatial-temporal distribution of electron density in 0.04 ms with different voltages. (a) Applied voltage is 10 kV, (b) applied voltage is 18 kV
图 4 放电电压10 kV，不同位置处放电空间中的温度随时间的变化
Figure 4. The discharge voltage is 10 kV, and the temperature in the discharge space at different positions changes with time
图 5 不同电压下，放电空间中间点温度变化
Figure 5. The temperature change of the midpoint of the discharge space with different applied voltages
图 6 不同初始温度时，放电空间中间点温度变化
Figure 6. The temperature change of the midpoint of the discharge space with different initial temperatures
图 7 不同电压下，CH4的平均摩尔分数变化
Figure 7. Change of average mole fraction of CH4 with different applied voltages
图 8 不同电压下，CH3的平均摩尔分数变化
Figure 8. Change of average mole fraction of CH3 with different applied voltages
图 9 不同电压下，CH3O的平均摩尔分数随时间变化
Figure 9. Change of average mole fraction of CH3O with different applied voltages
图 10 放电电压18 kV，不同CH4与O2摩尔比时放电空间中间点温度的变化
Figure 10. Change of temperature at the middle point of discharge
图 11 放电电压10 kV，不同Ar摩尔分数时放电空间中间点温度的变化
Figure 11. Change of temperature at the middle point of discharge space with different Ar mole fractions at a discharge voltage of 10 kV
表 1 DBD非平衡态等离子体辅助甲烷燃烧反应简化机理
Table 1. Simplified mechanism of DBD non-equilibrium plasma assisted methane combustion reaction
序号 反应 A(Kg,cm,K,mol)a,b nc Ea/(cal·mol−1)c Δε/(eV)d Ref. R1 CH4(+M)=>CH3+H(+M)e — [4]
kf
kf0
6.30×1014
1.00×1017
0
0
104000
86000R2 CH3+H(+M)=>CH4(+M)e — [4] kf
kf05.20×1012
8.25×10140
0−1310
−19310R3 CH4+H=>CH3+H2 2.2×104 3 8750 — [4] R4 CH3+H2=>CH4+H 9.57×102 3 8750 — [4] R5 CH4+OH=>CH3+H2O 1.60×106 2.1 2460 — [4] R6 CH3+H2O=>CH4+OH 3.02×105 2.1 17422 — [4] R7 CH3+O=>CH2O+H 6.80×1013 0 0 — [4] R8 CH3+O2=>CH3O+O 5.00×1013 0 25652 — [4] R9 CH3+OH=>CH2+H2O 7.60×106 2 5000 — [4] R10 CH3O+H=>CH2O+H2 2.00×1013 0 0 — [4] R11 CH3O+M=>CH2O+H+M 2.40×1013 0 28812 — [4] R12 CH2+O=>CO+H2 3.00×1013 0 0 — [4] R13 CH2+OH=>CH+H2O 1.13×107 2 3000 — [4] R14 CH2O+H=>HCO+H2 9.00×1013 0 3991 — [4] R15 CH2O+OH=>HCO+H2O 3.00×1013 0 1195 — [4] R16 CH+O=>CO+H 5.70×1013 0 0 — [4] R17 CH+OH=>HCO+H 3.00×1013 0 0 — [4] R18 CH+O2=>HCO+O 3.30×1013 0 0 — [4] R19 CH+CO2=>HCO+CO 8.40×1013 0 200 — [4] R20 HCO+H=>CO+H2 4.00×1013 0 0 — [4] R21 HCO+M=>CO+H+M 1.60×1014 0 14700 — [4] R22 CO+OH=>CO2+H 1.51×107 1.3 −758 — [4] R23 CO2+H=>CO+OH 1.57×109 1.3 21000 — [4] R24 O2+H=>O+OH 1.55×1014 0 16800 — [4] R25 O+OH=>O2+H 1.20×1013 0 690 — [4] R26 O+H2=>OH+H 1.80×1010 1 8826 — [4] R27 OH+H=>O+H2 8.00×109 1 6760 — [4] R28 OH+H2=>H2O+H 1.17×109 1.3 3626 — [4] R29 H+H2O=>OH+H2 5.09×109 1.3 18588 — [4] R30 OH+OH=>O+H2O 6.00×108 1.3 0 — [4] R31 O+H2O=>OH+OH 5.90×109 1.3 17029 — [4] R32 H+O2+M=>HO2+Me 1.60×1018 0.8 0 — [4] R33 H+HO2=>OH+OH 1.50×1014 0 1004 — [4] R34 H+HO2=>H2+O2 2.50×1013 0 700 — [4] R35 OH+HO2=>H2O+O2 2.00×1013 0 1000 — [4] R36 HO2+HO2=>H2O2+O2 8.00×1013 0 0 — [4] R37 H2O2+M=>OH+OH+M 1.30×1017 0 45500 — [4] R38 OH+OH+M=>H2O2+M 9.86×1014 0 −5070 — [4] R39 H2O2+OH=>HO2+H2O 1.00×1013 0 1800 — [4] R40 H2O+HO2=>H2O2+OH 2.86×1013 0 32790 — [4] R41 OH+H+M=>H2O+M 2.20×1022 −2 0 — [4] R42 H+H+M=>H2+M 1.80×1018 −1 0 — [4] R43 O2+O+M=>O3+M 8.60×1013 0 721.3 — [4] R44 O3+O2=>O2+O+O2 1.54×1014 0 2.306 $ \times $ 104— [4] R45 O3+N2=>O2+O+N2 4.00×1014 0 2.267 $ \times $ 104— [4] R46 O3+O=>O2+O+O 2.48×1015 0 2.273 $ \times $ 104— [4] R47 O3+O3=>O2+O+O3 4.40×1014 0 2.306 $ \times $ 104— [4] R48 O2+O+O3=>O3+O3 1.67×1015 −0.5 −1391 — [4] R49 O3+H=>O2+OH 8.43×1013 0 933.9 — [4] R50 O3+H=>O+HO2 4.52×1011 0 0 — [4] R51 O3+OH=>O2+HO2 1.85×1011 0 831 — [4] R52 O3+H2O=>O2+H2O2 6.62×1001 0 0 — [4] R53 O3+HO2=>OH+O2+O2 6.62×1009 0 993.9 — [4] R54 O3+O=>O2+O2 4.82×1012 0 4094 — [4] R55 O3+CH3=>CH3O+O2 5.83×1010 0 0 — [4] R56 e+O2=>e+O2* ke1 — — 1.627 [8] R57 O2*+H=>OH+O 4.0×1013 0 1.4 $ \times $ 104— [4] R58 OH+O=>H+ O2* 5.80×1012 0 2.454 $ \times $ 104— [4] R59 CH3+ O2*=>CH3O+O 2.11×1013 0 1.4372 $ \times $ 104— [4] R60 O2*+M=>O+O+M 5.82×1021 0 9.539 $ \times $ 104— [4] R61 O2*+H2=>H+HO2 3.28×1017 0 3.619 $ \times $ 104— [4] R62 O2*+OH=>O+HO2 2.39×1016 0 3.396 $ \times $ 104— [4] R63 O2*+CO=>O+CO2 1.0×1012 0 1.5 $ \times $ 104— [4] R64 O2*+CH4=>CH3+HO2 7.59×1013 0 3.616 $ \times $ 104— [4] R65 CH+O=>HCO++e 3.00×1011 0 1.5 $ \times $ 104— [4] R66 HCO++H2O=>H3O++CO 5.00×1015 0 4000 — [4] R67 H3O++e=>H2O+H 2.29×1018 −0.5 2000 — [4] R68 H3O++e=>H2+OH 10.25×1019 −0.5 4000 — [4] R69 O2+e=>O+O+e ke2 — — 12.06 [8] R70 H2O+e=>H2+O+e ke3 — — 13.0 [8] R71 CO2+e=>CO+O+e ke4 — — 6.5 [8] R72 H2+e=>H+H+e ke5 — — 8.9 [8] R73 CH4+e=>CH3+H+e ke6 — — 10.0 [8] R74 e+O2=>e+e+O2+ ke7 — — 12.06 [8] R75 CH4+e=>CH3++e+e ke8 — — 12.6 [8] R76 CH3+e=>CH3++e+e ke9 — — 10.0 [8] R77 O2++e=>O+O 3.6132×1019 −1 0 — [4] R78 CH4++e=>CH3+H 3.0712×1019 −0.5 0 — [4] R79 CH4++e=>CH2+H+H 3.0712×1019 −0.5 0 — [4] R80 CH3++e=>CH2+H 6.3231×1019 0.5 0 — [4] R81 N2++N2+O2=>N4++O2 1.81×107 0 0 — [7] R82 N2++N2+N2=>N4++N2 1.81×107 0 0 — [7] R83 N4++O2=>O2++N2+N2 1.51×108 0 0 — [7] R84 N2++O2=>O2++N2 3.61×107 0 0 — [7] R85 O2++N2+N2=>N2O2++N2 3.26×105 0 0 — [7] R86 N2O2++N2=>O2++N2+N2 2.58×108 0 0 — [7] R87 N2O2++O2=>O4++N2 6.02×108 0 0 — [7] R88 O2++O2+N2=>O4++N2 8.69×105 0 0 — [7] R89 O2++O2+O2=>O4++O2 8.69×105 0 0 — [7] R90 O2−+O4+=>3O2 6.02×1010 0 0 — [7] R91 O2−+O4++O2=>3O2+O2 7.25×1010 0 0 — [7] R92 O2−+O4++N2=>3O2+N2 7.25×1010 0 0 — [7] R93 O2−+O2++N2=>2O2+N2 7.25×1010 0 0 — [7] R94 O2−+O2++O2=>2O2+O2 7.25×1010 0 0 — [7] R95 O+O2+O2=>O3+O2 9.06×101 0 0 — [7] R96 O+O2+N2=>O3+N2 9.06×101 0 0 — [7] R97 e+O4+=>2O2 8.43×1011(300/Te)5 0 0 — [7] R98 e+O2+O2=>O2+O2− 7.25×106(300/Te) 0 0 — [7] R99 e+N2=>e+e+N2+ ke10 — — 15.6 [8] R100 e+N2=>e+N2 ke11 — — — [8] R101 e+O2=>e+O2 ke12 — — — [8] a 反应速率系数ke1- ke12用电子碰撞截面σk[8]和电子能量分布函数计算；
b 表中R1-R101中二体反应速率系数单位为cm3·s−1·mol−1，三体反应速率系数单位为cm6·s−2·mol−2，Te的单位是K[3]；
c n为指数，Ea的单位为cal·mol−1；
d Δε为电子碰撞反应中损失的电子能量，单位为eV；
e 三体反应：CH4，6.5；CO，0.75；CO2，1.5；H2，1；H2O，6.5；N2，0.4；O2，0.4。
下载: 导出CSV
表 2 混合气体表面反应
Table 2. Surface reaction of mixed gas
序号 表面反应 γse 序号 表面反应 γse 1 N2+=>N2 0.1 7 CH3+=>CH3 0.1 2 O2+=>O2 0.1 8 HCO+=>HCO 0.1 3 N4+=>2N2 0.1 9 H3O+=>H3O 0.1 4 O4+=>2O2 0.1 10 H2O+=>H2O 0.1 5 N2O2+=>N2O2 0.1 11 O2*=>O2 0 6 CH4+=>CH4 0.1 12 O2−=>O2 0
下载: 导出CSV
表 3 气体组分
Table 3. Gas composition
Ф CH4占比 CO2占比 O2占比 N2占比 0.1 1.74% 1.74% 17.36% 79.17% 0.2 2.96% 2.96% 14.79% 79.30% 0.3 3.87% 3.87% 12.88% 79.39% 0.4 4.57% 4.57% 11.41% 79.46% 0.5 5.12% 5.12% 10.24% 79.51%
下载: 导出CSV
-
[1] Bechane Y, Fiorina B. Numerical analysis of turbulent flame enhancement by nanosecond repetitively pulsed plasma discharges[J/OL]. Proceedings of the Combustion Institute, (2022-7-26) [2022-11-1]. https://www.sciencedirect.com/science/article/pii/S1540748922000293. [2] Barleon N, Cheng L, Cuenot B, et al. Investigation of the impact of NRP discharge frequency on the ignition of a lean methane-air mixture using fully coupled plasma-combustion numerical simulations[J/OL]. Proceedings of the Combustion Institute, (2022-8-17) [2022-11-1]. https://www.sciencedirect.com/science/article/pii/S1540748922000797. [3] Li S,Wang X B,Liu Y,et al. Numerical analysis of the effect of surface recombination on N-atom in discharge and post-discharge region[J]. Physics of Plasmas,2020,27(6):063502 doi: 10.1063/5.0006986 [4] Larsson A,Zettervall N,Hurtig T,et al. Skeletal Methane-Air Reaction Mechanism for Large Eddy Simulation of Turbulent Microwave-Assisted Combustion[J]. Energy & Fuels,2017,31(2):1904−1926 [5] Smith G P, Golden D M, Frenklach M, et al. GRI-Mech 3.0 home page [EB/OL]. (1999-7-30) [2022-11-1]. http://www.me.berkeley.edu/grimech. [6] Wang Z H,Yang L,Li B,et al. Investigation of combustion enhancement by ozone additive in CH4/air flames using direct laminar burning velocity measurements and kinetic simulations[J]. Combustion and Flame,2012,159(1):120−129 doi: 10.1016/j.combustflame.2011.06.017 [7] Pancheshnyi S,Nudnova M,Starikovskii A,et al. Development of a cathode-directed streamer discharge in air at different pressures: Experiment and comparison with direct numerical simulation[J]. Physical Review E,2005,71(1):016407 doi: 10.1103/PhysRevE.71.016407 [8] LXcat Electron Scattering Database [EB/OL]. (2022-10-24) [2022-11-1]. http://www.lxcat.laplace.univ-tlse.fr/. [9] Golubovskii Y B,Maiorov V A,Behnke J,et al. Modelling of the homogeneous barrier discharge in helium at atmospheric pressure[J]. Journal of Physics D:Applied Physics,2002,36(1):39−49 [10] Li S,Wang Y,Wang L. Numerical study on pulse modulated RF argon discharge at atmospheric pressure[J]. Nuclear Fusion and Plasma Physics,2021,41(04):591−597 (李帅星,王一男,王莉. 大气压脉冲调制射频氩气放电等离子体特性的数值研究[J]. 核聚变与等离子体物理,2021,41(04):591−597(in chinese) doi: 10.16568/j.0254-6086.202104002 Li S, Wang Y, Wang L. Numerical study on pulse modulated RF argon discharge at atmospheric pressure [J]. Nuclear Fusion and Plasma Physics, 2021, 41(04): 591-597. doi: 10.16568/j.0254-6086.202104002 -
计量
- 文章访问数: 32
- HTML全文浏览数: 32
- PDF下载数: 1
- 施引文献: 0