四极杆组件是由4根平行对称的杆电极组成，正对的极杆两两相连形成两组电极，相对极杆间最小距离为2r₀，r₀称为场半径。设四极杆组件截面中心为坐标原点，令x轴方向上的两根极杆电位为Φ，y轴方向上的两根极杆电位为−Φ（Φ= U+Vcoswt，U和V分别为四极杆上施加电压的直流分量和交流分量的幅值，w为角速度，t为时间）。

电极空间任一点（x,y）上的电位为

式中，Φ为t时刻（x,y）点的电位。

质荷比M=m/e的离子沿z轴进入四极场，将受电场作用，其运动方程为

式中，m为离子质量，e为离子电荷。

可以看出，由于Φ是随时间周期性变化的，则离子在四极场中x、y方向作振荡运动，z方向作匀速运动。

令

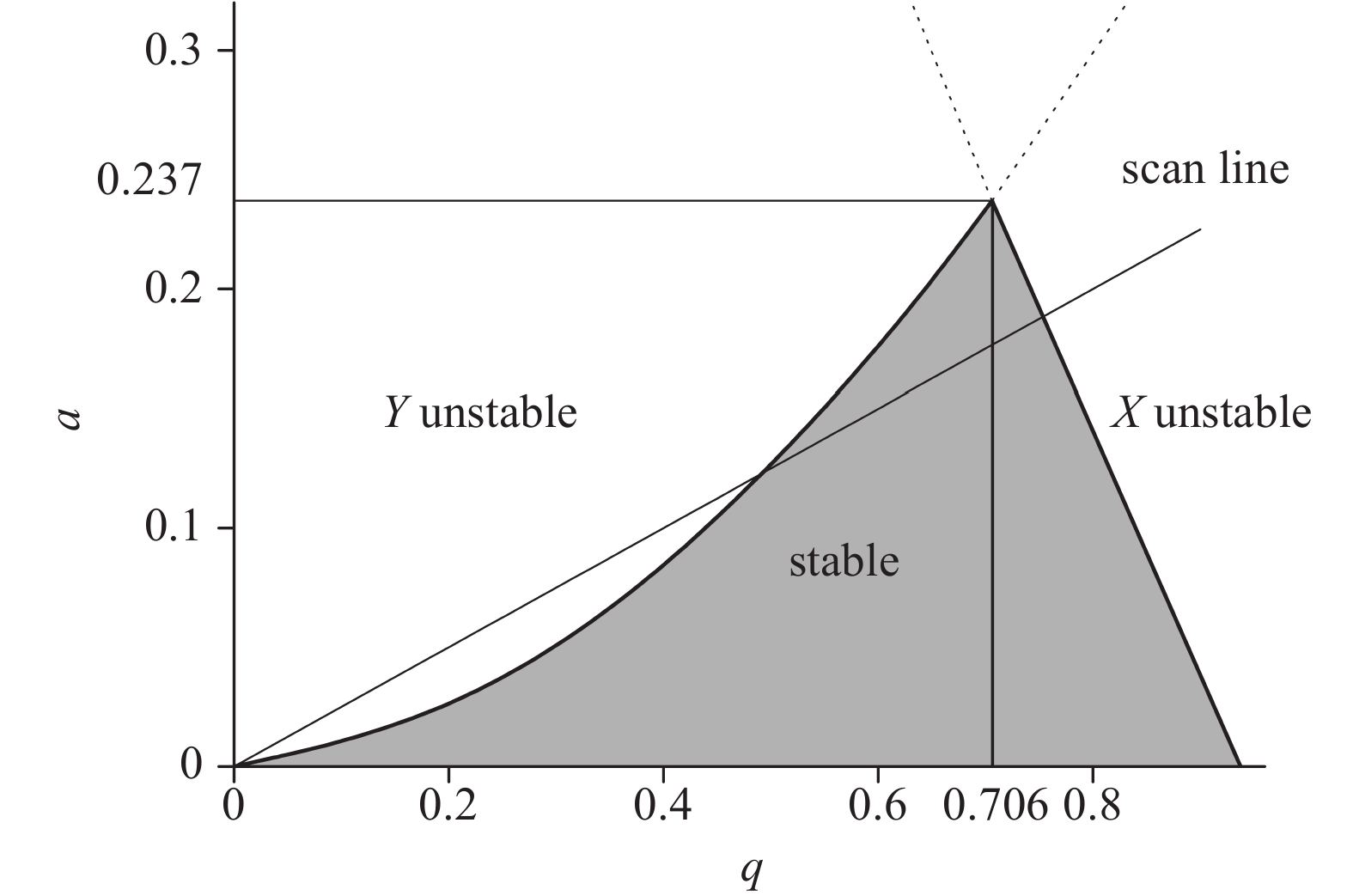
将式（3）代入式（2）并求解，得到离子的第一稳定区如图1所示。

当选定U、V的比值后，在稳定图上会形成一条通过原点的直线，称作质量扫描线。扫描线切割稳定区于两个交点，只有位于交点之间质荷比的离子，才能以有限的振幅通过四极场，到达离子检测器；而其他离子在x或y方向作增幅振荡，最终与四极杆碰撞被收集或移出电场区，不能到达离子检测器。这就是四极场实现质量分析的原理。

当扫描线通过稳定区顶点时交点变为一个，此时最佳的分辨率但离子通过率极低，顶点坐标为（0.237,0.706），相应的U/V=0.1678。

四极电场的模拟方法主要有以下三种。

直接数值计算法，其代表软件为MATLAB。该方法是根据离子在四极场内的运动方程，采用如四阶Runge-Kutta法等进行微分方程求解，得到离子不同时刻位置和速度^[8]。该方法计算精度较高，但计算速度较慢。

有限差分网格计算（FDM）方法，代表软件为SIMION^[9]。该方法通过有限差分法求解拉普拉斯方程，从而得到空间内的电场分布；确定离子的初始位置和速度后，就可以得到任意时刻离子的位置和速度。SIMION软件允许用户自行设计电极，可以模拟复杂装置的离子轨迹模拟。

有限元网格计算（FEM）方法，代表软件为COMSOL^[10]。该方法通过将模型划分为网格，先计算四极电场，然后通过电场数据驱动计算离子轨迹。COMSOL适用于多物理场的耦合计算。

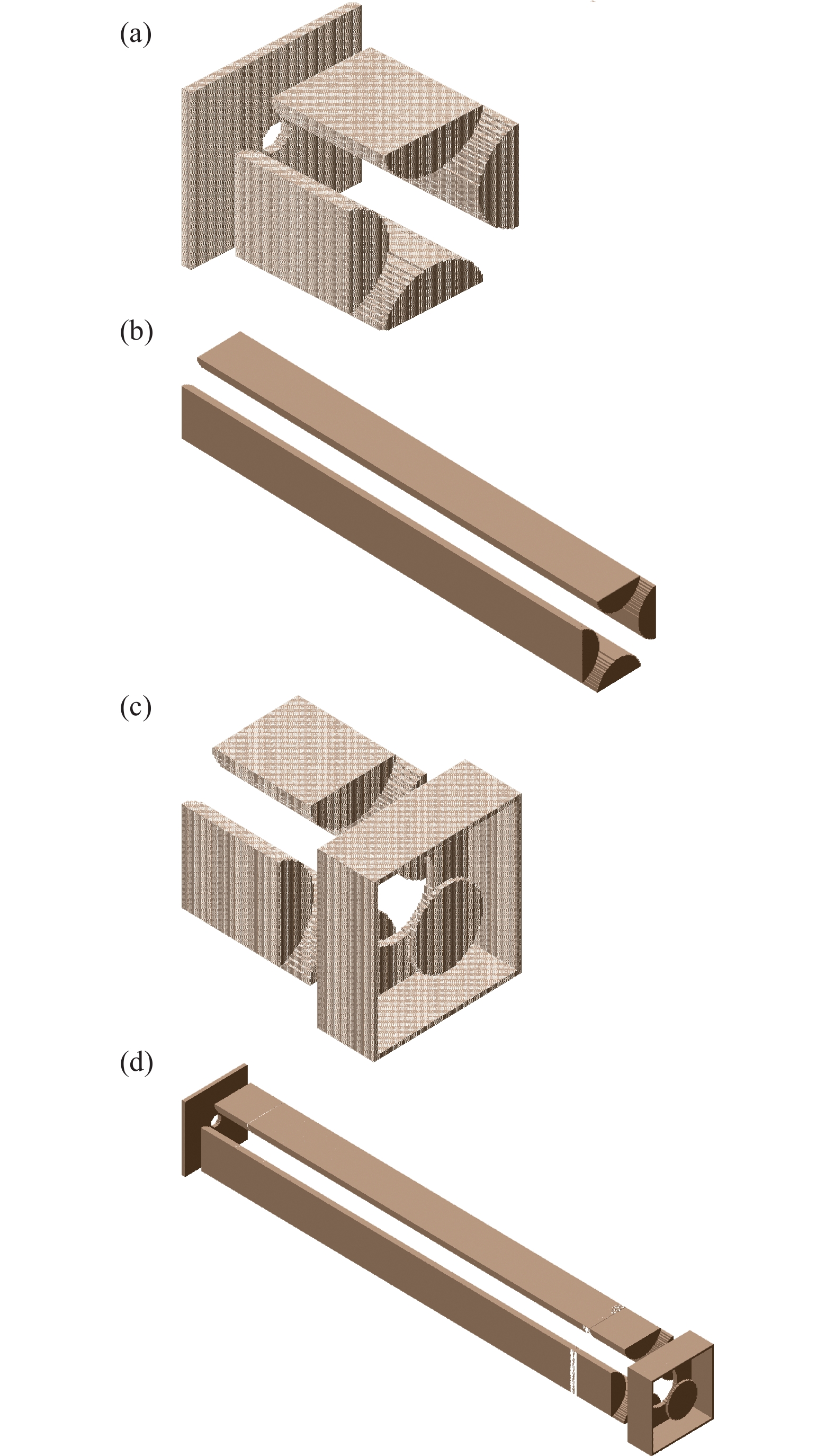
为了研究不同尺寸结构四极杆组件对性能的影响，采用SIMION进行了建模。考虑到边缘场的影响，模型包括了离子入射透镜、四极杆组件和离子出射透镜。由于四极杆组件较长且为平面对称结构，完全采用3D电势阵列建模对计算机RAM的需求会急剧上升，因此采用如下方案进行模型的建立。

将四极杆组件切割为三段，首尾两段分别随入射透镜和出射透镜建立3D电势阵列，中间一段建立为2D电势阵列，从而形成一个完整的四极杆组件研究模型。所建立模型如图2所示。

仿真模型参数如表1所示。

质谱计的灵敏度和分辨率是表征仪器性能的重要指标。灵敏度是四极质谱计离子检测器收集离子信号强度与被测气体分压力之比，这里只讨论四极场的影响，可以用离子通过率来表征。分辨率是四极质谱计分辨不同质荷比离子能力的量度，采用50%峰高处的∆m（Full Width at Half Maxima, FWHM）来表征。

当前实际四极质谱计多采用等峰宽电路以在不同质荷比离子处达到近似相等的分辨率，而文中仿真在全质量范围采用了恒定的直交比，这一点是需要特别注意以免混淆的。

分别采用5 gu/mm、10 gu/mm和20 gu/mm网格密度对Φ8 mm×100 mm四极杆组件进行建模，保持其他参数一致，则三种网格密度模型在1~1000 u质量范围的离子通过率如图3所示。

由图3可知，三种网格密度模型在5~500 u区间离子通过率基本一致，该区域之外则10 gu/mm和20 gu/mm模型离子通过率大于5 gu/mm模型，且5 gu/mm曲线在800 u处的凸起在另外两条曲线中前移至700 u；10 gu/mm和20 gu/mm曲线离子通过率在1~1000 u基本一致，因此可以认为对于离子轨迹的计算，10 gu/mm网格密度已经能够满足计算精度，文中仿真均采用10 gu/mm模型。

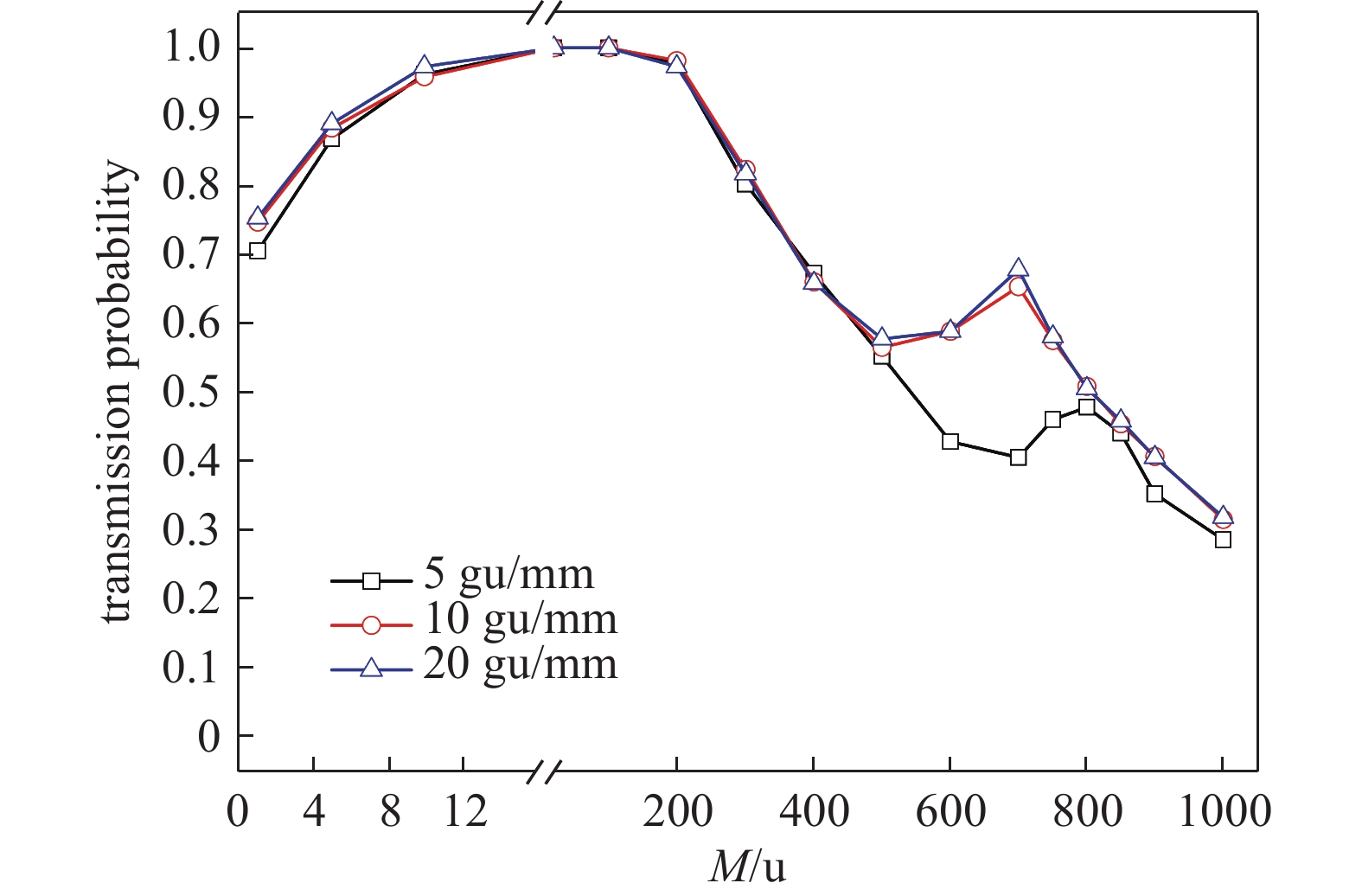
场半径直接影响四极质谱计的径向尺寸，对仪器的选择有重要影响。改变场半径，固定其他参数，U/V=0.97×0.1678=0.1628，仿真计算离子通过率，取U/V=0.99×0.1678=0.1661，仿真计算分辨率，其结果如图4所示。

由图4(a)可知，不同场半径下在20~200 u间离子通过率均接近100%，表明在所选定的直交比下场半径对中间质荷比离子通过率影响不大；低质荷比段，离子通过率随场半径增加而增大，场半径为8 mm时1 u离子通过率达到1。与r₀=3 mm模型相比，r₀=4 mm、r₀=8 mm模型1 u处通过率分别增大42%和90%，表明大场半径有利于低质荷比离子传输；高质荷比段，r₀=8 mm模型通过率最低，1000 u处相比r₀=3 mm模型减小22%，这可能来源于边缘场的影响，场半径3 mm和4 mm模型曲线基本一致，但4 mm在650 u处有凸起，经多次重复仿真，该现象始终存在。目前尚无恰当的解释。

由图4(b)可知，r₀=3 mm和r₀=4 mm模型在1~200 u分辨率曲线基本重合，在1~40 u分辨率优于r₀=8 mm模型，在100~200 u三种场半径模型分辨率相同。能够通过四极杆组件的离子最大振幅应小于场半径，对于r₀=3 mm和r₀=4 mm模型，其允许通过的不稳定离子最大振幅近似，又仿真中分辨率变化最小为0.05 u，因此出现了前两者曲线重合的现象；将场半径增加到8 mm，容许通过的最大振幅翻倍，部分无法通过小场半径的离子得以通过，1~40 u分辨率变差；100~200 u时，不稳定离子在四极场中经历了足够多的射频周期，已经完成了分离，因此增大场半径不会使分辨率变差，这一点将在杆长影响一节详细分析。

根据式（4）^[4]，对于同样质荷比的离子，频率一定时，场半径增大会导致所需的交流电压增大，四极杆端面电极在边缘场中的影响也会增大，离子碰撞电极的比例会增加且更易损失在四极杆前端。

式中，V_pp为交流电压峰峰值。

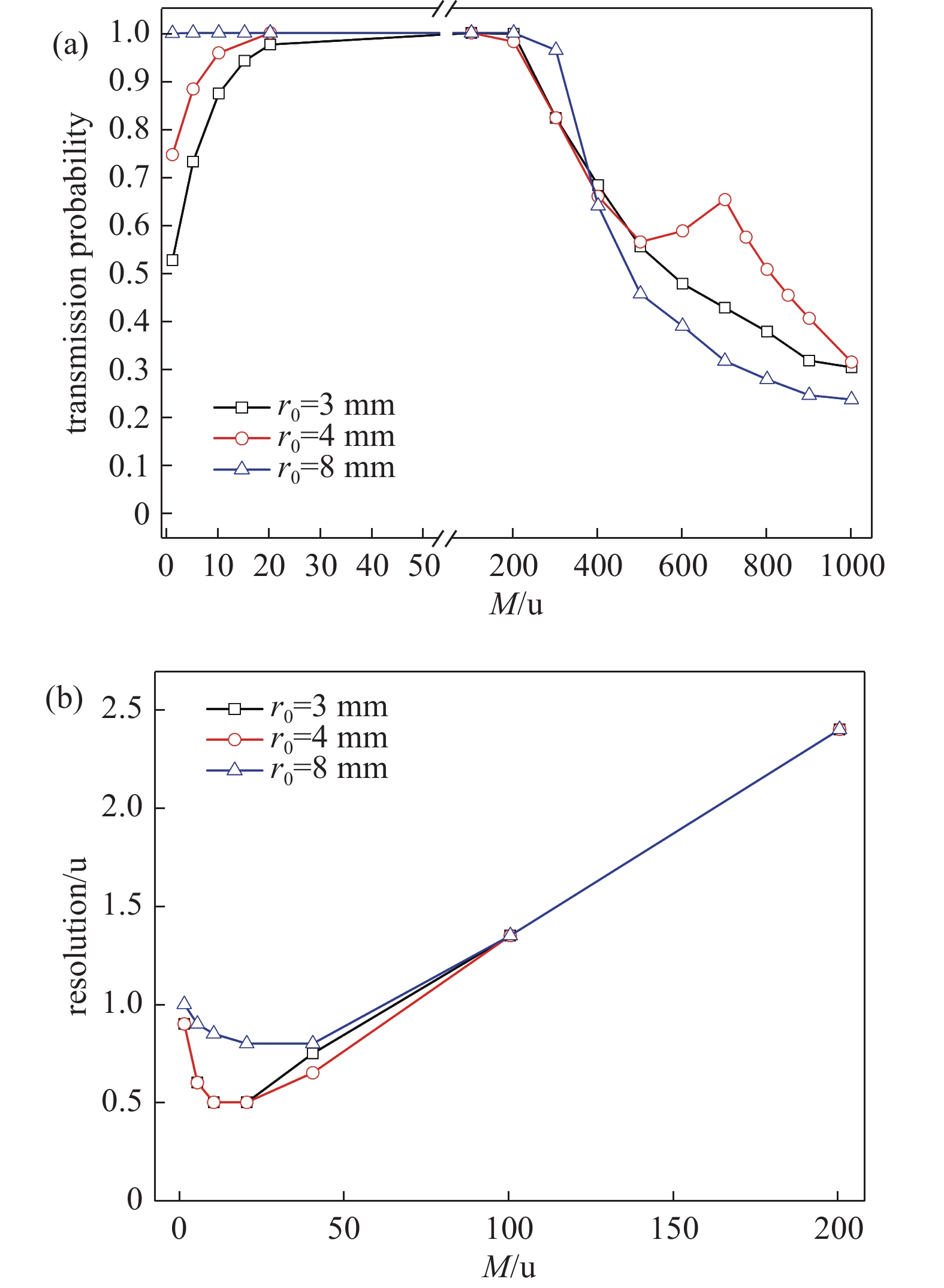
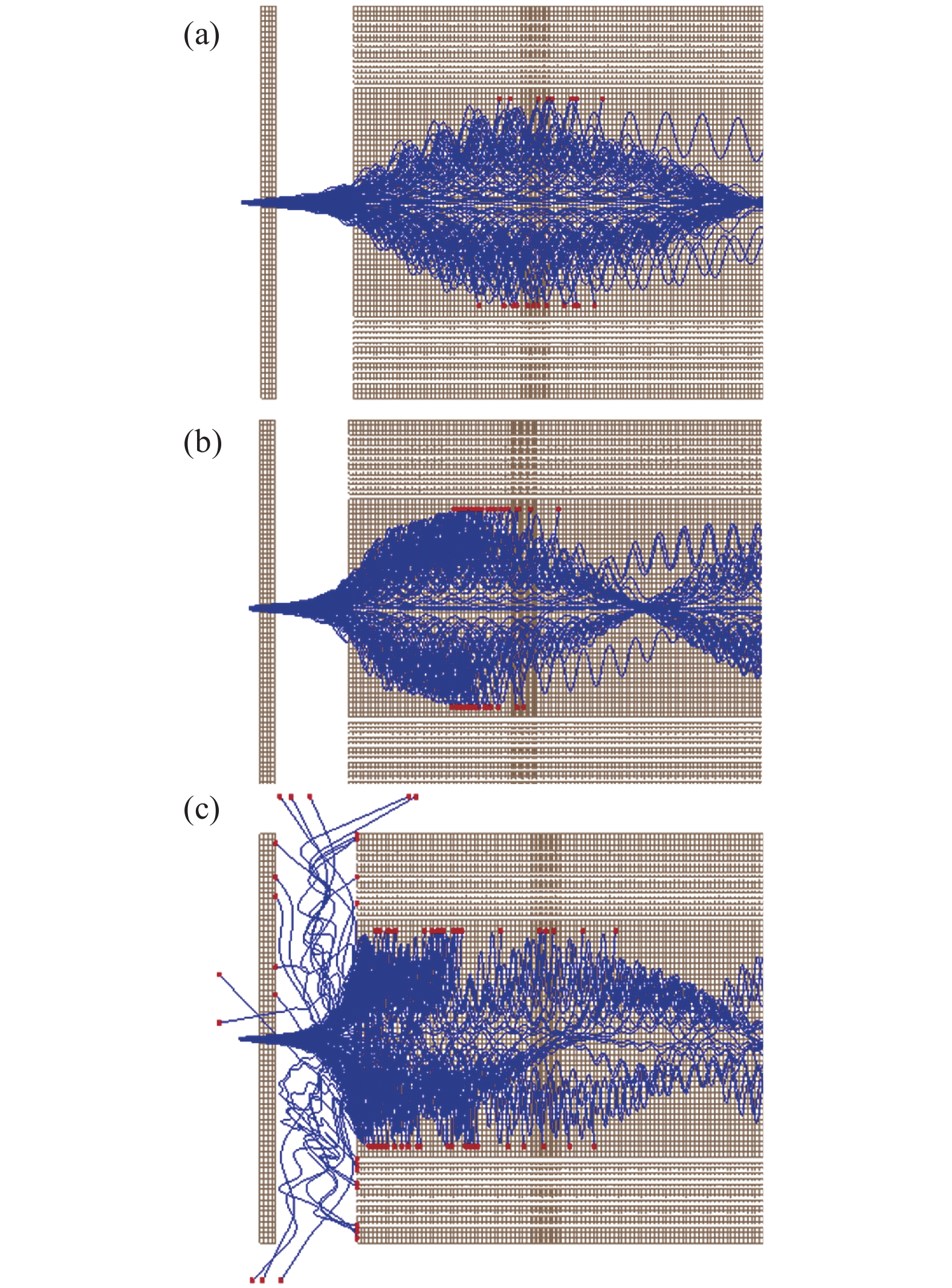
对损失在极杆上的离子进行分析，以500 u为例，仿真结果见图5，图中红点为离子损失位置。离子在边缘场度过6个射频周期（6 T），r₀=3 mm模型离子主要损失在四极杆入口6~13 T内，r₀=4 mm模型离子主要损失在四极杆入口7.5~13.5 T内，而r₀=8 mm模型离子主要损失在四极杆入口6~34 T内，并有部分离子损失在入口前。这与预期结果一致。

为了进一步验证这一结果，采用固定场半径，射频频率分别取1.0、1.3、2.0 MHz进行仿真。根据式（4），f与r₀在式中起同样作用，仿真结果如图6所示，离子损失位置变化与频率关系同场半径相似，再次验证了预期结果。

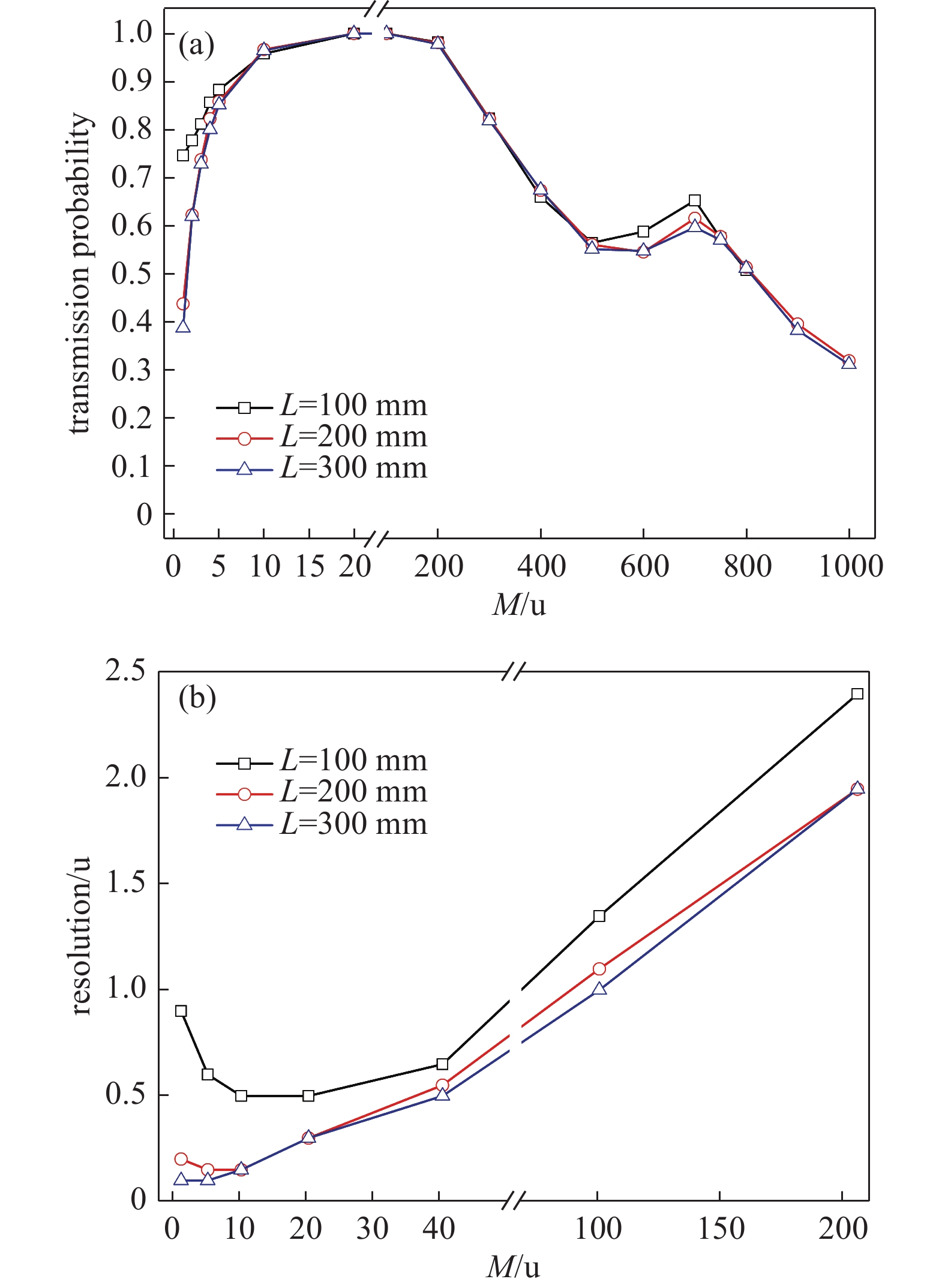
四极杆长度的延长会使离子在四极场中的运动周期数增加，部分作增幅振动的离子振幅逐渐增大，能够通过短杆而无法通过长杆。场半径取4 mm，固定其他参数，杆长分别取100、200、300 mm，仿真计算离子通过率和分辨率，其结果如图7所示。

由图7（a）可知，随着杆长L的增加，10~1000 u区间离子通过率曲线基本重合，仅在凸起附近有明显差异，但相对100 mm最大变化也小于10%；1~3 u离子通过率随长度变化有明显差异，在1 u处300 mm比100 mm减小48%。这是由于进入四极场的离子，在经过一定射频周期后不稳定离子碰撞四极杆或离开四极场实现分离，剩下的稳定离子将作周期振荡全部通过四极场；仿真中不同质荷比的离子以相同能量进入四极场，但因速度的不同在四极场内经历的射频周期数有差异，同样杆长质荷比越小的离子经历的射频周期数越少；而要分离不稳定离子需要一定的射频周期，对于图7所示曲线，10~1000 u质荷比离子在100 mm杆长已达到不稳定离子分离所需周期数，而这一长度还未满足1~3 u质荷比离子所需周期数。

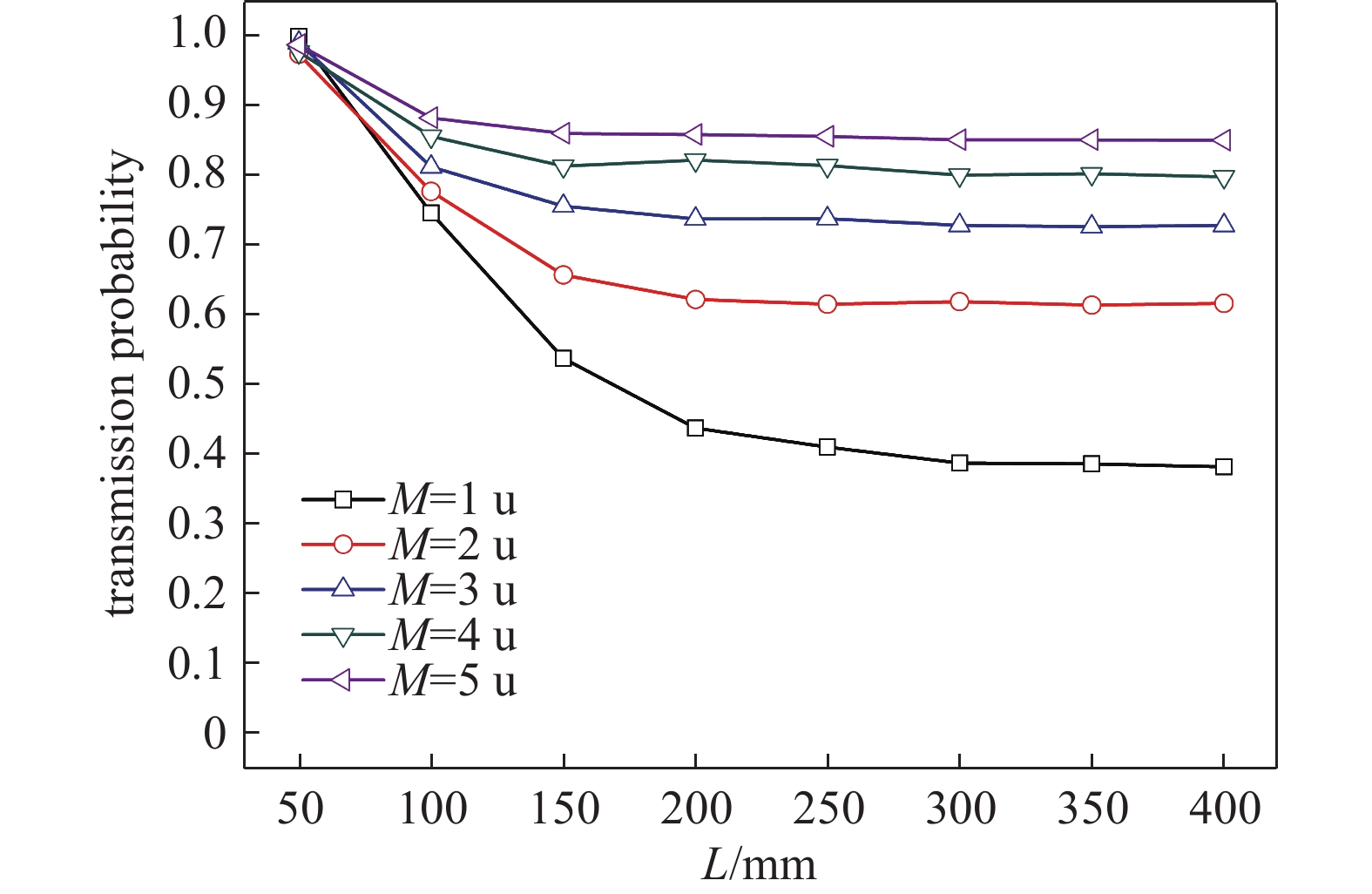
为了验证这一分析，对1~5 u质荷比离子通过率随杆长变化开展了进一步研究，结果如图8所示。图中1 u离子在L≥300 mm时通过率达到稳定，2 u、3 u离子在L≥200 mm时通过率达到稳定，4 u、5 u离子在L≥150 mm时通过率达到稳定。根据动能公式

式中，E为离子动能，m为离子质量，v为离子速度。

则相同动能的1~5 u离子其速度比为1∶$\dfrac{1}{{\sqrt 2 }}$∶$\dfrac{1}{{\sqrt 3 }}$∶$\dfrac{1}{2}$∶$\dfrac{1}{{\sqrt 5 }}$，按离子需要同样数量的射频周期数实现分离，则离子稳定分离所需的杆长比同样为1∶$\dfrac{1}{{\sqrt 2 }}$∶$\dfrac{1}{{\sqrt 3 }}$∶$\dfrac{1}{2}$∶$\dfrac{1}{{\sqrt 5 }}$。图8中1、2、4 u离子稳定分离杆长比为300∶200∶150=1∶$\dfrac{2}{3}$∶$\dfrac{1}{2}$，与上述理论计算结果基本一致。

图7(b)中，杆长200 mm和300 mm的分辨率曲线基本重合，说明200 mm的杆长已能够实现离子完全分离；而100 mm杆长1~200 u分辨率均较差，这是由于分辨率仿真时U/V=0.99×0.1678=0.1661，而离子通过率仿真时U/V=0.97×0.1678=0.1628， U/V的增大导致不稳定离子完全分离所需的杆长也随之增加，100 mm杆长已无法满足该范围离子分离要求。

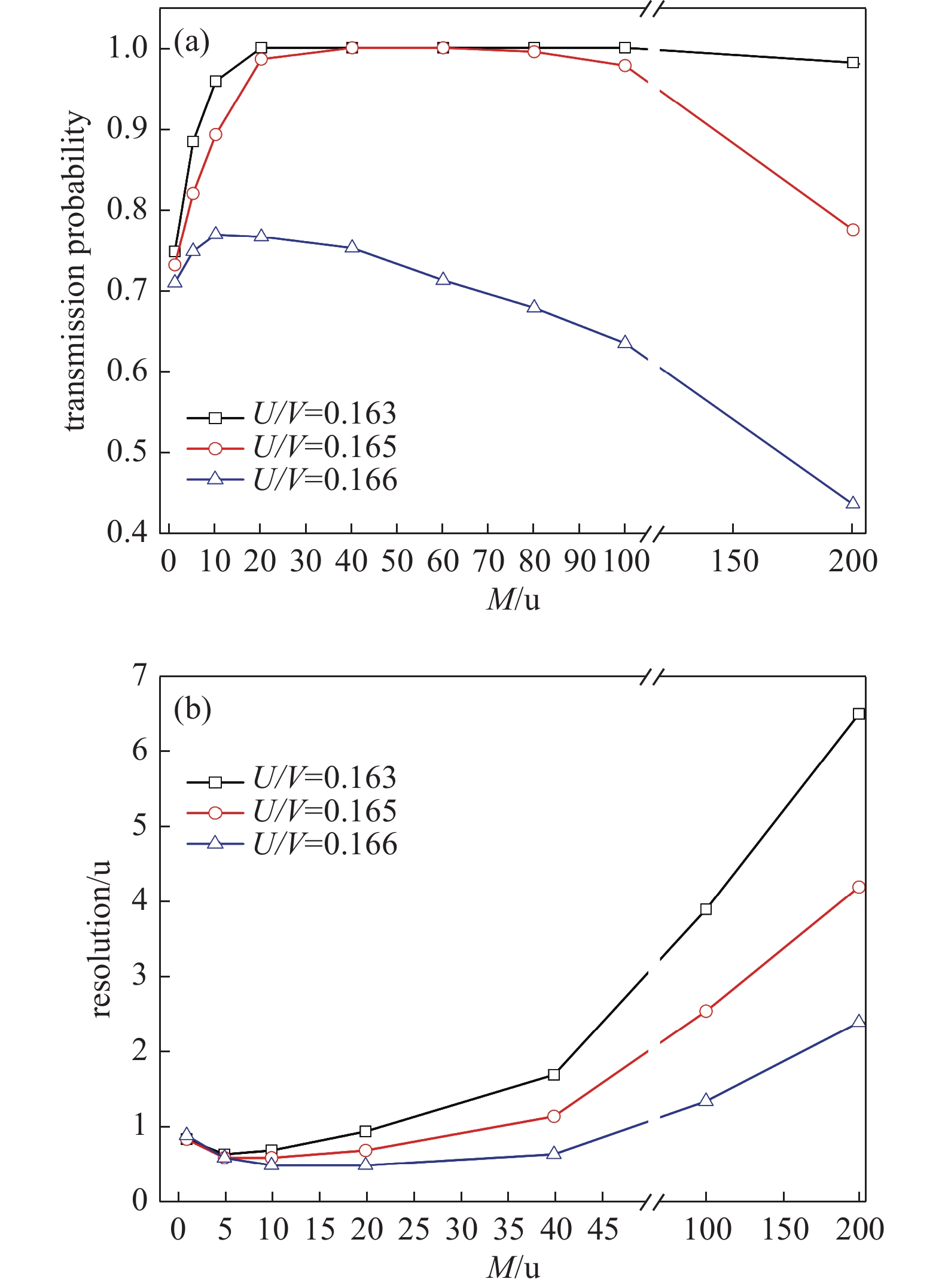
增大四极杆上电压直交比会导致离子所受电场力增大，离子运动振幅增加，传输率下降。场半径取4 mm，固定其他参数，U/V分别取0.163、0.165、0.166，仿真计算1~200 u离子通过率和分辨率，其结果如图9所示。

由图9(a)可知，随着U/V从0.163增大到0.165，不同质荷比离子通过率均下降，且100%传输区间由20~200 u缩小到20~100 u；继续增大到0.166，100%传输区间缩小为0，传输率最大值0.768约在10 u处；低质荷比段通过率分别下降7%和20%，高质荷比段下降21%和56%。由图9(b)可知，随着U/V的增大，分辨率是逐渐改善的，且质荷比越大，分辨率改善越明显，10 u处分别为0.163曲线的86%和71%，200 u处为65%和37%，而1~5 u三条曲线基本重合。上述结果表明调节电参数可以方便显著的改变四极质谱计性能，且对高质荷比段影响更大，对低质荷比影响较小。

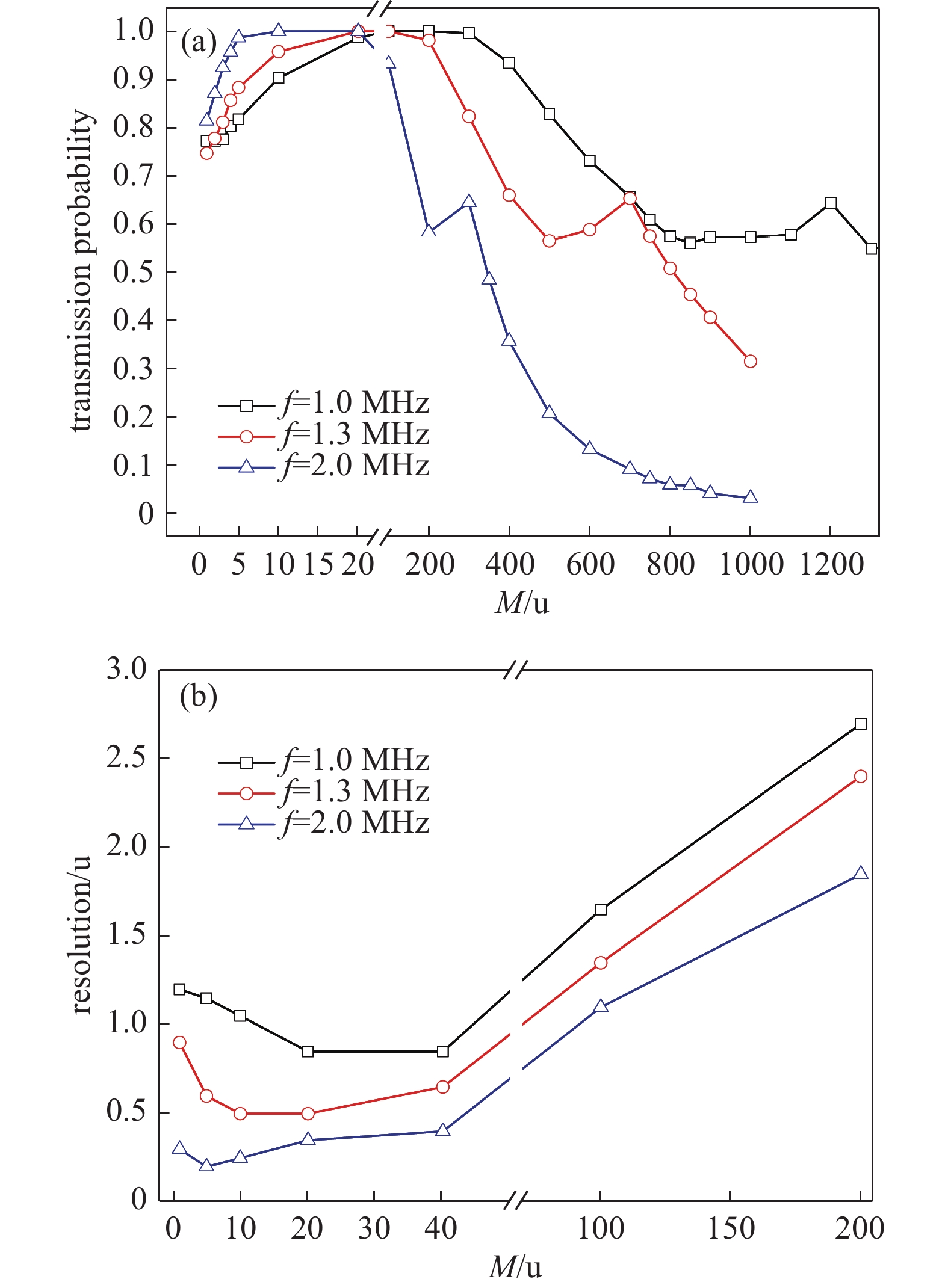
射频电源频率的变化会改变离子在四极场中经历的射频周期数。场半径取4 mm，固定其他参数，频率f分别取1.0 MHz、1.3 MHz和2.0 MHz，仿真计算离子通过率和分辨率，其结果如图10所示。

由图10(a)可知，频率的增加可以一定程度上提高1~20 u离子的通过率，却会显著降低100~1000 u离子的通过率；图4(a)中观察到的凸起，在2.0 MHz曲线前移至300 u。已有两点（1.3,650）和（2.0,300），f=1.0 MHz时，按线性关系凸起应在800 u，但在1.0 MHz曲线800 u处未观察到此现象；以频率平方的倒数计算，凸起应在1100~1200 u处，延长1.0 MHz曲线至1300 u，确实在1200 u处观察到了凸起。这一结果表明凸起的位置与频率的平方有明确的关系。由图10(b)，频率的增加可以显著改善1~200 u离子分辨率，且三条曲线基本平行，说明频率对分辨率的改善在全质荷比上规律是相同的。频率的增加使离子在四极场中经历的射频周期数增加，同样杆长使离子分离更加充分，从而得以改善分辨率。

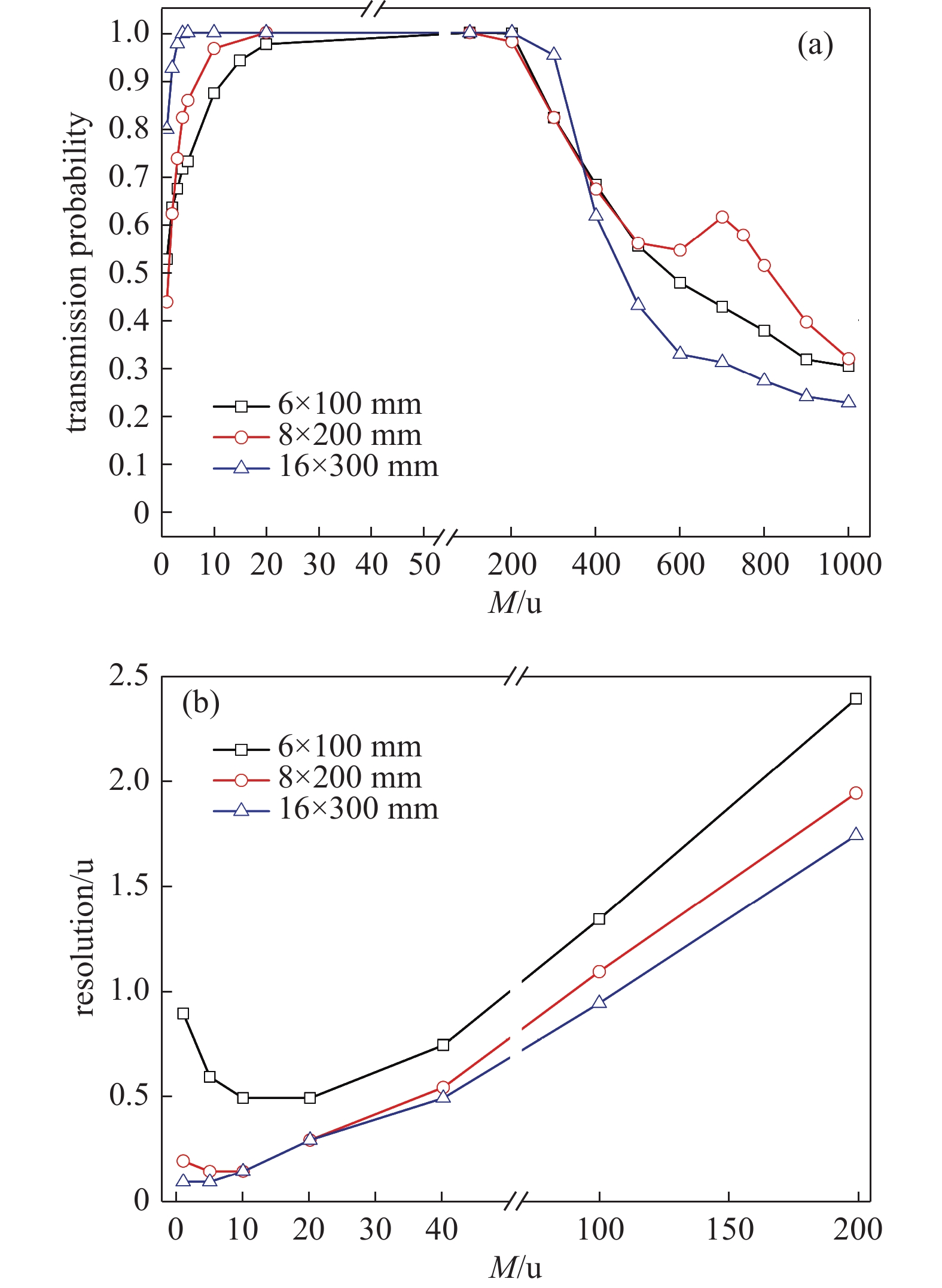
对Φ6 mm×100 mm、Φ8 mm×200 mm和Φ16 mm×300 mm（以下分别简称小杆、中杆和大杆）三种四极杆组件仿真计算离子通过率和分辨率，其他参数保持一致，结果如图11所示。

由图11(a)可知，不同尺寸四极杆组件的离子100%通过率区间分别为20~200 u、10~200 u和3~200 u，大杆的100%通过率区间最大。低质荷比段，离子通过率随四极杆组件尺寸增大而增大，但中杆在1 u处反而降低17%；高质荷比段，200~500 u段小杆和中杆离子通过率曲线重合，500~1000 u中杆曲线凸起离子通过率大于小杆，400~1000 u大杆离子通过率小于前两者。将图11(a)与图4(a)对比，可以发现100 u以上曲线形状位置基本一致，说明场半径决定大质荷比离子通过率曲线形状，即场半径对不同质荷比离子通过率的影响不同；10 u以下，图11(a)相比图4(a)中杆和大杆离子通过率均有明显的下降，质荷比越小下降幅度越大，说明图4(a)中的杆长尚未满足小质荷比离子稳定分离的要求。

由图11(b)可知，中杆和大杆相对小杆分辨率均有明显改善，1~5 u和100~200 u段大杆分辨率优于中杆，而在10~40 u两者分辨率曲线重合；对比图11(a)，10~40 u为100%通过率区间，图11(b)所施加的直交比不足以使离子进一步分离，因而两者分辨率曲线重合。可以预测，当增大直交比后，图11(b)中重合的曲线会发生分离，大杆分辨率将会优于中杆。

将图11(b)与图4(b)对比，可以发现杆长对分辨率的影响要大于场半径的影响，增加杆长是提高分辨率的有效方法。

不计算固定四极杆的陶瓷极座时，以上三种四极杆组件外径分别为19.8、26.4、52.8 mm，质量为0.145、0.515、3.088 kg（钼杆，密度取9.7 g/cm³）。大杆体积和重量都远远大于小杆，这是重要的负面因素，进行四极杆组件选择时必须慎重考虑；但大杆也具有相应的优势，对低质荷比段离子传输有明显优势，全质荷比分辨率更佳，且抗污染性能更好^[11]。

使用SIMION仿真软件，以10 gu/mm的网格密度对四极杆组件进行了建模和计算分析，探究了四极杆组件关键参数变化对1~1000 u宽质荷比范围离子通过率和分辨率的影响。结果表明：

（1）场半径对不同质荷比离子通过率影响不同，主要决定大质荷比离子通过率曲线形状；大场半径有利于低质荷比离子传输但会降低分辨率；单级四极杆由于边缘场电压的影响，频率一定时增大场半径反而不利于高质荷比离子传输，而场半径对分辨率影响随质荷比增大逐渐减弱，直至不同场半径分辨率相同。

（2）同样能量的离子因质荷比不同实现稳定分离所需的杆长不同，质荷比越小，需要的杆长越长；达到稳定分离杆长前，离子通过率随杆长增加而减小，分辨率随杆长增加而提高；杆长对分辨率的影响大于场半径。

（3）直交比U/V的增加会引起离子通过率的减小和分辨率的提高，且对高质荷比段影响更大，对低质荷比影响较小；频率的增加能够在全质荷比提高分辨率，可以一定程度提高低质荷比离子通过率，却会显著降低高质荷比离子通过率。

（4）对三种模块化四极杆组件进行对比，大尺寸杆低质荷比段离子通过率最大、分辨率最佳，高质荷比段通过率最小但分辨率也最佳；中尺寸杆低质荷比段通过率和分辨率均大于小尺寸杆，高质荷比段分辨率优于小尺寸杆而两者通过率相同。

（5）在r₀=4 mm模型通过率曲线出现凸起点，经验证其位置与频率平方成反比，与杆长无明显关系，该现象出现原因尚不明确。

本研究探究了四极杆组件关键参数对不同质荷比离子性能的影响，这为不同应用目的四极质谱计的设计提供了参考。