首页
登录
注册
下载:
-
当微通道的特征尺寸与气体分子平均自由程相当或更小、且沿壁面切线方向存在温度梯度，壁面附近的气体分子会自发地由冷端向热端蠕动（thermal creep），随着流动的发展，热端因分子聚集而压力升高，冷端因分子数量减少而压力降低，热端与冷端形成压差后又产生由热端流向冷端的压力驱动流（Poiseuille flow），但从宏观效果看是气体自发地从冷端流向热端并使热端压力升高，该现象称为热流逸效应（thermal transpiration effect），于1879年被雷诺（Reynolds O）[1]发现。1909年努森（Knudsen M）[2]提出了利用热流逸效应为工作原理的气体输送和升压装置，后人称之为努森压缩机或努森泵（the Knudsen compressor/pump），但碍于当时技术条件的限制未得到发展。如今随着微/纳米技术的发展，这类无运动部件、仅依靠热能驱动的热流逸泵送技术重新进入人们的视野。
时至今日，应用热流逸效应几乎都要借助努森压缩机/泵，能耗和能效是评价其性能的重要指标。作为一种以热能驱动的特殊类型真空泵，目前努森真空泵能耗模型可分为两种：一种是Copic[3-5]、Muntz[6]、Vargo[7]和王博韬[8]等的做法，从泵本身能量转换的角度的出发，通过微通道材料的导热率计算维持冷热两端温差所需的耗热量；另一种则是根据被泵送气体（抽真空对象）获取能量的角度，按照被泵送气体的导热率计算其从微通道冷端流向热端达到一定温差时所需的耗热量[9]。但这些模型都是针对最简单的单级结构。为获取较大真空度，往往需要将多个努森真空泵串联组成泵组（称为多级努森真空泵）来使用，为此有必要探究如何将现有的单级能耗模型扩展至更具实际应用价值的多级努森真空泵。对于真空泵，评价其性能一般要强调抽吸气体的能力，因此评价耗能通常用“消耗单位功量/获得的流量”这一指标，加之多级努森真空泵以热能驱动，故其性能宜采用“热流比”来评价，表征其单位时间的能耗与单位时间内抽出的气体分子数量之比。此外，为兼顾人们对能源利用效率的常规理解，仍然有必要从能量转换的角度来看问题，此时多级努森真空泵的运行效率可定义为真空泵所做的最大功（即泵送气体的流动功）与产生热流逸效应的驱动力（热能）之比[10]。
本文拟从Muntz[6]的能耗模型及Copic[5]的效率模型出发，着重考虑多级串联结构的级联特性，建立多级努森真空泵的能耗和效率模型。进而以空气作为研究对象，探讨努森数、压比、温差和级数等参数对能耗和效率的影响，以期为多级努森真空泵的优化设计及应用提供指导。
-
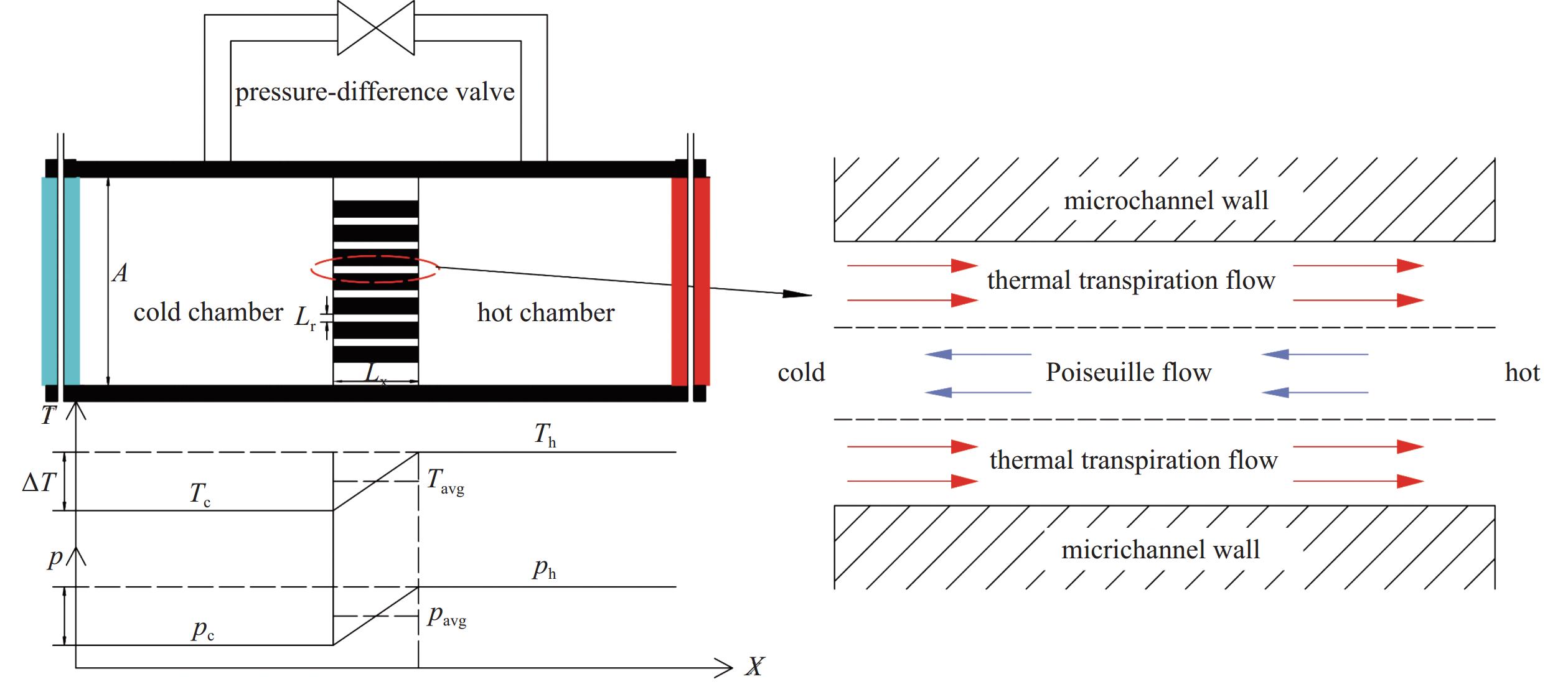
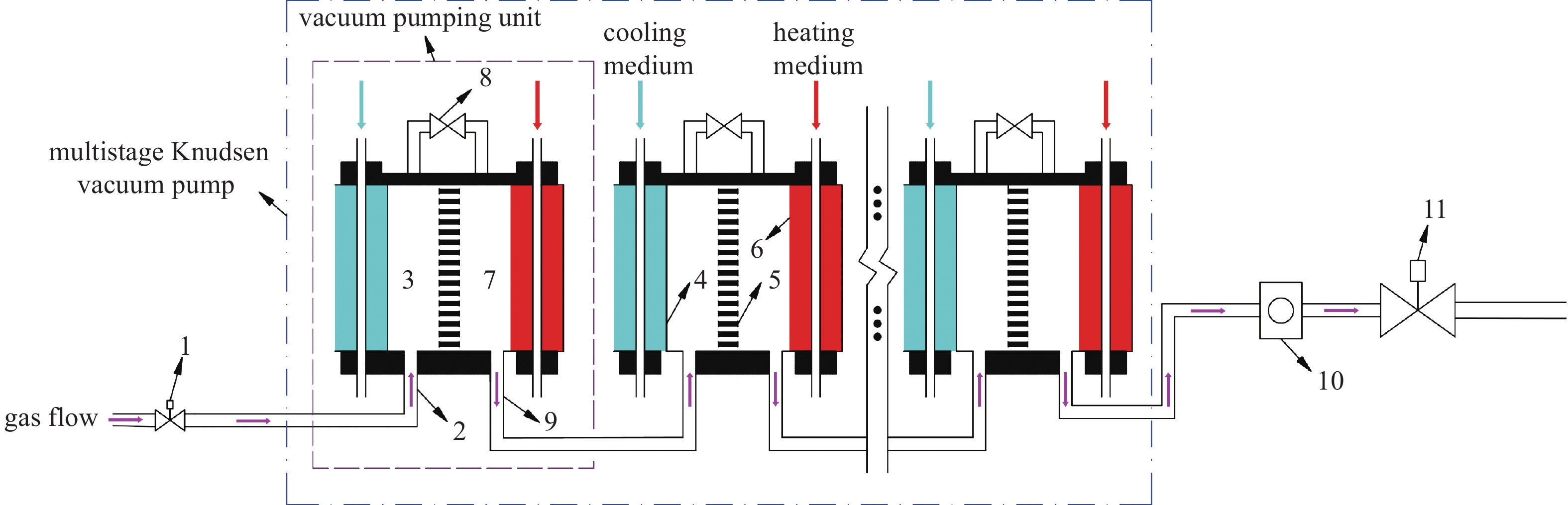
在真空系统中具有通用性的多级努森真空泵如图1所示，其由若干个泵组单元（单级努森泵）通过级联（串联连接）方式组成。参考图1，冷腔温度Tc与热腔温度Th分别由冷却器4和加热器6维持，当微通道组达到热流逸效应发生的条件时，每个努森泵内的气体工质流动和压力变化如图2所示，热流逸流（thermal transpiration flow）和压力驱动流（Poiseuille flow）的综合效果表现为气体工质自发地从本级泵组单元的冷腔流向热腔，使得本级泵组单元的热腔因气体分子聚集而压力ph升高、冷腔因气体分子减少而压力pc降低，然后经出口管流向下一级泵组单元。气体压力经泵组单元逐级提升至大气压力，而真空端的压力则因热流逸效应不断将气体分子移出而逐渐降低。最终，真空端的气体工质经每一级努森泵被源源不断的抽吸并排至大气，直至达到所需真空度。
-
根据Muntz[6]的理论，驱动努森真空泵内部气体运动的动力都来自于微通道两端的温差，因此对于由N个泵组单元串联而组成的多级努森真空泵而言，输入的总功为通过这N个泵组单元的微通道壁面传递的热量之和，即
式中，K为微通道材料导热系数，W·(m·K)−1；A为微通道组的横截面积，m2；F为微通道组通流面积占比，%；ΔT为冷热腔的温差，K；Lx,i 为第i级微通道组长度，m。
结合文献[8]关于多级努森真空泵流量的计算，可得多级努森真空泵的热流比为
式中，(
$\overline{M}$ N)des为多级努森真空泵分子流量，#·s−1；Ω为被抽运气体的粘性碰撞横截面，m2；Tavg为微通道两端冷热腔的平均温度，K；m为气体分子质量，kg；kb为玻尔兹曼常数，kb=1.38065×10−23 J·k−1[11]；μ为气体的摩尔质量，kg·mol−1；NA为阿伏伽德罗常数，本文取NA=6.02×1023 mol−1；KnN为整体努森数；QT,i、Qp,i分别为热流逸系数和泊肃叶系数[12]；ki为累计到第i级的压差系数[8]，可反映抽真空的能力。由于努森真空泵工作时其内部气体流态一般为过渡流（0.1<Kn<10），且对应的气体分子碰撞模型多采用硬球碰撞模型[11]。在上述两个条件下，式（2）中的
因此热流比可简化为
为达到预定的真空度，需要先设定最后一级泵组单元（第N级）的热腔压力与第一级泵组单元的冷腔压力（近真空室端）之比
$ {(p}_{N} $ )des（简称压比），那么$ {(p}_{N} $ )des的值为各级压力比的乘积，即若已知设定压比，因多级努森真空泵的级数N与压差系数ki是相互关联的，故可由式（4）求得压差系数ki，即
将式（5）代入式（3），若假设多级努森泵在运行时内部气体的流态保持不变、每一级泵组单元所采用的微通道材料都相同（即微通道组通流面积占比F与导热系数K都相同）、且每一级泵组单元冷、热腔两端温差也保持一致，则热流比可表为级数N的显函数形式
此外，根据Copic[5]的理论，多级努森真空泵所做的有用功Wuse为气体工质吸收壁面热量后所获得的能量，即
式中，Cp为泵送气体的定压比热容，kJ·kg−1·K−1。
由此可得从能量转换角度考虑的多级努森真空泵运行效率为
-
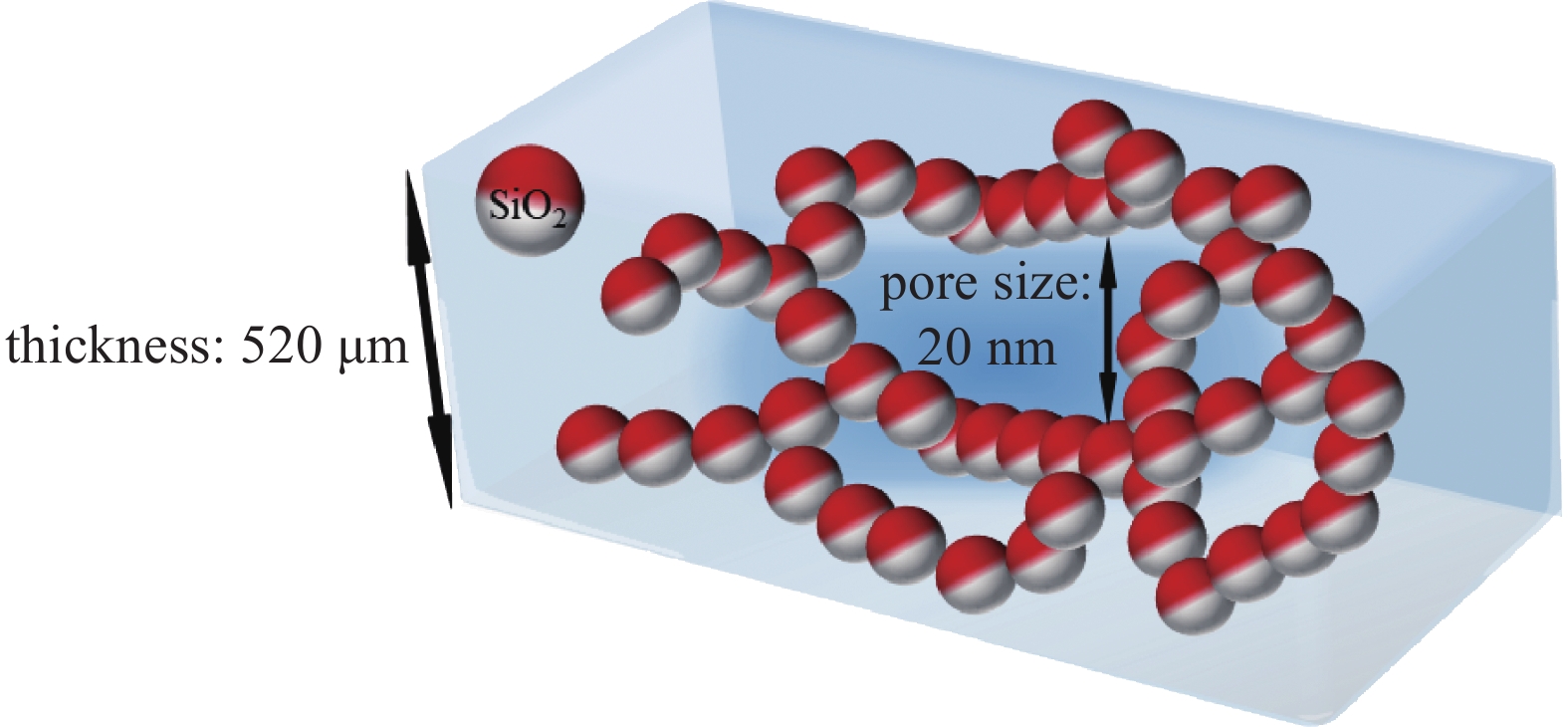
努森真空泵中的微通道组通常用便于制备的多孔材料代替，气凝胶是一类特殊的连续多孔固体材料，具有纳米级的颗粒和孔隙结构。作者选择Vargo[13]在实验中所采用的二氧化硅气凝胶多孔膜作为努森真空泵微通道的材料，如图3所示，其结构厚度（视为Lx）和平均孔径（视为Lr）分别为520 μm和20 nm，导热系数为0.017 W·m−1·K−1。多孔膜的孔隙率一般保持在65%~80%[14]，本文取70%[15]。
鉴于本文讨论介质为空气的抽真空，故设定各级冷腔温度为293 K（恒定不变），最后一级末端连接大气环境，压力取105 Pa（恒定不变）[8,16]。由于多级努森真空泵一般采用定流法设计[13]，因此每级的微通道孔径都不相同，但由式（2）的分析可知孔径大小的不同对热流比以及运行效率的结果并未造成太大影响，因此可不必考虑各级多孔膜的膜面积与微通道孔径的变化。
-
图4（a）展示了多级努森真空泵为达到指定的真空度（本文以压比
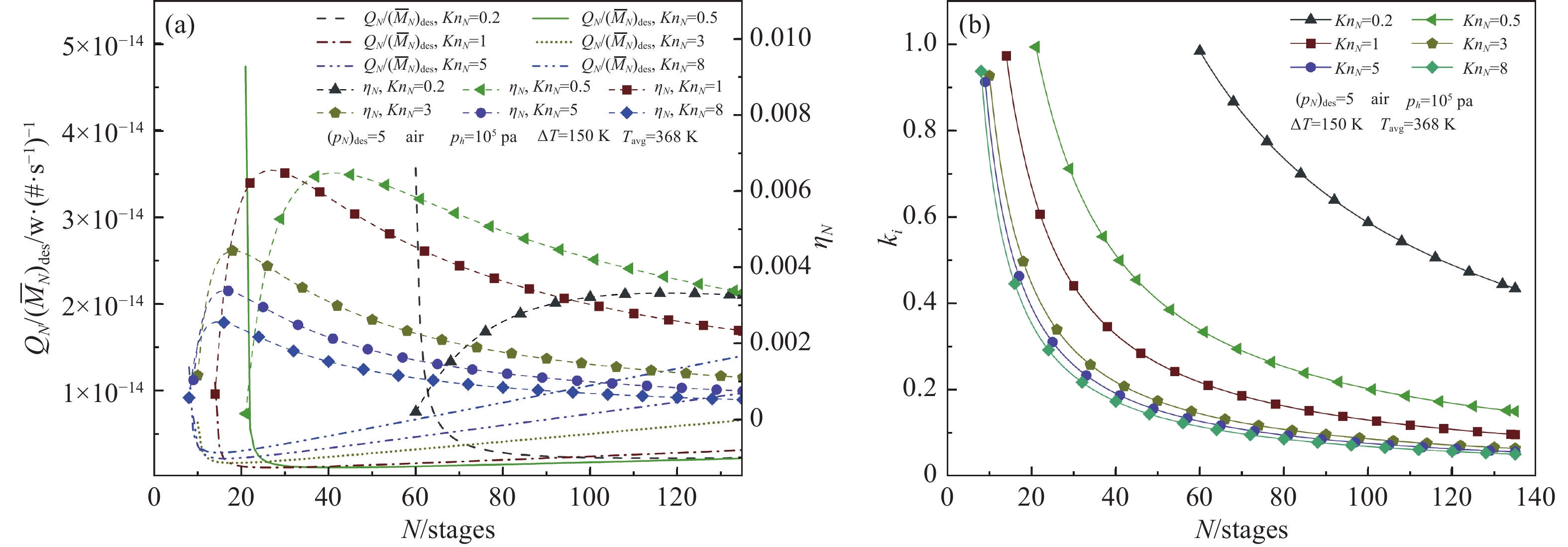
$ {(p}_{N} $ )des来表达）时，热流比及运行效率随级数和努森数变化的情况。从图中可以看出，无论努森数KnN取何值，随着级数N的增加，热流比QN/($\overline {M}$ N)des都呈现先迅速减小、后平缓增大的趋势；而运行效率$ {\eta }_{N} $ 与热流比QN/($\overline {M}$ N)des恰好相反，呈先增大后减小的趋势。与大KnN数工况相比，小KnN下QN/($\overline {M}$ N)des的增大趋势更为缓慢。上述分析表明，存在一个使多级努森真空泵运行效率最大（热流比最小）的级数，可称之为最优级数。对应于不同的KnN，最大运行效率（最小热流比）所需的最优级数不同。当压比
$ {(p}_{N} $ )des=5，KnN=0.2、0.5、1、3、5、8时，多级努森真空泵获得最大运行效率（最小热流比）的所需级数分别为118、41、27、18、16、15级。可见，随着KnN数的增加，获得最大运行效率（最小热流比）所需的级数逐渐减少。进一步分析图4（a），KnN=1时$ {\eta }_{N} $ 的极值最大，分别是KnN=0.2、0.5、3、5、8时的1.97、1.02、1.48、1.94、2.55倍；与之对应，KnN=1时QN/($\overline {M}$ N)des的极值最小，分别是KnN=0.2、0.5、3、5、8时的50.68%、98.87%、67.66%、51.68%、39.17%。即在ΔTi=150 K和$ {(p}_{N} $ )des=5条件下，最佳运行效率与最小热流比对应的KnN数和级数N分别为1和27左右。这说明在多级努森泵的工作过程中，存在使其获得最大运行效率（最小热流比）的努森数，且所对应的级数也较为适宜。由于单级努森真空泵的压差有最大限制，反映到多级努森真空泵则表现为最小级数限制[8]。由图4（b）可知，KnN=0.2、0.5、1、3、5、8时，使多级真空泵可运行的最小级数分别为60、21、14、10、9、8级，为达到相应的压比
$ {(p}_{N} $ )des，累计到第i级的压差系数ki会随着级数的增加而减小，且减小的趋势逐渐平缓。随着KnN数的增大，ki会逐渐减小；根据式（5），若级数不变，那么将导致每一级的压比都减小。对比图4（a）和（b）还可看出，最小级数对应的热流比QN/($\overline {M}$ N)des是最大的，另外最小热流比对应的级数（即最优级数）随KnN数的增大逐渐接近最小级数。所以对于多级泵级数的选取，应该尽量避免选择最小级数，同时需要考虑最优级数的范围，以获得最大运行效率与最小热流比。 -
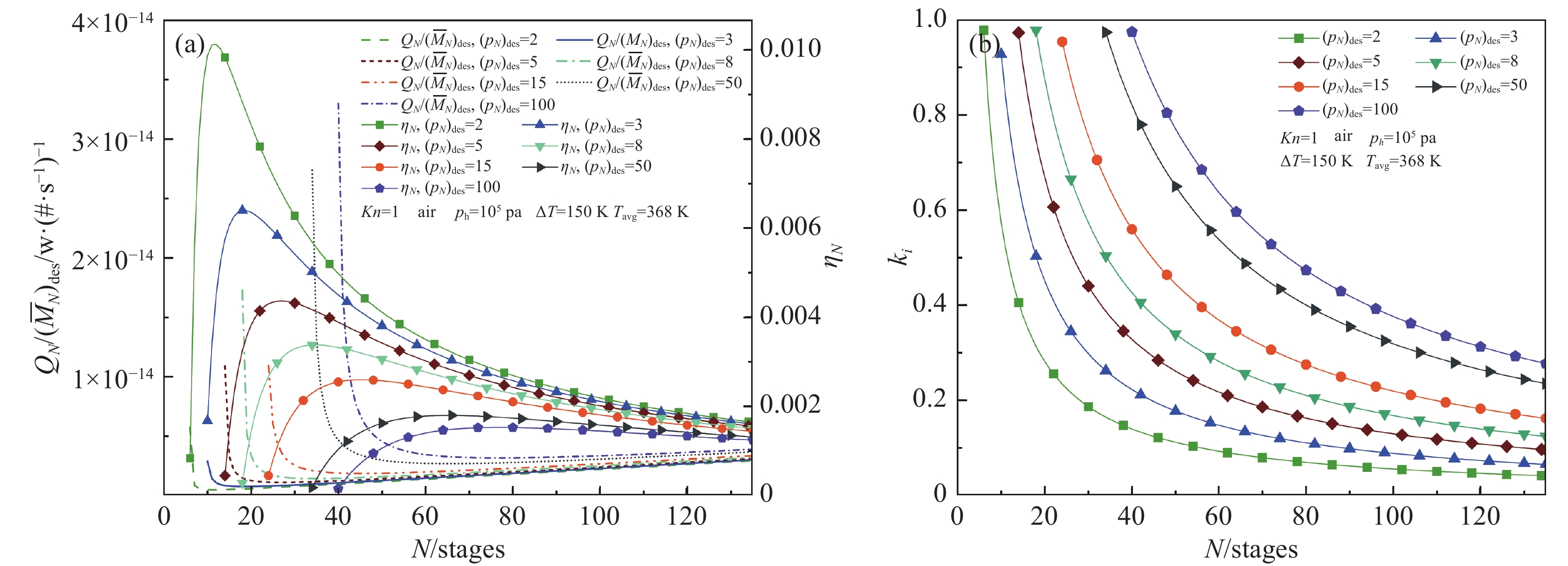
考察图5（a），在不同压比
$ {(p}_{N} $ )des下，随级数N的增加，热流比QN/($\overline{M}$ N)des先减小后平缓增加，存在一个极小值；而运行效率$ {\eta }_{N} $ 则是先增加后减小且变化趋势逐渐平缓，存在一个极大值；与从图4（a）得到的结果类似，也存在一个使多级努森真空泵运行效率最大（热流比最小）的最优级数。随着$ {(p}_{N} $ )des的增大，对应的QN/($\overline{M}$ N)des极小值逐渐增大、$ {\eta }_{N} $ 极大值逐渐减小，QN/($\overline{M}$ N)des极小值与$ {\eta }_{N} $ 极大值对应的工作总级数逐渐增大。$ {(p}_{N} $ )des=2、3、5、8、15、50、100时，获得$ {\eta }_{N} $ 极大值（QN/($\overline{M}$ N)des极小值）所需的级数分别为12、18、27、35、45、65、77级。当$ {(p}_{N} $ )des=2时，QN/($\overline{M}$ N)des的极小值是$ {(p}_{N} $ )des=3、5、8、15、50、100时的63.14%、43.12%、33.37%、25.63%、17.74%、15.07%；对应的，$ {\eta }_{N} $ 的极大值分别为1.59、2.32、3.00、3.90、5.64、6.64倍。因此，在设计多级努森真空泵的时，应充分考虑使用场景的压比要求（即真空度要求）；当用于低压比（低真空度）情形时，级数为12级左右时热流比较低且运行效率较高，这从能效的角度论证了多级努森真空泵用于粗真空场景较有优势。但需要注意（参考图5（a）），无论压比取何值，当多级努森真空泵的级数接近最小级数或远大于最优级数时，热流比大幅增加且运行效率大幅降低。因此在选择级数时，应尽量使级数保持在最优级数附近。图5（b）展示了不同压比条件下，多级努森泵中压差系数ki的变化情况。可以看到，随着级数N的增加，压差系数ki都会减小且趋势逐渐平缓，最小级数对应着最大压差系数。此时压差接近于这N级串联泵组单元的降压极限，即接近于所能获取的真空度极限。另外还可看出，压比越大，对应的最小级数就越大，最小级数和最优级数逐渐远离。根据前文关于图5（a）的分析，这对热流比和运行效率均有不利影响，故在设计多级努森真空泵时要避开最小级数。
-
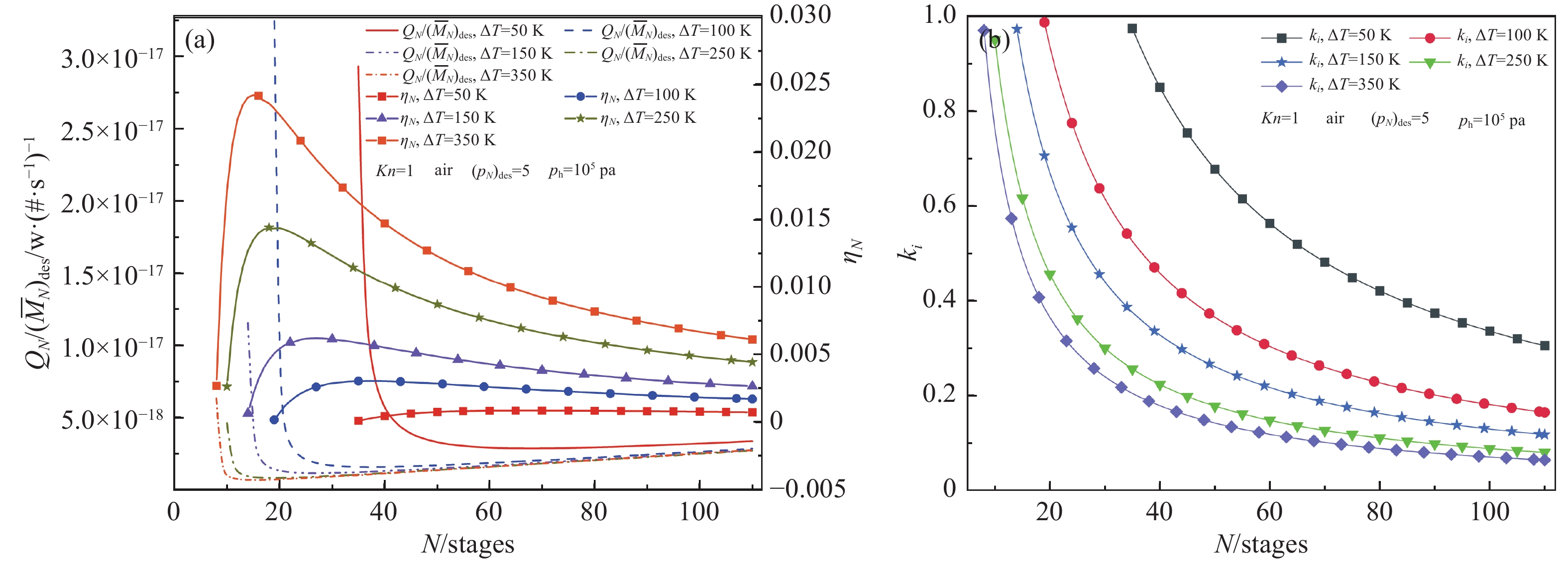
考察图6（a），在不同的温差ΔT下，随级数N的增加，热流比QN/(
$\overline{M}$ N)des先急剧减小后平缓增加，存在一个极小值；而运行效率$ {\eta }_{N} $ 则是先增大后减小，存在一个极大值。因此，同样存在一个使多级努森真空泵运行效率最大（热流比最小）的最优级数。不难看出，随着温差ΔT增大，QN/($\overline{M}$ N)des的极小值逐渐减小，$ {\eta }_{N} $ 的极大值逐渐增大，需要注意的是QN/($\overline{M}$ N)des极小值和$ {\eta }_{N} $ 极大值对应的最优级数减小。ΔT=50、100、150、250、350 K时，获得$ {\eta }_{N} $ 极大值所需的级数分别为68、37、27、19、15级。当ΔT=350 K时，QN/($\overline{M}$ N)des极小值分别是ΔT=50、100、150、250 K的24.22%、43.70%、59.56%、83.40%；对应的$ {\eta }_{N} $ 极大值分别是ΔT=50、100、150、250 K的28.90、8.00、3.92、1.68倍。因此，温差作为驱动多级努森真空泵的动力源，可根据实际应用场景适当选用较大温差。同样的，无论温差取何值，应尽量使级数保持在最优级数附近，以此保证获得更大的运行效率和更小的热流比。此外，如图6（b）所示，在不同温差下，随着级数N的增加，压差系数ki均减小。与前文的分析结果类似，同样是最小级数对应着最大压差系数，且最小级数对应高热流比和低运行效率。但另一方面，温差越大，对应的最小级数就越小，且最小级数和最优级数逐渐趋近。
故由以上分析可知，如要降低多级努森真空泵的最优级数以简化其结构，则应尽可能提高冷热腔的温差ΔT。
-
本文建立了描述多级努森真空泵能耗及效率的数学模型，进而分析了多级努森真空泵热流比及运行效率与级数、努森数、压比和温差等关键参数之间的关系，主要结论如下：
（1）在满足运行温差ΔTi=150 K且获得指定压比
$ {(p}_{N} $ )des=5（即需要的真空度）的条件下，使运行效率最高（热流比最小）的最优级数约为27级。当努森数从0.2增至8时，对应的最优级数从118级减少至15级。（2）在满足运行温差ΔTi=150 K和努森真空泵内流动条件的情形下，使运行效率最高（热流比最小）的最优级数约为12级。当压比（真空度）从2增至100时，对应的最优级数从12级增加至77级。
（3）在满足努森真空泵内流动条件且获得指定压比
$ {(p}_{N} $ )des=5的情况下，使运行效率最高（热流比最小）的最优级数约为15级。当温差从50 K增至350 K时，对应的最优级数从68级减少至15级。（4）多级努森真空泵存在最小级数限制，努森数（温差）越小、或压比越大，所需的最小级数也就越多；当努森数或温差增大时，最小级数与最优级数逐渐趋近，而当压比增大时，最小级数与最优级数逐渐远离。
（5）努森数（温差）越大、或压比越小，则多级努森真空泵的热流比就越低（运行效率就越高）且对应的最优级数也就越小。可见，若从能效的角度来考虑多级努森真空泵的设计，为获得最大运行效率（最小热流比）需综合考虑努森数、压比和温差的影响，确定最优级数的范围。
多级努森真空泵能效分析
Energy Efficiency Analysis of Multistage Knudsen Vacuum Pump
-
摘要: 基于热流逸效应工作的努森真空泵相较于传统真空泵，因具有无运动部件且结构简单的优点而倍受关注，其应用通常采用多级串联结构。文章以努森真空泵能耗和效率模型为基础，着重考虑级数与热量传递和压力分配的关系，建立了多级努森真空泵气体工质流态处于过渡流时的能耗（热流比）与运行效率模型，进而研究了影响热流比及运行效率与级数、努森数、压比、温差等参数的关系。结果表明，努森数从0.2增至8，对应的最优级数从118级减少至15级；压比从2增至100，对应的最优级数从12级增加至77级；温差从50 K增至350 K，对应的最优级数从68级减少至15级。努森数（温差）越大、或压比越小，热流比就越低（运行效率就越高）且对应的最优级数就越小，所需的最小级数也越少。若从能效优化的角度来设计多级努森真空泵，需综合考虑努森数、压比和温差的影响，确定最优级数范围。Abstract: Compared to traditional vacuum pumps, the Knudsen vacuum pump, based on the thermal transpiration effect, is paid lots of attention to because of the advantages of no moving parts and simple structure. The Knudsen vacuum pump is commonly used by type of many unit pumps in series. According to the energy consumption and efficiency model of the single-stage Knudsen vacuum pump and focusing on the relationship of the number of stages with heat transfer and pressure distribution, energy consumption (heat requirements per pumped molecule) and operation efficiency model are established for multistage Knudsen vacuum pump when the pumped gas medium is in transition flow regime. Furthermore, the investigation is carried out on correlations between heat requirements per pumped molecule and operating efficiency and those parameters such as number of stages, Knudsen number, pressure ratio and temperature difference. The results show that as the Knudsen number increases from 0.2 to 8, the corresponding optimum number of stages decreases from 118 to 15. As the pressure ratio increases from 2 to 100, the corresponding optimum number of stages increases from 12 to 77. As the temperature difference increases from 50 K to 350 K, the corresponding optimum number of stages decreases from 68 to 15. The larger the Knudsen number (temperature difference) or the smaller the pressure ratio, the lower the heat requirements per pumped molecule (the higher the operating efficiency) and the smaller the corresponding optimum number of stages as well as the minimal number of stages required. Considering the design of a multistage Knudsen vacuum pump from the perspective of energy efficiency optimization, it is necessary to take into account the comprehensive effects of Knudsen number, pressure ratio and temperature difference in order to determine the range of optimum number of stages.
-
-
图 2 努森真空泵内的流动和压力特性
Figure 2. Characteristics of flow and pressure in Knudsen vacuum pump
图 4 不同努森数条件下多级努森真空泵能效参数、结构参数之间的相互关系。（a）热流比、运行效率与级数，（b）压差系数与级数
Figure 4. Correlations of energy efficiency parameters, structural parameters and both kinds for multistage Knudsen pump at different Knudsen numbers. (a) The heat flow ratio and operation efficiency, (b) pressure difference coefficient
图 5 不同压比条件下多级努森真空泵能效参数、结构参数之间的相互关系。（a）热流比、运行效率与级数，（b）压差系数与级数
Figure 5. Correlations of energy efficiency parameters, structural parameters and both kinds for multistage Knudsen pump at different pressure ratios. (a) The heat flow ratio and operation efficiency, (b) pressure difference coefficient
图 6 不同温差条件下多级努森真空泵能效参数、结构参数之间的相互关系。（a）热流比、运行效率与级数，（b）压差系数与级数
Figure 6. Correlations of energy related parameters, structural parameters and both kinds for multistage Knudsen pump at different temperature differences. (a) The heat flow ratio and operation efficiency, (b) pressure difference coefficient
-
[1] Reynolds O. On certain dimensional properties of matter in the gaseous state. Part I. & Part II[J]. Philosophical Transactions of the Royal Society of London,1879,170:727−845 doi: 10.1098/rstl.1879.0078 [2] Knudsen M. Eine revision der Gleichgewichtsbedingung der gase. Thermische Molekularströmung[J]. Annalen der Physik,1909,336:205−229 doi: 10.1002/andp.19093360110 [3] Copic D, Mcnamara S. Efficiency derivation for the Knudsen pump with and without thermal losses[J]. Journal of Vacuum Science & Technology A,2009,27(3):496−502 [4] Copic D. A MEMS Knudsen pump for high gas flow applications[D]. Louisville: University of Louisville, 2008 [5] Copic D, Brehob E, McNamara S. Theoretical efficiency of a microfabricated knudsen pump[C]//University /Government /Industry Micro Nano Symposium, 2008. UGIM 2008.17th Biennial. IEEE, 2008: 107-110 [6] Muntz E P, Sone Y, Aoki K, et al. Performance analysis and optimization considerations for a Knudsen compressor in transitional flow[J]. Journal of Vacuum Science & Technology A: Vacuum, Sur-faces, and Films,2002,20(1):214−224. [7] Vargo S E, Muntz E P, Shiflett G R, et al. Knudsen compressor as a micro- and macroscale vacuum pump without moving parts or fluids[J]. Journal of Vacuum Science & Technology A Vacuum Surfaces & Films,1999,17(4):2308−2313 [8] 王博韬. 热流逸效应的抽真空特性及其在真空制冷中的应用[D]. 南宁: 广西大学, 2018(in chinese) WANG Botao. Vacuum pumping characteristics and vacuum cooling application of thermal transpiration effect[D]. Nanning: Guangxi University, 2018 [9] Young M, Han Y L, Muntz E P, et al. Characterization of a radiantly driven multistage Knudsen compressor[C]// ASME 2003 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineering, 2003: 393-400 [10] Klein T A. Energy conversion using thermal transpiration: Optimization of a Knudsen compressor[D]. Cambridge: Massachusetts Institute of Technology, 2012 [11] 沈青. 稀薄气体动力学[M]. 北京: 国防工业出版社, 2003(in chinese) SHEN Qing. Rarefied gas gynamics[M]. Beijing: National Defense Industry Press, 2003 [12] 杨林. 努森压缩机优化分析及努森压缩制冷系统研究[D]. 南宁: 广西大学, 2015(in chinese) YANG Lin. Performance analysis of Knudsen compressor and refrigeration systems with the Knudsen compressors[D]. Nanning: Guangxi University, 2015 [13] Vargo S E, Muntz E P. Initial results from the first MEMS fabricated thermal transpiration-driven vacuum pump[C]// AIP Conference Proceedings. American Institute of Physics, 2001, 585(1): 502-509 [14] Nakaye S, Sugimono H. Demonstration of a gas separator composed of Knudsen pumps[J]. Vacuum,2016,125:154−164 doi: 10.1016/j.vacuum.2015.12.015 [15] Gupta N K, Gianchandani Y B. Thermal transpiration in mixed cellulose ester membranes: Enabling miniature, motionless gas pumps[J]. Microporous and Mesoporous Materials,2011,142(2-3):535−541 doi: 10.1016/j.micromeso.2010.12.042 [16] 覃日帅, 蒙仕达, 王博韬, 等. 多级热流逸式真空泵流量与压力特性分析[J]. 真空科学与技术学报,2022,42(11):815−821(in chinese) doi: 10.13922/j.cnki.cjvst.202204023 Qin Rishuai, Meng Shida, Wang tao, et al. Analysis of Flow Rate and Pressure Characteristics for Multistage Thermal Transpiration Based Vacuum Pump[J]. Chinese Journal of Vacuum Science and Technology,2022,42(11):815−821 doi: 10.13922/j.cnki.cjvst.202204023 -
图( 6)
计量
- 文章访问数: 106
- HTML全文浏览数: 106
- PDF下载数: 2
- 施引文献: 0