在推导残余气体噪声之前，需要对气体分子与壁面的碰撞过程做出如下假设^[11]：（1）分子与壁面完全非弹性碰撞，碰撞后遵循余弦角分布的随机再发射；（2）气体温度视为均匀；（3）气体压力视为均匀的，间隙压力不受来自检验质量或其他部件的局部放气的影响；（4）由于LISA要求腔体内真空度达到10⁻⁵ Pa，所以忽略气体分子间相互作用力。

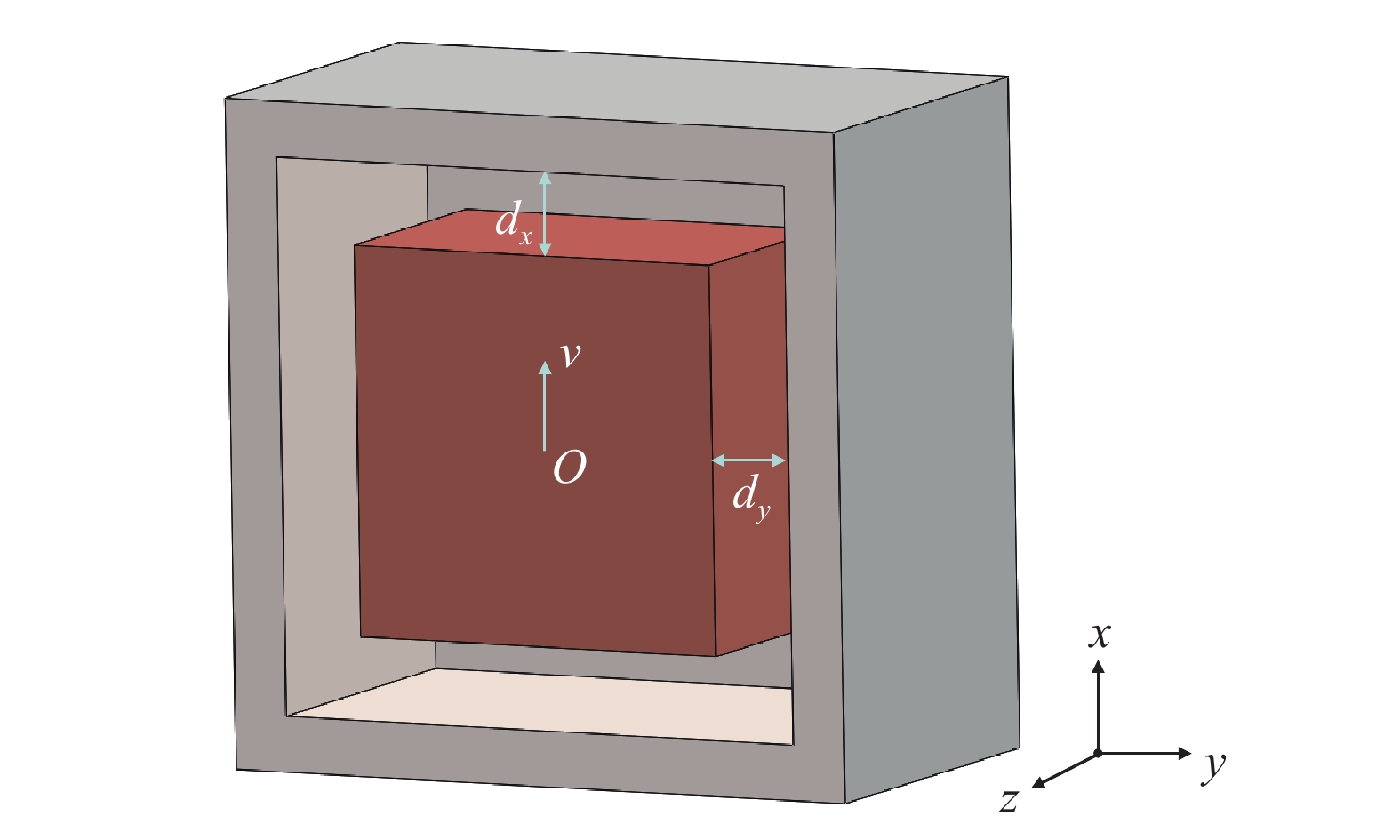
由于LISA中真实GRS结构过于复杂，本文中简化为立方体结构。如图1所示，假设TM位于GRS中心位置，TM与GRS在x、y、z轴上的间隙距离分别为$ {d}_{x} $、$ {d}_{y} $、$ {d}_{{\textit{z}}} $。当TM沿x轴方向以速度$ v=\dot{x}\left(t\right) $运动时，x轴的间隙会被挤压或拉伸，假设间隙变化量为x。由于间隙中的气体分子数密度守恒，分子会从被挤压面流向拉伸面，从而增强气体分子与壁面的碰撞概率。

根据以上描述，可以得到气体分子数密度改变率的恒等方程^[12]：

式中：n是分子密度的平均值；τ是分子扩散出x轴间隙所需要的时间，称为逃逸时间，是关于$ {d}_{x} $的函数。

在频域中TM速度表示为$ v=i\omega x $，代入式（2）得到^[9]：

将式（2）与理想气体定律$ P=n{k}_{B}T $结合，作用在与x轴正交面上的气体阻尼力可表示为^[9]：

作用于与x轴正交的TM表面上的剪切阻尼力可计算为^[9]：

如果$ \omega \gg 1/ \tau $，那么TM运动速度太快，分子来不及逃逸出间隙，$ {F}_{x} $变成一个弹性力。当$ \omega \ll {1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-\nulldelimiterspace} \tau } $，$ {F}_{x} $就是一个与频率无关的阻尼力。将式（3）与涨落耗散理论相结合，可得到力噪声^[9]：

除了对TM上的力噪声进行分析，还要计算TM上的扭矩噪声。当TM以速度$ v=\dot{\theta }r $沿z轴旋转时，平行于z轴的表面将受到增强的阻尼力的影响，其中r为表面上任何一点到z轴的距离。经过简单的积分运算，可得到扭矩噪声^[9]：

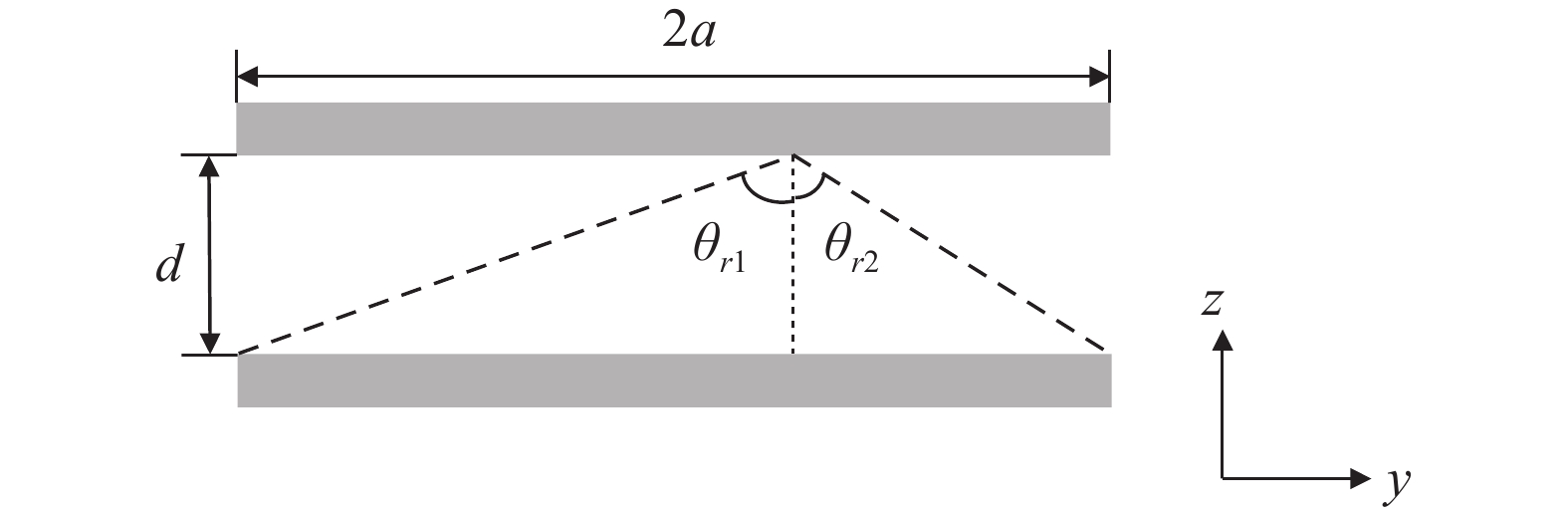
本文仿真采用两块面积相等的正方形板，如图2所示，假设边长为2a，在板间距离$d \ll a $的情况下，经过多次碰撞后，分子会从边界扩散出板，称总的碰撞的时间为逃逸时间。

在笛卡尔坐标系下，出射分子的速度分布可以写成^[9]：

对$ {\nu }_{x} $从$ -\infty $到$ \infty $进行积分得到：

分子逃逸出来之前与板的碰撞次数可以估算为$ \bar{{R}_{r}^{2}}/(4\left\langle{r}_{r}^{2} \right\rangle) $，其中$ \bar{{R}_{r}^{2}} $是矩形上任意点到边缘上任意点的距离在轴上投影的均方值，$\left\langle {r}_{r}^{2} \right\rangle $是分子发生连续两次碰撞的产生的侧向位移的均方值^[9]。

其中$ \varsigma =\dfrac{d}{2a} $。分子连续经历两次碰撞的概率为^[9]：

则逃逸时间为^[9]：

若考虑气体分子在板上的滞留时间，逃逸时间的计算还应加上单次的滞留时间与碰撞次数的乘积。

由于LISA引力波探测要求整体真空度小于10⁻⁵，板间气体流态处于分子流，几乎可以忽略气体分子之间的相互作用，只考虑气体分子与板的碰撞^[13]。本文采用MATLAB软件对板间分子运动进行MC仿真，通过对单个分子的运动轨迹进行研究，记录每次碰撞所需的时间以及横向位移等数据。

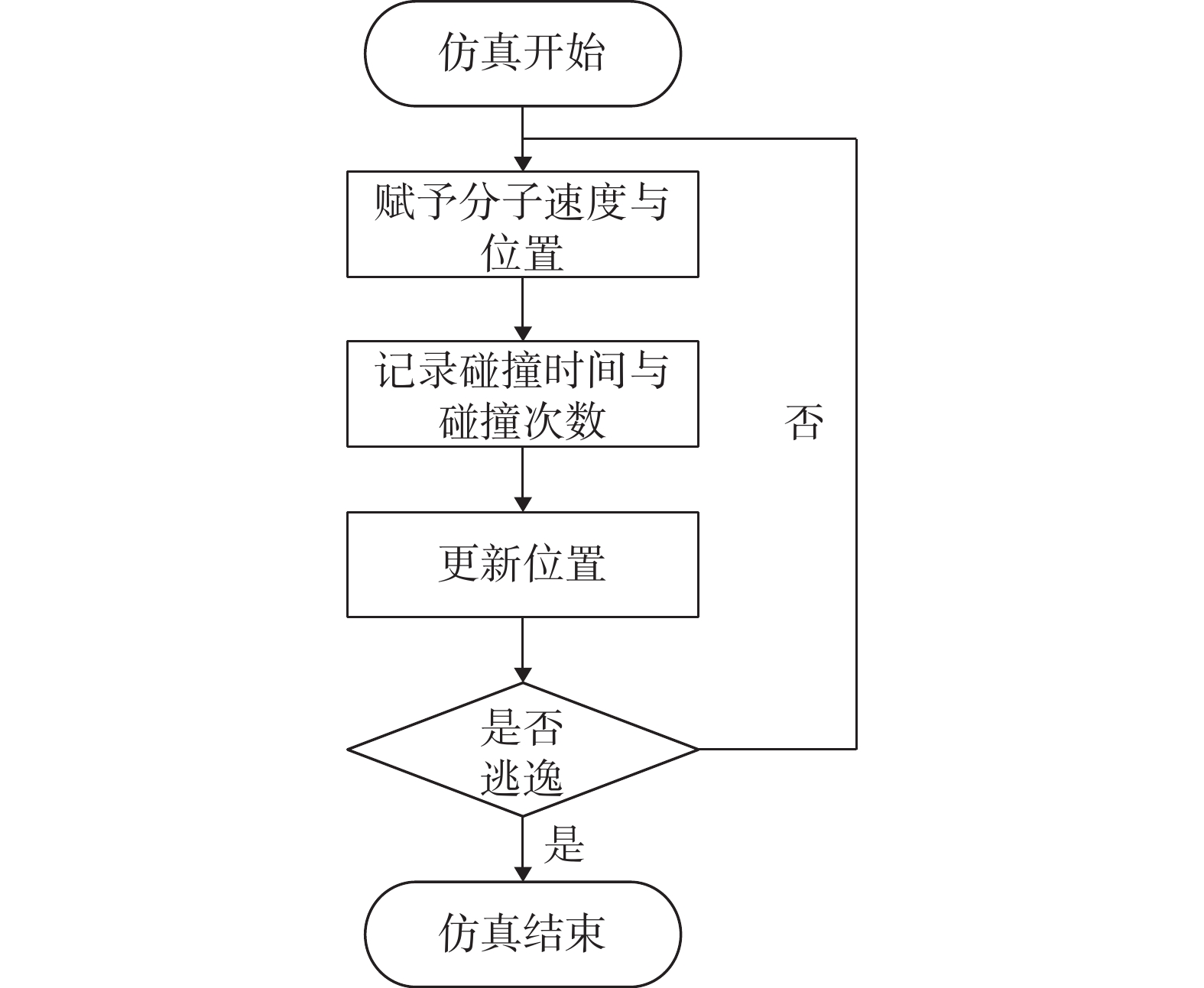
具体蒙特卡洛模拟流程如图3流程图所示。首先在板间给分子一个随机初始位置($ {x}_{0}，{y}_{0}，{{{{\textit{z}}}}}_{0} $)，分子的速度按照麦克斯韦-玻尔兹曼分布。在每次碰撞之后，记录碰撞所需的时间和碰撞次数，更新分子位置，记录分子在x-y平面发生的横向位移。然后依据分子的新坐标判定分子是否已经逃逸出平板距离，如果已经逃逸，就记录总时间和总碰撞次数；如果没有逃逸，就按照余弦定律给分子一个新的速度，继续仿真并重复上述步骤。每次碰撞时，考虑气体分子在板上停留的时间。一共重复模拟10⁴个分子，最终得到平均逃逸时间和平均碰撞次数。

余弦定律是指碰撞于固体表面的分子，飞离表面的方向与原来的方向无关，并按与表面法线方向所成角度$ \theta $的余弦而分布。其表达式为^[14-16]：

式中$ {\mathrm{d}}\omega $是角度$ \theta $ 与$ \theta+\mathrm{d}\theta $的两锥面间所包括的立体角。为了解释此定律，克努曾提出了“吸附层”假说^[13]，认为凡是与表面碰撞的分子都会在表面被暂时吸附，停留一段时间后再重新逸出，这段时间就叫做滞留时间，重新逸出后速度自然与原方向无关。

滞留时间的存在使得分子在碰撞之后会在固体表面吸附一段时间，单位时间内单个分子与固体表面的碰撞频率就会降低，从而对气体噪声产生影响。克努曾曾经提出一种可靠的间接测量滞留时间的方法^[17]，是基于气体分子在低压下不会互相碰撞时，通过狭窄毛细管的速度测定。分子流通过毛细管时，分子碰撞管壁停留一段时间，然后按余弦定律向各个方向重新蒸发。克努曾计算出分子通过长度为$ l $ 直径为$ d $的毛细管所需的平均时间，其值为：

其中$ \bar{u} $ 为分子的平均速度。式（14）中的第一项是由于再蒸发的余弦定律产生的，第二项则是由滞留时间 $ {\tau }_{R} $ 导致的。测得$ \bar{t} $后，反推出：

克努曾实验^[17]用的气体分子为氩气，在90 K时，$ {\tau }_{R} $ 为$ 3.1\times {10}^{-5} $ s，在78 K 时，$ {\tau }_{R} $ 为$ 75\times {10}^{-5} $ s。用氮气进行实验，得出氮气在玻璃上的滞留时间也有相同的数量级。因此，在本文仿真中，滞留时间采用$ 1\times {10}^{-5} $ s，即每次分子与固体壁面碰撞都会在表面停留$ 1\times {10}^{-5} $ s。

在先进LIGO的设计中，采用了半径17 cm的圆形检验质量，距离检验质量端面5 mm的位置有同样面积大小的反应质量，两个端面间的距离远远小于端面的半径，符合压膜阻尼的产生条件^[4]。在MAO等^[9]的研究中，已经证明了在满足$ d\ll R $ 时，端面的几何形状的差异可以忽略不计，所以本文选择与LIGO 检验质量端面面积相同的正方形板进行仿真。由于引力波测量装置真空度要求都在高真空，腔室内的气体分子主要是水和氢气，水与氢气的量约为5:3，温度为294 K，板间距离从10⁻⁴~10⁻¹ m之间对数均匀取13个值。

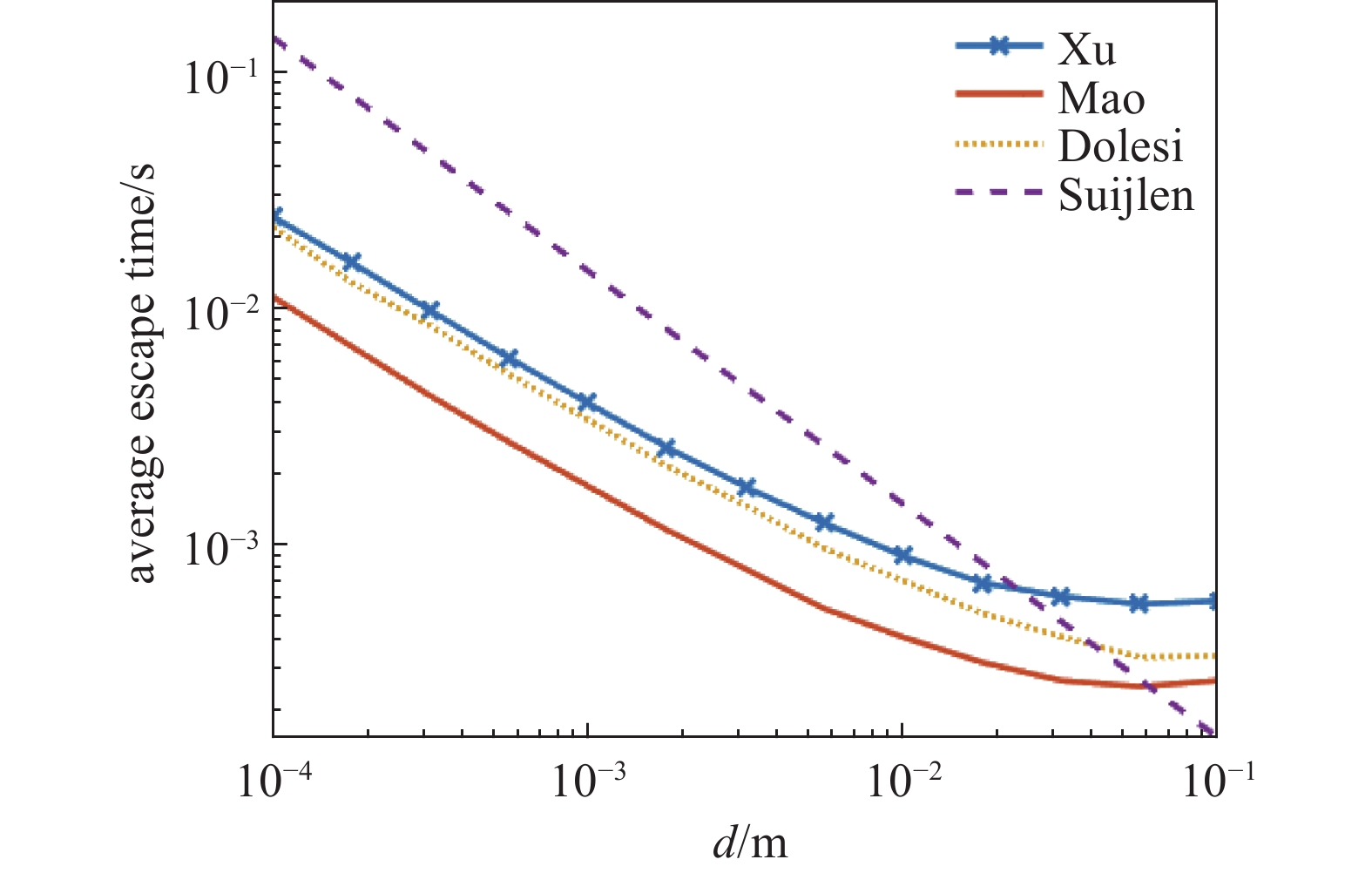
如图4所示， 在不考虑滞留时间的情况下，气体分子的平均逃逸时间随板间距离d 的增大而减小，逐渐趋于一个稳定值。这是由于当板间距离变大时，气体分子与板的碰撞次数减少，更容易逃逸出间隙，最终趋于稳定值是因为压膜阻尼产生的条件$ \mathrm{\mathit{d}}\ll\mathrm{\mathit{R}} $ 不再满足，从有限空间下的碰撞变成无限空间下的气体分子碰撞^[18]，即气体分子与板碰撞一次就逃逸不再碰撞。

本文仿真采用的是混合气体分子，水分子与氢气分子比例为5:3，而Mao等^[9]的研究中认为高真空下氢气是主要残余气体，所以只研究了单一气体。但是根据LISA Pathfinder的研究，如表2所示，引力波探测装置内并不只有氢气，甚至氢气不是主要残余气体，残余气体中最主要的成分仍然是水分子，其次是氢气分子，除此之外还有氮气、氧气、二氧化碳等等。由于本文采用了混合气体作为仿真对象，平均气体分子的质量变大，速度减小，逃逸出间隙时间更长，更符合实际。

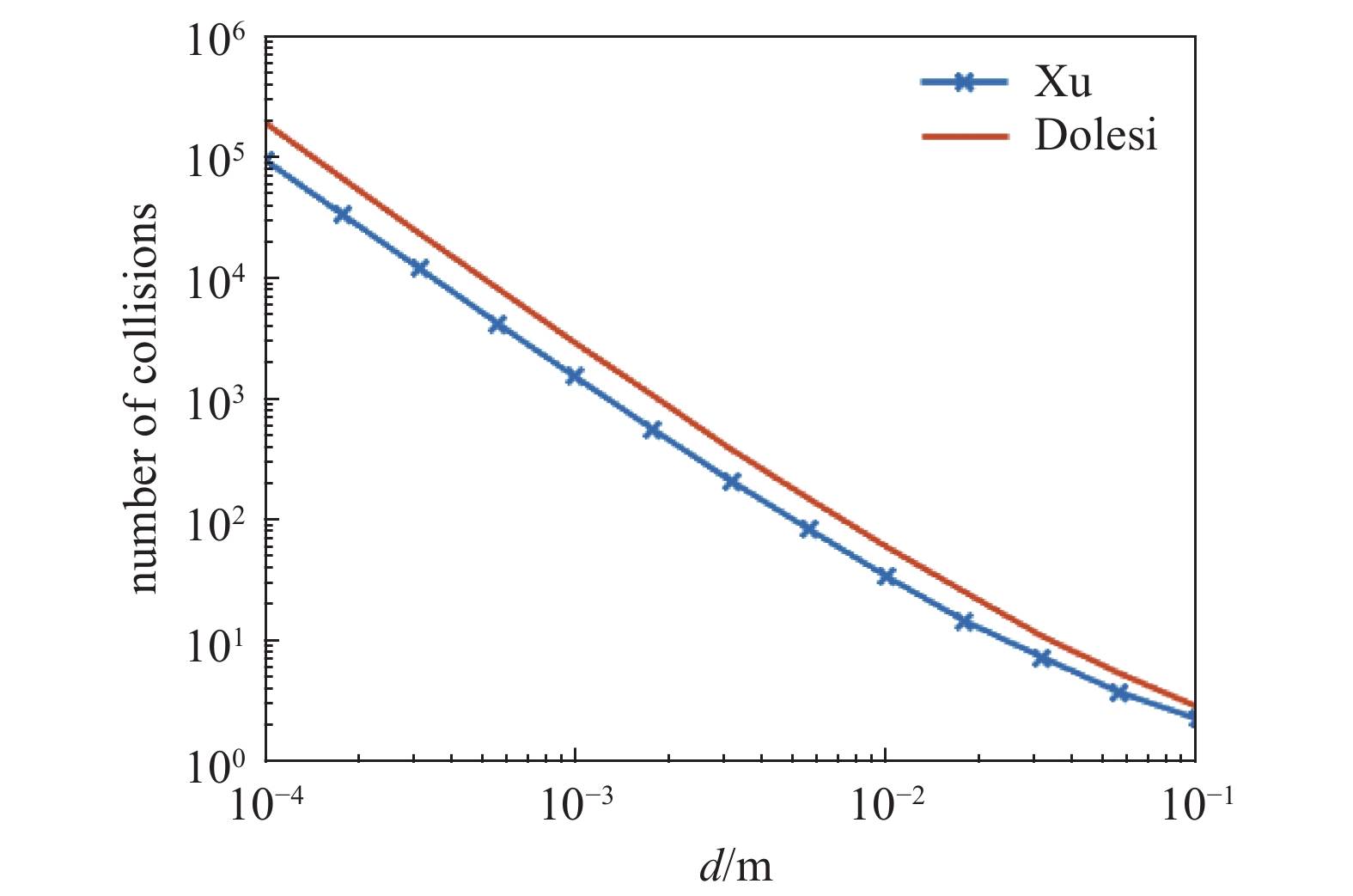
从图5可以看出，板间距离越近，气体分子离开间隙碰撞的次数越多。混合气体只改变仿真气体分子的质量、速度和逃逸时间，并不会改变气体分子与板的碰撞次数。在碰撞次数相同的情况下，气体分子的逃逸时间越长，气体分子与板碰撞的频率就越低，因此混合气体因素会对残余气体噪声产生一定影响。

根据式（4），在LISA Pathfinder引力波探测其中，对于2 kg的检验质量在293 K、水分子与氢气分子比例为5:3情况下，$ {m}_{0} $约为12 amu，估计残余气体阻尼产生的加速度噪声为：

则惯性传感器中的压强p应低于$ 1.15\times {10}^{-5}\,{\mathrm{Pa}} $，才能满足由残余气体阻尼产生的噪声小于$ 3\times {10}^{-15}\,{\mathrm{m}}/{\mathrm{s}}^{2}/{\mathrm{H{{z}}}}^{1/2}$的预算。

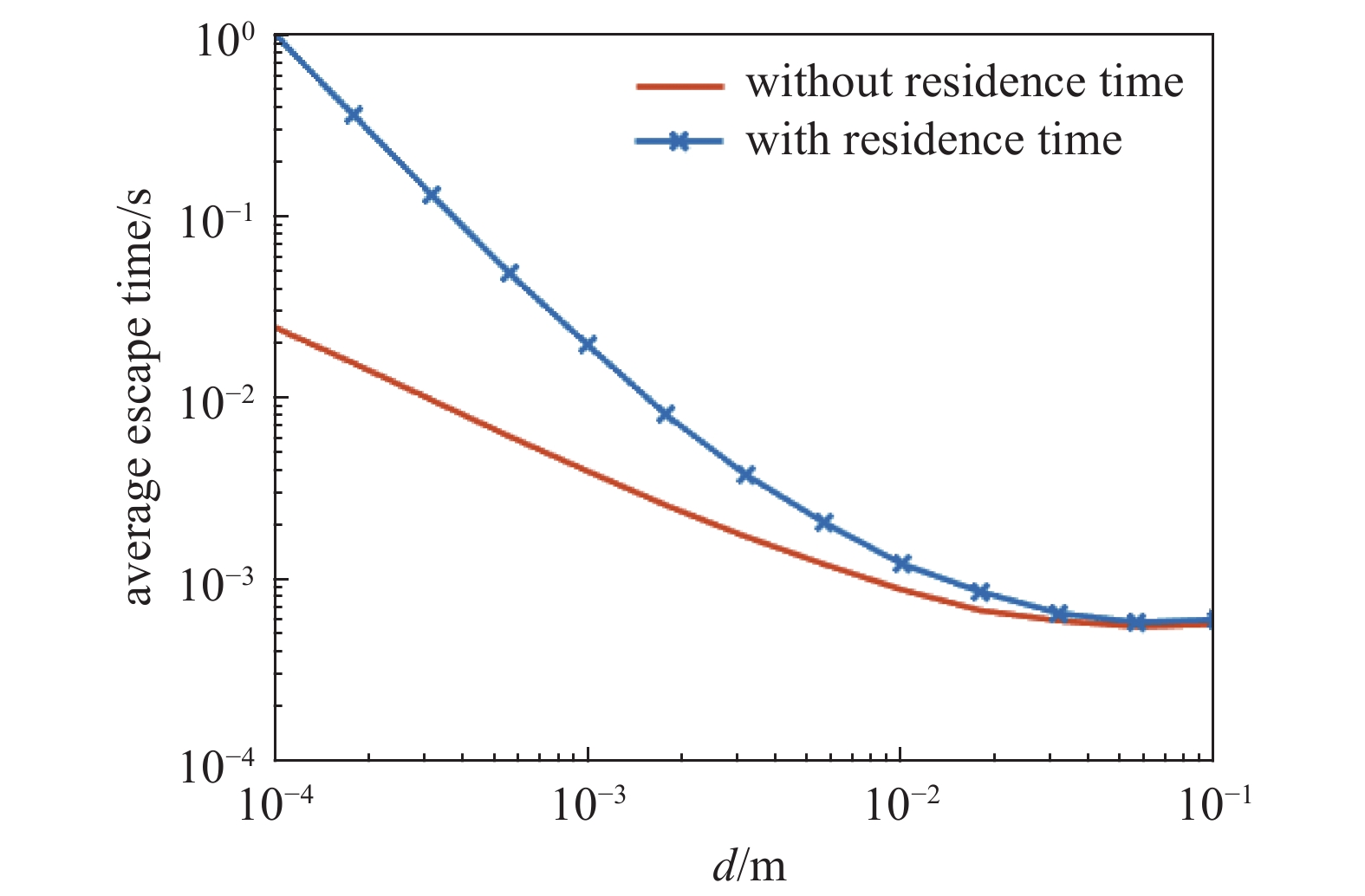
在混合气体条件下，仿真中加上滞留时间效应，结果如图6所示。由于只是增加了滞留时间效应，对分子在板间的运动并未产生影响，所以碰撞次数没有改变。逃逸时间总体趋势仍是随板间距离增加而减小，但考虑滞留时间的情况下的逃逸时间数值比不考虑要大得多，且降低的趋势更陡。这是因为考虑滞留时间之后，由于滞留时间为定值，气体分子在板上总的滞留时间依赖于碰撞次数，而逃逸时间是气体分子在板间运动的时间与总的滞留时间的和，所以考虑了滞留时间之后，逃逸时间很大程度上依赖于碰撞次数。

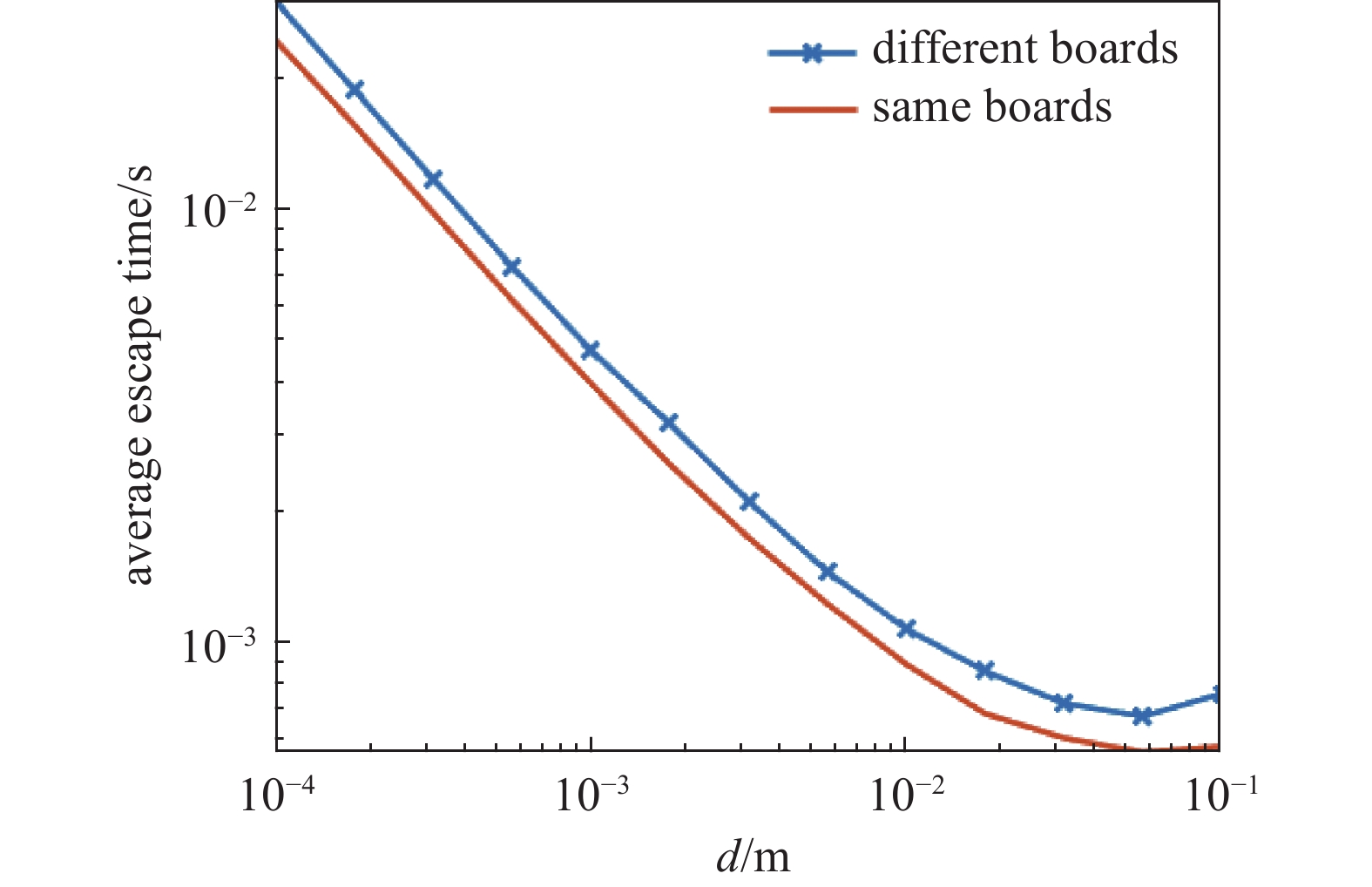
由于引力波探测装置中，GRS和TM的材料不同，表面处理也不一样，而且在太空极端环境下，两个板间存在一定温差，这些不同点会给与板碰撞的气体分子不同的反射速度^[20]。本仿真将其中一块板的碰撞速度分布保持不变，将另一块板碰撞后的气体分子速度分布除以$ \sqrt{2} $，旨在研究不同板对残余气体分子噪声的影响。结果如图7所示，由于只是改变了其中一个板的速度分布，气体分子在板间的运动时间更长，但是并不会改变气体分子的运动轨迹，因此逃逸时间比相同板更长，而碰撞次数没有改变。随着间距增大到 10⁻² m以上，逐渐不符合$ \mathit{\mathrm{\mathit{d}}}\ll\mathrm{\mathit{R}} $的假设，仿真结果失去规律。

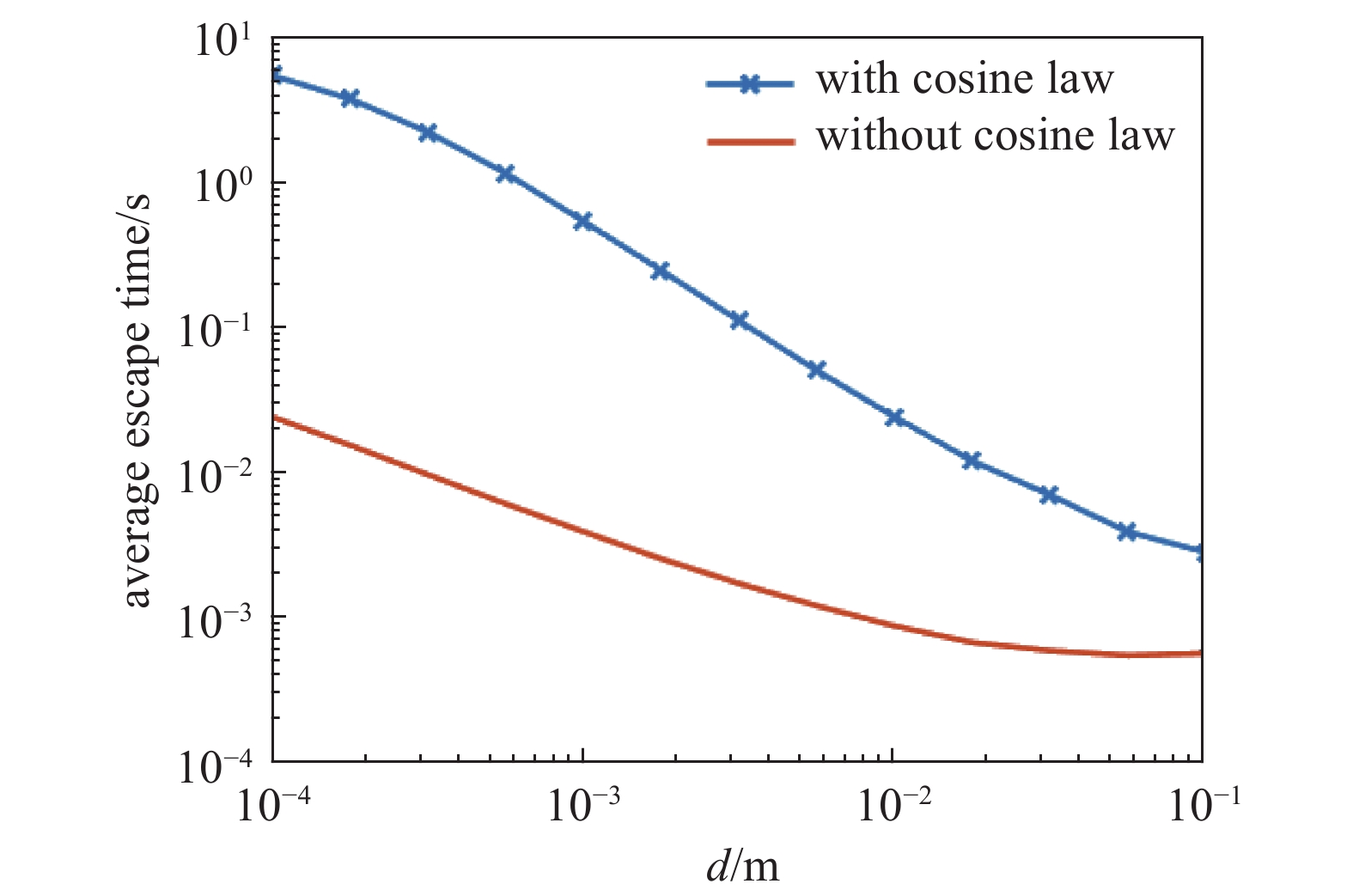
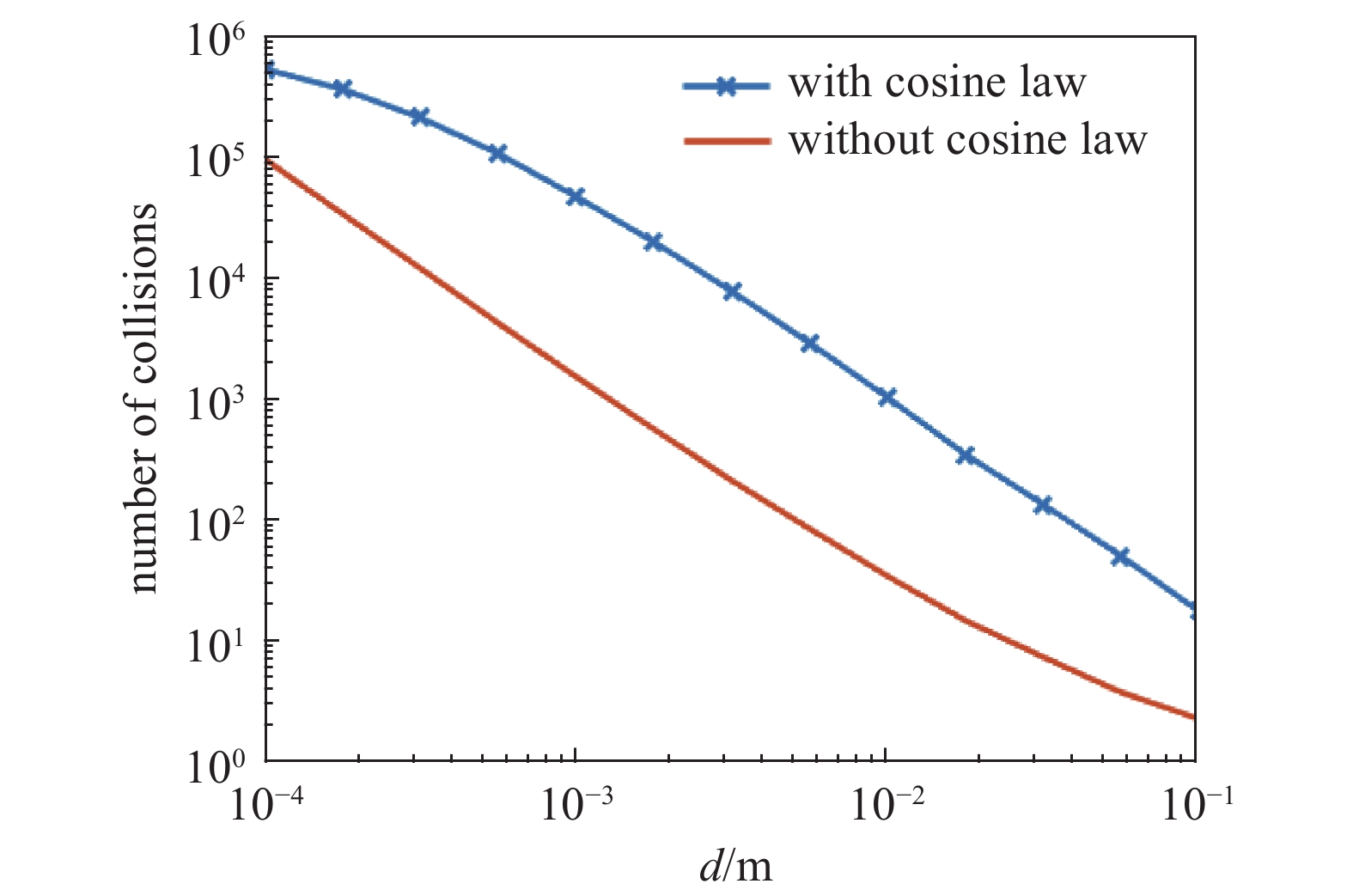
在仿真中考虑角度余弦之后，即每次气体分子与壁面碰撞后，气体分子的速度不再按麦克斯韦分布随机赋值，而是按照余弦定律赋予随机方向。仿真结果如图8、图9所示。在考虑角度余弦的情况下，气体分子逃逸出间隙所需的碰撞次数是不考虑的7-8倍，所需的时间也随着碰撞次数增加而增加，整体趋势仍随着间距减小而增大，但是与不考虑相比，不同点在于间距较大时，线型较为陡峭，而随着间距小于10⁻³ m，逃逸时间不再按直线增加。

本文通过理论推导完善了残余气体噪声模型，得出了残余气体噪声与气体分子逃逸时间之间的关系，推导了逃逸时间的计算公式，通过MC仿真方法探究了残余气体分子在正方形板间的逃逸时间与板间距离的关系，主要考虑了混合气体、气体分子在碰撞时的滞留时间、异性板和角度余弦等因素，发现逃逸时间与气体分子的成分有关，残余气体噪声随平均分子质量线型增加，当气体组分为水分子与氢气分子比例为5:3情况下，惯性传感器中压强p应低于$1.15\times {10}^{-5}\,\,{\mathrm{Pa}}$，才能满足LISA中由残余气体阻尼产生的噪声小于$3\times {10}^{-15}\,\,{\mathrm{m}}/{\mathrm{s}}^{2}/{\mathrm{H{{z}}}}^{1/2}$的预算；考虑滞留时间会在小间隙时大幅增加气体分子的逃逸时间，增加的逃逸时间与碰撞次数成正比，但对碰撞次数本身没有影响，所以单个气体分子的碰撞频度会大幅降低；异性板也会对逃逸时间造成影响，但是只考虑不同板碰撞后速度不同的影响是线性的、可计算的，残余气体噪声随之线性变化；角度余弦的加入会对逃逸时间和碰撞次数都产生较大影响。由于现在取的滞留时间值为定值，且未考虑碰撞损失，后续将对滞留时间、碰撞损失等进行进一步仿真设计。