首页
登录
注册
-
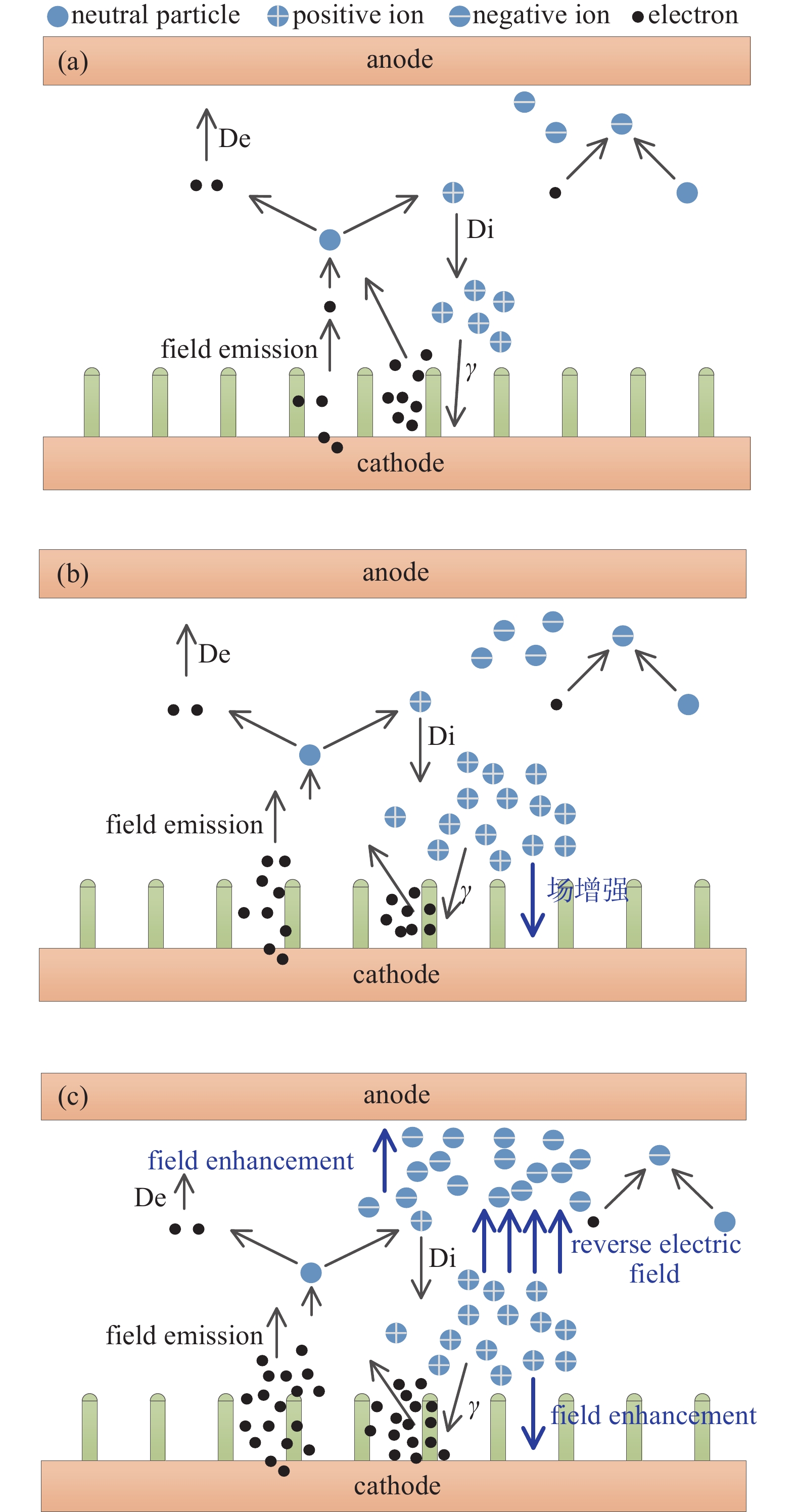
微电晕器件将放电空间限制在亚毫米量级以下，可以使低温等离子体在常压下稳定运行，随着研究不断深入可应用于生物医学、电离式气体传感器、微型质谱仪、微化学分析等方面，具有响应快、低功耗等特点[1-4]。微电晕放电属于局部自持放电，与击穿的瞬间高能放电相比，放电过程更为缓慢、具有可调制性，然而目前对微电晕器件放电机理的认识仍然不足，如何在降低功耗提高放电效率的同时保持放电过程长期稳定的问题依然存在，因此对微电晕放电机理的研究可为微电晕器件的设计、优化及调制提供依据[5-6]。而目前对微尺度下气体放电过程中不同参数的演变规律在实验诊断中难以获取，基于仿真模型的数值模拟依然是研究微尺度气体放电的重要工具[7-8]。
目前对微尺度气体放电机理的研究也在不断进行，2014年廖瑞金等[9]基于流体力学模型建立了电晕放电混合模型，研究得到放电过程中正负离子数密度的变化过程，发现了负离子对放电过程起抑制作用，而中性粒子含量较少。2018年Fu等[10]基于二维流体模型计算了阴极表面具有不同突起时的微间隙气体放电电压-电流曲线，研究了突起尺寸和纵横比对间隙击穿电压的影响，发现突起尺寸对击穿电压的影响比突起的纵横比产生的影响更大。2020年王林华等[11]通过推到计算得出在间距为1 μm−10 μm时由于阴极表面的离子密度很大会产生很强的离子增强效应，然后画出离子增强效应二次系数 γ'与 Townsend 二次系数 γ的比值随间距变化的曲线发现1−5 μm时，放电由场致发射主导，10 μm−100 μm时的放电过程可用Townsend理论解释。2021年Cejas等[12]基于流体模型的研究了大气压空气放电，结果表明当阴极场强超过45 V/μm时场致发射会引起辉光放电转变为电弧。2022年李彦森等[13]研究了不同气压下微间距气体放电的过程，发现pd值超过80 Pa∙cm后击穿电压U随pd的变化曲线与传统Paschen曲线基本一致，且间隙5 μm以下的间隙击穿由场致发射主导。2023年陈芸等[14]求解了阴极表面离子数密度公式，发现气压越高离子密度越大，间距越大离子密度越小，离子密度越大离子增强效应越强，越容易击穿，且在5 μm以下时最为强烈，间距大于10 μm后符合Townsend理论。2023年常泽洲等[15]通过二维粒子仿真及实验发现间距小于5 μm时，阴极表面场强足够产生场致发射且场致发射电流占阳极电流95%以上。目前微尺度击穿机理已经得到较为充分的研究，认为二次电子发射和场致发射在不同微间隙范围内维持放电并主导击穿过程，但是对于微尺度的低能放电过程，当前机理研究主要考虑了离子轰击阴极的二次电子过程[16-17]，而场致发射的作用尺度和影响机制尚不清晰。对此本文基于流体-化学混合模型框架，融合F-N发射及二次电子发射，建立了二维微电晕放电模型，仿真计算两种电子发射模型的放电过程，通过分析电子密度分布、空间电离速率变化、离子及电场分布等参量揭示场致发射对电晕放电过程的影响，阐明场致发射、二次电子发射、电子碰撞反应在微尺度不均匀场中的耦合机制，完善微电晕放电机理。
-
流体力学模型主要通过求解粒子的连续性、动量和能量方程来分析空气放电过程中粒子数密度、速率和能量，并将上述方程与泊松方程联立求解获得自洽的电场。本文在流体-化学混合模型的基础上又考虑了场致发射与二次电子发射过程。因此本文的控制方程如下。
电子连续控制方程为：
式中，
${n_{\mathrm{e}}}$ ，$ {{{\varGamma }}_{\mathrm{e}}} $ ，$ {R_{\mathrm{e}}} $ ，$ {\mu _{\mathrm{e}}} $ ，$ {D_{\mathrm{e}}} $ 分别为电子数密度、电子通量、电子净生成率、电子迁移率、电子扩散率；$ \nabla $ 为拉普拉斯算子；$E$ 为电势；$M$ 为产生与消耗电子的化学反应的个数；${x_j}$ 与${k_j}$ 分别为反应$ \mathit{{j}} $ 中的目标物质的摩尔分数与化学反应速率；$ {N_{\mathrm{n}}} $ 为中性粒子的数密度。电子动量方程为：
式中，
$ {m_{\mathrm{e}}} $ ，$ {u_{\mathrm{e}}} $ ，$ {p_{\mathrm{e}}} $ 为电子的质量、漂移速度、压力张量；$q$ 为电荷；$ {v_{\mathrm{m}}} $ 为电子动量的传递碰撞频率。电子能量守恒方程：
式中，
$ k\mathrm{_B} $ 为玻尔兹曼常数，$ T_{\mathrm{e}} $ 为电子温度；${n_k}$ 、$ \eta_k$ 、$ M_k$ 分别为粒子$k$ 的密度、电子碰撞过程中的能量损失系数、质量；$T$ 为气体温度；$ j_{\mathrm{e}}\cdot E $ 为电子由于焦耳加热效应获得的能量。重粒子（正负离子、中性粒子）连续控制性方程：
式中，
$ {\rho _{{\mathrm{z}}}} $ 为总混合物粒子数密度；$ j_k$ 为扩散通量矢量；$ {u_\mathrm{m} } $ 为质量平均流体速度矢量；$ w_k $ 、$ R_k$ 、$ V_k$ 分别为粒子$k$ 的质量分数、反应速率表达式、多分量扩散速度。泊松方程：
式中，
${\varepsilon _0}$ 为真空介电常数；$ \varepsilon\mathrm{_r} $ 为相对介电常数；$V$ 为电势；$ {\rho _ {\mathrm{b}} } $ 为表面电荷密度。 -
仿真模型以空气为背景气体，设置N2-O2比例为
$4:1$ 。由于许多粒子的产生与猝灭过程极其短暂，简化空气放电的化学反应及粒子种类并不会对整体产生明显的影响[18]。因此本仿真添加了包括${\text{e}}$ ，${{\text{N}}_2}$ ，${{\text{O}}_2}$ ，${\text{O}}$ ，${{\text{O}}_3}$ ，${{\text{N}}_2}{{\text{A}}_3}$ ，${{\text{N}}_2}{{\text{a}}_1}$ ，${\text{N}}_2^ + $ ，${\text{N}}_4^ + $ ，${\text{O}}_2^ + $ ，${\text{O}}_4^ + $ ，${{\text{N}}_2}{\text{O}}_2^ + $ ，${\text{O}}_2^ - $ 共13种物质之间的33个反应[19-20]，包括电离、复合、吸附等过程，具体的化学反应式如表1所示。 -
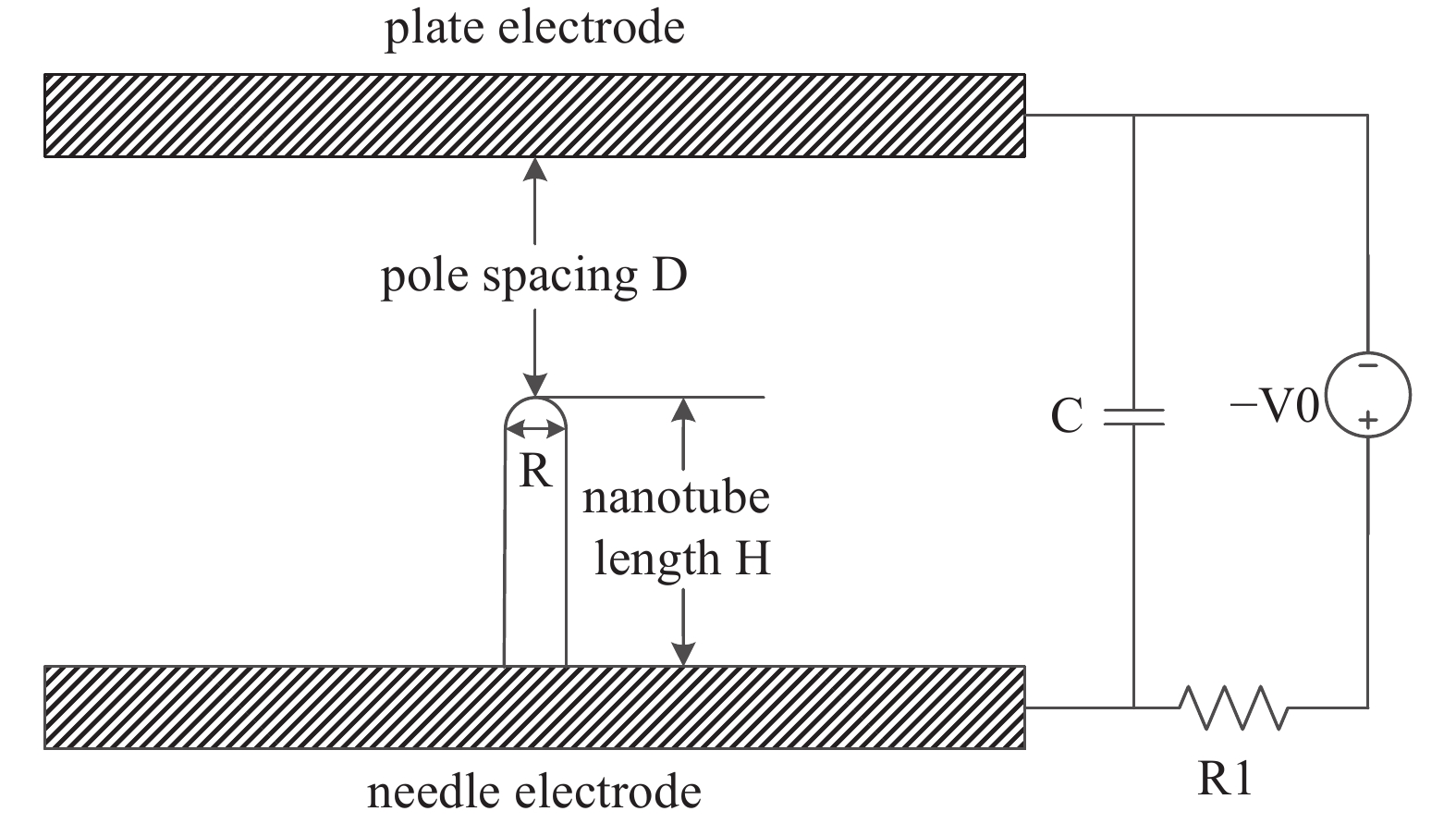
二维仿真模型如图1所示，其中纳米管的长度为 H = 20 µm、直径为 R=0.1 µm,极板长度为 L = 30 µm，电压为 V0 = −200 V。温度与压强分别为293.15 K、1 atm。为研究放电过程中放电机理的耦合关系，在仿真过程中固定电极的形貌，只改变极间距D。
（1）阴极二次电子发射
本文将二次电子发射考虑在内，因此正离子在模型的边界不仅会发生表面反应，还会引起电极二次电子发射现象，在目前仿真中二次发射系数与平均电子能量取值范围分别为0.001−0.5和1−5 eV[21]，但本模型中纳米尖端处的场强要大于平板处，因此 尖端处的势垒更低,二次发射系数要大于其他部分。具体数值如表2所示。
（2）阴极场致电子发射
纳米线的场增强因子[22]由纳米线高度、极间距和纳米线半径计算得到，发射电流密度
$ {j_{\mathrm{FN}}} $ 的变化根据阴极表面瞬态场强由F-N模型[23]描述，计算公式如下所示。式中，
$\beta $ 为场增强因子；${E_\varphi }$ 为表面功函数；常数$ {A_{\mathrm{FN}}} $ =1.541×10−6，$ {B_{\mathrm{FN}}} $ =6.830×109；${t^2}\left( y \right)$ 与$v\left( y \right)$ 为：（3）边界条件
边界条件也是仿真模型极为重要的部分，包括了电子、离子、中性粒子边界条件。
电子通量包含二次发射、电子迁移、场致发射，在阴极和阳极边界条件为：
式中，
$ {{{\varGamma }}_{\mathrm{e}}} $ 为电子的密度通量；$ {{{\varGamma }}_{\mathrm{i}}} $ 为离子的密度通量；${q_i}$ 为第$i$ 个离子的带电量；$ {{{\varGamma }}_{\mathrm{FE}}} $ 为场致发射通量，由式（9）进一步推导得到；$ {v_{\mathrm{th,e}}} $ 为电子的热速率；$ {m_{\mathrm{e}}} $ 是电子的质量。离子通量在阴极和阳极两电极的边界条件为：
式中，
$ {{{\varGamma }}_{\mathrm{i}}} $ 为离子的密度通量；$ {v_{\mathrm{th,i}}} $ 是离子的热速率；${m_i}$ 是离子的质量；$\alpha $ 为电离系数；${\mu _i}$ 为第$i$ 个离子的迁移率。中性粒子在放电电极上的边界条件为：
式中，
$ {{{\varGamma }}_{\mathrm{n}}} $ 为离子的密度通量；$ {v_{\mathrm{th,n}}} $ 是离子的热速率；$ {m_{\mathrm{n}}} $ 是离子的质量。 -
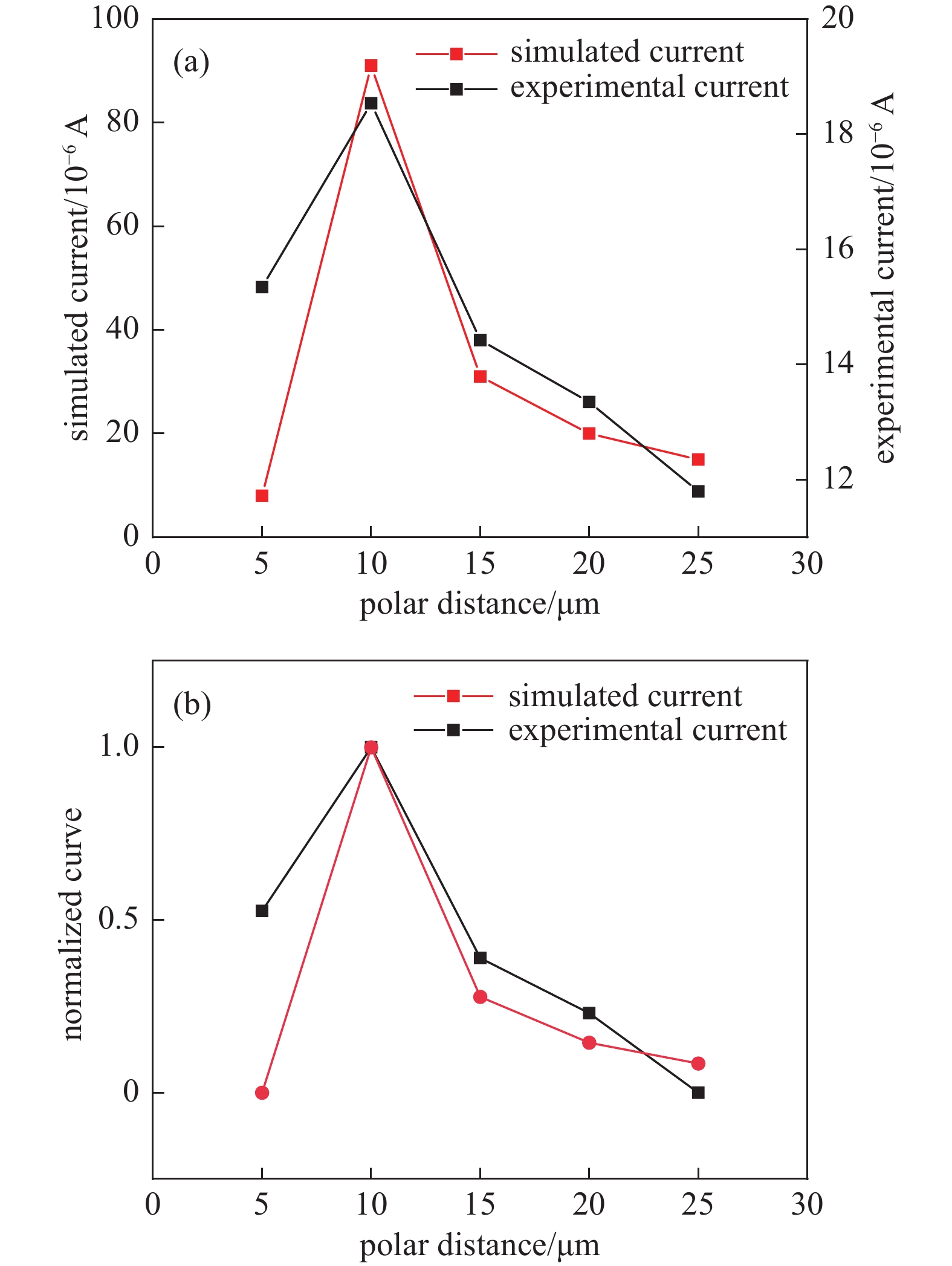
本文搭建了实验平台以验证所建立模型的有效性。针电极采用纳米管高度为20 µm的硅纳米线阵列，表面平整硅片作为板极。利用分辨率为1 µm的内径千分尺控制两极板间距。外加200 V直流电压由IT6576D高精度直流电源提供。放电电流由6482型双通道皮安表测量，测量精度0.1%，量程1 pA~20 mA。调节千分尺，分别测试间距25 μm，20 μm，15 μm，10 μm，5 μm下的放电电流。为了保证实验数据的准确性，不同间距分别进行5次实验求取平均值。
实验电流数据与仿真电流数据如图2所示，由于仿真条件参数与实验参数不严格一致，放电电流在数量上存在较大偏差，但从电流对比和归一化对比可以看出，放电强度随间距的变化趋势相似，可以定性验证本文仿真模型的准确性。
-
为分析场致发射对微电晕放电的作用及影响程度，本文固定激励电压，一维纳米电极形貌以及电路阻容参数，通过等距调节放电极间距D （25 μm，20 μm，15 μm，10 μm，5 μm）仿真计算两种模型放电过程，其中一种模型同时考虑阴极的二次电子发射和场致电子发射，另一种模型没有考虑场致电子发射过程。
-
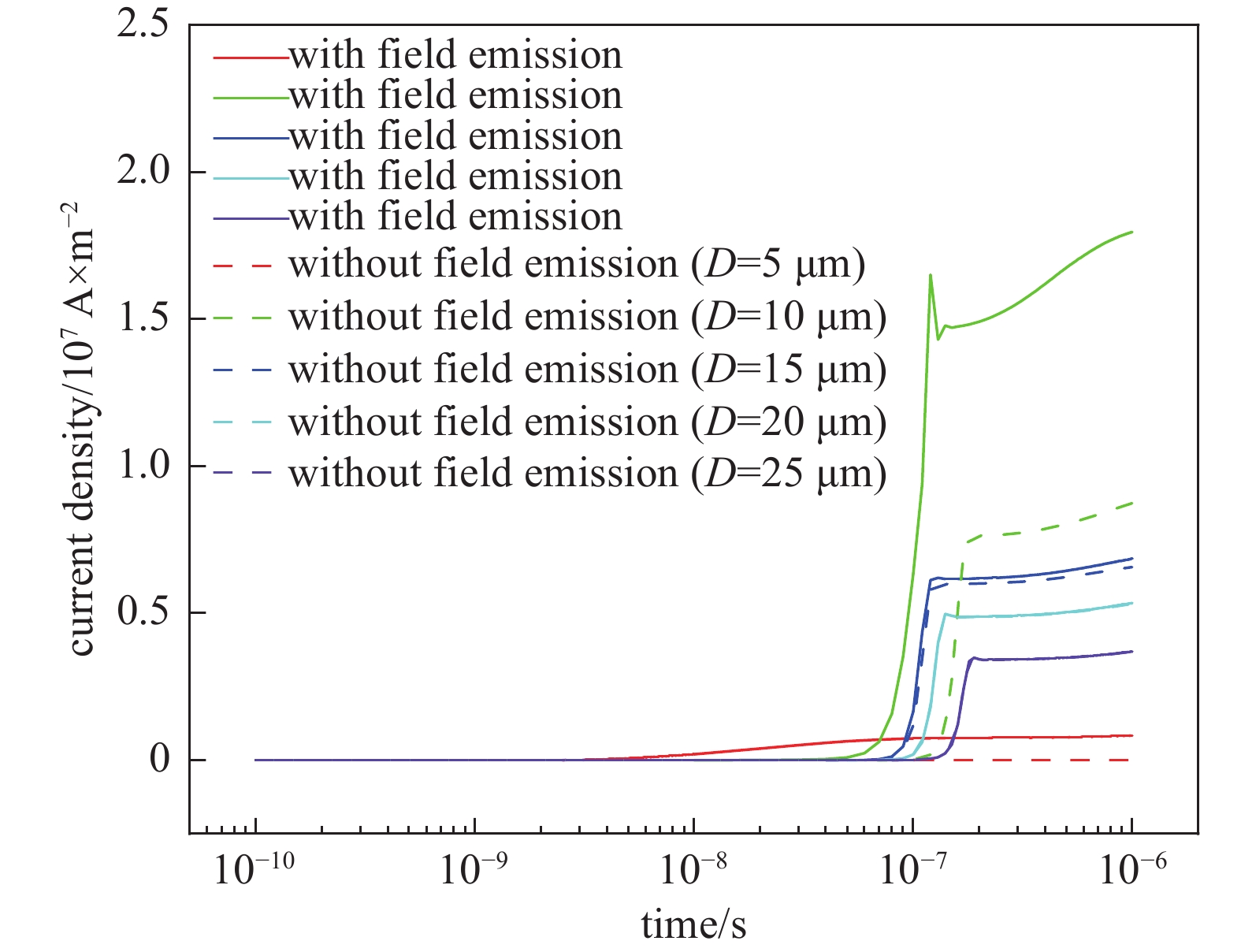
在图3中可以看到两种模型的共同点，随着极间距等距减小，放电电流密度先增大后减小，对于25 μm，20 μm和15 μm三个极间距，两种模型放电电流密度的差距非常小。间距减小到10 μm时，相比无场致发射模型，有场致发射模型电流密度增长比例达98%，而场致发射电子流密度占电流密度不超过1% （如表3所示）。间距为5 μm时，放电强度骤减，这是由于随着间距进一步缩短，电子从阴极到阳极的过程中碰撞总电离次数降低，抑制了空间电离的发展。综上，场致发射对微电晕放电的影响不是简单的线性累加。
由图3和表3可知，放电强度是二次发射、场致发射和空间电离耦合作用的结果，因此本文以放电最强的10 μm放电模型为对象，详细分析微电晕放电的发展过程及场致发射对微电晕放电的影响。
-
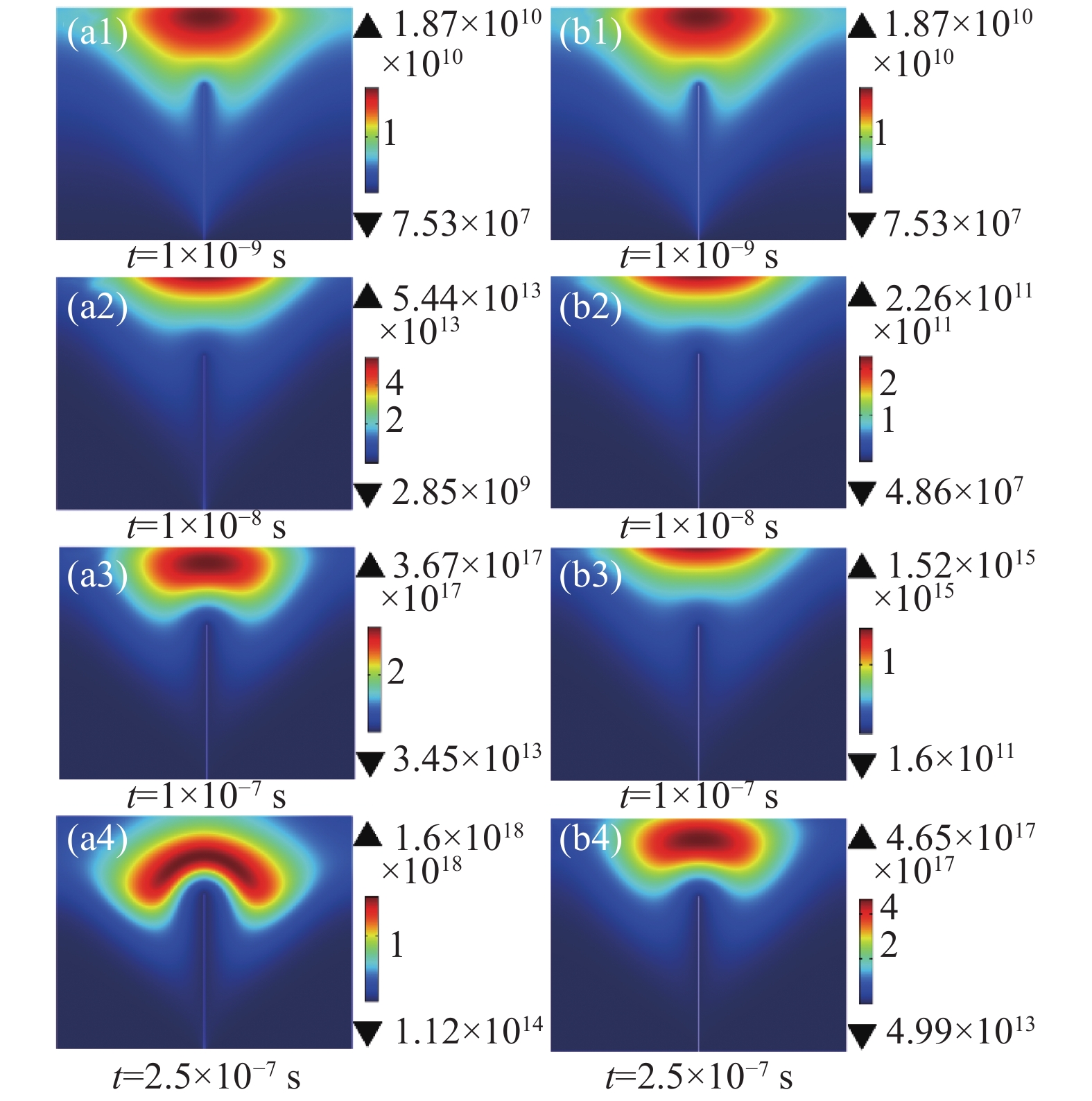
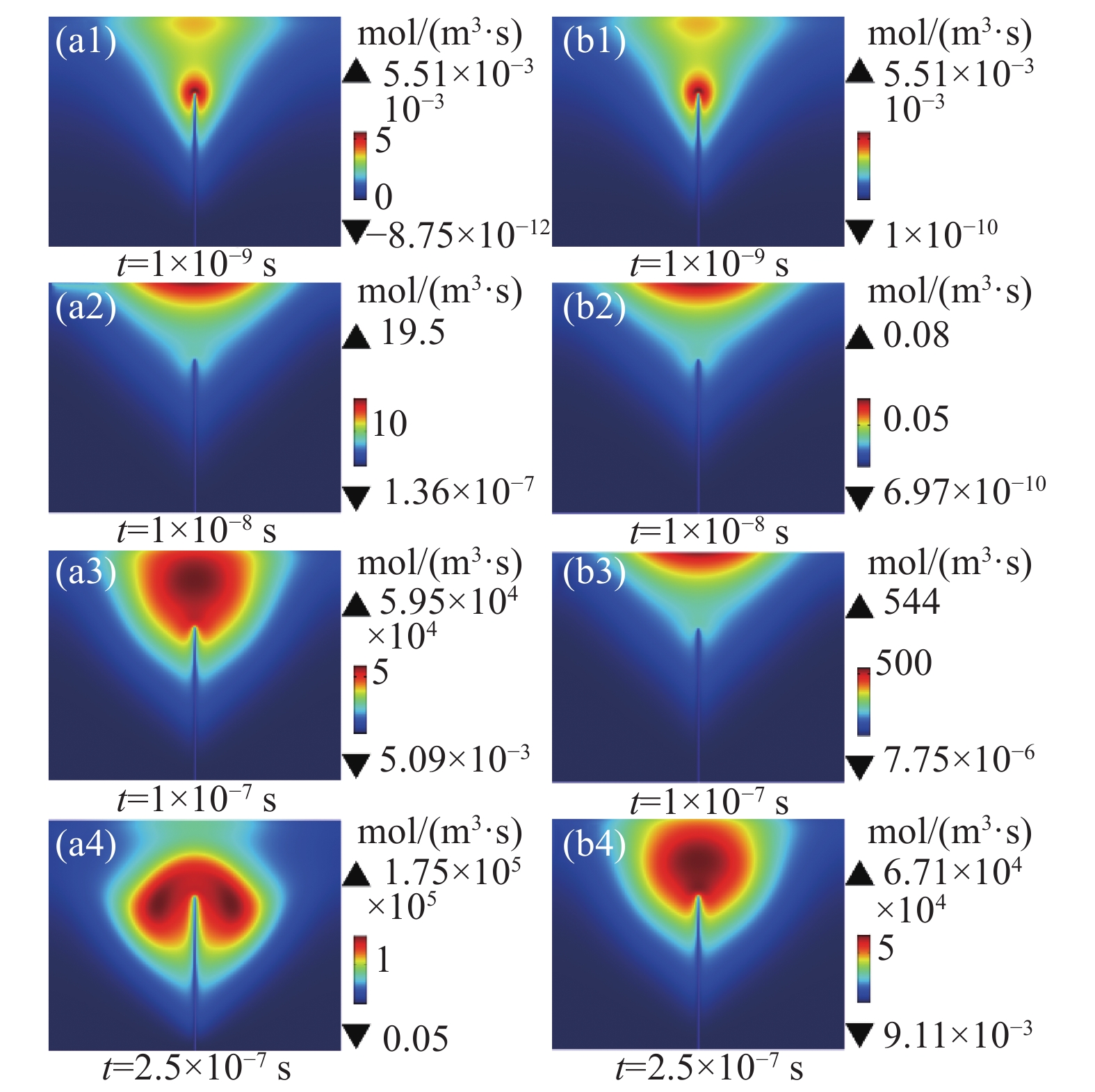
电子密度是电子漂移运动的宏观体现，电子通过漂移完成能量累积与传递，推动气体分子的电离过程。图4为两种情况下相同时刻的空间电子密度分布图，由图可以看出两种情况下的电子密度分布整体呈现出相同的规律，即电子团由纳米尖端开始向阳极发展，到达阳极后保持一段时间，之后向纳米尖端发展，但两种情况下电子团的发展速度及数值有很大差异。
空间电子密度分布如此变化，主要是因为电路中电容的存在使得微电晕器件两端电压在初始阶段缓慢上升，电场较小不足以导致空间电离。随着电场增大空间电离概率增大， 电子在电场的作用下向阳极迁移并电离中性粒子产生电子与正离子。产生的电子与原来的电子向阳极继续迁移并电离其他中性粒子，而正离子向阴极迁移并在电场中获得能量轰击阴极表面产生更多的二次电子发射，这又进一步促使空间电离速率增大，如此循环使得空间放电不断发展。但此时的阴极场强不足以导致场致发射，因此两种情况下的放电还没出现差异，如图4(a1)和图4(b1)所示，直至1E-9s，场致发射开始产生影响，如图5所示，两种情况下放电过程出现差异。场致电子发射与二次电子发射同时产生种子电子，使得有场致发射情况下的空间电离速率更大，有更多的正离子产生并轰击阴极产生二次发射，更强的促进空间电离，这使得有场致发射的情况下电子密度更大，如图4(a2)和图4(b2)所示。随着放电的发展因碰撞速率不断增大使得到达阳极的电子的电子能降低，使得附着反应加快了电子的消耗，产生了更多的负离子，负离子积聚使得阳极表面场强增大，电子在阳极表面的复合加快，阳极表面的电子密度减小，电子团呈现出向纳米尖端发展 ，而有场致发射的情况下，空间电离速率及二次发射增长更快，空间放电过程更为剧烈，上述过程发展更快，如图4(a3）和图4(b3)。而后随着空间放电趋于稳定，空间电子密度分布及数值基本保持不变，如图4(a4）和图4(b4)。
-
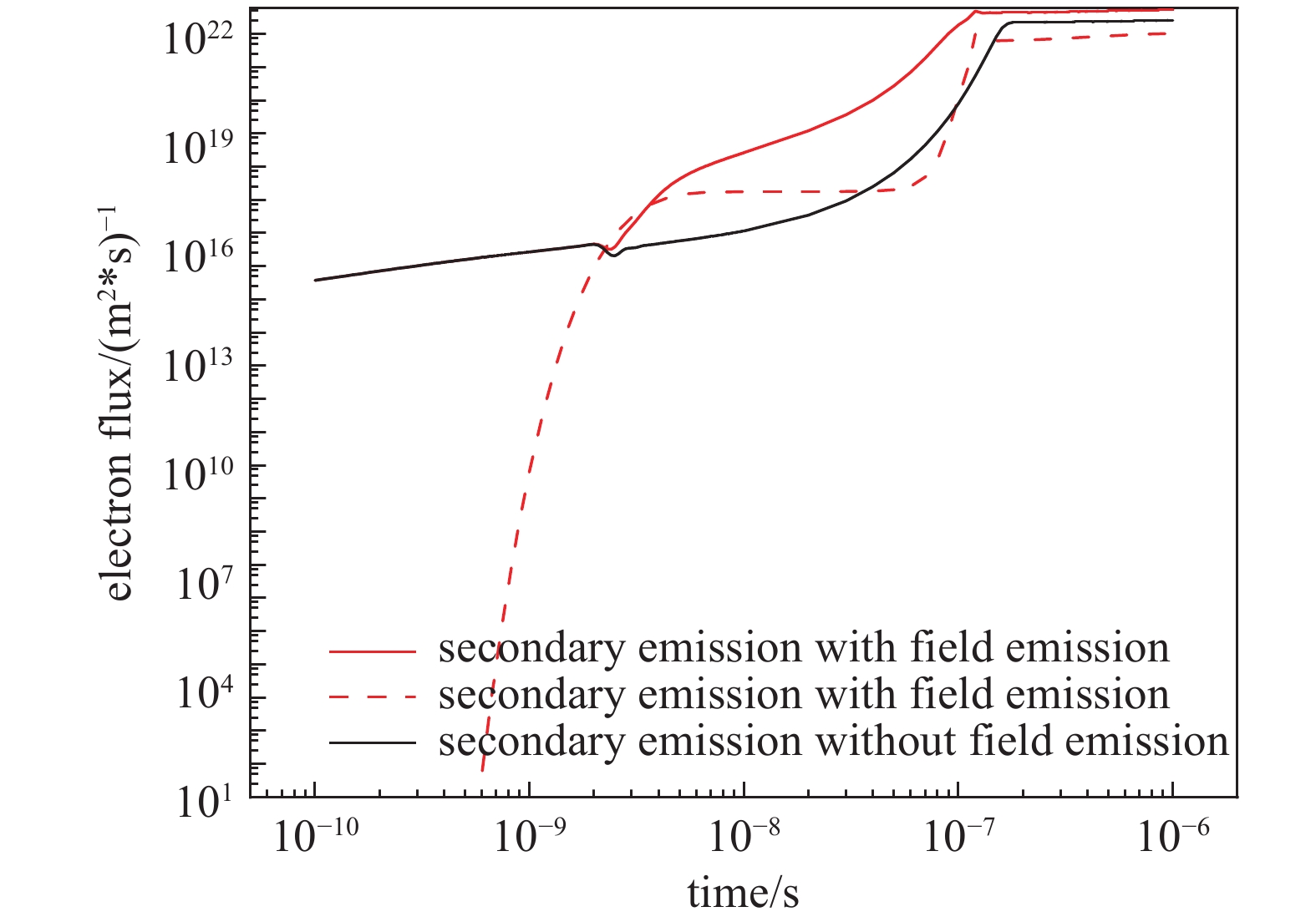
电子碰撞电离速率与电子能量和碰撞截面密切相关，可用于分析场强以及种子电子密度的变化对空间放电的影响。图6为两种情况下相同时刻的空间电离速率分布图。在放电起初由于空间场强较小、纳米尖端因尖端场增强效应具有较大的场强，因此空间电离主要集中于纳米尖端上方，随着电子远离尖端电子能降低，碰撞电离越来越微弱。放电不断发展，电场不断增大，使得电子在远离纳米尖端后依旧可以在电场的作用下获得足够能量，且在空间中发生弹性碰撞时不会损失大量能量，因此电子在向阳极迁移过程中可以积累能量，在到达阳极表面后足以电离中性粒子，如图6(a1）和图6(b1)。随后电场继续增强，电子在向阳极迁移的过程中不断电离产生新的电子，新的电子与原来的电子又电离产生电子，发展至阳极表面后使得阳极表面的电离速率极大提高，如图6(a2)和图6(b2)，但此时的空间的电场并未发生畸变，两种情况下的电场分布相同，因此导致电离速率在数值上出现极大差异的主要原因为阴极产生的种子电子不同，在图5中可以看到1E-8s与1E-7s之间两种情况下的二次发射通量存在巨大差距，但有场致发射的情况下场致发射通量远小于二次发射电子通量，这也说明场致发射的存在引起了两种情况出现差异，但不是场致发射直接引起的，而是由场发射增强空间电离以及二次发射间接导致。随着电离速率的继续增大，使得电子到达阳极时因非弹性碰撞损失更多能量而导致电子能降低，以及电场的畸变削弱了空间电场，这共同使得阳极附近的电离速率降低，而有场致发射的情况下电离更为激烈，电场畸变更强，因此有场致发射下空间电离速率最大值的空间位置最先远离阳极，图6(a3)和图6(b3)，最终两种情况下的空间电离速率最大值分布于极板之间，如图6(a4）和图6(b4)。
-
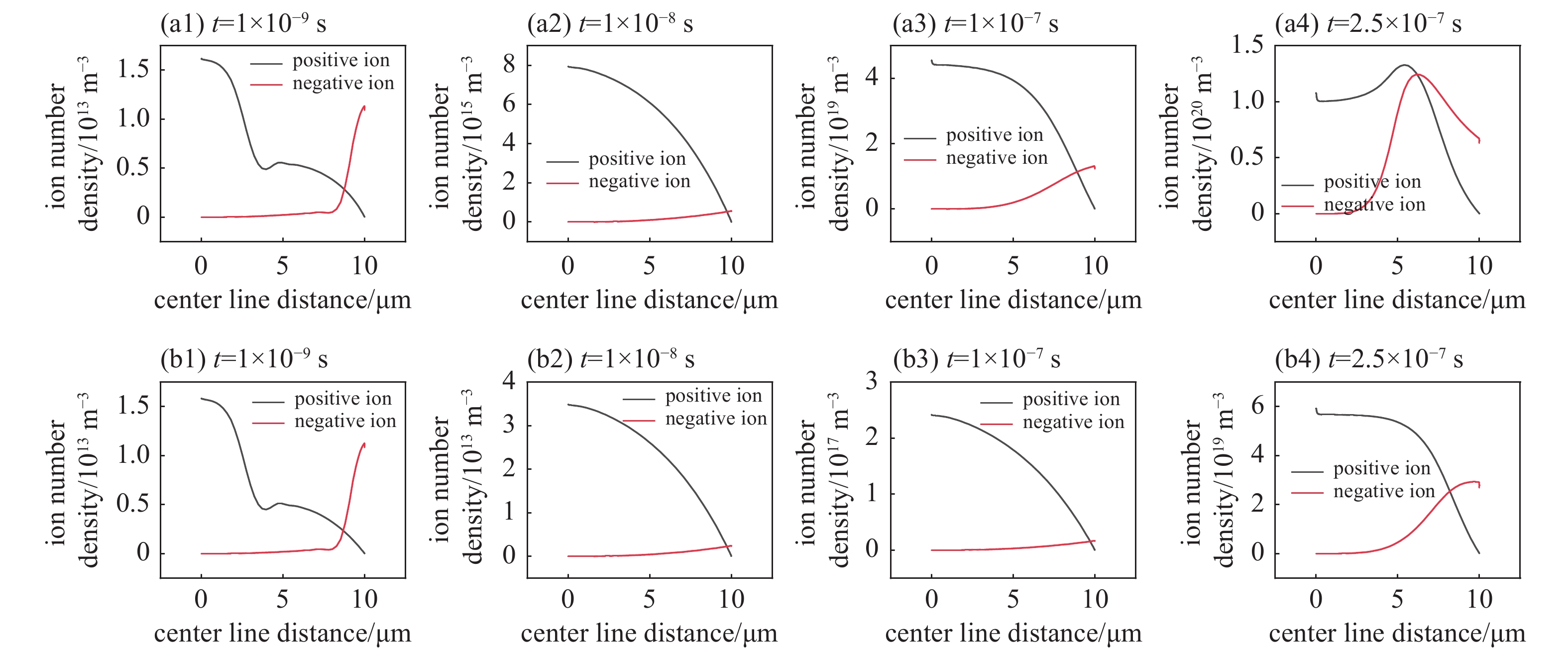
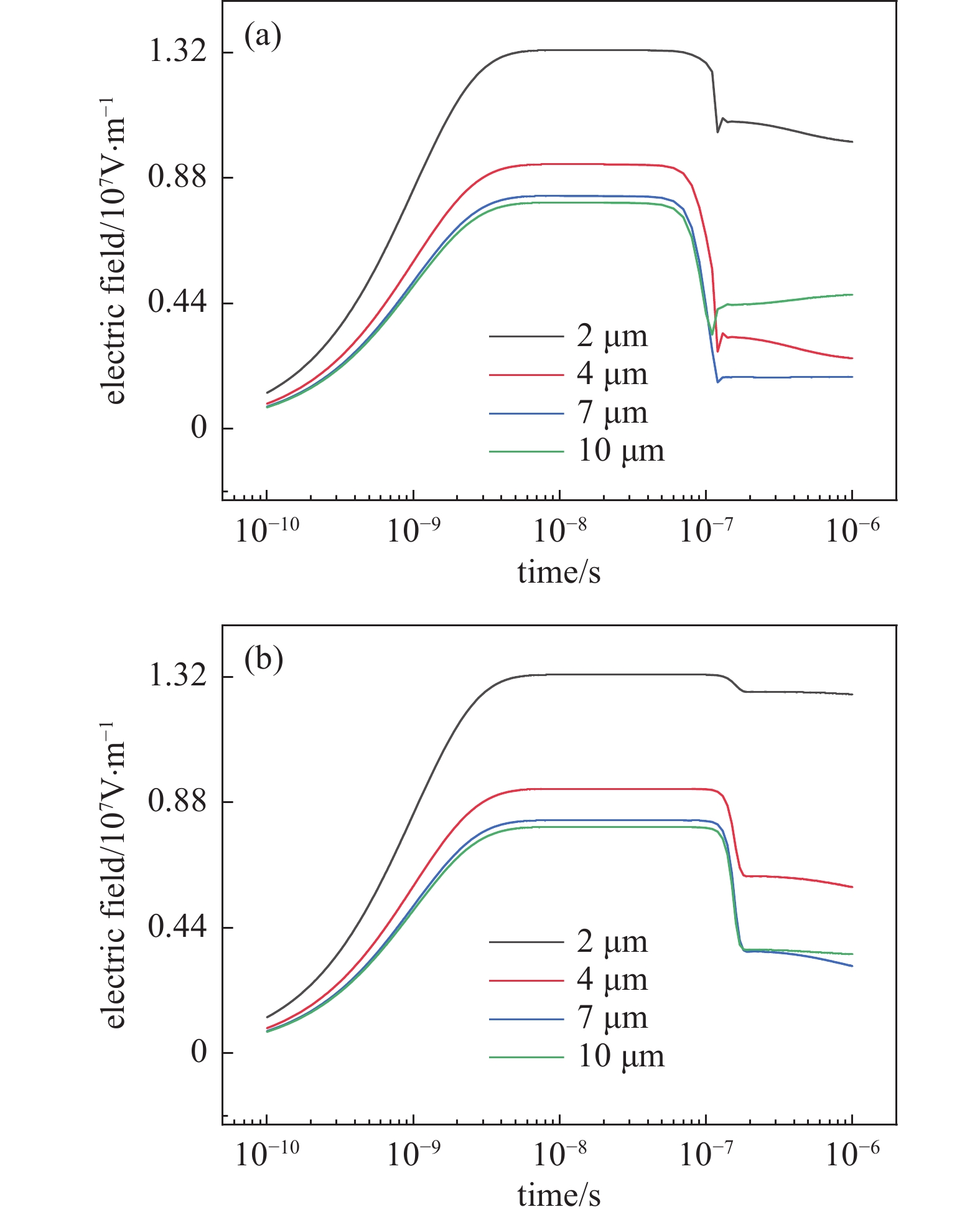
带电粒子（正负离子、电子）的分布与速率直接受到电场的影响，反过来离子产生的空间电荷效应也直接影响电场畸变，两者之间反应了物质与场之间的耦合作用。图7为有无场致发射两种情况下中轴线上正负离子数密度。图8为阴极纳米尖端处电场强度与电势随时间的变化曲线。图9为两种情况下中轴线上纳米尖端上方2 μm、4 μm、7 μm、10 μm处的场强随时间变化的曲线。可以看到在放电前期纳米尖端与空间场强随施加电势的增长而增长，直至电势最大值保持稳定，放电后期，纳米尖端场强增大、空间不同位置场强不同程度的降低，且有场致发射的情况下场强发生变化的起始时间更早，过程更短，变化幅度更大。这主要是因为两种情况下空间中正负离子密度发展过程存在差异造成的。图7(a1)和图7(b1)为场致发射开始对放电过程产生影响时刻的正负离子沿轴线的分布，可见两种情况下放电发展至此时还未出现差异，电场分布、正负离子空间分布与数值都相同。图7(a2)和图7(b2)为电压达到最大值后电场保持稳定阶段的正负离子分布。可以看到此时刻两种情况下正负离子的分布没有差异，但数值上有场致发射的情况更大，这是因为有场致发射的情况下空间电离速率更大，产生的正离子更多，二次发射增强，放电发展的更快，但此时的正离子密度依然不足以使电场畸变。图7(a3)和图7(b3)为电场发生畸变阶段的正负离子分布，可以看到两种情况下的正负离子的分布相似，但由于放电过程中场致发射对空间电离速率及二次发射增强，使得有场致发射情况下的正离子积聚更快，比无场致发射的情况下更早的引起电场畸变，而此时附着反应产生的负离子较少，也就更多的体现为正离子对阴极场强的增强与对空间及阳极场强的削弱。图7(a4)和图7(b4)为电场稳定阶段的正负离子分布，可见正负离子密度差距相对减小，这是由于放电后期空间电离速率较大，使得电子到达阳极后电子能大幅降低，加快了附着反应，负离子密度上升，正负离子之间的反向电场削弱了空间电场，使得阴极与阳极处场强都大于空间场强，而有场致发射情况下的正负离子数密度更大，畸变更强。
-
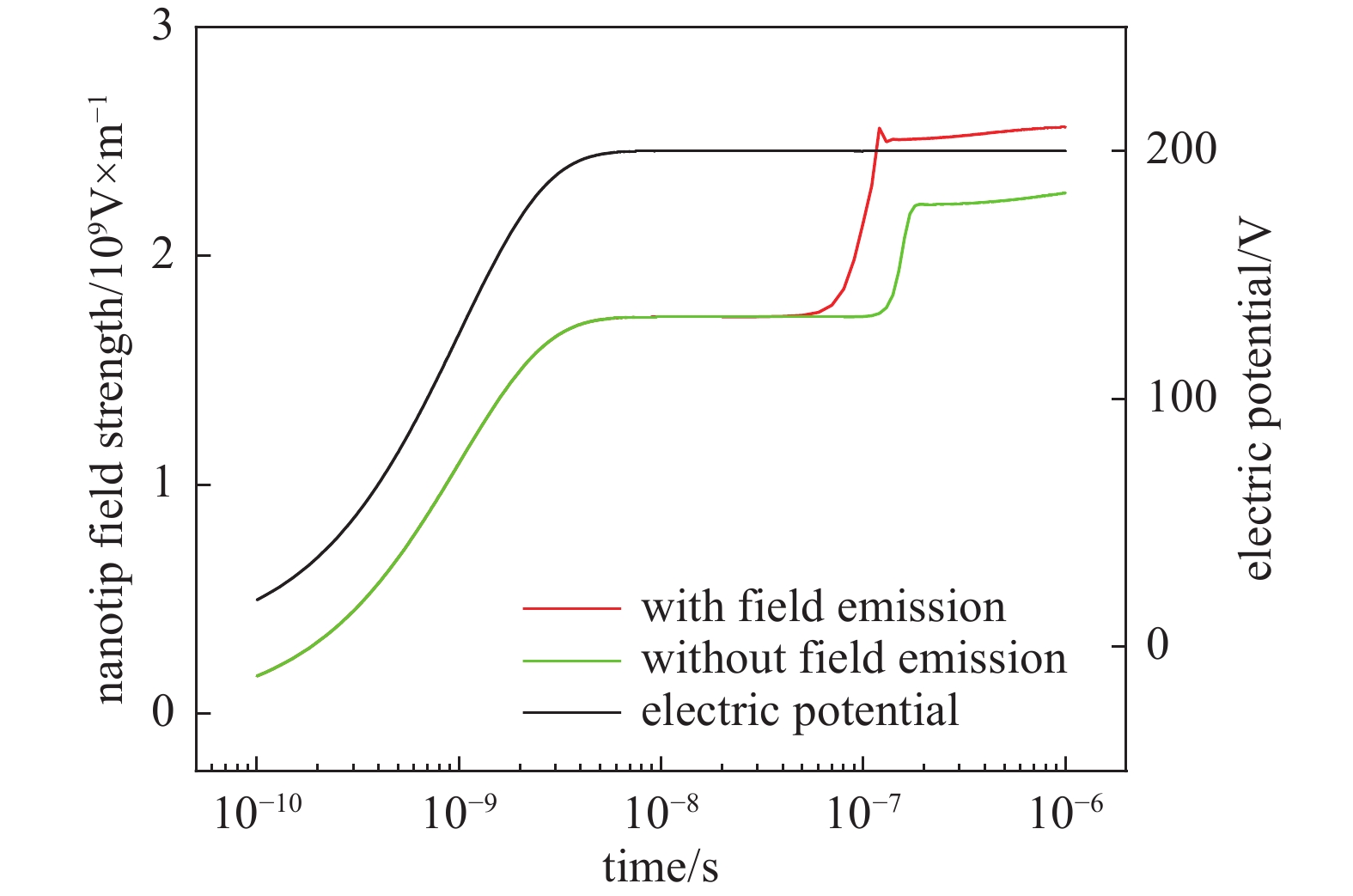
经以上对两种情况下的电子密度分布、空间电离速率及离子与场强的空间分布的分析，我们可以看出在空间放电过程中碰撞电离、二次发射及场致发射这三个导致空间放电的主要机制之间有着复杂的链锁影响。在图5中可以看到场致发射在整个放电形成过程中先是随施加电压形成的电场的增大而增大，随后电压达到最大值场致发射保持恒定，放电不断发展，空间正负离子的积聚导致电场畸变，场致发射进一步增大，最终放电趋于稳定，场致发射不在变化。在场致发射增长阶段，场致发射电子通量较小，对放电影响可以忽略；随后施加电压形成的电场达到最大值，场致发射保持恒定，此时场致发射增多了种子电子，增强了空间电离，产生更多的正离子，正离子增多使得二次发射电子增多，这进一步增强空间电离并不断循环，二次发射不断增大，远超场致发射，场致发射影响逐渐减小，如图10(a）所示；随着空间正离子密度不断增大，空间电荷增大了阴极场强，场致发射再次增长，此时场致发射提供更多的种子电子，这再次增强了空间电离及二次发射过程，使得空间正离子密度更快的增长，阴极场强继续增大，场致发射也持续增长，但空间电离速率的增长也导致了到达阳极的电子经非弹性碰撞后电子能降低，使得阳极表面的负离子产生速率增大并积聚如图10(b)所示；最终正负离子的空间分布使得阴极与阳极表面电场增强，空间电场削弱，这增强了表面反应抑制了空间电离，且电子能的降低也抑制了空间电离的发展，最终空间中带电粒子的产生与消耗达到平衡，空间放电得以维持与稳定，如图10(c)所示。
-
针对目前对微电晕放电机理研究存在的不足，本文建立了描述阴极电子发射过程的二维针-板放电模型，分析了不同极间距下场致发射对微电晕放电的影响，以及极间距为10 μm时场致发射对微电晕放电形成过程的响，得到以下结论：
（1）通过改变极间距发现场致发射对电晕放电形成的影响随着间距的减小而增大，且有无场致发射两种情况的放电随着间距的变化表现出不同的规律，因此场致发射对微电晕放电的影响随着间距的减小不可忽视。
（2）对比两种情况下的放电过程发现场致发射的存在会增强空间电子碰撞电离，使得空间正离子密度增长更快更多，正离子的增多又增大了二次电子发射，这又进一步增强了空间电子碰撞，空间正离子以更快的速率产生并积累，这增强了阴极表面场强，场致发射进一步增强，使得空间电子碰撞电离更为激烈。
（3）放电发展过程的最后，电子在激烈的非弹性碰撞后损失大量能量，且积累的正负离子之间形成反向电场削弱空间电场，这都抑制了空间碰撞电离的发展，空间电场、粒子密度不再增长，场致发射、二次发射趋于平稳。
（4）场致发射所产生的电流占总电流比例较小，但通过比较两种情况的放电过程可以发现，场致发射使得放电形成过程更短，且电流密度更大，因此微电晕器件有望通对结构优化，利用场致发射增强电离过程，提高灵敏度以及电流信号。
微尺度下场致发射对电晕放电的影响机理
Mechanism of the Influence of Field Emission on Corona Discharge at Microscale
-
摘要: 场致离子化微电晕器件基于一维纳米材料的电场增强效应，可产生大气压非平衡微等离子体，适用于气体检测以及生物医疗等领域，具有响应快、低功耗等特点。但微尺度下的电晕放电属于局部自持的低能放电，其场致发射的作用及影响机制尚不清晰。因此文章基于流体-化学混合模型框架，融合F-N发射模型，建立了常温常压N2-O2混合气体的二维微电晕放电模型。通过与无场致发射放电模型对比，探索不同间距下场致发射对放电动态过程的影响，发现针-板间距减至15 μm时，两种模型放电过程差异很小，表明放电以二次电子发射机制为主导，当间距减至10 μm时，两种模型的放电强度相差近1倍，场致发射的作用及影响不可忽略；通过进一步对电子密度分布、空间电场分布、电流密度等参量进行动态分析，发现场致发射、空间碰撞电离反应和离子轰击二次电子发射之间存在链锁影响规律。Abstract: Based on the electric field enhancement effect of one-dimensional nanomaterials, field-ionized micro-corona devices can generate atmospheric pressure non-equilibrium micro-plasma, which is suitable for gas detection and biomedical fields with fast response and low power consumption. However, the corona discharge at the microscale is a local self-sustaining low-energy discharge, and the role and influence mechanism of its field emission are still unclear. Therefore, in this paper, based on the fluid-chemical mixing model, the F-N emission model is introduced and coupled to establish a two-dimensional microcorona discharge model for the N2-O2 gas mixture at room temperature and pressure. By comparing with the discharge model without field emission, the effect of field emission on the dynamic process of discharge under different spacing is explored. It is found that when the pin-plate spacing is reduced to 15 μm, the difference in the discharge process between the two models is very small, indicating that the discharge is dominated by the secondary electron emission mechanism, and when the spacing is reduced to 10 μm, the difference in the discharge intensity between the two models is nearly a factor of one, and the role and influence of field emission cannot be neglected; And through further dynamic analysis of electron density distribution, space electric field distribution, current density and other parameters, it is found that there is a chain influence law between field-induced emission, space collision ionization reaction and ion bombardment secondary electron emission.
-
-
图 2 仿真数据与实验数据对比。（a）实际值，（b）归一化曲线
Figure 2. Comparison of simulation data with experimental data. (a) actual value, (b) normalized curve
图 4 两种情况下相同时刻电子密度分布。（a1）-（a4）有场致发射，(b1)-(b4)无场致发射
Figure 4. Electron density distribution at the same moment in both cases. (a1)-(a4) With field-induced emission, (b1)-(b4) without field-induced emission
图 5 两种情况下纳米尖端的二次电子及场致发射电子通量
Figure 5. Secondary electron and field emission electron fluxes at the nano-tip in two cases
图 6 两种情况下相同时刻碰撞电离速率。（a1）-（a4）有场致发射，（b1）-（b4）无场致发射
Figure 6. Collisional ionization rate at the same moment in both cases. (a1)-(a4) With field-induced emission, (b1)-(b4) without field-induced emission
图 7 有无场致发射两种情况下中轴线上正负离子数密度。（a1）-（a4）有场致发射，（b1）-（b4）无场致发射
Figure 7. Positive and negative ion number density on the central axis with and without field emission. (a1)-(a4) With field emission, (b1)-(b4) without field emission
图 8 两种情况下纳米尖端的场强及电势
Figure 8. The field strength and potential of the nano-tip in the two cases
图 9 两种情况下中轴线不同位置场强随时间变化。（a）有场致发射，（b）无场致发射
Figure 9. Variation of field intensity with time at different positions of the central axis in two cases. (a) With field-induced emission, (b) without field-induced emission
图 10 放电过程中不同机制之间演化过程。（a）场发射平稳阶段，（b）离子增强场发射阶段，（c）放电平稳阶段
Figure 10. Evolutionary processes between different mechanisms in the discharge process. (a) Field emission steady phase, (b) Ion-enhanced field emission phase, (c) discharge steady phase
表 1 等离子体化学反应式
Table 1. Plasma chemical reaction formula
反应类型 等离子体化学反应式 弹性碰撞 e+N2=>e+N2 e+O2=>e+O2 碰撞激发 e+N2=>e+N2A3 e+N2=>e+N2a1 碰撞电离 e+N2=>2e+N2+ e+O2=>2e+O2+ e+N2A3=>2e+N2+ e+N2a1=>2e+N2+ 潘宁电离 N2A3+N2a1=>e+N2+N2+ N2a1+N2a1=>e+N2+N2+ N2A3+N2a1=>e+N4+ N2a1+N2a1=>e+N4+ 附着 e+2O2=>O2+O2− 复合 e+N2+N2+=>2N2 e+O4+=>2O2 e+O2+=>2O O4++O2−+O2=>3O2+O2 O4++O2−+N2=>3O2+N2 O2++O2−+O2=>2O2+O2 O2++O2−+N2=>2O2+N2 O4++O2−=>3O2 电荷转移 O2++O2+N2=>O4++N2 O2++O2+O2=>O4++O2 N2O2++O2=>O4++N2 N2O2++N2=>O2++2N2 O2++2N2=>N2O2++N2 O2+N2+=>O2++N2 N2++N2+O2=>N4++O2 N2++N2+N2=>N4++N2 O2+N4+=>O2++N2+N2 中性物质化学转变 O+O2+N2=>O3+N2 O+O2+O2=>O3+O2 O+O3=>O2+O2 
下载: 导出CSV
表 2 表面反应
Table 2. Surface reaction
反应式 阴极 阳极 纳米管 平板 γ ϵi γ ϵi γ ϵi e+N2+=>N2 0.05 4 0.002 2 0 0 e+N2O2+=>N2+O2 0.05 4 0.002 2 0 0 e+N4+=>2N2 0.05 4 0.002 2 0 0 e+O2+=>O2 0.05 4 0.002 2 0 0 e+O4+=>2O2 0.05 4 0.002 2 0 0 e+O2-=>O2 0 0 0 0 0 0 N2A3=>N2 0 0 0 0 0 0 N2a1=>N2 0 0 0 0 0 0
下载: 导出CSV
表 3 两种情况下放电稳定时针尖电流密度及增长比例
Table 3. Needle tip current density and growth ratio at discharge stabilization in two cases
间距 无场致发射
总电流密度有场致发射 总电流密度
增长比例总电流密度 场致发射电流密度 5 μm 0.13 A/m2 8×105 A/m2 3536.2 A/m2 61000000% 10 μm 7.66×106 A/m2 1.52×107 A/m2 1.6×105 A/m2 98% 15 μm 6.03×106 A/m2 6.20×106 A/m2 2.5×103 A/m2 2.8% 20 μm 4.88×106 A/m2 4.89×106 A/m2 1.6×102 A/m2 0.2% 25 μm 3.41×106 A/m2 3.41×106 A/m2 6.0 A/m2 0.01%
下载: 导出CSV
-
[1] Shimizu K, Fukunaga H, Blajan M. Biomedical applications of atmospheric microplasma[J]. Current Applied Physics,2014,14(7):S154−S161 [2] 欧阳吉庭, 张宇, 秦宇. 微放电及其应用[J]. 高电压技术,2016,42(3):673−684(in chinese) Ouyang J T, Zhang Y, Qin Y. Micro-discharge and its applications[J]. High Voltage Engineering,2016,42(3):673−684 [3] Kim J Y, Kaganovich I, Lee H C. Review of the gas breakdown physics and nanomaterial-based ionization gas sensors and their applications[J]. Plasma Sources Science & Technology,2022 ,31(3):33001 [4] Dirk J, Franzke J, Manz A. Scaling and the design of miniaturized chemical-analysis systems[J]. Nature,2006,442(7101):374−380 doi: 10.1038/nature05059 [5] Fu Y, Wang H, Zheng B, et al. Direct current microplasma formation around microstructure arrays[J]. Applied Physics Letters,2021,118(17):174101 doi: 10.1063/5.0046312 [6] Yuan X, Tang J, Duan Y X. Microplasma technology and its applications in analytical chemistry[J]. Applied Spectroscopy Reviews,2011,46(7):581−605 doi: 10.1080/05704928.2011.604814 [7] 孟国栋, 折俊艺, 应琪, 等. 微米尺度气体击穿的数值模拟研究进展[J]. 电工技术学报,2022,37(15):3857−3875(in chinese) Meng G D, She J Y, Ying Q, et al. Research progress on numerical simulation of gas breakdown at microscale[J]. Transactions of China Electrotechnical Society,2022,37(15):3857−3875 [8] 牛海清, 徐乐平, 李小潇, 等. SF6气体正极性电晕放电特性仿真研究[J]. 高电压技术,2021,47(11):4063−4071(in chinese) Niu H Q, Xu L P, Li X X, et al. Simulation and study of positive corona characteristics in SF6 gas[J]. High Voltage Engineering,2021,47(11):4063−4071 [9] 廖瑞金, 刘康淋, 伍飞飞, 等. 棒-板电极直流负电晕放电过程中重粒子特性的仿真研究[J]. 高电压技术,2014,40(4):965−971(in chinese) Liao R J, Liu K L, Wu F F, et al. Simulative study on characteristic of heavy particles in negative bar-plate dc corona discharge[J]. High Voltage Engineering,2014,40(4):965−971 [10] Fu Y, Peng Z, Verboncoeur J P. Gas breakdown in atmospheric pressure microgaps with a surface protrusion on the cathode [J]. Applied Physics Letters, 2018, 112(25)254102 [11] 王林华, 孙岩洲, 董克亮, 等. 微间隙气体放电击穿过程分析[J]. 电子器件,2020,43(6):1197−1202(in chinese) doi: 10.3969/j.issn.1005-9490.2020.06.002 Wang L H, Sun Y Z, Dong K L, et al. Analysis of breakdown process of micro-gap gas discharge[J]. Chinese Journal of Electron Devices,2020,43(6):1197−1202 doi: 10.3969/j.issn.1005-9490.2020.06.002 [12] Cejas E, Prevosto L, Minotti F O, et al. Cathode-sheath model for field emission sustained atmospheric pressure discharges[J]. Physics of Plasmas,2021,28(3):033506 doi: 10.1063/5.0035710 [13] Li Y S, Sun Y Z, Wang L H, et al. Research on the characteristics of micro-spacing gas discharge at different pressures [J]. Chinese Journal of Vacuum Science and Technology, 2022, 42(01):75−81(李彦森, 孙岩洲, 王林华, 等. 不同气压下微间距气体放电特性分析[J]. 真空科学与技术学报, 2022, 42(01):75−81(in chinese) [14] 陈芸, 孙岩洲, 李彦森, 等. 微间距气压对场致发射影响的分析与计算[J]. 电气工程学报,2023,18(1):251−257(in chinese) doi: 10.11985/2023.01.028 Chen Y, Sun Y Z, Li Y S, et al. Analysis and calculation of the infuence of air pressure on field emission at micro-gap[J]. Journal of Electrical Engineering,2023,18(1):251−257 doi: 10.11985/2023.01.028 [15] 常泽洲, 孟国栋, 应琪, 等. 阴极曲率半径对微米尺度气隙击穿的影响规律研究[J]. 电工技术学报,2023,38(4):1032−1041(in chinese) Chang Z Z, Meng G D, Ying Q, et al. Study on the influence of cathode radius on the breakdown characteristics across microgaps in air[J]. Transactions of China Electrotechnical Society,2023,38(4):1032−1041 [16] 柴钰, 弓丽萍, 张晶园, 等. 微纳电离式矿井甲烷传感器安全放电及敏感机理仿真[J]. 电工技术学报,2019,34(23):10(in chinese) Chai Y, Gong L P, Zhang J Y, et al. Simulation of safe discharge and sensitive mechanism of micro-nano ionized mine methane sensor[J]. Transactions of China Electrotechnical Society,2019,34(23):10 [17] 柴钰, 张妮, 刘杰, 等. 微尺度下N2–O2电晕放电的动态特性二维仿真[J]. 物理学报,2020,69(16):10(in chinese) doi: 10.7498/aps.69.20200095 Chai Y, Zhang N, Liu J, et al. Two-dimensional simulation of dynamic characteristics of N2–O2 corona discharge at micro scale[J]. Journal of Physics,2020,69(16):10 doi: 10.7498/aps.69.20200095 [18] Kossyi I A, Kostinsky A Y, Matveyev A A, et al. Kinetic scheme of the non-equilibrium discharge in nitrogen-oxygen mixtures[J]. Plasma Sources Science and Technology,1992,1(3):207 doi: 10.1088/0963-0252/1/3/011 [19] Pancheshnyi S, Nudnova M, Starikovskii A. Development of a cathode-directed streamer discharge in air at different pressures: Experiment and comparison with direct numerical simulation[J]. Phys. Rev. E,2005,71(1):016407 doi: 10.1103/PhysRevE.71.016407 [20] Poggie J, Adamovich I, Bisek N, et al. Numerical simulation of nanosecond-pulse electrical discharges[J]. Plasma Sources Science and Technology,2013,22(1):015001 [21] Liu X Q. Cathode electronics [M]. Beijng: Science Press, 1980(刘学悫 . 阴极电子学[M]. 科学出版社, 1980(in chinese) [22] 王新庆, 王淼, 李振华. 单根纳米导线场发射增强因子的计算[J]. 物理学报,2005(03):1347−1351(in chinese) doi: 10.3321/j.issn:1000-3290.2005.03.060 Wang X Q, Wang M, Li Z H. Calculation of the field emission enhancement factor for single nanowires[J]. Acta Physica Sinica,2005(03):1347−1351 doi: 10.3321/j.issn:1000-3290.2005.03.060 [23] 王党树, 邓翾, 刘树林, 等. 甲烷/空气混合气体在针板电极下的微间隙放电特性[J]. 电工技术学报,2023,38(13):3388−3399(in chinese) Wang D S, Deng X, Liu S L, et al. Microgap discharge characteristics of methane / air under the needle plate electrode[J]. Transactions of China Electrotechnical Society,2023,38(13):3388−3399 -
计量
- 文章访问数: 254
- HTML全文浏览数: 254
- PDF下载数: 5
- 施引文献: 0