首页
登录
注册
下载:
-
微纳尺度下的热流逸效应是指当通道的特征尺寸与气体的平均自由程相当或者更小时，并且沿微通道壁面存在切向温度梯度，冷端气体会自动向热端流动，在微尺度下这表现出一种泵送现象[1-2]。努森压缩机具有结构简单、无运动部件、可利用低温热能等优点[3]，可广泛用于输送气体[4]、压缩气体[5]以及分离气体[6]等。因此，研究努森压缩机微纳尺度热流逸效应的影响机制，获得微纳通道内气体流动特性，是提高其性能的关键。
国内外学者围绕努森压缩机开展了大量研究，在微纳流动特性、性能变化规律等方面取得一系列成果。Ye等[7]研究发现随着微通道半圆形障碍物尺寸的增大，压升和中心通道处泊肃叶流流速均减小。Zhang等[8]采用直接模拟蒙特卡罗（DSMC）方法对矩形微通道的努森泵进行模拟，研究了不同努森数下通道内氧气和氮气在不同比例下的流动特性，研究表明，气体物理性质的变化不影响努森泵内的速度场、温度场等分布，热流逸效应的强弱与气体的分子质量有关。Bond等[9]研究了弯曲通道中热流逸气体流动，结果发现，气体最大质量流量的增加，对普朗特数影响显著，而对粘度指数影响较小。Bond等[10]又设计了正弦曲线形和矩阵形通道的努森泵，并与之前的泵进行了对比，研究表明，矩阵形通道与矩形通道表现几乎相同，均有较好的性能，并且矩阵通道具有控制气体流动方向的能力。Balaj等[11]考虑在进口和出口压力相等的情况下的气体流动在施加线性壁面温度梯度的平行板之间，找到了质量速率与壁温的关系并推导了质量速度的解析表达式。
努森压缩机的微纳结构对其性能有着重要的影响。由于发散和收敛微通道与矩形微通道高度相似并且性能较好而备受关注。Varade等[12]研究了发散微通道内气体在滑移流区域内的流动，结果显示发散角增大会导致压升和中心线速度减小。Tatsios等[13] 研究了稀薄气体在发散和收敛的非封闭微通道内的热流逸效应，发现当净质量流量为零时，压升随着通道倾角的增大而增大，当进出口压力相等时，通道倾角的增加会导致质量流量减小。Mozaffari等[14]采用DSMC方法研究了发散通道中稀薄气体的热流逸效应，通道在固定横纵比下，研究了不同发散角下气体马赫数、压力、温度、剪切应力等流场特性。Hemadri等[15]对在发散和收敛微通道内稀薄气体的热流逸效应进行了研究，在变截面的微通道中发现了努森数的最小值，在此基础上研究了几何截面和流体性质对努森数最小值的影响。
综上所述，现有研究主要关注矩形和弯曲通道内的热流逸效应、微纳流动和性能变化规律。大多数研究采用DSMC方法，但存在统计噪声和高计算成本等问题。相比之下，对于发散和收敛的微通道流动的研究相对较少。因此，本文采用适应于滑移流区域的梯形微通道内气体流动的二维数值模型，分析了不同倾角和冷热腔室温差对气体克努森数分布、气体压升以及气体流动特性的影响规律，为努森压缩机微通道的构建和性能优化设计提供了指导。
-
本文采用COMSOL多物理场仿真软件的滑移流模型建立努森压缩机的二维数值模型，滑移流模型是通过纳维-斯托克斯方程的修正边界条件进行建模，使用PARDISO求解器进行求解，此求解器求解速度快，并且占用内存小，同时COMSOL软件可以在一个界面下实现了所有的物理场以及从建模到仿真到后处理乃至优化的全部流程，操作相对方便。
-
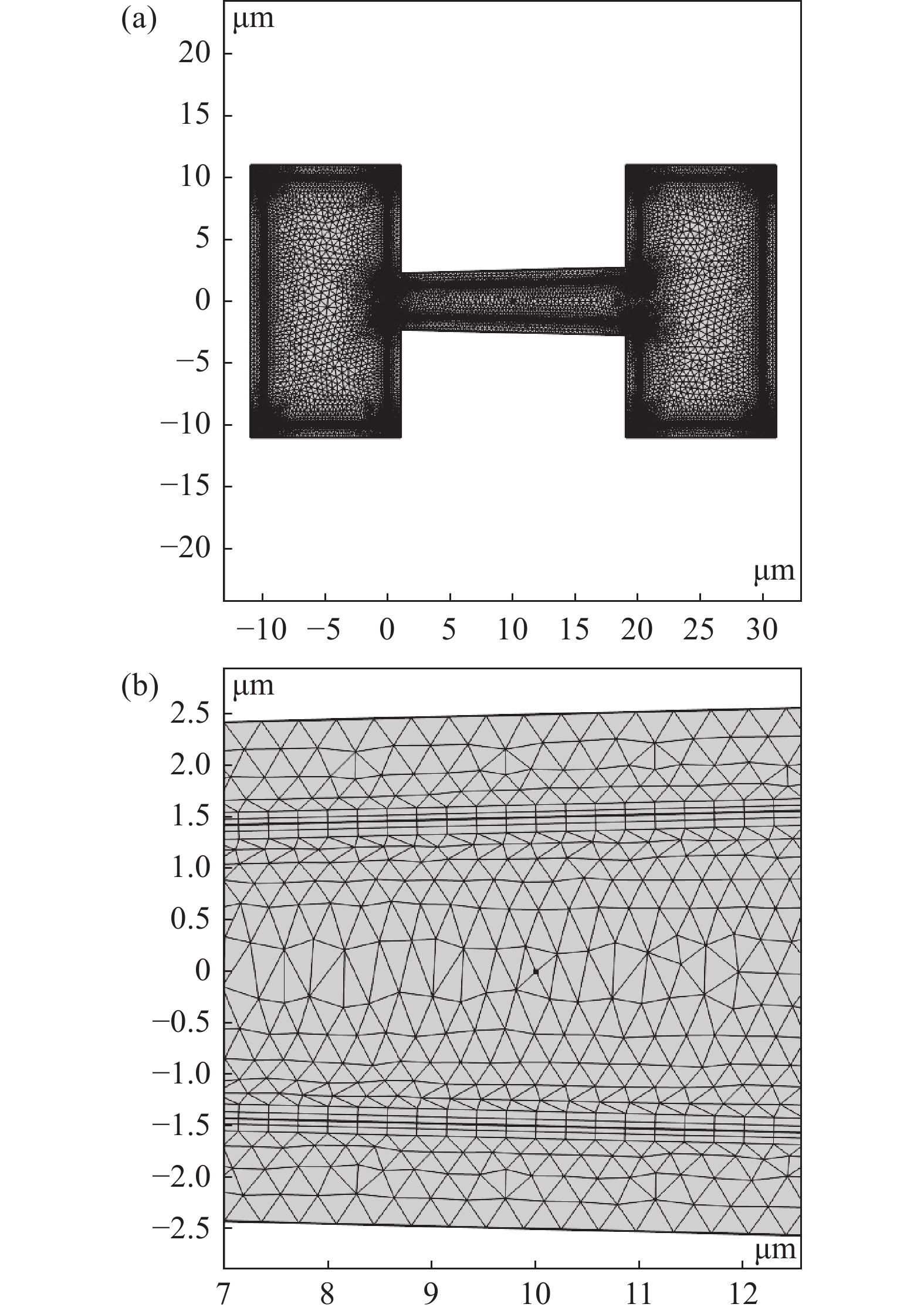
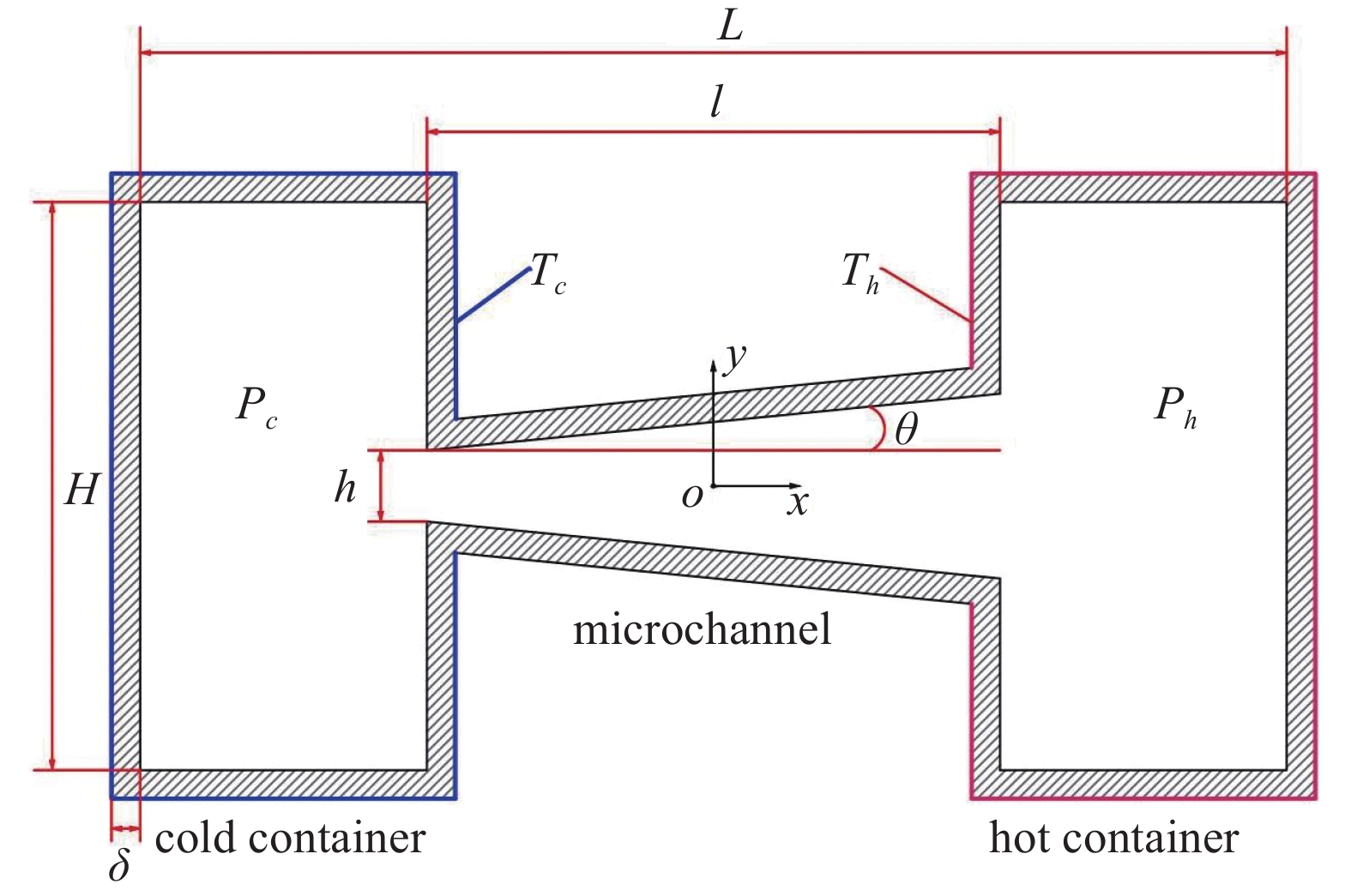
考虑到微通道宽度对努森压缩机的升压性能以及流动特性影响较小[2]，并且考虑计算复杂性，本文将忽略微通道宽度的影响，建立梯形微通道的努森压缩机的二维模型。图1为梯形微通道的努森压缩机二维平面图。如图所示,该努森压缩机由冷腔、微通道、热腔组成。其外壳厚度δ = 1 μm，考虑到硅基材料的导热系数较小，能较好地维持微通道壁上的温度梯度，有利于产生热流逸现象，故假定外壳为硅基材料。腔室的整体长度L = 40 μm，高度H = 20 μm，梯形微通道的水平长度l = 20 μm，梯形微通道短边的高度h = 2.5 μm，倾角用θ表示。
-
宏观尺度流体运动的数学模型的构建常使用纳维-斯托克斯方程（N-S方程）[16]，即传统流体力学中的质量守恒、动量守恒和能量守恒三个方程，如式（1）~（3）所示。N-S方程的前提是将流体视作连续介质，进而研究流体在外力下参数（温度、速度、压强等）的变化规律[17]。
式中：ρ为气体的密度，kg/m3 ；uk为瞬时速度分量，m/s ；
$ \displaystyle\sum {k}_{i} $ 为单位面积表面力的二阶应力张量，N/m4 ；gi为单位质量体积力，m/s2 ；e为内能，J ；qk为传导和辐射热流矢量之和,W 。本研究中，气体的克努森数处于0.001~0.1之间，处于滑移流区。在滑移流区域内，N-S方程仍然适用，但是考虑壁面附近存在速度滑移和温度跳跃的现象，故本文采用具有滑移和跳跃边界条件的N-S方程来预测气体的流动行为。速度滑移和温度跳跃的方程如下[18-19]：
式中：us为滑移速度，m/s ；uw为移动壁速度，m/s ；αv为切向动量调节系数，本文中切向动量调节系数在Sharipov[20]工作的基础上取αv=0.9，λ为气体平均自由程，m ；μ为气体粘度，Pa·s ；τ为粘性应力张量，N/m2 ；ρ为气体的密度，kg/m3 ；Tg为气体温度，K ；Tw为壁温，K ；γ为气体的比热比，k为气体的导热系数，W/(m·K) ；Cp为恒压下的热容，J/(kg·K)；Kn为气体的克努森数；L为微通道的特征长度，m。
-
本模型忽略外部温度场对微通道内部温度的影响，假设微通道外壁为绝热壁，冷腔和热腔的外壁温度分别用Tc和Th表示，梯形微通道短边的高度设定为h = 2.5 μm。当研究倾角对梯形微通道热流逸效应的影响时，设置Tc = 300 K和Th = 400 K，倾角θ变化范围为0°~5.72°，倾角间隔为1.43°；当研究温差对梯形微通道热流逸效应影响时，设置Tc = 300 K和θ = 1.43°，Th 的变化范围为320~400 K，间隔为20 K。氮气性质稳定，常温下是气态，并且分子直径较小，有利于产生热流逸效应，故腔内部设定的气体为氮气，其物性参数均可在COMSOL软件中获取。初始条件下，将模型内气体压力设置为p0，通道中心O点设为压力约束点pO = 0 Pa。当流动达到平衡状态时，冷腔和热腔的压强分别用pc和ph表示。腔体和微通道的特征尺寸都较小，内部气体极度稀薄，这种情况下，气体分子和壁面的相互作用较为强烈，气体在内壁上存在速度滑移和温度跳跃的现象，故将模型内壁设置成滑移壁。
-
图2为梯形微通道努森压缩机的二维模型的网格图。如图所示，采用了三角形非结构化网格进行网格划分，对边界处进行了角细化与边界层网格处理。
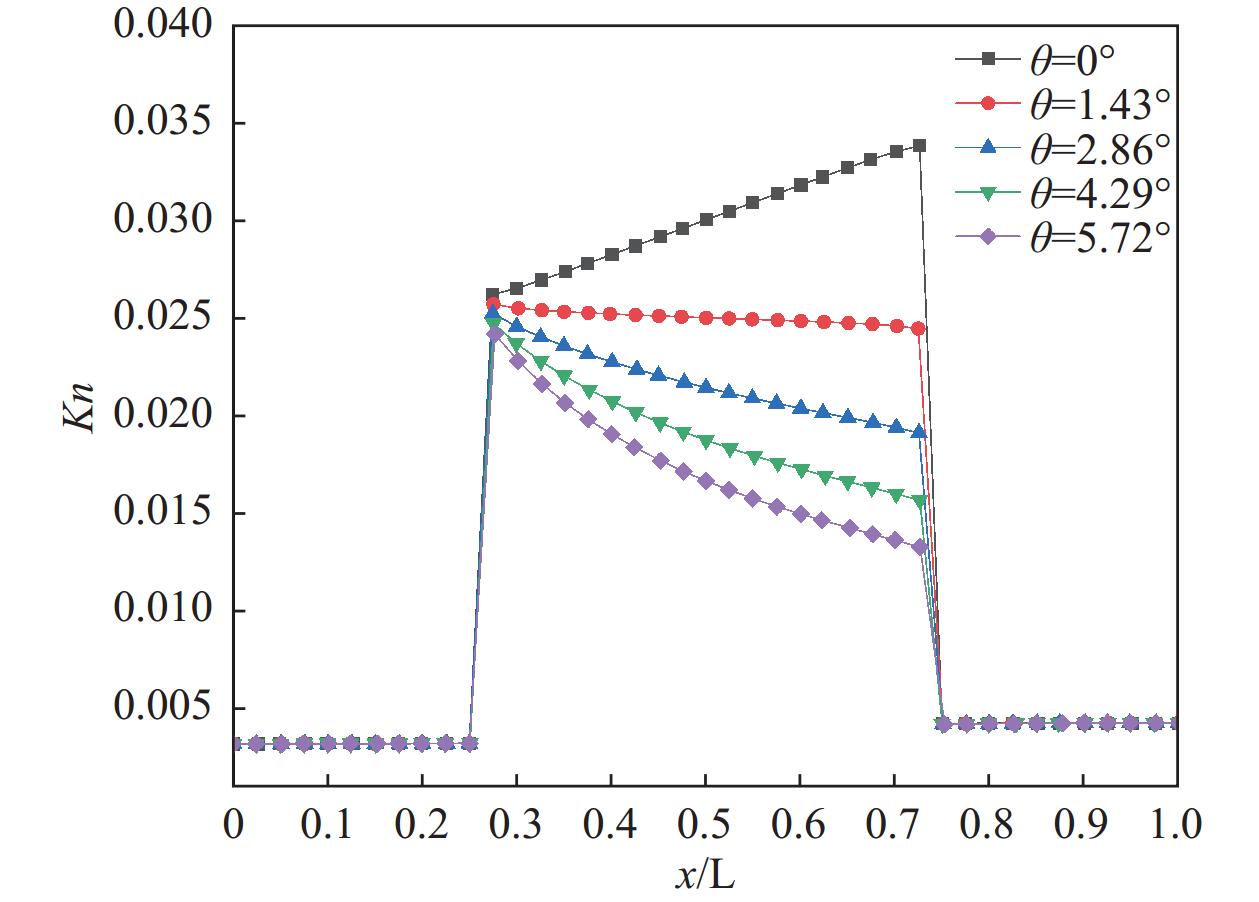
针对倾角θ = 1.43°的梯形微通道努森压缩机进行二维数值模拟，当计算结果收敛稳定后，对冷腔和热腔内气体压差进行了网格无关性验证，结果如图3所示。由图可见，随着网格数量的增加，两端腔室内氮气的压差值逐渐减小并趋于稳定，当网格数达到65000个时，两端腔室内气体压差稳定在92.994 Pa，因此，为节约计算空间并保证模拟的准确性，本文针对梯形微通道二维模型的计算网格数维持在65000个水平。
-
为验证本模型的可行性和准确性，将本模型的平行板间微通道内压力驱动的泊肃叶流模拟结果同文献[21]的结果进行了对比分析，本模型平板间距为1.36 μm，通道长度为272 μm，定壁温，通道出口常温常压（T = 298 K，p = 101325 Pa），进口压力为出口大气压力的1.5倍，工质采用空气，这些条件均与参考文献[21]中的条件一致。图4为出口截面速度分布的对比结果图。如图4所示，二者得到的微通道出口截面速度分布基本一致，最大速度差为0.023 m/s， 最大相对误差仅为6.813%。因此，本文建立的模型具有较高的准确性
-
梯形微通道倾角的变化直接影响努森压缩机微通道内的克努森数、压升、速度等特性。因此本文研究5种不同的倾角（θ = 0°、θ = 1.43°、θ = 2.86°、θ = 4.29°以及θ = 5.72°）下努森压缩机微通道内的流动和性能特性。本文的冷腔和热腔外壁温度分别设定为Tc = 300 K和Th = 400 K。
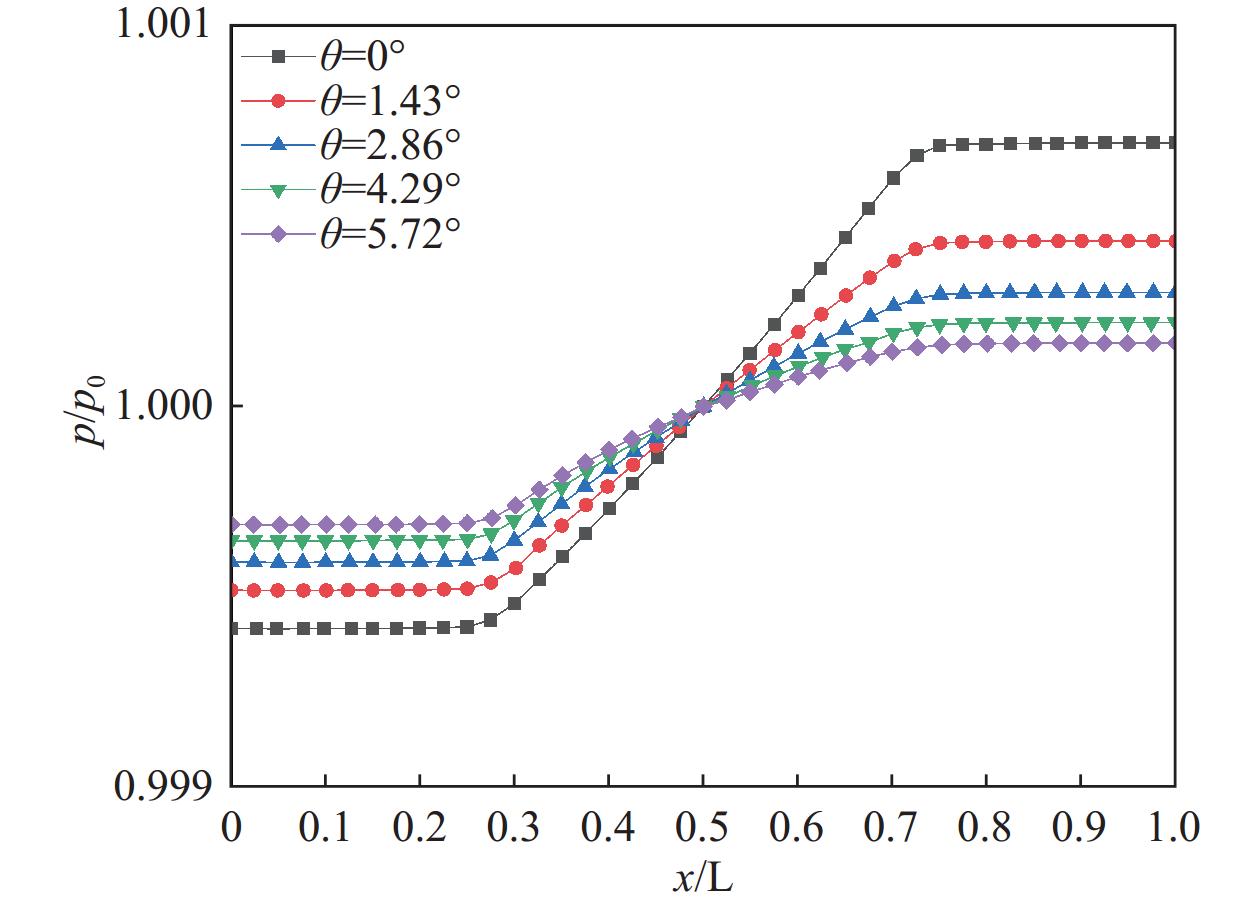
图5为沿梯形微通道中心线的氮气克努森数变化情况。气体的克努森数处于0.001与0.1范围之间，氮气处于滑移流流态。当微通道倾角分别为θ = 0°、θ = 1.43°、θ = 2.86°、θ = 4.29°以及θ = 5.72°时，微通道中心处的氮气克努森数分别为Kn = 0.030、Kn = 0.025、Kn = 0.021、Kn = 0.019以及Kn = 0.017，说明梯形微通道倾角的增加会导致氮气克努森数减小，并且减小速度逐渐减小。当倾角θ = 0°时，温度逐渐增大，导致克努森数沿着x轴正方向线性增加；当倾角大于0°时，沿着x轴正方向克努森数逐渐减小，并且倾角越大，克努森数减小速度越快，同时克努森数逐渐成非线性变化。因为微通道特征尺寸增大，通道内氮气稀薄程度减小，即克努森数与通道特征尺寸成反比。
图6为沿梯形微通道中心线的氮气无量纲压力比变化情况。由图可知，当梯形微通道的倾角分别为θ = 0°、θ = 1.43°、θ = 2.86°、θ = 4.29°以及θ = 5.72°时，两端腔室内氮气的压差分别为129.181 Pa、92.972 Pa、71.837 Pa、58.018 Pa以及48.291 Pa，压差随着微通道倾角的增大而减小，倾角增加5.72°的同时压差减小80.890 Pa，且气体压力的增长速率逐渐减小。因为随着梯形微通道倾角的增大，通道特征尺寸增大，使得通道内气体稀薄程度减小，热流逸效应减弱，故使得压升减小。
沿梯形微通道中心线泊肃叶流流速的分布情况如图7所示，由图可见，当梯形微通道的倾角分别为θ = 0°、θ = 1.43°、θ = 2.86°、θ = 4.29°以及θ = 5.72°时，微通道内泊肃叶流最大速度值分别为0.096 m/s、0.100 m/s、0.103 m/s、0.104 m/s以及0.106 m/s，由此说明随着梯形微通道倾角的增大，微通道内泊肃叶流的流速增大，因为通道倾角增大，通道的特征尺寸增大，流动阻碍减小，更有利于气体流速的提升。
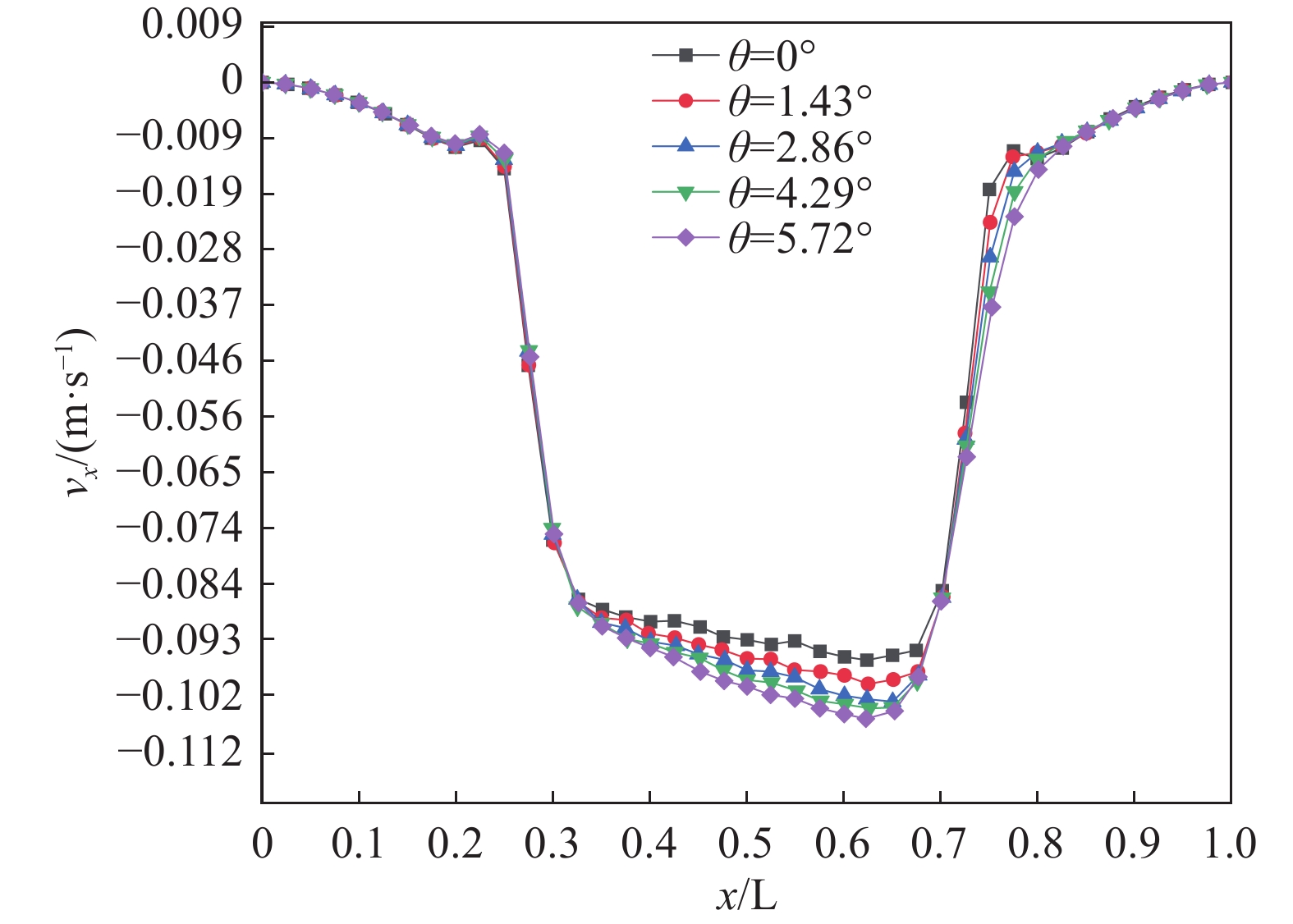
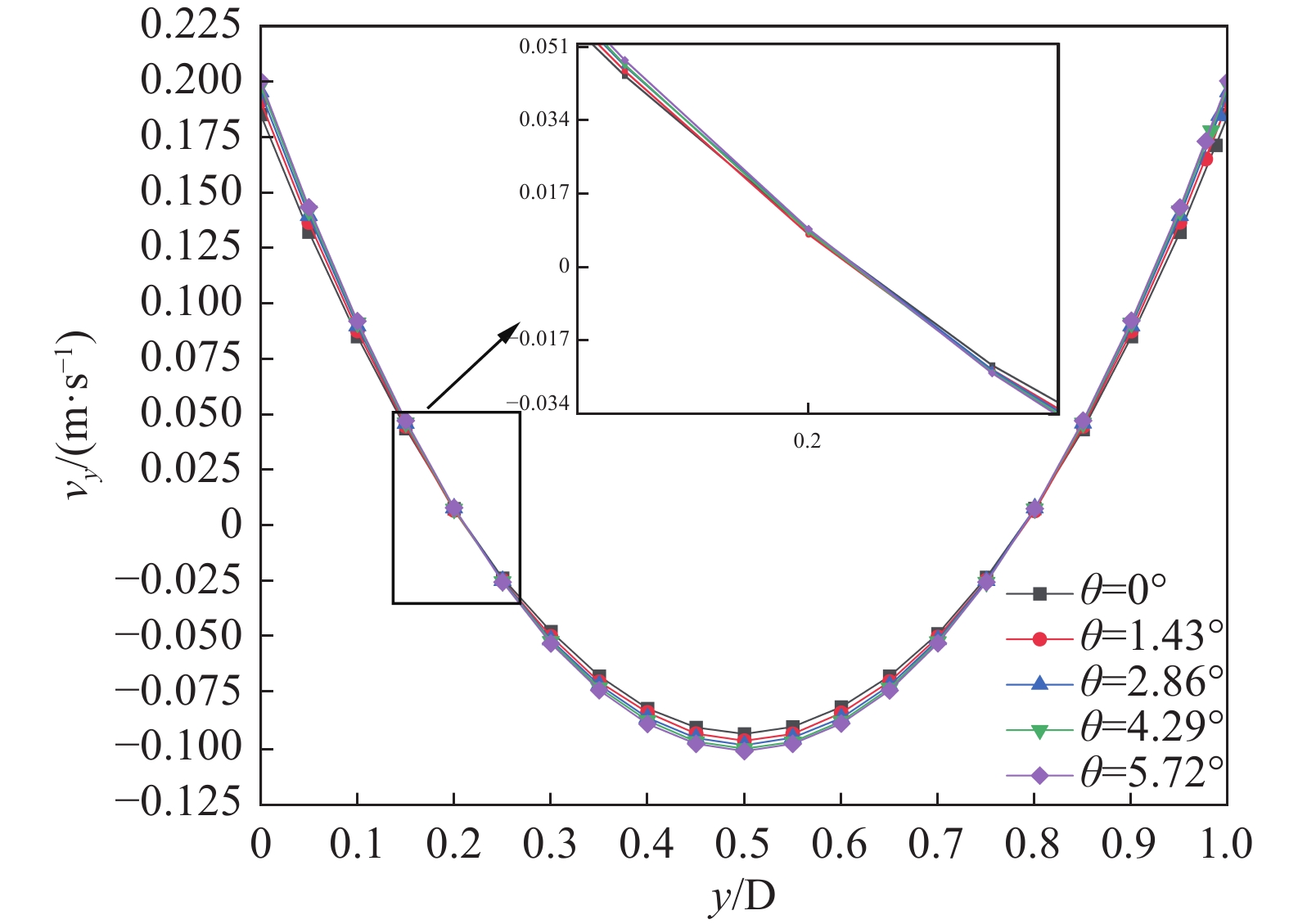
沿梯形微通道垂直中心线处速度在x方向分量的分布曲线如图8所示，由图可知，垂直中心线处的速度成抛物线型分布，当梯形微通道的倾角分别为θ = 0°、θ = 1.43°、θ = 2.86°、θ = 4.29°以及θ = 5.72°时，微通道近壁面处的热流逸流流速分别为0.185 m/s、0.191 m/s、0.196 m/s、0.198 m/s以及0.200 m/s，随着倾角的增大，热流逸速度增大，但增加速度减小。倾角θ从0°增加到2.86°，热流逸速度增加0.011 m/s，但当倾角θ从2.86°增加到5.72°，热流逸速度仅增加0.004 m/s。在微通道中心线处的泊肃叶流流速分别为0.093 m/s、0.096 m/s、0.098 m/s、0.099 m/s以及0.100 m/s，泊肃叶流流速随着倾角的增大而增大，但其值小于对应的热流逸流流速，从而导致冷热腔之间产生压升。梯形微通道倾角的增大，有利于气体流动，因为两者向相反的方向流动阻碍减小，故二者的流速都逐渐增大。
-
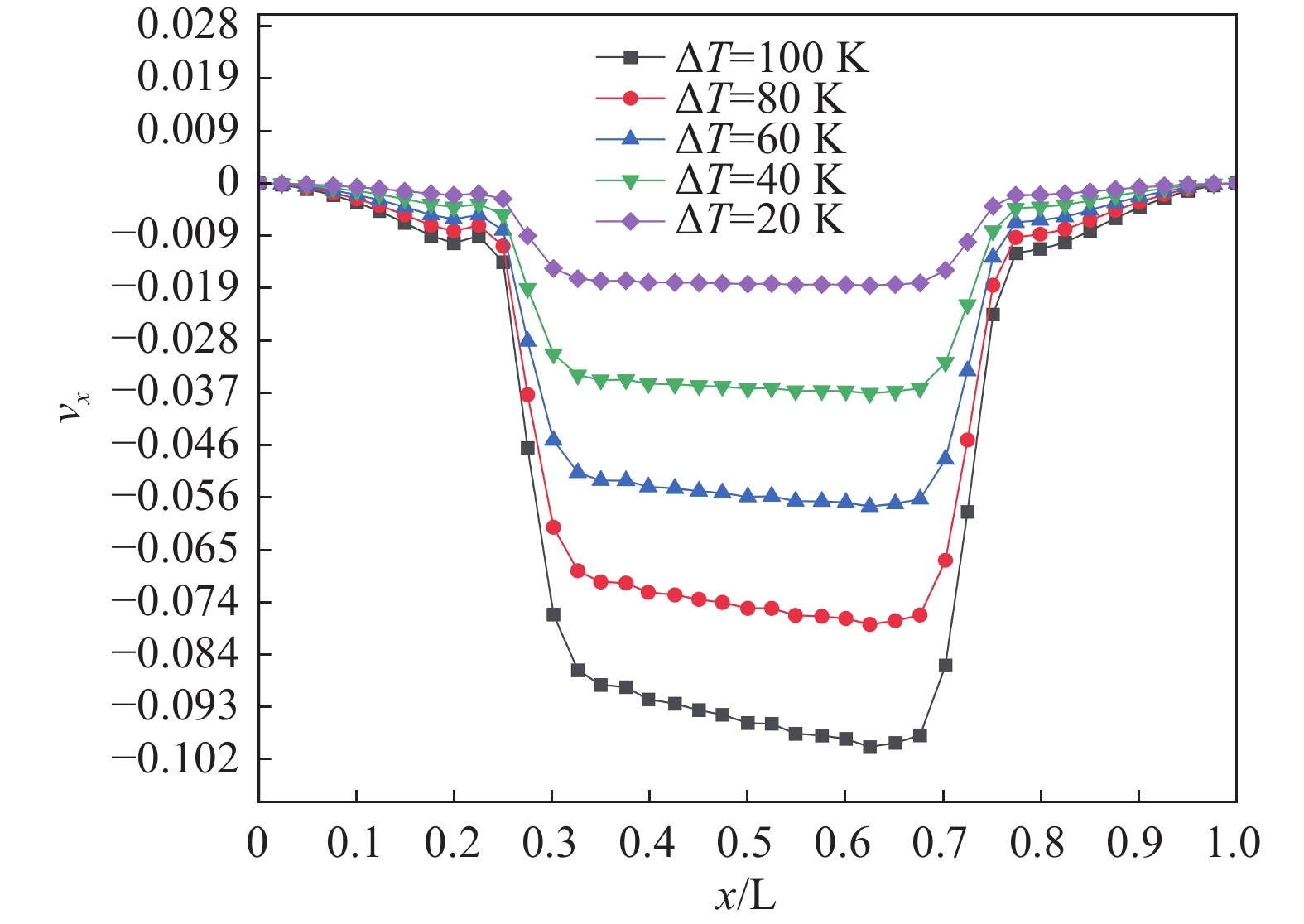
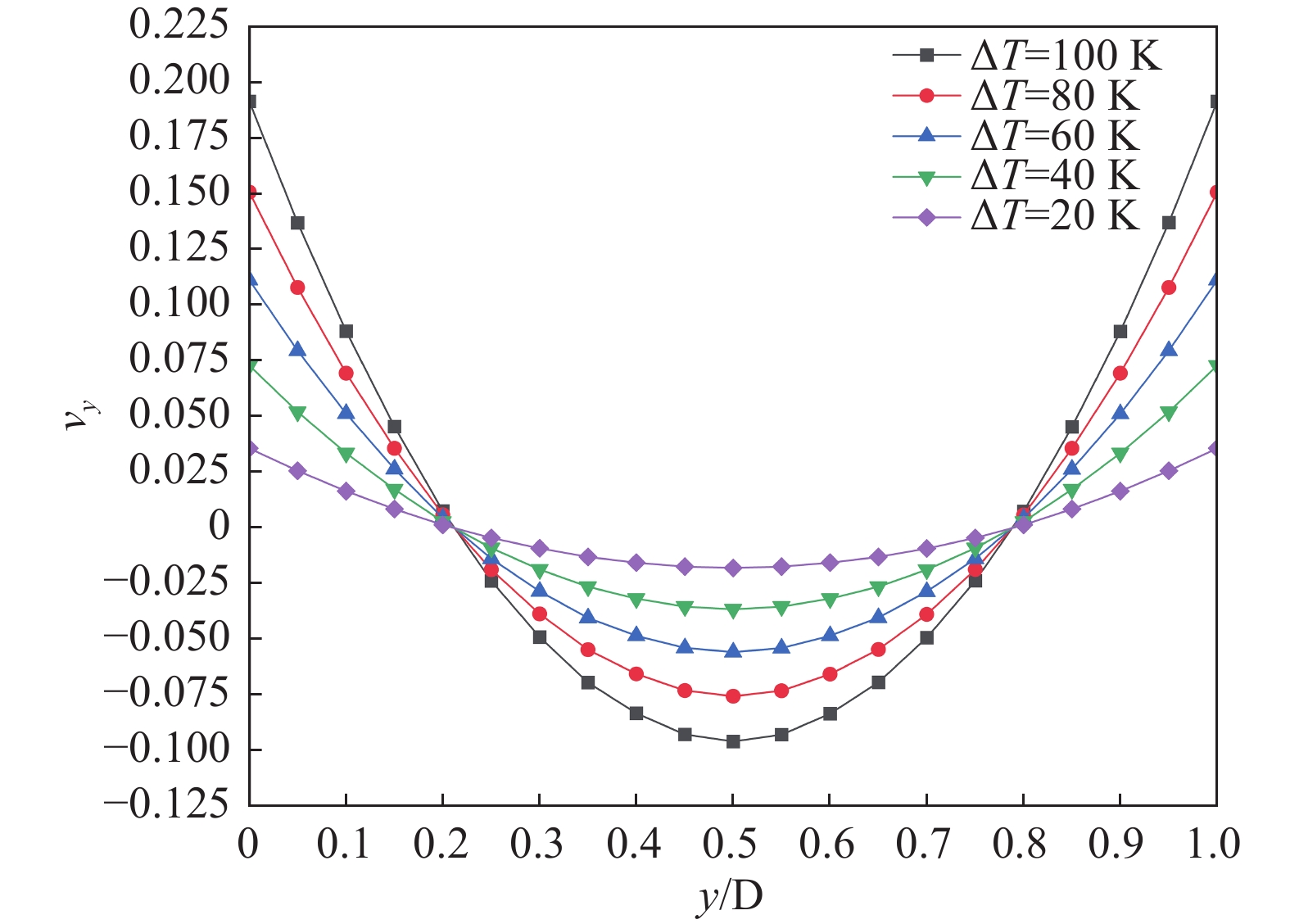
冷热腔温差的变化会直接影响努森压缩机微通道内克努森数、压升、速度等特性。因此本文研究5种不同的温差（∆T = 20 K、∆T = 40 K、∆T = 60 K、∆T = 80 K以及∆T = 100 K）下努森压缩机微通道内的流动和性能特性。
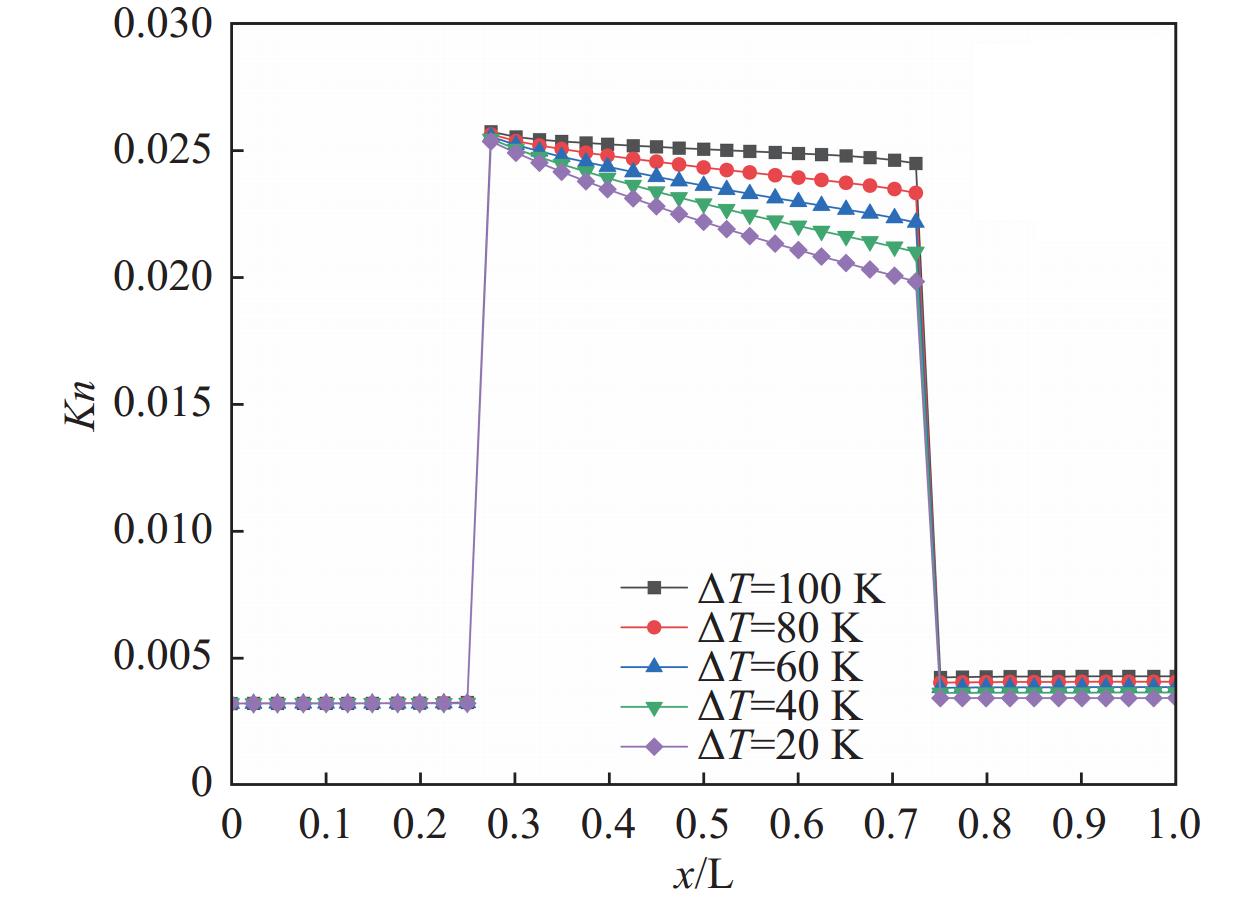
图9所示为沿微通道中心线的氮气克努森数变化情况，克努森数范围处在0.001与0.1之间，氮气处于滑移流流态。由图可见，当冷热腔温差分别为∆T = 20 K、∆T = 40 K、∆T = 60 K、∆T = 80 K以及∆T = 100 K时，微通道出口处的氮气克努森数分别为Kn = 0.020、Kn = 0.021、Kn = 0.022、Kn = 0.023以及Kn = 0.024，冷热腔的温差每增加20 K，克努森数增大0.001，这与克努森数与温差成正比关系一致。
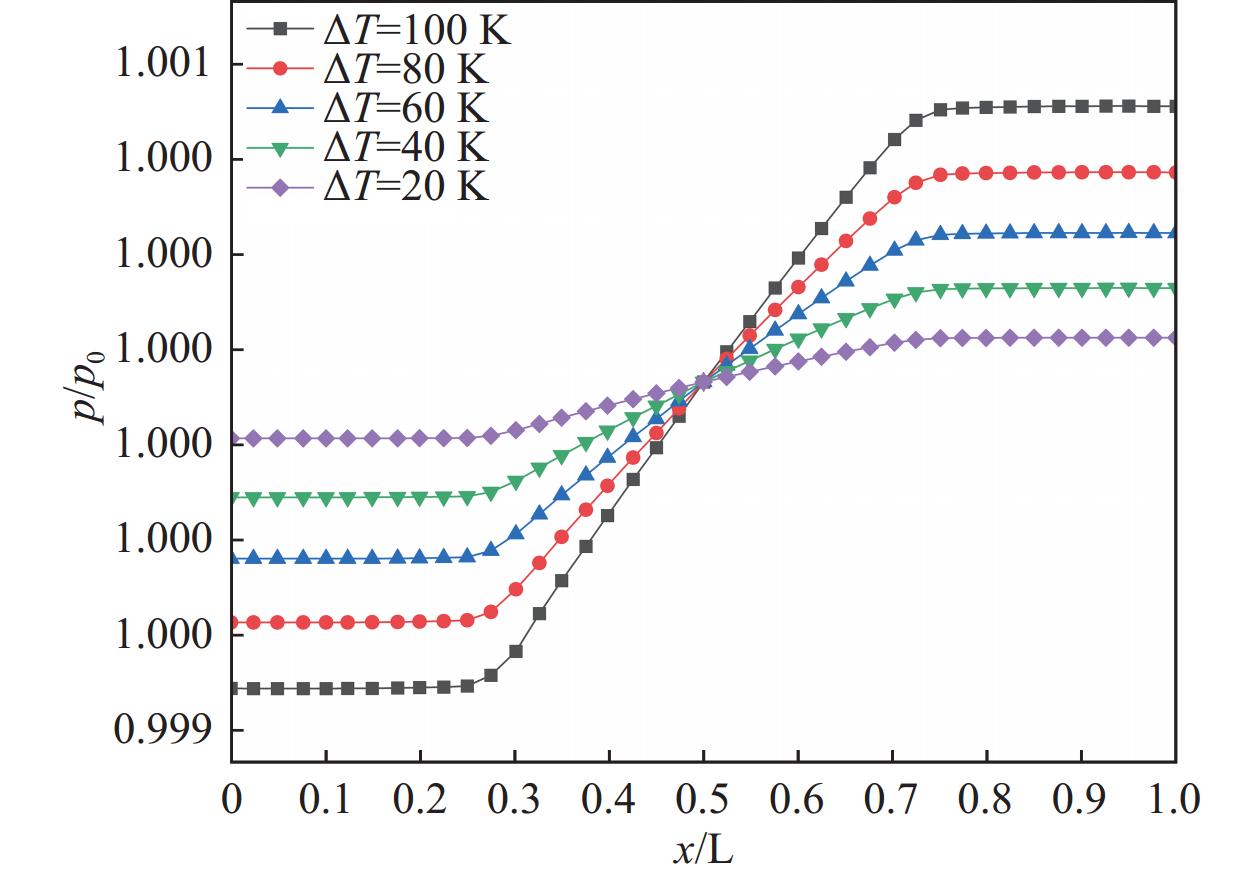
图10所示沿梯形微通道中心线的氮气无量纲压力比变化情况。由图可知，在同一温差下，微通道内氮气无量纲压力比呈线性增加，当冷热腔温差分别为∆T = 20 K、∆T = 40 K、∆T = 60 K、∆T = 80 K以及∆T = 100 K时，两端腔室内气体的压差值为16.081 Pa、33.420 Pa、52.014 Pa、71.870 Pa以及92.974 Pa，随着温差增大，压升增大，并且通道内气体压力增大速率增大。因为温差增大，内壁的温度梯度增大，使得热流逸效应增强，所以气体压升和压力增大效率都会增大。由此说明，在冷热腔室温差在一定范围内增大，可以提高升压性能。
沿梯形微通道中心线泊肃叶流流速的分布情况如图11所示，由图可知，当冷热腔温差分别为∆T = 20 K、∆T = 40 K、∆T = 60 K、∆T = 80 K以及∆T = 100 K时，梯形微通道内泊肃叶流流速最大值分别为0.018 m/s、0.037 m/s、0.057 m/s、0.078 m/s以及0.100 m/s，温差每增加20 K，泊肃叶流流速最大值增加约0.020 m/s，因为温差增大使得热流逸效应增强，有利于微通道内气体流动。
沿梯形微通道垂直中心线处速度在x方向分量的分布曲线如图12所示，由图可知，该分布曲线呈抛物线型，当冷热腔温差分别为从20 K升至100 K时，微通道近壁面处的热流逸流流速从0.036 m/s升至0.191 m/s，增加了430.556%，微通道中心线处的泊肃叶流流速从0.018 m/s 升至0.096 m/s，增加了433.333%。随着温差增大，气体流速增大，因为温差增大，使得内壁温度梯度增大，气体热流逸效应增大。由此说明，冷热腔室温差在一定范围内增加有利于微通道内气体流动。
-
（1）在滑移流区，克努森数可反应热流逸效应的强弱。梯形微通道的倾角θ = 0时（即矩形通道），克努森数沿微通道x轴正方向是线性增加的；当倾角大于0°时，沿着x轴正方向克努森数在逐渐减小，并且倾角越大，克努森数减小的速度越快，同时克努森数逐渐成非线性变化。
（2）随着梯形微通道倾角的增大，内部气体的稀薄程度减小，热流逸效应减弱，其升压性能减小，倾角增加5.72°，压差减小80.890 Pa，而通道内气体泊肃叶流与热流逸流流速均增大，但热流逸速度的增加速度减小，倾角θ从0°增加到2.86°，热流逸速度增加0.011 m/s，而倾角θ从2.86°增加到5.72°，热流逸速度仅增加0.004 m/s。
（3）在同一温差下，微通道内气体无量纲压力比呈线性增加，随着冷热腔室温差的增大，内部气体的稀薄程度增大，热流逸效应增强，其升压性能显著提高，并且通道内泊肃叶流与热流逸流流速均增大，温差每增加20 K，泊肃叶流和热流逸流最大流速值分别增加约0.021 m/s和0.039 m/s，冷热腔的温差增加有利于通道内气体流动，提高升压性能。
滑移流区域梯形微通道内气体热流逸效应及流动特性
Thermal Transpiration Effect and Flow Characteristics of Gas in Trapezoidal Microchannel in Slip Flow Region
-
摘要: 努森压缩机是一种有效的非机械式气体升压微泵，在输送气体、压缩气体等方面具有巨大的应用潜力。基于具有滑移和跳跃边界条件的纳维-斯托克斯方程，建立适应于滑移流区域梯形微通道内气体流动二维数值模型。分析了倾角和冷热腔室温差对微通道内部气体克努森数分布、压升以及流动特性的影响规律。结果表明：微通道倾角从0°升高到5.72°，压升从129.181 Pa降低到48.291 Pa，降低了62.618%。此外，倾角越大，气体克努森数越小，但气体流速逐渐增大，泊肃叶流和热流逸流最大流速分别为0.106 m/s和0.200 m/s。当冷热腔室温差从20 K升高到100 K，努森压缩机的压升从16.081 Pa升高到92.974 Pa，提高478.161%。，温差每增加20 K，克努森数增大0.001，泊肃叶流和热流逸流最大流速分别增加约0.020 m/s和0.039 m/s。研究结果为努森压缩机复杂微通道的构建及性能优化设计提供指导。Abstract: The Knudsen compressor is an effective non-mechanical gas-boosting micropump, which has great potential for applications in transporting and compressing gases. In this paper, a two-dimensional numerical model of the gas flow inside a trapezoidal microchannel adapted to the slip flow region is established based on the Navier-Stokes equations with slip and jump boundary conditions. The effects of the inclination angle and the temperature difference between the hot and cold chambers on the Knudsen number distribution, pressure rise and flow characteristics of the gas inside the microchannel are analyzed. The results show that when the inclination angle of the microchannel increases from 0° to 5.72°, the pressure rise decreases from 129.181 Pa to 48.291 Pa, which is 62.618% lower. In addition, the larger the inclination angle is, the smaller the gas Knudsen number is, but the gas flow rate gradually increases, and the maximum flow velocities of the Poiseuille flow and the thermal transpiration flow are 0.106 m/s and 0.200 m/s, respectively. The temperature difference between the hot and cold chambers increases from 20 K to 100 K, and the pressure rise of the Knudsen compressor increases from 16.081 Pa to 92.974 Pa, which is an increase of 478.161%. For every 20 K increase in temperature difference, the Knudsen number increases by 0.001, and the maximum flow velocity of the Poiseuille flow and the thermal transpiration flow increase by about 0.020 m/s and 0.039 m/s, respectively. The results of this study provide guidance for the construction of complex microchannels in the Knudsen compressor and the optimal design of its performance.
-
-
图 1 梯形微通道努森压缩机的二维平面图
Figure 1. 2D plan view of the Knudsen compressor with the trapezoidal microchannel
图 2 模型的网格划分。（a）全局网格，（b）梯形微通道网格局部放大图
Figure 2. Meshing of the model. (a) Global mesh, (b) partial enlarged view of the trapezoidal microchannel mesh
图 5 沿通道中心线的克努森数分布
Figure 5. Knudsen number distribution along the centerline of the channel
图 8 沿微通道垂直中心线的速度分布
Figure 8. Velocity distribution along the vertical centerline of the microchannel
图 9 沿通道中心线的克努森数分布
Figure 9. Distribution of Knudsen number along the centerline of the channel
-
[1] Shao J, Ye J, Zhang Y, et al. Effect of the microchannel obstacles on the pressure performance and flow behaviors of the hydrogen Knudsen compressor[J]. International Journal of Hydrogen Energy,2019,44(40):22691−22703 doi: 10.1016/j.ijhydene.2019.03.075 [2] Pitipat P, Chanon P, Tanawit T, et al. Performance improvement of glass microfiber based thermal transpiration pump using TPMS[J]. Micromachines,2022,13(10):1632−1632 doi: 10.3390/mi13101632 [3] Jiang L, Junlong X, Jianjun Y, et al. Flow and transmission characteristics of the multistage hydrogen Knudsen pump in the micro-power system[J]. International Journal of Hydrogen Energy,2022,47(44):19206−19216 doi: 10.1016/j.ijhydene.2022.04.064 [4] Jiang L, Junlong X, Jianjun Y, et al. Non-equilibrium evolution and characteristics of the serrated microchannel hydrogen knudsen compressor[J]. International Journal of Hydrogen Energy,2022,47(7):4804−4813 doi: 10.1016/j.ijhydene.2021.11.087 [5] Kosyanchuk V, Kovalev V, Yakunchikov A. Multiscale modeling of a gas separation device based on effect of thermal transpiration in the membrane[J]. Separation and Purification Technology, 2017, 180 58-68 [6] Kugimoto K, Hirota Y, Kizaki Y. Motionless heat pump-A new application of thermal transpiration [J]. AIP Conference Proceedings, 2016, 1786(1): 080004 [7] Ye J, Shao J, Hao Z, et al. Characteristics of thermal transpiration effect and the hydrogen flow behaviors in the microchannel with semicircular obstacle[J]. International Journal of Hydrogen Energy,2019,44(56):29724−29732 doi: 10.1016/j.ijhydene.2019.04.079 [8] Zhang Z, Wang X, Zhao L, et al. Study of flow characteristics of gas mixtures in a rectangular Knudsen pump[J]. Micromachines,2019,10(2):79 doi: 10.3390/mi10020079 [9] Bond D, Wheatley V, Goldsworthy M. Numerical investigation of curved channel Knudsen pump performance[J]. International Journal of Heat and Mass Transfer,2014,76:1−15 [10] Bond D, Wheatley V, Goldsworthy M. Numerical investigation into the performance of alternative Knudsen pump designs[J]. International Journal of Heat and Mass Transfer,2016,93:1038−1058 [11] Varade V, Duryodhan V, Agrawal A, et al. Low mach number slip flow through diverging microchannel[J]. Computers and Fluids,2015,111:46−61 [12] Tatsios G, Quesada L G, Rojas-Cardenas M, et al. Computational investigation and parametrization of the pumping effect in temperature-driven flows through long tapered channels[J]. Microfluidics and Nanofluidics,2017,21(5):99 doi: 10.1007/s10404-017-1932-5 [13] Mozaffari S M, Roohi E. On the thermally-driven gas flow through divergent micro/nanochannels[J]. International Journal of Modern Physics C,2017,28(12):1750143 doi: 10.1142/S0129183117501431 [14] Hemadri, Vadiraj, Varade, et al. Investigation of rarefied gas flow in microchannels of non-uniform cross section[J]. Physics of fluids,2016,28(2):022007 doi: 10.1063/1.4942183 [15] Balaj M, Roohi E, Akhlaghi H. Effects of shear work on non-equilibrium heat transfer characteristics of rarefied gas flows through micro/nanochannels[J]. International Journal of Heat and Mass Transfer, 2015, 83 69-74 [16] Barber R, Sun Y, Gu X, et al. Isothermal slip flow over curved surfaces[J]. Vacuum,2004,76(1):73−81 doi: 10.1016/j.vacuum.2004.05.012 [17] S. E B. The Navier–Stokes–Voigt equations with position-dependent slip boundary conditions[J]. Zeitschrift für angewandte Mathematik und Physik,2023,74(1):6 [18] Ye J, Shao J, Xie J, et al. The hydrogen flow characteristics of the multistage hydrogen Knudsen compressor based on the thermal transpiration effect[J]. International Journal of Hydrogen Energy,2019,44(40):22632−22642 doi: 10.1016/j.ijhydene.2019.04.155 [19] Jianjun Y, Xiaoyi J, Shuangling T, et al. Three dimensional channel effect on the flow characteristics and the performance of hydrogen Knudsen compressors[J]. International Journal of Hydrogen Energy,2020,46(34):18128−18136 [20] Sharipov, F. Data on the velocity slip and temperature jump on a gas-solid interface[J]. Journal of Physical and Chemical Reference Data, 2011, 40(2): 023101 [21] 张月卓. 微通道气体流动换热特性数值模拟分析[D]. 大连:大连理工大学, 2019 (in Chinese) Yuezhuo Z, Numerical simulation and analysis of gas flow and heat transfer in microchannel[D]. Dalian University Of Technology, 2019 -
图( 12)
计量
- 文章访问数: 208
- HTML全文浏览数: 208
- PDF下载数: 1
- 施引文献: 0