为设计合理的叶片结构，本文利用COMSOL软件中数学粒子追踪模块，基于蒙特卡洛方法，模拟分子流态下气体粒子在不同叶片间气体流域中的传输过程^[21-23]，计算气体粒子传输几率，对比分析不同叶片结构的抽气性能。

模拟计算基于如下假设：

（1）气体分子的流态为自由分子流，被抽介质为氮气。

（2）不考虑分子流态下气体分子经过管道时，会出现的分子向管路中心聚集的束流效应现象和角度发散现象。

（3）入射的气体分子在入口平面上均匀分布，入射方向服从余弦分布，入射速度服从麦克斯韦速度分布。

（4）不考虑管道内壁对气体分子的吸附，气体分子碰撞到内壁后漫散射。

基于以上假设，分析叶片间气体粒子正、反向传输几率和压缩比。涡轮分子泵的最大抽速${S_{\max }}$和最大压缩比${K_{\max }}$由下式计算：

式中，$\bar v$为气体分子热运动平均速率，$A$为吸气面积，${p_1}$、${p_2}$分别为组合叶列入口、出口侧的压力，${M_{12}}$、${M_{21}}$分别为气体通过组合叶列的正、反向传输几率。

由式（1）、（2）可知，涡轮分子泵的抽气能力主要由正、反向传输几率决定。为了得到组合叶列的传输几率${M_{12}}$、${M_{21}}$，可由单级叶列传输几率迭代求出，此时${M_{12}}$、${M_{21}}$分别对应${P_{\text{n}}}$、${Q_{\text{n}}}$。组合叶列传输几率的简化计算公式为：

式中，${P_{\text{n}}}$、${Q_{\text{n}}}$分别表示前n级组合叶列正、反向传输几率，${P_{{\mathrm{n}} - 1}}$、${Q_{{\mathrm{n}} - 1}}$分别表示前n−1级组合叶列正、反向传输几率，${P_{{\text{dn}}}}$、${Q_{{\text{dn}}}}$分别表示第n级单叶列正、反向传输几率。

径向涡轮分子泵内部抽气结构可分为两种：一是由内部抽气向四周排气，二是由四周抽气向中间排气。第一种结构，抽气级叶列线速度较小且有效抽气面积小，因此抽速较小，而压缩级叶列线速度大，压缩比增加较快。第二种结构，抽气级叶列有效抽气面积较大且线速度高，因此抽速较大，而压缩级叶列线速度较小，压缩比上升慢，压缩比较小。

径向涡轮分子泵在设计多级叶列时，应同时考虑抽速与压缩比。在进气端选择可获得较大抽速的叶列参数；在排气端选择压缩比较大的叶列参数。有研究表明，在满足抽速设计指标的前提下，第一种抽气结构的压缩比比第二种高接近2个数量级^[12]，因此本研究选取第一种内部抽气向四周排气径向结构的涡轮分子泵为研究对象。

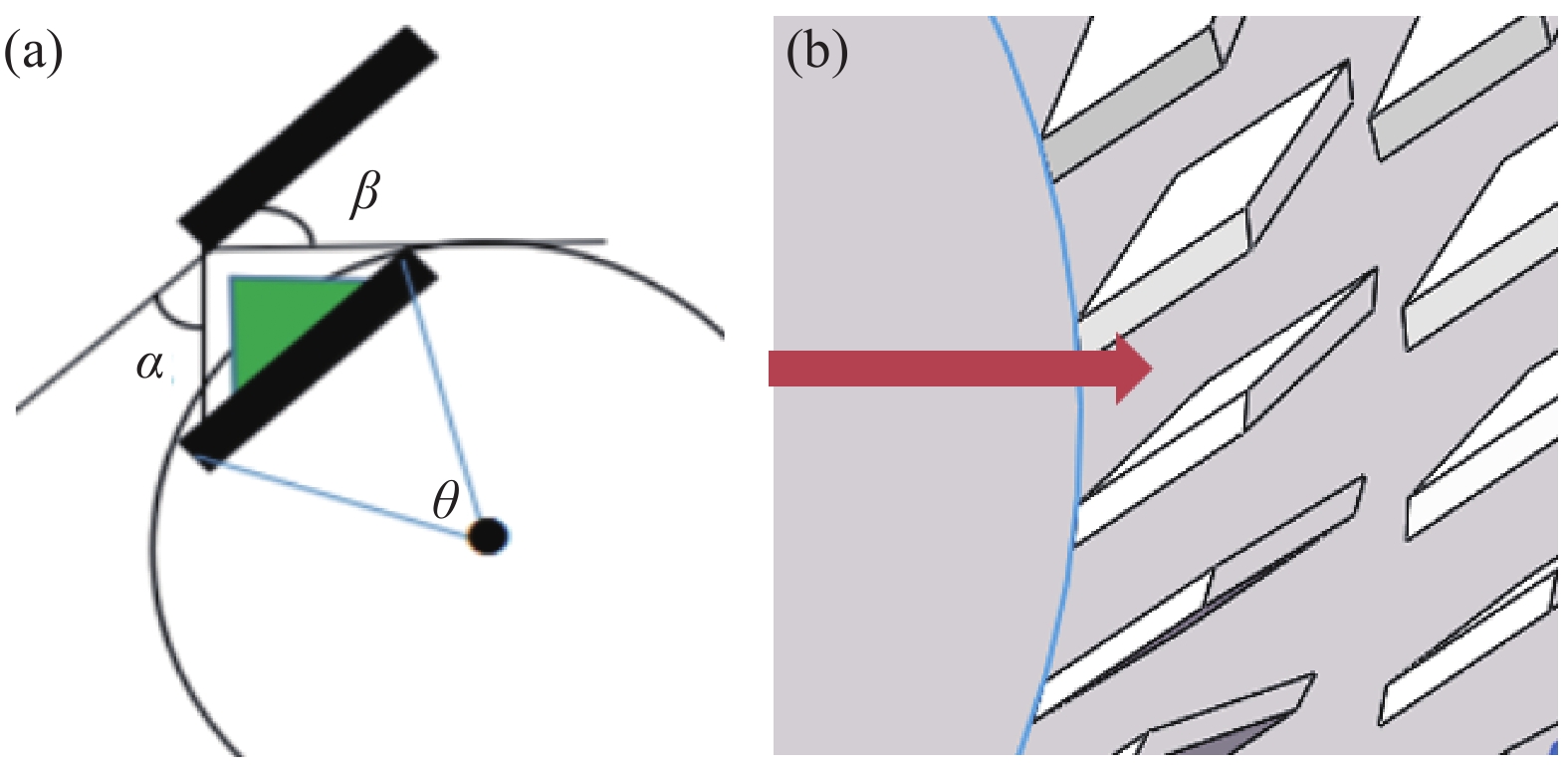
如图1（a）所示，当气体粒子抵达高速旋转的叶片附近时，角度$\alpha $范围内的气体粒子直接被叶片反弹回左侧，角度$ \beta $范围内的气体粒子直接穿过叶列抵达下一级。剩余部分的气体粒子既可能穿过，也可能被反弹。随着转子旋转，气体粒子不停地由内侧向外侧运动，从而产生抽气效果。

根据涡轮分子泵的基本抽气原理，泵入口侧的涡轮叶列应设计成大倾角、大节弦比、大抽气面积以保证抽速；出口侧的涡轮叶列应设计成小倾角、小节弦比以提高压缩比；在抽气级、压缩级中间应设计适当的倾角、节弦比作为过渡级。

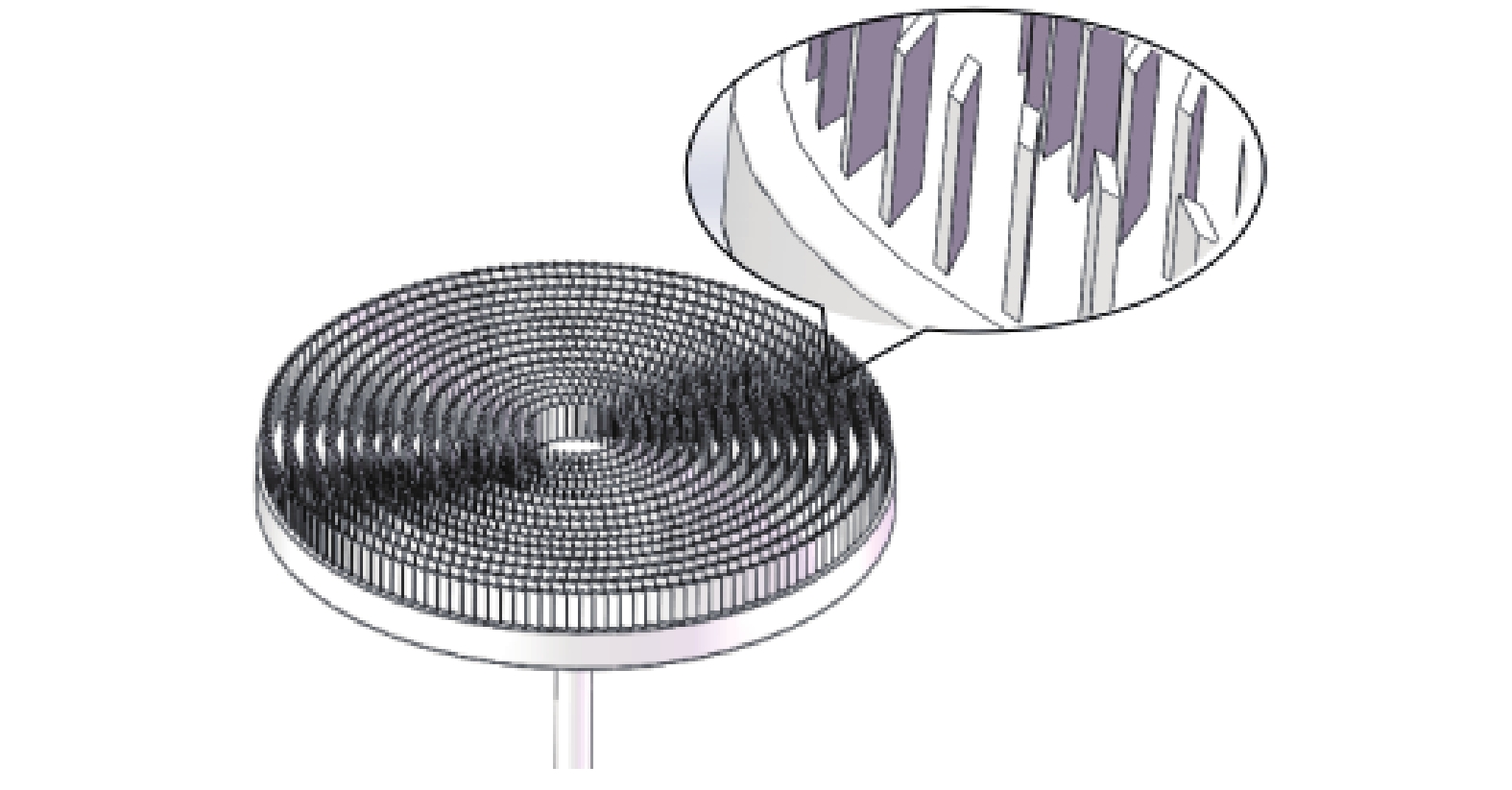
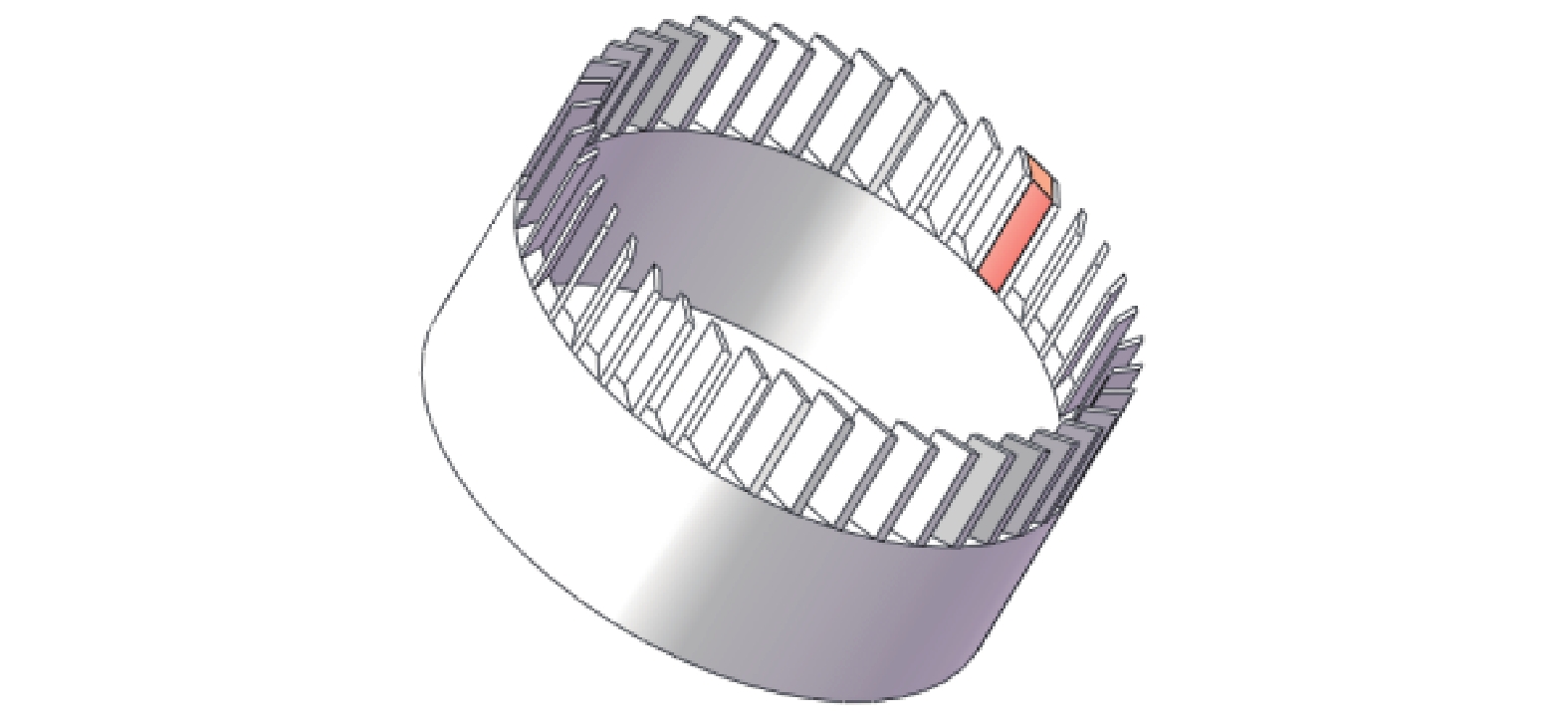
以抽速6 L/s由内向外抽气的径向涡轮分子泵为例，各级叶列所在半径为10.3~35 mm，转子相关参数设计如下：抽气级，叶片角度为30°~40°，节弦比取1，叶片间距1 mm，叶片宽度1 mm，叶片厚度0.15 mm，叶片高5.5 mm，共5级；过渡级，叶片角度为25°~30°，节弦比取0.8，叶片间距1.2 mm，叶片宽度1.5 mm，叶片厚度0.2 mm，叶片高5.5 mm，共6级；压缩级，叶片角度为20°，节弦比取0.7，叶片间距1.4 mm，叶片宽度2 mm，叶片厚度0.2 mm，叶片高5.5 mm，共4级。其转子结构如图2所示。

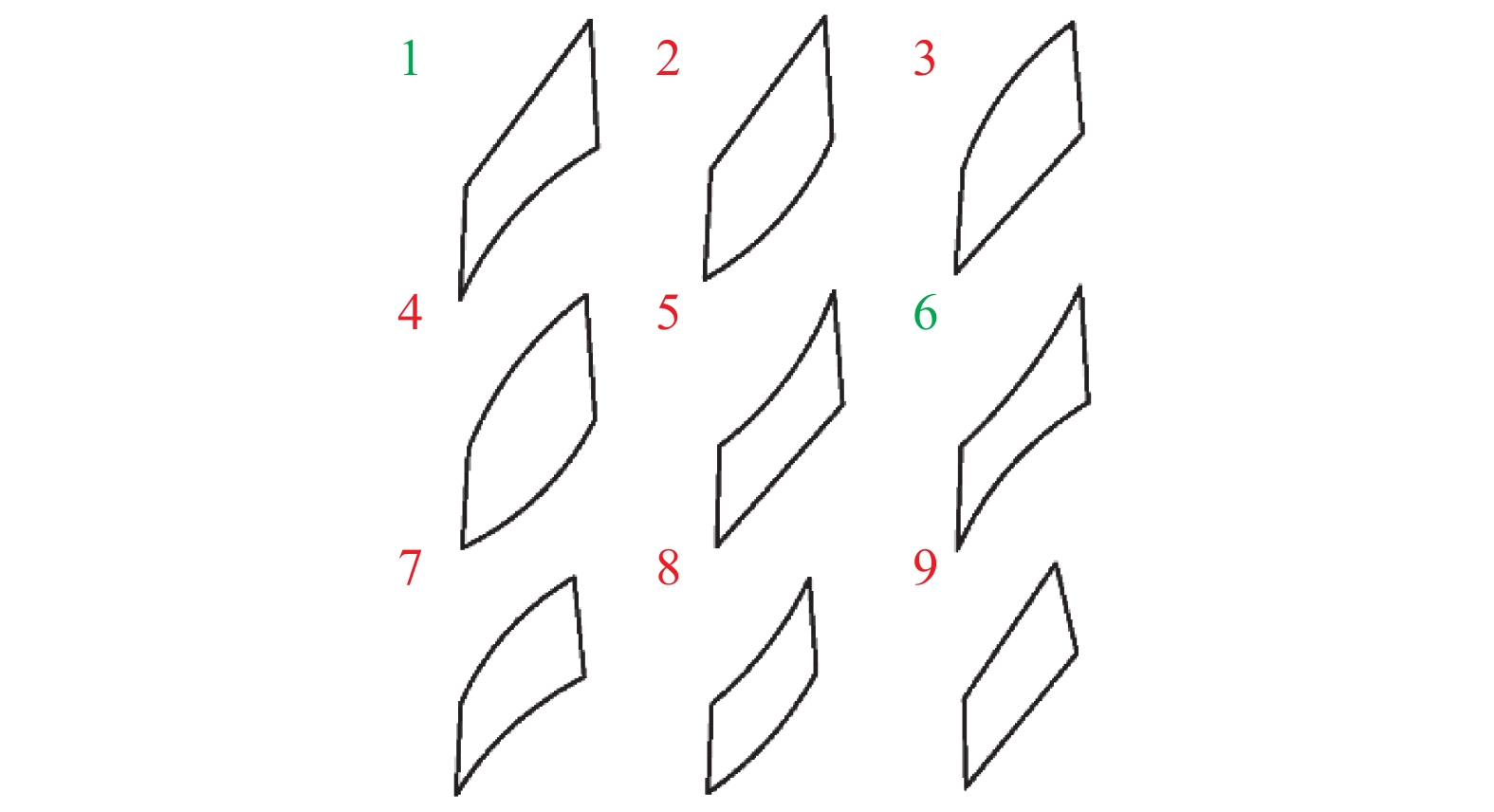
为了提高叶列间气体传输效率，对叶片形状进行改进优化^[24]。由于叶片形状决定了气体分子的反射运动，选取叶片间流场为研究对象，如图3所示。改变叶片两侧形状，可获得8种形状的叶片间流场，第9种为未改变形状的原始叶片间流场：（1）叶片内侧外凸；（2）叶片内侧内凹；（3）叶片外侧内凹；（4）叶片两侧内凹；（5）叶片外侧外凸；（6）叶片两侧外凸；（7）叶片内侧外凸及外侧内凹；（8）叶片内侧内凹及外侧外凸；（9）原始叶片。9种叶片间流场横截面如图4所示。

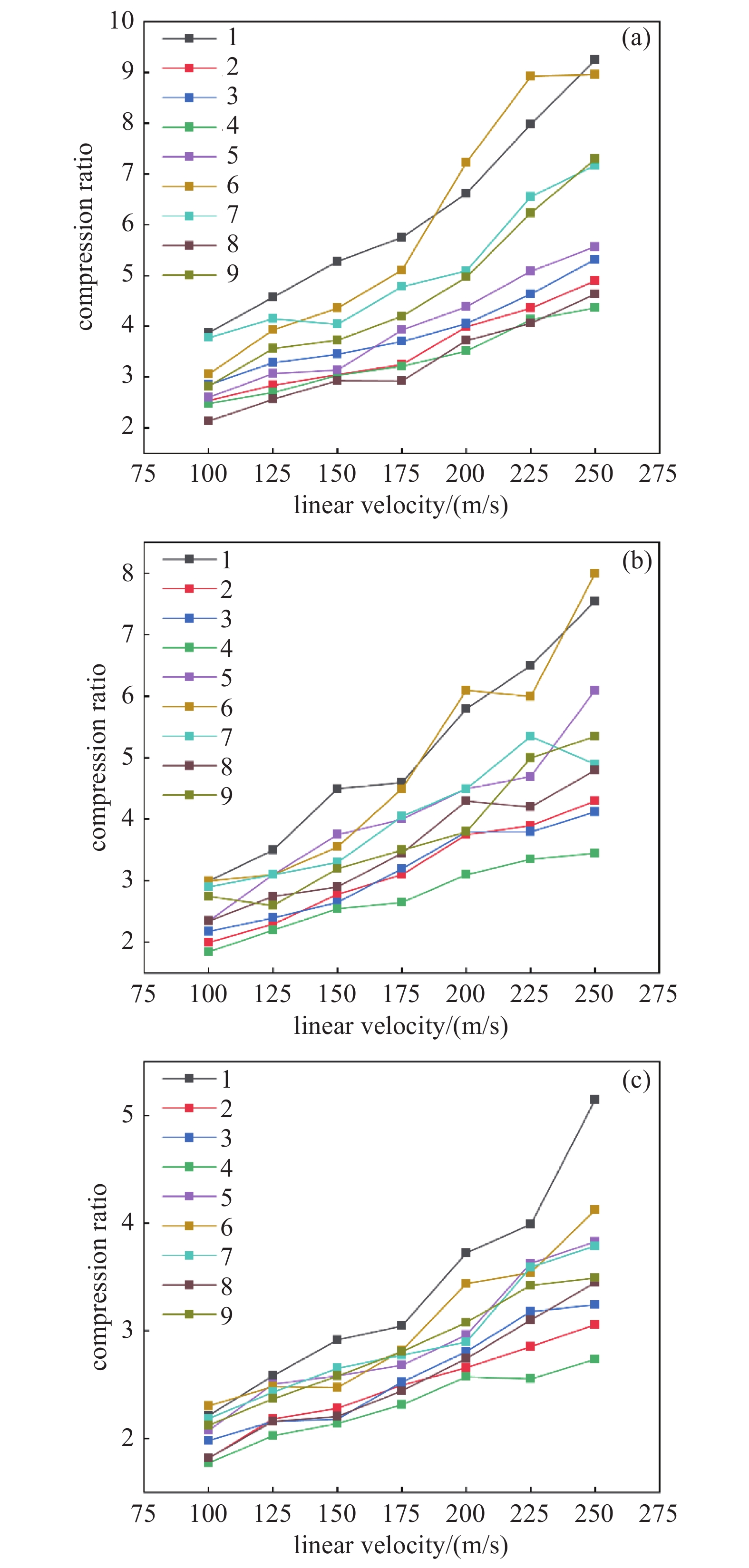
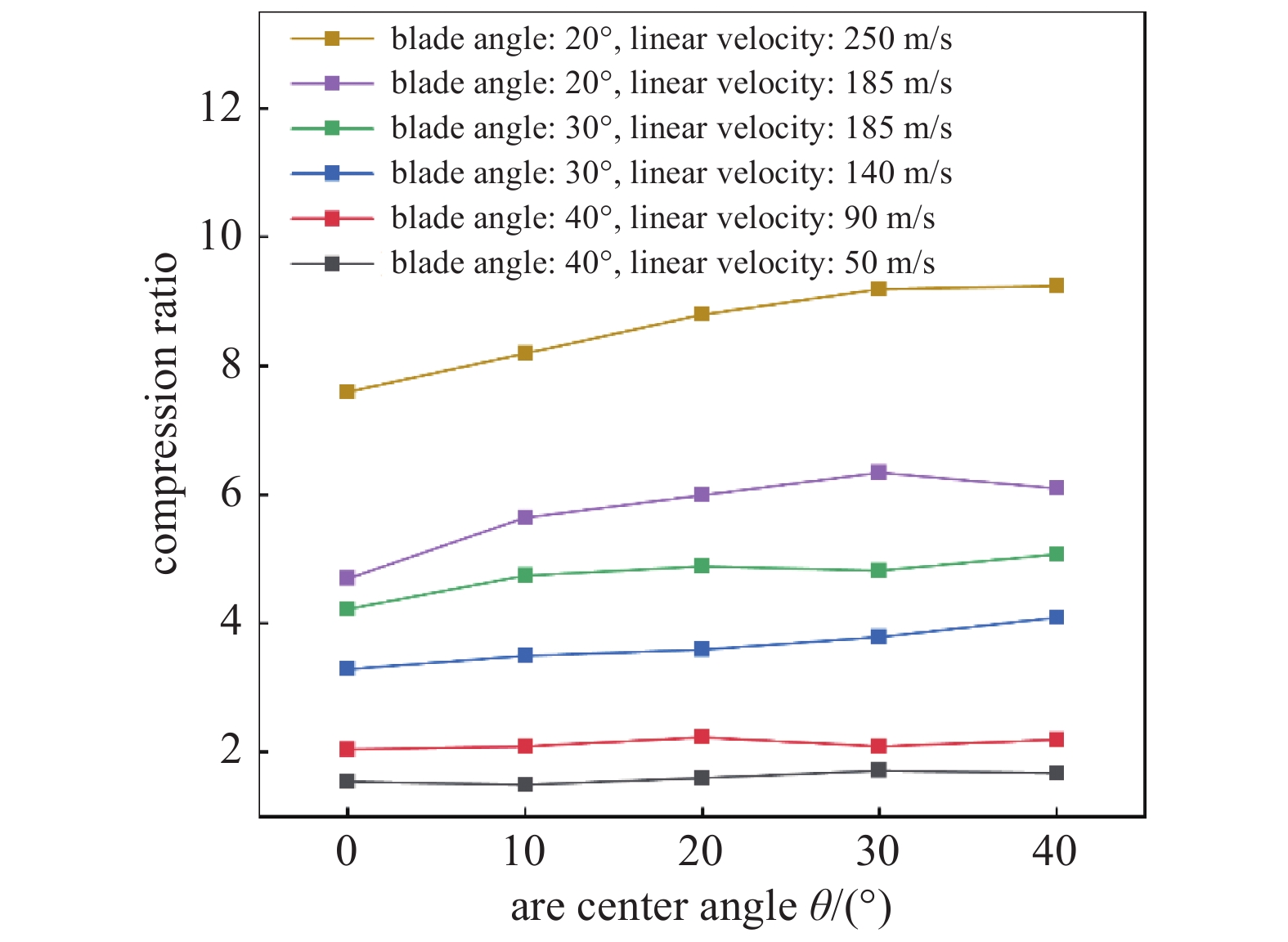
上述9种叶片间流场结构会对气体分子正、反向传输几率产生影响，为了更好地判断最佳叶列结构，分别以20°、30°、40°叶片角转子叶列为例，入射气体为氮气，气体分子热运动速度设为417 m/s。叶列线速度取100~250 m/s，进行模拟。取形状改动后叶片圆弧对应圆心角$\theta $为40°，利用COMSOL模拟计算得到9种不同叶片间流场结构的压缩比随线速度变化趋势，如图5所示。结果表明，20°、30°、40°三种叶片角下，第1种和第6种叶列结构的压缩比较优，考虑到叶列结构改动对抽速、叶片强度、加工成本等的影响，选第1种结构进行后续研究。

叶片单侧圆弧的大小会对抽气性能产生影响，为分析不同线速度下，圆弧圆心角$\theta $与压缩比之间的关系，针对20°、30°、40°叶片角、0°~40°圆弧圆心角、50、90、140、185、250 m/s叶列线速度开展研究。具体参数设置为：抽气级叶片角取40°，线速度取50、90 m/s；过渡级叶片角取30°，线速度取140、185 m/s；压缩级叶片角取20°，线速度取185、250 m/s（见图6）。

如图6所示，随着$\theta $增大，压缩比也呈增加趋势。但由于圆弧弧度过大会使叶片间有效抽气面积减小，因此$\theta $不宜过大。综合考虑，抽气、过渡、压缩级叶列优化的圆弧圆心角$\theta $分别选取20°、20°~40°、30°~40°。

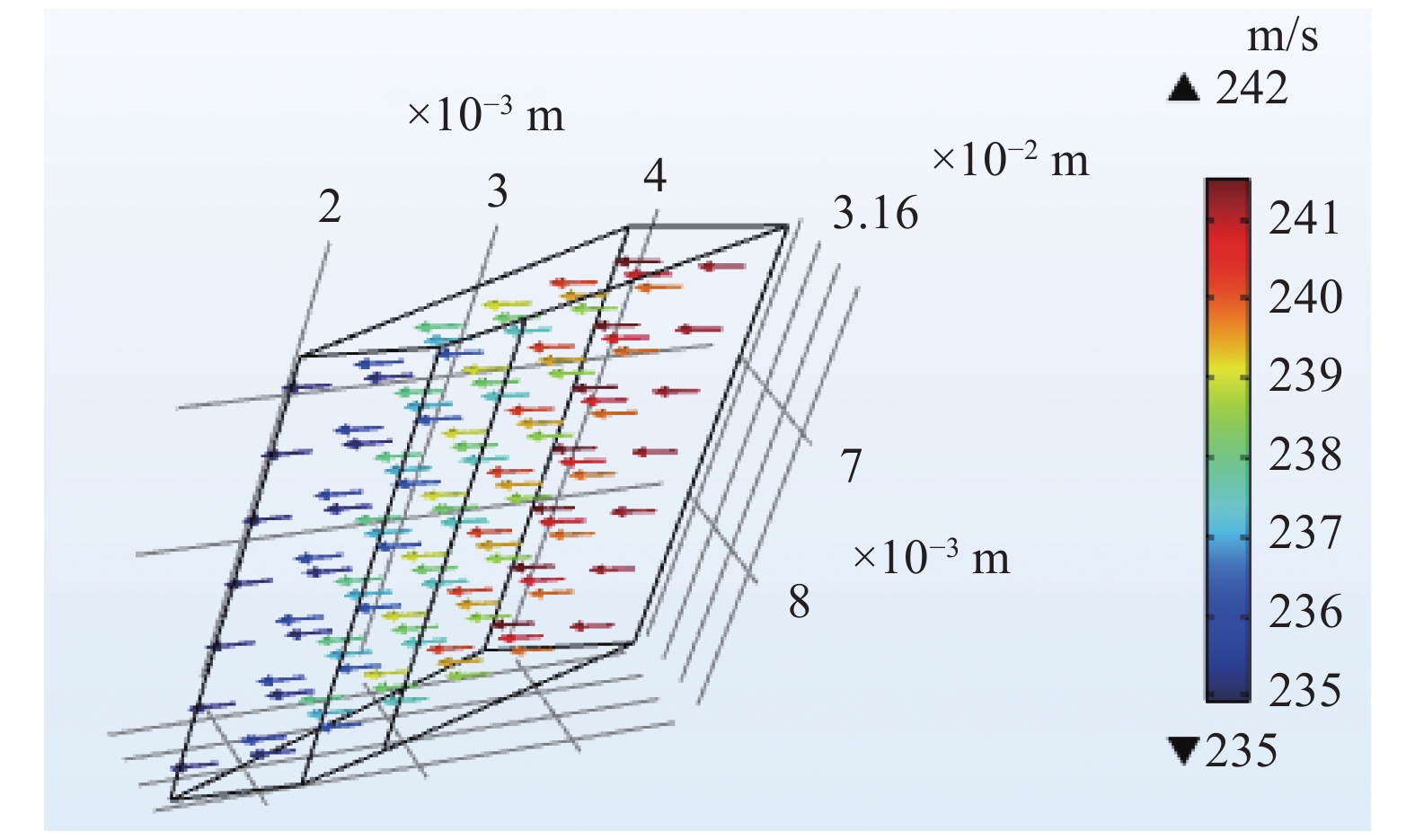
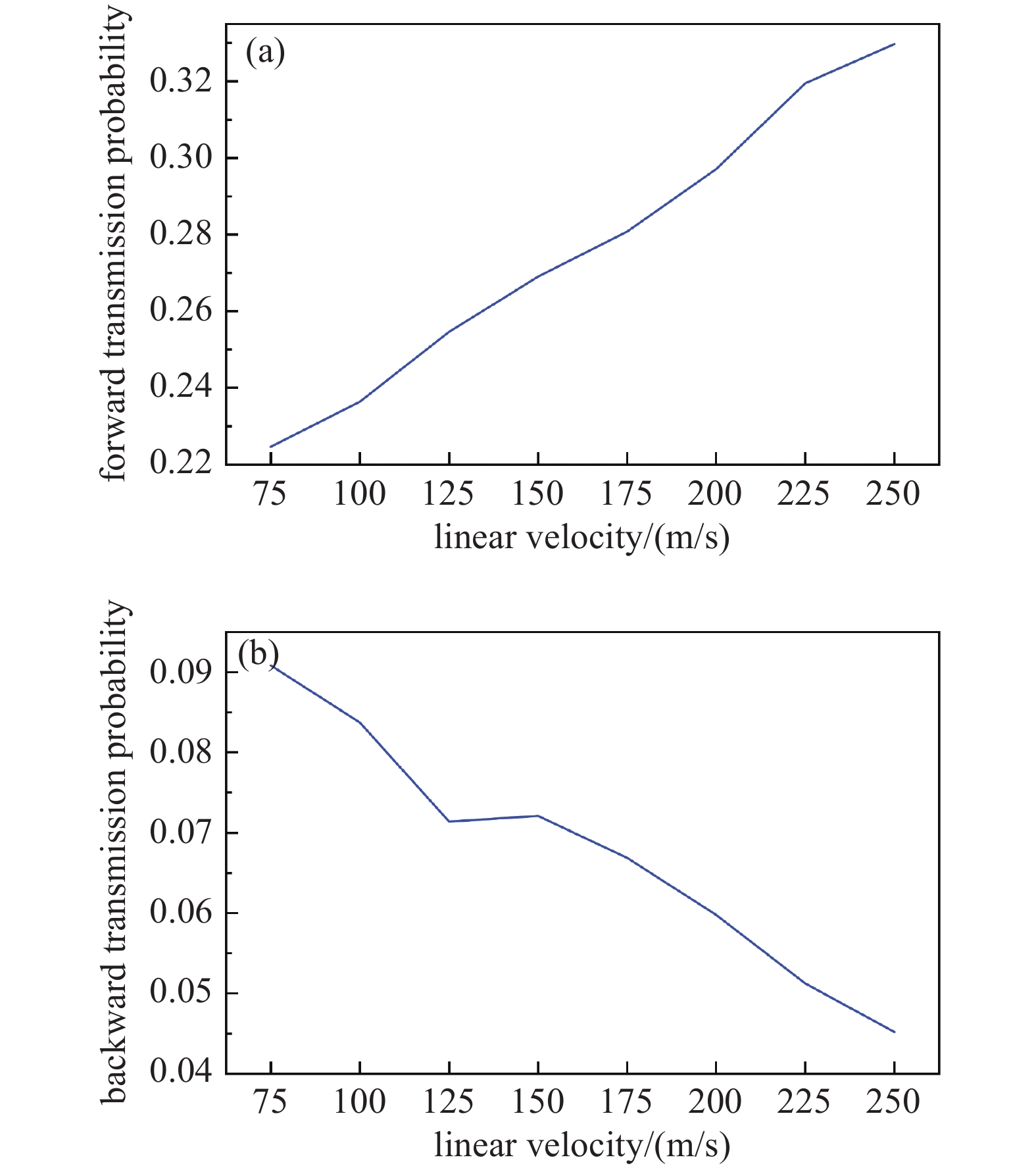
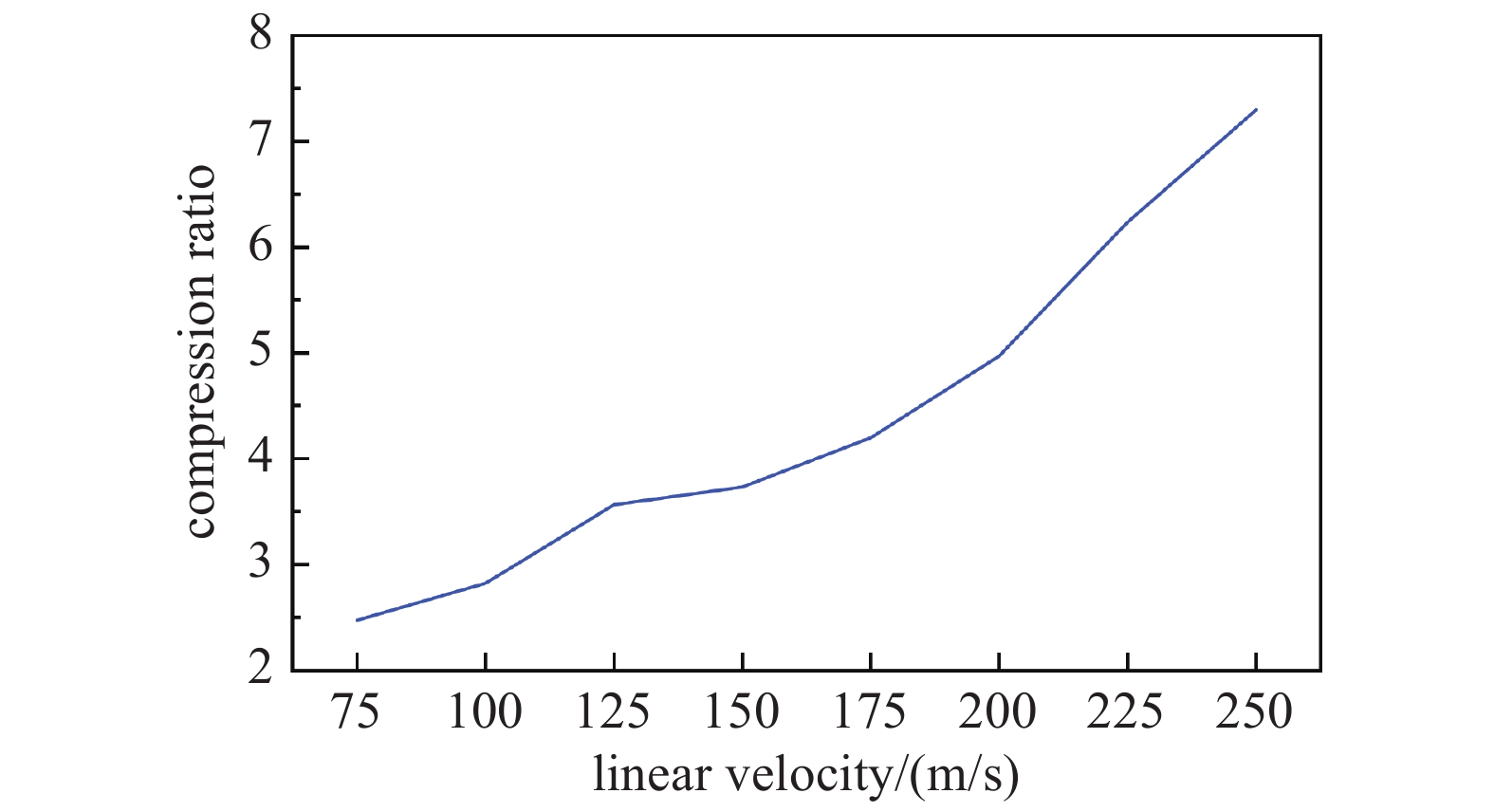
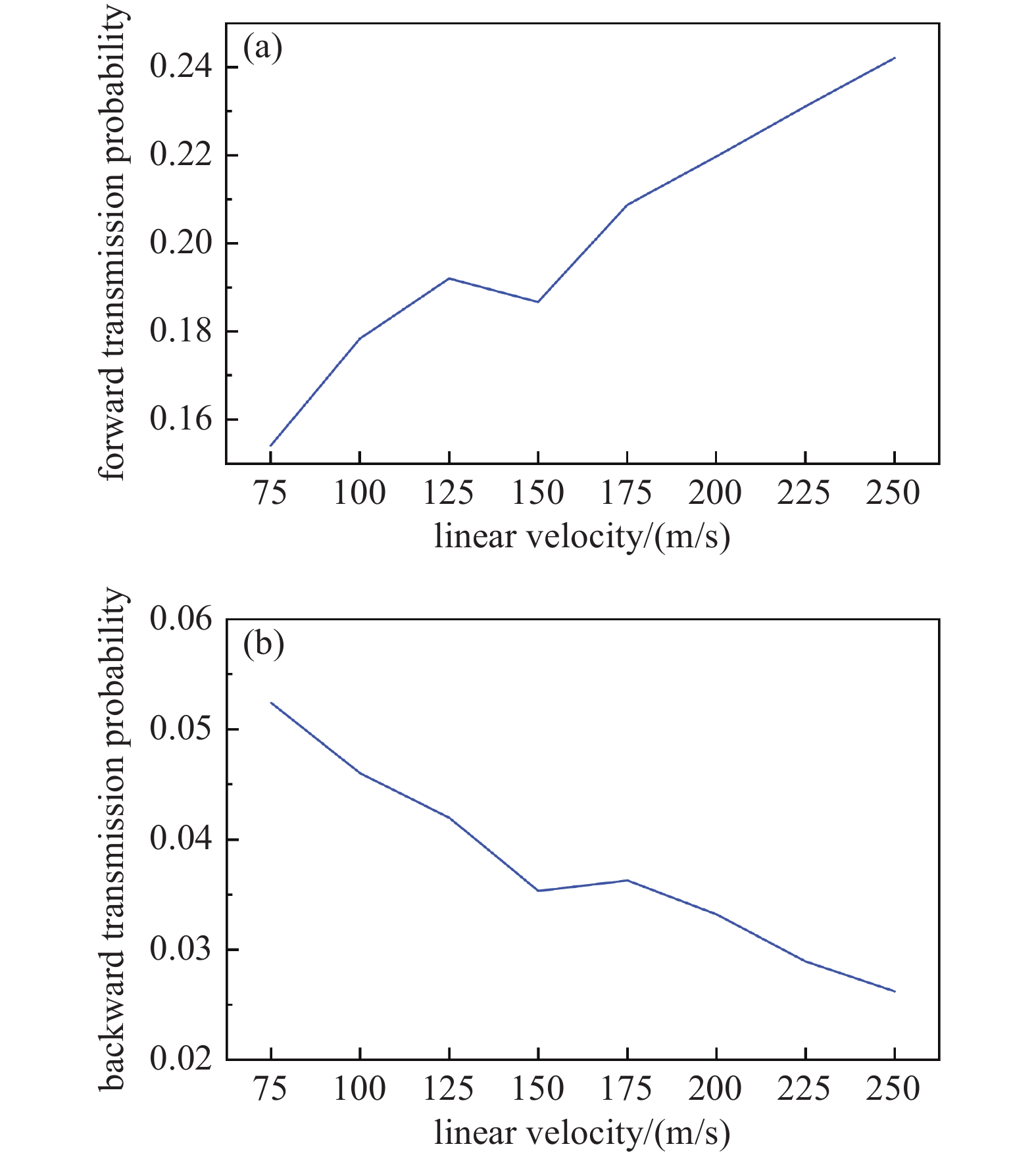
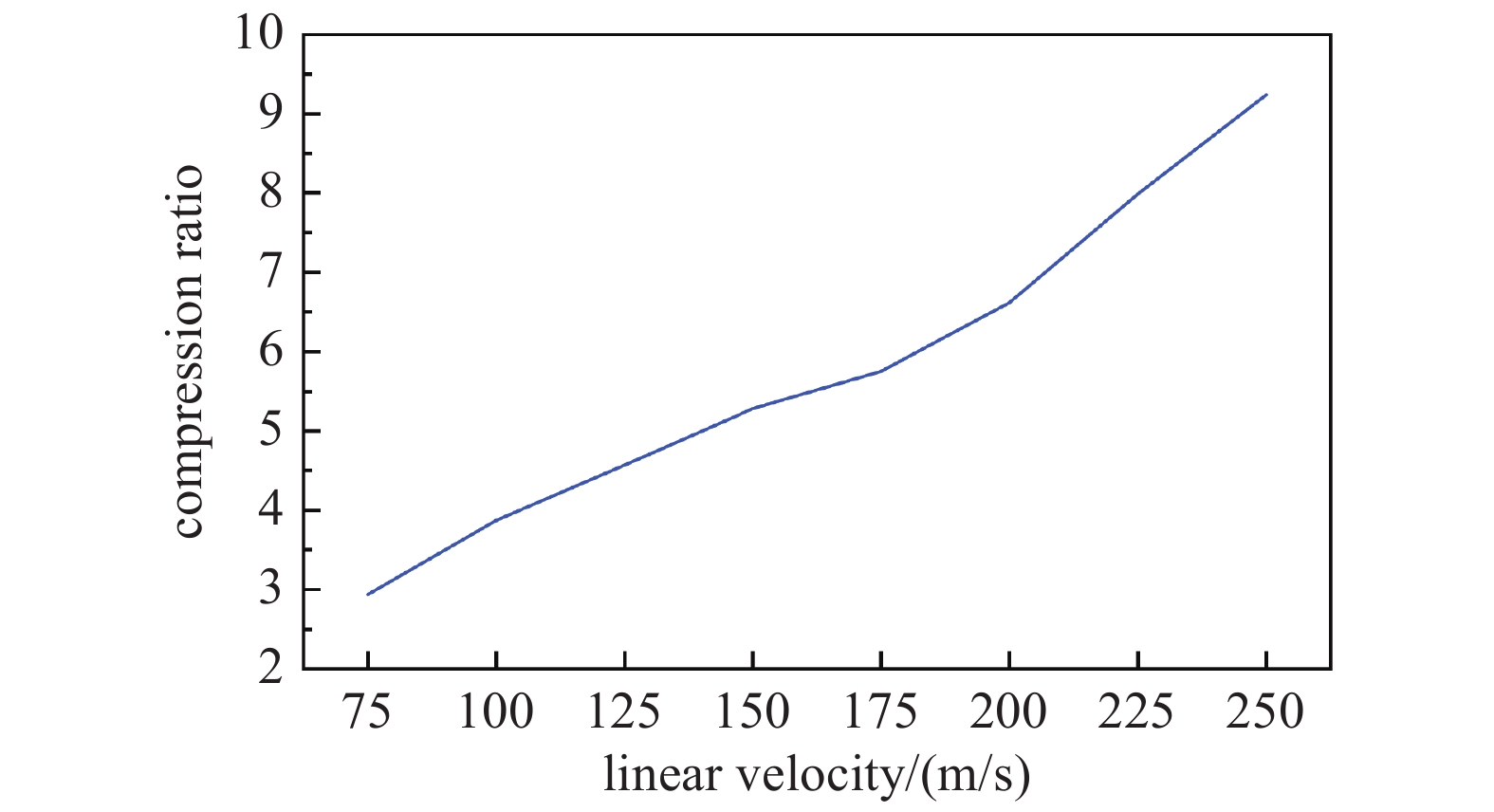
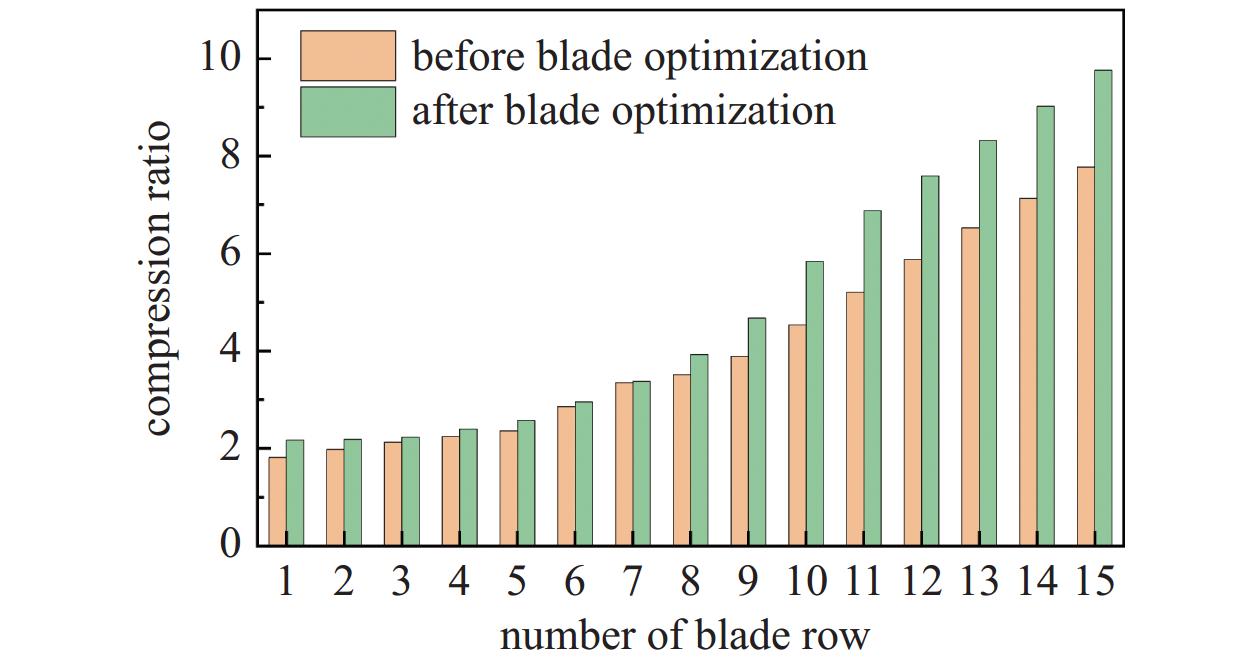
使用COMSOL软件分别对不同线速度原始叶列进行模拟计算，结果见图7。结合2.1节所述叶片参数，通过参数化扫描得到压缩比和线速度之间的关系，分析叶片间气体粒子的正向传输几率${M_{{\text{12}}}}$、反向传输几率${M_{21}}$和组合叶列压缩比，得出线速度与各参数之间的关系，图8、图9所示为20°叶片角原始叶列结果示例。

根据不同叶片角原始叶列的模拟结果可知，原始叶列4级压缩级各级的压缩比分别为5.88、6.53、7.13、7.78；抽气级与过渡级各级压缩比乘积分别为40.68、3111.57。根据式（2）~（4），并考虑到内外圈过流面积增加约5.2倍，计算可知原始叶列总压缩比约为5.18×10⁷。

转子基本结构参数不变，对第1种改进叶片进行优化分析，得到第1种叶列结构叶片间气体粒子正、反向传输几率、压缩比与线速度之间的关系，图10、11所示为20°叶片角优化叶列结果示例。

对比优化前后的正、反向传输几率模拟结果，发现优化后的正、反向传输几率均有所降低。这是由于叶片单侧圆弧的存在导致叶片间流场有效抽气面积减小。

根据不同叶片角优化叶列的模拟结果可知，优化叶列4级压缩级各级的压缩比分别为7.59、8.32、9.02、9.76；抽气级与过渡级各级压缩比乘积分别为65.08、7359.74。根据式（2）~（4），并考虑到内外圈过流面积增加约5.2倍，计算可知优化叶列总压缩比约为5.91×10⁸，比原始叶列提升1个数量级。

优化前后叶列各级压缩比对比如图12所示。叶片形状改动前后抽气级叶列压缩比相差不大，压缩级叶列压缩比相差显著。这是由于径向涡轮分子泵转子每一级叶列所在半径不同。半径越大，线速度越大，传输效果越好。抽气级叶列所在半径较小，增益效果不明显；压缩级叶列所在半径大，增益效果明显。在压缩级阶段，各叶列单级压缩比分别提升29.11%、27.39%、26.54%、25.53%。此外，由于叶片结构改动增加了叶片齿根处厚度，叶片强度也得到提升，延长了转子使用寿命，且能承受更高转速，获得更大抽速和压缩比。

优化叶列涡轮分子泵的抽速可由1.1节中式（1）、（3）、（4）迭代计算得到。优化叶列${P_1} = 0.263$，${Q_1} = 0.122$，故：

由式（3）、（4）继续迭代计算，可知组合优化叶列的正反向传输几率差值P₁₅−Q₁₅=0.165。

将差值及$\bar v$=417 m/s、$A$=355.8 mm²代入式（1）中得：$S$=6.12 L/s。经计算检验，优化后的抽速满足6 L/s的设计指标。

针对径向涡轮分子泵转子叶片结构进行优化研究，利用COMSOL软件对不同叶片结构抽气性能进行仿真分析，结论如下：

（1）在相同转速条件下，径向涡轮分子泵转子叶片来流方向侧设为圆弧形凸面可有效增加叶列压缩比，而对抽速影响不大；

（2）叶列压缩比随叶片侧边圆弧圆心角$\theta $增大呈增加趋势，且压缩级增加趋势显著大于过渡级和抽气级；

（3）本研究内部抽气径向涡轮分子泵压缩级叶列线速度大，优化后压缩比提升效果明显；同时优化结构增加了叶片齿根截面厚度，可提高叶片强度，延长转子使用寿命、承受更高工作转速。