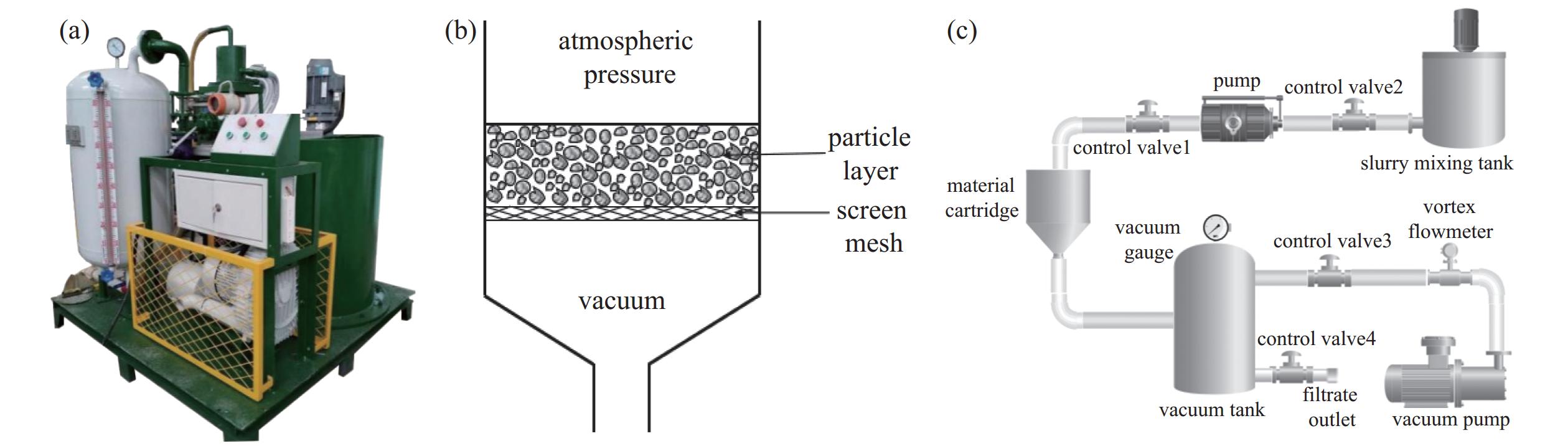
本文设计并搭建了如图1(a)所示的实验装置。该装置由真空系统和筛分过滤系统两部分构成，真空系统由真空泵、真空罐以及其他连接和辅助设备组成，用于提供和维持真空环境，筛分过滤系统由物料筒和泥浆搅拌罐组成，用于进行物料的过滤和搅拌，物料筒示意图如图1（b）所示，实验工作流程如图1(c)所示。

实验中用到的工具和仪器包括：最大气流量为315 m³/h的3RB350-1型漩涡真空泵一个；总容积为300 L的Q235B材质DN600-300型真空罐一个；总高为180 mm，内径为200 mm的Q235材质物料筒一个；中国安平县星火金属网厂生产的有效过滤面积为0.03 m²的100目、150目和200目的API金属丝编织筛网各3个；控制阀若干；量程35～380 m³/h的CKLUGD-D50-TD-C涡街流量计一个；由80目、100目、120目、200目的304不锈钢筛网组成的标准分样筛1套；量程为0.01~500 g的酷贝i-2000数字电子秤一个；烧杯和量杯若干。

实验管段中多孔介质床内流体的流速和压降满足一定的关系，其速度－压降关系表达式^[21]如下：

式（1）中，$ A $与$ B $为拟合系数；$ \Delta p $为压降，pa；$ v $为流速，m/s。

拟合实验数据确定$ A $与$ B $，然后可计算得到实验管段中多孔介质床的粘性阻力系数和惯性阻力系数，其计算公式^[22]为：

式中，$ \mu $为动力黏度，pa.s；$ \Delta l $为多孔介质区域的厚度，m；$ \rho $为工质密度，$ \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $；$ D $为粘性阻力系数；$ {C_2} $为惯性阻力系数。

为了探明颗粒配比、颗粒层厚度、筛网目数、气流速度和颗粒床对真空筛分多孔介质床粘性阻力系数和惯性阻力系数的影响，本文基于1.2所述的理论模型，计算出不同实验条件下真空筛分多孔介质床的粘性阻力系数和惯性阻力系数。真空筛分多孔介质床阻力系数实验分为干颗粒实验和湿颗粒实验两个阶段，制定的实验方案如下。

（1）实验物料调配：开始实验前使用四种目数的标准分样筛筛分满足实验要求尺寸的石英砂颗粒，按照表1所示的实验设计比例配置颗粒物试样并充分混合，得到石英砂颗粒混合样本^[23]。将其中一份样本不加水，作为干颗粒样本；另一份样本加入适量清水进行充分浸泡，得到湿颗粒样本。

（2）实验过程：称取不同质量的颗粒样本（干颗粒或湿颗粒），平铺在物料筒的筛网上，测量颗粒层高度L并记录；然后开启真空泵，并调节真空罐内真空度达到设定值，开始计时并记录数据。每一次实验在真空度达到设定值并稳定5秒后，记录气流量和真空度。每组实验在相同条件下重复3次，记录数据取平均值。

（3）数据处理：基于记录的数据采用拟合方法得到拟合系数$ A $和$ B $，基于多孔介质床结构参数和流体介质物性参数，采用式（2）和（3）可计算出不同实验条件下真空筛分多孔介质床的粘性阻力系数和惯性阻力系数。

每组实验重复三次取平均值，采用式（2）和（3）计算得到95组多孔介质床阻力系数实验数据，表2为部分粘性阻力系数和惯性阻力系数实验数据，其中颗粒配比取值比例1~比例5分别用1,2,3,4,5表示，颗粒床取值0表示干颗粒，取值1表示湿颗粒。

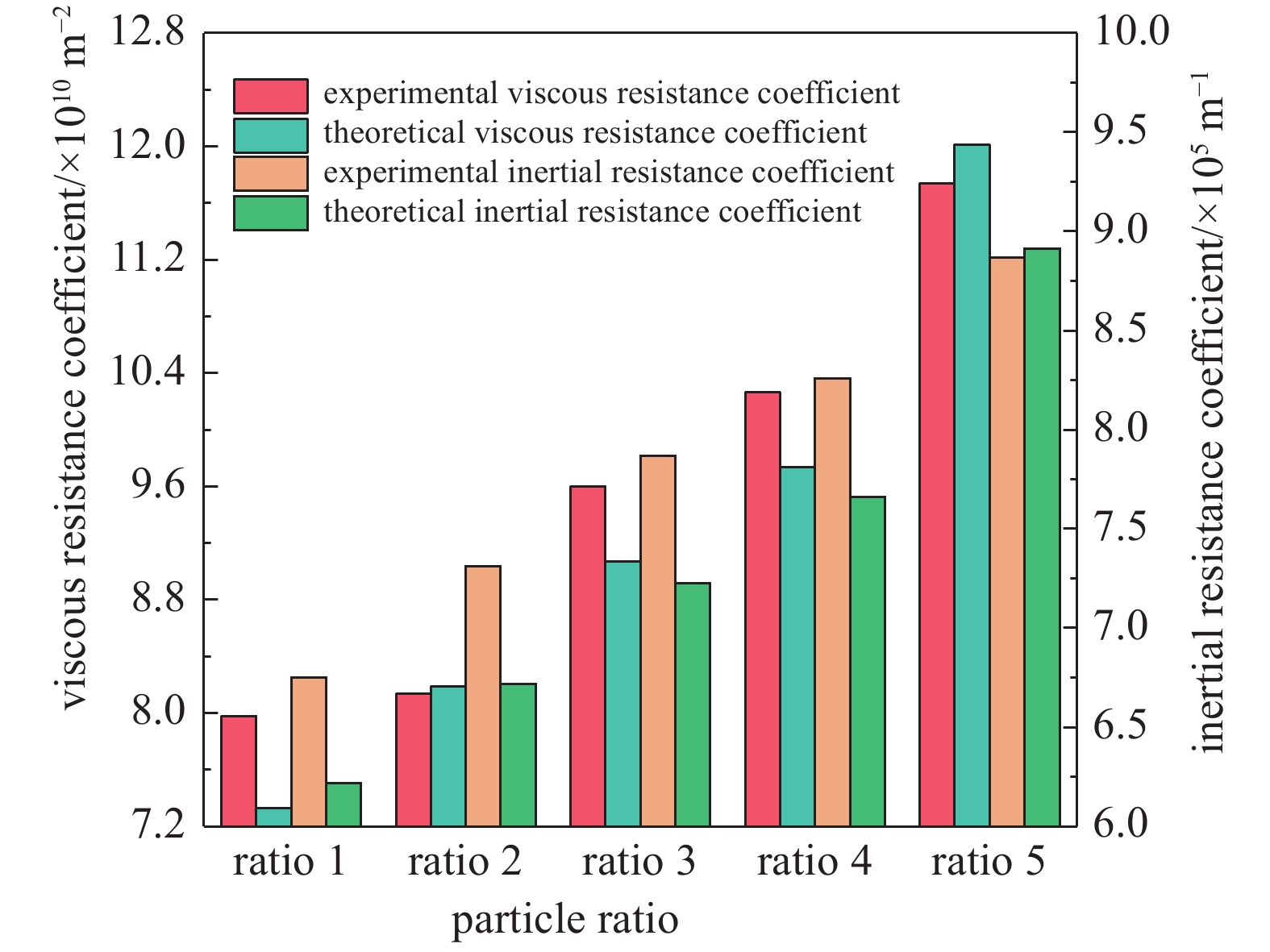
为了验证本文计算得到的多孔介质床流动阻力系数的可靠性，以100目筛网、颗粒层厚度为3.5 mm、颗粒床为干颗粒、颗粒配比分别为1~5为例，将实验研究计算得到的流动阻力系数与Ergun方程理论^[6]计算值进行对比分析，对比结果如图2所示。根据图示结果分析可知，粘性阻力系数和惯性性阻力系数与理论计算值最大相对误差未超过为9%，在允许接受的范围内，因此本文通过实验数据拟合得到的流动阻力系数具有可靠性。

（1）筛网目数对流动阻力系数的影响

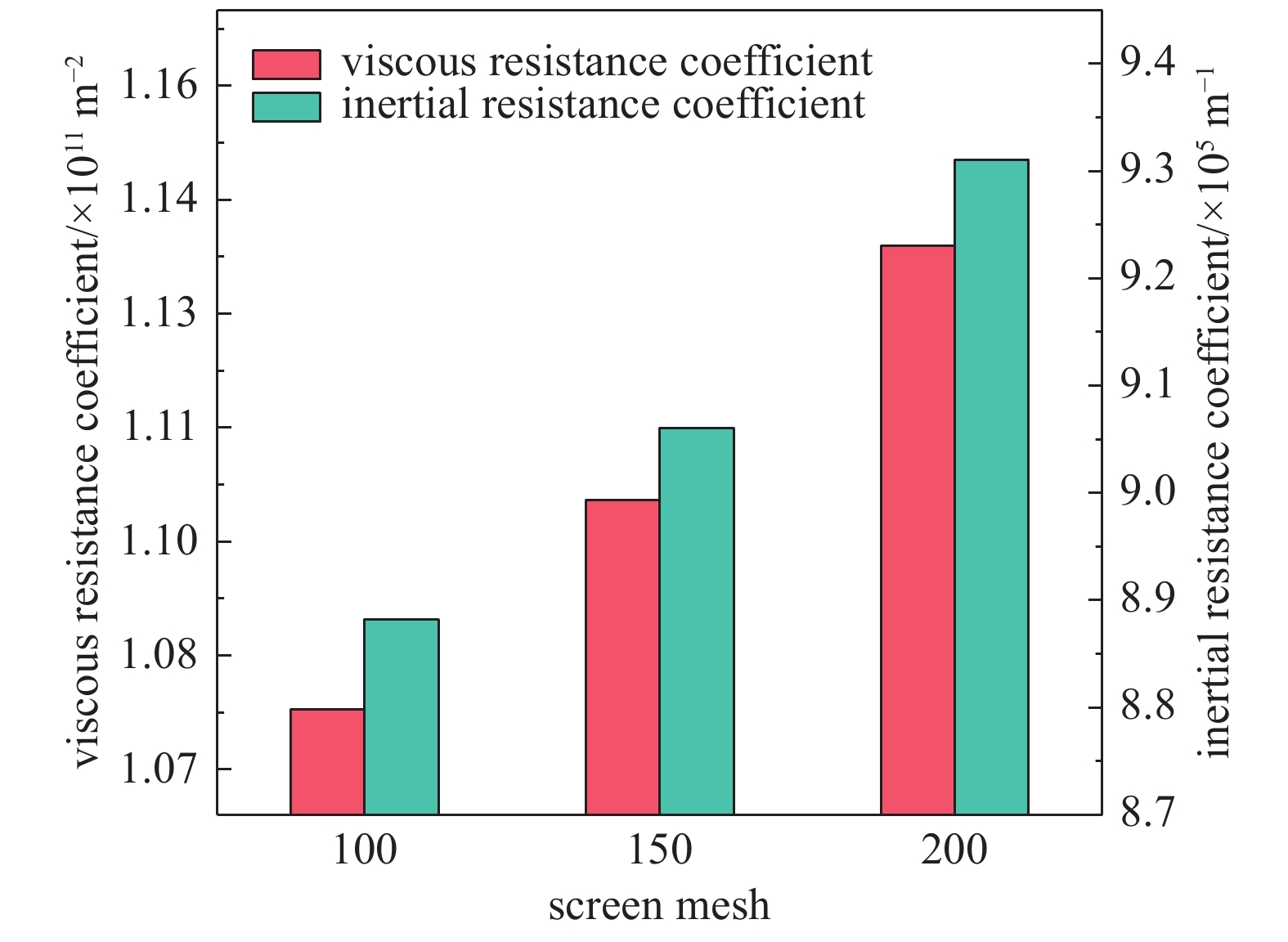
图3展示了不同筛网目数下多孔介质床粘性阻力系数和惯性阻力系数的变化关系。实验中，颗粒配比为比例3，颗粒层厚度7.1 mm，筛网目数分别为100目，150目和200目，颗粒床为干颗粒。从图3可知，无论是粘性阻力系数还是惯性阻力系数，都随着筛网目数的增加而增加。粘性阻力系数随着筛网目数从100目增加到200目，增加了5.50%；惯性阻力系数增加了5.06%。这是因为筛网目数增加时，筛网的孔隙直径减小，增加了流体透过多孔介质床的阻力，相应的粘性阻力系数和惯性阻力系数亦增加。

（2）颗粒层厚度对流动阻力系数的影响

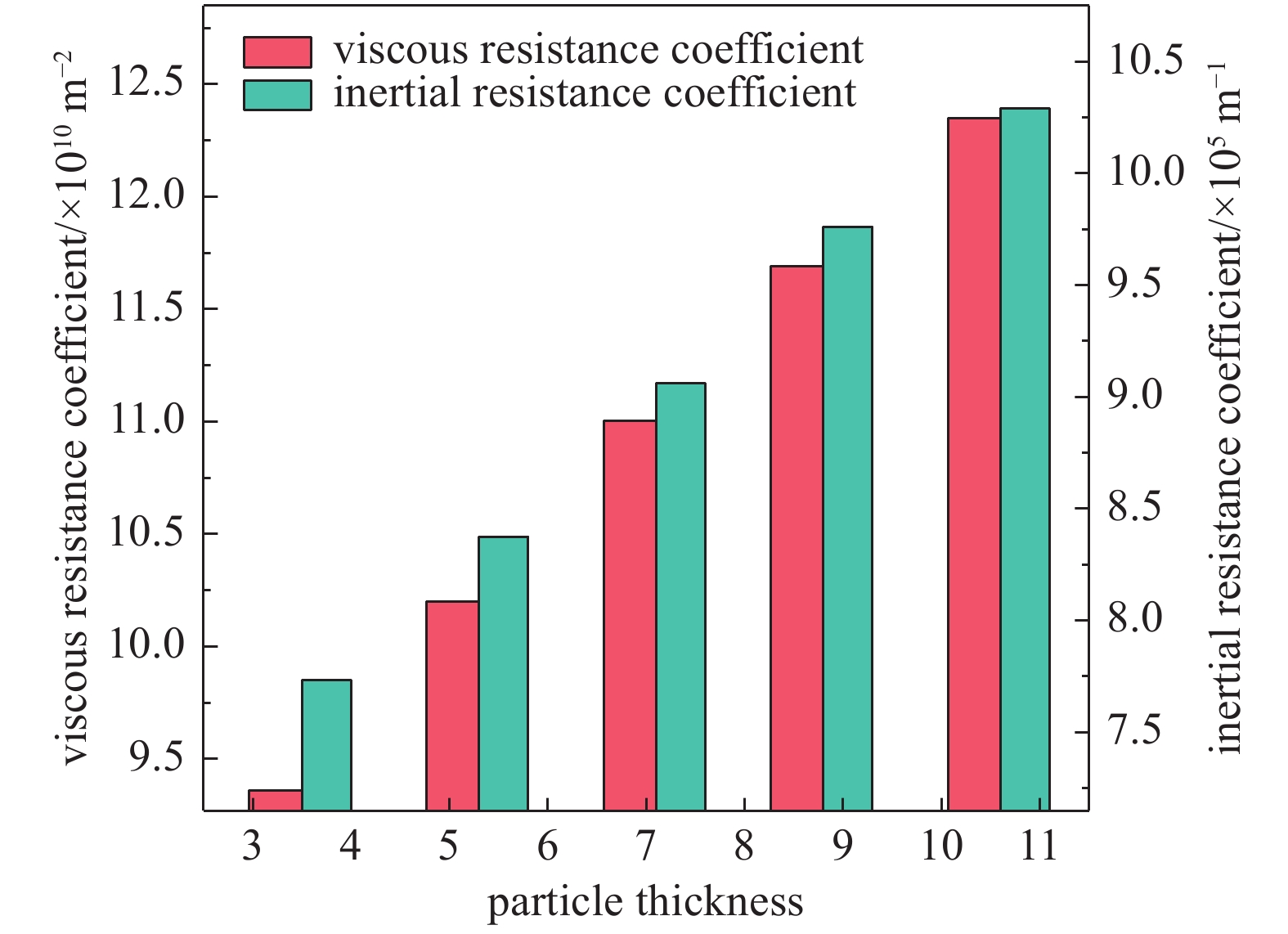
图4展示了不同颗粒层厚度下多孔介质床粘性阻力系数和惯性阻力系数的变化关系。实验中颗粒配比为比例3，筛网目数为150目，颗粒床为干颗粒，颗粒层厚度从3.5 mm增加到10.6 mm。从图3可知，粘性阻力系数和惯性阻力系数均随着颗粒层厚度的增加而增加。粘性阻力系数随着颗粒层厚度从3.5 mm增加到10.6 mm，增加了约31.94%，惯性阻力系数增加了约33.08%。这表明，随着颗粒层厚度的增加，流体透过多孔介质床的阻力增加了，相应的粘性阻力系数和惯性阻力系数亦增加。

（3）颗粒配比对流动阻力系数的影响

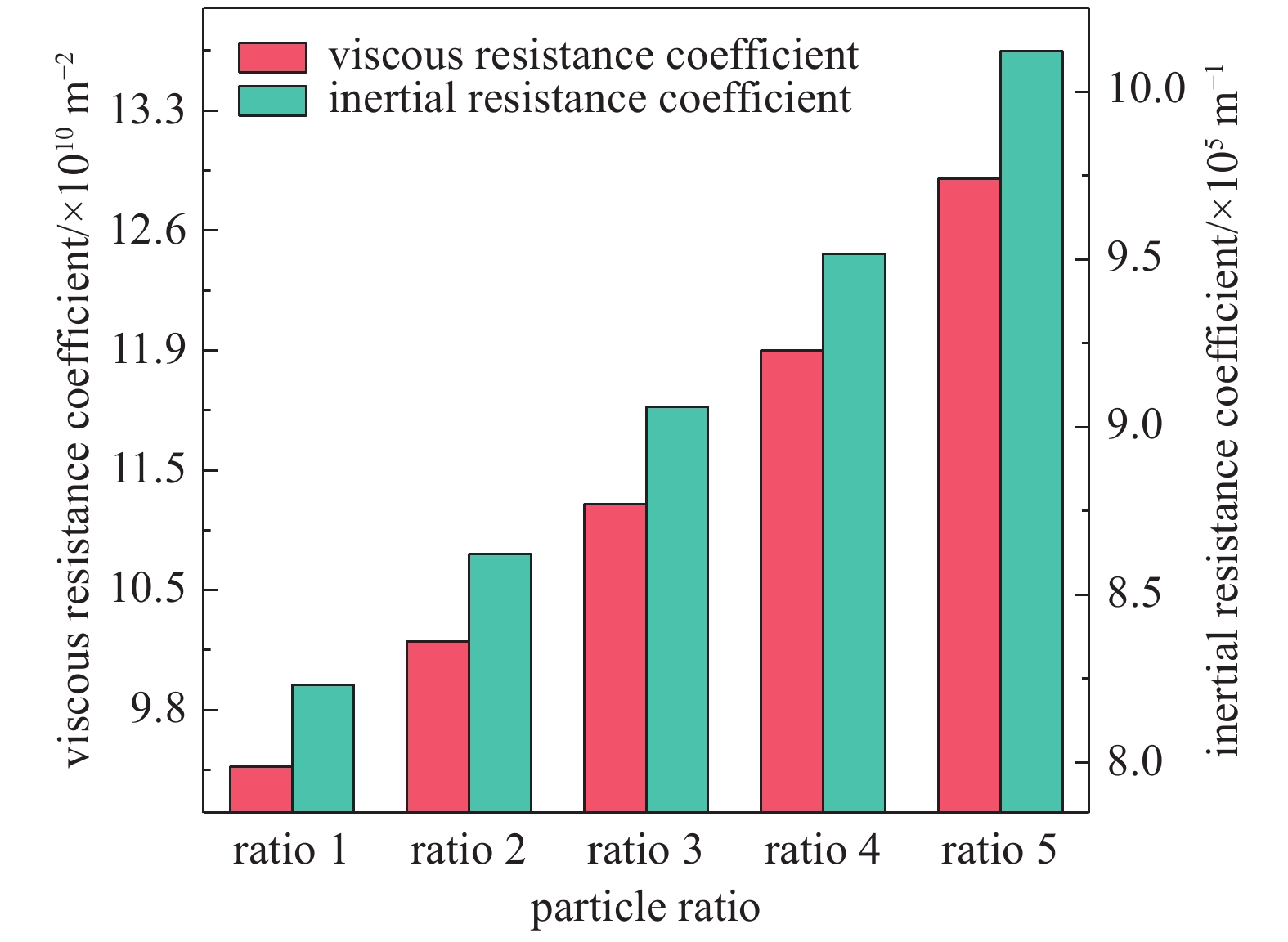
图5展示了不同颗粒配比下多孔介质床粘性阻力系数和惯性阻力系数的变化关系。实验中，筛网目数为150目，颗粒层厚度为7.1 mm，颗粒床为干颗粒，颗粒配比从比例1增加到比例5。从图4可知，颗粒配比为比例5时，粘性阻力系数最大；而颗粒配比为比例1时，粘性阻力系数最小。惯性阻力系数随颗粒配比的变化与粘性阻力系数呈现相同的变化趋势。这是因为颗粒配比为比例5的石英砂混合物中75~120 μm和120 μm~150 μm的石英砂含量最高，颗粒配比为比例1的石英砂混合物中75~120 μm的石英砂含量最低。细石英砂颗粒成分的增加，石英砂混合物的孔隙率减小，流体透过多孔介质床的阻力也增大，相应的粘性阻力系数和惯性阻力系数亦增加。

（4）颗粒床对流动阻力系数的影响

图6展示了不同颗粒床下多孔介质床粘性阻力系数和惯性阻力系数的变化关系。实验中，筛网目数为150目，颗粒层厚度为7.1 mm，颗粒配比为比例2，颗粒床分别为干颗粒和湿颗粒。从图5可以发现，颗粒床为湿颗粒时，多孔介质床的粘性阻力系数显著高于干颗粒的情况。例如，颗粒床为湿颗粒时，多孔介质床的粘性阻力系数比颗粒床为干颗粒时高出约94.27%。惯性阻力系数的变化趋势与粘性阻力系数一致。

通过对实验结果进行讨论，发现颗粒配比、颗粒层厚度、筛网目数、颗粒床对多孔介质床流动粘性阻力系数和惯性阻力系数有不同程度的影响，但是并不能判断影响真空筛分多孔介质床因素的敏感性。机器学习模型特征重要性可以反映特征对目标变量的影响大小，即特征在模型中的贡献度。因此，本研究将采用机器学习特征重要性方法对多孔介质床粘性阻力系数和惯性阻力系数因素敏感性进行分析。

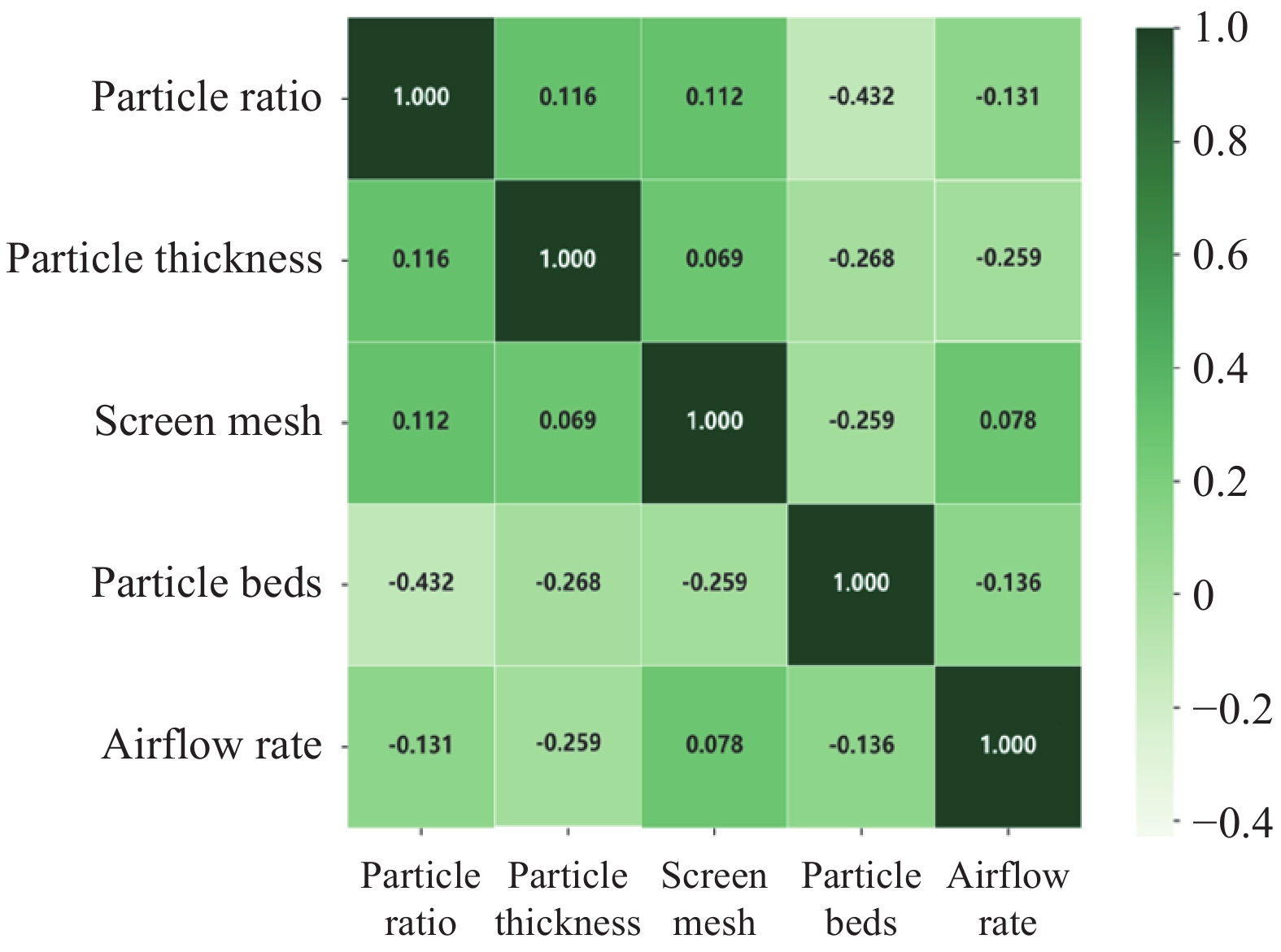
实验测试了筛网目数、颗粒层厚度、颗粒配比、颗粒床和气流速度分别对多孔介质床粘性阻力系数和惯性阻力系数的影响，但是不能揭示各影响因素的相关性。常用的数据相关性分析方法有皮尔逊相关系数法。皮尔逊（Pearson）相关系数是衡量两个连续变量之间线性相关性的常用指标，它可以在数值范围[−1, 1]之间取值，Pearson相关系数的绝对值越接近于1，表明两个变量之间的线性关系越强；反之，绝对值越接近于0，则表明两个变量之间的线性关系越弱或不存在。依据表2所示的95组实验数据在Anaconda 平台采用Python语言进行Pearson相关系数分析，各影响因素之间的Pearson相关系数热力图如图7所示。

从图7可以发现，颗粒配比、颗粒层厚度、筛网目数、颗粒床和气流速度之间的相关系数绝对值均小于0.5，说明这五个因素之间的线性相关性较弱。

根据2.1 皮尔逊相关性分析的结果，即颗粒配比、颗粒层厚度、筛网目数、颗粒床和气流速度之间并不存在较强的线性相关性，可以将这五个参数作为机器学习模型的输入，真空筛分多孔介质床的粘性阻力系数和惯性阻力系数作为输出。

由于机器学习模型特征重要性可以反映特征对目标变量的影响大小。BP神经网络^[24]一种模仿人类大脑接收和处理信息的算法，它们在许多领域形成了最先进的基础，给定足够的输入数据和计算能力来训练更高级的架构，BP神经网络可以学习数据中复杂的非线性模式。随机森林是一种以决策树为基学习器的并行式集成学习算法，能够多样性和不平衡数据，具有较高的准确性和鲁棒性。XGBoost^[25]采用梯度下降的思想迭代地训练一系列决策树模型，并通过加权组合这些模型的预测结果来获得最终的预测，它通过并行化和正则化来提高训练速度，并且在许多竞赛中表现出色。鉴于以上三种算法各自的优势和特性，因此本文采用这三种机器学习算法分析了各影响因素的特征重要性排名，结果如表3所示。

根据表3，BP神经网络、随机森林和XGBoost模型的特征重要性排序可以看出，三种模型排位前三的特征重要性具有一致性，即气流速度、颗粒床和颗粒配比均排在前三位，这三个特征的特征重要性取值均在0.18以上，而排在后两位的特征是颗粒层厚度和筛网目数。因此，影响真空筛分多孔介质床阻力系数的因素敏感性顺序为气流速度>颗粒床>颗粒配比>颗粒层厚度>筛网目数。

为使真空筛分多孔介质床流动阻力系数达到优化区间内的全局最优水平，采用XGBoost与遗传算法（GA）相结合的方法对真空筛分多孔介质床流动阻力系数进行优化研究。优化模型中气流速度$V$、颗粒床$B$、颗粒配比$R$、颗粒层厚度$Th$、筛网目数$M$为优化变量；粘性阻力系数$ D $和惯性阻力系数$ {C_2} $为优化目标，$ D $和$ {C_2} $越小表示真空筛分多孔介质床流动性能越好。优化模型如下式(4)所示：

式中: (${V_{\min }}$，${V_{\max }}$)、(${B_{\min }}$，${B_{\max }}$)、(${R_{\min }}$，${R_{\max }}$)、($T{h_{\min }}$，$T{h_{\max }}$)、(${M_{\min }}$，${M_{\max }}$)分别为气流速度$V$、颗粒床B、颗粒配比R、颗粒层厚度Th、筛网目数M的约束区间。具体优化参数约束区间如表4所示。

为获得优化模型式（4）的决策解，首先利用XGBoost构建预测粘性阻力系数$ \text { D } $和惯性阻力系数$ C_{2} $以及优化参数的映射关系模型，以$ \text { D } $和$ C_{2} $最小为目标，确定参数优化模型，并采用GA进行优化求解。

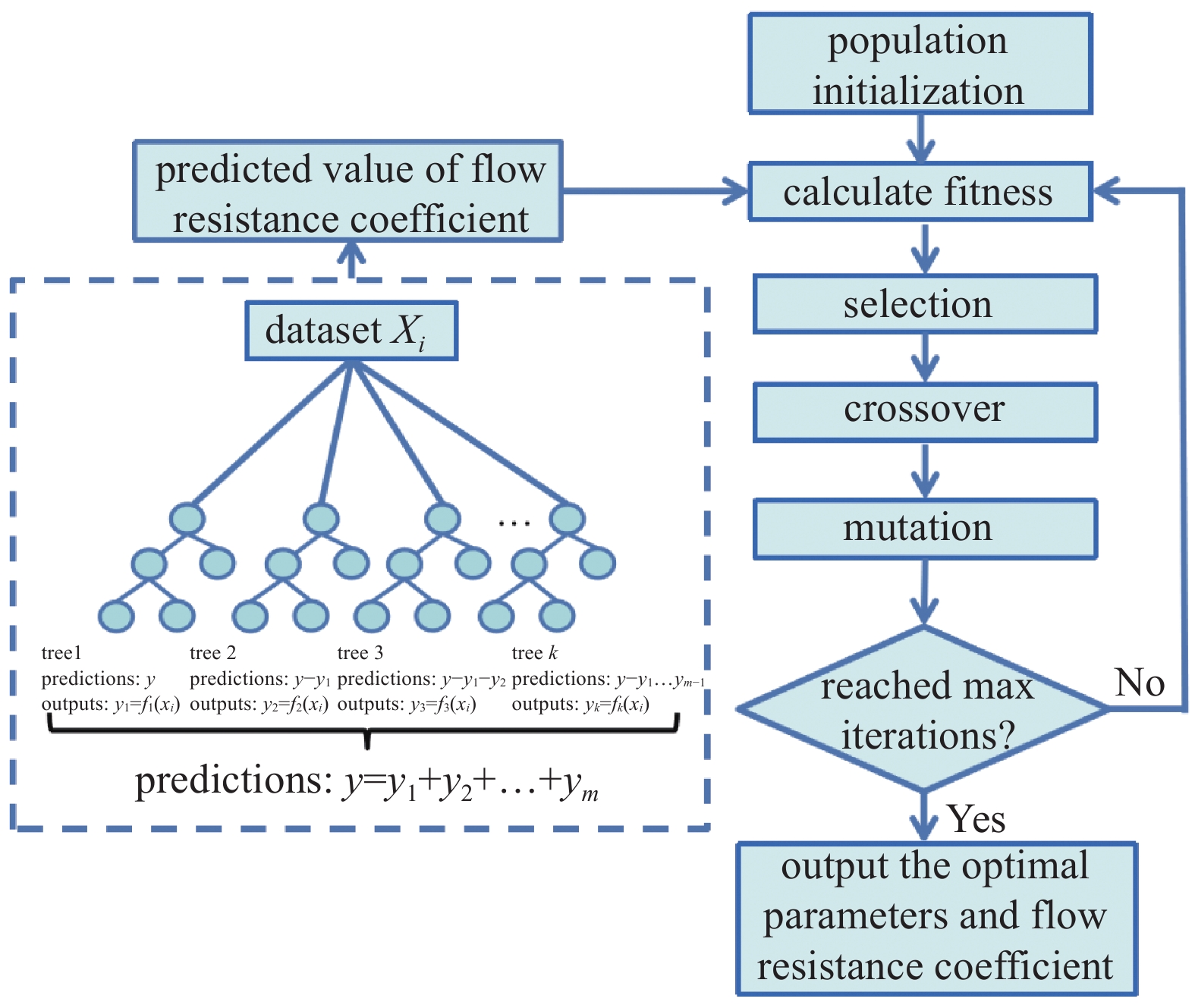
遗传算法（GA）是一种模拟自然进化过程的优化算法，它将优化问题的解空间映射为染色体编码空间，通过迭代地执行选择、交叉和变异等操作，实现染色体信息的交换和更新，从而逐步逼近最优解。由于GA算法的具有简单易行，收敛速度快，较好的全局搜索能力等特点，本文将遗传算法和XGBoost相结合，训练好的XGBoost预测结果将作为个体的适应度，然后通过GA算法寻找数据的全局最优值，优化流程如图8所示。

采用XGBoos建立粘性阻力系数$ \text { D } $及惯性阻力系数 $ C_{2} $预测模型，模型样本数据共95组，采用随机抽样的方法选取训练集和测试集，训练集样本75组，测试集样本25组。为减小误差，采用Min-Max归一化方法对数据进行归一化处理。为提高模型预测精度，采用网格搜索（Grid Search CV）方法对XGboost模型进行超参数进行优化。同时，利用网格搜索方法内置的交叉验证方法对模型的性能进行评估，从而选择最优的超参数。XGBoost和GA算法参数设置如表5所示。

模型预测精度是真空筛分多孔介质床流动阻力系数参数优化的前提。以决定系数R²、均方根误差为评价指标，对XGBoost模型的预测结果进行分析，结果见表6。由表6可知， XGBoost模型，在粘性阻力系数训练集上R²达到了99.74%，在测试集上R²达到了 98.71%；在惯性阻力系数训练集上R²均在98%以上；说明XGBoost模型在回归应用中具有良好的性能。

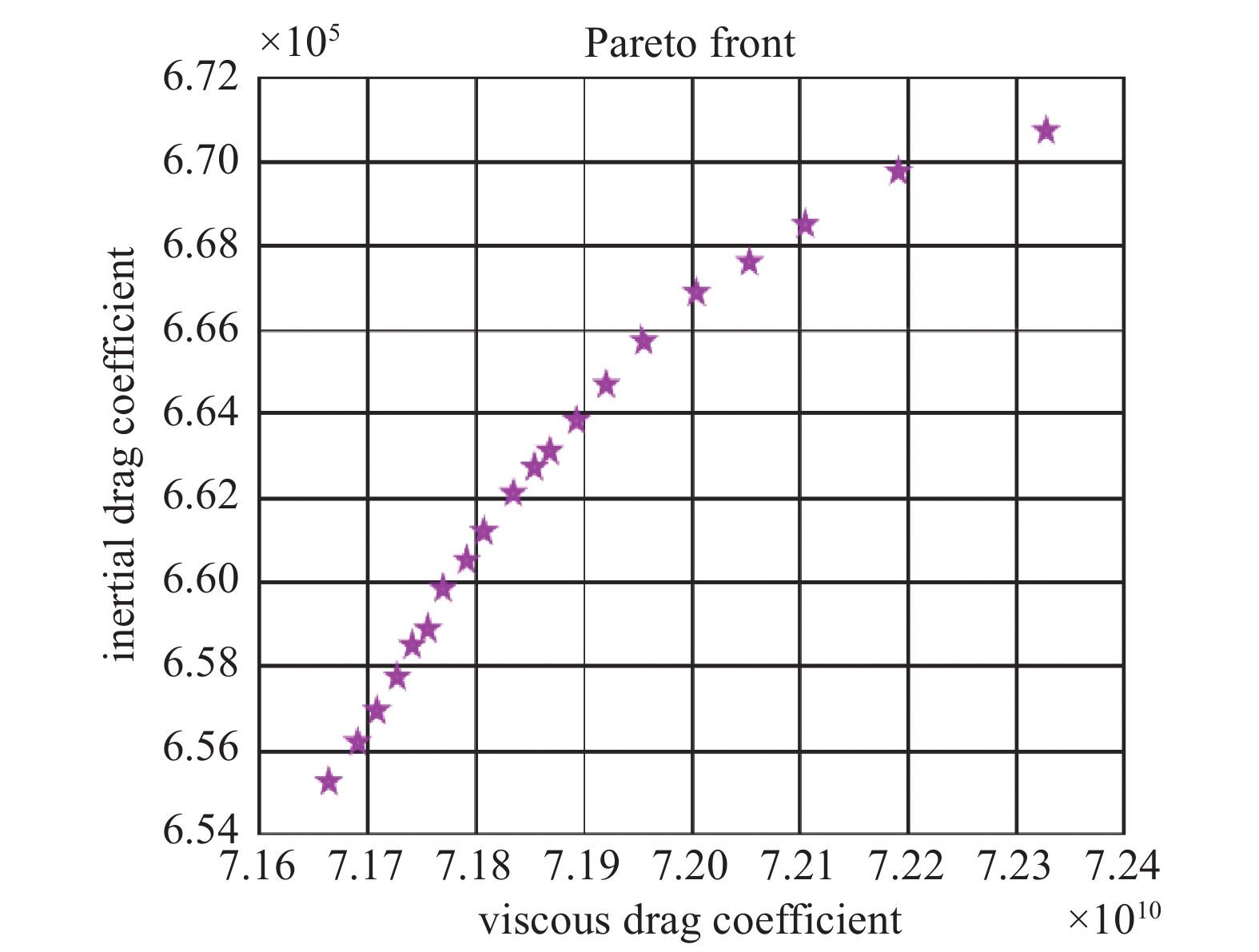
利用遗传算法GA进行多目标的迭代优化，将训练好的XGBoost 预测模型作为多目标优化的适应度函数，经过1000次迭代，获得20组真空筛分多孔介质流动阻力系数遗传算法寻优的Pareto前沿解，如图9所示。图中星号为选取的Pareto最优解。

从图9可知，在Pareto解集中，粘性阻力系数在${\text{[7}}{\text{.16}} \times {\text{1}}{{\text{0}}^{10}}{\text{,7}}{\text{.23}} \times {\text{1}}{{\text{0}}^{10}}{\text{]}}$之间分布，惯性阻力系数在${\text{[6}}{\text{.55}} \times {\text{1}}{{\text{0}}^5}{\text{,6}}{\text{.74}} \times {\text{1}}{{\text{0}}^5}{\text{]}}$之间分布。

从表7可知，Pareto的非劣解集一共20组，为筛选出Pareto的最优解，本文通过熵权-TOPSIS方法对遗传算法优化得到的Pareto非劣解集进行排序，排序最高的即为最优解^[26]。该方法是一种结合熵权法和TOPSIS法的多属性决策分析方法。首先，通过熵权法计算各属性的权重，以反映各属性在决策中的重要性。然后，利用TOPSIS法将标准化后的属性值进行排序，确定正理想解和负理想解。接着，计算每个决策方案与正理想解和负理想解的距离，进而得出每个方案的接近程度。最后，根据接近程度进行排序，从而找出最优的决策方案。Pareto的非劣解集熵权-TOPSIS评价结果如表8所示。

从表8可以发现,20组Pareto的非劣解集中排序第一的是方案12，结合表7可知，多孔介质真空筛分最优工艺参数为：颗粒配比为1，筛网目数100，颗粒层厚度3.5 mm，干颗粒床，气流速度1.20 m/s；最优粘性阻力系数为7.176×10¹⁰ m⁻²,惯性阻力系数为6.635×10⁵ m⁻¹。

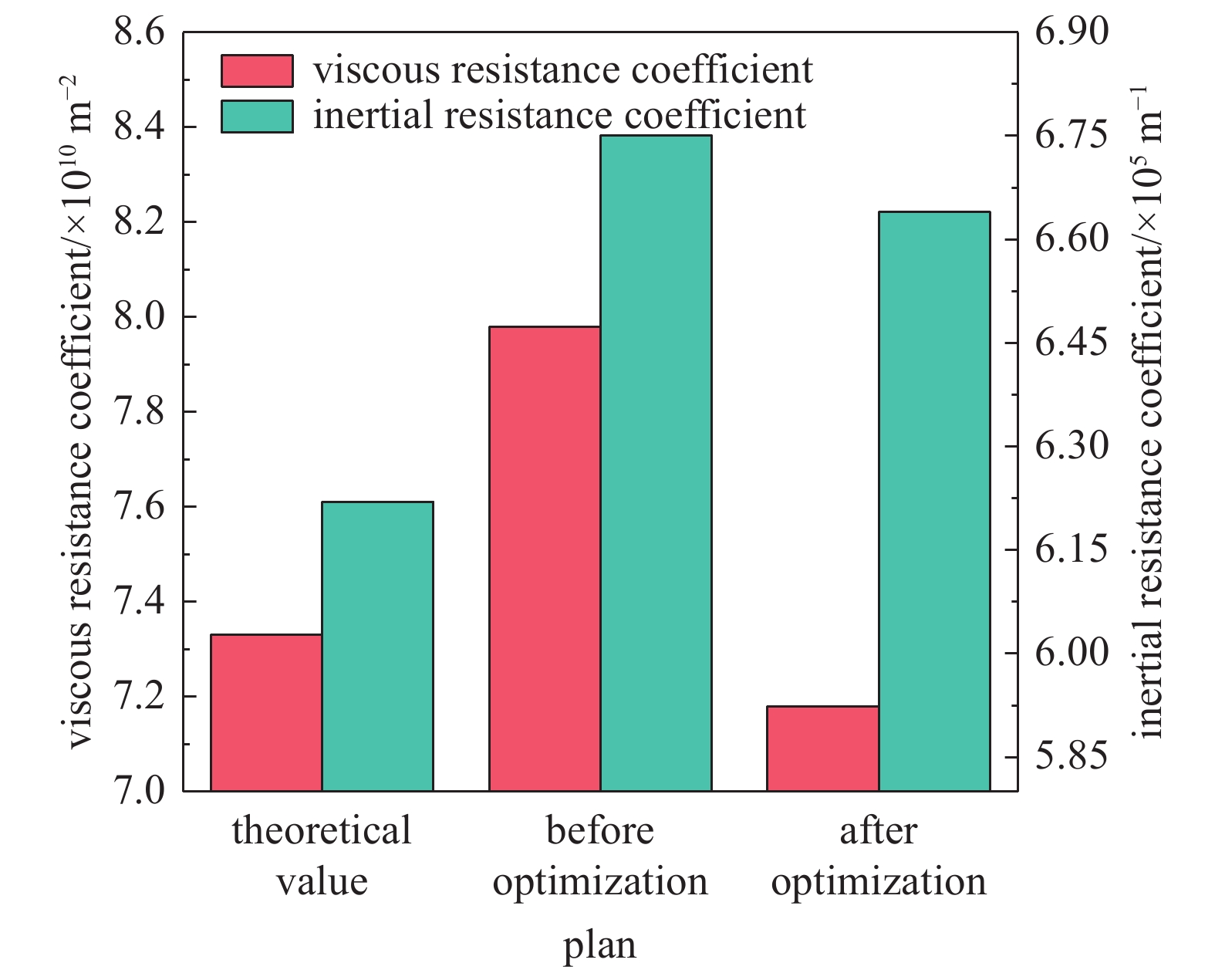
为验证优化所得的真空筛分流动阻力系数的准确性，本研究将优化后的流动阻力系数与基于Ergun方程^[6]的理论计算值进行了对比，分析结果如图10所示。

从图10可以发现，优化前粘性阻力系数与惯性阻力系数相较于理论计算值的误差分别为8.91%和8.58%。然而，经过优化后，粘性阻力系数和惯性阻力系数与理论计算值的误差显著降低，粘性阻力系数的误差缩小至2.06%，而惯性阻力系数的误差降至6.73%。这一结果表明，优化后的流动阻力系数与理论计算值之间的误差更小，从而验证了优化过程的有效性和准确性，为后续的工程应用提供了更为可靠的依据。

本研究设计搭建了真空筛分实验装置并进行实验，采用三种机器学习算法，识别出了影响真空筛分多孔介质床的阻力系数因素敏感性，并采用遗传算法GA，以XGBoost的预测模型作为多目标优化的适应度函数，建立真空筛分多孔介质床流动阻力系数多目标优化模型，得到以下主要结论：

（1）搭建了真空筛分实验装置，在不同的实验条件下获得了95组多真空筛分多孔介质床阻力系数实验数据，经分析数据具备较强的稳定性。但是由于本文实验研究中并未考虑介质粘度对真空筛分多孔介质床的影响，因此，在将该模型应用于涉及不同介质粘度的真空筛分多孔介质床情况时，可能会存在一定的偏差。

（2）分析了BP神经网络、随机森林和XGBoost三种模型的特征重要性排序结果，识别了影响真空筛分多孔介质床阻力系数因素的敏感性。研究发现影响真空筛分多孔介质床阻力系数的因素敏感性顺序为气流速度>颗粒床>颗粒配比>颗粒层厚度>筛网目数。

（3）采用遗传算法GA，以XGBoost预测模型作为多目标优化的适应度函数，建立真空筛分多孔介质床流动阻力系数多目标优化模型，得到多孔介质真空筛分最优工艺参数为颗粒配比为1，筛网目数100，颗粒层厚度3.5 mm，干颗粒床，气流速度1.20 m/s；最优粘性阻力系数为7.176×10¹⁰ m⁻²，惯性阻力系数为6.635×10⁵ m⁻¹。