首页
登录
注册
-
螺杆真空泵是一种综合性能优秀的干式真空泵，具有无油污染、抽速范围宽、结构紧凑、可直排大气、可抽除含水蒸气及粉尘的介质气体等优点[1-3]，逐渐取代传统真空泵并广泛应用于石油化工、半导体、动力电池、平板显示等场景[4-6]。螺杆真空泵转子的螺旋型结构使真空泵内气体存在复杂的周期性变化过程，研究与设计难度高[7-10]。工作过程中泵腔内气体温度由于气体压缩、气动加热等因素升高，影响气体流动状态[11-12]。气体温升还会将气体热能传递给转子和泵体，使转子和泵体受热变形，间隙尺寸减小，气体泄漏量降低，进而提升极限压力和抽速等性能指标，但过小的间隙会导致转子刮擦磨损甚至卡死。
许多学者通过数值模拟，推导热力学方程等方法，基于无泄漏假设研究螺杆真空泵的热力过程。谭昱全等[13]使用热-结构耦合模拟，得出转子热变形量并计算间隙分布；徐飞等[14]设计了单头等螺距螺杆真空泵，建立活塞模型研究其工作热力过程，对内压缩阶段和反冲阶段进行分析计算；张世伟等[15]将等螺距螺杆真空泵的工作过程分解成四个阶段，视内压缩为绝热压缩，分析各阶段热力学参数的变化；赵凡等[16-17]进一步研究变螺距螺杆真空泵，基于热力学角度对比分析不同螺旋展开规律的变螺距螺杆转子。
部分学者分析螺杆真空泵的传输理论，研究有质量传输的热力学过程。翟云飞等[18-19]按极限工况计算泄漏量，进而分析热力过程，提出简化的工作腔模型并进行数值模拟；巫修海等[20-21]建立内压缩螺杆真空泵工作特性数学模型，对间隙面积和通道拓扑连接进行分析，按等熵流动喷管模型计算泄漏流量，得到抽速、功率曲线等结果。卢阳等[22-23]基于质量守恒关系建立微分方程组，使用等熵流动喷管模型，利用四阶Runge-Kutta法求解计算。李丹童等[24-25]提出基于工作腔模型和热阻网格的研究方法，考虑泵内气体与转子、泵腔之间的换热，得到不同入口压力下气体、转子和泵腔的温度分布。
目前研究多基于绝热假设，缺少考虑充分冷却的等温过程及更接近实际的多变过程。此外，无泄漏假设下的压力与温度分布也是模拟和理论研究的重要基础条件。因此，基于不同理论热力过程分析无泄漏下螺杆真空泵的气体输运过程，探究适用于螺杆真空泵的分析计算方法具有重要研究意义[26-29]。
本研究选取一段式变螺距螺杆转子，进行气体输运过程中吸气、内压缩、反冲压缩和排气四个阶段的热力学计算，其中内压缩考虑等温过程、绝热过程、多变过程三种热力过程；以实例分析变螺距螺杆转子各热力学参数随时间的变化关系，研究相同工况条件下等螺距与变螺距螺杆真空泵的排气温度与入口压力的关系；将理论计算结果作为初始条件和边界条件，使用数值模拟方法分析等螺距与变螺距螺杆真空泵的温度场、压力场及转子变形，通过剖析螺杆转子变形规律，为螺杆真空泵的设计制造提供理论支持。
-
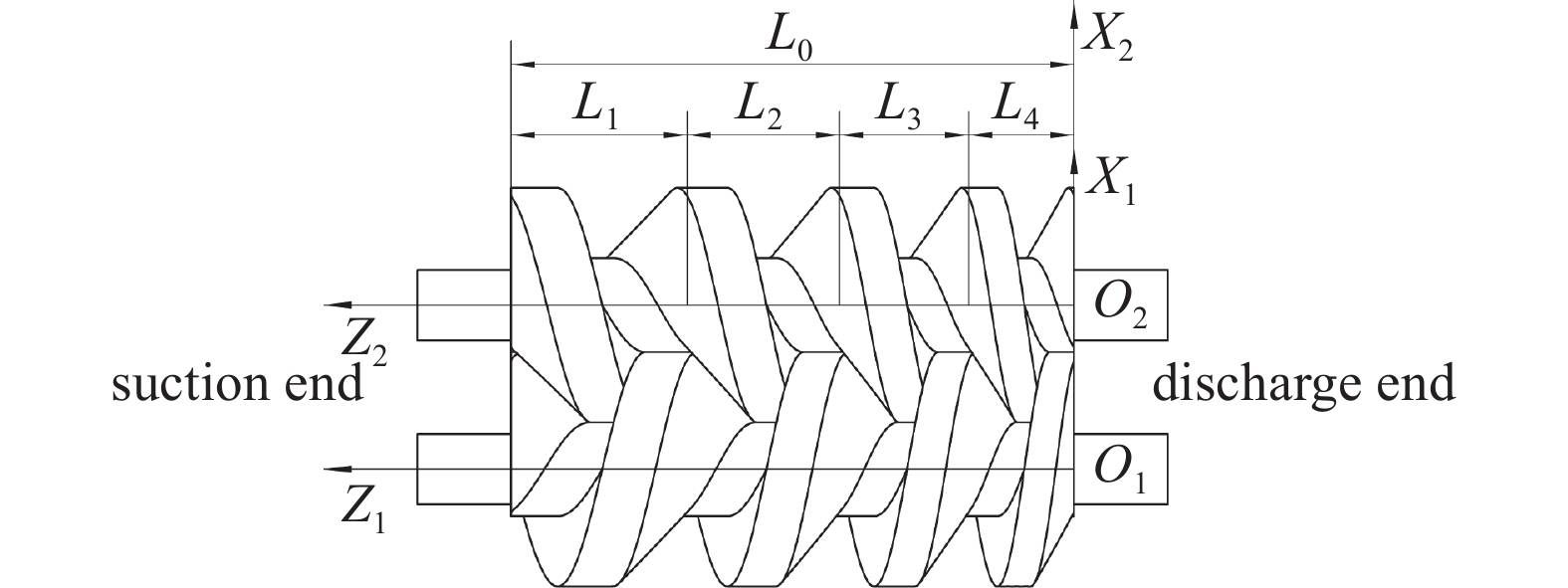
如图1所示，以变螺距转子为例，排气端面为基准建立坐标系。图中L0为转子总长度、L1-L4分别为转子第1级到第4级的导程。此外，Pi为吸气端局部导程、Pe为排气端局部导程、λ为变螺距系数、θ为螺旋展开角、ω为转子旋转角速度、t为时间、τ0为旋转时间周期、Z(θ)为转子沿Z+方向的长度、nπ为总螺旋展开角、n为转子级数且不限制是正整数。基于二次型变螺距方程，可以建立上述参数之间的关系。
-
为便于各阶段气体热力过程的推导计算，做出如下假设[15,30]：（1）气体介质视为理想气体，遵从理想气体状态方程；（2）忽略各储气容积间的泄漏和储气容积向吸气口的返流，同一储气容积内的气体质量保持不变；（3）忽略吸、排气口处的压力脉动，吸、排气压力为恒定值；（4）气体温度为0 K时，设热力学能U和焓值H为0 J；（5）比热容简化为常数，取低压下空气在300 K时的比定压热容和比定容热容。
螺杆真空泵的工作过程可以分为吸气阶段、内压缩输运阶段、反冲压缩阶段和排气阶段[31-34]。下面对各工作阶段进行推导计算。
-
在吸气阶段，螺杆转子吸气端形成的工作腔储气容积逐渐增大，将吸气过程看作是等温等压恒稳过程进行分析。
吸气过程工作腔轴向长度L(t1)：
式中，θ0为吸气阶段起始位置螺旋展开角，θ1为吸气阶段t1时刻螺旋展开角。
吸气容积V(t1)：
式中，S为螺杆泵截面的有效吸气面积。
根据理想气体方程推导不同压力入口下的吸入气体密度ρ0：
式中，p0为入口压力值，μ为摩尔质量，R为摩尔气体常数，T0为入口气体温度。
气体质量M(t1)：
气体压强p(t1)：
气体温度T(t1)：
气体内能U(t1)：
式中，cv为比定容热容。
气体焓H(t1)：
式中，cp为比定压热容。
-
吸气阶段结束后，变螺距螺杆转子的储气容积逐渐减小，在输运气体的同时进行内压缩过程。本阶段以绝热压缩、多变压缩和等温压缩3种压缩形式进行计算，分别用AC、VC和IC表示。内压缩输运过程发生在吸气阶段之后，该阶段方程推导中t1为吸气阶段最大极限值τ0。
内压缩过程工作腔轴向长度L(t2)：
式中，
$ \theta _2^{'} = {\theta _2} + 2\pi $ ，θ2为t2时刻螺旋展开角。气体体积V(t2)：
气体质量M(t2)：
气体压强p(t2)：
气体温度T(t2)：
气体内能U(t2)：
气体焓H(t2)：
-
反冲压缩阶段可以认为是在储气工作腔与排气口连通的瞬间完成，只需要关注气体状态参数的初值与终值，视作绝热的准稳态过程进行计算[15]。首先计算反冲气体在排气口外的状态参数，再计算原被抽气体与反冲气体混合后的混合气体状态参数。该阶段方程推导中t2为内压缩输运阶段最大极限值nτ0/2。
设原气体内压缩结束时各状态参数下标为3，原气体体积V3：
原气体质量M3：
原气体温度T3：
原气体内能U3：
设反冲气体的压力为pr、温度为Tr、质量为Mr，可得到反冲气体的体积Vr：
反冲气体内能Ur：
反冲气体焓Hr：
反冲压缩结束时，混合气体总质量MT：
外界气体推动反冲气体进入排气端储气容积所作的功Wr：
混合气体总内能UT：
混合气体温度TT：
混合气体满足理想气体状态方程：
推导得到反冲气体质量Mr：
混合气体总焓HT：
-
在排气阶段，储气工作腔容积迅速减小将气体介质排出，忽略排气口处的流动阻力损失，看作等温等压恒稳过程进行分析。
排气过程工作腔轴向长度L(t4)：
排气腔内气体质量M(t4)：
排气腔内气体温度T(t4)：
排气腔内气体内能U(t4)：
排气腔内气体焓H(t4)：
-
分别选取转子总长和级数相等的等螺距螺杆真空泵和一段式变螺距螺杆真空泵，选用渐开线型螺杆转子端面型线，螺杆转子结构特性参数和气体物性参数见表1。其中，有效吸气面积指泵腔截面面积减去两转子截面面积的差，作为几何抽速的参考。等螺距螺杆转子除导程外，其余参数均和变螺距螺杆转子相同。
-
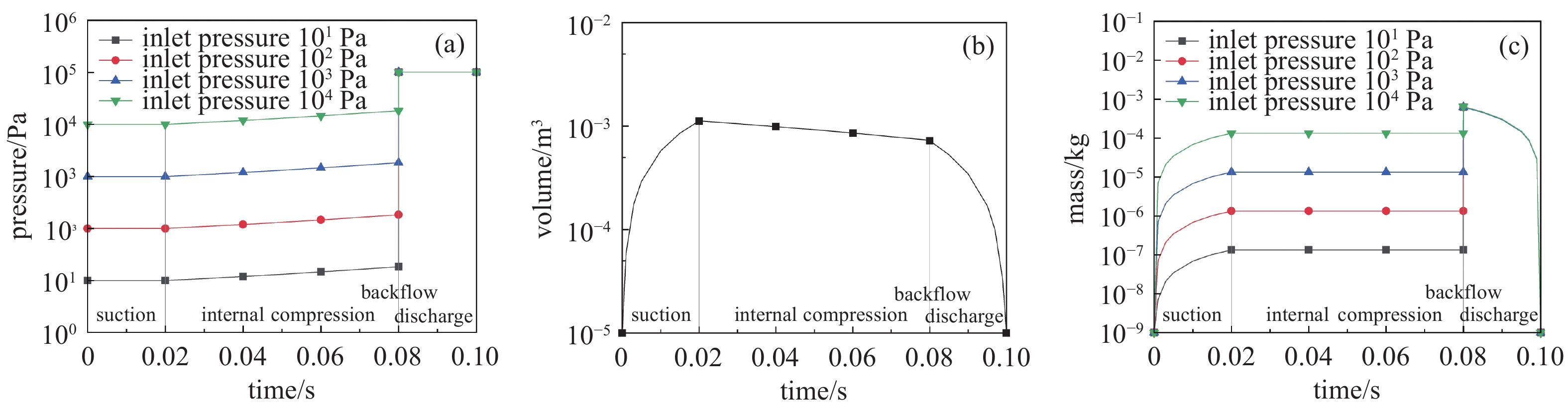
图2为按绝热压缩计算，一段式螺杆真空泵内气体压力、储气容积和气体质量随时间的变化规律。吸气阶段气体压力保持稳定，气体容积及气体质量逐渐升高，直至稳定。内压缩输运阶段，由于储气容积逐渐减小，气体压力呈缓慢增长趋势；因为忽略气体泄漏和返流，所以气体质量保持不变。反冲压缩阶段，在排气口接通瞬间，气体压力跃升至略高于大气压力，气体质量因反冲气体的加入而增加。排气阶段，气体压力略高于大气压力且保持恒定，储气容积减小将气体排出，表现为气体质量快速减少。根据不同入口压力下的质量曲线，入口压力越高，吸入气体的质量越大，气体反冲作用越弱。
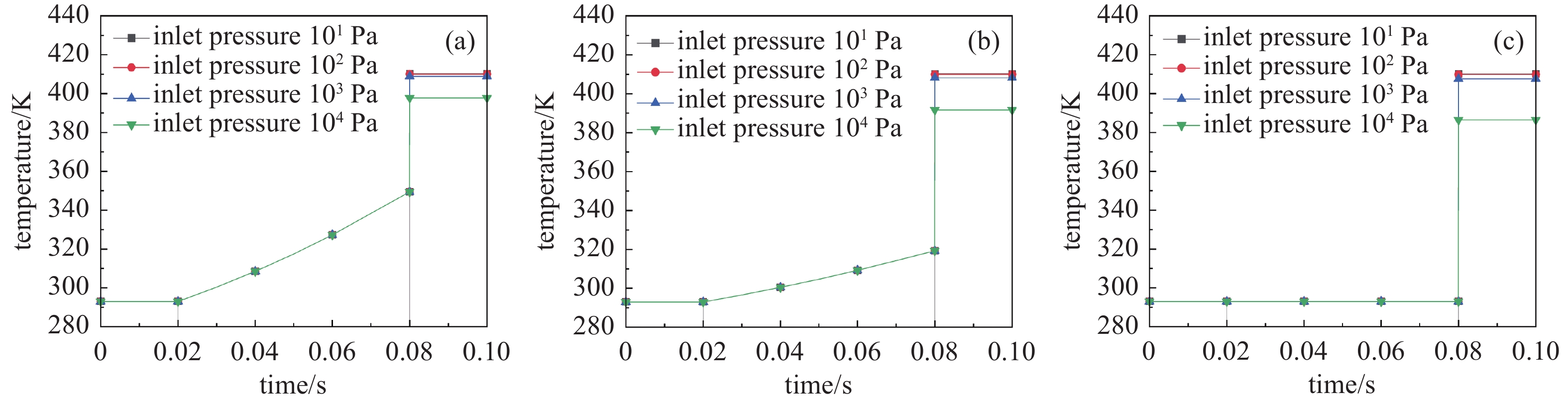
由图3可知，吸气阶段，三种压缩方式下吸入气体温度与室温相等。内压缩输运阶段，按绝热压缩或多变压缩计算时，气体温度随时间迅速增长，绝热压缩的气体温度高于多变压缩的气体温度。反冲压缩阶段，反冲气体对被抽气体做功，导致三种压缩形式下的气体温度均发生陡增，且等温过程增加最显著，多变及绝热过程次之。排气阶段，气体以内压缩结束时的气体温度排出泵腔。
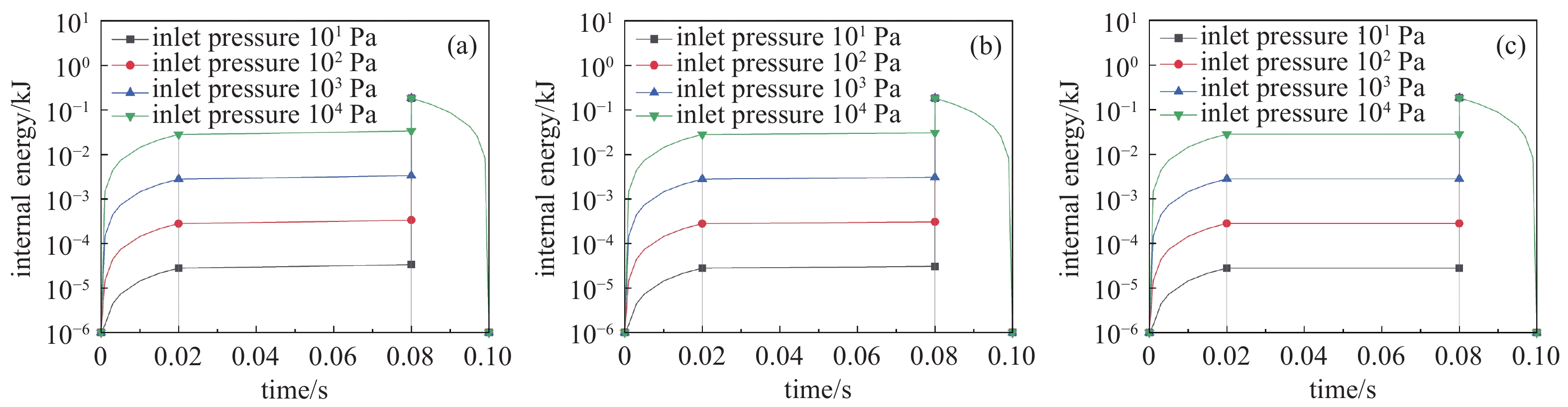
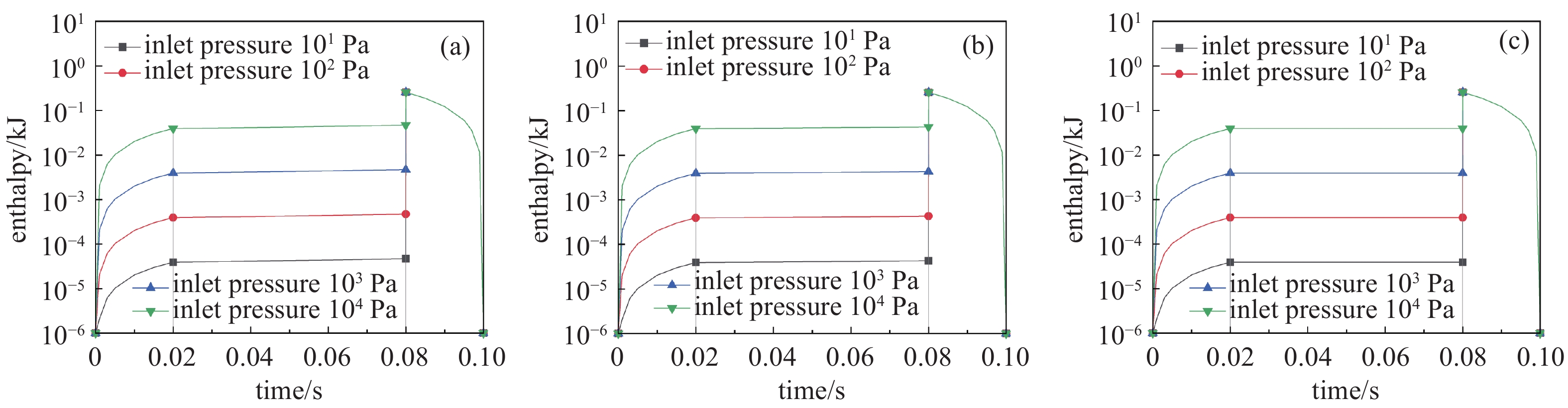
由图4和图5可知，吸气阶段，随着吸气量逐渐增多，三种内压缩形式下气体内能值和焓值均跨数量级迅速升高至稳定值。内压缩输运阶段，按绝热压缩和按多变压缩计算时，气体内能值和焓值均缓慢增加；按等温压缩计算时，气体内能值和焓值始终保持不变。反冲压缩阶段，三种内压缩形式下气体内能值和焓值均因反冲气体的作用而在短时间内急剧上升。排气阶段，气体内能值和焓值随着泵内气体的排出而跨数量级迅速降低。
-
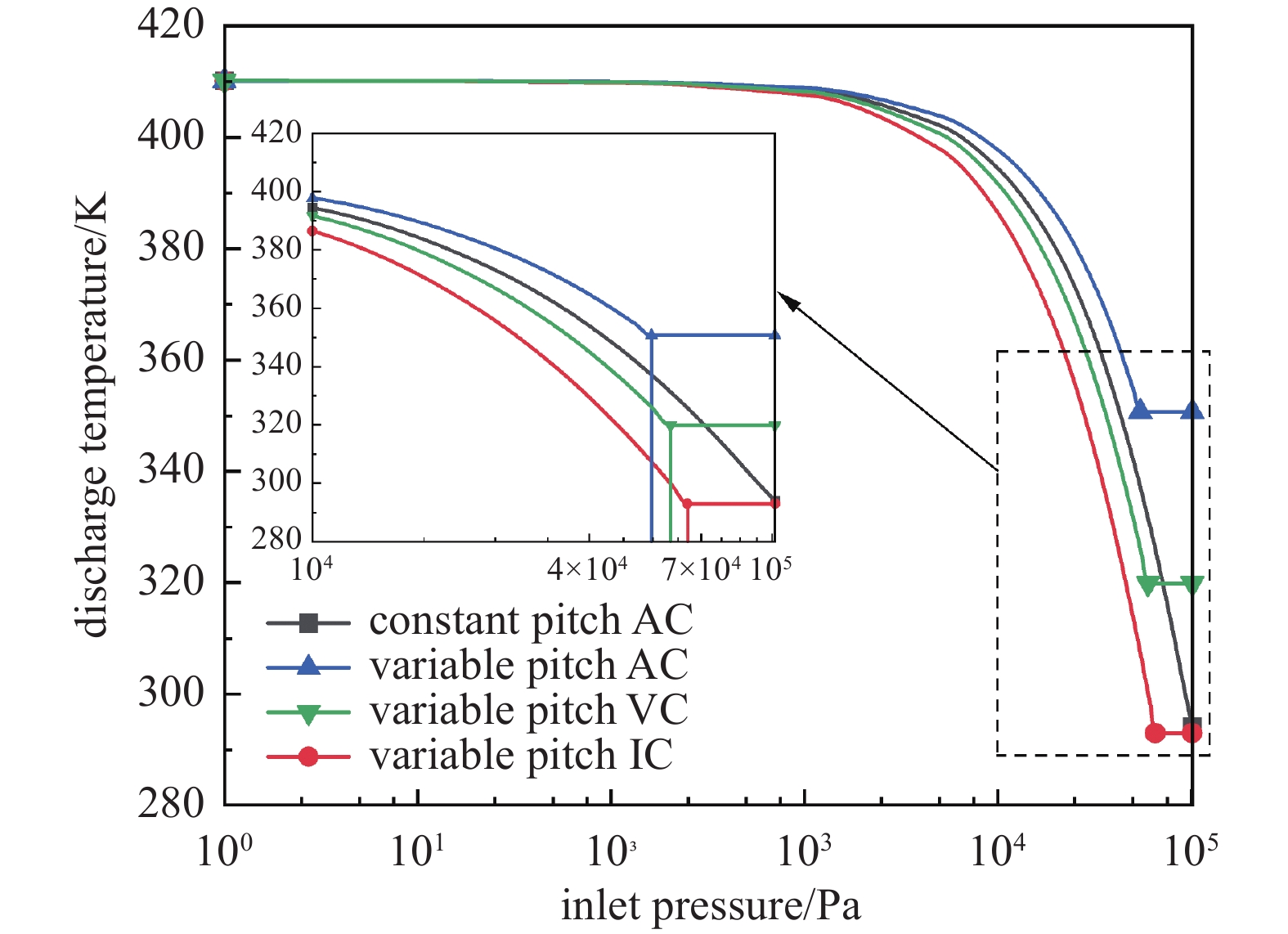
图6给出了等螺距与变螺距螺杆真空泵按不同压缩形式计算的排气温度结果，两种螺杆真空泵采用相同的热力学关系式，区别在于等螺距螺杆真空泵无内压缩输运阶段。对于变螺距螺杆真空泵，入口压力越低，三种压缩形式的排气温度越接近；随着入口压力的升高，排气温度均呈现先缓慢后迅速的下降趋势，直至入口压力过大而达到过压缩工况，排气温度恒定，不再随入口压力的升高而变化。绝热压缩的排气温度最高，达到过压缩工况的入口压力最低，其次为多变压缩和等温压缩。等螺距螺杆真空泵随入口压力升高，排气温度也呈先缓慢后迅速的下降趋势。
上述结果说明，在无泄漏模型中使气体温度升高的主要因素是反冲压缩，且入口压力越低，两端压差越大，反冲压缩的作用越明显。从绝热、多变到等温过程，气体与外界的热交换逐渐增强，表现为排气温度的逐渐降低。实际过程为处于等温与绝热过程之间的多变过程，若能通过实验或经验得到多变指数，采用多变压缩计算能得到更准确的结果。从避免转子发生剐蹭故障的目的出发，采用绝热压缩可计算气体温度的上限，预测转子变形量的最大值。
-
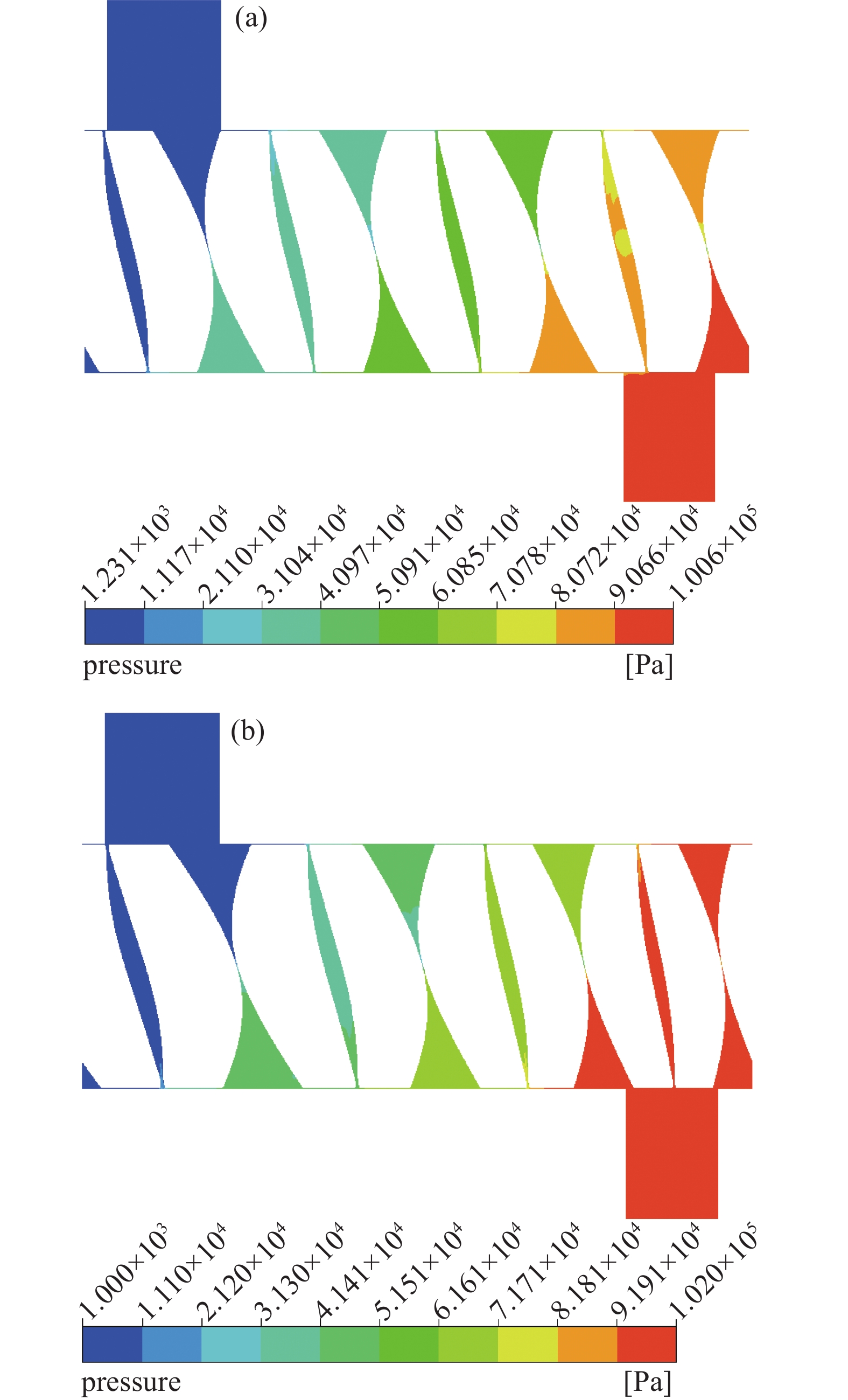
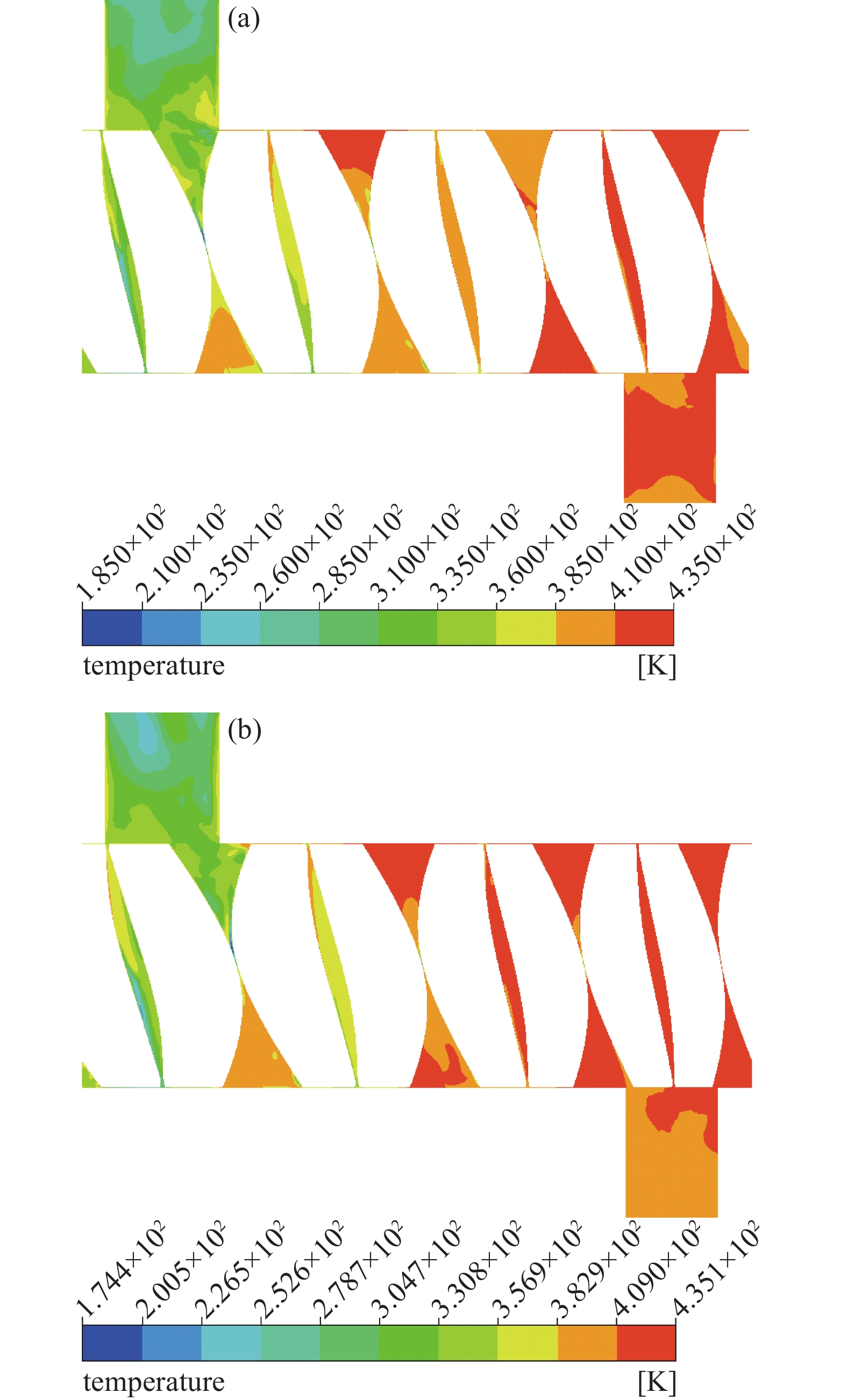
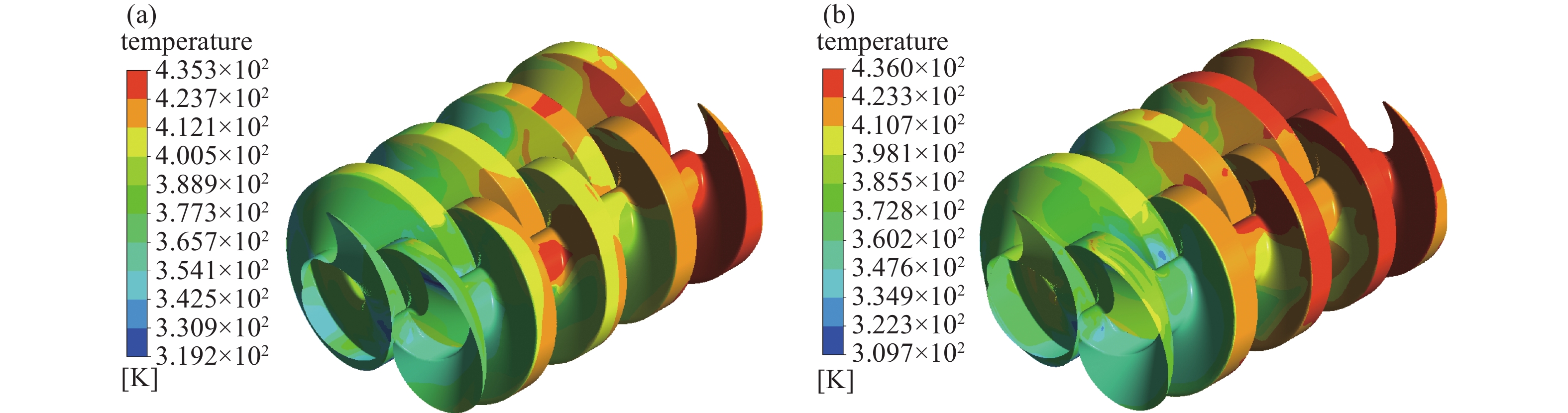
根据表1给出的结构参数，分别绘制等螺距与变螺距螺杆真空泵转子与泵腔的三维模型。对转子端面型线的曲线元使用等距、圆角连接、平移旋转等方法进行调整，得到有间隙的螺杆转子三维模型，将泵腔与转子间隙，转子之间间隙控制在0.2~0.3 mm范围内。最后提取流体域，使用Ansys Fluent进行流场模拟。分别划分不同啮合相位的结构网格，网格数约为724万。选取入口压力为1000 Pa、入口温度为293.15 K、出口压力为101325 Pa时按绝热压缩计算的排气温度作为出口温度，其中等螺距为408.50 K，变螺距为408.85 K。进出口管道边界分别为压力入口和压力出口，转子通过动网格功能实现转动。气体介质为可压缩理想空气。模拟得到的流场压力和温度分布结果如图7~图10所示。
基于已绘制的转子模型，使用Ansys Workbench进行稳态流−热−固耦合模拟。稳态热模块中，在转子表面施加流场得到的壁面温度；稳态结构模块中，在转子表面施加流场得到的压力载荷，在转子两端面分别施加入口压力和出口压力。此外，按实际工况施加地球重力、旋转速度、轴承作用表面的约束条件等。最终得到的等螺距与变螺距螺杆转子变形结果如图11~图14所示。
-
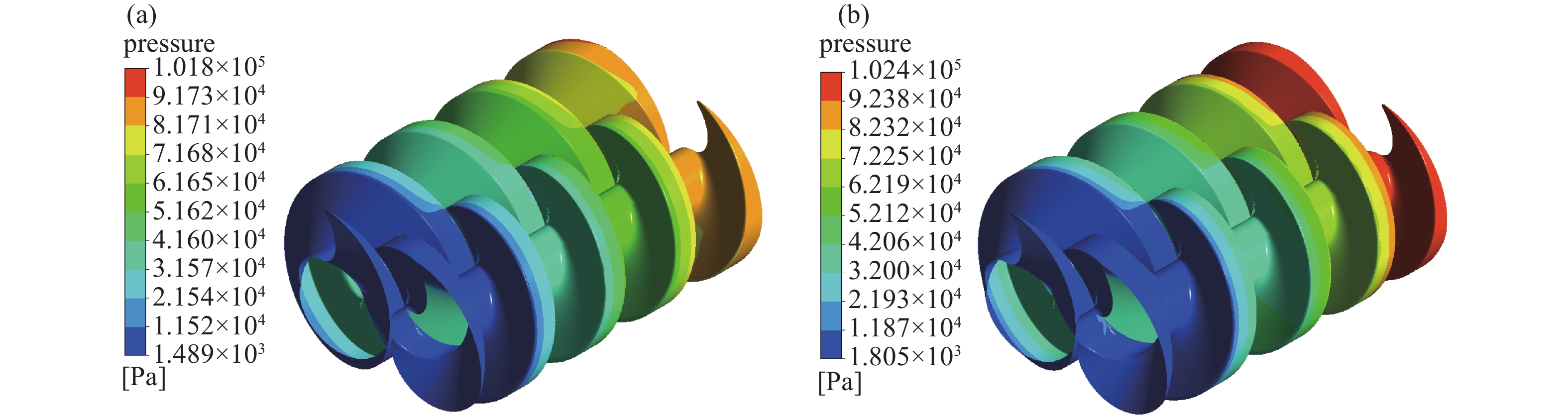
从图7可知，两种螺杆泵内的压力从吸气端至排气端均逐渐升高。各压力区域的边界多位于级间间隙处，同一储气容积（或称同一级）内的压力差异较小，图9更加清晰地表示了上述情况。等螺距螺杆泵无内压缩，除排气级外各级压力在理论上应当相等，但流场仿真模拟中考虑了因间隙造成的级间气体泄漏及进出口返流，故等螺距螺杆泵各级压力从吸气端到排气端呈阶梯上升趋势，高于理论计算结果。变螺距螺杆泵存在内压缩，理论上应呈现从吸气端到排气端先缓慢后急剧的变化趋势，但在级间气体泄漏和进出口返流的综合影响下，其各级压力分布呈现与等螺距螺杆泵相似的阶梯状上升趋势，亦高于理论计算值。以上结果表明流场模拟可以综合考虑级间泄漏和进出口返流，能更准确地描述泵内的气体压力分布。
图8显示，两种螺杆泵内的温度从吸气端至排气端均逐渐升高，变螺距螺杆泵的进出口温度区间跨度大，且最高温度高于等螺距螺杆泵，最低温度低于等螺距螺杆泵。从图10可知，温度分布无明显阶梯分布，结合图8，可发现吸气端温度较低，其余区域温度较高，排气端温度最高。变螺距螺杆泵存在内压缩，且排气端导程小，使热量容易向吸气端传递，所以变螺距螺杆泵内气体温度梯度更大，排气端附近的温度高于等螺距螺杆泵。图8显示温度最高的区域在排气端储气容积而非排气口，且高于理论值，表明了气体反冲及气体返流综合作用导致的排气端储气容积内气体温升效果。
-
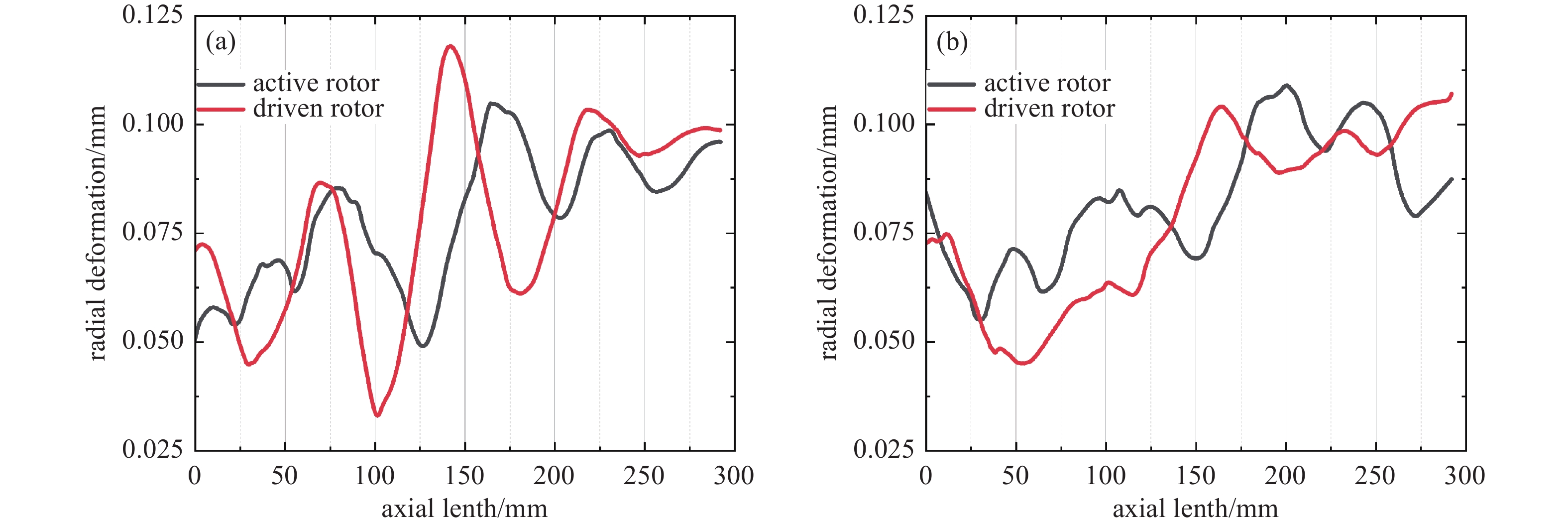
图11表明，主动转子的总变形量从吸气端到排气端逐渐升高，从动转子的总变形量在中间最大而两端较小，与图10的温度分布相似。从动转子最大总变形位于中间，是由于转子于此处发生弯曲，引起的形变相对热膨胀更大。主动转子吸气端尖点和从动转子排气端尖点由于两侧压差较大且尺寸较薄，工作过程中形变较大，故有些产品将尖点切除避免刮擦。上述结果表明螺杆转子结构复杂，需综合考虑温度、压力及转子结构进行变形分析。
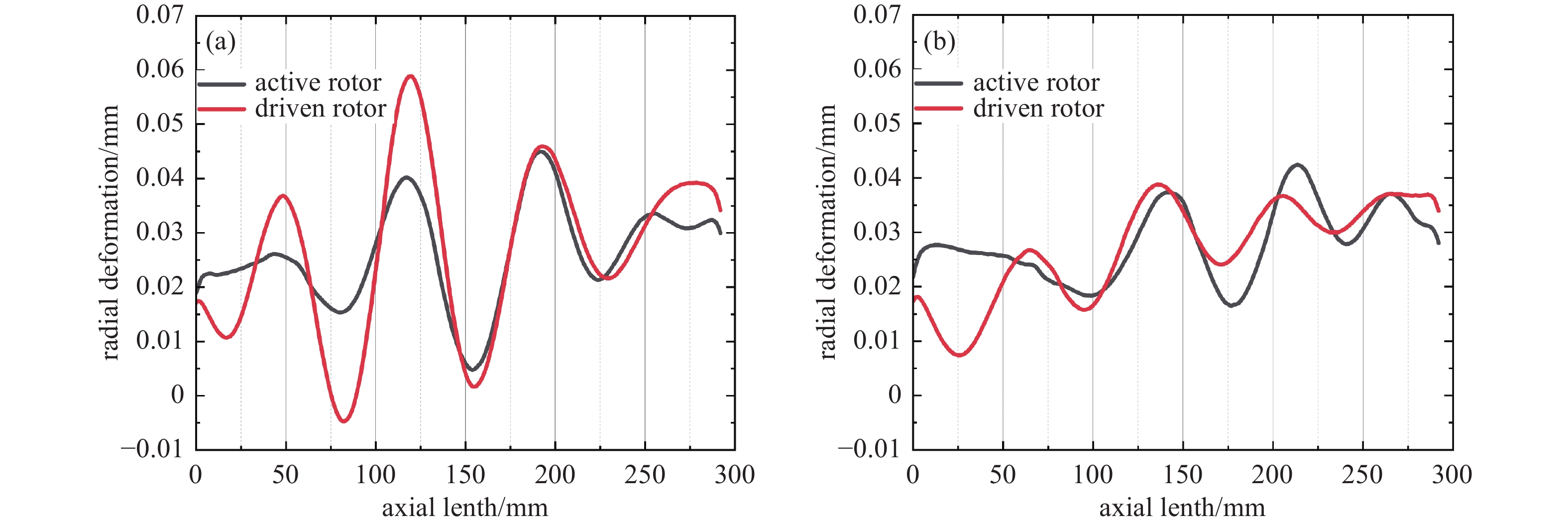
齿顶、齿根螺旋线的径向变形会改变螺杆转子的齿顶间隙和啮合间隙。从图12和图13可知，两种转子齿顶、齿根螺旋线的径向变形量从吸气端到排气端均逐渐上升，且由于转子的弯曲使螺旋线上各点相对原圆柱坐标系的径向变形呈波浪形分布。等螺距转子的径向变形范围更大，变化更剧烈，两种转子极限径向变形量相差约35%，而平均径向变形量仅相差约5%。这是因为等螺距转子吸气端导程较小，齿宽较窄，转子齿形更容易发生弯曲，综合轴的弯曲效果，故使极限径向变形更大。
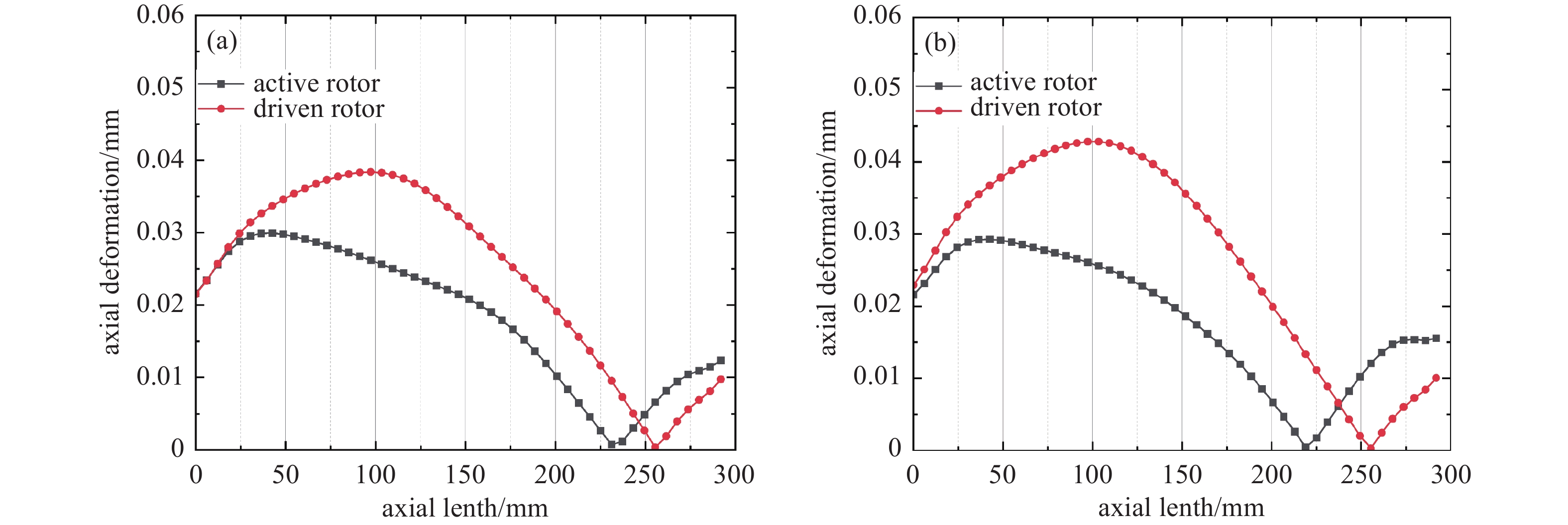
图14是转子轴线上轴向变形量的绝对值曲线，其中变形量零点左侧的变形指向吸气端，变形量零点右侧的变形指向排气端。相同长度下变螺距转子轴向变形大于等螺距转子，两种转子的轴向变形量均呈现先升高、后下降、再上升的趋势，吸气端轴向变形量比排气端更大。这是由于转子轴温度从吸气端到排气端逐渐升高，排气端膨胀变形向吸气端累积，且转子轴两端存在轴向约束，导致转子轴发生弯曲，使轴向变形量呈现出上述效果。因此，螺杆转子吸气端面的预留间隙应大于排气端面。
-
以一段式变螺距螺杆真空泵为研究对象，研究了绝热、多变及等温三种内压缩形式下气体压力、温度、内能、焓等热力学参数的变化规律；选取相同转子长度的等螺距与变螺距螺杆真空泵，以理论计算结果为模拟边界条件，进行流热固耦合模拟，研究螺杆真空泵内气体压力、温度及转子变形规律，结论如下：
（1）理论计算发现，变螺距螺杆转子的入口压力越低，三种压缩形式的排气温度越接近；随着入口压力升高，排气温度均呈现先缓慢后迅速的下降趋势，直至发生过压缩工况后趋于稳定。绝热压缩达到过压缩的入口压力最低，排气温度最高，随后依次为多变压缩和等温压缩，过压缩后排气温度分别为350.7 K、319.8 K、293.2 K。等螺距螺杆真空泵的排气温度也随入口压力的升高呈现先缓慢后迅速的下降趋势。
（2）流场仿真模拟发现，压力从吸气端到排气端呈现阶梯上升趋势，各级压力高于理论计算结果，除第一级外相差一个数量级以上，同一级内各处的压力趋于一致；温度无显著阶梯分布，各级温度高于理论计算结果，气体反冲和返流综合作用导致排气级内气体温度高于排气口。流场模拟能更准确地描述泵内气体压力和温度的分布。
（3）转子流−热−固耦合模拟发现，螺杆转子弯曲明显影响变形量的分布，转子结构因素在变形分析中不可忽略；相同长度的等螺距转子比变螺距转子更易发生弯曲，极限径向变形量相差约35%，而平均径向变形量相差约5%；螺杆转子尖点易变形，吸气端比排气端轴向变形量高约0.006~0.013 mm，变形规律与工程实际情况具有一致性。
螺杆真空泵内气体热力过程的数值计算及模拟分析
Numerical Calculation and Simulation Analysis of Gas Thermodynamic Process in Screw Vacuum Pump
-
摘要: 螺杆真空泵内气体的热力过程能直接反映其抽气性能，具有重要研究价值。以某种变螺距螺杆真空泵为对象，在绝热、多变和等温三种内压缩形式下，研究泵内气体压力、温度、内能和焓等热力学参数随时间的变化规律。计算等螺距与变螺距两种螺杆真空泵在相同工况下排气温度随吸气压力的变化趋势，模拟分析两种泵的温度场、压力场及转子变形量的分布。理论计算表明，两种螺杆泵的排气温度均随入口压力升高呈现先缓慢后迅速的下降趋势，变螺距螺杆泵的排气温度在发生过压缩后保持不变，相同入口压力下的排气温度从高到低依次为绝热过程、多变过程、等温过程。流场模拟能够考虑级间泄漏和进出口返流情况，描述泵内气体压力和温度分布更加准确。流场模拟的温度与压力结果均高于理论计算值。变形模拟表明，螺杆转子弯曲是影响变形的重要因素，相同长度的等螺距转子更易发生弯曲，模拟得到的螺杆转子变形规律与工程实际具有一致性。Abstract: The thermodynamic process within screw vacuum pumps directly reflects its performance, holding significant research value. This study focuses on two types of screw vacuum pumps, analyzing the thermodynamic parameters including pressure, temperature, internal energy, and enthalpy of gas based on adiabatic, polytropic, and isothermal processes. The correlation between exhaust temperature and suction pressure for constant and variable pitch screw vacuum pumps was calculated. Additionally, the distribution of temperature, pressure, and deformation of rotors was analyzed through numerical simulation. The calculations indicate that as the suction pressure increases, the exhaust temperatures initially decrease slowly and then rapidly. For the variable pitch screw vacuum pump, the exhaust temperature remains constant after over-compression; the order of exhaust temperature at the same suction pressure is adiabatic, polytropic, and isothermal processes. The numerical simulation gives more accurate results for covering the effect of leakage and backflow, with higher temperatures and pressures than theoretical calculations. Deformation simulation indicates that bending is a significant factor affecting the deformation of the screw rotors, with constant pitch rotors being more prone to bending. The deformation pattern of the screw rotor obtained from numerical simulations can be verified in practical engineering.
-
Key words:
- Screw vacuum pump /
- Thermodynamics process /
- Exhaust temperature /
- Numerical simulation .
-
-
图 2 工作参数随时间的变化曲线。（a）压力，（b）容积，（c）质量
Figure 2. Variation of operating parameters over time. (a) Pressure, (b) volume, (c) mass
图 3 三种内压缩形式下气体温度随时间的变化曲线。（a）绝热，（b）多变，（c）等温
Figure 3. Variation of gas temperature with time for three forms of internal compression. (a) Adiabatic, (b) polytropic, (c) isothermal
图 4 三种内压缩形式下气体内能随时间的变化曲线。（a）绝热，（b）多变，（c）等温
Figure 4. Variation of the internal energy with time in three forms of internal compression. (a) Adiabatic, (b) polytropic, (c) isothermal
图 5 三种内压缩形式下气体焓随时间的变化曲线。（a）绝热，（b）多变，（c）等温
Figure 5. Variation of the enthalpy of a gas with time in three forms of internal compression. (a) Adiabatic, (b) polytropic, (c) isothermal
图 6 螺杆真空泵排气温度与入口压力的关系曲线
Figure 6. Relationship curve between exhaust temperature and inlet pressure of screw vacuum pump
图 7 螺杆真空泵内部压力分布。（a）等螺距，（b）变螺距
Figure 7. Internal pressure distribution of screw vacuum pump. (a) Constant pitch, (b) variable pitch
图 8 螺杆真空泵内部温度分布。（a）等螺距，（b）变螺距
Figure 8. Internal temperature distribution of screw vacuum pump. (a) Constant pitch, (b) variable pitch
图 9 螺杆转子表面压力分布云图。（a）等螺距，（b）变螺距
Figure 9. Pressure distribution of screw rotor surface. (a) Constant pitch, (b) variable pitch
图 10 螺杆转子表面温度分布云图。（a）等螺距，（b）变螺距
Figure 10. Temperature distribution of screw rotor surface. (a) Constant pitch, (b) variable pitch
图 11 螺杆转子总变形云图。（a）等螺距，（b）变螺距
Figure 11. Total deformation of screw rotors. (a) Constant pitch, (b) variable pitch
图 12 齿顶螺旋线径向变形。（a）等螺距，（b）变螺距
Figure 12. Radial deformation of the helix at the top of the tooth. (a) Constant pitch, (b) variable pitch
图 13 齿根螺旋线径向变形。（a）等螺距，（b）变螺距
Figure 13. Radial deformation of the helix at the root of the tooth. (a) Constant pitch, (b) variable pitch
图 14 螺杆转子轴向变形。（a）等螺距，（b）变螺距
Figure 14. Axial deformation of screw rotors. (a) Constant pitch, (b) variable pitch
表 1 计算实例相关参数
Table 1. Relevant parameters of calculation example
变量 单位 数值 齿顶圆半径R1 m 0.0712 齿根圆半径R2 m 0.0236 基圆半径r0 m 0.0177 有效吸气面积S m2 0.0127 转子总长度L0 m 0.292 变螺距吸气端导程Pi m 0.094 变螺距排气端导程Pe m 0.052 等螺距各级导程Ls m 0.073 转子级数n 4 旋转周期τ0 s 0.02 入口气体温度T0 K 293.15 反冲气体压力pr Pa 101325 反冲气体温度Tr K 293.15 多变指数α 1.2 定压比热容cp kJ·kg−1·K−1 1.005 定容比热容cv kJ·kg−1·K−1 0.718 
下载: 导出CSV
-
[1] 姜燮昌. 干式螺杆真空泵的结构、性能与应用[J]. 真空,2018,2018(4):6−12 (in Chinese) Jiang X C. Structure, performance and applications of dry screw vacuum pump[J]. Vacuum,2018,2018(4):6−12 [2] Andreas Tengler. The benefits of oil-free vacuum pumps in industrial processes[J]. World Pumps,2005,2005:18−21 [3] Pfaller D, Brümmer A, Kauder K. Optimized rotor pitch distributions for screw spindle vacuum pumps[J]. Vacuum,2011,85(12):1152−1155 doi: 10.1016/j.vacuum.2011.03.002 [4] 郭蓓, 薛建国, 牛瑞, 等. 干式螺杆真空泵研究现状与展望[J]. 真空,2009,2009(5):37−40 (in Chinese) Guo B, Xue J G, Niu R, et al. Current situation and outlook for R&D of dry screw vacuum pump[J]. Vacuum,2009,2009(5):37−40 [5] 刘明昆, 李丹童, 邢子文. 双螺杆真空泵内压缩转子结构研究现状[J]. 真空,2022,59(4):28−32 (in Chinese) Liu M K, Li D T, Xing Z W. Research progress of the inner compression rotor structure of twin-screw vacuum pumps[J]. Vacuum,2022,59(4):28−32 [6] 刘坤, 巴德纯, 张振厚, 等. 面向应用的真空干泵模块化与集成化发展趋势[C]. 珠三角光电产业与真空科技创新论坛暨广东省真空学会2016年学术年会论文集,2016 (in Chinese) Liu K, Ba D C, Zhang Z H, et al. Application-oriented vacuum dry pump modularization and integration trends[C]. Proceedings of the Pearl River Delta Optoelectronics Industry and Vacuum Science and Technology Innovation Forum and the 2016 Annual Academic Conference of Guangdong Vacuum Society, 2016 [7] 潘成程, 徐飞, 谭昱全, 等. 双螺杆真空泵封闭容积间压力和泄漏特性研究[J]. 真空,2015,52(3):21−25 (in Chinese) Pan C C, Xu F, Tan Y Q, et al. Study on the characteristic of leakage and pressure within the lead of two screw vacuum pump[J]. Vacuum,2015,52(3):21−25 [8] 周宝洪. 干式螺杆真空泵的螺杆设计与计算[J]. 真空,2001,03:46−48 (in Chinese) doi: 10.3969/j.issn.1002-0322.2001.01.011 Zhou B H. Screw design and computing of dry twin-screw vacuum pump[J]. Vacuum,2001,03:46−48 doi: 10.3969/j.issn.1002-0322.2001.01.011 [9] 张世伟, 赵凡, 张杰, 等. 无油螺杆真空泵螺杆转子设计理念的回顾与展望[J]. 真空,2015,52(5):1−12 (in Chinese) Zhang S W, Zhao F, Zhang J, et al. Review and prospect of design ideas for the screw rotors in the oil-free twin-screw vacuum pumps[J]. Vacuum,2015,52(5):1−12 [10] 张世伟, 孙坤, 韩峰. 螺杆真空泵设计的常见问题分析[J]. 真空,2021,58(1):23−28 (in Chinese) Zhang S W, Sun K, Han F. Discussion on several common problems in screw vacuum pump design[J]. Vacuum,2021,58(1):23−28 [11] Hsieh C F, Zhou Q J. Fluid analysis of cylindrical and screw type roots vacuum pumps[J]. Vacuum,2015,121:274−282 doi: 10.1016/j.vacuum.2015.04.037 [12] 刘春姐. 螺杆型干式真空泵转子特性的研究[D]. 沈阳: 东北大学, 2006 (in Chinese) Liu C J. Study on rotor characters of dry vacuum screw pump[D]. Shenyang: Northeastern University of China, 2006 [13] 谭昱全, 潘成程, 徐飞, 等. 双螺杆真空泵腔内间隙的模拟计算[J]. 真空,2015,52(5):13−17 (in Chinese) Tan Y Q, Pan C C, Xu F, et al. Calculation of clearances inside the twin screw vacuum pump[J]. Vacuum,2015,52(5):13−17 [14] 徐飞, 潘成程, 谭昱全, 等. 双螺杆真空泵工作过程中容积及气体状态变化分析[J]. 真空科学与技术学报,2015,35(11):1300−1304 (in Chinese) Xu F, Pan C C, Tan Y Q, et al. Modeling and analysis of air compression in single-thread twin-screw vacuum pumps[J]. Chinese Journal of Vacuum Science and Technology,2015,35(11):1300−1304 [15] 张世伟, 张杰, 张英锋, 等. 等螺距螺杆真空泵内气体热力过程的研究[J]. 真空科学与技术学报,2015,35(8):926−933 (in Chinese) Zhang S W, Zhang J, Zhang Y F, et al. Thermodynamic analysis of pumping by twin-screw vacuum pump with fixed pitch rotors[J]. Chinese Journal of Vacuum Science and Technology,2015,35(8):926−933 [16] Zhao F, Zhang S, Sun K, et al. Thermodynamic performance of multi-stage gradational lead screw vacuum pump[J]. Applied Surface Science,2018,432(B):97−109 [17] 赵凡. 无油螺杆真空泵四种变螺距转子的性能研究[D]. 沈阳: 东北大学, 2016 (in Chinese) Zhao F, Performance study of four types of variable pitch rotors for oil-free screw vacuum pumps[D]. Shenyang: Northeastern University of China, 2016 [18] 翟云飞. 螺杆真空泵内气体热力过程的模拟与实验研究[D]. 沈阳: 东北大学, 2020 (in Chinese) Zhai Y F. Simulative and experimental studies of gas thermodynamic processes in the twin screw vacuum pump[D]. Shenyang: Northeastern University of China, 2020 [19] 翟云飞, 张世伟, 孙坤, 等. 螺杆真空泵内气体热力过程的解析计算与实验研究[J]. 真空,2020,57(3):54−60 (in Chinese) Zhai Y F, Zhang S W, Sun K, et al. Analytical calculation and experimental studies on gas thermodynamic processes in screw vacuum pump[J]. Vacuum,2020,57(3):54−60 [20] 巫修海. 内压缩干式螺杆真空泵关键技术研究[D]. 杭州: 浙江理工大学, 2016 (in Chinese) Wu X H. Research on key technology for dry screw vaccum pump with internal compression[D]. Hangzhou: Zhejiang Sci-Tech University, 2016 [21] 巫修海, 陈文华, 张宝夫. 内压缩干式螺杆真空泵工作特性数学建模[J]. 真空科学与技术学报,2016,36(9):987−994 (in Chinese) Wu X H, Chen W H, Zhang B F. Modeling and evaluation of characteristics of dry screw vacuum pump with internal compression[J]. Chinese Journal of Vacuum Science and Technology,2016,36(9):987−994 [22] 卢阳, 郭蓓, 周瑞鑫. 双螺杆真空泵工作过程数值模拟[J]. 西安交通大学学报,2015,49(7):67−71 (in Chinese) Lu Y, Guo B, Zhou R X. Numerical simulation for working process in twin screw vacuum pump[J]. Journal of Xi'an Jiaotong University,2015,49(7):67−71 [23] Lu Y, Fu Y, Guo B, et al. Numerical simulation of the working process in the twin screw vacuum pump[J]. Iop Conference Series: Materials Science and Engineering,2017,232:1−11 [24] 李丹童, 何志龙, 邢子文. 干式螺杆真空泵内部泄漏过程建模及分析[J]. 真空科学与技术学报,2021,41(10):959−968 (in Chinese) Li D T, He Z L, Xing Z W. Modeling and analysis for the leakage process in dry screw vacuum pumps[J]. Chinese Journal of Vacuum Science and Technology,2021,41(10):959−968 [25] Li D T, He Z L, Wang C, et al. Simulation of dry screw vacuum pumps based on chamber model and thermal resistance network[J]. Applied Thermal Engineering,2022,211:118460 doi: 10.1016/j.applthermaleng.2022.118460 [26] Lu Y, Guo B, Geng M F. Study on design of rotor profile for the twin screw vacuum pump with single thread tooth[J]. IOP Conference Series: Materials Science and Engineering,2015,90:012007 doi: 10.1088/1757-899X/90/1/012007 [27] 肖红云. 变螺距螺杆真空泵抽气机理研究及转子结构优化[D]. 合肥: 合肥工业大学, 2017 (in Chinese) Xiao H Y. Study on exhaust mechanism and rotor structure optimization of screw vacuum pump with variable pitch[D]. Hefei: Hefei University of Technology, 2017 [28] 孙瑾亭. 变螺距螺杆真空泵结构设计及优化[D]. 合肥: 合肥工业大学, 2018 (in Chinese) Sun J T. Structure design and optimization of variable pitch screw vacuum pump[D]. Hefei: Hefei University of Technology, 2018 [29] 徐飞. 双螺杆真空泵结构设计及分析[D]. 合肥: 合肥工业大学, 2015 (in Chinese) Xu F. Structure design and analysis for twin-screw vacuum pump[D]. Hefei: Hefei University of Technology, 2015 [30] 刘坤, 宁英超, 孟冬辉, 等. 一种单螺旋转子型线及其热变形研究[J]. 真空科学与技术学报,2015,35(12):57−62 (in Chinese) Liu K, Ning Y C, Meng D H, et al. Profile and thermal deformation of single screw rotor[J]. Chinese Journal of Vacuum Science and Technology,2015,35(12):57−62 [31] Wei J, Liang X L, Sun W, et al. Numerical simulation of flow field dynamics characteristics for one novel twin-screw kneader[J]. Applied Mechanics and Materials,2012,271-272:1049−1055 doi: 10.4028/www.scientific.net/AMM.271-272.1049 [32] Tran V T, Le T L, Nguyen H L. Force analysis for a variable-pitch rotor meshing pair in twin-screw vacuum pump generating on cnc turning machine[J]. Applied Mechanics and Materials,2019,894:41−50 doi: 10.4028/www.scientific.net/AMM.894.41 [33] Reddy G C. CFD studies on flow through screw compressor[D]. Rourkela: National Institute of Technology, 2007 [34] 吴文坤. 干式螺杆真空泵内部温度场分析及调控机制的研究[D]. 沈阳: 东北大学, 2020 (in Chinese) Wu W K. Research on internal temperature field analysis and control mechanism of dry screw vacuum pump[D]. Shenyang: Northeastern University of China, 2020 -
计量
- 文章访问数: 456
- HTML全文浏览数: 456
- PDF下载数: 4
- 施引文献: 0