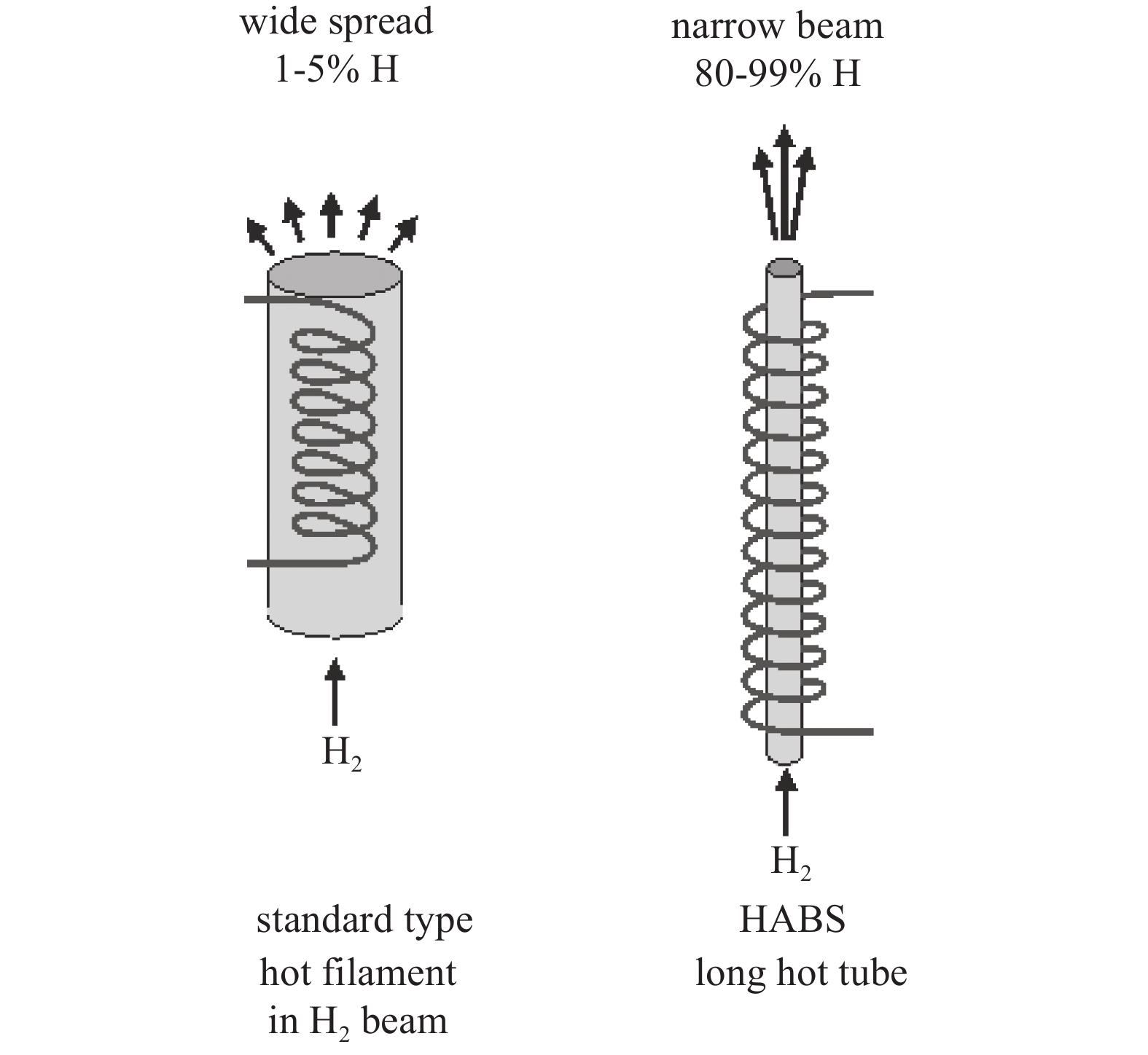
气体裂解源通常包括氢、氧、氮等气体裂解源，其中氮源通常为射频等离子裂解源。本文以氢裂解源为例介绍气体裂解源。原子氢多用于衬底表面的低温处理，比如去除GaAs、InP衬底上的碳污染（200℃）和氧污染（400℃），以提高MBE外延品质；原子氢还用于辅助MBE外延，比如原子氢增强的GaAs MBE外延^[1-5]。氢原子主要是由等离子体或热表面的氢气解离产生，而通过热裂解的方式可以提供无任何离子或激发态分子的氢原子。如图1所示，这是一个典型的钨灯丝热裂解原子氢源和毛细管热裂解原子氢源工作原理图。

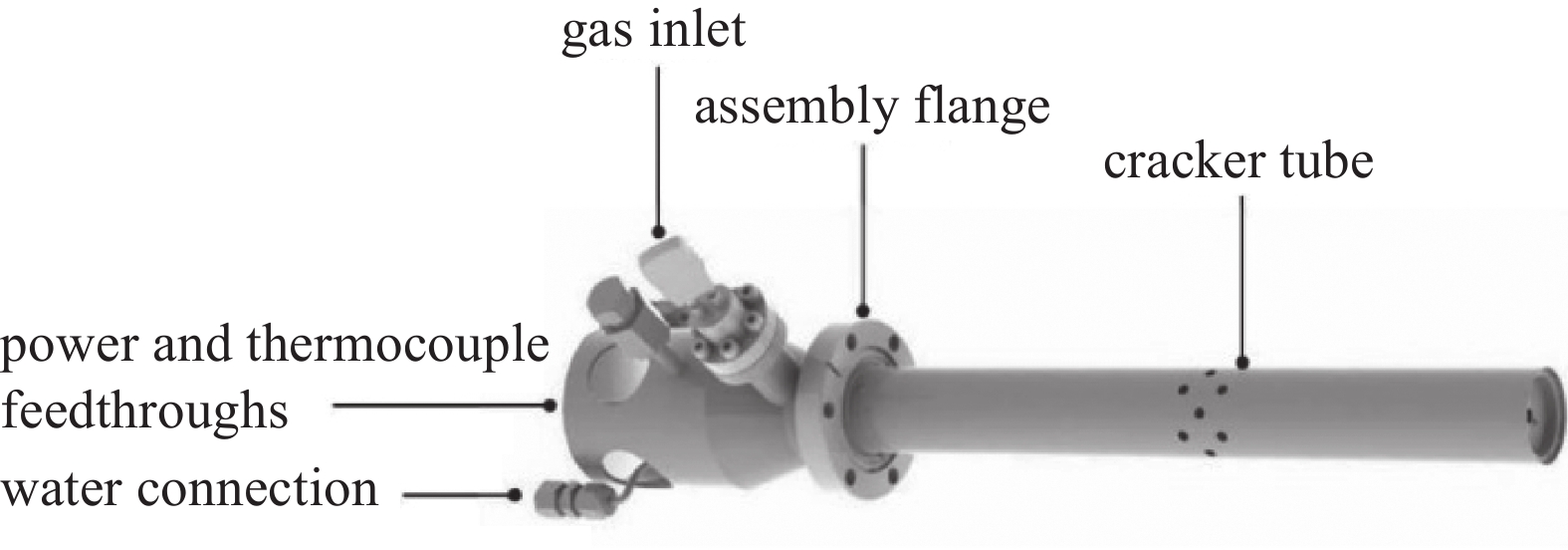
典型裂解源适用于大流量工业用气源，氢气通过流导很小的管路后再进入装有热丝的裂解腔，经过热钨丝的催化及加热实现氢气裂解，具有束流量大、无高能离子电子的特点。但其束流准直性差，裂解效率较低，在45 W热丝达到2000℃时通常在40%左右；而毛细管热裂解源是将氢气通过流导极小的热毛细钨管，氢气在钨壁上发生裂解。如图2所示，小流量科研用氢裂解源具有裂解效率高，束流准直性好，无高能离子电子的优点^[6-8]；缺点是不适合半导体工业需要的大尺寸衬底处理高均匀性和高通量的需求，提高气量后裂解效率快速衰减，同时采用金属毛细管还存在金属蒸气污染的风险。

源的强度可以通过氢气流量和加热功率控制，通常气体流量由泄漏阀或质量流量调节控制器。加热功率决定了毛细管的温度，细长的钨毛细管最高工作温度为2100℃，通常工作气流在0.1 sccm以内。

带阀固体裂解源如图3，通常包括砷、磷、铯、锢、锑、硫、汞固体裂解源等，本节以砷裂解源为例。GaAs是制作发光二极管、激光二极管、光电探测器等光电器件的关键材料，广泛应用于照明、通信、显示等领域。As在GaAs中属于基质元素，与Ga共同形成晶格。通过MBE技术，可以实现对砷化镓的精确掺杂，从而控制半导体的电子性质^[9-12]。在不同的半导体材料之间可以生长异质结构，如在GaAs上生长InGaAs层使用As₂而非As₄可以减少由于点缺陷造成的深层能级浓度^[13-17]，并减少材料中由于缺陷而产生的束缚激子对光致发光光谱的影响。这在制造高性能的光电器件和高频器件中非常重要。

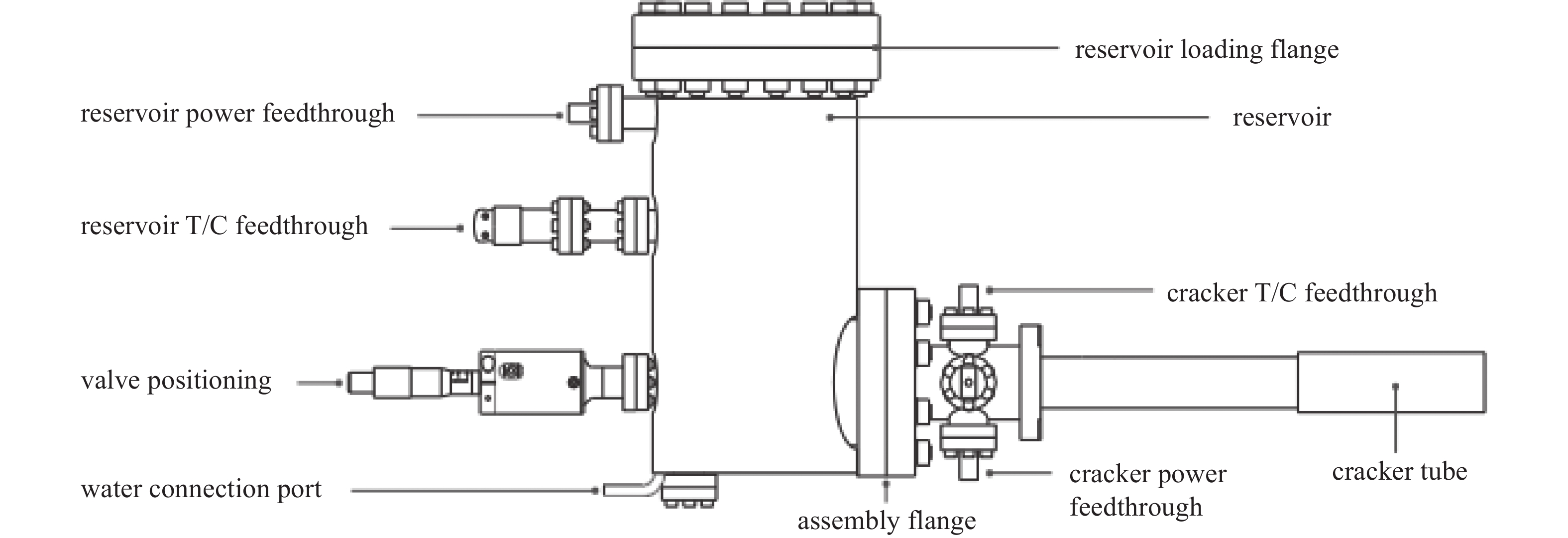
带阀门的砷裂解源如图4所示，由三个主要部分组成：储液罐、隔离阀和裂解腔。固体砷通过法兰端口加载到储层坩埚中，储层外部用循环水冷却，以便有效散热。坩埚加热后固体砷变为砷蒸汽，通过可控制的隔离阀进入钽丝电阻加热的进料管和裂解腔。裂解阶段产生开裂的砷二聚体，并经过几何形状优化的扩散器在衬底上提供均匀的通量。

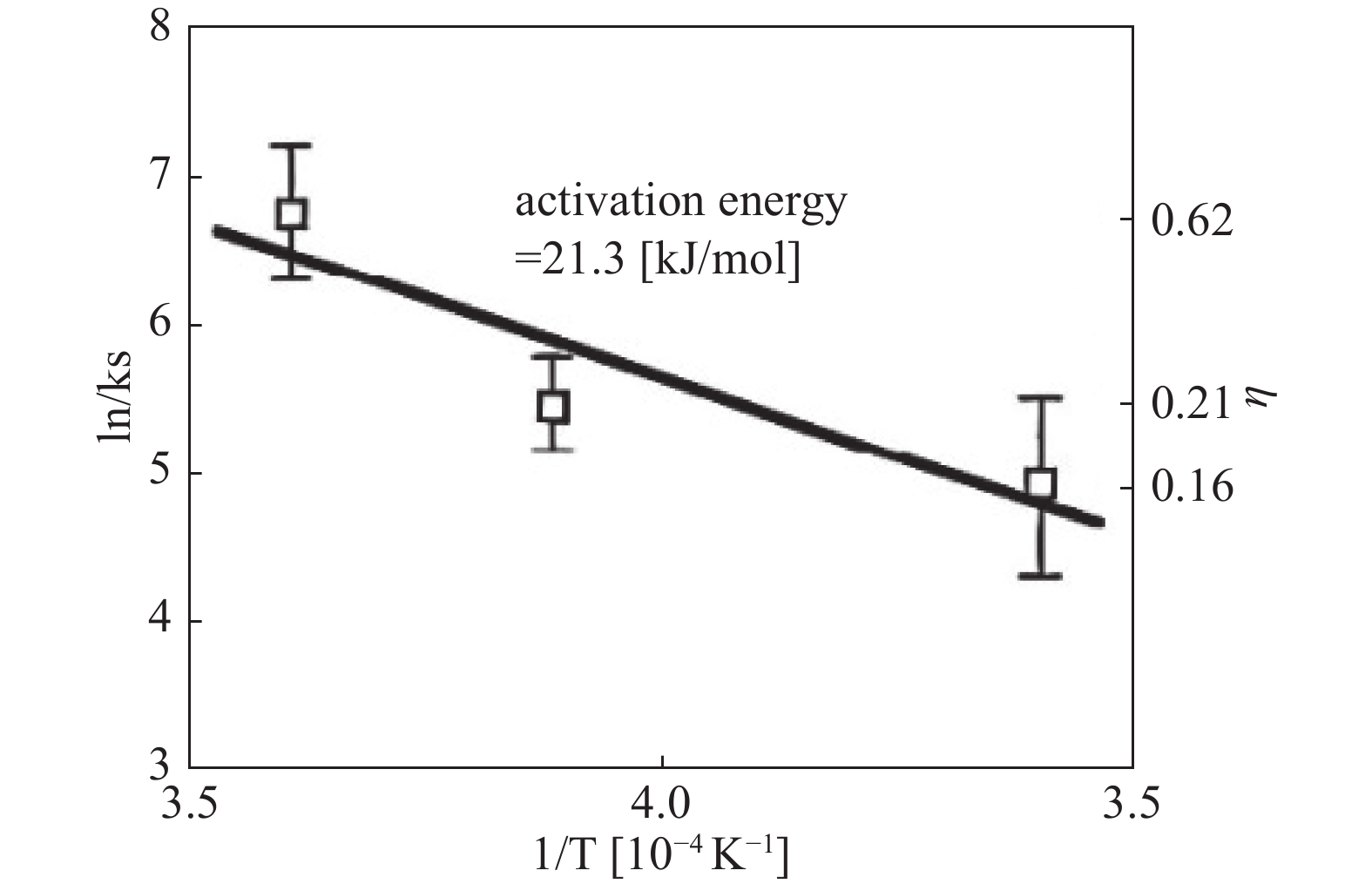
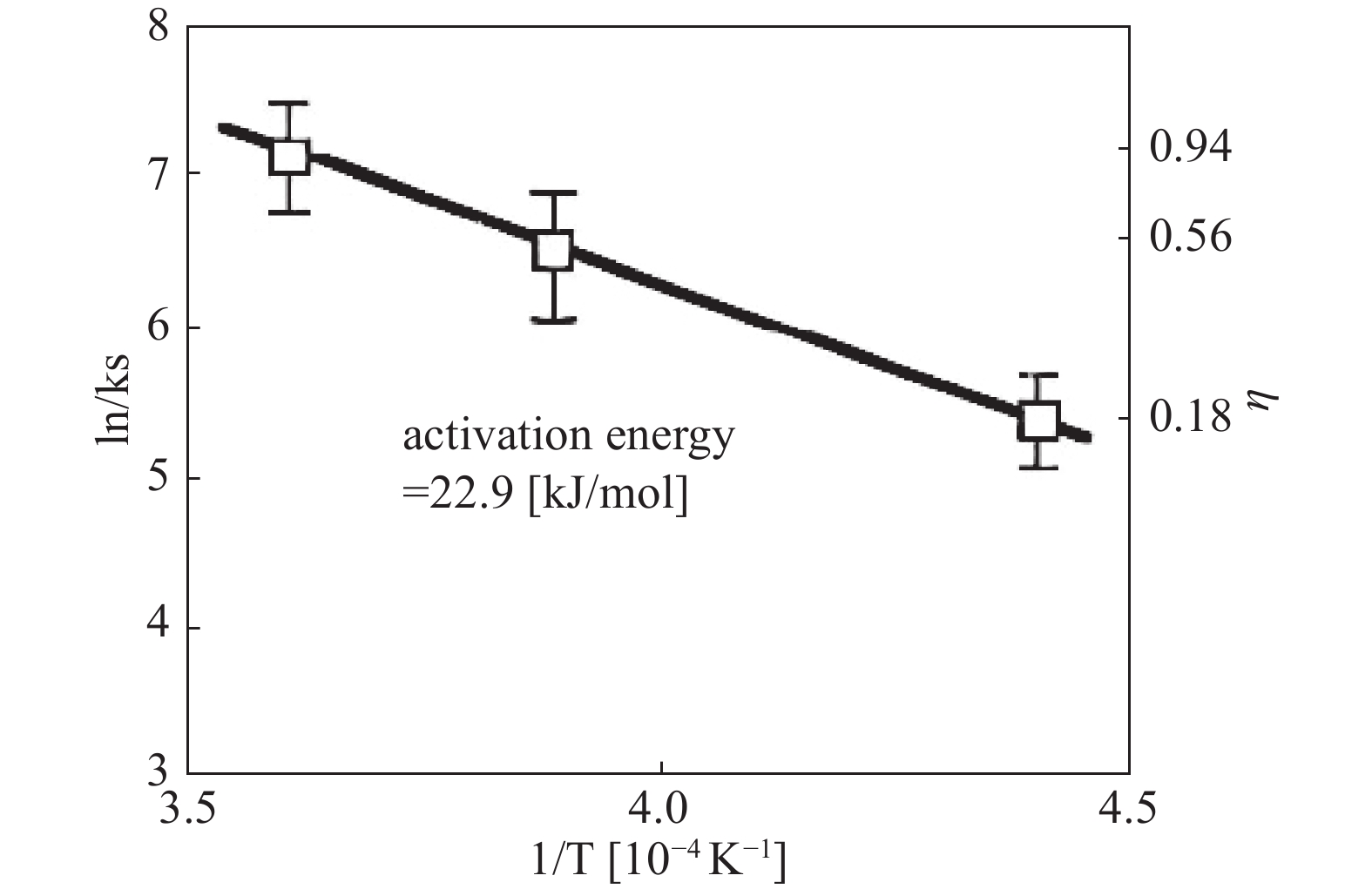
Otsuka T 等^[18]研究了热钽和钨丝对氢分子的解离作用。实验确定了在2000℃、2300℃和2500℃的热丝温度和0.5至100 Torr的H₂压力下，热钽和钨丝解离H₂所需的电能。在高压区域，气体相中H₂和H符合热力学平衡。随着压力的降低，H₂的解离从热力学平衡控制转变为表面反应速率控制。通过Arrhenius图（图5，图6），确定了在钽丝上H₂解离的活化能为21.3 kJ/mol，在钨丝上为22.9 kJ/mol，表明热钨丝上H₂的解离概率很大且优于钽丝。反应概率在表面反应速率控制下，在钽上为0.16 ~ 0.62，在钨上为0.18 ~ 0.94。

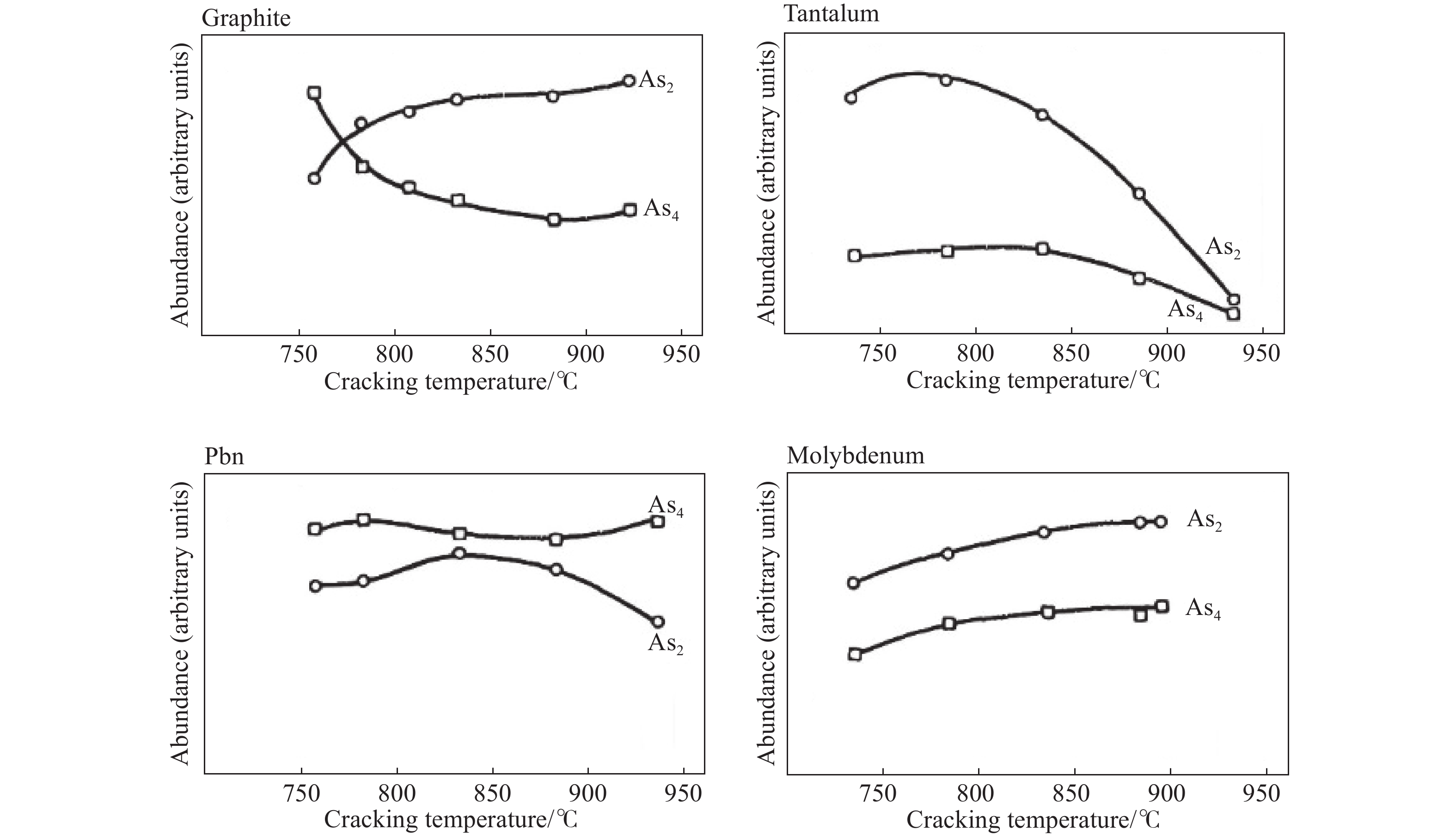
Lee R L等^[19]研究了不同材料对分子束外延中砷裂解炉裂解效率的影响。文章讨论了三种获得As₂的方法：GaAs蒸发、砷化氢的热分解和As₄的裂解。As₄的裂解方法最为适合，并研究比较了四种不同的裂解挡板材料—石墨、钽、硼氮化物（PBN）和钼对于裂解后相对丰度的影响，如图7结果显示不同的挡板材料对裂解效率有明显影响。

对于石墨、钼和PBN，高温下更有利于As₄的分解，其中PBN挡板效果最差。而对于钽挡板，存在一个最佳温度窗口，在850℃以上二聚体含量会下降。通过使用残余气体分析仪测量裂解炉的束流组成，发现石墨挡板在高温下提供了最高的二聚体通量。除了钽之外，其他材料在高温下都达到了各自的二聚体/四聚体组成比率的渐近值，这些值低于平衡极限，表明裂解反应受动力学限制，钽挡板的特殊情况可能是由于高温下砷与钽的反应所致。

直接仿真蒙特卡洛方法^[20-23]通过构建分子动力学的统计计算模型实现对稀薄气体流动的高效模拟。该方法采用有限数量仿真粒子表征气体分子的群体动力学行为，其核心算法通过解耦迁移运动与碰撞作用两个物理过程来降低计算维度。在离散时间步长框架下，系统首先对所有仿真粒子实施匀速直线运动的坐标更新，并通过边界条件约束处理粒子与计算域固壁的相互作用；随后采用概率密度函数建立局部网格单元内的分子碰撞抽样准则，以蒙特卡洛接受-拒绝机制替代传统的确定性力学追踪，从而显著减少碰撞计算的时间复杂度。在非平衡态向准稳态演化的过程中，该方法通过时空耦合的统计采样技术，将仿真粒子的微观运动特征（如速度分布、内能状态）映射至宏观流动参数，最终获得包括温度梯度场、压强分布场等在内的全域气体动力学特征。这种基于分子混沌假设与分步确定性求解的策略，使得算法整体计算效率优化至线性复杂度，为航天器再入大气层、微机电系统流场分析等复杂工况提供了有效的数值模拟工具。

计算中DSMC方法基于将粒子的连续运动及其碰撞分成两个连续阶段：

1）所有粒子移动到由它们的速度和时间步长Δt确定的距离。如果粒子穿过边界曲面，则直接进入无限边界真空环境不再反弹回来。

2）模拟对应于时间间隔Δt的粒子碰撞，粒子碰撞后得到的速度代替了碰撞前的速度。

物理空间的模拟体积被划分为若干单元。在每个单元中模拟一定数量粒子的运动和碰撞。时间以时间步长Δt离散地变化，与粒子碰撞之间的平均时间相比，时间步长Δt较小。在每个时间步长内，对计算气流宏观参数（密度、速度、温度、压力）所需的信息进行采样。

总能碰撞（TCE，total collision energy）模型^[24]是最为广泛使用的一种。该化学反应建模框架基于分子碰撞能量传递理论，通过离散数学重构方法将Arrhenius连续速率控制方程映射为概率型反应截面函数，其核心转换需以各反应的速率系数实验数据作为本征参数。当前DSMC化学动力学模型的发展呈现基础模型有限但深化应用活跃的特征：尽管通用型全局反应截面模型体系发展相对滞后，但在精细反应流模拟方向已涌现出多项创新性解决方案。典型的高精度计算方法采用准经典轨迹（QCT，Quasi-Classical Trajectory）理论的量子态分辨计算数据，或基于态−态（state-to-state）碰撞截面实测数据建立反应截面的概率分布函数，这类直接根于分子碰撞量子态演化的模型架构提升了振动弛豫、解离重组等非平衡过程的模拟保真度。Bird G A^[25]于2011年提出了一种全新的化学反应模型：量子−动理学（Q-K，quantum kinetic）模型以分子振动量子能态演化为基础，通过构建量子态跃迁概率矩阵直接预测化学反应路径，摆脱传统宏观速率方程与热力学平衡假设的双重约束。其核心架构包含两大创新模块：利用量子化振动能级分布计算化学键断裂/重组概率，以及基于量子态分辨的抽样算法确定反触发逻辑。此类量子特性显式建模方法，使该模型在高温离解反应、激波诱导非平衡流等存在显著振动−平动能量松弛的应用场景中，较传统模型具备更精确的微观反应动力学描述能力。量子振动模型的引入为发展更加接近真实的物理的程序开辟了道路，当碰撞后振动能级是解离能级时，解离反应自然发生。

Q-K模型基于量子振动理论框架，采用简谐振子近似构建非平衡能态演变方程。在振动能弛豫机制处理中，通过引入量子碰撞温度实现对平动温度分量与振动弛豫特征时间的耦合建模，可直接导出松弛碰撞数这一关键动力学参数。计算表明：当双分子体系的振动叠加态满足阈值条件时，松弛碰撞数将决定振动量子态能量向平动模式传递的概率加权系数，最终驱动系统达到统计平衡态^[26]。量子碰撞温度可写为：

式中i_max为碰撞分子对所具有的最大能级，$ \omega $为气体黏性系数中的温度指数。采用量子碰撞温度T_coll定义振动松弛碰撞数如下^[27]：

其中，Z_ref为参考温度T_ref下的振动松弛碰撞数，该松弛碰撞数可通过TCE模型中求解振动碰撞数的方式获得^[28]：

参考温度T_ref通常用振动特征温度表示，式3中C₁和C₂为常数。在Q-K模型中，离解反应的化学过程通过量化振动能级跃迁概率与键能的匹配关系进行建模，其处理方法可概括为以下几个方面。

离解反应的触发机制可表述为：当碰撞能量超过分子键解离阈值对应的振动能级时发生分子断裂。以反应式AB + T $\rightleftharpoons $ A + B + T为例，其中AB为离解分子，T为引发能量转移的第三体碰撞粒子，A和B则为离解过程中生成的自由基产物。碰撞后的最大振动能级i_max由式（4）确定^[29-30]：

式中$ \left\lfloor ... \right\rfloor $表示截断取整，E_c是碰撞分子对的碰撞能，$ \theta\mathrm{_v} $为分子振动特征温度，k为Boltzmann常数。在分子碰撞动力学框架下，总有效碰撞能可表述为反应体系内碰撞对的相对运动平动能与分子AB初始振动态能量之和，其数学表征为：$ E_{\mathrm{C}}=\varepsilon_{\mathrm{v},\mathrm{AB}+\mathrm{T}}+\varepsilon_{\mathrm{v},\mathrm{AB}} $，解离的判断条件为：

$ \theta_{\mathrm{d}} $为分子AB的特征离解温度。Q-K模型对于高温高速运动的粒子计算较为精准，化学反应发生在二体碰撞时，多用于航天返回舱与大气摩擦气体分解的计算，Q-K模型的量子振动分解判定机理对于裂解源的高温裂解也同样适用。

Mankelevich YA等^[31]研究了双原子分子（H₂, N₂, O₂）在金属热丝（HF，Hot Filament）表面上的解离过程，并提出了一个统一的两步反应机制。在统一的两步反应机制框架内，通过对金属热丝表面的气体温度和选定物质浓度分布的联合实验进行模拟研究，从理论上研究了双原子分子（H₂，N₂，O₂）的解离。

同核双原子物质X₂（H₂ ，N₂）在热丝表面上的催化解离。该机制涉及四个“有效”反应：裸金属表面位置S^*的分子解离（反应1），X在金属SX处提取原子生成分子（反应-1），从SX表面位置X原子解吸（反应2）和X加到自由S^*位置（反应-2）。

在任何特定的平衡条件下，稳态[S^*]和[SX]， [S^*]和[SX]的净产量/损失率应为零。{(r₁−r₋₁)−(r₂−r₋₂)}= 0。有效反应1，−1和2，−2的速率R_i的不平衡决定了热丝表面X原子的净非均相生成速率（催化源项Q，单位为cm⁻² s⁻¹）：

式中的[X]和[X₂]分别为紧邻热丝表面的浓度即[X(d = 0)]和[X₂(d = 0)]， [S₀]为单位面积表面总位点密度，即[S₀] = [SX] + [S^*]。

Plotnikov M等^[32]依据 Mankelevich YA等^[31]提出的模型，提出了一种新的DSMC算法，该算法包含了一个两步氢气解离模型，并提出了一种在DSMC方法框架内模拟异质反应的新技术，其中反应速率常数依赖于气体和表面温度。两步模型考虑了四个反应过程，包括氢气分子在金属表面上的解离和复合，以及氢原子的吸附和脱附。在该模型中,氢分子解离的概率与金属表面活性位点的占用相关。气相粒子（不参与化学反应）与表面相互作用时的动量和能量交换过程使用具有调节系数α的镜面漫反射模型来描述（AC2模型）。因此，粒子从表面漫射反射，其动量和能量完全适应的概率为α，或以1-α的概率镜面反射（Baule公式，AC2模型）。

这里m是气相粒子的质量，M是表面原子的质量。根据表面点位分子的类型用公式确定调节系数的值。如果粒子与自由表面点发生碰撞，则用钽原子的质量作为表面原子的质量。如果粒子与已占据的位置相撞，那么质量使用占据点位的分子或原子的质量。此种壁面碰撞模型称为AC3混合模型。

如果一个氢气分子碰到一个空的活性位点，则估计其吸附并解离的概率：

其中A为表面积，$ {\theta }_{{\mathrm{r}}} $为空位数，m_Hx为粒子质量，k为反应速率系数，E为反应活化能。其中一个氢原子返回气相，从表面反射出充分的动量和能量，而其余则吸附在自由表面上。吸附氢原子的寿命从指数分布中采样：

在这段时间结束时，原子回到气相。在DSMC算法的每个时间步，选择寿命结束的吸附原子。然后计算这些原子的速度，并考虑到时间步长的其余部分来执行它们的运动。

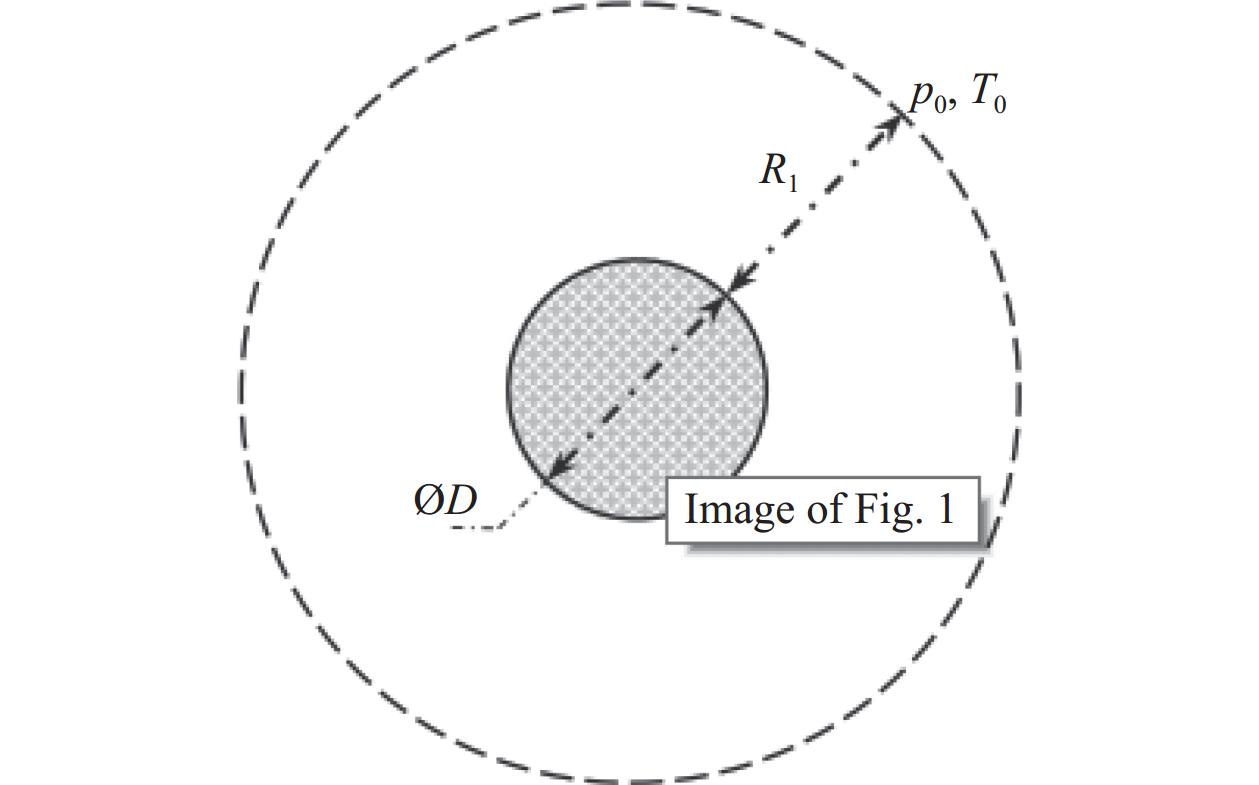
研究以加热的无限长钽丝置于氢气氛围中为例进行了算法验证，二维模型如图8。几何模型为直径3 mm的无限长圆柱钽丝，计算域从丝表面延伸至外边界间距2 mm，外边界压力设定为5−50 Torr并依压力梯度对应温度965–1690 K。网格采用径向非均匀划分，近壁面网格尺寸为平均自由程的四分之一（L≈0.004–0.02 cm，Knudsen数范围0.004–0.02）；分子相互作用采用变软球（VSS）模型，能量交换通过Larsen-Bognakke模型处理；表面催化反应采用两步模型，活性位点密度基于钽晶格常数确定为9.183×10¹⁴ cm⁻²，反应速率常数遵循阿伦尼乌斯公式，其中离解反应（S^* + H₂→SH + H）反应速率系数为3.08×10⁻¹² T^1/2 cm³/s、活化能1.442×10⁻¹⁹ J；蒙特卡洛算法时间步长取为10⁻⁹−10⁻⁸ s，采样次数达10⁵−10⁶次以确保统计收敛，初始条件外边界分子氢密由理想气体定律计算，原子氢密度依据实验数据插值表获取；表面相互作用通过自由位点采用Baule公式适应系数，占据位点使用固定值的AC3混合模型差异化处理碰撞事件，并引入490 K的温跃值修正离解速率预指数因子，最终构建了涵盖稀薄效应、表面覆盖度动态及温度梯度的多尺度耦合模型框架。模型的一个显著特点是随着压力的增加，产生的原子氢数量会逐渐停止增加，这也是实验中观察到的现象。氢气解离的概率随着压力的增加而降低，这是由于金属表面上活性位点的占用率增加。

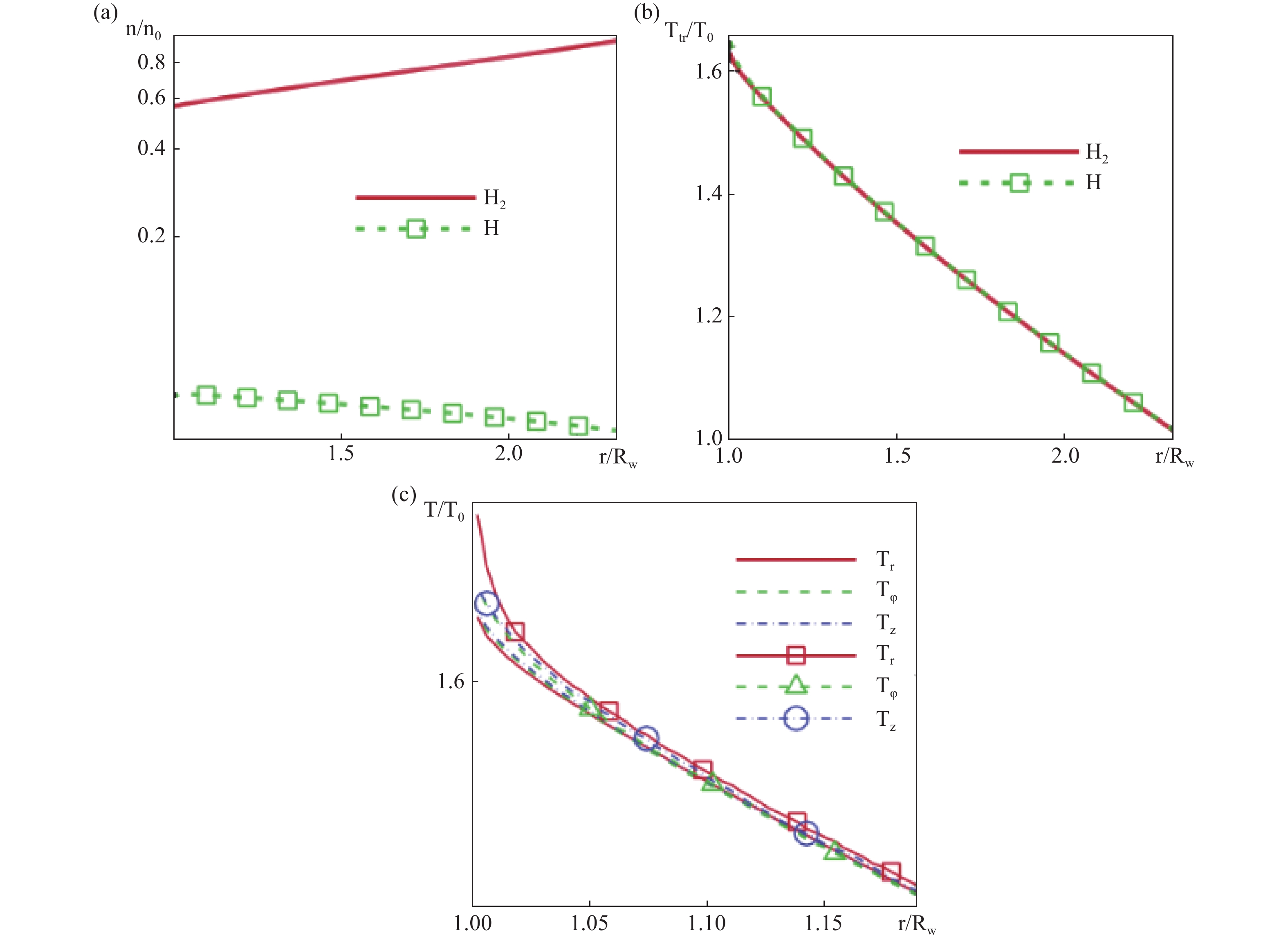
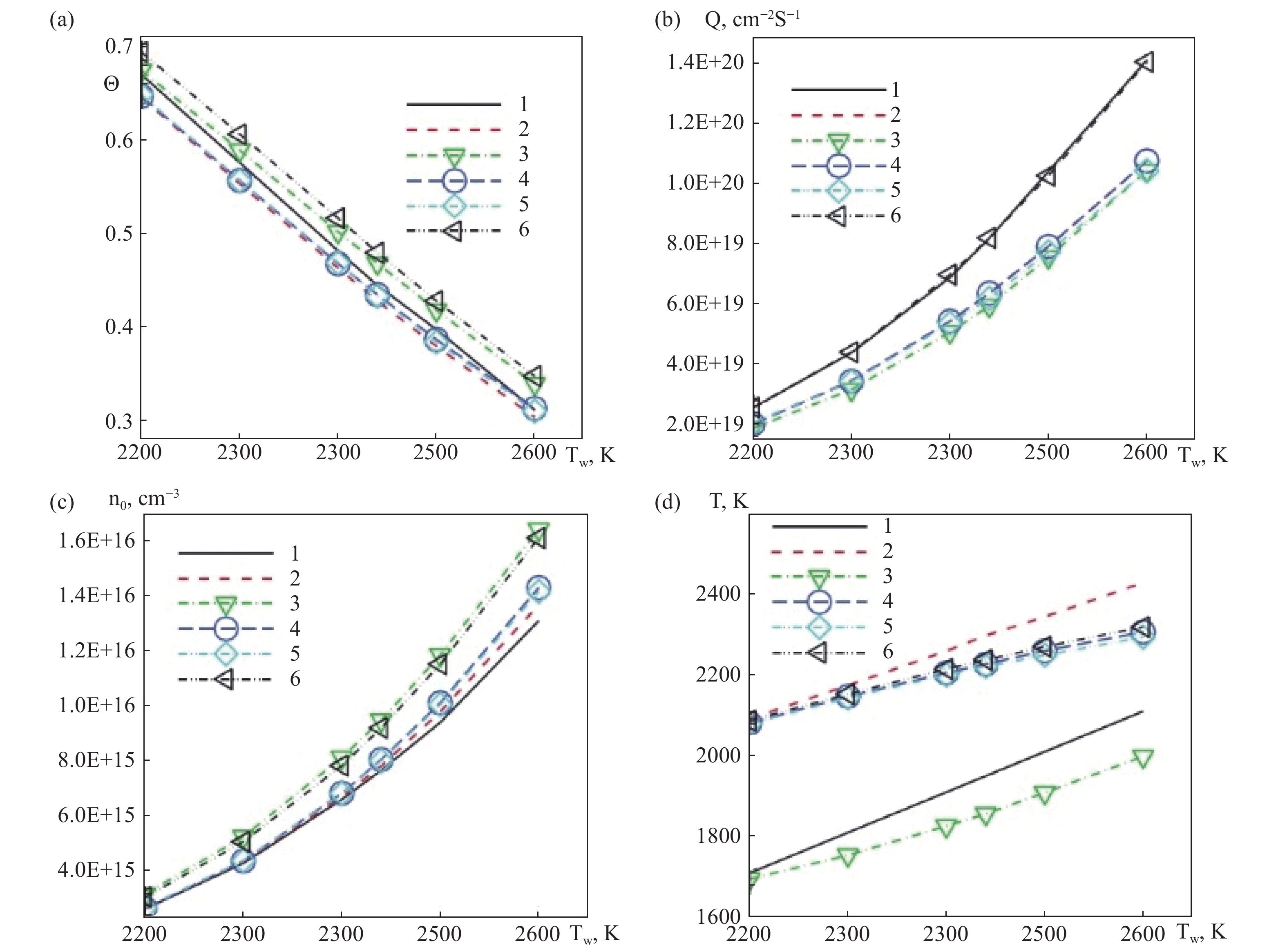
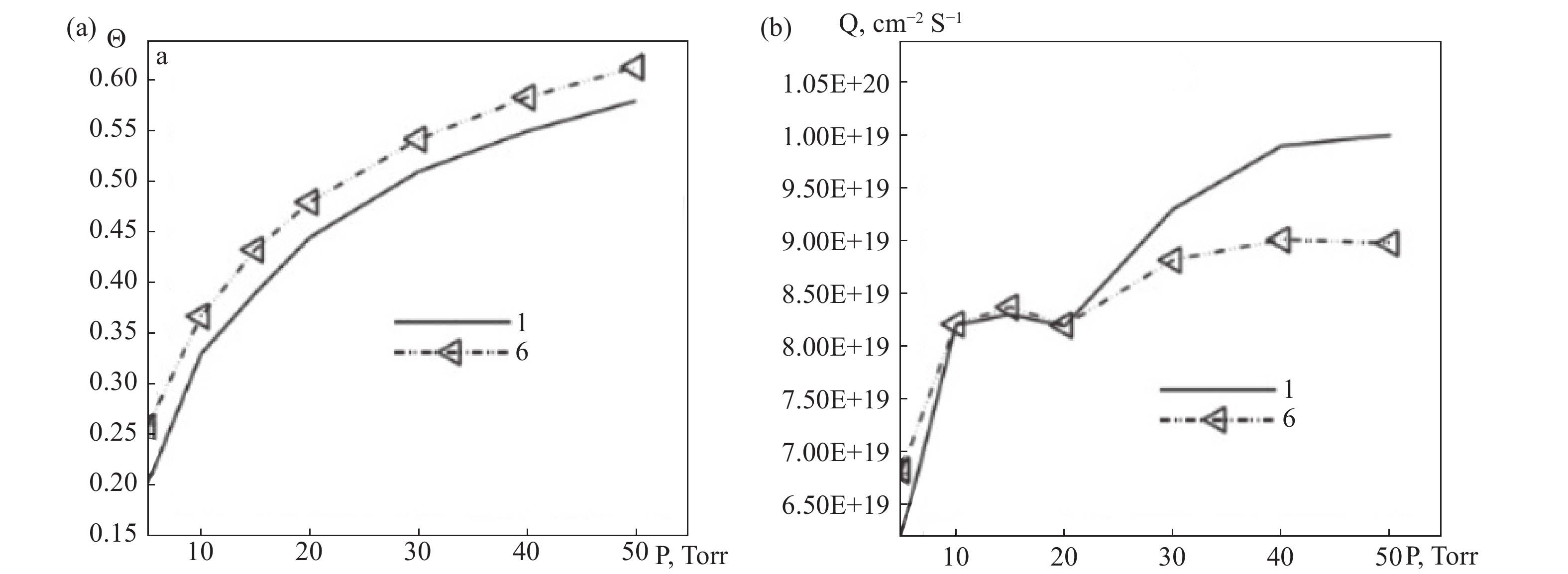
分子氢在近壁区的数密度随离解反应显著下降，如图9（a），表面2 mm区域内原子氢密度从6×10¹⁵ cm⁻³递减至边界条件预设值1.64×10¹⁵ cm⁻³，距离热钽丝表面较远的区域，原子氢的密度降低主要由其沿半径方向的扩散过程驱动；气体平动温度在表面附近趋近钽丝温度T_w=2440 K，但受外边界温度约束T₀=1390 K，离表面0.5 mm处H₂与H的温度快速均衡至约1950 K，如图9（b），其中径向温度分量T_r因高碰撞率在近壁区微高于切向分量，如图9（c）；催化原子源功率Q随T_w呈指数增长2200 K至2600 K时Q提升10倍，但高压下受吸附位饱和θ→1限制产生增长瓶颈如图10（b）、图11（b）；表面覆盖度θ随T_w升高因吸附原子寿命缩短而显著降低T_w=2400 K时θ≈0.6，如图10（a），随压力增加因活性位快速填充趋近饱和p₀=50 Torr时，θ>0.95如图11（a）；对比表明，经典镜漫反射模型（AC1）因高能粒子占比过高导致近壁气体温度虚高T_gas≈2250 K，如图10 d，由Baule公式（8）计算的调节系数是第二种选择（AC2）。而混合相互作用模型（AC3）通过处理自由/占据位点碰撞，适应系数分别取Baule值/固定值更吻合实验结果，揭示DSMC在捕捉稀薄效应分子返流、动态吸附平衡与温度梯度耦合机制上的独特优势。

数值实验结果表明气体温度、表面活性位点的占用度以及异质反应的模拟方法对催化源功率有显著影响。气体温度升高直接增强反应动力学速率，但同时通过热泳效应改变近壁面氢原子分布，导致反应物浓度场的空间重构。表面活性位点占用度呈现非线性调控特征，低占用度状态下反应速率受游离位点数量主导，而高占用度时吸附物种的动态平衡制约反应进程。异质反应模拟方法的算法选择则体现多尺度特征：微观概率模型的能量层级分离气体温度控制前因子，表面温度主导活化能；位点状态分类反射，游离态与吸附态碰撞差异；以及动态调节系数基于质量差的多态传能模型的优化，显著改善了催化源功率的预测精度。

本文以氢、砷裂解源为例介绍了其基本原理及各自的特点，研究不同材料对砷裂解效率的影响，如石墨、钼和 PBN 在高温下更有利于分解，钽挡板存在最佳温度窗口。介绍了基于量子振动的Q-K模型及双原子分子在金属热丝表面的解离过程及相关反应机制，包括统一的两步反应机制和新的 DSMC 算法。该算法包含两步氢气解离模型及模拟异质反应的新技术，考虑氢气分子在金属表面的解离、复合、氢原子的吸附和脱附等过程，描述气相粒子与表面相互作用时的动量和能量交换过程。

随着化合物半导体芯片制造行业的发展，对裂解源的性能要求会不断提高。未来研究可进一步优化裂解源的结构设计，提高裂解效率和束流质量；深入研究不同材料和工艺条件对裂解过程的影响，开发更高效的模拟方法和模型，以更好地理解和控制裂解源内部的复杂物理化学过程，满足半导体制设备不断发展的需求。