在ECR系统中充入放电气体氩气，气体在通过电场的作用下放电，产生的等离子体在特定磁场作用下，电磁波和作回旋运动的电子发生共振，产生高密度的等离子体。

ECR中，由微波加热获得的高能电子通过与氩原子发生碰撞，电离氩原子生成氩离子和自由电子，从而形成和维持等离子体。考虑电子（e）、激发态的氩原子（Ar^s）、氩原子（Ar）和氩离子（Ar⁺）的等离子体反应，其反应方程式^[10]如表1所示。

ECR中，电离率通常低于10%，此时电子−离子的碰撞频率相对较低，对等离子体整体影响较小，故忽略。而Hussein M A等^[11]指出离子−离子碰撞的主要作用是将能量从平行于磁场的方向重新分配到垂直于磁场的方向，故亦可忽略。

根据ECR的共振条件：

式中，${f_{{\mathrm{ce}}}}$为电子回旋频率，$B$为共振时的磁场强度，在一般的ECR系统中，微波功率为2.45 GHz，当$f = {f_{{\mathrm{ce}}}} = $2.45 GHz时，得共振时的磁感应强度${B_{{\text{res}}}}$≈875 Gs。

ECR中，磁场的分布和变化是等离子体产生和维持有重要影响。以Maxwell方程组模拟放电系统中加热等离子体的电磁场：

式（2）~（4）中，${\boldsymbol{B}}$为磁感应强度；${\boldsymbol{J}}$为等离子体电流密度；${\boldsymbol{A}}$为磁矢势；$\sigma {\boldsymbol{E}}$为电子在电场中运动引起的电流密度；$\sigma {\boldsymbol{v}} \times {\boldsymbol{B}}$为电子在磁场中运动引起的电流密度；${{\boldsymbol{J}}_{\text{e}}}$为线圈电流密度，其表达式为：

式中，$N$为线圈匝数，${I_{{\text{coil}}}}$为线圈电流，$A$为线圈横截面面积，${{\boldsymbol{e}}_{{\text{coil}}}}$为线圈电流的单位矢量。

在ECR等离子体中，采用描述电子密度${n_{\text{e}}}$和能量密度${n_\varepsilon }$的漂移扩散方程，这可以描述电子在一般环境下的宏观运动。

式（6）、（7）分别为粒子守恒方程和能量守恒方程，描述了电子在空间和时间上的分布变化，其中包括了电子由于电场或磁场引起的漂移、由于浓度梯度引起的扩散现象，以及电子产生或消失的源项对电子的影响。式中， ${\boldsymbol{E}}$为电场强度； ${{\boldsymbol{R}}_{\text{e}}}$为电子产生项，表示电子和中性电子碰撞产生新电子的过程；${{\boldsymbol{\varGamma}} _{\text{e}}}$为电子通量；${{\boldsymbol{\varGamma}} _\varepsilon }$为能量通量；${{\boldsymbol{S}}_{{\text{en}}}}$为能量源项，ECR放电模型的能量源为微波；${\boldsymbol{Q}}$为外部输入的电子能量；${{\boldsymbol{Q}}_{{\text{in}}}}$为内部生成的电子能量；$q$为电子电荷量。

其中，电子通量和能量通量的计算式

式中，$ \text{ }{{\boldsymbol{\mu}} }_{\text{e}} $为电子迁移率；${{\boldsymbol{D}}_{\text{e}}}$为电子扩散系数；$ {{\boldsymbol{\mu}} }_{\varepsilon } $电子能量迁移率； ${{\boldsymbol{D}}_\varepsilon }$为电子能量扩散系数，其关系为：

为了简化计算，假设等离子体在整个放电腔内是均匀的，并且电子能量依照麦克斯韦分布，当ECR等离子体达到平衡时，抽取等离子体内的电子，电子发射电流密度${J_{{\text{em}}}}$和电子发射电流${I_{{\text{em}}}}$由Boltzmann关系确定^[12]，假设电子从开放的等离子体表面发射，则发射方程：

式中，${S_{\text{e}}} = \pi r_{\text{e}}^2$为电子发射口面积，${r_{\text{e}}}$为电子发射口半径。

热电子电流密度${J_{{\text{em}}}}$：

式中，${j_{{\text{ex}}}}$是等离子体中电子电流密度，${\varphi _{{\text{pl}}}}$和${\varphi _{\text{c}}}$分别是放电系统中等离子体电位和收集极电位，$k$是Boltzmann常数，${T_{\text{e}}}$ 是电子温度。

电子电流密度${j_{{\text{ex}}}}$：

式中，$e$为电子电荷量，${n_{\text{e}}}$为等离子体中的单位体积内的电子数，即电子密度，${m_{\text{e}}}$为电子的静止质量。

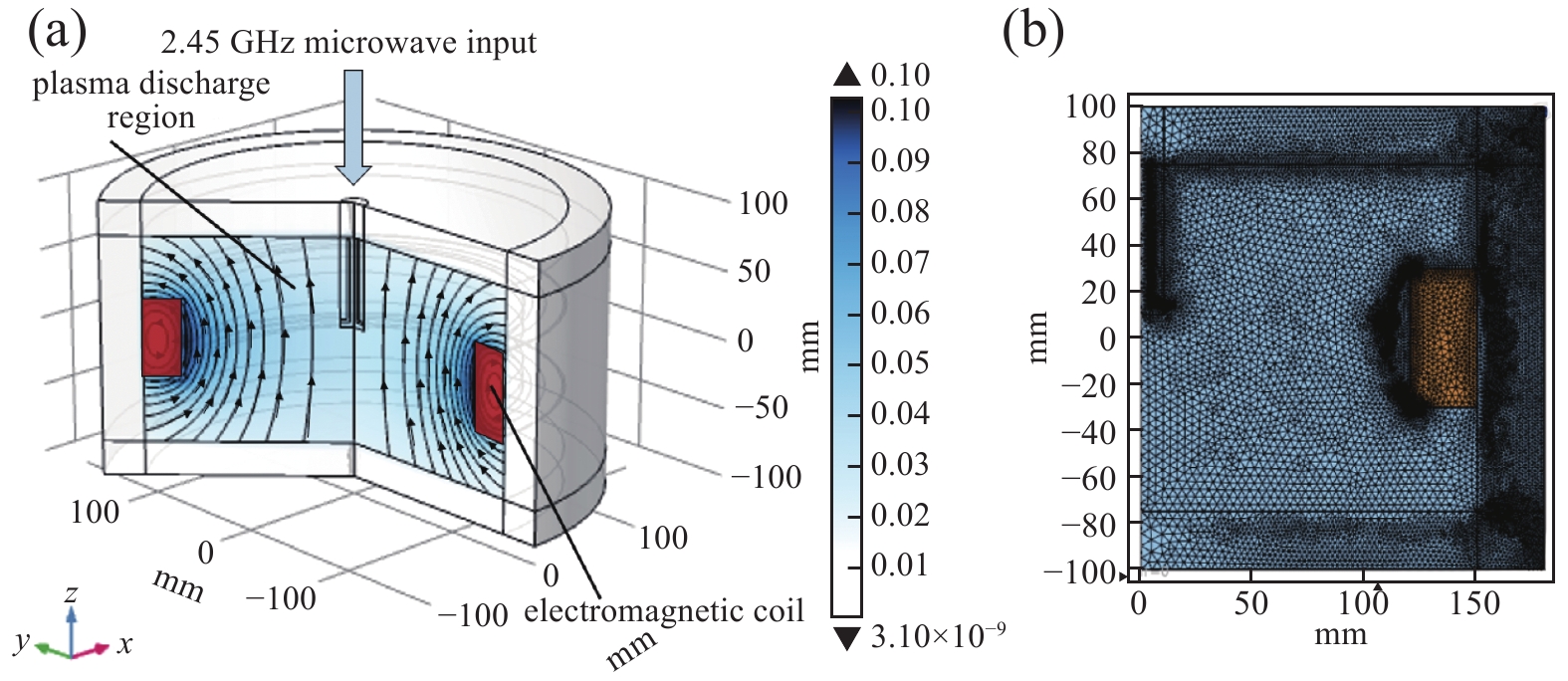
ECR等离子体放电系统几何图形是以圆柱坐标（z，r）设立的对称几何体。该装置为Φ300×Φ150 mm的腔体，这一空心腔体是氩气放电的区域。设置环状的电磁线圈域，线圈的位置和线圈电流决定了磁场的分布情况。中间是输入微波的同轴电缆。其装置尺寸见表2。

放电装置的结构与磁场分布如图1（a）所示，为了达到ECR共振条件所需的磁感应强度${B_{{\text{res}}}}$≈875 Gs，线圈匝数为5000匝，通过线圈的电流为2.0A，计算得出最大磁感应强度大于1000 Gs，满足ECR共振条件所需的磁感应强度要求。

2.45 GHz微波从放电系统顶部，半径为10 mm的同轴电缆中输入至放电腔内，为了使磁场强度最大的区域落在放电区域中部，设置尺寸为10 mm×60 mm的线圈域，线圈域和同轴电缆的材料设置为铜。其余区域为空气域。

设定电磁波、电磁场，与等离子体模型中的粒子密度、温度参数进行耦合，形成由电磁波加热，电磁场共振的宏观等离子体反应模型，该模型通过COMSOL Multiphysics进行求解，求解模型的网格如图1（b）所示，分区域划分为：内壁面边界采用1.5 mm边界网格、微波同轴电缆区域采用1 mm三角形网格、微波输出端边界采用0.5 mm边界网格，靠近共振点的区域采用自适应细化边界网格，ECR腔体和其他区域采用预定义的细化或超细化三角形网格。

为了降低真空度对电子轨迹的影响，ECR等离子体放电系统中的工作气压不宜过大。取微波功率为100 W，工作气压取0.005、0.01、0.02、0.04 Pa进行仿真计算，研究放电特性。

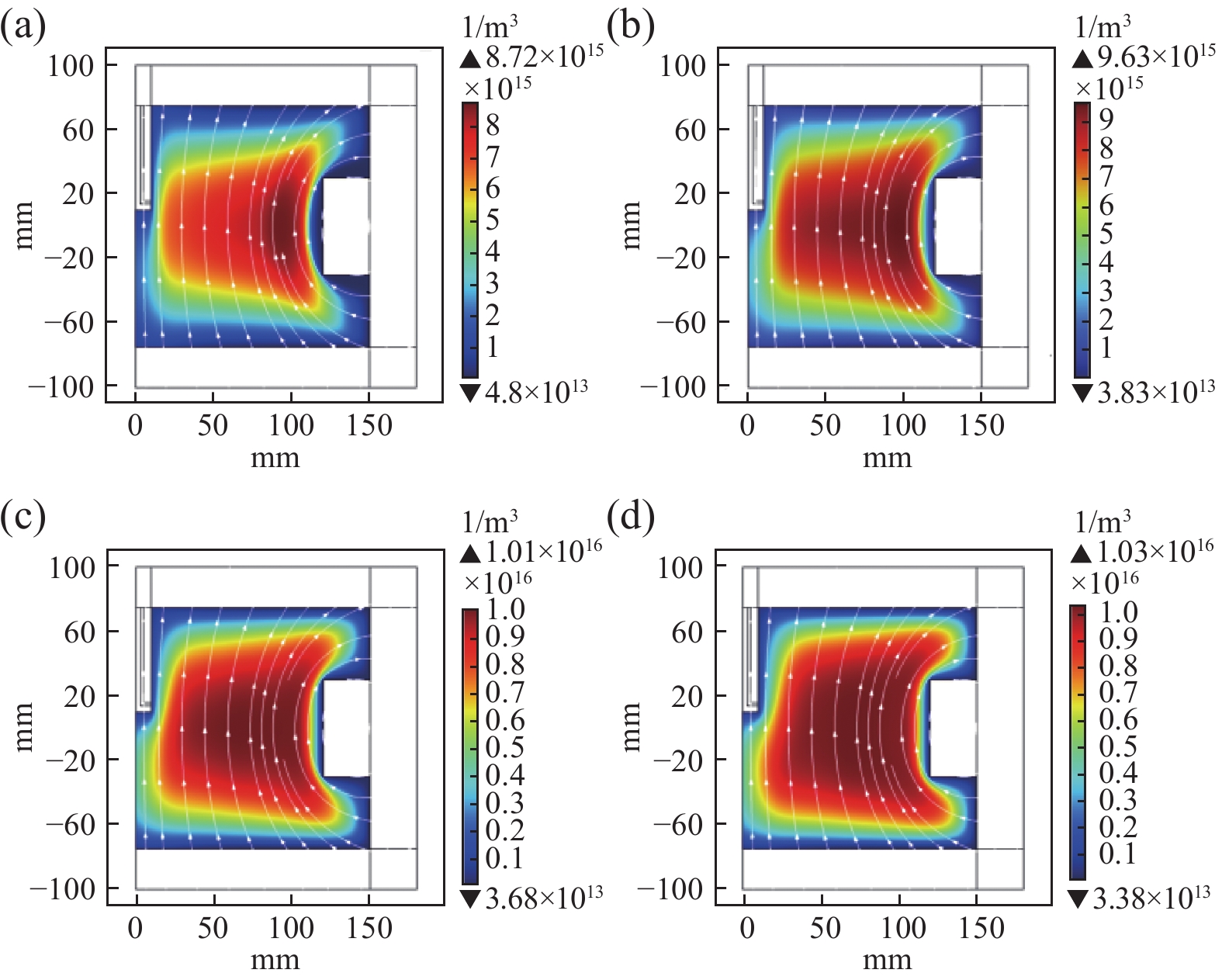
不同工作气压下电子密度如图2所示，电子密度峰值分别为8.72×10¹⁵ m⁻³、9.63×10¹⁵ m⁻³、10.0×10¹⁵ m⁻³、10.03×10¹⁵ m⁻³。

由图2可知，电子密度在径向和轴向均存在显著的密度梯度，其分布与磁场线形状基本吻合。证明在该区域内，微波和作回旋运动的电子间发生共振，继续电离周围的气体分子。

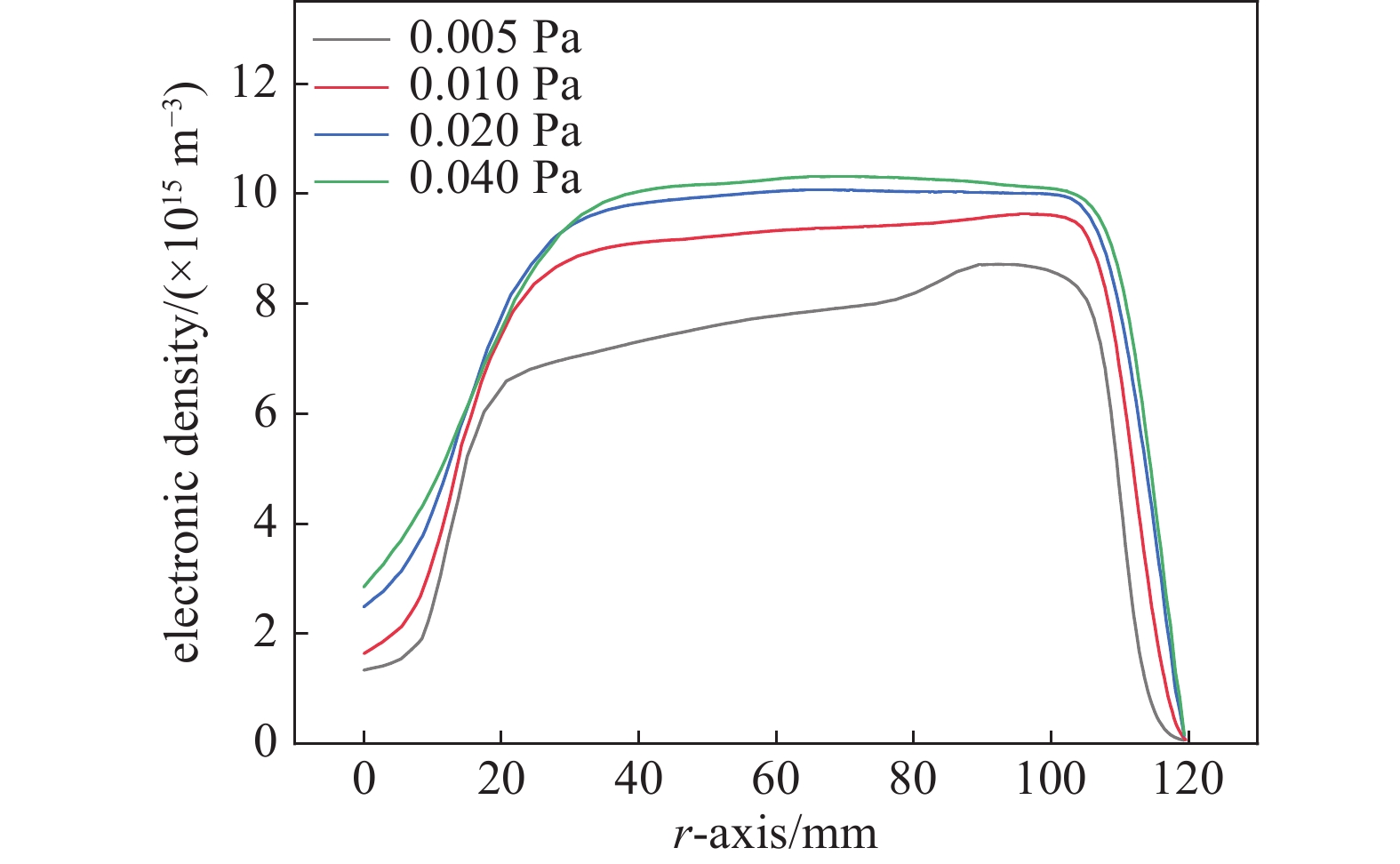
不同工作气压下放电系统中部（0，r）电子密度沿径向距离分布如图3所示。在相同的位置下，工作气压越高，电子密度越高；不同工作气压下，磁场位形和微波功率分布保持相对稳定，电子密度沿径向距离的分布趋势相似。

对比不同工作气压下的电子密度可以发现，随着气压增加，电子密度更高的区域向更广泛的区域扩展。高气压使电子和中性气体分子碰撞频率增加，电子密度提高。然而，在气压继续增加时，碰撞频率增大，能量损失加重，导致电子密度增加迟缓。

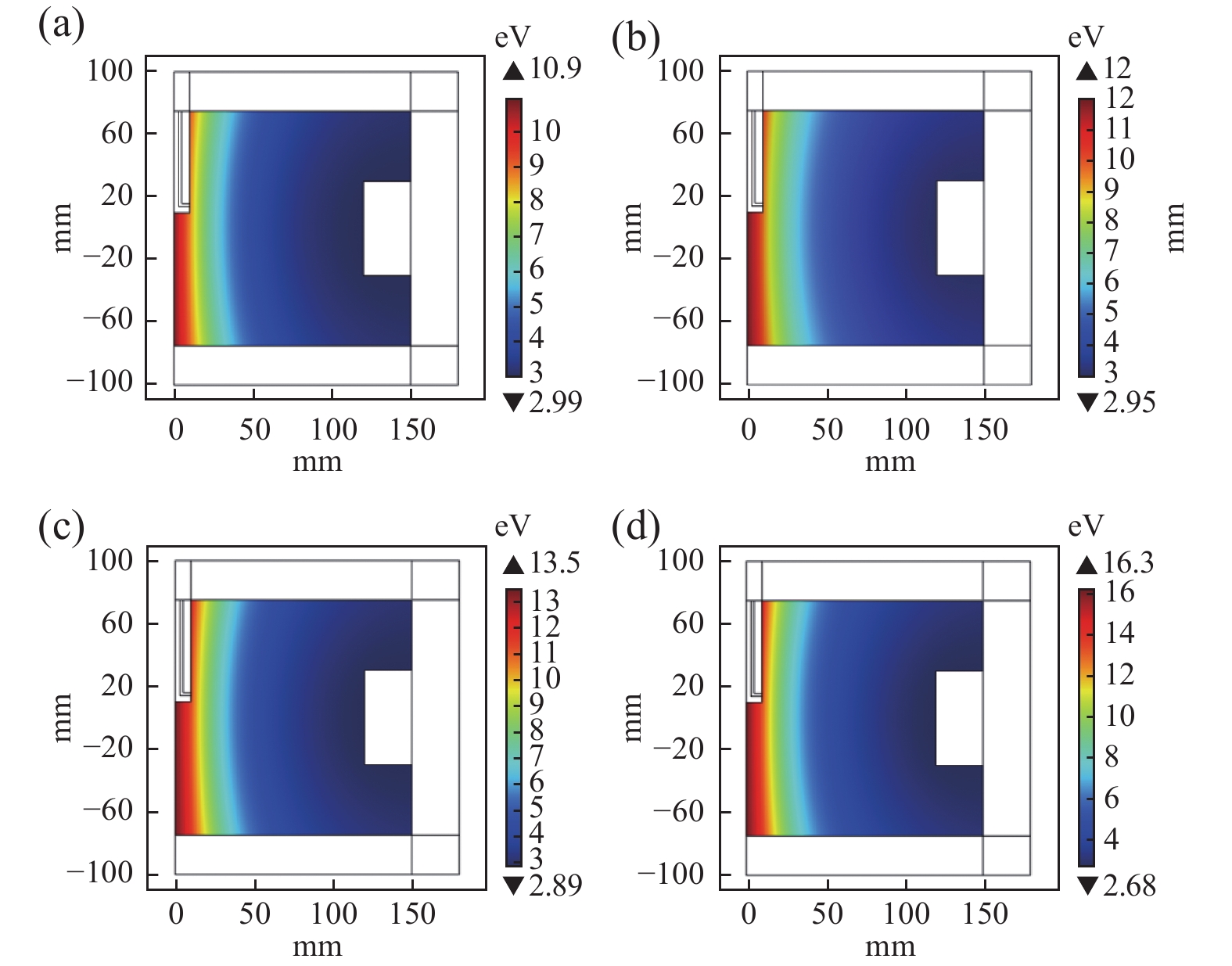
不同工作气压下电子温度对应的能量分布情况如图4所示，是电子温度乘以Boltzmann常数（$k{T_{\text{e}}}$）表示的能量，峰值分别为10.9 eV、12 eV、13.5 eV、16.3 eV。

由图4可知，电子温度沿腔体径向向外逐渐递减，高温电子集中靠近微波能量的输入端。当微波进入等离子体时，电子吸收部分能量，由于越靠近共振点，电子间碰撞越剧烈，能量沿着径向逐渐耗散，电子温度减小。

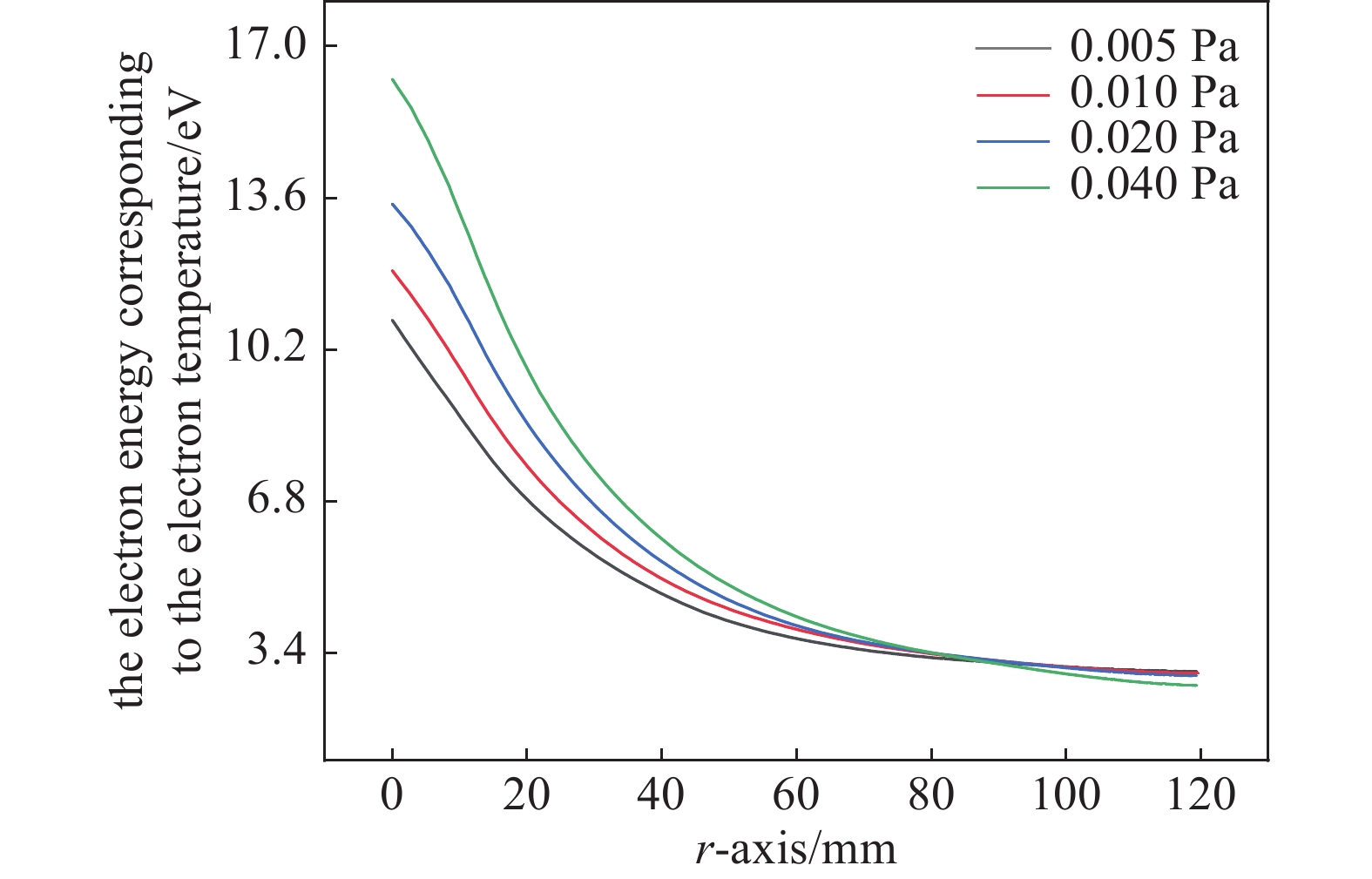
不同工作气压下放电系统中部（0，r）电子温度沿径向距离分布如图5所示。随着气压增加，高温区域会扩大和增强，但由于磁场条件没有变化，电子温度的变化维持在相对恒定的水平。

在不同气压下，电子温度分布比较均匀，远离微波输入端的区域保持低温，随着气压增大，温度梯度变得更大，由此可知，此处局部加热效应更强。

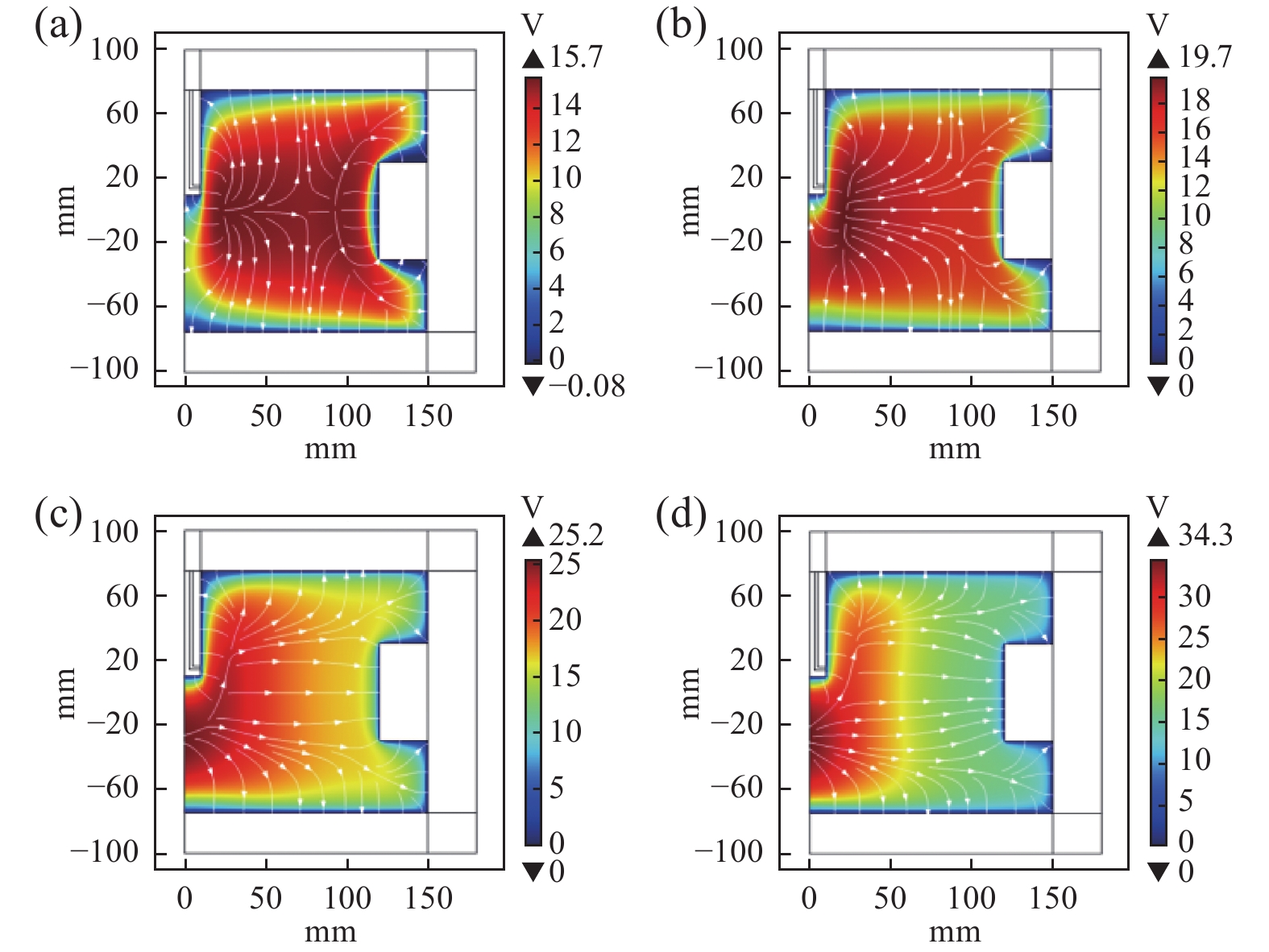
不同工作气压下等离子体电势分布情况如图6所示，电势峰值分别为15.7 V、19.7 V、25.2 V、34.3 V。

由图6可知，由于微波在腔体中央输入，在微波输入附近，由于微波能量沉积和局部加热效应显著，电势较高；随着气压增加，电子碰撞频繁，能量传输变得更为局部化，导致电场从较为均匀分布向局部化增强转变，远离输入区域的电子能量较低，电势也较低。磁场分布对电子运动轨迹的限制，以及空间电荷效应的增加，进一步加剧了电场和电势梯度的增强。

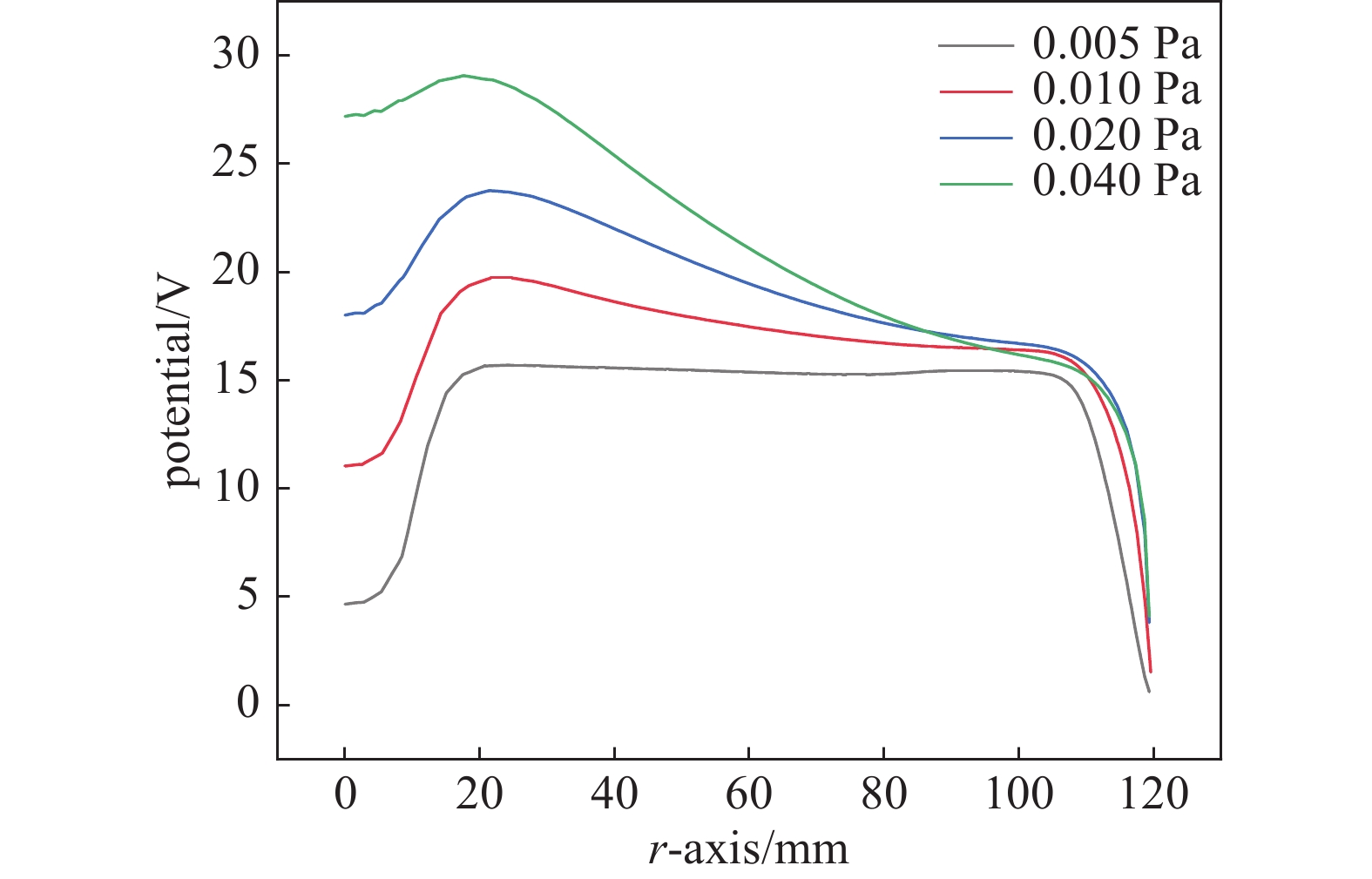
不同工作气压下放电系统中部（0，r）电子温度沿径向距离分布如图7所示。随着气压的增加，电势峰值逐渐升高，高电势区域逐渐扩展。

气压增加时，电子与中性粒子的碰撞增多，导致能量损耗增加，但同时电场的作用也增强，因此电势逐步升高。这是由于较高气压下，更多的电子被局部加热并且形成更强的电场。不同工作气压下的电势分布表明，由于气压增大时碰撞频率的提升导致的电荷积累效应增强，使得等离子体中的电势差和电场强度增大。

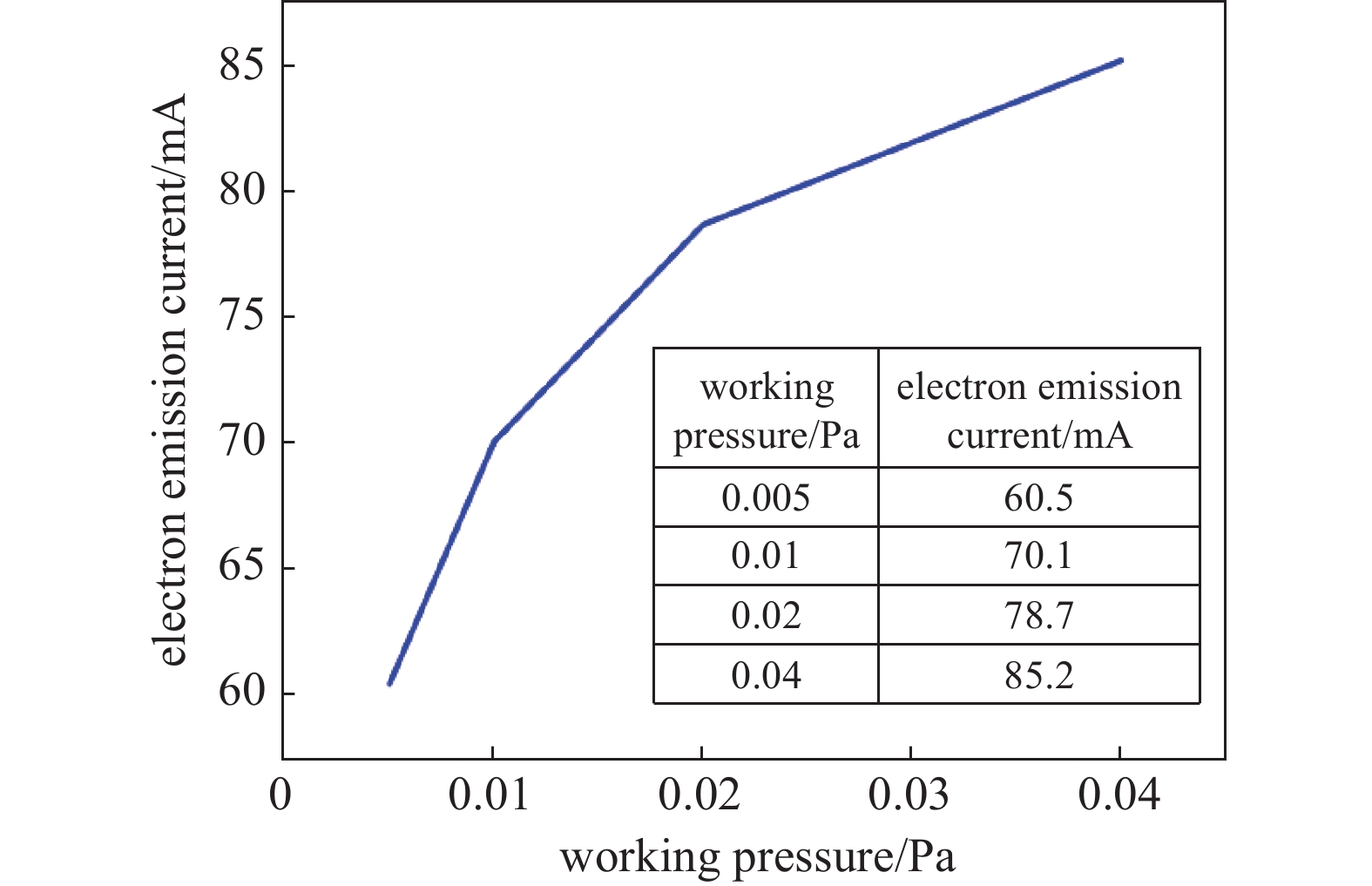
通过ECR放电系统释放出的电子电流即电子发射电流。随着阴极电子发射电流的增加，发射出的电子数量增多，电子束流增大。电子发射电流随工作气压变化如图8所示。

通过仿真分析发现，在工作压力为0.005~0.04 Pa的范围下，可得到的电子发射电流为60.5~80.2 mA，因此，该ECR等离子体放电系统能该气压范围内能产生稳定且足够强的电子发射电流，满足电子枪的束源要求。电子密度峰值在工作气压为0.005~0.015 Pa的区间内变化较为明显。与其正相关的电子发射电流亦然，为了利用改变工作气压的方式控制束流大小，且由于电子枪内电子光学系统和电子束加工室内存在严格的真空度要求，因此在下一步工作中，考虑将工作气压控制在0.01 Pa左右。

仿真结果表示，电子密度峰值从8.72×10¹⁵ m⁻³增至10.03×10¹⁵ m⁻³，电子温度对应的能量峰值从10.9 eV增至16.3 eV，电势从15.7 V增至34.3 V。以上数据表明：随着工作气压增大，等离子体中自由电子束流增多，碰撞频率增加，更多的气体分子被电离，从而产生更多的电子，电子密度亦呈上升趋势。电子温度随着气压增大逐渐上升，表明虽然电子和中性气体分子的碰撞增加，但电子能量并没有显著损失，微波能量能有效地被传递给电子，意味着电子具备更高的能量。电势的增强意味着产生更强的电场，决定了电子束的提取与加速。

适当的工作气压可以在保证电子温度和电势的前提下，产生稳定且高强度的电子束流。因此，选择合适的工作气压能够在保持系统效率的同时，满足电子枪对束源的要求。