首页
登录
注册
-
在真空系统中，为了更快地达到理想的真空度，通常在设计时要求连接管路短而粗。这样做的目的是降低管道的流阻，从而使气体能够快速地被抽走。在多数的真空系统中，真空管道长径比一般不是太大，可以近似的认为管道内的真空压力（本文的真空压力单位均为帕斯卡Pa，表示在界面上，气体作用力的法线分量和受力面积的比值）是均匀分布的。然而在生物医药、科学研究和仪器设备等领域，经常碰到又细又长的真空管道结构，也即大家常说的细长管。在细而长的腔体或管路内，各处的真空压力则不相等甚至相差很大，这种情况下就需要对细长管内的真空压力分布进行专业的分析计算。
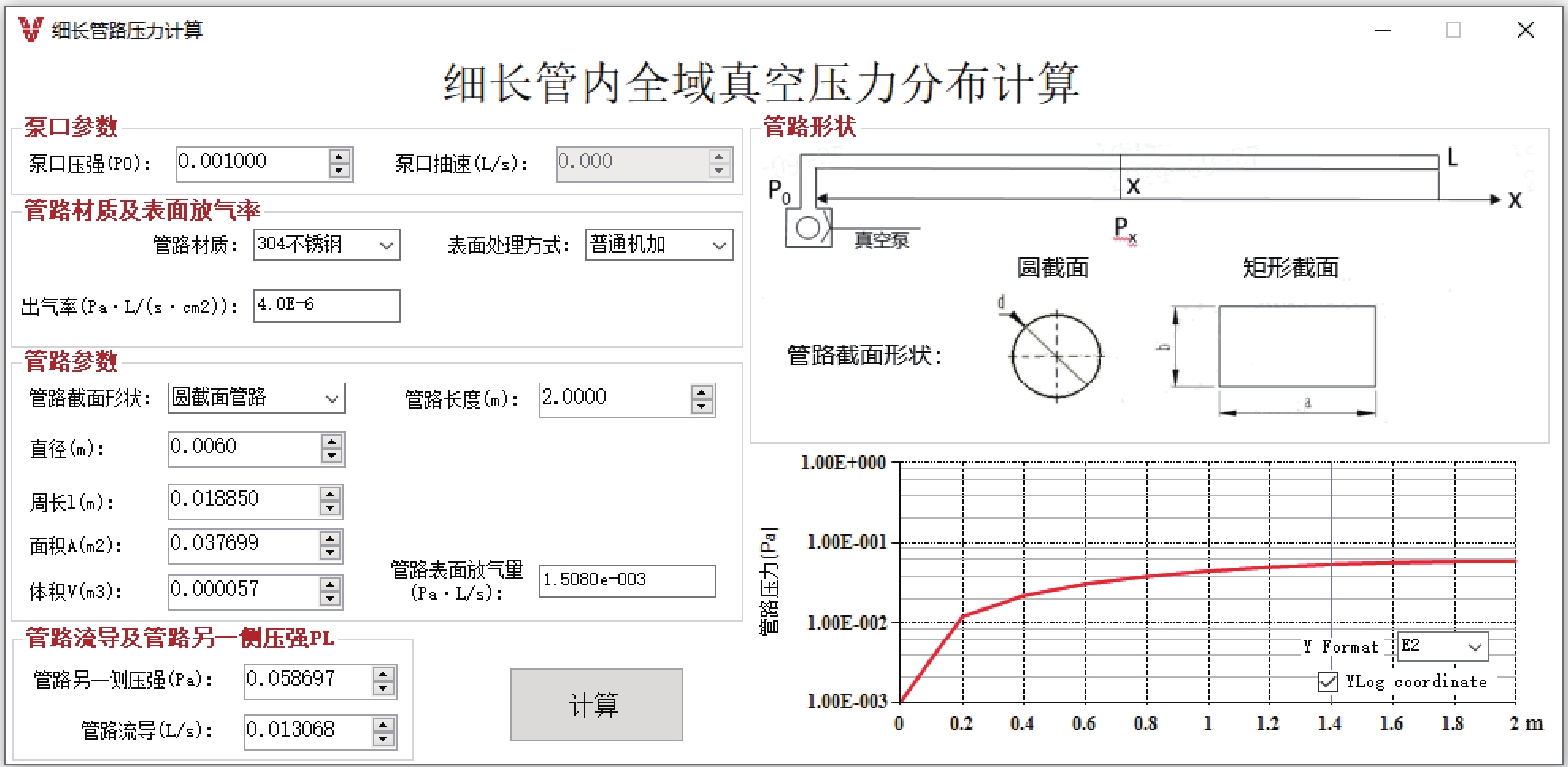
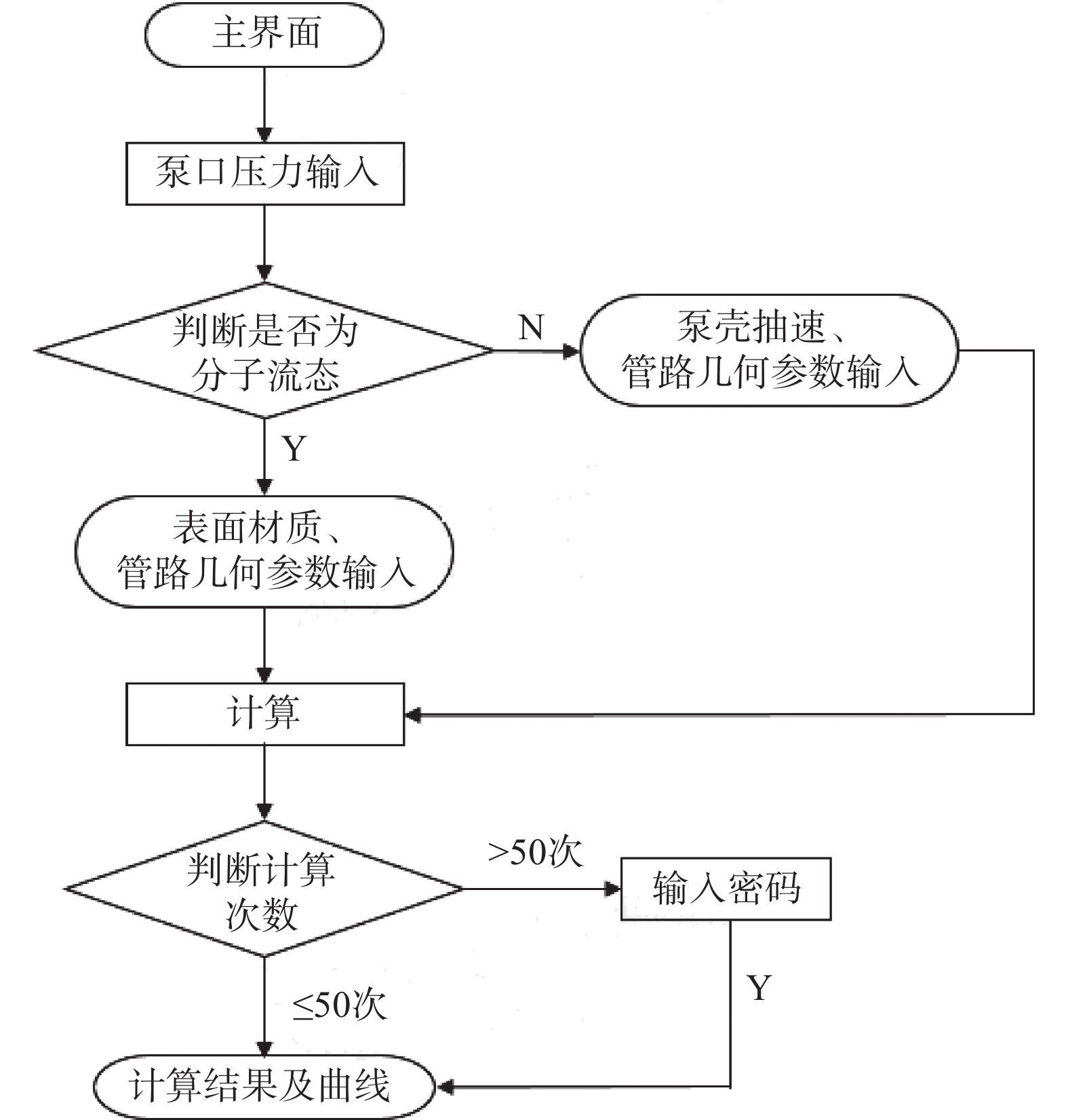
本文在对高中低真空下的气体流动理论推导的基础上，对细长真空元件内的真空压力分布规律进行了研究并得出了系统性的结论。然后针对实际工程当中计算过程复杂，计算耗时较长，管路内压力分布无法测量等问题，进行软件编程计算。并通过Molflow、fluent软件的数值模拟和搭建试验台进行实测验证两种方式，对软件计算法进行了确认和修正，证明本文设计的细长管压力梯度计算算法和软件是有效和可行的。通过本课题的研究得出了细长管内真空压力分布的几个重要规律。通过软件的开发和使用，能够快速得出细长腔体或管路内压力的分布，为解决实际工程问题提供了可靠、便捷的解决办法。
-
气体的流动状态可以分为湍流、粘滞流、过渡流（粘滞−分子流）以及分子流。各种流态之间划分区间并没有完全绝对和准确的界限，对于典型的流态有各自的判别方法，如湍流一般采用雷诺数进行判别，粘滞流和分子流采用气体分子平均自由程与管道的特征尺寸的比值，即克努曾数作为判断依据。真空工程实践中常常也采用简略的方法判别流态，认为高真空管路中流动的气体处于分子流态，低真空管路中的气体处于粘滞流态[1-2]。
-
粘滞流中通常气体分子的数密度较大，可以近似的认为满足连续流体特性，且粘滞流气体出现在高压力、小流速的情况下，通常在低真空管路中发生[1]。此时由于流速较慢，惯性力较小，气体的内摩擦力使得气体各层之间在同一方向的速度不相等，即管路截面速度分布并不相等，管路中心位置气体流动最快，然后沿管路径向逐渐减小，靠近管壁位置认为速度为0。图1为粘滞流态气体在管路中流动的示意图。
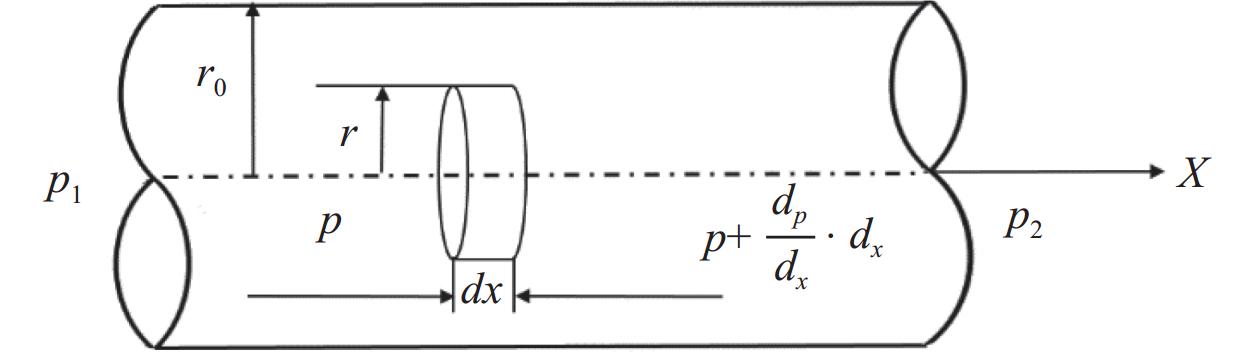
根据流量连续方程，稳定流动状态下，单位时间内流过真空系统任一截面的气量相等，可得：
因此，在已知泵口压力及该压力对应的抽速时，即可计算出总的气流量Q。
根据泊肃叶公式：
其中
$ \overline{p}=\frac{p_1+p_2}{2} $ ，$ \frac{\pi}{8}\frac{r_0^4}{\eta}\cdot\overline{p} $ 为圆截面长管流导U，η为气体黏滞系数，将管道半径用直径D代替后可得：根据连续性方程，流体稳定流动时，同一时间内流过管路任一截面的质量流量相等。通过对截面上流过的气体质量进行积分可得到流过整个截面的气体质量流量[3]：
式中
$ \frac{\mathrm{d}p}{\mathrm{d}x} $ 是管路横截面处的压力梯度，r0为管路半径。利用气体状态方程将ρ用P、T形式表达可得：式中
$ \mu $ 为气体摩尔质量，将式（4）中的ρ用式（5）代替后可改写成：根据稳定流动的特性，同一时间内，流过任一截面的M相等，式（6）中除
$ p\frac{\mathrm{d}p}{\mathrm{d}x} $ 外均为常数，因此：对上式进行积分x由0积到l可得到管路各位置x处的压力。
K为常数，从式（9）可已看出管路内的压力分布沿管道轴线方向呈抛物线形。
-
当细长真空系统元件中的气体处于分子流态，且分子运动处于动态平衡时，在不考虑漏气量、渗气量且无反应气体产生时，总气载量：
其中q为材料的表面放气率，与材料的表面处理工艺相关，A为细长真空系统元件的表面积。
根据均匀出气的细长真空腔室内的压力分布：
式中L、l为管路几何参数，分别为管路总长度和形状截面周长；U是流导，代表管道通气能力的大小；S是泵入口侧的有效抽速。
当真空系统元件中的气体处于动态平衡时，材料表面的放气量就等于泵端抽走的气载量：
将式（12）中的S表示为与q、l、L及p0相关的表达引入（11）后，可得细长管路内压力随位置的变化关系。
管路两端的压差：
从式（13）得出，在细长真空系统元件中，管路内的压力分布呈抛物线形。从式（14）得出，在该类真空系统中，管路两端的压差与管路形状、长度有关，与泵的抽速无关。
-
本文在理论推导及程序计算之外，还通过采用不同流态下适用的仿真软件，对细长管内的压力分布进行了计算机数值模拟，并对程序计算结果与数值模拟结果进行了对比，达到验证程序计算准确性的目的。
-
图4为数值模拟建立的细长管真空系统模型。管路长度为L，内径为D，泵口压力为p0，细长管远端压力为pL，流体介质为20℃空气。
-
分子流采用Molflow软件进行模拟，该软件是基于蒙特卡洛模型开发的一款用于计算任意形状腔体在高真空下的真空度的软件[4-7]。本文采用三维结构进行仿真。假设气体在表面均匀分布，且入射角度遵循朗伯余弦定律。入、出口边界条件设置如表1。
-
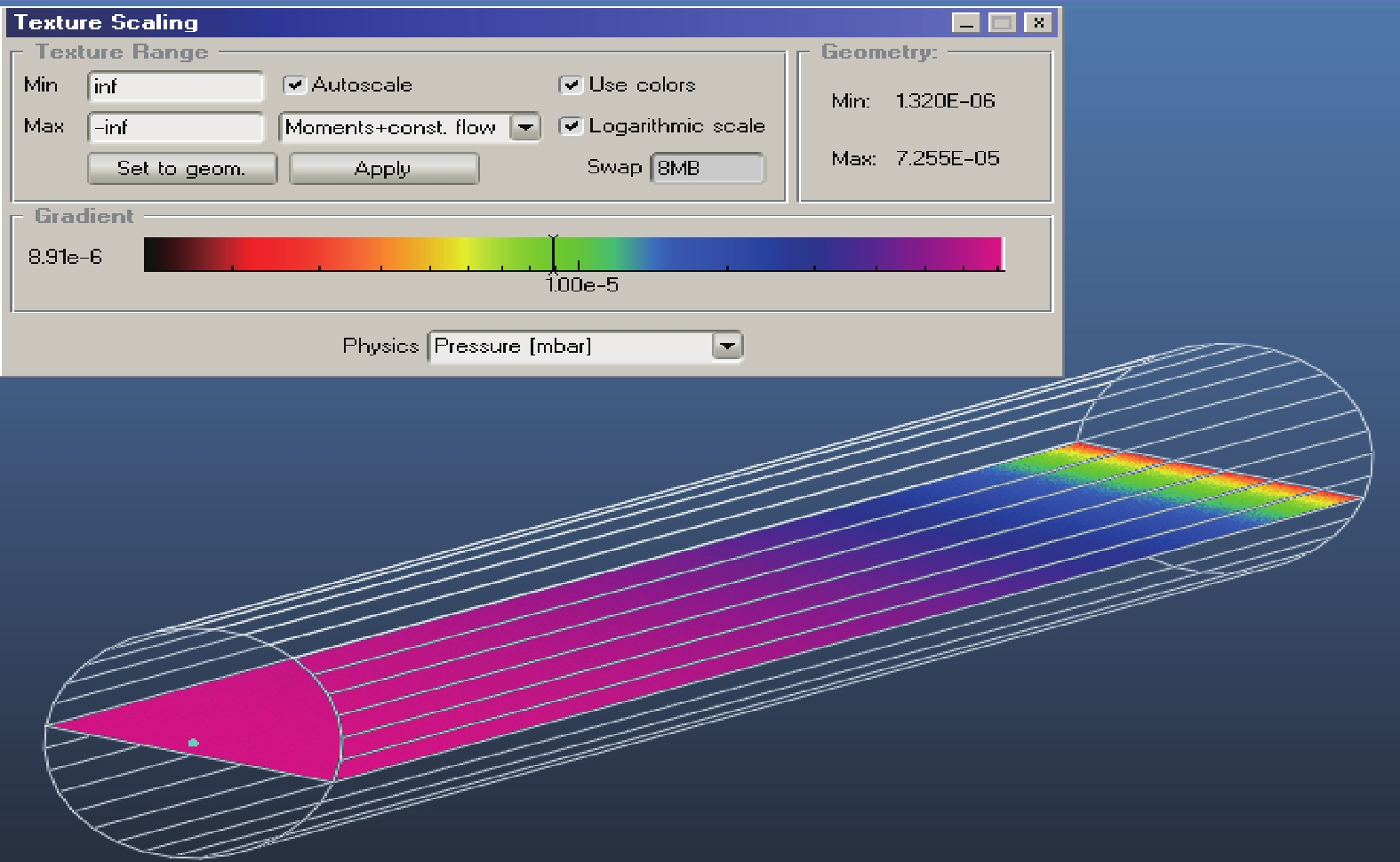
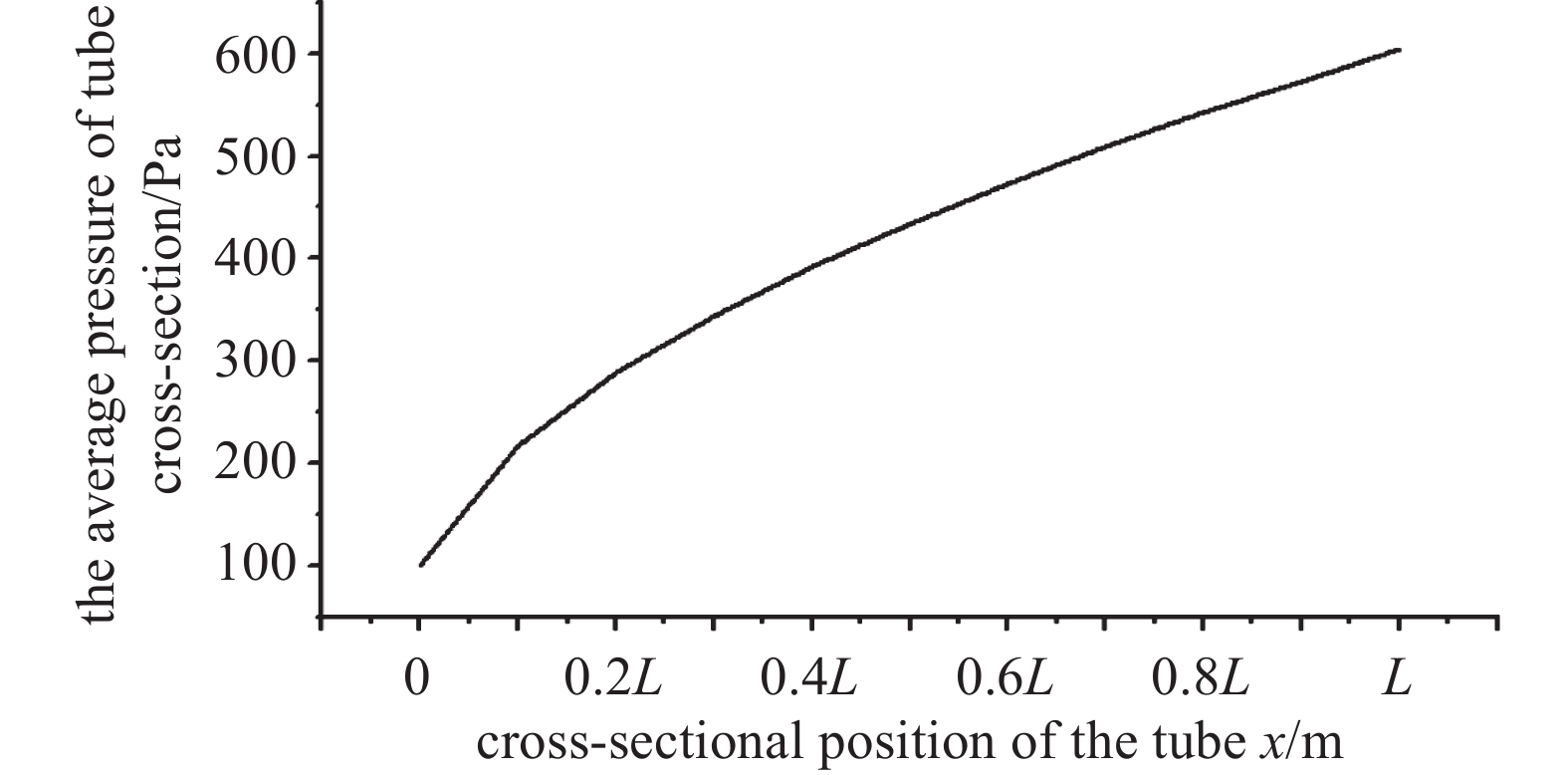
管路直径0.016 m，长度1.8 m，泵侧压力为2.9×10−4 Pa时，管路中截面压力分布云图，如图5所示。从图5可以看出，管路内的压力分布并不均匀，且管路长度方向的压力梯度的变化也不均匀。离泵口的距离越近，压力梯度越大。
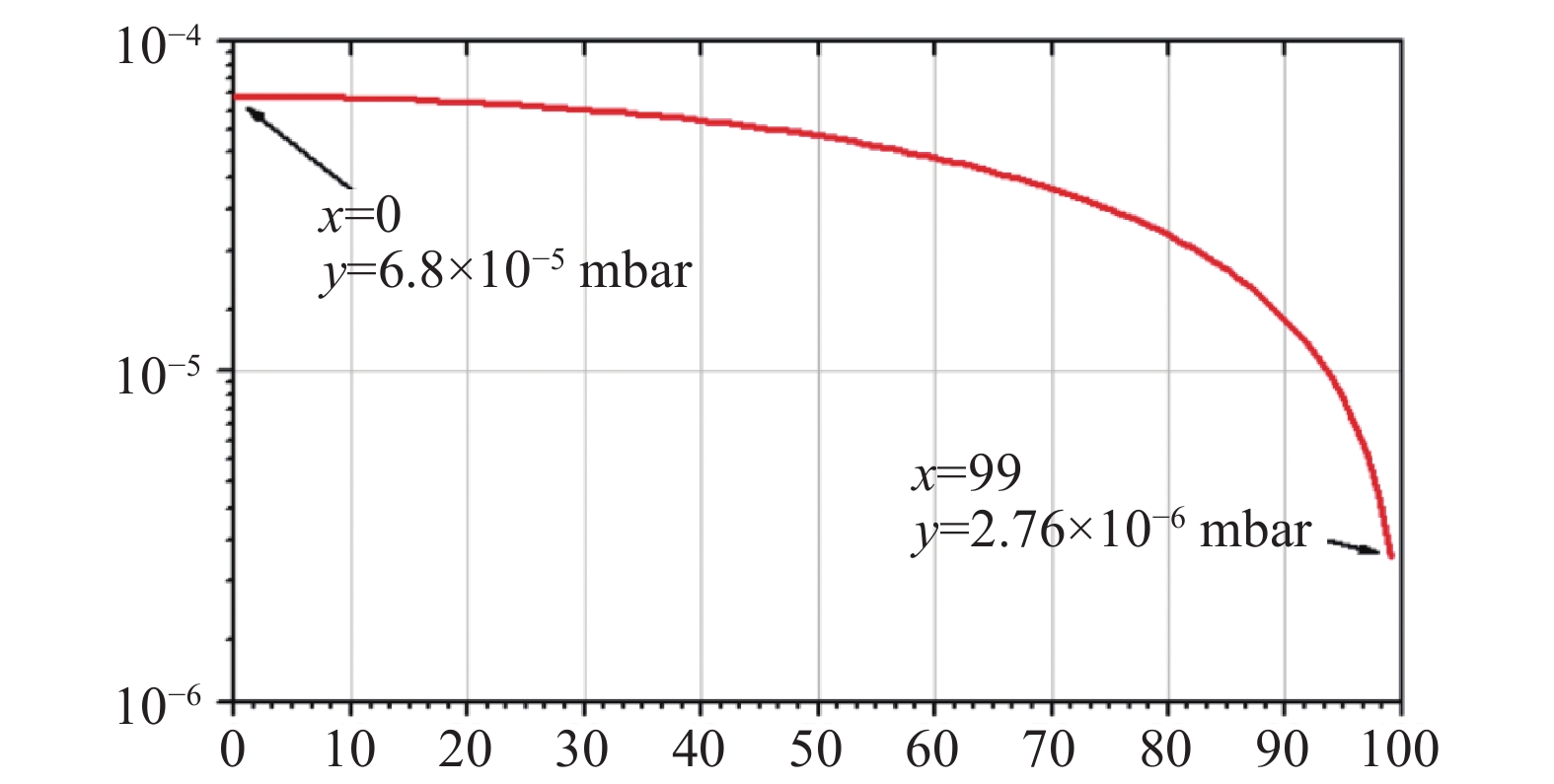
管路中截面压力分布曲线如图6所示。管路内压力分布呈抛物线形，与理论分析一致。从曲线斜率的变化可以看出，泵的抽空能力主要影响靠近泵口侧管路内的真空度，管路越长、末端离泵口越远，影响越小。
-
管路x=L处截面平均压力pL如表2所示。不同的管路参数时，数值模拟结果与程序计算结果均匹配良好。
从结果上来看，管径相同，管路越长，两端的压差越大；管路长度相同，管径越小，两端压差越大。管路长度增加到原始长度的10倍时，两端压差增加到约100倍；管径缩小到原来的一半，两端压差增加到近4倍。
管路参数相同，泵入口侧压力不同时，管路两端的压差不变。
-
粘滞流态管路中的气体压力分布采用fluent软件进行模拟[8-11]，模拟方法为求解N-S方程。选用二维轴对称模型进行计算，边界层层数15层。入、出口边界条件设置如表3。其中管路x=L处的流速由泵口的抽速计算而来。
-
管路直径D为0.012 m，长度L为5 m，泵口压力为100 Pa，泵口抽速为0.01 m3/s时，管路内压力分布云图如图7所示。
将管路沿长度L方向平均切分为10段，共划分了9个截面，将管路沿轴线截面压力处的平均压力绘制成曲线，如图8所示。从曲线可以看出，管路内压力梯度在靠近泵侧最大，且随着管路的长度的增加逐渐减小。
-
管路x=L处截面平均压力pL如表4所示。三种不同的管路参数时，数值模拟结果与程序计算结果误差在3%以内，两种计算方式匹配良好。
-
本文还通过实验设备，对细长管两端的压差进行了测试。实验设备如图9所示。真空泵采用CBVAC中科九微的两款分子泵，型号分别为JFB-100/301脂润滑一体式分子泵和JZB-160/500直排大气分子泵。连接方式为分子泵排气口通过真空管道连接一个前级泵；分子泵进气口通过一个三通分别连接细长管样品和真空规计1，该真空规计用于测量泵口侧的真空度；细长管的末端连接另一个真空规计2，该真空规计用于测量细长管末端的真空度。选用两种不同尺寸的细长管进行实际测试验证，尺寸参数分别为，细长管规格1：D=0.016 m，L=1.8 m；细长管规格2：D=0.025 m，L=2.5 m。
-
实测结果如表5所示。
-
三种测量（计算）方式在相同的泵口压力及气载量下，结果对比如表6所示。三种测量（计算）结果误差在可接受范围内。
-
本研究通过理论计算、数值模拟和实验测量等方法，系统研究了细长真空管内的压力分布规律，并开发了相应的工程计算软件。主要结论如下：
（1）分子流态下，细长真空元件两端压差仅取决于气量及管路几何参数（截面形状和长度），提升泵抽速对改善压差并无作用，需要避免盲目追求大抽速泵而造成的资源浪费和成本增加。
（2）缩短管路长度和增加管路直径可有效改变管路内压力分布梯度。真空系统设计中，可通过本文算法或计算软件，快速优化管路和泵的配置，提高设计效率和质量。
最后，需要指出的是，本文在研究分子流态时，忽略了管道的渗透气量以及可能存在的微小漏气量，理论计算会存在一定的偏差，这个在实际运用中还需要进一步具体研究。
细长管内真空压力分布的算法研究和工程实践
Calculation Algorithm Research and Engineering Practice of Vacuum Pressure Distribution in the Slender Tube
-
摘要: 研究针对细长真空管在实际工况中存在的远端压力计算复杂、耗时较长以及管内压力难以测量等技术难题，采用理论推导、数值模拟与实验测试相结合的方法，系统研究了细长真空管内的压力分布规律。结果表明：细长管两端的压差与管路的几何参数相关；且细长真空管内的压力呈现典型的抛物线分布特征，其中泵口侧压力梯度变化最为显著；通过缩短管道长度或增大管径可有效优化管内压力分布。研究成果为真空系统的优化设计提供了理论依据和技术支撑，对提高抽气效率、优化细长管内的真空压力分布以及保证工艺一致性具有重要的工程应用价值。Abstract: This paper focuses on issues such as the complexity and time-consuming calculation of the pressure at the end of a slender vacuum tube in actual working conditions, as well as the inability to measure the pressure inside the tube. Through three methods including software programming calculation based on theoretical derivation, numerical simulation, and experimental test, the pressure distribution law within the slender vacuum tube is investigated. The results show that the pressure difference between the ends of the slender tube is related to the geometric parameters of the slender tube, and the pressure distribution in the slender vacuum tube presents a typical parabolic distribution characteristic, in which the pressure gradient on the pump port side changes most significantly; the pressure distribution in the tube can be effectively optimized by shortening the length of the tube or increasing the diameter. The results of this research provide a theoretical basis and technical support for the optimal design of the vacuum system and have important engineering application value for improving pumping efficiency, optimizing the vacuum pressure distribution in the slender tube, and ensuring the consistency of the process.
-
Key words:
- Slender tube /
- Pressure distribution /
- Pressure gradient .
-
-
图 1 气体处于粘滞流态在管路中流动的示意图
Figure 1. The schematic diagram of gas flow in the tube in viscous flow
图 5 D0.016-L1.8管路中截面压力分布云图
Figure 5. The distribution contour of pressure on cross section of tube D0.016-L1.8
图 6 D0.016-L1.8管路中截面压力分布曲线
Figure 6. The distribution curve of pressure on cross section of tube D0.016-L1.8
图 7 管路D0.012-L5压力分布云图
Figure 7. The distribution contour of pressure in slender tube of D0.012-L5
图 8 管路截面平均压力随位置的变化曲线
Figure 8. The curve of the average pressure of tube cross-section varying with position
表 1 入、出口边界条件
Table 1. The boundary condition of inlet and outlet
管路直径
D/m管路长度
L/m表面放气率
q/Pa·L/(s·cm2)泵口压力
p0/Pa0.006 0.15 4×10−6 1×10−3 0.006 1.5 4×10−6 1×10−3 0.012 1.5 4×10−6 1×10−3 0.016 1.8 4×10−6 2.9×10−4 0.016 1.8 4×10−6 2.9×10−3 0.016 1.8 4×10−6 2.9×10−2 
下载: 导出CSV
表 2 分子流态数值模拟与程序计算对比
Table 2. Comparison of numerical simulation and program calculation in molecules flow
管路直径
D/m管路长度
L/m泵入口侧压力
p0/Pa数值模拟结果
pL/Pa程序计算结果
pL/Pa程序计算
pL−p00.006 0.15 1×10−3 1.319×10−3 1.325×10−3 3.250×10−4 0.006 1.5 1×10−3 3.398×10−2 3.345×10−2 3.245×10−2 0.012 1.5 1×10−3 9.014×10−3 9.113×10−3 8.113×10−3 0.016 1.8 2.9×10−4 6.789×10−3 6.862×10−3 6.572×10−3 0.016 1.8 2.9×10−3 9.376×10−3 9.472×10−3 6.572×10−3 0.016 1.8 2.9×10−2 3.550×10−2 3.557×10−2 6.572×10−3
下载: 导出CSV
表 3 粘滞流态数值模拟入、出口边界条件参数
Table 3. The boundary conditions of inlet and outlet for numerical simulation of viscous flow
管路直径
D/m管路长度
L/m泵口压力
p0/Pa管路x=L流速
m/s泵口抽速
m3/s0.006 0.15 120 22.6 0.001 0.006 1.5 120 9.01 0.001 0.012 5 100 14.6 0.01 0.016 1.8 1000 41.9 0.01
下载: 导出CSV
表 4 粘滞流态数值模拟与程序计算对比
Table 4. Comparison of numerical simulation and program calculation in viscous flow
管路直径
D/m管路长度
L/m泵入口侧
压力p0/Pa泵口抽速
m3/s数值模拟
结果pL/Pa程序计算
结果pL/Pa0.006 0.15 120 0.001 190.4 187.4 0.006 1.5 120 0.001 467.1 470.1 0.012 5 100 0.01 604.6 608.2 0.016 1.8 1000 0.01 1211.7 1187.4
下载: 导出CSV
表 5 不同长度细长管时两端压力/Pa
Table 5. Two side pressure of slender tubes with the different width
细长管参数/m 泵口压力p0/Pa 远端压力pL/Pa 抽空时间/min D=0.016，L=1.8 2.9×10−4 6.3×10−3 20 D=0.025，L=2.5 4.3×10−3 1.5×10−2 5
下载: 导出CSV
表 6 实测结果、程序计算、数值模拟结果对比
Table 6. The result comparison among experiment test, program calculation and numerical simulation
细长管
参数/m泵口压力
p0 /Pa实测远端
压力pL/Pa程序计算远端
压力pL/Pa数值模拟远端
压力pL/PaD=0.016，L=1.8 2.9×10−4 6.3×10−3 6.86×10−3 6.79×10−3 D=0.025，L=2.5 4.3×10−3 1.5×10−2 9.49×10−3 9.55×10−3
下载: 导出CSV
-
[1] 达道安. 真空设计手册第三版[M]. 北京: 国防工业出版社, 2004 (in Chinese) Da D A. The third edition of vacuum design manual[M]. Beijing: National defence industrial press, 2004 [2] 刘金策. 基于fluent的真空系统元件气体流动模拟计算方法的研究[M]. 沈阳: 东北大学, 2010 (in Chinese) Liu J C. A study on calculation method of vacuum system components gas flow simulation based on fluent[M]. Shenyang: Northeastern University, 2010 [3] 王宝霞, 张世伟. 真空工程理论基础[M]. 沈阳: 东北大学, 2011 (in Chinese) Wang B X, Zhang S W. Theoretical basis of vacuum engineering[M]. Shenyang: Northeastern University, 2011 [4] 张波, 王洁, 尉伟, 等. 蒙特卡洛计算分子流态下真空管道的传输几率[J]. 真空科学与技术学报,2014,34(6):571−574 (in Chinese) Zhang B, Wang J, Wei W, et al. Monte carlo calculation of transmission probability in vacuum tube under molecular flow conditions[J]. Journal of vacuum science and technology,2014,34(6):571−574 [5] 张世伟, 姬国钊, 韩进, 等. 气体分子以分子流态通过直圆管道时的位置分布计算[J]. 真空科学与技术学报,2010,30(6):626−631 (in Chinese) Zhang S W, Ji G Z, Han J, et al. Calculation of positional distributions of molecular flux at orifice of cylindrical pipe[J]. Journal of vacuum science and technology,2010,30(6):626−631 [6] 隋吉秋. 空间环境模拟器真空抽气过程的计算研究[M]. 沈阳: 东北大学, 2016 (in Chinese) Sui J Q. Computational study on the vacuum pumping process in a space environment simulator[M]. Shenyang: Northeastern University, 2016 [7] 牟如意, 张世伟, 张志军, 等. 涡轮分子泵入口接管束流效应的蒙特卡洛计算[J]. 真空科学与技术学报,2017,37(8):753−759 (in Chinese) Mu R Y, Zhang S W, Zhang Z J, et al. Monte carlo simulation of beaming effect of molecular flow via inlet tube of turbo molecular pump[J]. Journal of vacuum science and technology,2017,37(8):753−759 [8] 刘斌. 流体仿真从入门到精通[M]. 北京: 清华大学出版社, 2022 (in Chinese) Liu B. From beginner to proficient in fluid simulation[M]. Beijing: Tsinghua University, 2022 [9] 江帆, 黄瑞. 基于FLUENT 的异径管管内流体流动特性分析[J]. 焊管,2022,45(11):27−30 (in Chinese) Jiang F, Huang R. Analysis of fluid flow characteristics inside reducing pipes based on fluent[J]. Journal of welded pipe and tube,2022,45(11):27−30 [10] 党睿, 王亚丽, 马元博, 等. 气体管内流动相似性的FLUENT数值模拟研究[J]. 榆林学院学报,2018,28(6):56−59 (in Chinese) Dang R, Wang Y L, Ma Y B, et al. Fluent numerical simulation study on flow similarity within gas pipes[J]. Journal of Yulin University,2018,28(6):56−59 [11] 周佳, 朱目成, 巫帅珍, 等. 180°方形截面弯管内流动特性研究[J]. 化工机械,2016,43(2):214−217 (in Chinese) doi: 10.3969/j.issn.0254-6094.2016.02.019 Zhou J, Zhu M C, Wu S Z, et al. Study on flow characteristics within a 180° square-section elbow[J]. Journal of Chemical Machinery,2016,43(2):214−217 doi: 10.3969/j.issn.0254-6094.2016.02.019 -
计量
- 文章访问数: 67
- HTML全文浏览数: 67
- PDF下载数: 0
- 施引文献: 0