高超声速飞行器高速飞行时面临强烈的气动加热, 激波波后流场温度可高几千甚至上万开尔文, 高温气体发生离解、电离产生等离子体, 并沿高速流动向下游扩展, 形成等离子体鞘. 由于等离子体会与电磁场、电磁波相互作用, 影响电磁传输特性和电磁目标特性, 严重影响飞行器远程通信和飞行安全. 因此飞行器等离子体鞘产生机理及其与电磁场相互作用机制, 一直都是人们广泛关注的热点问题.

由于等离子体在电磁场中会受到宏观的洛伦兹力和焦耳热作用, 因此通过电磁场与高超声速流动的相互作用, 向流场输运可控的动量与能量, 可以有效地提升飞行器的气动性能, 这就是磁流体力学(MHD)在高超声速领域的典型运用^[1]. 随着稀土磁工业和高超声速飞行技术的蓬勃发展, 磁流体力学控制在高超声速领域的广阔应用前景引发人们极大的研究热情. 其涉及多个学科交叉领域, 可应用于高超声速飞行器气动控制、气动热环境管理、无线电通信、等离子体隐身、磁流体发电机等多个方面, 受到美国、俄罗斯、日本等航天大国高度重视.

流场中具有一定电导率的等离子体的分布特性, 是其与电磁场耦合作用的关键性因素之一^[2]. 由于高超声速飞行器飞行速度快, 面临较为严酷的气动热环境, 常利用表面烧蚀效应进行防热设计^[3]. 表面材料烧蚀会产生质量引射, 参与流场热化学反应, 改变流场结构, 进而影响高超声速飞行器流场等离子体分布; 与此同时, 烧蚀材料中含有少量碱金属元素, 也会改变流场介质的电磁学特性^[4], 进而影响电磁流动作用效果.

近二十年来, 国内外在高超声速流动与电磁场相互作用方面开展了大量研究, 取得很多有价值的结论, 但大多没有考虑表面材料烧蚀对等离子体的影响. 例如, 2006年, Otsu等^[5]采用完全气体模型模拟简化等离子体环境(无烧蚀及化学反应)及其磁流体控制, 得到了多种条件下磁场强度等对流场结构的影响规律; 2009年, Boettcher^[6]开展了球头高超声速流动与外加磁场作用数值模拟研究, 得到了磁场对气动热环境的影响规律, 其等离子体及其电学特性采用简化近似处理, 无法有效模拟飞行器表面材料特性及其对等离子体的影响; 2013—2016年, Fujino等^[7,8]、Robin等^[9]考虑高温热化学非平衡效应, 开展了地球大气和火星大气再入等离子体环境及其电磁流动研究, 分析了大钝体磁阻力伞和磁控热防护效果, 这项研究没有考虑壁面材料可能存在的烧蚀效应. 2019年, Robin等^[10]开展了钝体高速流场与磁场相互作用的试验研究, 针对无烧蚀表面和中等磁场强度, 进行了磁场对飞行器受热的热防护效果的探讨. 2020年, Daniel等^[11]开展了无烧蚀条件下的磁球体磁阻力试验测量研究, 发现磁阻力与磁场强度呈非线性关系.

高超声速流动表面材料烧蚀效应对等离子体影响及其与磁流体力学控制的耦合研究较为少见. 2011年, Bisek和Poggie ^[12]开展了高超声速钝烧蚀体磁流体力学控制模拟研究, 通过表面烧蚀向流场注入碱金属粒子, 进而改变等离子体的电导率. 但这项研究采用的是简化烧蚀边界, 仅考虑了壁面附近的碱金属的质量通量, 没有考虑表面材料烧蚀引射、质量/能量输运对流场的影响, 也没有考虑流场中烧蚀组分和碱金属粒子的电离反应过程; 其计算状态的磁相互作用数很小, 磁场与流动几乎没有耦合干扰作用, 因此结论的有效性仍有待商榷. 2013—2017年, 柴栋等^[4]、曾学军等^[13]开展了含碱金属烧蚀对高超声速流场特性及其等离子体分布影响的研究, 发现烧蚀材料中的碱金属元素电离使等离子体电子数密度显著增大. 2017年, 李开 ^[14]开展了高超声速钝体磁控热防护试验研究, 发现在一定磁场作用下, 钝体表面材料烧蚀程度明显降低, 热防护效果十分明显, 证实了磁控热防护的有效性.

本文考虑烧蚀产物参与流场等离子体生成过程, 结合含碱金属的混合电离气体导电机理, 建立含碱金属烧蚀等离子体计算方法; 基于导电流体与电磁场相互作用机理, 通过耦合求解带电磁源项的三维热化学非平衡流动控制方程、电场泊松方程、磁矢量泊松方程, 同时考虑高超声速飞行器表面烧蚀引射、壁面微元质量/能量平衡机制, 建立了含碱金属烧蚀的高超声速磁流体力学控制计算方法. 在此基础上, 结合常见的碳-碳材料和硅基酚醛树脂材料烧蚀热解过程, 较为系统地开展表面烧蚀对等离子体的影响及其与电磁场相互作用的研究, 分析烧蚀等离子体的分布变化机理, 得到该条件下流动与电磁场的相互作用规律.

高超声速飞行器飞行过程中, 如果速度较高, 流场中高温气体发生离解和电离. 对于干燥空气, 除中性粒子的离解、置换等反应外, 需要重点考虑的电离机制包括缔合电离反应、碰撞电离和附着电离反应等^[15] (见表1, M为碰撞体), 其他电离反应机制还包括电荷交换、电子交换和互中和反应等. 表1为干燥空气主要电离反应.

如果飞行器采用壁面烧蚀防热设计, 还需要考虑烧蚀产物参与的流场等离子体生成过程. 烧蚀防热材料种类有很多种, 常见的有碳-碳材料和硅基酚醛树脂材料. 对于碳-碳材料, 主要烧蚀产物为C, CO, CO₂等, 进入流场之后, 形成C/N/O的化学反应体系^[16]. 除中性粒子的离解、置换等反应外, 主要电离反应见表2.

对于硅基酚醛树脂材料, 烧蚀热解产物更加复杂, 包括CO, CO₂, H₂O, OH, H₂, CH₂, CH, SiO, Si等, 形成C/H/N/O/Si的化学反应体系. 除表1和表2的主要电离反应外, 还需要额外考虑H的电离反应H + e ⇔ H⁺ + e + e.

由于烧蚀材料含有微量的碱金属(如Na等)杂质会显著改变流场中等离子体分布^[4,13], 因此还需要考虑碱金属参与的电离反应(见表3).

依据化学反应关系(中性粒子反应和电离反应等), 含碱金属烧蚀等离子体第$ i $组分化学生成率$ {w_i} $可写为^[15]

式中$ {N_{\text{r}}} $为化学反应数, $ {M_i} $为等离子体第$ i $组分的分子量(或原子量), $ {Q_j} $为第$ j $个化学反应的摩尔生成率, $ {\gamma _{ij}} $和$ \gamma _{ij}^* $为第$ j $化学反应式中第$ i $组分的反应物和生成物系数.

由于上述反应机制是在流动过程中发生的, 因此存在化学反应的非平衡效应. 通过离解、电离等化学反应非平衡过程的模拟, 得到等离子体流场中各气体组分密度分布, 可直接用于等离子体电导率的计算. 基于多种电离成分碰撞与迁移的导电机理, 空气电离的等离子体电导率可写为 ^[2,14]

当s为离子时, 碰撞频率$ \upsilon _{{\text{e, }}s}^{\text{m}} $为^[2,14,17]

当s为中性粒子时, $ \upsilon _{{\text{e, }}s}^{\text{m}} $为^[2,14,16]

式中$ {k_{\text{b}}} $为玻尔兹曼常数; $ {\varepsilon _0} $为真空介电常数; $ {T_{\text{e}}} $为电子温度; $ {m_{\text{e}}},\; e $为电子质量和电荷; $ {n_{\text{e}}} $和$ {n_s} $为电子和s组分的数密度; $ \sigma _{{\text{e, }}s}^{\text{m}} $为电子与s组分的有效碰撞截面. 研究表明, 在纯空气电离时, 采用(2)式计算的电导率, 与试验结果符合程度最好^[2].

Macheret和Shneider ^[18]发现在电离度较低时, 电导率与气体电离度近似呈正比, 给出了轻电离气体的电导率$ {\sigma _{}} = {\sigma _0}X $, $ X $为气体电离度, $ {\sigma _0} $为电导率系数. 在纯空气时, 电导率系数 $ {\sigma _0} \approx 2.7 \times {10^5} $, 采用这一方法能较为简便地计算出气体电导率, 并与(2)式的计算结果符合较好^[2].

由于目前尚未见到同时包含空气、烧蚀组分和碱金属电离的电导率精准模型及其相关试验测量数据, 因此这里结合上述两种电导率计算方法及其构建原理, 拓展得到混合气体的电导率:

其中$ {X_{{\text{all}}}} $为混合气体电离度, $ {\sigma _{{\text{all}}}} $为混合气体电导率系数. 结合(2)式对$ {\sigma _{{\text{all}}}} $进行标定, 以提升准度$ {\sigma _{{\text{all}}}} = {\sigma _{{\text{air}}}}/{X_{{\text{air}}}} $, $ {X_{{\text{air}}}} $为空气的电离度. 该方法可能不十分精准, 但能在电离度较低时, 近似表达包含空气、烧蚀组分和碱金属成分的电离特征.

由于混合气体电导率与电子温度$ {T_{\text{e}}} $紧密相关, 因此还需要考虑等离子体流动过程中热力学非平衡效应. 由于电子温度与振动温度之间的松弛时间, 远小于平转动温度与振动温度之间的松弛时间, 这里采用双温模型表征热力学变化过程. 电子温度与振动温度达到平衡态, 用统一的振动-电子温度$ {T_{\text{v}}}_{\text{e}} $表达, $ {T_{\text{e}}} \approx {T_{\text{v}}} \approx {T_{{\text{ve}}}} $, 振动-电子能与平转动能之间松弛可写为^[15]

其中$ {\rho _i} $为第$ i $组分密度; $ e_{{\text{V}}i}^ * $, $ e_{{\text{V}}i}^{} $和$ {\tau _{{\text{V}}i}} $分别为第i组分的平衡振动-电子能、非平衡振动-电子能和平转动-振动松弛特征时间.

等离子体与电磁场宏观作用的基本原理在于等离子体具有一定导电性, 当其在磁场中运动时, 会受到宏观的洛伦兹力作用, 其内部感应电流会产生焦耳热作用^[19–21]:

式中, $ {\boldsymbol{F}} $为流体微元受到的洛伦兹力, $ {E_{\text{M}}} $为磁场对流体微元能量输运, $ {E_{{\text{MV}}}} $为磁场对振动-电子模态的能量输运; $ {\boldsymbol{J}} $, $ {\boldsymbol{B}} $和$ {\boldsymbol{U}} $分别为感应电流密度、磁感应强度和流体速度; $ {\boldsymbol{F}} \cdot {\boldsymbol{U}} $表征洛伦兹力做功, $ {{\boldsymbol{J}}^2}/\sigma $为感应电流焦耳热, $ \gamma $为电磁焦耳热作用在气体分子振动-电子能量模态上的比率.

(7)式中${\boldsymbol{J}}$, $ {\boldsymbol{B}} $可通过离散耦合求解电场泊松方程^[21]和磁矢量势泊松方程^[7,22,23]计算:

其中, $ \phi $为电势, $ {{\boldsymbol{A}}_{{in} }} $为磁矢量势, $ {\mu _{\text{e}}} $为磁导率, $ {{\boldsymbol{B}}_{{\text{in}}}} $为感应(诱导)磁场, $ {{\boldsymbol{B}}_{{\text{ext}}}} $为由机载磁场发生装置产生外加磁场.

与常见黏性速度边界不同, 考虑表面材料烧蚀时, 壁面出现法向引射速度:

其中$ {\boldsymbol{n}} $为法向单位矢量. $ {\dot m_{\text{w}}} $为总的质量引射率, 由表面微元的质量关系得到:

其中$ {c_{s, {\text{w}}}}, {\dot m_{s, {\text{w}}}}, {j_{s, {\text{w}}}} $分别为s组分壁面质量分数、净质量生成率和向壁面的扩散通量, $ {\dot m_{\text{g}}} $和$ {c_{s, {\text{g}}}} $分别为材料热解的壁面生成率和s组分质量比例. 烧蚀表面还需满足能量平衡关系:

式中, $ {q_{\text{w}}}, {q_{\text{r}}}, {\dot m_{\text{w}}}{H_{\text{w}}}, {\dot m_{\text{l}}}{h_{\text{l}}}, {q_{\text{c}}}, {\dot m_{\text{g}}}{h_{\text{g}}} $分别为气动加热热流、向外辐射热流、引射能量通量、机械流失能量通量、机体内部热传导热流和材料热解能量通量; $ {\dot m_{\text{l}}}, {H_{\text{w}}}, {h_{\text{l}}}, {h_{\text{g}}} $为机械流失质量率、壁面总焓、 熔化层机械流失焓和热解焓.

对于碳-碳烧蚀材料^[24], 本文主要考虑碳的氧化和升华反应带来的质量和能量变化. 当表面温度在3000 K以下时, 主要考虑的反应为

上述3个反应速率分别为

其中$ {T_{\text{w}}} $为壁面温度, $ {M_{{{\text{O}}_{2}}}}, {M_{\text{O}}} $分别为氧气分子量和氧原子量.

硅基酚醛树脂烧蚀材料^[25]的主要烧蚀机制是酚醛树脂热解和碳硅反应. 本文酚醛树脂热解的主要产物是C₂H₂, H₂O, CO, H₂和CO₂, 质量百分比分别为40.8%, 34.07%, 11.32%, 8.12%和5.69%, 热解速率为$ {\dot m_{\text{g}}} = 10.2{{\text{e}}^{ - 4300/{T_{\text{w}}}}} $; 碳硅反应主要考虑$ {\text{Si}}{{\text{O}}_{2}}{\text{ + C}} \Rightarrow {\text{SiO + CO}} $, 由此带来的质量生成率为$ {\dot m_{{\text{SiO}}}} = {\dot m_{{\text{CO}}}} = 1.25 \times {10^8}{{\rm e} ^{ - 46300/{T_{\text{w}}}}} $.

在烧蚀过程中, 由烧蚀带来的碱金属生成率为$ {\dot m_{{\text{Na}}}} = D/(1 - D)\displaystyle\sum\nolimits_{s \ne {\text{Na}}} {{{\dot m}_s}} $, 其中$ D $为碱金属在烧蚀材料中的质量占比.

通过电磁源项的形式, 引入电磁场对流场的宏观力、热作用, 并考虑热化学非平衡效应, 流动控制方程包括各组分气体密度连续性方程、总密度连续性方程、3个动量守恒方程、总能量守恒方程和振动能量守恒方程, 其无量纲守恒形式可写为^[20]

其中$ {\boldsymbol{Q}} = {({\rho _i}, \rho , \rho u, \rho v, \rho w, \rho {E_{\text{t}}}, \rho {E_{\text{v}}})^{\text{T}}} $, $ {\rho _i} $为第$ i $气体组分密度; $ u, v, w $为直角坐标速度三分量; $ {E_{\text{t}}} $为内能; $ {E_{\text{v}}} $为振动-电子能; $ Re $为雷诺数; $ {\boldsymbol{F}}, {\boldsymbol{G}}, {\boldsymbol{H}} $和$ {{\boldsymbol{F}}_{\text{V}}}, {{\boldsymbol{G}}_{\text{V}}}, {{\boldsymbol{H}}_{\text{V}}} $分别为直角坐标三方向的无黏项和黏性项. $ {\boldsymbol{W}} $为热化非平衡源项, ${{\boldsymbol{W}}_{{\text{MHD}}}}$为电磁作用源项, 其形式为

其中$ {f_x}, {f_y}, {f_z} $为洛伦兹力$ {\boldsymbol{F}} $的三分量; ${Q_{\text{m}}}$为磁相互作用数, 表征了磁场与流动耦合作用效果, $ {Q_{\text{m}}} = {\sigma _{0}}B_0^2 L/({\rho _0}{u_0}) $, 其中$ {\sigma _{0}} $, $ B_0^{} $, $ L $, $ {\rho _0} $和$ {u_0} $为电导率、磁感应强度、作用尺度、密度和流速特征量.

将(1)—(7)式代入(13)式, 耦合求解流动控制方程(13)、电磁场方程(8)和烧蚀边界方程(9)—(12), 共同构成了含碱金属烧蚀等离子体电磁流动数值模拟方法. 其中对于流动控制方程(13), 时间离散采用全隐式LU-SGS方法, 对无黏项、黏性项和源项均进行隐式处理, 以增强稳定性; 空间离散采用较低耗散的AUSMPW+方法, 以提升数值模拟的精准度. 对于电磁场方程(8), 引入虚拟时间, 采用基于薄层近似的近似因式分解, 实现三维隐式TDMA数值离散, 以提升数值模拟稳定性和效率. 对于烧蚀边界层方程(9)—(12), 基于牛顿迭代, 建立分层隐式迭代计算方法, 实现边界的隐式离散模拟.

由于同时考虑表面材料烧蚀的高超声速流动/等离子体/电磁相互作用的研究极为少见, 这里从两个方面对计算方法进行验证.

采用球头模型, 球头半径为1.0 m. 计算飞行高度65 km, 飞行速度8000.0 m/s. 与文献[24]一致, 壁面采用C-C烧蚀材料, 考虑热力学激发、C-C烧蚀产物参与流场化学反应及其非平衡效应. 由于文献[24]并未明确给出计算网格和数值离散方法, 本文采用结构网格和低耗散AUSMPW+数值离散方法, 以保证数值模拟具有较高精准度, 这可能与文献存在一定差异.

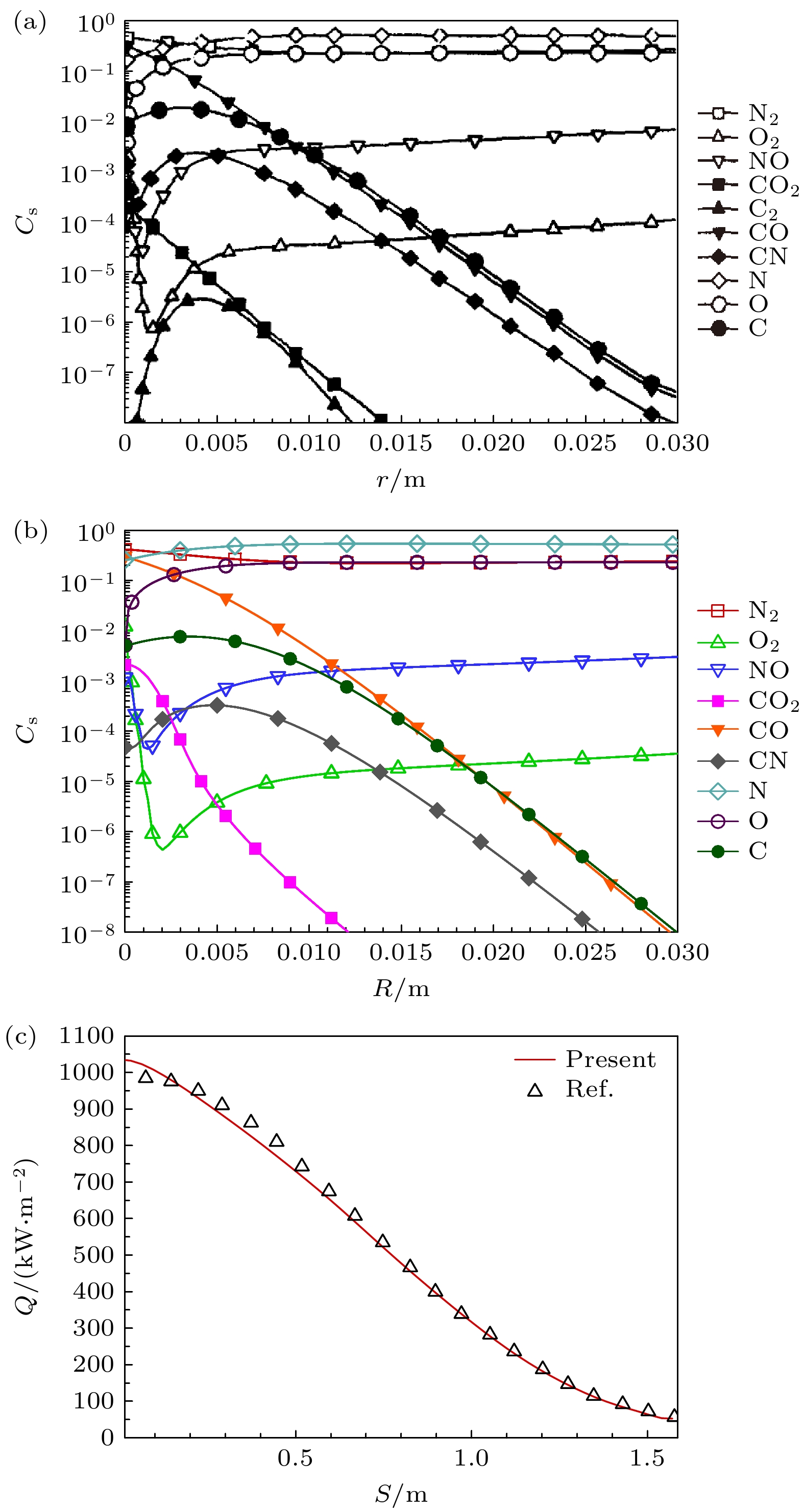
图1给出了本文计算结果与文献[24]结果比较. 由图1可以看出, 本文计算得到的烧蚀流场主要组分、表面热流的分布变化规律与文献[24]符合较好. 这说明本文采用的计算方法可较好地模拟高温非平衡流动与表面烧蚀的耦合作用.

采用OREX试验外形^[16,26], 选取再入时间7471.5 s的飞行工况, 对应飞行高度为59.6 km, 飞行马赫数17.61. 外加磁场采用磁偶极子模型, 其表达式为^[16,26]

式中($ {\boldsymbol{r}}, {\boldsymbol{\alpha }} $)为极坐标的单位矢量, $ {B_0} $为特征磁感应强度.

由于OREX再入速度较高, 本文考虑高速飞行过程中的热化学非平衡效应, 这与文献[16]的处理一致. 不同的是, 本文在电磁场方程(8)的处理时, 引入虚拟时间项, 采用基于薄层近似的近似因式分解, 实现三维隐式TDMA数值离散, 这种方法无需步进因子等人工参数, 且稳定性好.

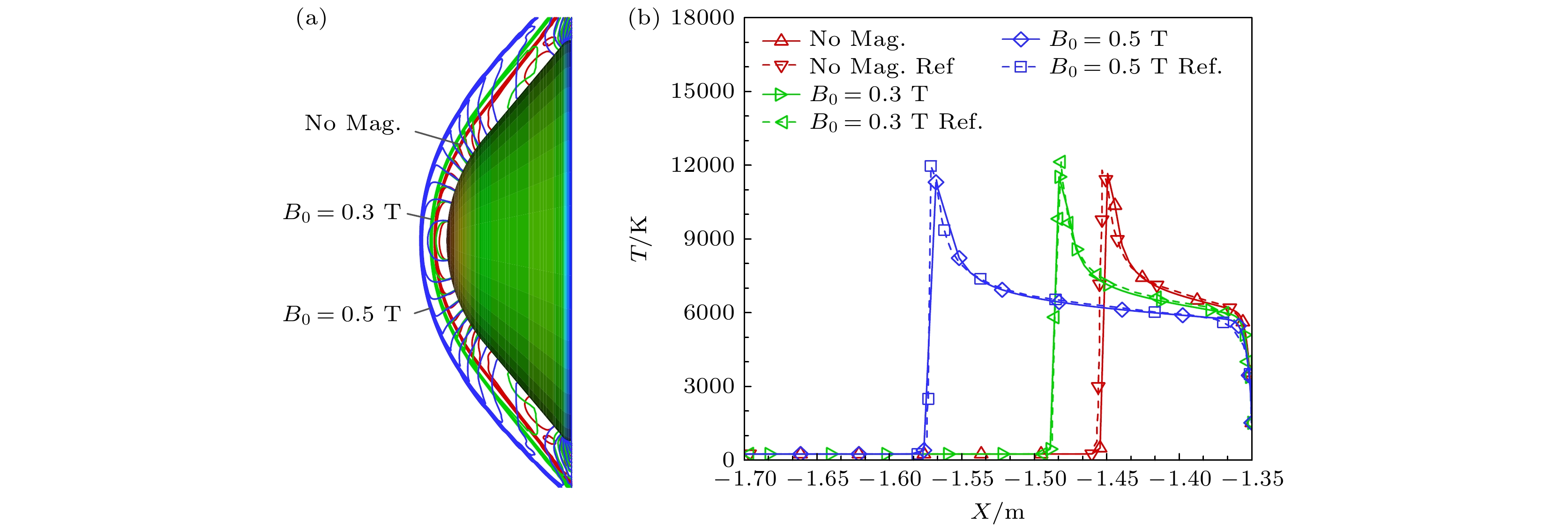
图2给出非平衡流场磁流体力学控制的流场结构和驻点线温度分布. 可以看出, 随磁场的增强, 激波脱体距离逐渐增大; 3种磁场条件下, 本文计算结果均与文献[16, 26]结果符合较好. 这说明本文采用的计算方法, 可较好地模拟高温非平衡流场与电磁场的耦合作用.

由于涉及的物理化学现象十分复杂, 考虑到计算量问题, 本文选取RAM-C钝锥外形作为研究对象, 头部半径0.1524 m, 钝锥角9°, 总长约1.3 m, 该外形有电子数密度的飞行数据^[27,28]. 计算状态为飞行高度61—81 km, 速度4—8 km/s, 这是飞行器需要进行热防护的主要作用区间. 表面烧蚀材料选用常见的C-C材料和硅基酚醛树脂材料, 由于制备工艺不同, 烧蚀材料中碱金属杂质含量差异较大, 例如RAMC-1端头的碱金属杂质比在0.005左右, 而RAMC-2端头碱金属杂质含量很低, 几乎可以忽略. 因此本文选取碱金属杂质含量在0.01—0.001之间变化. 外加磁场选用偶极子磁场模型, 该模型可较好地模拟同等特征尺寸(直径和长度)条件下的螺线管磁场^[23], 磁感应特征强度取$ {B_0} = 0.4\; {\text{T}} $, 这在工程上较为容易实现.

图3给出了无烧蚀、无磁场条件下RAM-C钝体末端电子数密度分布与试验比较, NCW和FCW分别为完全非催化和催化壁面, CNEQ和TCNEQ分别为化学非平衡和热化学非平衡. 由于真实壁面一般为有限催化, 介于完全非催化(NCW)和催化(FCW)之间, 因此本文计算结果与试验数据^[27,28]符合较好, 具有较高的准确性.

由于等离子体特性是高超声速流动与电磁场相互作用的基础, 因此首先开展碳-碳(标示为C-C)和硅基酚醛树脂(标示为Si-PR)材料不同碱金属含量条件下的等离子体特性和生成机制研究.

图4给出了高度71 km、速度5 km/s、无碱金属(碱金属质量占比D = 0)条件下不同表面材料的流场电子数密度云图. 图5给出了该条件驻点线电子数密度和电导率分布, R为离开壁面的距离. 可以看出, 表面C-C材料烧蚀的电子数密度和电导率, 与表面无烧蚀的结果差别不明显; 而采用Si-PR烧蚀材料, 驻点附件区域电子数密度降低1/3—1/2, 等离子体层厚度明显增大. 还可以看出, 等离子体层电子数密度在10¹¹ cm^–3量级, 电导率在10 S/m量级, 由此得到磁相互作用数仅0.68, 可以预计, 其磁场作用效果将不明显.

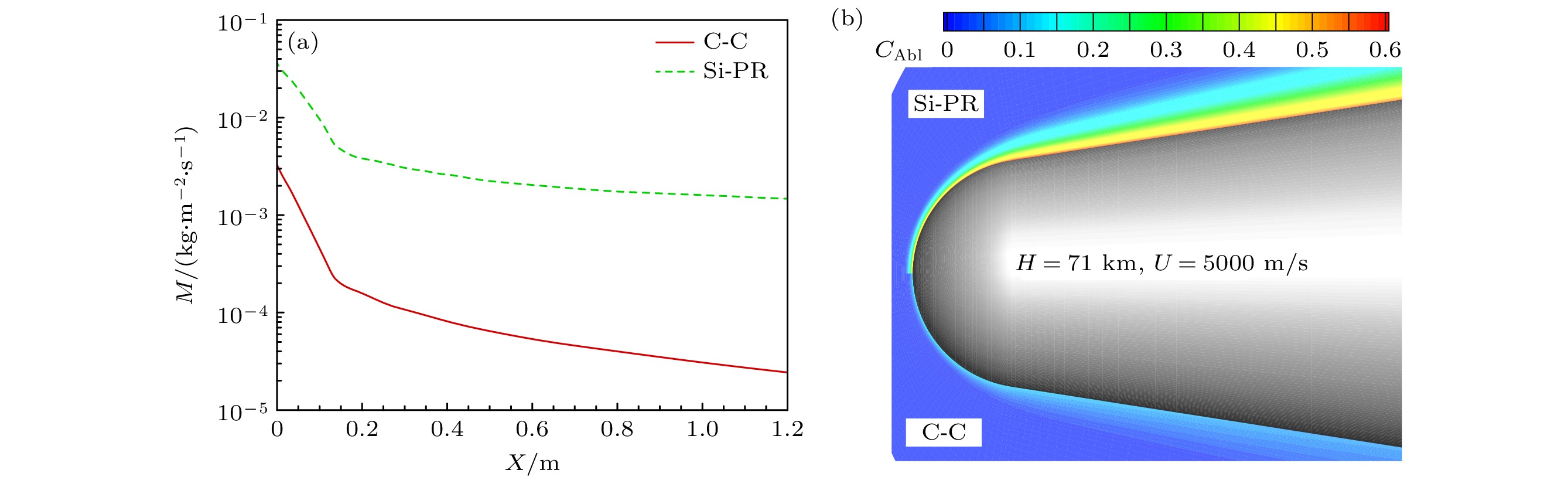
为了进一步分析不同表面材料等离子体差异产生的机理, 图6给出了不同表面材料的表面烧蚀质量引射率M和流场中烧蚀产物分布, C_Abl为烧蚀产物总的质量分数; 图7给出了驻点线主要电离组分分布, X_s为摩尔分数, C_s为质量分数.

可以看出, 对于C-C材料, 其表面烧蚀质量引射率相对较小(图6(a)), 流场中烧蚀产物的质量占比小(图6(b)), 烧蚀产物C等含量很小(图7(c)), 其缔合电离C+O⇔CO⁺+e与电子碰撞电离C+e ⇔C⁺+2 e产生的CO⁺和C⁺, 均远远小于空气主要电离组分NO⁺和O₂⁺(图7(a)), 因此流场等离子体电子数密度分布与无烧蚀纯空气流场差异不明显(图4(a)), 均以NO⁺的电离为主、O₂⁺的电离为辅. 这可以结合空气电离机制进行解释: 由于缔合电离O+N+2.76 eV ⇔ NO⁺ +e所需的活化能远低于其他电离反应, 因此该电离反应主导了高温空气的等离子体生成过程, 等离子体中NO⁺含量高; 尽管N+N+5.82 eV⇔N₂⁺+e所需的活化能, 与O+O+6.96 eV⇔O₂⁺+e差别不大, 但由于同等条件下O₂离解(O₂⇔O+O)较N₂离解(O₂⇔O+O)容易得多, 因此流场O含量一般高于N的含量, 因此流场中O₂⁺高于N₂⁺.

对于硅基酚醛树脂材料, 其表面烧蚀量较大(图6(a)), 质量引射作用较强, 流场中烧蚀产物的质量占比大(图6(b)), 这一方面“稀释”了流场中等离子体含量, 使驻点附近区域电子数密度降低, 气体电导率下降, 另一方面壁面上会产生较强速度引射((9)式), 使激波脱体距离增大, 等离子体层厚度增大(图4(b)). 由于烧蚀产物中C的含量较高(图7(c)), 其缔合电离C+O⇔CO⁺+e与电子碰撞电离C+e ⇔C⁺+2e相对较强, 因此烧蚀电离产物CO⁺和C⁺含量相对较大(图7(b)), 其影响不容忽视. 由图7(b)还可看出, 等离子体中H⁺占比很小, 远低于其他电离子组分, 这说明对于硅基酚醛树脂材料, 由于电离反应H + e +13.6 eV⇔ H⁺ + 2所需活化能较高, H的电离程度很小, 因此可忽略该电离反应的影响.

图8给出了不同碱金属杂质含量下, 驻点线电子数密度和电导率分布, D为碱金属杂质质量占比. 可以看出, 碱金属杂质对等离子体的影响极其显著, 随碱金属含量的提高, 流场中电子数密度迅速升高, 气体电导率迅速增大, 这主要是由于碱金属元素随表面材料烧蚀进入流场后, 电离生成的Na⁺占据了主导, 显著高于其他电离组分(图8(e)); 相比于C-C材料, 硅基酚醛树脂材料的电子数密度和气体电导率上升的幅度更大, 这与硅基酚醛树脂材料烧蚀质量引射率较大(图6)存在关联; 当碱金属杂质质量占比D = 0.01时, 流场中电子数密的增加1—2个数量级, 混合气体电导率提高1个量级, 达到10² S/m. 这种电导率量级的等离子体, 可较好应用于流动与电磁场相互作用研究^[29,30], 因此本文研究流动与磁场相互作用时, 将重点针对D = 0.01的烧蚀材料.

由于不同烧蚀材料等离子体生成机制存在差别, 碱金属含量对等离子体分布的影响极大, 因此本节开展了不同烧蚀材料、不同碱金属含量条件下的高速流动/等离子体/电磁场相互作用研究.

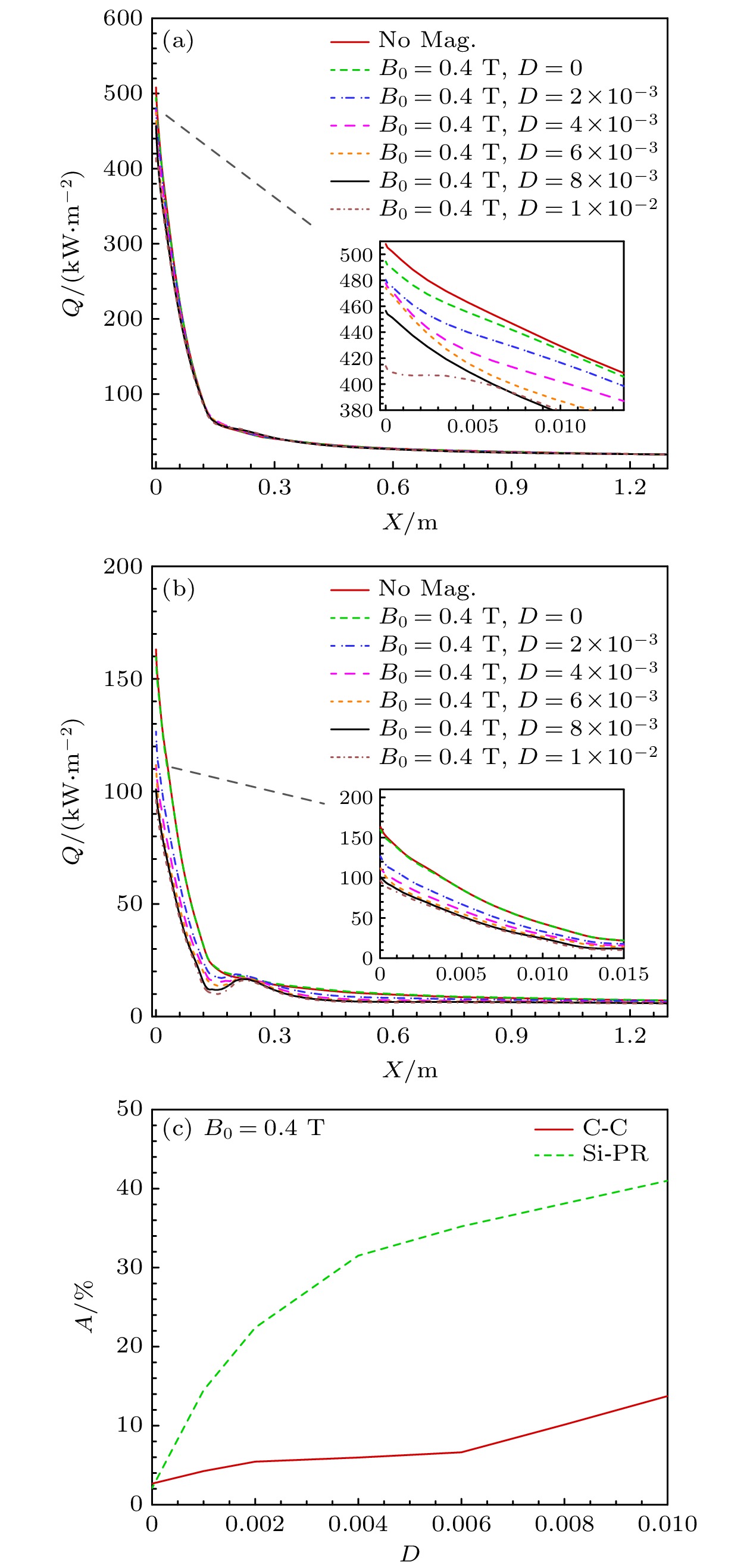
图9和图10分别给出了高度71 km、速度5 km/s时两种烧蚀材料、不同碱金属含量条件下磁场对驻点线温度温度和表面热流分布的影响, 图中D为碱金属质量占比, No Mag.为无磁场时的计算结果, B₀为外加偶极子磁场的磁感应强度, A为驻点热流下降的百分比.

可以看出, 在外加磁场作用下, 激波脱体距离增大, 头部驻点附近区域的表面热流呈下降趋势; 磁场的作用效果, 与烧蚀材料中碱金属含量紧密相关, 当碱金属含量为零, 磁场对流动的宏观作用不明显, 这与图4的分析一致; 随碱金属含量升高, 磁场的作用效果逐渐增强, 激波脱体距离和头部热流下降的百分比非线性增大; 采用不同烧蚀材料, 磁场的作用效果存在差别; 当碱金属质量占比为0.01, 表面采用Si-PR材料时, 激波增大约1倍, 驻点热流下降35%以上, 而采用C-C材料时, 激波仅增大了10%左右, 热流仅下降了约10%.

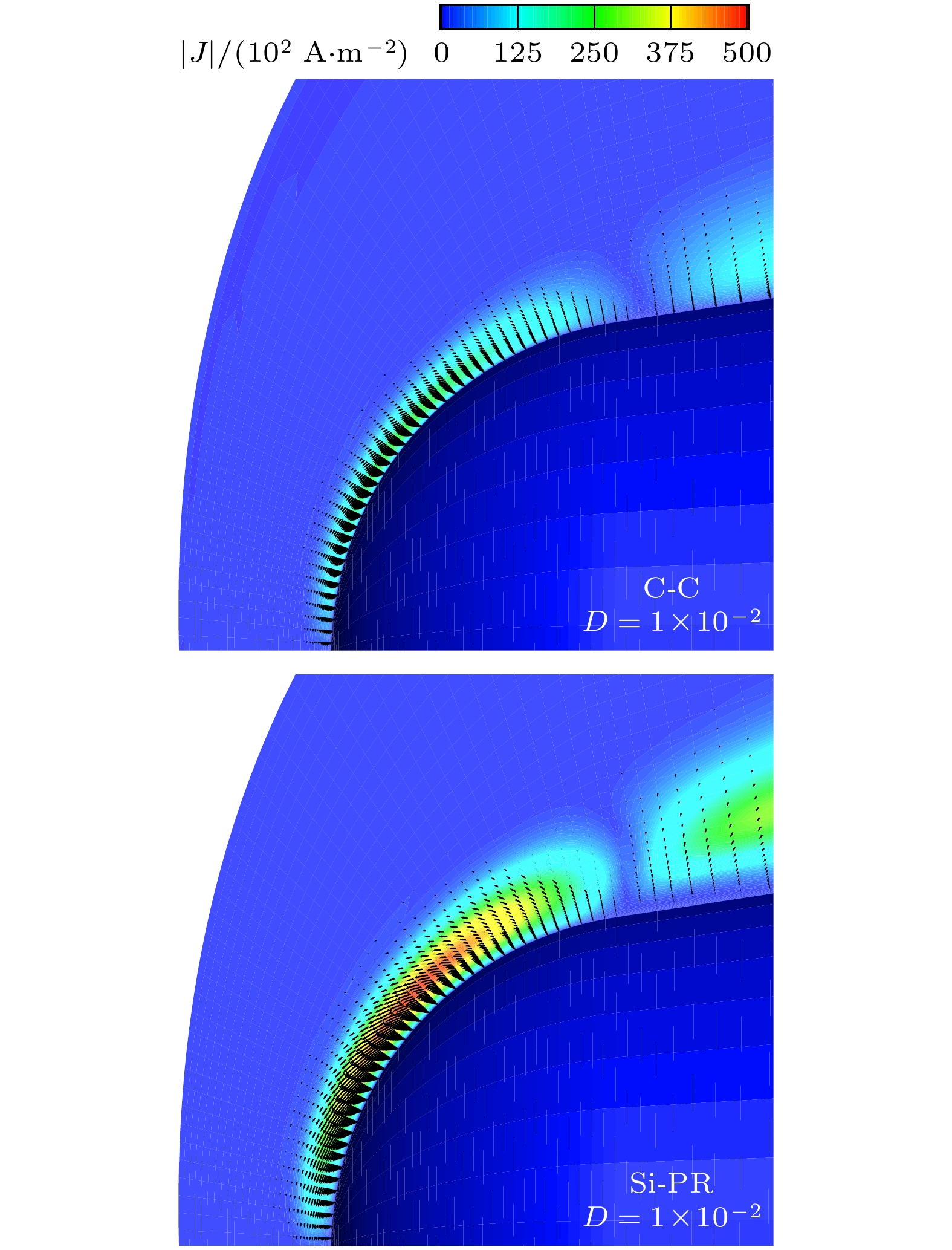
产生这种现象的原因, 可结合图6、图8和图11进行分析. 图11给出了磁场作用下, 两种烧蚀材料流场环形感应电流和洛伦兹力矢量分布, 图中$ \left| J \right| $为环形感应电流大小, 用云图颜色表征; 黑色箭头为流体微元受到的洛伦兹力矢量, 其长度表征了洛伦兹力的相对大小. 由图6可知, Si-PR材料的烧蚀质量引射率显著高于C-C材料, 相同碱金属含量条件下, Si-PR烧蚀引入碱金属元素更多, 其电离产生的碱金属离子在一定程度上主导了等离子体的电子数密度, 气体电导率更高(图8), 与磁场作用产生的环形感应电流更强, 流体微元受到的洛伦兹力更大(图11), 因此激波脱体距离更远, 高温气体更远离壁面(图9), 表面热流下降的百分比更大(图10).

由于高温流场等离子体和壁面烧蚀过程均与来流条件存在密切关联, 因此本节还开展了不同飞行高度、速度的流体与电磁场相互作用研究. 为了便于分析, 主要针对表面材料为碱金属含量0.01的酚醛树脂材料, 此时电磁场与流动相互作用较为明显.

图12给出了速度U = 5 km/s时不同高度条件下磁场使驻点热流下降的百分比. 可以看出, 当碱金属含量为0时, 磁场的作用效果不明显; 当碱金属质量占比为0.01时, 随飞行高度升高, 磁场作用效果逐渐增强, 磁控热流下降幅度由61 km时的14%, 上升至81 km时的60%.

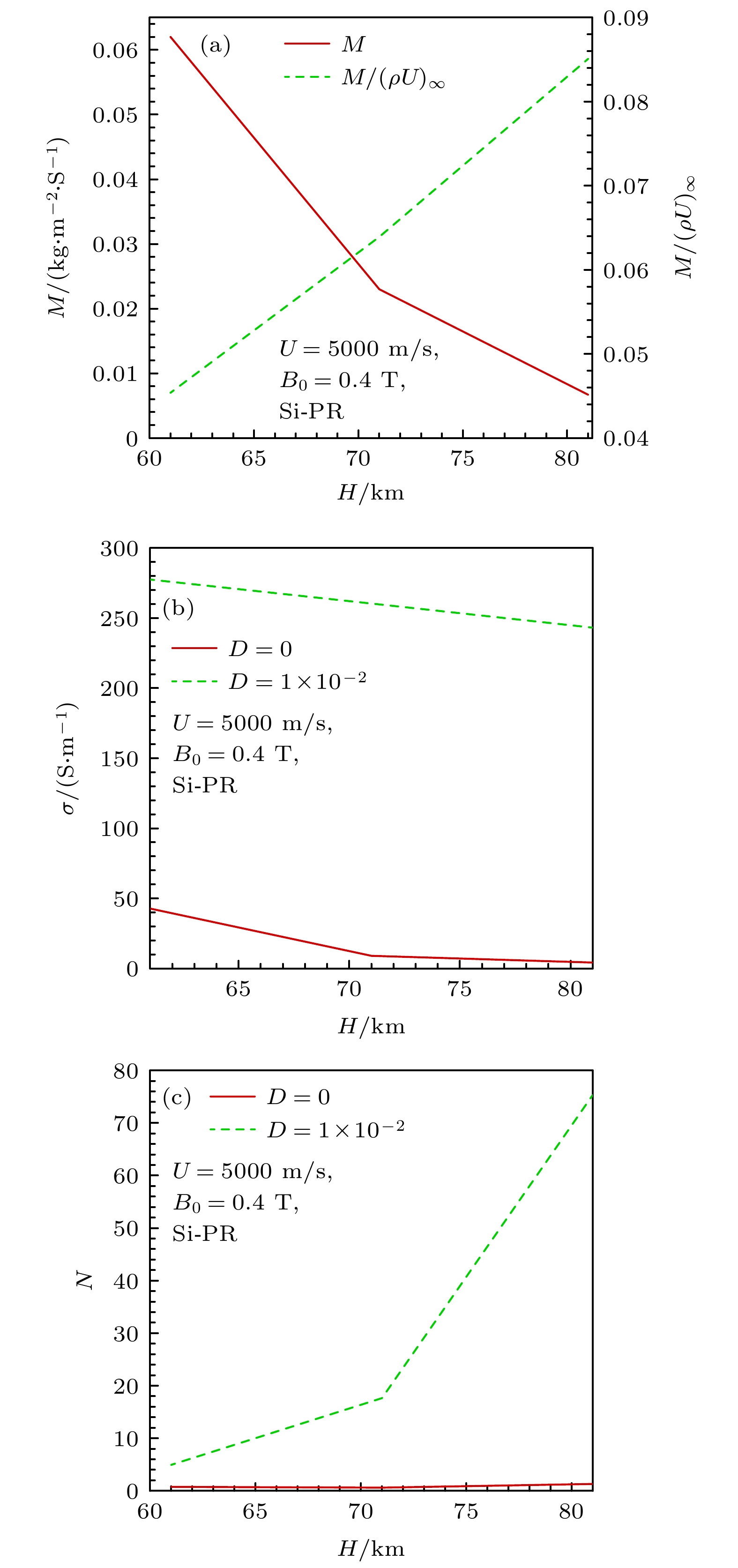
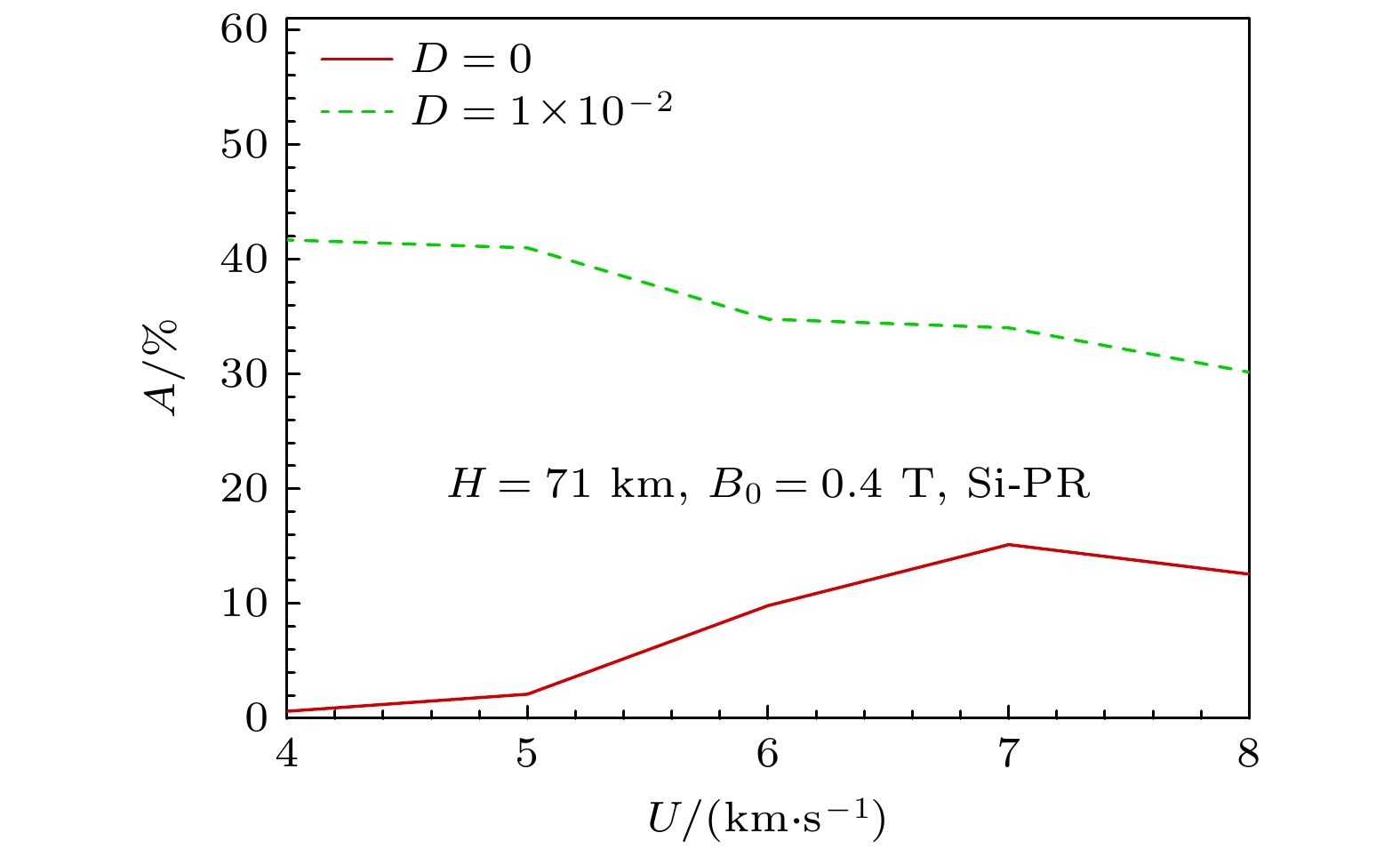
为了分析图12现象产生的原因, 图13给出不同飞行高度的壁面烧蚀引射质量、流场电导率峰值及其对应的磁相互作用数, 图中M为质量引射率, $ M/{(\rho U)_\infty } $为质量引射率与来流流量的比值, N为磁相互作用数. 可以看出, 随高度上升, 尽管烧蚀质量引射率呈下降趋势, 但由于气体密度下降, 质量引射率与来流流量的比值增大, 烧蚀(尤其是碱金属)对等离子体影响增大. 当D = 0.01时, 碱金属电离使等离子体电导率达到200 S/m以上, 且随飞行高度上升下降幅度不大; 在这电导率条件下, 磁相互作用数受气体密度主导, 随飞行高度上升, 气体密度降低, 磁相互作用数显著增大, 磁场作用效果增强. 当D = 0.0时, 气体电导率较小, 磁相互作用数接近于0, 磁场作用效果不明显.

图14给出了高度H = 71 km时不同速度条件下磁场使驻点热流下降的百分比. 可以看出, 碱金属含量为0时, 随速度升高, 磁控热流下降的百分率先升高后降低; 当速度低于5 km/s时, 磁场作用效果不明显; 当速度达到7 km/s时磁场作用效果最强, 热流下降百分比可达15%以上; 当速度高于7 km/s, 磁控热流下降的百分比反而略微减小. 碱金属含量为0.01时, 不同速度条件下, 磁场作用效果均较为显著, 磁控热流下降百分比达到30%以上; 随飞行速度下降, 磁场作用效果略微上升. 由此可见, 由于速度较低时纯空气电离度较低, 通过含碱金属烧蚀来提高混合气体电离度进而提升磁场作用效果的效率更高.

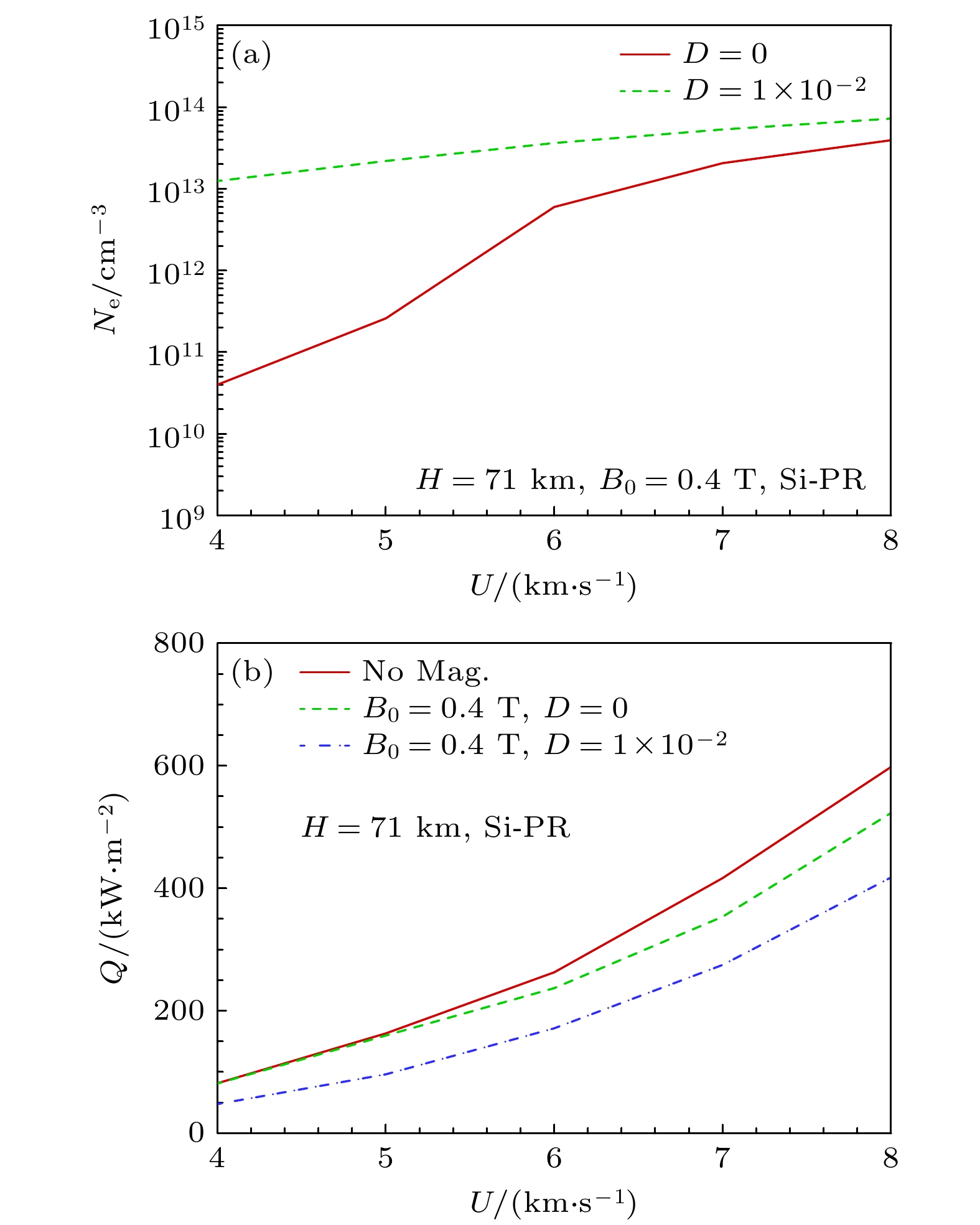
为了分析图14现象产生的原因, 图15给出了不同速度条件下的流场电子数密度峰值和驻点热流. 可以看出, 随速度升高, 流场中电离程度增大: 无碱金属时, 电子数密度上升幅度较大, 在速度7 km/s以上时达到10¹³ cm^–3量级, 接近碱金属0.01的状态; 碱金属占比为0.01时, 电子数密度上升相对缓慢, 但均高于无碱金属的状态, 均在10¹³ cm^–3以上. 速度越高, 电离程度越大, 气体电导率越高, 磁场使热流下降的绝对值越大. 但由于速度升高时无磁场时的热流上升更快, 因此速度较高时磁控热流下降的百分比反而减小.

1)烧蚀效应对流场等离子体分布的影响, 受烧蚀质量引射率和碱金属质量占比共同作用. 当碱金属含量为零时, 流场等离子体浓度主要受空气电离主导, 由于烧蚀质量引射的“稀释”和“外推”作用, 其峰值电子数密度下降, 等离子体层厚度增加; 当碱金属含量较高时, 碱金属电离反应占主导, 电子数密度增大1—2个数量级.

2)不同材料烧蚀对等离子体的影响存在差别. C-C材料的烧蚀质量引射率较小, 碳的电离反应对等离子体的影响小, 无碱金属时与空气无烧蚀等离子体差别不大; Si-PR的烧蚀质量引射率较大, 流场中碳含量相对较高, 电离生成CO⁺, C⁺的摩尔分数接近空气主要电离组分NO⁺, ${\mathrm{O}}_2^+ $, 其影响不容忽视; 流场H的电离很小, 基本可以忽略.

3)烧蚀材料中碱金属可以显著提升磁场作用效果. 磁场作用下, 激波脱体距离增大, 热流下降; 随着碱金属占比增大, 磁场作用效果增强; 二者呈非线性关系, 受烧蚀材料类型影响, 采用C-C材料时磁场作用效果的变化幅度小于Si-PR材料.

4)对于含碱金属材料(碱金属质量占比为0.01的Si-PR)烧蚀的高超/电离/电磁流动来说, 同一速度条件下, 随飞行高度上升, 磁场作用效果显著增强, 飞行高度81 km时磁控热流下降可达60%; 同一飞行高度, 随飞行速度下降, 空气本身的电离度降低, 但磁场使热流下降的百分数反而增大. 由此可见, 在速度较低时, 通过含碱金属烧蚀来提升磁场作用效果的效率更高.