首页
登录
注册
-
微波放电中和器作为微波离子推力器系统的重要组成部分, 在维持航天器电位平衡、中和羽流方面发挥着关键作用[1,2]. 微波放电中和器利用电子回旋共振(electron cyclotron resonance, ECR)加热机制形成高能电子, 进而电离中性气体产生等离子体, 在外部虚拟阳极的作用下引出电子, 与离子束流混合实现中和效果.
目前, 国内外以μ1[3,4]和μ10[5,6]为代表的ECR离子推力器系统中的微波放电中和器为原型开展了大量实验和仿真研究[7–16]. 其中, 针对电子引出机制的研究以PIC-MCC (particle-in-cell with Monte Carlo collision)仿真为主. 在对前者的研究中, 发现了静电漂移对电子引出的影响, 解释了电子跨磁力线引出的原理[17,18]. 在对后者的研究中, 将电子引出通道分为磁阱通道和双鞘层通道, 并对不同磁场结构下的中和器伏安特性曲线进行合理解释[19]; 以此为依据, 西北工业大学对ECR中和器进行了结构改进, 成功提升了电子束流[20].
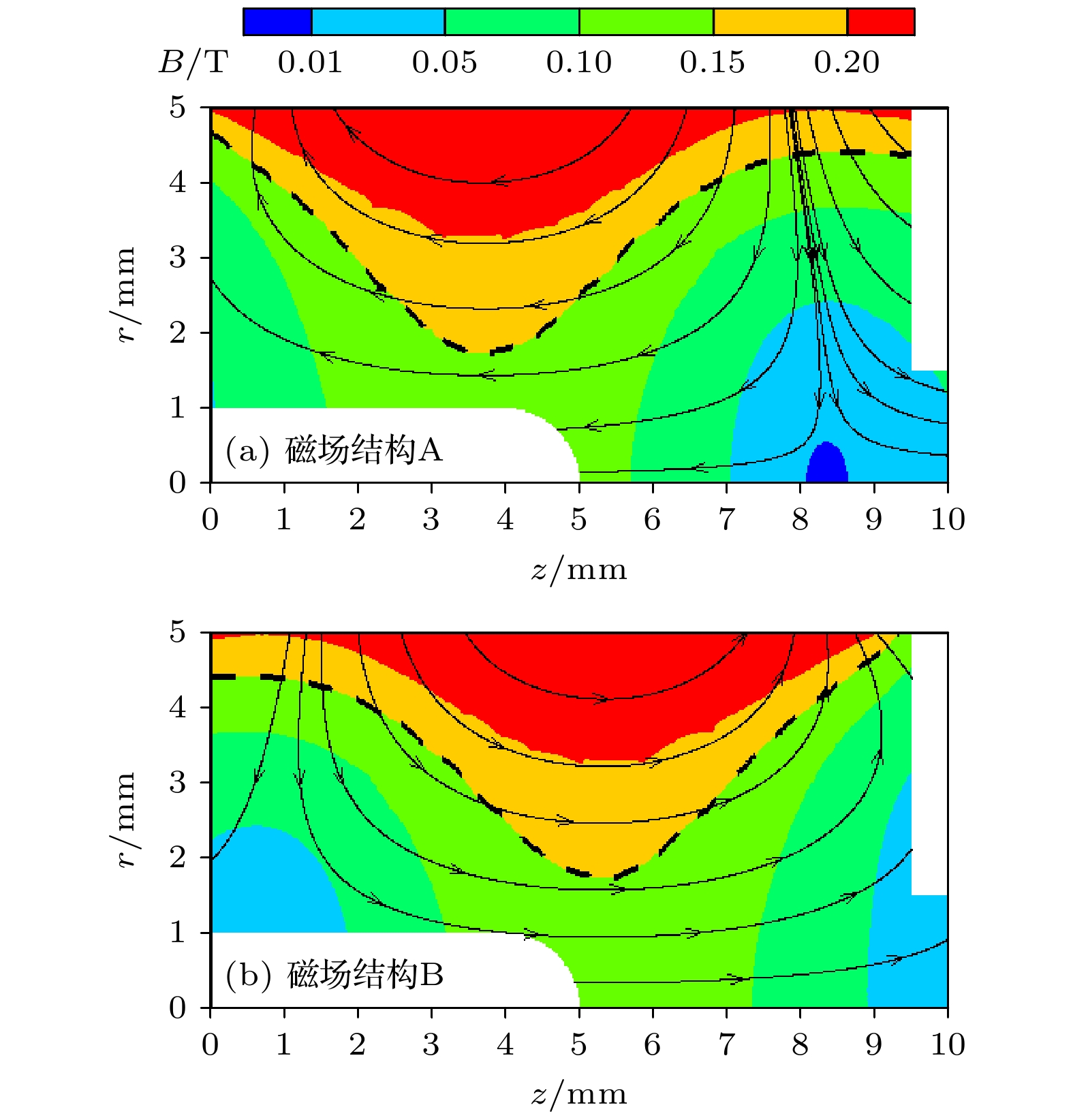
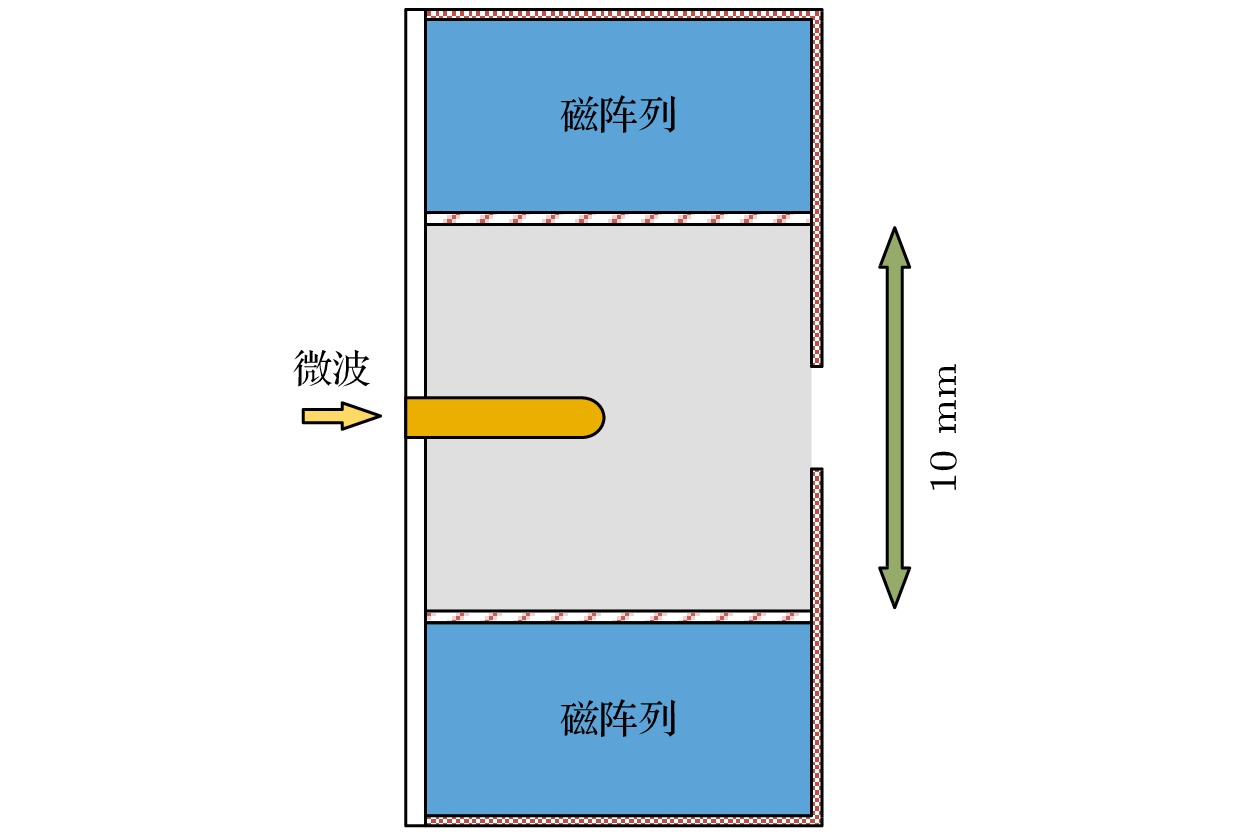
为了突破微波离子推力器系统的小型化瓶颈, 西安交通大学开发了磁阵列微波离子推力器系统[21]. 其中, 磁阵列微波放电中和器结构如图1所示, 由微波接头、天线、磁阵列、内壳体、外壳体和孔板组成. 在磁场结构定型的过程中, 发现调转磁阵列朝向, 从磁场结构A变为磁场结构B后, 两种磁场结构的伏安特性曲线存在明显差异. 图2为两种磁场结构, 其中黑虚线为电子回旋共振区(B = 0.15 T), 黑线为磁力线.
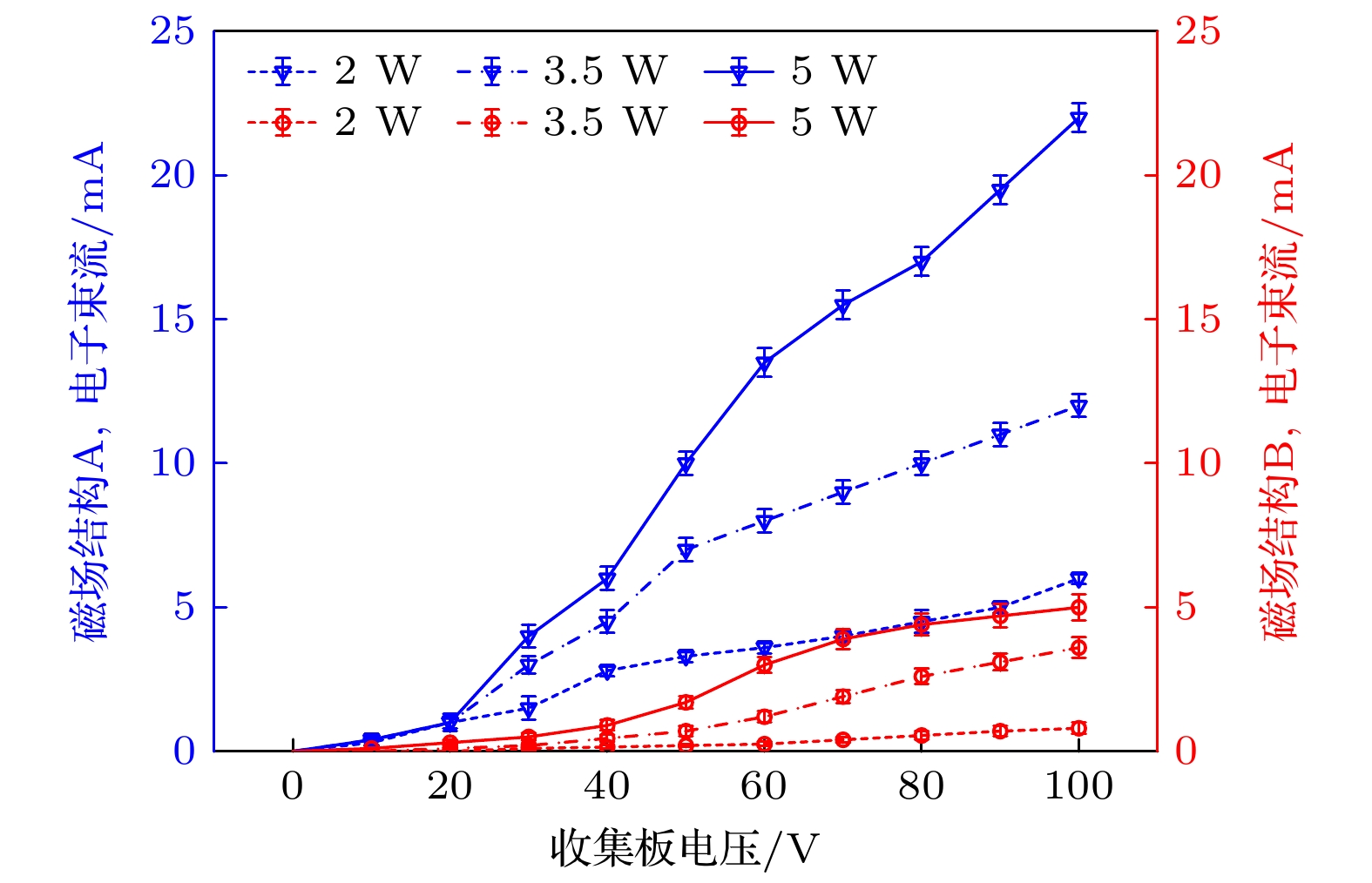
图3为实验测得的伏安特性曲线, 可见磁场结构B的中和器在输入功率小于2 W时几乎无法引出电子. 同时, 从整体趋势上看, 引出电子能力对微波功率不敏感. 然而, 磁阵列微波放电中和器采用了从外部构筑内部磁场的设计思路, 与现有ECR中和器的结构差异较大, 无法运用既有研究成果对实验现象进行合理解释.
鉴于磁阵列微波放电中和器放电室直径仅为10 mm, 介入式探针诊断对等离子体干扰较大, 本文将采用一体化的PIC-MCC方法[22]对中和器进行仿真研究, 获得两种磁场结构下的等离子体参数分布, 进一步分析磁阵列类型中和器的电子引出机制, 为后续中和器性能优化提供理论参考.
-
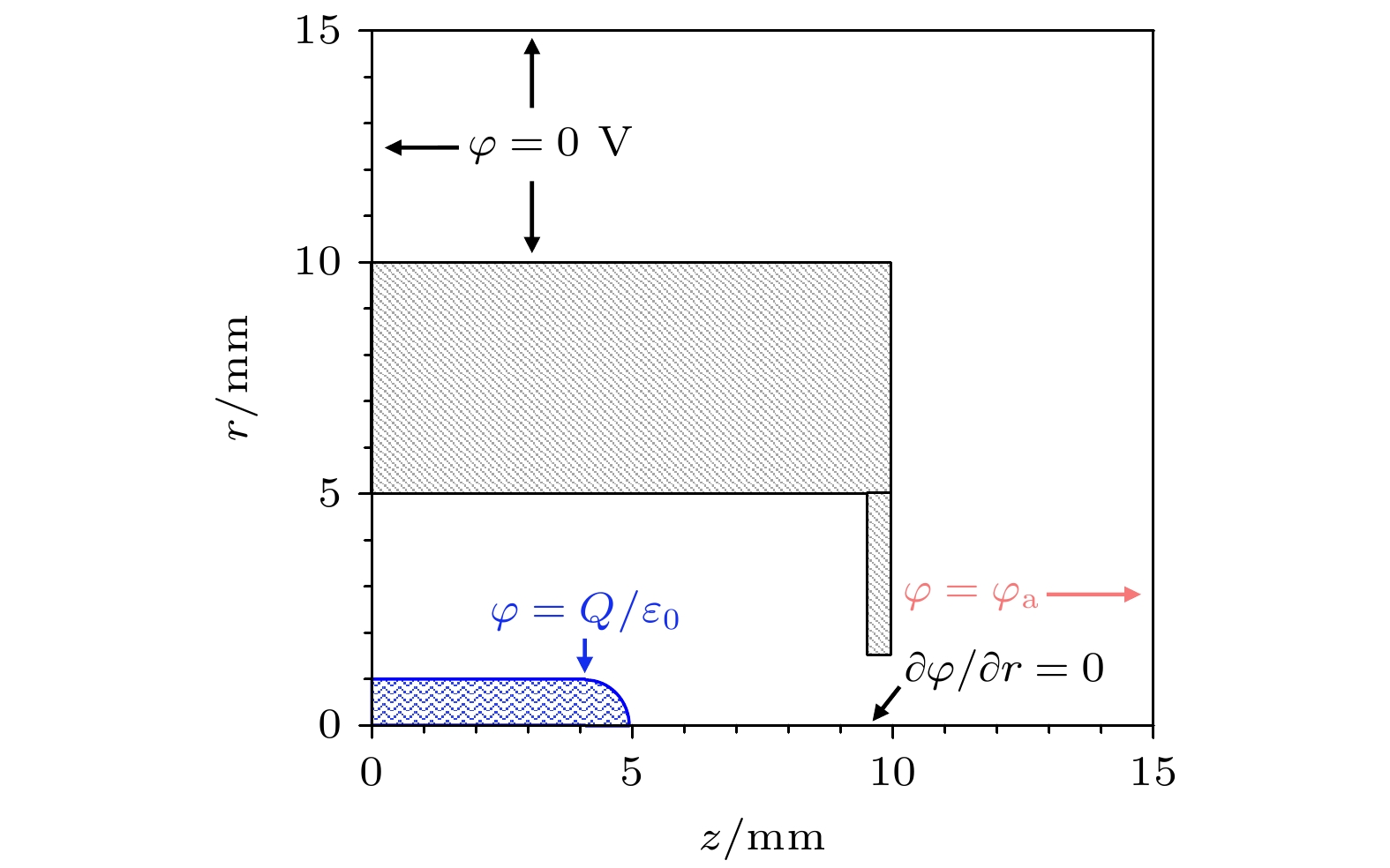
一体化PIC-MCC仿真的计算域如图4所示. 计算域大小为15 mm×15 mm, 包含了中和器和近场区域, 右边界为虚拟阳极, 与中和器相距5 mm. 计算域中, r < 5 mm区域的网格步长为0.025 mm; 5 mm < r < 10 mm区域的网格步长为0.05 mm; r > 10 mm区域的网格步长为0.1 mm. 同时, 图4标注了求解泊松方程的边界条件, 其中天线电势由累积电荷自洽计算[22]. 碰撞模型中, 考虑电子-中性粒子的弹性、激发和电离碰撞; 离子-中性粒子的弹性和电荷交换碰撞; 中性粒子之间的弹性碰撞.
仿真分为初始放电和电子引出两个阶段. 在初始放电仿真中, 所有实体边界均为0 V, 计算200万步(20 μs)至稳态后进入电子引出阶段. 在电子引出仿真中, 继承初始放电的等离子体分布, 在右边界(虚拟阳极
$ {\varphi }_{{\mathrm{a}}} $ )分别施加40 V和80 V的电压, 统计右边界收集的电子和离子电流, 相减得到实际电流. 仿真的参数设置如表1所示. 为了反演真实物理现象, 仿真中采用了真实的介电常数; 相应地, 降低了微波功率来减轻计算负担. -
在
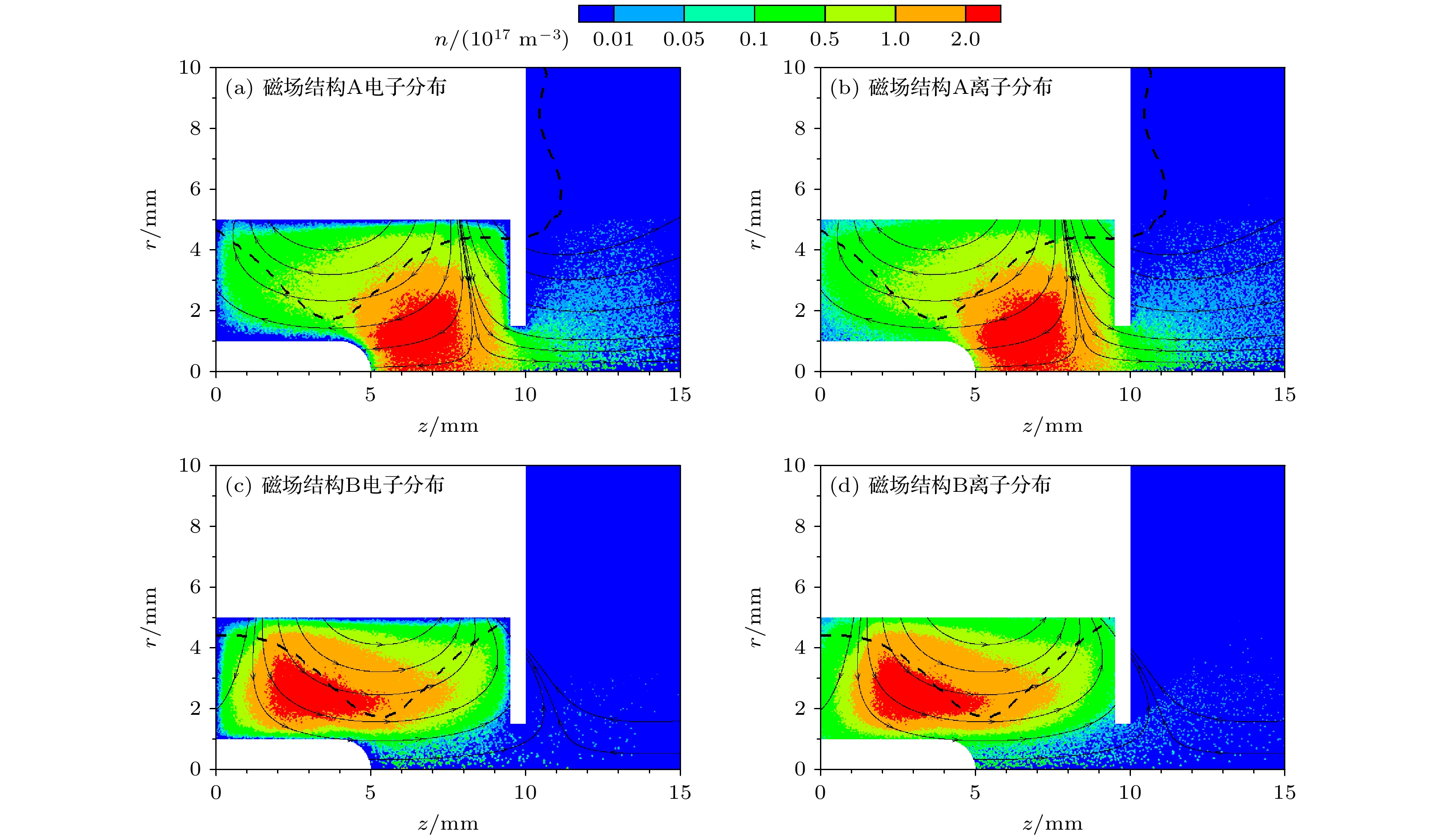
$ {\varphi }_{{\mathrm{a}}} $ = 0 V条件下, 由初始等离子体演化至稳态后等离子体密度分布如图5所示. 两种磁场结构的最高等离子体密度均可达2×1017 m–3, 等离子体分布形貌存在明显区别, 磁场结构A的主等离子体区向下游偏移, 磁场结构B的主等离子体区向上游偏移, 偏移方向与磁场梯度方向相同. 因偏移方向不同, 导致磁场结构A中有等离子体溢出孔外; 而磁场结构B在轴线处的等离子体较少. -
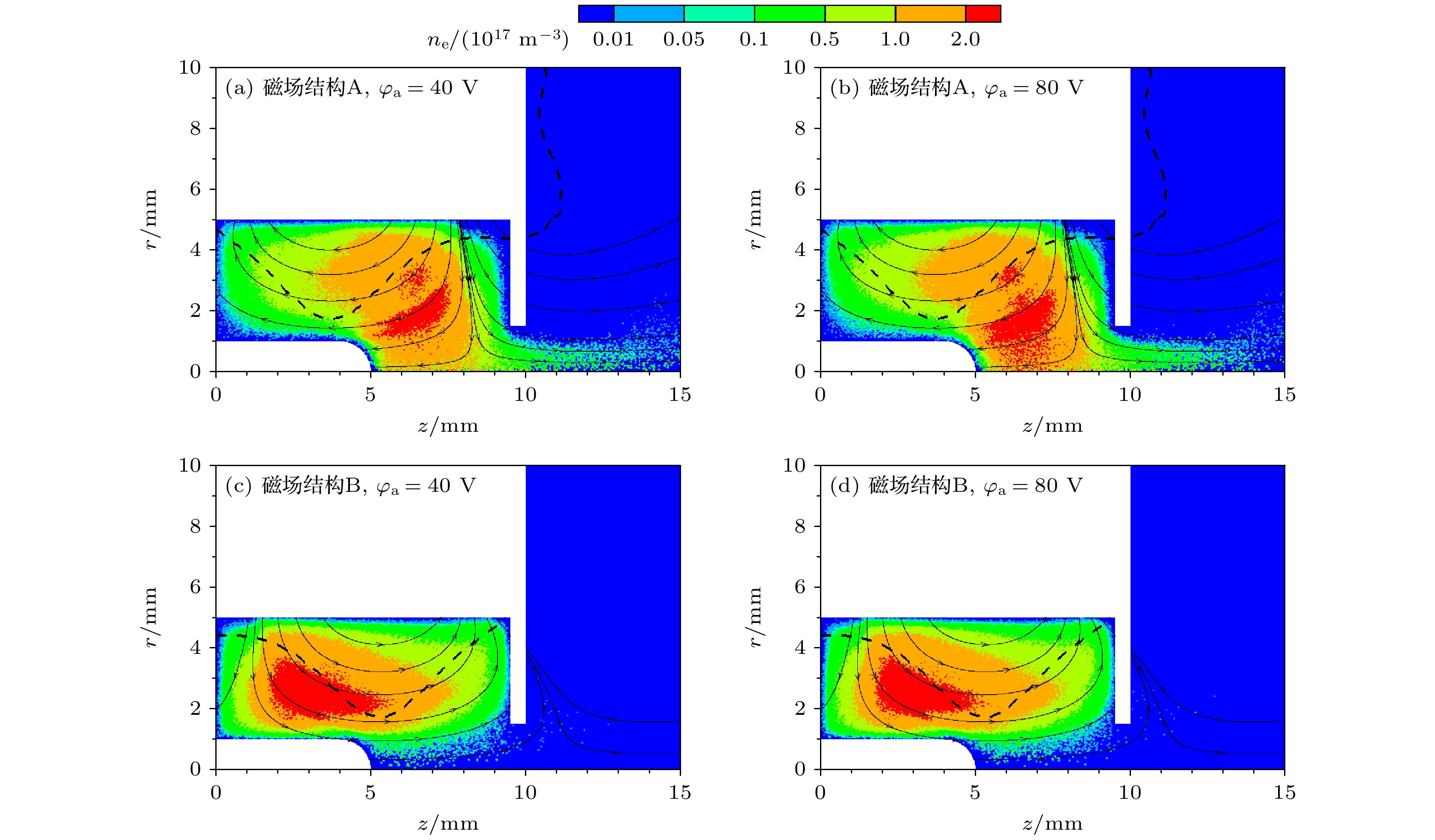
图6分别展示了
$ {\varphi }_{{\mathrm{a}}} $ = 40 V和$ {\varphi }_{{\mathrm{a}}} $ = 80 V时的电子束流引出情况. 明显地, 磁场结构A能够看到电子束流, 而磁场结构B中仅能看到极少量电子. 仿真结果与实验结果均得出了磁场结构B难以引出电子的结论. 同时, 与初始放电的等离子体分布对比, 磁场结构A的等离子体形貌发生明显变化, 而磁场结构B的等离子体形貌几乎不变. 这表明在电子引出过程中微波放电等离子体会自洽地寻找新平衡, 最终重新获得稳定的分布, 在实验中的表现为磁场结构A的反射功率逐渐下降, 磁场结构B的反射功率几乎不变. -
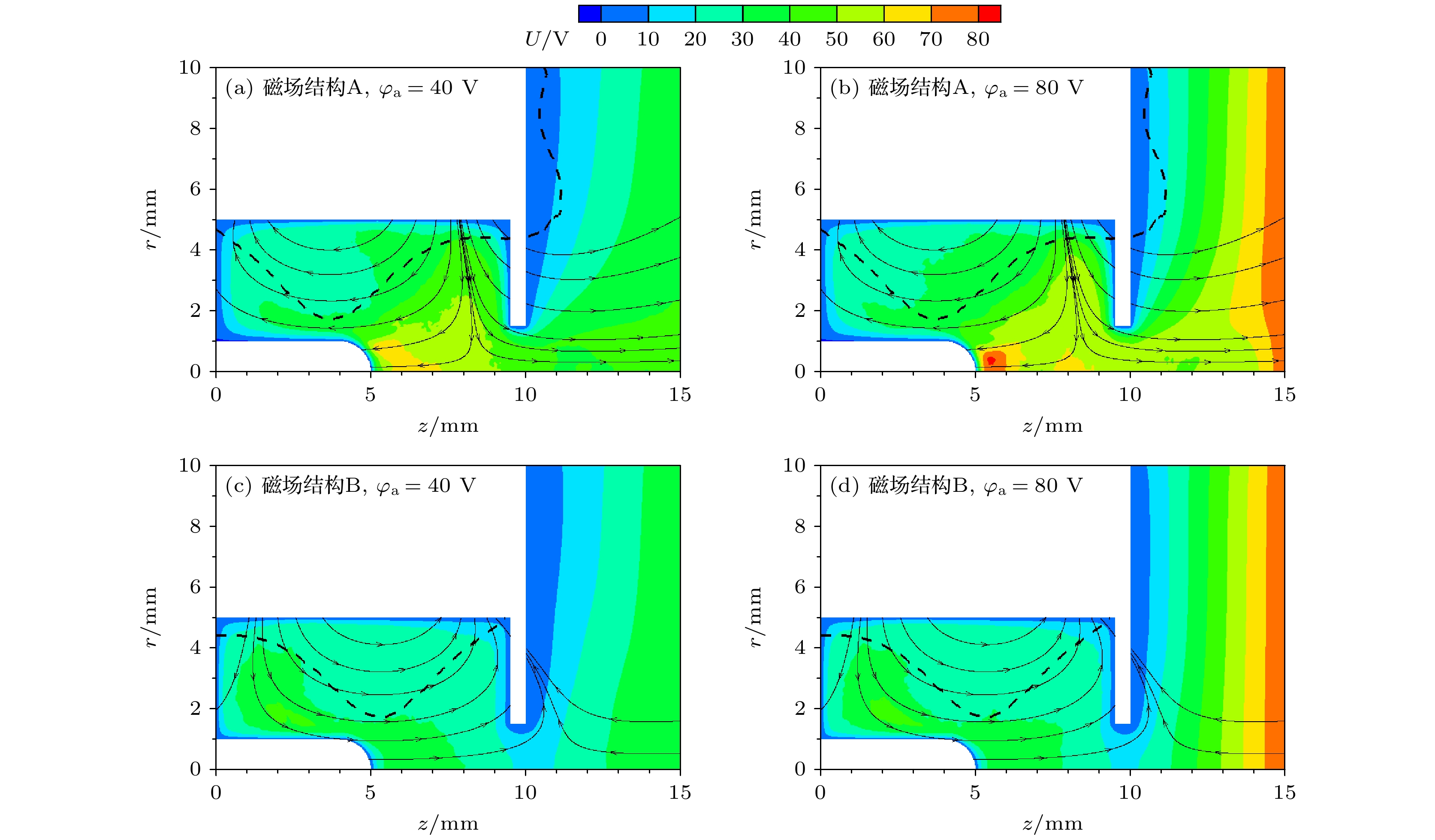
图7展示了不同工况下电子引出时的电势分布. 在磁场结构A中, 放电室内最高电势随
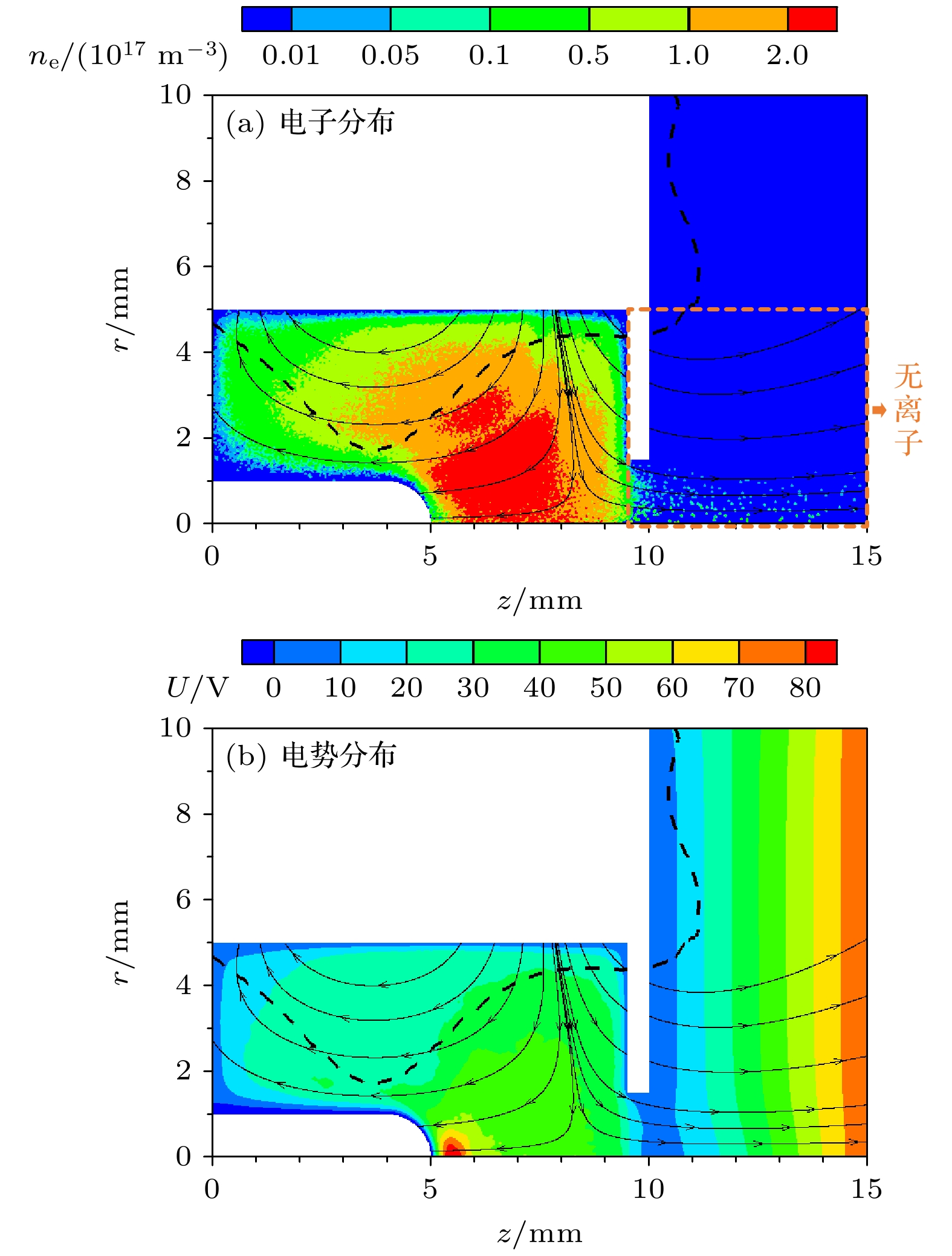
$ {\varphi }_{{\mathrm{a}}} $ 增大而增大, 引出孔附近电势明显提升; 在磁场结构B中, 引出孔附近存在明显的电势阱, 且电势阱深度不随$ {\varphi }_{{\mathrm{a}}} $ 变化而变化. 由于微波放电中和器属于依靠阳极电势的被动引出类型, 电子需要先克服等离子体电势离开引出孔才能被阳极电场捕获. 因此, 引出孔附近的电势分布决定了中和器的电子引出能力, 只有降低或打破电势阱才能使电子顺利引出.从电势阱变化可做进一步推断: 中和器引出电子的过程必须有离子参与. 本文在磁场结构A,
$ {\varphi }_{{\mathrm{a}}} $ = 80 V条件下(图6(b))对仿真模型进行修改, 人为使离子在进入引出孔后消失, 仿真结果如图8所示. 在放电室和阳极板之间出现了电势阱, 无法建立电子引出通道, 电子引出电流骤降, 只有少量电子可以沿磁力线引出. 由此可知, 离子对电子引出过程具有重要影响. 结合图3的伏安特性曲线可以推测, 随微波功率提升, 等离子体密度增大, 一方面有更多的电子可供引出, 另一方面有更多的离子迁移至引出孔附近, 抬升电势并吸引更多电子汇聚, 最终使得电子电流增大. 另外, 磁场梯度可以引导离子顺梯度漂移, 直接决定了放电室内的等离子体分布, 这解释了两种磁场结构的伏安特性曲线差异.综上所述, 微波放电中和器有效引出电子需要满足两个条件: 1)磁场梯度指向引出孔, 引导等离子体迁移; 2)引出孔附近需要有足够的离子抬升电势, 降低或打破电势阱.
-
本文采用一体化PIC方法对磁阵列微波放电中和器的初始放电和电子引出过程进行了仿真, 仿真结果与实验现象相符合. 通过分析中和器工作过程中等离子体参数分布的变化, 阐明了磁场结构对中和器电子引出特性的影响机制, 总结了中和器有效引出电子的必要条件. 未来, 将在现有磁阵列微波放电中和器的基础上, 进一步优化磁阵列结构, 使整个放电室的磁场梯度指向下游, 提升中和器性能.
磁阵列微波放电中和器的电子引出机制
Electron extraction mechanism of magnet array microwave discharge neutralizer
-
摘要: 微波放电中和器作为微波离子推力器系统的重要组成部分, 在维持航天器电位平衡、中和羽流方面发挥着重要作用, 其电子引出性能直接关系到电推力器系统的工作状态. 在磁阵列微波放电中和器的磁场结构定型实验中, 发现调转磁阵列朝向后引出电流的伏安特性曲线差异极大. 由于磁阵列微波放电中和器的放电室直径仅10 mm, 介入式探针诊断对等离子体干扰大, 本文采用了一体化粒子模拟方法对中和器的工作过程进行仿真, 仿真结果与实验现象相符合. 通过对比不同磁场结构、工作电压下的等离子体参数分布, 发现引出孔附近的电势分布决定着中和器的电子引出能力; 并进一步揭示了离子在中和器电子引出过程中发挥的关键作用, 阐明了磁场结构对中和器电子引出能力的影响机制. 最后, 本文总结了微波放电中和器有效引出电子的两个必要条件: 1)磁场梯度指向引出孔, 引导等离子体迁移; 2)引出孔附近有足够的离子抬升电势, 降低或打破电势阱.Abstract: Microwave discharge neutralizer is an important part of microwave discharge ion thruster system, which plays a vital role in maintaining potential balance between spacecraft and neutralizing ion beam. Its electron extraction property directly affects the operation condition of ion thruster system. In order to break through the power limit of miniature microwave discharge ion thruster, a magnet array microwave discharge ion thruster system is designed and tested. In the experiment on finalizing magnetic field structure of magnet array microwave discharge neutralizer, an interesting phenomenon is found that the I-V curves of electron current, after rotating the magnetic array orientation, are very different. Defining forward direction of magnet array can normally extract electrons, then backward direction of magnet array can hardly extract electrons. Because the diameter of discharge chamber is only 10 mm, it is too small to perform Langmuir probe diagnosis. And thus, an integrative particle-in-cell method is used to simulate the neutralizer operation processes of two different magnetic field structures, and for the sake of accuracy, real vacuum permittivity is used. The simulation results show good consistence with experimental phenomenon. In the initial discharge process, it is found that the magnetic field gradient leads to different plasma distributions; in electron extraction process, it is found that the potential distribution near the orifice determines the electron extraction property of the neutralizer. Through comparing the plasma parameter distributions under different magnetic field structures and operating voltages, an assumption that the ion is an important factor in electron extraction process is proposed. Then, a simulation that ions disappear artificially outside the orifice is conducted, and the simulation results show that electrons cannot be effectively extracted without ions near the orifice. According to the simulation and experiment results, two necessary conditions are summarized for electron extraction of the neutralizer. The first condition is magnetic field structure: the magnetic field gradient should point towards the orifice to guide plasma migration towards the orifice, the second one is potential distribution: there should be enough ions to lift the potential near the orifice for reducing or breaking the potential well. These two conditions can help understand the electron extraction mechanism of microwave discharge neutralizer and provide theoretical reference for optimizing the performance of neutralizer in future.
-
Key words:
- electron cyclotron resonance /
- neutralizer /
- electron extraction .
-
-
图 1 磁阵列微波放电中和器结构简图
Figure 1. Structure diagram of magnet array microwave discharge neutralizer.
图 2 磁阵列微波放电中和器的磁场结构
Figure 2. Magnetic field of magnet array microwave discharge neutralizer.
图 3 磁阵列微波放电中和器伏安特性曲线
Figure 3. I-V curves of magnet array microwave discharge neutralizer.
图 5 初始放电仿真结果 (a)磁场结构A的电子密度分布; (b)磁场结构A的离子密度分布; (c)磁场结构B的电子密度分布; (d)磁场结构B的离子密度分布
Figure 5. Initial discharge simulation results: (a) Electron density distribution of magnetic field structure A; (b) the ion density distribution of magnetic field structure A; (c) the electron density distribution of magnetic field structure B; (d) the ion density distribution of magnetic field structure B.
图 6 电子引出仿真结果 (a)磁场结构A,
$ {\varphi }_{{\mathrm{a}}} $ = 40 V; (b)磁场结构A,$ {\varphi }_{{\mathrm{a}}} $ =80 V; (c)磁场结构B,$ {\varphi }_{{\mathrm{a}}} $ = 40 V; (d)磁场结构B,$ {\varphi }_{{\mathrm{a}}} $ = 80 VFigure 6. Simulation results of electron beam in extraction stage: (a) Magnetic field structure A,
$ {\varphi }_{{\mathrm{a}}} $ =40 V; (b) Magnetic field structure A,$ {\varphi }_{{\mathrm{a}}} $ = 80 V; (c) Magnetic field structure B,$ {\varphi }_{{\mathrm{a}}} $ = 40 V; (d) Magnetic field structure B,$ {\varphi }_{{\mathrm{a}}} $ = 80 V.
图 7 电子引出阶段电势变化 (a)磁场结构A,
$ {\varphi }_{{\mathrm{a}}} $ = 40 V; (b)磁场结构A,$ {\varphi }_{{\mathrm{a}}} $ =80 V; (c)磁场结构B,$ {\varphi }_{{\mathrm{a}}} $ = 40 V; (d)磁场结构B,$ {\varphi }_{{\mathrm{a}}} $ = 80 VFigure 7. Potential distribution in extraction stage: (a) Magnetic field structure A,
$ {\varphi }_{{\mathrm{a}}} $ = 40 V; (b) magnetic field structure A,$ {\varphi }_{{\mathrm{a}}} $ = 80 V; (c) magnetic field structure B,$ {\varphi }_{{\mathrm{a}}} $ = 40 V; (d) magnetic field structure B,$ {\varphi }_{{\mathrm{a}}} $ =80 V.
图 8 假设引出孔外无离子的仿真结果 (a)电子分布; (b)电势分布
Figure 8. Electron beam (a) and potential distribution (b) assuming no ion outside orifice.
表 1 参数设置
Table 1. Simulation parameter setting.
参数 设定值 微波频率/GHz 4.2 微波功率/W 1 氙气流量/sccm 0.3 初始等离子体密度/m–3 1 × 1016 初始宏粒子数量 10000 时间步长/s 1 × 10–11 
下载: 导出CSV
-
[1] Nono A, Morishita T, Hosoda S, Tsukizaki R, Nishiyama K 2023 Acta Astronaut. 212 130 doi: 10.1016/j.actaastro.2023.07.045 [2] 杨涓, 牟浩, 耿海, 吴先明 2023 推进技术 44 2208095 Yang J, Mou H, Geng H, Wu X M 2023 J. Propuls. Tech. 44 2208095 [3] Koizumi H, Komurasaki K, Aoyama J, Yamaguchi K 2018 J. Propuls. Power. 34 960 doi: 10.2514/1.B36459 [4] Koizumi H, Komurasaki K, Aoyama J, Yamaguchi K 2014 Trans. JSASS Aerospace Tech. 12 1884 [5] Tsukizaki R, Ise T, Koizumi H, Togo H, Nishiyama K, Kuninaka H 2014 J. Propuls. Power. 30 91 [6] Barquero S, Tabata K, Tsukizaki R, Merino M, Navarro-Cavallé J, Nishiyama K 2023 Acta Astronaut. 211 750 doi: 10.1016/j.actaastro.2023.06.036 [7] Sekine H, Minematsu R, Ataka Y, Ominetti P, Koizumi H, Komurasaki K 2022 J. Appl. Phys. 131 093302 doi: 10.1063/5.0069600 [8] Motoki T, Takasaki D, Koizumi H, Ataka Y, Komurasaki K, Takao Y 2022 Acta Astronaut. 196 231 doi: 10.1016/j.actaastro.2022.04.015 [9] Sato Y, Koizumi H, Nakano M, Takao Y 2020 Phys. Plasmas. 27 063505 doi: 10.1063/5.0002336 [10] Tsuru T, Kondo S, Yamamoto N, Nakashima H 2009 Trans. JSASS Aerospace Tech. 7 163 [11] Yamamoto N, Maeda Y, Nakashima H, Watanabe H, Funaki I 2016 Trans. JSASS Aerospace Tech. 59 100 [12] Foster J E, Patterson M J 2005 J. Propuls. Power. 21 862 doi: 10.2514/1.4932 [13] 夏旭, 杨涓, 耿海, 吴先明, 付瑜亮, 牟浩, 谈人玮 2022 物理学报 71 045201 doi: 10.7498/aps.71.20211519 Xia X, Yang J, Geng H, Wu X M, Fu Y L, Mou H, Tan R W 2022 Acta Phys. Sin. 71 045201 doi: 10.7498/aps.71.20211519 [14] Masui H, Tashiro Y, Yamamoto N, Nakashima H, Funaki I 2006 Trans. JSASS Aerospace Tech. 49 87 [15] Kubota K, Watanabe H, Yamamoto N, Nakashima H, Miyasaka T, Funaki I 2014 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference Cleveland, OH, July 28–30, 2014 pp1–12 [16] 孟海波, 杨涓, 黄文斌, 夏旭, 付瑜亮, 胡展 2019 宇航学报 40 1478 doi: 10.3873/j.issn.1000-1328.2019.12.012 Meng H B, Yang J, Huang W B, Xia X, Fu Y L, Hu Z 2019 J. Astronaut. 40 1478 doi: 10.3873/j.issn.1000-1328.2019.12.012 [17] Hiramoto K, Nakagawa Y, Koizumi H, Takao Y 2017 Phys. Plasmas 24 064504 doi: 10.1063/1.4989734 [18] Sato Y, Koizumi H, Nakano M, Takao Y 2019 J. Appl. Phys. 126 243302 doi: 10.1063/1.5127805 [19] Fu Y L, Yang J, Geng H, Wu X M, Hu Z, Xia X 2021 Vacuum 184 109932 doi: 10.1016/j.vacuum.2020.109932 [20] 付瑜亮 2022 博士学位论文(西安: 西北工业大学) Fu Y L 2022 Ph. D. Dissertation (Xi’an: Northwestern Polytechnical University [21] 付瑜亮, 张思远, 杨谨远, 孙安邦, 王亚楠 2024 物理学报 73 095203 doi: 10.7498/aps.73.20240017 Fu Y L, Zhang S Y, Yang J Y, Sun A B, Wang Y N 2024 Acta Phys. Sin. 73 095203 doi: 10.7498/aps.73.20240017 [22] Fu Y L, Yang J, Mou H, Tan R W, Xia X, Gao Z Y 2022 Comput. Phys. Commun. 278 8395 -
计量
- 文章访问数: 95
- HTML全文浏览数: 95
- PDF下载数: 1
- 施引文献: 0