高级搜索

基于迭代算法的不同状态散射光场聚焦

,  , 

downloadPDF

上一篇

下一篇

段美刚, 赵映, 左浩毅. 基于迭代算法的不同状态散射光场聚焦[J]. 物理学报, 2024, 73(12): 124203-1. doi: 10.7498/aps.73.20231991
引用本文: 段美刚, 赵映, 左浩毅. 基于迭代算法的不同状态散射光场聚焦[J]. 物理学报, 2024, 73(12): 124203-1. doi: 10.7498/aps.73.20231991
shu
Mei-Gang Duan, Ying Zhao, Hao-Yi Zuo. Focusing scattering light field with different states based on iterative algorithm[J]. Acta Physica Sinica, 2024, 73(12): 124203-1. doi: 10.7498/aps.73.20231991
Citation: Mei-Gang Duan, Ying Zhao, Hao-Yi Zuo. Focusing scattering light field with different states based on iterative algorithm[J]. Acta Physica Sinica, 2024, 73(12): 124203-1. doi: 10.7498/aps.73.20231991
shu

基于迭代算法的不同状态散射光场聚焦

  • 1.

    太原科技大学应用科学学院, 太原　030024

  • 2.

    四川大学物理学院, 成都　610065

    • 通讯作者: E-mail: duanmg.sxu@foxmail.com.;  E-mail: zuohaoyi@scu.edu.cn.

  • 中图分类号: 42.25.-p, 42.25.Fx, 42.30.-d, 42.30.Wb

Focusing scattering light field with different states based on iterative algorithm

  • 1.

    School of Applied Sciences, Taiyuan University of Science and Technology, Taiyuan 030024, China

  • 2.

    College of Physics, Sichuan University, Chengdu 610065, China

    • Corresponding authors: E-mail: duanmg.sxu@foxmail.com;  E-mail: zuohaoyi@scu.edu.cn.

  • MSC: 42.25.-p, 42.25.Fx, 42.30.-d, 42.30.Wb

  • 摘要: 透过散射介质传递光学信息在生物医学、航空航天等领域具有广阔的应用前景. 但是, 当光通过散射介质后会引起波前畸变, 导致光学信息失真. 基于波前振幅调制技术是利用优化算法不断对入射光波前振幅进行调整, 找到可使目标区域光强最大对应的波前振幅分布. 实验主要研究通过波前振幅调制使透过散射介质的空间光实现光聚焦, 讨论在不同持续时间的散射光场中控球后卫算法与遗传算法对散射光场的调控能力. 实验结果表明, 在散射介质持续时间相同的情况下, 控球后卫算法可以实现比遗传算法更高增强因子的聚焦点以及更均匀的多点聚焦.
    Abstract: Transmitting optical information through scattering medium has broad application prospects in biomedical, aerospace and other fields. However, the light passing through the scattering medium will cause wavefront distortion and optical information blurring. Wavefront shaping technology uses a mathematical matrix to characterize the characteristics of scattering medium, which can achieve refocusing and imaging after light propagation through the scattering medium. It mainly includes optical phase conjugation, optical transmission matrix and wavefront shaping based on iterative optimization. However, the iterative wavefront shaping is considered to be a cost-effective method. Based on the wavefront amplitude modulation technology, the wavefront amplitude of the incident light is continuously adjusted by using the optimization algorithm to find the corresponding wavefront amplitude distribution that can maximize the light intensity in the target area. The system generates binary patterns implemented with digital-micromirror device (DMD) based on on-off state of micromirror, where “on” represents 1 and “off” refers to 0. The DMD has a high refresh rate and can achieve high speed wavefront amplitude modulation by using the iteration algorithm. In the experiment, the scattering medium is prepared with TiO2, water and gelatin, whose persistence times are controlled with the water-gelatin ratio (WGR). In addition, the Pearson correlation coefficient (Cor) curve obtained through 300-s-measurement under different WGR conditions, which shows that the greater WGR, the shorter the persistence time is. The experiment mainly studies the focusing of the spatial light through scattering media by wavefront amplitude modulation, and discusses the ability of point guard algorithm (PGA) and genetic algorithm (GA) to control the scattered light field with different persistence times in 64 × 64 segments. The experimental results show that the PGA can achieve higher enhancement factor and more uniform multi-point focusing than the GA after 1000 iterations in the scattering medium with the same persistence time. The relative standard deviation value is inversely proportional to the WGR value when multi-point focusing can be completed. We also demonstrate that GA can only achieve single-point focusing when WGR = 40, and it cannot accomplish multi-point focusing in self-made scattering medium. This study not only verifies a method to achieve focusing scattering light field, but also provides a new scheme for testing the performance of the iterative wavefront shaping.
  • 加载中

  • 图 1  散射光场聚焦示意图　(a)光透过散射介质的散斑; (b)调制后的光透过散射介质的聚焦; (c) PGA流程图

    Figure 1.  Schematics of focusing of scattering field: (a) Speckle formed by light passing scattering medium; (b) focusing by modulated light passing scattering medium; (c) the flowchart of PGA.

    下载: 全尺寸图片 幻灯片

    图 2  不同WGR下散斑相关系数随时间的变化

    Figure 2.  Variation curves of speckle correlation with time under different WGR.

    下载: 全尺寸图片 幻灯片

    图 3  不同WGR下每隔30 s散斑随时间的变化图

    Figure 3.  Variation of speckle with time every 30 s under different WGR.

    下载: 全尺寸图片 幻灯片

    图 4  实验装置

    Figure 4.  Experimental setup.

    下载: 全尺寸图片 幻灯片

    图 5  不同WGR下PGA和GA的单点聚焦实验结果　(a) PBR值随迭代次数的变化; (b)迭代过程中的最佳聚焦效果; 比例尺为150 μm

    Figure 5.  Experimental results of single-point focusing of PGA and GA under different WGR: (a) Variation curves of PBR value with iteration times; (b) the best focusing effect in iterative process; Scalar: 150 μm.

    下载: 全尺寸图片 幻灯片

    图 6  不同WGR下PGA和GA的多点聚焦实验结果　(a) 2点聚焦; (b) 3点聚焦; 比例尺为150 μm

    Figure 6.  Experimental results of multi-point focusing of PGA and GA under different WGR: (a) Two-point focusing; (b) three-point focusing; Scalar: 150 μm.

    下载: 全尺寸图片 幻灯片

    图 7  不同WGR下多点聚焦的平均PBR和相对标准偏差RSD (N是焦点个数)　(a) PGA和GA的平均PBR; (b) PGA的相对标准偏差RSD;

    Figure 7.  Average PBR and relative standard deviation RSD of multi-point focusing under different WGR: (a) The average PBR of PGA and GA; (b) the relative standard deviation RSD of PGA. N is the number of focal points.

    下载: 全尺寸图片 幻灯片
  • [1] Yaqoob Z, Psaltis D, Feld M S, Yang C 2008 Nat. Photonics 2 110 doi: 10.1038/nphoton.2007.297
    [2] Lai X T, Li Q Y, Chen Z Y, Shao X P, Pu J X 2021 Opt. Express 29 43280 doi: 10.1364/OE.446630
    [3] 赵富, 胡渝曜, 王鹏, 刘军 2023 物理学报 72 154201 doi: 10.7498/aps.72.20230551 Zhao F, Hu Y Y, Wang P, Liu J 2023 Acta Phys. Sin. 72 154201 doi: 10.7498/aps.72.20230551
    [4] Yang J M, He Q Z, Liu L X, Qu Y, Shao R J, Song B W, Zhao Y Y 2021 Light Sci. Appl. 10 149 doi: 10.1038/s41377-021-00591-w
    [5] Zhao Y Y, He Q Z, Li S N, Yang J M 2021 Opt. Lett. 46 1518 doi: 10.1364/OL.417606
    [6] Duan M G, Yang Z G, Zhao Y, Fang L J, Zuo H Y, Li Z S, Wang D Q 2022 Opt. Laser. Technol. 156 108529 doi: 10.1016/j.optlastec.2022.108529
    [7] 韩平丽, 刘飞, 张广, 陶禹, 邵晓鹏 2018 物理学报 67 054202 doi: 10.7498/aps.67.20172009 Han P L, Liu F, Zhang G, Tao Y, Shao X P 2018 Acta Phys. Sin. 67 054202 doi: 10.7498/aps.67.20172009
    [8] 孙雪莹, 刘飞, 段景博, 牛耕田, 邵晓鹏 2021 物理学报 70 224203 doi: 10.7498/aps.70.20210703 Sun X Y, Liu F, Duan J B, Niu G T, Shao X P 2021 Acta Phys. Sin. 70 224203 doi: 10.7498/aps.70.20210703
    [9] 李元铖, 翟爱平, 张腾, 赵文静, 王东 2022 光学学报 42 1411002 doi: 10.3788/AOS202242.1411002 Li Y C, Zhai A P, Zhang T, Zhao W J, Wang D 2022 Acta Opt. Sin. 42 1411002 doi: 10.3788/AOS202242.1411002
    [10] 李琼瑶, 扎西巴毛, 陈子阳, 蒲继熊 2020 光学学报 40 0111016 doi: 10.3788/AOS202040.0111016 Li Q Y, Zhaxi B M, Chen Z Y, Pu J X 2020 Acta Opt. Sin. 40 0111016 doi: 10.3788/AOS202040.0111016
    [11] 张诚, 方龙杰, 朱建华, 左浩毅, 高福华, 庞霖 2017 物理学报 66 114202 doi: 10.7498/aps.66.114202 Zhang C, Fang L J, Zhu J H, Zuo H Y, Gao F H, Pang L 2017 Acta Phys. Sin. 66 114202 doi: 10.7498/aps.66.114202
    [12] 张熙程, 方龙杰, 庞霖 2018 物理学报 67 104202 doi: 10.7498/aps.67.20172688 Zhang X C, Fang L J, Pang L 2018 Acta Phys. Sin. 67 104202 doi: 10.7498/aps.67.20172688
    [13] 罗嘉伟, 伍代轩, 梁家俊, 沈乐成 2024 激光与光电子学进展 61 1011008 doi: 10.3788/LOP231483 Luo J W, Wu D X, Liang J J, Shen Y C 2024 Laser Optoelectron. Prog. 61 1011008 doi: 10.3788/LOP231483
    [14] Zhou S H, Xie H, Zhang C C, Hua Y Z, Zhang W H, Chen Q, Gu G H, Sui X B 2021 Optik 244 167516 doi: 10.1016/j.ijleo.2021.167516
    [15] 朱磊, 邵晓鹏 2020 光学学报 40 0111005 doi: 10.3788/AOS202040.0111005 Zhu L, Shao X P 2020 Acta Opt. Sin. 40 0111005 doi: 10.3788/AOS202040.0111005
    [16] Vellekoop I M, Mosk A P 2007 Opt. Lett. 32 2309 doi: 10.1364/OL.32.002309
    [17] Vellekoop I M, Lagendijk A, Mosk A P 2010 Nat. Photonics 4 320 doi: 10.1038/nphoton.2010.3
    [18] Conkey D B, Brown A N 2012 Opt. Express 20 4840 doi: 10.1364/OE.20.004840
    [19] Woo C M, Zhao Q, Zhong T, Li H H, Yu Z P, Lai P X 2022 APL Photonics 7 046109 doi: 10.1063/5.0085943
    [20] Feng Q, Yang F, Xu X Y, Zhang B, Ding Y C, Liu Q 2019 Opt. Express 27 36459 doi: 10.1364/OE.27.036459
    [21] Conkey D B, Piestun R 2012 Opt. Express 20 27312 doi: 10.1364/OE.20.027312
    [22] Duan M G, Zhao Y, Yang Z G, Deng X, Huangfu H L, Zuo H Y, Li Z S, Wang D Q 2023 Opt. Comm. 548 129832 doi: 10.1016/j.optcom.2023.129832
    [23] Duan M G, Zhao Y, Huangfu H L, Deng X, Zuo H Y, Luo S R, Li Z S, Wang D Q 2023 Results Phys. 52 106767 doi: 10.1016/j.rinp.2023.106767
    [24] Vellekoop I M, Mosk A P 2008 Opt. Commun. 281 3071 doi: 10.1016/j.optcom.2008.02.022
    [25] Conkey D B, Caravaca-Aguirre A M, Piestun R 2012 Opt. Express 20 1733 doi: 10.1364/OE.20.001733
    [26] Vellekoop I M, Aegerter C M 2010 Proc. SPIE 7554 755430 doi: 10.1117/12.841159
  • 加载中
图( 7)
计量
  • 文章访问数:  283
  • HTML全文浏览数:  283
  • PDF下载数:  6
  • 施引文献:  0
出版历程
  • 收稿日期:  2023-12-20
  • 刊出日期:  2024-06-20

基于迭代算法的不同状态散射光场聚焦

  • 收稿日期:  2023-12-20

摘要: 透过散射介质传递光学信息在生物医学、航空航天等领域具有广阔的应用前景. 但是, 当光通过散射介质后会引起波前畸变, 导致光学信息失真. 基于波前振幅调制技术是利用优化算法不断对入射光波前振幅进行调整, 找到可使目标区域光强最大对应的波前振幅分布. 实验主要研究通过波前振幅调制使透过散射介质的空间光实现光聚焦, 讨论在不同持续时间的散射光场中控球后卫算法与遗传算法对散射光场的调控能力. 实验结果表明, 在散射介质持续时间相同的情况下, 控球后卫算法可以实现比遗传算法更高增强因子的聚焦点以及更均匀的多点聚焦.

English Abstract

    全文HTML

    1.   引　言

    • 光在散射介质(浓雾、云层和生物组织等)中传播时, 由于散射介质折射率的不均匀性, 使得光子逐渐失去对初始传播方向的记忆并随机地向各个方向传播[1]. 这就导致光透过散射介质后形成随机的散斑图案, 难以实现对目标信息的准确获取[2]. 近年来, 经过国内外大量研究者的不断探索, 发现波前整形技术(wavefront shaping, WFS)可以通过对入射光波前的振幅、相位或者偏振态的调整来实现畸变波前的校正, 调控后的散射光场可以形成更具实用价值的焦点或者图形模式[3–10]. 在生物医学成像、消防救援和航天探测等方面具有广阔的应用前景. 因此, 该技术迅速得到广泛的关注.

      为抑制光学散射效应造成的成像分辨率较低的影响, 研究者们提出多种散射成像技术, 主要包括: 基于迭代优化的波前整形技术[11]、光学传输矩阵法[12]和光学相位共轭法[13]的散射成像技术. 基于迭代优化的波前整形技术被认为是众多散射成像技术中性价比较高的一种方法, 主要是利用优化算法通过不断迭代找到最优波前, 实现光透过散射介质的信息传递[14,15]. 在迭代优化过程中, 散射介质可以被看作是一个“黑匣子”, 无需考虑其散射特性. 另外, 这种反馈系统具有实验光路简单, 无需采集先验数据, 可以根据散射介质的状态进行实时反馈等优点. 2007年, Vellekoop和Mosk [16]首次利用反馈优化算法结合空间光调制器(spatial light modulator, SLM)实现光透过强散射介质的聚焦, 最终获得相较于优化前散斑亮度提高1000倍的焦点, 远超出光学透镜能够达到的聚焦效果, 这项工作拉开散射光场调控的序幕. 2010年, Vellekoop 等[17]利用迭代优化波前整形技术实现光透过散射介质聚焦, 焦点的直径仅为传统光学透镜聚焦点的1/10大小, 突破光学透镜的衍射极限. 随着研究的深入, 研究者们对迭代波前整形技术的时效性和抗噪性能提出更高的要求. 2012年初, Conkey和Brown[18]首次将遗传算法(genetic algorithm, GA)引入到散射光场的调控中. GA在执行过程中将SLM上各调制单元的相位值进行整体优化, 极大地提高了波前整形的效率和稳定性. 通过与传统的连续相变算法(continuous sequential algorithm, CSA)相比, 数值模拟和实验结果都表明GA在噪声环境中的增强因子仍具有非常明显的优势. 虽然在之后的研究中提出大量的优化算法用于散射光场聚焦, 但由于GA对噪声的不敏感性, 被认为是散射光场调控领域最受欢迎的方法[19–21]. 在实际应用中, 散射介质的特性变化较快且周围通常存在很强的干扰, 这就需要所用的方法既要有较快的调控速度又要很强的抗噪声能力.

      因此, 一种可用于振幅优化的新算法——控球后卫算法(point guard algorithm, PGA)[22,23]被提出. 在算法执行过程中, PGA只需要考虑边界值(boundary value, BV)对调控性能的影响, 具有较好的稳定性, 且能高质量的完成散射光场的调控. 在该研究中, 将PGA 和GA从实验上对不同退相关时间散射光场的调控速度和抗噪性能进行对比. 另外, 实验还研究了在单点聚焦和多点聚焦中不同持续时间的散射光场与焦点增强因子和焦点均匀度的关系.

    2.   基本原理

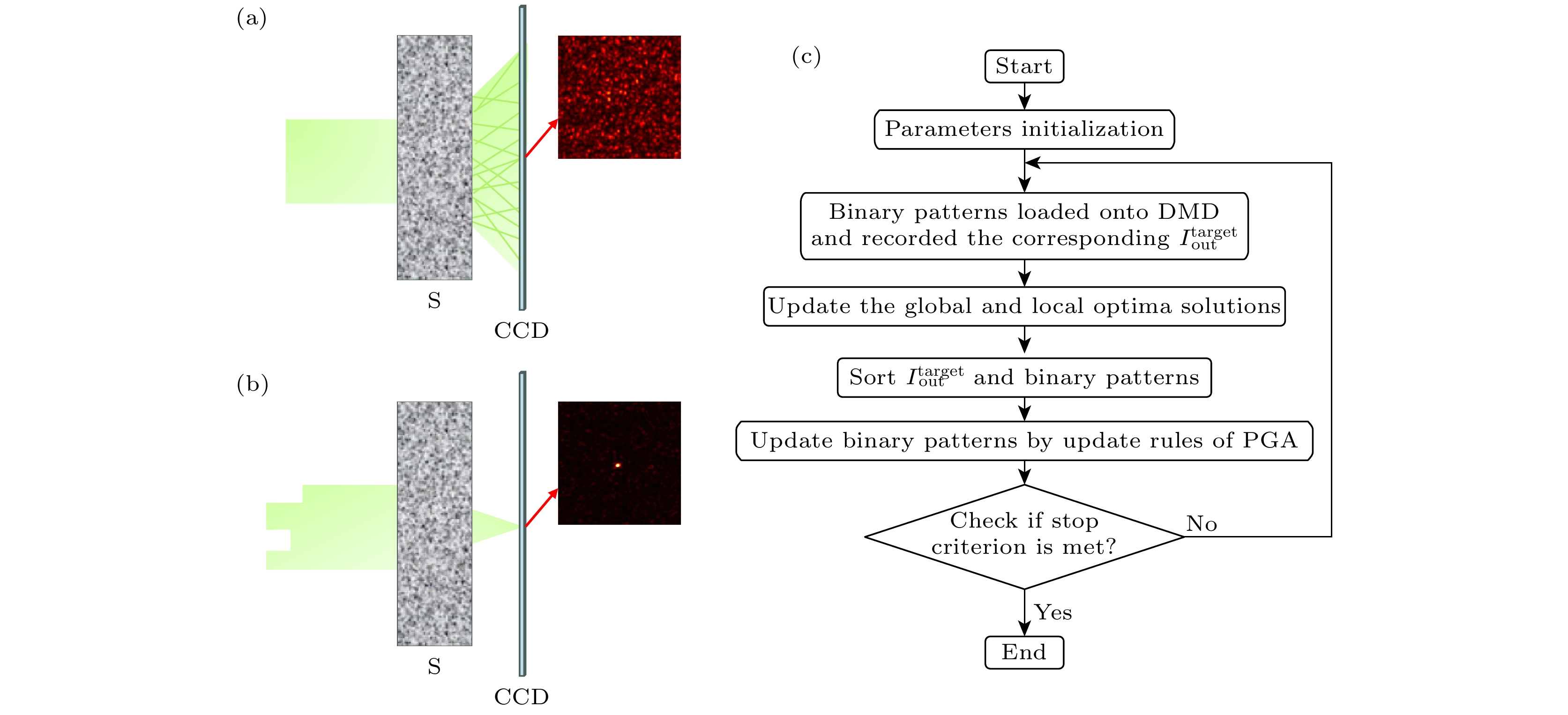
    • 由于强散射介质多重散射的原因, 光透过散射介质在电荷耦合器件(charge coupled device, CCD)上接收到的光场分布如图1(a)所示, 是一种随机散斑模式. 基于振幅的迭代优化波前整形技术是利用数字微镜阵列(digital-micromirror device, DMD)调整入射光波前振幅, 使光透过散射介质后在CCD上形成如图1(b)所示的焦点模型. 将入射光波和出射光波离散化之后, 输入场与输出场之间的关系可表示为[24]

      式中, $ E_m^{{\text{out}}} $表示第m个输出通道的复振幅; $ E_n^{{\text{in}}} $ 表示第n个输入通道的复振幅, 可表示为$ E_{n}^{{\text{in}}} = {A_n} \exp ({\rm i}{\varphi _n}) $, $ {A_n} $和$ {\varphi _n} $分别是经调制后第n个输入通道的振幅和相位; $ {t_{mn}} $为第n个输入通道经散射介质后在第m个输出通道的传输矩阵元. 因此, 基于振幅的散射光场调控是在$ {t_{mn}} $未知的情况下, 寻找DMD上每个调制段匹配的振幅$ {A_n} $. 基本步骤可概括为: 由DMD调幅后的光束经过透镜投射到浑浊介质上, 并由探测器捕获输出光场. 根据输出光场的反馈, 利用优化算法不断调整加载到DMD上的二进制模式, 直到获得所需的输出光场. 整个迭代优化过程是基于光的干涉叠加原理完成的, 通过打开DMD上有益于输出目标光场的控制段, 关闭不利于输出目标光场的控制段. 控制段的开关状态是由加载到DMD上的数字0和1实现. 其中, 0表示关闭状态(出射光反射到光路之外的位置), 1表示打开状态(出射光进入光路).

      在职业篮球赛中, 控球后卫(point guard, PG)的主要职责是通过对球的控制, 选择在恰当的时机将球传给合适的队友来组织全队的进攻. PG会根据自己周围是否存在对手的防守来判断是自己运球还是传球给队友. 如果PG周围有对手的防守, 他会把球传给队友. 为了减小传球过程中被对手抢断的概率, PG在传球前会向目标队友方向移动一段距离. 如果PG周围没有对手的防守, 他会自己运球到其他位置. PG的初始位置可用如下矩阵表示:

      其中每一行代表一个PG, 每个PG的位置由d个元素组成. 用随机数R判断PG的控球行为, 其取值范围是[0, 1]; 用边界值BV表示是否有来自对手的干扰, 其取值范围是[0.4, 0.8]. 为了反映PG的位置, 用接球段数(catching segments, CS)来反映队友上前接球时移动的距离, 用带球段数(bring segments, BS)来反映PG带球时移动的距离.

      如果R < BV, 表示PG周围存在对手的防守, PG会选择传球. 更新规则如下: 首先, 从适应度值排在前50%的个体中随机选取一个接球手, 将该街球手的位置标记为 $ {X_{k}} $(表示第k个个体). 然后, 从$ {X_{k}} $中随机选取CS个元素, 并将这些元素的值标记为$ {X_{{k, j}}} $(表示第k个个体的第j个元素的值). 该队友上前接球时移动的距离与随机选取元素的个数成正比. 最后, 将$ {X_{i, j}} $(表示第i个个体的第j个元素的值)的值用$ {X_{{k, j}}} $取代, 得到新的$ {X_{i}} $.

      如果R > BV, 表示PG周围没有对手的防守, PG会选择自己带球到合适的位置. 更新规则如下: 首先, 从$ {X_i} $中随机选取BS个元素, 并将这些元素标记为$ {X_{i, j}} $. 然后, 翻转这些元素的值, 即0变为1, 1变为0. 将$ {X_{i}} $中这些值翻转之后得到新的$ {X_i} $.

      在波前整形中, PG的位置代表DMD上加载的二进制掩码, 利用PGA实现散射光场聚焦的流程如图1(c)所示. 可概括如下.

      步骤1　参数初始化, 主要包括PG个数(p), DMD控制段数(d), 最大迭代次数(iter)以及随机产生PG的初始位置.

      步骤2　将二进制掩码逐个加载到DMD上, 并用CCD记录每个掩码对应的目标区域的光强度值. 将新得到的光强度值与上一次迭代得到的光强度值进行比较(光强度值在开始时都设置为0), 用于更新全局和局部最优解. 如果当前的光强度值较大, 我们将更新光强度值和相应的二进制掩模, 以获得新的PG个体. 如果当前的光强度值较小, 光强度值和相应的二进制掩模保持不变. 然后, 将新得到的光强度值按降序的方式进行排列. 同时, 更新相应的二进制掩模排序.

      步骤3　使用PGA的位置更新规则对PG的位置进行更新.

      步骤4　检查是否满足停止条件(最大迭代次数). 如果满足停止条件, 则输出最佳结果. 如果没有满足停止条件, 则重复步骤2和步骤3.

    3.   实验结果与分析

    • 在本节中, 主要研究内容是对比PGA和GA在光透过不同状态散射介质单点聚焦和多点聚焦的增强因子和焦点均匀度.

      • 3.1.   散射样品的制备

    • 散射样品是由明胶、去离子水和二氧化钛(TiO2)组成. 通过改变去离子水和明胶的比例(water-gelatin ratio, WGR)控制样品的黏度, 可以达到对散射样品散射特性时间变化的控制, 即是对噪声强度大小的控制. 样品制备包括: 将40 mL水加热至40 ℃, 分散0.05 g粒径大小为2—3 μm的TiO2, 并将悬浊液用旋涂仪通过离心的方法搅拌均匀. 然后, 在悬浊液中加入不同质量的分析纯明胶(gelatin, AR). 最后, 将制备好的样品置于玻璃比色皿(20 mm×27 mm×5 mm)中, 等待样品冷却形成不同持续时间的散射介质.

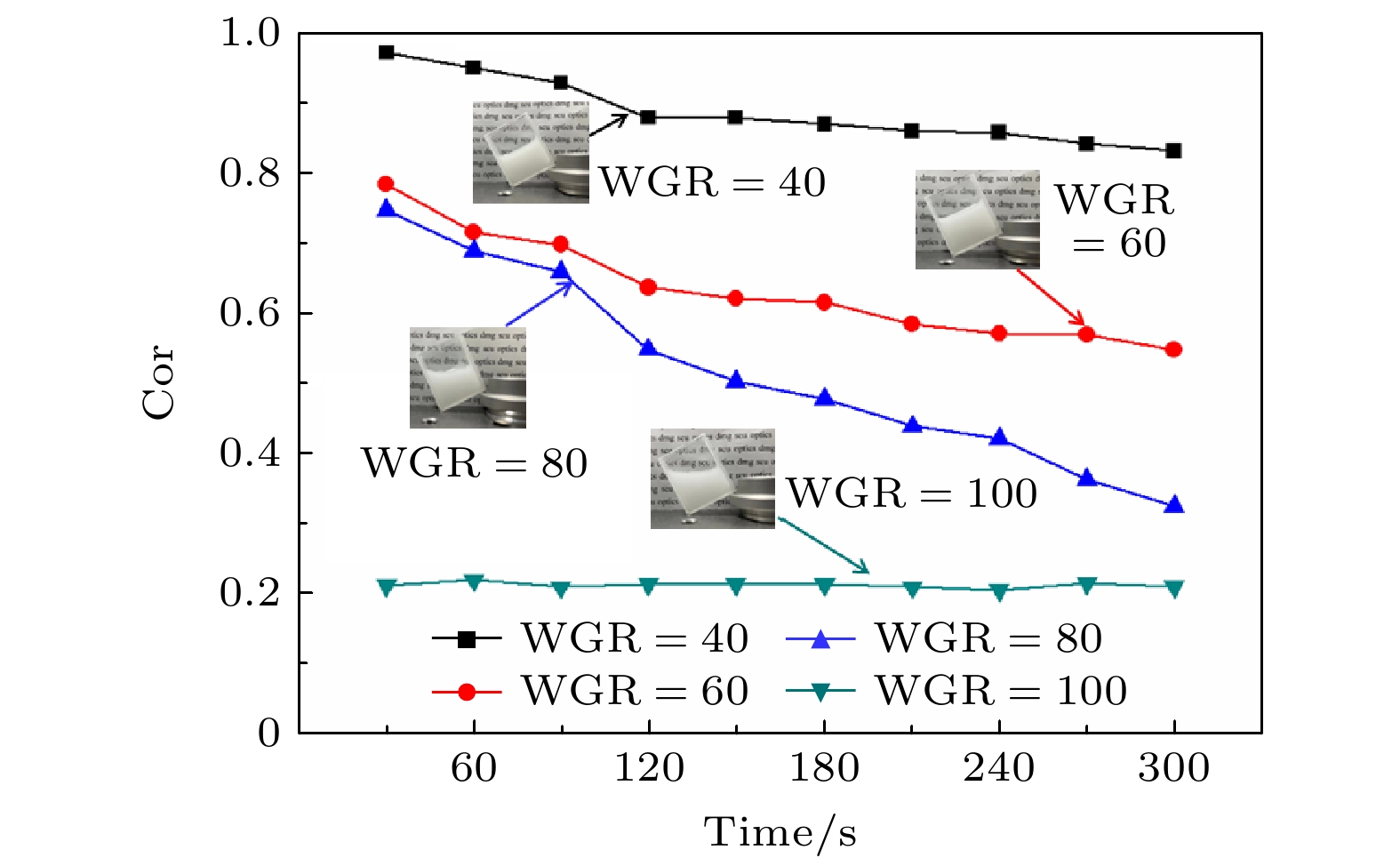
      在本实验中, 使用的散射介质分别是WGR为40, 60, 80和100的胶体. 为了说明不同WGR散射介质的散射特性变化情况, 每隔30 s测一次散斑特性, 并计算其与初始散斑之间的皮尔逊相关系数(Cor), 表达式如下:

      式中, $ {x_{i, j}} $为每隔30 s 时间CCD捕获到的散斑数据, $ {y_{i, j}} $为0 s时CCD捕获到的初始散斑数据, $ \overline x $和$ \overline y $分别是$ {x_{i, j}} $和$ {y_{i, j}} $的平均值, i和j分别是CCD捕获到散斑图像的横纵坐标. 图2是在不同WGR条件下测量300 s得到的Cor变化曲线. 为了减小由随机性引起的误差, 每条曲线是20次实验的平均结果. 从图2可以看到, WGR值越大, Cor值变化越快, 散射介质的持续时间越短(散射介质的持续时间是指散斑状态维持稳定的时间[25,26]). 这主要是由于明胶越少, 胶体的黏性越小, TiO2在胶体中受到的束缚力越小, 分子运动的变化就越快, 使得散射介质的散射特性变化越快. 图3是在不同WGR下每隔30 s测得的散斑形状. 值得注意的是, WGR = 100时, 从图3展示的介质状态可以看出, 散射介质已经处于一个流体状态, 说明胶体的黏性很低, 介质中的TiO2在快速地进行无规则运动. 此时, 在CCD上观察到散斑的变化非常快, 其状态可在极短的时间内发生变化. 经过测量后, 发现无论经过多长时间得到的散斑图与最初散斑图之间的Cor值一直维持在0.2左右, 这主要是因为Cor值的获得是通过计算两张散斑图中对应像素点之间的相关性得到. 虽然散斑的变化很快, 但CCD拍到的散斑图背景之间仍存在一定的相关性, 这就使得Cor值一直维持在某个数左右.

      • 3.2.   实验装置

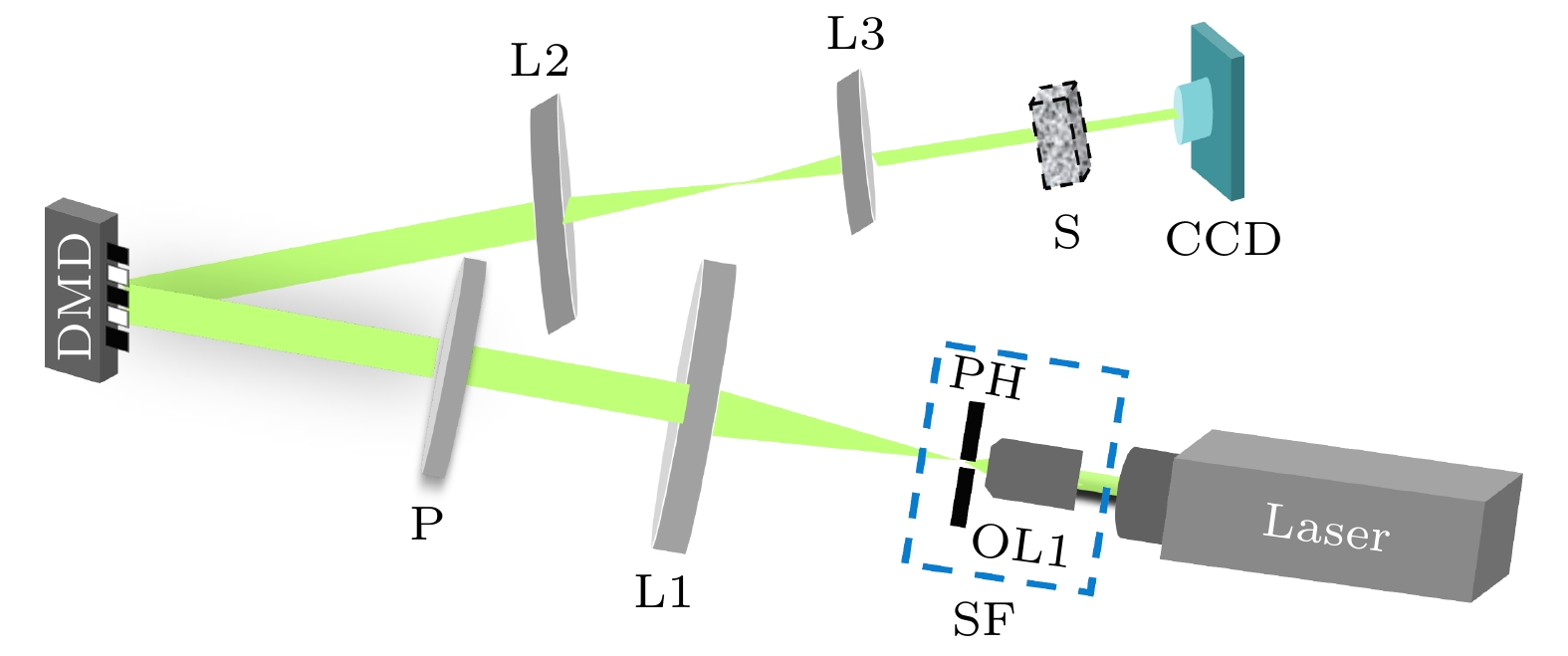
    • 光透过不同WGR的TiO2散射介质的聚焦实验装置如图4所示. 首先, 用波长为532 nm的连续激光器(MSL-FN-532 nm-200 mW, CNI)产生一束准直光束, 准直后的光束经过物镜OL1(40×, NA = 0.65)进行扩束, 扩展后的光束中心部分通过一个直径为25 μm的小孔PH. 图4蓝色框中的组件(OL1和PH)形成一个空间滤波器(SF). 然后将透过小孔的光束通过透镜L1 (f = 250 mm)产生一束平行光. 该平行光束用于覆盖DMD (型号: V-9601, Aunion Tech Co., Ltd.)的掩码区域, DMD和L1之间的线偏振片P用于调节投射到DMD上的光强度. 经DMD调整后的光束通过 透镜L2 (f = 200 mm)和L3 (f = 50 mm)缩束, 缩束后的光波照射到散射样品(S)的前表面, 透过散射介质的散射光由一个分辨率为600 × 960像素的CCD (型号: Point Grey Research, Blackfly BFLY-U3-23S6M, 8 bit)收集. DMD的分辨率为1920 × 1200像素, 刷新频率为16.393 kHz. DMD中心像素周围1024×1024像素的范围作为实验过程中的有效调制区域. 每个像素的大小为10.8 μm × 10.8 μm, 而且每个像素的可以被随机分配的值为0或1. CCD的工作范围为中心像素周围256 × 256像素, 每个像素的大小是8 μm × 8 μm.

      • 3.3.   光透过不同WGR散射介质的聚焦

    • 在实验中, DMD的有效调制区域被分为64×64个控制段. 单点聚焦的目标区域是CCD中心周围3×3像素, 多点聚焦相邻两焦点的距离为CCD上16个像素点, 每个焦点的大小仍是3×3像素.

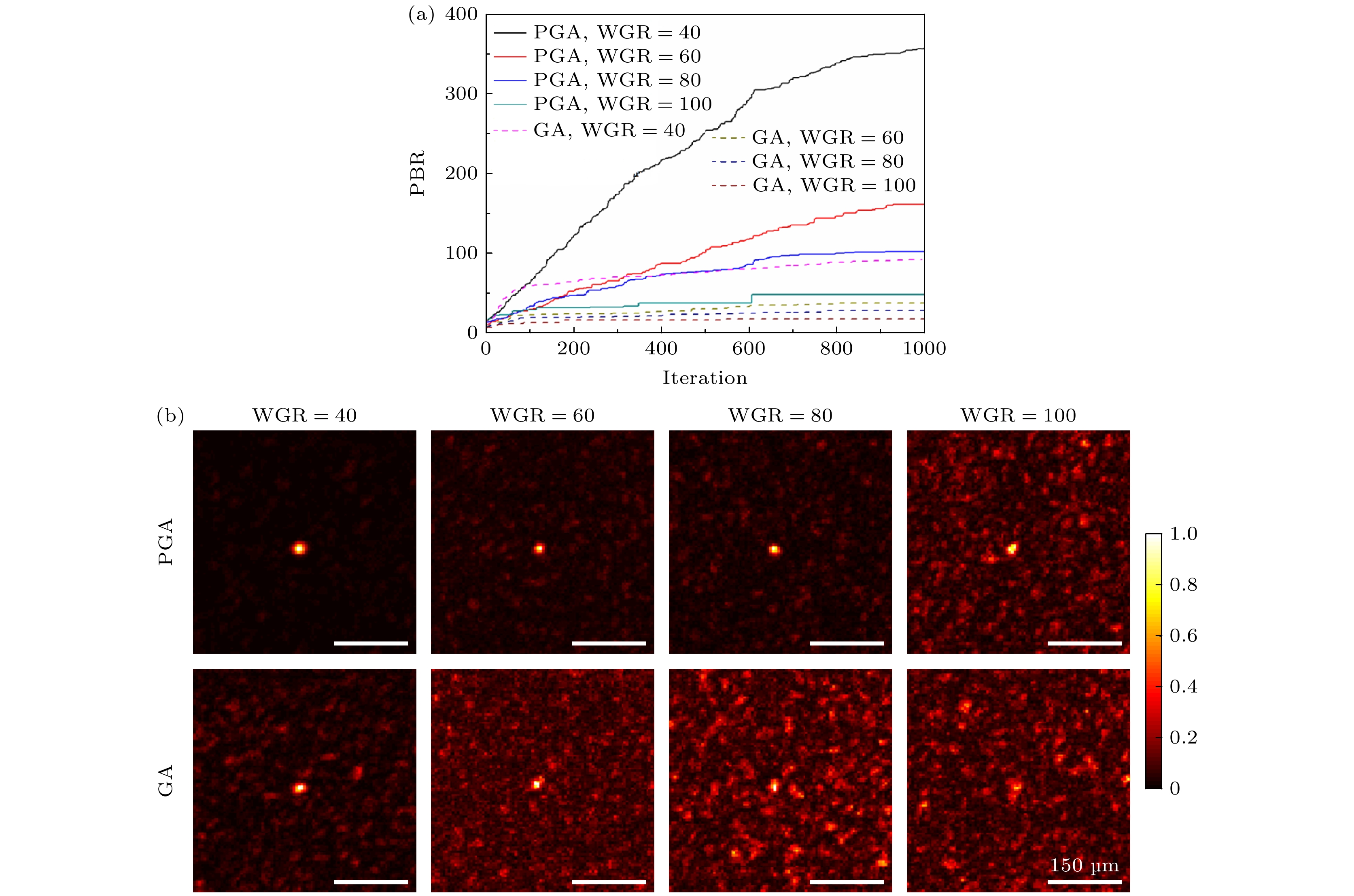
      图5是PGA和GA在种群数为20, 经过1000次迭代后得到的单点聚焦实验结果. 单点聚焦的目标函数是峰背比(peak-to-background ratio, PBR), 表达式如下:

      式中, $ I_{{\text{out}}}^{{\text{target}}} $是目标区域的光强度, $ {I_{{\text{ref}}}} $是背景的平均强度. 图5(a)是在不同WGR下PBR值随迭代次数的变化. 通过对比发现在相同WGR的条件下, PGA的PBR值增长速度总是快于GA. 而且, WGR = 80的PGA经过1000次迭代获得的最高PBR值仍比WGR = 40的GA要高. 图5(b)是PGA和GA在1000次迭代过程中的最佳聚焦模式. 可以看到, 在WGR = 80时, GA的焦点已被散斑所覆盖, 而PGA在WGR = 100时仍可以找到比较清晰的焦点. 以上实验结果均说明, PGA的抗噪声能力要优于GA, 而且PGA的收敛速度也快于GA. 值得注意的是, 由于硬件采集速率的限制, 实验中PGA和GA迭代1000次的运行时间几乎相同.

      为了进一步说明PGA对透过不同WGR散射介质的光场调控能力, 进行了多点聚焦实验, 目标函数如下:

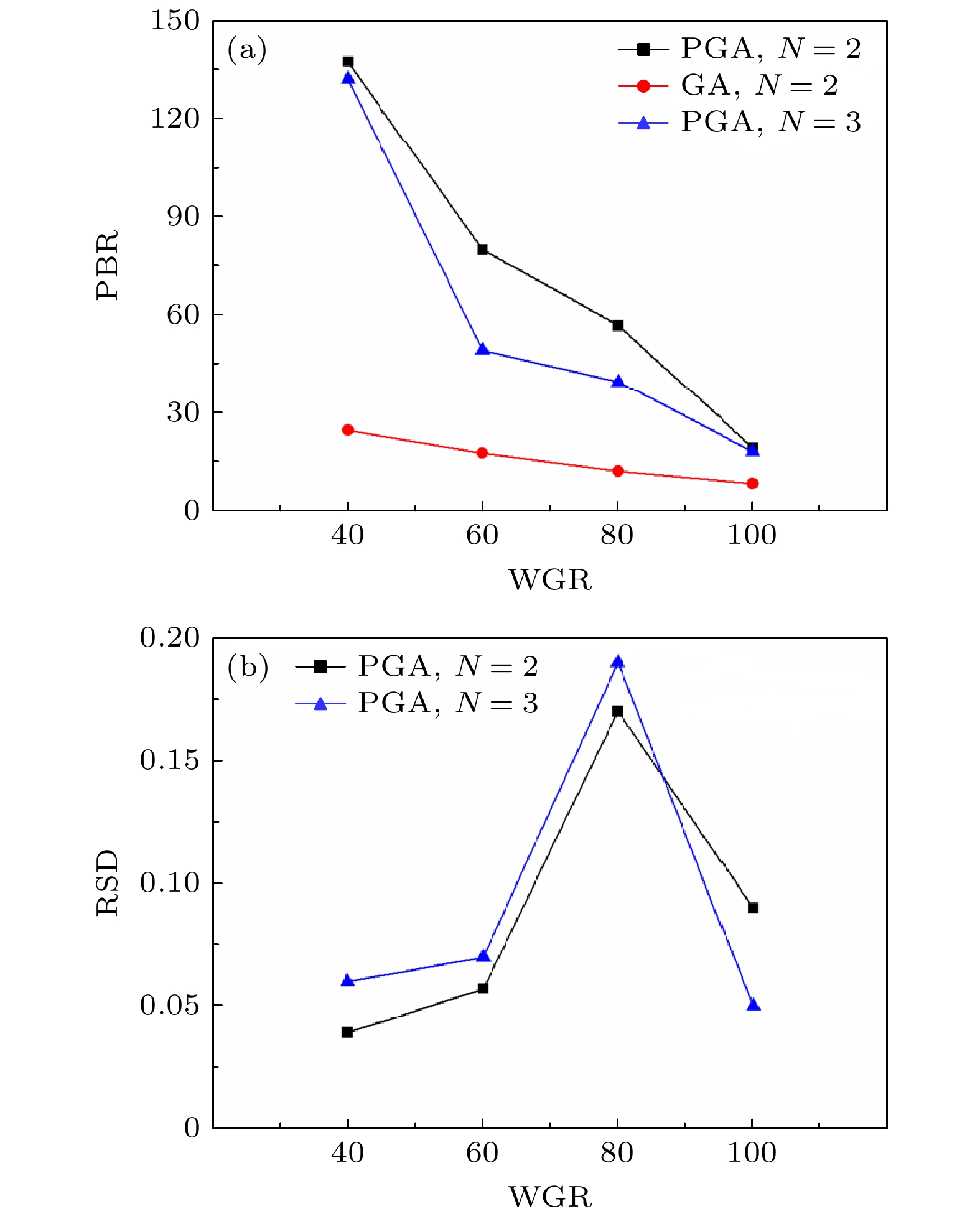
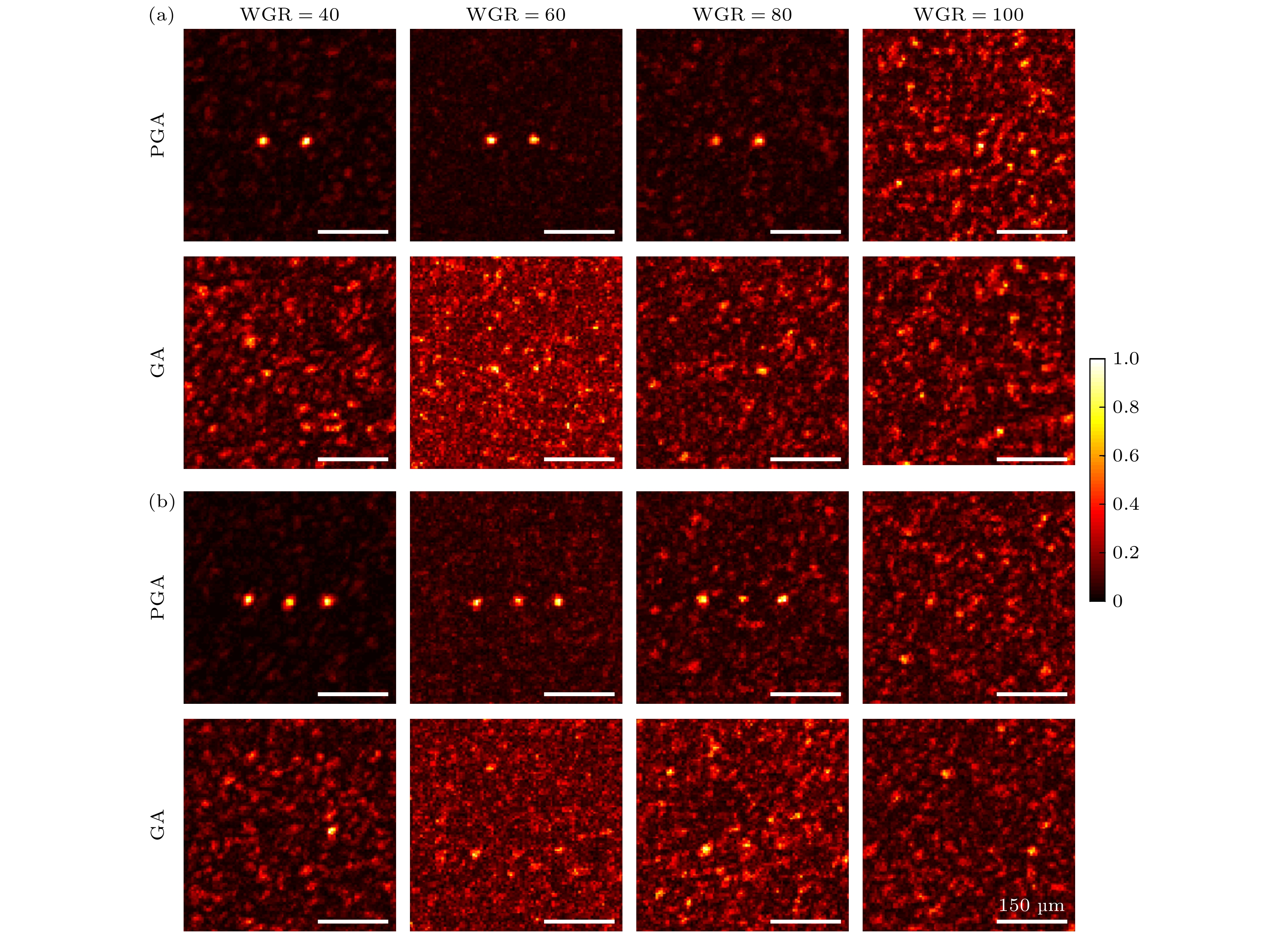
      式中, N是焦点个数, $ I_{{\text{out}}}^{{\text{target}}, n} $是第n个焦点目标区域的光强度, $ {I_{{\text{ref}}}} $是背景的平均强度. 图6是PGA和GA在经过1000次迭代后2点聚焦和3点聚焦的最佳结果. 从图6可以看到, GA在进行多点聚焦时几乎是没有调制结果的, 而PGA只有在面对WGR = 1/100快速变化的散射光场时, 多点聚焦实验才会失败. 这主要是由于在进行多点聚焦时, 算法更易受外界条件干扰的影响. 从这一点也说明PGA的抗干扰能力要强于GA. 图7(a)是不同WGR下, 多点聚焦时各焦点的平均PBR的变化曲线. 从图7(a)可以看出: 平均PBR值与WGR值成正比; 对于PGA, 平均PBR值随着焦点个数的增加在减小. 这主要是由于焦点个数越多, 优化过程越复杂, 算法对外界的干扰也越敏感, 这就使得单个焦点能达到的最大PBR值变小. 为了评估各多点聚焦焦点亮度的均匀性, 计算了不同WGR下PGA焦点PBR的相对标准偏差(relative standard deviation, RSD), 结果如图7(b). RSD值越小, 焦点强度越均匀. 在可完成多点聚焦的情况下, RSD值与WGR值成反比, 主要是由于WGR值越小, PGA受到外界干扰越明显, 多点聚焦的效果就越差, 这就使得各焦点强度之间的均匀性越差. 而在WGR = 100时, RSD的值突然变小, 这主要是由于PGA对光场几乎没有调控作用, 各焦点目标区域的强度几乎等于优化前的强度.

    4.   结　论

    • 本文主要是对PGA和GA在不同持续时间散射光场中的聚焦质量进行对比. 实验结果表明, 经过1000次迭代, GA只能在接近静态散射介质的情况下实现单点聚焦, 对于多点聚焦GA无法实现对光场的精准调控. 而PGA在持续时间较短的散射介质干扰下, 仍能实现单点聚焦和多点聚焦, 该研究结果为基于反馈优化波前整形技术推向实际应用提供了新的思路. 此外, 本文所提出的调制方法是通过DMD上微镜的开关状态来控制光的空间分布, 所以该方案仅适用于相干光源.

    参考文献 (26)

目录

/

返回文章
返回