透过复杂散射介质的高质量光学成像^[1]目前仍是一项艰巨的挑战, 一方面是由于散射直接会将入射光进行强烈散射导致目标信息淹没于背景中^[2], 另一方面是散射对波长的敏感性使得频谱信息混叠产生严重的色彩畸变, 导致彩色成像受限; 因此解决透散射介质实现彩色高分辨率成像的问题迫在眉睫.

无论是通过增大光学系统口径还是使用镜面拼接的方式^[3]来实现空间高分辨率成像^[4], 其面临的体积、重量、成本^[5]以及高精度的共相^[6]等难题都限制了目前的高分辨率成像技术的发展. 而借助于傅里叶域内频谱信息拼接来实现高分辨率成像的傅里叶叠层成像技术^[7], 将相位信息的测量难度由系统转移到计算领域, 整合了相位恢复和合成孔径的思想, 利用入射光角度的变化实现更高频信息的搬移^[8], 并通过空域记录的光强信息和频域中某种固定的映射关系来进行交替迭代求解, 实现低数值孔径(numerical aperture, NA)的高分辨率成 像结果. 自该方法提出以来, 鉴于其在测量精度^[9]、成像效率^[10]和成像通量^[11]上无可比拟的优势, 迅速受到了各国科研工作者的关注. 由于传统变光源成像技术所存在的光源调控难^[12], 不适合宏观尺度下的高分辨率成像, 研究者们提出了基于孔径扫描模式的傅里叶叠层成像系统^[13,14]. 无论是变光源还是孔径扫描模式, 其所存在的调控难度和机械扫描控制精度大幅度限制了其成像效果. 据此衍生出基于散斑照明的傅里叶叠层成像技术^[15], 则将需要通过扫描光瞳和进行光源调控的频谱搬移方式优化为控制照明光路中的散射介质平动^[16-18], 大大简化了成像难度, 提升了傅里叶叠层成像技术的普适性. 但是以上的几类成像方式, 基本都是集中于小NA复原出大NA的成像效果, 而很少关注透过散射介质^[19]实现超分辨率成像^[20]. 此外, 由于相位恢复求解中对于相干性的要求导致难以实现宽谱, 尤其是彩色成像^[21], 这也就限制了傅里叶叠层成像技术在生命科学^[22]中的应用.

针对目前傅里叶叠层成像难以透过散射介质实现彩色成像这一问题, 本文提出了一种偏振彩色傅里叶叠层超分辨率彩色成像技术. 通过对透过散射形成的散射光场中偏振特性的分析和提取^[23], 利用彩色三通道散射光场的偏振共模抑制特性进行了散射介质和低分辨率退化图像的有效分析, 结合傅里叶叠层成像技术实现了透过散射介质的超分辨率彩色成像. 实验结果表明, 该方法不仅能够有效地去除散射介质带来的图像退化, 而且能够消除傅里叶叠层中对于成像带宽的限制, 实现超分辨率彩色成像, 大幅扩展傅里叶叠层成像技术的应用.

光波在散射介质中传播时, 由于强散射所导致的帷幔效应致使成像效果急剧变差, 且所接收到的图像呈现以下3个特点: 1) 信噪比低, 强散射现象会导致背景干扰呈现指数增长, 而目标信息呈现负指数衰减, 致使目标信息难以解译^[24]; 2) 分辨率差, 光波与粒子相互作用会导致携带目标信息的光波产生复杂的相位信息改变, 丢失目标信息进而导致成像分辨率的急剧恶化^[25]; 3) 色彩畸变严重, 散射对波长的敏感使得不同波长信息产生混叠, 导致宽谱彩色成像时色彩畸变严重^[26]. 在透过散射介质所形成的强散射区内, 探测器所接收到的信号$ {I}_{{\mathrm{t}}{\mathrm{o}}{\mathrm{t}}{\mathrm{a}}{\mathrm{l}}}\left(x, y\right) $是由目标信息$ {I}_{{\mathrm{o}}{\mathrm{b}}{\mathrm{j}}}\left(x, y\right) $和背景散射信息$ {I}_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}}\left(x, y\right) $两部分组成, 且由于实验过程中采用的白光非相干光源照明, 目标与背景的干涉部分较小, 对最终成像的结果影响可近似忽略, 因此探测器采集到的图像如(1)式所示:

而散射光场中背景散射光信息的强度分布如(2)式所示:

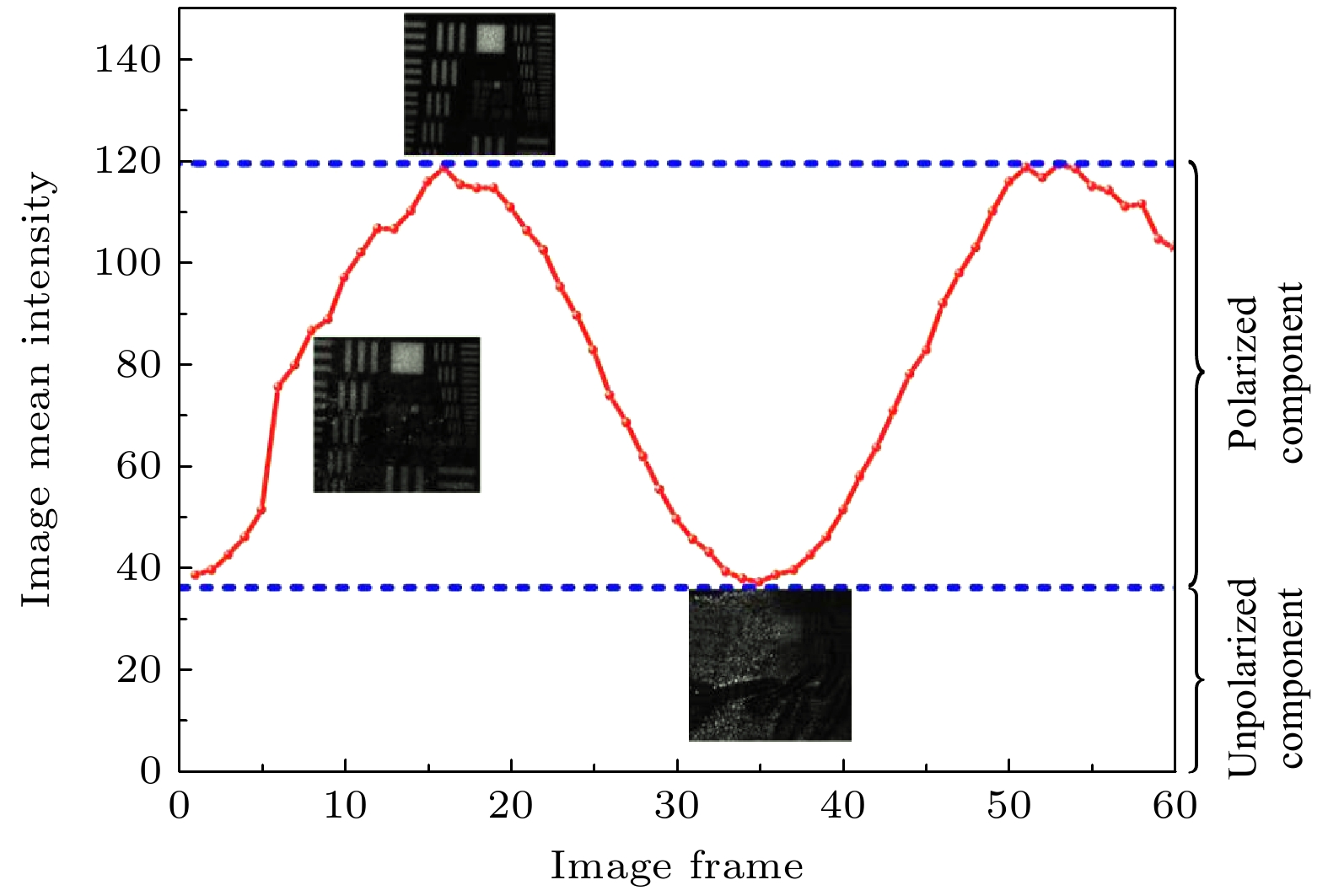
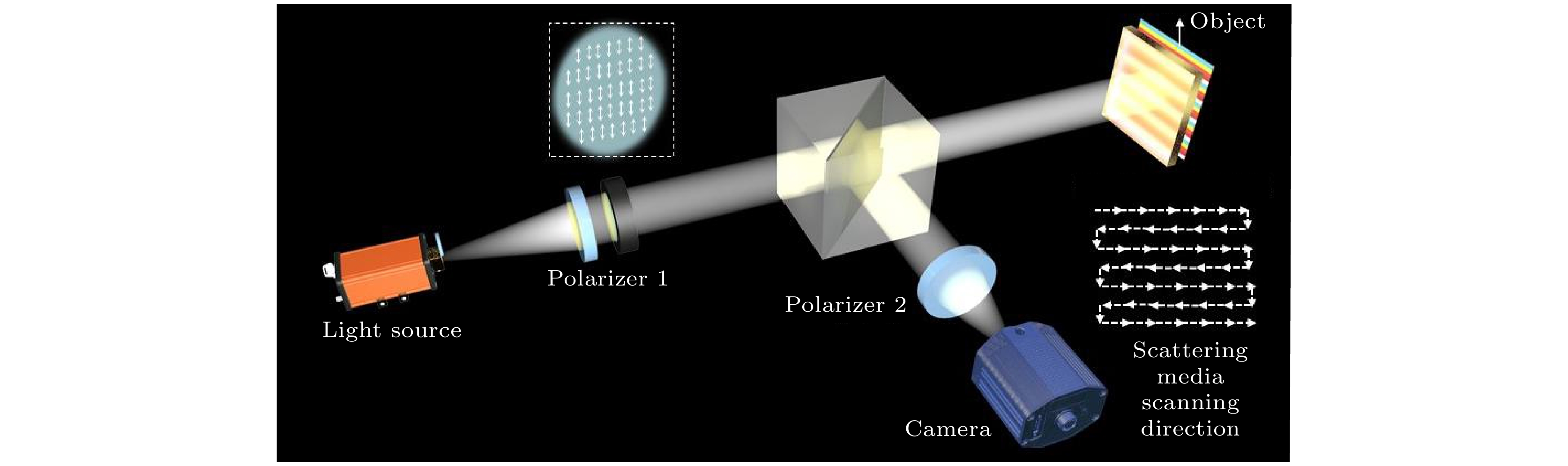
随着传输距离或散射介质散射程度的增强, 所形成背景散射越强. 这里$ {R}_{{\mathrm{c}}{\mathrm{a}}{\mathrm{m}}}\left(z\right) $为场景中任一点到探测器的距离; $ {I}_{{\mathrm{s}}{\mathrm{o}}{\mathrm{u}}{\mathrm{r}}{\mathrm{c}}{\mathrm{e}}}\left(z\right) $为光源的辐照度; b为介质的散射系数, 表征了介质在某一个角度方向$ \theta $上的后向散射饱和度; c为衰减因子; $ \theta \in \left[0, {\mathrm{\pi }}\right] $是光波在散射介质中的散射角, 根据Fresnel公式可知, 在不同散射角时x和y方向上所产生的振幅和相位存在差异性, 这就导致背景散射光场呈现出明显的偏振特性^[27].

为了验证和说明散射光场的强度和偏振特性变化情况, 根据如图1所示的原理图搭建光学成像系统并进行数据采集. 实验中利用白光光源后安装偏振片来产生完全偏振光照明, 光路中采用毛玻璃作为散射介质, 通过旋转偏振片2进行不同偏振方位角图像的采集.

如图2所示, 对偏振片2每旋转3°进行光场信息的记录, 共采集了60幅图像, 其强度变化情况如图2所示. 根据不同偏振方位角散射光场图像及均值强度分布曲线可知, 散射光场强度随偏振方位角的变化有显著的明暗变化, 并且整体服从余弦函数分布规律. 然而值得注意的是, 无论是背景散射信息还是目标信息部分都呈现部分偏振特性, 即由完全偏振和完全非偏振两部分组成, 在忽略了相干部分后, (1)式可进一步优化如(3)式的表示形式:

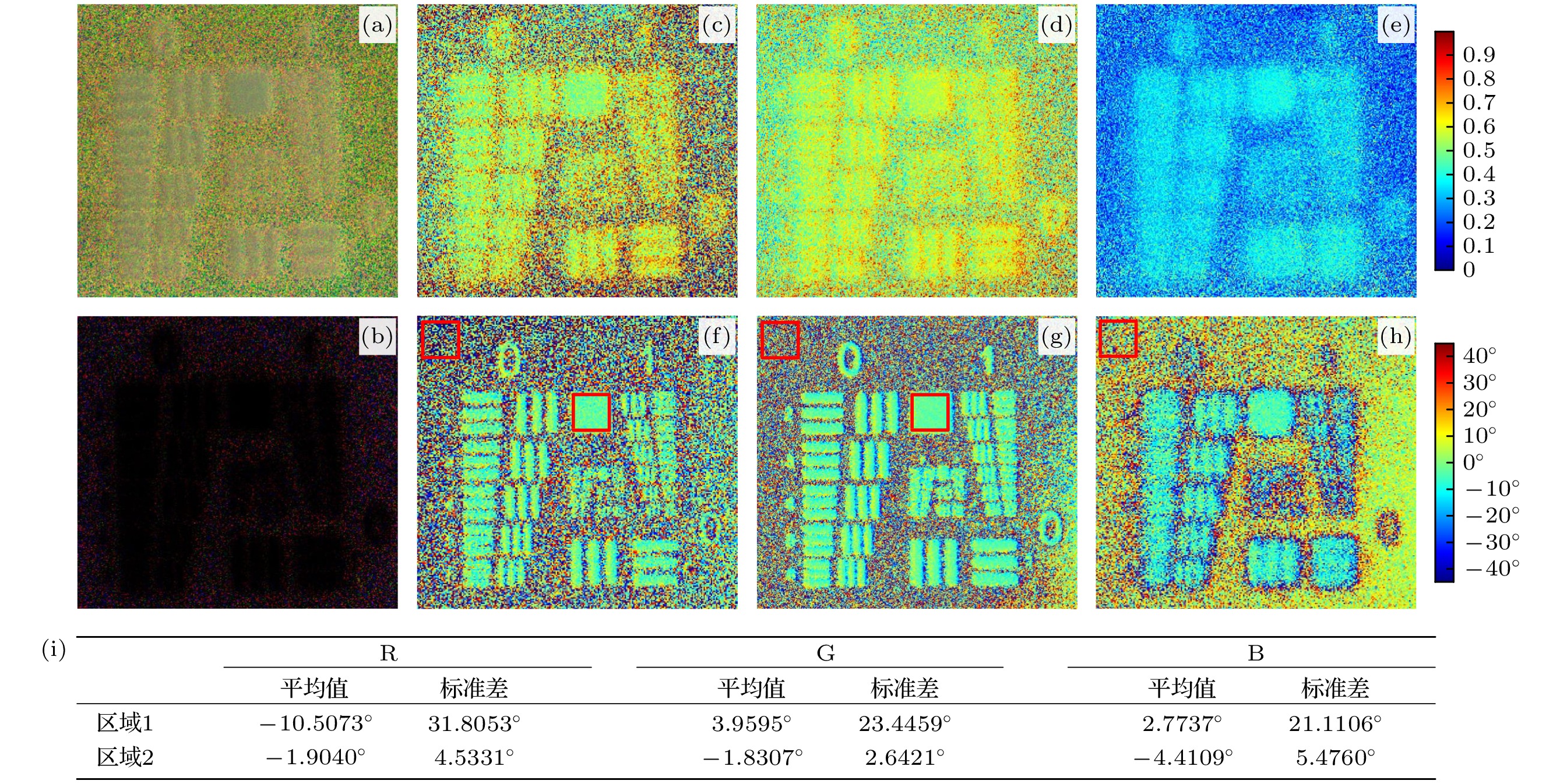
偏振度是用来描述偏振光在总光强中所占比例的参数, 能够量化表示光的偏振状态特性. 而偏振角则是描述偏振光矢量振动方向的角度参数, 它是光矢量在特定平面上振动方向与参考方向间的夹角, 能够反映偏振光振动方向的特性. 为了进一步深入分析透过散射介质后散射光场偏振特性分布情况, 其偏振度和偏振角图像如图3(a)和图3(b)所示, 图3(c)—(e)及图3(f)—(h)分别为RGB三通道的偏振度及偏振角图像. 散射光场中无论是背景散射信息还是目标信息, 都呈现出明显的偏振特性, 且偏振度值在0.3—0.8之间. 此外, 由图3(a)、图3(c)、图3(d)和图3(e)可得, 靶标条纹信息所在的目标区域的偏振特性明显弱于背景散射区域, 即在光波透过散射介质后目标与背景的信息呈现明显的偏振差异性, 且RGB三通道的偏振特性由于散射与波长的强相关性, 导致其结果也呈现差异性. 由图3(b)、图3(f)、图3(g)、图3(h)中及图3(i)的数值分析中可得, 目标信息的偏振角信息相对一致, 都集中于5°左右较小的一个范围内, 变化趋势相对平稳且规律, 而背景散射部分的偏振角信息则分布相对较为广泛. 因此, 充分考虑散射光场中两部分信息的偏振差异性并进行信号分离, 从而获得散射介质的强度信息分布和目标图像的强度信息分布, 为超分辨率重建提供基础, 从物理上解决透过散射介质的超分辨率成像问题.

由于探测器所接收到的透过散射介质形成的散射光场在偏振域内呈现明显的偏振特性, 深入分析光场中目标信息和背景散射信息的偏振差异性, 综合利用偏振的共模抑制特性有效分离出背景散射信息和目标信息, 如(4)式所示:

其中$ {I}_{{\mathrm{P}}{\mathrm{S}}{\mathrm{I}}}\left(x, y\right) $和$ {I}_{{\mathrm{P}}{\mathrm{D}}{\mathrm{I}}}\left(x, y\right) $分别为偏振求和图像和偏振差分图像^[28]. 对于理想偏振成像系统来说, $ {I}_{{\mathrm{P}}{\mathrm{S}}{\mathrm{I}}}\left(x, y\right) $相当于传统的场景强度图像. $ {I}_{{\mathrm{P}}{\mathrm{D}}{\mathrm{I}}}\left(x, y\right) $为到达探测器像元上的呈正交分布的偏振光的最大光强和最小光强之差, 如图2所示. 偏振差分图像不仅能够有效地去除非偏振光的影响, 提升场景信号的信噪比, 而且能够最大限度地反映散射光场的差异性. 但是由于介质的强散射作用导致散射场中的光强最大和最小不严格呈现正交分布, 因此为了有效地提升散射光场目标和背景干扰信息分离的准确性, 以及重建图像的质量, 本文基于偏振角信息的分布特性和目标——背景的信息无关性, 结合盲元信号分离技术分别获取背景$ {I}_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}}\left(x, y\right) $和目标$ {I}_{{\mathrm{o}}{\mathrm{b}}{\mathrm{j}}}\left(x, y\right) $的信息:

其中$ {\phi }_{m\times n} $为每个像素点上目标信息的电矢量振动占优的方向.

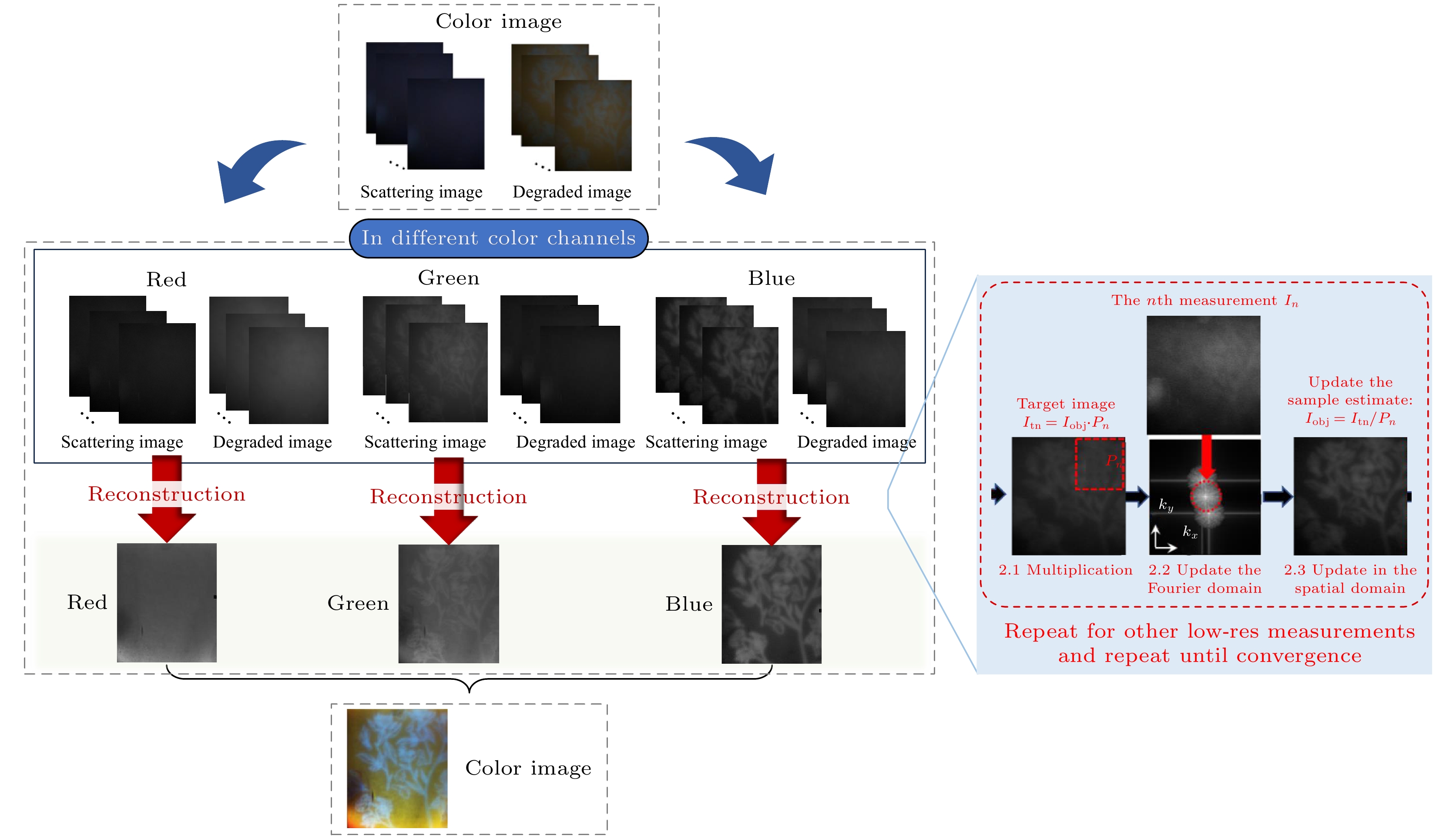
通过3.1节分析可知, 散射光场偏振特性的获取和利用可以有效解译出背景散射信息和退化的目标信息, 因此我们通过如图1所示实验装置来移动散射介质采集一系列图像对来实现频谱信息的搬移, 进而通过迭代算法来实现频谱信息的拼接, 进而获得场景的超分辨率成像, 如图4所示. 对于傅里叶叠层重建过程而言, 其超分辨率重建过程的核心是从含有不同频谱信息的散射光场中解译出的一系列退化低分辨率目标信息$ {I}_{{\mathrm{o}}{\mathrm{b}}{\mathrm{j}}} $, 结合分离出的不同背景散射信息$ {I}_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}} $所引入的高频分量对低分辨率目标信息不断重复相位恢复的迭代过程直至收敛而得到, 具体过程如图4右侧插图所示.

散射介质的移动产生了不同的照明模式, 由此可获得相应的测量图像$ {I}_{{\mathrm{t}}{\mathrm{o}}{\mathrm{t}}{\mathrm{a}}{\mathrm{l}}}(x, y) $. 获取的图像根据偏振特性可分为目标信息和背景信息(散射介质), 对应于图4中的清晰位置图像(scattering images)和模糊位置图像(degraded images), 在本文中可分别视为低分辨率目标图像$ {I}_{{\mathrm{o}}{\mathrm{b}}{\mathrm{j}}}(x, y) $和散射照明模式$ {I}_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}, n}(x, y) $. 因此测量图像可近似看作光学系统的光学传递函数(OTF)影响下目标信息与散射介质信息经傅里叶变换后的乘积, 因OTF可以在傅里叶空间中表示, 测量图像$ {I}_{{\mathrm{t}}{\mathrm{o}}{\mathrm{t}}{\mathrm{a}}{\mathrm{l}}}(x, y) $可表示为

1)通道分离

将采集的清晰位置(scattering images)和模糊位置(degraded images)两组RGB序列图像拆分为图4所示对应的三通道图像(Red, Green, Blue), 方便下面对RGB三个通道的图像分别进行重建处理.

2)初始估计

首先对待估计的样本进行初始猜测(sample estimate $ {I}_{{\mathrm{e}}{\mathrm{s}}{\mathrm{t}}{\mathrm{i}}{\mathrm{m}}{\mathrm{a}}{\mathrm{t}}{\mathrm{e}}}(x, y) $), 该初始猜测可以是一个低分辨率测量的插值图像, 也可以是随机的猜测. 本文中高分辨率目标的单通道的初始猜测$ {I}_{{\mathrm{e}}{\mathrm{s}}{\mathrm{t}}{\mathrm{i}}{\mathrm{m}}{\mathrm{a}}{\mathrm{t}}{\mathrm{e}}, k}(x, y) $是通过将对应通道的低分辨率图像进行求和平均得到的:

其中k为通道数(下文中k均为通道数序号), $ {I}_{{\mathrm{o}}{\mathrm{b}}{\mathrm{j}}, k}(x, y) $为探测器采集的k通道的低分辨率目标图像, N为对应通道低分辨率图像的数量.

3)迭代更新

目标图像$ {I}_{t, n}(x, y) $的生成. 在空间域内, 将初始猜测图像$ {I}_{{\mathrm{e}}{\mathrm{s}}{\mathrm{t}}{\mathrm{i}}{\mathrm{m}}{\mathrm{a}}{\mathrm{t}}{\mathrm{e}}, k}(x, y) $与照明模式$ {I}_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}, n, k}(x, y) $相乘生成空间域中的目标图像: $ {I}_{t, n, k}(x, y)= {I}_{{\mathrm{o}}{\mathrm{b}}{\mathrm{j}}, k}(x, y){{*}}{I}_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}, n, k}(x, y) $.

图像估计值的频域更新. 对目标图像$ {I}_{t, n, k}(x, y) $进行傅里叶变换得到对应的频域图像$ \mathcal{F} ({I}_{t, n, k}(x, y)) $, 使用测量得到的低分辨率图像$ {I}_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}, n, k}(x, y) $进行如下更新:

图像估计值的空域更新. 对更新后的频域图像$ \mathcal{F}\left({I}_{t, n, k}\right(x, y){)}^{{\mathrm{u}}{\mathrm{p}}{\mathrm{d}}{\mathrm{a}}{\mathrm{t}}{\mathrm{e}}{\mathrm{d}}} $进行逆变换, 在空间域内得到更新的目标图像$ {{I}_{t, n, k}(x, y)}^{{\mathrm{u}}{\mathrm{p}}{\mathrm{d}}{\mathrm{a}}{\mathrm{t}}{\mathrm{e}}{\mathrm{d}}} $用于目标估计值的更新. 最后, 在空间域内使用以下的等式对目标估计值进行更新, 得到更高分辨率的目标估计.

4)重复至收敛

将RGB三个通道分别输入, 对所有不同的照明模式$ {I}_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}, n, k}(x, y) $重复1)—3)的更新过程, 直到算法收敛(连续恢复的两幅图像的均方误差小于预定值), 则该过程停止.

5)通道合成

将RGB三通道的重建图像进行合并生成最终的高分辨率彩色图像$ {I}_{{\mathrm{o}}{\mathrm{b}}{\mathrm{j}}}(x, y) $.

为了验证本文方法的有效性, 搭建如图1所示的实验光路图, 通过白光LED加装起偏器来实现完全偏振光照明, 通过旋转彩色工业相机前面的检偏器来采集不同偏振方位角的散射光场信息. 以220目的毛玻璃作为散射介质置于分辨率靶标之前, 并按照如图1所示轨迹进行移动, 每次移动2.5 μm, 移动49次共采集50组的0°, 45°, 90°, 135°的偏振方位角图像用以进行重建.

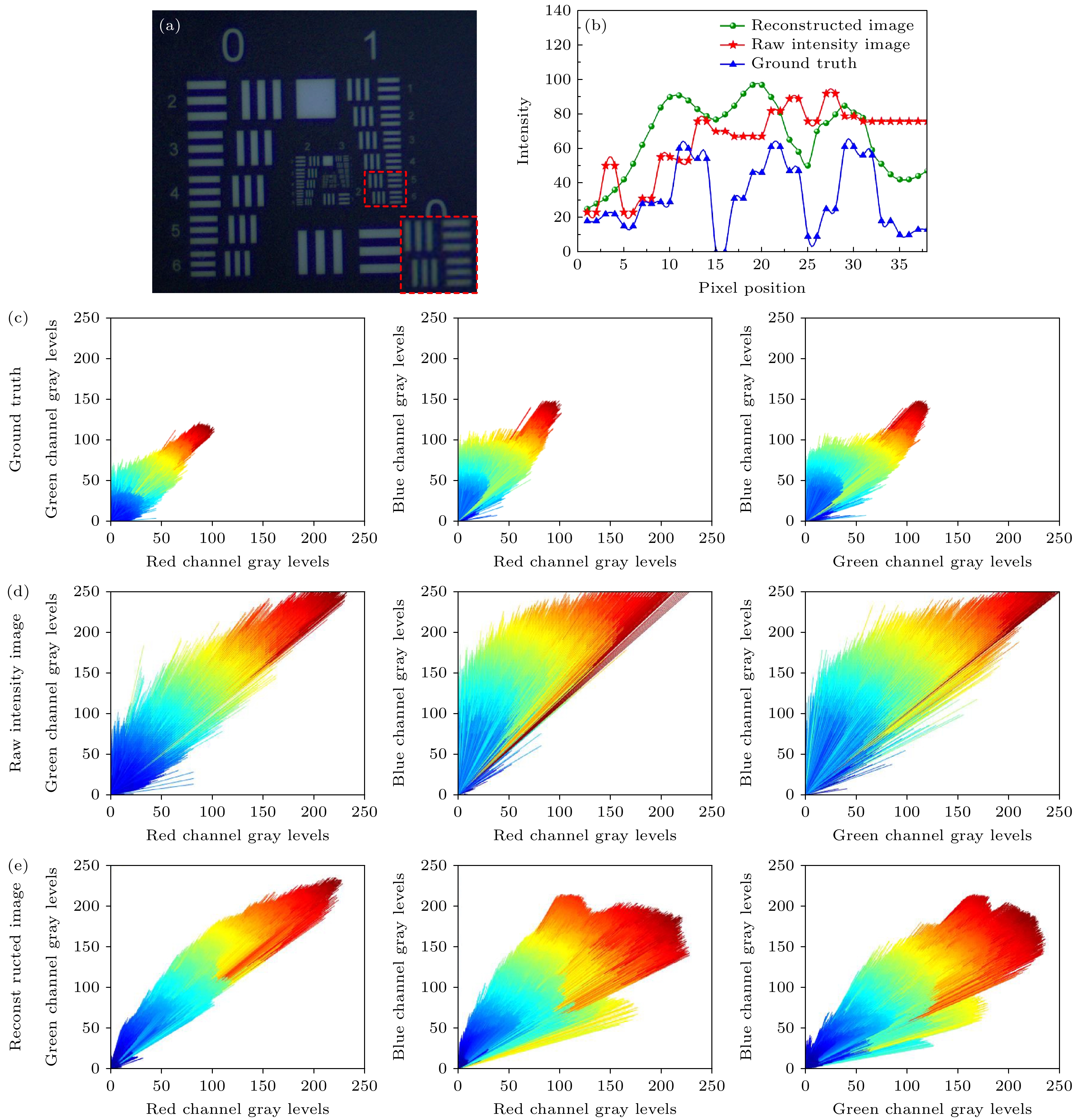
图5(a)所示为实验采集到的原始强度图像, 由于散射介质的强散射作用, 导致场景目标信息被覆盖, 图像的分辨率和清晰度大大降低; 同时由于散射的色偏效应, 致使采集到的图像产生颜色失真, 难以观测到真实的目标信息. 图5(b)为通过本文算法重建的结果, 直观上看图像的分辨率得到了明显的提升. 具体来说, 实验采集的原始强度图像的极限可分辨线对为1组3, 即可分辨198.43 μm; 通过本文算法处理之后的重建图像却能够将1组6明显分辨出来, 即可分辨140.31 μm线对. 图5(e)为传统偏振去散射方法^[29]的重建结果, 可以看出传统偏振去散射方法并没有提升分辨率. 此外, 图5(c), (d), (f)所示为图5(a), (b), (e)的1组5和6的线对细节对比图像, 本文算法所重建图像的边缘对比信息可知, 重建图像的对比度明显得到了提升. 图6(b)为在1组6元素的像素强度值分布图, 对比发现重建图像的波峰波谷变化位置与真值数据高度吻合, 其在白色条纹与黑色背景交界处的像素强度值变化剧烈, 明显优于系统采集的原始强度图像, 说明重建算法有效增强了成像结果的层次感. 总的来说, 文中所提出的算法不仅能够有效地去除散射提升成像对比度和清晰度, 而且能够提升成像系统的空间分辨率. 此外, 如图5所示, 散射光场偏振特性的深度解译虽然能够获得透过散射介质的高分辨率成像, 有效去除散射提升成像对比度和清晰度, 但目前方法仍会受限于散射介质的散射程度, 随着散射程度的增加, 场景中目标和散射介质偏振特性的差异性急剧减小, 导致信息分离精度降低, 难以重建分辨率受限.

对比图5和图6(a)所示结果可知, 实验直接获得的原始强度图像色彩畸变严重(图5(a)), 具体来说, 其在各通道的值都得到了明显增强, 而蓝色通道的强度值明显高于其他通道, 导致图像整体呈现蓝色, 色彩畸变严重, 如图6(d)所示. 而如图5(b)所示的重建结果从视觉直观上看得到了与目标靶板真值图像近似的颜色信息. 具体从图6(c)和图6(e)可得, 文中所提重建算法一定程度上在去除散射时候抑制了蓝色通道的信息, 并且R, G, B三通道中像素强度值分布均匀, 不存在某一通道占优情况, 图像质量得到了极大的提升. 此外, 为了进一步分析本文所提算法在颜色校正上的有效性, 利用CIEDE2000(color improvement evaluation with delta E2000)的色差$ {{\Delta }}{E}_{00} $和颜色测量委员会(color measurement committee, CMC)提出的色差公式来对直接采集的原始强度图像与重建结果进行分析^[30]. 无论对于色差$ {{\Delta }}{E}_{00} $还是CMC, 值越大说明图像与原始真值图像的色差差异性越大. 对比分析可知直接采集的原始强度图像的色差CIEDE2000和CMC值分别为42.57和253.08, 而重建图像的值分别为29.85和127.72, 以上结果都说明了本文所提算法在去除散射, 提升对比度以及解决散射过程中的色偏效应的有效性.

为了深入分析与对比本文算法的普适性和有效性, 实验选取了纸质、塑料、病叶和编织布等不同材质的目标, 结果如图7所示. 无论是哪种材质的目标, 整体上来看重建算法有效提升了成像质量. 以图7中的区域1为例, 受介质的强散射作用, 直接采集的原始强度图像对比度和分辨率大幅下降, 细节信息难以分辨. 此外, 图中纹理等目标区域信息因为散射对波长的敏感性而呈现蓝色, 而背景区域也呈现了明显的颜色畸变现象. 而重建图像中的树叶的脉络信息清晰可辨, 边缘信息得到有效的增强. 图7中其余无论是整体图像还是细节区域的结果都存在类似的结论, 也充分证明了本文所述方法的普遍适用性.

傅里叶叠层成像技术能够通过频谱拼接方式实现超分辨率成像, 但是目前传统方法由于信息相关性的限制, 难以实现透过散射介质的彩色超分辨率成像. 本文深度挖掘散射光场的多维光场信息, 利用散射光场中目标信息与背景散射信息在偏振域内的差异性和唯一性, 结合偏振的波长敏感性, 解算散射光场中目标与背景信息占优的散射光场偏振特性分析模型, 结合偏振的共模抑制特性, 获取宽谱成像条件下目标退化信息与背景散射信息. 最后通过傅里叶叠层成像技术在频谱信息拼接方面的优势实现了透过散射介质超分辨率彩色成像, 重建高对比度、高分辨率的彩色场景图像. 实验结果表明, 本文所提方法能够有效地抑制散射对波长的敏感性, 提升成像的对比度和空间分辨率, 获得高保真度的彩色呈现高效果, 该方法为透过散射介质的超分辨率成像提供了一种新的思路和相应的理论支撑.