高级搜索

小尺度靶丸冲击波调控的冲击波测量技术优化及应用

,  ,  ,  ,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

杨为明, 段晓溪, 张琛, 理玉龙, 刘浩, 关赞洋, 章欢, 孙亮, 董云松, 杨冬, 王哲斌, 杨家敏. 小尺度靶丸冲击波调控的冲击波测量技术优化及应用[J]. 物理学报, 2024, 73(12): 125203-1. doi: 10.7498/aps.73.20232000
引用本文: 杨为明, 段晓溪, 张琛, 理玉龙, 刘浩, 关赞洋, 章欢, 孙亮, 董云松, 杨冬, 王哲斌, 杨家敏. 小尺度靶丸冲击波调控的冲击波测量技术优化及应用[J]. 物理学报, 2024, 73(12): 125203-1. doi: 10.7498/aps.73.20232000
shu
Wei-Ming Yang, Xiao-Xi Duan, Chen Zhang, Yu-Long Li, Hao Liu, Zan-Yang Guan, Huan Zhang, Liang Sun, Yun-Song Dong, Dong Yang, Zhe-Bin Wang, Jia-Min Yang. Optimization and application of shock wave measurement technology for shock-timing experiments on small-scale capsules[J]. Acta Physica Sinica, 2024, 73(12): 125203-1. doi: 10.7498/aps.73.20232000
Citation: Wei-Ming Yang, Xiao-Xi Duan, Chen Zhang, Yu-Long Li, Hao Liu, Zan-Yang Guan, Huan Zhang, Liang Sun, Yun-Song Dong, Dong Yang, Zhe-Bin Wang, Jia-Min Yang. Optimization and application of shock wave measurement technology for shock-timing experiments on small-scale capsules[J]. Acta Physica Sinica, 2024, 73(12): 125203-1. doi: 10.7498/aps.73.20232000
shu

小尺度靶丸冲击波调控的冲击波测量技术优化及应用

  • 1.

    中国工程物理研究院, 激光聚变研究中心, 绵阳　621900

  • 2.

    中国工程物理研究院, 等离子体物理全国重点实验室, 绵阳　621900

    • 作者简介: 杨为明: 835093137@qq.com .
    通讯作者: E-mail: zhebinw@vip.sina.com.;  E-mail: yjm70018@sina.cn.

  • 中图分类号: 52.57.-z, 52.35.Tc, 52.50.Lp, 47.40.-x

Optimization and application of shock wave measurement technology for shock-timing experiments on small-scale capsules

  • 1.

    Research Center of Laser Fusion, China Academy of Engineering Physics, Mianyang 621900, China

  • 2.

    National Key Laboratory of Plasma Physics, China Academy of Engineering Physics, Mianyang 621900, China

    • Corresponding authors: E-mail: zhebinw@vip.sina.com;  E-mail: yjm70018@sina.cn.

  • MSC: 52.57.-z, 52.35.Tc, 52.50.Lp, 47.40.-x

  • 摘要: 激光聚变研究中, 冲击波调控技术是实现靶丸压缩过程的熵增调谐, 保证高性能内爆的关键实验技术. 本文在十万焦耳激光装置上首次实现了0.375 mm半径小尺度内爆靶丸下双台阶辐射驱动的高精度冲击波调控实验测量. 针对小靶丸下任意反射面速度干涉仪(VISAR)诊断有效反射区域不足的问题, 通过建立的球形反射面VISAR图像光强的理论计算方法, 提出了利用锁孔(keyhole)锥反射效应提升VISAR诊断空间区域的实验技术路线, 使得小靶丸尺度下有效 VISAR 数据区域提升了近3倍. 在实验中首次获得了整形内爆实验条件下低温液氘靶的冲击波测量实验数据, 实现了高精度冲击波调控实验测量. 实验发现, 小时空尺度内爆设计条件下, 由于反射冲击波的作用, 激光参数的较小偏差都会对冲击波追赶后的传输行为产生显著影响, 揭示了我国当前小靶丸尺度下高性能整形内爆物理过程中冲击波传输的多因素敏感性, 以及冲击波调控实验对于内爆设计验证的重要性. 本文提出的小靶丸冲击波调控实验技术, 不仅为我国十万焦耳激光装置上整形脉冲下熵增调谐实验的开展提供了技术基础, 也对基于球汇聚压缩的超高压物理研究具有重要意义.
    Abstract: In laser fusion research, the precision of shock-timing technology is pivotal for attaining optimal adiabatic tuning during the compression phase of fusion capsules, which is crucial for ensuring the high-performance implosion. The current main technological approach for shock-timing experiments is to use keyhole targets and VISAR (velocity interferometer system for any reflector) diagnostics to measure the shock velocity history. Nonetheless, this approach encounters limitations when scaling down to smaller capsules, primarily due to the reduced effective reflection area available for VISAR diagnostics. In this work, a novel high-precision shock-timing experimental methodology is used to realize a double-step radiation-driven implosion of a 0.375 mm radius capsule on a 100 kJ laser facility. By calculating the intensity of VISAR images with spherical reflective surfaces, a new experimental technical route is proposed, i.e. using the keyhole cone reflection effect to enhance the VISAR diagnostic spatial area, which can effectively increase the effective data collection region by nearly threefold for small-scale capsules. The technique has been adeptly used to measure shock waves in cryogenic liquid-deuterium-filled capsules under shaped implosion experimental conditions, thus obtaining high-precision shock-timing experimental data. The experimental data reveal that the application of this technology can markedly enhance both the image quality and the precision of data analysis for shock wave velocity measurements in small-scale capsules. Furthermore, it is discovered that under similar laser conditions, there exist considerable variations in the shock velocity profiles. Simulation analysis shows that the difference in chasing behavior of the “N+1” reflected shock wave caused by small changes in laser intensity is the main reason for the significant difference in merging speed. It is demonstrated that small changes in laser parameters can significantly affect the transmission behavior of the shock wave. This experiment highlights the complex sensitivity of shock wave transmission in high-performance forming implosion physics process on a current small capsule scale, making it essential to conduct shock-timing experiments to accurately adjust actual shock wave behavior. This research not only lays a robust technical foundation for promoting adiabatic tuning experiments ofour 100 kJ laser facility but also has profound significance for the ultra-high pressure physics research based on the spherical convergence effect.
  • 加载中

  • 图 1  (a) 球形反射面下VISAR诊断光路入射和收光示意图; (b) 成像系统F数为3时不同半径球形反射面的VISAR数据测量空间方向的光强分布; (c) 成像系统F数为4.5时不同半径球形反射面的VISAR数据测量空间方向的光强分布

    Figure 1.  (a) Diagnostic diagram of VISAR for spherical reflector; (b) spatial intensity distribution of VISAR data for spherical reflectors with different radii under the f/3 of imaging system; (c) spatial intensity distribution of VISAR data for spherical reflectors with different radii under the f/4.5 of imaging system.

    下载: 全尺寸图片 幻灯片

    图 2  (a) 利用keyhole锥壁反射效应时球形反射面的VISAR诊断示意图; (b) 有10°锥角/无锥角时VISAR光强随倾角的变化; (c) 成像系统F数为3、半锥角为10°下不同半径球形反射面的VISAR数据测量空间方向的光强分布

    Figure 2.  (a) Diagnostic diagram of VISAR for spherical reflector with cone reflection; (b) comparison of the relationship between VISAR data intensity and inclination angle with 10° cone angle or without cone angle; (c) spatial intensity distribution of VISAR data for spherical reflectors with different radii under the f/3 of imaging system and 10° cone angle.

    下载: 全尺寸图片 幻灯片

    图 3  (a) 无锥角和(b) 10°锥角keyhole靶冲击波调控实验原理示意图; (c) 无锥角和(d) 10°锥角keyhole靶冲击波调控实验设计辐射温度波形(蓝色实线)、VISAR仿真图像

    Figure 3.  Schematic diagram of shock-timing experiment under (a) non-cone angle and (b) 10° cone angle keyhole target; design of laser waveform (blue solid line) and VISAR simulation image of shock-timing experiment under (c) non-cone angle and (d) 10° cone angle keyhole target.

    下载: 全尺寸图片 幻灯片

    图 4  不同keyhole锥角的冲击波调控实验获得的VISAR原始图像

    Figure 4.  VISAR raw images obtained from shock-timing experiments with different cone angles of keyhole target.

    下载: 全尺寸图片 幻灯片

    图 5  液氘中的冲击波速度历程

    Figure 5.  Shock velocity history in deuterium.

    下载: 全尺寸图片 幻灯片

    图 6  实验实际注入黑腔的单束激光平均波形及测量的辐射温度

    Figure 6.  Average waveform of single laser beam injected into hohlraum and measured radiation temperature.

    下载: 全尺寸图片 幻灯片

    图 7  258发次冲击波传输轨迹的实验后模拟

    Figure 7.  Simulation of shock propagation trajectory of shot 258.

    下载: 全尺寸图片 幻灯片

    图 8  274发次冲击波传输轨迹的实验后模拟

    Figure 8.  Simulation of shock propagation trajectory of shot 274.

    下载: 全尺寸图片 幻灯片
  • [1] Lindl J 1995 Phys. Plasmas 2 3933 doi: 10.1063/1.871025
    [2] Lindl J D, Amendt P, Berger R L, Gail Glendinning S, Glenzer S H, Haan S W, Kauffman R L, Landen O L, Suter L J 2004 Phys. Plasmas 11 339 doi: 10.1063/1.1578638
    [3] Atzeni S, Meyer-ter-vehn J 著 (沈百飞 译) 2008 惯性聚变物理 (北京: 科学出版社) 第41页 Atzeni S, Meyer-ter-vehn J (translated by Sheng B F) 2008 The Physics of Inertial Fusion (Beijing: Science Press) p41
    [4] Robey H F, MacGowan B J, Landen O L, LaFortune K N, Widmayer C, Celliers P M, Moody J D, Ross J S, Ralph J, LePape S, Berzak Hopkins L F, Spears B K, Haan S W, Clark D, Lindl J D, Edwards M J 2013 Phys. Plasmas 20 052707 doi: 10.1063/1.4807331
    [5] Dewald E L, Rosen M, Glenzer S H, Suter L J, Girard F, Jadaud J P, Schein J, Constantin C, Wagon F, Huser G, Neumayer P, Landen O L 2008 Phys. Plasmas 15 072706 doi: 10.1063/1.2943700
    [6] Haan S W, Pollaine S M, Lindl J D, Suter L J, Berger R L, Powers L V, Alley W E, Amendt P A, Futterman J A, Levedahl W K, Rosen M D, Rowley D P, Sacks R A, Shestakov A I, Strobel G L, Tabak M, Weber S V, Zimmerman G B 1995 Phys. Plasmas 2 2480 doi: 10.1063/1.871209
    [7] Hu S X, Goncharov V N, Boehly T R, McCrory R L, Skupsky S, Collins L A, Kress J D, Militzer B 2015 Phys. Plasmas 22 056304 doi: 10.1063/1.4917477
    [8] Boehly T R, Munro D, Celliers P M, Olson R E, Hicks D G, Goncharov V N, Collins G W, Robey H F, Hu S X, Marozas J A, Sangster J C, Landen O L, Meyerhofer D D 2009 Phys. Plasmas 16 056302 doi: 10.1063/1.3078422
    [9] Celliers P M, Bradley D K, Collins G W, Hicks D G, Boehly T R, Armstrong W J 2004 Rev. Sci. Instrum. 75 4916 doi: 10.1063/1.1807008
    [10] Boehly T R, Goncharov V N, Seka W, Barrios M A, Celliers P M, Hicks D G, Collins G W, Hu S X, Marozas J A, Meyerhofer D D 2011 Phys. Rev. Lett. 106 195005 doi: 10.1103/PhysRevLett.106.195005
    [11] Robey H F, Boehly T R, Celliers P M, et al. 2012 Phys. Plasmas 19 042706 doi: 10.1063/1.3694122
    [12] Robey H F, Muncro D H, Spears B K, Marinak M M, Jones O S, Patel M V, Haan S W, Salmonson J D, Landen O L, Boehly T R, Nikroo A 2008 J. Phys. Conf. Ser. 112 022078 doi: 10.1088/1742-6596/112/2/022078
    [13] Robey H F, Celliers P M, Moody J D, Sater J, Parham T, Kozioziemski B, Dylla-Spears R, Ross J S, LePape S, Ralph J E, Hohenberger M, Dewald E L, Berzak Hopkins L, Kroll J J, Yoxall B E, Hamza A V, Boehly T R, Nikroo A, Landen O L, Edwards M J 2014 Phys. Plasmas 21 022703 doi: 10.1063/1.4863975
    [14] Robey H F, Celliers P M, Kline J L, et al. 2012 Phys. Rev. Lett. 108 215004 doi: 10.1103/PhysRevLett.108.215004
    [15] Zheng W G, Wei X F, Zhu Q H, Jing F, Hu D X, Yuan X D, Dai W J, Zhou W, Wang F, Xu D P, Xie X D, Feng B, Peng Z T, Guo L F, Chen Y B, Zhang X J, Liu L Q, Lin D H, Dang Z, Xiang Y, Zhang R, Wang F, Jia H T, Deng X W 2017 Matter Radiat. Extremes 2 243 doi: 10.1016/j.mre.2017.07.004
    [16] 晏骥, 张兴, 郑建华, 袁永腾, 康洞国, 葛峰骏, 陈黎, 宋仔峰, 袁铮, 蒋炜, 余波, 陈伯伦, 蒲昱东, 黄天晅 2015 物理学报 64 125203 doi: 10.7498/aps.64.125203 Yan J, Zhang X, Zheng J H, Yuan Y T, Kang D G, Ge F J, Li C, Song Z F, Yuan Z, Jiang W, Yu B, Chen B L, Pu Y D, Huang T X 2015 Acta Phys. Sin. 64 125203 doi: 10.7498/aps.64.125203
    [17] 蒲昱东, 康洞国, 黄天晅, 高耀明, 陈家斌, 唐琦, 宋仔峰, 彭晓世, 陈伯伦, 蒋炜, 余波, 晏骥, 江少恩, 刘慎业, 杨家敏, 丁永坤 2014 物理学报 63 125211 doi: 10.7498/aps.63.125211 Pu Y D, Kang D G, Huang T X, Gao Y M, Chen J B, Tang Q, Song Z F, Peng X S, Chen B L, Jiang W, Yu B, Yan J, Jiang S E, Liu S Y, Yang J M, Ding Y K 2014 Acta Phys. Sin. 63 125211 doi: 10.7498/aps.63.125211
    [18] 黄天晅, 吴畅书, 陈忠靖, 晏骥, 李欣, 葛峰峻, 张兴, 蒋炜, 邓博, 侯立飞, 蒲昱东, 董云松, 王立锋 2023 物理学报 72 025201 doi: 10.7498/aps.72.20220861 Huang T X, Wu C S, Chen Z J, Yan J, Li X, Ge F J, Zhang X, Jiang W, Deng B, Hou L F, Pu Y D, Dong Y S, Wang L F 2023 Acta Phys. Sin. 72 025201 doi: 10.7498/aps.72.20220861
    [19] Ge F J, Pu Y D, Wang K, Huang T X, Sun C K, Qi X B, Wu C S, Gu J F, Chen Z J, Yan J, Jiang W, Yang D, Dong Y S, Wang F, Zhou S Y, Ding Y K 2023 Nucl. Fusion 63 086033 doi: 10.1088/1741-4326/acdfe3
    [20] Philpott M K, George A, Whiteman G, De’Ath J, Millett J C F 2015 Meas. Sci. Technol. 26 125204 doi: 10.1088/0957-0233/26/12/125204
    [21] Barker L M 1998 AIP Conf. Proc. 429 833 doi: 10.1063/1.55598
    [22] Li Z C, Jiang X H, Liu S Y, Huang T X, Zheng J, Yang J M, Li S W, Guo L, Zhao X F, Du H B, Song T M, Yi R Q, Liu Y G, Jiang S E, Ding Y K 2010 Rev. Sci. Instrum. 81 073504 doi: 10.1063/1.3460269
    [23] Li Z C, Zhu X L, Jiang X H, Liu S Y, Zheng J, Li S W, Wang Z B, Yang D, Zhang H, Guo L, Xin J, Song T M, Ding Y K 2011 Rev. Sci. Instrum. 82 106106 doi: 10.1063/1.3657158
    [24] Theobald W, Miller J E, Boehly T R, Vianello E, MeyerhoferD D, Sangster T C 2006 Phys. Plasmas 13 122702 doi: 10.1063/1.2397581
    [25] Celliers P M, Collins G W, Da Silva L B, Cauble R, Gold D M, Foord M E, Holmes N C, Hammel B A, Wallace R J, Ng A 2000 Phys. Rev. Lett. 84 5564 doi: 10.1103/PhysRevLett.84.5564
    [26] Zaghoo M, Boehly T R, Rygg J R, Celliers P M, Hu S X, Collins G W 2019 Phys. Rev. Lett. 122 085001 doi: 10.1103/PhysRevLett.122.085001
    [27] Erskine D, Eggert J, Celliers P, Hicks D 2017 AIP Conf. Proc. 1793 160016 doi: 10.1063/4971756
    [28] Ramis R, Schmalz R and Meyer-Ter-Vehn J 1988 Comput. Phys. Commun. 49 475 doi: 10.1016/0010-4655(88)90008-2
    [29] Eidmann K 1994 Laser Part. Beams 12 223 doi: 10.1017/S0263034600007709
    [30] Landen O L, Caseya D T, DiNicola J M, et al. 2020 High Energy Density Phys. 36 100755 doi: 10.1016/j.hedp.2020.100755
  • 加载中
图( 8)
计量
  • 文章访问数:  392
  • HTML全文浏览数:  392
  • PDF下载数:  4
  • 施引文献:  0
出版历程
  • 收稿日期:  2023-12-21
  • 刊出日期:  2024-06-20

小尺度靶丸冲击波调控的冲击波测量技术优化及应用

    通讯作者: E-mail: zhebinw@vip.sina.com.; 
    通讯作者: E-mail: yjm70018@sina.cn.
    作者简介: 杨为明: 835093137@qq.com
  • 1. 中国工程物理研究院, 激光聚变研究中心, 绵阳　621900
  • 2. 中国工程物理研究院, 等离子体物理全国重点实验室, 绵阳　621900
  • 收稿日期:  2023-12-21

摘要: 激光聚变研究中, 冲击波调控技术是实现靶丸压缩过程的熵增调谐, 保证高性能内爆的关键实验技术. 本文在十万焦耳激光装置上首次实现了0.375 mm半径小尺度内爆靶丸下双台阶辐射驱动的高精度冲击波调控实验测量. 针对小靶丸下任意反射面速度干涉仪(VISAR)诊断有效反射区域不足的问题, 通过建立的球形反射面VISAR图像光强的理论计算方法, 提出了利用锁孔(keyhole)锥反射效应提升VISAR诊断空间区域的实验技术路线, 使得小靶丸尺度下有效 VISAR 数据区域提升了近3倍. 在实验中首次获得了整形内爆实验条件下低温液氘靶的冲击波测量实验数据, 实现了高精度冲击波调控实验测量. 实验发现, 小时空尺度内爆设计条件下, 由于反射冲击波的作用, 激光参数的较小偏差都会对冲击波追赶后的传输行为产生显著影响, 揭示了我国当前小靶丸尺度下高性能整形内爆物理过程中冲击波传输的多因素敏感性, 以及冲击波调控实验对于内爆设计验证的重要性. 本文提出的小靶丸冲击波调控实验技术, 不仅为我国十万焦耳激光装置上整形脉冲下熵增调谐实验的开展提供了技术基础, 也对基于球汇聚压缩的超高压物理研究具有重要意义.

English Abstract

    全文HTML

    1.   引　言

    • 激光聚变是目前人类获取聚变能源的最有潜力途径之一, 也是人们研究高能量密度物理现象的重要实验手段. 在激光间接驱动的惯性约束聚变研究中, 通常使用整形激光脉冲注入黑腔产生特定时间演化的X射线辐射场, 来驱动球形靶丸内爆压缩聚变燃料, 达到高温高密度条件实现聚变燃烧. 为了提升燃料的可压缩性, 点火设计通常使用强度逐步增加的多个冲击波, 使整个压缩过程接近等熵过程[1–4]. 然而, 目前的整形内爆模拟计算中的一部分模型存在较大的不确定性, 包括黑腔能量耦合[5], 靶丸能量吸收[6], 材料物性参数[7]等. 在实验过程中直接利用理论设计给出的激光和靶参数难以实现点火, 必须通过实验对理论设计参数进行验证. 冲击波调控实验就是通过实验来表征和调控多冲击波的匹配关系来达到该目的, 它是激光聚变研究四类调谐实验平台之一.

      冲击波调控实验技术的关键是在内爆实验 条件下实现靶丸中多冲击波的原位高精度诊断. 美国提出锁孔(keyhole)靶 [8]和成像型任意反射面 速度干涉仪(velocity interferometer system for any reflector, VISAR)[9]诊断的技术路线, 先后在 OMEGA和NIF激光装置上开展了一系列冲击波调控技术验证实验. Boehly等[8,10]在OMEGA装置上, 采用分解实验排除了点火强辐射环境下诊断窗口致盲的实验技术风险, 采用直接驱动方式验证了NIF尺寸靶丸中的汇聚冲击波测量的诊断技术有效性. Boehly等[11]在NIF装置上采用增加冷冻屏蔽罩的方式解决了低温结霜的实验技术问题. Robey等采用数值模拟评估了keyhole靶黑腔的辐射温度原位替代性[12], 采用实验验证了DT冰和液氘物性参数的替代性问题[13]. 基于keyhole靶和VISAR诊断的实验技术在NIF装置上逐渐发展成为一个成熟的keyhole实验平台, 通过该平台的高精度冲击波调控实验, 美国不断优化点火设计的激光和靶参数, 实现了内爆性能的显著提升[14].

      我国激光聚变研究中整形脉冲条件下的综合内爆实验研究主要依托十万焦耳激光装置[15]开展, 并取得了一系列的内爆物理实验成果[16–19]. 其中面向高性能内爆的熵增调谐需求的冲击波调控实验技术研究, 相比美国百万焦耳级的NIF装置, 具有更强的技术挑战性. OMEGA和NIF装置上的冲击波调控实验表明, VISAR诊断的有效空间区域和靶丸的曲率半径成正比[8,11]. NIF冲击波调控实验中靶丸内半径为1 mm, VISAR诊断的有效空间区域约300 μm, 容易实现高精度诊断应用. 而我国十万焦耳激光装置受限于驱动能力, 内爆靶丸的典型尺度只有NIF靶丸大小的1/3[18], VISAR诊断的有效空间区域仅为80 μm. 而且随着球形冲击波向靶丸内传输, 有效空间区域还将进一步减小, 导致VISAR数据的干涉条纹数减少, 这将严重影响图像质量和数据分析精度[20,21]. 因此十万焦耳装置上开展冲击波调控实验面临的主要问题是小时空尺度球形波阵面演化的诊断区域不足的问题.

      本文对十万焦耳激光装置中keyhole靶结构下小时空尺度球形波阵面的VISAR诊断图像进行了深入研究, 发展了理论计算方法, 提出了利用锥面反射效应提升VISAR诊断区域的实验技术, 并应用于低温液氘靶的冲击波测量实验, 首次获得了高质量的冲击波调控实验数据. 研究表明, 利用锥面反射使VISAR数据的空间范围提高了近3倍, 大幅提升了VISAR测量质量及可靠性. 另外, 通过冲击波调控实验数据发现, 由于反射冲击波的作用, 激光参数的较小偏差都会对冲击波追赶后的传输行为产生显著影响. 因此, 对于国内十万焦耳激光装置小时空尺度下的整形内爆设计中, 需要通过冲击波调控实验对激光驱动多冲击波及反射冲击波进行精细表征和调控, 保证压缩过程的熵增满足理论设计要求.

    2.   小尺度靶丸下的冲击波测量技术优化

      2.1.   VISAR数据光强分布的理论计算

    • VIASR是研究高速瞬态物理过程的重要光电仪器系统, 它基于多普勒效应, 将待测反射面的速度变化转化为探针光的频率变化, 然后利用将频率变化转化为干涉条纹的明暗变化, 采用高速光学条纹相机对其进行记录, 从而获得干涉条纹随时间演化的过程, 最终通过数据反演获得待测反射面的速度历程. 对VISAR图像, 通常只关注反映速度信息的干涉条纹偏移信号, 而对于图像强度的时空演化很少进行定量研究. 而图像强度的来源及演化是决定VISAR诊断有效性的基础, 这在非平面冲击波的测量中尤为重要. 冲击波调控实验中需要对靶丸中的球形汇聚冲击波的速度历程进行测量, 这里的待测波阵面就是一个典型的非平面冲击波. 本文从VISAR诊断的基本原理出发, 对冲击波调控实验中VISAR数据的光强进行定量计算.

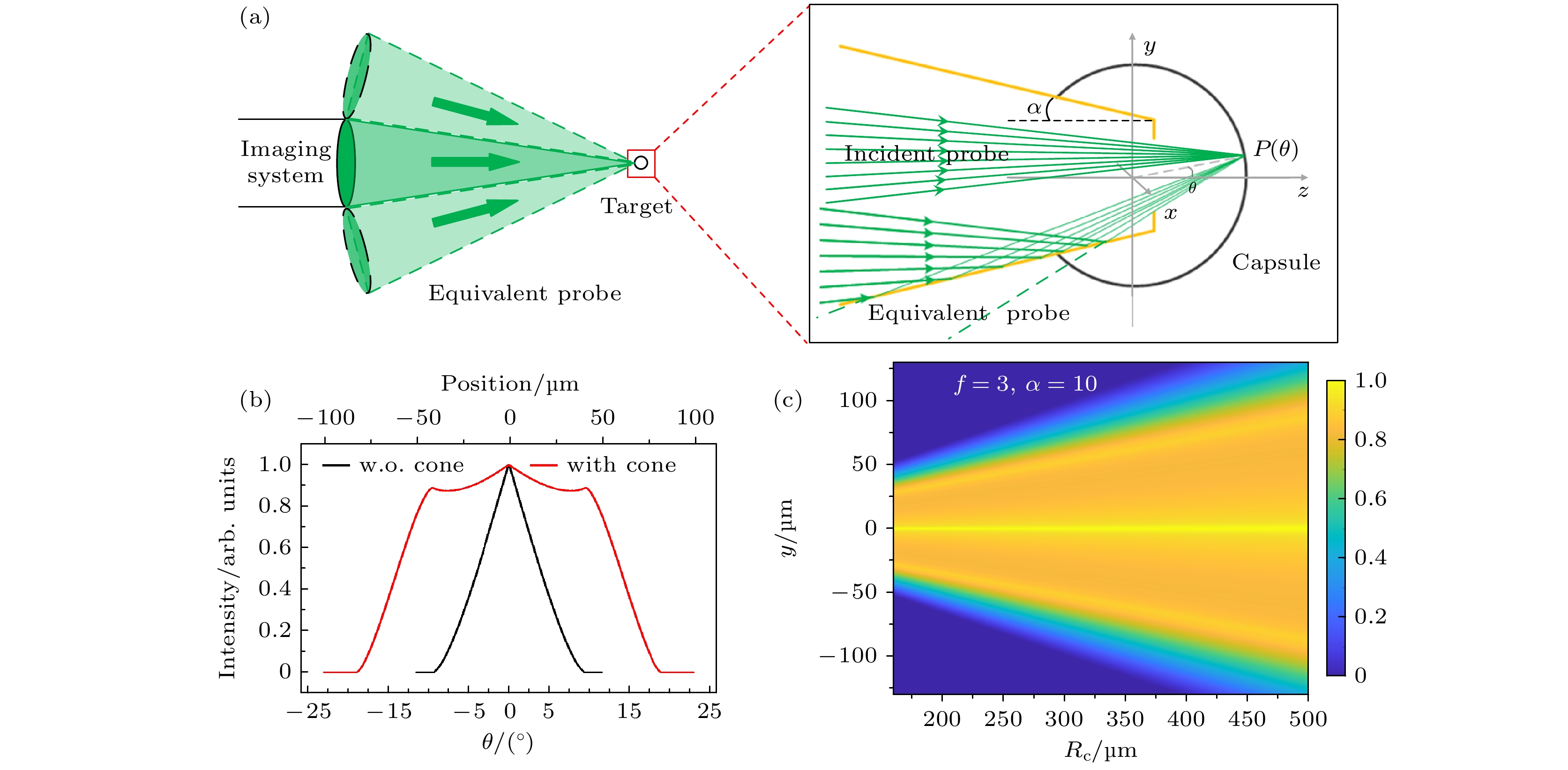
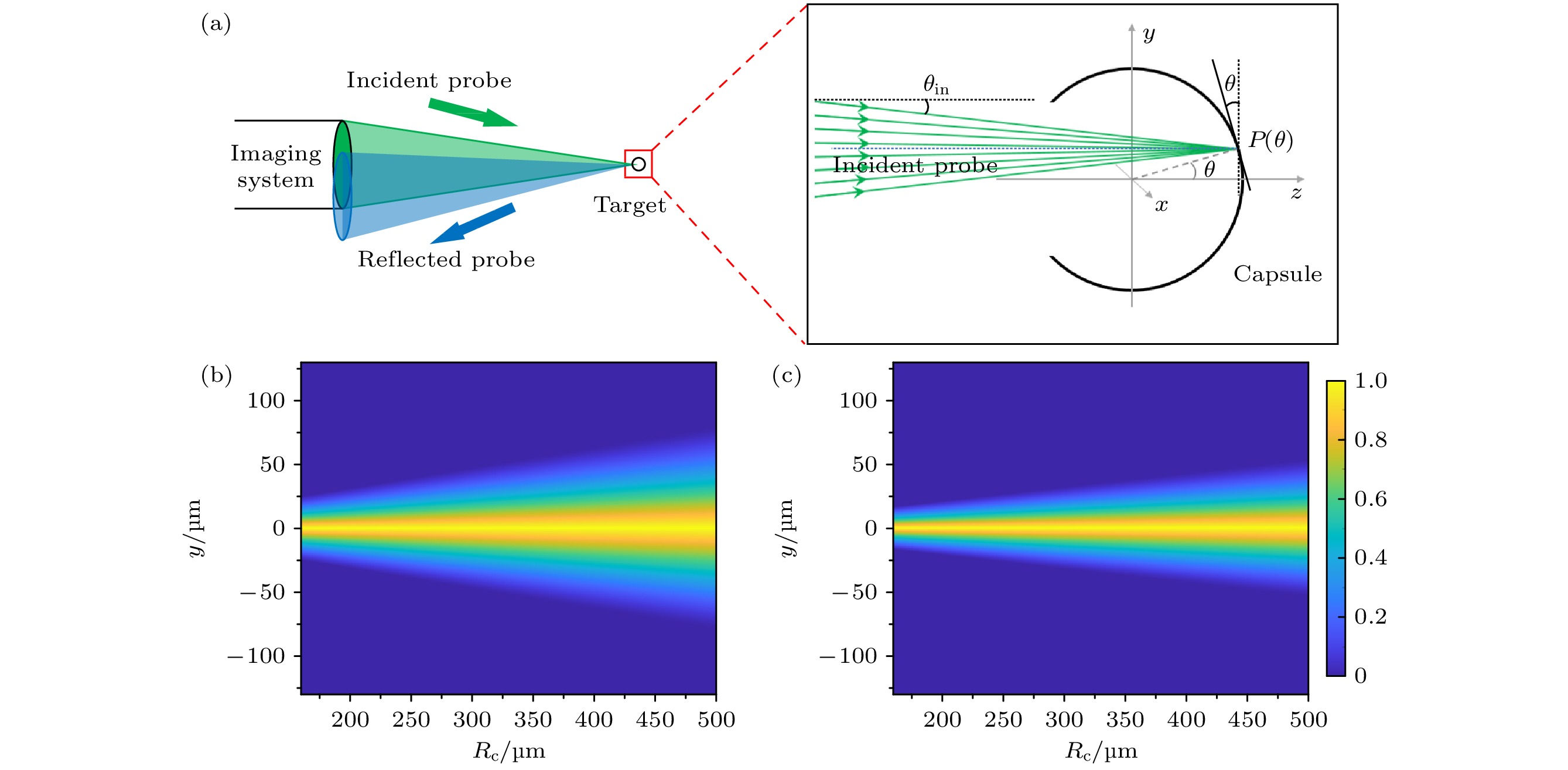
      采用光线追踪模型来定量计算球形反射面的VISAR数据信号强度, 图1(a)展示了球形反射面下VISAR诊断光路入射和收光示意图. 在模型中, 探针光是从成像系统末端出射的一个汇聚面光源, 面光源的任意位置都有光线照射任意待测位置P, 如图中绿色箭头所示. 因此探针光中任意光束的入射角可以表示为

      其中r0是光源的半径, fp是探针光源的F数, x和y分别是光源出射面(即成像系统末端面)的空间坐标. 那么对于待测点P, 总的入射光强为所有光线强度Iin(x, y)的总和, 为

      然后探针光线经P点反射, 假设P点反射面和探针光光轴垂线存在倾角θ, 在球面上也等于该点对球心的张角, 如图1(a)所示, 则反射光线的反射角为

      最后VISAR数据信号强度来源于从待测反射面反射后能被成像系统收集的光线贡献, 即反射角度小于成像系统收光角的光线, 可计算为

      其中${\varphi _0} $是成像系统最大收光角, $ {\varphi _0} = \arctan (1/2{f_{\rm c}}) $; fc是成像系统的F数.

      对于倾角为0°的平面反射面, 由(3)式可知反射角等于入射角, 此时所有光线均能返回收光系统. 由(4)式可知光强只取决于探测点的反射率, 为

      当倾角不为0°时, 并不是所有探针光光线都能返回收光系统, 如图1(a)中的蓝色区域表示的反射探针光束所示, 此时只有图中两个代表入射光锥和反射光锥的交叠区域内的光线可以返回收光系统贡献VISAR数据的信号强度. 假设上述面光源发出的光线强度均匀, 那么VISAR数据信号强度正比于和倾角θ相关的重叠区域面积. VISAR诊断系统的常规配置中, 面光源尺寸和成像系统末端透镜尺寸一致, 即探针光的入射F数等于成像系统的收光F数($ {f_{\text{P}}} = {f_{\text{c}}} $). 那么在小角近似下, P点对应的VISAR数据光强可以表示为

      从(6)式可以看到, 对于存在一定倾角的反射测量, VISAR数据光强将不再是一个只和反射率相关的值, 还和倾角θ以及成像系统F数等实验布局密切相关. 对于球形波阵面上的任意P, 反射面的倾角和空间位置相关, 设反射球面半径为rc, 则不同空间位置(xP, yP), 反射面角度θP为

      将(7)式代入(6)式, 可以获得球位型下不同空间位置的VISAR数据光强. 图1展示了上述理论计算的不同球形反射面半径下, VISAR测量方向上不同空间位置的光强图, 图1(b)和图1(c)分别对应成像系统F数分别为3和4.5的结果. 可以看到F数固定的情况下, 不同空间位置的光强分布呈中间强两侧弱; 随着收光系统F数的减小, 即对应入射立体角和收光立体角的增大, 可观测区域也将增大. 定义图像有光强的位置为VISAR可观测区域, 可以看到, 随着反射球面的半径变小, 可观测区域不断变小, 这是由于随着半径变小, (7)式计算的倾角θP不断变大导致.

      当前我国激光聚变整形内爆实验受限于十万焦耳激光装置输出能量, 其靶丸几何内半径为0.375 mm, 显著小于美国点火靶丸的毫米半径尺寸. VISAR收光系统的F数fc最早设计为4.5, 此时可测量区域理论上最大约为80 μm. 考虑探测器的响应灵敏度、光路传输的效率、噪声以及瞄准偏差等因素的影响, 实际应用中VISAR可测量区域将更小. 如何实现小靶丸尺度下多冲击波传播行为的精密测量成为我国当前激光聚变精密实验的特有难点之一.

      • 2.2.   小曲率半径球面冲击波的VISAR诊断优化

    • 基于上述分析, 优化VISAR诊断图像的一种直观的技术路线就是降低F数. 影响VISAR数据光强的F数有两个, 一个是成像系统的F数fc, 决定反射光的收光角度范围; 另一个是入射探针光的汇聚F数fp, 决定入射光的角度范围. 因此, 降低两种F数均可提升球形波阵面的观测区域. 我们首先将成像系统F数减小为3, 从(6)式可知此时可测量区域理论上最大约为120 μm. 然而考虑到碎片防护等工程因素, VISAR成像系统F数进一步减小空间有限, 因此需要设计新的技术路线进一步提升VISAR测量区域.

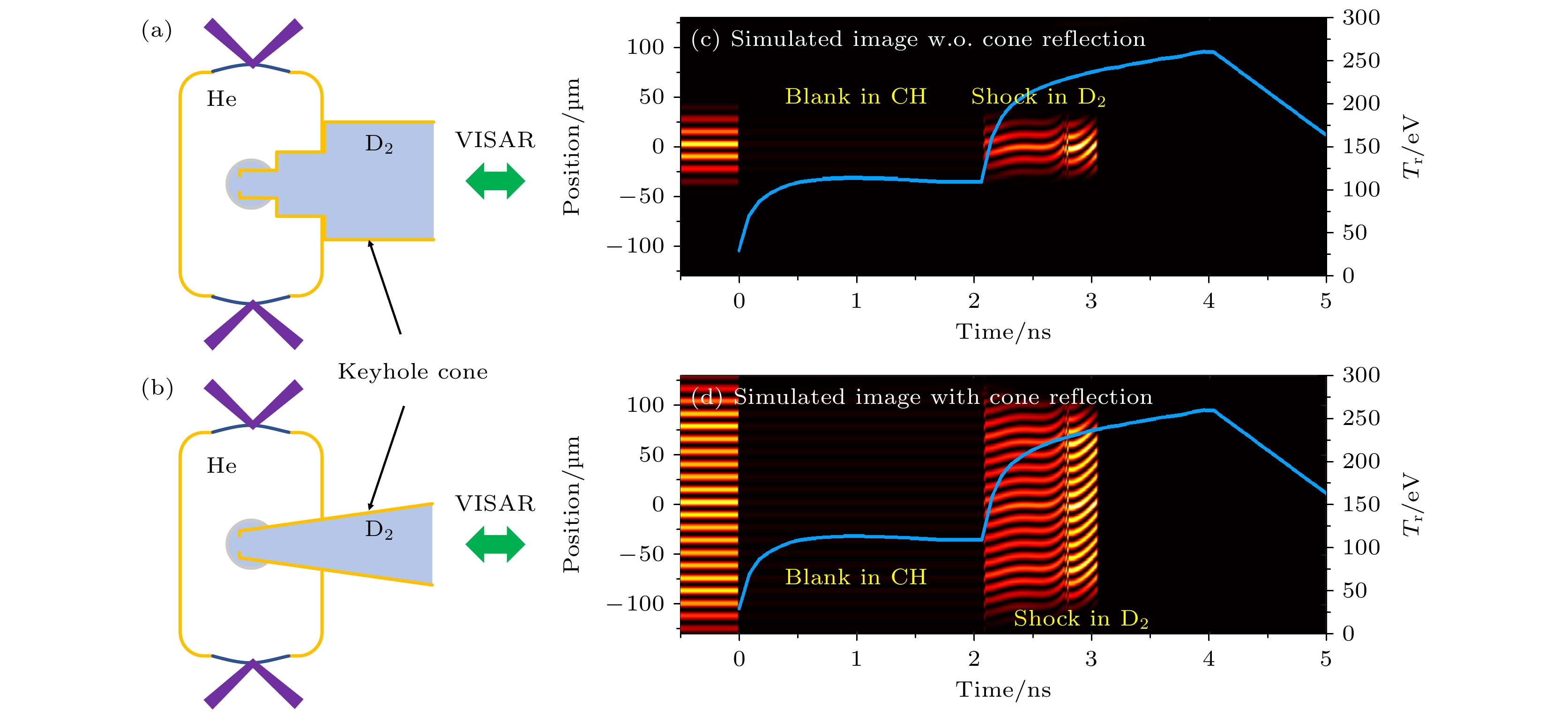
      我们提出利用keyhole靶的金锥锥壁反射效应等效地降低入射探针光的汇聚F数, 实现VISAR测量区域增大的技术路线. 如图2(a)所示, 引入一个角度合适的金锥, 此时探针光除了直接入射靶丸中的待测位置, 还会通过金锥反射入射待测反射面, 即等效于增加了一个额外光源, 如图2(a)中虚线区域所示, 从而增加了入射光的角度范围. 假设锥面半锥角为α, 则等效探针光源增加的入射角度范围有

      此时对于任意探测点P, 增加光源部分贡献的VISAR强度为

      其中Rcone是金锥的反射率. 将(1)式、(3)式代入(9)式, 并叠加上(6)式, 可得利用keyhole靶金锥反射后总的VISAR数据强度分布. 图2(b)展示了有/无锥角反射效应下不同倾角的光强分布, 其中锥角为10º、成像系统F数为3、金锥反射率为1. 由图2(b)可以看到, 利用金锥反射效应, VISAR系统可测量角度显著提升, 其中最大角度提升两倍, 而且由(9)式可知, 通过改变锥角还可以进一步提升最大测量角度. 图2(c)展示了利用keyhole靶金锥反射效应后, 不同反射半径下, VISAR测 量的光强分布图. 和图1(b)对比可以看出, 考虑金锥反射后, VISAR可测量区域提升了2倍, 在半径0.375 mm时, VISAR可测量区域约240 μm, 而且中间区域图像强度变得更加均匀, 显著提升了VISAR对小靶丸尺度下球形冲击波的诊断适 用性.

    3.   实验验证及应用

      3.1.   实验排布

    • 为了验证金锥对VISAR诊断图像测量区域的提升效果, 在激光聚变研究中心的十万焦耳激光装置上开展了基于液氘keyhole靶的冲击波调控实验. 图3为实验原理示意图. 实验中48路激光束分两端注入黑腔内产生高温X射线辐射场, 辐射场烧蚀碳氢(CH)靶丸产生球形汇聚冲击波在靶丸中传输. 实验采用的激光波形为典型双台阶整形激光, 产生的辐射驱动波形如图3(c)和图3(d)中蓝色实线所示. 实验用靶为keyhole靶结构, 如图3(a)和图3(b)所示, 黑腔大小为Φ2600 μm×4100 μm, 两端注入孔为1400 μm, 黑腔注入孔由0.5 μm的碳氢薄膜密封, 内充有3个大气压的He气以减缓激光焦斑处的烧蚀等离子体向黑腔中心的移动速度. 黑腔上安装了一个伸入靶丸中的金锥, 金锥顶部开260 μm诊断孔, 靶丸和金锥内充满液氘, 采用带倾角的石英窗口进行密封. 实验中分别采用金锥半锥角为0°和10°的keyhole靶开展实验, 来验证金锥对VISAR诊断图像测量区域的提升效果. 靶丸为壳厚65 μm、内径750 μm的球形靶丸, 靶丸外表面镀120 nm厚的铝膜. 诊断方面采用平响应XRD[22,23]监测时间分辨的黑腔辐射温度. 采用VISAR诊断系统进行冲击波测量, 探针光通过金锥顶部诊断孔入射靶丸内部来测量冲击波速度历程.

      • 3.2.   实验图像仿真

    • 实验前对VISAR图像进行了模拟仿真. 首先采用辐射流体程序对靶丸中的冲击波传输历程进行计算, 获得冲击波速度和波阵面位置的演化历程; 然后在假设冲击波阵面是理想球面的条件下, 将keyhole靶结构参数以及成像系统F数输入根据第2节内容构建的光线追踪模拟程序, 结合靶材料的反射率、吸收率等光学性质, 获得未干涉的光强时空演化; 最后根据多普勒效应及Mach-Zehnder干涉仪原理给出VISAR干涉图像. 图3(c)和图3(d)展示了两种keyhole靶锥角设计下冲击波调控实验的VISAR仿真图像. 可以看到两个图像的时间演化一致, 但空间宽度存在显著差异, 10º锥角设计下由于锥角反射效应的作用, VISAR图像数据区域增加了近3倍, 预期可以显著提升小靶丸冲击波调控实验中VISAR诊断的适用性.

      • 3.3.   实验结果

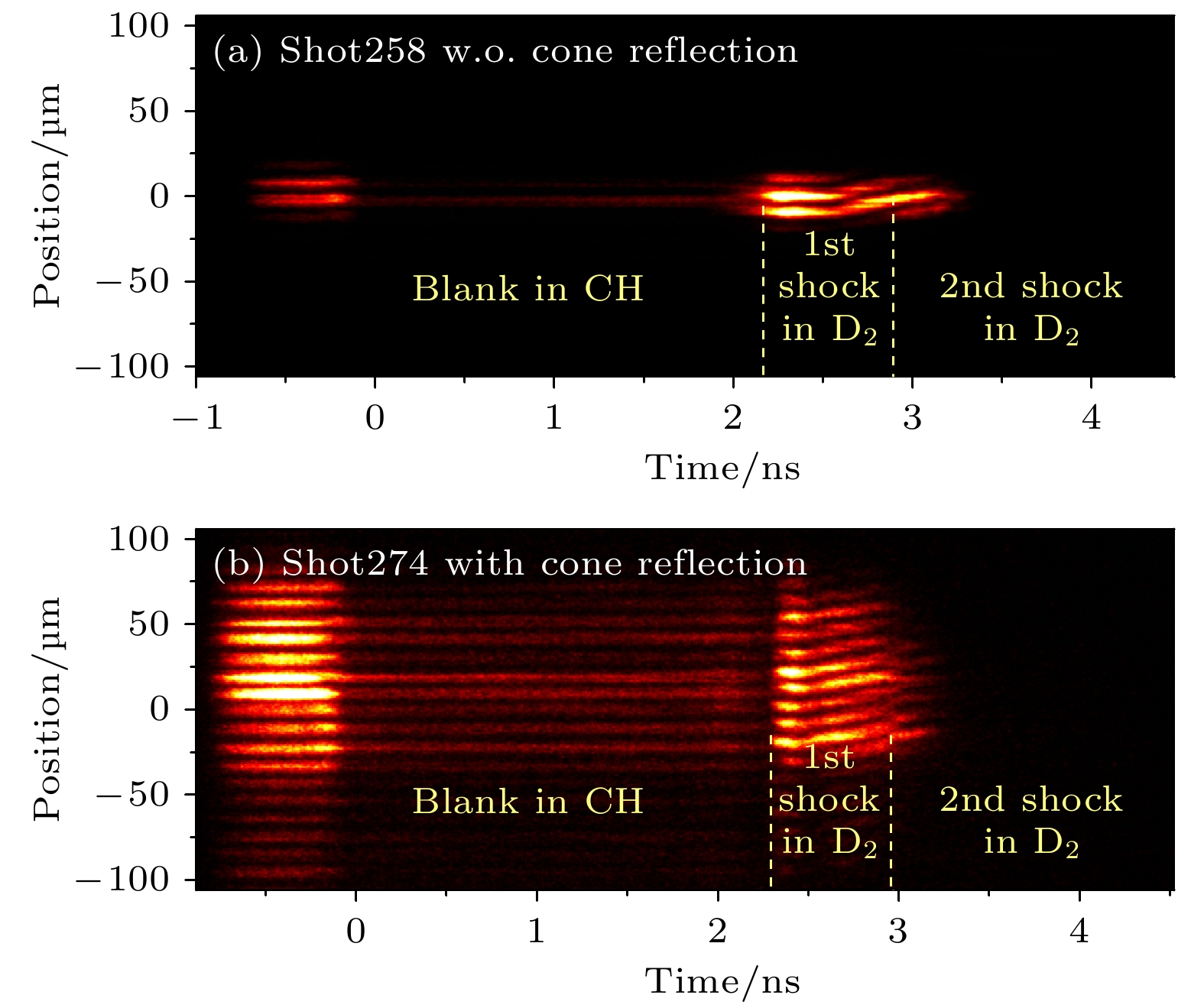
    • 图4展示了我国十万焦耳装置上基于低温液氘靶的冲击波调控实验结果. 实验通过VISAR诊断获得了冲击波在靶丸液氘中的传输图像, 图4(a)和图4(b)分别是两种keyhole锥角的冲击波调控实验获得的VISAR原始图像. 首先看VISAR图像的空间区域, 可以看到, 利用金锥反射后VISAR测量区域有显著提升, 这和图3中的模拟图像一致. 在锥角为0°时, VISAR图像只存在于中间区域, 宽度约50 μm, 比仿真预测还要少, 干涉条纹数目仅2—3根, 这对高质量数据获取及分析带来了较大的风险性; 在利用10°张角的金锥反射效果后, VISAR图像的测量区域增加至约180 μm, 条纹数目显著增加, 不仅消除了小靶丸尺度条件下VISAR测量失效的风险, 同时有效降低了VISAR测量图像中常见的小区域随机散斑等噪声干扰的影响[27]. 实验结果直接验证了利用金锥反射效应等效降低汇聚光源F数, 进而实现小靶丸尺度下球面冲击波传输的VISAR诊断区域显著提升的技术路线的有效性.

    4.   分析与讨论

      4.1.   双冲击波追赶过程

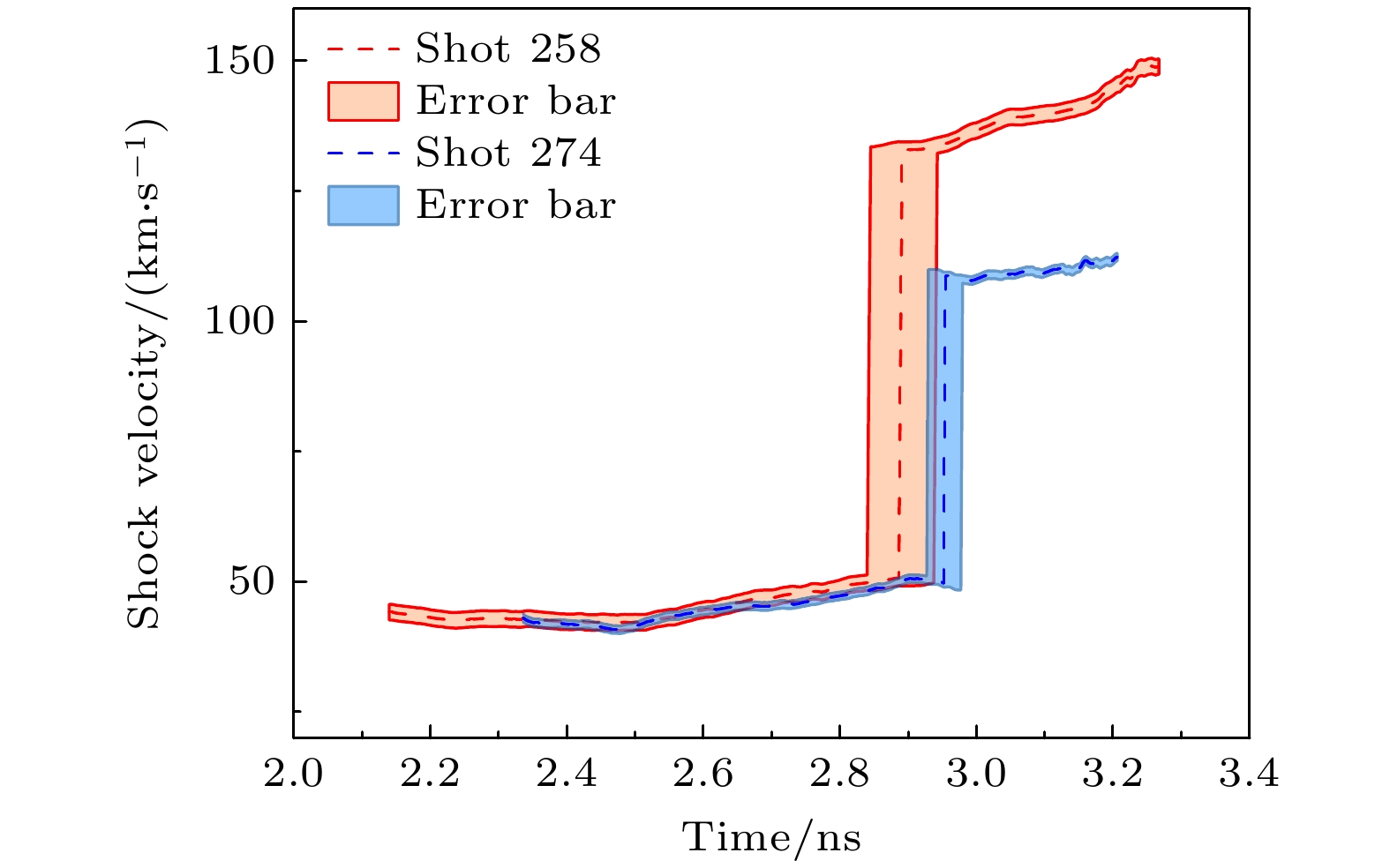
    • 从图4的时间演化过程可以看到, 两发次实验VISAR图像在时间演化上均可以分为三个阶段. 第一阶段是主激光注入前, VISAR反射信号主要来源于CH层外表面的Al膜反射, 由于激光脉冲设置了0.5 ns的烧膜预脉冲, 烧膜剩余能量提前注入黑腔壁产生X射线会破坏Al膜, 所以在–0.15 ns左右Al膜静态信号即完全消失. 第二阶段是冲击波在CH层中传输时的图像, 第一台阶激光注入黑腔产生的辐射场压缩靶丸, 在CH中产生冲击波, 但此时激光注入黑腔产生的高能X射线将波前未压缩CH离化, 导致对532 nm波长的探针光完全吸收[24], 此时VISAR无法对CH中冲击波进行测量, 因此测量到的VISAR数据信号来源于CH-液氘界面的弱反射. 第三阶段是2.2 ns后冲击波从CH中穿出进入液氘后在液氘中传输时的图像. 由于液氘对X射线吸收效应极弱, 因此对探针光仍然保持很好的透明性, 同时冲击下的液氘出现金属化现象具有较好的反射性质[25,26], 此时VISAR数据信号全部来源于液氘冲击波阵面的反射. VISAR干涉条纹随着液氘中冲击波速度的变化而发生偏移, 两发图像可以看到冲击波在液氘中的完整追赶过程. 图5展示了两发图像数据处理后获得的液氘中的冲击波速度历程, 可以看到, 利用了金锥反射效应的274发数据, 在速度不确定度和时间判别不确定度方面均有明显提升. 冲击波速度不确定度由258发次的±1.5 km/s减小至0.74 km/s, 时间判别不确定度从±50 ps减小至25 ps. 最终由此获得的冲击波汇聚位置的不确定度由258发的±2.8 μm降低至±1.3 μm, 该技术的应用显著地提升了多冲击波追赶的精密表征能力.

      • 4.2.   “N+1”反射冲击波的影响

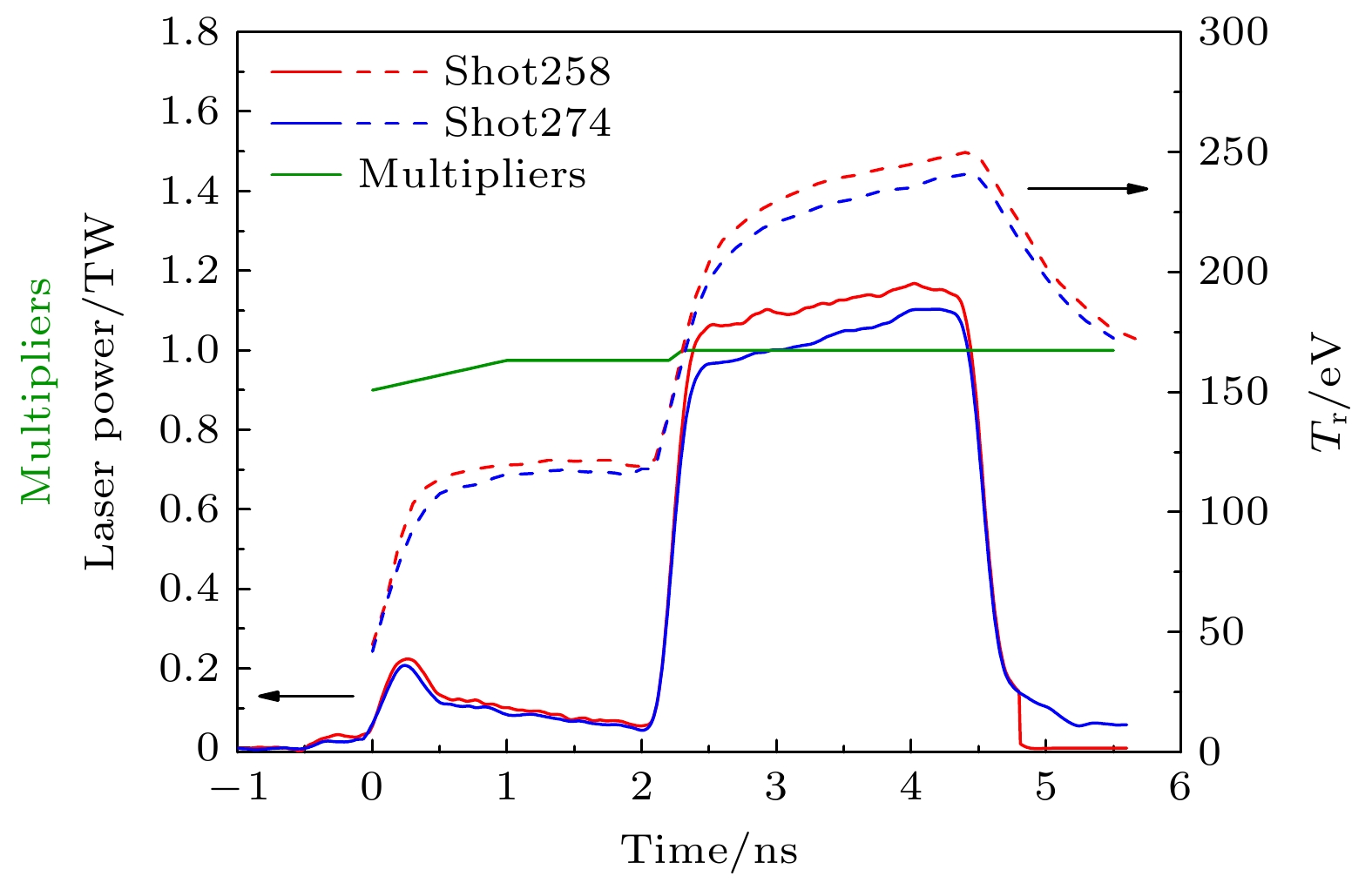
    • 从图4的原始图像和图5的数据处理结果可看到, 两发实验的物理过程是基本一致的, 但双冲击波的速度历史定量上存在显著差异. 两发次液氘中的第一冲击波速度基本一致, 均在40 —50 km/s范围内, 但258发次的冲击波进液氘时刻、冲击波追赶时刻均比274发次略早, 追赶后的第二冲击波也存在较大差异, 258发次追赶后冲击波速度约133 km/s, 274发次追赶后只有108 km/s. 为了分析两者差异的原因, 首先对比了两发次实验的靶丸实际参数, 258发内径746.0 μm, CH壳层厚64.0 μm, 274发内径749.0 μm, CH壳层厚63.6 μm, 两发次靶丸参数差异均小于0.5%, 具有很好的一致. 然后对比了激光注入波形及黑腔辐射温度, 如图6所示. 由图6可以看到, 两发次激光第一台阶脉冲(即预脉冲)功率中258发较274发稍高, 稍高的功率和258发冲击波进液氘时刻更早、速度略高的现象是自洽的; 第二台阶脉冲(即主脉冲)功率相差较大, 258发比274发的平均功率高约10%, 对应的峰值辐射温度高约2.5%, 定性上似乎和258发冲击波追赶时间更早、追赶后速度更高的现象是自洽的. 但我们从量上估计, 辐射温度2.5%的差异远不足以导致实验观测到的冲击波速度差异超过20%.

      为了理解两发实验第二冲击波速度的巨大差异, 采用一维辐射流体程序Multi1 D[28,29]进行了实验后模拟. 模拟思路和美国冲击波调控实验分析类似[11], 通过调整靶丸感受的辐射温度, 即将实验测量的辐射温度乘上如图6中的绿色实线所示乘积因子, 使冲击波速度历程和实验数据符合较好. 从乘积因子时间演化来看, 预脉冲阶段需乘上小于1的乘积因子, 这表明靶丸感受的辐射温度小于从注入口测量的辐射温度; 主脉冲阶段乘积因子为1, 表明此时靶丸感受的辐射温度与实验测量一致. 乘积因子代表着黑腔能量到靶丸感受能量的转换性能, 它与黑腔等离子体环境密切相关. 两发次实验采用相同的乘积因子后, 模拟结果均可较好地符合冲击波实验数据, 如图7和图8所示, 说明了两发实验中黑腔等离子体环境差别很小. 这验证了靶物理设计具有较强的皮实性, 即在相同的黑腔与靶设计下, 相近激光参数注入下黑腔内等离子体环境变化是可控的.

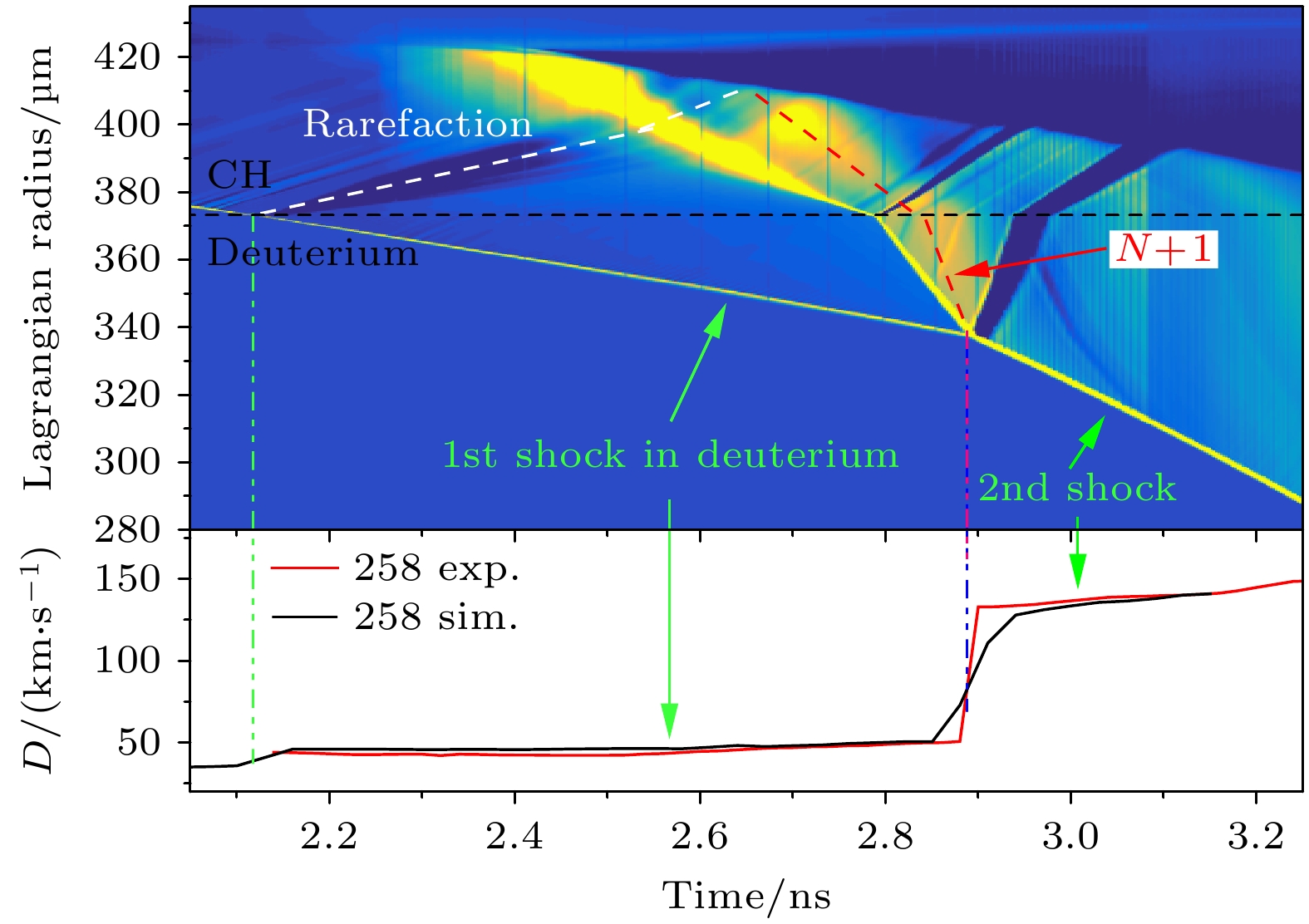
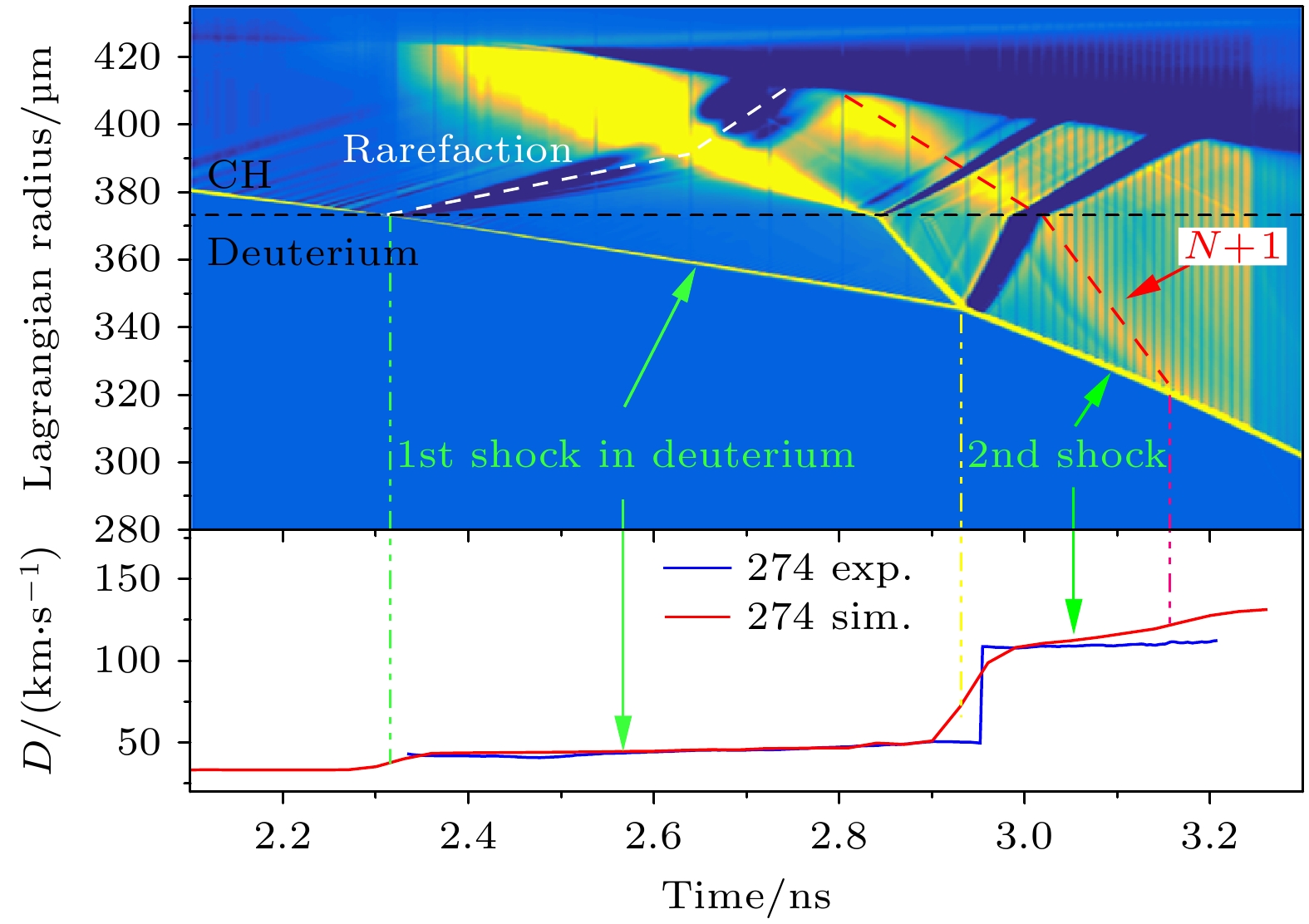
      为了理解实验中第二冲击波速度历史的差异, 进一步分析了靶丸冲击波速度演化过程. 图7和图8分别展示了两发次的模拟结果, 同时给出了模拟获得的冲击波传输过程的压强梯度流场图, 可以清晰看到第一冲击波和追赶后第二冲击波的传输轨迹. 另外, 从图7和图8的模拟流场图可以看到, 第一冲击波穿过CH/液氘界面时, 由于阻抗失配的原因, 向液氘中传输一个冲击波的同时也会向CH中传输一个稀疏波(rarefaction), 如图中白色虚线所示; 稀疏波传到烧蚀面产生增压作用再向靶丸内产生一个反射冲击波, 也称为“N+1”冲击波[30], 如图红色虚线所示. “N+1”冲击波追上波头会产生显著的加速现象. 258发和274发由于预脉冲激光功率的差异, 导致258发第一冲击波进液氘的时刻以及产生稀疏波的时刻比274发早; 同时由于主脉冲功率的差异, 258发次的“N+1”冲击波比274发更强. 最后导致258发的“N+1”冲击波提前追赶, 并和双台阶辐射驱动产生的第一、第二冲击波同时汇聚, 导致追赶后的冲击波速度偏强; 而274发“N+1”冲击波追赶发生在第一、第二冲击波汇聚之后更晚的时间, 如图8所示, 所以实验测的汇聚冲击波传输过程还没有受到“N+1”冲击波影响. 因此, 我们认为两发次追赶后第二冲击波的速度差异主要是由于“N+1”反射冲击波的传输过程差异引起的.

      由此可见, 采用小靶丸设计时, 靶丸的内爆压缩过程在更小的时空尺度发生, 这导致冲击波和稀疏波等波系在有限的时空内发生复杂的相互作用和耦合. 从而激光驱动源的微小变化可能导致冲击波出现明显的差异, 冲击波匹配过程对实验输入参数呈现了更复杂的敏感性. 因此建立高精度的小靶丸冲击波调控实验平台, 精密表征和调控小尺度靶丸中的冲击波传输历程, 对理解小时空尺度靶丸的内爆压缩过程具有重要意义.

    5.   结　论

    • 我国当前整形内爆实验主要基于十万焦耳激光装置上开展, 国内靶丸时空尺度的缩小不仅在诊断上对冲击波测量提出了更高要求, 而且在物理上因为“N+1”冲击波传输, 使得实验条件的较小变化都会对内爆压缩过程产生更显著的影响. 作为激光聚变四大调谐技术之一, 冲击波调控实验技术对实现整形内爆熵增调控、提高聚变燃料压缩度具有关键作用. 相比美国百万焦耳激光装置上的毫米半径内爆靶设计, 我国激光聚变受限于十万焦耳激光装置输出能量, 高性能整形内爆靶半径不超过0.4 mm, 如何实现小靶丸下的多冲击波调控的精密测量是我国当前激光聚变精密实验面临的特有难题.

      本文建立了球形反射面的VISAR图像光强的理论计算方法, 提出了利用keyhole锥反射提升VISAR诊断空间区域的实验技术路线, 使得小靶丸尺度下有效VISAR数据区域提升了近3倍, 不仅解决了VISAR测量失效的重大风险, 同时有效降低了VISAR测量图像中常见的小区域随机散斑等噪声干扰的影响, 保障了测量精度. 在十万焦耳激光装置上开展了双冲击波测量技术验证实验, 首次获得了整形内爆实验条件下基于低温液氘keyhole靶的原位冲击波调控实验数据, 冲击波汇聚位置精度±1.3 μm, 成功验证了冲击波调控技术有效性. 通过深入分析相近激光条件下靶丸中的冲击波速度历程的显著差异, 发现小尺度内爆靶设计下, 由于反射冲击波产生的“N+1”冲击波追赶效应, 激光参数的较小偏差都会对冲击波追赶后的传输行为产生显著影响, 从而揭示了我国当前小靶丸尺度下高性能整形内爆物理过程中冲击波传输的多因素敏感性. 本工作建立的小尺度靶丸下的冲击波调控实验技术不仅为我国十万焦耳激光装置上熵增调谐实验的开展提供了关键技术基础, 也为基于球汇聚压缩的超高压物理研究提供重要技术基础.

    参考文献 (30)

目录

/

返回文章
返回