-
Laves相是一类化学计量比为AB2的金属间化合物, 结构为立方MgCu2(C15)、六方MgZn2(C14)和六方MgNi2(C36). 在20世纪30年代, 德国科学家Laves发现了这类具有特定的晶格结构和相似性, 且C36是C14到C15结构原子排序中的一个中间相. Schulze将这些类型统称为“Laves相”金属间化合物[1,2]. 这类金属间化合物具有耐腐蚀、抗蠕变、磁性和电学功能等性能, 可作为磁性材料、磁光材料、储氢材料等.
钴基高温合金在低应力和中等温度下的热腐蚀性能非常重要, 但其应用受到高温时强度较低的限制[2,3]. 通过添加W, Ta, Mo, Hf等关键合金元素, 可以改善钴基高温合金的这一缺陷, 提高其综合性能[4]. 其中Co-Hf是钴基合金的一个重要子系统, 有抗高温蠕变、较高的疲劳寿命、耐腐蚀性以及对各种形式磨损具有良好耐久性等性能. Burzo等[5]给出了温度在0—800 K内 Co2Hf的磁化率曲线, 发现在居里温度以上(约100 K), Co2Hf的磁化率随着温度的升高而降低. Chen等[6]研究了C15相Co2Hf的溶解度极限和结构缺陷, 利用电子探针显微分析和X射线衍射等方法测定了Co的溶解度(原子百分比)为65.0%—72.0%, 从晶格常数、密度、X射线衍射强度等方面进一步发现了Co2Hf的结构缺陷主要是反位取代. 同时, Chen等[7]采用共振超声光谱法测定了C15相Co2Hf的弹性常数、德拜温度, 并研究了力学性能. 在Co的原子百分比为66.7%时, 杨氏模量和体积模量达到最大值, 分别为210.79 GPa和225.17 GPa, 剪切模量随着Co含量的增大而减小, 在Co的原子百分比为66.92%时, 泊松比达到最大值0.3462. Concas等[8]用SQUID磁强计实验仪器测量了C15相Co2Hf磁化率随温度的变化, 发现了Co2Hf的磁化率 χ在T → 0 K时, 达到最大值, 而χ–1在高温区 (T > 250 K)时存在线性行为, 符合Curie-Weiss式χ = a/(T – b), 所计算的态密度和结构参数, 与实验结果吻合较好.
在Co基合金中, Ta被认为是不可或缺的合金元素, 可以提高γ ′相的溶解温度和相稳定性[9–12], 但过量添加导致结构不稳定, 不利于高温使用. Dragsdorf 和Foreing[13]对不同质量比的钴钽合金进行了X射线衍射研究, 证实了C15, C14, C36型Co2Ta Laves相的存在. Baheti 等[14]在Co-Ta体系中获得了Co2Ta相的互扩散系数和扩散系数比. Shinagawa等[15]对Co-Ta二元相图进行了实验研究, 并基于现有结果和文献中的实验数据进行热力学评价. Wang等[16]综述了Co-Ta体系, 并对其热力学描述进行重新评价. 他们运用第一性原理方法对Co-Ta体系中稳定相C14, C15, C16, C36以及μ相的形成焓进行了详细计算, 发现基态结构为C36, 计算的相图与实验数据和其他理论模拟结果相吻合较好. Zhou等[17]考虑了自旋极化, 其形成能也表明C36是最稳定的结构.
然而, 对于Co2Hf的稳定性问题, 一直存在着争议. Asano和Ishidat[18]认为, B亚格点为Co时, C15结构比C14稳定. 对于Laves相MCo2 (M = Hf, Ta), 发现C15是稳定的结构[19–21]. Wang等[22]发现Al和W的掺杂使C15和C36结构的Co2Hf形成能差从–20 meV/atom增至Co2(Hf, Al, W)的形成能差为–10 meV/atom. 因此, Co2(Hf, Al, W)合金中, C15和C36两相之间的能垒较小. 在有限温度下, 第一性原理分子动力学模拟表明, 热振动对C36结构的自由能贡献比C15大, 因此, 随着温度升高, 使得C36结构相对于C15更为稳定. 实验也证实了Co-9Al-9W-2Hf合金中存在C36-Co2(Hf, Al, W)相. 而Levy等[23]利用第一性原理高通量计算出Co2Hf的最稳定结构是C14. 可能的原因是3个结构在有限温度下的自由能较为接近. 因此, 为了系统分析磁性和温度效应对相稳定的影响, 基于弹性理论和晶格振动, 更全面地考虑自由能, 通过第一性原理计算有限温度下的电子结构和自由能, 深入研究Co2(Hf, Ta)合金的稳定结构和热物理性质.
-
Laves相分为3种结构类型, 分别是C14 (P63/mmc), C15 (
$Fd \bar{3}m $ ), C36 (P63/mmc). 这3种结构类型如图1所示, 晶体信息汇总见表1. 根据这些结构信息, 构建了本文中Laves相Co2Hf和Co2Ta的初始晶胞模型, 根据合金的原子半径或实验参数, 对晶格参数进行评估. -
本文基于密度泛函理论, 选择CASTEP[24]产生的超软赝势(OTFG-USPP), 采用广义梯度近似下Perdew-Burke-Ernzerhof泛函[25,26]来考虑原子实与价电子以及交换关联效应. 采用Monkhorst-Pack方法[27]对Brillouin区进行k点采样. 根据收敛性测试, 平面波的截断能设置为435.4 eV, 设置并测试统一的k点密度, 对于C14, C15, C36结构, k点分别选择为6×6×4, 6×6×6, 6×6×2. 采用Broyden-Fletcher-Goldfarb-Shanno (BFGS)优化方法[28], 对晶体结构进行结构优化. 采用严格的收敛判据, 能量、力、应力和离子位移的收敛标准分别为1.0×10–5 eV/atom, 0.03 eV/Å, 0.05 GPa及0.001 Å. 根据应力-应变方法[29], 计算了合金Co2(Hf Ta)的弹性常数及弹性模量. 采用了有限位移方法[30]计算声子色散关系, 并获得了有限温度下的晶格振动对自由能的贡献. 采用准简谐近似下的Debye-Grüneisen模型[31,32]计算了Co2Hf和Co2Ta合金在一定压强和温度下的热物理性质. 计算赫姆霍兹自由能的公式 :
式中
$ {E}_{0} $ 表示零点能;$ {S}_{{\mathrm{v}}{\mathrm{i}}{\mathrm{b}}} $ 表示振动熵, 通过声子谱计算导出;$ {S}_{{\mathrm{e}}{\mathrm{l}}{\mathrm{e}}} $ 表示电子熵, 则通过Mermin统计进行计算[33]. -
为了研究Co2Hf和Co2Ta化合物的3种构型在不同磁态下的稳定性, 定义了形成能:
其中, E是由N种元素所组成Laves相合金的平均能量, i是元素类型, xi是合金中i型原子的占比, Ei是平均到每原子的单质能量. 获得平衡晶格参数、体积、能量差、磁矩和形成能, 如表2所列.
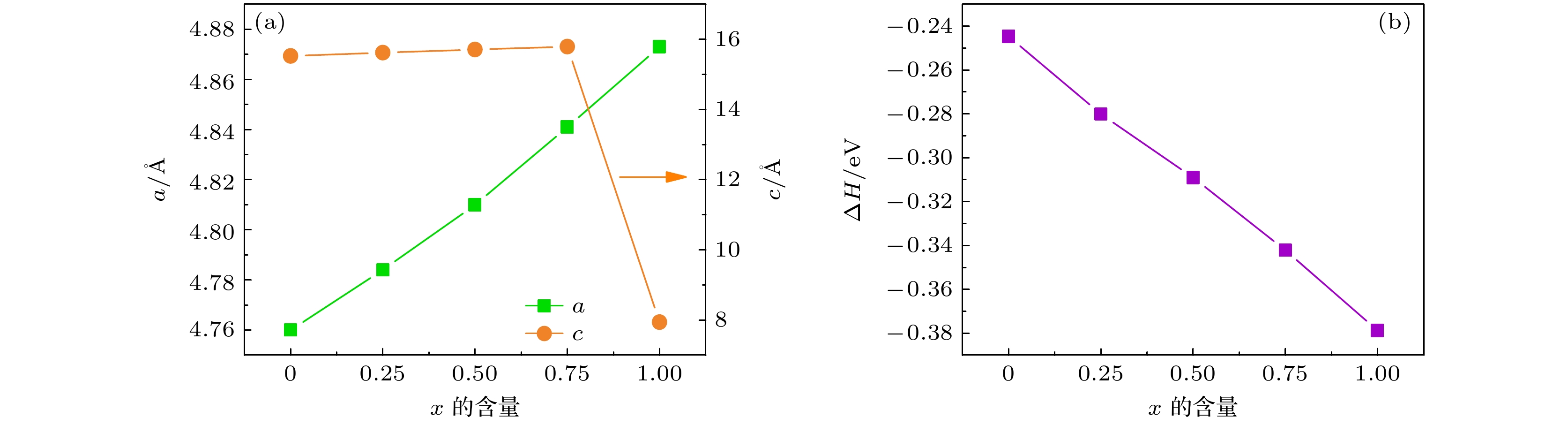
本文计算的晶格参数与文献报道的相对误差在1.3%之内. 不考虑自旋极化时的晶格参数均小于自旋极化下的晶格参数, 即磁有序使晶格参数变大. 由于Co占据在不同的亚格点上, 相应的局域磁矩不同, 但磁矩大小相差较小, 在Co2Hf 和Co2Ta合金不同相中, Co的局域磁矩分别在 0.58—0.79 μB/atom和0.33—0.68 μB/atom之间. 局域磁矩的存在, 使体系在0 K下更为稳定, 相对能量差ΔE强烈依赖于结构, 如C14相Co2Hf的ΔE 为0.017 eV/atom, 而C36相Co2Ta的ΔE仅为0.003 eV/atom, 根据铁磁态和顺磁态的能量差与居里温度的关系(
$ {T}_{{\mathrm{c}}}= {2\Delta {{E}}}/({3{k}_{{\mathrm{B}}}}) $ ), 估算得到的C14 Co2Hf和C36 Co2Ta的居里温度分别是200 K和35 K. 在低温下, Co2M (M = Hf, Ta)表现出铁磁性结构. 然而, 随着温度的升高, 在居里温度附近, 发生磁相变. 在这个过程中, 磁的有序排列由于热运动而被破坏, 导致局域磁矩无序分布, 总磁矩趋于零. 当前的计算结果显示, 在顺磁态下, Co的局域磁矩为0, 呈现无磁性. 据此, 可推测高温下考虑非自旋极化的处理是合理的. 形成能表明稳定的Co2Hf是铁磁C14结构, Co2Ta的基态是C36结构. 对于Co2Ta合金的C15和C36结构, 其形成能分别为–0.2442 eV/atom和–0.2447 eV/atom, 非常接近, 导致难以判定Co2Ta的稳定结构.弹性常数是判断材料是否力学稳定的重要参数之一, 零压下立方晶体的广义弹性力学稳定性判据为:
$ {c}_{11} > 0,\; {c}_{44} > 0,\; {c}_{11} > |{c}_{12}|,~ ({c}_{11} + 2{c}_{12}) > 0 $ , 零压下六方晶体的广义弹性力学稳定性判据:$ {c}_{44} > 0, {c}_{11} > |{c}_{12}|, ({c}_{11}+{c}_{12}){c}_{33} > 2{c}_{13}^{2} $ [35], 零压下对于三角晶系, 其弹性力学稳定性判据是:${c}_{44} > 0, \;{c}_{11} > |{c}_{12}|$ ,$ ({c}_{11} + {c}_{12}){c}_{33} > 2{c}_{13}^{2}$ ,$ ({c}_{11} + {c}_{12}){c}_{44}-2{c}_{14}^{2}- {2 c}_{15}^{2} > 0 $ [32]. 表3列出了Co2(HfxTa1–x)在不同结构下的弹性常数, 其弹性常数均满足上述判据, 这表示目前所研究的结构在弹性力学上均稳定.从表3可以明显看出, Co2Hf的弹性常数小于Co2Ta的相应结果, 这暗示了Co—Ta的成键强于Co—Hf键. 不同磁态的弹性常数变化较大, 其主要原因是弹性常数对键长较为敏感, 而局域磁性通常诱导了体系体积增大, 多数原子间的键长增大, 而个别键长减小, 使得组成的连续介质的原子键长变化呈现较大的各向异性.
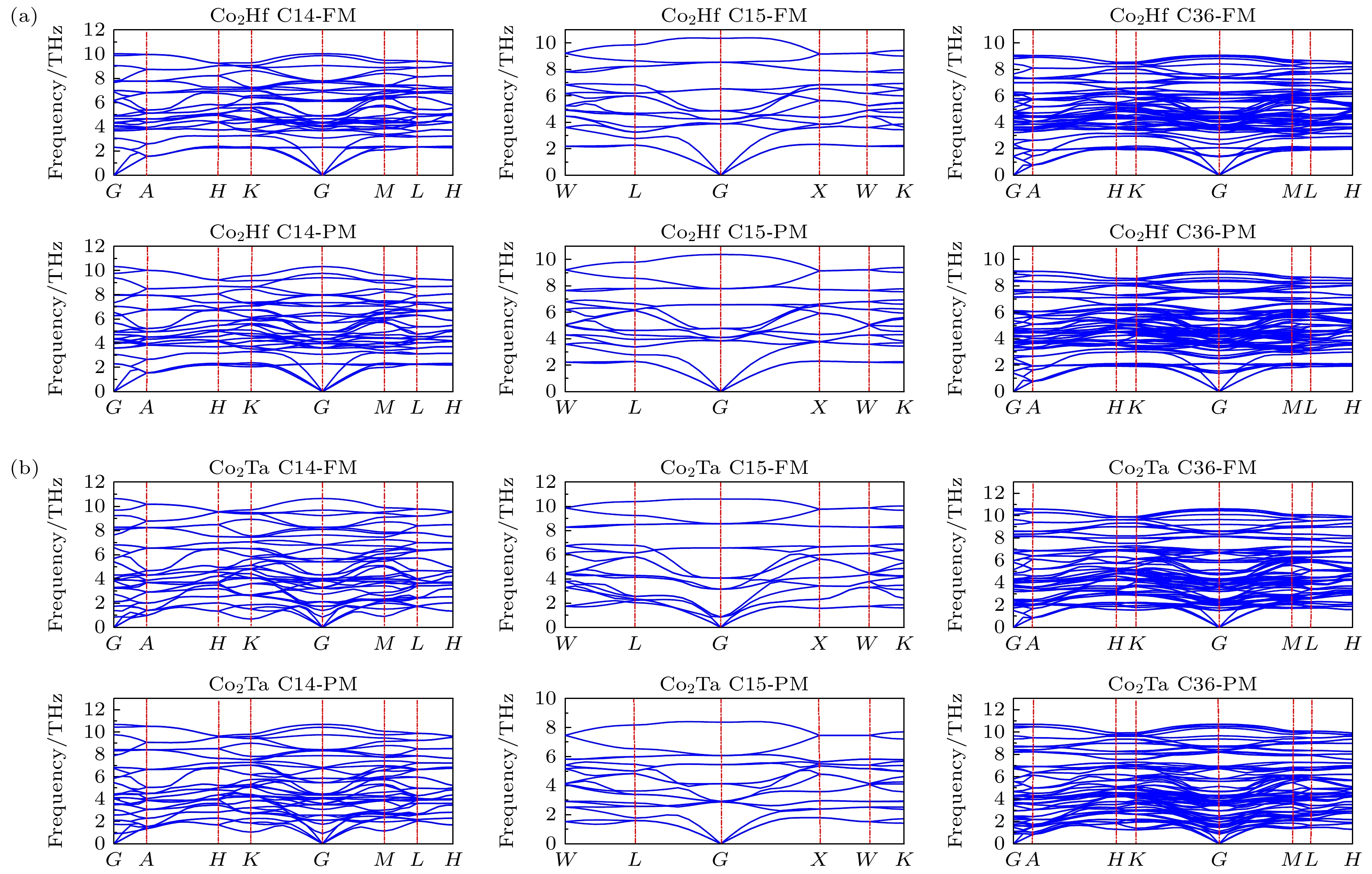
为了进一步从晶格动力学方面研究Co2Hf和Co2Ta的稳定性, 图2描述了两种磁态下3种结构沿布里渊区高对称点的声子色散关系. 对于C14, C15和C36结构, 原胞中原子数(N )分别为12, 6和24. 因此, 在由3个声学声子模和3N – 3个光学模组成的声子谱中应该有3N个声子模. 根据声子模与原子数的关系(3N ), 原子数较多的C36结构有较多的声子模 [36]. 在稳定的结构中, 声子无虚频. 虚频的存在通常表示结构中存在不稳定的振动模式, 通常代表结构的失稳性. 在图中曲线呈现类似频带的形状, 在所有高对称点上得到频率全为正的谱线, 没有发现负频, 表明Co2Hf, Co2Ta的C14, C15, C36相在不同磁态下结构均是动力学稳定的.
由于Co2Hf和Co2Ta两者之间稳定结构的差异, 在Co2Ta基体中掺入不同浓度的Hf时, 会引发相变. 对于C14, C15和C36结构, 根据亚格点的不同, Hf替代Ta, 对比同一含量下的总能, 取能量最低结构. 图3给出了晶格参数和形成能随Hf浓度的变化, Hf含量在0.75—1之间c发生了明显的递减, 这标志发生了相变, 结构从C36变为了C14. 从图3(b)可以看出, 随着Hf含量的增加, Co2(Hf Ta)结构的形成能变得更负.
-
弹性常数是描述物质抵抗形变和应力的重要物理参数, 计算的弹性常数结合弹性理论, 可得到 材料的体积模量、剪切模量、杨氏模量等弹性性质参数.
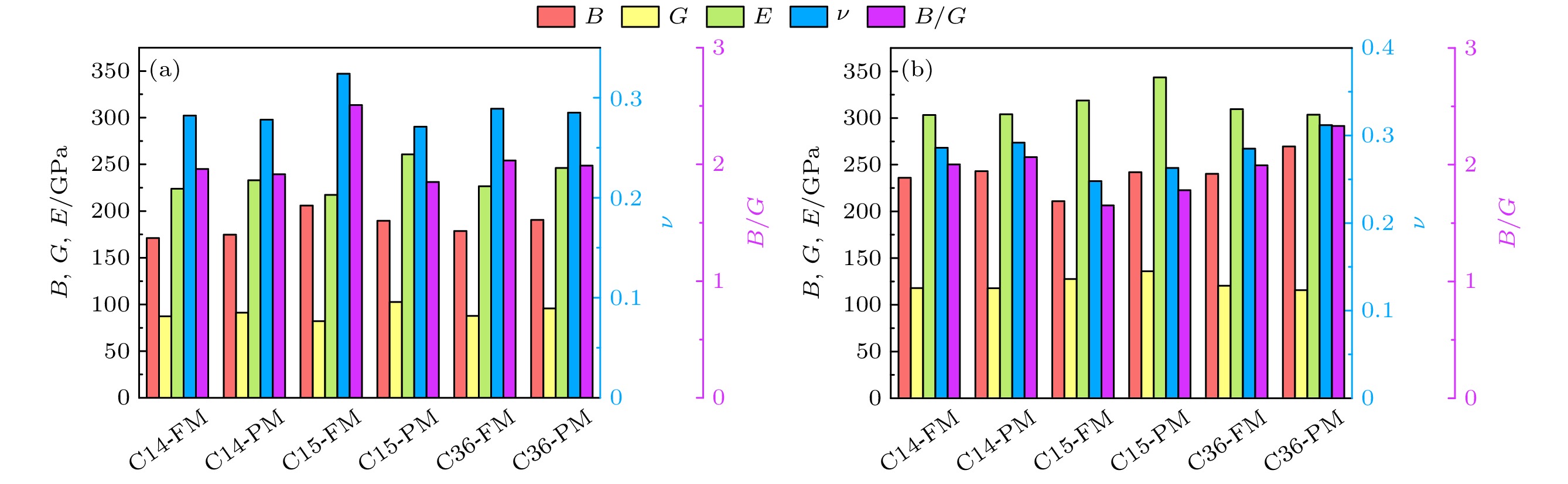
弹性常数c11和c33分别反映了a轴和c轴对单向压缩的阻力, c44和c66分别代表(100)和(001)抗剪切变形的平面阻力[37]. 对于Co2Hf的C14结构、顺磁态的C36结构, 及铁磁Co2Ta的C14和C36结构, c11 < c33, 表明这些结构在c 轴上抗击压缩的能力比a轴强. 对于FM Co2Hf的C36结构、PM Co2Ta的C14结构, c11 > c33, 表示这些结构在a 轴上抗击压缩的能力比c轴强. Co2Hf的C36结构和Co2Ta的C14结构, 考虑自旋极化对a轴和c轴对单向压缩的阻力有一定的影响. 利用Voigt-Reuss-Hill平均方法, 计算了体模量B、剪切模量G、杨氏模量E和泊松比ν, 结果如图4所示. 通常用B/G值[38]和泊松比
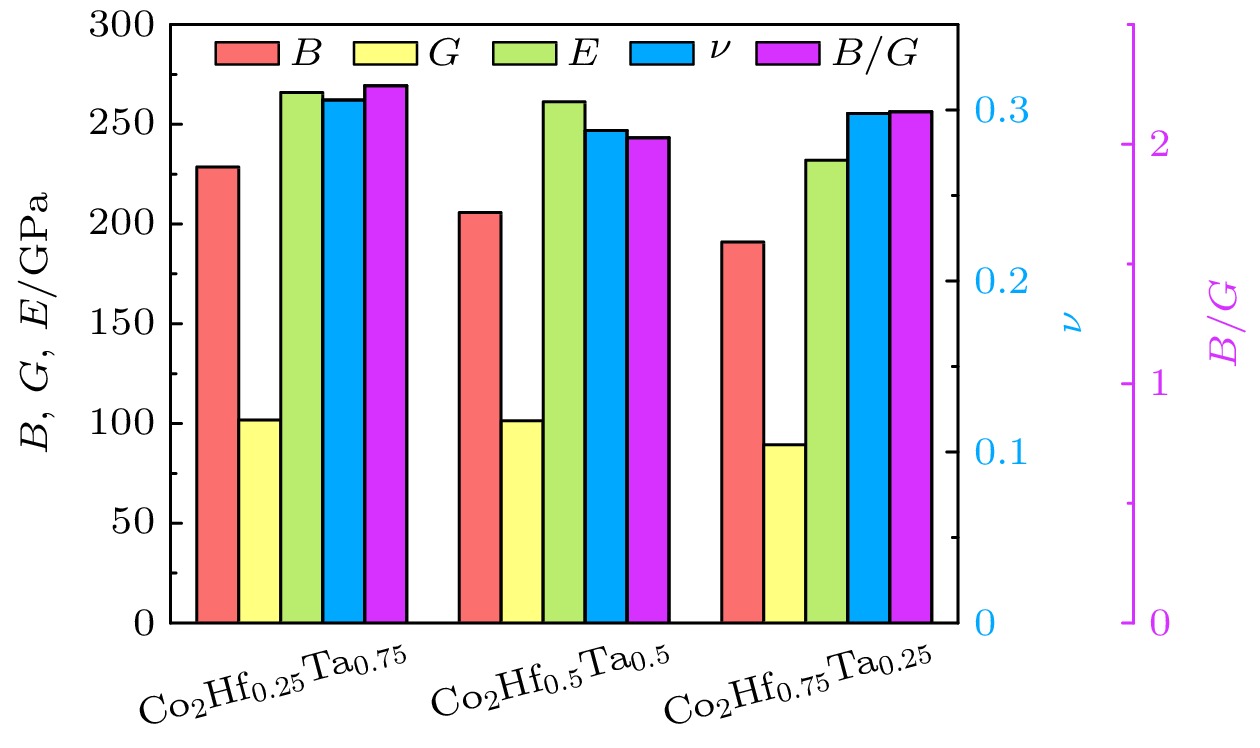
$ {\mathrm{\nu }} $ [39]区分固体的延脆性, 关键参数B/G = 1.75 ($ \nu $ = 0.33). 如图4所示, 所有结构的B/G值都略大于1.75, 而$ \nu $ 值接近0.3, 说明Co2Hf和Co2Ta Laves相具有本征脆性.对于Co2Hf Ta合金, Co2Hf0.25Ta0.75, Co2Hf0.75Ta0.25的c11 > c33, a轴上抗击压缩的能力比c轴强. Co2Hf0.5Ta0.5的c11 和c33相差不大. 从图5可以看出, Co2Hf0.25Ta0.75的体模量、剪切模量和杨氏模量均相对较大.
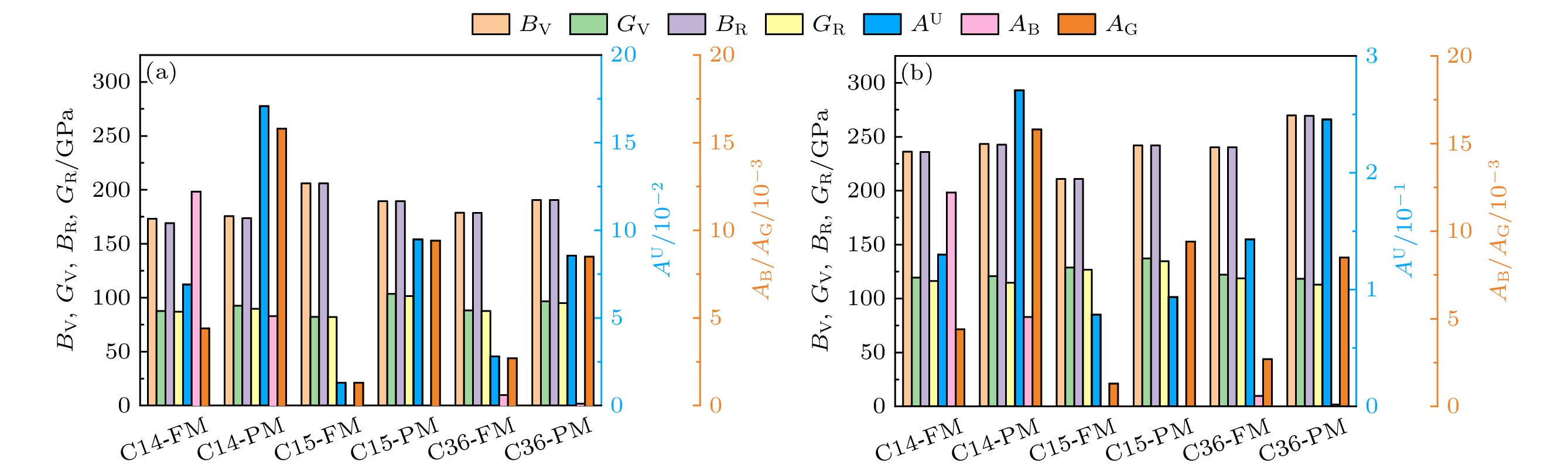
根据Ostoja-Starzewshi和Ranganathan提出的通用弹性各向异性参数AU [40]和Chung-Buessem 各向异性参数[41], 量化了弹性各向异性程度. 用Voigt 近似和Reuss近似得到的体模量和剪切模量分别为BV, GV, BR和GR, 立方晶系的弹性模量公式为
$ {B}_{{\mathrm{V}}}={B}_{{\mathrm{R}}}=\dfrac{{C}_{11}+2{C}_{12}}{3} $ ,$ {G}_{{\mathrm{V}}}=\dfrac{{C}_{11}-{C}_{12}+3{C}_{44}}{5} $ ,$ {G}_{{\mathrm{R}}}=\dfrac{5\left({C}_{11}-{C}_{12}\right){C}_{44}}{4{C}_{44}+3\left({C}_{11}-{C}_{12}\right)} $ , 六方晶系的弹性模量为$ {B}_{{\mathrm{V}}}=\left({1}/{9}\right)\left[2\left({C}_{11}+{C}_{12}\right)+4{C}_{13}+{C}_{33}\right] $ ,$ {G}_{{\mathrm{V}}}= \left({1}/{30}\right)({C}_{11}+{C}_{12}+2{C}_{33}-4{C}_{13}\,-\, 4{C}_{13}+12{C}_{44} $ +$12{C}_{66}) $ ,$ {B}_{{\mathrm{R}}}={C}^{2}/({C}_{11}+{C}_{12}+2{C}_{33}- 4{C}_{13}) $ ,$ {G}_{{\mathrm{R}}}= \left({5}/{2}\right)\left({C}^{2}{C}_{44}{C}_{66}\right)/\left[3{B}_{\rm V}{C}_{44}{C}_{66}\;+\;{C}^{2}{(C}_{44}{+C}_{66})\right] $ , 其中$ {C}^{2}=\left({C}_{11}+{C}_{12}\right){C}_{33}-2{C}_{13}^{2} $ . AU的表达式为: AU = 5(GV/GR) + (BV/BR) – 6. Chung-Buessem参数在压缩系数AB和剪切系数AG中的表达式为: AB = (BV – BR)/(BV + BR), AG = (GV – GR)/(GV + GR). AU = AB = AG= 0表示该固体是一种弹性各向同性材料. 各向异性指标的偏差均反映了各向异性的程度, 偏差越大, 各向异性越强. 计算得到Co2Hf, Co2Ta的Laves相各向异性指标如图6所示. 所得的各向异性指数AU表明, Co2Hf和Co2Ta均是顺磁态C14结构的AU值最大, FM-C15的AU值最小. 因此, 顺磁态C14结构的弹性各向异性最强, 铁磁态的C15结构的弹性各向异性最低. 对于Co2Hf和Co2Ta的C15结构, BV = BR, 使得AB = 0, 表明其具有各向异性的抗压缩能力.为了直观地展示弹性各向异性, 图7给出了三维杨氏模量随晶向的变化. 杨氏模量是描述固体材料抵抗形变能力的物理量, 对于各向同性系统, 曲面是球形, 而与球形形状的偏差反映了弹性各向异性的程度. 从图7可以看出, C14构型的杨氏模量近似为球形, C15呈曲边正方形, 而C36结构呈陀螺形, 铁磁态下的C14Co2Hf与其他结构相比, 各向同性性质明显, 且C36结构的Co2Ta的顺磁态具有高的弹性各向异性, 这与图6各向异性参数AU所示结果一致. 而在掺杂合金Co2(HfxTa1–x)下, 铁磁态的C36结构Co2Hf0.5Ta0.5比 Co2Hf0.25Ta0.75和Co2Hf0.75Ta0.25具有更强的弹性各向异性.
-
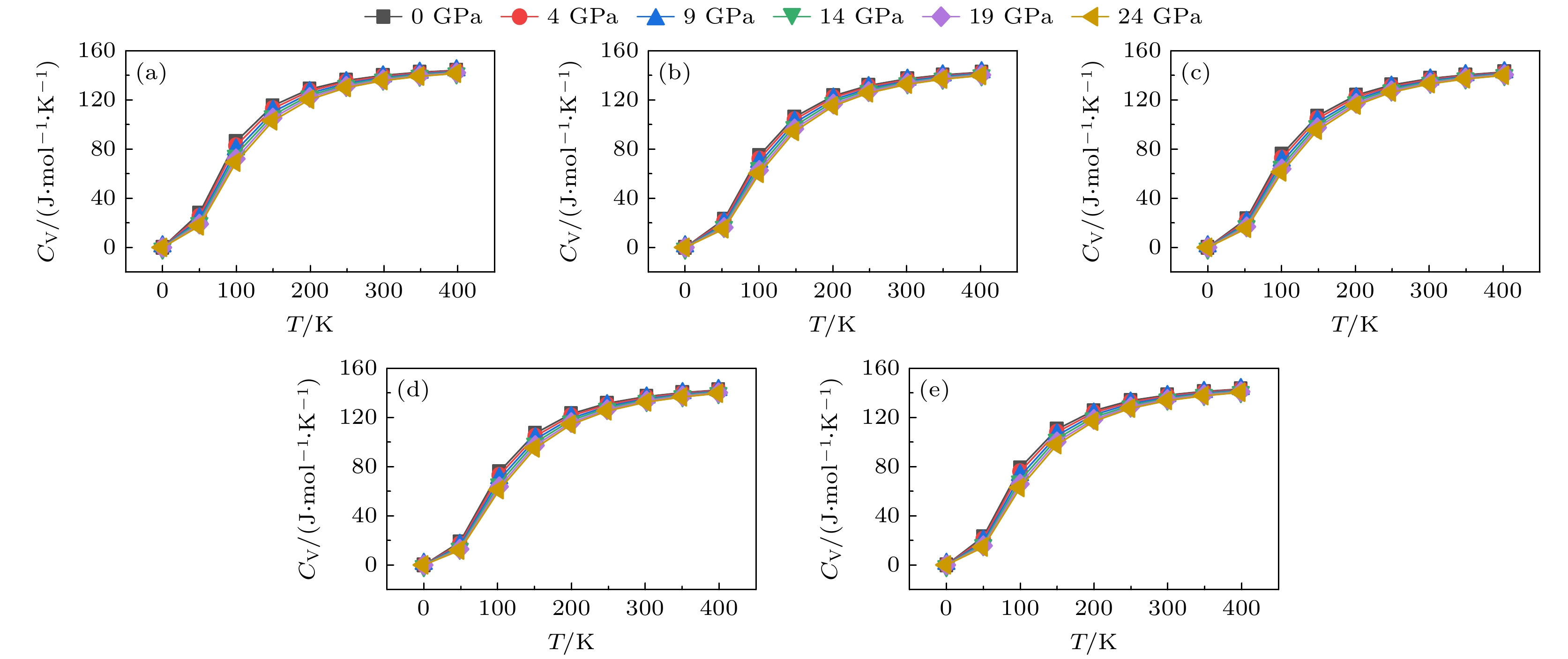
正如前文讨论, 在顺磁态下, 钴的局域磁矩趋近于零. 表明在高温下, 计算考虑非自旋极化是合理的. 因此, 下面所计算的高温下的热力学性质均采用了无自旋极化的结构. 在此之前, 通过计算得出Co2Hf具有稳定的顺磁C15结构, 而Co2Ta和Co2(Ta1–xHfx) (x = 0.25, 0.50, 0.75)具有顺磁态的C36结构. 在准简谐近似下, 计算的热容CV如图8所示, 同时也展示了热容随压强(0—24 GPa)的变化. 在温度T< 200 K时, CV增长迅速, 随着温度升高 (T > 200 K), CV增大变缓慢. 在高温时, CV逐渐收敛于一个特定值的倾向, 即热容的极值, 对应于杜隆-珀替定律常数.
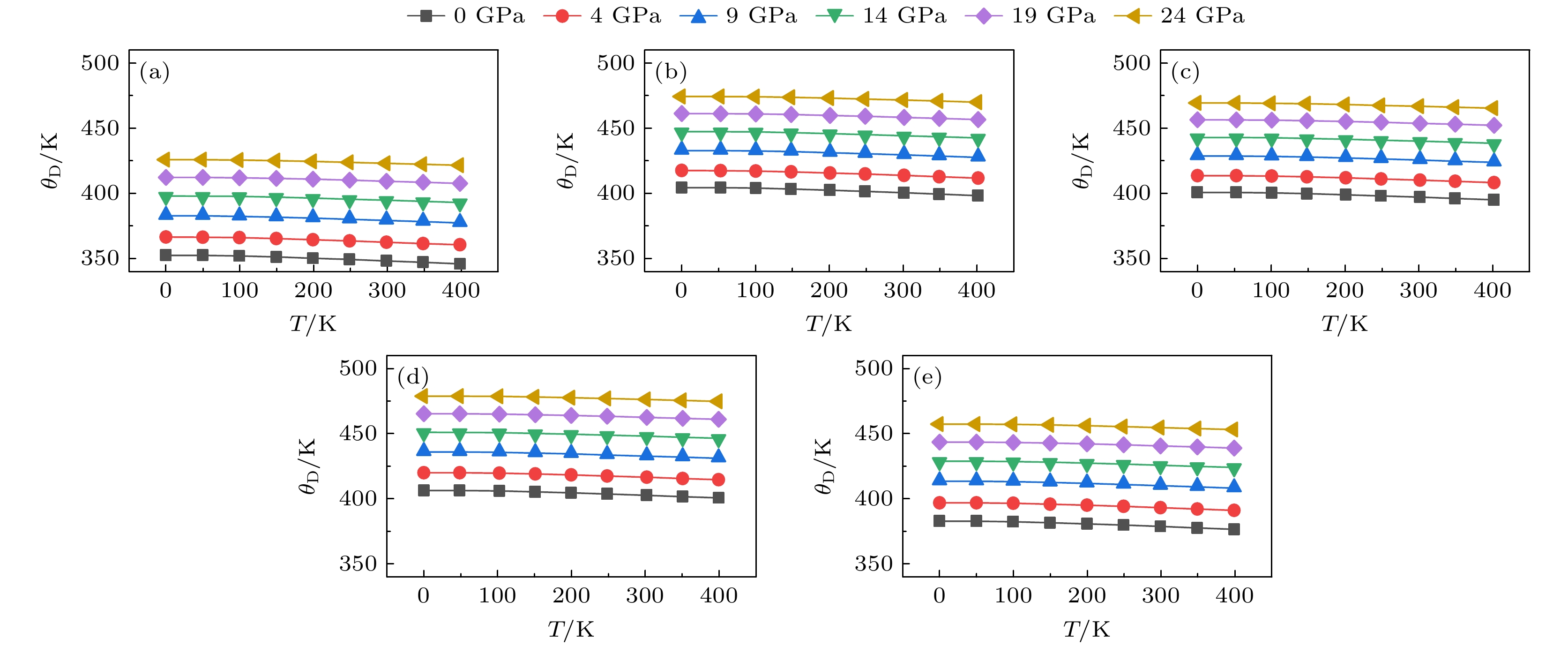
图9展示了德拜温度(
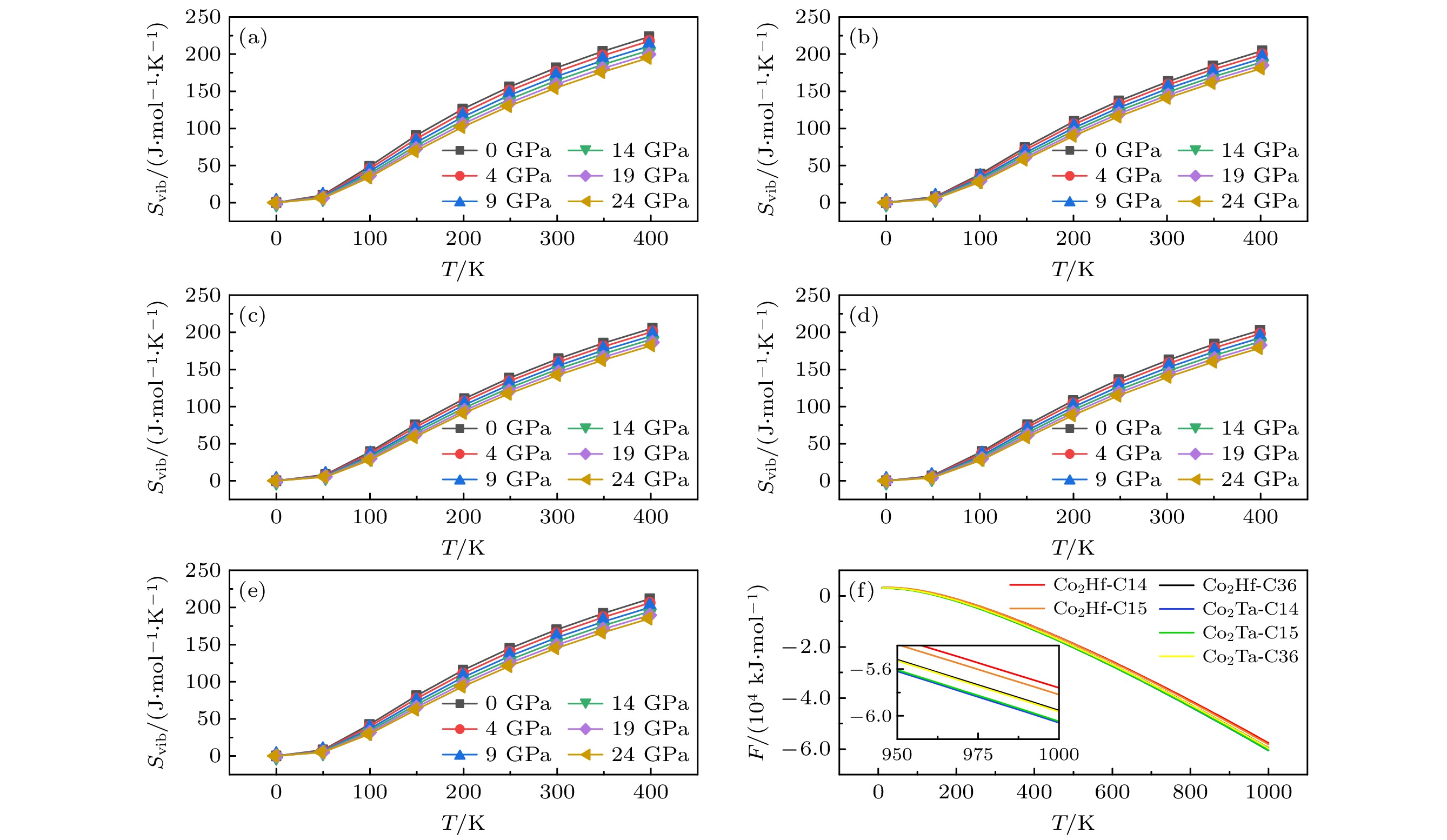
$ {\theta }_{{\mathrm{D}}} $ )随温度和压强的变化关系. 从图9可看出,$ {\theta }_{{\mathrm{D}}} $ 在温度范围0—400 K时近似为常数. 当温度一定时,$ {\theta }_{{\mathrm{D}}} $ 随着压强的增大而增大. 在零温零压下, C15 Co2Hf的$ {\theta }_{{\mathrm{D}}} $ 为352.5 K, C36相Co2Ta的$ {\theta }_{{\mathrm{D}}} $ 为404.48 K, Co2Hf0.25Ta0.75的$ {\theta }_{{\mathrm{D}}} $ 为400.77 K, Co2Hf0.5Ta0.5的$ {\theta }_{{\mathrm{D}}} $ 为406.39 K, Co2Hf0.75Ta0.25的$ {\theta }_{{\mathrm{D}}} $ 为382.82 K, 因此, Hf的加入可能对Co2Hf Ta合金德拜温度的变化产生影响.图10表明振动熵随温度单调递增和压强与振动熵负相关. 在特定温度和压强下, Co2Hf0.5Ta0.5 振动熵最小, 而C15结构的Co2Hf振动熵最大, 相应地, 在相同条件下, C15结构的赫姆霍兹自由能有较大变化. 根据图10(f), 自由能包括了振动熵和电子熵的贡献, 在1000 K时, C36结构的Co2Hf (黑线) 对应自由能最小, 而Co2Ta-C14 (蓝线) 对应的自由能也最小. 这与0 K下计算的基态结构不同, 表明振动熵和电子熵对结构稳定性的影响非常显著, 即随着温度的升高, Co2Hf的稳定结构变为C36, 而Co2Ta的稳定结构变为C14.
-
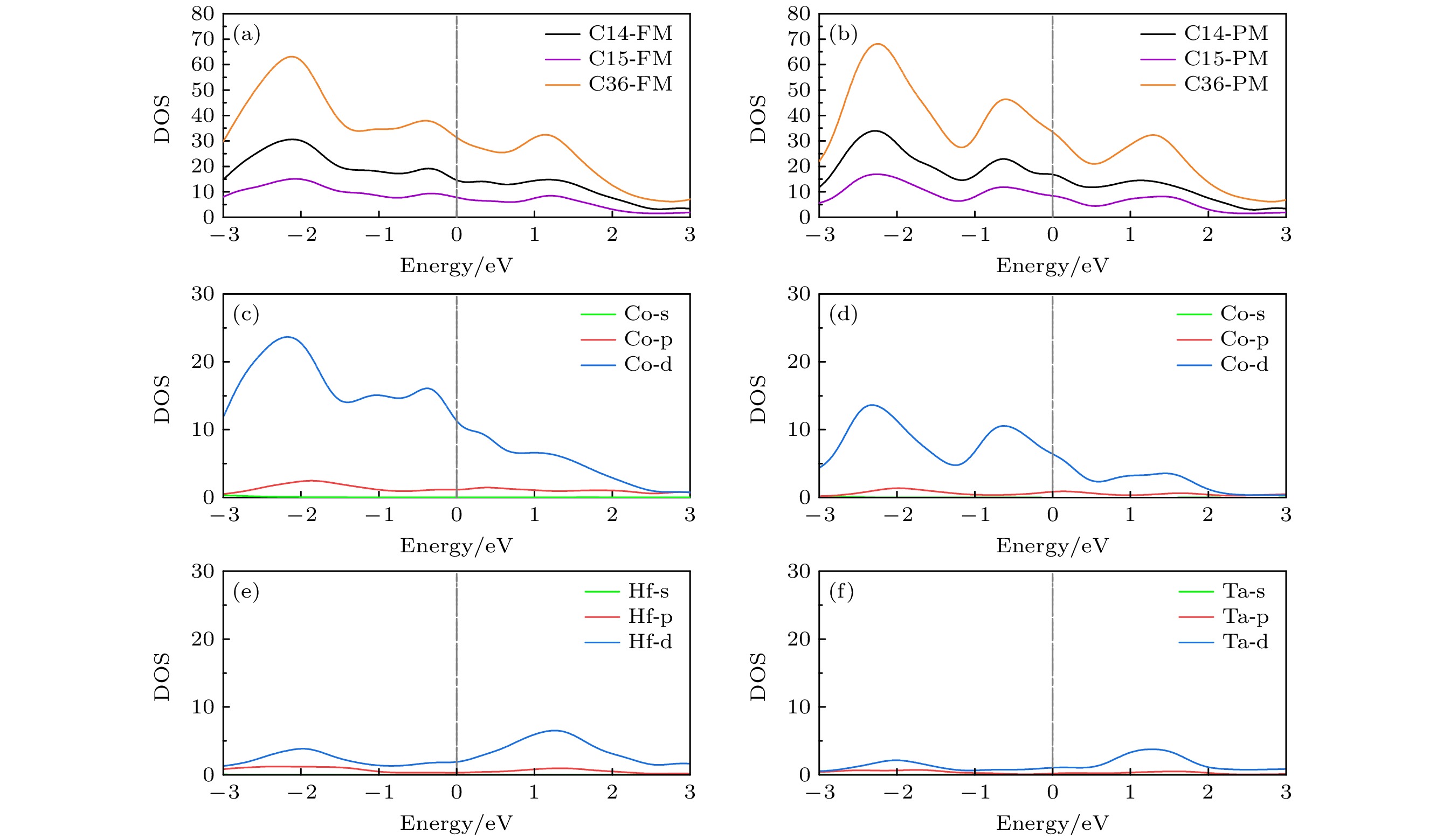
图11给出Co2Ta和Co2Hf的总态密度(DOS)和分态密度(PDOS). 可以看出两种合金的Laves相有非常相似的电子态密度分布. 在费米面附近, C15的态密度相对最小, 但C15并不是基态结构, 也进一步说明了这3种结构具有相似的稳定性. 不同磁态下的电子态密度也较为相似(未展示). C14 Co2Hf的Co-3d电子主要在–3—2 eV之间的价态区域贡献, 而Co2Ta在–3—2 eV和–1—0 eV有明显的局域性. 对于Co2Ta, 在–2 eV附近, Co 3p轨道和Ta 5d轨道出现杂化.
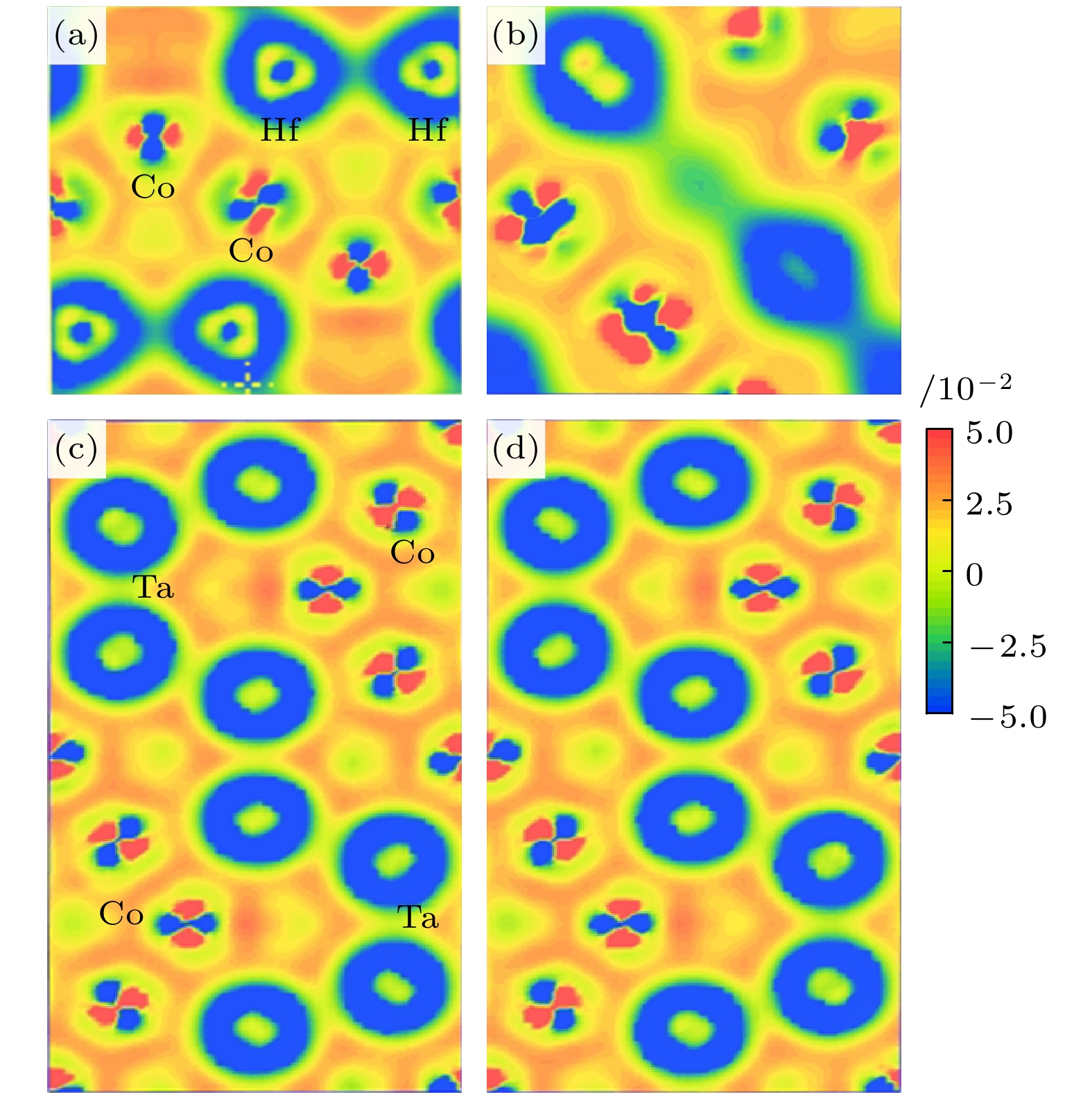
差分电荷密度图可以用来直观地展示晶体结构中原子之间的电荷转移以及在晶格间电荷重新分布. 从图12可以看出Co原子周围电荷密度的局域程度比Hf/Ta原子要强, 且展示了d电子的电子云分布的特征, Co与Hf和Co的成键有一定的方向性, 呈现了共价键的特征.
-
本文采用第一性原理方法, 研究了Co2(HfxTa1–x)化合物的晶格常数、形成能、弹性性质、热力学性质和电子结构性质. 结果表明Co2Hf的基态为铁磁C14结构, 而Co2Ta的基态为铁磁C36结构. 振动熵和电子熵对结构稳定性有重要影响, 随着温度的增加, 自由能的计算表明Co2Hf的相对稳定结构变为C36, 而Co2Ta变为C14. 对于Co2(HfxTa1–x)合金, 当Hf的含量在75%—100%之间基态结构发生了C36-C14的转变.
弹性常数的计算表明Co2(HfxTa1–x)合金在a轴和c轴上抗击压缩的能力有差异, Co2Hf和Co2Ta Laves相表现了本征脆性. Co2(Hf Ta)合金中不同组分的力学性能研究为合金设计提供了理论依据. 引入了通用参数AU、Chung-Buessem参数和三维杨氏模量图, 量化了Co2(HfxTa1–x)弹性各向异性程度. 通过热容、德拜温度和振动熵分析, 发现Co2Hf和Co2Ta Laves相在高温下呈现出特定的热力学行为, 德拜温度在温度范围0—400 K时近似为常数, 振动熵随温度单调递增和压强与振动熵负相关. 电子态密度分析展示了Co2Ta和Co2Hf的3个Laves相有较为接近相稳定性, 差分电荷密度图揭示了Co原子具有较强的局域性和方向性.
Laves-Co2(Hf Ta)合金的相稳定性及热物性
Phase stability and thermo-physical properties of Laves-Co2(Hf Ta) alloys
-
摘要: 基于第一性原理计算方法, 在考虑磁效应的基础上, 对不同温度下合金Co2(Hf Ta)中的稳定结构、电子性质和热力学性质展开了研究. 通过第一性原理计算形成能、弹性性质及声子色散关系, 结果表明合金Co2(HfxTa1–x) 在x ≤ 0.75时基态是C36, 当x > 0.75时基态是C14. 这一发现提示了合金成分对其基态结构的影响, 并为合金的稳定性提供了重要线索. 值得注意的是, 考虑了振动熵和电子熵的贡献后, Co2Hf相对稳定的结构变为C36, Co2Ta变为C14, 这表明温度会对合金结构稳定性的影响. Co2(HfxTa1–x)合金在弹性方面呈现出本征脆性. 热力学分析表明其在高温下热容趋于稳定, 德拜温度近似为常数, 振动熵随温度递增且与压强负相关. 电子态密度分析揭示了Co2(Hf Ta)合金三个结构的相稳定性.
-
关键词:
- Co2(Hf Ta) /
- Laves相稳定性 /
- 热物性质 /
- 第一性原理计算
Abstract: There exists still the controversy over the stable structure of Laves-phase Co2(Hf Ta) alloys with the C14, C15 or C36 structures. In this study, the stability, electronic and thermodynamic properties of Laves-phase Co2(Hf Ta) are investigated. In order to fully understand the influence of magnetic state and temperature on phase stability, we systematically study the free energy change at finite temperature, elastic stability, and phonon dispersion. The low Curie temperature can be estimated, which suggests that the Co2(Hf Ta) alloys possess the paramagnetic state in a wide temperature range. Results indicate that the lattice vibration and electronic excitation have an important effect on the phase stability. The ground state of Co2Hf compound has a C14-type structure, while the ground state of Co2Ta has a C36-type structure, without the effect of temperature. After doping Hf with different concentrations (0.25, 0.50, 0.75) into Co2Ta, the most stable structure still possesses the C36-type structure. After considering the contribution of vibration entropy and electron entropy, the relatively stable structures of Co2Hf and Co2Ta undergo the C36 and C14 phase transition, respectively. In addition, the thermodynamic properties, including Debye temperature, heat capacity, and vibration entropy, which vary with pressure and temperature, are studied. The electronic properties of Co2Hf and Co2Ta compounds are analyzed by the charge difference and density of states. The similar electronic density of states between different phases suggest that the Lave phases have the similar stability. The Hf-Co bonding with a certain direction is revealed. Our results are of great significance in understanding the structure and properties of Co2Hf and Co2Ta compounds.-
Key words:
- Co2(Hf Ta) /
- Laves phase stability /
- thermo-physical properties /
- first-principles calculation .
-

-
图 7 Co2Ta1–xHfx稳定结构的杨氏模量 (E)的三维图(颜色刻度值以GPa为单位) (a) 铁磁态C14相Co2Hf; (b) 顺磁态C15相Co2Hf; (c) 铁磁态C36相 Co2Ta; (d)—(f) 铁磁C36相 Co2Hf0.25Ta0.75, Co2Hf0.5Ta0.5, Co2Hf0.75Ta0.25
Figure 7. Anisotropy of Young’s modulus (E) of Co2Ta1–xHfx along different crystalline directions: (a) Ferromagnetic C14 Co2Hf; (b) paramagnetic C15 Co2Hf; (c) ferromagnetic C36 Co2Ta; (d)–(f) ferromagnetic C36 Co2Hf0.25Ta0.75, Co2Hf0.5Ta0.5 and Co2Hf0.75Ta0.25. The color scale is in GPa.
图 8 不同压强下热容随温度的变化 (a) C14-PM Co2Hf; (b) C36-PM Co2Ta; (c) C36- PM Co2Hf0.25Ta0.75; (d) C36-PM Co2Hf0.5Ta0.5; (e) C36-PM Co2Hf0.75Ta0.25
Figure 8. Heat capacity with temperature under different pressures: (a) C14-PM Co2Hf; (b) C36-PM Co2Ta; (c) C36-PM Co2Hf0.25Ta0.75; (d) C36-PM Co2Hf0.5Ta0.5; (e) C36-PM Co2Hf0.75Ta0.25.
图 10 不同压强下, 振动熵与温度的变化关系, 其中(a) C15 Co2Hf; (b) C36 Co2Ta; (c)—(e) C36 Co2Hf0.25Ta0.75, Co2Hf0.5Ta0.5, Co2Hf0.75Ta0.25; (f) Co2Hf和Co2Ta 的自由能随温度的变化
Figure 10. Vibrational entropy versus temperature under different pressures: (a) C15 Co2Hf; (b) C36 Co2Ta; (c)–(e) C36 Co2Hf0.25Ta0.75, Co2Hf0.5Ta0.5, Co2Hf0.75Ta0.25. (f) The free energy versus temperature for Co2Hf and Co2Ta.
图 11 Co2Hf和Co2Ta总态密度和分态密度(垂直虚线表示费米能级) (a), (b) C14, C15, C36相的Co2Hf和 Co2Ta的总电子态密度; (c), (e) C14相 Co2Hf的分态密度; (d), (f) C36相Co2Ta的分态密度
Figure 11. Total density of states and partial density of states of Co2Hf and Co2Ta : (a), (b) The total electronic density of states of Co2Hf and Co2Ta in C14, C15 and C36 phases; (c), (e) the partial density of states of C14 phase Co2Hf; (d), (f) the partial density of states of C36 phase Co2Ta. The vertical dotted line represents the Fermi level.
图 12 差分电荷密度图 (a) Co2Hf 的C14结构
$ (11 \bar{2} 0)$ 面; (b) Co2Hf 的C15结构的(110)面; (c), (d) 代表为铁磁和顺磁Co2Ta的C36 的$(11 \bar{2}0) $ 面Figure 12. Differential charge density diagram: (a) C14-FM
$ (11\bar{2}0) $ plane of C14 structure of Co2Hf; (b) C15-FM (110) plane of C15 structure of Co2Hf; (c), (d) the$ (11\bar{2} 0)$ plane of C36 with ferromagnetic and paramagnetic Co2Ta.表 1 Laves相晶体结构的基本信息; 表中x = 1/6, z (C14-A1) = 9/16, z (C36-A1) = 21/32, z (C36-A2) = 3/32, z (C36-B3) = 1/8理想原子位置附近, 随A和B的不同, 6h和4e, 4f位的位置参数x和z会有微小的变化[2]
Table 1. Details on Laves phase crystal structure. Depending on A and B sites, the position parameters x and z of the 6h and 4e, 4f sites slightly vary around the ideal atom position values of x = 1/6, z (C14-A1) = 9/16, z (C36-A1) = 21/32, z (C36-A2) = 3/32, z (C36-B3) = 1/8[2].
结构名称 结构类型 空间群 原子 亚格点位置以及占位 x y z C15 MgCu2 227 A 8a 0 0 0 B 16d 5/8 5/8 5/8 C14 MgZn2 194 A 4f 1/3 2/3 z B1 6h x 2x 1/4 B2 2a 0 0 0 C36 MgNi2 194 A1 4f 1/3 2/3 z A2 4e 0 0 z B1 6h
x2x 1/4 B2 6g 1/2 0 0 B3 4f 1/3 2/3 z 表 2 Co2Hf和Co2Ta Laves相的晶格常数a和c、体积V、钴的局域磁矩M、形成能ΔH、有无自旋极化状态下的能量差ΔE, 及可利用的实验或模拟数据
Table 2. Lattice constants a, c, volume V, local magnetic moment M, formation energy ΔH, energy difference ΔE with and without spin polarization state , and available experimental or simulated data of Co2Hf and Co2Ta Laves phases.
体系 结构 a/Å c/Å V/(Å3·atom–1) M/(μB·atom–1) ΔH/(eV·atom–1) ΔE/(eV·atom–1) Refs. Co2Hf C14 4.873 7.939 13.605 0.69
0.79–0.3788 –0.017 C15 4.870 13.615 0.76 –0.3752 –0.002 4.824
4.909
13.945Cal.[22]
Cal.[34]C36 4.876 15.837 13.585 0.68
0.70
0.58–0.3779 –0.007 4.816 15.650 Cal.[22] Co2Ta C14 4.766 7.750 12.703 0.33
0.68–0.2378 –0.002 4.797 7.827 12.730 Exp.[13] C15 4.759 12.702 0.40 –0.2442 –0.005 4.791 12.957 Cal.[34] C36 4.760 15.529 12.698 0.39
0.41
0.27–0.2447 –0.003 表 3 Co2Hf和Co2Ta的C14, C15和C36结构以及Co2(Ta1–xHfx)基态结构的弹性常数cij (GPa), 其中, 结构部分, FM和PM代表铁磁和顺磁态, 数字156, 186表示空间群
Table 3. Elastic constants cij (GPa) of C14, C15, C36Co2Hf and Co2Ta as well as Co2(Ta1–xHfx), where the structural part, FM and PM represent ferromagnetic and paramagnetic states, and the numbers 156, 186 represent the space group.
体系 结构 c11 c33 c44 c12 c13 $c_{66}, {c_{14}}^* $ 

Refs. Co2Hf C14-FM 274.14 332.76 81.86 86.14 126.48 94.00 C14-PM 299.75 348.07 73.80 90.11 113.04 104.82 C15-FM 308.80 85.60 154.53 C15-PM 298.50 106.00 139.12 C15 270.20 85.50 117.50 Cal.[34] C36-FM 308.11 293.50 80.53 121.99 113.90 93.06 C36-PM 329.08 343.58 81.90 120.83 117.89 104.12 Co2Ta C14-FM 407.15 430.80 97.10 138.20 151.11 134.48 C14-PM 442.04 421.53 89.27 167.32 137.34 137.36 C15-FM 357.11 141.47 137.90 C15-PM 395.37 151.94 165.32 C15 383.50 143.90 173.40 Cal.[34] C36-FM 424.64 429.32 98.18 154.27 143.77 135.19 C36-PM 444.08 481.10 88.70 174.90 177.34 134.59 Co2Hf0.25Ta0.75 156-FM 390.67 383.02 80.43 153.72 146.41 –1.13 Co2Hf0.5Ta0.5 186-FM 358.36 362.80 84.35 132.40 126.78 Co2Hf0.75Ta0.25 156-FM 327.16 312.04 77.66 130.90 122.88 0.68 *: c66, c14数据列, 其中后3行时c14数值, 其他行为c66数值. -
[1] Schulze G E 1939 Zeitschrift Für Elektrochemie und Angewandte Physikalische Chemie 45 849 doi: 10.1002/bbpc.19390451202 [2] Stein F, Leineweber A 2021 J. Mater. Sci. 56 5321 doi: 10.1007/s10853-020-05509-2 [3] 张硕鑫, 刘士余, 严达利, 余浅, 任海涛, 于彬, 李德军 2021 物理学报 70 117102 doi: 10.7498/aps.70.20210191 Zhang S X, Liu S Y, Yan D L, Yu Q, Ren H T, Yu B, Li D J 2021 Acta Phys. Sin. 70 117102 doi: 10.7498/aps.70.20210191 [4] Zhang Y, Fu H, He J, Xie J 2022 J. Alloys Compd. 891 162016 doi: 10.1016/j.jallcom.2021.162016 [5] Burzo E, Gratz E, Pop V 1993 J. Magn. Magn. Mater. 123 159 doi: 10.1016/0304-8853(93)90026-X [6] Chen K C, Peterson E J, Thoma D J 2001 Intermetallics 9 771 doi: 10.1016/S0966-9795(01)00068-1 [7] Chen K C, Chu F, Kotula P G, Thoma D 2001 Intermetallics 9 785 doi: 10.1016/S0966-9795(01)00067-X [8] Concas G, Congiu F, Belošević-Čavor J, Cekić B 2007 Zeitschrift für Naturforschung A 62 452 doi: 10.1515/zna-2007-7-816 [9] Wang C, Chen X, Yang P, Zhang Q, Yang S, Lu Y, Guo Y, Liu X 2022 J. Alloys Compd. 925 166723 doi: 10.1016/j.jallcom.2022.166723 [10] Ooshima M, Tanaka K, Okamoto N L, Kishida K, Inui H 2010 J. Alloys Compd. 508 71 doi: 10.1016/j.jallcom.2010.08.050 [11] Omori T, Oikawa K, Sato J, Ohnuma I, Kattner U R, Kainuma R, Ishida K 2013 Intermetallics 32 274 doi: 10.1016/j.intermet.2012.07.033 [12] Povstugar I, Choi P P, Neumeier S, Bauer A, Zenk C H, Göken M, Raabe D 2014 Acta Mater. 78 78 doi: 10.1016/j.actamat.2014.06.020 [13] Dragsdorf R, Foreing W 1962 Acta Crystallogr. 15 531 doi: 10.1107/S0365110X62001371 [14] Baheti V A, Roy S, Ravi R, Paul A 2013 Intermetallics 33 87 doi: 10.1016/j.intermet.2012.09.020 [15] Shinagawa K, Chinen H, Omori T, Oikawa K, Ohnuma I, Ishida K, Kainuma R 2014 Intermetallics 49 87 doi: 10.1016/j.intermet.2014.01.015 [16] Wang P, Koßmann J, Kattner U R, Palumbo M, Hammerschmidt T, Olson G B 2019 Calphad 64 205 doi: 10.1016/j.calphad.2018.12.002 [17] Zhou C, Guo C, Li C, Du Z 2019 Calphad 66 101649 doi: 10.1016/j.calphad.2019.101649 [18] Asano S, Ishida S 1988 J. Phys. F: Metal Phys. 18 501 doi: 10.1088/0305-4608/18/3/020 [19] Stein F, Palm M, Sauthoff G 2004 Intermetallics 12 713 doi: 10.1016/j.intermet.2004.02.010 [20] Von Keitz A, Sauthoff G 2002 Intermetallics 10 497 doi: 10.1016/S0966-9795(02)00025-0 [21] Thoma D, Perepezko J 1995 J. Alloys Compd. 224 330 doi: 10.1016/0925-8388(95)01557-4 [22] Wang L, Kong Y, Oehring M, Song M, Pyczak F 2022 J. Alloys Compd. 906 164261 doi: 10.1016/j.jallcom.2022.164261 [23] Levy O, Hart G L, Curtarolo S 2010 Acta Mater. 58 2887 doi: 10.1016/j.actamat.2010.01.017 [24] Segall M, Lindan P J, Probert M A, Pickard C J, Hasnip P J, Clark S, Payne M 2002 J. Phys.: Condens. Matter 14 2717 doi: 10.1088/0953-8984/14/11/301 [25] Clark S J, Segall M D, Pickard C J, Hasnip P J, Probert M I, Refson K, Payne M C 2005 Z. Krist. -Cryst. Mater. 220 567 doi: 10.1524/zkri.220.5.567.65075 [26] Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke K 2008 Phys. Rev. Lett. 100 136406 doi: 10.1103/PhysRevLett.100.136406 [27] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188 doi: 10.1103/PhysRevB.13.5188 [28] Pfrommer B G, Côté M, Louie S G, Cohen M L 1997 J. Comput. Phys. 131 233 doi: 10.1006/jcph.1996.5612 [29] Wang Q, Li Q, Ding H, Tian F 2022 Comput. Condens. Matter 32 e00721 doi: 10.1016/j.cocom.2022.e00721 [30] Sun Y, Zhou Y, Gurunathan R, Zhang J Y, Hu M, Liu W, Xu B, Snyder G J 2021 J. Mater. Chem. C 9 8506 doi: 10.1039/D1TC00902H [31] Wu R, Wang Y P, Shao L, Wang W, Tang B Y 2021 Chin. J. Chem. Eng. 40 315 doi: 10.1016/j.cjche.2020.11.033 [32] Gao J, Liu Q, Jiang C, Fan D, Zhang M, Liu F, Tang B 2022 Chin. J. High Press. Phys 36 051101 doi: 10.11858/gywlxb.20220575 [33] Jana A, Sridar S, Fries S G, Hammerschmidt T, Kumar K H 2020 Intermetallics 116 106640 doi: 10.1016/j.intermet.2019.106640 [34] Chen S, Sun Y, Duan Y H, Huang B, Peng M J 2015 J. Alloys Compd. 630 202 doi: 10.1016/j.jallcom.2015.01.038 [35] Özer T 2020 Canadian J. Phys. 98 357 doi: 10.1139/cjp-2018-0448 [36] Cheng T M, Yu G L, Zhang X X 2022 Physica B 645 414268 doi: 10.1016/j.physb.2022.414268 [37] Xu Y, Cao Y, Hu C, Zhang C, Tian C, Alzoabi S, Santos N, Zhou S 2021 Solid State Sci. 115 106580 doi: 10.1016/j.solidstatesciences.2021.106580 [38] Xu N, Chen Y, Chen S, Zhang W, Li S, Song R, Zhang J 2023 J. Mater. Res. Technol. 26 4825 doi: 10.1016/j.jmrt.2023.08.218 [39] Jian Y, Huang Z, Xing J, Sun L, Liu Y, Gao P 2019 Mater. Chem. Phys. 221 311 doi: 10.1016/j.matchemphys.2018.09.055 [40] Ranganathan S I, Ostoja-Starzewski M 2008 Phys. Rev. Lett. 101 055504 doi: 10.1103/PhysRevLett.101.055504 [41] Hong D, Zeng W, Liu F S, Tang B, Liu Q J 2019 Physica B 558 100 doi: 10.1016/j.physb.2019.01.036 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: