高级搜索

纳米氧化锌改性纤维素绝缘纸力学和热学性能的分子动力学模拟

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

张钰业, 张镱议, 韦文厂, 苏至诚, 兰丹泉, 罗世豪. 纳米氧化锌改性纤维素绝缘纸力学和热学性能的分子动力学模拟[J]. 物理学报, 2024, 73(12): 127701-1. doi: 10.7498/aps.73.20240208
引用本文: 张钰业, 张镱议, 韦文厂, 苏至诚, 兰丹泉, 罗世豪. 纳米氧化锌改性纤维素绝缘纸力学和热学性能的分子动力学模拟[J]. 物理学报, 2024, 73(12): 127701-1. doi: 10.7498/aps.73.20240208
shu
Yu-Ye Zhang, Yi-Yi Zhang, Wen-Chang Wei, Zhi-Cheng Su, Dan-Quan Lan, Shi-Hao Luo. Molecular dynamics simulation of mechanical and thermal properties of nano-zinc oxide modified cellulose insulating paper[J]. Acta Physica Sinica, 2024, 73(12): 127701-1. doi: 10.7498/aps.73.20240208
Citation: Yu-Ye Zhang, Yi-Yi Zhang, Wen-Chang Wei, Zhi-Cheng Su, Dan-Quan Lan, Shi-Hao Luo. Molecular dynamics simulation of mechanical and thermal properties of nano-zinc oxide modified cellulose insulating paper[J]. Acta Physica Sinica, 2024, 73(12): 127701-1. doi: 10.7498/aps.73.20240208
shu

纳米氧化锌改性纤维素绝缘纸力学和热学性能的分子动力学模拟

  • 1.

    广西大学电气工程学院, 广西电力输配网防雷工程技术研究中心, 南宁　530004

  • 2.

    广西大学, 省部共建特色金属材料与组合结构全寿命安全国家重点实验室, 南宁　530004

    • 作者简介: 张钰业: 2212391083@st.gxu.edu.cn .
    通讯作者: E-mail: yiyizhang@gxu.edu.cn.; 

  • 中图分类号: 77.22.Gm, 77.84.Lf

Molecular dynamics simulation of mechanical and thermal properties of nano-zinc oxide modified cellulose insulating paper

  • 1.

    Guangxi Power Transmission and Distribution Network Lightning Protection Engineering Technology Research Center, School of Electrical Engineering, Guangxi University, Nanning 530004, China

  • 2.

    State Key Laboratory of Featured Metal Materials and Life-cycle Safety for Composite Structures, Guangxi University, Nanning 530004, China

    • Corresponding author: E-mail: yiyizhang@gxu.edu.cn.; 

  • MSC: 77.22.Gm, 77.84.Lf

  • 摘要: 随着电力负荷激增和电压水平不断提高, 绝缘纸的力学性能和热稳定性面临着严峻挑战. 然而, 由于缺乏直接的科学理论或模拟指导, 传统低效的“试错性”试验难以快速高效地研发新型纤维素复合绝缘纸. 针对这一问题, 本文提出通过分子动力学模拟, 研究纳米氧化锌(nano-ZnO)对纤维素的力学和热学性能的提升效果. 首先设计了nano-ZnO/纤维素复合材料模型, 然后从微观角度分析了不同nano-ZnO含量的改性纤维素的力学性能和热稳定性, 从而确定nano-ZnO和纤维素的最佳配比. 结果表明, 相比于未改性模型, nano-ZnO改性纤维素模型的力学性能、内聚能密度、玻璃化转变温度和导热系数均有提升, 弹性模量最高提升了45.31%, 导热系数最高提升了41.49%. 因为nano-ZnO的加入能够有效填充纤维网络中的空隙, 并增强纤维素链之间的作用力和导热通道, 从而提升纤维素的热力学性能. 本工作为可快速制备出具有优良热力学性能的改性纤维素绝缘纸提供有价值的理论参考.
    Abstract: With the surge in electrical loads and increasing voltage levels, the mechanical performance and thermal stability of insulating paper are facing severe challenges. However, due to the lack of direct scientific theories or simulation guidance, traditional inefficient “trial-and-error” experiments are difficult to effectively develop new types of cellulose composite insulating papers. For solving this problem, in this work we are to enhance the effects of nanoscale zinc oxide (nano-ZnO) on the mechanical and thermal properties of cellulose through molecular dynamics simulations. Initially, we model the nano-ZnO/cellulose composite material , then carry out a microscopic analysis of the mechanical performance and thermal stability of modified cellulose with varying nano-ZnO content, thus determining the optimal ratio of nano-ZnO to cellulose. The results indicate that compared with the outcomes from the unmodified model, the mechanical performance, cohesive energy density, glass transition temperature, and thermal conductivity of the nano-ZnO-modified cellulose model are all improved, with the highest increase in elastic modulus reaching 45.31% and the highest increase in thermal conductivity attaining 41.49%. The addition of nano-ZnO effectively fills the gaps in the fiber network and enhances the interactions between cellulose chains and thermal conduction channels, thereby improving the thermodynamic performance of cellulose. This work provides valuable theoretical references for rapidly preparing modified cellulose insulating papers with excellent thermodynamic performance.
  • 加载中

  • 图 1  nano-ZnO和纤维素的复合模型　(a) P0; (b) P2; (c) P4; (d) P6; (e) P8; (f) P10

    Figure 1.  Composite model of nano-ZnO and cellulose: (a) P0; (b) P2; (c) P4; (d) P6; (e) P8; (f) P10.

    下载: 全尺寸图片 幻灯片

    图 2  不同nano-ZnO含量的nano-ZnO/纤维素模型的体积模量、剪切模量和弹性模量

    Figure 2.  Volume modulus, shear modulus, and elastic modulus of nano-ZnO/cellulose model with different nano-ZnO content.

    下载: 全尺寸图片 幻灯片

    图 3  (a)不同nano-ZnO含量的nano-ZnO/纤维素模型的内聚能密度; (b) Nano-ZnO填充无定形区域空隙时产生的氢键; (c) Nano-ZnO出现团聚现象时产生的氢键; (d) 6种模型的氢键数量

    Figure 3.  (a) Cohesion energy density of nano-ZnO/cellulose models with different nano-ZnO contents; (b) hydrogen bonding when Nano-ZnO fills voids in amorphous regions; (c) hydrogen bonds generated when Nano-ZnO is agglomerated; (d) the number of hydrogen bonds in the six models.

    下载: 全尺寸图片 幻灯片

    图 4  (a) 6种模型的MSD曲线; (b)各模型样品的最大MSD值

    Figure 4.  (a) MSD curves for six models; (b) the maximum MSD value of each model sample.

    下载: 全尺寸图片 幻灯片

    图 5  nano-ZnO/纤维素复合模型的玻璃化转变温度　(a) P0; (b) P2; (c) P4; (d) P6; (e) P8; (f) P10

    Figure 5.  Glass transition temperature of nano-ZnO/cellulose models: (a) P0; (b) P2; (c) P4; (d) P6; (e) P8; (f) P10.

    下载: 全尺寸图片 幻灯片

    图 6  反向非平衡分子动力学(RNEMD)方法模型图

    Figure 6.  Model diagram of reverse non-equilibrium molecular dynamics (RNEMD) method.

    下载: 全尺寸图片 幻灯片

    图 7  不同添加量下的nano-ZnO/纤维素模型的导热系数模拟结果

    Figure 7.  Thermal conductivity simulation results of nano-ZnO/cellulose models with different doping ratios.

    下载: 全尺寸图片 幻灯片

    表 1  分子动力学计算纯纤维素绝缘纸和改性纤维素绝缘纸的力学参数

    Table 1.  Mechanical parameters of pure cellulose insulating paper and modified cellulose insulating paper calculated by molecular dynamics.

    模型 λ μ E/GPa G/GPa K/GPa K/G
    P0 1.7942 2.7210 6.5232 2.7210 3.6082 1.3261
    P1 2.6659 3.9442 9.4791 3.9442 5.2954 1.3426
    P2 1.1556 3.8840 8.6586 3.8840 3.7449 0.9642
    P3 2.2157 2.7362 6.6967 2.7362 4.0398 1.4764
    P4 0.5645 2.7983 6.0663 2.4300 2.7983 0.8684
    P5 2.6101 2.3187 5.8653 4.1559 2.3187 1.7923
    下载: 导出CSV
  • [1] Shadfar H, Pashakolaei M G, Foroud A A 2021 Int. T. Electr. Energy 31 24 doi: 10.1002/2050-7038.12996
    [2] Chen Q G, Li C P, Cheng S, Sun W, Chi M H, Zhang H 2022 IEEE T. Dielect. El. In. 29 591 doi: 10.1109/TDEI.2022.3157900
    [3] Tang C, Chen R, Zhang J Z, Peng X, Chen B H, Zhang L S 2022 IET Nanodielectrics 5 63 doi: 10.1049/nde2.12032
    [4] Yang L, Gao J, Peng X, Qin J S, Tang C 2021 Cellulose 28 6023 doi: 10.1007/s10570-021-03956-x
    [5] Tang C, Zhang S, Wang X B, Hao J 2018 Cellulose 25 3619 doi: 10.1007/s10570-018-1813-4
    [6] Chen Q J, Kang M C, Xie Q H, Wang J H 2020 Cellulose 27 7621 doi: 10.1007/s10570-020-03305-4
    [7] Ji D Y, Li T, Hu W P, Fuchs H 2019 Adv. Mater. 31 19 doi: 10.1002/adma.201806070
    [8] Sun X, Chi M H, Weng L, Shi J H, Zhang X R 2021 J. Mater. SCI-Mater. El. 32 26548 doi: 10.1007/s10854-021-07031-w
    [9] Gao F, Zhang X R, Weng L, Cheng Y J, Shi J H 2022 Pigm. Resin Technol. 51 441 doi: 10.1108/PRT-03-2021-0039
    [10] Han Z Q, Qi S L, Liu W, Han L, Wu Z P, Wu D Z 2013 Ind. Eng. Chem. Res. 52 3042 doi: 10.1021/ie400286w
    [11] Wei W C, Chen H Q, Zha J W, Zhang Y Y 2023 Front. Chem. Sci. Eeg. 17 991 doi: 10.1007/s11705-022-2259-7
    [12] 吕程 2014 博士学位论文 (重庆: 重庆大学) Lv C 2014 Ph. D. Dissertation (Chongqing: Chongqing University
    [13] 张松, 唐超, Chen G, 周渠, 吕程, 李旭 2015 中国科学: 技术科学 45 1167 doi: 10.1360/N092015-00207 Zhang S, Tang C, Chen G, Zhou Q, Lv C, Li X 2015 Sci. Sin. Tech. 45 1167 doi: 10.1360/N092015-00207
    [14] Huang M, Han Q B, Lv Y Z, Wang L, Shan B L, Ge Y, Qi B, Li C R 2018 IEEE T. Dielect. El. In. 25 1135 doi: 10.1109/TDEI.2018.007058
    [15] Zhang Y Y, Xu C Q, WEI W C, Deng Y K, Nie S X, Zha J W 2023 High Volt. 8 599 doi: 10.1049/hve2.12271
    [16] Wei W C, Zhang Y Y, Chen H Q, Xu C Q, Zha J W, Nie S X 2023 Mater. Design 233 11 doi: 10.1016/j.matdes.2023.112176
    [17] 王久亮, 刘宽, 秦秀娟, 邵光杰 2004 哈尔滨工业大学学报 02 226 doi: 10.3321/j.issn:0367-6234.2004.02.025 Wang J L, Liu K, Qin X J, Shao G J 2004 J. Harbin Instit. Tech. 02 226 doi: 10.3321/j.issn:0367-6234.2004.02.025
    [18] 李酽, 李娇, 陈丽丽, 连晓雪, 朱俊武 2018 物理学报 67 140701 doi: 10.7498/aps.67.20180182 Li Y, Li J, Chen L L, Lian X X, Zhu J W 2018 Acta Phys. Sin. 67 140701 doi: 10.7498/aps.67.20180182
    [19] 李酽, 张琳彬, 李娇, 连晓雪, 朱俊武 2019 物理学报 68 070701 doi: 10.7498/aps.68.20181961 Li Y, Zhang L B, Li J, Lian X X, Zhu J W 2019 Acta Phys. Sin. 68 070701 doi: 10.7498/aps.68.20181961
    [20] Banerjee A, Bose N, Lahiri A 2023 IEEE T. Ind. Appl. 59 479 doi: 10.1109/TIA.2022.3215955
    [21] Lu J Y, Jiang Q S, Zhang J 2009 21st Chinese Control and Decision Conference Guilin, China, June 17–19, 2009 p4823
    [22] Naskar M, Dharmendra H M, Meena K P 2021 5th International Conference on Condition Assessment Techniques in Electrical Systems Kozhikode, India, December 3–5, 2021 p186
    [23] Kong Y, Li L B, Fu S Y 2022 J. Mater. Chem. A 10 14451 doi: 10.1039/D2TA03164G
    [24] Du D Y, Tang C, Tang Y J, Yang L, Hao J 2021 Compos. Struct. 261 6 doi: 10.1016/j.compstruct.2020.113283
    [25] Zhang Z X, Zhou H B, Li W T, Tang C 2021 Processes 9 9 doi: 10.3390/pr9050766
    [26] Zhang Y Y, Li Y, Zheng H B, Zhu M Z, Liu J F, Yang T, Zhang C H, Li Y 2020 Cellulose 27 2455 doi: 10.1007/s10570-019-02960-6
    [27] Mo Y, Yang L J, Yin F, Gao Y Y 2022 Polym. Composite 43 1698 doi: 10.1002/pc.26489
    [28] Inagak T, Siesler H W, Mitsui K, Tsuchikawa S 2010 Biomacromolecules 11 2300 doi: 10.1021/bm100403y
    [29] Mazeau K, Heux L 2003 J. Phys. Chem. B 107 2394 doi: 10.1021/jp0219395
    [30] Wang X B, Tang C, Wang Q, Li X P, Hao J 2017 Energies 10 11 doi: 10.3390/en10091377
    [31] Bond S D, Leimkuhler B J, Laird B B 1999 J. Comput. Phys. 151 114 doi: 10.1006/jcph.1998.6171
    [32] 吕健, 詹怀宇, 晋华春 2008 中国造纸 5 54 doi: 10.3969/j.issn.0254-508X.2008.02.014 Lv J, Zhan H Y, Jin H C 2008 China Pulp Paper 5 54 doi: 10.3969/j.issn.0254-508X.2008.02.014
    [33] Tanaka F, Okamura K 2005 Cellulose 12 243 doi: 10.1007/s10570-004-5864-3
    [34] Chang K S, Chung Y C, Yang T H, Lue S J, Tung K L, Lin Y F 2012 J. Membrane Sci. 417 119 doi: 10.1016/j.memsci.2012.06.019
    [35] 王有元, 杨涛, 廖瑞金, 张大伟, 刘强, 田苗 2012 高电压技术 38 1199 Wang Y Y, Yang T, Liao R J, Zhang D W, Liu Q, Tian M 2012 High Volt. Eng. 38 1199
    [36] Liu X J, Rao Z H 2019 Int. J. Heat. Mass Tran. 132 362 doi: 10.1016/j.ijheatmasstransfer.2018.12.009
    [37] 王振华, 卢咏来, 张立群 2009 橡胶工业 56 581 doi: 10.3969/j.issn.1000-890X.2009.10.001 Wang Z H, Lu Y L, Zhang L Q 2009 China Rubber Ind. 56 581 doi: 10.3969/j.issn.1000-890X.2009.10.001
  • 加载中
图( 7) 表( 1)
计量
  • 文章访问数:  408
  • HTML全文浏览数:  408
  • PDF下载数:  5
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-01-31
  • 刊出日期:  2024-06-20

纳米氧化锌改性纤维素绝缘纸力学和热学性能的分子动力学模拟

    通讯作者: E-mail: yiyizhang@gxu.edu.cn.; 
    作者简介: 张钰业: 2212391083@st.gxu.edu.cn
  • 1. 广西大学电气工程学院, 广西电力输配网防雷工程技术研究中心, 南宁　530004
  • 2. 广西大学, 省部共建特色金属材料与组合结构全寿命安全国家重点实验室, 南宁　530004
  • 收稿日期:  2024-01-31

摘要: 随着电力负荷激增和电压水平不断提高, 绝缘纸的力学性能和热稳定性面临着严峻挑战. 然而, 由于缺乏直接的科学理论或模拟指导, 传统低效的“试错性”试验难以快速高效地研发新型纤维素复合绝缘纸. 针对这一问题, 本文提出通过分子动力学模拟, 研究纳米氧化锌(nano-ZnO)对纤维素的力学和热学性能的提升效果. 首先设计了nano-ZnO/纤维素复合材料模型, 然后从微观角度分析了不同nano-ZnO含量的改性纤维素的力学性能和热稳定性, 从而确定nano-ZnO和纤维素的最佳配比. 结果表明, 相比于未改性模型, nano-ZnO改性纤维素模型的力学性能、内聚能密度、玻璃化转变温度和导热系数均有提升, 弹性模量最高提升了45.31%, 导热系数最高提升了41.49%. 因为nano-ZnO的加入能够有效填充纤维网络中的空隙, 并增强纤维素链之间的作用力和导热通道, 从而提升纤维素的热力学性能. 本工作为可快速制备出具有优良热力学性能的改性纤维素绝缘纸提供有价值的理论参考.

English Abstract

    全文HTML

    1.   引　言

    • 变压器作为电网中电能传输和转换的核心部件, 其安全稳定运行保证着电力的有效传输[1]. 绝缘纸是油浸式变压器的关键绝缘材料, 其性能关乎变压器的安全稳定运行. 电力变压器在运行过程中, 油纸绝缘系统的温度一般长期维持在60—80 ℃左右, 绝缘纸长期处于此条件下极易发生热老化导致性能下降甚至失效[2]. 绝缘纸的力学性能是确保电气设备在各种工作条件下稳定运行的关键, 不仅保证了纸张的耐久性和可靠性, 也直接影响着设备的安全性和性能表现. 因此提升绝缘纸的力学性能对于保护电气设备、确保电气安全以及延长设备使用寿命都至关重要. 因此, 绝缘纸具有良好的热力学性能是决定电力变压器长期可靠运行的主要因素[3]. 纤维素绝缘纸作为变压器的主要绝缘材料已有近80年的历史[4], 相比于合成纤维绝缘纸, 纤维素绝缘纸因具有良好的机械性能和电学特性, 可再生性、可生物降解性和来源丰富性等特点[5–9], 长期被广泛应用于电力变压器油纸绝缘系统[10,11]. 然而, 纯纤维素绝缘纸的热力学性能相对较低, 已难以满足电压等级不断提升的变压器的需求, 急需开发具有优良热力学性能的改性纤维素绝缘纸, 以确保变压器的安全可靠运行.

      为提升纤维素绝缘纸的热力学及电气性能, 向其引入纳米材料已被证明是一种理想的方法. 吕程[12]制备了掺杂纳米二氧化钛的改性绝缘纸, 研究表明经纳米二氧化钛改性的绝缘纸与未改性的绝缘纸相比, 工频下击穿场强、局部放电、起始放电电压都有提高; 张松等[13]发现, 在绝缘纸中加入纳米氧化铝, 其会与纤维素的表面发生相互作用, 结果表明经纳米氧化铝改性的绝缘纸热稳定性有了较好的提升; Huang等[14]将纳米二氧化钛空心微球加入到绝缘纸中, 然后对其进行浸油处理, 研究结果表明, 改性绝缘纸的介电常数相比未改性绝缘纸, 降低了34%, 油纸绝缘系统的击穿电压提升了15.5%. 其他纳米颗粒, 如纳米碳化硅[15]、纳米聚酰亚胺[16]等掺杂纤维素对绝缘纸进行改性也有报道. 与其他纳米颗粒相比, nano-ZnO具有独特的化学和物理性质, 是一种多功能性的新型无机材料. 因其表面活性高, 比表面积大, 具备较高的导热性和良好的热稳定性, 使其在陶瓷、化工、电子、光学、生物、医药等许多领域有重要的应用价值和前景, 已成为许多科研人员关注的焦点[17–19]. Banerjee等[20]在聚丙烯材料中加入了nano-ZnO颗粒, 研究表明, 随着nano-ZnO颗粒的加入, 聚丙烯的介电性能得到了改善, nano-ZnO填料的表面疏水性好, 漏电流小, 材料的热稳定性和紫外吸收都得到了提升. Lu等[21]发现nano-ZnO膜具有较高的湿度敏感性和良好的重现性, 研究了经六甲基二氮杂烷(HMDS)处理的nano-ZnO的感湿性能, 实验结果表明, HMDS处理后的nano-ZnO可用于高湿环境下的乙醇检测. Moumita等[22]制备了醋酸乙烯酯(EVA)/氧化锌(ZnO)纳米复合材料, 对其绝缘性能进行了研究, 结果表明, 在EVA基体中加入nano-ZnO后, 体积电阻增大, 复合材料的热稳定性上限温度提高了52 ℃.

      近年来, 随着高分子理论和计算模拟技术的发展, 分子动力学模拟已成为开发新材料最重要的方法之一, 具有效率高、成本低、环境干扰小等优点, 可以有效预测材料的性能参数与微观作用机理, 有助于减少实验试错次数, 降低实验成本, 对真实实验具有指导意义, 已被广泛应用于新材料开发[23,24]. 研究人员通过分子动力学模拟对聚合物的热分解、力学性能和介电特性[25–27]等进行了广泛的研究. 然而, 目前以nano-ZnO作为纤维素绝缘纸的改性添加剂并配合分子动力学模拟对纤维素绝缘纸进行研究还未见报道.

      为可快速制备出具有优良热力学性能的改性纤维素绝缘纸实验提供理论方案, 本工作以nano-ZnO颗粒作为纳米填料对纤维素进行改性, 通过分子动力学模拟软件(materials studio, MS), 讨论不同nano-ZnO添加量对纤维素力学性能、内聚能密度、均方位移、玻璃化转变温度、导热系数等性能参数的影响, 预测最佳的nano-ZnO添加量, 旨在将模拟结果作为真实实验的科学性理论指导.

    2.   模型的建立与仿真

      2.1.   模型建立

    • 绝缘纸的主要成分是纤维素, 占比约90%, 其在绝缘纸中以两种状态存在: 结晶区和无定形区. 纤维素分子在结晶区呈现致密有序结构, 而在无定形区则表现为不规则分布. 在分子内部, 相互作用力较小, 特别是分子间的相互作用力较为微弱, 导致空隙较多. 在油浸式变压器的运行过程中, 绝缘纸的热老化绝大部分是从无定形区域开始的[28]. 本文定义纤维素分子链中葡萄糖残基的数目为聚合度(degree of polymerization, DP), 且Mazeau和Heux [29]的模拟和实验结果表明, 不同长度的纤维素链的分子构象和物理化学性质没有明显差异. 因此, 本文采用DP为10的纤维素链建立无定形区模型, 每个无定形区由两条纤维素链组成, 从而可以考虑纤维素链之间存在的相互作用. 所有的模拟过程在Materials Studio 2019软件中包含的“Build Polymers”和“Amorphous Locator”模块中进行的. 首先, 在MS软件的“Build”模块中建立DP为10的纤维素链模型, 然后在“Build”模块中从数据库中导入ZnO超级晶体, 形成纳米结构, nano-ZnO的半径为5 Å. 最终在“Amorphous Locator”模块中构建纤维素和nano-ZnO的复合模型, 根据nano-ZnO所占质量分数, 分别表示为纯纤维素(P0)、2%-nano-ZnO/纤维素(P2)、4%-nano-ZnO/纤维素(P4)、6%-nano-ZnO/纤维素(P6)、8%-nano-ZnO/纤维素(P8)和10%-nano-ZnO/纤维素(P10). 最终模型在“Amorphous Locator”模块中构建, 如图1所示.

      • 2.2.   仿真参数设置

    • 为使仿真的过程更贴近现实中绝缘纸在油浸式变压器中工作的模型, 使仿真的结果更加合理, 对已建立的纤维素非晶态区nano-ZnO/纤维素复合模型进行结构和能量优化. 优化的工序主要为结构几何优化, 循环退火以及模型弛豫三个循序渐进的步骤. 首先在“Forcite”模块中, 使用共轭梯度法和COMPASS力场对复合模型的几何形状进行优化. 接着对所构建的模型进行循环退火, 每50 K对模型进行两个退火循环, 从650 K冷却到250 K, 然后再次加热到650 K, 并在每个阶段对能量最小化结构进行优化, 持续5个循环. 经过此处理, 模型的内应力减小, 系统变得稳定, 更趋于真实材料. 最后是进行模型弛豫, 在分子模拟中, 每个目标温度都是基于弛豫后得到的模型, 这就需要在NVT正则系综下进行200 ps的平衡模拟, 然后在相同温度下进行200 ps的NPT等压(1 GPa)等温系综下的分子动力学模拟, 每个积分步骤为1 fs. 在这个系统平衡后, 下一阶段的起始构象取自上一阶段模拟的最终平衡构象, 接着在NPT系综中模拟0.0001 GPa下的200 ps分子运动, 最后进行各种性能计算和数据分析.

      整个模拟过程中使用了COMPASS力场[30]. 压力控制采用Berendsen方法, 温度控制采用Nose-Hoover方法[31], 初始速度采用玻尔兹曼分布随机分配, 范德瓦耳斯力采用Atom Based方法. 经过以上优化, 模型的密度和能量高度收敛[5], 使得模型接近真实的nano-ZnO/纤维素复合绝缘纸材料.

    3.   仿真实验结果与分析

      3.1.   力学性能分析

    • 油浸式变压器中的绝缘纸长期处于强机械振动和机械冲击的工作环境中, 对绝缘纸的机械强度和抵抗变形的能力造成巨大挑战[32]. 力学性能也是衡量材料宏观机械强度的重要指标, 在分子动力学的模拟过程中, 可以在模型平衡的状态下, 通过持续施加较小的应力, 从而在仿真计算过程中计算材料的力学性能相关的参数. 微观强度参数如弹性模量(E)、剪切模量(G)、体积模量(K )、体积模量与剪切模量之比(K/G)等. E是应力与应变的比值, 一般用来度量材料的刚性, 材料的刚性与弹性模量成正比, 刚性越强意味着材料抵抗变形的能力就越强. G是剪切应力与应变的比值. K是描述均质各向同性固体的弹性参数, K越大, 则表征材料的不可压缩性更好. 体系的韧性可以用K/G值来衡量, 通常K/G值越大则材料具有较强的韧性.

      绝缘纸属于固体材料, 广义的胡克定律可以用于定义固体材料的应力与应变关系[33], 因而可以借助广义的胡克定律来分析绝缘纸的应力与应变关系:

      式中, ${\sigma _i}$为应力, ${C_{ij}}$为计算得到的6阶弹性刚度系数矩阵, ${\varepsilon _j}$为应变张量.

      本文是采用MS软件中“Forcite”模块的Mechanical Properties功能, 在设定的条件下进行分子动力学模拟, 计算材料的晶体结构和原子间相互作用从而得到弹性刚度系数矩阵. 首先建立模拟系统, 在MS软件中建立与目标材料相应的分子动力学模拟系统. 其次设置仿真参数, 在已建立的绝缘纸非晶态区nano-ZnO/纤维素复合模型进行结构和能量优化, 接着进行分子动力学仿真, 系统平衡后在NPT系综中模拟标准大气压下进行仿真时长200 ps的分子运动机械性能测试. 利用模拟过程中得到的原子位移和应力信息, 采用MS软件中用于提取弹性常数的算法计算Cij弹性刚度系数矩阵, 计算误差率小于3%.

      $\lambda $和$\mu $为Lame常数, 表达式分别为

      根据(2)式和(3)式, 可以求出固体材料的力学参数:

      式中E为弹性模量, G为剪切模量, K为体积模量.

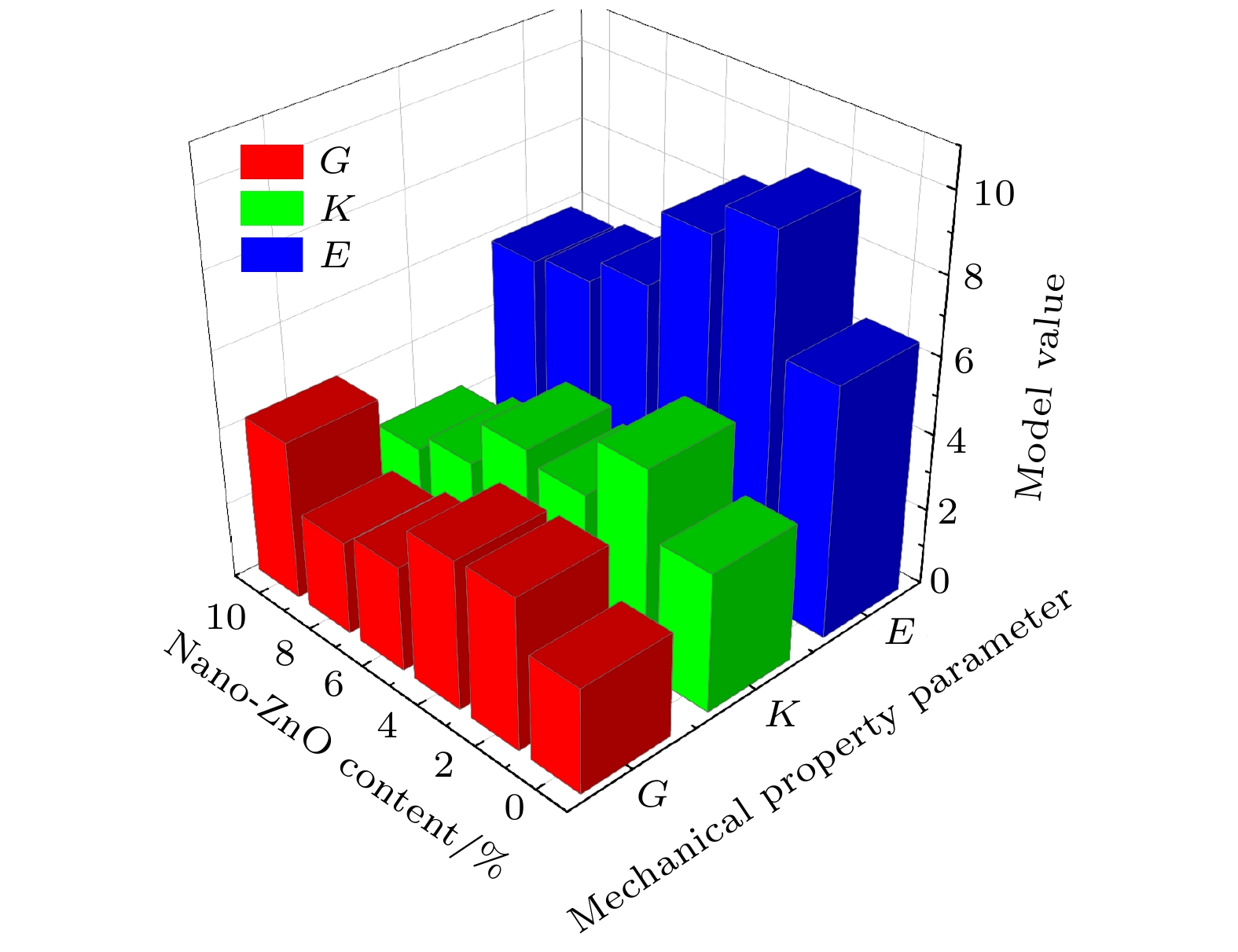
      通过分子动力学仿真模拟, 计算得到6组不同nano-ZnO含量模型的力学参数E, G, K, K/G值, 分别取10次模拟结果的平均值, 结果如表1所列.

      为了方便比较, 更直观地得出结论, 给出了模拟中得到的弹性模量、剪切模量、体积模量与不同nano-ZnO含量的关系, 如图2所示. 从图2可以看出, 添加nano-ZnO可增强纤维素的体积模量、剪切模量和弹性模量, 表明材料刚度和抗变形能力有所提升. 当nano-ZnO质量分数为2%时, 无论是弹性模量或是其他参数, 力学性能的提升最明显, 表明2%的nano-ZnO含量是最优添加量. 在最优含量的nano-ZnO粒子填充下, 纳米粒子可以补充纤维素网络, 填充空隙, 提高纸张的紧密度; 同时由于nano-ZnO具有较大的比表面积和许多活性位点, 可与纤维素之间产生了范德瓦耳斯力, 与纤维素之间有着良好的界面结合, 从而提高了绝缘纸的抗拉强度. 然而, 随着nano-ZnO含量的进一步增大, 会导致形成更多的界面缺陷而产生不连续性结构, 从而降低了复合材料的力学性能. 这是因为过量的纳米粒子在纤维表面及内部出现了团聚现象, 造成纳米粒子与纤维素纤维之间的界面结合减弱, 使得材料结构变得更为疏松, 从而导致绝缘纸的力学性能下降. 然而, 剪切模量G在P10出现了增大, 这可能是因为随着纳米颗粒增加到一定的量, 导致纤维结构中纳米颗粒密集填充, 使得整体复合结构出现刚性增强的现象, 导致模型的抗剪切应变能力增强.

      • 3.2.   内聚能密度

    • 内聚能密度通常用来表征聚合物分子间相互作用能的大小, 是单位体积液体蒸发所需要的内能. 因为材料内部分子间的反应会对材料本身的性质产生巨大的影响, 尤其对于纤维素材料而言, 分子链之间的作用力对纤维素复合材料的热力学性能有着重要的影响. 内聚能密度越大, 分子间作用力就越大, 分子链越紧密, 纤维素复合材料的抗变形能力(弹性模量)就会越强, 纤维素复合材料的玻璃化转变温度也会越高. 内聚能密度的计算表达式为

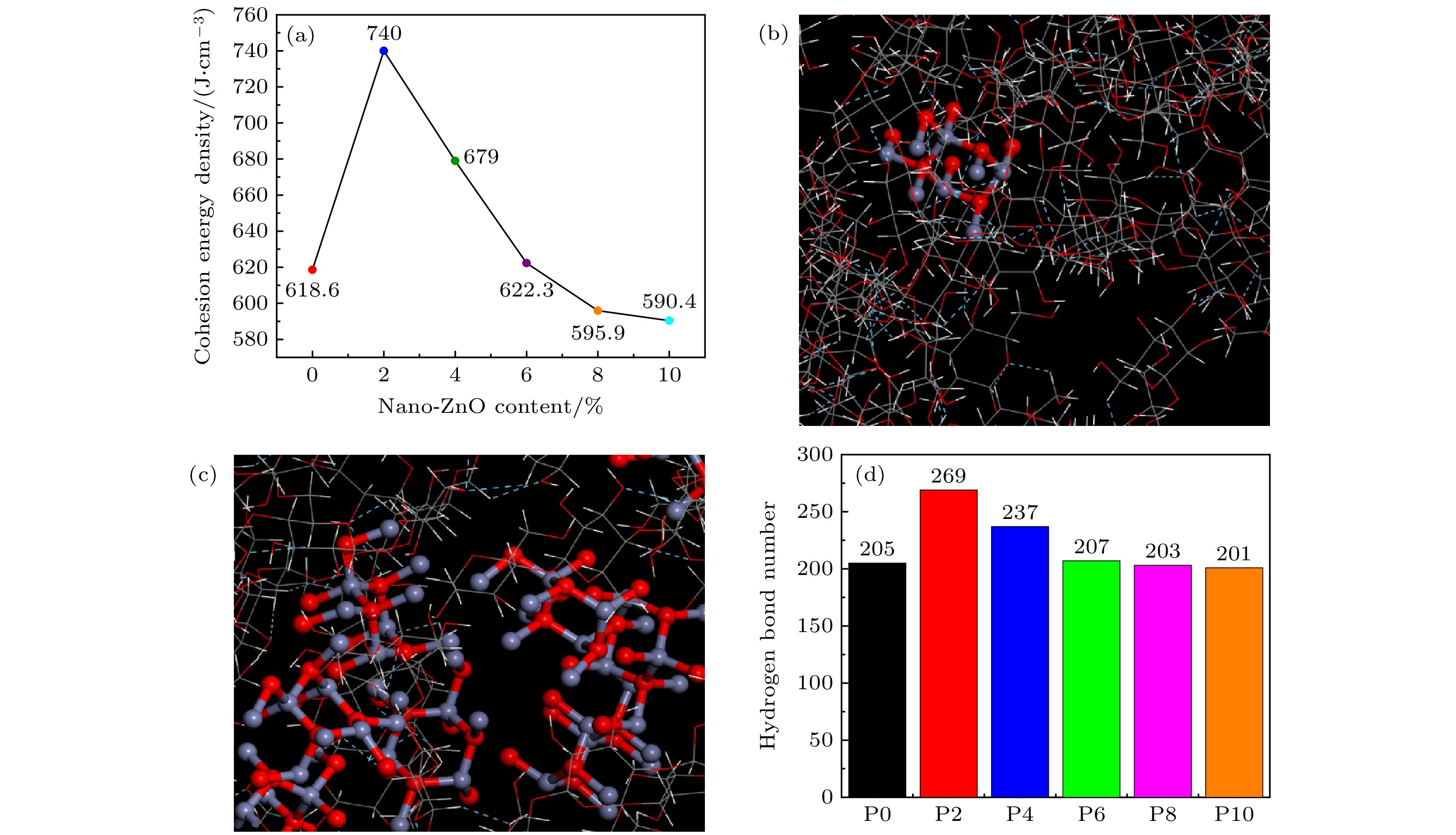
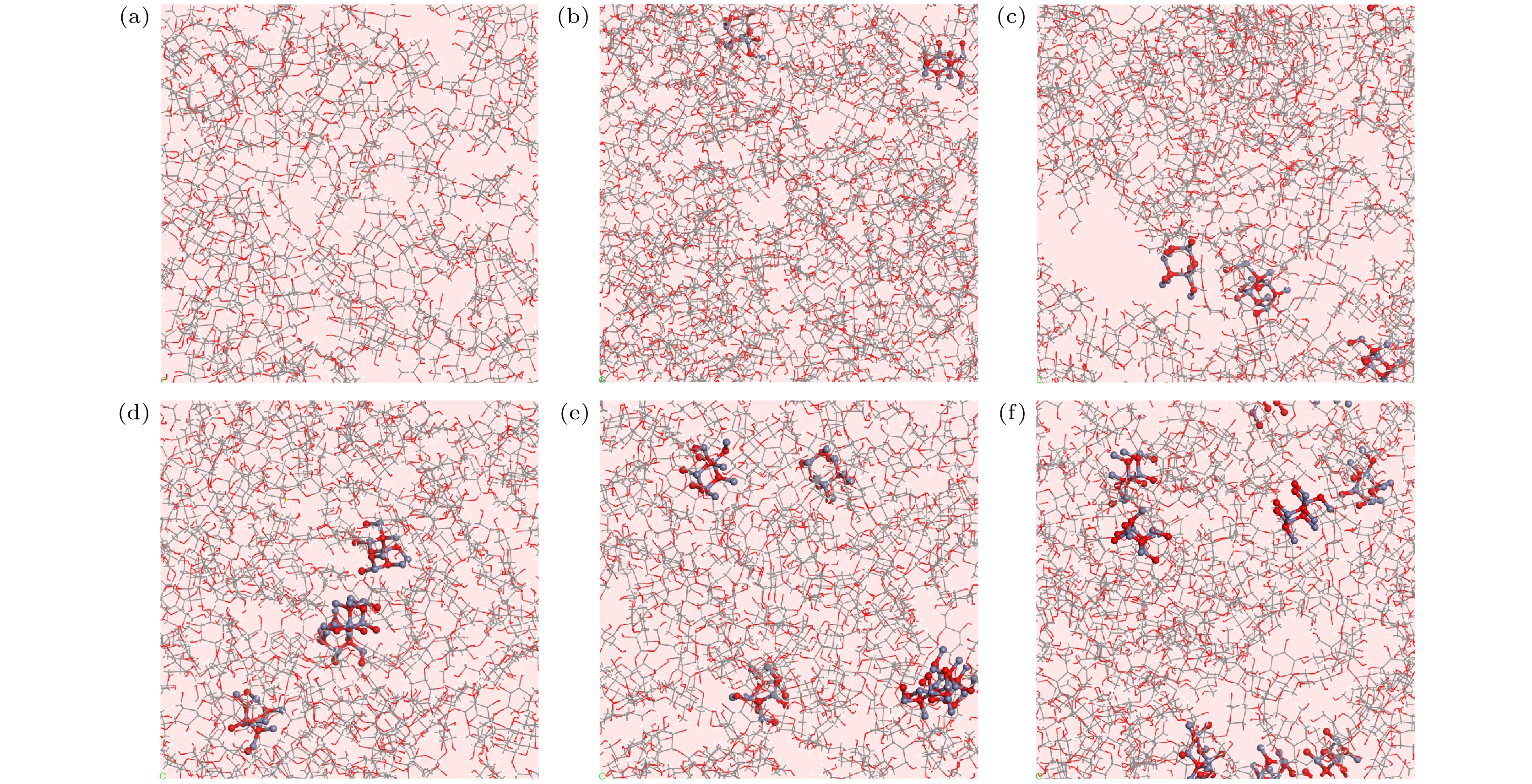
      式中, ${E_{{\text{coh}}}}$为系统的内聚能, $V$为系统的摩尔体积, ${E_{\rm {int} {{er}}}}$为系统分子间的能量, ${E_{{\text{total}}}}$为系统的总能量, ${E_{{\text{intra}}}}$为系统分子链的内能.

      对不同含量的nano-ZnO/纤维素复合模型分别进行内聚能密度的分子动力学模拟计算, 对应的结果如图3(a)所示. 由图3(a)可以看出, 与未改性的纤维素模型相比, 复合材料的内聚能密度随着掺入nano-ZnO含量增加呈现先增大后减小的变化趋势. 当添加量为2%时, 体系的内聚能密度达到最大值. 这是因为nano-ZnO填充了纤维素绝缘纸无定形区域的一些空隙, 并与周围的纤维素分子形成氢键. 系统中氢键数量的增加增强了与纤维素的结合, 从而在微观尺度上提高了纤维素链的内聚能密度. 在这里, 本文强调氢键数量指的是纤维素链之间的氢键以及Nano-ZnO与纤维素链之间的氢键, 形成的氢键位置如图3(b), (c)中蓝色虚线所示, 所计算出的氢键数量如图3(d)所示, 氢键数量的变化趋势与图3(a)的内聚能密度相一致. 因此可以从微观尺度上归因于添加适量的nano-ZnO后纤维素的力学性能和热稳定性得到提升. 但当nano-ZnO过量, 则会造成纳米粒子与纤维素之间的相容性下降. 该计算结果与前面的力学性能参数的计算结果展现的趋势相一致.

      • 3.3.   均方位移

    • 在构建的聚合物模型中, 每个原子和分子段的迁移率可用均方位移(MSD)表示. 分子链运动越强, MSD值越高. 在热应力的作用下, 分子链会更容易发生旋转和位移. 具有N个原子系统的MSD计算式为

      式中, $N$为系统中的原子数, ${{\boldsymbol{R}}_i}(t)$和${{\boldsymbol{R}}_i} (0)$分别表示系统中任意原子$i$在时刻$t$和初始时刻的位移矢量.

      对nano-ZnO/纤维素复合材料模型在NPT等温等压系综下(温度设为363 K)进行了时长为200 ps的集成模拟, 然后计算模型的MSD值. 模拟结果如图4所示, 随着时间的增加, 添加不同nano-ZnO含量的复合模型的MSD与纯纤维素模型相比, 呈现下降趋势. nano-ZnO/纤维素复合模型的MSD小于纯纤维素模型, 其中, P2模型具有最小值. 因此, 可以认为当nano-ZnO的添加量为2%时, 可以很好地抑制nano-ZnO/纤维素复合材料的原子和分子链的迁移性, 从而提高材料的热力学性能.

      总体而言, 低温区域相邻温度下的MSD曲线差异不显著, 但随着温度的升高, 出现了不同程度的跳跃. 这是因为温度的升高有助于克服分子链之间的相互作用力, 加剧了分子链的运动, 符合热力学定律. 此外, 修正模型的MSD值低于未修正模型的MSD值. 在改进后的模型中, 跳跃发生的温度高于未改进的模型, 这表明nano-ZnO的加入可以减弱分子链的运动, 提高纤维素的热稳定性.

      • 3.4.   玻璃化转变温度

    • 当温度升高到一定值时, 高分子材料的非晶态区域发生玻璃化转变. 玻璃化转变温度(Tg)是材料从坚硬和相对脆的状态转变为熔融或橡胶状状态的温度. 在相变过程中, 发生二级相变以及材料热容的连续变化. 材料的强度在达到Tg之前是相对稳定的. 而当温度升高到Tg以上时, 分子的运动、自由度、硬度等都发生明显的变化, 从而使其力学、热力学、电磁和光学性质发生变化[34]. 因此, 将Tg作为评价材料稳定性的标准. 在MS软件的分子动力学计算中, 可以从材料的比容温关系曲线中得到绝缘纸的玻璃化转变温度(Tg). 在650—250 K范围内, 对所建立的纤维素复合材料模型进行了分阶段冷却的NPT分子动力学模拟, 每段冷却温度降低50 K. 前一阶段(较高温度)的最后一个平衡构象作为下一阶段(较低温度)的起始构象, 共进行9个阶段的分子动力学模拟. 首先在每个温度段进行100 ps的NPT系综模拟, 以进一步放松聚合物链. 然后进行200 ps NPT标准大气压(0.0001 GPa)下的模拟, 对各种性能进行了数据分析和计算.

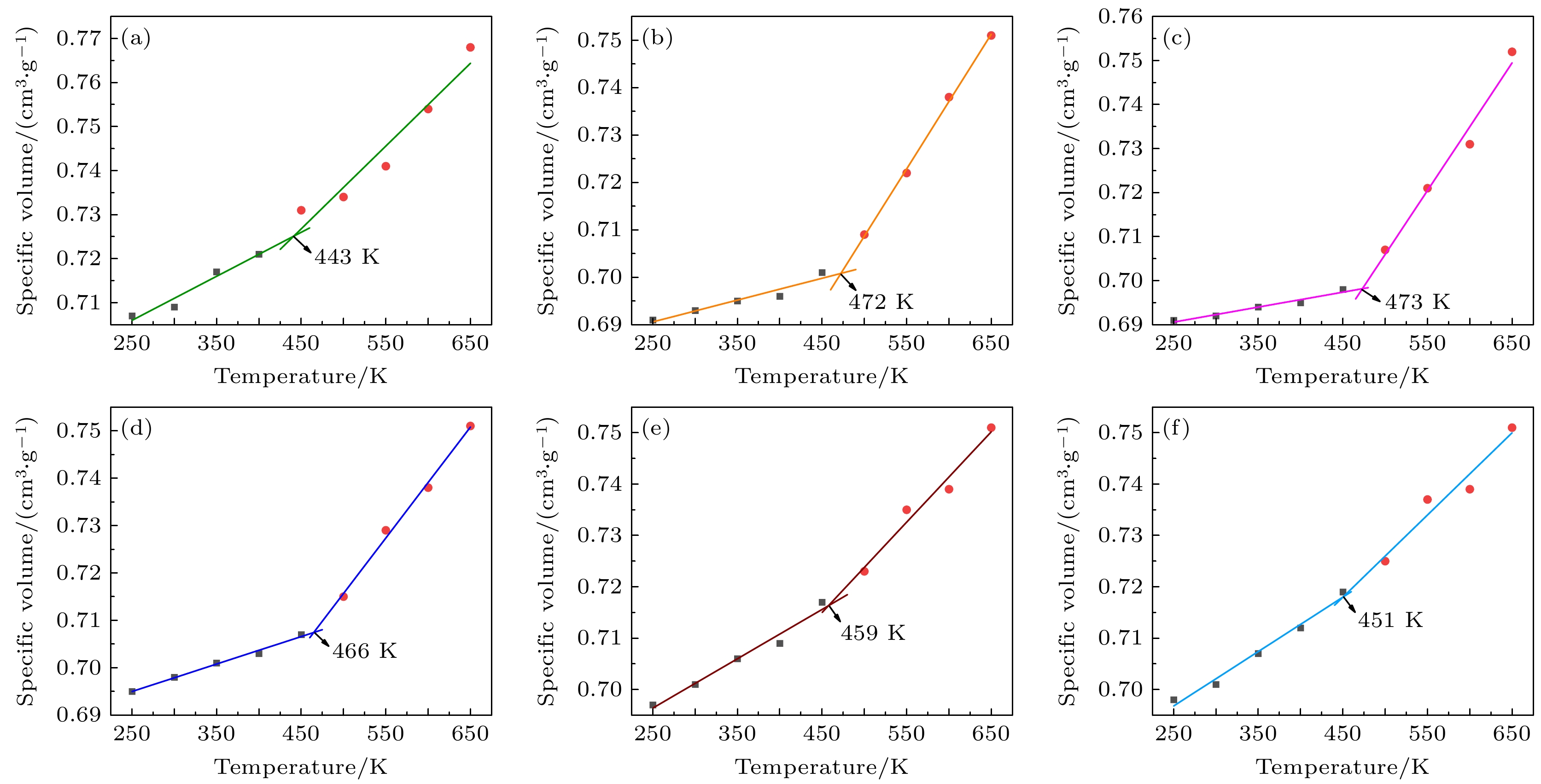
      以比体积拐点为边界点, 分别在边界点前后进行线性拟合. 边界点是材料模型玻璃化状态转变的过渡点. 玻璃化转变温度(Tg)的模拟曲线如图5所示. 从图5可以看出, P0模型的Tg为443 K, 这结果与Wang等[35]测得的纯纤维素绝缘纸的Tg几乎一致, 验证了本文构建模型的准确性. 在nano-ZnO/纤维素复合模型中, 当nano-ZnO添加量为4%时对应的Tg为473 K, 相比与纯纤维素的模型提升了30 K, 其次是添加量为2%的P2复合模型, 为472 K, 与提升最大的模型相近. 然而, 随着纳米材料含量超过4%, 玻璃化转变温度开始降低, 这是因为过量的纳米颗粒会增强填料与纤维基质之间的相互作用, 加速了纤维素链的运动和重排, 从而降低了玻璃化转变温度. 结果表明, 在纤维素中加入nano-ZnO可以提高Tg. 复合材料的力学特性和热稳定性与Tg有着密不可分的关联. nano-ZnO具有较高的比表面积和优良的分散性, 当其添加到纤维素中时, 可以形成均匀分布的纳米颗粒, 并填充在纤维素纸的纤维网状结构之间. 这种填充效应可以增大纤维素纸的整体密度和结构的紧致程度, 从而提高纤维素纸的玻璃化转变温度. 因此, 可以认为nano-ZnO能够改善纤维素绝缘纸的热力学性能.

      • 3.5.   热导率

    • 分子动力学已经被广泛应用于计算聚合物材料的导热系数. 反向非平衡分子动力学方法(RNEMD)因为其温度梯度收敛时间较快而得到广泛应用[36]. 导热系数的计算基于傅里叶导热定律, 如下式所示:

      式中$k$为导热系数, ${\text{d}}{Q_x}$为$x$方向的能量通量, ${\text{d}}T/{\text{d}}x$为温度梯度, 负号表示与梯度相反方向的能量通量.

      能量通量是通过在系统中两个固定层在每个时间间隔$\Delta t$之间交换能量$\Delta E$施加的, 计算公式为

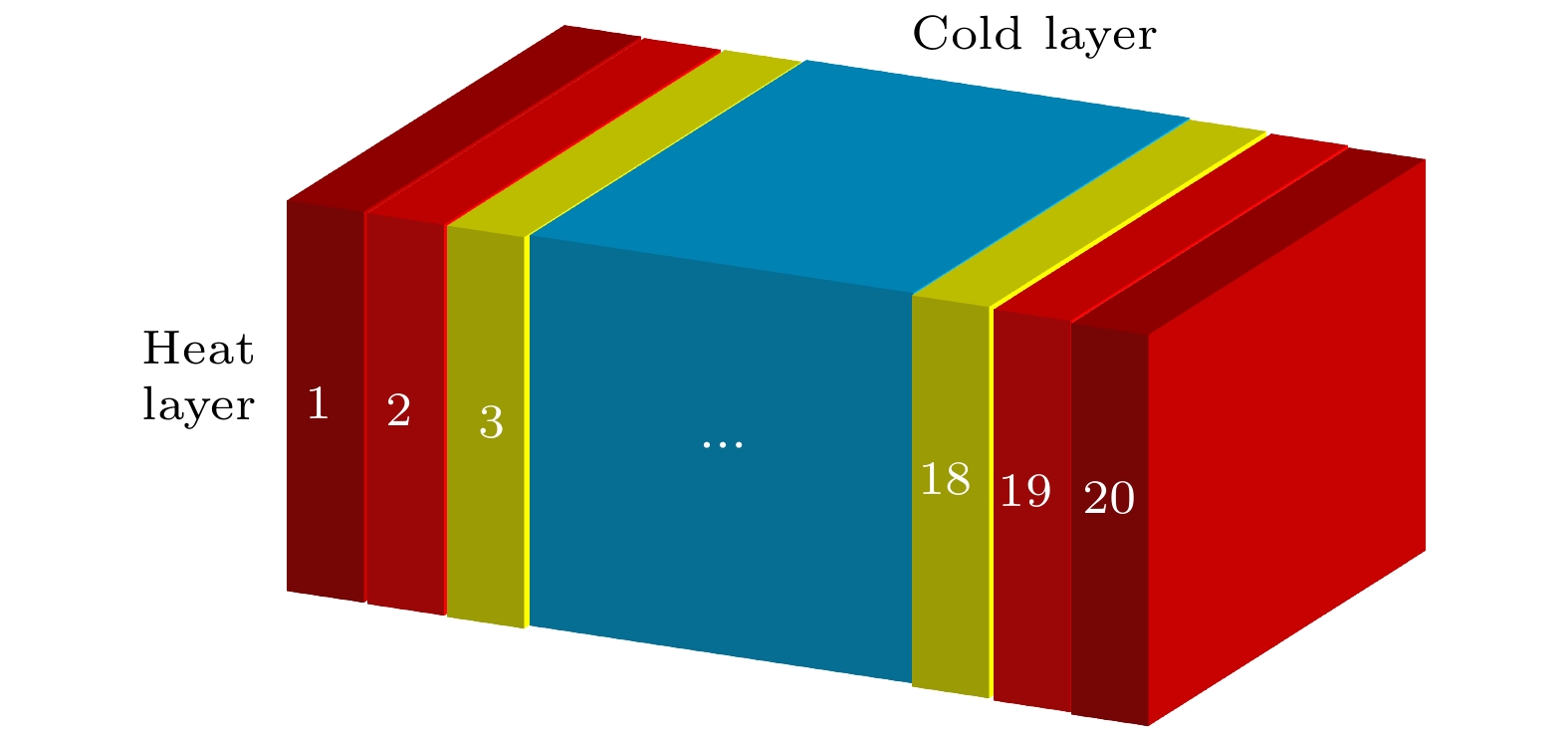
      式中, ${\text{d}}{Q_x}$为$x$方向的能量通量, $A$为垂直于通量方向的面积, $\Delta t$为时间间隔, $\Delta E$为时间间隔交换的能量.

      如图6所示, RNEMD是将模型在一个方向上划分成20个区域. 热层位于左右边界层, 冷层位于中间层. 热量是通过冷热层之间的动能交换传递的. 经过多次交换, 最终在体系中形成稳定的温度梯度. 为了计算一个方向的导热系数, 该模型首先在NVT正则系综中模拟了时长为100 ps的分子运动, 然后在NPT等温等压系综中模拟了时长为100 ps的分子运动. 为了计算复合结构的整体导热系数, 需要计算模型在x, y, z三个方向的导热系数, 取平均值作为模型的导热系数. 由于工作环境和负载变化等诸多因素, 变压器某些部位的温度有时会升至393 K左右. 因此, 本文选择363 K的平均值来研究nano-ZnO/纤维素的导热系数.

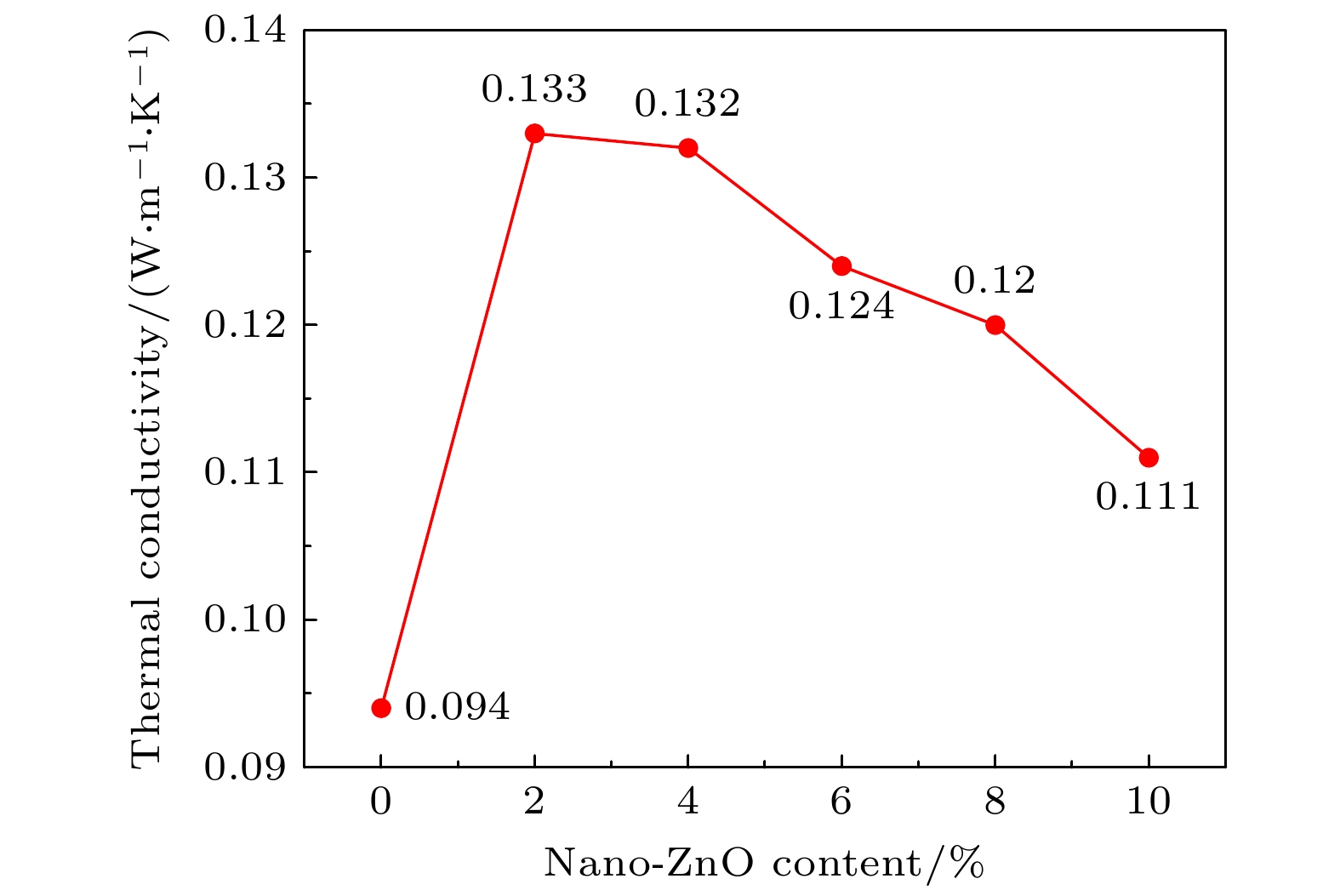
      本文分别计算了6种复合模型在x, y, z方向上的导热系数. 取各方向3次计算的平均值作为最终的导热系数. 纤维素复合材料模型的总导热系数为这3个方向的平均值, 最终各模型的导热系数模拟结果如图7所示. 从图7可以看出, 随着nano-ZnO含量增加, nano-ZnO/纤维素复合材料的导热系数呈现先增大后减小的趋势. 当添加量为2%时, 复合材料的导热系数达到最大值, 比未改性绝缘纸的导热系数高41.49%. nano-ZnO改性纤维素复合模型的导热系数均高于未改性的纯纤维素模型, 说明添加nano-ZnO可以提高纤维素绝缘纸的导热系数.

      根据导热路径理论, 随着导热填料的加入, 由于氧化锌的高导热性, 一些导热填料开始相互接触, 形成局部导热链或网络, 加速了纸张内部的热扩散, 导致导热系数增加[37]. 当填料的添加量超过4%时, 随着填料含量的不断增大, 导热结构内部逐渐出现团聚现象, 增加了复合结构的热阻, 阻碍了声子在结构内部的传播, 从而导致模型的面内热导率降低. 氧化锌颗粒的团聚同时会在复合结构中增加热阻, 导致整体结构抗热能力不均, 从而降低了复合材料整体的热稳定性.

    4.   结　论

    • 本文采用nano-ZnO对纤维素绝缘纸进行改性, 借助分子动力学模拟, 从微观角度分析了不同nano-ZnO的含量下对新型绝缘纸热力学性能影响的模拟计算. 结果表明, nano-ZnO可以提高绝缘纸的热力学性能.

      在现有的研究中, 当复合材料模型中的nano-ZnO含量达到2%时, 其热力学的综合性能达到最佳. 其中, 力学性能的弹性模量相比于未改性的纤维素绝缘纸提高了45.31%, 剪切模量提高了44.95%, 体积模量提高了46.76%; 内聚能密度相比于未改性的绝缘纸提高了19.62%, 均方位移的最大值降低了26.46%, 玻璃化转变温度提高了6.55%, 导热系数提高了41.49%. 这些分子动力学模拟的结果有望将“模拟设计直接指导试验探究”的方法应用到对高性能绝缘纸的研发当中, 对绝缘纸改性起到理论指导性的作用, 改变以往的绝缘纸改性研究依靠大量“尝试性”重复试验, 多偏向试错、摸索性的实验研究手段, 其过程繁琐且缺乏足够的科学理论依据的现状, 有利于推动电工新材料研发进程. 未来研究将更注重于贴合可行性研究试验的模拟工作, 以期为真实试验提供更有价值的理论指导.

    参考文献 (37)

目录

/

返回文章
返回