高级搜索

界面电子结构对核壳量子点/聚乙烯纳米复合绝缘电导与空间电荷特性的影响

,  , 

downloadPDF

上一篇

下一篇

王赫宇, 李忠磊, 杜伯学. 界面电子结构对核壳量子点/聚乙烯纳米复合绝缘电导与空间电荷特性的影响[J]. 物理学报, 2024, 73(12): 127702-1. doi: 10.7498/aps.73.20232041
引用本文: 王赫宇, 李忠磊, 杜伯学. 界面电子结构对核壳量子点/聚乙烯纳米复合绝缘电导与空间电荷特性的影响[J]. 物理学报, 2024, 73(12): 127702-1. doi: 10.7498/aps.73.20232041
shu
He-Yu Wang, Zhong-Lei Li, Bo-Xue Du. Effect of interfacial electronic structure on conductivity and space charge characteristics of core-shell quantum dots/polyethylene nanocomposite insulation[J]. Acta Physica Sinica, 2024, 73(12): 127702-1. doi: 10.7498/aps.73.20232041
Citation: He-Yu Wang, Zhong-Lei Li, Bo-Xue Du. Effect of interfacial electronic structure on conductivity and space charge characteristics of core-shell quantum dots/polyethylene nanocomposite insulation[J]. Acta Physica Sinica, 2024, 73(12): 127702-1. doi: 10.7498/aps.73.20232041
shu

界面电子结构对核壳量子点/聚乙烯纳米复合绝缘电导与空间电荷特性的影响

  • 天津大学电气自动化与信息工程学院, 智能电网教育部重点实验室, 天津　300072

    • 作者简介: 王赫宇: heyuwang@tju.edu.cn .
    通讯作者: E-mail: lizhonglei@tju.edu.cn.;  E-mail: duboxue@tju.edu.cn.

  • 中图分类号: 77.84.Lf, 73.21.La, 77.22.Jp, 72.20.-i

Effect of interfacial electronic structure on conductivity and space charge characteristics of core-shell quantum dots/polyethylene nanocomposite insulation

  • Key Laboratory of the Ministry of Education on Smart Power Grids, School of Electrical and Information Engineering, Tianjin University, Tianjin 300072, China

    • Corresponding authors: E-mail: lizhonglei@tju.edu.cn;  E-mail: duboxue@tju.edu.cn

  • MSC: 77.84.Lf, 73.21.La, 77.22.Jp, 72.20.-i

  • 摘要: 为研究核壳量子点的界面电子结构对聚乙烯绝缘电导与空间电荷特性的影响, 分别制备了CdSe@ZnS/LDPE, ZnSe@ZnS/LDPE两种核壳量子点纳米复合绝缘, 研究了复合绝缘的直流电导和空间电荷的演变规律, 并分析了核壳量子点的界面电子结构对电荷陷阱分布特性的影响机理. 研究发现, 相比于LDPE绝缘, ZnSe@ZnS/LDPE复合绝缘在高温强场条件下直流电导率可降低47.2%, 空间电荷积累量降低了40.3%, 且陷阱能级增大, 表现出对载流子更强的捕获作用. 基于密度泛函理论, 计算了核壳量子点与聚乙烯绝缘的能带特征. 结果表明, 核壳纳米量子点的核层-壳层界面、壳层-绝缘界面的能带偏移导致导带底与价带顶发生突变, 分别对电子和空穴具有限域作用, 且限域效应随着量子点核层与壳层带隙差异增大而逐渐增强, 从而限制高温强场下载流子迁移、抑制空间电荷积聚.
    Abstract: To investigate the effect of the interface electronic structure of core-shell quantum dots on the conductivity and space charge characteristics of polyethylene insulation, nanocomposite insulations, namely CdSe@ZnS/LDPE and ZnSe@ZnS/LDPE, are synthesized. The study focuses on elucidating the evolution patterns of DC conductivity and space charge in the nanocomposite insulation, and analyzing the effect of the interfacial electronic structure of core-shell quantum dots on the distribution of charge traps. Comparative analysis reveals that in contrast to LDPE insulation, ZnSe@ZnS/LDPE nanocomposite insulation demonstrates a substantial reduction in DC conductivity by 47.2% and a decrease in space charge accumulation by 40.3% under the conditions of elevated temperature and strong electric field. The increase of trap energy level means an enhanced trap effect on charger carriers. According to density functional theory, the band structure characteristics of core-shell quantum dots integrated with polyethylene are computationally assessed. The findings underscore that the band misalignment at the core-shell interface and the shell-insulation interface induces shifts in the conduction band bottom and at the valence band top, respectively. These shifts impose a confinement effect on electrons and holes, with the extent of this effect escalating with the augment of the difference in band gap between the core layer and the shell layer. Consequently, this phenomenon curtails carrier migration, thereby inhibiting space charge accumulation under the conditions of elevated temperature and strong electric fields.
  • 加载中

  • 图 1  核壳量子点/聚乙烯纳米复合绝缘制备流程

    Figure 1.  Preparation method of quantum dots/PE composite insulation.

    下载: 全尺寸图片 幻灯片

    图 2  核壳量子点/聚乙烯复合绝缘的理化性能表征(1 cps = 1 counts/s)　(a) CdSe@ZnS量子点TEM图; (b) CdSe@ZnS量子点粒径分布; (c) ZnSe@ZnS量子点TEM图; (d) ZnSe@ZnS量子点粒径分布; (e) QD1/PE绝缘TEM图; (f) QD1/PE绝缘EDS谱图; (g) QD2/PE绝缘TEM图; (h) QD2/PE绝缘EDS谱图; (i) 核壳量子点/聚乙烯复合绝缘XPS全谱; (j)—(m) Cd, Zn, Se和S元素精细谱; (n) 核壳量子点/聚乙烯复合绝缘UV-Vis吸收谱; (o)—(q) 核壳量子点/聚乙烯复合绝缘光学带隙

    Figure 2.  Characterization of physical and chemical properties of core-shell quantum dots/polyethylene composite insulation: (a) TEM of CdSe@ZnS QDs; (b) particle size distribution of CdSe@ZnS QDs; (c) TEM of ZnSe@ZnS QDs; (d) particle size distribution of ZnSe@ZnS QDs; (e) TEM of QD1/PE insulation; (f) EDS of QD1/PE insulation; (g) TEM of QD2/PE insulation; (h) EDS of QD2/PE insulation; (i) XPS full spectra of composite insulation; (j)–(m) XPS fine spectra of Cd, Zn, Se, and S; (n) UV-Vis absorption spectra of composite insulation; (o)–(q) optical gap of composite insulation.

    下载: 全尺寸图片 幻灯片

    图 3  聚乙烯绝缘和核壳量子点/聚乙烯复合绝缘的电导特性　(a)—(c) PE, QD1/PE和QD2/PE绝缘电导特性; (d)—(f) 基于跳跃电导模型的PE, QD1/PE和QD2/PE绝缘电导特性; (g)—(i) 基于P-F发射效应的PE, QD1/PE和QD2/PE绝缘电导特性; (j)—(l) 基于肖特基发射效应的PE, QD1/PE和QD2/PE绝缘电导特性

    Figure 3.  Conductivity characteristics of polyethylene insulation and core-shell quantum dot/polyethylene composite insulation: (a)–(c) Current density characteristics of PE, QD1/PE and QD2/PE insulation; (d)–(f) conductivity characteristics of PE, QD1/PE and QD2/PE insulation based on hopping conductivity model; (g)–(i) conductivity characteristics of PE, QD1/PE and QD2/PE insulation based on P-F emission effect; (j)–(l) conductivity characteristics of PE, QD1/PE and QD2/PE insulation based on Schottky emission effect.

    下载: 全尺寸图片 幻灯片

    图 4  聚乙烯绝缘和核壳量子点/聚乙烯复合绝缘的空间电荷特性　(a) PE绝缘极化过程; (b) QD1/PE绝缘极化过程; (c) QD2/PE绝缘极化过程; (d) 极化过程平均空间电荷密度变化情况; (e) PE绝缘去极化过程; (f) QD1/PE绝缘去极化过程; (g) QD2/PE绝缘去极化过程; (h) 去极化过程平均空间电荷密度变化情况

    Figure 4.  Space charge characteristics of polyethylene insulation and core-shell quantum dot/polyethylene composite insulation: (a) Polarization of PE insulation; (b) polarization of QD1/PE insulation; (c) polarization of QD2/PE insulation; (d) average space charge density during the polarization process; (e) depolarization process of PE insulation; (f) depolarization process of QD1/PE insulation; (g) depolarization process of QD2/PE insulation; (h) average space charge density during the depolarization process.

    下载: 全尺寸图片 幻灯片

    图 5  聚乙烯绝缘和核壳量子点/聚乙烯复合绝缘的陷阱特性

    Figure 5.  Trap characteristics of polyethylene insulation and core-shell quantum dots/polyethylene composite insulation.

    下载: 全尺寸图片 幻灯片

    图 6  核壳量子点与聚乙烯绝缘的能带结构与态密度　(a) CdSe晶体模型; (b) CdSe能带结构与态密度; (c) ZnSe晶体模型; (d) ZnSe能带结构与态密度; (e) ZnS晶体模型; (f) ZnS能带结构与态密度; (g) PE晶体模型; (h) PE能带结构与态密度

    Figure 6.  Band structures and density of states of core-shell quantum dots and polyethylene: (a) CdSe crystal model; (b) CdSe band structure and DOS; (c) ZnSe crystal model; (d) ZnSe band structure and DOS; (e) ZnS crystal model; (f) ZnS band structure and DOS; (g) PE crystal model; (h) PE band structure and DOS.

    下载: 全尺寸图片 幻灯片

    图 7  核壳量子点/聚乙烯绝缘的界面结合能、差分电荷密度与界面能带结构　(a) 不同界面的结合能变化情况; (b) ZnS-聚乙烯界面的差分电子密度; (c) CdSe-ZnS界面的差分电子密度; (d) ZnSe-ZnS界面的差分电子密度; (e) PE-ZnS界面能带结构; (f) CdSe-ZnS界面能带结构; (g) ZnSe-ZnS界面能带结构

    Figure 7.  Binding energy, electron density difference, and band structure of interface for core-shell quantum dot/polyethylene insulation: (a) Binding energy of different interfaces; (b) electron density difference between ZnS and PE; (c) electron density difference between CdSe and ZnS; (d) electron density difference between ZnSe and ZnS; (e) band structure between PE and ZnS; (f) band structure between CdSe and ZnS; (g) band structure between ZnSe and ZnS.

    下载: 全尺寸图片 幻灯片

    图 8  核壳量子点界面结构对聚乙烯绝缘中载流子迁移的影响

    Figure 8.  Effect of interface structure with core-shell quantum dots on carrier migration in polyethylene-based insulation.

    下载: 全尺寸图片 幻灯片

    表 1  核壳量子点与聚乙烯的能带结构特征

    Table 1.  Band characteristics of core-shell quantum dots and polyethylene.

    结构 能带间隙
    Eg/eV    		 带隙类型 电子有效质量
    $m_{\rm n}^*{\mathrm{ /a.u.}}$    		 空穴有效质量
    $m_{\rm p}^*{\mathrm{ /a.u.}}$    		 电子亲和能
    χ/eV    		 功函数
    W/eV
    CdSe 2.06 直接带隙 0.14 0.39 4.85 5.38
    ZnSe 2.77 直接带隙 0.18 0.54 4.37 5.10
    ZnS 3.44 直接带隙 0.24 0.55 3.96 4.71
    PE 8.80 直接带隙 >10 >10 –2.45 5.42
    下载: 导出CSV
  • [1] 俞葆青, 夏兵, 杨晓砚, 万宝全, 查俊伟 2023 物理学报 72 068402 doi: 10.7498/aps.72.20222320 Yu B Q, Xia B, Yang X Y, Wan B Q, Zha J W 2023 Acta Phys. Sin. 72 068402 doi: 10.7498/aps.72.20222320
    [2] Li Z L, Du B X 2018 IEEE Electr. Insul. Mag. 34 30 doi: 10.1109/MEI.2018.8507715
    [3] 杜伯学, 韩晨磊, 李进, 李忠磊 2019 电工技术学报 34 179 doi: 10.19595/j.cnki.1000-6753.tces.180073 Du B X, Han C L, Li J, Li Z L 2019 Trans. Chin. Electrotech. Soc. 34 179 doi: 10.19595/j.cnki.1000-6753.tces.180073
    [4] 何金良, 党斌, 周垚, 胡军 2015 高电压技术 41 1417 doi: 10.13336/j.1003-6520.hve.2015.05.001 He J L, Dang B, Zhou Y, Hu J 2015 High Voltage Eng. 41 1417 doi: 10.13336/j.1003-6520.hve.2015.05.001
    [5] Mazzanti G, Diban B 2021 IEEE Trans. Power Delivery 36 3784 doi: 10.1109/TPWRD.2021.3049269
    [6] Lewis T J 2014 IEEE Trans. Dielectr. Electr. Insul. 21 497 doi: 10.1109/TDEI.2013.004173
    [7] Tanaka T, Kozako M, Fuse N, Ohki Y 2005 IEEE Trans. Dielectr. Electr. Insul. 12 669 doi: 10.1109/TDEI.2005.1511092
    [8] Takada T, Hayase Y, Tanaka Y 2008 IEEE Trans. Dielectr. Electr. Insul. 15 152 doi: 10.1109/T-DEI.2008.4446746
    [9] Zhu X, Wu J, Wang Y, Yin Y 2020 IEEE Trans. Dielectr. Electr. Insul. 27 450 doi: 10.1109/TDEI.2019.008497
    [10] Li S T, Zhao N, Nie Y J, Wang X, Chen G, Teyssedre G 2015 IEEE Trans. Dielectr. Electr. Insul. 22 92 doi: 10.1109/TDEI.2014.004524
    [11] Ye C, Zhang D S, Chen B, Tung C H, Wu L Z 2023 Chem. Phys. Rev. 4 011304 doi: 10.1063/5.0126893
    [12] Han C L, Du B X, Li J, Li Z L, Tanaka T 2020 IEEE Trans. Dielectr. Electr. Insul. 27 1204 doi: 10.1109/TDEI.2020.008930
    [13] Yang M, Wang S, Fu J, Zhu Y, Liang J, Cheng S, Hu S, Hu J, He J, Li Q 2023 Adv. Mater. 35 2301936 doi: 10.1002/adma.202301936
    [14] Smith A M, Lane L A, Nie S M 2014 Nat. Commun. 5 4506 doi: 10.1038/ncomms5506
    [15] Tanaka T 2019 IEEE Trans. Dielectr. Electr. Insul. 26 276 doi: 10.1109/TDEI.2018.007599
    [16] Lei Z P, Fabiani D, Bray T, Li C Y, Wang X Y, Andritsch T, Credi A, La Rosa M 2021 IEEE Trans. Dielectr. Electr. Insul. 28 753 doi: 10.1109/TDEI.2021.009223
    [17] Moyassari A, Unge M, Hedenqvist M S, Gedde U W, Nilsson F 2017 J. Chem. Phys. 146 204901 doi: 10.1063/1.4983650
    [18] Chen X, Zhao A X, Li J M, Deng J B, Zhang G J, Zhao X F 2019 J. Appl. Phys. 126 035101 doi: 10.1063/1.5089863
    [19] Lü Z P, Ma Y T, Zhang C, Peng J Y, Wu K, Dissado L A 2021 IEEE Trans. Dielectr. Electr. Insul. 28 616 doi: 10.1109/TDEI.2021.009324
    [20] Simmons J G, Tam M C 1973 Phys. Rev. B 7 3706 doi: 10.1103/PhysRevB.7.3706
    [21] Cheng S, Zhou Y, Li Y, Yuan C, Yang M, Fu J, Hu J, He J, Li Q 2021 Energy Storage Mater. 42 445 doi: 10.1016/j.ensm.2021.07.018
    [22] 董久锋, 邓星磊, 牛玉娟, 潘子钊, 汪宏 2020 物理学报 69 217701 doi: 10.7498/aps.69.20201006 Dong J F, Deng X L, Niu Y J, Pan Z Z, Wang H 2020 Acta Phys. Sin. 69 217701 doi: 10.7498/aps.69.20201006
    [23] Emtage P R, Tantraporn W 1962 Phys. Rev. Lett. 8 267 doi: 10.1103/PhysRevLett.8.267
    [24] Hoang A T, Pallon L, Liu D, Serdyuk Y V, Gubanski S M, Gedde U W 2016 Polymers 8 87 doi: 10.3390/polym8030087
    [25] Zhou L, Wang X, Zhang Y, Zhang P, Li Z 2019 Materials 12 2657 doi: 10.3390/ma12172657
    [26] Akram S, Bhutta M S, Zhou K, Meng P F, Castellon J, Wang P, Rasool G, Aamir M, Nazir M T 2021 IEEE Trans. Dielectr. Electr. Insul. 28 1514 doi: 10.1109/TDEI.2021.009563
    [27] Fishchuk I I, Kadashchuk A K, Vakhnin A, Korosko Y, Bässler H, Souharce B, Scherf U 2006 Phys. Rev. B 73 115210 doi: 10.1103/PhysRevB.73.115210
    [28] Li C, Duan L, Li H, Qiu Y 2014 J. Phys. Chem. C 118 10651 doi: 10.1021/jp5022906
    [29] 屠德民, 王霞, 吕泽鹏, 吴锴, 彭宗仁 2012 物理学报 61 01704 doi: 10.7498/aps.61.017104 Tu D M, Wang X, Lv Z P, Wu K, Peng Z R 2012 Acta Phys. Sin. 61 01704 doi: 10.7498/aps.61.017104
    [30] 张睿智, 陈文灏, 杨璐娜 2012 物理学报 61 187201 doi: 10.7498/aps.61.187201 Zhang R Z, Chen W H, Yang L N 2012 Acta Phys. Sin. 61 187201 doi: 10.7498/aps.61.187201
    [31] Hewa-Kasakarage N N, Kirsanova M, Nemchinov A, Schmall N, El-Khoury P Z, Tarnovsky A N, Zamkov M 2009 J. Am. Chem. Soc. 131 1320 doi: 10.1021/ja8082895
    [32] Chen X H, Chen Y T, Ren F F, Gu S L, Tan H H, Jagadish C, Ye J D 2019 Appl. Phys. Lett. 115 202101 doi: 10.1063/1.5126325
  • 加载中
图( 8) 表( 1)
计量
  • 文章访问数:  488
  • HTML全文浏览数:  488
  • PDF下载数:  5
  • 施引文献:  0
出版历程
  • 收稿日期:  2023-12-29
  • 刊出日期:  2024-06-20

界面电子结构对核壳量子点/聚乙烯纳米复合绝缘电导与空间电荷特性的影响

    通讯作者: E-mail: lizhonglei@tju.edu.cn.; 
    通讯作者: E-mail: duboxue@tju.edu.cn.
    作者简介: 王赫宇: heyuwang@tju.edu.cn
  • 天津大学电气自动化与信息工程学院, 智能电网教育部重点实验室, 天津　300072
  • 收稿日期:  2023-12-29

摘要: 为研究核壳量子点的界面电子结构对聚乙烯绝缘电导与空间电荷特性的影响, 分别制备了CdSe@ZnS/LDPE, ZnSe@ZnS/LDPE两种核壳量子点纳米复合绝缘, 研究了复合绝缘的直流电导和空间电荷的演变规律, 并分析了核壳量子点的界面电子结构对电荷陷阱分布特性的影响机理. 研究发现, 相比于LDPE绝缘, ZnSe@ZnS/LDPE复合绝缘在高温强场条件下直流电导率可降低47.2%, 空间电荷积累量降低了40.3%, 且陷阱能级增大, 表现出对载流子更强的捕获作用. 基于密度泛函理论, 计算了核壳量子点与聚乙烯绝缘的能带特征. 结果表明, 核壳纳米量子点的核层-壳层界面、壳层-绝缘界面的能带偏移导致导带底与价带顶发生突变, 分别对电子和空穴具有限域作用, 且限域效应随着量子点核层与壳层带隙差异增大而逐渐增强, 从而限制高温强场下载流子迁移、抑制空间电荷积聚.

English Abstract

    全文HTML

    1.   引　言

    • 高压直流输电是海上新能源并网、大容量远距离输电和跨区域电网互联的重要手段, 是推进我国能源结构转型的关键支撑, 是实现“碳达峰、碳中和”战略目标的首要举措[1]. 作为高压直流输电工程中的关键装备, 高压直流电缆决定了输电系统可靠性与稳定性. 高压电缆绝缘性能直接影响了电能传输的效率与安全性[2]. 聚乙烯(polyethylene, PE)绝缘具有良好的耐电性能, 并且经过交联反应后形成交联聚乙烯可进一步提升耐热性能与机械性能, 聚乙烯已成为当今高压电缆挤包式绝缘的主要材料[3]. 然而, 高压直流电缆绝缘层电场分布由材料的电导率决定, 通常情况下电导率随温度升高呈指数级增大, 导致直流电缆正常运行时发生电场反转现象[4]; 另一方面, 绝缘长期在直流应力下将发生空间电荷积聚现象, 进一步使绝缘内部电场发生畸变, 可导致绝缘失效[5]. 因此, 降低聚乙烯电缆绝缘高温强场下电导率、抑制空间电荷积聚现象, 是提升聚乙烯电缆绝缘性能的关键.

      纳米电介质改性方法自1994年被提出[6], 成为了对聚合物绝缘载流子迁移行为进行调控的有效手段[7]. 通过金属氧化物纳米颗粒向聚合物绝缘引入深陷阱能级, 形成对电子具有捕获效果的局域态, 对聚合物绝缘中的电荷迁移形成抑制作用[8]. 通过向XLPE绝缘中添加质量分数为0.5%的纳米MgO颗粒, 纳米颗粒形成的电荷屏蔽层削弱了绝缘缺陷部位的电场强度, 抑制了局部放电对绝缘的破坏过程[9]. 对于填充TiO2纳米颗粒的PE/TiO2纳米复合材料的研究指出, TiO2纳米颗粒通过界面极化起到了对电荷的捕获作用, 有效地降低了PE绝缘空间电荷密度[10].

      低维纳米材料具有一系列独特的效应, 包括量子限域效应、表面效应、量子隧道效应、库伦阻塞效应等[11], 因此受到学者的广泛关注. 二维层状纳米填充物由于具有更高的比表面积, 形成了更强的量子限域效应, 使其具有微填充、强性能的特点. 以氧化石墨烯(GO)为代表的二维量子阱结构已被应用于提升聚乙烯绝缘直流电气性能, 向聚乙烯绝缘中添加质量分数为0.01%的GO使得绝缘直流击穿场强提升19.9%, 并且可向绝缘中引入中心能级约0.89 eV的深陷阱[12]. 利用低维纳米材料的量子尺寸效应, 可实现聚合物绝缘能带间隙与缺陷调控, 通过金属氧化物团簇结构, 向聚合物绝缘中引入了更深的陷阱能级, 有效地降低了高温条件下的直流电导[13]. 量子点(quantum dots, QDs)的粒径尺寸与德布罗意波长相近, 电子能级呈现出简并态, 被称为零维纳米材料. 量子点具有显著的电荷限域效应与库仑阻塞效应[14], 因此应用于聚合物绝缘性能提升[15]. 通过向聚苯乙烯绝缘中添加质量分数为0.1% CdSe@ZnS核壳量子点, 研究发现在50 kV/mm强场下的空间电荷积聚得到抑制[16]. 因此, 核壳纳米量子点的界面结构可对绝缘的载流子迁移与空间电荷积聚行为产生影响.

      密度泛函理论计算可从原子与分子角度揭示电子结构对性质的影响规律. 通过对聚乙烯半结晶结构模型进行计算获得电子结构特征, 揭示了聚乙烯中空穴迁移率显著低于电子迁移率, 并指出相较于载流子沿聚乙烯链迁移, 载流子在链间迁移更为困难[17]. 通过对聚乙烯与金属电极之间的异质结构能级特征进行计算, 发现空穴载流子的注入势垒显著地高于电子载流子, 揭示了强场作用下的金属电极发射与载流子迁移机理[18]. 因此, 基于密度泛函理论计算可获得核壳纳米量子点/聚乙烯绝缘之间异质结构能级特征, 揭示界面电子结构对绝缘载流子迁移的影响.

      本文选取了CdSe@ZnS和ZnSe@ZnS两种典型II-VI型核壳量子点, 制备了核壳量子点/聚乙烯纳米复合绝缘材料, 研究了复合绝缘的直流电导、空间电荷和陷阱特性的演变规律, 并建立了核壳量子点/聚乙烯界面结构模型, 计算获得了界面电子结构特征, 分析了核壳量子点的界面电子结构对电子、空穴载流子迁移特性的影响机理.

    2.   核壳量子点/聚乙烯复合绝缘制备方法与表征

      2.1.   试样制备方法

    • 选用低密度聚乙烯(low-density polyethylene, LDPE)基料为中国石油兰州石化公司生产, 牌号2420H, 密度为0.920 g/cm3, 重均分子量1.594×105. 选取两种不同组分的核壳量子点, 分别为CdSe@ZnS和ZnSe@ZnS, 阿拉丁试剂提供. 两种核壳量子点均具有表面油溶性配体十八烷胺, 具有良好的非极性试剂溶解性, 以1 mg/mL浓度分散于甲苯溶剂.

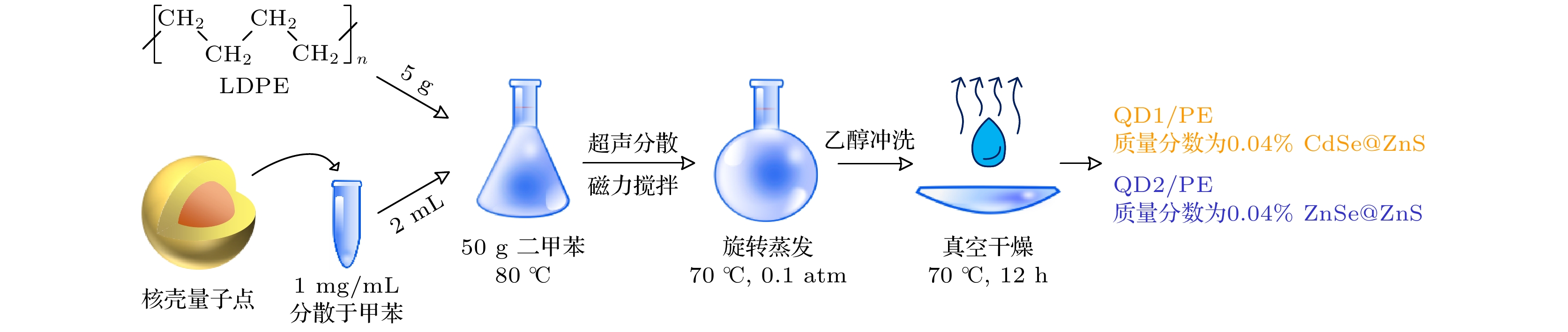
      本文制备核壳量子点/聚乙烯复合绝缘方法如图1所示. 取5 g低密度聚乙烯粒料置于50 g二甲苯溶剂, 在80 ℃温度下充分溶解. 随后加入2 mL量子点溶剂(即2 mg CdSe@ZnS或2 mg ZnSe@ZnS), 经过在80 ℃水浴条件下进行10 min超声振荡, 使量子点纳米颗粒均匀分散. 在80 ℃温度下保持磁力搅拌15 min, 并将核壳量子点/聚乙烯/二甲苯溶液体系转移至旋转蒸发仪, 在70 ℃, 0.1 atm (1 atom=1×105 Pa)条件下进行减压蒸馏. 待减压蒸馏完成后, 使用无水乙醇冲洗析出产物. 将析出产物在70 ℃, 0.1 atm条件下持续12 h真空干燥, 以充分去除残留的有机试剂, 得到核壳量子点/聚乙烯复合绝缘材料. 质量分数为0.04% CdSe@ZnS/LDPE和质量分数为0.04% ZnSe@ZnS/LDPE两种试样名称分别记为QD1/PE和QD2/PE.

      • 2.2.   纳米复合绝缘表征

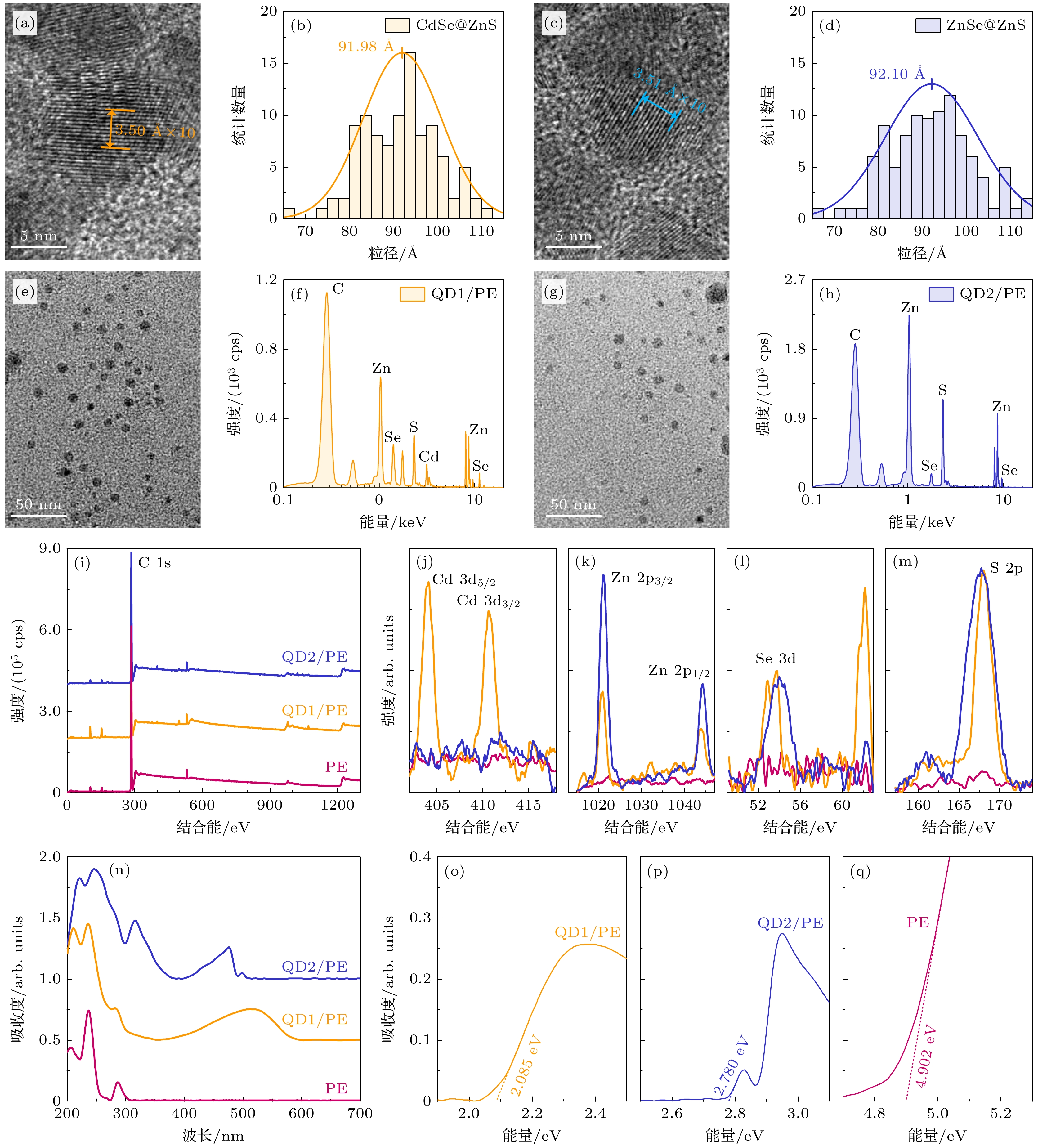
    • 采用透射电子显微镜(TEM, FEI Tecnai G2F20)分别表征了核壳量子点和复合绝缘材料的微观形貌特征. 图2(a)与图2(c)分别为CdSe@ZnS核壳量子点和ZnSe@ZnS核壳量子点微观形貌, 图中可观察到明显的晶格条纹形貌, 晶格间距分别为3.50 Å和3.51 Å, 与壳层ZnS纤锌矿的晶格常数a相匹配. 图2(b)与图2(d)分别统计了两种核壳量子点的粒径分布情况, 基于正态分布对两者粒径分布进行拟合, 结果表明CdSe@ZnS量子点平均粒径为(91.98 ± 8.95) Å, ZnSe@ZnS量子点平均粒径为(92.10 ± 10.54) Å.

      将溶解于二甲苯的纳米复合绝缘涂抹与碳膜铜网, 基于TEM观测了量子点在绝缘中的分散情况, 图2(e)与图2(g)分别展示了CdSe@ZnS量子点分散于QD1/PE复合绝缘和ZnSe@ZnS量子点分散于QD2/PE复合绝缘的微观形貌, 可见核壳量子点纳米颗粒在聚乙烯绝缘基体中的分散均匀性良好. 在图2(f)和图2(h)中, 采用能量色散光谱(EDS, Bruker Nano Esprit 2)表征了复合绝缘材料中的元素分布情况, 可见在QD1/PE复合绝缘中存在明显的Cd, Zn, Se和S元素特征能谱峰, 而在QD2/PE复合绝缘中存在明显的Zn, Se和S元素特征能谱峰.

      采用X射线光电子能谱(XPS, Thermo Scientific K-Alpha)表征了经过热压成型的薄片状复合绝缘试样中的元素特征, XPS全谱如图2(i)所示, 各元素精细谱经过10次扫描如图2(j)—(m)所示. 复合绝缘在XPS全谱中在284.1 eV处显示出明显的C1s元素峰, 表征了聚乙烯分子链的主碳链. 根据图2(j)所示, 对于QD1/PE绝缘在404.1 eV和410.8 eV处可见明显的Cd元素峰, 分别对应于Cd 3d5/2和Cd 3d3/2轨道, 对应了QD1/PE中添加核壳量子点的核层CdSe结构. 根据图2(k), 对于两种复合绝缘均在1021.2 eV和1044.3 eV出现明显的Zn元素峰, 分别对应于Zn 2p3/2和Zn 2p1/2轨道. 由图2(l)可见, 在53.8 eV处存在明显的Se 3d轨道特征峰. 图2(m)展示了S 2p轨道在167.9 eV处的特征峰, 对应于核壳量子点中壳层ZnS结构. 基于XPS谱图, 证明了核壳量子点/聚乙烯复合绝缘经过热压成型后, 其中核壳量子点仍然稳定存在.

      采用紫外-可见光(UV-Vis, Hitachi U4150)吸收谱表征了核壳量子点/聚乙烯复合绝缘的光学特征, 结果如图2(n)所示. 由图2(n)可见, 聚乙烯绝缘在可见光波段没有明显的吸收峰, 其特征吸收峰均出现于300 nm及以下的波段. 对于QD1/PE和QD2/PE两种复合绝缘, 在可见光波段出现了明显的特征吸收峰. QD1/PE绝缘在520 nm处出现特征吸收峰, 而QD2/PE绝缘在485 nm处出现特征吸收峰. 采用吸收峰前沿切线方法, 分别计算了聚乙烯绝缘和核壳量子点/聚乙烯复合绝缘的光学带隙特征, 结果如图2(o)—(q)所示. 由于激子结合能的存在, 因此光学带隙将势必低于能带间隙. QD1/PE绝缘和QD2/PE绝缘分别具有2.085 eV和2.780 eV的光学带隙, 而PE绝缘的光学带隙为4.902 eV.

      • 2.3.   实验方法

    • 采用三电极实验系统测试了复合绝缘在不同直流电场强度(5—70 kV/mm)与不同温度(10—70 ℃)下的直流电导特征. 实验方法如下: 制备厚度150 μm的薄片绝缘试样, 采用无水乙醇清除试样表面, 将绝缘试样放置于电极夹具; 待实验环境温度稳定后, 对绝缘试样施加直流电场; 采用皮安表记录30 min极化过程的电流, 选取稳态电流得到电流密度.

      采用脉冲电声(pulsed electro-acoustic, PEA)[19]法测试了绝缘试样在50 kV/mm直流电场强度、25 ℃温度下的空间电荷特性. 实验方法如下: 制备厚度150 μm的薄片绝缘试样, 采用无水乙醇清除试样表面, 将绝缘试样放置于电极夹具; 在5 kV/mm的直流电场强度下对空间电荷测量基线进行校准; 将直流场强升高至50 kV/mm持续30 min, 在此场强作用下载流子可向聚乙烯绝缘中明显发生注入现象[19], 以此获得极化过程中绝缘空间电荷动态特性; 随后关闭高压直流电源, 使绝缘试样两侧电极接地, 持续30 min, 获得去极化过程中绝缘内部空间电荷消散特性.

      采用等温放电电流(isothermal discharge current, IDC)方法表征复合绝缘的电荷陷阱能级深度与陷阱密度分布. 实验方法如下: 制备厚度150 μm的薄片绝缘试样, 采用无水乙醇清除试样表面, 将绝缘试样放置于电极夹具; 在50 kV/mm直流场强、25 ℃温度下极化30 min; 随后关闭高压直流电源, 使绝缘试样两侧电极接地, 保持25 ℃恒温, 持续60 min, 利用皮安表记录去极化过程中的释放电流, 获得绝缘试样的等温放电电流特性.

      等温放电电流方法考虑了存在陷阱分布的固体绝缘能带模型, 当绝缘在高电场下充分注入载流子, 使得绝缘中的陷阱能级被充分填充; 当去除外施电场后, 在等温条件下释放电流随时间的衰减过程. 根据Simmons模型, 等温放电电流I与陷阱密度-能级分布函数Nt(E)之间存在如下关系[20]:

      其中I为等温放电电流, Nt(E)为陷阱密度-能级分布函数, e为电子电荷量, L为试样厚度, S为电极面积, kB为玻尔兹曼常数, T为热力学温度, t为时间.

      陷阱能级深度与去极化时间满足如下关系[20]:

      其中Et为陷阱能级深度; v为入陷电子逃逸速率, 取值1012 s–1.

      因此, 可以得到陷阱密度与陷阱能级之间的关系为

    3.   实验结果

      3.1.   电导特性

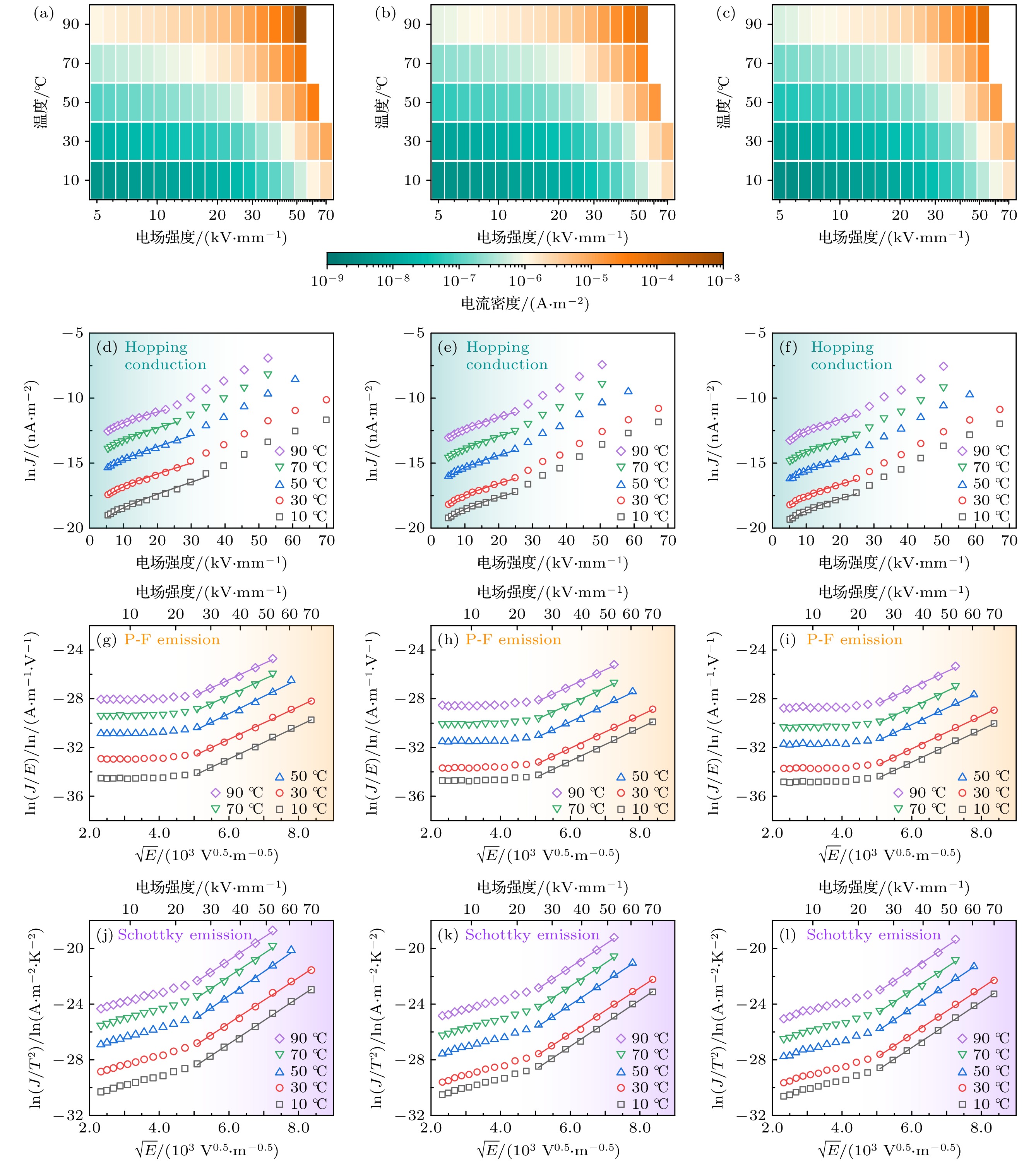
    • 聚乙烯绝缘和核壳量子点/聚乙烯复合绝缘的电流密度J随外施直流场强E和温度T的变化关系如图3(a)—(c)所示. 随着温度或外施场强的增加, 电导电流密度明显增大. 相较于常温低场条件(30 ℃, 5 kV/mm), 在高温强场条件下(90 ℃, 55 kV/mm)绝缘试样的电流密度可增大5个数量级的差异.

      在90 ℃温度、10 kV/mm场强条件下, PE绝缘体积电导率为6.43×10–13 S/m; 而QD1/PE和QD2/PE的分别具有3.78×10–13 S/m和3.26×10–13 S/m的体积电导率, 两者均明显低于PE绝缘, 说明了核壳量子点对聚乙烯绝缘内部的载流子迁移起到抑制作用. 在低电场强度下, 量子点难以发挥对载流子的限域作用, 而仅充当了载流子散射中心的效果[15]. 载流子受外施电场影响的迁移过程受到量子点的散射, 使载流子迁移率降低, 因此降低了纳米复合绝缘在低电场强度下电导率.

      对于聚乙烯绝缘, 绝缘体内载流子迁移机理主要包括欧姆电导、跳跃电导、Poole-Frenkel (P-F)发射效应和肖特基发射效应. 本文重点研究纳米复合绝缘在高温强电场条件下的电导特性, 此时电导机制受到空间电荷限制作用, 因此主要包含跳跃电导机制和P-F发射效应[21]; 另外, 载流子在高温强场条件下可克服金属电极与绝缘基体的接触势垒, 发生注入现象, 因此肖特基发射效应也是影响高温强场条件下绝缘电导的关键因素.

      对于聚乙烯绝缘, 由于内部聚集态结构的差异, 导致禁带中存在局域态, 在电场调制作用下载流子在局域态之间以“跳跃”的形式发生迁移行为, 在绝缘内部形成跳跃电导. 绝缘内部以跳跃电导形式主导的电流密度J随电场强度E的变化规律可表示为[22]

      其中n为载流子浓度, q为电荷量, λ为平均跳跃距离, ν为热振动频率, Ea为跳跃电导活化能, T为绝对温度. 在一定温度条件下, 可将(4)式简化描述为

      其中α1和α2均为常数.

      基于跳跃电导模型, 拟合了PE, QD1/PE和QD2/PE绝缘的电导特性, 结果如图3(d)—(f)所示. PE绝缘在10 ℃温度条件下, 当外施电场强度低于35 kV/mm时, 其跳跃电导的形式较为显著; 随着温度升高至90 ℃, PE绝缘在外施场强低于25 kV/mm时电导机制呈现明显的跳跃电导形式. 但对于QD1/PE和QD2/PE两种复合绝缘, 在10—90 ℃的温度范围内, 跳跃电导机制均呈现在场强低于25 kV/mm的区域.

      在更高的电场作用下, 绝缘能带结构受到外施电场的调制作用更为显著, 绝缘内部陷阱捕获的载流子受热激发至绝缘导带中形成电导电流, 即为P-F发射效应. 外施电场的增加, 使得载流子跃迁至导带的能量降低. 因此在高电场条件下, 由P-F发射效应导致的电导电流将更为显著. P-F发射的电流密度可表示为[22]

      在一定温度条件下, 可简化描述为

      其中μ为载流子迁移率, Nc为绝缘导带态密度, $q\varphi_{\mathrm{T}} $为陷阱能级, ε为介电常数, β1和β2均为常数.

      另一方面, 在高温强场条件下, 电极与绝缘之间存在肖特基发射效应. 这是由于载流子受热激发获得足够的能量以克服界面势垒, 从而产生注入的过程. 肖特基发射产生的电流密度可表示为[23]

      (8)式可被简化描述为

      其中A为理查德常数, $q\varphi_{\mathrm{B}} $为金属电极-绝缘基体接触势垒, γ1和γ2均为常数.

      基于P-F发射模型, 拟合了PE, QD1/PE和QD2/PE绝缘的电导特性, 结果如图3(g)—(i)所示. 基于肖特基发射模型, 同样对PE, QD1/PE和QD2/PE绝缘的电导特性进行了拟合, 结果如图3(j)—(l)所示. 可见在10—90 ℃的温度范围内, P-F发射效应和肖特基发射效应均出现在高于25 kV/mm的区域. 说明在更高的场强下, 电场对绝缘能带结构的调制作用促进了载流子越过势垒; 一方面载流子更容易越过金属电极-绝缘基体之间的接触势垒, 以肖特基发射的形式进行迁移; 另一方面, 载流子更容易越过绝缘基体内陷阱势垒, 以P-F发射的形式进行迁移. 关于聚乙烯绝缘在高场下的电导机制, 是难以通过单一模型进行描述[24], 强电场下的电流以P-F发射效应和肖特基发射效应为主[25], 同时跳跃电导的机制也可能参与到其中[26]. 基于图3(g)—(l)的拟合结果, 也同样可以验证这一观点, 高电场下的聚乙烯绝缘受到空间电荷的影响作用, 形成了P-F发射效应与肖特基发射效应共同作用的电导电流. 对于QD1/PE和QD2/PE纳米复合绝缘, 在高电场强度的作用下, 电导电流密度仍明显小于PE绝缘. 说明在高场强条件下, 核壳量子点对载流子起到了限域作用, 可视为向绝缘中引入能级更深的局域态. 在相同条件下, 纳米复合绝缘内的载流子更难以跨越势垒, 抑制了载流子迁移, 使得纳米复合绝缘电导低于未改性的PE绝缘.

      • 3.2.   空间电荷特性

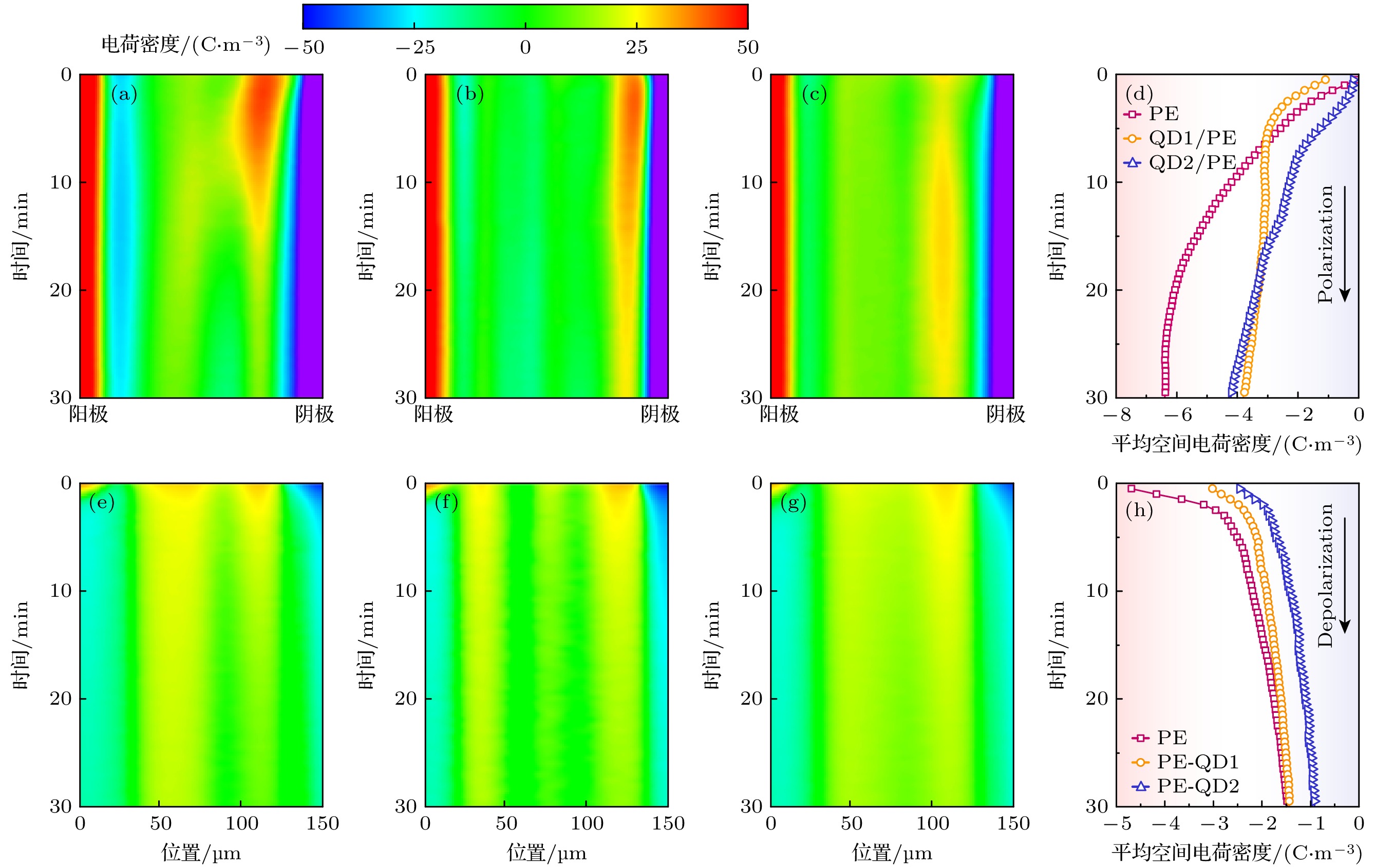
    • 聚乙烯绝缘和复合绝缘在50 kV/mm直流电场下的空间电荷特性如图4(a)—(c)所示. 根据图4(a), 对于PE绝缘试样, 在施加直流电压后阴极与阳极附近均出现异极性极化电荷; 阴极位置的正电荷进一步增强了阴极附近的电场强度, 加剧了载流子向绝缘内的注入; 随着极化时间的增加, 阴极侧的正极性电荷逐渐减少, 表明阴极发生了负极性电荷注入现象, 极化电荷与注入电荷发生复合, 表现为正极性电荷逐渐减少. 根据图4(b), 对于QD1/PE绝缘, 在施加直流电压后, 在阳极和阴极附近同样出现异极性极化电荷, 这与PE绝缘现象相一致; 随着极化时间的增加, 阴极侧的极化电荷同样具有减少的趋势, 表明同极性电荷注入发生复合. 根据图4(c), 对于QD2/PE绝缘, 其内部的空间电荷积聚情况明显减弱, 在持续30 min的极化过程中, 没有观察到显著的电荷注入现象. 为研究绝缘内部空间电荷的积聚与消散特性, 绝缘试样内部平均空间电荷密度随时间的变化情况表示为

      其中ρ(t)为绝缘试样内平均空间电荷密度随时间的变化, d为试样厚度, q(x, t)为试样内x位置、t时刻的空间电荷密度.

      聚乙烯绝缘和复合绝缘在极化过程和去极化过程中试样内部的平均空间电荷密度变化情况分别如图4(d)和图4(h)所示. PE绝缘在极化过程中, 负极性空间电荷量不断增加, 说明了电子由阴极向绝缘内的注入现象显著, 在25 min后逐渐趋近稳定于–6.4 C/m3. 而QD1/PE和QD2/PE绝缘中空间电荷量显著低于PE绝缘, 说明了CdSe@ZnS量子点或ZnSe@ZnS量子点可捕获电极注入的同极性电荷, 形成的反向电场削弱了电极附近的整体电场强度, 使得电荷注入过程受到抑制. 在30 min时刻, QD1/PE和QD2/PE绝缘内部的空间电荷积累量分别较PE绝缘降低了40.3%和34.1%.

      图4(e)—(g)为PE, QD1/PE和QD2/PE绝缘试样在去极化过程中的空间电荷分布情况. 图4(h)为去极化过程中平均空间电荷密度的变化情况. PE绝缘内部空间电荷在30 min的去极化过程中电荷平均电荷密度由–4.6 C/m3衰减至–1.5 C/m3, 其电荷消散速率高于QD1/PE绝缘和QD2/PE绝缘. 三种绝缘试样中, QD2/PE在经过30 min的去极化后, 具有最低的平均空间电荷密度为–1.0 C/m3. 纳米复合绝缘中的空间电荷消散速率较慢, 可归因于量子点壳层对核层所捕获的载流子的限制作用, 壳层结构抑制了核层与绝缘基体之间的相互作用, 对内部载流子起到了限域作用, 表现出了空间电荷消散速率减慢的现象.

      因此, 核壳量子点/聚乙烯复合绝缘展现出更强的对空间电荷注入的抑制作用, 注入的同极性电荷形成反向电场, 阻止了电荷进一步注入与积聚; 而受到核壳量子点捕获的载流子需要更长的脱陷时间, 使得纳米复合绝缘的电荷消散速率低于PE绝缘.

      • 3.3.   电荷陷阱特性

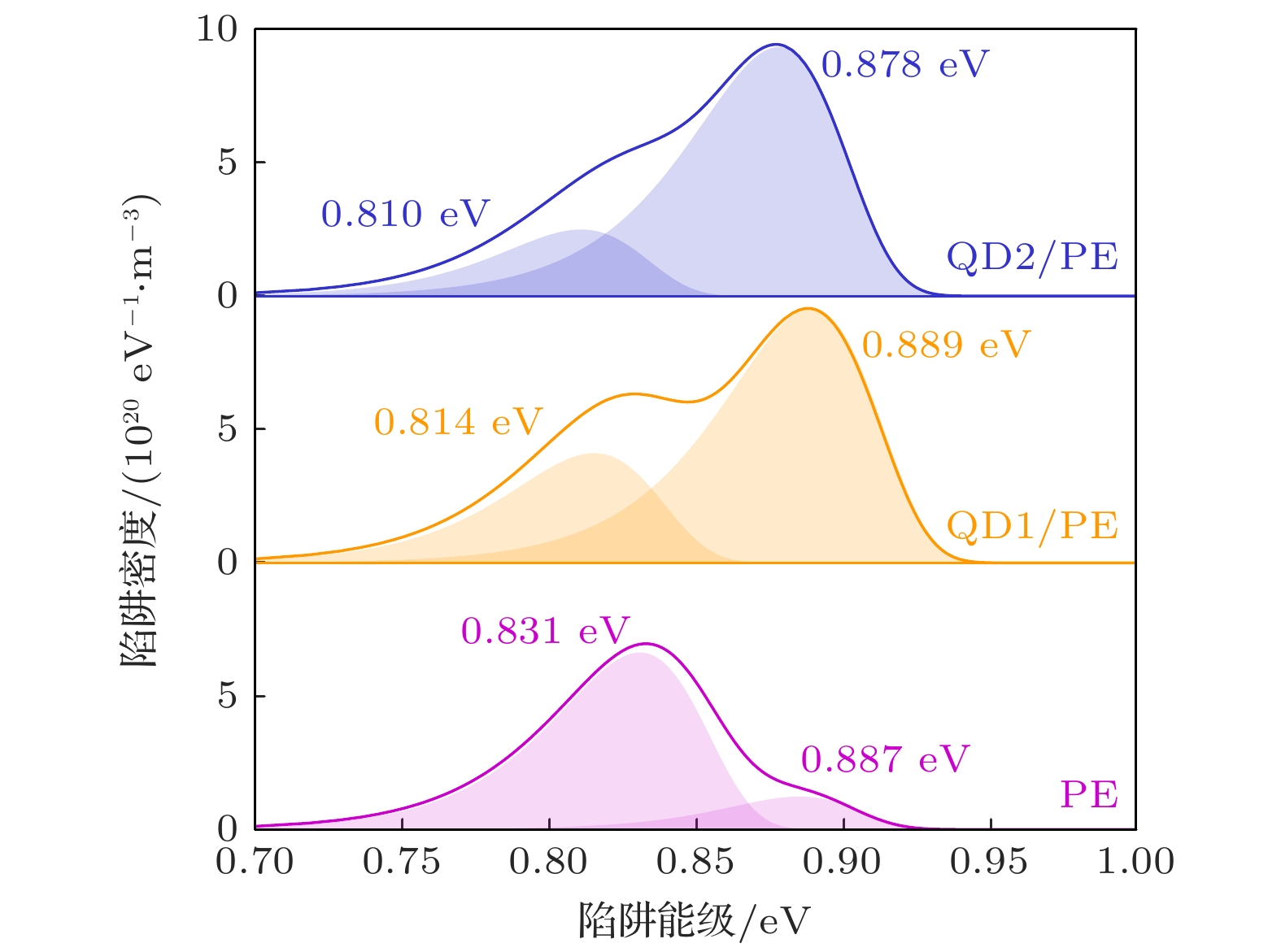
    • 基于等温放电电流方法获得了核壳量子点/聚乙烯复合绝缘的陷阱能级与陷阱密度特性, 并与PE绝缘进行对比, 如图5所示. 图5分别表示了每种绝缘试样的深陷阱与浅陷阱特征. PE绝缘在能级深度为0.831 eV处具有6.60×1020 eV–1·m–3的陷阱密度. 核壳量子点/聚乙烯复合绝缘最为显著的陷阱能级明显较PE绝缘更深. QD1/PE绝缘的深陷阱特性更为显著, 深陷阱中心能级为0.889 eV, 陷阱密度达到9.50×1020 eV–1·m–3. 相较于QD1/PE绝缘, QD2/PE的深陷阱也同样显著, 深陷阱中央能级为0.878 eV水平, 陷阱密度为9.40×1020 eV–1·m–3.

      另外, 由图5可以发现, QD1/PE和QD2/PE的浅陷阱中央能级分别为0.814 eV和0.810 eV, 均低于PE绝缘的浅陷阱中央能级水平. 浅陷阱特征与跳跃电导的活化能有关, 较低的浅陷阱能级反映出更低的温度敏感性[27]. 纳米复合绝缘中浅陷阱能级的降低与核壳量子点对载流子的散射作用相关[15]. 载流子在低电场条件下在绝缘基体中的迁移是以浅陷阱中的跳跃行为为主, 而核壳量子点的引入对低电场下的载流子迁移具有抑制作用, 表现为浅陷阱能级变浅. 而另一方面, 深陷阱特征并不会影响到低电场下的跳跃电导活化能[28], 深陷阱能级的增加与核壳量子点对载流子的限域作用有关. 量子点的核壳捕获的载流子更难以重新被激发至绝缘基体, 体现为深陷阱能级加深.

      根据核壳量子点/聚乙烯复合绝缘的陷阱能级与陷阱密度特征可知, 核壳纳米量子点向聚乙烯绝缘中引入了更深的陷阱能级, 对载流子起到了更强的捕获作用. 对于电导特征, 在低场下, 载流子在浅陷阱中跳跃迁移, 而纳米复合绝缘的浅陷阱深度降低, 使得跳跃电导的活化能降低, 降低了电导的温度敏感性以及高温条件下的绝缘电导率; 在高场条件下, 核壳量子点向聚乙烯绝缘内部引入更深的陷阱能级, 使得入陷载流子难以被重新激发脱陷, 因此在相同条件下的核壳量子点/聚乙烯复合绝缘电导电流密度更低. 对于空间电荷积聚特征, 这些深陷阱形成的局域态能级使得载流子更容易从电极进入绝缘体内, 因此, 复合绝缘在极化过程初期平均电荷密度增加速率更高; 但是核壳量子点引入更深的陷阱能级使得载流子难以进一步发生迁移, 因此表现出对电荷注入过程的抑制作用[29]. 在空间电荷消散过程中, 由于外施电场对能级的影响消失, 入陷载流子主要以跳跃的形式消散, 核壳量子点/聚乙烯复合绝缘中积聚的空间电荷在更深的能级之中, 因此核壳量子点/聚乙烯复合绝缘的电荷消散速率比未改性的绝缘稍慢.

    4.   仿真计算与讨论

      4.1.   核壳量子点与聚乙烯绝缘能带结构

    • 基于密度泛函理论, 分别对CdSe, ZnSe, ZnS和PE的晶体结构进行平面波赝势第一性原理计算. 理论计算基于CASTEP程序, 以杂化泛函PBE0描述交换-相关势, 使用范数守恒赝势描述电子平面波函数展开, 截断能650.0 eV, 以1.0 × 10–6 eV/atom作为自洽场收敛条件, k点设置为6 × 6 × 6, 忽略自旋-轨道耦合效应. 对晶体结构模型进行几何结构优化, 能量收敛判据为1.0×10–5 eV/atom, 最大受力0.03 eV/Å, 最大压力0.05 GPa, 最大位移0.001 Å.

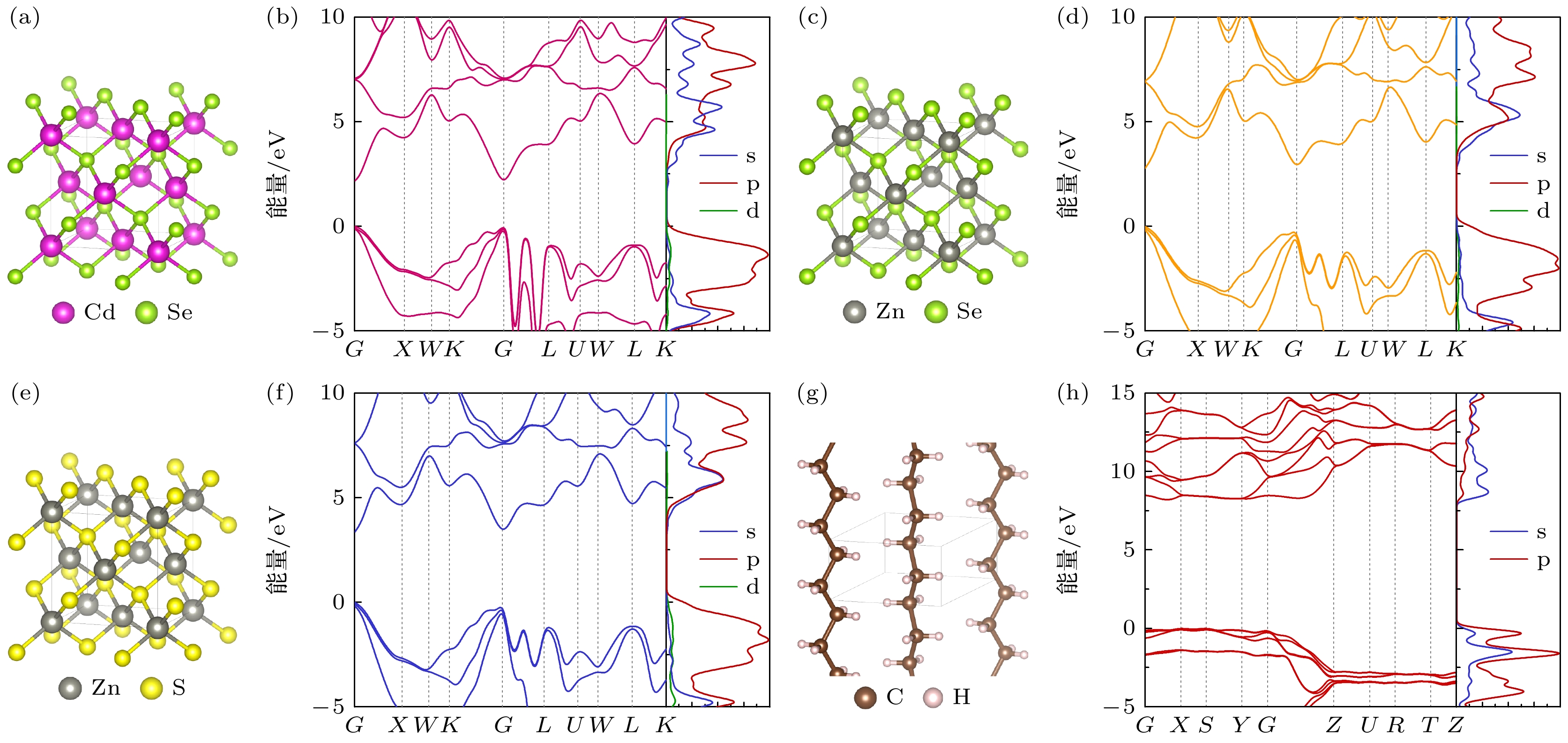
      CdSe, ZnSe和ZnS晶体均属于F-43M空间群, 经过几何优化处理, 三者的晶格参数分别为6.037, 5.658, 5.403 Å; PE晶体属于PNAM空间群, 晶格参数为7.380(a), 4.924(b), 2.540(c) Å. 上述四种晶体结构模型分别如图6(a)、图6(c)、图6(e)和图6(g)所示. 计算获得了上述晶体结构的能带结构与态密度特征, 结果如图6(b)、图6(d)、图6(f)和图6(h)所示. 其中, CdSe, ZnSe和ZnS均为II-VI型半导体, 价电子层具有较为相似的结构, 因此三者的E-k色散关系较为相似, 价带顶与导带底均在Gamma点出现, 呈现直接型带隙特征. 对于这三种II-IV型半导体, 外层共有8个价电子, 由4个s轨道电子和4个p轨道电子以sp3杂化形式形成共价键结合, 成键态形成以p轨道为主导的价带顶, 而反键态形成以s, p轨道共同主导的导带底. PE晶体的价带顶与导带底呈现平缓的特征, 说明空穴和电子的迁移行为均较为困难, 呈现出载流子限域效应. 聚乙烯中碳原子均呈现sp3杂化与氢原子1s形成共价键, 因此价带顶处p轨道态密度高于s轨道态密度, 而导带底处s轨道态密度高于p轨道态密度.

      晶体内的载流子迁移率与载流子有效质量和散射概率呈反比关系. 能带结构中的E-k色散关系与载流子有效质量可表示为

      其中k为波矢量; E0为导带底或价带顶能量; $\hbar $为约化普朗克常数; m*为电子有效质量或空穴有效质量, 电子有效质量记为$m_{\mathrm{n}}^* $, 空穴有效质量记为$m_{\mathrm{p}}^* $.

      核壳量子点与聚乙烯的能带结构特征如表1所列. 由表1可见, CdSe具有最低的电子有效质量和空穴有效质量, 分别为0.14 a.u.和0.39 a.u., 说明载流子在其中具有最高的迁移率. ZnSe和ZnS的电子/空穴有效质量依次增大. 而PE绝缘的价带顶和导带底平缓, 使得载流子难以发生迁移行为, 其电子有效质量和空穴有效质量均大于10 a.u.

      • 4.2.   核壳量子点/聚乙烯界面电子结构对载流子迁移的影响

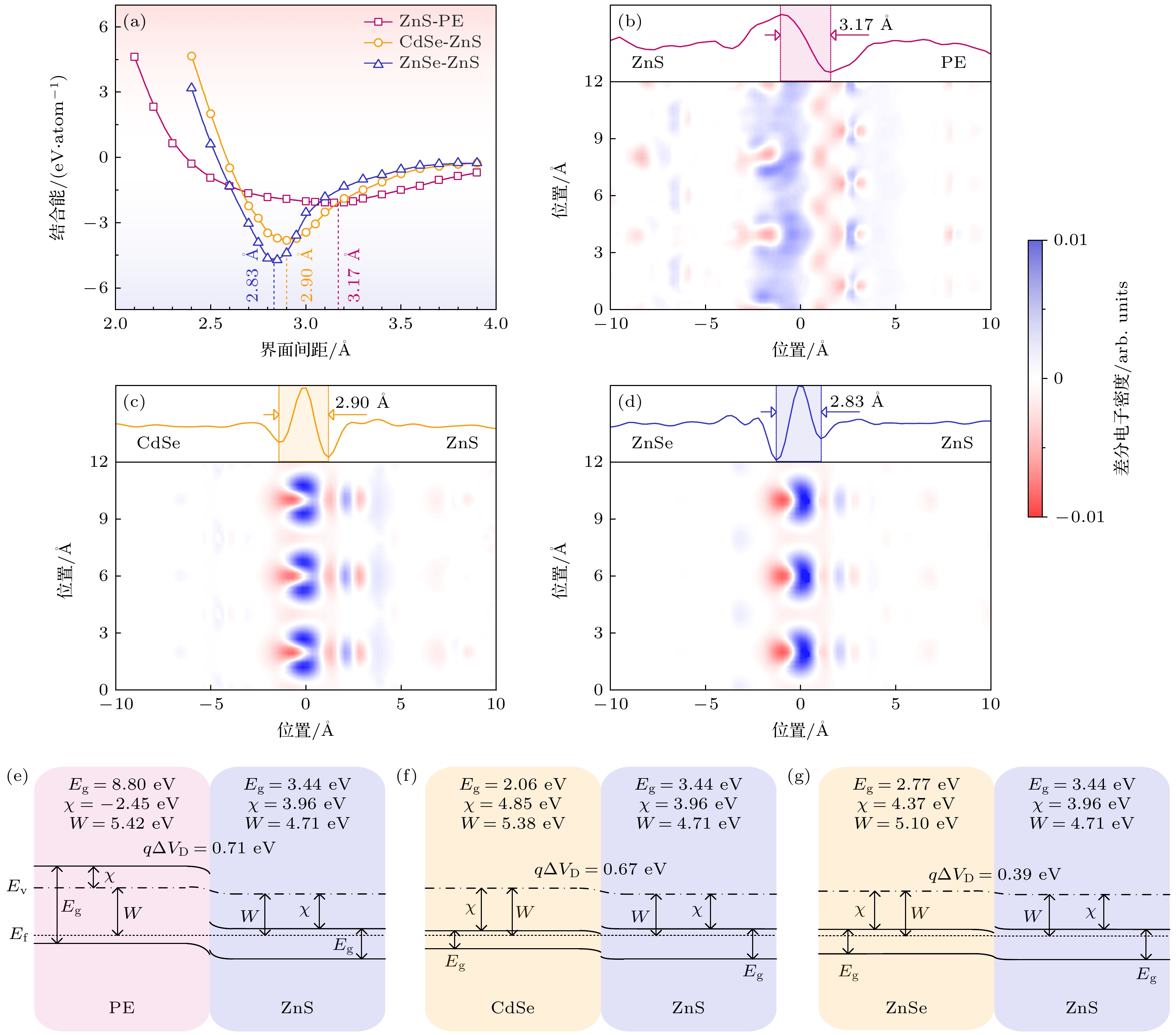
    • 为了研究核壳量子点/聚乙烯界面电子结构, 分别建立了ZnS-PE, CdSe-ZnS和ZnSe-ZnS三种界面周期性模型, 图7(a)展示了三种不同界面的结合能随层间原子间距的变化情况. 对于ZnS-PE界面模型, 层间结合能以非键相互作用为主导, 因此其界面结合能较低, 界面间距较大. 当界面间距为3.17 Å时, 界面结合能取得极小值, 得到最稳定的界面结构. CdSe-ZnS和ZnSe-ZnS界面存在未配位原子, 界面结合能以共价键作用为主, 因此界面结合能较高, 界面间距与键长相关. CdSe-ZnS界面间距为2.90 Å时、ZnSe-ZnS界面间距为2.83 Å时, 两者的界面结合能各自取得最小值, 形成稳定的界面结构. 另外, 由于ZnSe的共价键长为2.44 Å, 低于CdSe共价键长2.60 Å, 所以ZnSe-ZnS界面间距略低于CdSe-ZnS界面间距.

      采用差分电子密度(electron density difference)表征了量子点核壳层之间、量子点与聚乙烯之间由于接触发生的电子转移特性. 差分电子密度可表示为

      其中Δρ(r)为实空间r位置的差分电子密度, ρ12(r)为双层界面模型的电子密度, ρ1(r)和ρ2(r)分别为单层模型的电子密度.

      量子点壳层ZnS与聚乙烯之间的界面差分电子密度如图7(b)所示, 可见聚乙烯在界面结构中呈现失电子特性, 而ZnS则呈现出得电子特性, 说明了在ZnS-PE界面中, 电子倾向于由PE转移至ZnS, 而空穴则ZnS转移至PE. 由于PE的空穴有效质量显著高于ZnS, 因此在界面层形成了载流子限域层, 抑制了载流子在ZnS-PE界面的进一步迁移. CdSe-ZnS和ZnSe-ZnS界面的差分电子密度如图7(c)和图7(d)所示, 由于两种界面结构具有相似的对称性和价电子结构, 界面处的电荷转移特性也较为相似. 界面两侧结构均呈现处出失电子特性, 而电子集中于界面层. 界面处的对称性缺失引入了界面缺陷态, 界面态能级对电子形成了限域作用[30], 而且由于ZnS的导带能级高于CdSe和ZnSe, 进一步增强了对电子的束缚作用, 使得界面态入陷电子难以脱离.

      根据表1所列的能带特征参数与图7所示的界面电子结构特征, 图7(e)—(g)为PE-ZnS, CdSe-ZnS, ZnSe-ZnS三种界面结构的能带模型. PE绝缘基体与壳层ZnS形成接触界面, PE能带结构向下弯曲, 而ZnS能带结构向上弯曲. 存在于导带底的电子载流子, 受到能带弯折的影响, 由PE绝缘向壳层ZnS发生迁移. PE-ZnS界面价带顶形成不连续的“凹口”与“尖峰”结构, 对空穴载流子形成了显著的限域作用[31]. 建立了核壳量子点界面结构对聚乙烯绝缘载流子迁移的影响模型, 如图8所示. 图8所示的核壳量子点的核层与壳层形成的接触界面属于n-n型半导体接触, 核层能带结构出现下弯, 而壳层能带结构出现上弯. 导带底电子载流子将会受到此界面的限域作用, 而难以继续迁移[32]. 价带顶空穴载流子受到内建接触电势的影响而向壳层发生迁移. 核壳量子点自身的核壳界面提供了对电子载流子的限域作用, 而壳层与绝缘基体的界面提供了对空穴载流子的限域作用.

      另外依据Tanaka提出的介电量子点模型[15], 载流子主要以场致发射的形式进入量子点, 所以在较低电场强度的条件下, 核壳量子点难以对载流子发挥限域作用. 在低电场条件下, 量子点在聚合物基体的载流子迁移过程中发挥了散射中心的作用. 此时聚合物基体中的载流子主要以浅陷阱跳跃迁移的形式形成电导, 量子点对载流子的散射作用使得载流子迁移率降低, 因此降低了纳米复合绝缘在低电场条件下的体积电导率.

      综上所述, 核壳量子点对载流子的散射作用, 降低了纳米复合绝缘在低电场条件下的载流子迁移率; 核壳纳米量子点的核层-壳层界面、壳层-绝缘界面的能带偏移导致导带底与价带顶发生突变, 分别对电子和空穴具有限域作用, 且限域效应随着量子点核层与壳层带隙差异增大而逐渐增强, 从而限制高温强场下载流子迁移、抑制空间电荷积聚.

    5.   结　论

    • 本研究选取了CdSe@ZnS和ZnSe@ZnS两种典型II-VI型核壳量子点, 制备了核壳量子点/聚乙烯纳米复合绝缘材料, 研究了核壳量子点界面电子结构对绝缘内部载流子迁移的影响规律及机理. 本文结论如下:

      1)在10—90 ℃温度范围内, 当场强低于25 kV/mm时纳米复合绝缘的电导机制为跳跃电导; 而当场强超过25 kV/mm, P-F发射效应和肖特基发射效应在纳米复合绝缘的电导机制中较为显著. 相较于PE绝缘, 在温度90 ℃、场强50 kV/mm条件下, QD1/PE和QD2/PE复合绝缘的直流电导率分别可降低39.2%和47.2%.

      2) QD1/PE和QD2/PE纳米复合绝缘的空间电荷积聚量低于PE绝缘, 在25℃温度、50 kV/mm场强条件下分别较PE绝缘降低了40.3%和34.1%, 这主要归因于核壳量子点可引入电荷深陷阱, PE绝缘的陷阱能级深度为0.831 eV, 而QD1/PE和QD2/PE绝缘的深陷阱能级分别增大至0.889 eV和0.878 eV. 表明核壳量子点增强了对电极注入同极性电荷的捕获作用, 进而削弱了电极-绝缘界面电场, 对空间电荷的注入起到抑制作用.

      3)基于密度泛函理论, 建立了核壳纳米量子点/聚乙烯复合绝缘中的核层-壳界面模型与壳层-绝缘基体界面模型. 理论计算结果表明, 壳层与绝缘基体之间的接触界面对空穴载流子起到了限域作用, 而电子载流子由绝缘基体向壳层发生迁移; 核层与壳层之间形成n-n型半导体接触, 对电子载流子起到限域作用, 而空穴载流子由核层向壳层发生迁移. 核壳量子点对电子和空穴载流子的限域效应, 提高了载流子捕获能力, 限制了载流子迁移, 抑制了空间电荷的注入.

    参考文献 (32)

目录

/

返回文章
返回