首页
登录
注册
-
高电荷态离子(highly charged ions, HCIs)精密谱学一直是原子物理的前沿研究方向之一[1,2]. 双电子复合(dielectronic recombination, DR)是一个共振过程, 精确测量双电子复合共振结构可以解析出高电荷态离子的激发态能级, 进而开展如量子电动力学检验[3,4]、同位素移动测量[5–7]、超精细诱导跃迁寿命测量[8]等重要研究. 随着电子冷却技术的产生和发展[9,10], 离子冷却储存环逐渐成为继核聚变反应装置Tokamak和电子束离子阱之后, 研究电子-离子复合精密谱学最理想的工具之一. 相比其他实验方法, 重离子冷却储存环可以通过冷却技术获得高亮度、高品质离子束, 并能长时间储存和操控离子, 从而为DR谱学实验提供了极高的能量分辨(meV)、极大的能量调制范围(meV—keV)、纯的单一电荷态离子以及绝对测量等独一无二的实验条件[11,12]. 过去十多年, 人们在重离子储存环上开展了一系列高电荷态离子的双电子复合精密谱学实验研究, 包括德国TSR上的类锂Sc18+离子的超精细分裂[8]、德国ESR上的类锂重离子U89+, Pb79+, Au76+精细结构[4]、瑞典CRYRING上的类铜Pb53+的超精细分裂等[3], 基于储存环的双电子复合谱学实验也因此正在发展成为新一代的精密谱学测量方法——电子离子共振谱学技术. 此外, 精确的双电子复合速率系数是天体物理和聚变等离子体模型中最基本的输入参数, 双电子复合过程伴随的退激辐射往往可以作为诊断等离子体中电子温度和密度的有效探针[13,14].
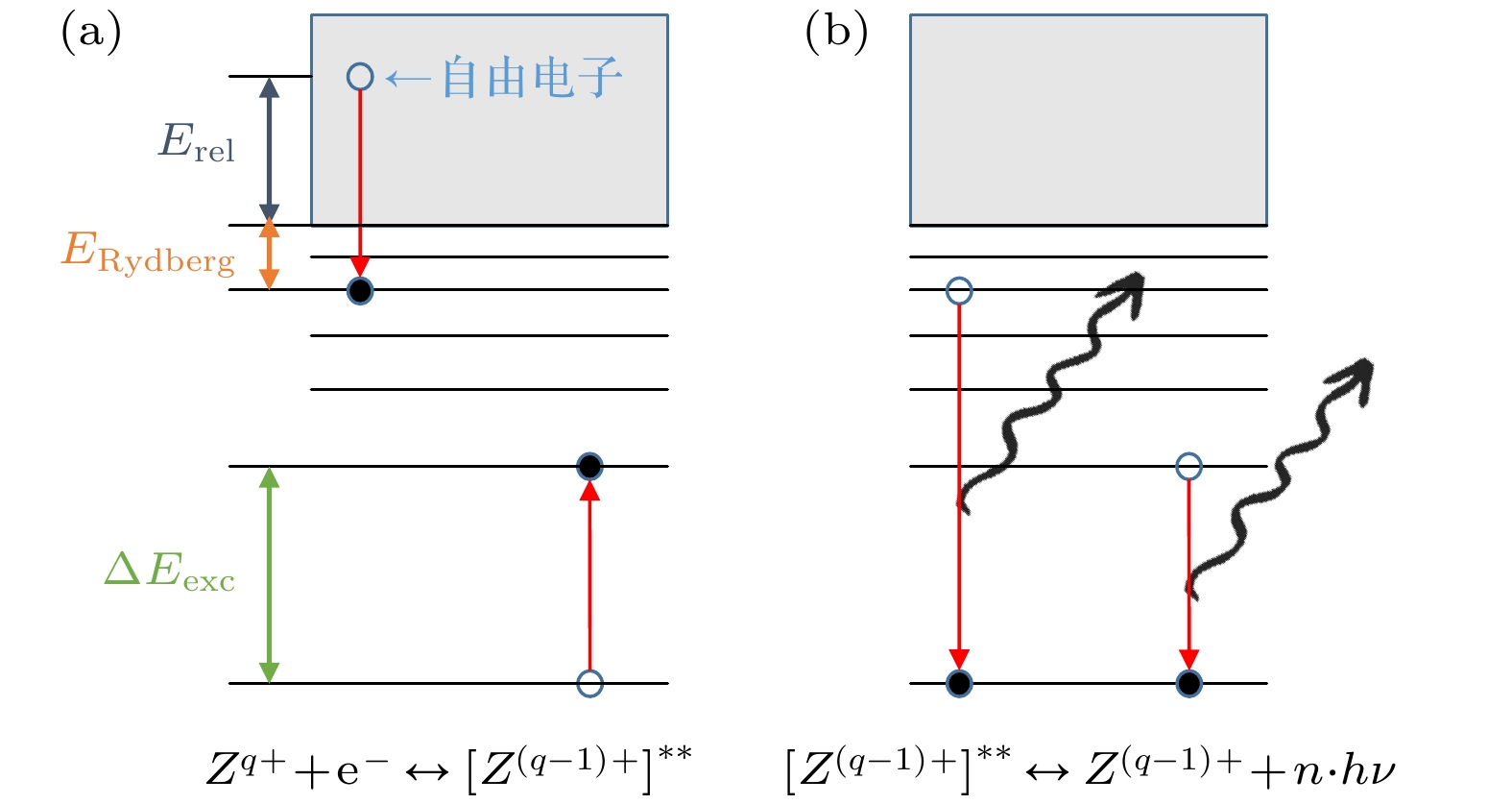
图1给出了双电子复合过程示意图, 自由电子被非全裸离子
$ {Z}^{q+} $ 俘获的同时, 共振激发离子的某个束缚电子, 形成双激发态离子$ {{[Z}^{(q-1)+}]}^{{\mathrm{*}}{\mathrm{*}}} $ , 最后这个双激发态离子通过发射光子退激到低于其电离阈的稳定态, DR过程可用方程(1)表示:图1中标出的能量分别为电子-离子质心系相对能量
$ {E}_{{\mathrm{r}}{\mathrm{e}}{\mathrm{l}}} $ , 被俘获电子所处的里德伯能级对应的电离能$ {E}_{{\mathrm{R}}{\mathrm{y}}{\mathrm{d}}} $ 和内壳层电子的激发能$ {{{\Delta }}E}_{{\mathrm{e}}{\mathrm{x}}{\mathrm{c}}} $ , 发生DR过程的前提是满足能量守恒$ {\Delta E}_{{\mathrm{e}}{\mathrm{x}}{\mathrm{c}}}={E}_{{\mathrm{r}}{\mathrm{e}}{\mathrm{l}}}+{E}_{{\mathrm{R}}{\mathrm{y}}{\mathrm{d}}{\mathrm{b}}{\mathrm{e}}{\mathrm{r}}{\mathrm{g}}} $ , 共振的DR过程也因此对原子能级结构非常敏感, 通过调制电子和离子的相对能量, 并测量共振复 合DR谱, 就可以解析出高电荷态离子能级结构 信息.兰州重离子加速器冷却储存环CSRm上已经成功开展了一系列重离子的DR实验[15–22]. 而相比CSRm 上的35 keV电子冷却装置, 重离子储存实验环CSRe上的300 keV电子冷却装置开展高电荷态离子双电子复合精密谱学实验具备独特优势: 它可以被用来测量更重和更高电荷态的离子, 可以将电子-离子质心系下的碰撞能量由100 eV增大至1000 eV, 将成为世界上主要开展超高电荷态离子和放射性核素双电子复合精密谱学的实验装置. 300 keV电子冷却装置上的电子-离子复合实验的重点研究方向包括: 开展天体物理相关的高电荷态离子双电子复合反应速率精确测量; 开展强库仑场中量子电动力学效应研究; 推动电子-离子谱学技术在研究放射性核素物理性质中的应用. CSRe上使用了自主研制的多丝正比探测器, 可以实时地、无破坏地进行离子束流包络监测, 指导优化离子束, 降低离子束的温度、动量分散和束流包络, 提升离子束流的品质. 为了验证CSRe上新安装的电子束能量调制系统和复合离子探测器的工作性能, 选用Kr25+离子进行了DR测试实验, 实验测量了质心系下相对碰撞能量0—70 eV的DR速率系数谱, 在这个能量范围内, 主要的双电子复合通道有
对比实验结果与FAC (flexible atomic code)的理论计算, 发现二者整体符合很好, 差别小于20%, 在实验数据的不确定度(约30%)范围之内[22], 且除了
$ 3{\mathrm{s}}\to 3{\mathrm{l}}\;(\Delta n=0) $ 通道外,$ 3{\mathrm{s}}\to 4{\mathrm{l}}\;(\Delta n=1) $ 也是谱线的重要来源. 此外, 由实验测量的DR速率系数谱得到了等离子体速率系数, 并与理论计算结果进行了对比, 提供了用于等离子体建模的基准数据. 本次实验结果表明, CSRe上的双电子复合实验平台具有良好的稳定性和可靠性, 可以用于未来的更高电荷态离子的双电子复合实验研究. -
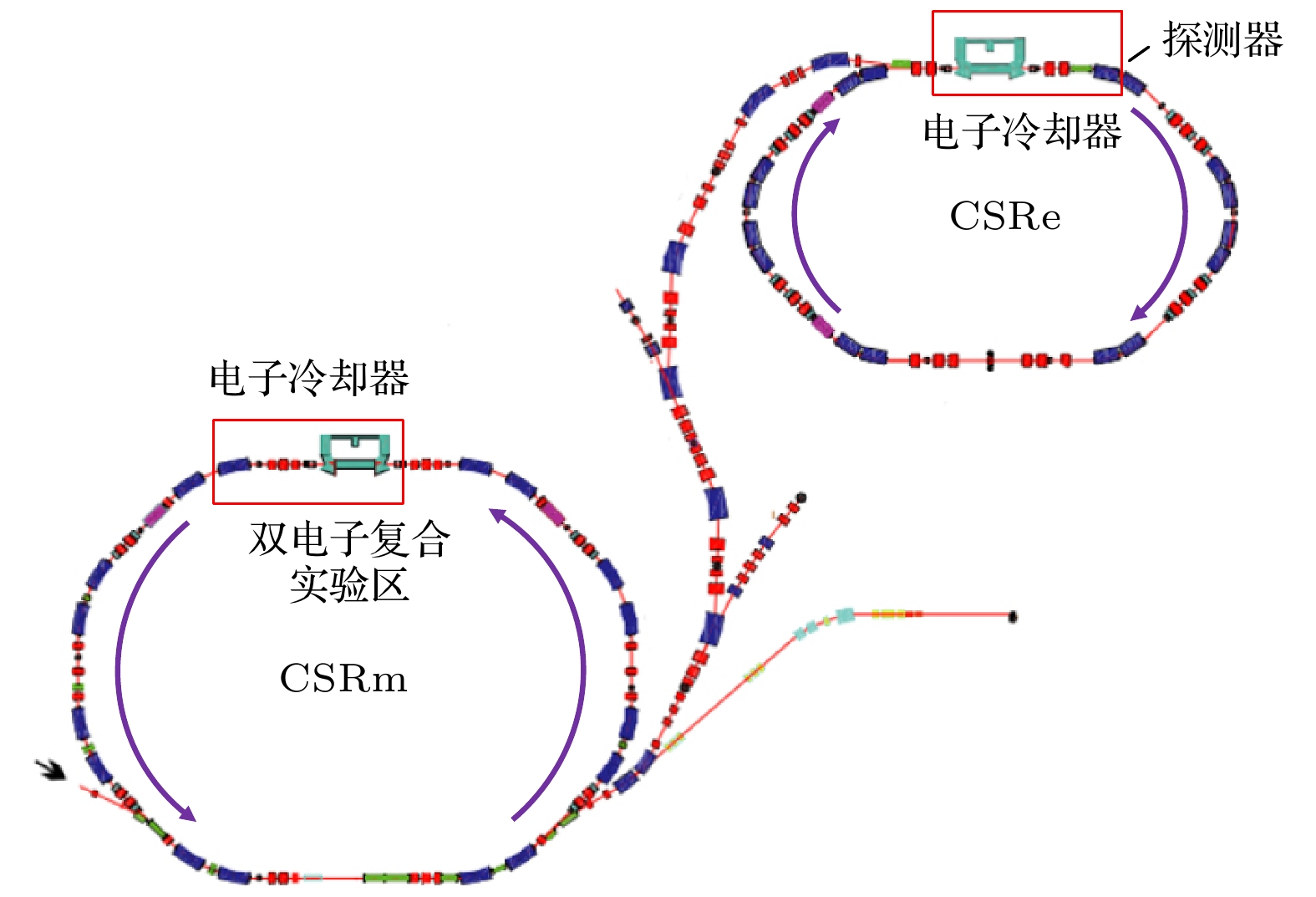
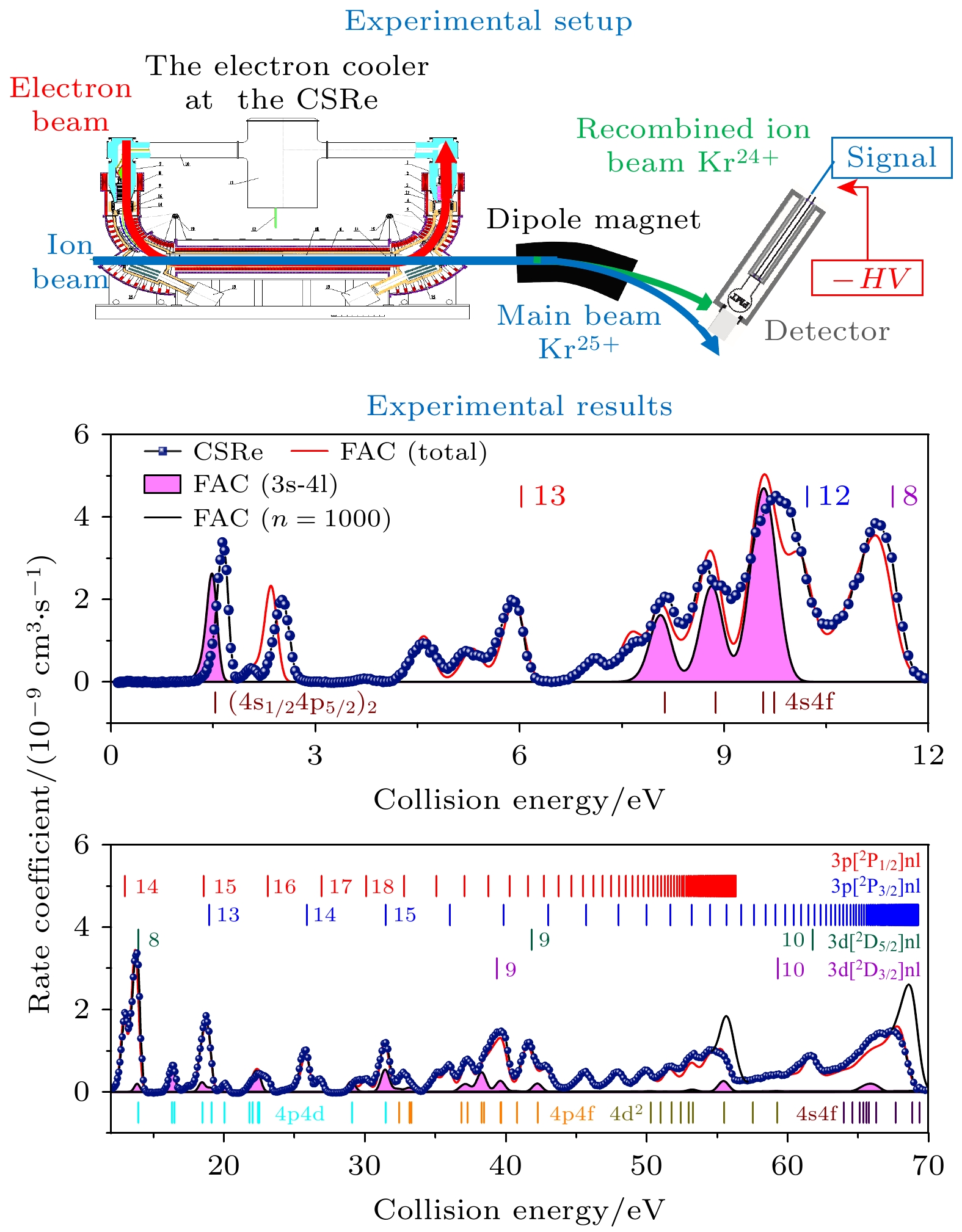
高电荷态离子双电子复合精密谱学实验是国家“九五”大科学工程兰州重离子加速器冷却储存环(HIRFL-CSR)的核心科学目标之一, 其实验装置示意图参见图2. HIRFL-CSR上的主环CSRm和实验环CSRe均配备了用于重离子束冷却的电子冷却器, 通过调制电子束能量可以获得非零的电子-离子质心系碰撞能量, 从而开展双电子复合精密谱学实验. 储存环CSRm上的离子注入能量在几MeV/u量级, 电子束能量调制系统的能量调制范围为–1.5—1.5 kV, 对应于电子离子质心系的碰撞能量为0—100 eV. 在CSRm双电子复合实验中, 电子回旋共振离子源ECR产生的离子束经由扇聚焦回旋加速器SFC加速至数MeV/u后注入到CSRm中进行冷却、储存, 在达到实验要求的流强后, 先经过2—3 s的电子束预冷却以优化束流品质, 随后再开展实验测量. 相比CSRm上的双电子复合实验, CSRe上的重离子束流是经过CSRm冷却、积累、加速等过程得到的. 因此, CSRe中离子束流能量更高, 能够达到几百MeV/u, 离子与环内残余气体(主要是H2, He)的电荷交换截面随着离子束能量的升高迅速减小[23]. 此外, 环内真空度也更高, 残余气体造成的本底很小, 实验中多次测量的可重复性很好, 实验装置的整体稳定性良好. 同时, CSRe电子冷却器使用自主研发的电子束能量高压调制系统具备优异的性能, 其电子能量调制范围能够达到–15—15 kV, 对应的电子离子质心系碰撞能量为0—1 keV, 因而在储存环CSRe上可以进行更高电荷态离子的DR精密谱学实验.
在CSRe上进行DR实验时, 电子-离子相互作用段下游的复合离子探测器被放置在与真空环境分离的腔室里, 这一方面可以在储存环实验和真空烘烤的过程中方便地更换和移除探测器; 另一方面, 由于离子束能量较高, 腔室上的薄不锈钢窗可以保护探测器不受低能的杂散电子、离子和光子的影响. 此外, 与CSRm上仅使用晶体闪烁体探测器（YAP:Ce）不同, 在CSRe电子冷却器的下游, 装配有塑料闪烁体探测器(plastic scintillation detector, PSD)和多丝正比探测器(multiwire proportional chamber, MWPC)用于探测经过复合或电离而改变电荷态的离子. 相较于PSD而言, MWPC具有位置分辨能力, 在获取复合离子计数的同时可以提供离子的位置信息, 因而在实验中可以用MWPC实时地监测离子束的横向包络, 为离子束束流优化提供指导. CSRe上Kr25+离子的双电子复合实验参数如表1所列(1 G = 10–4 T).
-
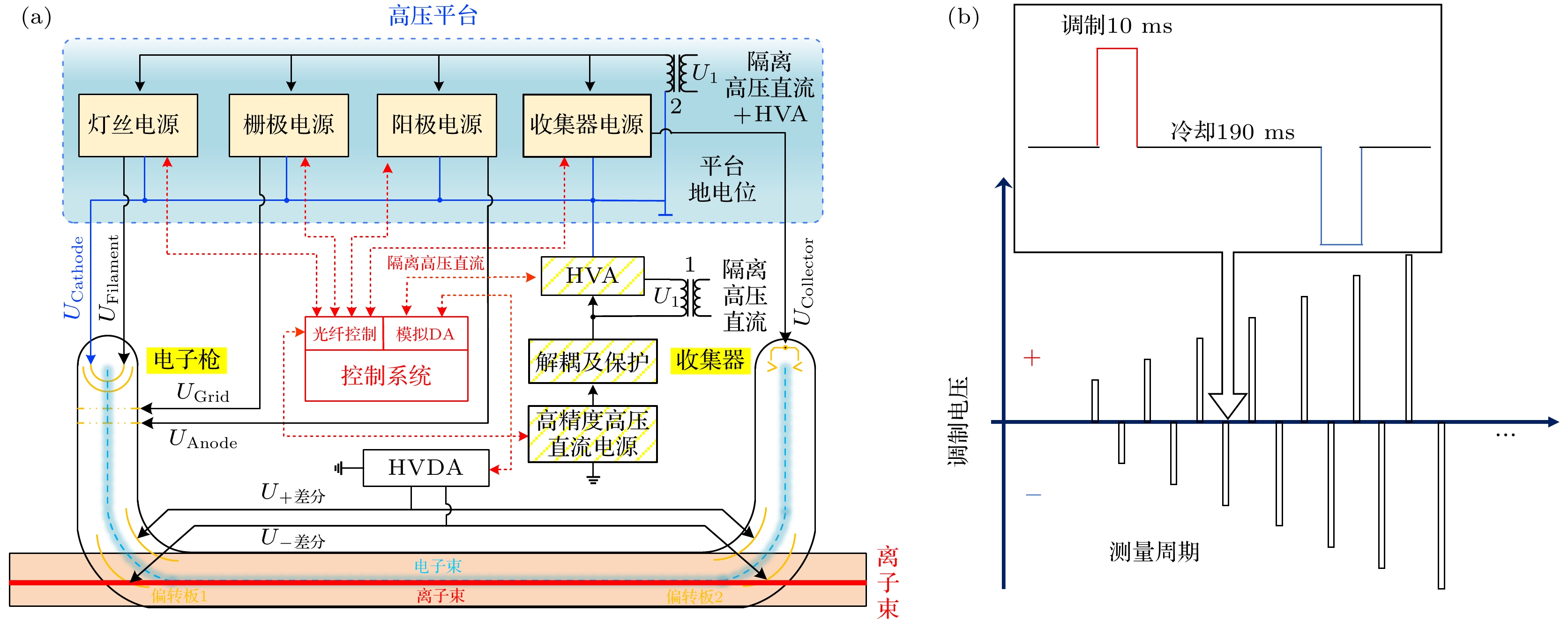
在储存环DR实验中, 通过电子束能量调制系统调节电子束能量, 可以得到非零的电子-离子碰撞能量. 为了在更高的束流能量下开展双电子复合实验, CSRe上的电子冷却器安装了最新自主研制的电子束能量调制系统, 可以输出300 kV的电压, 相对于冷却点的电子束电压调制范围为–15—15 kV, 对应质心系下的电子-离子碰撞能量调制范围为0—1 keV. 与CSRm的能量调制系统组成模块相似[24], CSRe能量调制系统中的高压电源系统由10个电压模块串联组成, 每一模块都有一个可以精确控制的电压源. 此外, 系统还附有专门的电压调制电路, 可以在500 μs内, 以总电压最大值10%的幅度快速调制电子束的能量. 在能量调制时, 考虑到高压电源系统的峰值电流为300 mA, 在每个模块内部安装了特殊的高压放大器来提供10 kW的功率, 整个调制系统可以提供100 kW的调制功率, 从而获得300 kV的高压. 10个受控模块的结构都相同, 其中电源部分由一个可以输出0—30 kV电压的接地高压模块与一个高压放大器串联而成, 高压模块与高压放大器分别由辅助电源和±6 kV的电源供电[25], 电子束能量调制系统示意图见图3(a). 需要注意的是, 在调制电压作用一定时间后, 由于电子束对于离子束的库仑冷却力会使得离子束的速度朝着调制电子束的速度偏移, 因此在能量调制10 ms后, 会让电子束维持在冷却能量190 ms以维持离子束的能量稳定, 之后再进行电子束能量调制, 实验中的能量调制时序如图3(b)所示.
-
在CSRe电子冷却器下游的腔室中安装了用于探测复合离子的闪烁体PSD探测器[26–28]和多丝正比MWPC探测器[29], 这两种探测器性能优异, 探测效率接近于100%. 在CSRe上, 探测器被放置于真空环境外的腔室中, 可以在储存环进行高温烘烤时轻易地将探测器从腔室中移出, 此外, 离子束需要经过厚度约30 μm的不锈钢窗之后才能打到探测器上, 这种设计可以过滤掉一部分杂散光和杂散离子. PSD由闪烁体、光电转换倍增器件和电子学系统三个部分构成, 在闪烁体和光电转换器之间一般配有光导用以传输闪烁光子. 当高电荷态离子入射到闪烁体时会引起闪烁体原子分子激发电离, 在退激后发出闪烁光子, 闪烁光子经过光导传输到光电转换器如光电倍增管上, 光电倍增管将闪烁光转换为电信号并放大传输到电子学系统处理.
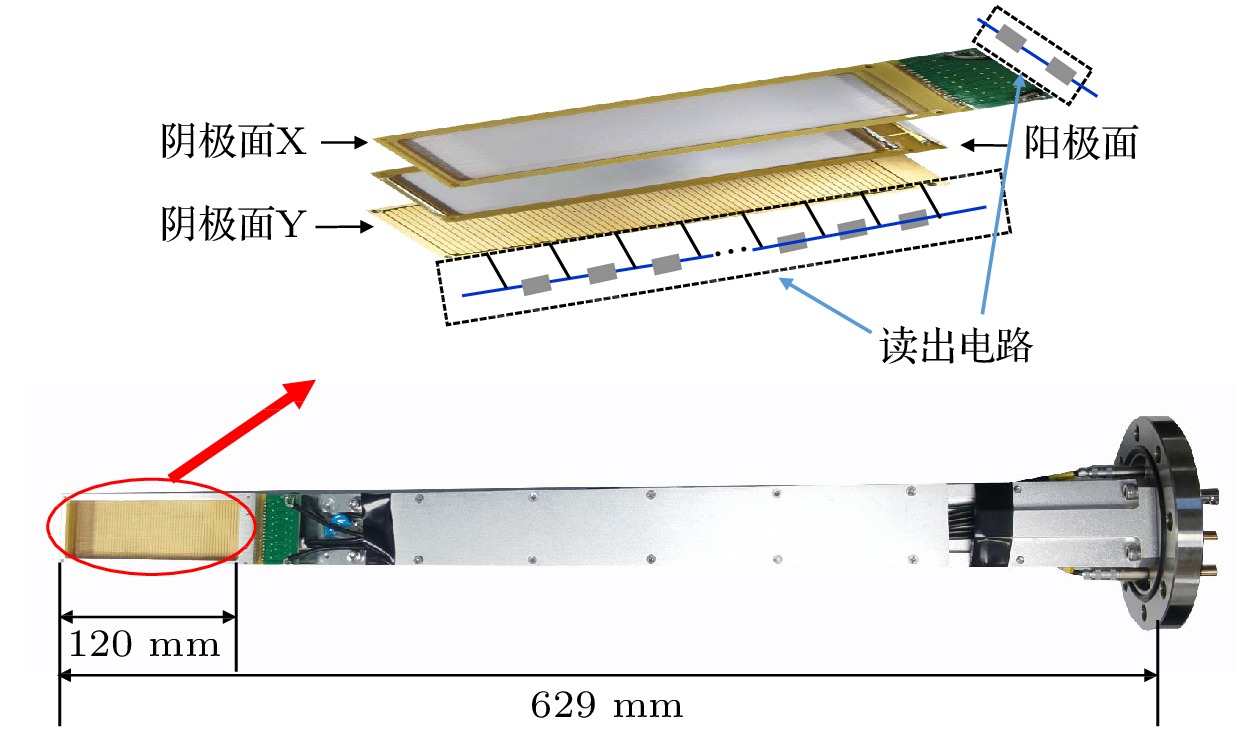
本文主要是利用MWPC探测器开展实验, 在DR实验中使用的MWPC探测器结构如图4所示, 阳极面由20根水平的、直径为20 μm的镀金钨丝组成, 彼此间距2 mm; Y层阴极面则是由80根水平的、直径为20 μm的镀金钨丝组成, 丝的间距为0.5 mm; 至于X层阴极平面, 使用了1.8 mm宽的印刷电路板取代纵向丝, 不仅解决了纵向丝固定的问题, 同时还可以将延迟读出模块嵌入背面以节省空间, 印刷电路板间隔0.2 mm, 共60条. 阳极和两个阴极平面的距离均为4 mm, 工作气体由80%的氩气和20%的二氧化碳气体混合而成, 气体流量为1.60 L/h.
MWPC的阳极信号的半高全宽约为26 ns, 经放大、甄别和电平转换后用作复合离子的计数测量, 计数率可以达到106/s, 探测效率接近100%, 具备优异的性能. 另外, MWPC的位置分辨能力可以实现实时的束流包络监测. 在阴极丝之间接入长度相同的延迟电阻, 由信号到达阴极两端的时间可以计算出离子的入射位置, 且两个阴极平面阴极丝的方向相互垂直以分别给出x方向和y方向的位置信息[30]. 在阴极面X, 阴极两端之间的距离为L, 读出电路两端输出信号的时间t1, t2, 由此, 可通过下式
求得入射离子的x坐标, 同理也可求得入射离子的y坐标.
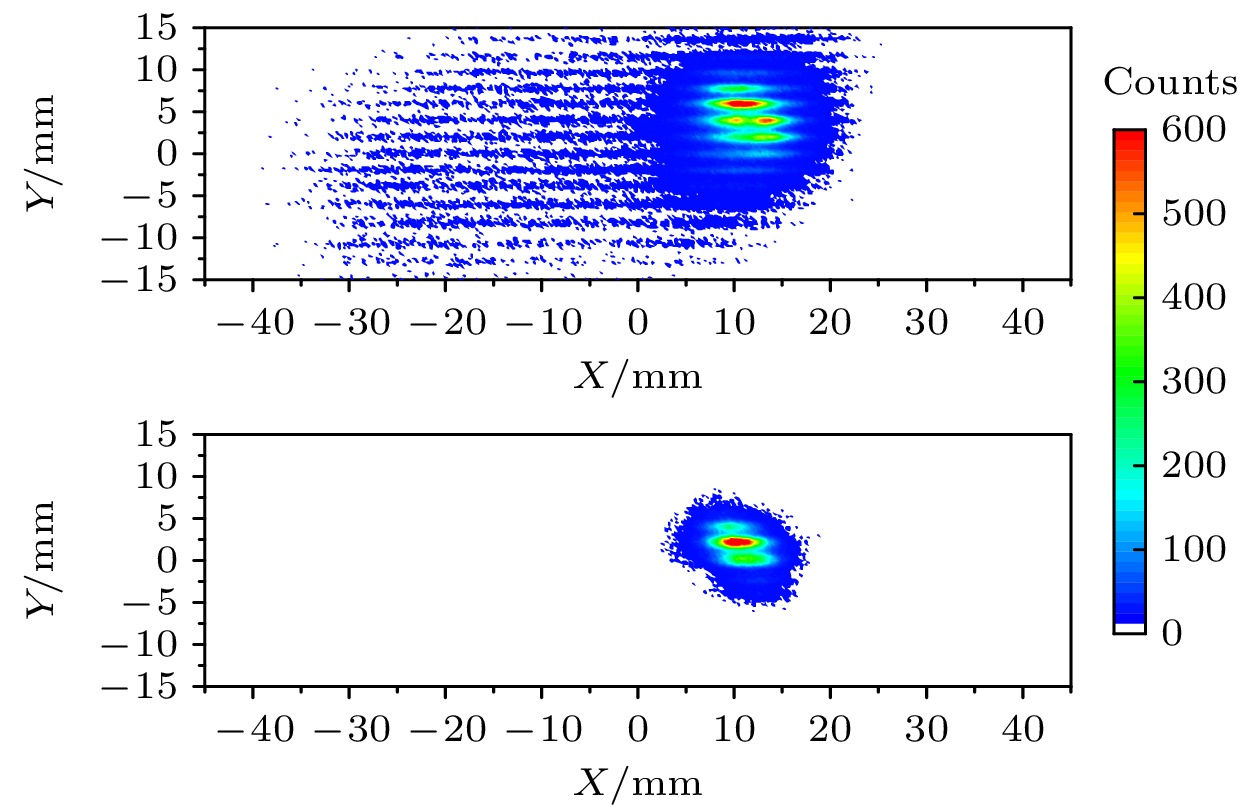
图5为MWPC探测的电子束冷却前和冷 却后的三维束流位置图, 可以清晰地看出经过电子冷却后, 离子束的包络显著缩小, 被很好地限制在MWPC的探测敏感区内, 证明了探测器的可靠性.
-
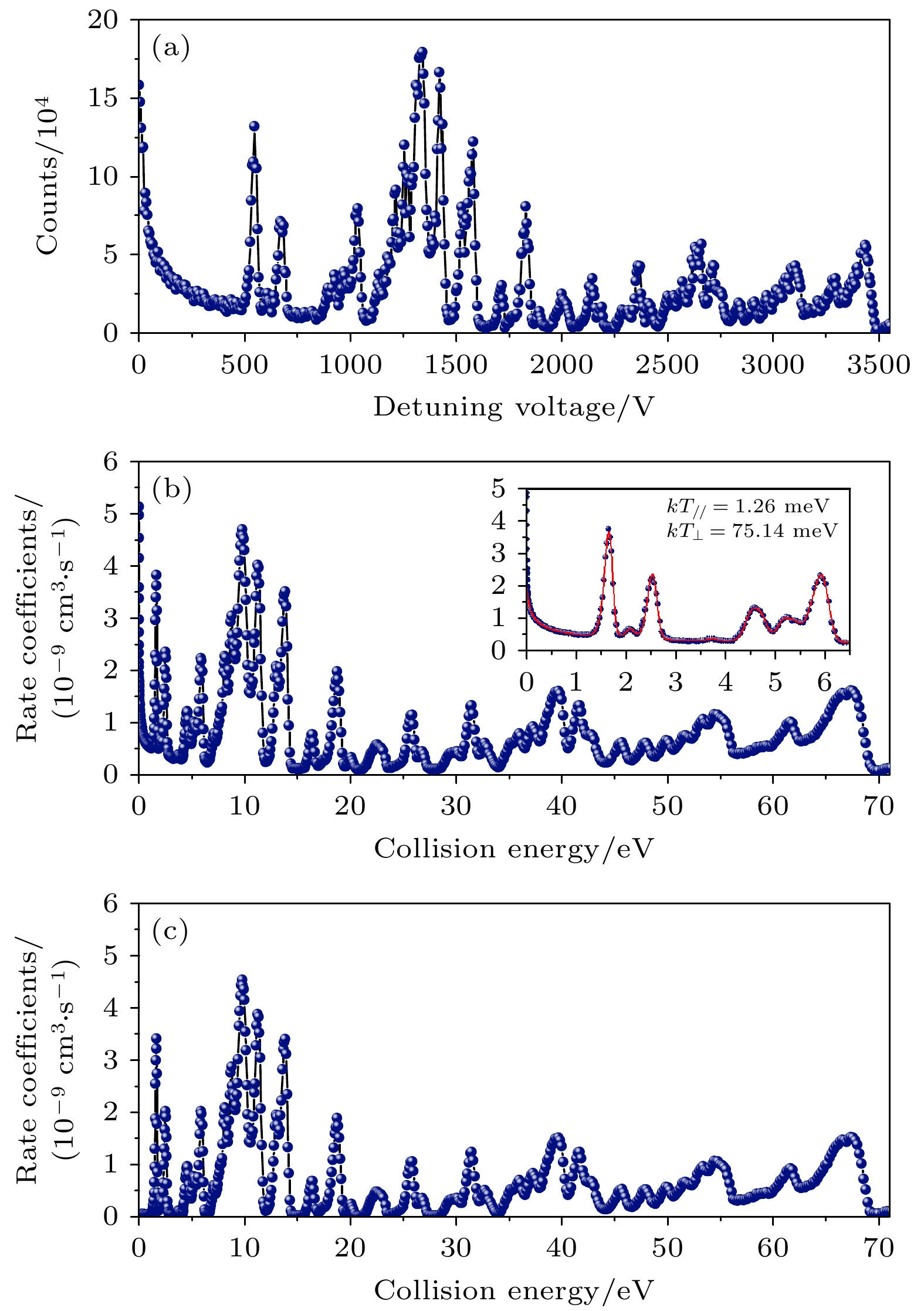
对电子束能量进行调制后, 发生复合的离子在冷却器下游经过磁场偏转被探测器探测, 最终得到电子束调制能量下的复合离子计数率谱图, 如图6(a). 在冷却阶段, 经过电子束的冷却, 离子的速度可以近似认为与冷却电子的速度相同. 当电子束处于调制阶段时, 考虑相对论效应后, 电子束与离子束在质心系下的碰撞能量可以表示为[22]
其中
$ {E}_{{\mathrm{r}}{\mathrm{e}}{\mathrm{l}}} $ 为质心系碰撞能量;$ {m}_{{\mathrm{e}}},\; {m}_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}},\;{ \beta }_{{\mathrm{e}}}, \; { \beta }_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}}, { \gamma }_{{\mathrm{e}}}, { \gamma }_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}} $ 分别为电子和离子的静质量、相对论因子和洛伦兹因子; c为真空中的光速, 且碰撞能量的计算需要考虑空间电荷势的修正[31]. 为了得到图6(b)所示的依赖于质心碰撞能量的复合速率系数谱, 还需要将实验中测得的计数率转换为复合速率系数. 在考虑相对论效应影响后, 储存环上DR实验测量的复合速率系数可以表示为其中
$ \alpha \left({E}_{{\mathrm{r}}{\mathrm{e}}{\mathrm{l}}}\right) $ 为复合速率系数; R为复合离子计数;$ {N}_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}} $ 为储存环中离子数目;$ {n}_{{\mathrm{e}}} $ 代表电子束空间密度; C = 128.8 m, L = 4.0 m分别为储存环的周长和电子离子相互作用段的长度.除了发生了DR的离子之外, 辐射复合(radiative recombination, RR)产生的复合离子同样会被下游的离子探测器探测, 在实验中, 需要去除RR和离子与残余气体碰撞的贡献才能得到绝对DR速率系数谱, 对于Kr25+离子, 辐射复合通道为
通常使用经验公式拟合RR速率系数加本底[32]:
其中
$ \alpha_i ~(i = 0, 1, 2, 3, 4) $ 为拟合所使用的拟合参数. 最终得到了纯粹的DR速率系数谱, 如图6(c)所示.由于实验分辨远大于双电子复合共振的自然线宽, 实验测量的DR峰结构由扁平的麦克斯韦电子束速度分布决定[33]. 拟合测得的低能端的复合速率系数谱, 即图6(b)碰撞能量范围0—6.5 eV的部分, 可得电子束的纵向和横向温度分别为kT// = 1.26 meV和kT⊥=75.14 meV, 图中红色曲线为拟合得到的谱线.
-
双电子复合过程的理论计算通常使用AUTOSTRUCTURE和FAC程序包, 这两种理论模型经过多年的发展已经较为成熟[15,34,35], 本文主要采用FAC理论结果与实验进行对比. FAC程序是基于全相对论组态相互作用开发的, 使用独立共振近似模型计算双电子复合过程[36,37]. DR是一个两步共振过程, 包含共振俘获过程和辐射退激过程, 其中, 如图1(a)所示的共振俘获作为自电离的逆过程, 原子单位制下的强度可以表示为[36]
其中
$ {g}_{i}, {g}_{j} $ 分别是自电离过程初态和末态的统计权重;$ {E}_{ij} $ 是共振能量;$ {A}^{a} $ 则为自电离速率. 共振俘获过程形成的双激发态离子, 由于其能量高于自电离阈, 除了发射光子形成低于电离阈的稳定状态外, 还可以通过自电离回到初态, 共振俘获DR过程的占比, 可近似写为[36]其中
$ {A}^{{\mathrm{r}}} $ 代表辐射退激速率,$ {k}' $ 代表自电离末态,$ k $ 代表低于电离阈的所有电子态,$ a $ 代表可以进一步电离的电子态. 由(8)式和(9)式得到了理论计算得到的DR截面, 将其与实验电子束的扁平麦克斯韦速度分布卷积即可得到理论计算的DR速率系数:其中包含电子束纵向温度和横向温度
$ {T}_{/ /}, {T}_{\perp } $ 的$ f\left(v, {T}_{/ /}, {T}_{\perp }\right) $ , 代表实验中的扁平麦克斯韦电子束速度分布, 电子束的横向温度与纵向温度可以通过拟合低能量段的速率系数谱得到, 如图6(b)所示. -
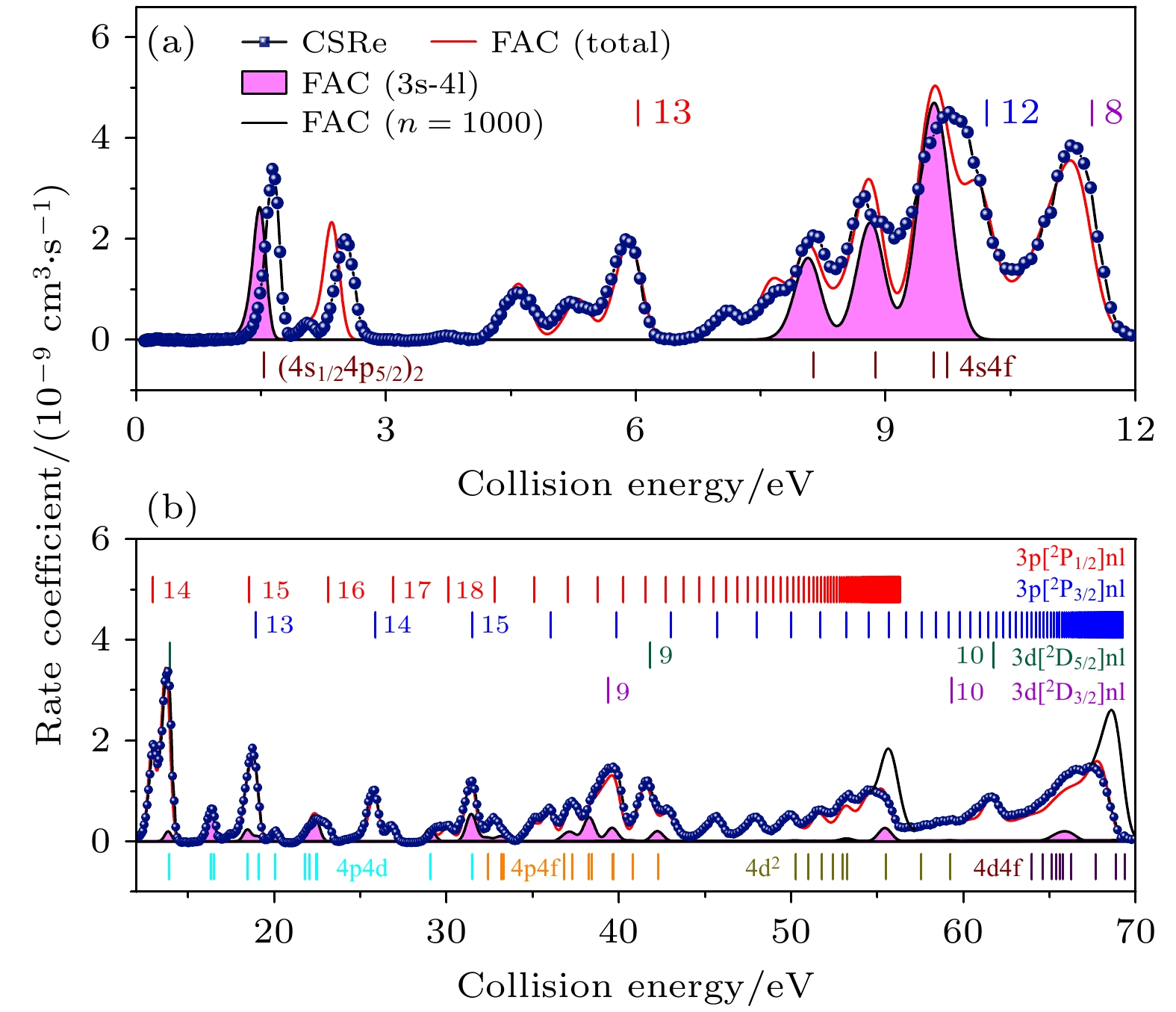
实验最终得到了如图7所示的DR速率系数谱, 对比了质心能量范围0—70 eV的FAC理论计算与实验得到的Kr25+离子的DR速率系数, 其中黑色(蓝色数据点)线为CSRe上多丝正比室探测器测得的DR速率系数, 红色实线为FAC理论计算的结果, 图中不同颜色的短竖线代表不同的里德伯系列, 竖线的横坐标代表对应的双激发态共振能量, 由里德伯公式计算得到:
其中
$ n $ 为俘获到里德伯能级的自由电子的主量子数,$ q $ 为所测离子的核电荷数,$ {R}_{y}=13.60569\;{\mathrm{e}}{\mathrm{V}} $ 为里德伯常数,$ {E}_{{\mathrm{e}}{\mathrm{x}}{\mathrm{c}}} $ 为内壳层电子的激发能. 从图7可以得出, 2p63p[2P1/2]nl与2p63p[2P3/2]nl系列共振的线系限约为56 eV和69 eV, 能级跃迁2p63s[2S1/2]→2p63d[2D3/2]与2p63p[2D5/2]的能量分别为144.340 eV与146.796 eV, 超过了图谱显示范围, 因而其线系限没有在图中得以体现. 俘获自由电子的里德伯能级的最小主量子数可以使用里德伯公式估算. DR共振2p63p[2P1/2]nl, 2p63p[2P3/2]nl, 2p63d[2D3/2]nl与2p63p[2D5/2]nl线系的最小主量子数分别为13, 12, 8, 8. 此外,$ 3{\mathrm{s}} \to 3{\mathrm{l}} ~(\Delta n= 0) $ 共振是谱线结构的主要来源, 而$ 3{\mathrm{s}}\to 4{\mathrm{l}}\;(\Delta n=1) $ 的共振也对谱线有很大的贡献. 为了能够更加细致地对比实验与理论得到的DR速率系数谱, 拟合0—35 eV范围的实验结果得到了共振能量和强度, 结果如表2所列, 其中, 混合峰的共振能量取值为各峰的共振强度加权平均值. 在3 eV之上, 实验数据与理论计算结果符合得非常好, 两组数据展示的双电子复合共振结构在共振能量上基本一致, 1.695 eV与2.573 eV两个共振峰的共振能量存在较大差别, 差值分别为0.165 eV与0.168 eV. 此外, 在其余$ \Delta n=1 $ 的共振位置处, 实验与理论的谱线差别在0.1 eV以内, 造成这些差别的原因是, 组态混合与较强的电子关联效应给$ 3{\mathrm{s}}\to 4{\mathrm{l}}~(\Delta n=1) $ 的双激发态理论计算带来很大困难[22].需要注意的是, 处于高里德伯态的双激发态离子由于其能量与电离阈能量非常接近, 在离开相互作用区域后, 会在探测器上游因横向磁场引发的运动电场而发生电离, 即发生场电离效应, 高里德伯态的截止主量子数为
$ {n}_{{\mathrm{c}}} $ . 由于发生场电离效应的复合离子电荷态和主束离子相同, 不会被复合离子探测器探测到, 最终导致实验测得的复合速率系数在线系限附近比实际情况低一些, 如图7所示, 实验结果在3p[2P1/2]与3p[2P3/2]的线系限处比理论计算即黑色直线的结果小一些. 此外, 考虑到处于双激发态的高里德伯态离子会通过辐射退激的方式退激发到末态, 而退激发之后的离子能够被探测器探测到, 所以, 离子只要满足辐射退激跃迁寿命小于其离开相互作用区到被探测器探测的间隔, 就依然会对计数产生贡献[31], 将跃迁寿命刚好等于这个间隔的主量子数标记为$ {n}_{{\mathrm{l}}{\mathrm{i}}{\mathrm{f}}{\mathrm{e}}} $ . 因此, 在对比实验与理论结果时, 需要采取$ {n}_{\boldsymbol{c}} $ 与$ {n}_{{\mathrm{l}}{\mathrm{i}}{\mathrm{f}}{\mathrm{e}}} $ 中较大的值作为理论计算的截止主量子数. 如图7所示, 在线系限处, 黑色直线为截止主量子数取1000的理论计算结果, 而红色直线为截止主量子数取100的结果. 在一般情况下, 场电离效应决定的截止主量子数较大, 由下式给出[38]:其中q为离子的电荷态,
$ {v}_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}} $ 为离子运动速度, B为磁场强度. 本次实验的截止主量子数取值100. 由于理论计算得到的线系限附近的复合速率系数比较准确, 在通过复合速率系数计算等离子体速率系数时, 可以将线系限处的实验结果, 替换为理论计算的结果, 如图7所示的黑色曲线, 从而得到准确的等离子体速率系数. -
与重离子储存环实验中各向异性的电子束速度分布不同, 在等离子体环境下, 电子的速度分布为各向同性的麦克斯韦速度分布, 与等离子体温度
$ T $ 有关. 由于实验中使用的电子束温度远小于等离子体温度, 采用以下近似得到实验测量的DR截面:将截面与电子束速度分布卷积得到有关温度的等离子体速率系数[38]:
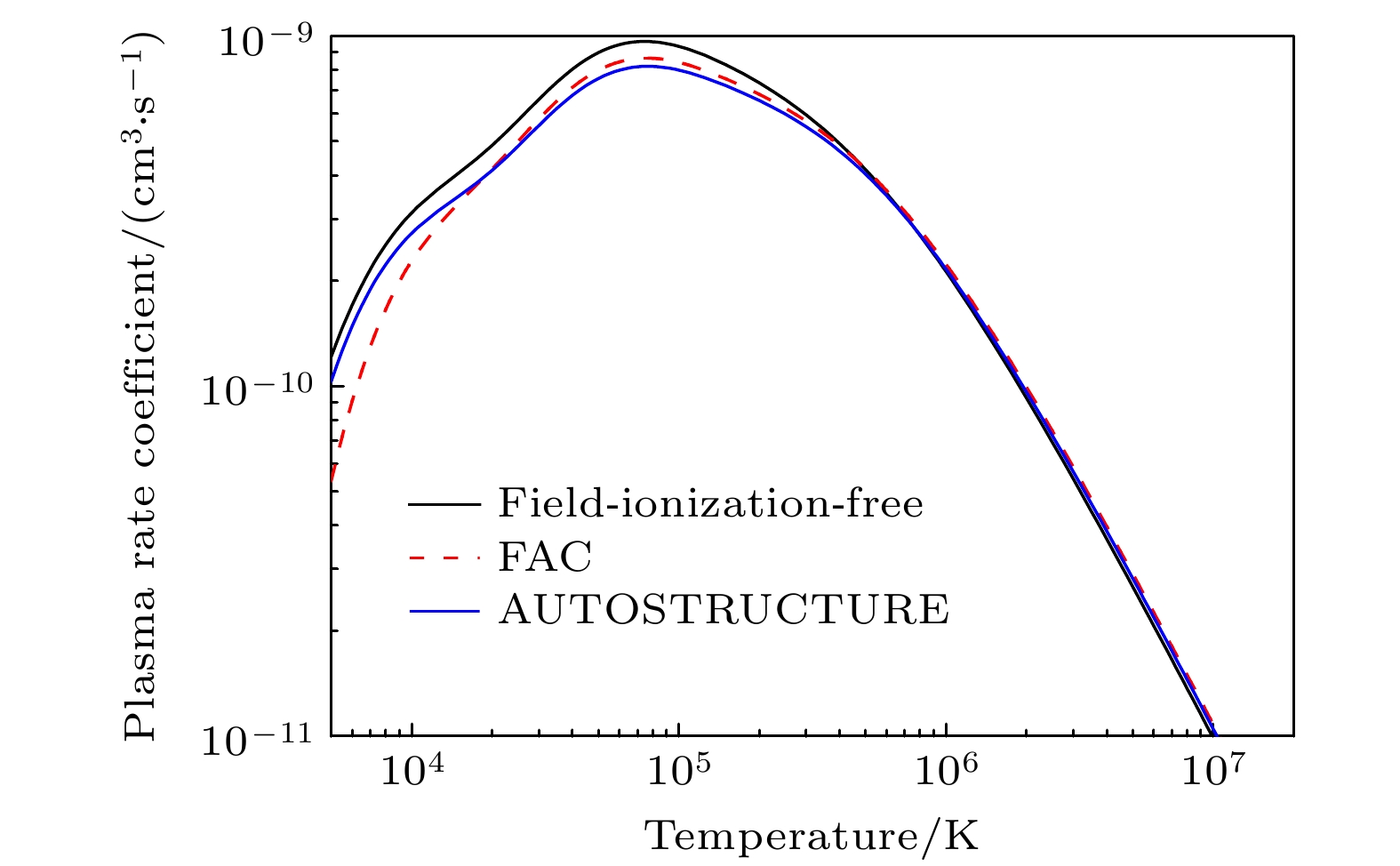
由于场电离效应的存在, 将线系限附近的实验结 果替换为FAC理论计算的结果. 如图8所示, 理论计算的结果在温度低于104 K时略低于实验导出的等离子速率系数, 主要原因是上文中提到的低能量共振位置与共振强度理论计算不准确. 我们还将AUTOSTRUCTURE程序理论、FAC理论导出的等离子体速率系数和上述方法得到的实验等离子体速率系数进行了对比, 整体符合得很好, 在温度小于106 K的区间, 相差不到20%, 在温度大于106 K小于107 K的区间, 相差不到10%.
为了方便等离子体建模, 可以使用温度相关的经验公式拟合等离子体速率系数[15,39]:
其中
$ {c}_{i} $ 与$ {E}_{i} $ 为拟合参数, 拟合的结果见表3. -
我们对兰州重离子加速器冷却储存环CSRe的电子冷却器进行了升级改造, 适于开展高电荷态离子双电子复合精密谱学实验. 更换了300 kV高压系统, 增加了电子能量快速调制系统, 该系统支持从–15 kV到+15 kV的调制高压, 比CSRm上的双电子复合实验平台提高了一个数量级. 此外, 我们自主研发并安装了塑料闪烁探测器和多丝正比探测器, 用于测量复合离子. 利用类钠Kr25+离子开展了测试实验, 测量了质心能量范围0—70 eV的DR速率系数谱, 并与FAC理论计算结果进行了对比, 发现除了
$ 3{\mathrm{s}}\to 3{\mathrm{l}}(\Delta n=0) $ 通道外,$ 3{\mathrm{s}}\to 4{\mathrm{l}} (\Delta n=1) $ 也是谱线的重要来源. 对实验获得的DR速率系数谱线进行拟合, 得到了共振能量和共振强度, 并与理论计算结果进行对比, 除了低能量处两个共振峰的共振能量有一定的偏移外, 实验结果与理论结果整体上符合得很好. 由实验测量的DR速率系数导出的等离子体速率系数与FAC和AUTOSTRUCTURE的理论计算结果符合得也很好.本次实验结果表明当前CSRe双电子复合实验平台的电子束能量调制系统和MWPC探测器的性能良好, 具有非常好的稳定性和可重复性, 为我们接下来开展高电荷态离子双电子复合精密谱学实验检验强场量子电动力学效应以及原子核性质精密测量等前沿实验提供了保障.
重离子储存环CSRe上类钠Kr25+离子的双电子复合精密谱学实验研究
Dielectronic recombination experiment of Na-like Kr25+ at heavy ion storage ring CSRe
-
摘要: 高电荷态离子的双电子复合精密谱学实验研究, 不仅对天体等离子体和聚变等离子体的研究具有重要意义, 而且可以作为一种新的精密谱学工具, 用来检验强场量子电动力学效应、测量同位素移动及提取原子核电荷半径等. 在兰州重离子储存环CSRe上, 安装了专门用于电子-离子复合精密谱学实验的电子束能量调制系统, 质心系下电子-离子碰撞能量的调制范围达到0—1 keV. 在CSRe电子冷却器下游安装了自主研制的塑料闪烁体探测器和多丝正比探测器, 用于探测复合离子. 在此基础上, 使用Kr25+离子在CSRe上进行了首次双电子复合测试实验, 实验测量了质心系能量0—70 eV的双电子复合速率系数. 为了更好地理解实验测量结果, 利用FAC (flexible atomic code)程序计算了Kr25+离子的双电子复合速率系数, 并与实验做了细致对比, 整体符合很好, 而且发现
$ 3{\mathrm{s}}\to 4{\mathrm{l}} \;(\Delta n=1) $ 的共振跃迁对实验谱线有很大的贡献. 实验结果表明, CSRe双电子复合实验平台具有非常好的稳定性和可重复性, 能够为下一步开展更高电荷态离子的双电子复合精密谱学实验、检验强场量子电动力学效应以及原子核性质精密测量等前沿实验提供支持.Abstract: The experimental study of precision spectroscopy of dielectronic recombination (DR) of highly charged ions is not only important for astronomical plasma and fusion plasma, but also can be used as a new precision spectroscopy to test the strong-field quantum electrodynamic effect, measure isotope shift, and extract the radius of atomic nuclei. An specially designed electron beam energy detuning system for electron-ion recombination precision spectroscopy experiments has been installed on the heavy ion storage ring CSRe in Lanzhou, China, where the electron-ion collision energy in the center-of-mass system can be detuned to 1 keV, and an independently-developed plastic scintillator detector and multiwire proportional chamber detector have been installed downstream of the electron cooler of the CSRe for detecting recombined ions. The multiwire proportional chamber detector has the ability to non-destructively monitor the profile of the ion beam in real-time while acquiring the recombined ion counts, providing guidance for optimizing the ion beam. On this basis, the first test experiment on dielectronic recombination of Kr25+ ions is carried out at the CSRe, and the dielectronic recombination rate coefficients in a range of 0–70 eV in the frame of center-of-mass are measured. In order to fully understand the experimental results, we calculate the dielectronic recombination rate coefficient of the Kr25+ ion by using the flexible atomic code (FAC) and make a detailed comparison with the experimental result, showing that they are in good agreement with each other, and only the resonance energy values of the two resonance peaks at 1.695 eV and 2.573 eV are significantly different. In addition, the DR resonance energy values and intensities are obtained by fitting the experimental results in a range of 0–35 eV, and we find that the transition 3s→4l (∆n = 1) contributes significantly to the experimental spectral lines. Furthermore, we compare the plasma rate coefficients derived from the DR rate coefficients with those derived from the AUTOSTRUCTURE and FAC theories, which differ by 20 percent in a temperature range less than 106 K. The experimental results show that the DR experimental platform of the CSRe has very good stability and reproducibility, and can provide support for the future DR experiments of highly charged ion, i.e. for testing strong-field quantum electrodynamics effect and measuring the properties of atomic nuclei. -
-
图 1
$ {Z}^{q+} $ 离子的双电子复合过程示意 (a) 第一步共振过程, 离子在俘获一个自由电子的同时将一个内壳层电子激发, 从而形成自电离态$ {{[Z}^{(q-1)+}]}^{{\mathrm{*}}{\mathrm{*}}} $ ; (b) 第二步过程, 自电离态离子通过辐射光子从而退激发到稳定态Figure 1. Schematic of DR of
$ {Z}^{q+} $ ions: (a) The first resonance step, in which the ion captures a free electron and simultaneously excites an inner shell electron, resulting in the formation of the autoionized state$ {{[Z}^{(q-1)+}]}^{{\mathrm{*}}{\mathrm{*}}} $ ; (b) the second step, in which the ion is deexcited to the stable state by radiative decay.
图 2 储存环CSRm与CSRe上的双电子复合实验平台示意图
Figure 2. Schematic view of the DR experimental platforms at the storage ring CSRm and CSRe.
图 3 (a) CSRe上的高压电源调制系统示意图; (b) 电子束能量调制时序图, 插图为放大后的一个周期内的调制电压变化图
Figure 3. (a) Schematic diagram of the high voltage power supply modulation system of the CSRe; (b) the timing sequence of electron beam detuning voltage which is used in the DR experiment of Kr25+.
图 4 储存环CSRe上的多丝正比探测器实物图, 黑色虚线方框内为延迟读出电路
Figure 4. Physical view of the MWPC detector, the black dashed box shows the delayed read-out circuitry.
图 5 多丝正比探测器实时探测到的冷却前后的离子束包络分布图
Figure 5. Experimentally measured beam profiles before and after electron-cooling by the MWPC detector.
图 6 (a) 复合离子探测器探测的复合离子计数-电子束调制能量谱; (b) 总的复合速率系数-质心系碰撞能量谱, 插图中的红色曲线为拟合结果, 拟合得到了电子束的横向温度与纵向温度; (c) 减去背景与RR的贡献后得到的绝对DR速率系数-碰撞能量谱
Figure 6. (a) Counts of recombined ions detected by the ion detector as a function of the electron beam detuning voltage; (b) total recombined rate coefficient at the center-of-mass collision energy; (c) the absolute DR rate coefficient by subtracting the contributions of the background and RR. In addition, the red curve in the inset of panel (b) is the fitting results.
图 7 蓝色点线和红色实线分别为CSRe测量的Kr25+离子双电子复合速率与FAC计算的理论结果, 阴影部分为
$ \Delta n=1 $ 的部分. 竖线为基于里德伯公式估算的双电子复合共振位置Figure 7. Experimental (dotted blue line) and theoretical (red solid line) dielectronic recombination rate coefficients of the Na-like Kr25+ ions. The shaded part is the part with
$ \Delta n=1 $ core excitation.
图 8 Kr25+离子的实验(黑色实线)与FAC(红色虚线)及AUTOSTRUCTURE[22](蓝色实线)理论导出的等离子体速率系数谱对比
Figure 8. Comparision of plasma rate coefficients of sodium-like Kr25+ ions between experimental results (black solid line) and calculations by FAC (red dashed line) and AUTOSTRUCTURE (blue line) code.
表 1 CSRe上Kr25+离子双电子复合实验参数
Table 1. Parameters of the DR experiment of Kr25+ at CSRe.
实验参数 实验装置(CSRe) 储存环周长/m 128.8 相互作用长度/m 4.0 离子束能量/(MeV·u–1) 80 离子束流强/μA 300—450 电子束流强/mA 287.5 电子束半径/cm 2.60 横向电子温度/meV 75.14 纵向电子温度/meV 1.26 冷却段磁场强度/G 390 枪区磁场强度/G 1250 
下载: 导出CSV
表 2 实验测量拟合结果与理论计算结果对比
Table 2. Comparison of experimental measurement fitting results with theoretical calculations.
双激发态组态 共振能量/eV 共振强度/(10–19 eV·cm2) FAC 实验 FAC 实验 4s[2S1/2]4d5/2 (J = 2) 1.530 1.695±0.001 75.2 93.8±0.6 3d[2D3/2]8s (J = 1) 2.090 2.119±0.009 7.1 8.4±0.6 3d[2D3/2]8s (J = 2) 2.405 2.573±0.001 62.2 56.1±0.6 3p[2P1/2]13s 3.869 3.804±0.049 1.5 1.9±0.6 3d[2D5/2]8s (J = 3) 4.530 7.3 3p[2P1/2]13p1/2 4.565a 4.4 Blend 4.543a 4.561±0.012 11.7 17.4±1.2 3d[2D3/2]8p1/2 (J = 2) 4.660 6.4 3d[2D5/2]8s (J = 2) 4.690 11.0 3d[2D3/2]8p1/2 (J = 1) 4.754 3.9 Blend 4.693a 4.789±0.013 21.2 15.8±1.2 3d[2D3/2]8p3/2 5.338 5.216±0.021 14.8 13.8±1.7 3p[2P1/2]13d 5.384a 5.448±0.032 7.2 11.5±1.4 3p[2P1/2]13f 5.838a 5.747±0.029 12.4 13.9±1.5 3p[2P1/2]13l (l ≥ g) 6.003a 6.000±0.006 40.4 44.7±1.9 3d[2D5/2]8p1/2 (J = 2, 3) 7.129a 7.154±0.022 14.6 12.5±1.3 3p[2P3/2]12s (J = 1, 2) 7.465a 7.494±0.095 2.0 6.8±2.3 3d[2D5/2]8p3/2 (J = 2, 3, 4) 7.705a 7.767±0.034 26.8 18.6±2.2 4s[2S1/2]4f5/2 (J = 2) 8.129 8.161±0.028 37.9 39.2±5.2 3d[2D5/2]8p3/2 (J = 1) 8.063 2.3 3p[2P3/2]12p1/2 8.245 2.2 3p[2P3/2]12p3/2 (J = 1, 2, 3) 8.404a 3.8 3d[2D3/2]8d3/2 8.596 12.7 Blend 8.466a 8.391±0.045 21.0 20.1±5.2 4s[2S1/2]4f5/2(J = 3) 8.880 8.790±0.010 53.9 58.2±1.3 3d[2D3/2]8d5/2 8.813a 21.1 3p[2P3/2]12d 9.404a 8.9 Blend 8.988a 9.143±0.014 30.0 41.2±1.3 4s[2S1/2]4f5/2 (J = 4) 9.577 9.546±0.018 65.7 60.6±4.0 4s[2S1/2]4f5/2 (J = 3) 9.737 9.842±0.023 55.8 75.1±3.2 3p[2P3/2]12l (l ≥ f ) 10.139a 10.138±0.020 77.5 67.0±3.8 3d[2D3/2]8f 10.721a 10.694±0.041 39.8 51.9±2.0 3d[2D5/2]8d 11.227a 11.224±0.023 33.1 58.3±2.8 3d[2D3/2]8l (l ≥ g ) 11.313a 11.504±0.009 70.7 60.3±4.5 3p[2P1/2]14d 12.443a 12.732±0.044 3.5 10.1±1.7 3p[2P1/2]14l (l ≥ f ) 12.907a 13.101±0.013 19.4 41.0±1.4 3d[2D5/2]8f 13.276a 13.616±0.018 25.4 39.2±1.8 3d[2D5/2]8l (l ≥ g) 13.770a 13.964±0.006 83.4 67.5±2.2 4p[2P1/2]4d5/2 (J = 3) 16.337 12.3 4p[2P1/2]4d5/2 (J = 2) 16.500 4.0 Blend 16.377a 16.482±0.013 16.3 14.1±1.0 3p[2P3/2]13p 17.491a 17.36±0.14 2.4 2.0±1.0 3p[2P1/2]15p 17.601a 17.74±0.12 0.8 3.0±0.8 Blend 17.517a 17.579±0.036 3.2 3.3±0.3 3p[2P1/2]15d 18.131a 1.4 3p[2P3/2]13d 18.313a 3.6 Blend 18.262a 18.226±0.057 5.1 7.2±1.4 4p[2P1/2]4d5/2 (J = 1) 18.466 5.2 3p[2P1/2]15l (l ≥ f) 18.533a 8.8 Blend 18.508a 18.609±0.031 14.0 21.6±1.0 3p[2P3/2]13l (l ≥ f) 18.930a 18.976±0.008 25.5 32.2±1.6 4p[2P3/2]4d5/2 (J = 2) 20.038 20.162±0.022 5.1 4.2±0.3 4p[2P3/2]4d5/2 (J = 0) 21.802 1.7 4p[2P3/2]4d5/2 (J = 1) 22.054 4.2 Blend 21.984a 22.086±0.025 5.9 5.1±0.3 4p[2P3/2]4d5/2 (J = 3) 22.444 4.3 4p[2P3/2]4d5/2 (J = 2) 22.502 5.4 Blend 22.476a 22.614±0.020 9.7 8.7±0.3 3p[2P1/2]16l 23.005a 23.164±0.018 9.5 7.3±0.3 3p[2P3/2]14p 24.715a 1.4 3p[2P3/2]14d 25.371a 2.2 Blend 25.111a 25.480±0.052 3.6 7.1±1.0 3p[2P3/2]14l (l ≥ f) 25.865a 25.941±0.013 20.7 21.2±1.0 3p[2P1/2]17l 26.821a 26.917±0.022 7.2 7.0±0.4 3p[2P1/2]18l 30.020a 30.277±0.024 6.1 6.8±0.3 3p[2P3/2]15l 31.348a 31.695±0.011 16.4 22.6±0.9 4p[2P1/2]4f5/2 (J = 3) 32.424 1.6 3p[2P1/2]19l 32.739a 7.5 Blend 32.683a 32.804±0.028 9.2 9.5±0.5 a Weighted energy: $ {E}_{{\mathrm{d}}}= {\displaystyle\sum {E}_{{\mathrm{d}}}{S}_{{\mathrm{d}}}}\Big/{\displaystyle\sum {S}_{{\mathrm{d}}}} $ 
下载: 导出CSV
表 3 实验与FAC理论计算得到的复合速率系数导出的等离子体速率系数拟合参数, ci与Ei的单位分别为cm3·s–1与eV, 括号内的数字为10的幂
Table 3. Fitted coefficients for the plasma rate coefficients of DR experiment and FAC, the ci are in units of cm3·s–1, and the Ei are in eV. The numbers in the square brackets are power of 10.
i 实验 FAC ci Ei ci Ei 1 1.01[–1] 37.1 4.65[–2] 24.7 2 2.28[–1] 63.9 2.07[–1] 53.4 3 1.95[–3] 1.74 7.35[–2] 92.9 4 3.30[–2] 121 1.05[–2] 6.15 5 3.99[–2] 15.5 8.90[–4] 1.42 6 4.34[–2] 9.07 1.57[–3] 2.36 7 3.88[–3] 4.17 5.37[–2] 5.37
下载: 导出CSV
-
[1] Gillaspy J D 2001 J. Phys. B: At. Mol. Opt. Phys. 34 R93 doi: 10.1088/0953-4075/34/19/201 [2] Kozlov M, Safronova M, López-Urrutia J C, Schmidt P 2018 Rev. Mod. Phys. 90 045005 doi: 10.1103/RevModPhys.90.045005 [3] Lindroth E, Danared H, Glans P, Pešić Z, Tokman M, Vikor G, Schuch R 2001 Phys. Rev. Lett. 86 5027 doi: 10.1103/PhysRevLett.86.5027 [4] Brandau C, Kozhuharov C, Müller A, et al. 2003 Phys. Rev. Lett. 91 073202 doi: 10.1103/PhysRevLett.91.073202 [5] Schuch R, Lindroth E, Madzunkov S, Fogle M, Mohamed T, Indelicato P 2005 Phys. Rev. Lett. 95 183003 doi: 10.1103/PhysRevLett.95.183003 [6] Brandau C, Kozhuharov C, Harman Z A, et al. 2008 Phys. Rev. Lett. 100 073201 doi: 10.1103/PhysRevLett.100.073201 [7] 啜晓亚, 黄忠魁, 汶伟强, 等 2018 原子核物理评论 35 196 doi: 10.11804/NuclPhysRev.35.02.196 Chuai X Y, Huang Z K, Wen W Q, et al. 2018 Nucl. Phys. Rev. 35 196 doi: 10.11804/NuclPhysRev.35.02.196 [8] Kieslich S, Schippers S, Shi W, et al. 2004 Phys. Rev. A 70 042714 doi: 10.1103/PhysRevA.70.042714 [9] Budker G, Kiselev A, Konkov N, Naumov A, Niffontov V, Ostreiko G, Petrov V, Yudin L, Yasnov G 1965 V International Conference on High Energy Accelerators Proceedings Frascati, September 9–16, 1965 p455 [10] Poth H 1990 Phys. Rep. 196 135 doi: 10.1016/0370-1573(90)90040-9 [11] Mitchell J, Ng C, Forand J, Levac D, Mitchell R, Sen A, Miko D, McGowan J W 1983 Phys. Rev. Lett. 50 335 doi: 10.1103/PhysRevLett.50.335 [12] Dittner P, Datz S, Miller P, et al. 1983 Phys. Rev. Lett. 51 31 doi: 10.1103/PhysRevLett.51.31 [13] Müller A 2008 Advances In Atomic, Molecular, and Optical Physics (Academic Press) pp293–417 [14] Schippers S 2015 Nucl. Instrum. Methods Phys. Res. , Sect. B 350 61 doi: 10.1016/j.nimb.2014.12.050 [15] Huang Z K, Wen W Q, Xu X, et al. 2018 Astrophys. J. Suppl. Ser. 235 2 doi: 10.3847/1538-4365/aaa5b3 [16] Khan N, Huang Z K, Wen W Q, Mahmood S, et al. 2018 Chin. Phys. C 42 064001 doi: 10.1088/1674-1137/42/6/064001 [17] Wang S X, Xu X, Huang Z K, et al. 2018 Astrophys. J. 862 134 doi: 10.3847/1538-4357/aacc69 [18] Wang S X, Huang Z K, Wen W Q, et al. 2019 Astron. Astrophys. 627 171 doi: 10.1051/0004-6361/201935648 [19] Huang Z K, Wang S X, Wen W Q, et al. 2020 X-Ray Spectrom. 49 155 doi: 10.1002/xrs.3077 [20] Wen W Q, Huang Z K, Wang S X, et al. 2020 Astrophys. J. 905 36 doi: 10.3847/1538-4357/abc1e4 [21] Khan N, Huang Z K, Wen W Q, et al. 2022 J. Phys. B: At. Mol. Opt. Phys. 55 035001 doi: 10.1088/1361-6455/ac4cce [22] Huang Z K, Wen W Q, Wang S X, et al. 2020 Phys. Rev. A 102 062823 doi: 10.1103/PhysRevA.102.062823 [23] Shevelko V P, Stöhlker T, Tawara H, Tolstikhina I Y, Weber G 2010 Nucl. Instrum. Methods Phys. Res., Sect. B 268 2611 doi: 10.1016/j.nimb.2010.06.019 [24] Yan K, Zhou Y, Ma X, Tang M, Gao D, Zhao H, Huang Z, Wen W, Mao L 2023 Nucl. Instrum. Methods Phys. Res. , Sect. A 1046 167699 doi: 10.1016/j.nima.2022.167699 [25] Skorobogatov D, Bryzgunov M, Kondaurov M, Putmakov A, Reva V, Repkov V 2019 Proceedings of the 12th Workshop on Beam Cooling and Related Topics Novosibirsk, Russia, September 24–27, 2019 pp86–88 [26] Menz E B, Hahn C, Pfäfflein P, Weber G, Stöhlker T 2020 J. Phys. Conf. Ser. 1412 232006 doi: 10.1088/1742-6596/1412/23/232006 [27] Westman S, Kerek A, Klamra W, Norlin L O, Novak D 2002 Nucl. Instrum. Methods Phys. Res., Sect. A 481 655 doi: 10.1016/S0168-9002(01)01415-2 [28] Miersch G, Habs D, Kenntner J, Schwalm D, Wolf A 1996 Nucl. Instrum. Methods Phys. Res., Sect. A 369 277 doi: 10.1016/0168-9002(95)00785-7 [29] Klepper O, Kozhuharov C 2003 Nucl. Instrum. Methods Phys. Res., Sect. B 204 553 doi: 10.1016/S0168-583X(02)02131-6 [30] Ye Y L, Di Z Y, Li Z H, Wang Q J, Zheng T, Chen T, Jiang D X, Ge Y C, Pang D Y, Li X Q 2003 Nucl. Instrum. Methods Phys. Res., Sect. A 515 718 doi: 10.1016/j.nima.2003.08.113 [31] Kilgus G, Habs D, Schwalm D, Wolf A, Badnell N R, Muller A 1992 Phys. Rev. A 46 5730 doi: 10.1103/PhysRevA.46.5730 [32] Schippers S, Bartsch T, Brandau C, Müller A, Gwinner G, Wissler G, Beutelspacher M, Grieser M, Wolf A, Phaneuf R A 2000 Phys. Rev. A 62 022708 doi: 10.1103/PhysRevA.62.022708 [33] Danared H 1995 Phys. Scr. 59 121 doi: 10.1088/0031-8949/1995/T59/014 [34] Badnell N R 2011 Comput. Phys. Commun. 182 1528 doi: 10.1016/j.cpc.2011.03.023 [35] Badnell N 2006 Astrophys. J. 651 L73 doi: 10.1086/509739 [36] Gu M F 2008 Can. J. Phys. 86 675 doi: 10.1139/p07-197 [37] Gu M F 2003 Astrophys. J. 590 1131 doi: 10.1086/375135 [38] Schippers S, Müller A, Gwinner G, Linkemann J, Saghiri A, Wolf A 2001 Astrophys. J. 555 1027 doi: 10.1086/321512 [39] Schippers S, Schnell M, Brandau C, Kieslich S, Müller A, Wolf A 2004 Astron. Astrophys. 421 1185 doi: 10.1051/0004-6361:20040380 -
计量
- 文章访问数: 276
- HTML全文浏览数: 276
- PDF下载数: 3
- 施引文献: 0