-
现实世界可被视为一个高度复杂的巨系统, 由各种不同类型的子系统构成, 包括社会系统[1,2]、生物系统[3,4]、电力系统[5,6]和交通系统[7,8]等. 为了全面深入地理解这些复杂系统, 网络科学应运而生[9-11]. 网络科学的主要研究目的是找出这些复杂系统的共性, 定量和定性地刻画它们所具有的普适性规律, 从而为理解和研究复杂系统提供理论基础和实证应用途径[12-14]. 为实现这一目的, 将复杂系统抽象成复杂网络通常是研究的第一步, 也是后续研究网络结构和动力学的基础.
传统的复杂网络通常将系统中的主体抽象为节点, 主体之间的成对作用关系抽象为连边. 然而, 对部分复杂系统而言, 只利用这种成对作用关系进行建模并不合理. 例如, 一篇论文经常由多名科学家共同合作完成[15,16], 完成一次新陈代谢需要多个反应物的参与[17], 一个社交群组往往包含多个成员间的互动[18,19]. 在这些情况下, 描述节点之间的作用关系需要超越成对关系, 建立具有高阶相互作用关系的网络模型, 即高阶网络[20-23].
相较于成对交互作用网络, 高阶网络不仅能更加精确地描述复杂系统的结构, 而且可揭示系统中的一些新型动力学现象[24-30]. 例如, 在同步动力学领域, 传统网络中的爆炸相变现象只在满足严格条件时才会发生[21,31], 而在高阶网络中这种现象却能自发出现; 即使存在负耦合的情况下, 高阶相互作用仍能有效地维持系统的同步, 并且在系统中形成与网络结构有关的集群[32]; 此外, 高阶相互作用还有助于产生多稳态[32,33]、嵌合状态[34,35]以及混沌动态[32,33,36]. 在传播动力学领域, 传播过程可以在网络的高阶结构上发生, 个体不但会受到其最临近邻居的影响, 还会受到它所参与的高阶交互关系对它的作用, 并且高阶传播还具有非连续相变的特性[28,37-40].
网络结构是研究复杂网络的基础, 结合统计量有利于定量化描述网络的结构特征. 利用网络结构特征, 可以衡量不同网络结构对动力学的影响, 还可进行图分类[41]、重要节点挖掘[42-44]、链路预测[45-47]、社团检测[48,49]等信息挖掘任务; 通过挖掘一些有共性的结构特征, 也可以建立基于通用统计特性的模型网络[50-53]. 然而, 由于高阶网络的结构复杂, 其统计指标也相对复杂, 同一类型的统计指标往往还存在多种定义. 因此, 刻画高阶网络的结构特征具有一定挑战性. 现有高阶网络研究主要集中于度相关的指标、聚集系数、节点之间的距离、中心性指标、熵和与代数拓扑相关的一系列指标. 这些指标既有从成对交互网络统计指标中拓展出来的, 也有高阶网络的特有指标. 本文首先介绍了两种最常见的高阶网络——超图和单纯形网络的基本定义, 然后综述了这两类高阶网络中常用的统计指标及其物理意义, 最后对于高阶网络统计指标的使用场景进行了总结和展望.
-
高阶网络考虑了两个及以上节点之间的高阶关系, 能够更全面地捕捉节点之间的复杂关联和多元交互关系. 高阶网络的两种主要表示形式为超图(hypergraph)和单纯形网络(simplicial network)[20,54].
-
相比于成对交互作用网络, 超图可以表示点边之间的多元关联关系. 超图可以定义为
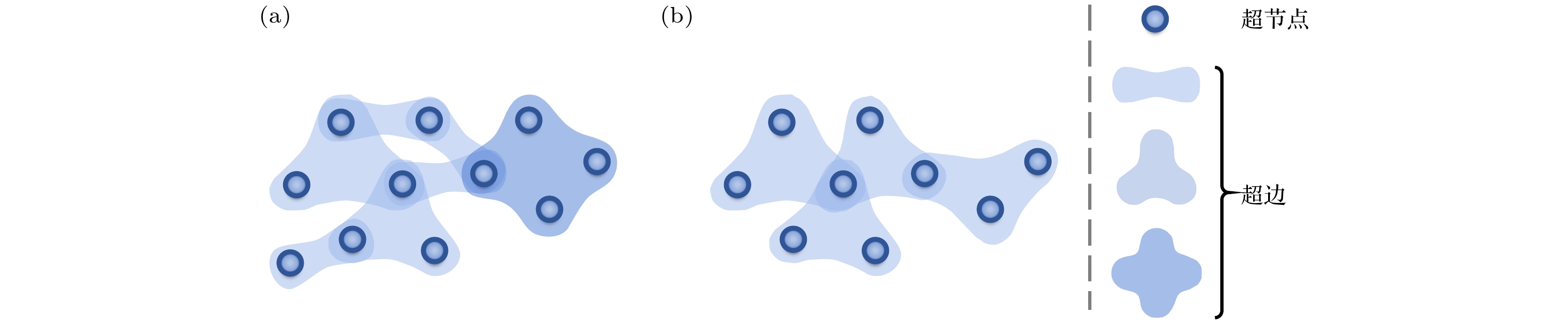
$ {\cal{H}} = (V, E) $ , 其中V为节点集, 每个节点被称为超节点(hypervertex); E为边集, 每条超边(hyperedge)$ e \in E $ 由它所连接的节点组成, 是节点集V的一个子集, 即$ e \subseteq V $ , 并且一条超边可以由任意数量的节点组成. 使用超图表示高阶网络不受闭包特性的限制, 例如, 超图$ {\cal{H}} $ 的一条超边e,$ e^{\prime} $ 是e的子集,$ e^{\prime} $ 不一定是超图$ {\cal{H}} $ 的超边. 如果一个超图中的每条边都恰好包含d个节点, 则称此超图为d-均匀超图(d-uniform hypergraph), 表示为$d{\text{-}} {\cal{H}} $ . 图1是两类超图的简单示例: 图1(a)是一个普通超图, 其中包含了11个超节点和7条超边; 图1(b)是一个3-均匀超图, 包含9个节点和4条超边, 并且每条超边中都包含3个超节点.目前, 超图的研究已经渗透到多个学科领域, 包括数据挖掘[55]、社交网络分析[56]、生物信息学[57]和通信网络[58]等. 在处理多元关系数据时, 超图展现出了其在表示复杂关系和高阶交互方面的优势. 一些研究突破包括新型超图模型的开发, 旨在更准确地捕捉实际系统的结构特征, 并且基于超图的算法已被应用于社区发现[59]、节点分类[60]和网络演化分析[61]等任务. 此外, 超图的研究还涉及到高阶图神经网络的发展, 这是融合了超图理论和深度学习的前沿方向, 其目标是提高数据的表示能力和预测精度[62].
-
单纯形网络是另一种常用的高阶网络表示方式, 它基于代数拓扑的单纯复形(simplicial complex)思想, 用单纯形(simplex)来表示高阶网络中的节点交互关系. 因此, 单纯形网络也可被认为是一个由若干个单纯形组成的单纯复形, 其维度是其中最高阶单纯形的阶数. 一个k阶单纯形由
$ k+1 $ 个节点组成, 例如节点为0阶单纯形, 边为1阶单纯形, 三角形为2阶单纯形, 四面体为3阶单纯形. 相比于超图, 单纯形网络有更严格的数学定义, 每个单纯形都要满足闭包性, 即一个k阶单纯形不仅包含k 阶交互关系, 还包含组成该单纯形的$ k+1 $ 个节点所能组成的所有低阶单纯形. 单纯形网络的构建方式主要有两种, 一种是将高阶交互数据构建为单纯形, 另一种是将传统成对交互作用网络中的团(clique, k阶团为$ k+1 $ 个节点组成的全连通子图)结构抽象为单纯形. -
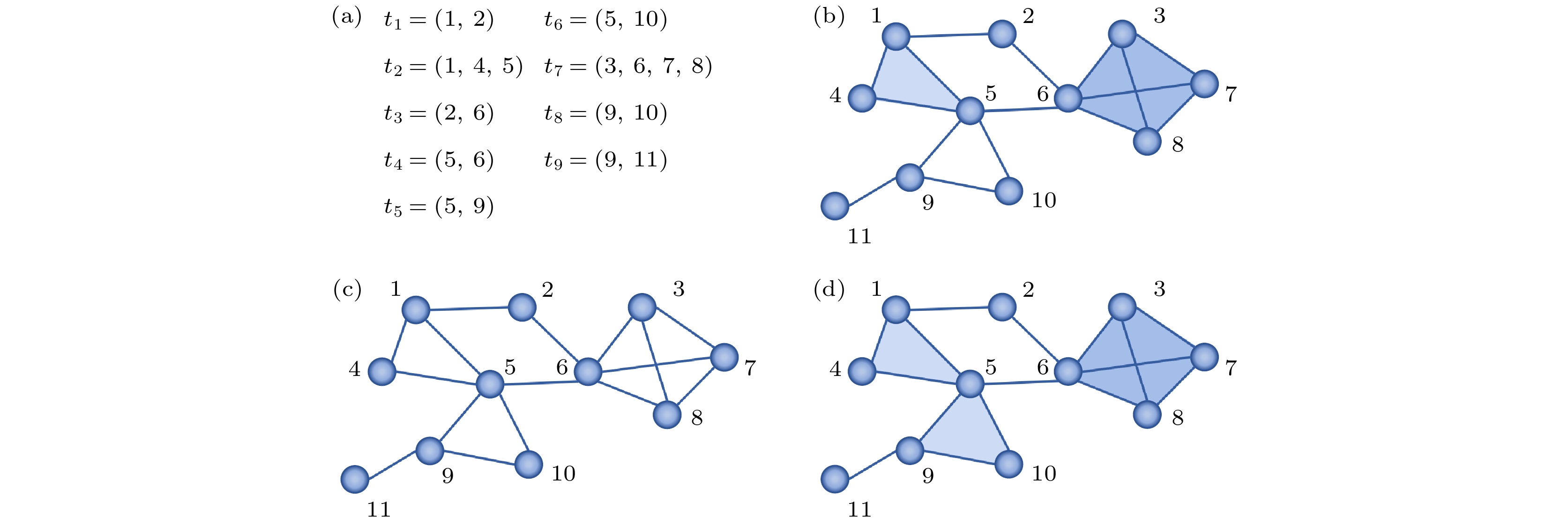
利用高阶交互数据可以构建单纯形网络, 如图2(a)中每个时间戳对应的数据都表示一个单纯形, 利用这些数据可以构建出图2(b)所示的单纯形网络. 基于单纯形网络可以提取出一个骨架/投影网络(skeleton/projected network), 该网络由原网络中所有的0阶单纯形和1阶单纯形组成, 是一个成对交互作用网络. 基于这个网络可以计算出所有的团结构, 借助单纯形网络中的高阶信息可以把这些团划分为开团(open clique)和闭团(closed clique): 如果一个团的所有节点都在同一个单纯形内, 则该团为闭团, 否则为开团. 例如, 图2(b)中的
$ (1, 4, 5) $ 3个节点组成了一个闭团, 对应图2(a)单纯形数据中的$ t_2 $ 时间戳;$ (5, 9, 10) $ 组成了一个开团, 因为这3个节点没有同时出现在任意一个单纯形中. -
将成对交互作用网络中的团结构抽象为单纯形可以构建团复形(clique complex). 对于给定的一个由节点和连边组成的成对交互作用网络, 计算网络中所有的团结构, 再将每个k阶团视为k阶单纯形, 可以得到这个网络所对应的团复形网络, 也是一个单纯形网络. 如图2(c)所示的这个成对交互作用网络, 可以计算出其中包含11个0阶团(节点)、16个1阶团(连边)、2个2阶团(三角形)、1个3阶团(四面体), 将这些团看作对应阶数的单纯形就可以得到如图2(d)所示的团复形网络. 团复形网络满足单纯形网络的所有性质, 同样满足闭包性, 并且其中任意两个单纯形的交集只有空集或团复形集合中的子集两种情况, 生成团复形网络的原始成对交互作用网络即为其骨架网络.
基于高阶数据的单纯形网络和团复形网络的主要区别在于: 基于高阶交互数据生成的单纯形, 其节点之间存在真实的高阶交互关系; 而团复形中的单纯形是基于对应阶数的团生成的, 即是基于一个成对交互作用网络生成的, 节点之间不一定存在真实的高阶交互关系. 因此, 两个网络的应用场景不同, 基于高阶数据的单纯形网络通常被用来探究具有高阶交互关系的复杂系统的特性和动力学; 团复形网络则用于为传统的成对交互作用系统提供更高阶的向量空间或高阶视角, 以研究高阶结构在网络中的作用和功能.
具体而言, 基于高阶数据的单纯形网络更多的是探索网络中的动力学行为的研究. 例如, 在高阶传播中, 研究者提出了多种单纯形网络上的传播模型[28,29], 也有研究分析了高阶相互作用的引入为 网络动力学带来的新特性[63], 单纯形网络还可以用于研究网络中的振荡和同步现象[26,64]. 此外, 在高阶网络重构[65]、高阶链路预测[66]等多种领域也有广泛的应用. 团复形网络常用于高阶结构相关的研究, 包括团、洞等高阶结构的计算[67], 以及探索脑网络中的高阶结构对大脑认知和信息传播的影响等[68,69], 也有研究者提出团复形网络的生成模型, 进行高阶网络建模和分析[70]. 不过, 无论是用高阶交互数据构建的单纯形网络, 还是由成对交互网络构建的团复形网络, 其最终的形式都属于单纯形网络, 后续介绍的基于单纯形网络的统计量均可使用.
-
本节对超图的一些核心统计指标进行了全面的概述. 这些指标在超图分析和应用中起着至关重要的作用, 有助于更深入地理解超图的结构和特性. 表1列出了这些指标的概览, 涵盖了多个维度. 其中, 度相关指标是描述超图中节点连接情况的基础指标, 它反映了节点在超图中的直接连接情况, 对于分析超图的连通性和复杂性具有重要意义. 其次, 介绍了关于节点的局部聚集系数和关于网络整体的全局聚集系数, 能够揭示超图中节点群聚的紧密程度, 对于理解超图的结构特性具有重要意义. 此外, 本节介绍了考虑多方面因素的超图节点距离的度量方式, 以及反映连边或者网络连接紧密程度的密度指标. 另外, 曲率作为超图的一个几何特性指标, 能够揭示超图的形态和弯曲程度, 在超图嵌入和形状分析等领域具有广泛应用. 本节还介绍了几种可用于衡量超图中节点的重要性和影响力的中心性指标. 最后, 熵作为信息论中的一个重要概念, 也被引入到超图分析中, 通过描述超图中信息的不确定性和复杂性, 来量化超图结构的复杂性. 这些指标为全面而深入地分析超图结构和特性提供了工具和方法.
-
度(degree)意在揭示节点和其他节点之间的关联程度, 超图中的度可以定义为超节点的邻居节点数量, 一个超节点的邻居节点被定义为与该超节点在同一个超边的超节点. 超节点的度可以通过超图的邻接矩阵计算得出, 即超节点
$ v_i $ 的度可以表示为其中N为超图中的超节点数量; A为超图的邻接矩阵, 如果超节点i和超节点j同时在l个超边内,
$ A_{ij} = l $ ,$ l \in [0, M] $ ;$ {\rm{sgn}} $ 为符号函数; M为超图中的超边数量. -
在超图中, 超度(hyperdegree)可以被定义为该超节点所包含的超边数量, 可以通过超图的关联矩阵计算得出, 即超节点
$ v_i $ 的超度可以表示为其中H为超图的关联矩阵, 如果超节点
$ v_i $ 在超边$ e_j $ 中$ H_{ij} = 1 $ , 反之$ H_{ij} = 0 $ . -
在超图中可以根据超边中节点的数量定义超边度(hyperedge degree), 也称为该超边的基, 超边
$ e_j $ 的超边度可以表示为 -
余平均度(excess average degree)用于反映节点的邻居节点的情况. 在成对交互作用网络中, 余平均度是计算节点的邻居节点的度平均值. 类似地, 在超图中, 余平均度被定义为节点的邻居节点的平均超度:
其中,
$ \tau(i) $ 为节点$ v_i $ 的邻居节点集合,$ HD(v_j) $ 为邻居节点$ v_j $ 的超度. -
聚集系数(clustering coefficient)是反映网络中节点的聚集程度的指标[50], 分为节点的聚集系数和网络的聚集系数; 前者是一个局部指标, 后者是针对网络整体的全局指标. 在成对交互作用网络中, 局部聚集系数指节点的邻居节点之间实际存在连边的数量占可以存在的所有连边数量的比例. 如果一个节点的两个邻居节点之间存在连边, 则代表这3个节点之间存在一个三角形, 所以局部聚集系数反映的也是该节点与邻居节点之间存在三角形的情况. 而全局聚集系数则通过将所有节点的聚集系数求平均值或者通过社会学中的传递系数[71]来计算.
利用这种思想可以在超图中计算聚集系数, 最简单的情况就是在d-均匀超图中计算聚集系数. 此时
$ C^{d}(v_i) $ 是超节点$ v_i $ 的聚集系数, 网络中的对应全局聚集系数是$ C_{\rm g}^{d} $ ,超图中计算聚集系数的难点之一就是两个超节点之间可能存在多条超边, 因此3个节点可能出现由多条不同超边组成的多个三角形结构. 两个节点之间已有的超边数量可以由其对应邻接矩阵得到, 但是由于在非均匀超图中的超边的阶数规模无法估计, 进而节点之间可能存在的超边数量无法估计, 导致无法准确地计算出聚类系数. 一种解决方法就是把超节点之间的关系投影到成对关系网络中, 只判断两个超节点是否存在超边关系, 不考虑存在超边的阶数和数量, 即利用超图的邻接矩阵A即可计算:
由于将局部聚集系数求平均所获得的全局聚集系数可能并不准确, 因此另一种方法是根据社会学中的传递系数来计算. 该方法将全局聚集系数定义为网络中所有三角形的数量和2阶路径数量的比例. Estrada和Rodríguez-Velázquez[72]将此方法推广到超图中, 定义了一种聚集系数
$ C_2({\cal{H}}) $ :其中,
$ CW_{a}({\cal{H}}) $ 表示的是网络中所有长度为a的闭合路径的数量; t表示不满足超三角形条件的长度为3的闭合路径数量,$ W_{2}({\cal{H}}) $ 表示所有长度为2的游走的数量;$ \mu_c(i) = (A^c)_{ii} = \displaystyle \sum\nolimits_{s = 1}^N(u_{is})^2\lambda_s^c $ ;$ u_{is} $ 为$ A^{c} $ 的第i个特征向量中的第s个值,$ \lambda_{s}^{c} $ 为$ A^{c} $ 的第s个特征值, c为常数. -
在无向无权超图中, 路径(path)被定义为一个超节点序列
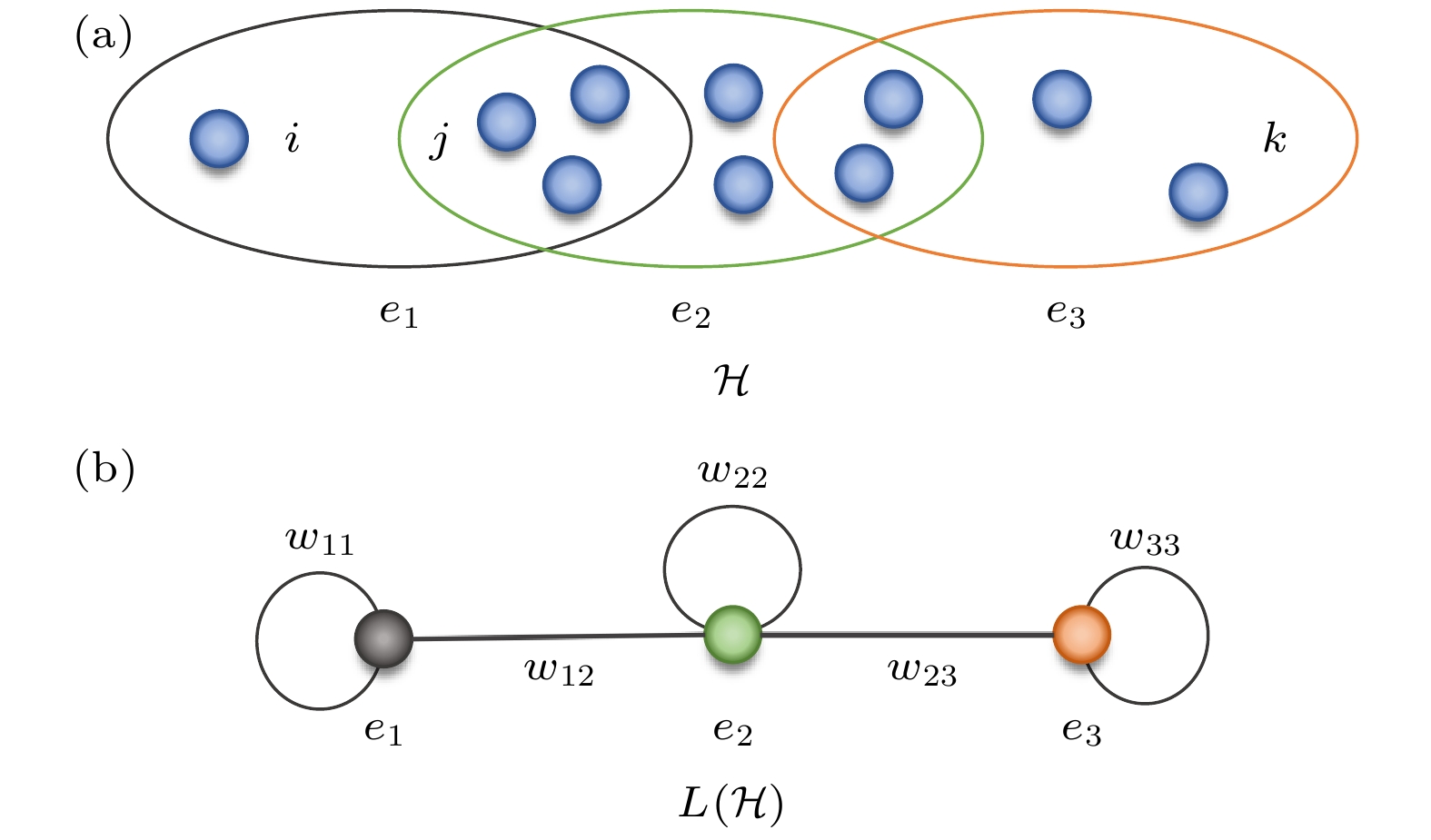
$ P = \{v_1, v_2, \cdots, v_p\} $ , 其中每两个相邻的超节点$ v_i $ 和$ v_{i+1} $ 之间都存在一条超边, P也被称为从超节点$ v_1 $ 到$ v_p $ 之间的一条路径, 路径所涉及的超边的数量被称为该路径的长度(length), 也可称为两个超节点之间的距离. 但是这种计算方法只考虑了超边的数量, 没有进一步考虑超边中超节点数量和超边之间重叠的超节点数量对度量超节点之间距离的影响.在一些基于随机游走(random walk)的算法中, 研究人员单独考虑了将超边的基作为超边的权重进行随机游走[73,74]; 还有一些研究是基于超边之间相交超节点的数量进行随机游走[75,76]. 最近, Vasilyeva等[77]提出了一个同时考虑超边的基和超边相交超节点的数量这两个因素的超节点距离指标, 他们将超图中的距离在超图映射的加权线图(weighted line graph)中进行计算, 加权线图是将超图中的超边当作节点, 加权线图中的连边表示两个超边之间存在重复超节点, 权重则为自行定义, 在下文会详细介绍. 图3(b)就是图3(a)对应的一个加权线图
$L ({\cal{H}}) $ , 图3(a)之中的3条连边在图3(b)中被当作节点,$ e_1 $ 和$ e_2 $ 之间在图3(a)中有重复的节点, 所以图3(b)中它们之间存在连边. 接下来可以根据加权线图来定义超图中节点$ v_i $ 和$ v_k $ 的距离为在这里
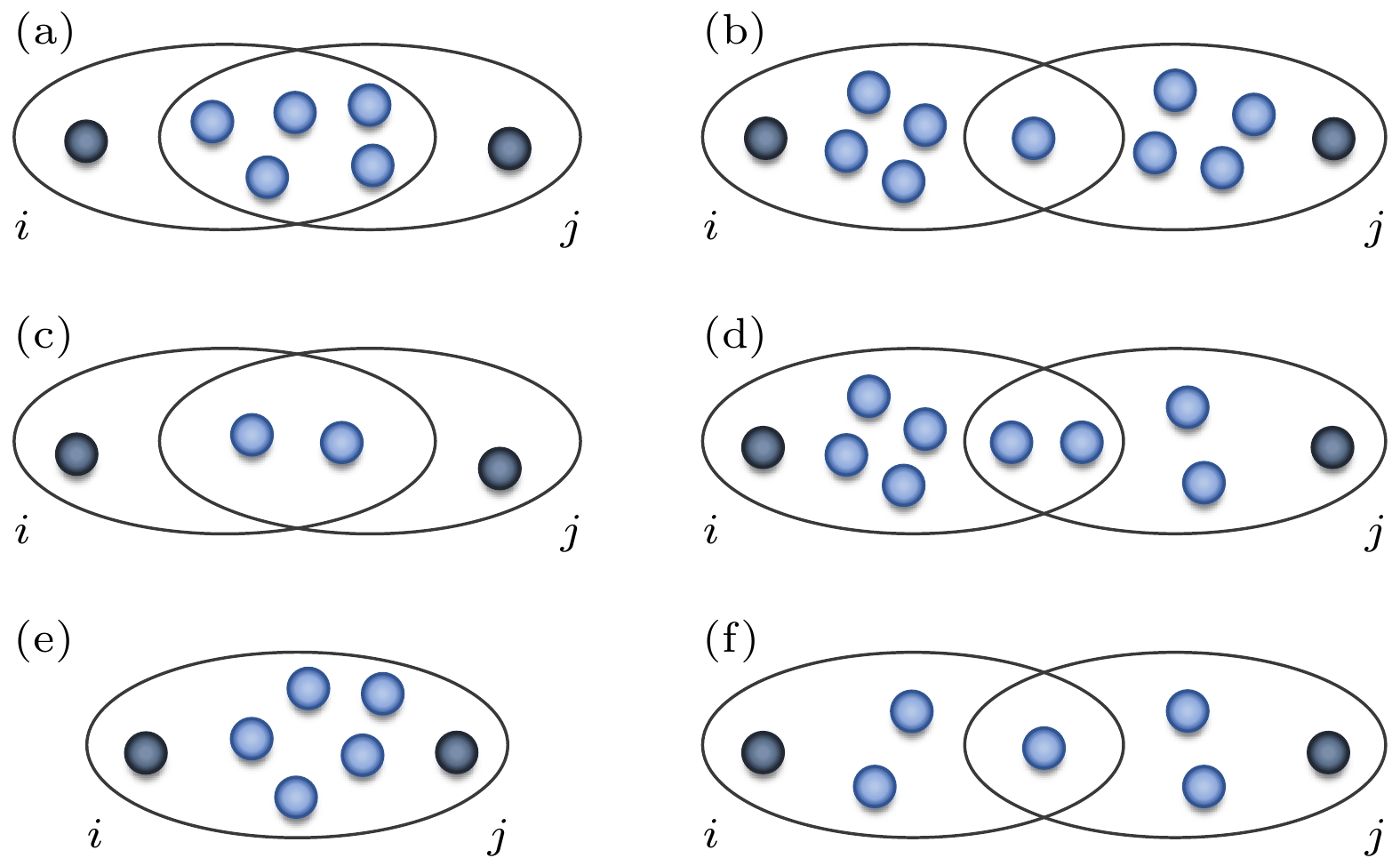
$ E_i $ 和$ E_k $ 分别为节点$ v_i $ 和$ v_k $ 所涉及的超边的集合,$ d^{\mathrm{L}}(e, \tilde{e}) $ 是超边e和$ \tilde{e} $ 在加权线图中的距离, 其计算方式和含权成对交互网络中计算两点之间的距离的方式相同.Vasilyeva等[77]考虑了两个超节点之间距离的4种情况: 1)对于由成对交互作用网络生成的团作为超边的超网络来说, 节点在成对交互作用网络中的距离应该和在超图中的距离相等; 2)当两个超节点之间经过超边的数量相同时, 超边的交点(重叠的超节点)数量越多距离应该越近, 如图4(a) 中超节点
$ v_i $ 和$ v_j $ 的距离要小于图4(b)中节点$ v_i $ 和$ v_j $ 的距离; 3)当两个节点之间经过超边的数量相同时, 所涉及的超边中的节点越多, 距离应该越大, 如图4(d)中节点$ v_i $ 和$ v_j $ 的距离要大于图4(c) 中节点$ v_i $ 和$ v_j $ 的距离; 4)两个节点之间涉及到的节点数量相同时, 超边数量越多, 距离应该越大, 如图4(f)中节点$ v_i $ 和$ v_j $ 的距离要大于图4(e)中节点$ v_i $ 和$ v_j $ 的距离. 根据这4种情况定义了加权线图中的权重, 也就是超图中两条超边$ e_i $ 和$ e_j $ 之间的权重$ w_{ij} $ :和成对交互作用网络一样, 超节点之间也可能存在多条路径, 两个节点之间距离最短的路径被称作最短路径(shortest path), 其长度为最短路径长度[78]. 两个节点之间的最短路径长度是固定的, 但是其最短路径可能不唯一.
-
密度(density)是理解网络的连接紧密程度以及节点之间相互关系的重要指标. 高密度网络中的节点更紧密地连接在一起, 而低密度网络中的连接相对稀疏. 在超图中, 同样可以用密度来衡量网络的紧密程度, 目前在超图中有如下关于密度的指标.
-
超边密度(hyperedge density)是为了计算网络中某一节点所连接的超边在网络中的重叠程度. 在一个非均匀超图中, 当一个节点
$ v_i $ 所在的超边个数为k时, 它的超边密度定义为其中,
$ z_i $ 为配位数(coordination number), 为节点$ v_i $ 直接连接的节点个数, 即节点i的度; 当节点所在的超边完全不重叠时, z取最大值, 有$ z_{\max} = {\displaystyle\sum\nolimits_{j \in E_i} |e_j|} - k $ ,$ E_i $ 为节点$ v_i $ 所在超边的集合.接下来, 可以进一步考虑一个节点所在的超边重叠最严重情况的配位数, 也就是配位数的下界
$ z_{\min} $ , 超边密度可以表示为$ D_{{\mathrm{dh}}}(i) $ :由于非均匀超图的超边的基差异比较大, 所以这里讨论的是均匀超图中的配位数的上下界. 在d-均匀超图中
$ z_{\max} = (d-1)k $ , 但是推导$ z_{\min} $ 的难度是随着d 增加的, 所以目前仅考虑最常见的也是最简单的3-均匀超图的配位数下界,$ z_{\min} = \lceil (1+ \sqrt{8 k+1})/2 \rceil $ , 更高维的均匀超图建议直接使用(10)式进行计算. Zlatić等[79]还讨论了一种特殊的3-均匀超图的超边密度, 该超图中的超节点共分为3种类型, 每条超边都包含3种不同类型的节点, 此时可以推导出节点的配位数的下界, 对于$ q(q-1) < k\leqslant q^2 $ ,$ z_{\min} = 2 q $ ; 对于$ q^2 < k\leqslant q(q+ 1) $ ,$ z_{\min} = 2 q+1 $ ; q取正整数. 无论是在均匀超图还是非均匀超图, 超图密度的取值范围都是$ [0, 1] $ . -
超图密度(hypergraph density) 是指已存在的超边数量与可能存在的所有超边数量之比. 对于d-均匀超图来说, 超边中的节点数量均是d个, 超图的密度定义为
对于非均匀超图来说, 由于超边的基不均匀, 可能存在的超边数量为
$ 2^{N} $ , 密度为$ M/2^{N} $ ; 由于分母随着节点数量呈指数级增长, 远多于实际存在的连边, 因此其超图密度通常很小. -
曲率(curvature)最初通过对描述光滑物体形状(如曲线或曲面)的函数进行二阶导数运算来计算. 在黎曼几何中, 曲率作为编码光滑流形的黎曼度量的几何不变量的张量, 是黎曼几何中的重点研究内容[80]. 曲率在图论中也有着特殊意义, 比如在平面几何中, 曲率可以通过计算曲线在该点的切线角度的变化率来得到; 如果曲率越大, 那么该点的切线角度变化越快, 曲线在该点也就越弯曲. 研究者将这些以往的曲率定义迁移到复杂网络中, 提出关于成对交互作用网络和超图的曲率定义.
-
Forman-Ricci曲率是针对边的统计指标, 在图中有如下应用. 首先, Forman-Ricci曲率可用于捕捉网络的几何特征和拓扑结构. 它提供了一种衡量网络形状和连通性的方法, 通过计算网络中所有边的Forman-Ricci曲率并分析它们的分布, 可以了解网络的整体拓扑结构. 其次, Forman-Ricci曲率还可用于研究网络中的连边重要性和社团发现. 通过与其他边缘度量指标如边缘介数中心性、分布度和嵌入度的相关性比较, 可以揭示网络中的关键连边和重要社团结构. 通过Forman-Ricci曲率的分析, 可以更好地了解复杂网络的结构、动态和演化, 从而在网络科学和实际应用中提供洞察和解决方案. 对于具有显著高或低Forman-Ricci曲率值的边, 它们可能在网络的连通性和信息流中扮演重要角色. 通过识别这些边, 可以了解哪些部分对维持网络整体结构和功能至关重要. 而对于网络的整体结构来说, 边的Forman-Ricci曲率总和或平均值可以作为衡量网络连通性的一个全局指标. 在一些情况下, 整个网络的Forman-Ricci曲率可以体现网络整体结构的情况, 如网络是否高度集群或者是否存在明显的社区结构. 在无向有权网络中, 一条连边
$ {\cal{E}} $ 的Forman-Ricci曲率定义如下[81]:其中
$ w_{\cal{E}} $ 表示边$ {\cal{E}} $ 的权重,$ w_i $ 和$ w_j $ 表示边$ {\cal{E}} $ 所连接的两个节点$ v_i $ 和$ v_j $ 的权重,$ E_i $ 表示节点i所在超边的集合,$ E_i \sim {\cal{E}} $ 则表示边集$ E_i $ 中去除掉连边$ {\cal{E}} $ . 如果在无向无权图中, 那么(15)式可以简化为其中
$ D_i $ 和$ D_j $ 表示节点$ v_i $ 和节点$ v_j $ 的度.而基于上述成对交互作用网络中曲率的定义, Leal等[82]和Eidi 等[83]分别对超图中的Forman-Ricci曲率进行了拓展. 他们根据上述定义, 认定一条超边e的Forman-Ricci曲率也和成对交互作用网络的计算思想一致, 并且由于一条超边e可以包含多个顶点, 那么在无向有权超图中的公式可以拓展为
同样地, 如果所有顶点和超边都没有权重, 即在无向无权超图中, 那么(17)式可以简化为
-
Ollivier-Ricci曲率[84]是根据几何曲率的概念来定义的. 它的计算涉及到节点间的Wasserstein距离和概率分布. 在成对交互网络中, Ollivier-Ricci曲率的计算方法如下: 首先, 对于一条边e两端的节点
$ v_u $ 和$ v_v $ 定义一个概率分布. 例如, 这个分布可以是均匀分布, 即节点$ v_u $ 和$ v_v $ 将概率均匀分配给它自己和它的邻居. 接着使用Wasserstein距离计算节点$ v_u $ 和$ v_v $ 的概率分布间的距离. 这通常涉及到解决一个最优传输问题. Ollivier-Ricci曲率可通过比较节点$ v_u $ 和$ v_v $ 的Wasserstein距离和其在图中的实际距离来计算. 具体来说, 其计算公式为其中,
$ W(\mu_u, \mu_v) $ 是节点$ v_u $ 和$ v_v $ 的概率分布$ \mu_u $ 和$ \mu_v $ 间的Wasserstein距离,$ d(v_u, v_v) $ 是节点$ v_u $ 和$ v_v $ 间在图中的最短路径长度.Wasserstein距离, 也称为“Earth Mover’s Distance”(EMD), 是用来度量两个概率分布间差异的一种方法. 在数学上, Wasserstein距离可以用多种方式定义, 其中一种常见的方法是基于线性规划来计算, 其计算公式为
其中,
$ N(u) $ 和$ N(v) $ 分别为节点$ v_u $ 和$ v_v $ 的邻居,$ d(v_i, v_j) $ 是网络中从节点$ v_i $ 到节点$ v_j $ 的最短路径长度,$ {\cal{E}}(v_i, v_j) $ 表示从节点$ v_i $ 到节点$ v_j $ 的转移的概率值,$ \varPi(\mu_u, \mu_v) $ 是所有可能的传输计划的集合, 这些计划满足$\displaystyle\sum\nolimits_j {\cal{E}}(v_i, v_j) = \mu_u(i) $ 和$ \displaystyle\sum\nolimits_i {\cal{E}}(v_i, v_j) = \mu_v(j) $ . Wasserstein距离度量了使两个概率分布相似所需的最小“工作量”或成本. Ollivier-Ricci曲率指标越大, 说明这条边连接的两个节点在网络中的拓扑位置越紧密或越重要.在有向超图
$ {\cal{H}}^d = \{V, E^d\} $ 中, Ollivier-Ricci曲率的定义如下[85]: 任意一条有向超边$ e^d $ 可表示为$ A = \{x_1, \cdots, x_n\} \stackrel{e^d}{\rightarrow} B = \{y_1, \cdots, y_m\}, (n, m)\leqslant |V| $ , 即在超边$ e^d $ 中,$ A = \{x_1, \cdots, x_n\} $ 和$ B = \{y_1, \cdots, y_m\} $ 是两个节点集合, 超边的方向是从节点集A指向节点集B, 节点集A中的每一个节点都指向节点集B中的节点. 那么该超边的Ollivier-Ricci曲率为其中,
$ \mu_{A^{\text {in}}} $ 为入节点的概率分布, 即:其中,
$ d_{v_i}^{{\mathrm{in}}} $ 表示节点$ {v_i} $ 的入度.同样地,
$ \mu_{B^{\text {out}}} $ 为出节点的概率分布, 其计算方法为其中,
$ d_{v_j}^{\text {out }} $ 表示节点$ {v_j} $ 的出度.进而可以计算二者的Wasserstein距离
$ W(\mu_{A^{\text {in }}}, \mu_{B^{\text {out }}}) $ :其中
$ u \rightarrow A $ 指的是指向节点集合A中任意一个节点的节点, 而$ B \rightarrow v $ 指的是被节点集合B中任意一个节点指向的节点.$ d(v_u, v_v) $ 是从$ v_u $ 到$ v_v $ 的最短超路径的长度,$ {\cal{E}}(v_u, v_v) $ 表示从顶点$ v_u $ 转移到顶点$ v_v $ 的概率,$ \varPi\left(\mu_{A^{{\mathrm{in}}}}, \mu_{B^{\text {out }}}\right) $ 是所有可能的传输计划的集合, 其需同时满足:如此一来便可计算超边的Ollivier-Ricci曲率. 与Forman-Ricci曲率相比, Ollivier-Ricci曲率考虑的是基于Wasserstein距离(最优传输成本)的度量, 它在概念上更接近于黎曼几何中的经典Ricci曲率. 这种度量能够更全面地反映网络的全局结构特征. 它不仅仅考虑了局部邻域, 而且在计算节点间的Wasserstein距离时, 可以捕捉到网络更广泛区域的特性. 但是, Ollivier-Ricci曲率的计算复杂度更高, 所以更不适合拓展到大型图上.
-
中心性(centrality)指标意在找到网络中重要或核心的节点, 此处将介绍多个超图的中心性指标, 其中描述的网络统一定义为一个拥有M条超边, N个节点的超图
$ {\cal{H}} = \{V, E\} $ . -
节点的度中心性(degree centrality)是最简单直观的中心性指标, 它衡量节点在超图中的连接程度, 度中心性高的节点在超图中与其他节点的连接较多, 可能在信息传播、交互和合作等方面发挥重要作用. 在无权超图中, 节点的度中心性和成对交互作用网络中的度中心性类似, 可被定义为节点所拥有的邻居节点的数量, 可以通过超图的邻接矩阵进行计算(详见(1)式), 也可以用其他的度相关指标进行定义(详见3.1节).
在超图中, 两个相邻节点之间可以存在多条超边, 因此, 可以根据节点之间存在的超边数量定义节点中心性, 此时节点i的中心性
$ C_d^h(i) $ 就定义为[86]进一步可以根据两个超节点之间更详细的关系定义超节点之间的权重, 进而定义加权的中心性指标, 在这种条件下, 加权度中心性定义为[86]
其中,
$ \omega_k $ 是每条超边的权重. 超边的权重可以通过多种方式进行度量, 可以根据结构来定义, 例如, 超边的多重性(超边在超图中的重复出现次数)与超边的基(超边度); 也可根据实际意义或需求来定义超边的权重.除了依靠节点之间的连接状况, 还可以通过节点之间的连接属性来区分, 社会学将连接分为强连接和弱连接[87], 其中, 强连接指的是紧密的、亲密的人际关系, 如家人、亲密的朋友, 这种连接关系中的成员通常互动频繁, 有共享的价值观和兴趣, 情感上比较亲近. 而弱连接指的是不太紧密或不太亲密的人际关系; 这种连接关系中的成员可能不经常互动, 共享的兴趣和价值观也可能较少, 但是在社会网络中起着重要的连接作用. 基于上述定义, Kapoor等[86]将强连接度中心性
$ C_{{\mathrm{s d}}}^h(i) $ 和弱连接度中心性$ C_{{\mathrm{w d}}}^h(i) $ 表示如下:其中, MEAN和SD表示所有权重的均值和标准差.
-
核心度中心性(coreness centrality)是基于超图的核心分解而定义的指标. 超图的核心分解将超图分解为多个核心, 其中每个核心是一组相互连接的节点和超边. 核心度中心性高的节点位于超图的核心结构中, 起到关键的组织和连接作用. 在成对交互作用网络中, 核心度中心性表示图在k-核分解[88]中分解到的最大层数, 扩展到超图上即在超图的k-核分解中分解到的最大层数, 此指标决定了节点与超图核的邻近程度.
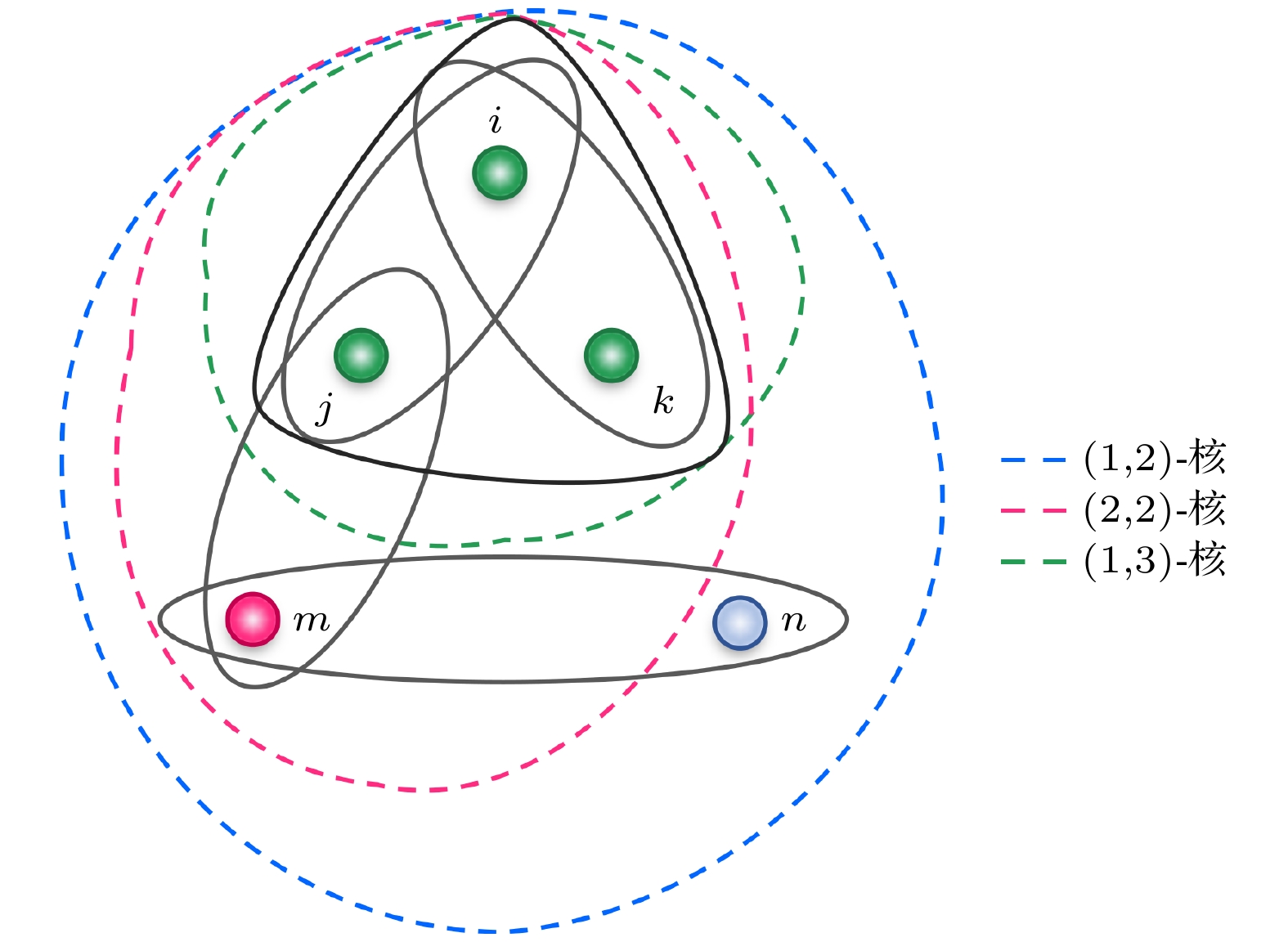
Mancastroppa等[61]提出了超核数的概念, 它是通过计算k-核分解的扩展算法——超核分解得到的. 由于超边所含节点数不一样, 所以该分解会存在两个参数——超边的数量k和超边度c, 简单来说,
$ (k, c) $ -超核中的所有节点都至少属于k个超边度大于等于c的超边. 很容易得出,$ (k, c) $ -超核包含$ (k+1, c) $ -超核和$ (k, c+1) $ -超核. 接着, 他们将节点i的c-壳的索引定义为$ C_c(i) = k $ , 使得节点$ v_i $ 属于$ (k, c) $ -超核, 但是不属于$ (k+1, c) $ -超核, 即节点$ v_i $ 连接了k个超边度为c 的超边. 那么$ (k, c) $ -壳$ S(k, c) $ 就可以被定义为所有$ C_c(i) = k $ 的节点集合, 即所有连接了k 个超边度为c的超边的节点集合. 继而可以刻画$ k_{{\mathrm{cax}}}^c $ 为使$ S(k, c) $ 不为空的k的最大值. 举例来说, 如图5中有5个节点和5条超边, 粉色的节点属于2条超边度为2的超边中, 所以它的$ C_2 = 2 $ .$ (2, 2) $ -壳$ S(2, 2) $ 即为绿色和粉色的节点集合, 因为它们都只连接了2条超边度为2的超边.$ k_{{\mathrm{cax}}}^2 $ 就是使得$ S(k, 2) $ 不为空的k的最大值, 在图5中等于2, 因为$ S(3, 2) $ 为空集, 没有节点连接3条超边度为2的超边. 因此, 超图的g-核心度中心性的定义为其中M是超图中的最大超边度,
$ g(c) $ 是任意权函数, 它可以对不同的高阶相互作用进行加权. 最简单的就是超边没有权重或权重相等, 即$ g(c) = 1 $ . -
Aksoy等[77]提出了s - 调和接近中心性(s -closeness centrality). 首先定义在超图上的游走形式为s - 游走, 并将其定义为一个节点序列, 这个节点序列中的邻接节点同在s个超边(而在普通网络中, 两点之间最多只能有1条连边, 所以在普通网络只有1-游走). 进而, 两条超边f和g之间的s - 距离就可以定义为超边之间最短的s - 游走长度, 即:
接下来定义某一条超边f的s - 调和接近中心性为
其中
$ E_s = \{e \in E: |e|\geqslant s\} $ , 即超边中节点个数大于等于s的超边. -
介数中心性(betweenness centrality)衡量了节点在网络信息传播和通信中的重要性. 节点的介数中心性越高, 意味着该节点在网络中扮演着更重要的桥梁角色, 连接了许多关键路径, 从而使得信息在网络中更易传播和流动. 成对交互作用网络上的介数中心性通过计算节点在最短路径上出现的次数来衡量节点在网络中的重要性. Xiao[89]将该成对交互作用网络上的介数中心性概念推广到超图上. 他首先定义了超路径(hyperpath)的概念为节点和超边的交错路径, 例如
$ v_1, e_1, v_2, e_2, \cdots, v_q, e_q, v_{q+1} $ 是一条长度为q的超路径, 接着很自然地推广出超图上的介数中心性指节点在最短超路径上出现的次数:其中,
$ g_k $ 代表从$ v_j $ 到$ v_k $ 的全部最短超路径的数量, 而$ g_k(i) $ 表示经过节点$ v_i $ 的所有最短超路径的数量.Lee等[90]也扩展了成对交互作用网络的介数中心性到超图中. 依据他们的观点, 一个代表着团队之间联系的3阶团, 可以被解释为由顶点对组成的3个成对交互关系组. 基于此, 他们提出衡量超边的介数中心性(h-BC). 为了计算这个指标, 首先需要把超图转换成二部图, 其中上层节点是超边所代表的顶点, 下层节点是原始网络中的节点. 接着, 构造一个最短路径树, 其中节点与超边所表示的节点依次相连. 那么此时超图中节点的介数中心性和超边的介数中心性都可以依据传统的成对交互网络的介数中心性进行计算.
-
在成对交互作用网络中, 特征向量中心性基于这样的理念: 一个节点的重要性不仅取决于它的邻居节点的数量, 还取决于这些节点的重要性. 这个概念在1972年由Phillip Bonacich提出[91], 并在社会网络分析中得到广泛应用. 特征向量中心性考虑了一个节点的邻居的重要性. 它基于这样的假设: 与重要节点相连接的节点也是重要的. 特征向量中心性是网络邻接矩阵的最大特征值λ对应的特征向量.
其中
$ \tau(i) $ 为节点$ v_i $ 的邻居节点集合.而推广到超图中, 目前只有关于均匀超图的 特征向量中心性的定义[92]. 在d - 均匀超图
$ d{\text{-}}{\cal{H}} = \{V, E\} $ 中, 节点$ v_i $ 的特征向量中心性计算如下:其中节点
$ v_i $ 和节点$ v_{j_1} , \cdots, $ $ v_{j_{k-1}} $ 同属于一条超边, F是任意函数, 一种简单的方法是直接求和, 即$ F\left(x_1, \cdots, x_{k-1}\right) = x_1+\cdots+x_{k-1} $ . 当然也可以选择别的函数, 在这种情况下, 中心性的存在性和唯一性可以通过非线性Perron–Frobenius理论来证明[93]. -
在复杂网络中, 可以使用熵(entropy)度量网络结构的复杂性或信息量, 本节介绍几种适用于超图的熵. 熵由Clausius[94]提出, 后来Claude Shannon第一次将熵的概念引入到信息论中, 从而定义了香农熵(Shannon entropy)[95]. 假设
$ p = \{p_1, p_2, \cdots, p_n \} $ 是一组概率分布, 并且满足$ 0 \leqslant p_i \leqslant 1 $ 和$\displaystyle \sum\nolimits_{i = 1}^n p_i = 1 $ , 那么香农熵就被定义为在超图中, 学者们基于香农熵提出了很多相关的超图熵定义. Bloch和Bretto[96]则是利用关联矩阵I来计算超图的熵, 他们定义了一个新的矩阵
$ {\boldsymbol{L}} = {\boldsymbol{II}}^t = ((|e_i \cap e_j|))_{i, j \in \{1 \cdots M\}} $ . 在这里Bloch和Bretto只给出了一种特殊超图的熵的计算方法——均匀且每条超边没有交集的超图. 由于每条超边没有交集且超边度一致, 故超图的秩$ r({\cal{H}}) $ (最大的超边度)恒为一个常数$ N/M $ , 进而L矩阵的迹为所有节点的超度之和${\mathrm{tr}}({\boldsymbol{L}}({\cal{H}})) = \displaystyle \sum\nolimits_{x \in V}d(x) $ . 所以超图的香农熵可以定义为但是上述方法只能够计算特殊类型的超图, 而Hu等[97]利用顶点超度数的概率分布来拟合香农熵公式, 从而计算超图熵. 假设超图
$ {\cal{H}} $ 中的节点超度序列为$ \{HD_1, HD_2, \cdots, HD_n\} $ , 那么超图熵则被定义为Wang等[98]则构建了加权超图的超图熵, 它是通过计算节点的权重差来得到的. 对于加权超图来说, 定义
$ q_i $ 为每一个节点的权重离平均权重的距离, 则节点的权重差分布为其中, ξ表示比较小的正值, 以避免除到零. 得到权重的差分布之后, 就可以计算超图熵:
-
本节对单纯形网络的重要统计指标进行了综述, 指标概览如表2所列, 主要从度相关指标、路径和距离相关指标、中心性指标、聚集系数和拓扑不变量等多个维度展开. 首先, 度相关指标详细地综述了关于单纯复形不同的邻接状态的捕捉方式, 并定义了对应度值的计算方法; 关于单纯形网络的路径, 本节介绍了两种游走的方式, 根据定义的路径可以进而计算出距离、离心率和直径等相关指标; 对于中心性指标, 本节也介绍了基于度定义的中心性指标以及结合路径的一些常见的中心指标的扩展; 关于聚集系数, 本节介绍了基于单纯形网络中节点的聚集系数和两种关于单纯形的聚类系数; 最后, 介绍了关于拓扑空间内描述单纯复形特征的拓扑不变量在单纯形网络中的相关指标.
-
传统成对交互作用网络中, 度衡量的是节点之间的连接状态, 但单纯形网络中存在不同阶数的单纯形, 因此度的定义会相对复杂[99-102], 本节将介绍单纯形网络中度的定义. 对于一个0阶单纯形(节点), 它与另一个0阶单纯形是否邻接取决于二者之间是否存在1阶单纯形(连边). 但是, 对于1阶单纯形来说, 它与另一个1阶单纯形是否邻接取决于二者是否有共同的0阶单纯形(节点), 或者是否在同一个2阶单纯形(三角形)之中. 因此, 对于两个k 阶单纯形
$ s^{(k)}_{i} $ 和$ s^{(k)}_{j} $ , 如果它们有一个公共的$ (k-1) $ 阶单纯形, 则称它们为下邻接, 记作$ s^{(k)}_{i}\sim {}_{{\mathrm{L}}}s^{(k)}_{j} $ ; 如果它们是一个$ (k+1) $ 阶单纯形的两个面, 则称它们为上邻接, 记作$ s^{(k)}_{i}\sim {}_{{\mathrm{U}}}s^{(k)}_{j} $ .定义一个k阶单纯形
$ s^{(k)} $ 的下邻接度$ {\mathrm{deg}}_{{\mathrm{L}}}(s^{(k)}) $ 为该单纯形连接的$ (k-1) $ 阶单纯形的数量, 即为$ k+1 $ ; 上邻接度$ {\mathrm{deg}}_{{\mathrm{U}}}(s^{(k)}) $ 为该单纯形作为一个k阶面的$ (k+1) $ 阶单纯形的数量; 基于这两个度的定义, 可以定义一个单纯形的度$ {\mathrm{deg}}(s^{(k)}) $ ,上述关于度的定义只是单纯形网络中最基本的度定义, 由于单纯形网络中的阶数比较复杂, 因此可以进一步定义一些关于不同阶数的度. 在上邻接和下邻接的基础上, 可以更加细致地定义网络中的任意一阶邻接关系, p邻接. 主要分为上p邻接和下p邻接, 分别用
$ {\mathrm{U}}_p $ 和$ {\mathrm{L}}_p $ 表示. 如果两个单纯形$ \sigma^{(k)}\sim{}_{{\mathrm{U}}_p}\sigma^{(k^\prime)} $ , 则一定存在一个p 阶单纯形$ \tau^{(p)} $ , 并且同时满足$ \sigma^{(k)}\subseteq\tau^{(p)} $ 和$ \sigma^{(k^\prime)}\subseteq\tau^{(p)} $ . 如果两个单纯形$ \sigma^{(k)}\sim{}_{{\mathrm{L}}_p}\sigma^{(k^\prime)} $ , 则一定存在一个p 阶单纯形$ \tau^{(p)} $ , 并且同时满足$ \tau^{(p)}\subseteq\sigma^{(k)} $ 和$ \tau^{(p)}\subseteq\sigma^{(k^\prime)} $ . 进而还可以定义两个单纯复形的严格上p邻接和严格下p邻接, 分别用$ {\mathrm{U}}_{p^*} $ 和$ {\mathrm{L}}_{p^*} $ 来表示. 如果两个单纯形$ \sigma^{(k)}\sim{}_{{\mathrm{L}}_{p^*}}\sigma^{(k^\prime)} $ , 需要同时满足$ \sigma^{(k)}\sim{}_{{\mathrm{L}}_p}\sigma^{(k^\prime)} $ 和$ \sigma^{(k)}\not\sim{}_{{\mathrm{L}}_{p+1}}\sigma^{(k^{\prime})} $ . 如果两个单纯形$ \sigma^{(k)}\sim{}_{{\mathrm{U}}_{p^*}}\sigma^{(k^\prime)} $ , 需要同时满足$ \sigma^{(k)}\sim{}_{{\mathrm{U}}_p}\sigma^{(k^\prime)} $ 和$ \sigma^{(k)}\not\sim {}_{{\mathrm{U}}_{p+1}}\sigma^{(k^{\prime})} $ . 基于以上的邻接关系, 可以定义一个单纯形$ \sigma^{(k)} $ 的上p邻接度($ {\mathrm{deg}}_{{\mathrm{U}}}^{p} $ )、下p邻接($ {\mathrm{deg}}_{{\mathrm{L}}}^{p} $ )、严格上p邻接度($ {\mathrm{deg}}_{{\mathrm{U}}}^{p^*} $ )和严格下p邻接度($ {\mathrm{deg}}_{{\mathrm{L}}}^{p^*} $ ):上述定义中, 上邻接和下邻接度计算的是所有与k阶单纯形
$ \sigma^{(k)} $ 上p邻接和下p邻接$ k' $ 阶单纯形$ \sigma^{(k')} $ 的数量, 也可以在此基础上计算规定阶数范围的单纯形度, 定义k阶单纯形$ \sigma^{(k)} $ 的$ (h, p) $ 度, 可以分为上$ (h, p) $ 邻接度和下$ (h, p) $ 邻接度, 记作$ {\mathrm{deg}}_{{\mathrm{L}}}^{h, p} $ ,$ {\mathrm{deg}}_{{\mathrm{U}}}^{h, p} $ , 同时也可以计算其对应的严格约束形式的度, 记作$ {\mathrm{deg}}_{{\mathrm{L}}}^{h, p…^{*}} $ ,$ {\mathrm{deg}}_{{\mathrm{U}}}^{h, p^{*}} $ :进一步地, 可以定义单纯形网络中更一般化的邻接关系及度——p邻接, 记作
$ {\mathrm{A}}_p $ . 如果两个单纯形$ \sigma^{(k)}\sim{}_{{\mathrm{A}}_p}\sigma^{(k^\prime)} $ , 需要同时满足$ \sigma^{(k)}\sim{}_{{\mathrm{L}}_{p^{*}}}\sigma^{(k^{\prime})} $ 和$ \sigma^{(k)}\not\sim{}_{{\mathrm{U}}_{p^{\prime}}}\sigma^{(k^{\prime})} $ , 这里$ p^{\prime} = k+k^{\prime}-p $ . 为了和传统的成对交互作用关系图对应, 当$ q = 0 $ 时, 如果两个节点$ v_i\sim{}_{{\rm U}_1}v_j $ , 则$ v_i $ 和$ v_j $ 邻接. 可以基于p邻接定义最大p 邻接, 记作$ {\mathrm{A}}_p^{*} $ . 如果两个单纯形$ \sigma^{(k)}\sim{}_{{\mathrm{A}}_{P^{*}}}\sigma^{(k^\prime)} $ , 除了满足p邻接的条件外, 还要满足对于任意一个和单纯形$ \sigma^{(k)} $ p邻接的单纯形$ \sigma^{(k^{\prime\prime})} $ 满足$ \sigma^{(k^{\prime})}\not\subset\sigma^{(k^{\prime\prime})} $ . 基于此, 定义一个k阶单纯形$ \sigma^{(k)} $ 的p邻接度$ {\mathrm{deg}}_{\mathrm{A}}^p $ 和最大p邻接度$ {\mathrm{deg}}_{\mathrm{A}}^{p^{*}} $ :最后, 可以在单纯形网络中定义一个无参数的度指标, 即最大单纯形度, 记作
$ {\mathrm{deg}}^*(\sigma^{(k)}) $ :其中,
$ {\mathrm{deg}}_{\mathrm{A}}^*(\sigma^{(k)}) = \displaystyle\sum\nolimits_{p = 0}^{k-1}{\mathrm{deg}}_{\mathrm{A}}^{p^*}(\sigma^{(k)}) $ ,$ {\mathrm{deg}}_{\mathrm{U}}^*(\sigma^{(k)}) = \displaystyle\sum\nolimits_{h = 1}^{\dim K-k}{\mathrm{deg}}_{\mathrm{U}}^{h, (k+h)^*}(\sigma^{(k)}) $ ,$ {\mathrm{dim}} K $ 为单纯形网络K的维度.以图2(b)单纯形网络中的1阶单纯形(1, 5)为例, 记为
$ \sigma^{(1)} $ , 该单纯形网络的维度$ {\mathrm{dim}} K = 3 $ ,$ k = 1 $ ,$ p = 0 $ ,$ h = 1, 2 $ . 因此$ {\rm{deg}}^*(\sigma^{(1)}) = {\rm{deg}}_{\mathrm{A}}^{0^*}(\sigma^{(1)}) +\; {\rm{deg}}_{\mathrm{U}}^{1, 2^*}(\sigma^{(1)}) + {\rm{deg}}_{\mathrm{U}}^{2, 3^*}(\sigma^{(1)}) = 4 + 1 + 0. $ $ {\rm{deg}}_{\mathrm{A}}^{0^*}(\sigma^{(1)}) $ 表示与$ \sigma^{(1)} $ 严格下0邻近但不是上邻接的单纯形$ \sigma^{(k')} $ 的数量, 有4个单纯形(1, 2), (5, 6), (5, 9), (5, 10);$ {\rm{deg}}_{\mathrm{U}}^{1, 2^*}(\sigma^{(1)}) $ 代表的是与$ \sigma^{(1)} $ 严格上2邻接的2阶单纯形(三角形)$ \sigma^{(2)} $ 的数量, 有1个单纯形(1, 4, 5);$ {\rm{deg}}_{\mathrm{U}}^{2, 3^*}(\sigma^{(1)}) $ 表示与$ \sigma^{(1)} $ 严格上3邻接的3阶单纯形(四面体)$ \sigma^{(3)} $ 的数量, 这里没有符合要求的3阶单纯形. 更详细的关于高阶度的计算方法可以查询文献[102]. -
计算网络中的最短路径, 首先从定义单纯形网络中的游走(walk)开始. 在单纯形网络中的研究主体不再只是节点, 而变成了单纯形, 本节主要介绍单纯形直接的游走和其相关统计指标[100,102].
-
Estrada和Ross[100]定义了一种
$ s_k $ 游走, 用来描述k阶单纯形之间的游走, 其主要特点是两个同阶单纯形只能通过低一阶的单纯形进行游走. 具体来讲,$ s_k $ 游走在$ \sigma^{(k)}_{1} $ 和$ \sigma^{(k)}_{r} $ 两个k阶单纯形之间定义了一个序列$ \{\sigma^{(k)}_{1}, \sigma^{(k-1)}_{1}, \sigma^{(k)}_{2}, \sigma^{(k-1)}_{2}, \cdots, \sigma^{(k-1)}_{r-1}, \sigma^{(k)}_{r}\} $ ,$ \sigma^{(k)}_{1} $ 和$ \sigma^{(k)}_{r} $ 两个单纯形不存在上邻接关系. 在这里k阶单纯形之间的游走只能依赖于$ (k-1) $ 阶单纯形, 根据单纯形网络中的定义可知, 这个$ (k-1) $ 单纯形是近邻的两个k阶单纯形的面. -
文献[86]定义了一个相对
$ s_k $ 游走来说更加广义的游走序列——p游走,$ \{\sigma^{(k_1)}_{1}, \sigma^{(p_1)}_{1},\sigma^{(k_2)}_{2}, \sigma^{(p_2)}_{2}, \cdots, \sigma^{(p_{r})}_{r}, \sigma^{(k_{r+1})}_{r+1}\} $ , 这里要求$ \sigma^{(k_i)}_{i} \sim{}_{{\mathrm{A}}_{p^{*}}} \sigma^{(k_{i+1})}_{i+1} $ , p取$ \{p_1, p_2, \cdots, p_r\} $ 中的最小值, r为游走的长度, 如果两个单纯形之间有一条p游走, 则称这两个单纯形最大p 连通. 当$ k_i = k $ ,$ p_i = k-1 $ 时, p游走即为$ s_k $ 游走. 也就是说, p游走是一个更一般化的游走,$ s_k $ 游走是p 游走的一种特殊形式, 因此, 下文介绍的基于路径的一系列统计指标均基于p游走, 如有需要, 通过设置参数就可转化为$ s_k $ 游走. -
接下来可以基于游走定义单纯形网络中的最短路径, 对于两个任意阶数的单纯形
$ \sigma^{(k)}_{a} $ 和$ \sigma^{(k)}_{b} $ , 两者之间p 游走的路径长度最小时, 该路径为最短路径, 其长度为两个单纯形之间的最短路径长度, 记为$ d_{p}(\sigma^{(k)}, \sigma^{(k')}) $ . -
度量单纯形的离心率可以从该单纯形与其他单纯形的距离来考虑, 通常把该单纯形到其余单纯形的最短路径长度计算出来, 选取其中最大值来表示该单纯形的离心率, 下面介绍基于最短路径定义的离心率. 基于p游走, 可以定义一个k 阶单纯形
$ \sigma^{(k)} $ 的p 离心率: -
网络的直径(diameter)是一个描述全局特征的统计指标, 所有节点的离心率的最大值即为直径. 直径也可以理解为网络中所有单纯形两两之间的最短路径长度的最大值:
-
通常, 定义度相关的中心性的思想是衡量节点与其他节点相连的程度. 最简单的方法是在传统成对交互作用网络中, 计算节点的度(即与其相连的边的数量), 然后将其除以除了自身节点以外的所有节点数量. 可以遵循此中心思想和单纯形网络中度的定义, 来定义一系列度中心性指标[102].
对于一个节点来说, 在单纯形网络里面是0阶单纯形, 是一个阶数最低的单纯形. 因此, 定义其度中心性只利用上邻接度即可, 记作
$ C_{\mathrm{deg}_{{\mathrm{U}}}^{h, h}}(v) $ ,其中,
$ f_0 $ 表示0阶单纯形的数量, 即节点数量. 可以发现, 当$ h = 1 $ 时, 该统计指标是成对交互作用网络定义的度中心性.除了节点的度中心性指标, 也可以在单纯形网络中进一步定义关于一个k阶单纯形的度中心性, 由于单纯形网络中有多种度定义, 本文介绍一种最常用的度中心性[102],
$ \mathrm{deg}^*(\sigma^{(k)}) $ 表示k阶单纯形$ \sigma^{(k)} $ 的最大单纯形度(详见(53)式),$ f_i $ 表示第i阶单纯形的数量,$ \dim K $ 表示单纯复形K的维数. -
特征向量中心性捕捉的是一个节点的邻居节点的重要性[103], 即如果一个节点的邻居节点是重要节点, 那么其自身也可能非常重要, 可以看作是度中心性的进一步考量. 计算特征向量中心性需要先构造邻接矩阵, 本文介绍的是基于k 阶单纯形的特征向量中心性, 所以, 首先给出的是k阶单纯形的邻接矩阵
$ {{A}}(k)_{ij} $ [100],第i个k阶单纯形
$ \sigma_i^{(k)} $ 的特征向量中心性为矩阵$ {{A}}(k)_{ij} $ 主特征向量(最大特征值对应的特征向量)的第i个分量对应的值. -
Katz中心性意在解决特征向量中心性在有向网络中的局限性[104], 主要思想是首先给每个节点赋予相同的中心性, 一般取值为1, 这样就解决了只有出度没有入度的节点中心性为0的局限, 在这里第i个k 阶单纯形的Katz中心性可以表示为[100,105]
这里
$ {\boldsymbol{A}}_k $ 表示k阶单纯形的邻接矩阵; m表示计算的迭代次数;$ \boldsymbol{e} $ 表示单位向量; α是一个常数, 其取值范围在$ (0, {1}/{\lambda_{1}}) $ ,$ \lambda_{1} $ 为矩阵$ {\boldsymbol{A}}_k $ 的最大特征值. 当$ \alpha\leqslant \rho({\boldsymbol{A}}_{k}) $ 时$ \bigl(\alpha^m{\boldsymbol{A}}_k^m\bigr) $ 可以收敛, 所以有其中,
$ \boldsymbol{I} $ 表示单位矩阵, 进而根据文献[105]可以推出用特征值和特征向量表示的Katz中心性,在这里
$ \psi_{k, j}(i) $ 和$ \psi_{k, j}(l) $ 分别表示矩阵$ {\boldsymbol{A}}_k $ 的第j个向量的第i和l个分量,$ \lambda_{k, j} $ 为该向量对应的特征值. -
接近中心性是衡量网络中两个节点接近程度的物理量[106], 在单纯形网络中可以用来衡量两个单纯形之间的接近程度[102]. 如果一个单纯形
$ \sigma_i^{(k_i)} \in K_p $ , 则有其中,
$ K_p $ 表示由阶数大于等于p的单纯形组成的集合, 分母表示其他单纯形到$ \sigma_i^{(k_i)} $ 的距离之和. -
介数中心性计算节点经过的最短路径的数量, 可以衡量一个节点起桥梁作用的程度[107]. 在单纯形网络中, 如果一个单纯形满足
$ \sigma_{h}^{(k_{h})}\in\bar{K}_{p, l}^{*}\subseteq\bar{K}_{p}^{*} $ , 则其介数中心性被定义为[102]其中,
$ Q_{p, l}^* $ 表示第l个最大p连通分量$ {\mathrm{bar}}{K}_{p, l}^{*} $ 中的单纯形数量,$ l_{ij, p} $ 表示两个单纯形$ \sigma_{i}^{(k_{i})} $ 和$ \sigma_{i}^{(k_{j})} $ 之间最短p游走的总数,$ l_{ij, p}(\sigma_h^{(k_h)}) $ 表示两个单纯形$ \sigma_{i}^{(k_{i})} $ 和$ \sigma_{i}^{(k_{j})} $ 之间最短p 游走中经过单纯形$ \sigma_h^{(k_h)} $ 的数量. -
节点的聚集系数可以反映该节点的邻居节点之间的聚集程度, 是一个常用的局部统计指标. 在单纯形网络中, Maletić等[108]定义了关于单纯形的聚集系数
$ C'_{\sigma_{i}^{k}} $ :其中
$ K_{nn}^{i} $ 表示单纯形$ \sigma_{i}^{k} $ 的邻居单纯形的集合.Serrano和Gómez[102]在此基础上引进了最大p邻接度和严格上邻接度用来定义了基于节点的聚集系数
$ C_s(v) $ 和基于单纯形的聚集系数$ C_s(\sigma^{(k)}) $ : -
贝蒂数(Betti number)是代数拓扑中的一个重要概念[22,109], 用于描述拓扑空间的拓扑不变量, 是拓扑数据分析中常用的统计指标. 贝蒂数表示单纯形网络中线性独立的
$ k(k \geqslant 0) $ 阶洞的数量, 记为$ \beta_k $ , 其中,$ \beta_0 $ 表示单纯形网络的连通分量数,$ \beta_1 $ 表示网络中1-洞的数量,$ \beta_2 $ 表示网络中由团包围而成的2-洞的数量, 等等. 通过计算贝蒂数$ \beta_k $ , 可以了解网络的拓扑特征, 如它的空间结构是否连通, 是否有闭合的洞等, 计算公式如下:其中,
$ m_k $ 为网络中k阶团的数量,$ r_k $ 为网络的k阶边界矩阵$ {\boldsymbol{B}}_k $ 的秩. 边界矩阵用来描述拓扑空间中单纯复形的边界信息,$ {\boldsymbol{B}}_k $ 表示$ (k-1) $ 阶单纯形和k阶单纯形的关联, 如果$ (k-1) $ 阶单纯形是k阶单纯形的子集, 则矩阵对应位置的元素为1, 否则为0.$ k = 1 $ 时, 边界矩阵$ {\boldsymbol{B}}_1 $ 即网络的关联矩阵. 边界矩阵的秩可以用高斯消去法计算, 首先将边界矩阵化为行阶梯形矩阵, 行阶梯形矩阵中非零行的数量就是边界矩阵$ {\boldsymbol{B}}_k $ 的秩$ r_k $ . -
欧拉示性数(Euler characteristic)是代数拓扑中另一个重要的拓扑不变量[22], 用于描述拓扑空间的特征. 在三维情况下, 欧拉示性数等于网络的节点数减去边数, 再加上三角形数量. 对于更高维的单纯复形, 欧拉示性数可以定义为交错和:
其中,
$ m_k $ 表示k阶团的数量. 通过欧拉-庞加莱公式, 可以将欧拉示性数和贝蒂数联系起来, 欧拉示性数等于贝蒂数的交错和, 即 -
本文详细阐述了超图和单纯形网络这两类高阶网络的基本概念, 并系统综述了在这两类网络中常用的统计指标及其物理意义. 高阶网络的统计指标具有广泛的应用场景. 它们能够更准确地量化描述各类复杂系统的结构信息, 进而揭示其内在的演化规律. 具体而言, 在超图的实证分析中, 统计指标的应用尤为重要. 由于超图中超边的基通常存在较大差异, 如何更细致地考虑结构因素来定义或拓展相关统计指标, 成为未来研究的一个重要方向. 同时, 如何在大规模超图中实现这些统计指标的高效计算, 也是亟待解决的问题.
单纯形网络的实证分析目前主要集中在网络的高阶度分布和高阶连通性研究上. 未来, 可以基于代数拓扑开发更多统计指标, 或提出新的基于代数拓扑理论的方法以深入分析单纯形网络的结构特性. 在网络信息挖掘方面, 高阶统计指标如高阶距离的定义和高阶度的概念, 可以进一步用于定义节点的中心性指标, 从而评估网络中的关键节点. 这不仅可以用于超边或单纯形的预测, 还可以利用这些统计特性进行高阶社团检测、图分类等任务. 在网络建模方面, 可以构建保持网络特定统计特性的配置模型和零模型, 或是根据演化特征构建生长模型. 目前面向超图建模的研究相对较多, 基于单纯形结构的模型开发是一个值得探索的领域.
此外, 高阶网络的结构信息与动力学关系的研究也具有重要意义. 利用高阶网络的结构信息或结构相关的模型, 有助于我们更深入地理解高阶动力学. 例如, 基于统计指标构造的中心性指标可用于研究高阶网络中的传播能力, 而高阶网络的结构相关模型则可用于高阶同步优化等动力学过程的研究. 本文仅介绍了基于无向无权高阶网络的统计指标, 因此, 研究包含权重、有向和时序特征的高阶网络, 将是一个极具挑战性的研究方向, 对于这些网络的研究也有望提供更丰富、更深入的网络分析手段.
感谢中国科学技术大学范天龙博士对本文的讨论.
高阶网络统计指标综述
Fundamental statistics of higher-order networks: a survey
-
摘要: 复杂网络是描述和理解现实世界中复杂系统的有力工具. 近年来, 为了更准确地描述复杂网络中的交互关系, 或者从高阶视角分析成对交互作用网络, 许多学者开始使用高阶网络进行建模, 并在研究其动力学过程中发现了与成对交互作用网络不同的新现象. 然而, 与成对交互作用网络相比, 高阶网络的研究相对较少; 而且, 高阶网络结构相对复杂, 基于结构的统计指标定义较为分散且形式不统一, 这些都给描述高阶网络的拓扑结构特征带来了困难. 鉴于此, 本文综述了两种最常见的高阶网络——超图和单纯形网络——常用的统计指标及其物理意义. 本文有助于加深对高阶网络的理解, 促进对高阶网络结构特征的定量化研究, 也有助于研究者在此基础上开发更多适用于高阶网络的统计指标.Abstract: Complex networks serve as indispensable instruments for characterizing and understanding intricate real-world systems. Recently, researchers have delved into the realm of higher-order networks, seeking to delineate interactions within these networks with greater precision or analyze traditional pairwise networks from a higher-dimensional perspective. This effort has unearthed some new phenomena different from those observed in the traditional pairwise networks. However, despite the importance of higher-order networks, research in this area is still in its infancy. In addition, the complexity of higher-order interactions and the lack of standardized definitions for structure-based statistical indicators, also pose challenges to the investigation of higher-order networks. In recognition of these challenges, this paper presents a comprehensive survey of commonly employed statistics and their underlying physical significance in two prevalent types of higher-order networks: hypergraphs and simplicial complex networks. This paper not only outlines the specific calculation methods and application scenarios of these statistical indicators, but also provides a glimpse into future research trends. This comprehensive overview serves as a valuable resource for beginners or cross-disciplinary researchers interested in higher-order networks, enabling them to swiftly grasp the fundamental statistics pertaining to these advanced structures. By promoting a deeper understanding of higher-order networks, this paper facilitates quantitative analysis of their structural characteristics and provides guidance for researchers who aim to develop new statistical methods for higher-order networks.
-
Key words:
- higher-order network /
- hypergraph /
- simplicial network /
- statistics .
-

-
图 2 单纯形网络相关示意图 (a) 一组时序高阶交互数据; (b) 一个11节点的单纯形网络; (c) 基于图(b)中单纯形网络的骨架网络; (d)一个11节点的团复形网络
Figure 2. Correlation diagrams of the simplicial network: (a) A set of temporal higher-order interaction data; (b) a simplicial network with 11 nodes; (c) a skeleton network based on the simplicial network in Fig. 2(b); (d) a clique complex with 11 nodes.
表 1 基于超图的统计指标总结
Table 1. Summary of statistical indicators of the hypergraph
指标类型 指标名称 度相关指标 度、超度、超边度、余平均度 聚集系数 节点的聚集系数、网络的聚集系数 距离相关指标 路径长度、超节点之间的距离 密度相关指标 超边密度、超图密度 曲率相关指标 Forman-Ricci曲率、Ollivier-Ricci曲率 中心性指标 度中心性、核心度中心性、接近中心性、
介数中心性、特征向量中心性熵相关指标 超图熵、超图的香农熵、加权超图的超图熵 表 2 基于单纯形网络的统计指标总结
Table 2. Summary of statistical indicators of the simplicial network
指标类型 指标名称 度相关指标 上邻接度、下邻接度、度、上 p 邻接度、下 p 邻接度、严格上 p 邻接度、严格下 p 邻接度、
上$(h, p)$ 邻接度、下

$(h, p)$ 邻接度、p 邻接度、最大 p 邻接度、最大单纯形度

路径和距离相关指标 $s_k$ 游走、p 游走、最短路径长度、离心率、直径

中心性指标 度中心性、特征向量中心性、Katz中心性、接近中心性、介数中心性 聚集系数 聚集系数 拓扑不变量 贝蒂数、欧拉示性数 -
[1] Marin A, Wellman B 2011 Social network analysis: An introduction (London: SAGE publications) pp11−25 [2] Kossinets G, Watts D J 2006 Science 311 88 doi: 10.1126/science.1116869 [3] Alon U 2003 Science 301 1866 doi: 10.1126/science.1089072 [4] Alm E, Arkin A P 2003 Curr. Opin. Struct. Biol. 13 193 doi: 10.1016/S0959-440X(03)00031-9 [5] Bose A, Clements K A 1987 Proc. IEEE 75 1607 doi: 10.1109/PROC.1987.13930 [6] Wu F F, Varaiya P 1999 Int. J. Electr. Power Energy Syst. 21 75 doi: 10.1016/S0142-0615(98)00031-3 [7] Williams J C, Mahmassani H S, Herman R 1987 Transp. Res. Rec. 1112 78 [8] Verma T, Araújo N A, Herrmann H J 2014 Sci. Rep. 4 5638 doi: 10.1038/srep05638 [9] Strogatz S H 2001 Nature 410 268 doi: 10.1038/35065725 [10] Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U 2006 Phys. Rep. 424 175 doi: 10.1016/j.physrep.2005.10.009 [11] Costa L D F, Rodrigues F A, Travieso G, Villas Boas P R 2007 Adv. Phys. 56 167 doi: 10.1080/00018730601170527 [12] Barabási A L 2013 Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 371 20120375 doi: 10.1098/rsta.2012.0375 [13] 汪小帆, 李翔, 陈关荣 2012 网络科学导论 (高等教育出版社) 第82页 Wang X F, Li X, Chen G R 2012 Network Science: An Introduction (Higher Education Press) p82 [14] 周涛, 柏文洁, 汪秉宏, 刘之景, 严钢 2005 物理 34 31 doi: 10.3321/j.issn:0379-4148.2005.01.007 Zhou T, Bai W J, Wang B H, Liu Z J, Yan G 2005 Physics 34 31 doi: 10.3321/j.issn:0379-4148.2005.01.007 [15] Courtney O T, Bianconi G 2017 Phys. Rev. E 95 062301 doi: 10.1103/PhysRevE.95.062301 [16] Lung R I, Gaskó N, Suciu M A 2018 Scientometrics 117 1361 doi: 10.1007/s11192-018-2908-2 [17] Pearcy N, Crofts J J, Chuzhanova N 2014 Int. J. Biol. Vet. Agric. Food Eng. 8 752 [18] Mastrandrea R, Fournet J, Barrat A 2015 PloS One 10 e0136497 doi: 10.1371/journal.pone.0136497 [19] Stehlé J, Voirin N, Barrat A, et al. 2011 PloS One 6 e23176 doi: 10.1371/journal.pone.0023176 [20] Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A, Young J G, Petri G 2020 Phys. Rep. 874 1 doi: 10.1016/j.physrep.2020.05.004 [21] Battiston F, Amico E, Barrat A, et al. 2021 Nat. Phys. 17 1093 doi: 10.1038/s41567-021-01371-4 [22] Bianconi G 2021 Higher-order Networks (Cambridge: Cambridge University Press) pp7–45 [23] Shi D, Chen G 2022 Natl. Sci. Rev. 9 nwac038 doi: 10.1093/nsr/nwac038 [24] Zhao D, Li R, Peng H, Zhong M, Wang W 2022 Chaos Solit. Fractals 155 111701 doi: 10.1016/j.chaos.2021.111701 [25] Wang W, Li W, Lin T, Wu T, Pan L, Liu Y 2022 Appl. Math. Comput. 420 126793 doi: 10.1016/j.amc.2021.126793 [26] Millán A P, Torres J J, Bianconi G 2020 Phys. Rev. Lett. 124 218301 doi: 10.1103/PhysRevLett.124.218301 [27] Lucas M, Cencetti G, Battiston F 2020 Phys. Rev. Res. 2 033410 doi: 10.1103/PhysRevResearch.2.033410 [28] Iacopini I, Petri G, Barrat A, Latora V 2019 Nat. Commun. 10 1 doi: 10.1038/s41467-018-07882-8 [29] Chowdhary S, Kumar A, Cencetti G, Iacopini I, Battiston F 2021 J. Phys.: Complex. 2 035019 doi: 10.1088/2632-072X/ac12bd [30] 陈浩宇, 徐涛, 刘闯, 张子柯, 詹秀秀 2024 物理学报 73 038901 doi: 10.7498/aps.73.20231096 Chen H Y, Xu T, Liu C, Zhang Z K, Zhan X X 2024 Acta Phys. Sin. 73 038901 doi: 10.7498/aps.73.20231096 [31] Gómez-Gardenes J, Gómez S, Arenas A, Moreno Y 2011 Phys. Rev. Lett. 106 128701 doi: 10.1103/PhysRevLett.106.128701 [32] Kovalenko K, Dai X, Alfaro-Bittner K, Raigorodskii A, Perc M, Boccaletti S 2021 Phys. Rev. Lett. 127 258301 doi: 10.1103/PhysRevLett.127.258301 [33] Tanaka T, Aoyagi T 2011 Phys. Rev. Lett. 106 224101 doi: 10.1103/PhysRevLett.106.224101 [34] Zhang Y, Latora V, Motter A E 2021 Commun. Phys. 4 195 doi: 10.1038/s42005-021-00695-0 [35] Kundu S, Ghosh D 2022 Phys. Rev. E 105 L042202 doi: 10.1103/PhysRevE.105.L042202 [36] Bick C, Ashwin P, Rodrigues A 2016 Chaos 26 094814 doi: 10.1063/1.4958928 [37] Wang W, Wang Z X, Cai S M 2018 Phys. Rev. E 98 052312 doi: 10.1103/PhysRevE.98.052312 [38] Guilbeault D, Becker J, Centola D 2018 Complex Spreading Phenomena in Social Systems (Cham: Springer) pp3−25 [39] Wang W, Liu Q H, Liang J, Hu Y, Zhou T 2019 Phys. Rep. 820 1 doi: 10.1016/j.physrep.2019.07.001 [40] Wang D, Zhao Y, Luo J, Leng H 2021 Chaos: Interdiscip. J. Nonlinear Sci. 31 053112 doi: 10.1063/5.0040518 [41] 王兆慧, 沈华伟, 曹婍, 程学旗 2011 软件学报 33 171 doi: 10.13328/j.cnki.jos.006323 Wang Z H, Shen H W, Cao Q, Cheng X Q 2011 J. Softw. 33 171 doi: 10.13328/j.cnki.jos.006323 [42] Lü L, Chen D, Ren X L, Zhang Q M, Zhang Y C, Zhou T 2016 Phys. Rep. 650 1 doi: 10.1016/j.physrep.2016.06.007 [43] 任晓龙, 吕琳媛 2014 科学通报 59 1175 doi: 10.1360/972013-1280 Ren X L, Lü L Y 2014 Chin. Sci. Bull. 59 1175 doi: 10.1360/972013-1280 [44] 李江, 刘影, 王伟, 周涛 2024 物理学报 73 048901 doi: 10.7498/aps.73.20231416 Li J, Liu Y, Wang W, Zhou T 2024 Acta Phys. Sin. 73 048901 doi: 10.7498/aps.73.20231416 [45] Lü L, Zhou T 2011 Phys. A: Stat. Mech. Appl. 390 1150 doi: 10.1016/j.physa.2010.11.027 [46] Liu B, Yang R, Lü L 2023 Chaos: Interdiscip. J. Nonlinear Sci. 33 083108 doi: 10.1063/5.0135640 [47] 吕琳媛 2010 电子科技大学学报 39 651 doi: 10.3969/j.issn.1001-0548.2010.05.002 Lü L Y 2010 J. Univ. Electron. Sci. Technol. China 39 651 doi: 10.3969/j.issn.1001-0548.2010.05.002 [48] Newman M E 2006 Proc. Natl. Acad. Sci. 103 8577 doi: 10.1073/pnas.0601602103 [49] Jiang Y, Jia C, Yu J 2013 Phys. A: Stat. Mech. Appl. 392 2182 doi: 10.1016/j.physa.2012.12.013 [50] Watts D J, Strogatz S H 1998 Nature 393 440 doi: 10.1038/30918 [51] Barabási A L, Albert R 1999 Science 286 509 doi: 10.1126/science.286.5439.509 [52] 许小可, 崔文阔, 崔丽艳, 肖婧, 尚可可 2019 电子科技大学学报 48 122 doi: 10.3969/j.issn.1001-0548.2019.01.020 Xu X K, Cui W K, Cui L Y, Xiao J, Shang K K 2019 J. Univ. Electron. Sci. Technol. China 48 122 doi: 10.3969/j.issn.1001-0548.2019.01.020 [53] Zeng Y, Liu B, Zhou F, Lü L 2023 Entropy 25 1390 doi: 10.3390/e25101390 [54] Bick C, Gross E, Harrington H A, Schaub M T 2023 SIAM Rev. 65 686 doi: 10.1137/21M1414024 [55] Feng Y, You H, Zhang Z, Ji R, Gao Y 2019 Proceedings of the AAAI Conference on Artificial Intelligence 33 3558 doi: 10.1609/aaai.v33i01.33013558 [56] Zhu J, Zhu J, Ghosh S, Wu W, Yuan J 2018 IEEE Trans. Netw. Sci. Eng. 6 801 doi: 10.1109/TNSE.2018.2873759 [57] Viñas R, Joshi C K, Georgiev D, Lin P, Dumitrascu B, Gamazon E R, Liò P 2023 Nat. Mach. Intell. 5 739 doi: 10.1038/s42256-023-00684-8 [58] Huang J, Zhang S, Yang F, Yu T, Prasad L N, Guduri M, Yu K 2023 IEEE Trans. Consum. Electron. 1 1775 doi: 10.1109/TCE.2023.3324680 [59] Ruggeri N, Contisciani M, Battiston F, De Bacco C 2023 Sci. Adv. 9 eadg9159 doi: 10.1126/sciadv.adg9159 [60] Wu H, Li N, Zhang J, Chen S, Ng M K, Long J 2024 Pattern Recognit. 146 109995 doi: 10.1016/j.patcog.2023.109995 [61] Mancastroppa M, Iacopini I, Petri G, Barrat A 2023 Nat. Commun. 14 6223 doi: 10.1038/s41467-023-41887-2 [62] Gao Y, Feng Y, Ji S, Ji R 2022 IEEE Trans. Pattern Anal. Mach. Intell. 45 3181 doi: 10.1109/TPAMI.2022.3182052 [63] Li Z, Deng Z, Han Z, Alfaro-Bittner K, Barzel B, Boccaletti S 2021 Chaos Solit. Fractals 152 111307 doi: 10.1016/j.chaos.2021.111307 [64] Gambuzza L V, Di Patti F, Gallo L, et al. 2021 Nat. Commun. 12 1255 doi: 10.1038/s41467-021-21486-9 [65] Wang H, Ma C, Chen H S, Lai Y C, Zhang H F 2022 Nat. Commun. 13 3043 doi: 10.1038/s41467-022-30706-9 [66] Benson A R, Abebe R, Schaub M T, Jadbabaie A, Kleinberg J 2018 Proc. Natl. Acad. Sci. 115 E11221 doi: 10.1073/pnas.1807677115 [67] Shi D, Chen Z, Sun X, Chen Q, Ma C, Lou Y, Chen G 2021 Commun. Phys. 4 249 doi: 10.1038/s42005-021-00748-4 [68] Reimann M W, Nolte M, Scolamiero M, et al. 2017 Front. Comput. Neurosci. 11 48 doi: 10.3389/fncom.2017.00048 [69] Sizemore A E, Giusti C, Kahn A, Vettel J M, Betzel R F, Bassett D S 2018 J. Comput. Neurosci. 44 115 doi: 10.1007/s10827-017-0672-6 [70] Kovalenko K, Sendiña-Nadal I, Khalil N, et al. 2021 Commun. Phys. 4 43 doi: 10.1038/s42005-021-00538-y [71] Holland P W, Leinhardt S 1971 Comp. Group Stud. 2 107 doi: 10.1177/104649647100200201 [72] Estrada E, Rodríguez-Velázquez J A 2006 Phys. A: Stat. Mech. Appl. 364 581 doi: 10.1016/j.physa.2005.12.002 [73] Carletti T, Battiston F, Cencetti G, Fanelli D 2020 Phys. Rev. E 101 022308 doi: 10.1103/PhysRevE.101.022308 [74] Carletti T, Fanelli D, Lambiotte R 2021 J. Phys.: Complex. 2 015011 doi: 10.1088/2632-072X/abe27e [75] Aksoy S G, Joslyn C, Marrero C O, Praggastis B, Purvine E 2020 EPJ Data Sci. 9 16 doi: 10.1140/epjds/s13688-020-00231-0 [76] Lu L, Peng X 2013 Internet Math. 9 3 doi: 10.1080/15427951.2012.678151 [77] Vasilyeva E, Romance M, Samoylenko I, Kovalenko K, Musatov D, Raigorodskii A M, Boccaletti S 2023 Entropy 25 923 doi: 10.3390/e25060923 [78] Gao J, Zhao Q, Ren W, Swami A, Ramanathan R, Bar-Noy A 2014 IEEE/ACM Trans. Netw. 23 1805 doi: 10.1109/TNET.2014.2343914 [79] Zlatić V, Ghoshal G, Caldarelli G 2009 Phys. Rev. E 80 036118 doi: 10.1103/PhysRevE.80.036118 [80] Bauer F, Hua B, Jost J, Liu S, Wang G 2017 Modern Approaches to Discrete Curvature (Cham: Springer) pp1−62 [81] Samal A, Sreejith R, Gu J, Liu S, Saucan E, Jost J 2018 Sci. Rep. 8 8650 doi: 10.1038/s41598-018-27001-3 [82] Leal W, Restrepo G, Stadler P F, Jost J 2021 Adv. Complex Syst. 24 2150003 doi: 10.1142/S021952592150003X [83] Eidi M, Farzam A, Leal W, Samal A, Jost J 2020 Theory Biosci. 139 337 doi: 10.1007/s12064-020-00328-0 [84] Bauer F, J Jost, S Liu 2012 Math. Res. Lett. 19 1185 [85] Eidi M, Jost J 2020 Sci. Rep. 10 12466 doi: 10.1038/s41598-020-68619-6 [86] Kapoor K, Sharma D, Srivastava J 2013 IEEE 2nd Network Science Workshop New York, USA, April 29–May 1, 2013 p152 [87] Granovetter M S 1973 Am. J. Sociol. 78 1360 doi: 10.1086/225469 [88] Dorogovtsev S N, Goltsev A V, Mendes J F F 2006 Phys. Rev. Lett. 96 040601 doi: 10.1103/PhysRevLett.96.040601 [89] Xiao Q 2013 Res. J. Appl. Sci. Eng. Technol. 5 568 doi: 10.19026/rjaset.5.4991 [90] Lee J, Lee Y, Oh S M, Kahng B 2021 Chaos: Interdiscip. J. Nonlinear Sci. 31 061108 doi: 10.1063/5.0056683 [91] Bonacich P 1972 J. Math. Sociol. 2 113 doi: 10.1080/0022250X.1972.9989806 [92] Benson A R 2019 SIAM J. Math. Data Sci. 1 293 doi: 10.1137/18M1203031 [93] Lemmens B, Nussbaum R 2012 Nonlinear Perron-frobenius Theory (Vol. 189) (Cambridge: Cambridge University Press) pp2−4 [94] Clausius R 1879 The Mechanical Theory of Heat (Macmillan) pp327−365 [95] Shannon C E 1948 Bell Syst. Tech. J. 27 379 doi: 10.1002/j.1538-7305.1948.tb01338.x [96] Bloch I, Bretto A 2019 Discrete Geometry for Computer Imagery: 21st IAPR International Conference Marne-la-Vallée, France, March 26–28, 2019 pp143–154 [97] Hu D, Li X L, Liu X G, Zhang S G 2019 Acta Math. Sin. Engl. Ser. 35 1238 doi: 10.1007/s10114-019-8093-2 [98] Wang H, Xiao G, Yan Y, Suter D 2018 IEEE Trans. Pattern Anal. Mach. Intell. 41 697 doi: 10.1109/TPAMI.2018.2803173 [99] Goldberg T E 2002 Sr. Thesis Bard Coll. 6 25 [100] Estrada E, Ross G J 2018 J. Theor. Biol. 438 46 doi: 10.1016/j.jtbi.2017.11.003 [101] Serrano D H, Hernández-Serrano J, Gómez D S 2020 Chaos Solit. Fractals 137 109839 doi: 10.1016/j.chaos.2020.109839 [102] Serrano D H, Gómez D S 2020 Appl. Math. Comput. 382 125331 doi: 10.1016/j.amc.2020.125331 [103] Bonacich P 2007 Soc. Netw. 29 555 doi: 10.1016/j.socnet.2007.04.002 [104] Katz L 1953 Psychometrika 18 39 doi: 10.1007/BF02289026 [105] Estrada E, Knight P A 2015 A First Course in Network Theory (Oxford: Oxford University Press) pp157−160 [106] Okamoto K, Chen W, Li X Y 2008 International Workshop on Frontiers in Algorithmics Changsha China, June 19–21, 2008 pp186–195 [107] Newman M E 2005 Soc. Netw. 27 39 doi: 10.1016/j.socnet.2004.11.009 [108] Maletić S, Rajković M, Vasiljević D 2008 Computational Science–ICCS 2008: 8th International Conference Kraków Poland, June 23–25, 2008 pp568–575 [109] Shi D, Lü L, Chen G 2019 Natl. Sci. Rev. 6 962 doi: 10.1093/nsr/nwz050 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: