-
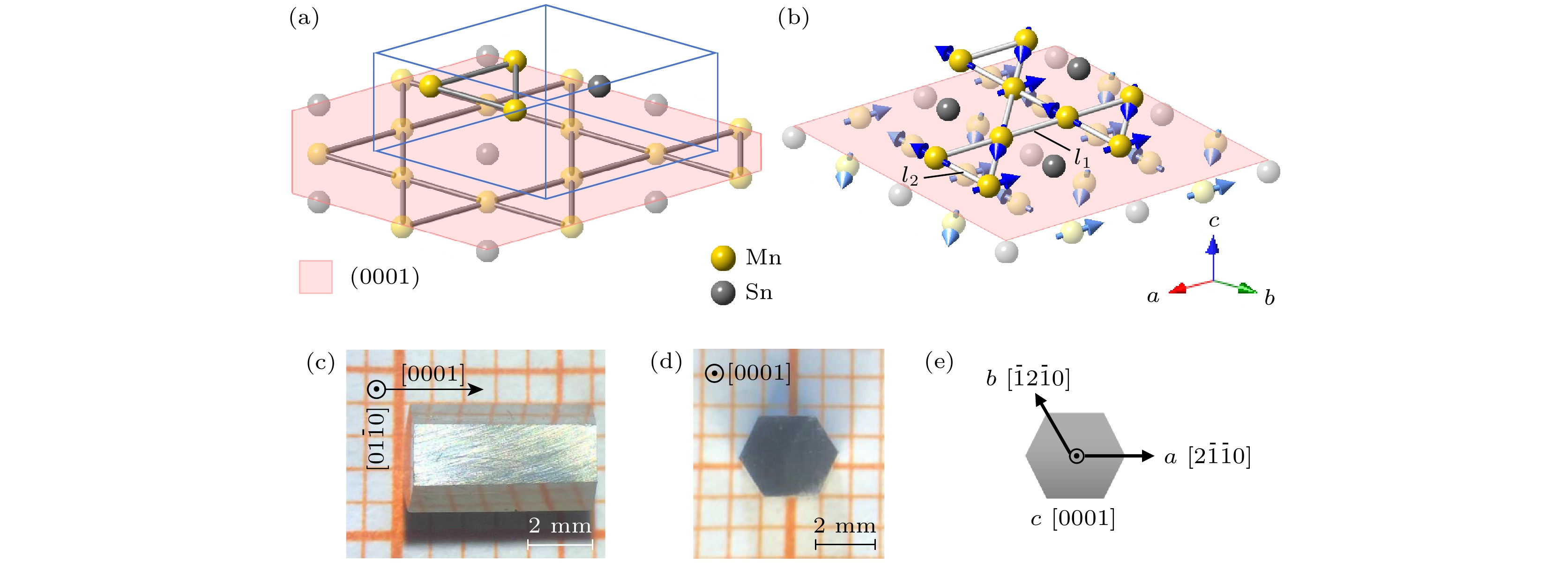
Mn3Sn具有非共线反铁磁结构并表现出反常霍尔效应[1-6]、拓扑霍尔效应[7-11]、反常能斯特效应[12,13]和磁光克尔效应[14,15]等新奇的物理现象, 这使得Mn3Sn成为反铁磁自旋电子学领域研究的热点[16-19]. Mn3Sn中这些新奇的物理行为与其特殊的反铁磁结构密切相关[20-27]. 研究表明, Mn3Sn具有Ni3Sn型六角密堆积晶体结构, 空间群为P63/mmc且非对称, 其晶胞由沿着c轴堆叠的两组Mn原子和Sn原子组成, Mn原子在a-b平面形成“kagome”结构(如图1(a)). 在奈尔温度(TN ≈ 420 K)以下, Mn原子在a-b平面表现出非共线自旋磁序, 并且相邻Mn原子之间的磁矩夹角为120°(如图1(b))[28], 这种特殊的非共线反铁磁结构打破了时间反演对称性[29], 使得在Mn3Sn这种强关联体系中观察到通常只有在弱关联体系中才能出现的物理现象. 因此, 理论上通过调控Mn3Sn的磁结构(自旋)就能实现对其相关物理性能的调控.
当前反铁磁自旋调控(包括Mn3Sn材料)面临的主要技术挑战是: 1) 如何使自旋翻转变得更容易, 即调控反铁磁性的外场要尽可能小[30]. 2) 如何在室温下实现大的自旋翻转信号, 这就需要使处于更高能态的反铁磁自旋发生翻转[31]. 因此, 能否在室温下实现反铁磁自旋翻转和自旋翻转强度的同时控制? 这成为反铁磁材料走向应用亟待解决的问题[32,33]. 为了解决这一关键科学问题, 人们发展了许多反铁磁自旋的调控方法, 包括利用自旋-轨道耦合作用和自旋-晶格耦合作用, 通过电场和光场对反铁磁自旋进行调控[34,35]; 利用磁交换耦合作用, 通过磁场对反铁磁自旋进行调控[36]; 近几年中, 人们在非共线反铁磁Mn3Sn中发现了大的反常霍尔效应[1], 并且这一行为在室温下仍然存在, 这一研究成果使得在室温下实现反铁磁Mn3Sn自旋调控成为可能. 在随后的研究工作中, 人们尝试通过各种方法调控Mn3Sn的物理性能. 例如, Singh等[3]通过对Mn3Sn单晶施加等静压的方式, 将室温下Mn3Sn的反常霍尔电阻率由3.5 μΩ·cm提高到4.5 μΩ·cm; Deng等[37]在Mn3Sn薄膜中实现了室温零磁场下的全电学调控, 他们采用约5×106 A/cm2的小写入电流密度, 实现了Mn3Sn的全电流感应确定性开关, 使Mn3Sn薄膜在室温下表现出大的反常霍尔信号; 另外他们还通过控制温度和Dzyaloshinskii-Moriya相互作用实现了Mn3Sn自旋织构的调控[37-40]; Wang等[41]通过在铁电氧化物PMN-PT上集成Mn3Sn薄膜, 使Mn3Sn薄膜材料在几十mT的小开关磁场下达到了与块体单晶完全相当的大反常霍尔效应. Ikhlas等[42]最近报道了Mn3Sn单晶在MPa级别单轴应力下的压磁效应, 表明对Mn3Sn施加单轴应力将会产生与应力成正比的净磁矩, 在沿着
$ \text{[01}\bar{1}\text{0]} $ 方向施加应力的情况下, 磁化率(χ)在0—270 MPa范围内是一个定值, 大约为0.0125 μB/(f.u.·T).我们早期的研究工作表明, 在极低温下(~2 K), 在反铁磁赤铁矿(hematite, Fe2O3)与反铁磁钛铁矿(ilmenite, FeTiO3)形成的(Fe2O3)1–x-(FeTiO3)x (HI)固溶物中, 由于两种不同磁各向异性的反铁磁格子之间的竞争关系, 使得系统的能量不能处于最低而形成一种亚稳态(通常我们称之为“磁阻挫”)[43]. 这种亚稳的磁阻挫态很容易在外场的驱动下发生变磁性转变(“雪崩式”翻转), 从而出现磁化强度在某一临界磁场下发生突变的磁化跳跃行为. 这一研究成果使我们看到了采用调控磁阻挫途径实现反铁磁自旋翻转的希望. 最近, 一种针对脆性材料的严重塑性变形技术被建立, 这种技术通过将材料束缚住再对其施加大单轴应力的方式, 成功地在NdFeB, SmCo和HI固溶物等脆性材料中实现了微结构控制[44-52]和严重塑性变形[53-55]. Mn3Sn单晶的滑移系统数量很少, 其延展性很差, 是一种脆性材料[56], 我们已经利用此项技术使Mn3Sn单晶发生塑性变形, 在单晶中实现了大的应变, 并且在室温下观察到了大的面外铁磁性[57]. 由于大的应变会在Mn3Sn中引入各向异性应变能, 这种各向异性应变能可以有效改变体系的反铁磁耦合作用, 从而实现对磁结构的调控, 进而调控其与磁结构相关的物性, 例如零场交换偏置行为、拓扑霍尔效应、大的面外铁磁性等[57-59]. 因此可猜测在Mn3Sn单晶中施加GPa级别的单轴应力, 其被磁化的难易程度即磁化率将会表现出新的变化规律.
本文采用高压压缩束缚变形技术, 在Mn3Sn单晶中施加了GPa级别的单轴应力. 我们发现在GPa级别的应力下, Mn3Sn单晶的χ不再是定值, 而是随着应力的增大而增大. 在沿着
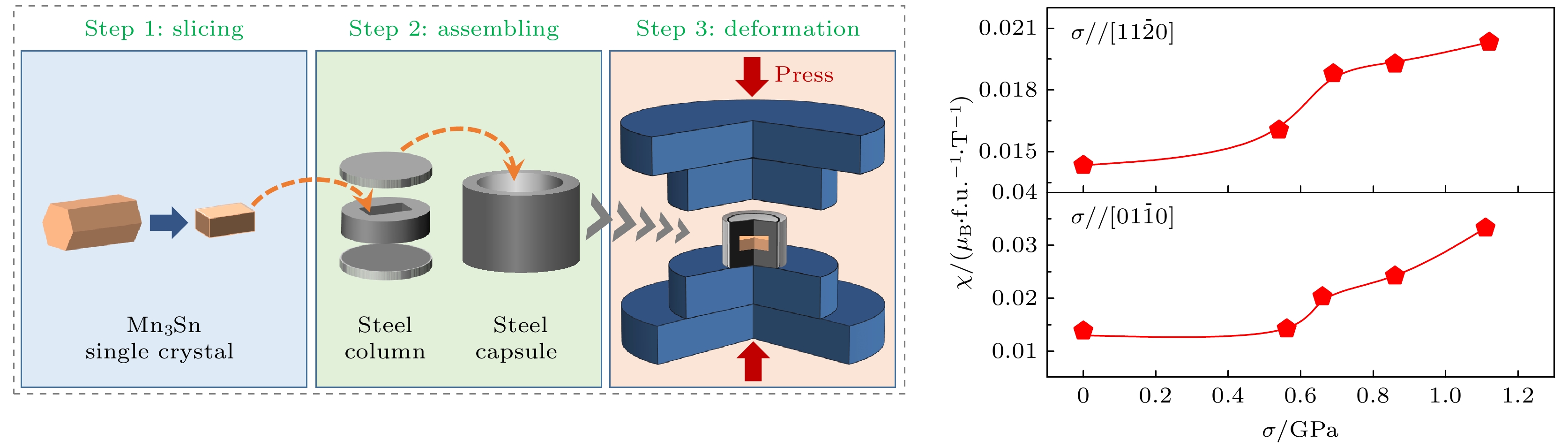
$ \text{[01}\bar{1}\text{0]} $ 方向施加应力的情况下, 当应力为0.86 GPa时, χ ≈ 0.0242 μB/(f.u.·T); 当应力为1.11 GPa时, χ ≈ 0.0332 μB/(f.u.·T), 这一结果也是Ikhlas等[42]报道的2.66倍. 当沿$ \text{[11}\bar{2}\text{0]} $ 方向施加1.12 GPa应力后, χ也达到了0.0203 μB/(f.u.·T). -
本文采用Sn助熔剂法制备Mn3Sn单晶[57], 首先将原料Mn块(纯度99.99%)和Sn块(纯度99.99%)以7∶3摩尔比混合后装入氧化铝坩埚中, 将氧化铝坩埚真空密封在石英管中, 之后将石英管放入马弗炉中, 在1000 ℃保持6 h, 再以1.25 ℃/h的速率降至900 ℃, 然后经过离心得到如图1(c), (d)所示的单晶. 单晶为表面呈金属光泽的六棱柱体, 横截面为正六边形, 尺寸约为3 mm×3 mm×6 mm, 利用能量色散X射线谱(EDX)确定了单晶的实际成分为Mn2.98Sn1.02, 为了方便表示, 本文中的单晶样品仍然用Mn3Sn表示. 晶体的
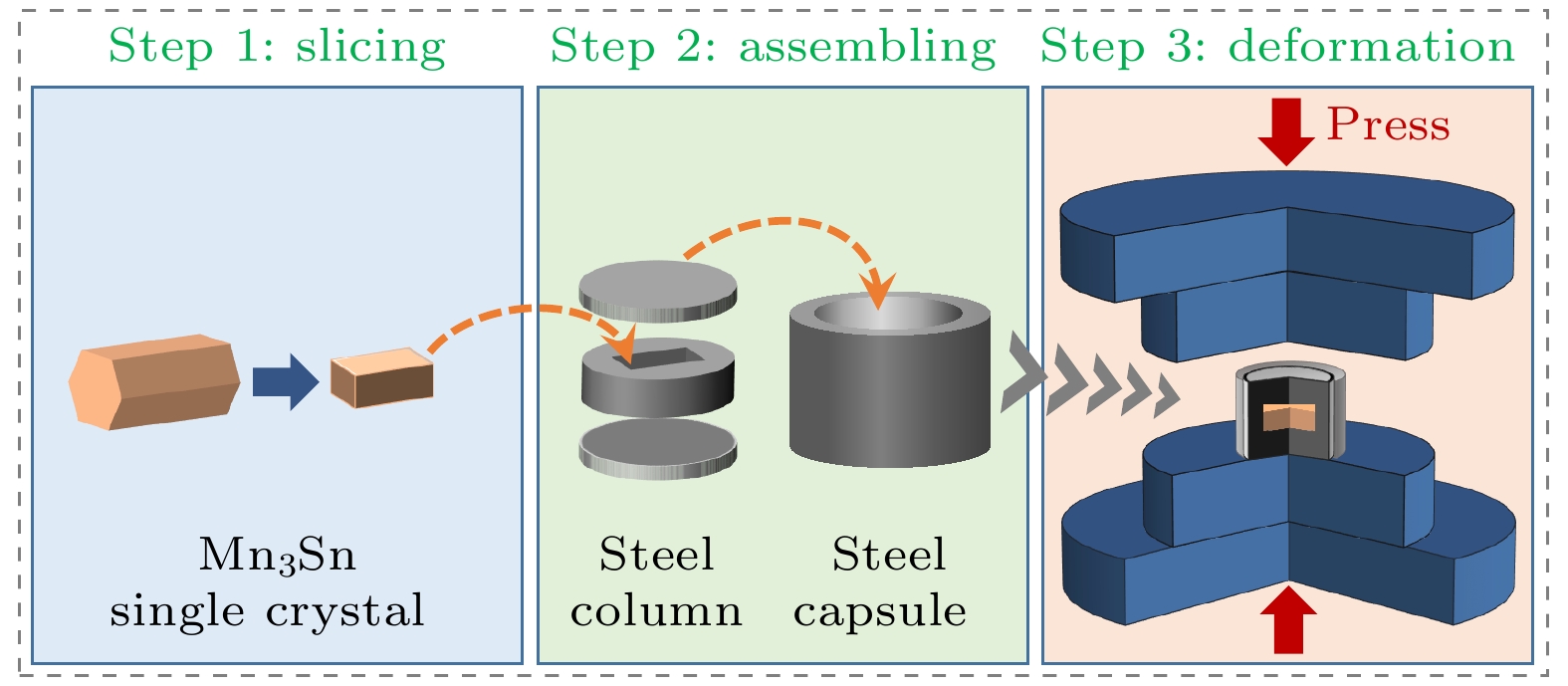
$ \text{[2}\bar{1}\bar{1}\text{0]}, \left[\bar{1}2\bar{1}0\right], \left[0001\right] $ 方向分别代表a, b和c轴, 如图1(e)所示.本文利用高压束缚变形方式对样品施加GPa级别的单轴应力, 其原理如图2所示. 首先将Mn3Sn单晶打磨成规则的立方体, 为防止单晶样品碎裂, 需要将样品镶嵌在不锈钢圆片中, 然后将其放入不锈钢套中, 最后对样品上下施加GPa级的单轴应力, 进行强束缚高应力压缩变形. 本文使用商用600 kN的轴向压力机器进行高压束缚变形, 采用X射线衍射(XRD)、透射电子显微镜(TEM)对样品的微观结构进行表征, 利用Rietveld法拟合X射线测试结果, 利用振动样品磁强计(VSM)测试样品磁性.
-
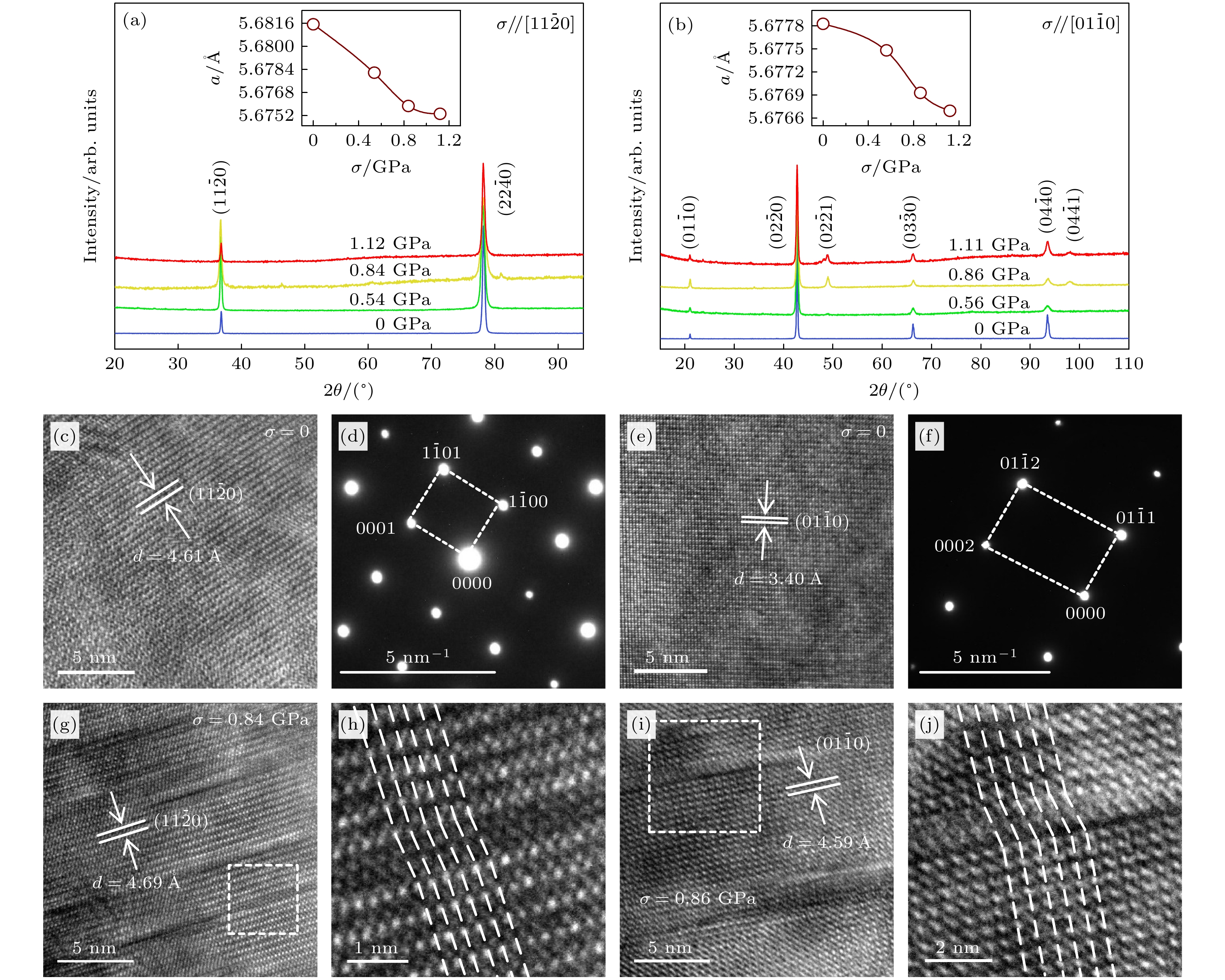
采用XRD方法分析样品的晶体结构. 图3(a), (b)展示了不同应力(σ)下Mn3Sn单晶的XRD图. 可以观察到当未施加应力(σ = 0)时, 只有
$ \left(11\bar{2}0\right) $ 和$ \text{(01}\bar{1}\text{0)} $ 晶面族的衍射峰, 未出现其他衍射峰, 样品的晶胞参数为a = 5.6740 Å, c = 4.5370 Å. 另外, 图3(d), (f)展示的$ \left(11\bar{2}0\right) $ 和$ \text{(01}\bar{1}\text{0)} $ 晶面的选区电子衍射(SAED)图谱均为规则排列的衍射斑点, 上述结果表明我们制备的样品为纯相的Mn3Sn单晶. 在施加应力后的XRD图中可以观察到, 沿$ \text{[11}\bar{2}\text{0]} $ 方向施加应力后,$ \left(11\bar{2}0\right) $ 的晶面中未出现其他相的峰; 沿$ \left[01\bar{1}0\right] $ 方向施加应力后, 在σ大于0.86 GPa时$ \text{(01}\bar{1}\text{0)} $ 晶面的XRD图中出现了微弱的$ \text{(02}\bar{2}\text{1)} $ 和$ \text{(0}4\bar{4}\text{1)} $ 峰, 这可能是变形过程中晶面滑移的结果[56]. 图3(a), (b)插图中展示了晶格常数a随应力的变化, 沿$ \text{[11}\bar{2}\text{0]} $ 晶向和$ \left[01\bar{1}0\right] $ 晶向施加应力后, 随着应力的增大a均减小. 当沿$ \text{[11}\bar{2}\text{0]} $ 方向施加应力时, 随着应力的增大, a由5.6815 Å (σ = 0 GPa)逐渐减小为5.6753 Å (σ = 1.12 GPa); 当沿$ \text{[01}\bar{1}\text{0]} $ 方向施加应力时, 随着应力的增大, a由5.6778 Å (σ = 0 GPa)逐渐减小为5.6766 Å (σ = 1.12 GPa). 晶格常数的减小是由于施加应力后单晶中产生了晶格畸变, 而体系的$ \text{[11}\bar{2}\text{0]} $ 方向是体系的能量最低态, 更易受外界应力的影响, 因此沿$ \text{[11}\bar{2}\text{0]} $ 方向施加应力时a减小的幅度更大[60]. 图3(c), (g)展示了沿$ \text{[11}\bar{2}\text{0]} $ 方向施加应力前后$ \text{(11}\bar{2}\text{0)} $ 晶面的高分辨透射电子显微镜(HRTEM)图, 图3(h)是图3(g)的放大图, 可以看到变形后样品中产生了层错缺陷. 沿着$ \left[01\bar{1}0\right] $ 方向施加单轴应力后在样品内部也可以观察到明显的层错, 如图3(i), (j)所示.为了进一步探索在Mn3Sn单晶上施加GPa级单轴应力对体系磁化率的影响, 测量了不同应力下的M-H曲线. 图4(a), (b)分别展示了Mn3Sn单晶在室温下磁场沿着
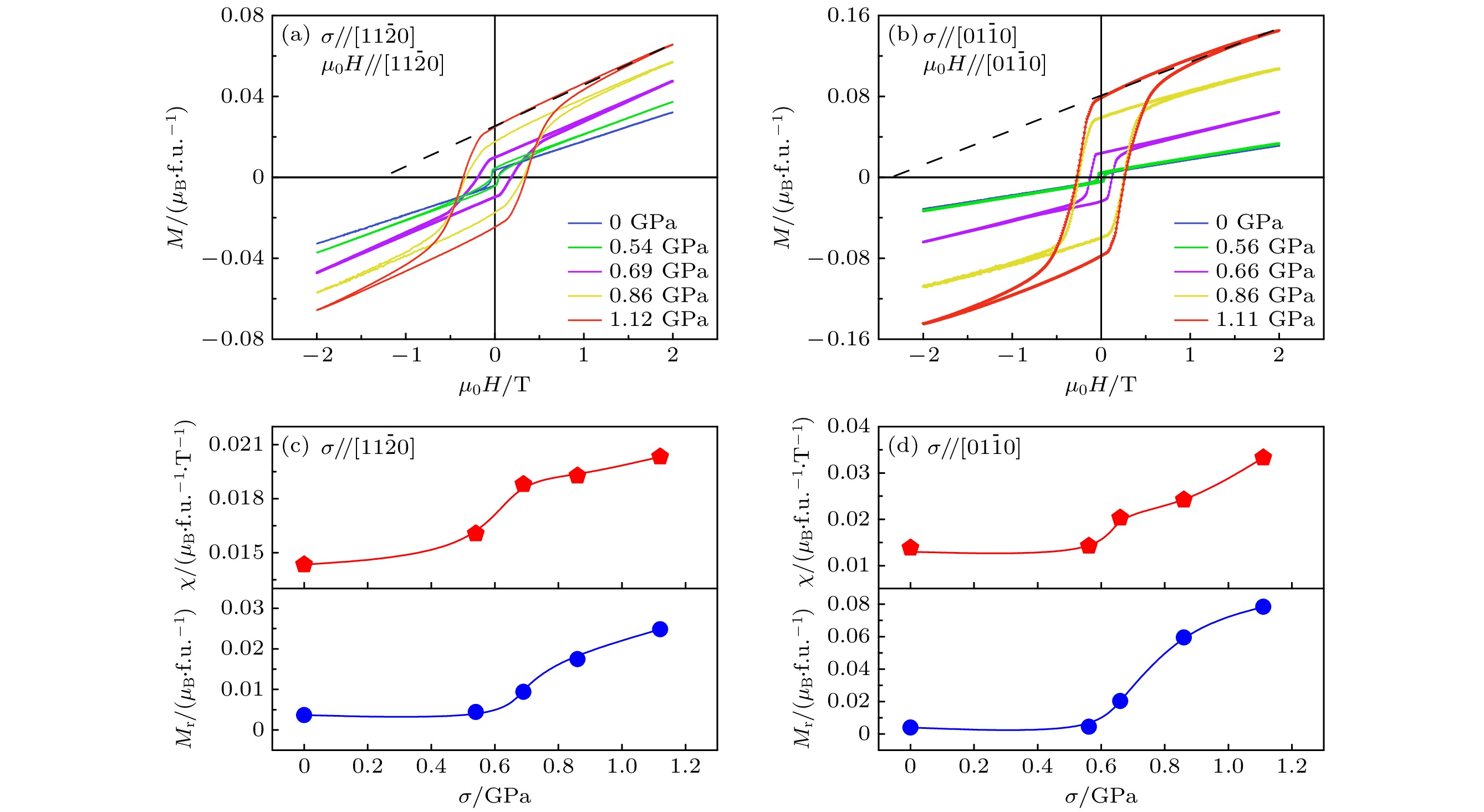
$ \text{[11}\bar{2}\text{0]} $ 和$ \left[01\bar{1}0\right] $ 方向的M-H曲线. 可以看出: 未施加应力时Mn3Sn单晶的M-H曲线中存在较小的磁滞; 随着应力的增大磁滞回线包围的面积显著增大, 矫顽力随着应力的增大而逐渐增大. 这可能是源于GPa级单轴应力在单晶中引入了层错缺陷, 从而引起了更大的矫顽力钉扎作用[61]. 图4(c), (d)展示了沿$ \text{[11}\bar{2}\text{0]} $ 和$ \left[01\bar{1}0\right] $ 方向施加应力时磁化率(χ)和剩余磁化强度(Mr)随σ的变化, 其中$ \chi = \dfrac{{\partial M}}{{\partial H}} $ 由第一象限内磁矩(M)和磁场(H)的线性关系式$ M = {M_{\text{r}}} + \chi {\mu _0}H $ 得到, 沿$ \text{[11}\bar{2}\text{0]} $ 和$ \left[01\bar{1}0\right] $ 方向施加应力后χ和Mr均随着σ的增大而增大. 这是由于Mn3Sn具有非共线反铁磁结构, 当未对其施加应力时, a-b平面内Mn原子磁矩向易轴偏转而存在微弱的铁磁分量, 当沿$ \text{[11}\bar{2}\text{0]} $ 和$ \left[01\bar{1}0\right] $ 两个方向施加高达GPa级单轴应力后, Mn原子磁矩沿易轴的分量增加, 体系的弱铁磁性增强.据Nakatsuji等[1]的报道, 在对Mn3Sn单晶施加MPa级单轴应力时, 体系的χ始终保持定值, 体系的Mr随σ增大而线性增大. 而我们对Mn3Sn单晶施加GPa级单轴应力后, χ随σ的增大而逐渐增大, Mr随应力的增大先缓慢提升, 在应力超过0.6 GPa后迅速增加. 当沿
$ \text{[11}\bar{2}\text{0]} $ 方向施加应力时, 随应力增大, 体系的χ由0.0143 μB/(f.u.·T) (σ = 0)增至0.0203 μB/(f.u.·T) (σ = 1.12 GPa); 当沿$ \left[01\bar{1}0\right] $ 方向施加0.86 GPa的应力后, χ ≈ 0.0242 μB/(f.u.·T), 当施加1.11 GPa应力后χ达到0.0332 μB/(f.u.·T), 为未变形样品的2.4倍.根据Singh等[3]的报道, 压力会导致kagome平面内Mn原子键长发生改变, 从而影响系统内的交换参数. 为了阐明Mn3Sn单晶的χ随GPa级单轴应力增加而增加行为背后的物理机制, 首先计算了不同应力下体系的三聚参数
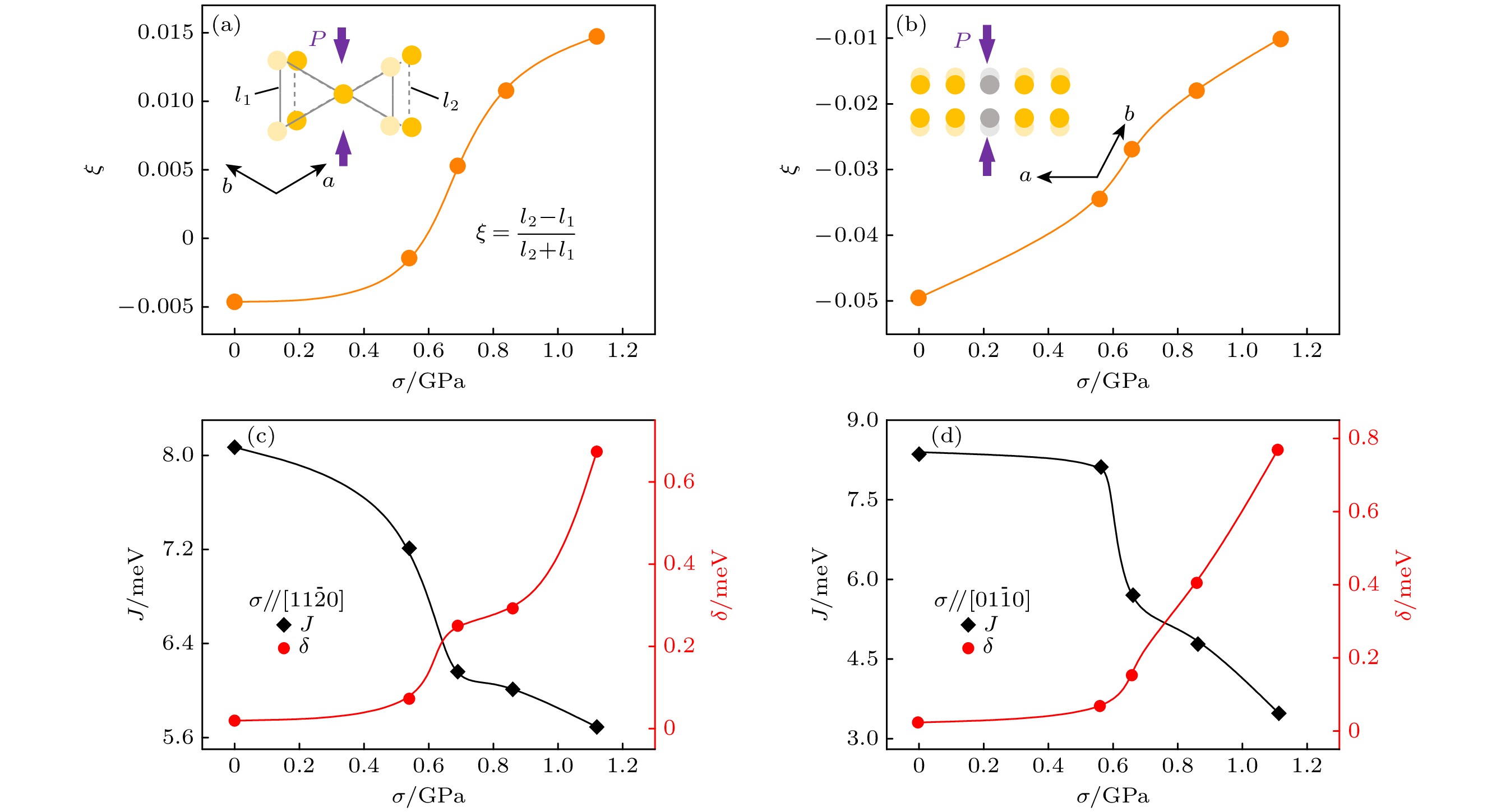
$ \xi = \dfrac{{{l_2} - {l_1}}}{{{l_2} + {l_1}}} $ [3], 其中l1和l2是对应于由kagome子晶格中的Mn原子组成的两个等边三角形的键长. ξ值的大小在表示Mn3Sn这样的六角系统的磁态方面起着至关重要的作用, ξ = 0时表示a-b平面内Mn原子形成理想的kagome晶格, ξ为非零值时表示Mn原子形成的三角形的键长变得不相等. 图5(a), (b)展示了沿$ \text{[11}\bar{2}\text{0]} $ 和$ \left[01\bar{1}0\right] $ 方向施加应力时ξ随σ的变化. 可以看出, 沿不同方向施加应力, ξ均随σ的增大而逐渐增大, 当沿$ \text{[11}\bar{2}\text{0]} $ 方向施加应力时ξ甚至发生了符号的改变. 这是因为应力使Mn3Sn体系内形成了扭曲的kagome晶格, 其中一个Mn三角形收缩, 而另一个则膨胀, 随应力增大Mn原子组成的两个等边三角形的键长相差越来越大, ξ也随之逐渐增大.通过M与H的关系式
$ {M_{({\mathrm{H}})}} = \dfrac{{\hbar \gamma S}}{{2 J}}(\delta - \varepsilon ) + \dfrac{{{\hbar ^2}{\gamma ^2}}}{{2 J}}{\mu _0}H $ 计算出不同应力下各向同性海森伯交换相互作用(J )及各向异性能(δ)的值, 其中ε为应变能, 自旋磁矩S = 3/2, 旋磁比γ = 2 μB/$ \hbar $ [62]. 图5(c), (d)展示了沿$ \text{[11}\bar{2}\text{0]} $ 和$ \left[01\bar{1}0\right] $ 方向施加应力时J和δ随σ的变化, 随着σ的增大, J逐渐减小, δ逐渐增大. 变形前$ \text{(11}\bar{2}\text{0)} $ 面内J = 8.07 meV, 施加1.12 GPa应力后减小为5.69 meV. 沿$ \text{[11}\bar{2}\text{0]} $ 方向对Mn3Sn单晶施加应力前, δ = 0.02 meV, 施加1.12 GPa应力后δ达到0.67 meV. 沿$ \text{[01}\bar{1}\text{0]} $ 方向施加应力后,$ \text{(01}\bar{1}\text{0)} $ 面内J随着σ的增大由8.36 meV减小到3.48 meV, δ由0.02 meV增大到0.77 meV. J的减小和δ的增大说明对Mn3Sn单晶施加GPa级单轴应力后, 体系的各向同性减弱, 各向异性增强.本研究中GPa级单轴应力使单晶Mn3Sn发生了塑性变形, 在单晶中引入了各向异性应变能, 变形后单晶中发生了晶格畸变, 打破了kagome晶格的面内六边形的对称性, 这使得Mn原子组成的两个等边三角形的键长发生改变, 从而影响系统内Mn原子之间的交换耦合, 促使Mn原子磁矩沿易轴偏转, 增强了体系的弱铁磁性. 根据文献[59]报道, 在不同温度下应力对Mn3Sn多晶磁结构的调控效果不同, 在50 K以下, 应力导致Mn3Sn出现受挫反铁磁结构, 在50—400 K时, 应力抑制了螺旋反铁磁结构, 并诱导了非共面反铁磁结构. 此外, 应力在单晶中引入了各向异性应变能, 增强了体系的各向异性, 导致体系的反铁磁耦合作用增强. 因此, 体系的Mr与σ不再是简单的线性依赖关系, 并且χ不再是定值, 随着应力的增大χ逐渐增大.
-
本文采用高压束缚变形技术, 成功地在Mn3Sn单晶上施加了高达GPa级的单轴应力, 研究结果证明GPa级的单轴应力会使Mn3Sn单晶的磁化率χ不再是一个定值, χ会随着应力的增大而增大. 当沿
$ \text{[11}\bar{2}\text{0]} $ 方向施加1.12 GPa应力后, χ达到0.0203 μB/(f.u.·T). 当沿着$ \text{[01}\bar{1}\text{0]} $ 方向施加0.86 GPa应力时, χ ≈ 0.0242 μB/(f.u.·T), 当施加1.11 GPa应力时, χ ≈ 0.0332 μB/(f.u.·T). 进一步引入三聚参数ξ分析χ变化的物理机制, 发现GPa级的单轴应力打破了kagome晶格的面内六边形的对称性, 从而改变Mn原子间的交换相互作用, 增强体系的反铁磁耦合作用, 进而使χ不再是一个定值. 这一发现将会反铁磁自旋调控提供新的思路.
吉帕级单轴应力下Mn3Sn单晶的磁化率增强
Enhancement of magnetic susceptibility of Mn3Sn single crystal under GPa-level uniaxial stress
-
摘要: 如何在室温下实现非共线反铁磁Mn3Sn自旋的调控是一项挑战. 本文通过对Mn3Sn单晶施加GPa级单轴应力调控其磁结构, 发现随着应力的增大, 晶格常数a逐渐减小. 此外, GPa级单轴应力下Mn3Sn的磁化率(χ)不同于MPa级单轴应力下的结果, 其值不再是一个定值, 而是随着应力的增大而增大. 当沿
$ \text{[11}\bar{2}\text{0]} $ 方向施加1.12 GPa应力后, χ达到0.0203 μB/(f.u.·T); 当沿$ \text{[01}\bar{1}\text{0]} $ 方向施加1.11 GPa应力后, χ达到0.0332 μB/(f.u.·T), 为未变形样品的2.4倍. 进一步的实验结果表明, GPa级的单轴应力打破了kagome晶格的面内六边形的对称性, 从而改变Mn原子间的交换相互作用, 增强体系的反铁磁耦合作用, 使χ不再是一个定值. 这一发现将会为反铁磁自旋调控提供新的思路.Abstract: How to achieve spin control of noncollinear antiferromagnetic Mn3Sn at room temperature is a challenge. In this study, we modulate the magnetic structure of Mn3Sn single crystals by subjecting them to uniaxial stress at the GPa level using a high-pressure combined deformation method. Initially, the single crystal is sliced into regular cuboids, then embedded in a stainless steel sleeve, and finally, uniaxial stress is applied along the$ \text{[11}\bar{2}\text{0]} $ direction and$ \text{[01}\bar{1}\text{0]} $ direction of the Mn3Sn single crystal. Under high stress, the single crystal undergoes plastic deformation. Our observations reveal lattice distortion in the deformed single crystal, with the lattice parameter gradually decreasing as the stress level increases. In addition, the magnetic susceptibility of Mn3Sn under GPa uniaxial stress (χ) is different from that under MPa uniaxial stress, and its value is no longer fixed but increases with the increase of stress. When 1.12 GPa stress is applied in the$ \text{[11}\bar{2}\text{0]} $ direction, χ reaches 0.0203$ {\text{μ}}_{\text{B}}\cdot{\text{f.u.}}^{{-1}}\cdot{\text{T}}^{{-1}} $ , which is 1.42 times that of the undeformed sample. In the case of stress applied along the$ \text{[01}\bar{1}\text{0]} $ direction, χ ≈ 0.0332$ {\text{μ}}_{\text{B}}\cdot{\text{f.u.}}^{{-1}}\cdot{\text{T}}^{{-1}} $ when the stress is 1.11 GPa. This result is also 2.66 times greater than the reported results. We further calculate the values of trimerization parameter (ξ), isotropic Heisenberg exchange interaction (J), and anisotropic energy (δ) of the system under different stresses. Our results show that ξ gradually increases, J gradually decreases, and δ gradually increases with the increase of stress. These results show that the GPa uniaxial stress introduces anisotropic strain energy into the single crystal, breaking the symmetry of the in-plane hexagon of the kagome lattice, which causes the bond length of the two equilateral triangles composed of Mn atoms to change. Thus, the exchange coupling between Mn atoms in the system is affected, the anisotropy of the system is enhanced, and the antiferromagnetic coupling of the system is enhanced. Therefore, the system χ is no longer a constant value and gradually increases with the increase of stress. This discovery will provide new ideas for regulating the anti-ferromagnetic spin.-
Key words:
- antiferromagnetic /
- uniaxial stress /
- single crystal /
- lattice distortion .
-

-
图 3 (a), (b)沿
$ \text{[11}\bar{2}\text{0]} $ ,$ \text{[01}\bar{1}\text{0]} $ 方向施加应力变形前后的XRD图; (c), (e)变形前$ \text{(11}\bar{2}\text{0)} $ ,$ \text{(01}\bar{1}\text{0)} $ 晶面的HRTEM图; (d), (f)变形前$ \text{(11}\bar{2}\text{0)} $ ,$ \text{(01}\bar{1}\text{0)} $ 晶面的SAED图; (g), (h)变形后$ \text{(11}\bar{2}\text{0)} $ 晶面的HRTEM图; (i), (j)变形后$ \text{(01}\bar{1}\text{0)} $ 晶面的HRTEM图Figure 3. (a), (b) XRD patterns before and after stress deformation along
$ \text{[11}\bar{2}\text{0]} $ and$ \text{[01}\bar{1}\text{0]} $ directions; (c), (e) HRTEM images of$ \text{(11}\bar{2}\text{0)} $ and$ \text{(01}\bar{1}\text{0)} $ crystal faces before deformation; (d), (f) SAED patterns of$ \text{(11}\bar{2}\text{0)} $ and$ \text{(01}\bar{1}\text{0)} $ crystal faces before deformation; (g), (h) HRTEM images of$ \text{(11}\bar{2}\text{0)} $ crystal face after deformation; (i), (j) HRTEM images of$ \text{(01}\bar{1}\text{0)} $ crystal face after deformation.图 4 (a), (b)沿
$ \text{[11}\bar{2}\text{0]} $ ,$ \text{[01}\bar{1}\text{0]} $ 方向变形前后样品的磁滞回线; (c), (d)沿$ \text{[11}\bar{2}\text{0]} $ ,$ \text{[01}\bar{1}\text{0]} $ 方向变形前后样品的磁化率χ和剩磁Mr随应力的变化Figure 4. (a), (b) Hysteresis loops of samples before and after deformation along
$ \text{}\text{[11}\bar{2}\text{0]}\text{} $ and$ \text{[01}\bar{1}\text{0]} $ directions; (c), (d) the changes of magnetic susceptibility χ and remanence Mr of sample demagnetization curve with stress before and after deformation along$ \text{}\text{[11}\bar{2}\text{0]}\text{} $ and$ \text{[01}\bar{1}\text{0]} $ directions.图 5 (a), (b)沿
$ \text{[11}\bar{2}\text{0]} $ ,$ \text{[01}\bar{1}\text{0]} $ 方向变形前后三聚参数ξ随应力的变化; (c), (d)黑色曲线为沿$ \text{[11}\bar{2}\text{0]} $ ,$ \text{[01}\bar{1}\text{0]} $ 方向施加应力前后单晶的各向同性海森伯交换作用J, 红色曲线为沿$ \text{[11}\bar{2}\text{0]} $ ,$ \text{[01}\bar{1}\text{0]} $ 方向施加应力前后单晶的各向异性能δFigure 5. (a), (b) Changes of trimerization parameters ξ with stress before and after deformation along
$ \text{}\text{[11}\bar{2}\text{0]}\text{} $ and$ \text{[01}\bar{1}\text{0]} $ directions. (c), (d) The black curve shows the isotropic Heisenberg exchange J of a single crystal before and after stress is applied in along$ \text{}\text{[11}\bar{2}\text{0]}\text{} $ and$ \text{[01}\bar{1}\text{0]} $ directions. The red curve shows the anisotropic energy δ of a single crystal before and after stress is applied in$ \text{[11}\bar{2}\text{0]}\text{} $ and$ \text{[01}\bar{1}\text{0]} $ directions. -
[1] Nakatsuji S, Kiyohara N, Higo T 2015 Nature 527 212 doi: 10.1038/nature15723 [2] Li X, Koo J, Zhu Z, Behnia K, Yan B 2023 Nat. Commun. 14 1642 doi: 10.1038/s41467-023-37076-w [3] Singh C, Singh V, Pradhan G, Srihari V, Poswal H K, Nath R, Nandy A K, Nayak A K 2020 Phys. Rev. Res. 2 043366 doi: 10.1103/PhysRevResearch.2.043366 [4] Higo T, Qu D R, Li Y F, Chien C L, Otani Y, Nakatsuji S 2018 Appl. Phys. Lett. 113 202402 doi: 10.1063/1.5064697 [5] Matsuda T, Higo T, Koretsune T, Kanda N, Hirai Y, Peng H, Matsuo T, Yoshikawa N, Shimano R, Nakatsuji S, Matsunaga R 2023 Phys. Rev. Lett. 130 126302 doi: 10.1103/PhysRevLett.130.126302 [6] Bai Y, Wang Z, Lei N, Muhammad W, Xiang L F, Li Q, Lai H L, Zhu Y Y, Wang W B, Guo H W, Yin L F, Wu R Q, Shen J 2022 Chin. Phys. Lett. 39 108501 doi: 10.1088/0256-307X/39/10/108501 [7] Rout P K, Madduri P V P, Manna S K, Nayak A K 2019 Phys. Rev. B 99 094430 doi: 10.1103/PhysRevB.99.094430 [8] Yan J, Luo X, Lv H Y, Sun Y, Tong P, Lu W J, Zhu X B, Song W H, Sun Y P 2019 Appl. Phys. Lett. 115 102404 doi: 10.1063/1.5119838 [9] Low A, Ghosh S, Changdar S, Routh S, Purwar S, Thirupathaiah S 2022 Phys. Rev. B 106 144429 doi: 10.1103/PhysRevB.106.144429 [10] Xiong D R, Jiang Y H, Zhu D Q, Du A, Guo Z X, Lu S Y, Wang C X, Xia Q T, Zhu D P, Zhao W S 2023 Chin. Phys. B 32 057501 doi: 10.1088/1674-1056/acb9ec [11] Ma H Y, Yin J X, Hasan M Z, Liu J P 2024 Chin. Phys. Lett. 41 047103 doi: 10.1088/0256-307X/41/4/047103 [12] Guo G Y, Wang T C 2017 Phys. Rev. B 96 224415 doi: 10.1103/PhysRevB.96.224415 [13] Ikhlas M, Tomita T, Koretsune T, Suzuki M T, Nishio-Hamane D, Arita R, Otani Y, Nakatsuji S 2017 Nat. Phys. 13 1085 doi: 10.1038/nphys4181 [14] Miwa S, Iihama S, Nomoto T, Tomita T, Higo T, Ikhlas M, Sakamoto S, Otani Y, Mizukami S, Arita R, Nakatsuji S 2021 Small Science 1 2000062 doi: 10.1002/smsc.202000062 [15] Higo T, Man H, Gopman D B, Wu L, Koretsune T, van’t Erve O M J, Kabanov Y P, Rees D, Li Y, Suzuki M T, Patankar S, Ikhlas M, Chien C L, Arita R, Shull R D, Orenstein J, Nakatsuji S 2018 Nat. Photonics. 12 73 doi: 10.1038/s41566-017-0086-z [16] Jungwirth T, Marti X, Wadley P, Wunderlich J 2016 Nat. Nanotechnol. 11 231 doi: 10.1038/nnano.2016.18 [17] Bauer G E W, Saitoh E, Van Wees B J 2012 Nat. Mater. 11 391 doi: 10.1038/nmat3301 [18] Cui B, Cheng B, Hu J F 2021 Chin. Sci. Bull. 66 2042 doi: 10.1360/TB-2021-0034 [19] 闫君, 孙莹, 王聪, 史再兴, 邓司浩, 史可文, 卢会清 2014 物理学报 63 167502 doi: 10.7498/aps.63.167502 Yan J, Sun Y, Wang C, Shi Z X, Deng S H, Shi K W, Lu H Q 2014 Acta Phys. Sin. 63 167502 doi: 10.7498/aps.63.167502 [20] 张源, 胡新宁, 崔春艳, 崔旭, 牛飞飞, 黄兴, 王路忠, 王秋良, 2023 物理学报 72 128401 doi: 10.7498/aps.72.20230328 Zhang Y, Hu X N, Cui C Y, Cui X, Niu F F, Huang X, Wang L Z, Wang Q L 2023 Acta Phys. Sin. 72 128401 doi: 10.7498/aps.72.20230328 [21] 张志东 2015 物理学报 64 067503 doi: 10.7498/aps.64.067503 Zhang Z D 2015 Acta Phys. Sin. 64 067503 doi: 10.7498/aps.64.067503 [22] Fang H W, Lyu M, Su H, Yuan J, Li Y W, Xu L X, Liu S, Wei L Y, Liu X Q, Yang H F, Yao Q, Wang M X, Guo Y F, Shi W J, Chen Y L, Liu E K, Liu Z K 2023 Sci. China Mater. 66 2032 doi: 10.1007/s40843-022-2348-9 [23] An N, Tang M, Hu S, Yang H L, Fan W J, Zhou S M, Qiu X P 2020 Sci. China Phys. Mech. Astron. 63 297511 doi: 10.1007/s11433-019-1525-6 [24] Li X K, Jiang S, Meng Q K, Zuo H K, Zhu Z W, Balents L, Behnia K 2022 Phys. Rev. B 106 L020402 doi: 10.1103/PhysRevB.106.L020402 [25] Yu T Y, Liu R, Peng Y R, Zheng P Y, Wang G W, Ma X B, Yuan Z H, Yin Z P 2022 Phys. Rev. B 106 205103 doi: 10.1103/PhysRevB.106.205103 [26] 赵巍胜, 黄阳棋, 张学莹, 康旺, 雷娜, 张有光 2018 物理学报 67 131205 doi: 10.7498/aps.67.20180554 Zhao W S, Huang Y Q, Zhang X Y, Kang W, Lei N, Zhang Y G 2018 Acta Phys. Sin. 67 131205 doi: 10.7498/aps.67.20180554 [27] 谭碧, 高栋, 邓登福, 陈姝瑶, 毕磊, 刘冬华, 刘涛 2024 物理学报 73 067501 doi: 10.7498/aps.73.20231766 Tan B, Gao D, Deng D F, Chen S Y, Bi L, Liu D H, Liu T 2024 Acta Phys. Sin. 73 067501 doi: 10.7498/aps.73.20231766 [28] Nagamiya T 1979 J. Phys. Soc. Japan 46 787 doi: 10.1143/JPSJ.46.787 [29] Kuroda K, Tomita T, Suzuki M T, Bareille C, Nugroho A A, Goswami P, Ochi M, Ikhlas M, Nakayama M, Akebi S, Noguchi R, Ishii R, Inami N, Ono K, Kumigashira H, Varykhalov A, Muro T, Koretsune T, Arita R, Shin S, Kondo T, Nakatsuji S 2017 Nat. Mater. 16 1090 doi: 10.1038/nmat4987 [30] Song C, You Y F, Chen X Z, Zhou X F, Wang Y Y, Pan F 2018 Nanotechnology 29 112001 doi: 10.1088/1361-6528/aaa812 [31] Baltz V, Manchon A, Tsoi M, Moriyama T, Ono T, Tserkovnyak Y 2018 Rev. Mod. Phys. 90 015005 doi: 10.1103/RevModPhys.90.015005 [32] Coileáin C Ó, Wu H C 2017 SPIN 07 1740014 doi: 10.1142/S2010324717400148 [33] Jungfleisch M B, Zhang W, Hoffmann A 2018 Phys. Lett. A 382 865 doi: 10.1016/j.physleta.2018.01.008 [34] Němec P, Fiebig M, Kampfrath T, Kimel A V 2018 Nat. Phys. 14 229 doi: 10.1038/s41567-018-0051-x [35] Wadley P, Howells B, Železný J, Andrews C, Hills V, Campion R P, Novák V, Olejník K, Maccherozzi F, Dhesi S S, Martin S Y, Wagner T, Wunderlich J, Freimuth F, Mokrousov Y, Kuneš J, Chauhan J S, Grzybowski M J, Rushforth A W, Edmonds K W, Gallagher B L, Jungwirth T 2016 Science 351 587 doi: 10.1126/science.aab1031 [36] Sokolov D A, Kikugawa N, Helm T, Borrmann H, Burkhardt U, Cubitt R, White J S, Ressouche E, Bleuel M, Kummer K, Mackenzie A P, Rößler U K 2019 Nat. Phys. 15 671 doi: 10.1038/s41567-019-0501-0 [37] Deng Y C, Liu X H, Chen Y, Du Z, Jiang N, Shen C, Zhang E Z, Zheng H Z, Lu H Z, Wang K Y 2023 Natl. Sci. Rev. 10 nwac154 doi: 10.1093/nsr/nwac154 [38] Liu X H, Feng Q, Zhang D, Deng Y C, Dong S, Zhang E Z, Li W, Lu Q, Chang K, Wang K Y 2023 Adv. Mater. 35 2211634 doi: 10.1002/adma.202211634 [39] Liu X H, Zhang D, Deng Y C, Jiang N, Zhang E Z, Shen C, Chang K, Wang K Y 2024 ACS Nano 18 1013 doi: 10.1021/acsnano.3c10187 [40] Jiang N, Deng Y C, Liu X H, Zhang D, Zhang E Z, Zheng H Z, Chang K, Shen C, Wang K Y 2023 Appl. Phys. Lett. 123 072401 doi: 10.1063/5.0163593 [41] Wang X N, Feng Z X, Qin P X, Yan H, Zhou X R, Guo H X, Leng Z G G, Chen W Q, Jia Q N, Hu Z X, Wu H J, Zhang X Y, Jiang C B, Liu Z Q 2019 Acta Mater. 181 537 doi: 10.1016/j.actamat.2019.10.020 [42] Ikhlas M, Dasgupta S, Theuss F, Higo T, Kittaka S, Ramshaw B J, Tchernyshyov O, Hicks C W, Nakatsuji S 2022 Nat. Phys. 18 1086 doi: 10.1038/s41567-022-01645-5 [43] Song P, Li G K, Ma L, Zhen C M, Hou D L, Wang W H, Liu E K, Chen J L, Wu G H 2014 J. Appl. Phys. 115 213907 doi: 10.1063/1.4881527 [44] Liu Y G, Xu L, Wang Q F, Li W, Zhang X Y 2009 Appl. Phys. Lett. 94 172502 doi: 10.1063/1.3126444 [45] Li X H, Lou L, Song W P, Huang G W, Hou F C, Zhang Q, Zhang H T, Xiao J W, Wen B, Zhang X Y 2017 Adv. Mater. 29 1606430 doi: 10.1002/adma.201606430 [46] Huang G W, Zhu G J, Lou L, Yan J C, Song W P, Hou F C, Hua Y X, Zhang Q, Li X H, Zhang X Y 2018 Mater. Lett. 217 219 doi: 10.1016/j.matlet.2018.01.104 [47] Zhang X Y 2020 Mater. Res. Lett. 8 49 doi: 10.1080/21663831.2019.1691668 [48] Zhang H T, Zhang T, Zhang X Y 2023 Adv. Sci. 10 2300193 doi: 10.1002/advs.202300193 [49] Lou L, Li Y Q, Li X H, Li H, Li W, Hua Y X, Xia W, Zhao Z, Zhang H T, Yue M, Zhang X Y 2021 Adv. Mater. 33 2102800 doi: 10.1002/adma.202102800 [50] Li X H, Lou L, Li Y Q, Zhang G S, Hua Y X, Li W, Zhang H T, Yue M, Zhang X Y 2022 Nano Lett. 22 7644 doi: 10.1021/acs.nanolett.2c02778 [51] Li X H, Lou L, Song W P, Zhang Q, Huang G W, Hua Y X, Zhang H T, Xiao J W, Wen B, Zhang X Y 2017 Nano Lett. 17 2985 doi: 10.1021/acs.nanolett.7b00264 [52] Huang G W, Li X H, Lou L, Hua Y X, Zhu G J, Li M, Zhang H T, Xiao J W, Wen B, Yue M, Zhang X Y 2018 Small 14 1800619 doi: 10.1002/smll.201800619 [53] Li W, Li L L, Nan Y, Li X H, Zhang X Y, Gunderov D V, Stolyarov V V, Popov A G 2007 Appl. Phys. Lett. 91 062509 doi: 10.1063/1.2768023 [54] Rong C B, Zhang Y, Poudyal N, Xiong X Y, Kramer M J, Liu J P 2010 Appl. Phys. Lett. 96 102513 doi: 10.1063/1.3358390 [55] Song P, Yao S, Zhang B X, Jiang B, Deng S S, Guo D F, Ma L, Hou D L 2022 Appl. Phys. Lett. 120 192401 doi: 10.1063/5.0091300 [56] Kandra J T, Lee J Y, Pope D P 1991 Mater. Sci. Eng. A 145 189 doi: 10.1016/0921-5093(91)90248-L [57] Zhang B X, Song P, Deng S S, Lou L, Yao S 2023 Chin. Phys. B 32 087502 doi: 10.1088/1674-1056/acca0b [58] Zhao M Y, Guo W, Wu X, Ma L, Song P, Li G K, Zhen C M, Zhao D W, Hou D L 2023 Mater. Horiz. 10 4597 doi: 10.1039/D3MH00754E [59] Deng J J, Zhao M Y, Wang Y, Wu X, Niu X T, Ma L, Zhao D W, Zhen C M, Hou D L 2022 J. Phys. D: Appl. Phys. 55 275001 doi: 10.1088/1361-6463/ac5da7 [60] Duan T F, Ren W J, Liu W L, Li S J, Liu W, Zhang Z D 2015 Appl. Phys. Lett. 107 082403 doi: 10.1063/1.4929447 [61] 周寿增, 董清飞 2004 超强永磁体: 稀土铁系永磁材料(第2版) (北京: 冶金工业出版社)第59—64页 Zhou S Z, Dong Q F 2004 Super Permanent Magnet: Rare Earth Iron Permanent Magnet Material (2nd Ed.) (Beijing: Metallurgical Industry Press) pp59–64 [62] Cable J W, Wakabayashi N, Radhakrishna P 1993 Solid State Commun. 88 161 doi: 10.1016/0038-1098(93)90400-H -


 首页
首页 登录
登录 注册
注册











 下载:
下载: