首页
登录
注册
-
自由电子激光(free electron laser, FEL)是当前国际公认的新一代先进光源, 与第三代同步辐射光源相比较而言具有超高峰值功率、超短脉冲和 更好的相干性等诸多优点, 可极大提升空间分辨率和缩短实验时间, 为研究更精细更复杂的物质结构和动态过程提供了有利的技术支持, 从而在材料、生物、化学和原子物理等领域都有重大的应用需求[1–5]. 其中, FEL可产生波长为13.5 nm的极紫外(extreme ultra-violet, EUV)辐射在EUV光刻技术领域同样具有极大应用前景[6].
EUV光刻是当前主流的先进光刻技术, 可实现更小的光刻节点. 在EUV光刻掩模缺陷检测、EUV光刻曝光等应用中均需要良好的照明均匀性, 均匀性是保证曝光场内获得均匀分辨率的重要条件[7–9]. FEL可作为一种性能优越的EUV光源, 在上述应用中能够发挥重要作用, 但同时FEL也具有非常高的空间相干性, 会对成像带来不利影响. 高相干性所带来的多光束干涉效应会使光斑强度呈点阵化分布, 导致成像分辨率下降[10–12]. 因此, 在光刻应用中需要对高相干性进行抑制, 降低高相干性的干涉效应. 此外, 除了高相干性带来的不利影响以外, FEL发射的辐射束具有类高斯强度轮廓[10,13], 光强分布是非均匀的, 也无法满足光刻所需的平顶分布的均匀照明.
目前在可见光波段及紫外波段进行相干性抑制及提高照明均匀性的方法主要有随机相位板[11]、微透镜阵列 [14]、扫描微镜[15,16]、旋转散射器[17]、反射式扩散器[18]等方法. 当波长下降至EUV波段时, 相应光学元件的设计和制造难度会随着目标波长的缩短而加大[12]. 匀光管也是实现照明视场光强分布高均匀性的主要方式之一[8,19]. 入射到匀光管内的光束在管内发生多次反射, 每次反射对应一个虚拟子光源, 大量虚拟子光源发出的光在出射端面叠加形成均匀的照明光场[8]. 同时, 具有一定发散度的光束入射到匀光管内不同位置处, 在管内的多次反射过程中会经历不同的路径长度, 不同路径之间的光程差可降低叠加后光束的空间相干性, 减小不同部分光束之间的干涉效应, 起到去相干作用[10].
本文设计了一种基于内表面反射的具有倾斜结构的新型匀光管, 可以降低FEL的高相干性以及解决FEL高斯强度轮廓特性所带来的光强分布集中的问题, 实现照明视场光强均匀分布, 同时还可以按需调整激光束斑尺寸, 使FEL发射的辐射束满足EUV光刻领域应用需求.
-
常规直线型匀光管结构以中心轴线作为旋转对称中心, 如圆柱型中空匀光管和圆锥型中空匀光管等. 由于常规匀光管引入的光程差范围有限, 较难满足去相干所需的光程差大于相干长度的需求. 同时, 常规匀光管结构在出口光线相位是沿离心距离线性变化的, 也无法满足去相干的需求[12]. 因此, 专门设计一种新型匀光管结构, 其在两正交平面内分别具有成对对称分布的倾斜单元. 与具有相同长度和内径的常规匀光管结构相比, 新型匀光管更有利于降低FEL光源的高空间相干性, 消除干涉效应所导致的斑点图案, 提高成像分辨率. 此外, 由于倾斜单元的引入, 使得高斯光源中心区域光线参与反射过程, 从而有助于消除FEL光源初始高斯光强分布特征, 提高照明视场光强分布均匀性.
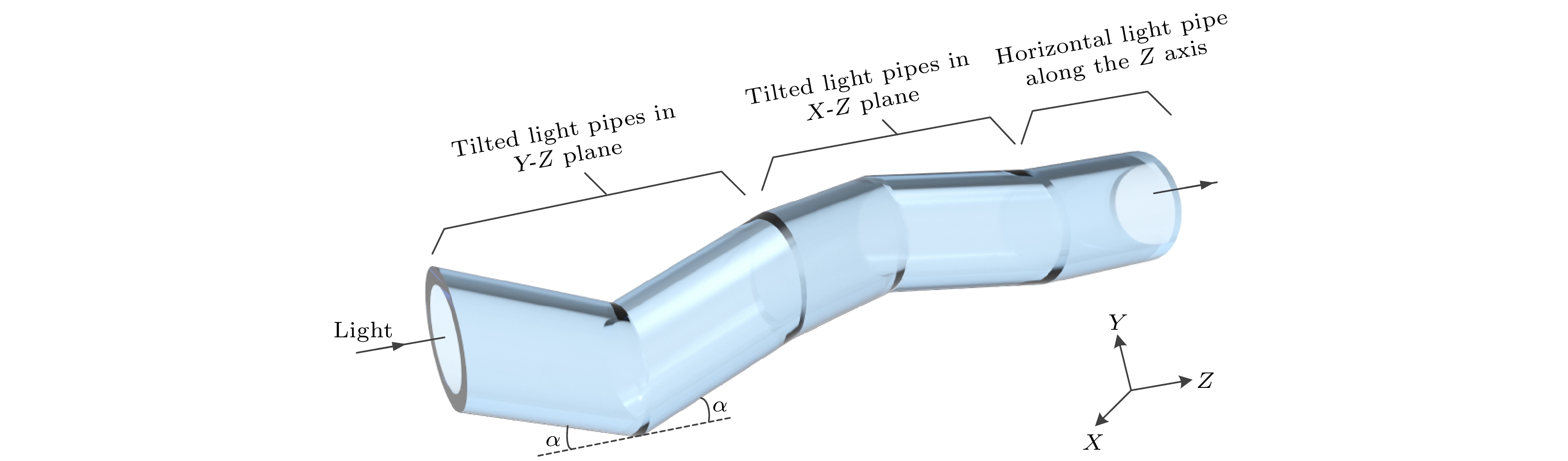
新型匀光管主要包含四节倾斜单元, 平均分布在两个正交平面内, 每个平面内的两节倾斜单元呈对称分布, 其倾斜角(定义为倾斜单元的轴线与水平轴夹角)相反, 如+α, –α (α为0°—90°之间数值). 分布在两正交平面内的四节倾斜单元长度相等、倾斜角绝对值相等, 使得经过四节倾斜单元后输出光束的轴线与原入射光轴相交. 此外, 在四节倾斜单元后端进一步增加一节水平匀光管, 其轴线与原入射光轴重合, 作用是用于导正光轴, 使从新型匀光管输出的光束仍沿原入射光轴. 因此, 所设计的新型匀光管共计包含五节单元, 如图1所示. 当倾斜角度较小时也可去除末端水平单元, 仅余前四节倾斜单元. 所有单元均为圆柱形内部中空结构, 光束在其内表面进行反射.
对于匀光管单元的长度, 需保证入射光束在每个平面内至少发生一次反射, 随后在末端水平匀光管内也至少发生一次反射. 通过匀光管后的输出光斑直径与匀光管出口处截面直径相同, 因此, 可根据目标照明视场需求, 确定匀光管出口直径和截面形状, 从而实现调整照明视场尺寸的目的.
通过在两正交平面内分别设置倾斜单元, 目的是在两维上同时进行光强的均匀化处理, 以及发挥相位扰乱作用, 以此获得高均匀性的照明光场和实现去相干的目的. 此外, 对于常规圆柱型匀光管, 从出口输出光束的发散度是与输入光束发散度相同的. 而对于新型匀光管, 由于设置的倾斜角可有效增加输出光束的发散度, 从而提高输出光束的光展量, 对控制下游光路中聚焦点处最小光斑尺寸可能发挥有利作用.
-
根据杨氏干涉原理可知, 当两个频率相同、振动方向相同的单色子光源S1和S2在空间某一点P相遇, P点到S1和S2的距离分别为r1和r2, 因此两光波在P点产生的光振动可以写成:
其中, a1和a2为子光源S1和S2在P点处的振幅, ω为频率, α1和α2为子光源S1和S2初始相位. 则P点的合振动为
合成波与子光源的频率和传播方向相同. 其中, 振幅A为
那么, P点的合成光强度分布为
其中,
$ I={A}^{2} $ , 相位差$ \delta ={\alpha }_{2}-{\alpha }_{1}=kn\left({r}_{2}-{r}_{1}\right)= \dfrac{2{\mathrm{\pi }}}{\lambda }n\left({r}_{2}-{r}_{1}\right) $ .如果输出光源S1和S2大小相等、强度也相等, 即I1 = I2 = I0, 则合成光强为
因此, 在空间P点叠加处的光强取决于叠加点的相位差δ: 当相位差
$ \delta =2 m{\mathrm{\pi }},\; m $ 为整数时, P点光强为最大值Imax = 4I0, 出现亮纹; 当相位差$ \delta = (2 m+1){\mathrm{\pi }}, m$ 为整数时, P点光强为最小值Imin=0, 出现暗纹.因此, 两个波之间的相位差对于干涉场的形成具有决定性作用.
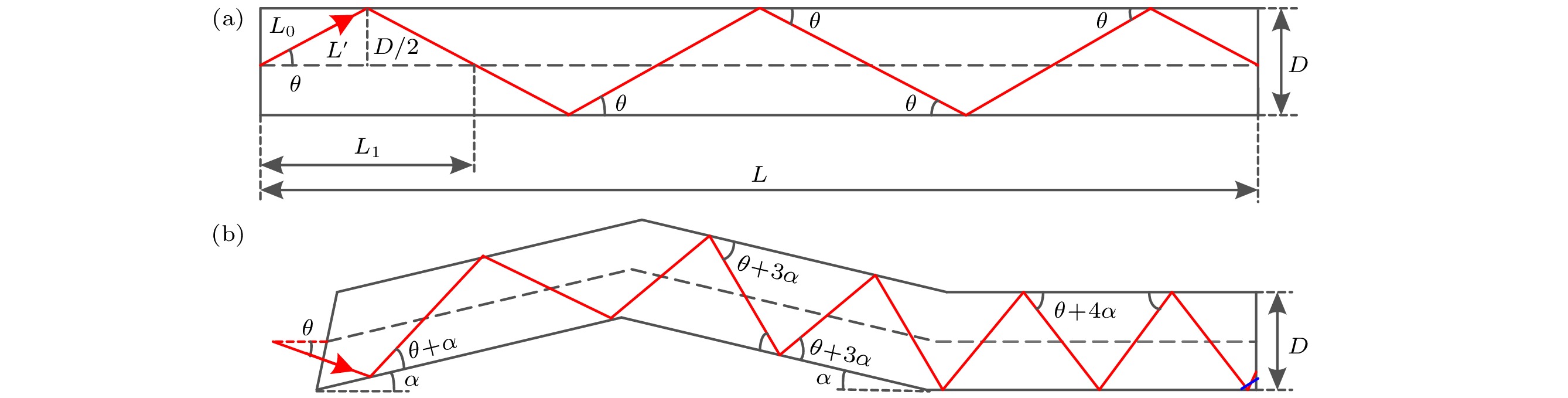
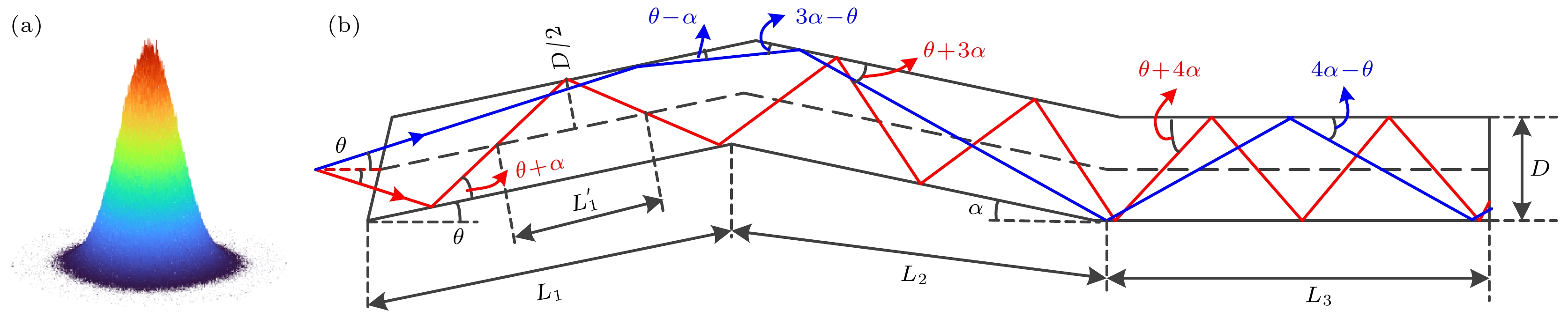
对于常规圆柱型匀光管而言, 如图2(a), 假定高斯光源最大发散半角定义为θ (单位为弧度). 此时入射到匀光管内的光线角度范围为0—θ. 光线在匀光管内发生的反射次数M可表示为
因此, 光线经过常规圆柱型水平匀光管的最大光程rmax为边缘光线传输路径之和, 约为
最小光程rmin对应中心光线传输路径, 有rmin =nL. 因此, 常规匀光管引入的光程差Δ为
其中, n为折射率.
当匀光管的总长度和内径保持不变时, 对于如图2(b)所示具有倾斜单元的匀光管而言, 此时最大角度范围从常规匀光管的角度θ扩大到约θ + 4α. 因此, 带有倾斜单元的匀光管能够引入的光程差简单估算为
对比(11)式和(12)式可发现, 由于倾斜单元的存在可增大光束在匀光管内表面上的掠入射角范围, 由此增加光束通过匀光管过程中所沿不同路径的多样性, 从而使光程差随之增大. 当两束子光束之间光程差大于其相干长度后, 两束子光之间将不再发生干涉. 因此, 由于新型匀光管可显著增加光程差, 对初始相位的空间扰乱程度随之增大, 进而降低光斑不同部分之间发生干涉效应的可能性, 实现去相干的目的, 使输出光束从原本的高空间相干光变为部分相干光或非相干光.
-
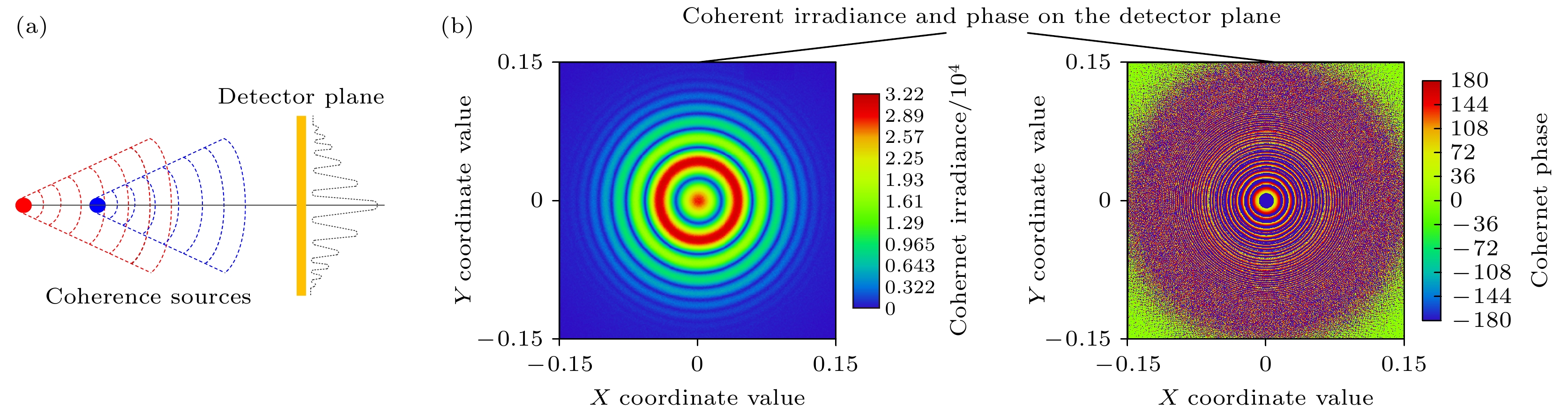
由于FEL为高空间相干光源, 为验证新型匀光管的去相干效果, 在匀光管入口处建立一个具有干涉条纹的相干光场, 观察干涉光场穿过匀光管之后的相位分布变化. 为此, 先行采用两个λ = 13.5 nm的高斯光源, 以沿光轴分布为例, 调整分布距离, 在匀光管入口处建立具有显著干涉条纹的干涉场, 如图3所示. 两光源沿光轴的分布方式, 可在形成干涉场的同时, 不会影响光场均匀性仿真.
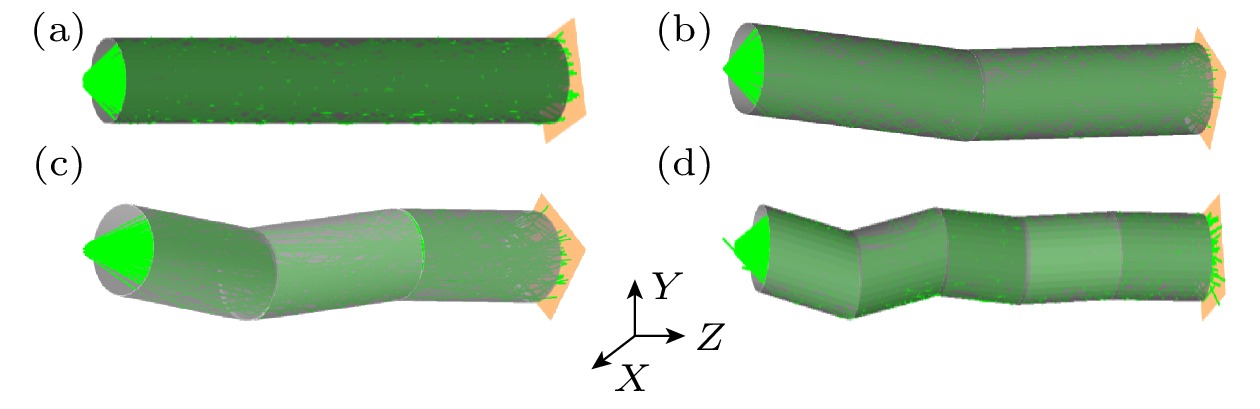
为验证新型匀光管对空间相干场的扰乱效果, 将其与如下3种匀光管结构进行对比分析: 1)常规圆柱型匀光管结构; 2)一节倾斜单元和一节水平单元组成的匀光管结构; 3)在一个平面内具有对称的两节倾斜单元、和一节水平单元组成的匀光管结构. 分别模拟4种不同匀光管结构出口处的相位分布结果. 每种结构中在远离入射光线下游的末端位置均设置一节水平单元, 并将所有倾斜单元的倾斜角度和长度设置为相同数值, 目的是保证输出光轴与入射光轴重合.
采用Zemax OpticStudio光学仿真软件, 模拟在相同匀光管总长度L、内径D、光线发散半角θ情况下, 对比图4中4种匀光管结构出口处的相位分布情况. 并在D和θ不变时, 调整L值, 从而改变光线在匀光管的反射次数后, 观察出口处相位分布的变化情况.模拟参数参考表1.
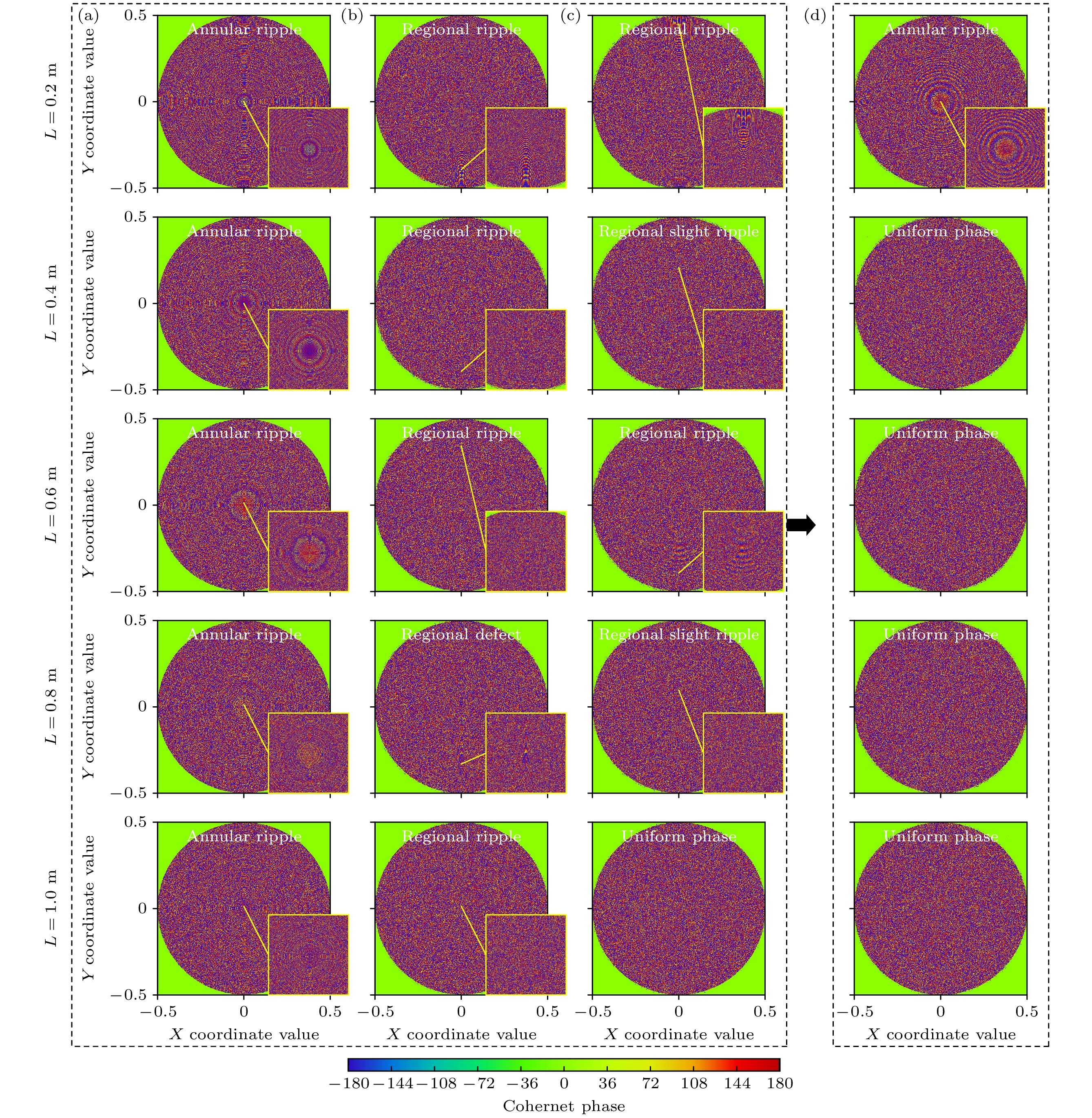
对于常规圆柱匀光管, 由于入射光源中心区域的光线未经历反射过程, 匀光管出口处光场中心区域仍保持初始相位, 经过常规圆柱匀光管后仍存在环状干涉条纹, 如图5(a)所示. 因此, 常规匀光管无法发挥扰乱相位的作用, 去相干能力最弱. 图4(b), (c)所示匀光管, 由于倾斜单元分布在一个平面内, 角度传输范围的展宽仅局限在一维上, 无法完全扰乱相位分布, 因此出口处光场中仍存在局部干涉波纹或相位缺陷, 如图5(b), (c)所示.
图4(d)所示新型匀光管由于能够在两维上将角度传输范围进行展宽, 因此在同等参数条件下具有最强的去相干效果, 出口处相位分布如图5(d)所示. L值较小时光线在匀光管内反射次数少, 去相干能力不足. 当L≥0.4 m后, 在匀光管出口处相位变得杂乱无序, 此时不同的相位差能够均匀分布, 代表着空间中任意点处光波叠加后的相位差随机变化, 激光高空间相干性得到衰减, 实现了去相干作用.
-
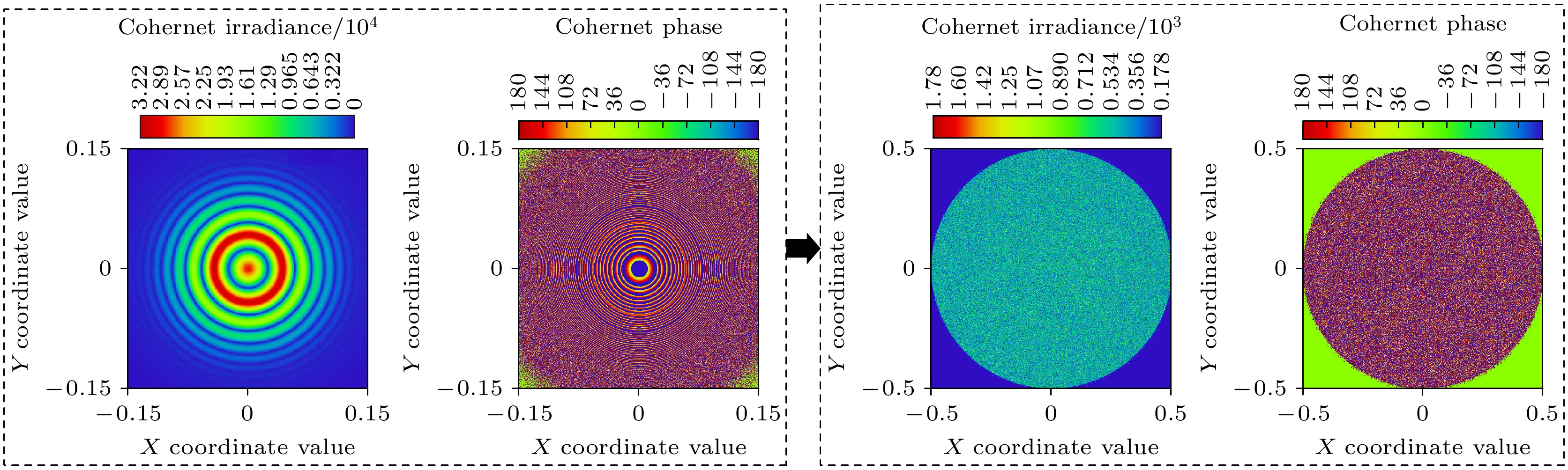
FEL发射具有类高斯强度轮廓的辐射束. 高斯强度轮廓特征为光强主要分布在光斑中心部分, 中心区域光强最大, 向外围光强逐渐衰减, 如图6(a)所示. 从中心向两侧振幅强度按照高斯函数规律变化. 具有高斯强度轮廓的光强过于集中, 分布不均匀, 无法满足平顶照明需求.
匀光管对高斯光束光强轮廓的均匀化处理是通过光束在管内多次反射过程来实现的. 对于常规圆柱型匀光管, 倾斜角度为0, 根据(7)式可知光线在匀光管内最大反射次数约为
$ M=L\theta /D $ . 对于具有倾斜角度α的新型匀光管而言, 如图6(b), 每一平面上均可简化分解为(+α倾斜单元)+(–α倾斜单元)+(水平单元)三部分的组合, 此时边缘光线在管内最大掠入射角不再为固定值θ, 而是随着倾斜单元的变化而变化, 最大掠入射角可增至约θ+4α.光线在匀光管内单次反射传输距离表达式为
在L1倾斜单元内的反射次数为
对于总长度为
$ L={L}_{1}+{L}_{2}+{L}_{3} $ 的匀光管而言, 光线经过匀光管所发生的最大反射次数$M' $ 约为与常规匀光管相比, 在相同长度L和内径D时, 新型匀光管由于引入了倾斜角度α, 因此其反射次数M' 将大于常规匀光管的反射次数M. 光线在匀光管内的反射次数决定了最后出口处的光强分布均匀性. 反射次数越多, 光场分布基本越均匀.
当L = 1 m, D = 1 mm, θ = α = 10 mrad时, 常规圆柱型匀光管可实现最大反射次数约为10次. 而新型匀光管在各单元长度相等时, 可实现的最大反射次数约超过40次.
-
采用Zemax OpticStudio光学仿真软件, 模拟在同等长度L、内径D、光束发散半角θ情况下, 对比图4中4种匀光管结构出口处光场分布情况. 并在D和θ不变时, 调整L值, 改变光线在匀光管内的反射次数后, 模拟匀光管出口光强均匀化效果. 模拟参数参考表1. 采用相干辐照模式模拟光场分布, 相干辐照度模式可同时体现强度和相位的共同作用结果.
对于图7(a)常规圆柱型匀光管, 由于光源中心区域光线未经历反射过程, 因此, 匀光管出口处主要能量仍分布在光场中心区域. 除图7(a)以外, 在图7(b)—(d)三种匀光管结构, 由于倾斜单元的贡献, 使照明光场中能量不再集中在中心区域. 同时, 随着长度增大, 使得反射次数随之增加, 光场中亮线逐步减少, 光强分布变得更为均匀.
根据光强分布均匀性公式[16,20]计算不同长度时匀光管出口处光照面内所有光强的均匀性数值, 如图7中图片左上角所示数据. 数值越小代表照明视场光强基本越均匀:
图7中所标注的均匀性数值与所选探测器像素数也有很大关系, 因此该数值仅作为参考, 用于观测变化情况. 图7(a)中常规圆柱型匀光管的均匀性数值最大, 均匀性最差. 图7(b)—(d)所示具有倾斜单元的匀光管结构, 计算得到的均匀性值显著下降, 光强分布变得均匀. 在相同长度和内径时, 4种结构中图7(d)结构由于在两维上将最大反射次数均进行了扩展, 因此其均匀性数值最小, 照明视场光强分布均匀性最佳, 能够实现最好的光强均匀化效果. 对于FEL光源输出光斑尺寸为200 μm、发散角为20 mrad、且具有高斯强度轮廓的情况下, 当L≥0.6 m后, 经过新型匀光管后可获得比较均匀的光强轮廓分布.
-
与可见光和红外波段不同的是, EUV波段光线反射率对于入射角非常敏感, 小的角度变化就会引起较大的反射率改变. 例如对于单层Ru@100 nm理想膜层, 掠入射角入射时0.1°的角度增量可损失EUV辐射中约0.5%的能量. Zemax OpticStudio光学仿真软件的膜层库中面向紫外至红外波段的常规膜系结构比较成熟, 但常规膜系无法应用于λ = 13.5 nm的EUV波段. 同时, 由于光线在匀光管内传输角度的多样性, 软件膜层库中具有固定反射率的膜层无法真实反映出EUV波段光线穿过匀光管的反射率变化.
具有小发散角的FEL以掠入射的方式通过匀光管. 掠入射时可采用如单层钌膜(Ru)、金膜(Au)等金属膜作为高反射率涂层材料. 反射率是掠入射角的函数, 掠入射角增大, 反射率则下降.
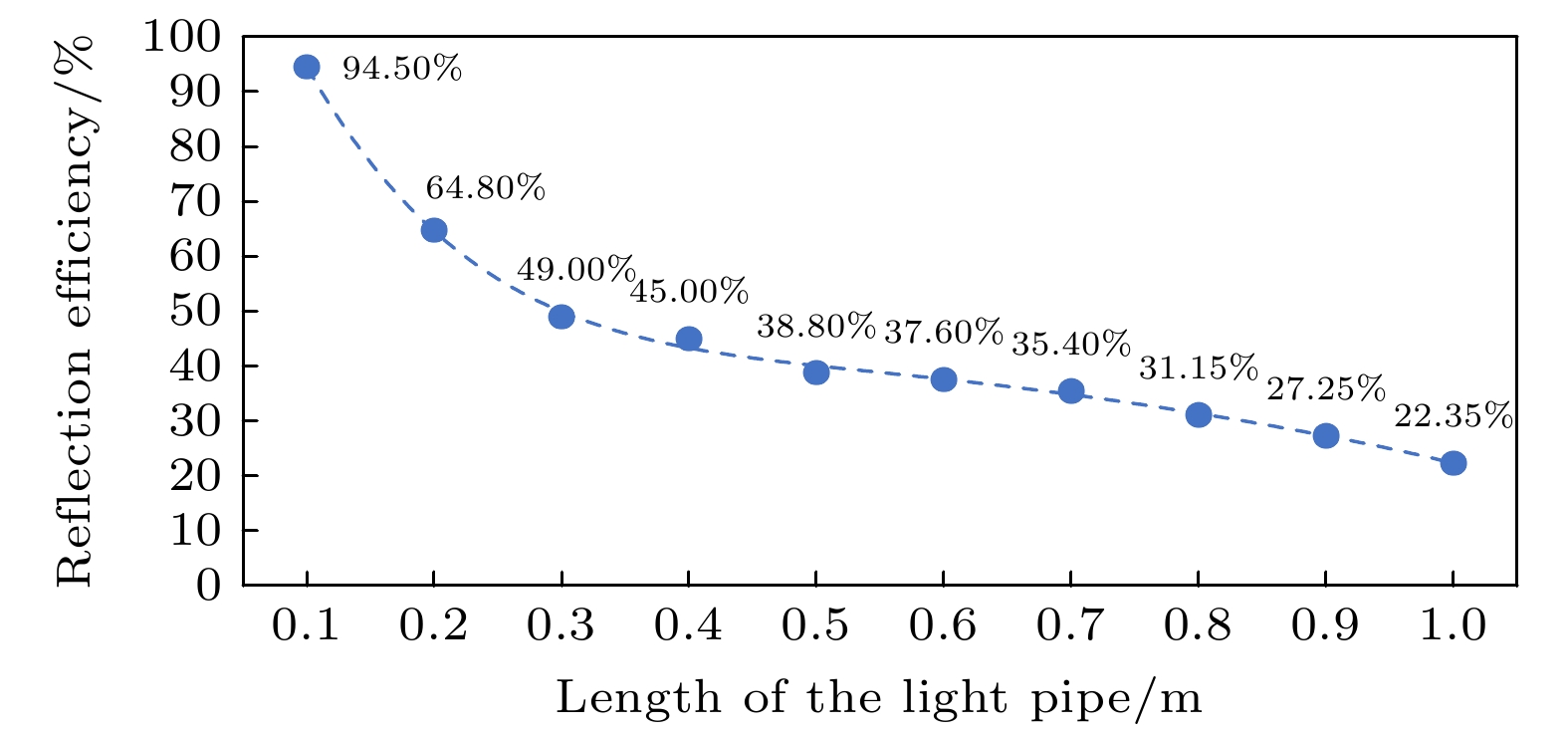
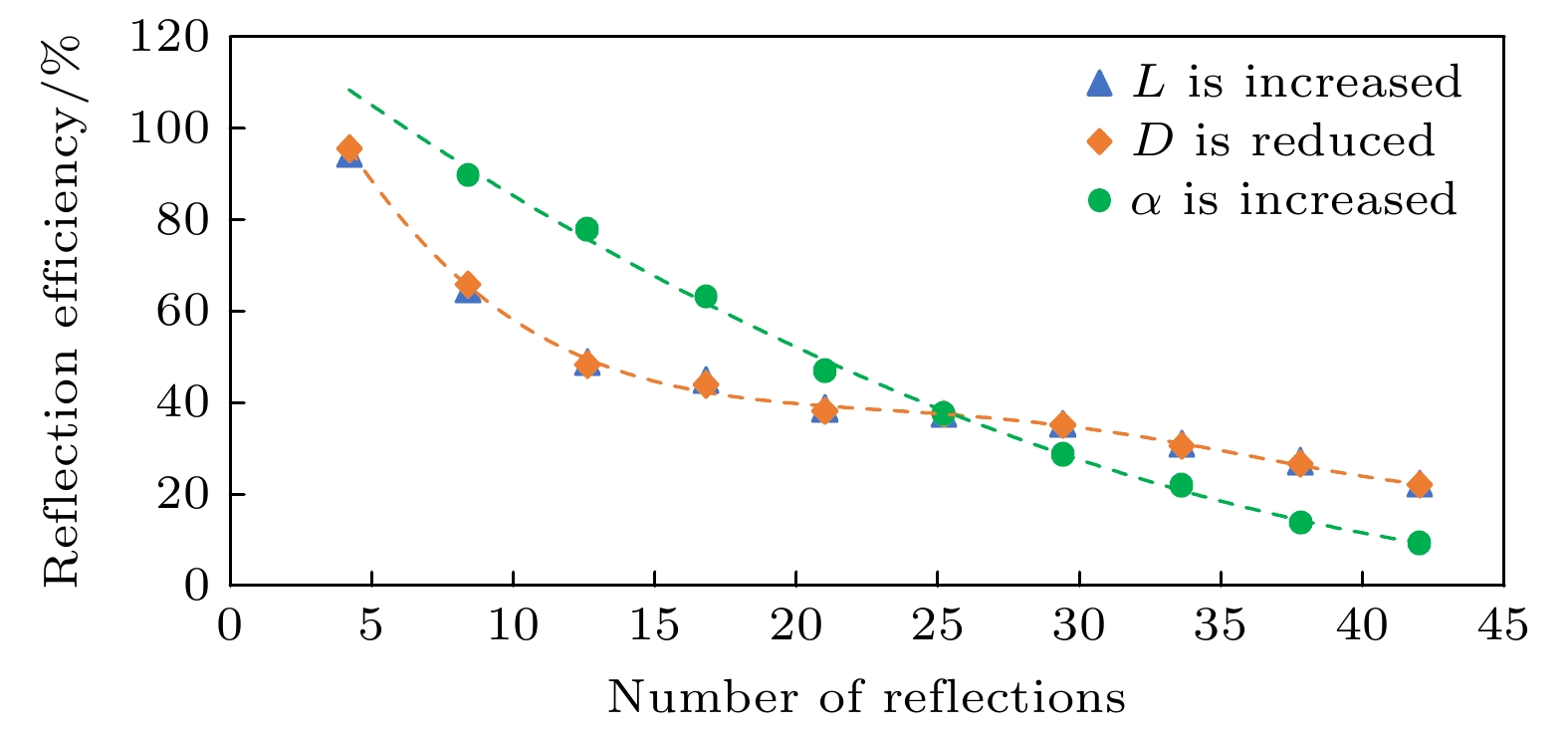
为了真实反映出匀光管对EUV辐射的传输效率, 从美国CXRO网站查询到以100 nm厚度钌膜为例, 在理想情况下(暂未考虑粗糙度)反射率随掠入射角的变化关系. 随后在Zemax OpticStudio光学仿真软件的膜层库采用Table指令, 专门设计一个包含光线在匀光管内所有掠入射角在内的专用膜层. 随后, 对匀光管内表面调用设计的专用膜层来计算匀光管的传输功率, 得到新型匀光管在不同长度时的反射效率, 如图8所示.
由于匀光管长度L的增大会带来反射次数的显著增加, 进而导致EUV辐射在匀光管内的损耗随之增大, 使得反射效率随之下降. 从上文可知当L = 0.6 m时可使匀光管出口处光强分布基本均匀, 此时匀光管反射效率约37.60%. 如出射光轴无需沿原入射光轴时, 可去除末端水平单元, 仅余前端四节倾斜单元, 此时可提高反射率至Rmax约44.58% (L保持0.6 m).
除反射次数增加会增大吸收损耗以外, 在新型匀光管中光束在两维上掠入射角范围的大幅增大也是导致反射传输效率下降的主要原因. 在EUV波段, 反射率对掠入射角的改变非常敏感, 掠入射角的增加会带来反射率的显著降低, 导致该匀光管的能量传输效率减小. 如需提高反射率可从如下几个方面: 1)增大匀光管内径或缩短长度以减少反射次数; 2)减小倾斜单元的倾斜角; 3)还可通过在匀光管上游设置具有曲率的反射镜减小进入匀光管的光束发散度.
因此, 在匀光管参数选择过程中需要综合考虑光场高均匀性与能量传输效率.
-
上文分析了调整匀光管总长度L对于光场分布的影响. 进一步分析调整匀光管内径D、倾斜角度α等数值对于光场光强分布的影响, 并与L变化进行对比. 当探测面在相干辐照度模式下实现均匀光场时, 代表同时获得均匀的光强和相位.
图9中横向分布分别为调整L, D和α值时的出口光场分布, 纵向分布为与各个L值所得反射次数基本等效所对应的D和α值. 照明光场匀化效果与匀光管总长度L、及倾斜角度α成正比, L值越大或α值越大, 匀光管均匀化效果越好, 出口处照明光场分布越均匀. 照明光场匀化效果与内径D成反比, 随着D值减小, 出口照明光场分布越均匀. 对于FEL光源输出光斑尺寸为200 μm、发散角为20 mrad、且具有高斯强度轮廓的光束时, 当匀光管参数满足L ≥ 0.6 m, D ≤ 1 mm且 α≥ 10 mrad, 如图中虚线框内所示, 可获得基本均匀的照明光场分布.
L , D 和 α参数改变时, 匀光管反射效率曲线如图10所示. 能量传输效率与参数变化息息相关. L值越大, 反射次数越多, 能量损耗越大, 因此反射传输效率越低. D值越小, 同理会增加反射次数, 降低传输效率. 从反射次数公式可看出内径D与长度L成线性关系, 同比例改变L与改变D对反射次数的影响是相同的, 因此可获得相近的反射效率.
但倾斜角度α对反射次数的影响比较复杂, 倾斜角度α与反射次数无法成简单线性关系. 同时, 倾斜角度α的增大, 除了增加反射次数外, 还会增大光线在内表面上的掠入射角从而降低能量反射率. 因此, 增大α值会导致更大的能量衰减幅度.
-
本文介绍了一种新型匀光管, 可设置在自由电子激光输出至光刻设备之间的引导整形光路中使用. 其结构主要包含在两正交平面内分别具有成对的、对称分布的倾斜单元. 将新型匀光管与常规圆柱型匀光管、一节倾斜单元匀光管、一个平面内具有成对倾斜单元的匀光管等代表性结构进行比较, 理论计算并仿真模拟了经过不同匀光管结构后的相位变化情况、及光强分布均匀性的改善. 经过对比发现, 在相同光源条件、相同匀光管内径和长度的情况下, 所设计的新型匀光管能够实现最理想的去相干和光强均匀化效果. 此外, 文中提供了一种EUV波段反射膜层新的设计方法, 能够精确反映EUV波段反射率随入射角的变化情况, 使Zemax OpticStudio仿真软件更为充分准确计算出新型匀光管的总传输效率. 目前对于波长为13.5 nm、光斑直径200 μm、发散度20 mrad的FEL高斯光源, 所设计的新型匀光管, 当长度不低于0.6 m、内径为1 mm, 且倾斜角度为10 mrad时, 可起到完全扰乱初始相位、去相干的目的, 获得较为均匀的照明视场. 当改变长度、或内径、或倾斜角度进一步增大反射次数后, 去相干和光强均匀化效果越好, 但是同时能量损耗也越大. 此外, 文中还具体分析了匀光管不同结构参数对照明光场分布的影响、及能量传输效率的影响. 通过本文所设计的新型匀光管进行光强均匀化的基础上, 还可结合其他光强均匀化器件进行光强二次均匀化处理, 进一步提高照明视场光强分布轮廓均匀性.
基于匀光管的极紫外消相干和光强均匀化仿真研究
Simulation study of decoherence and light intensity uniformization for extreme ultraviolet of uniform light pipe
-
摘要: 自由电子激光光源(free electron laser, FEL)可发出波长为13.5 nm的极紫外(extreme ultra-violet, EUV)辐射, 在EUV光刻领域能够发挥重要作用. 但FEL自身的高相干特性以及类高斯光强轮廓分布特征, 会对成像带来不利影响, 无法满足EUV光刻领域成像应用需求. 本文通过计算模拟的方法, 设计了一种匹配FEL应用的、用于EUV波段去相干和光强均匀化的新型匀光管结构. 模拟结果显示, 针对波长为13.5 nm、直径200 μm、发散度20 mrad的FEL-EUV高斯光束, 采用新型匀光管结构, 与常规匀光管结构相比, 在同等长度和内径时, 具有更显著的去相干能力和光场均匀化作用. 当新型匀光管内径为1 mm、总长度不低于0.6 m、倾斜角度为10 mrad时, 高相干光场完全被扰乱, 实现低相干光输出. 并可获得均匀照明光场, 光强分布不均匀性数值从常规圆柱型匀光管的28.38降低至0.97. 同时, 相应能量传输效率为37.6%, 最大传输效率达到44.58%. 结果表明, 新型匀光管结构能够满足EUV辐射去相干应用需求, 同时可提高照明视场光强分布均匀性, 在EUV光刻领域及其他成像应用具有很大应用前景.Abstract:
Free electron laser (FEL) is a high-quality laser source with wavelengths ranging from short-wave X-ray to long-wave infrared ray. Extreme ultra-violet (EUV) radiation at λ = 13.5 nm emitted by FEL can be used in manufacturing integrated circuit, such as EUV lithography exposure and mask defect inspection. However, the high spatial coherence characteristics and similar Gauss intensity profile distribution of FEL source has a negative effect on imaging, and cannot meet the requirements of imaging applications in EUV lithography. In this work, a newly light pipe for decoherence and intensity uniformity in an EUV spectral range is designed through the simulation calculations. The new light pipe consists of two pairs of tilted elements which are symmetrically distributed in the y-z plane and x-z plane, respectively. In this way, the beam transmission divergence in two dimensions can be widened at the same time, and the disturbance of the ray transmission track and spatial phase distribution is increased, so as to achieve the uniformization of light intensity and the reduction of spatial coherence. The simulation results show that for an EUV Gaussian beam at λ = 13.5nm, with a diameter of 200 μm, and a divergence of 20 mrad, the newly designed light pipe has more significant decoherence and illumination field uniformity than the conventional light pipe structure. When the new light pipe has an inner diameter of 1mm, a total length of not less than 600 mm, and a tilt angle of 10mrad , a basically uniform illumination field can be obtained, the coherence is completely disordered, and the non-uniformity of light intensity distribution in the illumination field decreases to 0.97 from 28.38 achieved by conventional cylindrical light pipe. At the same time, the light power transmission efficiency is about 37.6% and the maximum transmission efficiency is about 44.58%. The uniformity can be further improved by increasing the number of reflections. When the inner diameter and tilted angle of the light pipe are unchanged, the length of the light pipe increases to 1m, the non-uniformity of intensity distribution at the illumination field further decreases to 0.90, and the light power transmission efficiency is about 22.35%. The results show that the newly designed light pipe structure can meet the application requirements of decoherence and improve the uniformity of illumination field at EUV wavelength range, and it has great application prospects in EUV lithography and other imaging applications. -
Key words:
- extreme ultraviolet source /
- free electron laser /
- light pipe /
- phase /
- intensity uniformity .
-
-
图 2 光线在匀光管内的传输轨迹示意图 (a) 常规圆柱型水平匀光管; (b)带有倾斜单元的匀光管
Figure 2. Schematic diagram of ray transmission in the light pipe: (a) Conventional cylindrical light pipe; (b) light pipe with tilted elements.
图 3 通过两个具有高空间相干性的高斯光源建立干涉场 (a) 示意图; (b)软件模拟仿真的光场分布
Figure 3. Two Gaussian sources with high spatial coherence are used to obtain the interference field: (a) Schematic diagram; (b) optical field distribution simulated by software.
图 4 四种不同匀光管结构 (a) 常规圆柱型匀光管(结构一); (b) 单倾斜单元匀光管(结构二); (c) 具有在一个平面内一对呈对称分布的倾斜单元的匀光管(结构三); (d) 具有在两正交平面内分别具有一对呈对称分布的倾斜单元的新型匀光管(结构四)
Figure 4. Four light pipes with different structures: (a) Conventional cylindrical light pipe (first structure); (b) light pipe with single tilted element (second structure); (c) light pipe with a pair of tilted elements are symmetrically distributed in the y-z plane (third structure); (d) newly designed light pipe with a two pairs of tilted elements are symmetrically distributed in the y-z plane and x-z plane (fourth structure).
图 5 不同L值时4种匀光管出口处相位分布 (a) 结构一; (b) 结构二; (c) 结构三; (d) 结构四, 新型匀光管
Figure 5. Phase distribution at the outlet of four light pipes when different L values: (a) First structure; (b) second structure; (c) third structure; (d) newly designed light pipe (fourth structure).
图 6 匀光管内光路传输示意图 (a) 高斯光束振幅分布特征; (b) 光线经过新型匀光管的掠入射角变化
Figure 6. Schematic diagram of light transmission in the light pipe: (a) Gaussian beam amplitude distribution; (b) variation of the grazing incidence angle of ray in the newly designed light pipe.
图 7 具有不同长度的4种匀光管在出口处的光场分布 (a)结构一; (b) 结构二; (c) 结构三; (d) 新型匀光管(结构四)
Figure 7. Optical field distribution at the outlet of four light pipes with different length: (a) First structure; (b) second structure; (c) third structure; (d) newly designed light pipe (fourth structure)
图 8 反射效率随匀光管长度的变化曲线
Figure 8. Reflection efficiency curve with the different length of the light pipe.
图 9 分别改变L, D和α时匀光管出口光场分布
Figure 9. Optical field distribution at the outlet of light pipe when L, D and α are variables.
图 10 分别改变L, D和α时匀光管的反射效率
Figure 10. Reflection efficiency of light pipe when L, D and α are variables.
表 1 模拟参数
Table 1. Simulation parameters.
模拟参数 参数值 模拟参数 参数值 光源波长/nm 13.5 光源特征 高斯光源 光源数量/个 2 每个光源功率/W 1 每个光源分析光线数/条 1 × 106 光源发散角 2θ/mrad 20 匀光管总长度 L/mm 200—1000 匀光管内径 D/mm 1 匀光管倾斜单元倾斜角度 α/mrad 10 探测器尺寸/mm 1 × 1 探测器像素数 800 × 800 
下载: 导出CSV
-
[1] 赵振堂, 戴志敏, 张文志, 刘波, 邓海啸, 张满洲, 田顺强 2023 复旦学报 62 293 Zhao Z T, Dai Z M, Zhang W Z, Liu B, Deng H X, Zhang M Z, Tian S Q 2023 J. Fudan Univ. 62 293 [2] 杨家岳, 董文锐, 江凌, 袁开军, 王方军, 吴国荣, 乔德志, 张未卿, 杨学明 2023 中国科学: 化学 53 2103 Yang J Y, Dong W R, Jiang L, Yuan K J, Wang F J, Wu G R, Qiao D Z, Zhang W Q, Yang X M 2023 Sci. Sin. Chim. 53 2103 [3] 吴嘉程, 蔡萌, 陆宇杰, 黄楠顺, 冯超, 赵振堂 2023 光学学报 43 2114002 doi: 10.3788/AOS230893 Wu J C, Cai M, Lu Z J, Huang N S, Feng C, Zhao Z T 2023 Acta Opt. Sin. 43 2114002 doi: 10.3788/AOS230893 [4] 张少军, 郭智, 成加皿, 王勇, 陈家华, 刘志 2023 物理学报 72 105203 doi: 10.7498/aps.72.20222424 Zhang S J, Guo Z, Cheng J M, Wang Y, Chen J H, Liu Z 2023 Acta Phys. Sin. 72 105203 doi: 10.7498/aps.72.20222424 [5] 林宏翔, 魏晓慧, 廖天发, 王文辕, 杜鹃, 杨明亮 2022 光子学报 51 1014008 doi: 10.3788/gzxb20225110.1014008 Lin Z X, Wei X H, Liao T F, Wang W Y, Du J, Yang M L 2022 Acta Photon. Sin. 51 1014008 doi: 10.3788/gzxb20225110.1014008 [6] Norio N, Ryukou K, Hiroshi S, Kimichika T, Yasunori T, Yosuke H, Tsukasa M, Miho S, Takanori T, Olga A T, Takashi O, Hiroshi K 2023 Jap. J. Appl. Phys. 62 SG0809 doi: 10.35848/1347-4065/acc18c [7] 马晓喆, 张方, 黄惠杰 2021 中国激光 48 2005001 doi: 10.3788/CJL202148.2005001 Ma X Z, Zhang F, Huang H J 2021 Chin. J. Lasers 48 2005001 doi: 10.3788/CJL202148.2005001 [8] 刘佳红, 张方, 黄惠杰 2022 激光与光电子学进展 59 0922011 doi: 10.3788/LOP202259.0922011 Liu J H, Zhang F, Huang H J 2022 Laser Optoelectron. Prog. 59 0922011 doi: 10.3788/LOP202259.0922011 [9] Kenneth A G, Markus P B, Antoine W, Iacopo M, Senajith B R, Arnaud P A, Michael R D, Carl W C, Chao W L, Daniel J Z, James B M, Patrick P N, Anne R 2014 SPIE 9048 90480Y [10] Han-Kwang N, Rilpho L D, Gosse C D V 2020 US Paten 20 200 152 345 [11] Christopher N A, Ryan H M, Patrick P N 2011 SPIE 7969 796938 [12] 袁天语, 邵尚坤, 孙学鹏, 李惠泉, 华陆, 孙天希 2023 物理学报 72 034203 doi: 10.7498/aps.72.20221917 Yuan T Y, Shao S K, Sun X P, Li H Q, Hua L, Sun T X 2023 Acta Phys. Sin. 72 034203 doi: 10.7498/aps.72.20221917 [13] 班尼恩 V, 巴特瑞 P, 范格尔库姆 R, 阿门特 L, 彼得 D, 德维里斯 G, 栋克尔 R, 恩格尔伦 W, 弗里基恩斯 O, 格瑞米克 L, 卡塔伦尼克 A, 鲁普斯特拉 E, 尼恩惠斯 H K, 尼基帕罗夫 A, 瑞肯斯 M, 詹森 F, 克鲁兹卡 B 2019 CN Patent 110083019 [14] 肖艳芬, 朱菁, 杨宝喜, 胡中华, 曾爱军, 黄惠杰 2013 中国激光 40 0216001 doi: 10.3788/CJL201340.0216001 Xiao Y F, Zhu J, Yang B X, Hu Z H, Zeng A J, Huang H J 2013 Chin. J. Lasers 40 0216001 doi: 10.3788/CJL201340.0216001 [15] 李慧, 马钺洋, 尹皓玉, 韩晓泉, 黄宇峰, 吴晓斌 2024 激光与光电子进展 61 已录用 doi: 10.3788/LOP231676 Li H, Ma Y Y, Yin H Y, Han X Q, Huang Y F, Wu X B 2024 Laser Optoelectron. Prog. 61 in press doi: 10.3788/LOP231676 [16] Akram M N, Tong Z M, Ouyang G M, Chen X Y, Kartashov V 2010 Appl. Opt. 49 3297 doi: 10.1364/AO.49.003297 [17] Li D Y, Kelly D P, Sheridan J T 2013 Appl. Opt. 52 8617 doi: 10.1364/AO.52.008617 [18] Hsiao Y N, Wu H P, Chen C H, Lin Y C, Lee M K, Liu S H 2014 Opt. Rev. 21 715 doi: 10.1007/s10043-014-0116-8 [19] Sun M J, Lu Z K 2010 Opt. Eng. 49 024202 doi: 10.1117/1.3314310 [20] 李丽, 韩学勤, 赵士伟, 包鸿音, 王兴宾 2014 激光与光电子学进展 51 011401 doi: 10.3788/LOP51.011401 Li L, Han X Q, Zhao S W, Bao H Y, Wang X B 2014 Laser Optoelectron. Prog. 51 011401 doi: 10.3788/LOP51.011401 -
计量
- 文章访问数: 134
- HTML全文浏览数: 134
- PDF下载数: 4
- 施引文献: 0