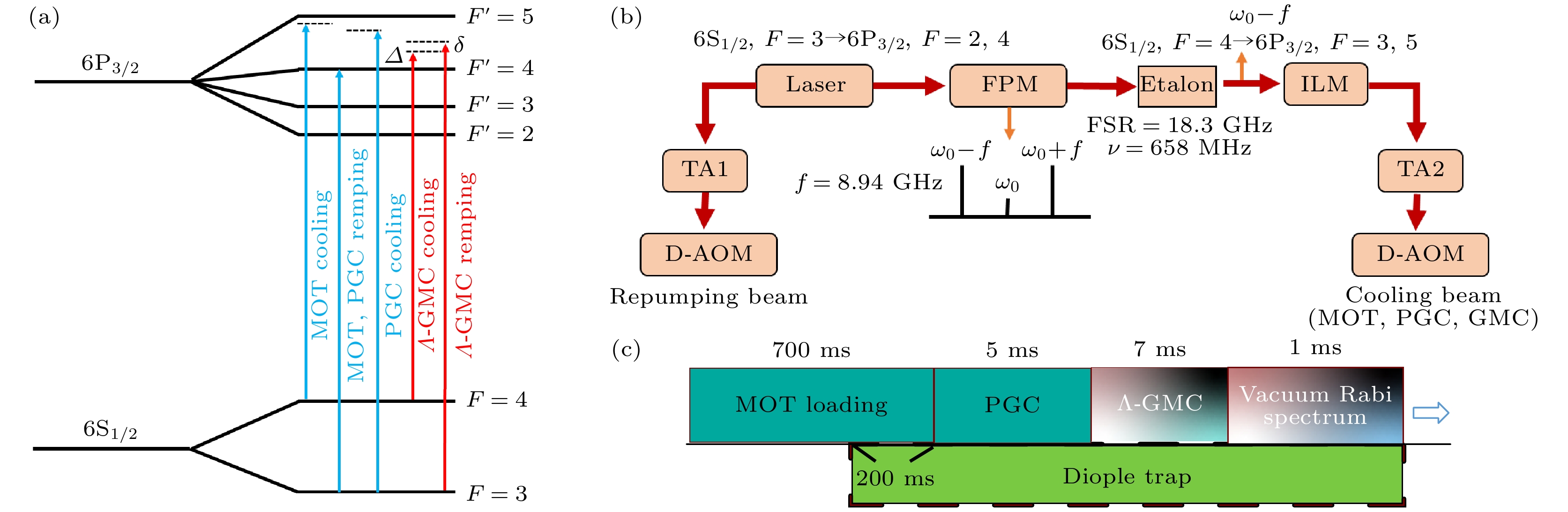
偏振梯度冷却(polarization gradient cooling, PGC)^[1–3]作为常用的亚多普勒冷却方法, 其冷却激光采用原子循环跃迁线($ F \leftrightarrow F' = F + 1 $), 原子样品温度总会受到光子反冲加热的限制. 近年来, 科学家们提出灰色黏团冷却(gray molasses cooling, GMC) 技术^[4–7]用于更低温度冷原子样品的实验制备, 与传统 PGC 的不同在于冷却激光采用原子非循环跃迁线($ F \leqslant F' $). 在 GMC 过程中, 当原子处于基态超精细塞曼子能级间的相干暗态且原子速度接近零时, 不与冷却光耦合散射荧光, 从而有效避免了光子反冲加热效应, 原子温度可突破光子反冲加热的限制. 另外, 处于基态的原子可减少由于光诱导的激发态原子间的碰撞损耗, 有助于提高原子的相空间密度.

当冷却光($ F \leftrightarrow F' = F $)和再泵浦光($ F - 1 $ $\leftrightarrow F' = F $)为$ \Lambda $构型, 且满足双光子拉曼共振时, 原子被冷却后处于两个基态($ F, F - 1 $)的相干叠加暗态. 该方案中由于包含$ \Lambda $型激光方案和相干拉曼过程, 被称为Λ-GMC. 已成功应用于多种类型的原子, 如 ⁶Li^[8–10], ²³Na^[11,12], ³⁹K^[13], ⁴⁰K^[14], ⁴¹K^[15], ⁸⁷Rb^[16], ¹³³Cs^[17] 等. 对于原子 ¹³³Cs 和 ⁸⁷Rb, 得益于 D2 线较大的超精细分裂, 可通过直接调节三维磁光阱(three dimensional magneto-optical trap, 3D-MOT)的激光失谐来实现Λ-GMC, 不需要新增额外的冷却光光源. 此外, 科学家们也在理论上基于$ \Lambda $型三能级系统, 于一维模型下利用光学布洛赫方程对自由空间^[8,13,16]和偶极阱内^[18]的Λ-GMC冷却进行了深入研究, 在拉曼共振条件附近出现了窄色散曲线特征, 其双光子红失谐时为冷却效果, 蓝失谐时为加热效果.

在光学腔和原子系综结合的腔量子电动力学(QED)系统中, 为了在一定原子运动范围内获得足够多的原子数目, 需要尽可能增大原子密度. 针对腔 QED 实验的需求, 首先于光学腔中心搭建了腰斑大小为15 μm的交叉偶极阱用于限制原子的运动范围; 其次设计搭建了可宽范围、快速调谐的激光系统; 再结合腔内 3D-MOT 装置^[19], 直接调节 MOT 激光的失谐, 实现Λ-GMC冷却. 既可辅助交叉偶极阱原子装载来增加阱内原子数目, 也可有效降低阱内原子温度. 相较于通过拉曼边带冷却降低光学腔内原子温度的方法^[20], 该方法更加简单.

本文所述腔QED系统内的光学微腔^[19]长度为1.27 mm, ${\text{TE}}{{\text{M}}_{00}}$模腰斑大小为46 μm. 在该光学微腔中心, 通过小角度3D-MOT成功俘获了冷原子云, 详细装置可见附录B. 此外, 实验搭建交叉偶极阱俘获小型原子系综与微腔相互作用. 偶极阱激光波长为1018 nm, 腰斑大小为15 μm; 两束激光交叉角为$ {30^ \circ } $, 可将偶极阱在光束传播方向上的尺寸减小至约58 μm, 有效减小了原子在偶极阱光束传播方向的运动范围.

图1(a)为铯原子 D2 线能级示意图. 在Λ-GMC过程中, 冷却光频率相对于跃迁线$ 6{{\text{S}}_{1/2}}|F = 4\rangle \leftrightarrow $$ 6{{\text{P}}_{3/2}}|F = 4\rangle $蓝失谐$ \varDelta $, 再泵浦光频率相对于跃迁线$ 6{{\text{S}}_{1/2}}|F = 3\rangle \leftrightarrow 6{{\text{P}}_{3/2}}|F = 4\rangle $蓝失谐$ \varDelta + \delta $. 实验中锁定一台激光器产生了 MOT, PGC 和Λ-GMC过程所需的全部频率激光不仅可以确保Λ-GMC过程中两束激光之间的相干性, 也可以实现大范围快速调谐.

激光产生过程如图1(b)所示. 首先, 一台主激光器其频率稳定于原子交叉峰$ 6{{\text{S}}_{1/2}}|F = 3\rangle \leftrightarrow $ $ 6{{\text{P}}_{3/2}}|F = 2, 4\rangle $, 部分激光输入索雷博(Thorlabs)公司生产的锥形放大器 TA1, 输出功率约为1 W; 再通过双通声光调制器(D-AOM)(单次通过频率移动88.1 MHz)实现跃迁线$6{{\text{S}}_{1/2}}F = 3 \leftrightarrow 6{{\text{P}}_{3/2}}F = $4附近的频率精细调谐, 可获得用于 MOT, PGC 和 Λ-GMC 过程的再泵浦激光. 其次, TA1 输出的少部分光(10 mW)穿过驱动频率为ω₀ = 8.9416 GHz 的光纤相位调制器(fiber phase modulator, FPM)后, 使用光学标准具(线宽为658 MHz, 自由光谱区为18.3 GHz)滤出负一级边带. 为了确保完全滤除激光模式中的杂散频率成分, 实验中 FPM 输出激光依次穿过两个标准具, 最终输出的激光功率约为1 mW. 随后, 该激光通过注入锁定放大, 输出功率约为40 mW; 并作为种子光输入到另一台锥形放大器 TA2 中, 输出激光频率共振于原子交叉峰$ 6{{\text{S}}_{1/2}}|F = 4\rangle \leftrightarrow 6{{\text{P}}_{3/2}}|F = 3, 5\rangle $. 通过调节 FPM 的驱动频率并结合双通 AOM(单次通过频率移动为113 MHz), 可获得 MOT, PGC 和Λ-GMC 过程中的冷却激光. 频率连续精确调谐范围大约为600 MHz, 主要由标准具的线宽决定; 调谐过程中 TA2 输出光功率不会产生明显变化. 激光装置中所有激光均由同一台激光器产生, 可以保障各个频率激光之间的相干性. 激光频率切换速率取决于FPM驱动频率的改变速率, 实验中通过将驱动信号在两台不同的信号源之间快速切换来实现, 切换时间约为5 ns.

利用$\Lambda\text{-}{\text{GMC}}$方法冷却原子的实验过程如 图1(c)所示, 主要分为以下几个步骤. 1)在光学微腔中心通过 3D-MOT 俘获冷原子云. FPM调制频率$ {\omega _0} = 8.9516 {\text{ GHz}} $, 冷却光频率与原子跃迁线$ 6{{\text{S}}_{1/2}}{\text{ }}F = 4 \leftrightarrow 6{{\text{P}}_{3/2}}{\text{ }}F = 5 $失谐$ - 10 {\text{ MHz}}$. 2)开启交叉偶极阱, 与冷原子云重合$200 {\text{ ms}}$进行原子装载. 3)快速关闭反亥姆霍兹线圈的电流, 同时将 MOT 激光功率降低至初始光强的1/3, 冷却光的频率由 MOT 激光的失谐$ - 10 {\text{ MHz}}$变为$ - 30 {\text{ MHz}}$(FPM调制频率为$ {\omega _0} = 8.9716 {\text{ GHz}} $), 进行PGC预冷却, 持续时间为$5~ {\text{ms}}$. 4)快速切换激光频率(FPM调制频率$ {\omega _0} = 9.1626 {\text{ GHz}} $)进行$\Lambda{\text{-GMC}}$冷却并辅助偶极阱原子装载. 5)测量真空拉比分裂光谱得到偶极阱中俘获的原子数目.

在GMC优化过程中，偶极阱中俘获的原子数和自由空间原子温度的变化趋势类似^[9], 本文通过偶极阱俘获的原子数目来优化影响$\Lambda {\text{-GMC}}$冷却效果的各个参数^[17,21], 主要包括: 激光作用时间$\tau $、三维磁场$ ( {{B_x}, {B_y}, {B_z}} ) $、单光子失谐$\varDelta $、双光子失谐$\delta $、冷却光功率${I_{{\text{cooling}}}}$和再泵浦光功率${I_{{\text{repumping}}}}$的比值以及冷却光功率${I_{{\text{cooling}}}}$.

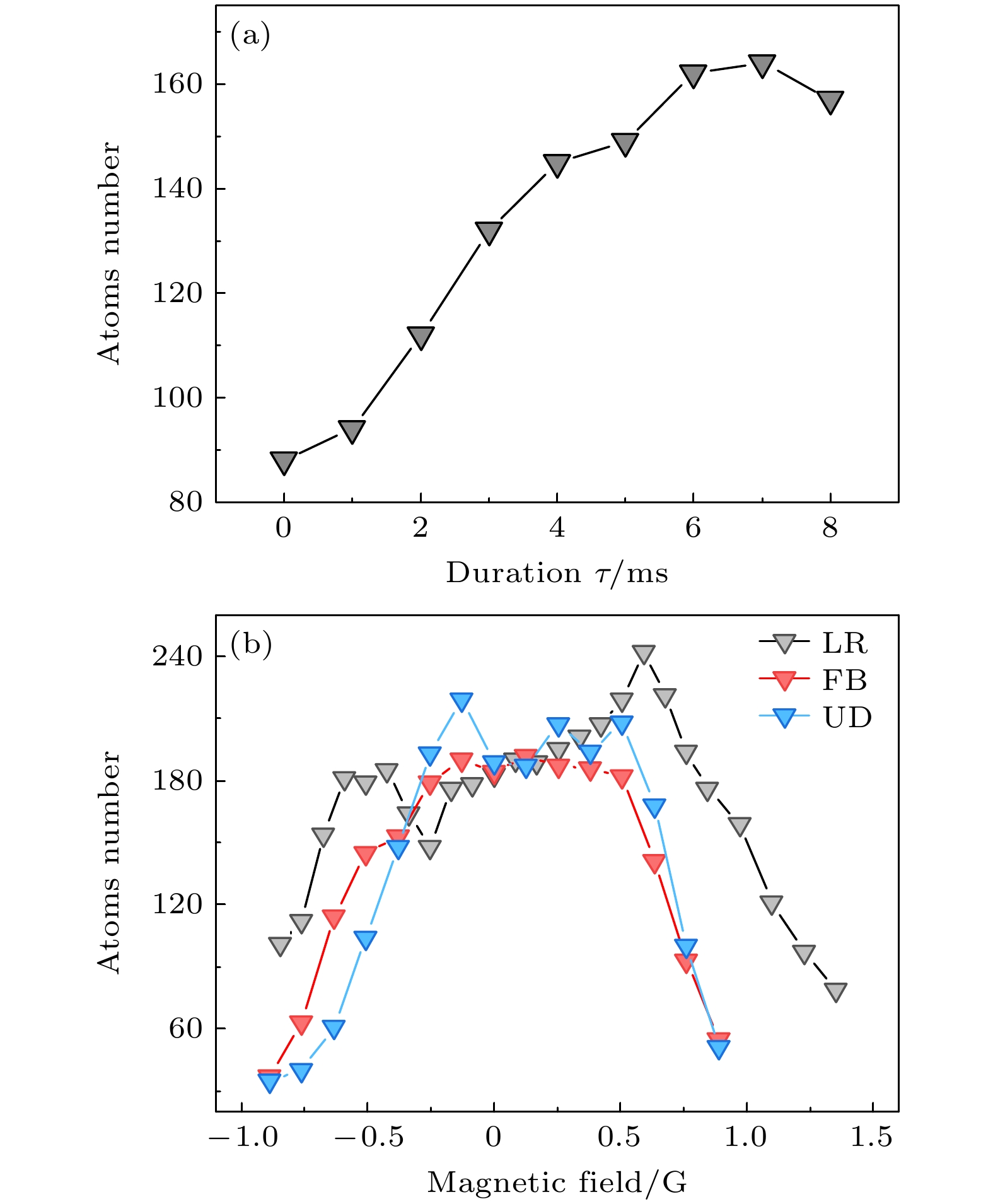
首先研究激光作用时间$\tau $对$\Lambda \text{-} {\text{GMC}}$冷却效果的影响. 此时, 双光子失谐为$\delta = 0$, 单光子失谐为$\varDelta = 5\varGamma $, 单束冷却光光强为$1.7{I_{{\text{sat}}}}$, 单束再泵浦光的光强为$0.6{I_{{\text{sat}}}}$, ${I_{{\text{sat}}}} = 1.1 {\text{ mW/c}}{{\text{m}}^{2}}$为铯原子 D2 线超精细态间跃迁的饱和光强. 偶极阱中的原子数目随激光作用时间 $\tau $ 的变化关系如图2(a) 所示, $\tau $ 大于$7~{\text{ms}}$后, 原子数目达到最大, 增加了约40%. 后续实验中设定激光作用时间 $\tau $为$7 {\text{ ms}}$.

其次, 研究三维磁场$ \left( {{B_x}, {B_y}, {B_z}} \right) $对$\Lambda\text{-}{\text{GMC}}$冷却效果的影响. 在$\Lambda \text{-} {\text{GMC}}$冷却过程中, 铯原子处于由两个基态所形成的相干暗态, 暗态的退相干速率对冷却效果起着重要作用. 退相干速率越小, 原子发出的荧光越少, 可以得到更低的原子温度. 由于杂散磁场的存在, 冷却过程中原子可能分布在不同的塞曼子能级, 暗态的退相干速率增加. 实验中需要有效减小原子所处环境的杂散磁场. 图2(b)为左右(LR)、前后(FB)、上下(UD)3个方向的剩磁大小与原子数的关系, 剩磁场为零的时候冷却效果最佳. 另一个影响暗态弛豫速率的因素为冷却激光和再泵浦激光之间的相干性. 实验中的冷却激光和再泵浦激光均来自同一台激光器, 额外的频率偏移由稳定信号发生器驱动 FPM 或 AOM 产生, 激光具有良好的相干性, 不是冷却效果的限制因素.

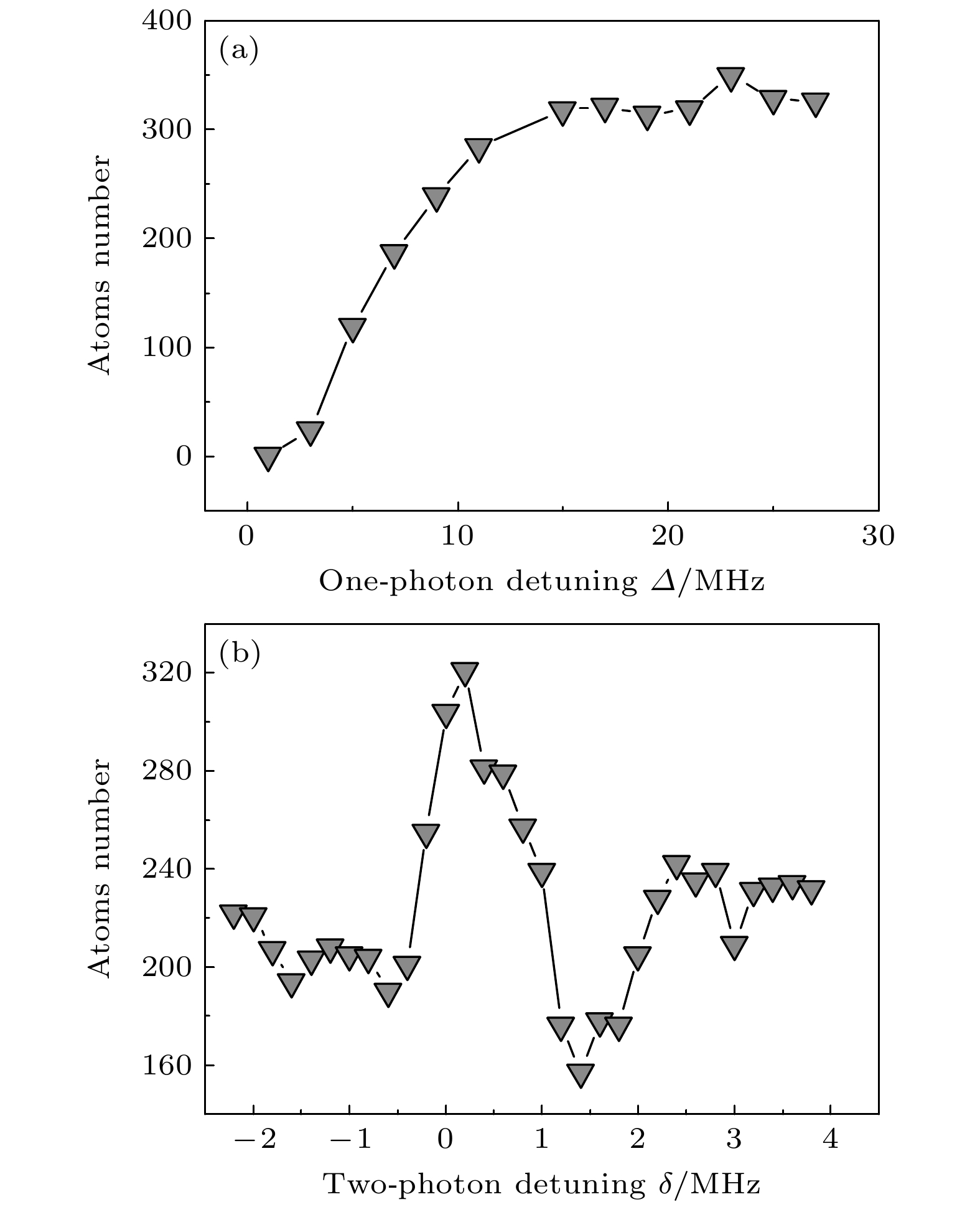
接下来研究失谐对冷却效果的影响, 包括单光子失谐$ \varDelta $ 和双光子失谐$ \delta $. 首先设置$\delta = 0$, 冷却光光强为$1.7{I_{{\text{sat}}}}$, 再泵浦光光强为$0.6{I_{{\text{sat}}}}$. 实验测量原子数和单光子失谐$ \varDelta $依赖关系, 如图3(a) 所示. 随着单光子失谐变大, 原子数逐渐增加. 当失谐大于$3\varGamma $时, 原子数趋于一个稳定值. 由于受到双通 AOM 的带宽限制, 实验测量的最大失谐为$ + 28 {\text{ MHz}}$. 随后, 设定$\varDelta = 5\varGamma $, 精细改变冷却激光的频率, 实验测量原子数与双光子失谐$ \delta $的依赖性关系, 如图3(b)所示. 当$ \delta = 0.2 {\text{ MHz}} $时, 达到拉曼共振条件, 冷却效果最好, 阱中俘获的原子数最多; 而当$ \delta = 1.4 {\text{ MHz}} $时, 冷却效果变差, 原子数目减小. 原子数对$ \delta $的依赖表现出一个窄范围内具有亚自然宽度的非对称法诺(Fano)轮廓, 该轮廓围绕拉曼共振点形成, 这是量子干涉效应出现的明显特征, 也意味着Λ-GMC冷却的实验实现^[9,20,22]. 偶极阱存在时得到的法诺谱线原子数最多和最少处的频率差为$ 1.2 {\text{ MHz}} $, 明显大于文献[17]报道结果$ 0.22 {\text{ MHz}} $, 这是由于原子在偶极阱内运动产生的光频移起伏导致基态相干暗态寿命缩短所导致的展宽效应.

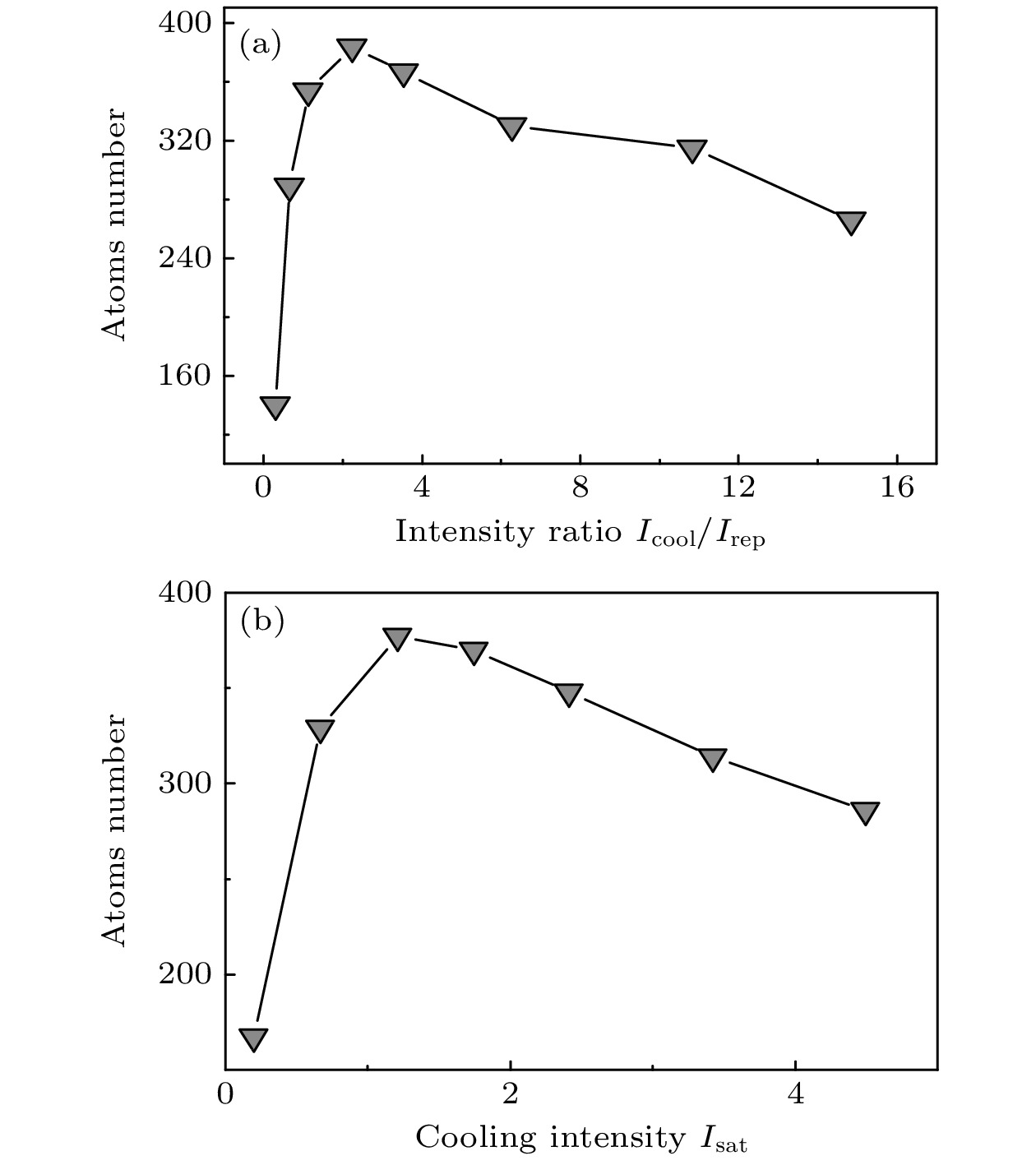
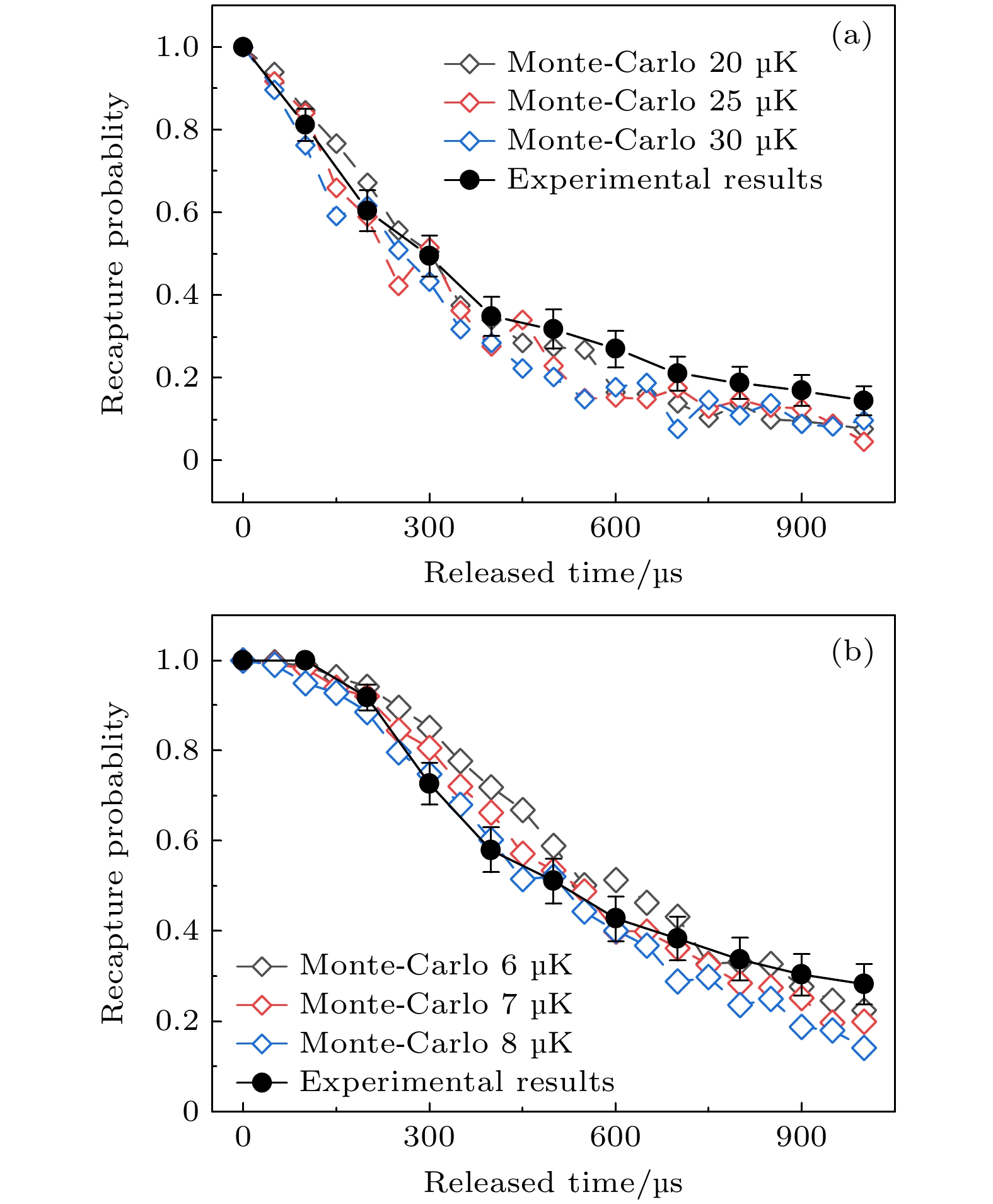
最后研究激光强度对冷却效果的影响. 设置双光子失谐$ \delta = 0.2 {\text{ MHz}} $, 单光子失谐为$\varDelta = 5\varGamma $, 再泵浦光的光强为0.6I_sat. 改变冷却光强度, 同时测量光强比(${I_{{\text{cool}}}}/{I_{{\text{rep}}}}$)与原子数的依赖性关系, 实验结果如图4(a) 所示. 当光强比${I_{{\text{cool}}}}/{I_{{\text{rep}}}}$=3时, 阱中俘获的原子数最多. 随着光强比${I_{{\text{cool}}}}/{I_{{\text{rep}}}}$逐渐变大, 原子数缓慢变小, 可能是由于冷却光太强激发了原子的其他超精细态之间的跃迁, 导致基态相干性变差, 从而影响了冷却效果. 随后我们保持光强比为 3, 同时扫描冷却光的强度大小, 实验结果如图4(b)所示. 当冷却光的强度为1.2I_sat时, 偶极阱中俘获的原子数最多.

经过上面的研究, 我们能够实现影响冷却效果的各个参数的优化, 偶极阱中的原子数相比未经过Λ-GMC冷却时增加了约4倍. 为了更好地评估冷却效果, 采用释放再俘获^[23]的方法分别测量了仅进行 PGC 冷却和 PGC+Λ-GMC组合冷却后阱中原子的温度. 图5(a)为仅进行 PGC 冷却时的实验结果, 其中黑色点线代表了实验测量数据, 其他点线为蒙特卡罗模拟结果. 对比实验数据和模拟结果, 可知原子最终的温度约为$ 25 {\text{ μK}} $. 图5(b)为经过 PGC+Λ-GMC组合冷却后的结果, 比较实验测量数据与模拟结果可知, 阱中原子的温度降至约$ 8 {\text{ μK}} $. 该温度高于文献[17]所报道实验结果$ 1.7 {\text{ μK}} $, 主要由于偶极阱内原子运动产生的光频移起伏导致基态相干暗态寿命缩短, 最终和光场相互作用产生加热现象所导致. 图5中原子释放时间大于$ 600 {\text{ μs}} $时, 实验测量的剩余原子百分比高于模拟结果. 当偶极阱关闭之后, 经过长时间飞行的部分原子仍然位于腔模内, 可被光学腔所探测, 导致实验测量原子数略微偏多.

本文基于自主设计搭建的激光系统, 于光学微腔中心通过铯原子 D2 线Λ-GMC冷却辅助偶极阱中的原子装载, 不仅可以增加与光学腔相互作用的原子数目, 还可有效降低阱内原子温度. 另外, 将该技术应用于单原子阵列装载实验中, 可通过Λ-GMC过程实现蓝失谐光辅助的受控碰撞阻挡效应^[24,25], 显著提升偶极阱中的单原子装载效率, 并有效降低原子温度. 该实验对确定性原子阵列与微腔相互作用系统^[19]中原子数目的增加具有重要的指导意义.

本文主要分析光频移、虚磁场和光辅助碰撞对Λ-GMC冷却效果的影响.

当偶极阱与原子云重叠时, 处于偶极阱附近的原子由于受偶极相互作用能级产生频移. 实验中阱深约为$ {U_0} = 330 {\text{ μK}} $, 铯原子两个基态$ 6{{\text{S}}_{1/2}}|F = 4\rangle $和$ 6{{\text{S}}_{1/2}}|F = 3\rangle $的光频移约为$ \Delta E_{{\text{light-shift}}\_{6}{{\text{S}}_{1/2}}|F} = 4\rangle = - 7.545 {\text{ MHz}} $和$ \Delta {E_{{\text{light-shift}}\_6{{\text{S}}_{1/2}}|F = 3\rangle }}\; = - 7.543 {\text{ MHz}} $, 各个塞曼子能级简并; 原子上能级激发态$ 6{\rm P_{3/2}}|F = 4\rangle $塞曼子能级$ m_{F = 0, 1, 2, 3, 4} $所对应的光频移约为$ \Delta {E_{{\text{light-shift}}}}_{\_{m_{F = 0, 1, 2, 3, 4}}} = - 3.242, - 3.261, - 3.319, - 3.319, - 3.416, - 3.551 {\text{ MHz}} $, 各个能级之间的频率差很小. 光频移引起的能级间的频率差可通过单光子失谐Δ补偿. 由图3(a)可知, 单光子失谐 Δ 大于$3\varGamma $时原子数趋于一个稳定值, 冷却效果此时随 Δ 变化不敏感, 文献[9]也得到类似实验结果. 当设置$\varDelta = 5\varGamma $时, 与偶极阱重叠的原子均可参与 Λ-GMC 冷却过程.

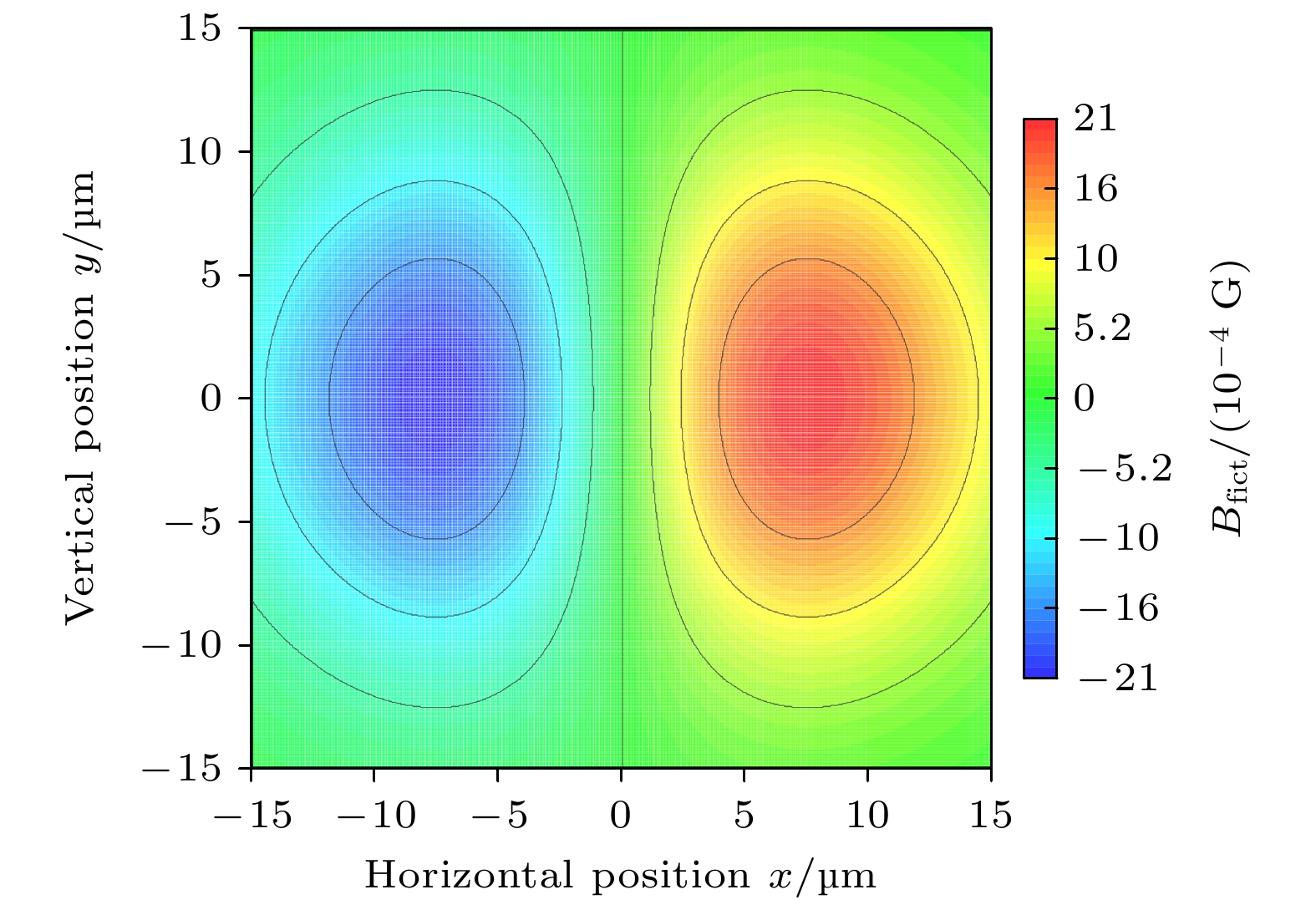
另外一个需要考虑的因素为虚磁场. 理论计算阱深为$ {U_0} = 330 {\text{ μK}} $, 腰斑大小为$ {\omega _0} = 15 {\text{ μm}} $, 线偏振聚焦光束下的虚磁场梯度分布^[26], 结果如图 A1 所示. 当原子温度为$ T = 25 {\text{ μK}} $时, 阱内原子位置方差$ \langle x \rangle = ({{{\omega _0}}}/{2})\sqrt{{T}/{{|{{U_0}}|}}} = 4.27 {\text{ μm}} $, 虚磁场$ {B_{\left\langle x \right\rangle }} $的变化范围为$ - 9.46 \times {10^{ - 4}}—9.46 \times {10^{ - 4}}\; {\text{G}} $, 引起的最大塞曼分裂大小为$ \Delta {E_{{\text{Zeeman}}}} = 331 {\text{ Hz}} $, 相比于图3(b)中阱内原子数最多和最少时所对应频率差$ 1.2 {\text{ MHz}} $, 该效应可忽略不计.

最后考虑由于光辅助碰撞引起的偶极阱内原子损耗, 该碰撞为非弹性碰撞. 腰斑大小为$ {\omega _0} = 15 {\text{ μm}} $的偶极阱可俘获小型铯原子系综^[27], Λ-GMC冷却光束蓝失谐于邻近原子跃迁线, 可诱导阱内原子间的可控蓝失谐辅助碰撞^[28], 每次碰撞仅丢失一个原子, 碰撞之后原子获得的能量为 $\hbar\varDelta $. 而传统的 PGC 过程诱导的红失谐辅助碰撞过程每次丢失原子数为2个, 且原子碰撞获得的能量不可控. 通过Λ-GMC冷却辅助偶极阱原子装载有利于偶极阱俘获更多原子数. 此外, Λ-GMC冷却过程中的大部分原子处于两个基态($ 6{{\text{S}}_{{\text{1/2}}}}|F = 3\rangle , 6{{\text{P}}_{{\text{3/2}}}}|F = 4\rangle $)的相干暗态, 有利于减小阱内原子的碰撞截面积, 降低原子碰撞损失率, 可有效增加阱内原子数.

实验中为了在腔长为1.27 mm光学腔中心俘获稳定原子云, 设计了如图 B1 所示的腔内小角度 3D-MOT 装置, MOT 光束由两束夹角为20°的激光和另外一束与之垂直的激光组成, 光束腰斑大小为$ 0.8{\text{ mm}} \times 1.6 {\text{ mm}} $, 腔轴方向的腰斑小于垂直于腔轴方向的腰斑, 以确保 MOT 光束在不被腔镜阻挡的同时获得最大腰斑.