-
Rydberg原子由于极大的电偶极矩和极化率[1], 并且Rydberg原子实验体系具有可重复、精确和稳定的特点, 被广泛应用于电场测量[2–4]. 基于高分辨率吸收光谱技术的不断提高以及实验仪器不断优化和改进, Rydberg原子许多不同于普通原子的奇异特性不断被发现, 通常这些特性与主量子数n 有紧密关系. 具有较高主量子数的Rydberg原子与电磁感应透明(EIT)技术的结合已经被用于检测和表征射频(RF)电场[5–7]. 基于EIT共振的Autler-Townes (AT)效应和非共振的Stark效应, 可以实现对RF电场的强度[6,8,9]、偏振[10,11]和相位[12,13]等信息的测量. 近年来, 基于原子体系的电场测量技术得到了迅速发展, 这些新技术包括可溯源到基本物理量的原子电场计[14]、功率传感器[15]、频谱分析仪[16,17]和通讯接收机[18,19]等. Shaffer 等[20]和Ripka等[21]分别于2018年和2021年描述了一种基于Rydberg原子电场感应的三光子读出方案, 并将残余多普勒能移降低到Rydberg态衰减时间对应的量级, 实现基于AT分裂机制用于较低场强的RF电场测量. 2022年, Liu等[22]基于ac Stark效应和非共振外差技术, 实现了对30 MHz射频电场的高灵敏度测量, 最小电场强度为37.3 µV/cm, 灵敏度为–65 dBm/Hz, 动态范围超过65 dB. 同年, Hu等[23]报道了在室温铯原子蒸气室中, 利用远离共振的ac Stark效应, 演示了2—5 GHz频率范围内的RF电场及连续可调的弱场测量, 实现最低电场强度达2.25 µV/cm, 灵敏度为712 nV·cm–1·Hz–1/2, 线性动态范围超过65 dB.
目前将铯原子激发到Rydberg态的主流方案是使用852 nm的探测光和510 nm的耦合光进行双光子激发[12,23], 这种方案比较成熟且激发效率高. 但是短波激光的产生通常采用半导体倍频激光器, 缺点是激光器体积较大且造价昂贵. Carr 等[24]提出基于全红外光激发的三光子方案, 使用两个红外光代替短波激光, 通过三步跃迁将原子激发到Rydberg态. 本工作采用1470 nm和780 nm激光代替510 nm激光, 采用四能级结构的方式制备了Cs原子的Rydberg态, 从而避免了短波激光器的使用, 同时可减少铯泡中原子因光电电离而导致的电离屏蔽效应[25]. 实验中使用的红外激光器体积较小, 且功率和模式更为稳定, 因此这种方案是测量射频电场重要的方式之一.
基于上述方案, 实验上对频率为30, 40, 50和60 MHz射频电场的EIT光谱分别进行测量, 获得了以1.25 V/m为步长, 电场幅度为0—250 V/m范围内的一系列光谱, 观察到EIT光谱的ac Stark 能移以及多个调制边带. 根据EIT主峰的能移, 讨论了频率对铯泡中电场屏蔽的影响, 得到对应的衰减系数. 基于EIT效应, 选择50 Hz—1 kHz范围内的低频电场调制到50 MHz的射频电场上, 并实现了保真度约95%的信号解调.
-
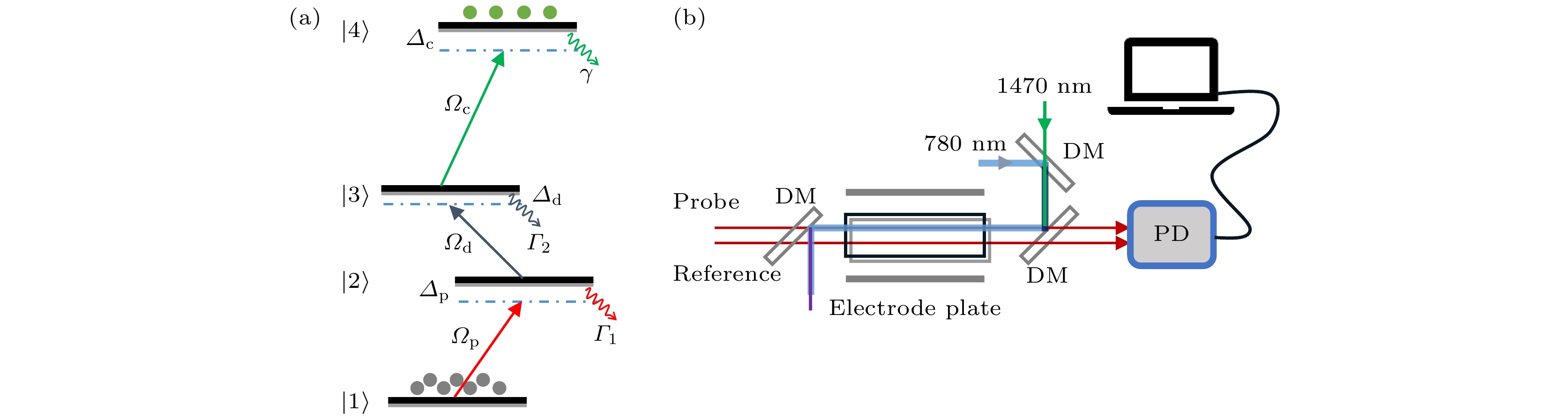
本工作是基于Cs原子Rydberg态的光学激发与探测, 实验采用阶梯型四能级Rydberg-EIT方案, 相关能级图如图1(a)所示. 其中|1
$\rangle $ 为Cs原子的基态, |2$\rangle $ 和|3$\rangle $ 为两个低激发态, |4$\rangle $ 为Rydberg态, 实验装置示意图如图1(b)所示. 波长为852 nm 的探测光和参考光平行穿过长度L = 70 mm, 直径Φ = 30 mm的圆柱形石英玻璃铯泡, 与探测光方向相反的1470 nm 的缀饰光和780 nm 的耦合光相互重叠并作用于铯泡中, 可以形成原子探测区域. 探测光聚焦在原子气室中用于驱动铯原子基态|6S1/2, F = 4$\rangle $ 到激发态|6P3/2, F = 5$\rangle $ 的跃迁, 束腰大约为200 μm, 拉比频率为Ωp. 缀饰光耦合两个中间态|6P3/2, F = 5$\rangle $ 和|7S1/2, F = 4$\rangle $ 之间的跃迁, 拉比频率为Ωd. 耦合光的束腰大约为200 μm, 拉比频率为Ωc ≈ 2π × 4 MHz, 用于驱动激发态|7S1/2, F = 4$\rangle $ 到Rydberg态|49P3/2$\rangle $ 的跃迁. DL pro型半导体激光器提供探测光, 线宽100 kHz, 利用饱和吸收光谱稳频技术[26]锁定激光频率在|6S1/2, F = 4$\rangle $ → |6P3/2, F = 5$\rangle $ 的共振跃迁线上, 1470 nm 的缀饰光由DL 100 pro型半导体激光器提供. 耦合光由TA pro 型激光器提供, 在|7S1/2, F = 4$\rangle $ → |49P3/2$\rangle $ 跃迁频率附近扫描耦合光的跃迁频率, 在光电探测器上记录852 nm 探测光的透射信号, 获得Rydberg原子EIT光谱, 实现Rydberg能级的光学探测. 为尽量减少电荷在极板角落处过于集中的情况, 实验中选用厚度为3 mm, 直径Φ = 120 mm的圆形铜板, 间距调节为40 mm且平行放置在铯泡两侧, 并使铯泡位于极板中心位置, 极板上外加的交流射频电场由RIGOL DG4062型信号发生器提供. 实验中通过调节信号发生器来改变RF的幅度和频率, 电场信号直接耦合到原子泡中的铯原子, 观测在不同情况下的电场对EIT光谱的响应同时对数据进行实时采集. -
原子系统与电场E相互作用的有效哈密顿量可描述为Heff = H0+HS, 其中H0和HS分别对应的是无外场时原子系统和Stark相互作用的哈密顿量. HS表示为
$-\mu^z_{ij}E$ , 其中$\mu_{ij}^z$ 是原子态i和j之间的偶极矩阵元沿电场E方向的分量. Alkali Rydberg Calculator (ARC) 软件包[27]使用库仑近似(CA)方法计算偶极矩阵元μij, 计算得到Rydberg态的精度优于1%, 而实验准确性通常在百分之几的水平上. 通过对角化Heff, 计算能量本征态, 增加基底的大小来检查收敛性, 直到在所需的精度(通常为0.1%)内获得收敛性. 从外加电场能量中减去无外场能量, 进一步得到Stark位移Δ. 对于非简并态i, Stark位移可以近似表示为其中非简并态i的极化率为
式中, E是外加频率为f的射频电场强度; h为普朗克常数; αi(f)是极化率, 把通过电场所有耦合到i态的j态进行求和; fij是i和j态之间的跃迁频率; Γj是j态的自发衰变速率. 考虑|7S1/2
$\rangle $ → |49P3/2$\rangle $ 的跃迁频率远大于外加射频电场的频率, 因此可用Cs原子的直流极化率来进行计算.随着电场幅度的增加, 谱线呈现出高阶项以及复杂的态混合和态转移现象, 微扰论不再成立. 需要采用非微扰的Floquet方法来定量解释光谱的位置和强度, 其计算精度受限于所使用的原子基组的大小. Floquet方法详细的理论描述可参考文献[28, 29]. 外加电场可表示为
$\varepsilon (t) = \varepsilon_{\rm ac}\sin(\omega_{\rm m} t) $ , 忽略激光场和退相干, 考虑绝热近似条件下, 包含精细结构的|49P3/2$\rangle $ 含时态矢量表示为式中, |ψ(
$\varepsilon $ )$\rangle $ 表示Stark 态; E($\varepsilon $ )为Stark 态哈密顿量的本征能量. 射频电场缀饰的Rydberg 态可表示为Floquet-Fourier形式:式中,
$\varepsilon_0 $ 表示准能量, ψN表示Fourier展开的谐波分量. 将电场代入(3)式后可以得到能级$\varepsilon _N$ 的表达式:当忽略退相干时, 交流电场会导致ac Stark能移和边带谱线. 实验中直流电场
$\varepsilon_{\mathrm{dc}}=0 $ , 外场仅施加交流电场, 不存在奇数边带. -
如图1(b)所示, 在圆形铜板之间施加电压, 由于极板直径远大于铯泡直径, 忽略边缘效应后可近似认为铯泡处于均匀电场中, 通过实验中观察到耦合光EIT信号中的感应差分Stark位移Δ, 进而实现基于Rydberg原子的电压测量. 由于Stark位移Δ是E的偶函数, 所以Δ与施加电压的极性无关. 使用ARC软件包[27]计算得到原子态的偶极极化率并进一步拟合得到直流极化率, Cs原子Rydberg态直流极化率的计算结果如表1所列. 由于|7S1/2
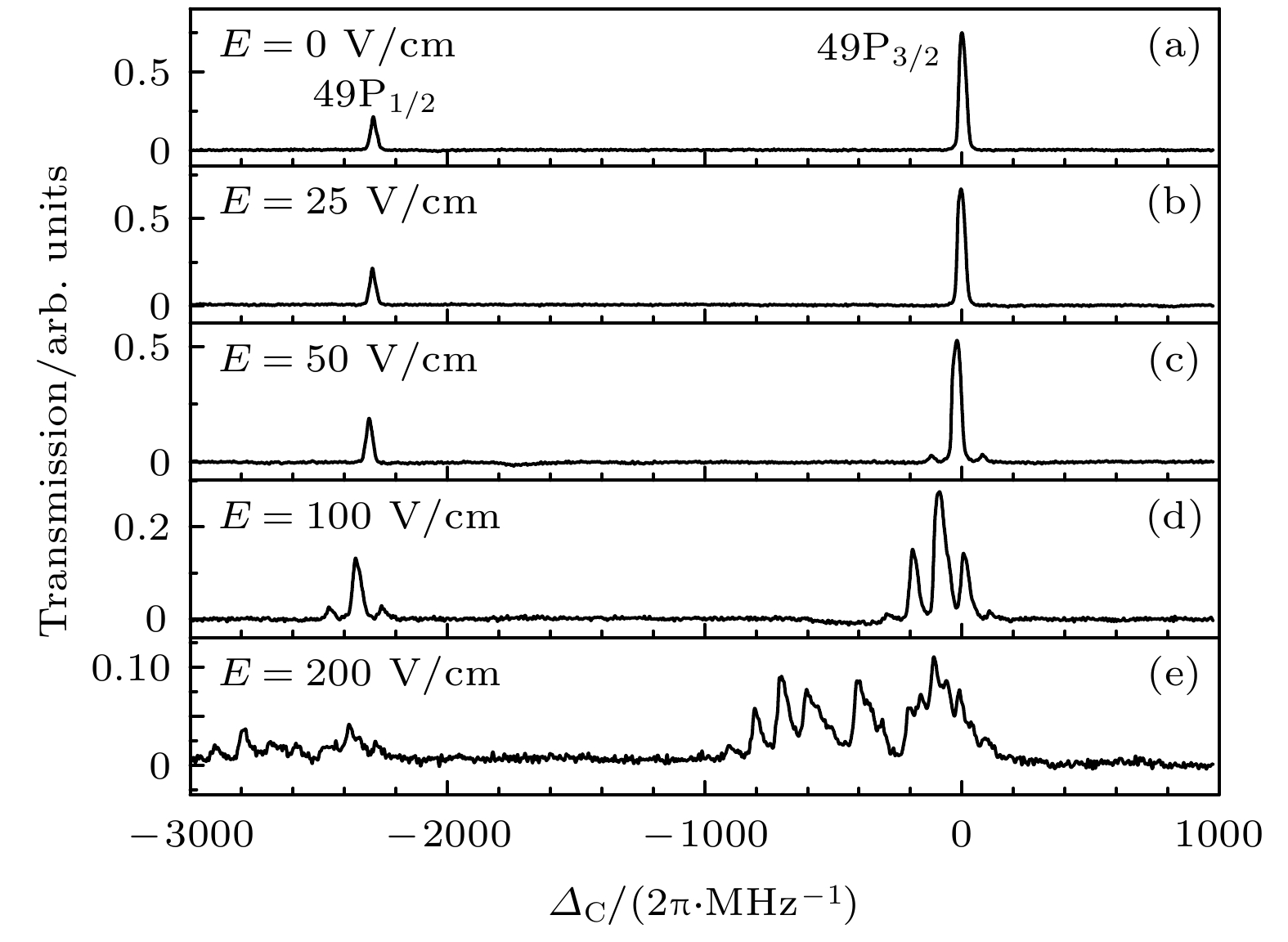
$\rangle $ 态极化率比Rydberg态的极化率至少小3个数量级, 因此实验中观测到的ac Stark效应可以忽略|7S1/2$\rangle $ 态极化率的贡献, 可全部看作是Rydberg态的ac Stark能移.如图2所示, 首先给出不同强度射频电场作用下Rydberg态的EIT光谱, 射频电场频率设定为50 MHz. 其中图2(a)是射频电场强度E = 0 V/m 时, 即无外场时Rydberg态的EIT光谱, 可利用此EIT光谱作为参考光谱, 光谱中呈现的次峰和主峰对应的Rydberg能级分别是|49P1/2
$\rangle $ 和|49P3/2$\rangle $ . 当电场强度E = 25 V/m时, EIT光谱形状未出现明显变化, 仅呈现出一定的Stark能移和谱线展宽, 这种展宽可能是由于激光传播路径经过极板间的非均匀场导致的, 此外, 局部电荷分布也可能导致额外的展宽, 这些可以理解为Rydberg原子碰撞电离[30]的结果. 当电场强度E = 50 V/m时, EIT光谱除了上述的Stark能移和谱线展宽, 还发现在主峰两侧产生边带, 边带与主峰的间距约100 MHz, 正是调制频率的2倍, 即二阶边带(N = ±2), 当电场强度进一步增加到100 V/m时, 次峰两侧也出现二阶边带, 而主峰出现更高阶的边带距离主峰约200 MHz, 即四阶边带(N = ±4). 由于一级Floquet边带峰不满足跃迁定则, 只存在双光子跃迁, 所以实验中的EIT光谱只出现偶数边带. 图3更清晰地展示了上述Stark能移、谱线展宽以及边带谱线位置的渐变情况. 当电场强度E = 200 V/m时, 由于Rydberg原子P态比S态具有更丰富的超精细能级结构, 在射频电场作用下Rydberg能级会产生一系列的Floquet态, 并呈现出高阶项, 以及态转移和态混合导致EIT谱线边带峰呈现不对称现象[29,31].为进一步了解射频电场中|49P3/2
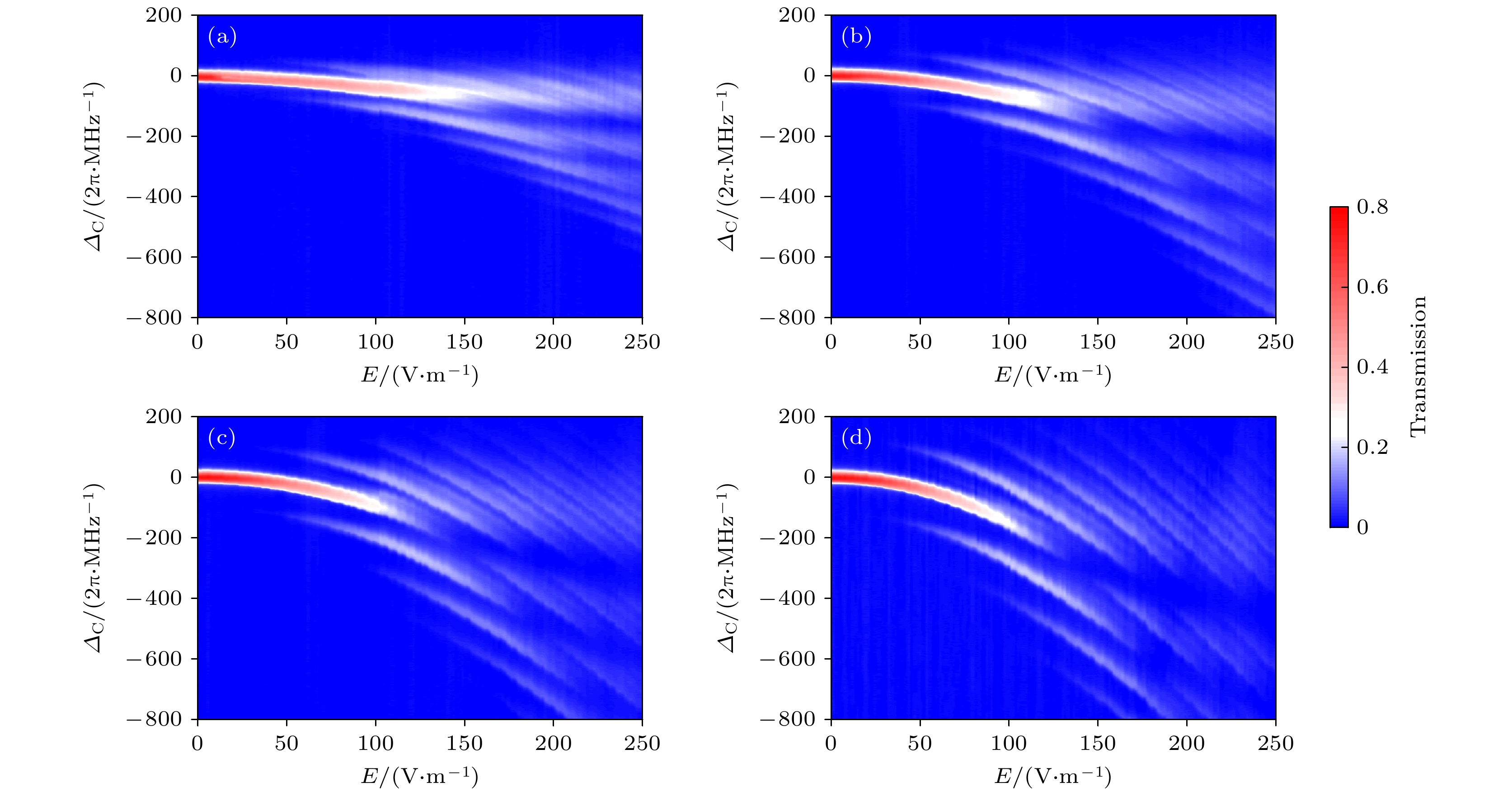
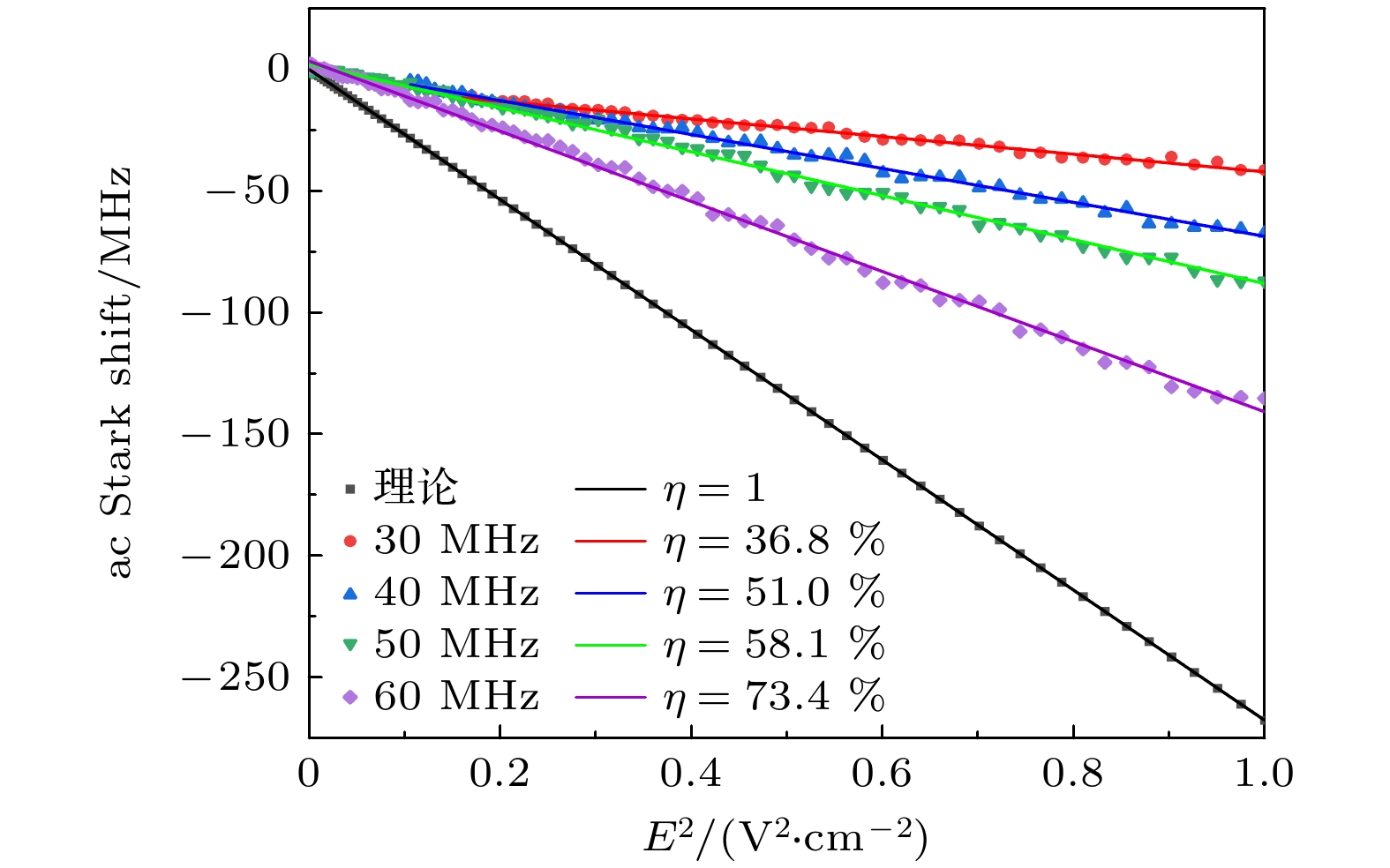
$\rangle $ 态的Rydberg原子EIT光谱特征, 实验以1.25 V/m为步长测量了一系列如图2所示的谱线, 正弦射频电场的频率分别选择30, 40, 50, 和60 MHz, 对应的EIT谱线随电场强度的变化如图3所示. 谱线的变化可分为三部分讨论, 首先在弱场区域(E < 60 V/m), 观测到EIT主峰位置在红失谐方向发生ac Stark能移, 且能移量与射频电场频率有关, 需要进一步考虑铯泡对电场的屏蔽效应. 其次在中强场区域(60 V/m < E < 120 V/m), 伴随电场逐渐增加, 图3(a)—(d)出现N = ± 2级的边带逐渐增强, 特别是图3(c)和图3(d)呈现出清晰的N = ±4级边带, 但主峰强度均随场强的增加而减弱, 在E = 150 V/m附近主峰完全消失, 这是由于外场作用下|49P3/2$\rangle $ 态与相邻多重态形成能级的避免交叉导致. 最后在强场区域(E > 120 V/m), |49P3/2$\rangle $ 能级与大量Stark能级的态混合会导致光谱图呈现出一定的波动结构, 而与临近Stark能级混 合后会出现线性Stark能移, 由图3中可以看出, 射频电场诱导的边带由非线性逐步转变为线性变化.如上文所述, 频率为MHz的射频电场会导致Rydberg的能量位移, 进而改变铯原子的EIT光谱能移, 根据(1)式可以计算Stark能移. 外加电场为正弦交流射频电场, ac Stark平均能移可用δ = –1/4αE 2 计算, 式中α为|49P3/2
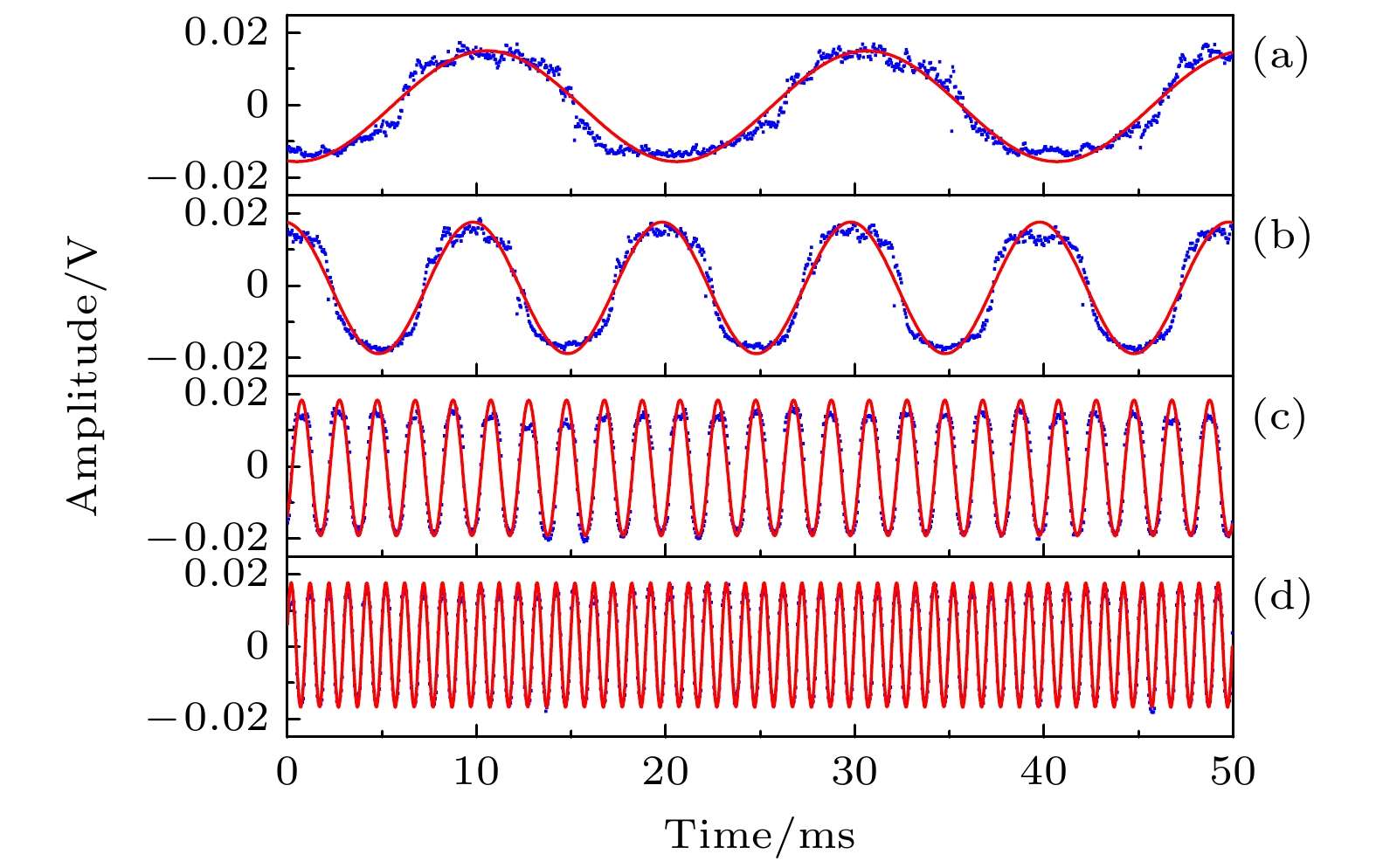
$\rangle $ 态的极化率. 为了探究外加不同频率电场在铯泡中的屏蔽效果, 假设理想的匀强电场E在铯泡中的衰减系数为η, 可将计算式表示为δ = –1/4α(ηE)2. 图4给出外加不同频率的射频电场情况下, EIT光谱主峰的ac Stark移动随$E^2 $ 的变化曲线, 散点为实验数据, 并对数据进行线性拟合, 对应频率分别是30, 40, 50和60 MHz, 拟合得到的皮尔逊相关系数分别是–0.99447, –0.99732, –0.99828和–0.99904, 均呈现出较好的线性关系. 根据拟合结果可以进一步计算衰减系数η, 分别是36.8%, 51.0%, 58.1%, 73.4%, 可以看出随着射频电场频率的增加, EIT光谱主峰的ac Stark能移增大, 表明铯泡中的原子可以感受到更多的电场, 电场屏蔽效应逐渐减小. 这是由于原子气室对于射频电场的屏蔽效应主要来源于气室内的电荷附着在内壁所形成的静电屏蔽层[32], 同时这种电荷分布需要一定时间, 射频电场频率越高, 电荷分布来不及完全建立, 电场屏蔽效应就越低.由于射频信号具有很好的穿透能力, 在射频通信中, 可以通过调制将频率较低的基带信号转换成频率更高的射频范围, 便于移动通信以及长距离的有效传输. 在实验中, 使用信号发生器产生一个50 MHz的射频电场, 分别将频率为50, 100, 500 Hz和1 kHz的低频电场调制到射频电场, 由于50 Hz—1 kHz的低频电场频率与射频电场相比较非常低, 因此低频电场幅度调制可认为是射频电场幅度随时间的缓变过程. 将780 nm的耦合光锁定在最佳工作位置, 由数字示波器记录光电探测器上传输的852 nm 探测光透射信号, 可以得到与之对应的正弦函数信号, 如图5所示. EIT信号峰值随电场频率发生变化, 利用正弦函数A sin(ωt +
$\varphi $ ) + B对数据进行拟合, 可以获得幅度和频率等参数. 表2列出拟合后的相关参数, 结果表示频率测量结果的相对误差不高于0.5%, 不确定度不高于0.09 Hz, 表明在50 Hz—1 kHz的低频电场范围内, 对正弦波调制信息的提取均呈现出高保真的结果.结果表明, 调制信号携带在探测光的传输中, 数字示波器可直接记录光电探测器的传输信号, Rydberg原子作为一个解调器, 不再需要复杂的电子解调装置. 基于Rydberg原子的ac Stark效应可实现对50 Hz—1 kHz范围内低频电场的解调, 并解调出保真度约95%的信号.
-
在室温条件下以铯原子 |6S1/2
$\rangle $ → |6P3/2$\rangle $ → |7S1/2$\rangle $ → |49P3/2$\rangle $ 形成的阶梯型四能级系统, 实现射频电场缀饰下铯Rydberg 原子EIT 光谱的连续探测. 在电场幅度较宽的动态范围内, 观察到EIT 光谱的能移以及多个边带, 获得的光谱结果可直接用来测定射频电场. 不同于传统偶极天线的测量方式, EIT谱线的偏移和避免交叉等光谱特征基于原子物理特性, 可溯源到基本物理常数, 不依赖探头的物理尺寸, 铯泡对待测电场的干扰极小. 基于Rydberg原子对外场敏感的特点, 实现50 Hz—1 kHz范围内的低频电场调制到射频电场, 并得到保真度约95%的解调信号. 表明射频电场缀饰下Rydberg原子的EIT光谱在射频电场计量和量子通信中具有广阔的应用前景.
射频电场缀饰下铯Rydberg原子的电磁感应透明光谱
Electromagnetically induced transparency spectra of cesium Rydberg atoms decorated by radio-frequency fields
-
摘要: 采用全红外光激发Rydberg原子的方案, 选择探测光(852 nm)、缀饰光(1470 nm)和耦合光(780 nm), 利用三光子激发方式实现了Cs原子Rydberg态(49P3/2)的制备. 实验上, 观测到射频电场作用下|7S1/2
$\rangle $ → |49P3/2$\rangle $ Rydberg 跃迁形成的电磁感应透明(EIT)效应, 实现对Rydberg 原子的光学探测, 根据EIT光谱的变化来探究射频电场的幅度和频率对光谱的影响. 研究表明, 随着射频电场幅度的增强, 观察到光谱现象从越发明显的ac Stark 能移逐步过渡到复杂混合态的多个调制边带, 并根据EIT主峰的频移进一步讨论频率对铯泡中电场屏蔽的影响. 采用将低频电场调制到射频电场的方式, 实现了基于Rydberg原子的50 Hz—1 kHz范围内电场解调, 并对解调信号的幅度和频率进行拟合, 保真度达到95%. 研究结果对Rydberg原子射频光谱探测和低频电场的可溯源测量等提供有价值的参考.-
关键词:
- Rydberg原子 /
- 电磁感应透明光谱 /
- 射频电场 /
- ac Stark 能移
Abstract:The large electric dipole moment of the Rydberg atom allows for strong coupling with weak electric fields, and is widely used in electric field measurements because of its reproducibility, precision and stability. The combination of Rydberg atoms and electromagnetically induced transparency (EIT) technology has been used for detecting and characterizing radio-frequency (RF) electric fields. In this work, by selecting probe light (852 nm), dressed light (1470 nm), and coupled light (780 nm), the Rydberg state (49P3/2) of Cs atom is prepared by using a three-photon excitation scheme through using all-infrared light excitation of Rydberg atoms. We experimentally observe the EIT spectra of the Rydberg states decorated by radio-frequency electric fields, which optically detects Rydberg atoms. The effect of the amplitude and frequency of the RF electric field on the spectrum is explored in light of changes in the EIT spectrum. The results show that in the region of weak electric field, only the ac Stark energy shift and spectral broadening occur. As the electric field is further enhanced, the sideband phenomenon occurs in both the primary peak and secondary peak of the EIT. In the region of strong field, the Rydberg energy level produces a series of Floquet states with higher-order terms, as well as state shifting and mixing, resulting in asymmetry in the spectra of the EIT sideband peaks. The effect of frequency on the shielding effect of the Cs vapor cell is further discussed based on the shift of the main peak of the EIT. The demodulation of the electric field in a range of 50 Hz–1 kHz with a fidelity of 95% is achieved by modulating the low-frequency electric field to the RF electric field. The results can provide valuable references for spectral detection and traceable measurements of low-frequency electric fields. -

-
图 3 不同正弦射频电场情况下测量的EIT谱线随电场强度的变化 (a) ωRF = 30 MHz; (b) ωRF = 40 MHz; (c) ωRF = 50 MHz; (d) ωRF = 60 MHz
Figure 3. The variation of EIT spectral lines measured with the electric field intensity under different sinusoidal radio-frequency electric fields: (a) ωRF = 30 MHz; (b) ωRF = 40 MHz; (c) ωRF = 50 MHz; (d) ωRF = 60 MHz.
表 1 ARC软件包计算Cs原子直流极化率
Table 1. Theoretical calculation of dc polarizabilities for Cs by Alkali Rydberg Calculator Python package.
Cs原子直流极化率α/(Hz·V–2·m–2) Rydberg 态 49P1/2, |mj|=1/2 49P3/2, |mj|=1/2 49P3/2, |mj|=3/2 极化率 α: dc 74979.842 107095.687 89150.196 表 2 拟合正弦函数得到的振幅、频率等参数
Table 2. The parameters of amplitude and frequency are obtained by fitting the sinusoidal function.
拟合参数 频率 50 Hz 100 Hz 500 Hz 1000 Hz 振幅/V 0.0153 ± 0.0001 0.0182 ± 0.0001 0.0188 ± 0.0002 0.0173 ± 0.0001 频率/Hz 49.78 ± 0.09 100.18 ± 0.08 500.01 ± 0.09 1000.02 ± 0.07 R 2 (COD) 0.94356 0.95435 0.93143 0.9554 -
[1] Gallagher T F 1994 Rydberg Atoms (Cambridge: Cambridge University Press [2] Adams C S, Pritchard J D, Shaffer J P 2020 J. Phys. B: At. Mol. Opt. Phys. 53 012002 doi: 10.1088/1361-6455/ab52ef [3] Liu B, Zhang L, Liu Z, Deng Z, Ding D, Shi B, Guo G 2023 Electromagn. Sci. 1 1 doi: 10.23919/emsci.2022.0015 [4] Yuan J, Yang W, Jing M, Zhang H, Jiao Y, Li W, Zhang L, Xiao L, Jia S 2023 Rep. Prog. Phys. 86 106001 doi: 10.1088/1361-6633/acf22f [5] Mohapatra A K, Jackson T R, Adams C S 2007 Phys. Rev. Lett. 98 113003 doi: 10.1103/PhysRevLett.98.113003 [6] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819 doi: 10.1038/nphys2423 [7] Kumar S, Fan H, Kübler H, Sheng J, Shaffer J P 2017 Sci. Rep. 7 42981 doi: 10.1038/srep42981 [8] Tanasittikosol M, Pritchard J D, Maxwell D, Gauguet A, Weatherill K J, Potvliege R M, Adams C S 2011 J. Phys. B: At. Mol. Opt. Phys. 44 184020 doi: 10.1088/0953-4075/44/18/184020 [9] Gordon J A, Simons M T, Haddab A H, Holloway C L 2019 AIP Adv. 9 045030 doi: 10.1063/1.5095633 [10] Sedlacek J A, Schwettmann A, Kübler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001 doi: 10.1103/PhysRevLett.111.063001 [11] Simons M T, Haddab A H, Gordon J A, Novotny D, Holloway C L 2019 IEEE Access 7 164975 doi: 10.1109/ACCESS.2019.2949017 [12] Jing M, Hu Y, Ma J, Zhang H, Zhang L, Xiao L, Jia S 2020 Nat. Phys. 16 911 doi: 10.1038/s41567-020-0918-5 [13] Artusio-Glimpse A, Simons M T, Prajapati N, Holloway C L 2022 IEEE Microwave Mag. 23 44 doi: 10.1109/MMM.2022.3148705 [14] Gordon J A, Holloway C L, Schwarzkopf A, Anderson D A, Miller S, Thaicharoen N, Raithel G 2014 Appl. Phys. Lett. 105 024104 doi: 10.1063/1.4890094 [15] Holloway C L, Simons M T, Kautz M D, Haddab A H, Gordon J A, Crowley T P 2018 Appl. Phys. Lett. 113 094101 doi: 10.1063/1.5045212 [16] Meyer D H, Kunz P D, Cox K C 2021 Phys. Rev. Appl. 15 014053 doi: 10.1103/PhysRevApplied.15.014053 [17] Zhang L H, Liu Z K, Liu B, Zhang Z Y, Guo G C, Ding D S, Shi B S 2022 Phys. Rev. Appl. 18 014033 doi: 10.1103/PhysRevApplied.18.014033 [18] Song Z, Liu H, Liu X, Zhang W, Zou H, Zhang J, Qu J 2019 Opt. Express 27 8848 doi: 10.1364/OE.27.008848 [19] Otto J S, Hunter M K, Kjærgaard N, Deb A B 2021 J. Appl. Phys. 129 154503 doi: 10.1063/5.0048415 [20] Shaffer J, Kübler H 2018 A Read-out Enhancement for Microwave Electric Field Sensing with Rydberg Atoms (Vol. 10674) (SPIE [21] Ripka F, Amarloo H, Erskine J, Liu C, Ramirez-Serrano J, Keaveney J, Gillet G, Kübler H, Shaffer J 2021 Application-driven Problems in Rydberg Atom Electrometry (Vol. 11700) (SPIE [22] Liu B, Zhang L H, Liu Z K, Zhang Z Y, Zhu Z H, Gao W, Guo G C, Ding D S, Shi B S 2022 Phys. Rev. Appl. 18 014045 doi: 10.1103/PhysRevApplied.18.014045 [23] Hu J, Li H, Song R, Bai J, Jiao Y, Zhao J, Jia S 2022 Appl. Phys. Lett. 121 014002 doi: 10.1063/5.0086357 [24] Carr C, Tanasittikosol M, Sargsyan A, Sarkisyan D, Adams C S, Weatherill K J 2012 Opt. Lett. 37 3858 doi: 10.1364/OL.37.003858 [25] Xu J H, Gozzini A, Mango F, Alzetta G, Bernheim R A 1996 Phys. Rev. A 54 3146 doi: 10.1103/PhysRevA.54.3146 [26] Pearman C P, Adams C S, Cox S G, Griffin P F, Smith D A, Hughes I G 2002 J. Phys. B: At. Mol. Opt. Phys. 35 5141 doi: 10.1088/0953-4075/35/24/315 [27] Robertson E J, Šibalić N, Potvliege R M, Jones M P A 2021 Comput. Phys. Commun. 261 107814 doi: 10.1016/j.cpc.2020.107814 [28] Anderson D A, Schwarzkopf A, Miller S A, Thaicharoen N, Raithel G, Gordon J A, Holloway C L 2014 Phys. Rev. A 90 043419 doi: 10.1103/PhysRevA.90.043419 [29] Anderson D A, Miller S A, Raithel G, Gordon J A, Butler M L, Holloway C L 2016 Phys. Rev. Appl. 5 034003 doi: 10.1103/PhysRevApplied.5.034003 [30] Daschner R, Ritter R, Kübler H, Frühauf N, Kurz E, Löw R, Pfau T 2012 Opt. Lett. 37 2271 doi: 10.1364/OL.37.002271 [31] Yoshida S, Reinhold C O, Burgdörfer J, Ye S, Dunning F B 2012 Phys. Rev. A 86 043415 doi: 10.1103/PhysRevA.86.043415 [32] Jau Y Y, Carter T 2020 Phys. Rev. Appl. 13 054034 doi: 10.1103/PhysRevApplied.13.054034 -


 首页
首页 登录
登录 注册
注册





 下载:
下载: