首页
登录
注册
-
锂离子电池是目前最重要的可充电储能设备之一. 在经济和可持续电化学储能设备需求的推动下, 人们对具有更好规格容量、循环稳定性、高倍率能力和安全性的锂离子电池(LIBs)的需求日益迫切, 这也进一步刺激了电极材料研究的发展[1].
二维(2D)纳米材料的范围不仅限于石墨烯, 还包括诸如BN, MoS2等多种非碳单层材料, 这些材料已经通过实验得到验证, 并在诸如电子学、能源存储等领域展示了潜在应用[2]. 在这些二维材料中, 二硫化钼(MoS2)作为一种潜在的锂离子电池电极材料备受关注. 经过实验验证, MoS2作为锂离子电池负极可表现出良好的性能, 尤其是在比容量方面显示出相对较高的水平[3]. 理论研究指出, 具有低扩散势垒的MoS2单层能够稳定地吸附锂离子[4]. 然而, MoS2单层本身是一种半导体材料, 其带隙相当大, 约为1.80 eV[5], 这种特性限制了其导电性, 从而使其在电化学方面的性能受到了限制. 尽管理论上已经证明, 通过将二维MoS2纳米带切割成锯齿状结构可以将其转变为金属[6], 从而显著增强了与锂离子的相互作用, 且不会牺牲锂离子的迁移性能[4]. 然而, 目前MoS2纳米带的大规模生产仍面临着巨大的挑战.
二硫化钒(VS2)是一种层状过渡金属二硫族化物(LTMDs)材料, 其晶体结构类似于MoS2. 其由钒(V)和硫(S)原子组成, 其中V原子形成一个八面体配位的结构, 而S原子则形成二维的硫层. 该材料的电荷密度波(CDW)特性和电子结构的多样性使其在20世纪70年代被发现. 由于大部分层状过渡金属二硫族化物的电子传递效率较差, 使得其电化学性能较差. 为提高电化学性能, 寻找具有金属性质的LTMDs已成为一种解决方案. 具有金属性的二硫化钒(VS2)是典型的LTMDs家族成员之一, 可望在离子电池中作为负极增强循环过程的电子传输[7]. 大块的VS2由多个单层VS2相互堆叠形成, 而单层VS2由一层钒原子夹在两层硫原子中间组成. 层间距离较大, 有利于离子在插入和脱插入过程中的扩散.
然而, 尽管其具有独特的物理和化学性质, 但在过去的十年中, 二硫化钒并没有得到太多的关注, 主要是因为其制备过程相对困难[8]. 通常采用气相转移法或物理气相沉积法等方法来制备二硫化钒单晶, 这些方法需要很高的温度、真空度和反应气氛, 并且制备出来的样品通常很小[9].
尽管如此, 近些年来, 随着实验技术的不断发展, 关于二硫化钒的研究又逐渐得到了重视. 研究人员们利用先进的材料合成和表征手段, 通过改变制备条件来获得更好的纯度和晶体质量, 从而使其性能得到更好的展现. 这些研究为二硫化钒的应用提供了更多可能性, 例如在能源存储、光催化、传感器等领域[10,11].
在一项2011年的研究中, 研究人员在实验中成功地将大块VS2剥离成单层数少于5个的超薄纳米片[12]. 值得注意的是, 单层VS2存在两种主要的结构, 分别是基于V和S原子不同配位构型的六角形单层VS2(记为H相)和三角形单层VS2 (记为T相). 理论分析表明, H相单层VS2的能级相较于T相低43 meV, 这表明H相结构为基态[13,14]. 因此, 我们重点研究用作LIB负极材料的H相单层VS2的结构和电子性能.
电池在充放电过程中, 由于锂化/脱锂过程会产生电池体积膨胀和收缩的情况, 可能导致负极断裂或负极形貌变化, 最终导致大量容量损失和循环不良. Yu等[15]通过单层VS2的电学性能进行分析, 计算出锂离子电池的理论容量, 但对于VS2的机械性能没有做详细说明. 在实际情况中, 以VS2作为电极材料时, 往往是多层VS2堆叠在一起, 只计算单层的VS2与实际情况有较大的差别. 通过计算VS2的杨氏模量, 分析VS2的机械性能, 构建了双层VS2, 确定最大能够吸附锂离子数量, 分析其电池容量和体积变化.
为研究VS2作为离子电池电极的导电性能和结构稳定性, 本文采用第一性原理密度泛函理论方法进行理论研究, 计算研究VS2几何结构的稳定性、结构刚度、吸附能、离子迁移势能、电池容量.
-
本文计算使用基于密度泛函理论(DFT)[16,17]第一性原理方法的Quantum ATK软件包, 研究了Li原子在VS2结构表面吸附性质、态密度、电子性质及迁移路径、杨氏模量及理论容量. 计算时选取投影缀加波赝势(PAW)和局域密度近似(LDA)分别计算电子、离子相互作用情况和电子交换相关情况. 布里渊区采用3 × 3 × 1点进行采样, 能量的收敛精度为10–5 eV, 力的收敛标准为0.01 eV/Å, 为减小层间的相互作用, 真空层取为20 Å.
本文分别计算Li原子在VS2表面硫(S)的空位(H)与桥位(B)、及钒(V)的顶位(T)吸附后的吸附能, 吸附能由下面公式得到:
式中
$ {E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}+{\mathrm{L}}{\mathrm{i}}} $ 是吸附Li原子后VS2总能量,$ {E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}} $ 是吸附前VS2总能量,$ {E}_{{\mathrm{L}}{\mathrm{i}}} $ 是Li原子的总能量, n是Li原子的个数.采用受激弹性带(nudged elastic band, NEB)方法计算Li原子在VS2表面空位(H)、桥位(B)两个位点间的迁移路径, 在初始和最终态之间创建一系列中间态(插值态), 来构建整个反应路径. 在计算中, 插值态上的原子受激并相互影响, 从而在能量最小化的同时确定反应过程的势垒和最低能垒路径. 通过计算每个插值态上的原子位置和能量, 得到整个反应路径的势垒和反应坐标.
根据广义近似的DFT方法, 可以通过应变-应力近似线性区域的计算来获得材料的各弹性常数. 在这种方法中, 应力和应变张量都是对称的3×3矩阵, 因此我们可以使用Voigt符号将其更紧凑地表示为6维向量:
应力向量:
应变向量:
材料的应力向量对于给定应变向量的线性响应可以表示为
其中C是一个对称的6×6矩阵, 包含了弹性常数. 根据晶体对称性, 我们可以进一步减少独立弹性常数的数量.
弹性常数矩阵C的具体形式如下:
要获取弹性常数, 需要应用小变形原理, 即沿着选定的应变向量对模拟单元进行扰动, 并计算得到结果应力向量. 线性应力贡献可以通过拟合每个Voigt应力分量和相应的应变曲线来得到. 然后, 通过解一个最小二乘线性方程组, 结合晶体对称性, 可以得到独立的弹性常数.
-
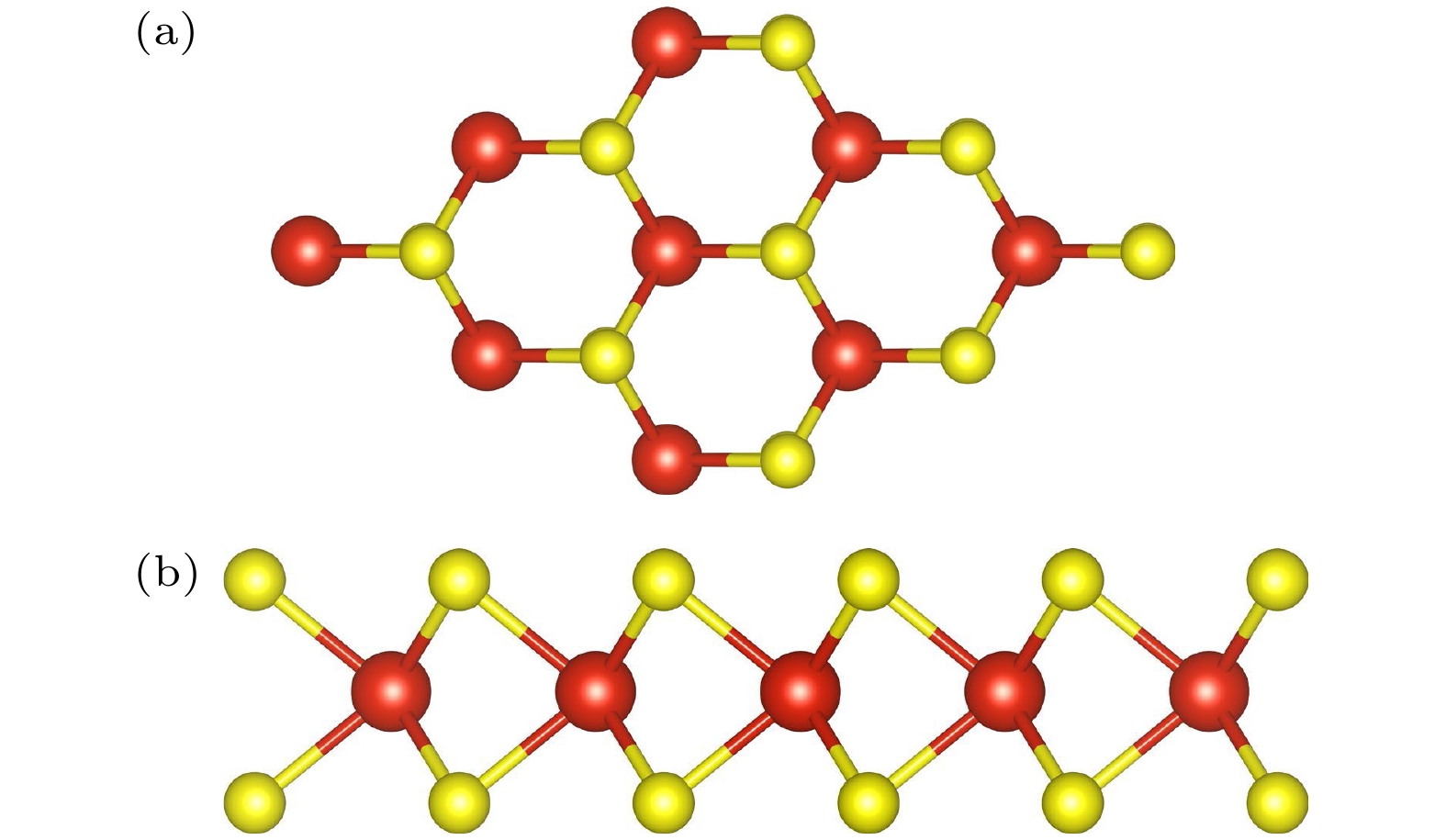
与其他过渡金属二硫化物(TMD)类似, VS2单层呈现三明治状结构, V层夹在两个S层之间. 一般来说, VS2有两种多晶型, 包括三角(T)相和六方(H)相, 这两种多晶型都对温度的变化和VS2层数的变化敏感. 在室温下, VS2单层更倾向于以H相结晶[14]. 因此, 本研究基于H相结构, 在H构型VS2 单层的优化结构中(图1(a)), 一个晶胞包含一个V原子和两个S原子, 晶格参数为
$ a=b=3.16 $ Å.V—S键长统一为2.36 Å, V—S—V键角为84.25°, 与文献[18, 19]非常一致. 并且本文对VS2自旋极化态与非极化态进行了计算, 计算结果表明 VS2单层具有自旋极化基态, 其能量比非极化态的低29 meV.
-
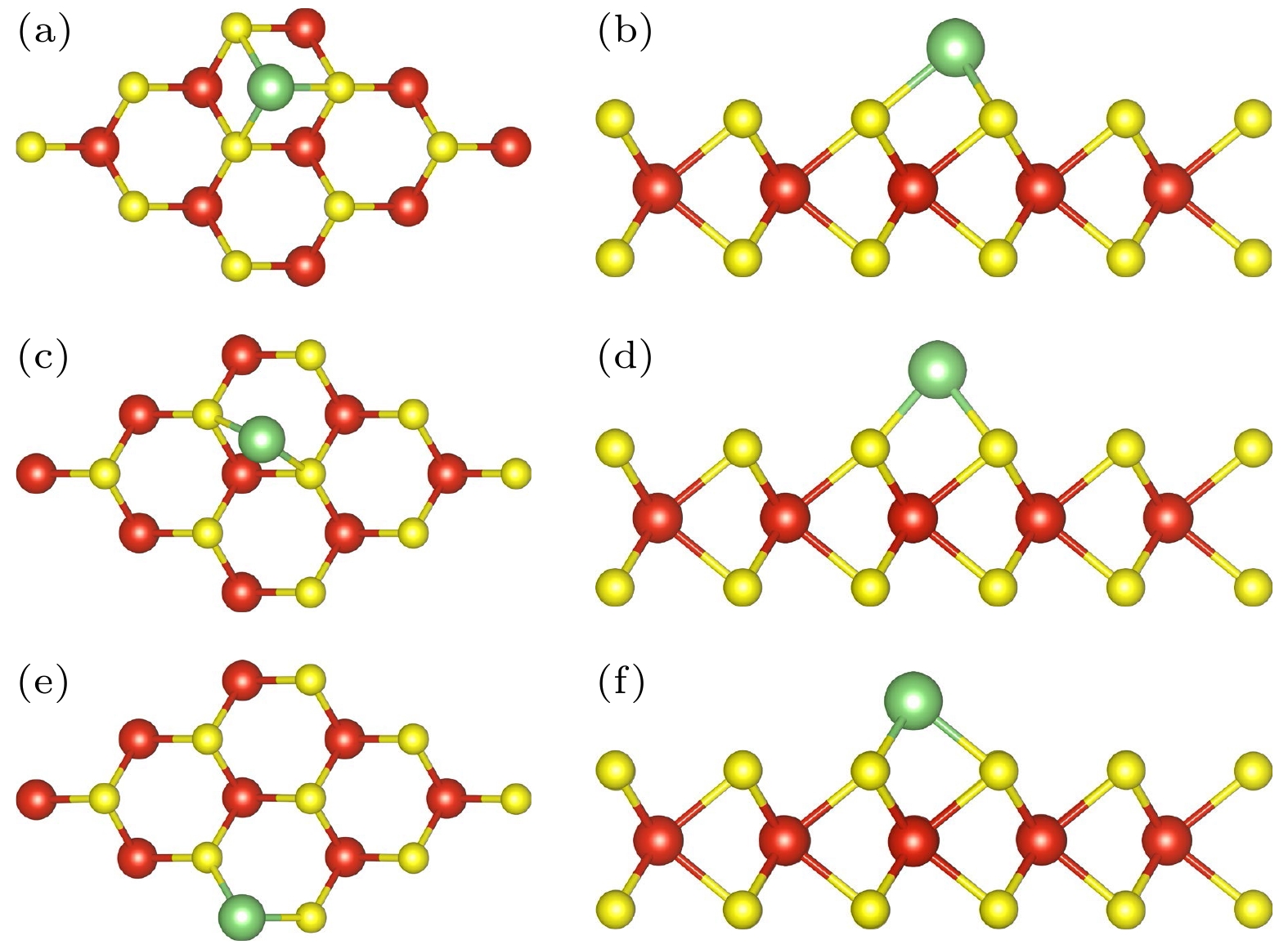
VS2中有钒(V)和硫(S)两种原子, 对VS2单层上S-T位、S-H位、S-B位、V-T位、V-H位、V-B位做Li原子吸附的优化后, 发现多个吸附位点中只留下3种吸附情况, 图2(a) S-H位、图2(c) S-B位、图2(e) V-T位, 其中最稳定存在的只有两个吸附位点, 即六边形中心上方的硫(S)原子空位(H)和钒(V)原子正上方顶位(T). 而考察V-H位和S-T位吸附位点, 通过不断精确优化后, Li原子都将会吸附到S-H位或V-T位, 即这两个位点上的锂原子在完全弛豫后移动到邻近的S-H或V-T位点, 因此这两个位点可能并不是锂离子吸附的局部最小位点, 并且吸附非常不稳定.
-
为从理论数据上探讨最优的吸附位点, 对钒(V)、硫(S)吸附位置做完优化, 计算吸附前后系统总能量, 在本论文中, 为简化研究计算, 采用单个Li原子吸附模型. 根据吸附能公式得:
$ {E}_{{\mathrm{a}}{\mathrm{d}}}={E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}+ {\mathrm{L}}{\mathrm{i}}}- {E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}}-{E}_{{\mathrm{L}}{\mathrm{i}}} $ , 计算得到几个位置的吸附能及Li吸附键长如表1所列.计算结果表明, 吸附后总能小于吸附前的总能, 吸附能为负值, 因此总的吸附过程是放热过程. 吸附后比未吸附的VS2具有更低的能量, 说明吸附后整个系统更加稳定, 并且Li的吸附更容易发生. 其中, 硫的桥位(S-B)的吸附能最大, 为–2.19 eV; 其次是硫的空位(S-H)的吸附能, 比硫的桥位(S-B)的吸附能小0.11 eV左右; 钒(V)顶位的吸附能最小, 为–2.40 eV, 说明Li在V上的吸附更加稳定, 与Tang等[20,21]研究结果一致.
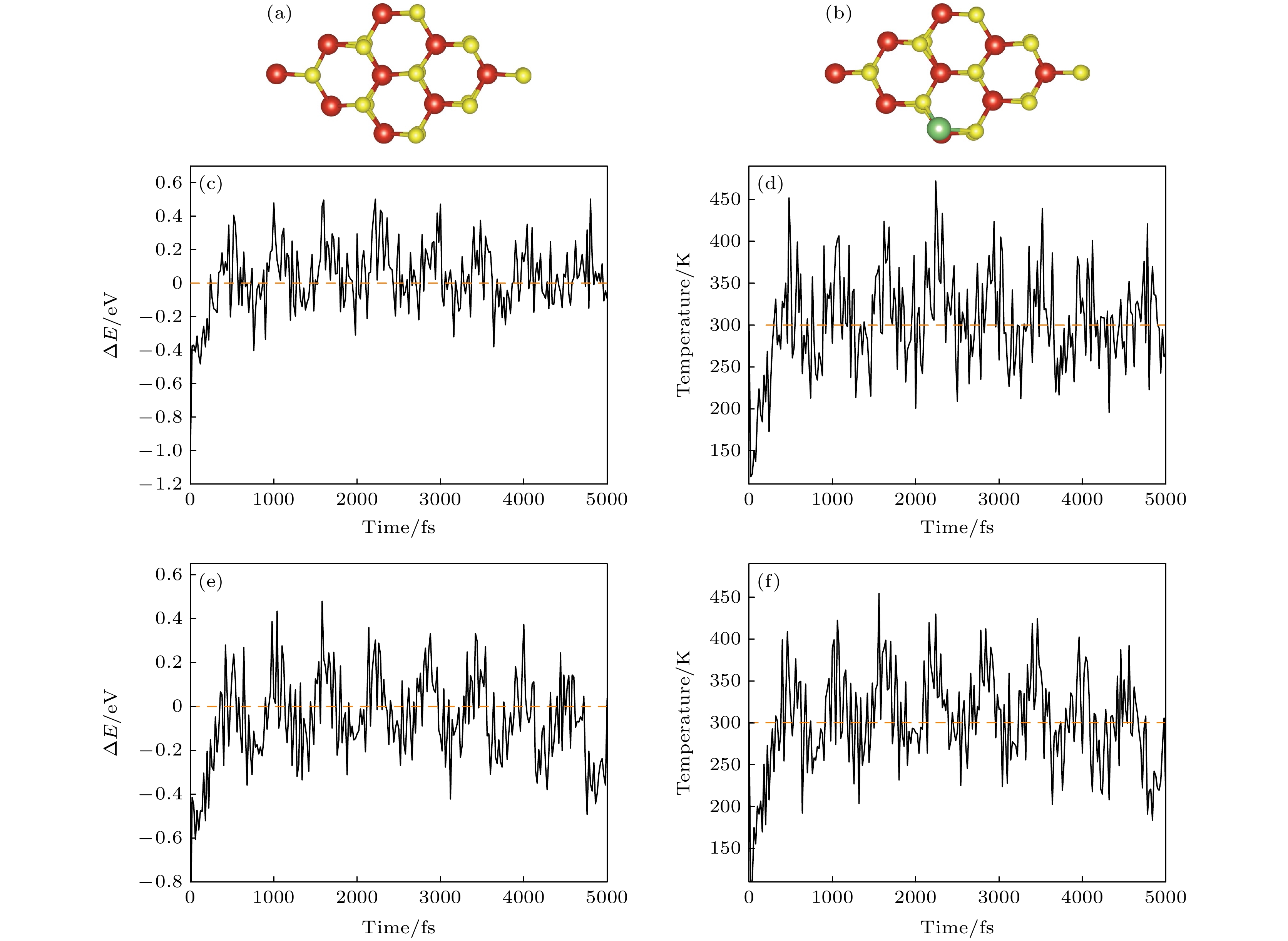
为了进一步评估吸附前后的热稳定性, 在正则系统中对H-VS2模型(图3(a))吸附钒的T后模型进行温度300 K、时间步长1 fs的第一性原理分子动力学(FPMD)模拟, 总时长为5000 fs, 其中图3(c)纵坐标中
$ \Delta E=E-23500\;{\mathrm{e}}{\mathrm{V}} $ , 图3(e)纵坐标中$ \Delta E=E-23697.8\;{\mathrm{e}}{\mathrm{V}} $ .大约500 fs后, 系统总能和温度总涨落的量级达到稳态, 可以观察到, FPMD期间的吸附前后能量(图3(c), (e))在–0.5—0.5之间振荡. 由于原子与晶格里的其他邻近原子相互作用, 分子的初始动能将会部分地转换成势能, 从而导致一开始时体系的温度降低, 可以观察到FPMD期间的温度迅速下降(图3(d), (f)), 降至150 K以下后以一个较快速度上升至300 K, 并之后在300 K附近进行振荡, 说明在常温下吸附前后结构都能够稳定存在.
总体来看, 总能量与温度分别在一个小范围内振荡, 并且没有发现漂移现象, 总体波动较小, 这表明Li在常温环境下具有很好的结构稳定性.
-
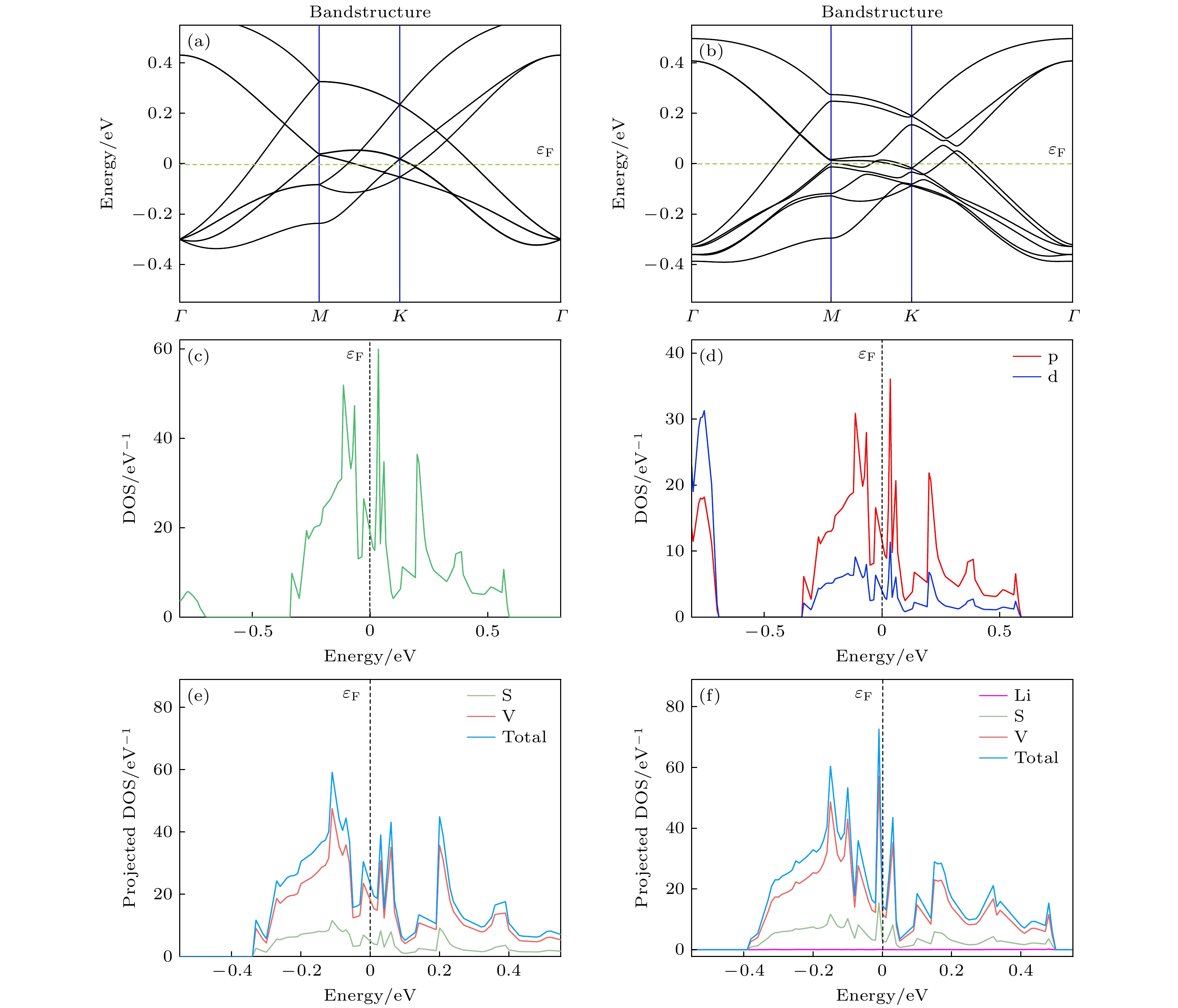
为检验VS2的导电性能, 计算VS2的能带图、态密度和分态密度. 从能带图(图4(a))上可以看出, VS2的价带和导带穿过费米能级, 说明VS2具有金属性, 意味着VS2具有优异的导电性能. 观察吸附后的能带图(图4(b)), 可以看出Li原子的吸附对VS2的能带几乎没有影响.
观察VS2的总的态密度图(图4(c)), 费米能级附近有态密度的存在, 这也就对应着能带图中VS2的价带和导带穿过费米能级. 同时, 观察p电子态和d电子态的态密度图(图4(d)), 可以看出费米能级附近态密度几乎由p态和d态的电子提供. 对比两种原子分态密度可以看出费米能级附近态密度大部分由钒(V)原子提供. 结合态密度图可以分析出, 在VS2费米能级附近的能带由V的3d态和S的3p态电子贡献. 也就表明, VS2的导电性能在很大程度上受V的3d态和S的3p态电子的影响.
由于Li原子吸附在V的顶位更稳定, 因此计算吸附V顶位的能带图和态密度图. 对比吸附前后的能带图, 分态密度图可以看出, Li的吸附对于VS2的导电性几乎没有影响. 表明在不考虑其他因素下, VS2在吸附后也能保持优异的导电性能.
-
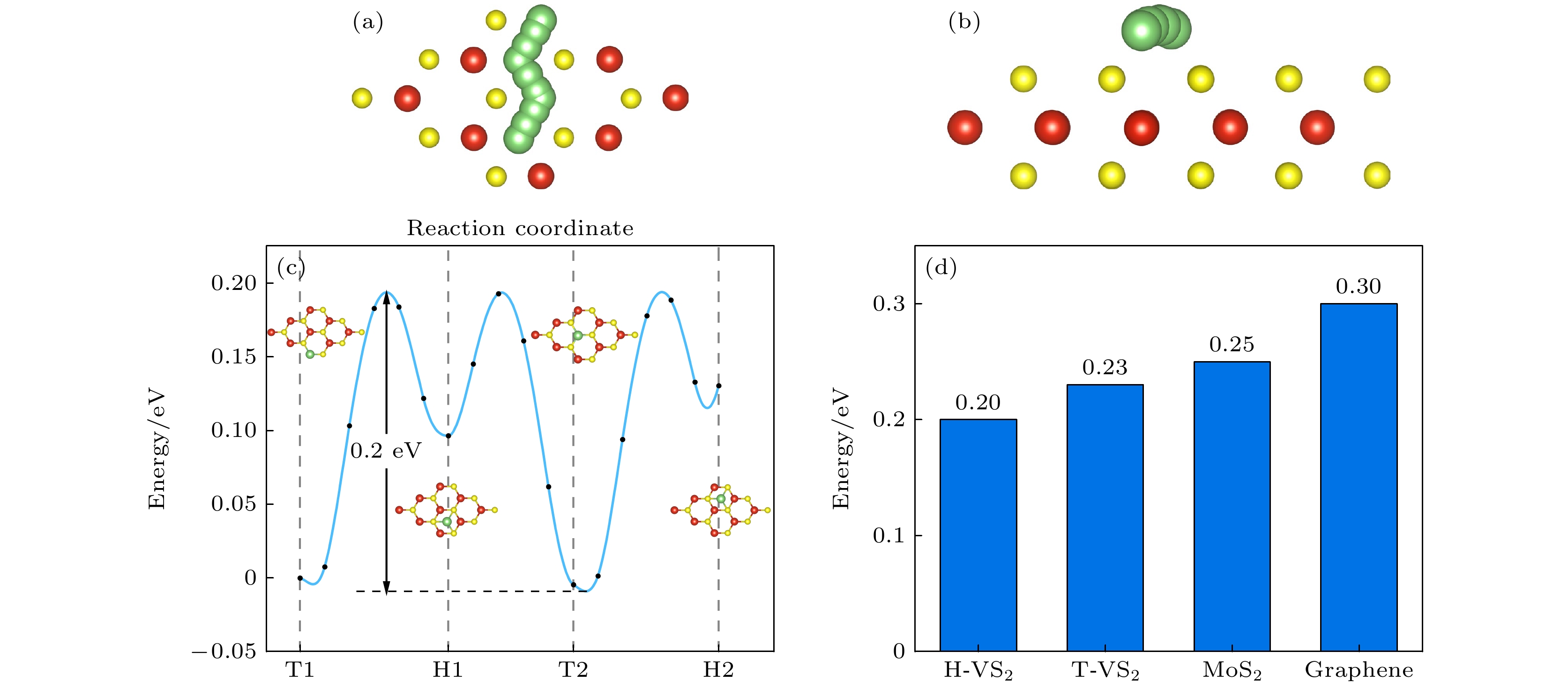
为研究Li原子在H相的VS2表面扩散, 进行Li单原子从V-T1—S-H1—V-T2—S-T2的研究, 用NEB方法寻找最优扩散路径. 由计算结果 (图5)发现Li从V-T2扩散到S-H2, 扩散势垒为0.20 eV, 与其他研究的扩散势垒基本一致[22]. 而T相VS2的扩散势垒为0.23 eV[22], Li在H相的VS2表面具有更小的扩散势垒, 意味着Li在H相VS2具有更快的扩散速率, 即导电性能更优异.
Li在石墨烯的表面的扩散势垒在0.30 eV, 而同样为二硫族化合物材料中MoS2的扩散势垒为0.25 eV[22] , Li在VS2表面的扩散势垒具有更小值.
同时, VS2是二维材料, 其层间距离较宽, 可以有利于Li离子在层间迁移, 使得Li离子能够快速传输, 这意味着Li离子在VS2表面的传输速率可能非常优异.
-
前面提到, VS2吸附Li原子的整个过程为发热过程, 这意味着锂的吸附是一个自发的过程, 但锂离子的嵌入与脱出将会导致VS2体积发生变化, 电极也将发生膨胀和收缩. 众所周知, 结构变形甚至电极粉碎会导致容量快速衰减, 并带来较差的循环能力. 对于高效负极材料来说, 优异的机械性能对于承受循环过程中锂化引起的体积膨胀至关重要. 因此, 我们计算了VS2的机械性能.
利用Quantum ATK的弹性常数计算模块, 可以直接算出各个弹性常数. 根据弹性对称矩阵系数矩阵, C11 = C22, C12 = C21, 其中C11和C22表示材料分别沿着x和y方向对单轴拉伸应变的刚度响应, 弹性常数C12描述了材料抵抗平面双轴拉伸应变的能力. 在Quantum ATK的弹性常数计算模块中, 采用的是体积, 而VS2为二维材料, 只需处理面积. 本论文中, 真空层采用的是20 Å, 通过转换为国际单位, 可以得到杨氏模量(Y)和泊松比(v)公式:
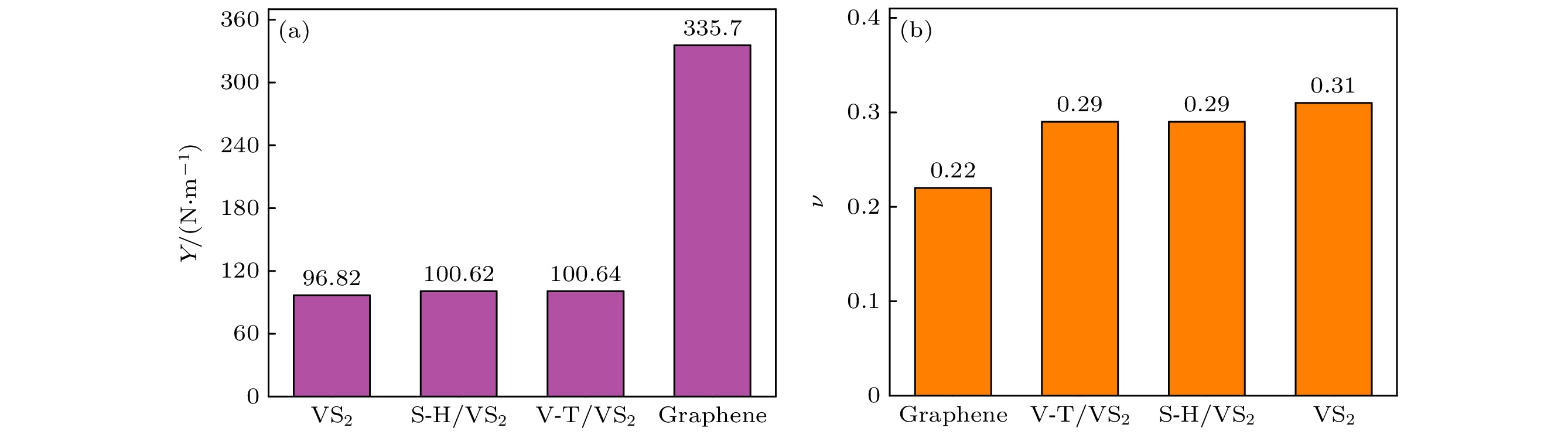
VS2吸附前后及石墨烯的弹性常数和杨氏模量如表2所列. 杨氏模量是描述固体材料抵抗形变能力的物理量, 是衡量材料产生弹性变形难易程度的指标, 其值越大, 即材料刚度越大, 在一定应力作用下, 发生弹性变形越小. 计算3×3×1的VS2超胞, 得到其杨氏模量为96.82
$ {\mathrm{N}}/{{\mathrm{m}}} $ , 表明其刚性较好, 与其他研究结果基本一致[23]. 比较吸附Li前后的杨氏模量, 发现系统吸附后的杨氏模量有所提升, 但总体的杨氏模量变化较小. 这表明VS2在作为电极材料时其刚性并不会由于Li的吸附而降低.VS2吸附前后与石墨烯的杨氏模量和泊松比对比如图6所示. -
最后, 我们探讨了基于VS2负极材料的锂离子电池的理论容量和嵌锂前后的层间距与体积变化率. 构建一个3×3×1的双层 VS2模型, 得到最稳定双层VS2层间距为3.67 Å. 在双层VS2层间吸附锂离子, 在层间最高能够吸附锂离子个数n = 18时, VS2的层间距变为6.24 Å, VS2体积膨胀率为30.6%. 因为实际电池负极是由多层VS2堆叠而成, 为考虑最接近实际的电池容量, 在双层中只计算其中一层VS2的摩尔质量, 法拉第常数F = 26800 mAh/mol, 根据
计算得到理论容量为466 mAh/g. 相比于石墨烯的理论容量(372 mAh/g)[24], VS2的理论容量更高, 说明了VS2作为锂离子电池负极材料具有巨大潜力.
-
本文通过DFT计算探索使用VS2单层作为锂离子电池负极材料的可能性. 系统地研究了VS2单层的单个Li原子结合能、扩散势垒以及杨氏模量. 通过对比观察能带图和态密度图, 可发现VS2单层是金属性的, 具有优异的导电性, 并且其导电性能与钒的3d态和硫的3p态电子相关. 同时, Li在VS2表面的扩散势垒只有0.20 eV, 比MoS2和石墨烯具有更小的Li的扩散势垒, 表明Li能够较快的迁移, 有利于LIB快速充电-放电过程. VS2作为电极材料的储存容量能够达到466 mAh/g, 并且完全锂化后VS2材料还具有较低的开路电压[25]. 多层VS2的制备已经在实验上实现突破, 相信随着不断的研究, 在不久的将来可以实现具有优异电化学性能的二维VS2负极材料.
VS2作为锂离子电池负极材料的第一性原理研究
First-principles study of VS2 as anode material for Li-ion batteries
-
摘要: 随着对锂离子电池(LIBs)性能要求的提高, 研究开发锂离子电池的新型电极尤显重要. 本文采用第一性原理计算研究二硫化钒(VS2)作为锂离子电池负极材料的可能性. 计算结果表明: VS2具有金属性, 费米能级附近的态密度主要来源于钒的3d轨道及硫的3p轨道; Li在VS2单层中优先吸附钒(V)的顶位, Li在VS2表面具有非常好的扩散性, 扩散势垒仅为0.20 eV, 低于石墨烯, 表明Li能够较快地迁移, 有利于LIB快速充电-放电过程; VS2机械性能良好, 杨氏模量为96.82 N/m, 且吸附Li后的杨氏模量与泊松比都未减小, 表明VS2在吸附Li以及Li离子扩散迁移过程中, 刚性并不会降低; 并且计算得到VS2的电池容量(466 mAh/g)比石墨烯更高. 研究表明VS2具有出色的导电性能和优异的机械刚性及较高的理论容量, 是一种非常有前景的锂离子电池负极材料.Abstract: With the increase of performance requirements for lithium-ion batteries (LIBs), it is particularly important to study and develop new electrodes for lithium-ion batteries. In this work, a 3×3×1 supercell of VS2 is constructed, and the possibility of using it as an anode material for lithium-ion batteries is study by the first-principles method based on density functional theory. Through the analysis of the energy band diagram, it is found that VS2 has metallic properties. Combining the density of states diagram, the analysis shows that the energy band near the Fermi level of VS2 is contributed by the 3d state of V and the 3p state electrons of S, which means that the conductive properties of VS2 are largely affected by the 3d state of V and the 3p state electrons of S. Of the vacancies, bridge sites, and top sites of lithium adsorbing vanadium (V), the top site has the lowest adsorption energy, indicating that lithium will preferentially adsorb the top site of vanadium (V). Through first-principles molecular dynamics simulations of the top position of adsorbed vanadium (V), it is found that at a temperature of 300 K, the total energy of the system and the magnitude of the total temperature fluctuation can reach a steady state, indicating that lithium can exist at the top position of stably adsorbed vanadium (V). Moreover, the interlayer spacing of the double-layer VS2 reaches 3.67 Å, which is larger than the interlayer spacing of graphene. From the top position to the vacancy, its diffusion barrier is only 0.20 eV. Its interlayer spacing is larger than the double-layer graphene’s, and its diffusion barrier is lower than graphene’s, indicating that lithium has very good diffusivity on the VS2 surface, and lithium can migrate quickly on the VS2 surface, which is conducive to the rapid charge-discharge process of LIB. In addition to excellent electrical conductivity, VS2 has good mechanical properties. The calculated Young's modulus is 96.82 N/m, and the Young's modulus and Poisson’s ratio do not decrease after adsorbing lithium, indicating that the rigidity of VS2 will not be reduced in the diffusion and migration process of lithium. On the other hand, it has excellent deformation resistance. In order to be more accurate and closer to the actual situation, a double-layer VS2 model is constructed, with a maximum number of lithium atoms adsorbed between layers being 18. The calculated theoretical capacity of VS2 (466 mAh/g) is higher than the theoretical capacity of graphene (372 mAh/g). Our results indicate that VS2 has excellent electrical conductivity and mechanical stiffness, making it a promising cathode material for lithium-ion batteries.
-
Key words:
- lithium-ion battery /
- energy of adsorption /
- first-principle .
-
-
图 1 (a)H-VS2的3×3×1结构俯视图; (b)H-VS2的3×3×1结构侧视图
Figure 1. (a) Top view of 3×3×1 structure of H-VS2; (b) side view of 3×3×1 structure of H-VS2.
图 2 (a)吸附H-VS2中S-H位俯视图; (b)吸附H-VS2中S-H位侧视图; (c)吸附H-VS2中S-B位俯视图; (d)吸附H-VS2中S-B位侧视图; (e)吸附H-VS2中V-T位俯视图; (f)吸附H-VS2中V-T位侧视图
Figure 2. (a) Top view of S-H sites in adsorbed H-VS2; (b) side view of S-H sites in adsorbed H-VS2; (c) top view of the S-B site in the adsorbed H-VS2; (d) side view of the S-B site in the adsorbed H-VS2; (e) top view of V-T site in adsorbed H-VS2; (f) side view of V-T site in adsorbed H-VS2.
图 3 分子动力学模拟后 (a) H-VS2俯视图; (b)吸附V-T俯视图; (c), (d) 300 K, 步长1 fs下总时间5 ps内H-VS2模型FPMD期间的能量与温度波动; (e), (f) 300 K, 步长1 fs下总时间5 ps内吸附V-T模型FPMD期间的能量与温度波动
Figure 3. After molecular dynamics simulation: (a) H-VS2 top view; (b) adsorbed V-T top view; (c), (d) energy and temperature fluctuations during FPMD of H-VS2 model within a total time of 5 ps at 300 K, step size 1 fs; (e), (f) energy and temperature fluctuations during FPMD of adsorbed V-T model within a total time of 5 ps at 300 K and step size 1 fs.
图 4 (a) VS2能带图; (b)吸附Li原子后VS2能带图; (c) VS2总态密度图; (d) VS2的p和d电子态密度图; (e) VS2分态密度图; (f)吸附Li原子后分态密度图
Figure 4. (a) VS2 energy band diagram; (b) VS2 energy band diagram after adsorption of Li atoms; (c) VS2 total state density diagram; (d) VS2-p and VS2-d electronic state density diagram; (e) VS2 partial density of state diagram; (f) partial density of state diagram after adsorption of Li atoms.
图 5 Li在VS2表面从V-T1—S-H1—V-T2—S-H2扩散路径 (a)俯视图; (b)侧视图; (c) Li在VS2表面的扩散势垒; (d) 扩散势垒对比图
Figure 5. Li diffusion path of V-T1—S-H1—V-T2—S-H2 on the VS2 surface: (a) Top view; (b) side view; (c) Li diffusion barrier on the VS2 surface; (d) comparative chart of diffusion barriers.
图 6 4×4×1超胞刚性对比 (a)杨氏模量对比图; (b) 泊松比对比图
Figure 6. Rigidity comparison of 4×4×1 supercell: (a) Young’s modulus comparison; (b) Poisson’s ratio comparison.
表 1 VS2的总能量
$ {E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}} $ 、Li在其表面吸附后总能量$ {E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}+{\mathrm{L}}{\mathrm{i}}} $ 、吸附能Ead、Li与VS2成键后的平均键长dTable 1. The total energy
$ {E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}} $ of VS2, the total energy$ {E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}+{\mathrm{L}}{\mathrm{i}}} $ after Li is adsorbed on its surface, the adsorption energy Ead, and the average bond length d of the bond between Li and VS2.吸附位置 $ {E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}} $ /eV
$ {E}_{{\mathrm{V}}{{\mathrm{S}}}_{2}+{\mathrm{L}}{\mathrm{i}}} $ /eV
Ead/eV d/Å S-H –23500.985 –23698.790 –2.303 2.38 S-B –23500.985 –23698.681 –2.194 2.31 V-T –23500.985 –23698.892 –2.405 2.37 
下载: 导出CSV
表 2 VS2吸附V-T和S-H后VS2及石墨烯的弹性常数和杨氏模量
Table 2. Elastic constants and Young’s modulus of VS2, VS2 and graphene after adsorption of V-T and S-H.
System C11 C22 C12 Y/ $ ({\mathrm{N}}\cdot {{\mathrm{m}}}^{-1}) $ 
v VS2 53.49 53.49 16.48 96.82 0.31 VS2吸附V-T 55.05 55.05 16.13 100.64 0.29 VS2吸附S-H 55.03 55.03 16.12 100.62 0.29 石墨烯 176.08 176.08 38.06 335.70 0.22
下载: 导出CSV
-
[1] Tarascon J M, Armand M 2001 Nature 414 359 doi: 10.1038/35104644 [2] Xu M S, Liang T, Shi M M, Chen H Z 2013 Chem. Rev. 113 3766 doi: 10.1021/cr300263a [3] Liu H, Su D, Zhou R, Sun B, Wang G, Qiao S Z 2012 Adv. Energy Mater. 2 970. doi: 10.1002/aenm.201200087 [4] Li Y F, Wu D H, Zhou Z, Cabrera C R, Chen Z F 2012 J. Phys. Chem. Lett. 3 2221 doi: 10.1021/jz300792n [5] Mak K F, Lee C, Hone J, Shan J, Heinz T F 2010 Phys. Rev. Lett. 105 136805 doi: 10.1103/PhysRevLett.105.136805 [6] Wang Z Y, Li H, Liu Z, Shi Z J, Lu J, Suenaga K, Joung S K, Okazaki T, Gu Z N, Zhou J, Gao Z X, Li G P, Sanvito S, Wang E G, Iijima S 2010 J. Am. Chem. Soc. 132 13840 doi: 10.1021/ja1058026 [7] 贺巧巧 2019 硕士学位论文(广州: 暨南大学) He Q Q 2019 M. S. Thesis (Guangzhou: Jinan University [8] 蒋晗涛 2022 硕士学位论文(长春: 东北师范大学) Jiang H T 2022 M. S. Thesis (Changchun: Northeast Normal University [9] 李传斌 2022 硕士学位论文(郑州: 华北水利水电大学) Li C B 2022 M. S. Thesis (Zhengzhou: North China University of Water Resources and Electric Power [10] 王羽偲嘉 2022 硕士学位论文(西安: 陕西科技大学) Wang Y C J 2022 M. S. Thesis (Xi'an: Shaanxi University of Science & Technology [11] 王振国 2021 博士学位论文 (上海: 华东师范大学) Wang Z G 2021 Ph. D. Dissertation (Shanghai: East China Normal University [12] Feng J, Peng Wu L C , Sun X , Hu S , Lin C, Dai J, Yang J L, Xie Y 2012 Adv. Mater. 15 1969 [13] Putungan D B, Lin S H, Kuo J L 2016 ACS Appl. Mater. Inter. 8 18754 doi: 10.1021/acsami.6b03499 [14] Zhang H, Liu L M, Lau W M 2013 J. Mater. Chem. A 1 10821 doi: 10.1039/c3ta12098h [15] Yu J, Zhou Z, Cabrera C R, Chen Z F 2013 J. Phys. Chem. C 117 25409 doi: 10.1021/jp410969u [16] Kresse G, Hafner J 1993 Phys. Rev. B 47 558 doi: 10.1103/PhysRevB.47.558 [17] Kresse G, Hafner J 1994 Phys-Condens Mat. 6 8245 doi: 10.1088/0953-8984/6/40/015 [18] Feng J, Sun X, Wu C Z, Peng L L, Lin C W, Hu S L, Yang J L, Xie Y 2011 J. Am. Chem. Soc. 133 17832 doi: 10.1021/ja207176c [19] Ma Y D, Dai Y, Guo M, Niu C W, Zhu Y T, Huang B B 2012 ACS Nano 6 1695 doi: 10.1021/nn204667z [20] Tang C M, Zhang M Z, Zhang K X, Gong J F 2021 Appl. Surf. Sci. 564 150468 doi: 10.1016/j.apsusc.2021.150468 [21] Wang D S, Liu Y H, Meng X, Wei Y J, Zhao Y Y, Pang Q, Chen G 2017 J. Mater. Chem. A 5 21370 doi: 10.1039/C7TA06944H [22] Mikhaleva N S, Visotin M A, Kuzubov A A, Popov Z I 2017 J. Phys. Chem. C 121 24179 doi: 10.1021/acs.jpcc.7b07630 [23] Liu B, Gao T, Liao P, Wen Y F, Yao M J, Shi S Q, Zhang W Q 2021 Phys. Chem. Chem. Phys. 23 18784 doi: 10.1039/D1CP02243A [24] Liu Y, Artyukhov V I, Liu M, Harutyunyan A R, Yakobson B I 2013 J. Phys. Chem. Lett. 4 1737 doi: 10.1021/jz400491b [25] Liu J Z, Guo P F 2015 J. Inorg. Mater. 30 1339 doi: 10.15541/jim20150345 -
计量
- 文章访问数: 342
- HTML全文浏览数: 342
- PDF下载数: 4
- 施引文献: 0