-
钙钛矿材料具有丰富多样的化学成分和物理性质, 例如铁电性、压电性、铁磁性、光电性. 在信息存储、发光二极管(LED)和太阳能电池等领域得到了广泛的应用[1–5] . 目前广泛研究的钙钛矿材料主要有以下3类, 第1类是无机钙钛矿, 目前工业化的无机钙钛矿材料成本低廉, 且制备工艺成熟. 例如具有铁电特性的传统无机钙钛矿材料钛酸钡(BTO, BaTiO3)和钛酸锆铅(PZT, PbZrxTi1–xO3), 这类材料已被广泛应用在电容器和压电器件上[6,7] . 而且, 无机钙钛矿材料的性能参数覆盖范围广, 故能较大范围地扩展其应用领域. 例如, Bi基层状钙钛矿氧化物Bi3TiTaO9和Bi3TiTaO9-6Ce的极化值分别为5.4 μC/cm2和8.0 μC/cm2, 相变温度分别为1164 K和1153 K[8]; 而BiFeO3的极化为100 μC/cm2, 相变温度约为830 K[9–11] . 然而, 传统钙钛矿材料仍然存在一些缺点, 例如, 它们中的大多数含有对环境不友好的重金属, 因此不环保; 很高的加工温度使得它们与微电子系统不兼容; 此外, 由于大多数钙钛矿氧化物铁电体很脆, 无法用于柔性器件[12] .
第2类材料是有机-无机杂化钙钛矿. 其中, 有机-无机杂化卤化铅钙钛矿因其加工成本低、易于制造、有较高的光电转换效率从而受到太阳能电池研究者的青睐[13] . 这类钙钛矿材料通常具有很高的光吸收系数、较好的双极迁移率、长载流子扩散长度、带隙可调等优点[13,14], 而具有成为有优异光电性能的光伏材料的巨大潜力. 例如, 以MAPbI3作为光吸收层的光电池功率转化率(PCE)从3.8%显著提高到24.4%(目前应用的钙钛矿-硅串联太阳能电池为 28%)[15]. 此外, 由于杂化钙钛矿材料能在结构上实现有机和无机特性的最佳组合, 从而成为许多领域研究的热点. 在具有极性空间群的有机-无机杂化钙钛矿材料中, 由于无机部分八面体位移和有机分子有序排列而往往表现出显著的铁电性、压电性等特性[16–18], 使得具有铁电特性的有机-无机杂化钙钛矿材料在光电探测、压电器件、信息存储元件等领域成为了候选者. 然而, 目前具有优异性能的有机-无机杂化钙钛矿主要集中在重金属尤其是有毒的铅元素, 不利于工业化生产, 并且对环境有害.
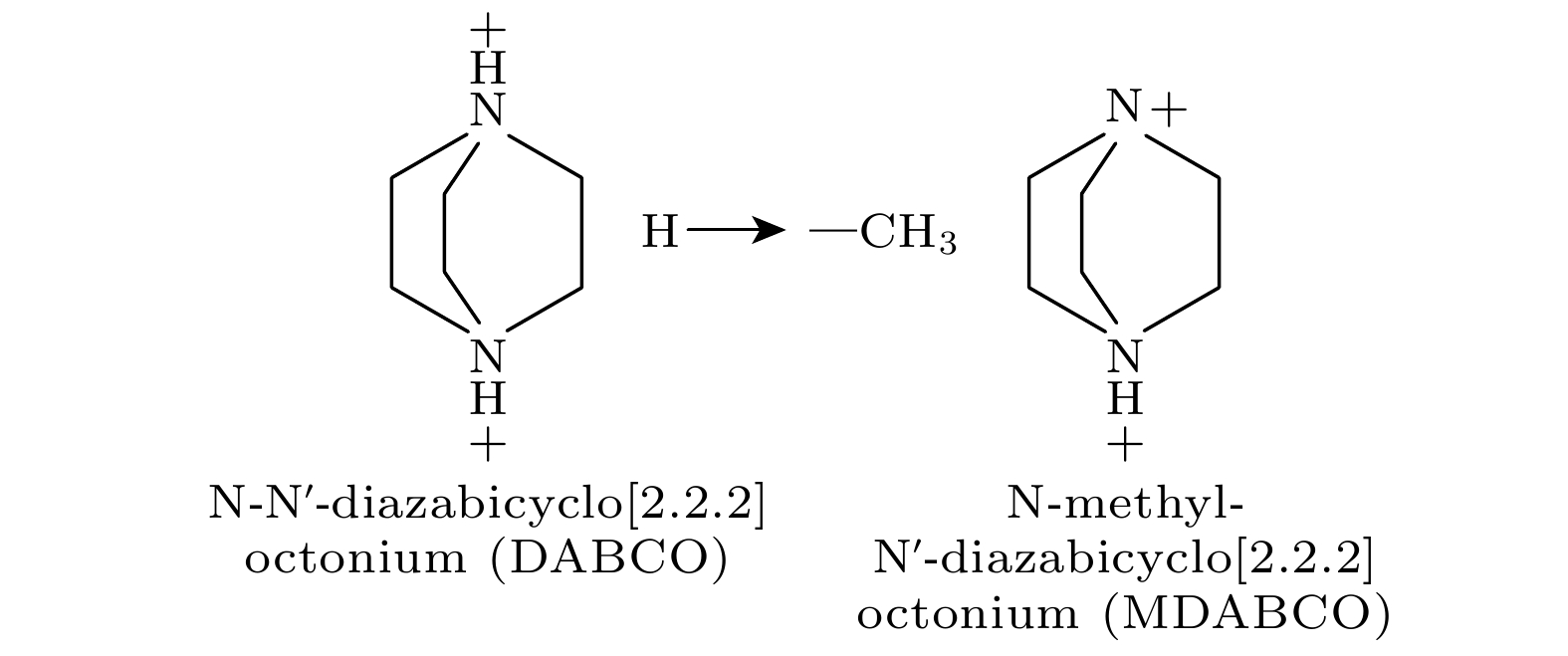
为了解决重金属钙钛矿有毒的问题, 近期Ye等[19]报道了一类钙钛矿材料: 无金属钙钛矿(有机钙钛矿). 该团队研究者设计并合成了一系列具有较高居里温度的无金属ABX3型三维钙钛矿有机铁电材料, 其顺电-铁电转变温度在355 —493 K之间. 这类有机钙钛矿铁电体具有通式 A-NH4-X3, 其中A为二价有机阳离子官能团, 如DABCO2+ (N-N′-diazabicyclo[2.2.2] octonium, dabconium), X为卤素阴离子. 进一步研究表明, 采用不同的基团取代A位有机阳离子DABCO2+上的一个氢原子, 而破坏原有DABCO2+的轴对称性, 形成极性分子, 从而诱导材料产生自发极化. 例如, 用一个甲基取代一个氢原子得到MDABCO2+, 结构如图1所示, 甲基取代形成了极性有机阳离子MDABCO2+, 使得MDABCO-NH4-I3具有铁电特性, 极化值达到22 μC/cm2, 相变温度高达448 K(传统的无机钙钛矿材料BTO的极化值和相变温度分别为26 μC/cm2和390 K)[20] . 有机钙钛矿铁电材料由于其结构可调性和分子多样性成为了铁电体领域的优秀候选者. 此外, 压电特性是铁电体材料具有的另一性能, 有机钙钛矿铁电体往往具有较大的压电应变分量[21], 并且MDABCO-NH4-I3薄膜被成功集成到压电纳米发电机中[22], 说明了有机钙钛矿实用于压电器件的可行性, 其在可穿戴电子产品上有广泛的应用前景. 近期, 在Ye等[19]报道的有机钙钛矿铁电材料MDABCO-NH4-I3基础上, Choi等[23] 用更大尺寸的
${\text{PF}}_6^ - $ 替代I–成功合成了MDABCO-NH4-(PF6)3, 在体系中引入N—H···F氢键, 实验结果表明有机钙钛矿中的矫顽力场可以通过调节分子间氢键的强度来增强.通过在有机钙钛矿的A位阳离子MDABCO2+中引入卤素官能团(F, Cl)取代—CH3中的一个H原子, 能够增大A位阳离子的偶极矩, 不仅可以提高DR-NH4-X3 (R = H, F, Cl; X = BF4)的自发极化, 还能够改善材料的光电响应能力[24]. Kasel等[25]采用—CH3, —OH, —CN等基团替代A位有机阳离子DABCO2+上的一个H原子, 构造了MDABCO2+, ODABCO2+, CNDABCO2+等有机阳离子, 研究发现A位阳离子对A-NH4-X3 (X = Cl, Br, I)的非线性光学(non-linear optical, NLO)性质起着重要作用, 在DABCO-NH4-X3的结构上引入—CN, 显著提高了有机钙钛矿的NLO性能. 本文基于MDABCO-NH4-(PF6)3有机钙钛矿化合物及以上研究背景, 设计将有机阳离子中的—CH3替换为—CN, —OH, —NO和—SH四种基团, 通过第一性原理计算, 研究了MDABCO-NH4-(PF6)3等一系列材料的结构稳定性、电子结构、力学性能、铁电性和压电性能等物理性质. 本研究对于新型有机钙钛矿的研究提供了有益的理论指导, 为后续的实验提供了理论基础.
-
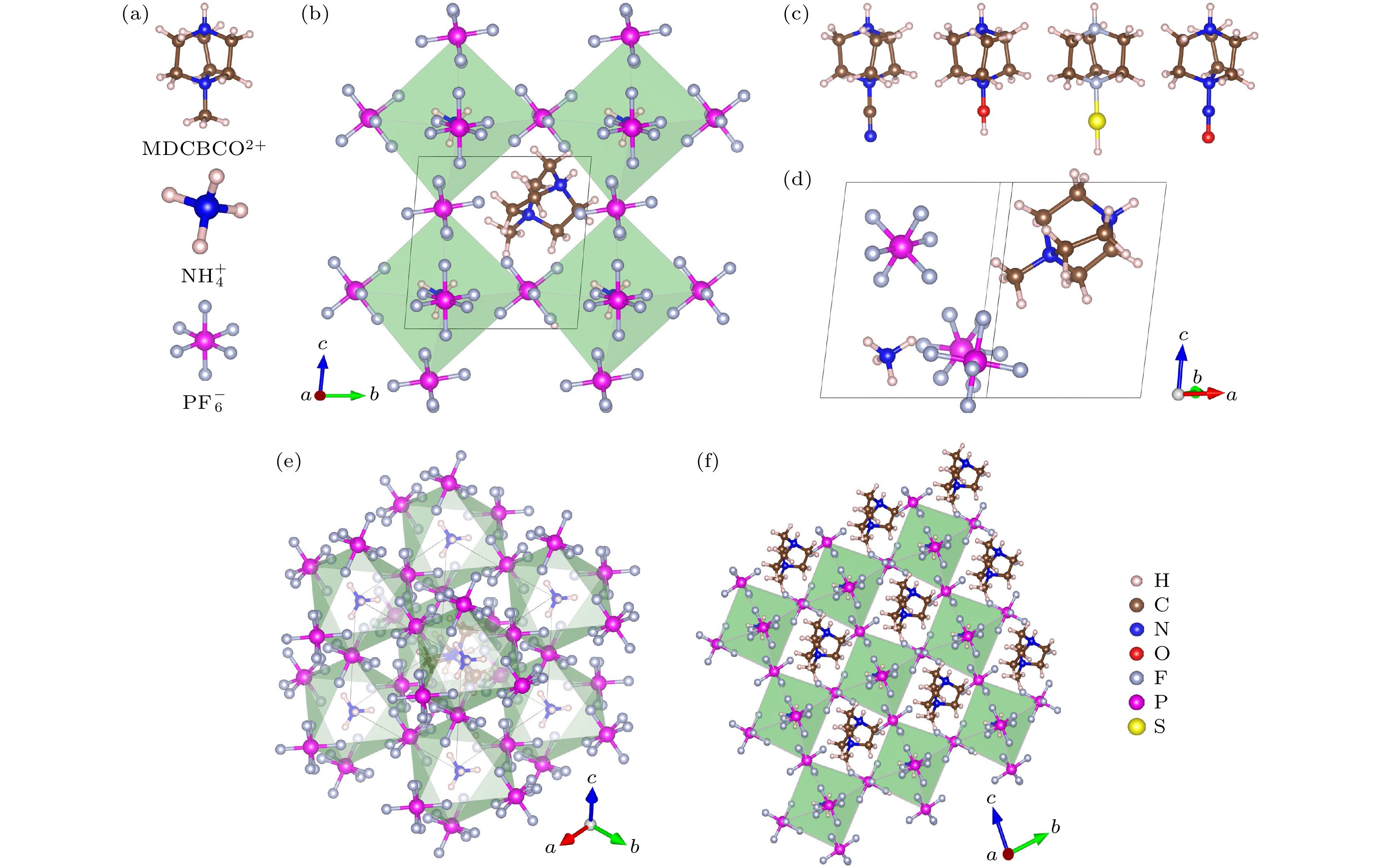
有机钙钛矿MDABCO-NH4-(PF6)3(以下将NH4-(PF6)3记为NP3)属于菱方结构空间群R3, 由MDABCO2+,
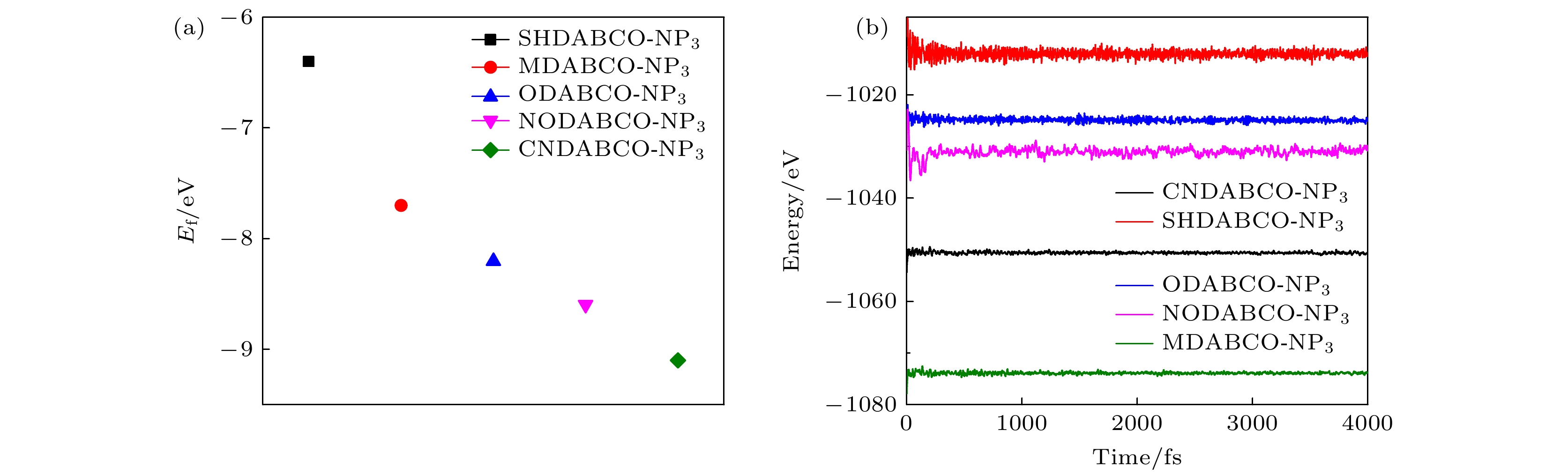
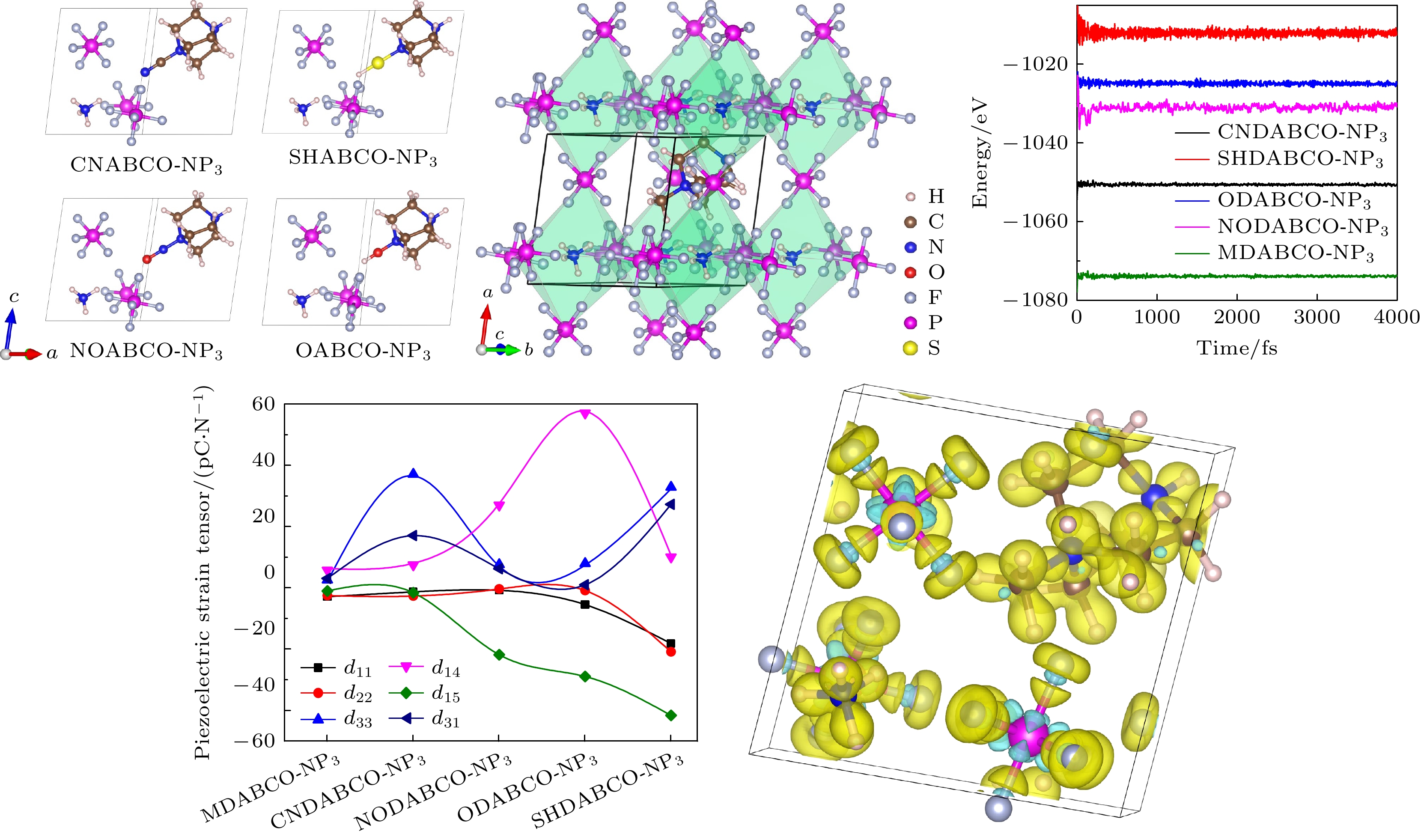
${\mathrm{NH}}_4^+ $ 和(PF6)6八面体组成, 如图2(a)所示.${\mathrm{NH}}_4^+ $ 位于(PF6)6八面体的中间, NH4(PF6)6八面体与相邻的6个八面体共用角, 形成角共享三维网络, MDABCO2+位于八面体空腔, 如图2(b), (e), (f)所示. 其中, 有机阳离子官能团MDABCO2+的两个氮原子在R3结构的三重轴[111]方向, 也即化合物的极化方向. 基于有机分子MDABCO2+官能团, 将—CH3基团替换为—CN, —OH, —NO和—SH基团, 形成了4种新的有机阳离子, 分别为NODABCO2+, ODABCO2+, CNDABCO2+和 SHDABCO2+, 如图2(c)所示. 首先, 对设计好的结构进行优化, 在优化的过程中采用了PBE和PBE+D3两种方法进行对比, 如表1所列. 结果表明, 采用PBE优化的晶格常数比PBE+D3(D3为对范德瓦耳斯力的修正)优化的晶格常数与实验值更接近, 相差在0.6%以下, 与Wang等[21]所报道的有机钙钛矿优化所采用的方法一致. 因此, 接下来采用PBE方法研究材料后面的所有性质. 除了MDABCO-NP3, 其他新设计的4种材料均未见报道. 因此, 需要通过结合能(Ef)来预测其他4种新型钙钛矿结构的稳定性, 其中MDABCO-NP3作为参考对象. 结合能公式如下:式中,
$ {E_{{{\text{A}}_x{\text{B}}_y{\text{C}}_z}}} $ ,$ {E}_{\text{A}},\; {E}_{\text{B}}和{E}_{\text{C}} $ 分别表示 A-NP3, 有机阳离子A2+,${\mathrm{NH}}_4^+ $ 和阴离子$ {{\mathrm{P}}{\mathrm{F}}}_{6}^{-} $ 的总能量. 如图3(a)所示, 所有体系的结合能都低于0, 表明理论上所有体系都容易合成. 为了探究材料的热稳定性, 测试了所有材料在300 K温度条件下的分子动力学, 如图3(b)所示. 结果表明, 在500 fs之后, 所有的材料能量都基本上在各自体系的能量值上下浮动, 且浮动的幅度很小, 这说明材料在300 K温度条件下非常稳定. 并且没有观察到结构发生松散, 5种材料始终保持原有的结构, 说明5种体系均具有较好的稳定性. -
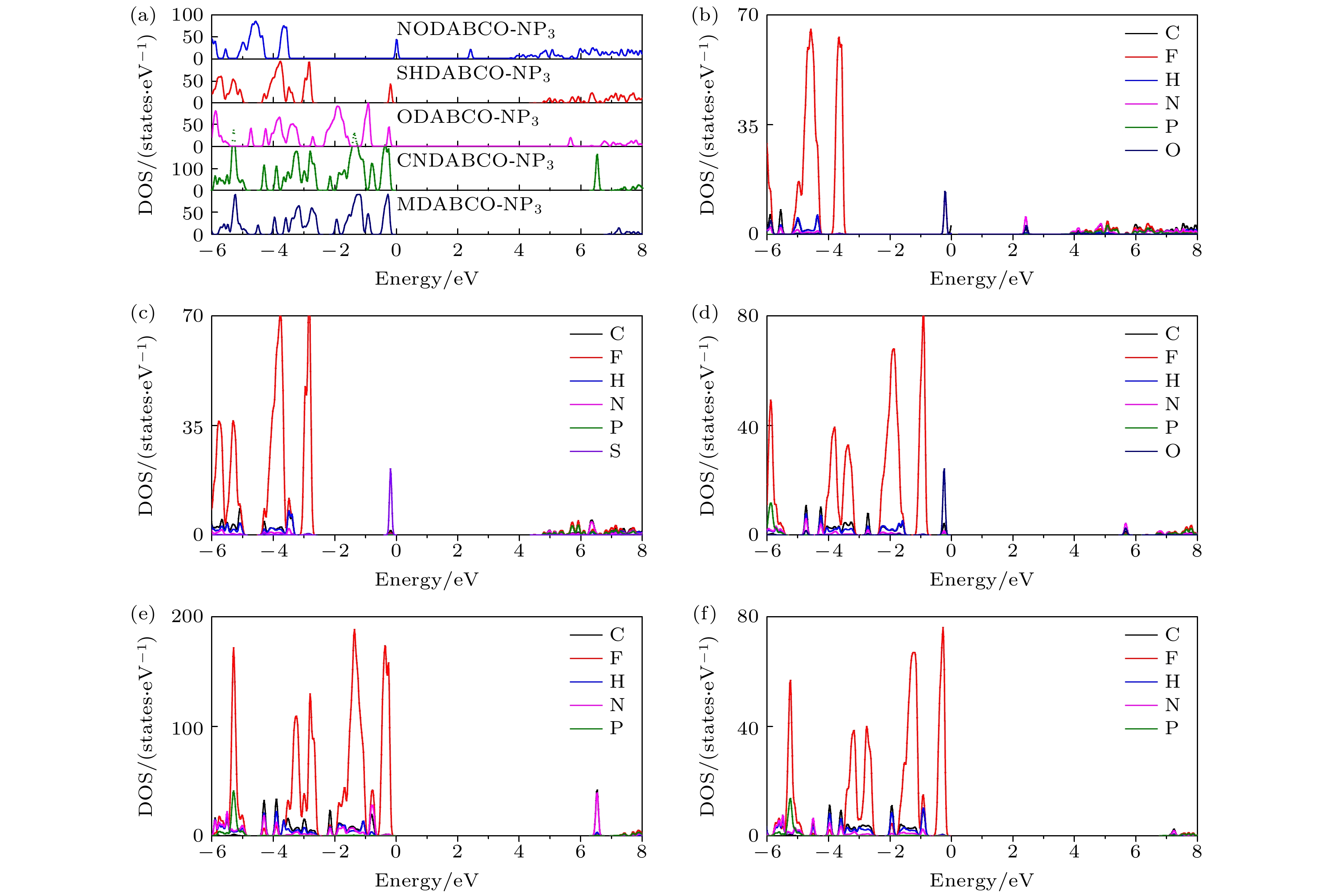
接下来, 针对有机钙钛矿的电子结构, 计算了总态密度和投影态密度, 如图4所示. 我们计算的MDABCO-NH4-(PF6)3的带隙为7.05 eV, 与Li等[30]所报道的结果(7.13 eV)基本一致. 可以看到, 价带主要是F元素贡献, 其中, NODABCO-NP3费米能级附近主要是N元素和O元素态密度所占据, SHDABCO-NP3费米能级附近主要是S元素态密度所占据, ODABCO-NP3的费米能级附近主要是O元素态密度所占据, CNDABCO-NP3和MDABCO-NP3的C元素存在于–4—0 eV, 其他材料中的C元素位于–4 eV能量以下, 这表明位于–4—0 eV的C元素的贡献来自—CN和—CH3中的C. 以上结果表明取代基团在价带顶起着主要作用, 因此可以推测, 取代基团将对物理性能起到较好的调控作用. 此外, 导带部分主要由P元素所占据. 价带和导带由不同的元素所占据, 表明电子跃迁在不同的分子结构上, 有利于电子-空穴对的分离.
-
为了探究有机阳离子对极化的影响, 利用DFT和现代极化理论(MTP)[31,32], 研究了5种有机钙钛矿材料的替代官能团对极化的影响. 从铁电相到顺电相, A-NP3中有机阳离子从有序到无序的变化是一个复杂的过程. 处于顺电相时, 很多氢原子的位置是不确定的, 用Berry方法计算铁电极化比较困难. 因此我们构建了5种有机阳离子和
${\mathrm{NH}}_4^+ $ 沿着[111]方向翻转, 形成–R3铁电结构, 如图5(a)所示. 在相变过程中, 有机阳离子和${\mathrm{NH}}_4^+ $ 沿[111]方向连续旋转${18}{{0}^ \circ }$ 形成稳定的+R3铁电结构, 如图5(a)—(c)所示. 其中$\lambda $ 是无量纲的参数, 对于每个$\lambda $ , 不对原子的位置进行优化, 但可以评估极化, 以监测其作为$\lambda $ 函数的连续演化. 可以理解的是, 只有$\lambda = 1$ 的状态具有真正的物理意义. 由于Born-Karman周期性边界条件[29], 自发极化会受到极化量子$ {P}_{q}=eR/\varOmega $ 的影响, 其中e是电子的电荷量, R是极化方向的晶格常数,$ \varOmega $ 是晶胞体积, 则自发极化的计算公式为其中n是任意整数,
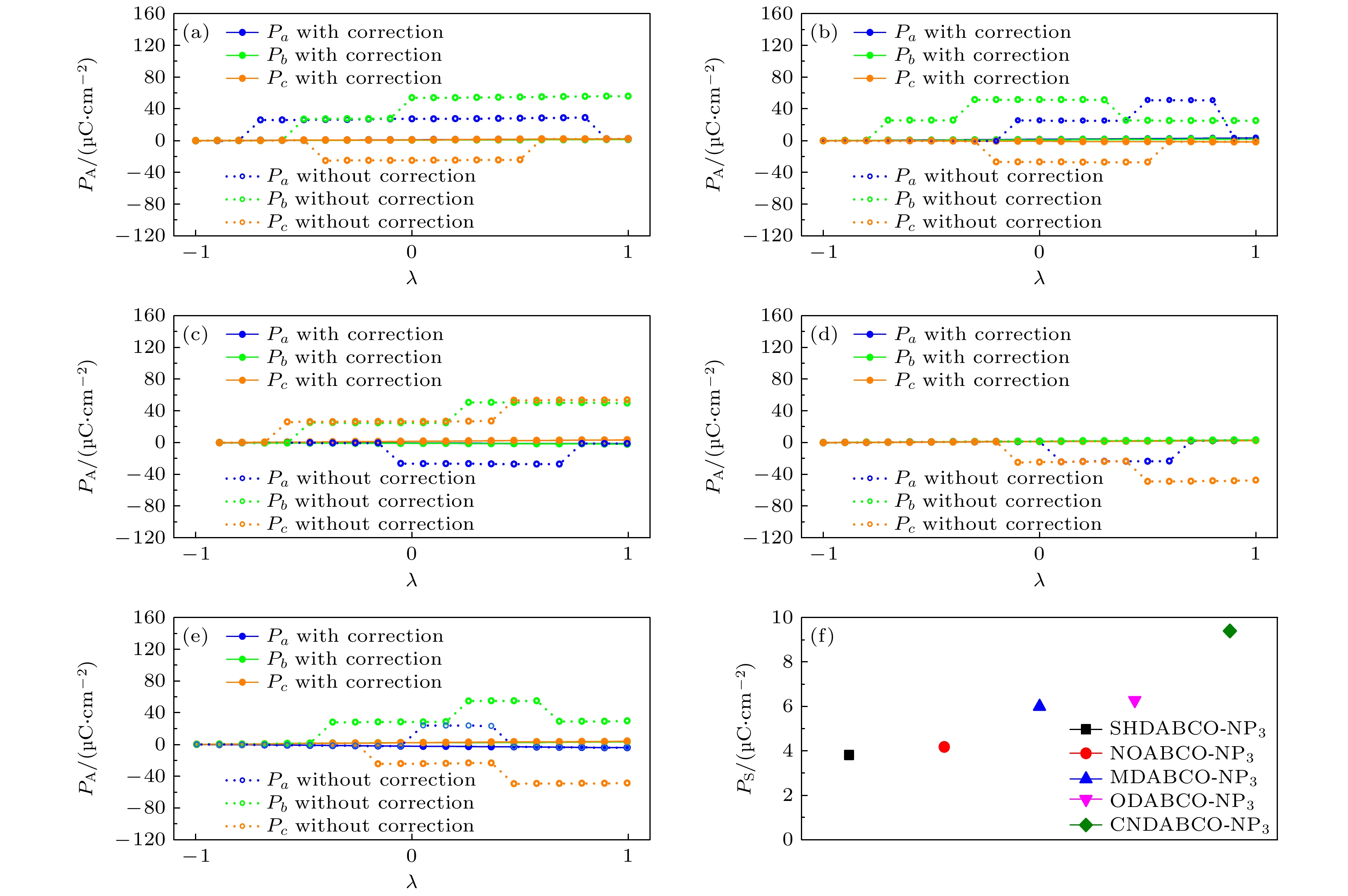
${P_{{\text{final}}}}$ 是铁电相的极化,${P_{{\text{initial}}}}$ 是参考相的极化.计算的所有体系的极化沿晶体a, b, c轴的极化分支分别为Pa, Pb, Pc, 总的极化值由3个方向的极化分量合成. –R3和+R3结构极化值作差的一半为PS, 结果如图6(f)和表2所示. MDABCO-NP3总的极化值为6.28 μC/cm2, 与Choi 等[23]所报道的结果(6.5 μC/cm2)相当. 考虑到5种阳离子的偶极矩大小不同[25], 分别为CNDABCO2+(7.6D), SHDABCO2+(4.7D), ODABCO2+(3.6D), NODABCO2+(3.3D), MDABCO2+(1.7D), 因而可能导致对总极化值的影响. 又由于CNDABCO-NP3体积最小(477.19 Å3), 并且CNDABCO2+的偶极矩明显大于其他阳离子, 所以CNDABCO-NP3的极化最大. 虽然SHDABCO2+和NODABCO2+的偶极矩较大, 但SHDABCO-NP3的晶胞体积(489.86 Å3)和NODABCO-NP3的晶胞体积(493.15 Å3)大于ODABCO-NP3的晶胞体积(478.75 Å3) 和MDABCO-NP3的晶胞体积(485.5 Å3), 体积的增大抵消了极化的增大.
Wang等[21]采用Born电荷模型分析了MDABCO-NH4-I3的极化特性, 结果表明, 在MDABCO-NH4-I3中, MDABCO2+偶极矩对总极化的贡献可以忽略不计. 然而, Wang和Yan[33]用Wannier function分析, 发现基于MDABCO2+有机阳离子电荷中心与基于其质量中心计算出的相对阴离子I–位移大小相差较大, 计算得出MDABCO2+有机阳离子的偶极矩对极化贡献达25%. 为了探究有机阳离子对极化值的贡献以及替代基团对有机阳离子极化的影响, 本文中还构造了仅将有机阳离子沿[111]方向旋转
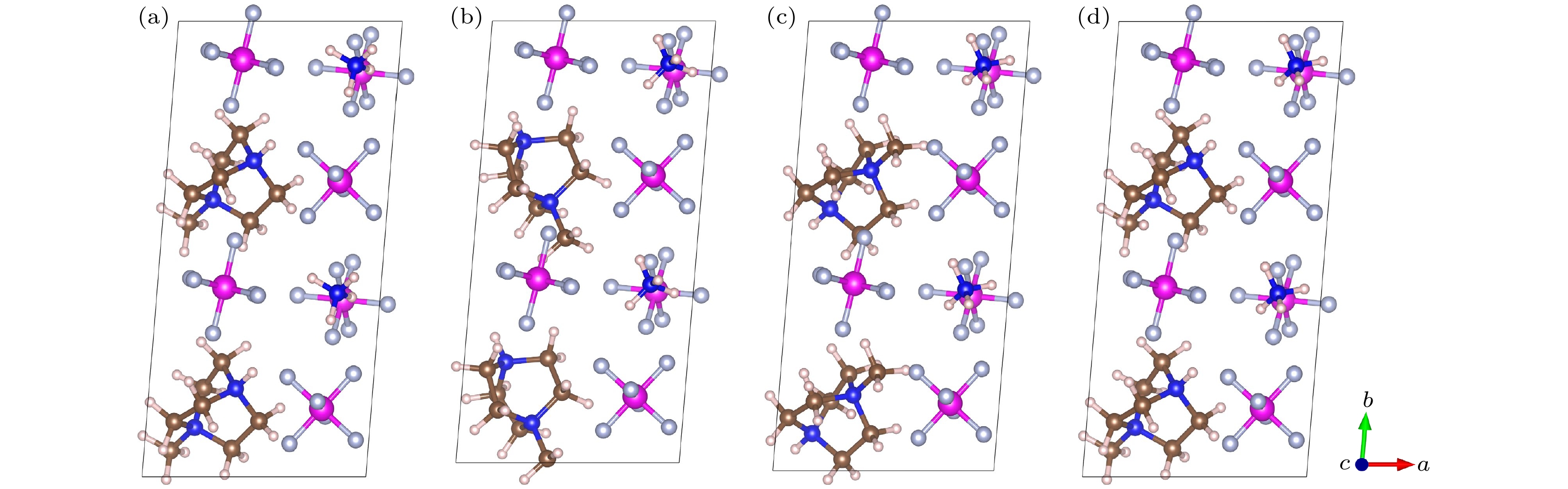
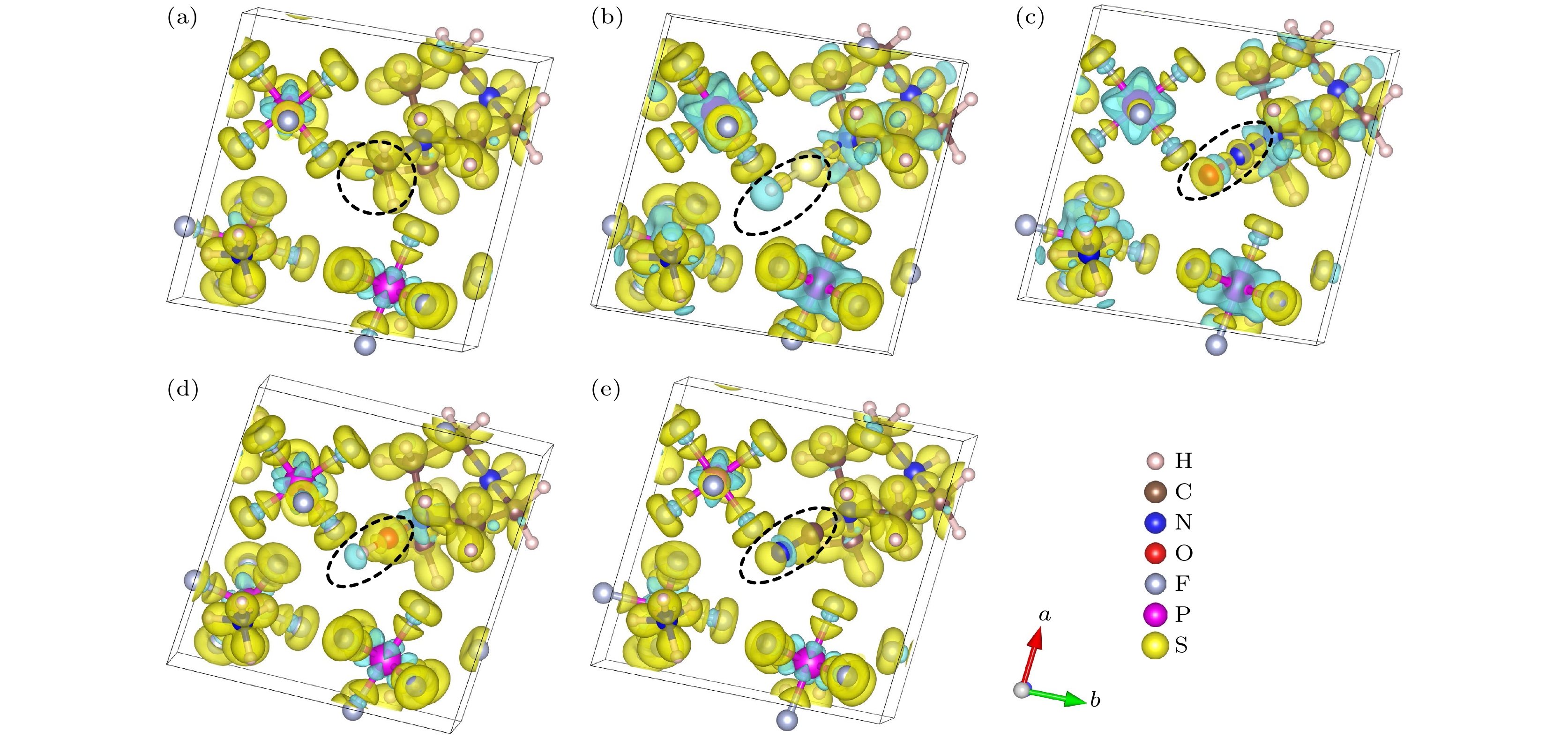
${18}{{0}^ \circ }$ 的类反铁电相到铁电相的转变路径, 如图5(d)所示, 并计算了极化值, 结果如图6(a)—(e)所示, 其极化值以及对总极化的贡献亦如表2所列. 由结果可知, 虽然偶极矩较大的CNDABCO2+阳离子的极化值大, 但其对总极化贡献的百分比相对较小. 而ODABCO-NP3和MDABCO-NP3的阳离子对总极化的贡献相对较大. 根据这几种有机阳离子偶极矩的数值大小关系, 可知在我们研究的这几个体系中, 偶极矩对极化的影响不占主导作用. ODABCO-NP3和MDABCO-NP3的阳离子对总极化的贡献大的原因主要是有机阳离子中H原子与阴离子${\text{PF}}_6^ - $ 中的F原子存在O—H···F(—OH)和C—H······F(—CH3)相互作用, 使得有机阳离子沿[111]方向的位移增大, 从而增大了阳离子对总极化的贡献.通过分析差分电荷密度, 可了解体系的电荷分布和成键情况. 图7给出了不同体系的差分电荷密度图. 从图7可看出, (a) MDABCO-NP3中—CH3的C—H键、(d) ODABCO-NP3中—OH的O—H键和(e) CNDABCO-NP3中—CN的C—N键明显比(b) SHDABCO-NP3中—SH的S—H键和(c) NODABCO-NP3中—NO的N—O键稳定. 说明取代基团中化学键的强弱也对材料的极化有影响, 取代基团中的化学键稳定, 材料的极化值较大.
-
弹性常数是一个重要的衡量材料力学性质的物理量, 基于此可推导出固体的许多力学性质, 如机械稳定性、弹性和材料刚度. 针对压电材料A-NP3, 需要了解其力学稳定性, 采用有限应变法计算材料的弹性常数. 基于DFT的第一性原理计算预测材料的弹性性能屡见报道[34–36]. 三方晶系的力学稳定性由7个独立的弹性常数C11, C12, C13, C14, C15, C33和C44决定. 三方晶系力学稳定性判据[37]:
结果如表3所列, 弹性常数Cij遵循上述稳定性准则. 因此, 进一步说明5种新型有机钙钛矿都具有机械稳定性.
此外, 通过以下关系式, 还计算了其他力学性能[38,39]:
其中
$B$ 是体模量,$E$ 是杨氏模量, G是剪切模量,$\nu $ 为泊松比, 如表2所列. 这些材料的体模量较小, 在外加应力作用下产生体积变形, 这种变形表明材料的可压缩性. 皮尤比和泊松比是定义材料延展性和脆性的重要参数[40], 延展性材料应该大于1.75(皮尤比)和0.26(泊松比)的临界极限值, 脆性材料小于这个临界极限值. 临界极限表明, 计算的5种有机钙钛矿均属于延展性材料类, 可以承受热冲击, 并且韧性材料更适合薄膜的制备.压电性通常用压电应力张量和压电应变张量来描述. A-NP3(空间群R3)的压电应变张量dij用矩阵表示为
dij有6个独立分量d11, d22, d33, d14, d15, d31. 其中d11, d22, d33表示电场方向和应变方向一致, 属于面外压电系数, 而d14, d15, d31属于面内压电系数. 对应的压电应力张量eij用矩阵表示为
压电应变张量[d]、压电应力张量[e]、弹性柔度张量[s]之间的关系为[d] = [e][s]. A-NP3(空间群R3)的弹性柔度张量矩阵表示为
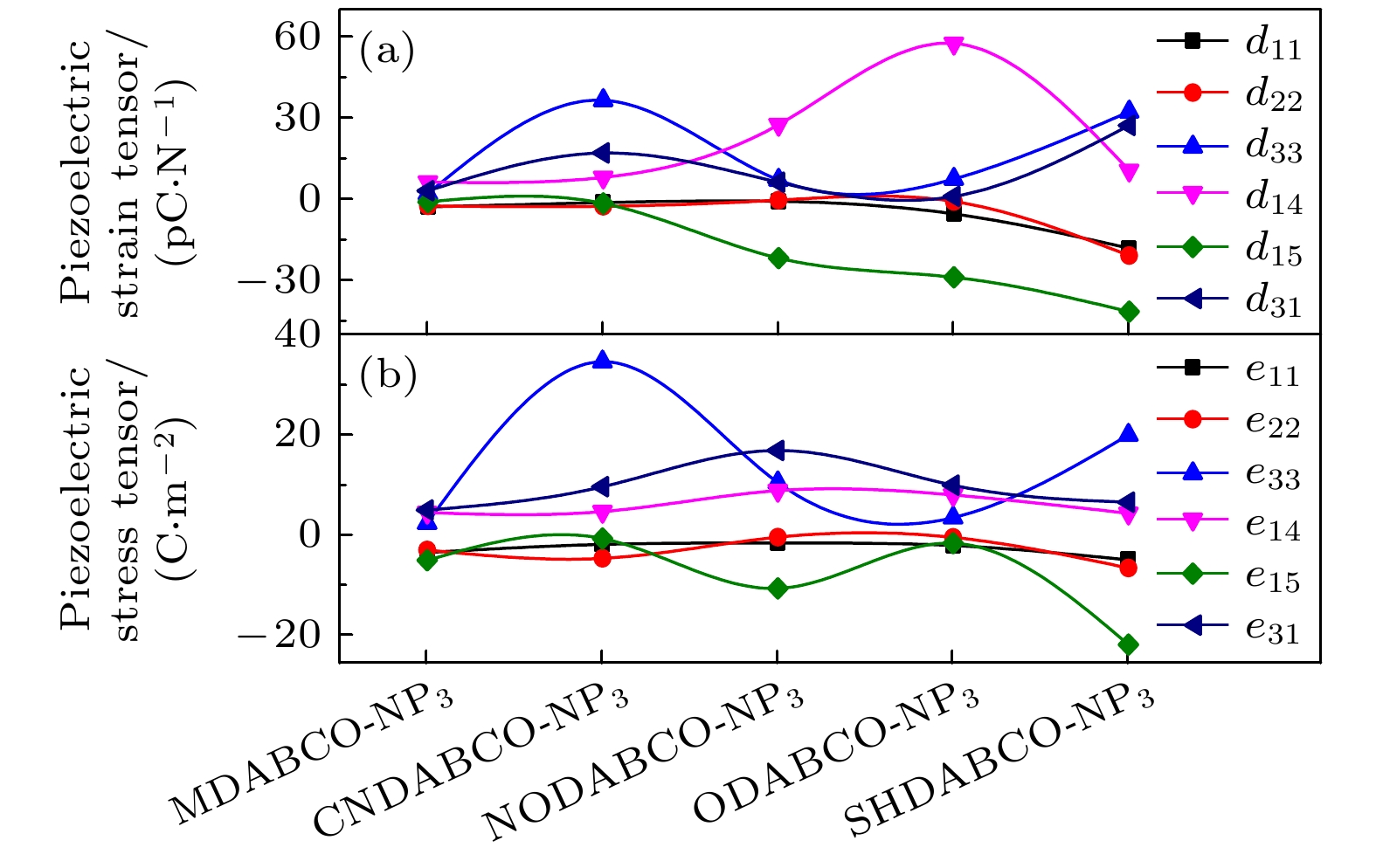
计算的A-NP3的压电应变张量和压电应力张量如图8、表4和表5所示, 柔性刚度张量见表6. 其中CNDABCO-NP3和SHDABCO-NP3的压电应变张量的最大分量为d33, 分别为36.5 pC/N和32.3 pC/N, 优于很多无机压电体, 并且高于目前已知的有机钙钛矿(MDABCO-NH4-I3对应的d33 = 14.4 pC/N)[19], 如表7所列. 此外, 其余3种晶体的压电应变张量的最大分量均为d14 , 分别为6.3 pC/N (MDABCO-NP3), 27.5 pC/N (NODABCO-NP3), 57.5 pC/N (ODABCO-NP3). 它们和无机晶体的压电应变张量的最大分量相当, 如表8所列. 上述对比表明, A-NP3具有较大的压电响应, 是各种压电应用的潜在候选材料. 压电应变张量分量
${d_{14}} = {e_{14}} \times {s_{44}} + 2{e_{11}} \times {s_{14}} - 2{e_{22}} \times {s_{25}}$ , 其中第2项和第3项比第1项小3个量级. 对于第1项${e_{14}} \times {s_{44}}$ , 由于A-NP3的e14差异很小, 所以d14随着阳离子的演化以s44为主. -
基于密度泛函理论的第一性原理计算, 在MDABCO-NP3的基础上, 将—CH3替换为其他不同的4种基团(—CN, —OH, —NO和—SH), 通过结合能和分子动力学预测了材料的稳定性, 为它们的实验可行性提供了有力的证据. 它们有较小的弹性张量和较大的压电应变分量, CNDABCO-NP3和SHDABCO-NP3有较大的d33, MDABCO-NP3, NODABCO-NP3, OHDABCO-NP3有较大的d14, 可与很多无机晶体相媲美. 同时体积模量和泊松比表明材料具有很好的柔韧性. 总之, 通过计算说明了本文研究的材料具有优异的压电性, 在压电应用上具有巨大的潜力. 此外, 有机阳离子对材料极化的影响较为明显, 可能的原因是氢键数目的改变增大了有机阳离子的位移, 但其微观机理需要进一步研究.
感谢天津大学理学院周伟副教授对计算提供的指导.
基团替代调控无铅有机钙钛矿铁电体的极化和压电特性的第一性原理研究
First principles study on polarization and piezoelectric properties of group substitution regulated lead-free organic perovskite ferroelectrics
-
摘要: 随着可穿戴电子产品要求提升, 无毒的有机钙钛矿铁电体成为潜在候选材料. 本工作应用第一性原理计算系统研究了无铅有机钙钛矿A-NH4-(PF6)3 (A = MDABCO, CNDABCO, ODABCO, NODABCO, SHDABCO)的电子态密度、自发极化、弹性特性和压电效应. 通过分子动力学和结合能计算发现, 有机钙钛矿在室温下具有稳定性且预测其在实验上易于合成. 对电子态密度研究发现, A-NH4-(PF6)3的价带主要来自F元素的贡献, 价带顶和导带底分别来自取代基团中的元素和N元素的贡献, 因此有利于电子-空穴对的分离. 依据Born稳定性判据, 有机钙钛矿具有稳定的机械性质. 除此之外, A位有机阳离子的取代基团可以改变材料中氢键的数量, 对总铁电极化的贡献有着明显影响. 最后通过压电性能计算, 揭示了有机钙钛矿具有良好的压电效果, 该效应源于材料引入的有机阳离子增加的材料的柔性. 计算结果为后续实验提供了理论基础.Abstract: Organic ferroelectrics are desirable for the applications in the field of wearable electronics due to their eco-friendly process-ability, mechanical flexibility, low processing temperatures, and lightweight. In this work, we use five organic groups as substitution for organic cation and study the effects of organic cations on the structural stability, electronic structure, mechanical properties and spontaneous polarization of metal-free perovskite A-NH4-(PF6)3 (A = MDABCO, CNDABCO, ODABCO, NODABCO, SHDABCO) through first-principles calculations. Firstly, the stabilities of the five materials are calculated by molecular dynamics simulations, and the energy values of all systems are negative and stable after 500 fs, which demonstrates the stabilities of the five materials at 300 K. The electronic structure calculation shows that the organic perovskite materials have wide band gap with a value of about 7.05 eV. The valence band maximum (VBM) and Cconduction band minimum (CBM) are occupied by different elements, which is conductive to the separation of electrons and holes. We find that organic cations have an important contribution to the spontaneous polarization of materials, with a contribution rate over 50%. The presence of hydrogen atoms in the substituting groups (MDABCO, ODABCO) enhances the hydrogen bond interaction between the organic cations and
${\rm PF}_6^- $ and increases the displacement of the organic cation, resulting in an increase in the contribution of the polarization of the organic cation to the total polarization. In addition, we observe large piezoelectric strain components, the calculated value of d33 is 36.5 pC/N for CNDABCO-NH4-(PF6)3, 32.3 pC/N for SHNDABCO-NH4-(PF6)3, which is larger than the known value of d33 of MDABCO-NH4-I3(14pC/N). The calculated value of d14 is 57.5 pC/N for ODABCO-NH4-(PF6)3, 27.5 pC/N for NODABCO-NH4-(PF6)3. These components are at a high level among known organic perovskite materials and comparable to many known inorganic crystals. The large value of d14 is found to be closely related to the large value of elastic compliance tensor s44. The analysis of Young’s modulus and bulk’s modulus shows that these organic perovskite materials have good ductility. These results indicate that these organic materials are excellent candidates for future environmentally friendly piezoelectric materials. -

-
图 2 (a) MDABCO2+,
${\mathrm{NH}}_4^+ $ ,${\text{PF}}_6^ - $ 结构示意图; (b) 沿a轴观察的MDABCO-NP3的原胞; (c) 不同基团取代之后的阳离子; (d) MDABCO-NP3的原胞; (e)沿着[111]方向观察到的MDABCO-NP3的原胞; (f) 沿a轴观察的MDABCO-NP3的晶胞Figure 2. (a) Structures of MDABCO2+,
${\mathrm{NH}}_4^+ $ ,${\text{PF}}_6^ - $ components; (b) the primitive cell of MDABCO-NP3 viewed along the a-axis; (c) cations substituted with different functionalities; (d) the primitive cell of MDABCO-NP3; (e) the primitive cell of MDABCO-NP3 viewed along [111] direction; (f) the unit cell of MDABCO-NP3 viewed along a-axis.图 4 (a) 5种材料的总态密度; (b)—(f)分别为NODABCO-NP3, SHDABCO-NP3, ODABCO-NP3, CNDABCO-NP3, MDABCO-NP3的投影态密度 ; 费米能级设置为0 eV
Figure 4. (a) Total density of states for A-NP3; (b)–(f) projected density of states of (b) NODABCO-NP3, (c) SHDABCO-NP3, (d) ODABCO-NP3, (e) CNDABCO-NP3, (f) MDABCO-NP3. Fermi level is set to zero.
图 5 –R3到+R3结构的转变过程 (a) –R3铁电相 (λ = –1)结构; (b)中间相变结构(λ =0); (c) +R3铁电相(λ = 1)结构; (d) 类反铁电(
$ {\lambda }' = -1$ )结构Figure 5. Transformation of –R3 to +R3 structure: (a) –R3 ferroelectric phase (λ = –1) structure; (b) intermediate phase transition structure (λ = 0); (c) +R3 ferroelectric phase (λ = 1) structure; (d) quasi-antiferroelectric phase structure (
$ {\lambda }' =-1$ ).图 6 计算的(a) MDABCO-NP3, (b) SHDABCO-NP3, (c) NODABCO-NP3, (d) ODABCO- NP3, (e) CNDABCO-NP3的经极化量子数修正的和未修正的极化值; (f) 5种材料总的极化值
Figure 6. Calculated polarization value of (a) MDABCO-NP3, (b) SHDABCO-NP3, (c) NODABCO-NP3, (d) ODABCO-NP3, (e) CNDABCO-NP3 with and without correction for polarization quantum; (f) the total polarization values of five materials.
表 1 采用PBE和PBE+D3方法优化后的A-NP3的晶格结构参数
Table 1. Structural optimization of A-NP3 by using PBE and PBE+D3 methods.
Material Method a/Å α/(°) V/Å3 MDABCO-NP3 PBE 7.89(0.57%) 84.91(0.06%) 485.51 PBE+D3 7.73(–1.46%) 84.55(–0.36%) 478.25 Exp 7.84 84.86 496.46 SHDABCO-NP3 PBE 7.93 83.84 489.86 PBE+D3 7.74 83.18 483.46 NODABCO-NP3 PBE 7.95 83.74 493.15 PBE+D3 7.84 81.25 485.65 ODABCO-NP3 PBE 7.85 85.2 478.75 PBE+D3 7.75 83.65 475.21 CNDABCO-NP3 PBE 10.58 85.21 477.19 PBE+D3 9.28 83.48 486.48 表 2 A位阳离子的极化PA (μC/cm2)和材料的总极化PS (μC/cm2)及阳离子的极化对总极化的贡献PA/PS
Table 2. Polarization of A-site cations (PA) and total polarization of materials (PS) and the contribution of cation polarization to total polarization (PA/PS).
Materials PA PS PA/PS SHDABCO-NP3 2.4 3.8 0.64 NODABCO-NP3 2.6 4.2 0.63 ODABCO-NP3 4.3 6.0 0.71 MDABCO-NP3 4.3 6.3 0.68 CNDABCO-NP3 5.7 9.4 0.61 表 3 计算的A-NP3的弹性刚度张量Cij、体积模量B、剪切模量G、杨氏模量E (GPa)、皮尤比(B/G)和泊松比
$ \nu $ Table 3. Calculated elastic tensor coefficients Cij , bulk modulu B, shear modulu G, Young’s modulu E(GPa), Pugh’s and Poisson’s ratios of A-NP3.
Materials C11 C33 C44 C12 C13 C14 C25 B G E B/G ν MDABCO-NP3 32.9 15.9 8.2 15.9 16.3 0.8 0.1 21.4 8.2 21.8 2.6 0.3 ODABCO-NP3 21.9 7.2 6.7 7.2 14.4 0.2 0.4 18.4 3.6 10.2 2.8 0.3 CNDABCO-NP3 35.2 19.4 6.6 19.4 22.8 0.6 1.3 25.7 6.7 18.4 4.0 0.4 SHDABCO-NP3 32.4 21.8 8.6 21.8 24.1 4.8 4.4 25.9 7.3 20.1 4.1 0.4 NODABCO-NP3 36.2 19.7 4.4 19.7 19.7 0.3 0.4 25.0 5.9 16.5 4.5 0.4 表 7 代表性无机、有机压电体对CNDABCO-NP3和SHDABCO-NP3的压电分量d33的对比.
Table 7. Comparison of piezoelectric component d33 of representative inorganic, organic piezoelectrics to CNDABCO-NP3 and SHDABCO-NP3.
表 8 代表性无机、有机压电体对MDABCO-NP3, NODABCO-NP3 和ODABCO-NP3的压电分量d14的对比
Table 8. Comparison of piezoelectric component d14 of representative inorganic, organic piezoelectrics to MDABCO-NP3, NODABCO-NP3 and ODABCO-NP3.
表 4 A-NP3的压电应变张量dij (pC/N)
Table 4. Piezoelectric strain tensor dij of A-NP3 (pC/N).
Materials d11 d22 d33 d14 d15 d31 MDABCO-NP3 –2.9 –2.6 2.0 –6.3 –1.0 3.0 ODABCO-NP3 –5.5 –0.9 7.4 –57.5 –28.9 0.9 CNDABCO-NP3 –1.3 –2.7 36.5 –7.9 –1.6 17.0 SHDABCO-NP3 –18.2 –20.9 32.3 –10.6 –41.6 27.2 NODABCO-NP3 –0.8 –0.4 7.1 27.5 –21.8 6.18 表 5 A-NP3的压电应力张量eij (C/m2)
Table 5. Piezoelectric stress tensor eij of A-NP3 (C/m2).
Materials e11 e22 e33 e14 e15 e31 MDABCO-NP3 –3.5 –3.0 2.4 4.5 –0.6 4.9 ODABCO-NP3 –2.1 –0.5 3.5 8.1 –1.7 9.9 CNDABCO-NP3 –1.9 –4.7 34.7 4.7 –0.8 9.7 SHDABCO-NP3 –5.2 –6.6 7.3 4.3 –21.9 6.5 NODABCO-NP3 –1.6 –0.5 10.5 8.9 –10.7 16.8 表 6 A-NP3的柔性刚度张量sij (10–12 m/N).
Table 6. Elastic compliance tensor sij of A-NP3 (10–12 m/N).
Materials s11 s33 s44 s12 s13 s14 s25 MDABCO-NP3 48.8 49.8 130.3 –16.8 –16.7 3.2 0.6 ODABCO-NP3 38.4 57.2 247.3 –9.0 –17.6 18 45.5 CNDABCO-NP3 56.9 85.4 157.3 –8.8 –35.7 –5.5 13.3 SHDABCO-NP3 124.7 142.4 218.9 –37.0 –79.2 –60.1 5.0 NODABCO-NP3 46.8 51.2 199.0 –16.6 –17.2 17.1 19.9 -
[1] Kieslich G, Sun S J, Cheetham A K 2014 Chem. Sci. 5 4712 doi: 10.1039/C4SC02211D [2] Sessolo M, Bolink H J 2011 Adv. Mater. 23 1829 doi: 10.1002/adma.201004324 [3] Bechmann R 2005 J. Acoust. Soc. Am. 28 347 doi: 10.1121/1.1908324 [4] Haertling G H 1999 J. Am. Cera. Soc. 82 797 doi: 10.1111/j.1151-2916.1999.tb01840.x [5] Zhao Y X, Zhu K 2016 Chem. Soc. Rev. 45 655 doi: 10.1039/C4CS00458B [6] Mischenko A S, Zhang Q, Scott J F, Whatmore R W, Mathur N D 2006 Science 311 1270 doi: 10.1126/science.1123811 [7] Peña M A, Fierro J 2001 Chem. Rev. 101 1981 doi: 10.1021/cr980129f [8] 郑隆立, 齐世超, 王春明, 石磊, 2019 物理学报 68 147701 doi: 10.7498/aps.68.20190222 Zheng L L, Qi S C, Wang C M, Shi L 2019 Acta Phys. Sin. 68 147701 doi: 10.7498/aps.68.20190222 [9] Neaten J B, Ederer C, Waghmare U V, Spaldin N A, Rabe K M 2005 Phys. Rev. B 71 14111 doi: 10.1103/PhysRevB.71.014111 [10] Lebeugle D, Colson D, Forget A, Viret M 2007 Appl. Phys. Lett. 91 22907 doi: 10.1063/1.2753390 [11] Palkar V R, Kundaliya D C, Malik S K 2003 J. Appl. Phys. 93 4337 doi: 10.1063/1.1558992 [12] Gao W X, Chang L, Ma H, You L, Yin J, Liu J M, Liu Z G, Wang J L, Yuan G L 2015 NPG Asia Mater. 7 e189 doi: 10.1038/am.2015.54 [13] Xu W J, Kopyl S, Kholkin A, Rocha J 2019 Coordin. Chem. Rev. 387 398 doi: 10.1016/j.ccr.2019.02.012 [14] Nandi P, Topwal D, Park N G, Shin H 2020 J. Phys. D: Appl. Phys. 53 493002 doi: 10.1088/1361-6463/abb047 [15] Köhnen E, Jost M, Morales-Vilches A B, Tockhorn P, Al-Ashouri A, Macco B, Kegelmann L, Korte L, Rech B, Schlatmann R, Stannowski B, Albrecht S 2019 Sustain. Energ. Fuels 3 1995 doi: 10.1039/C9SE00120D [16] Sahli F, Werner J, Kamino B A, Bräuninger M, Monnard R, Paviet-Salomon B, Barraud L, Ding L, Diaz Leon J J, Sacchetto D, Cattaneo G, Despeisse M, Boccard M, Nicolay S, Jeangros Q, Niesen B, Ballif C 2018 Nat. Mater. 17 820 doi: 10.1038/s41563-018-0115-4 [17] Yang W S, Park B, Jung E H, Jeon N J, Kim Y C, Lee D U, Shin S S, Seo J, Kim E K, Noh J H, Seok S I 2017 Science 356 1376 doi: 10.1126/science.aan2301 [18] Yun J S, Park C K, Jeong Y H, Cho J H, Paik J, Yoon S H, Hwang K 2016 Nanomater. Nanotechno. 6 20 doi: 10.5772/62433 [19] Ye H Y, Tang Y Y, Li P F, Liao W Q, Gao J X, Hua X N, Cai H, Shi P P, You Y M, Xiong R G 2018 Science 361 151 doi: 10.1126/science.aas9330 [20] Fu D W, Cai H L, Liu Y M, Ye Q, Zhang W, Zhang Y, Chen X Y, Giovannetti G, Capone M, Li J Y, Xiong R G 2013 Science 339 425 doi: 10.1126/science.1229675 [21] Wang H, Liu H H, Zhang Z Y, Liu Z H, Lv Z L, Li T W, Ju W W, Li H S, Cai X W, Han H 2019 npj Comput. Mater 5 17 doi: 10.1038/s41524-019-0157-4 [22] Wu H S, Wei S, Chen S W, Pan H C, Pan W P, Huang S, Tsai M, Yang P 2022 Adv. Sci. 9 2105974 doi: 10.1002/advs.202105974 [23] Choi H S, Li S N, Park I, Liew W H, Zhu Z Y, Kwon K C, Wang L, Oh I, Zheng S S, Su C L, Xu Q H, Yao K, Pan F, Loh K P 2022 Nat. Commun. 13 794 doi: 10.1038/s41467-022-28314-8 [24] Sun M J, Zheng C, Gao Y, Johnston A, Najarian A M, Wang P X, Voznyy O, Hoogland S, Sargent E H 2021 Adv. Mater. 33 2006368 doi: 10.1002/adma.202006368 [25] Kasel T W, Deng Z Y, Mroz A M, Hendon C H, Butler K T, Canepa P 2019 Chem. Sci. 10 8187 doi: 10.1039/C9SC03378E [26] Kresse, Furthmuller 1996 Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169 [27] Kresse, Hafner 1994 Phys. Review. B 49 14251 doi: 10.1103/PhysRevB.49.14251 [28] Kresse, Hafner 1993 Phys. Review. B 47 558 doi: 10.1103/PhysRevB.47.558 [29] Spaldin N A 2012 J. Solid State Chem. 195 2 doi: 10.1016/j.jssc.2012.05.010 [30] Li Z Z, Li Z H, Peng G Q, Shi C, Wang H X, Ding S Y, Wang Q, Liu Z T, Jin Z W 2023 Adv. Mater. 35 2300480 doi: 10.1002/adma.202300480 [31] King-Smith R D, Vanderbilt D 1993 Phys. Rev. B 48 4442 doi: 10.1103/PhysRevB.48.4442 [32] Vanderbilt D, King-Smith R D 1993 Phys. Rev. B 47 1651 doi: 10.1103/PhysRevB.47.1651 [33] Wang X M, Yan Y F 2022 arXiv: 2206.11137v1 [cond-mat. mtrl-sci] [34] Singh J, Kaur H, Singh G, Tripathi S K 2021 Mater. Today Energy 21 100820 doi: 10.1016/j.mtener.2021.100820 [35] Al-Qaisi S, Rai D P, Haq B U, Ahmed R, Vu T V, Khuili M, Tahir S A, Alhashim H H 2021 Mater. Chem. Phys. 258 123945 doi: 10.1016/j.matchemphys.2020.123945 [36] Kiely E, Zwane R, Fox R, Reilly A M, Guerin S 2021 CrystEngComm 23 5697 doi: 10.1039/D1CE00453K [37] Mouhat F, Coudert F 2014 Phys. Rev. B 90 224104 doi: 10.1103/PhysRevB.90.224104 [38] Haid S, Bouadjemi B, Houari M, Matougui M, Lantri T, Bentata S, Aziz Z 2019 Solid State Commun. 294 29 doi: 10.1016/j.ssc.2019.03.001 [39] Birch F 1938 J. Appl. Phys. 9 279 doi: 10.1063/1.1710417 [40] Kholil M I, Bhuiyan M T H 2020 Solid State Commun. 322 114053 doi: 10.1016/j.ssc.2020.114053 [41] Crisler D F, Cupal J J, Moore A R 1968 P. IEEE 56 225 doi: 10.1109/PROC.1968.6246 [42] Weis R S, Gaylord T K 1985 Appl. Phys. A 37 191 doi: 10.1007/BF00614817 [43] Joffe H, Berlincourt D, Krueger H, Shiozawa L 1960 14th Annual Symposium on Frequency Control Atlantic City, NJ, USA May 21–June 2 1960 p19 [44] Vanderbilt D, Hamann D R, Wu X F 2005 Phys. Rev. B 72 35105 doi: 10.1103/PhysRevB.72.035105 [45] X Y H 1991 Ferroelectric Materials and Their Applications (Netherlands: Amsterdam [46] Li F L, Tian S W, Wu G D, Jiang C, Wu F P, Zhao X 2019 Symposium on Piezoelectrcity, Acoustic Waves and Device Applications Shijiazhuang, China, November 1–4, 2019 p1 [47] Guy I L, Muensit S, Goldys E M 1999 Appl. Phys. Lett. 75 4133 doi: 10.1063/1.125560 [48] Irzhak D, Roshchupkin D, Fahrtdinov R 2012 Proceedings of ISAF-ECAPD-PFM 2012 Aveiro, Portugal, July 9–13 2012 p1 -


 首页
首页 登录
登录 注册
注册




 下载:
下载: