首页
登录
注册
下载:
-
超材料作为一种人工结构, 与传统材料相比, 通常具有独特的电磁性质, 如负磁导率和负介电 常数[1,2]. 其被广泛应用于电磁诱导透明[3]、高效光学传输器件[4]、完美透镜[5]、极化转换[6]等领域. 电磁诱导透明效应(electromagnetically induced transparency, EIT)最早发现于三能级或多能级原子系统中, 是一种量子破坏干扰, 可使原本不透明介质出现陡峭透明的透射峰, 且通常伴有较强的相色散, 造成明显的群指数和较大的群速度[7]. 因此基于超材料的类EIT效应在慢光缓存元件、高灵敏度传感器、窄带滤波器、光学调制器等微纳光子器件设计中具有广泛的应用前景[8–11]. 目前, 典型的基于类电磁诱导透明的超材料是通过明模和明模之间的破坏性干涉效或者是由明模与暗模之间的耦合来实现的[12–16]; 明模与暗模是两种不同的共振模式. 明模指的是可以直接受到入射光激发而显著产生的共振模式, 其强度相对较高. 而暗模则是通过间接激发方式在谐振腔中产生的共振模式.
传统的极化转换器在转换过程中会导致高损耗[17], 而且其相位调节能力有限, 这限制了其在相位突变触发延迟器件中的应用潜力[18]. 然而, 近年来, 基于类电磁诱导透明效应的极化转换器因其具备超薄厚度和卓越的透射性能而引起了广泛关注. Zhu等[19]利用两对正交的金属谐振线组成的超薄超表面, 通过两组明模之间耦合在微波频段下实现了单频点的极化转化. Yang等[20]研究了一种由N型和双裂环谐振器组成的超材料, 基于类电磁诱导透明效应在微波频段下实现了宽带传输和透射型极化转换, 但是极化转换效率较低. Gao等[21]设计了由4个非对称H型谐振器组成的结构, 基于EIT效应在太赫兹波段实现了透射型单频点的线极化到圆极化转换. 尽管这些设计可以实现透射和极化转换功能, 但是大多只能在单频点实现极化转换功能, 并且在极化转换点处伴随着较大的传输损耗.
针对之前极化转换EIT超材料存在的问题, 本文提出了一种由4个开口T型谐振器组成的EIT超表面. 该设计可以实现双极化透射和双频点极化转换功能. 它使用两组明模与明模的破坏性干涉来产生双极化下EIT-like效应. 通过分析表面电流分布、磁场分布和频率响应特性, 深入探究EIT的形成机理. 最后, 通过对仿真数据的计算和分析, 证明了所设计的在太赫兹频段下的EIT超材料, 不仅能在双极化下实现双频段透射窗口和双频点的线极化到圆极化的转换, 而且在入射角改变时, 仍存在双频段透射窗口.
-
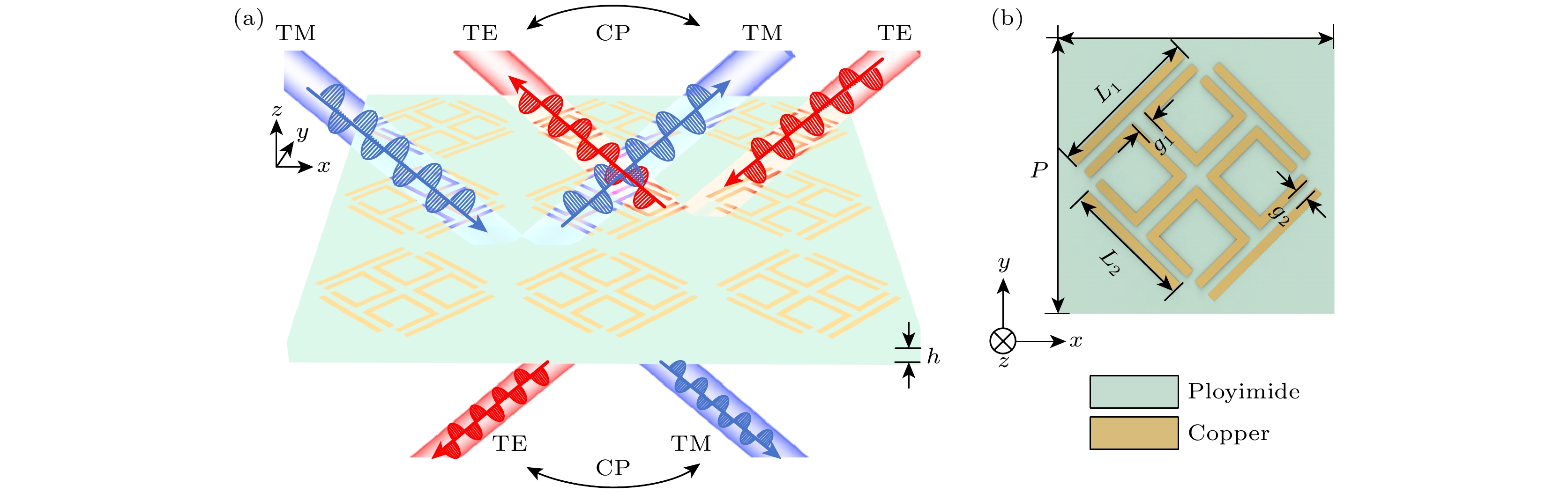
本设计的结构采用单层结构, 如图1所示. 从图1(a)可以观察到, 入射电磁波不仅能有效地穿过所提出的结构, 而且当极化方向与x轴相差45°的电磁波沿–z轴传播时, 还能实现双频点透射型和反射型线极化到圆极化转换的功能. 图1(b)直观地呈现了单元结构, 该结构由4个开口T型谐振器组成. 在仿真过程中, 该结构的单个单元受到沿z轴方向的x偏振平面波(波矢量k)的垂直激励. 所有维度的空间网格尺寸设置为1 nm, 频率采样点数为3000. 在x方向和y方向上都设置了周期边界条件, 以准确模拟结构的周期特性.
本文所提出的基于EIT的多功能频率选择表面(frequency selective surface, FSS)单元结构详情如图1所示, 沿+y和+x方向呈周期性排布. 该结构由一层PEC金属材料的FSS结构和一个Ployimide材料的介质层组成[19]. 经过仿真拟合优化后, 各层结构参数如下: 单元结构周期P = 300 μm, 介质层厚度H = 35 μm, 介电常数为2.2, L1 = 165 μm, L2 = 140 μm, g1 = 15 μm, g2 = 10 μm.
-
为了实现双频点极化转换和滤波功能, 通过两组具有相似共振频率的明模相互干涉产生透射窗口, 然后利用微变法构造非对称结构来实现TE和TM极化下的透射窗口偏移, 从而实现双频点极化转换.
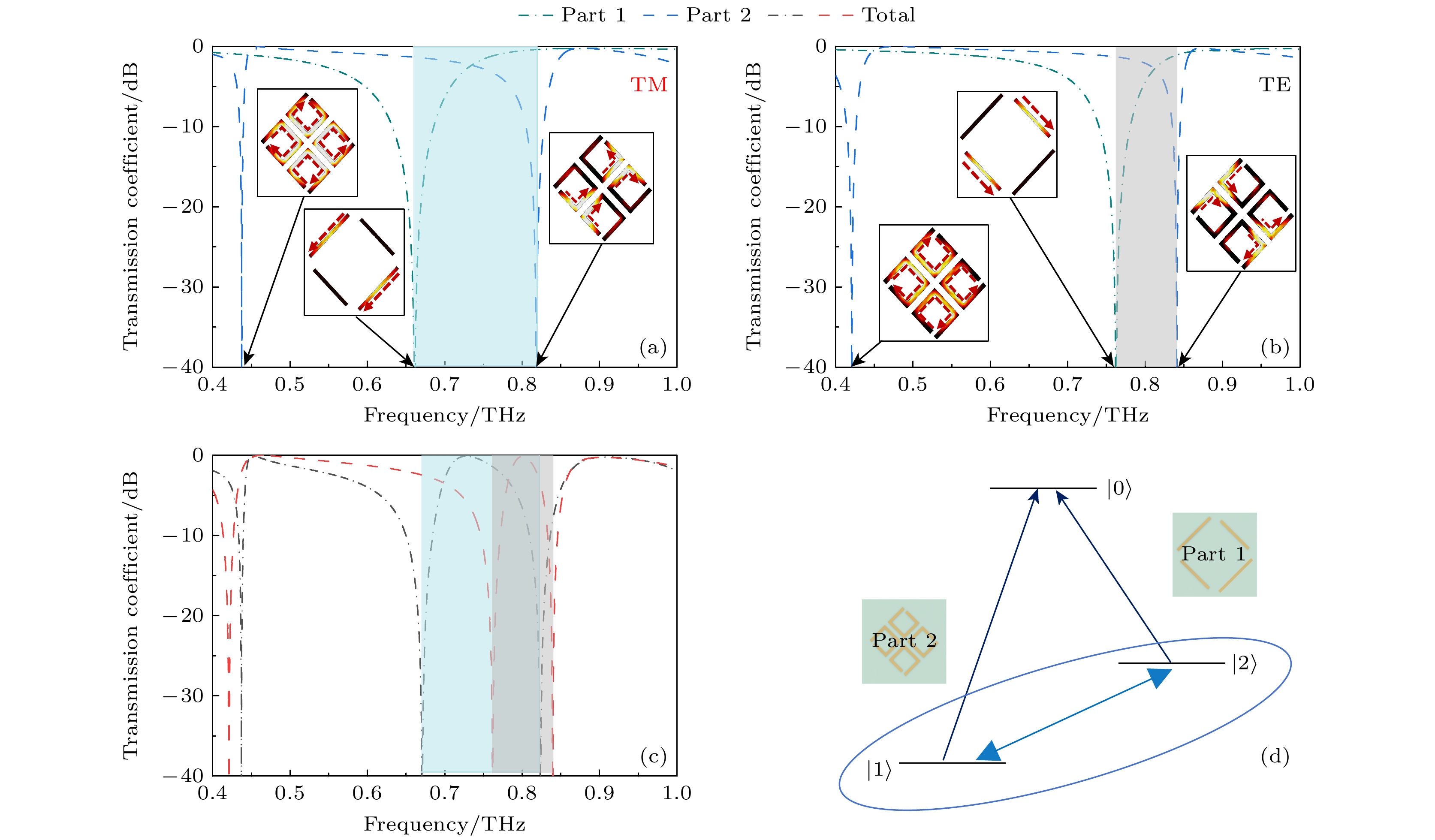
为了阐明这种电磁诱导透明效应的工作机理, 在CST Microwave Studio商业电磁仿真软件中进行数值解析, 分别研究了Part 1, Part 2和整体结构的TE, TM极化下的透射曲线、表面电流以及磁场分布. 如图2(a), (b)所示, 在TM极化波入射下, Part 1在0.66 THz处出现谐振, Part 2在0.438 THz和0.82 THz处出现谐振; 在TE极化波入射下, Part 1在0.763 THz处出现谐振, Part 2在0.421 THz和0.839 THz处出现谐振. 如图2(c)所示, 结构组合后, 可以看到TE极化波下, 在0.465 THz和0.8 THz处实现了EIT窗口; TM极化波下, 在0.45 THz和0.723 THz处也实现了EIT窗口. 可以看出, 两组明模的谐振频率相近, 且谐振窗口的品质因数不同, 满足EIT窗口的形成条件, 这是由于两组明模之间相干叠加, 在阻带内产生了透射峰. 通过原子系统能级可以更好地理解类EIT效应的形成过程. 在图2(d)中, 两个态
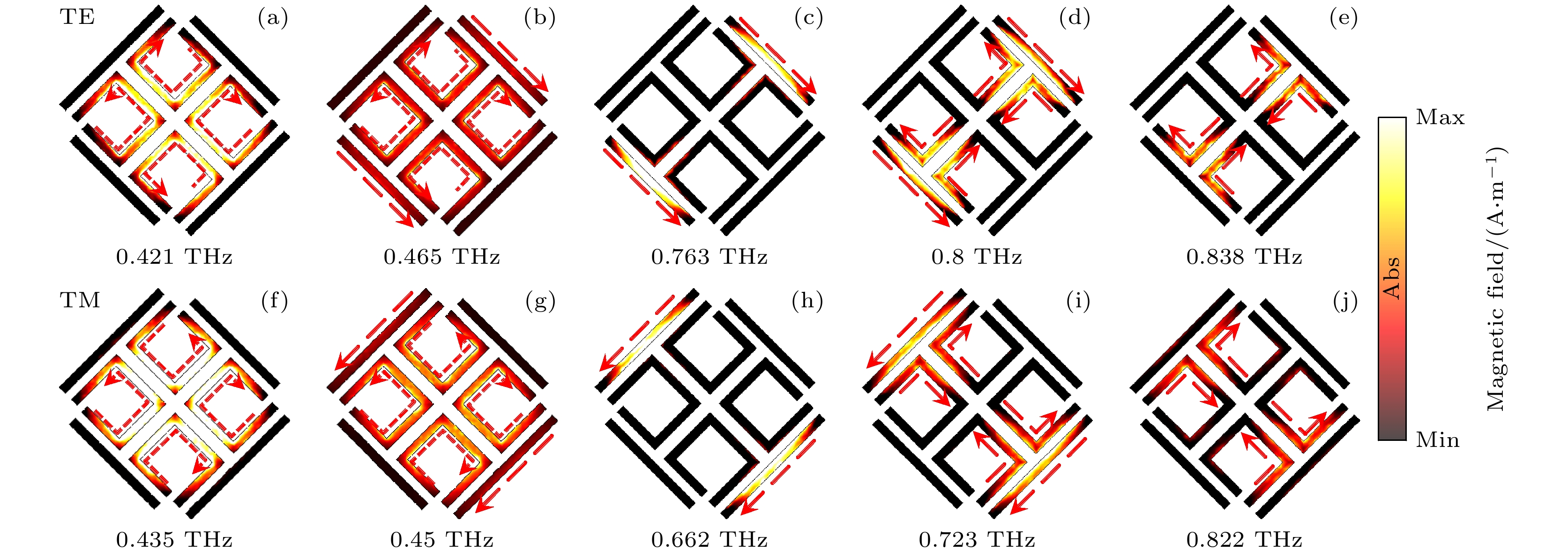
$ \left| 1 \right\rangle $ 和$ \left| 2 \right\rangle $ 分别表示激发后的两个谐振器. 基态$ \left| 0 \right\rangle $ 表示未被激发时的状态. 激发路径$ \left| 0 \right\rangle $ →$ \left| 1 \right\rangle $ 类似于被入射波直接激发Part 2; 同样, 另一条激发路径$ \left| 0 \right\rangle $ →$ \left| 2 \right\rangle $ 是 Part 2被激发的过程. 能级$ \left| 1 \right\rangle $ ↔$ \left| 2 \right\rangle $ 在这个过程中相当于一组相干叠加态. 通过对原子系统的分析, 发现当引入一个新的且合适的激发态后, 其与相邻能级的激发态将组合出一组新的相干叠加态, 这将大大降低原子系统在另一个频率范围内的光的吸收, 并产生一个新的EIT-like透射窗口.为了阐明在EIT效应和极化转换的作用机理, 图3描绘了在相同幅度尺度下TE和TM极化下的2个透明峰和4个透射衰减的磁场和透射峰处的表面电流以及磁场分布. 图3(a)—(e)为TM极化中磁场以及电流分布. 可以看出: 图3(a)中能量主要集中在开口谐振环中; 图3(b)中开口谐振环和副对角线的谐振线上均有能量; 图3(c)中能量主要集中在副对角线的谐振线上; 图3(d)中副对角线的谐振线和内部T型谐振器上均有能量; 图3(e)中能量主要集中在开口谐振环中, 即主要集中副对角线内部的T型谐振器上. 由此EIT窗口1是由于开口谐振环和副对角线的谐振线之间破坏性干扰所导致的, 透射窗口2是由于副对角线的谐振线和内部T型谐振器的破坏性干扰所导致. 图3(f)—(j)为TE极化下磁场以及电流分布, 结果刚好与TM极化下相反.
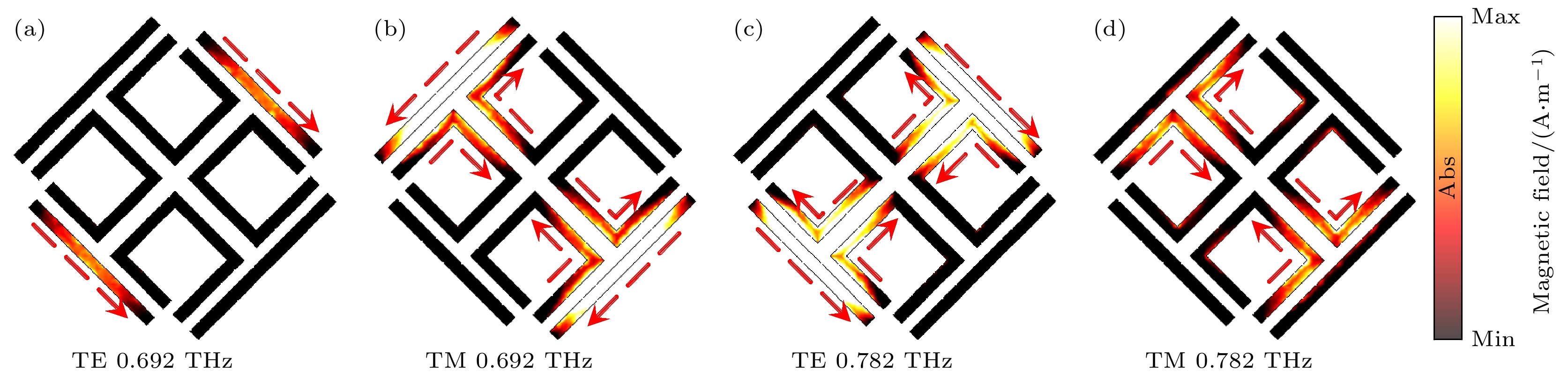
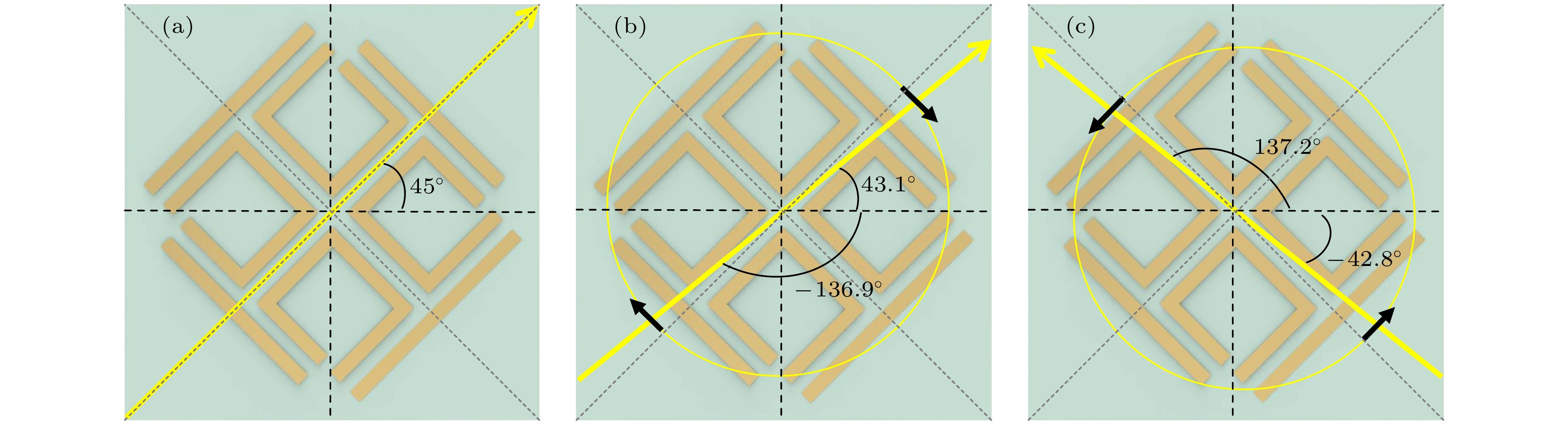
图4(a)—(d)分别显示了在极化转化频点处表面电流以及磁场随TE和TM极化波的分布. 对于TE入射波, 总电流沿着主对角线方向; 对于TM入射波, 总电流沿着副对角线方向. 由于这种正交方向产生了极化转换.
-
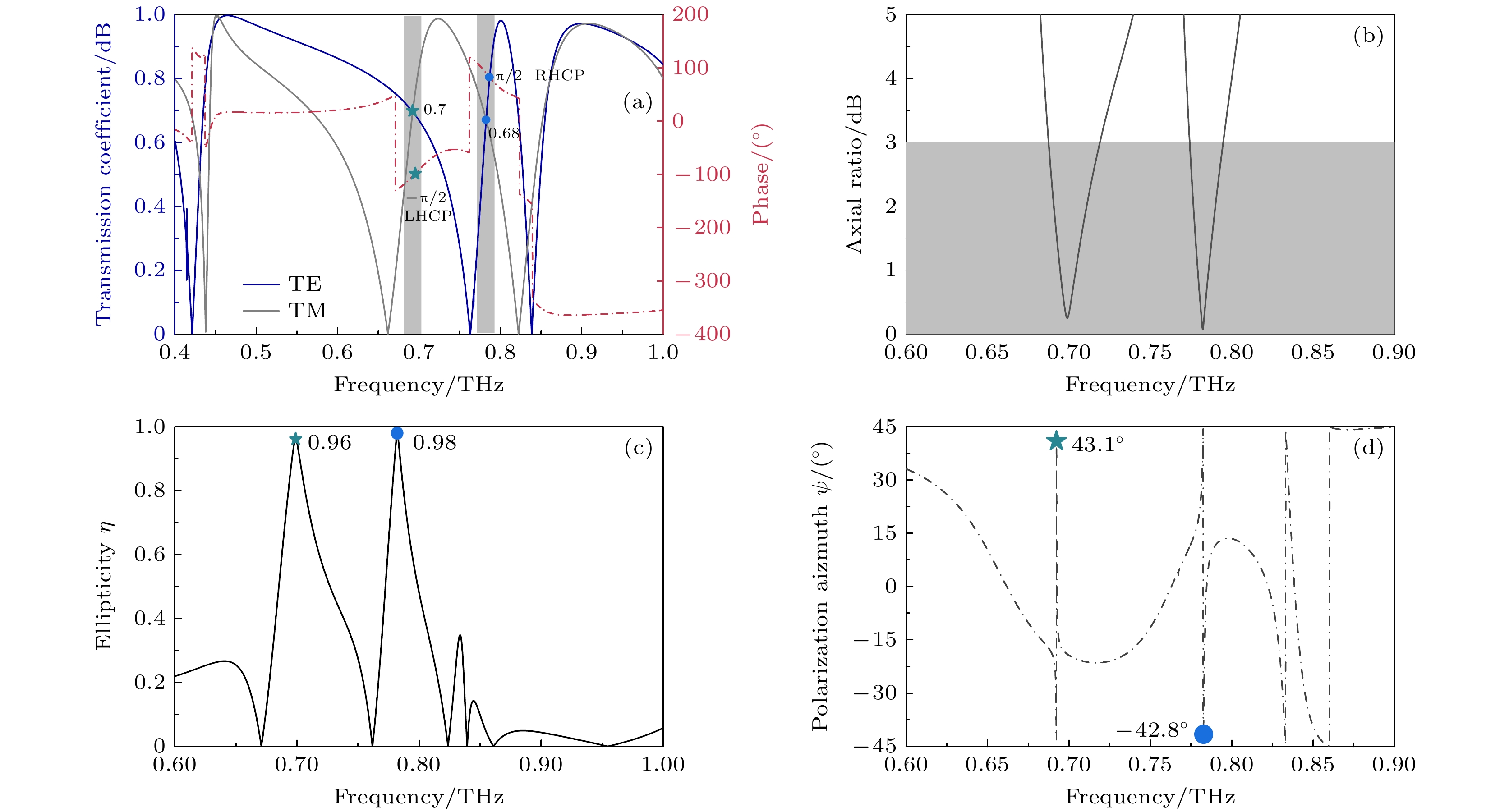
从图5(a)可以清晰地观察到, 当TE波和TM波入射时, 产生了两个明显的EIT窗口, 分别位于0.421—0.763/0.763—0.838 THz和0.45—0.723/0.723—0.822 THz, 相对带宽分别为57.7%/9.4%和46.5%/12.8%. 值得特别指出的是, 透射带和反射带对应的透射系数不仅在0.692 THz和0.782 THz处相等, 而且高达0.7和0.68, 这表明超材料具有低损耗透射的特性, 并且两种透射电磁波的传输相位差受到强相位色散的支配. 这为处理电磁波的极化提供了一种方法.
因此, 两个透射电磁波在同一频率下的透射系数符合以下条件[22]:
其中Tx , Ty, φx, φy和
$\Delta \varphi $ 分别表示两个透射电磁波的透射幅值、相位和相应的相位差.调整参数后, 最优相位差如图5(a)所示, 在0.692 THz和0.782 THz处Tx和Ty的传输系数相等而且相位差分别大约为–90°和90°. 因此, 可以很好地观察到LTC极化转换. 通过微量改变所呈现结构在每个方向上的不对称程度, 可以获得期望的相位差. 通过EIT行为的激发导致了LTC极化转换的实现.
利用椭圆度
$\eta $ , 轴比AR和极化方位角$\psi $ 来描述透射波, 可以很好地显示该结构LTC极化转换的优异性能. 因此, 引入4个Stokes参数如下[23]:式中, αin为入射电磁波电场方向与x轴夹角; tx, ty为x极化波和y极化波的透射系数;
$\Delta \varphi = {\varphi _x} - {\varphi _y}$ 为两种透射波的相位差.根据(3)式, 可以推导出极化方位角
$\psi $ 和椭圆度$\eta $ 如下[24]:同时, 小于3 dB的AR也可以用来表现LTC极化转换性能[25], 计算公式如下:
根据(3)式—(5)式, 椭圆度
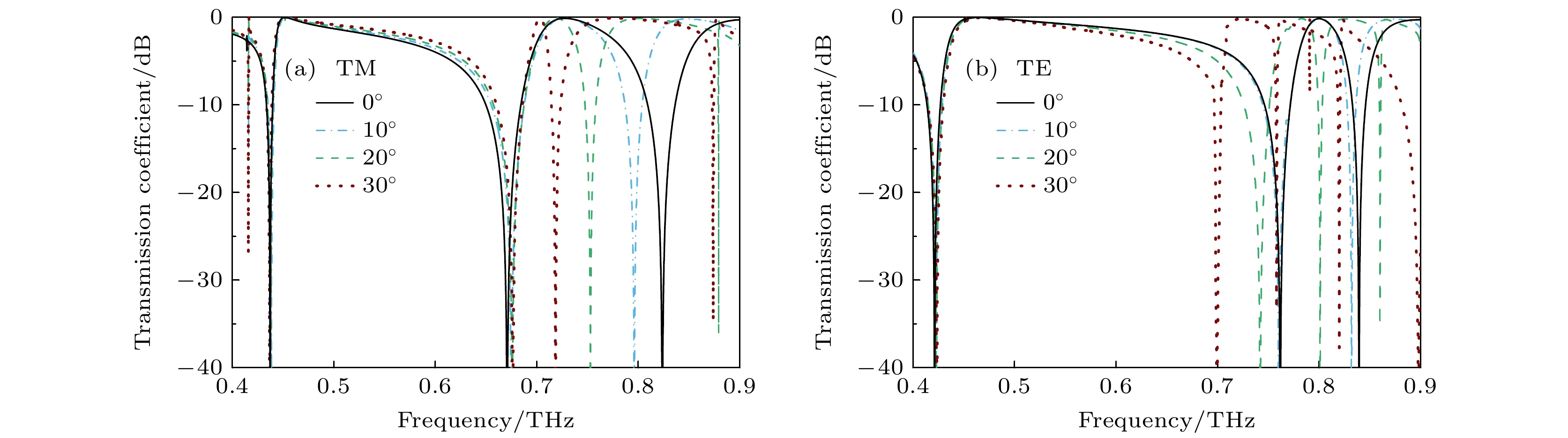
$\eta $ 、极化方位角$\psi $ 分别为0.96/0.98, 38.5°/–42.5. 如图6(b)所示, 该结构在0.692 THz和0.782 THz处的最佳AR分别为0.32 dB和0.12 dB, αin = 45°, 显示出近乎完美的LTC极化转换. 此外, 从图5(c)可以算出, 在对应处的椭圆度角χ分别为43.2°和44.1°, 这进一步证实了上述LTC极化转换的产生. 计算sin(2χ)分别为0.998, 0.999, 获得了99.8%和99.9%的LTC极化转化率. 此外, 在0.692 THz和0.782 THz处的极化方位ψ分别为43.1°和–42.8° (相应的输出端口x轴与主轴之间的角度差 αout为137.2°）. 表明图6(b)和图6(c)中电磁波圆极化的极化角与输入电磁波的极化角相比大约旋转了–90°和90°. 综上所述, 在EIT超材料中可以观察到完美的LTC极化转换.此外, 还研究了本设计对于入射角的敏感特性. 图7为改变入射角对EIT效应的影响. 从图7可以看到, 在TM极化波下, 入射角增大时第1个EIT窗口稳定而第2个EIT窗口频带变窄; 在TE极化波下, 入射角增大时第1个EIT窗口变窄而第2个EIT窗口产生红移. 即当入射角改变很小的角度透射谱的变化却很大. 因此本结构产生的EIT效应对入射角度比较敏感, 但仍然存在透射频带.
-
本文在太赫兹频段基于类电磁诱导透明效应提出了一种高效率极化转化滤波器, 通过非对称 结构激励了多能级明模路径, 突破了传统EIT干涉效应调制的维度瓶颈, 在传输模式调制的基础上于多个频带实现了线-圆极化的偏振调控功能. 研究结果表明, 在由4个开口T型谐振器构成的金属-介质超表面上, 可以实现双频点的线极化向圆极化的转换. 此外, 该设计在双极化下实现了电磁诱导透明象, 相对带宽分别为57.7%/9.4%和46.5%/12.8%, 且在0.692 THz和0.782 THz处发生了线性到圆的极化转换, 透射系数分别为0.7和0.68. 根据Stokes参数, 对应的椭圆率η分别为96%和98%. 这种基于类电磁诱导透明效应的极化转换滤波器具有低损耗和超薄的特点, 在天线阵列、天线罩和延迟器领域中具有广泛的应用前景.
基于类电磁诱导透明效应的极化转换滤波器
Polarization conversion filter based on electromagnetically induced transparency-like effect
-
摘要: 在太赫兹频段基于类电磁诱导透明效应(electromagnetically induced transparency, EIT)提出了一种高效率极化转化滤波器, 通过非对称结构激励了多能级明模路径, 在传统EIT干涉效应的基础上, 获得了正交的圆极化转换窗口. 通过两组具有相似共振频率的明模相互干涉产生透射窗口, 然后构造非对称结构来实现TE和TM极化下的透射窗口偏移, 从而实现双频点极化转换. 该超材料的单元结构由4个开口T型金属谐振组成. 通过分析表面电流分布、频率响应特性以及入射角特性, 探究了其工作机理. 研究结果显示, 该设计在不同极化下实现了电磁诱导透明现象. 随后, 基于两个入射极化的EIT共振, 在0.692 THz处实现了线极化到右旋圆极化转换和0.782 THz处实现了线极化到左旋圆极化转换, 透射系数分别为0.7和0.68. 这种基于EIT的极化转化具有低损耗和超薄的特点, 在紧凑型天线、衍生雷达相控阵和军事工业探测器领域有潜在应用价值.Abstract: Owing to the large losses in the conversion process of traditional polarization converters, there is an increasing demand for metasurfaces with excellent transmission performance. In this work, an efficient polarization conversion metasurface is proposed based on electromagnetically induced transparency-like (EIT-like) effect in the terahertz band. The multi-level bright mode paths are excited by an asymmetric structure to obtain orthogonal circular polarization conversion windows. The transmission window is generated by the mutual interference of two sets of bright modes with similar resonant frequencies. Then an asymmetric structure is constructed to achieve transmission window shift under TE polarization and TM polarization, thereby realizing dual-frequency polarization conversion. The metamaterial unit structure consists of four open metal resonant rings and four metal resonant strips. The working mechanism is explored by analyzing the surface current distribution, frequency response, and incident angle characteristics. The results show that electromagnetically induced transparency can be achieved under different polarizations. Furthermore, based on the EIT resonance between the two incident polarizations, the conversion from linear polarization to right-hand circular polarization is achieved at 0.692 THz, and the conversion from linear polarization to left-hand circular polarization is realized at 0.782 THz, transmission coefficients are 0.7 and 0.68 respectively. According to the Stokes parameters, the corresponding ellipticity η values are 96% and 98%, respectively. This EIT-based polarization conversion metasurface with low loss and ultra-thin characteristics has great potential applications in compact antennas, derived radar phased arrays, and military detectors.
-
Key words:
- metamaterials /
- electromagnetic induced transparency effect /
- polarization conversion /
- filters .
-
-
图 1 所提出的单元结构 (a) 功能示意图; (b) 单元结构图
Figure 1. Proposed unit structure: (a) Functional diagram; (b) cell structure diagram.
图 2 不同单元结构的透射谱 (a) TM极化波下的不同基本结构透射谱、表面电流以及磁场图分布图; (b) TE极化波下的不同结构透射谱、表面电流以及磁场图分布图; (c) 整体结构的透射谱; (d) 类EIT效应的能级系统
Figure 2. Transmission spectra of different unit structures: (a) Transmission spectra, surface currents, and magnetic field maps of different basic structures under TM polarized waves; (b) transmission spectra, surface currents, and magnetic field maps of different structures under TE polarized waves; (c) transmission spectrum of the overall structure; (d) energy level systems of class EIT effects.
图 4 极化转换点的表面电流以及磁场图
Figure 4. Surface current and magnetic field (absolute value) of the polarization transition point.
图 5 重要指标图 (a) 透射曲线和相位; (b) 透射曲线的轴比; (c) 透射曲线的椭圆度; (d) 透射曲线的极化方位角
Figure 5. Important indicators: (a) Transmission curve and phase; (b) axial ratio of transmission curve; (c) ellipticity of the transmission curve; (d) polarization azimuth of the transmission curve.
图 6 极化转换示意图 (a) 45°线极化入射波; (b) 0.692 THz透射波模拟极化; (c) 0.782 THz透射波模拟极化
Figure 6. Schematic diagram of polarization conversion: (a) 45° linearly polarized incident wave; (b) simulated polarization of 0.692 THz transmitted wave; (c) simulated polarization of 0.782 THz transmitted wave.
-
[1] Zheng D, Lin Y S 2020 Adv. Mater. Technol. 5 202000584 doi: 10.1002/admt.202000584 [2] Mutlu M, Ozbay E 2012 Appl. Phys. Lett. 100 051909 doi: 10.1063/1.3682591 [3] Yan D, Wang B B, Bai Z Y, Li W B 2020 Opt. Express 28 9677 doi: 10.1364/OE.389247 [4] Li A D, Chen W J, Wei H, Lu G W, Alù A, Qiu C W, Chen L 2022 Phys. Rev. Lett. 129 127401 doi: 10.1103/PhysRevLett.129.127401 [5] Huang Z R, Zheng Y Q, Li J H, Cheng Y Z, Wang J, Zhou Z K, Chen L 2023 Nano. Lett. 23 10991 doi: 10.1021/acs.nanolett.3c03258 [6] 王哲飞, 李超, 万发雨, 曾庆生, 傅佳辉, 吴群, 宋明歆 2024 光学学报 44 1624002 doi: 10.3788/AOS240839 Wang Z F, Li C, Wan F Y, Zeng Q S, Fu J H, Wu Q, Song M X 2024 Acta Opt. Sin. 44 1624002 doi: 10.3788/AOS240839 [7] Guan D F, You P, Zhang Q, Xiao K, Yong S W 2017 IEEE Trans. Microw. Theory Tech. 65 4925 doi: 10.1109/TMTT.2017.2727486 [8] Liang D C, Zhang H F, Gu J Q, Li Y F, Tian Z, Ouyang C M, Han J G, Zhang W L 2017 IEEE J. Select. Topics Quantum Electron. 23 4700907 doi: 10.1109/JSTQE.2017.2657681 [9] Deng Y D, Song Z Y 2020 Opt. Mater. 105 109972 doi: 10.1016/j.optmat.2020.109972 [10] Li F, Zhang T, Mao M, Zhang H F 2020 J. Opt. 22 095106 doi: 10.1088/2040-8986/abac21 [11] Prakash D, Gupta N 2022 Int. J. Microw. Wirel. Technol. 14 19 doi: 10.1017/S1759078721000039 [12] Han L, Tan Q L, Gan Y, Zhang W D, Xiong J J 2020 Results Phys. 19 103377 doi: 10.1016/j.rinp.2020.103377 [13] Wang Q, Kuang K L, Gao H X, Chu S W, Yu L, Peng W 2021 Nanomaterials 11 1350 doi: 10.3390/nano11051350 [14] Sarkar R, Devi K M, Ghindani D, Prabhu S S, Chowdhury D R, Kumar G 2020 J. Opt. 22 035105 doi: 10.1088/2040-8986/ab70f2 [15] Li H M, Liu S B, Liu S Y, Wang S Y, Zhang H F, Bian B R, Kong X K 2015 Appl. Phys. Lett. 106 114101 doi: 10.1063/1.4915313 [16] Li H M, Liu S B, Liu S Y, Wang S Y, Ding G W, Yang H, Yu Z Y, Zhang H F 2015 Appl. Phys. Lett. 106 083511 doi: 10.1063/1.4913888 [17] Srijan D, Lalita U 2023 NDT E. Int. 139 102908 doi: 10.1016/j.ndteint.2023.102908 [18] Lang T T, Yu Z Y, Zhang J H, Hong Z, Liu J J, Wang P 2023 Sensor Actuat. A-Phys. 360 114522 doi: 10.1016/j.sna.2023.114522 [19] Zhu L, Dong L, Guo J, Meng F Y, He X J, Zhao C H, Wu Q 2018 Plasmonics 13 1971 doi: 10.1007/s11468-018-0712-8 [20] Yang D, Shen Z Y, Xia Y Q 2021 Appl. Phys. B 127 87 doi: 10.1007/s00340-021-07635-4 [21] Gao C J, Guo Z H, Sun Y Z, Zhang H F 2022 Opt. Laser Technol. 151 108006 doi: 10.1016/j.optlastec.2022.108006 [22] Yang Y S, Guan D F, Fu Y F, Gu Z Y, Zhang J D, Qian Z P, Wu W 2024 IEEE Antenn. Wirel. Pr. 23 1035 doi: 10.1109/LAWP.2023.3342248 [23] Khanikaev B, Mousavi S H, Wu C H, Dabidian N, Alici K B, Shvets G 2012 Opt. Commun. 285 3423 doi: 10.1016/j.optcom.2012.03.023 [24] Sun Y Z, Zhang D, Zhang H F 2022 Opt. Express 30 30574 doi: 10.1364/OE.465895 [25] Meng D J, Wang S Y, Sun X L, Gong R Z, Chen C H 2014 Appl. Phys. Lett. 104 261902 doi: 10.1063/1.4886148 -
计量
- 文章访问数: 455
- HTML全文浏览数: 455
- PDF下载数: 4
- 施引文献: 0