高级搜索

超快光纤激光器中可控脉冲产生与湮灭动力学

,  ,  , 

downloadPDF

上一篇

下一篇

周瑞, 李阳, 朱润徽, 张祖兴. 超快光纤激光器中可控脉冲产生与湮灭动力学[J]. 物理学报, 2024, 73(17): 174201-1. doi: 10.7498/aps.73.20240673
引用本文: 周瑞, 李阳, 朱润徽, 张祖兴. 超快光纤激光器中可控脉冲产生与湮灭动力学[J]. 物理学报, 2024, 73(17): 174201-1. doi: 10.7498/aps.73.20240673
shu
Rui Zhou, Yang Li, Run-Hui Zhu, Zu-Xing Zhang. Controlled pulse generation and annihilation dynamics in ultrafast fiber lasers[J]. Acta Physica Sinica, 2024, 73(17): 174201-1. doi: 10.7498/aps.73.20240673
Citation: Rui Zhou, Yang Li, Run-Hui Zhu, Zu-Xing Zhang. Controlled pulse generation and annihilation dynamics in ultrafast fiber lasers[J]. Acta Physica Sinica, 2024, 73(17): 174201-1. doi: 10.7498/aps.73.20240673
shu

超快光纤激光器中可控脉冲产生与湮灭动力学

  • 南京邮电大学电子与光学工程学院、柔性电子(未来技术)学院, 南京　210023

    • 作者简介: 周瑞.E-mail: 1222025215@njupt.edu.cn .
    通讯作者: E-mail: zxzhang@njupt.edu.cn.

  • 中图分类号: 42.50.Md, 42.65.Tg, 42.65.Sf, 42.81.Dp

Controlled pulse generation and annihilation dynamics in ultrafast fiber lasers

  • School of Electronic and Optical Engineering, School of Flexible Electronics (Future Technology), Nanjing University of Posts and Telecommunications, Nanjing 210023, China

    • Corresponding author: E-mail: zxzhang@njupt.edu.cn.

  • MSC: 42.50.Md, 42.65.Tg, 42.65.Sf, 42.81.Dp

  • 摘要: 本文采用实时傅里叶变换光谱探测技术, 研究了基于泵浦强度调制的超快光纤激光器中锁模脉冲产生与湮灭动力学过程. 结果表明: 当泵浦调制电压处于高电平时, 激光器输出稳定的锁模脉冲. 随着调制电压跳变至低电平, 锁模脉冲的强度不断降低, 而后经历一段衰减振荡阶段后发生湮灭, 在~5 μs后孤子从噪声中重建, 这一过程伴随着调Q不稳定性的产生. 在低电平阶段, 激光腔内的湮灭过程连续发生, 其周期为~55 μs. 通过改变调制泵浦的占空比, 能够操控在低电平调制下孤子连续湮灭的次数. 进一步, 锁模与孤子湮灭的连续切换过程与泵浦调制频率有关, 调制频率的升高能够有效缩短两种状态的持续时间从而减少孤子湮灭的次数. 此外, 通过减小低电平的值, 能够降低激光腔内的增益, 使得孤子连续湮灭的周期缩短. 研究结果有利于深入了解孤子的形成与湮灭动力学, 并为超快激光器各种运行机制的发展提供了新的视角.
    Abstract: In this paper, the mode-locked pulse generation and annihilation dynamics in ultrafast fiber lasers based on pump intensity modulation are investigated by using real-time Fourier transform spectral probing. The results show that the laser outputs stable mode-locked pulses when the pump modulation voltage is at a high level. As the modulation voltage jumps to a low level, the intensity of the mode-locked pulse decreases, and then undergoes a period of decaying oscillation before annihilation occurs, and after ~5 μs the soliton is reconstructed from the noise, accompanied by the generation of the Q-modulation instability. In the low-level phase, the annihilation process in the laser cavity occurs continuously with a period of ~55 μs. By changing the duty cycle of the modulation pump, it is possible to control the the number of times solitons continuously annihilate under low-level modulation. Further, the continuous switching process of mode-locking and soliton annihilation is related to the modulation frequency of the pump, and the increase of the modulation frequency can effectively shorten the duration of the two states, thus reducing the number of soliton annihilations. In addition, by reducing the value of the low level, the gain in the laser cavity can be reduced, resulting in a shorter period of successive soliton annihilation. The results of the study are conducive to an in-depth understanding of the formation and annihilation dynamics of solitons, and provide new perspectives for developing various operation mechanisms of ultrafast lasers.
  • 加载中

  • 图 1  实验装置图(SG-信号发生器; LD-半导体光源; WDM-波分复用器; PC-偏振控制器; OC-光耦合器; PDG-偏振相关光栅; PI-ISO-偏振无关隔离器; DCF-色散补偿光纤; PD-光电探测器; OSA-光谱仪; OSC-示波器)

    Figure 1.  Diagram of experimental setup(SG-signal generator; LD-semiconductor light source; WDM-wavelength division multiplexer; PC-polarization controller; OC-90:10 optical coupler; PDG-polarization-dependent grating; PI-ISO-polarization-independent isolator; DCF-dispersion compensation fiber; PD-photodetector; OSA-optical spectrum analyzer; OSC-oscilloscope).

    下载: 全尺寸图片 幻灯片

    图 2  调制泵浦的性能表征　(a) 2, 5和10 kHz调制频率下的输入泵浦脉冲波形和载波信号波形; (b)调制电平和泵浦功率关系图

    Figure 2.  Performance characterization of modulated pump: (a) Input pump pulse waveform and carrier signal waveform at 2, 5, and 10 kHz modulation frequencies; (b) plot of modulation level versus pump power.

    下载: 全尺寸图片 幻灯片

    图 3  DFT准确性验证及脉冲状态切换过程脉冲序列　(a)用OSA记录的光谱(虚线)和从DFT测量结果提取出的单次光谱(实线); (b)切换过程相应的脉冲序列; (c), (d)孤子湮灭前后的细节放大图

    Figure 3.  DFT accuracy verification and pulse trains during pulse state switching process: (a) Spectra recorded with OSA (dashed line) and single spectra extracted from DFT measurements (solid line); (b) pulse sequence corresponding to the switching process; (c), (d) detailed enlargements of the soliton before and after its annihilation.

    下载: 全尺寸图片 幻灯片

    图 4  稳定锁模与孤子湮灭切换过程的实验实时数据　(a) DFT光谱演化图; (b)孤子湮灭前的细节放大; (c)相应的场自相关迹演化; (d)一个呼吸周期内最宽和最窄脉宽的光谱图; (e)孤子重建时的细节放大; (f)相应的场自相关迹演化; (g)调Q不稳定性状态下与稳定锁模状态下的光谱

    Figure 4.  Experimental real-time data for stable mode-locking and soliton annihilation switching processes: (a) DFT spectral evolution diagram; (b) detailed enlargement of the soliton before its annihilation; (c) corresponding field autocorrelation trace evolution; (d) spectrograms of the widest and narrowest pulse widths in one breathing period; (e) detailed zoom in on the reconstruction of the soliton; (f) corresponding field autocorrelation trace evolution; (g) spectra of the Q-switched instability state versus the stable mode-locked state.

    下载: 全尺寸图片 幻灯片

    图 5  不同占空比和调制频率下切换过程的脉冲序列和DFT光谱图　(a), (b)低电平调制占空比为30%; (c), (d)低电平调制占比为70%; (e), (f) 5 kHz调制频率; (g), (h) 10 kHz调制频率

    Figure 5.  Pulse trains and DFT spectra of the switching process at different duty ratios and modulation frequencies: (a), (b) 30% duty ratio for low-level modulation; (c), (d) 70% duty ratio for low-level modulation; (e), (f) 5 kHz modulation frequency; (g), (h) 10 kHz modulation frequency.

    下载: 全尺寸图片 幻灯片

    图 6  不同低电平下切换过程的脉冲序列、DFT光谱图及自相关迹演化　(a), (b), (c) 2.52 V; (d), (e), (f) 2.50 V; (g), (h), (i) 2.44 V

    Figure 6.  Pulse sequence, DFT spectra, and autocorrelation trace evolution of switching process at different low levels: (a), (b), (c) 2.52 V; (d), (e), (f) 2.50 V; (h), (g), (i) 2.44 V.

    下载: 全尺寸图片 幻灯片
  • [1] Yun L, Qiu Y, Yang C H, Xing J, Yu K H, Xu X X, Wei W 2018 Photon. Res. 6 1028 doi: 10.1364/PRJ.6.001028
    [2] Malinauskas M, Žukauskas A, Hasegawa S, Hayasaki Y, Mizeikis V, Buividas R, Juodkazis S 2016 Light Sci. Appl. 5 16133 doi: 10.1038/lsa.2016.133
    [3] Mao D, Zheng Y, Zeng C, Lu H, Wang C, Zhang H, Zhang W D, Mei T, Zhao J L 2021 Adv. Photon. 3 014002
    [4] Cao B, Gao C X, Liu K W, Xiao X S, Yang C X, Bao C Y 2023 Light Sci. Appl. 12 260 doi: 10.1038/s41377-023-01305-0
    [5] Wise F W, Chong A, Renninger W H 2008 Laser Photon. Rev. 2 58 doi: 10.1002/lpor.200710041
    [6] Fermann M E, Hartl I 2013 Nat. Photon. 7 868 doi: 10.1038/nphoton.2013.280
    [7] Huang L, Zhang Y S, Liu X M 2020 Nanophotonics 9 2731 doi: 10.1515/nanoph-2020-0269
    [8] Zhang Y S, Cui Y D, Huang L, Tong L M, Liu X M 2020 Opt. Lett. 45 6246 doi: 10.1364/OL.404778
    [9] Kieu K, Renninger W H, Chong A, Wise F W 2009 Opt. Lett. 34 000593 doi: 10.1364/OL.34.000593
    [10] Zhao L M, Tang D Y, Zhang H, Cheng T H, Tam H Y, Lu C 2007 Opt. Lett. 32 001806 doi: 10.1364/OL.32.001806
    [11] Renninger W H, Chong A, Wise F W 2008 Phys. Rev. A 77 023814 doi: 10.1103/PhysRevA.77.023814
    [12] Liu X M 2010 Phys. Rev. A 81 023811 doi: 10.1103/PhysRevA.81.023811
    [13] Li H, Ouzounov D G, Wise F W 2010 Opt. Lett. 35 002403 doi: 10.1364/OL.35.002403
    [14] Goda K, Tsia K K, Jalali B 2009 Nature 458 1145 doi: 10.1038/nature07980
    [15] Mahjoubfar A, Churkin D V, Barland S, Broderick N, Turitsyn S K, Jalali B 2017 Nat. Photon. 11 341 doi: 10.1038/nphoton.2017.76
    [16] Xu Y Q, Wei X M, Ren Z B, Wong K K Y, Tsia K K 2016 Sci. Rep. 6 27937 doi: 10.1038/srep27937
    [17] Lu M X, Wang X D, Li K X, Geng X, Pan J Y, Sun M Q, Li S W 2022 Laser Phys. 33 015101
    [18] Song Y G, Zou D F, Gat O, Hu M L, Grelu P 2023 Laser Photon. Rev. 17 2300066 doi: 10.1002/lpor.202300066
    [19] Sheng C, Liu H, Chen H Y, Zhu S N 2018 Nat. Commun. 9 4271 doi: 10.1038/s41467-018-06718-9
    [20] Cui H, Liu X M 2019 Photon. Res. 7 000423 doi: 10.1364/PRJ.7.000423
    [21] Zhou Y, Ren Y X, Shi J W, Mao H D, Wong K K Y 2020 Optica 7 965 doi: 10.1364/OPTICA.394706
    [22] Han D D, Wang Y J, Hui Z Q, Zhang Z X, Ren K, Zheng Y P, Zhao F, Zhu L P, Gong J M 2021 Infrared Phys. Techn. 116 103786 doi: 10.1016/j.infrared.2021.103786
    [23] Korobko D A, Ribenek V A, Itrin P A, Fotiadi A A 2023 Opt. Fiber Technol. 75 103216 doi: 10.1016/j.yofte.2022.103216
    [24] Jiang C, Zhou R, Fang Z, Wan Y, Sun B, Mou C B, Liu Y Q, Zhang Z X 2023 Opt. Lett. 48 5875 doi: 10.1364/OL.506326
    [25] 方振, 余游, 赵秋烨, 张昱冬, 王治强, 张祖兴 2023 物理学报 73 014202 doi: 10.7498/aps.73.20231030 Fang Z, Yu Y, Zhao Q Y, Zhang Y D, Wang Z Q, Zhang Z X 2023 Acta Phys. Sin. 73 014202 doi: 10.7498/aps.73.20231030
    [26] Peng J S, Boscolo S, Zhao Z H, Zeng H P 2019 Sci. Adv. 5 1110
    [27] Gui L, Wang P, Ding Y H, Zhao K J, Bao C Y, Xiao X S, Yang C X 2018 Appl. Sci. 8 201 doi: 10.3390/app8020201
  • 加载中
图( 6)
计量
  • 文章访问数:  242
  • HTML全文浏览数:  242
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-05-11
  • 刊出日期:  2024-09-05

超快光纤激光器中可控脉冲产生与湮灭动力学

    通讯作者: E-mail: zxzhang@njupt.edu.cn.
    作者简介: 周瑞.E-mail: 1222025215@njupt.edu.cn
  • 南京邮电大学电子与光学工程学院、柔性电子(未来技术)学院, 南京　210023
  • 收稿日期:  2024-05-11

摘要: 本文采用实时傅里叶变换光谱探测技术, 研究了基于泵浦强度调制的超快光纤激光器中锁模脉冲产生与湮灭动力学过程. 结果表明: 当泵浦调制电压处于高电平时, 激光器输出稳定的锁模脉冲. 随着调制电压跳变至低电平, 锁模脉冲的强度不断降低, 而后经历一段衰减振荡阶段后发生湮灭, 在~5 μs后孤子从噪声中重建, 这一过程伴随着调Q不稳定性的产生. 在低电平阶段, 激光腔内的湮灭过程连续发生, 其周期为~55 μs. 通过改变调制泵浦的占空比, 能够操控在低电平调制下孤子连续湮灭的次数. 进一步, 锁模与孤子湮灭的连续切换过程与泵浦调制频率有关, 调制频率的升高能够有效缩短两种状态的持续时间从而减少孤子湮灭的次数. 此外, 通过减小低电平的值, 能够降低激光腔内的增益, 使得孤子连续湮灭的周期缩短. 研究结果有利于深入了解孤子的形成与湮灭动力学, 并为超快激光器各种运行机制的发展提供了新的视角.

English Abstract

    全文HTML

    1.   引　言

    • 由于超快光纤激光器具有转换效率高、光束质量好等固有优势, 这使得其在光通信、精密光谱以及光学传感等诸多领域的应用愈加广泛[1–4]. 通过适当的色散管理, 能够在超快光纤激光器中得到传统孤子、自相似脉冲、拉伸脉冲以及耗散孤子等不同类型的脉冲[5,6]. 其中, 耗散孤子的概念源于保守效应与耗散效应之间的复合平衡[7,8]. 相较于其他类型的脉冲, 耗散孤子能够承受过度的非线性相移, 这使得其在实现更高的脉冲能量的同时往往也表现出复杂的不稳定性[9]. 事实上, 尽管在各种超快光纤激光器中实现耗散孤子锁模与湮灭的研究越来越多[10–13], 但是在这些系统中实现锁模状态和湮灭状态的连续切换缺乏具体的实验, 对于这两种状态的建立切换与精准调控的动力学研究更是寥寥可数.

      时间拉伸色散傅里叶变换(TS-DFT)技术是研究非线性光学系统实时瞬态过程的一种新兴技术, 常用于解决示波器和频谱仪等检测器分辨率有限的问题. 其基本原理为: 不同频率的光在大色散介质中以不同的速度传输, 这使得入射脉冲被拉伸展宽, 当在远场出射端满足一定色散条件时, 能够从时域上观察到入射脉冲的实时强度变化[14–16]. 目前, DFT技术已经成功的用于研究被动锁模光纤激光器中的各种非线性现象, 如孤子爆炸[17]、混沌孤子[18]以及异常波[19]等.

      2019年, Cui等[20]报道了传统孤子、拉伸脉冲和耗散孤子在超快光纤激光器中从诞生到湮灭的完整演化动力学, 发现在不同的色散条件下的孤子湮灭过程随着脉冲和泵浦功率的改变而有所差异. 2020年, Zhou等[21]利用DFT结合数值模拟研究耗散孤子分子时发现, 孤子分子可以通过瞬态湮灭和能量转移解离成一个孤子, 且背景噪声可以直接形成一对孤子, 然后通过强烈的排斥力形成孤子分子锁模. 2021年, Han等[22]利用DFT技术对无源锁模光纤激光器中耗散孤子的形成和破缺动力学进行了研究, 发现在耗散孤子形成和湮灭的过程中均能够观察到调Q不稳定性. 2023年, Korobko等[23]研究谐波锁模激光器发现, 利用外部连续波注入空腔可精确控制孤子数量, 并利用DFT技术观察了改变泵浦功率引发的孤子产生与湮灭动态. 然而, 上述研究虽然涉及了耗散孤子的稳定锁模和孤子湮灭两种状态, 但是无一例外均是不受操控的在特定泵浦功率下观察到的瞬时动力学过程. 到目前为止, 能够利用调制泵浦实现这两种状态连续切换的动力学过程尚未被详细研究, 孤子湮灭周期和次数的可控操控尚未实现.

      本文报道了基于泵浦强度调制的超快光纤激光器中稳定锁模与孤子湮灭可控切换动力学, 采用DFT技术, 重点研究了两种状态建立和切换时的瞬态动力学过程. 通过改变调制泵浦的占空比, 实现了一个调制周期内孤子湮灭次数的可控操纵. 此外, 在不同的调制频率和调制电压下, 观测并比较了孤子连续湮灭的动力学过程, 并对其周期进行了统计. 不同于孤子爆炸和异常波等非重复事件, 随着泵浦功率的周期性变化, 孤子的产生与湮灭可以连续、重复地出现, 证明了激光器可在不同输出特性下实现连续切换. 此外, 精心控制的外部泵浦来控制孤子产生与湮灭的数量能够实现对激光器重复频率的微调控, 并对实现可控阶数谐波锁模激光器的设计有指导意义.

    2.   实验装置及调制泵浦的性能表征

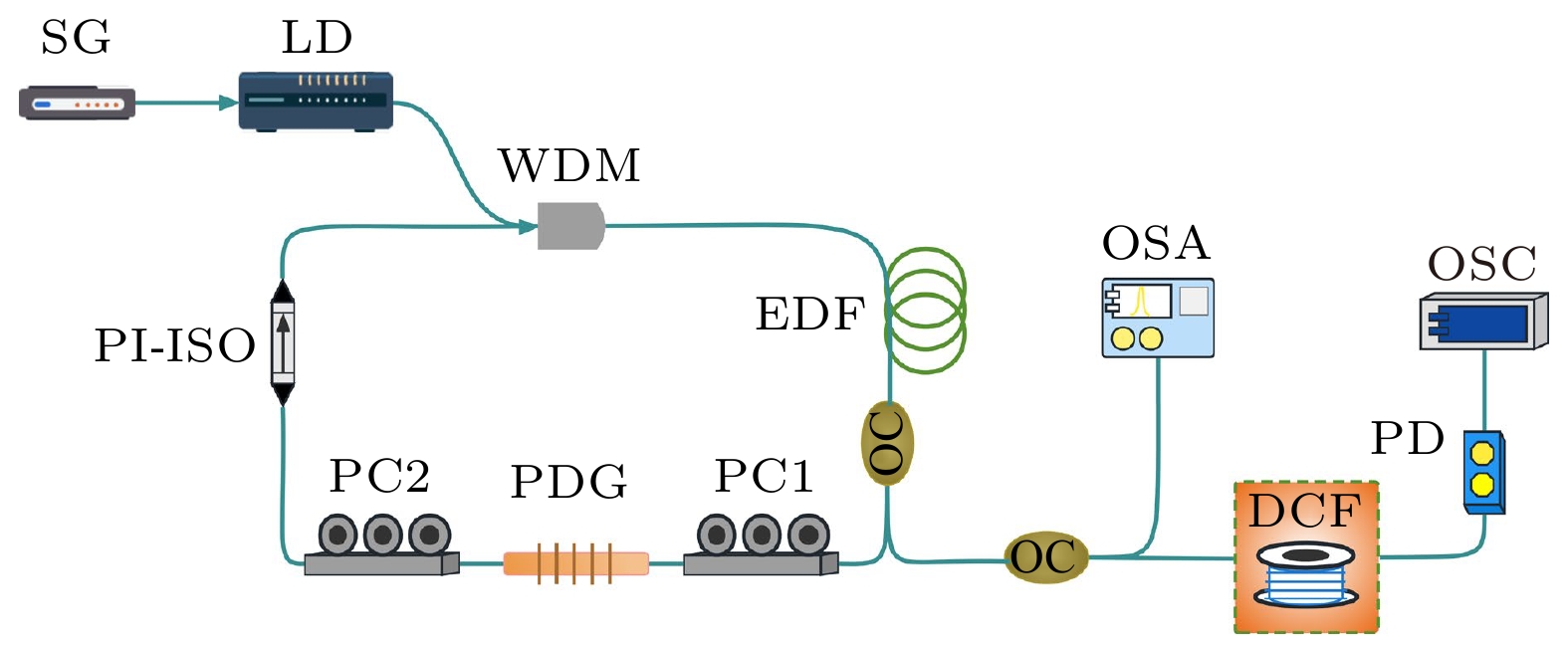
    • 实验装置如图1所示. 光纤激光器由信号发生器(SG)、 976 nm 半导体激光器(LD)、波分复用器(WDM)、掺铒光纤(EDF)、70:30 光耦合器(OC)、偏振相关光栅(PDG)、两个偏振控制器(PC)以及偏振无关隔离器(PI-ISO)组成. 其中, 增益光纤(EDF)长2 m, 在1.5 μm波段色散为61.15 ps²/km, 其与泵浦光源通过980/1550 nm WDM连接, 腔体的其余光纤组分是色散为–22.8 ps²/km的单模光纤(SMF-28 E). 谐振腔的总长度为6.17 m, 对应重复频率为33.529 MHz, 腔内净色散为 ~0.0272 ps². LD的输出波形和功率等特性能够通过SG进行调控, PC用于改变腔内的偏振状态, 其与具有较高偏振相关损耗的光栅(PDG)[24]集成, 等效于可饱和吸收体, 能够实现非线性偏振旋转(NPR)模式锁定. 输出脉冲由一个70:30的光耦合器(OC)从腔中提取, 再通过50:50的OC分成两束光. 其中一束光借助8 km的色散补偿光纤(DCF)进行拉伸展宽, 并通过18 GHz带宽的高速光电探测器(PD, aoshowsh, HSPD4018)将光信号转换为电信号后接入到带宽为11 GHz的示波器(OSC, LeCroy, SDA 11000)来记录实时光谱变化, 另一束则接入到光谱仪(OSA, YOKOGAEA, AQ6370D)进行光谱测量. 在1550 nm处DCF的色散为56 ps²/km, 故TS-DFT相对应的时间分辨率为33.3 ps, 光谱分辨率为0.2586 nm.

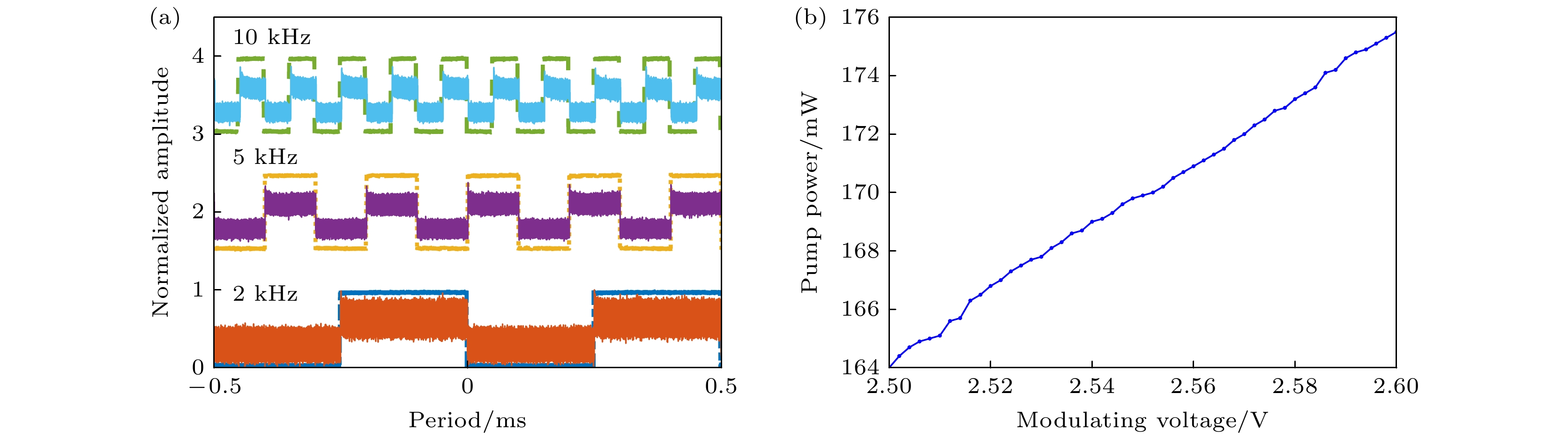
      在进行激光器实验前, 对调制泵浦的性能进行表征, 图2显示了在1 ms内不同信号发生器的载波信号波形和输出泵浦光源波形. 图2(a)中的非实线部分表明, 调制信号为矩形波, 高低电平分别为2.6 V和2.5 V, 调制深度为50%, 占空比为50%. 而实线部分为载波信号调制下的泵浦激光器输出波形, 由于此时的输出功率远超PD的功率阈值, 故该波形是经过了5:95的OC后接入示波器的结果. 图2(b)显示了泵浦激光器的输出功率与调制电平的对应关系, 在调制下泵浦激光器输出的最大功率为175.5 mW, 最小功率为164 mW, 调制深度为6.55%. 图2表明, 在信号发生器调制信号的作用下, 不仅能够调控泵浦激光源的输出功率, 还能够改变激光源功率变化的周期和幅度等特性[25].

    3.   脉冲切换过程

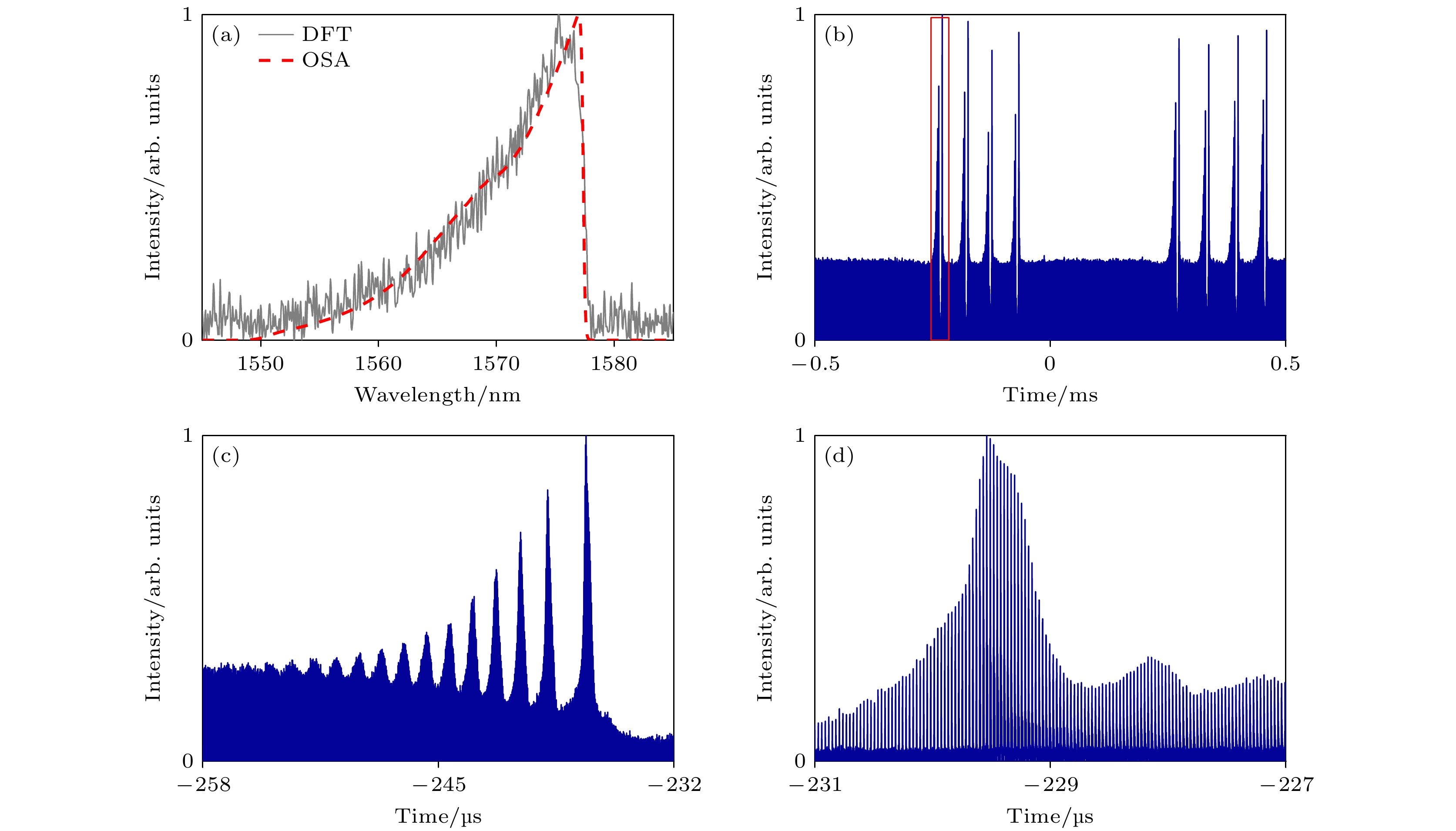
    • 首先, 泵浦调制频率设置为2 kHz, 当调制电平处于高电平2.6 V时, 激光器输出稳定的锁模脉冲. 图3(a)中的虚线部分是使用光谱仪测量得到的稳定锁模状态下线性坐标的光谱, 其中心波长为1573.58 nm, 半宽全高(FWHM)为7.6 nm. 由于EDF增益的不对称性, 导致脉冲在长波长获得了更大的增益放大, 同时光谱强度在长波长边缘处快速下降, 这符合耗散孤子的典型光谱特征. 为了验证DFT技术的准确性, 在相同的状态下从经过拉伸的脉冲序列中提取出单次光谱, 如图3(a)中的实线部分所示, 可以看到DFT获取的光谱与OSA直接测量的光谱整体十分吻合. 图3(b)显示了在1 ms的时间尺度内锁模脉冲产生与湮灭过程相应的脉冲序列, 其切换周期为0.5 ms, 这与调制频率(2 kHz)相对应, 证明了状态的改变是由于泵浦功率的变化引起的. 在锁模阶段, 脉冲的强度维持稳定, 而孤子在湮灭前后的状态往往伴随着剧烈的能量变化.

      对图3(b)中孤子湮灭前后的部分(红色框内)进行了细节放大, 如图3(c)所示, 随着调制电平由高电平2.6 V切换至低电平2.5 V, 激光器在腔内脉冲能量持续降低后进入到一段~23 μs的衰减呼吸振荡阶段, 随后孤子湮灭. 事实上, 在低电平调制下, 孤子每次湮灭时的强度变化是不规则的. 这是由于湮灭强度主要受到呼吸瞬态动力学的影响, 其具体的强度往往是由色散、非线性、增益、损耗及光谱滤波等因素共同决定的, 任何微小变化都可能影响湮灭时的强度. 此外, 高调制频率下激光腔内增益流的不稳定性也会导致孤子湮灭时强度的不规则性变化. 图3(d)展示了在~5 μs后孤子从噪声中重建的过程, 这一过程伴随着明显的调Q不稳定性.

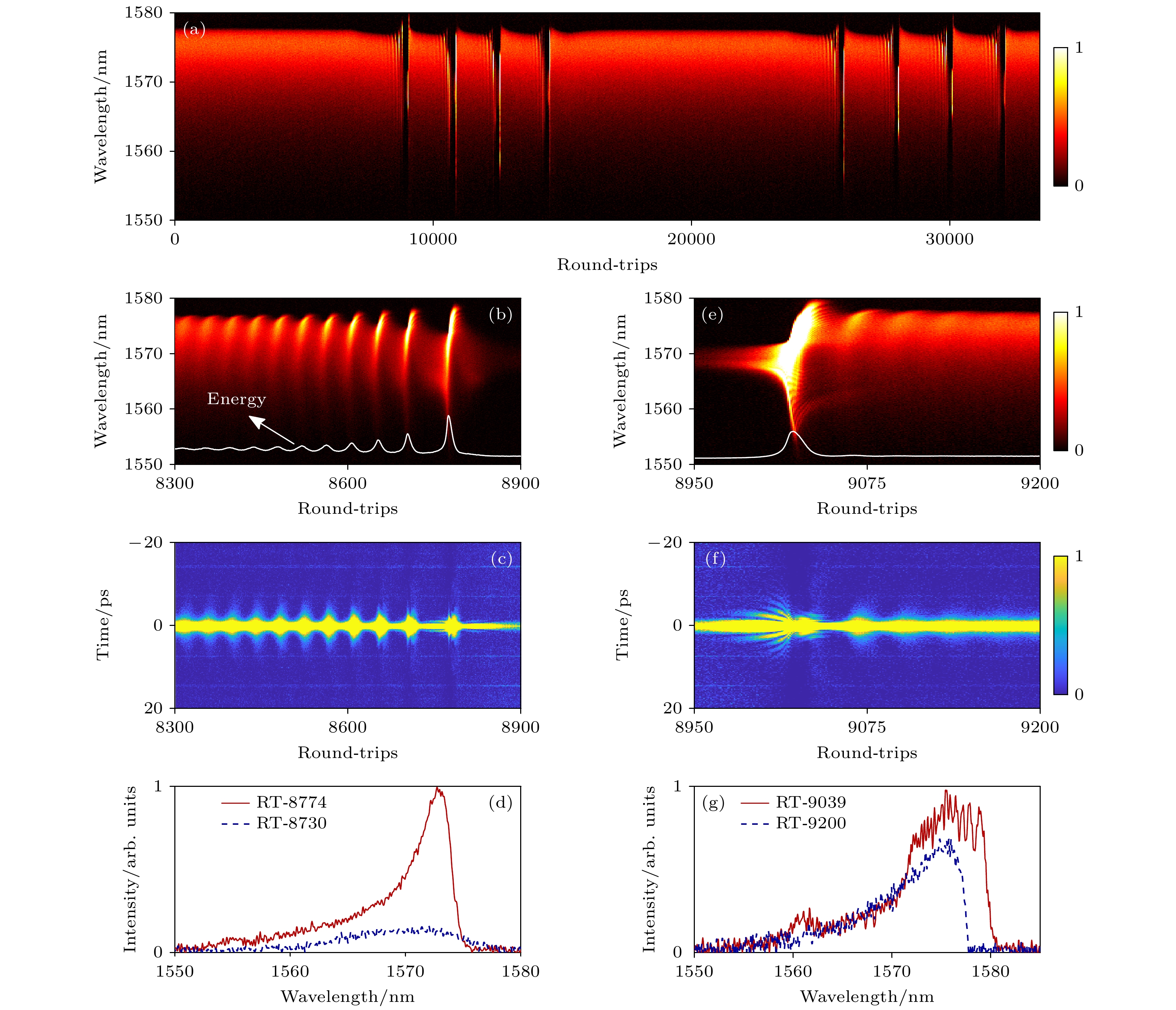
      为了对状态切换过程中光谱的变化进行实时观测, 将TS-DFT记录的时间序列以每29.8 ns(对应锁模脉冲周期)为一圈进行分割, 从而逐圈分析实验数据. 如图4(a)所示, 将图3(b)中的数据重新绘制为时间光谱图, 能够观察到锁模和孤子湮灭两个状态连续切换的动态过程. 从图4(a)明显看出, 当调制泵浦处于高电平时, 激光腔内输出稳定的耗散孤子, 其能量和波长几乎不变. 随着调制电平切换至低电平, 腔内的能量急剧减少, 然而由于弛豫效应的存在, 泵浦功率的降低并没有使得激光器直接脱离模式锁定状态, 而是在中心波长向短波长漂移了一段时间后表现出衰减呼吸振荡. 进一步, 对8300—8900圈的DFT光谱进行放大, 可以看到此时腔内输出呼吸振幅不断增大的呼吸耗散孤子, 如图4(b)所示. 呼吸耗散孤子的产生是通过Hopf分岔将不动点转化为极限环的结果, 其显著特点是谱宽和能量的周期性振荡. 事实上, 弱噪声脉冲在形成稳定孤子前会受到可饱和吸收体的损耗调制, 当噪声波动引起可饱和吸收体的瞬态饱和时, 会发生调Q不稳定性, 这也是导致呼吸振荡行为发生的主要原因. 因此, 若提高可饱和吸收体的饱和功率, 在相同条件下会使得孤子的湮灭与振荡现象更加明显. 进一步, 通过对单圈的光谱密度进行积分, 能够得到该过程中腔内的脉冲能量变化, 如图4(b)中的白色曲线所示, 能量周期性的增强衰弱与DFT光谱所表现出的展宽收缩高度对应.

      图4(c)是对单次光谱进行傅里叶变换所得到相应的场自相关迹演化, 由于噪声的影响, 基于TS-DFT反演得到的脉冲宽度与实际脉宽存在一定的偏差, 但不影响脉冲的整体演化特点. 可以看出, 随着圈数的增加, 孤子脉宽周期性收缩展宽幅度的不断增大, 直至~8863 RT(round-trip)孤子发生湮灭. 为了更好地展示耗散孤子在湮灭前的呼吸活动, 提取了最后一个呼吸周期内最大和最小谱宽的光谱, 如图4(d)所示. 在上述过程中, 呼吸振幅的持续增强是通过控制弱脉冲的强度实现的[26].

      随后在经历了~168 RT后, 孤子从噪声中重建, 并表现出明显的调Q不稳定性. 事实上, 随着调制电平切换至低电平, 脉冲能量随着泵浦功率的降低而减少, 这使得脉冲具有较低增益的同时锁模的损耗增大. 当腔内的增益小于损耗时, 腔内的能量会突然下降, 这导致了孤子湮灭现象的发生[20]. 然而, 此时的泵浦功率仍能够诱导EDF中的Er3+ 集居数反转积累, 在一段时间后, 增益可能再次大于损耗, 从而增加了腔内的能量, 孤子得以重建. 图4(e)是对孤子重建后动态过程的细节放大, 当调Q不稳定性出现时, 腔内脉冲的能量逐渐上升, 耗散孤子的光谱也会产生波动. 图4(f)是相应的自相关迹, 可以看出在能量上升至最高时, 腔内出现了多个孤子的竞争演化[27], 这种竞争在~70 RT后结束, 进而逐渐进入到单孤子的稳定锁模状态. 为了更好地比较孤子重建状态与稳定锁模状态下光谱的变化情况, 提取9039 RT和9200 RT时的光谱, 如图4(g)所示. 与正常锁模状态下光谱相比, 调Q不稳定性发生时的光谱强度更大且在两侧出现了明显的干涉图样, 这种现象可以归因于自相位调制效应.

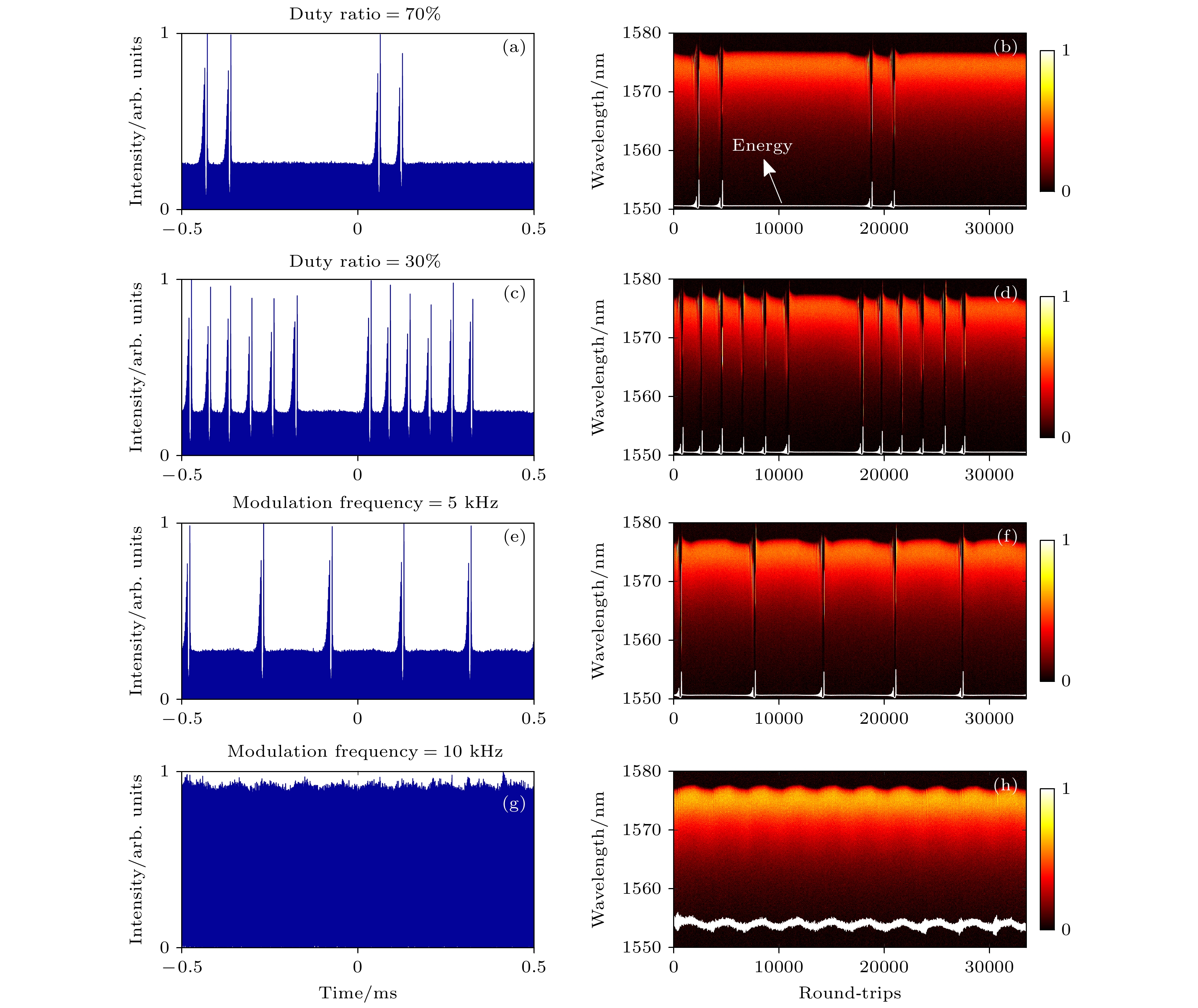
      在不改变其他实验条件的情况下, 将一个调制周期内的占空比由原来的50%分别调整至70%和30%, 观察在不同占空比下锁模状态和孤子湮灭状态的连续切换过程. 如图5(a)所示, 当占空比为70%时, 高电平调制下稳定锁模的时间得到延长而低电平调制下的孤子湮灭次数由原本的4次缩减至2次. 为了进一步研究改变调制泵浦占空比对于该状态切换过程带来的影响, 绘制了相应的DFT光谱演化图, 如图5(b)所示. 在高电平下, 腔内维持稳定的锁模脉冲, 随着切换至低电平, 孤子的湮灭过程包括与上述实验过程中相同的3个阶段, 即长波长收缩、衰减呼吸和调Q不稳定性. 图中的白色曲线描述了整个切换过程中腔内的脉冲能量变化. 进一步, 通过降低占空比至30%, 可以使得在一个调制周期内缩短稳定锁模时间的同时增加孤子湮灭的次数. 图5(c), (d)分别显示了占空比为30%时的脉冲序列及相应的DFT光谱图, 随着低电平调制时间的加长, 腔内损耗与增益间动态平衡被打破的次数增多. 上述过程说明通过改变一个调制周期内的占空比, 能够在固定的时间内实现对孤子湮灭次数的可控操作.

      在维持高低电平占空比均为50%的基础上, 分别研究5 kHz和10 kHz调制频率下两种状态的切换过程. 与2 kHz调制频率相比, 调制频率的升高缩短了两种状态间的持续时间, 此时高调制频率加快了腔内增益谱的重塑. 图5(e), (f)分别显示了在5 kHz调制频率下的切换过程对应的脉冲序列及光谱演化图, 可以看出, 在低电平调制下, 孤子湮灭仅发生一次, 在湮灭后~5.8 μs孤子重建, 这与2 kHz调制频率下孤子湮灭后重建的时间基本保持一致, 这说明调制频率的升高对于该过程的影响很小. 进一步提升调制频率至10 kHz, 如图5(g), (h)所示, 此时高低电平均处于锁模状态, 仅因为能量方面的差异而产生波长偏移. 此时孤子湮灭不再出现的原因是: 在10 kHz调制频率下, 占空比为50%的低电平调制时间仅为50 μs, 与孤子连续湮灭的周期相近, 这会导致在脉冲能量随着低电平到来而持续降低的过程中腔内的增益尚未减少至低于损耗时调制信号就已然切换至高电平, 泵浦功率的瞬间升高打破了低电平下腔内脉冲能量持续降低的状态, 从而阻碍了孤子湮灭现象的发生. 此外, 泵浦调制频率的过度升高也是导致该现象的原因之一, 高低电平的快速切换会加剧腔内的增益流的不稳定性, 从而使得Er3+集居反转数的变化引起的增益谱重塑过程更加复杂.

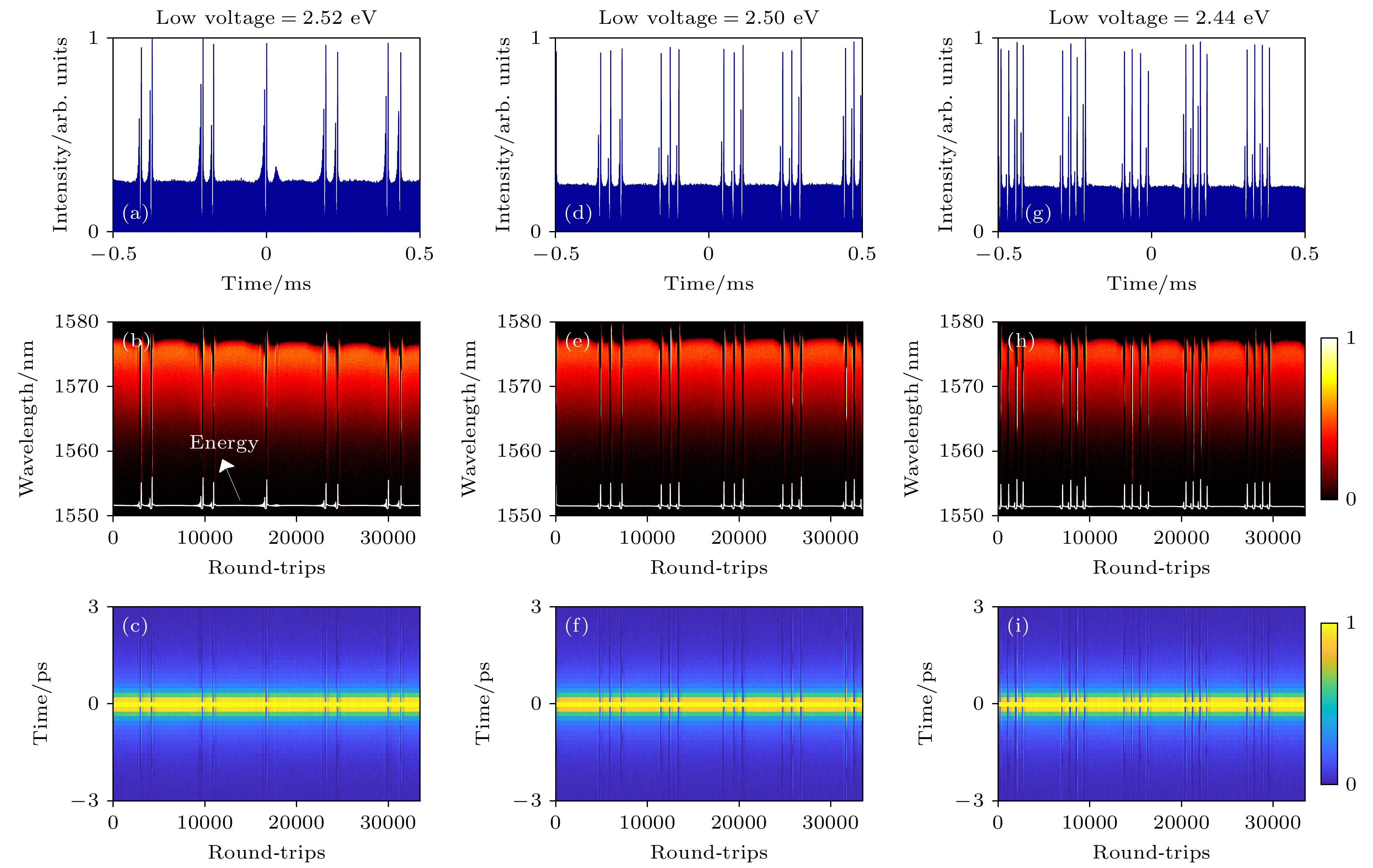
      为了进一步探究不同调制电平对于锁模和孤子湮灭状态切换过程的影响, 在保持调制频率为5 kHz, 占空比为50%的基础上改变低电平的数值, 观察相应的动力学过程. 图6(a)是高电平为2.6 V, 低电平为2.52 V时状态切换相应的脉冲序列, 可以看出, 此时高电平调制下腔内输出稳定的锁模脉冲, 低电平下孤子发生连续的湮灭, 湮灭次数为2次. 不同的是, 在高低电平切换的第3个周期中, 注意到孤子在低电平湮灭一次后并没有继续, 而是表现出明显的呼吸迹象, 这可能是高调制频率下泵浦激光器功率输出的不稳定性以及腔内非线性动力学瞬态变化所引起的. 图6(b), (c)分别给出了上述切换过程相应的DFT光谱演化图、能量演化图及自相关迹. 在维持其他条件不变的情况下, 将低电平的调制电平降低至2.50 V, 此时高电平调制下依旧为锁模状态, 而低电平调制下孤子湮灭的周期由原本的35.37 μs缩小至32.69 μs, 这导致低电平调制的100 μs内湮灭次数由原本的2次增至3次, 图6(e), (f)为相应的动力学演化. 进一步降低低电平的值至2.44 V, 此时孤子湮灭的周期进一步收缩, 为20.55 μs, 一个调制周期内孤子湮灭次数也增至4次, 相应的动力学过程见图6(h), (i). 可注意到, 随着低电平的持续降低, 孤子的湮灭周期持续缩小, 孤子湮灭次数不断增加. 这是因为降低低电平加剧了腔内脉冲能量的衰减, 缩短了增益小于损耗所需的时间, 进而表现出增益与损耗间维持动态平衡周期的不断改变.

    4.   结　论

    • 本文提出并研究了一种实现脉冲产生与湮灭可控的超快光纤激光器, 并利用DFT技术研究了在泵浦调制作用下两种状态建立和切换时的动力学过程. 在高电平下, 腔内输出稳定的锁模脉冲, 随着调制电平切换至低电平, 激光器进入连续的孤子湮灭状态. 通过改变调制泵浦的占空比, 能够对孤子湮灭次数进行有效的控制, 而提升泵浦调制频率可以缩短两种状态分别持续的时间, 但超出一定的频率上限会阻碍低电平调制下孤子湮灭现象的发生. 此外, 通过改变低电平的值, 能够进一步降低激光腔内的增益从而缩短孤子湮灭的周期. 研究结果对于深入理解耗散孤子的产生和湮灭动力学具有重要意义, 并为超快光纤激光器的设计和应用提供了新的视角.

    参考文献 (27)

目录

/

返回文章
返回